Synthesis, Analysis, and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing
Abstract
1. Introduction
2. Materials and Methods
2.1. Scissor-Structural Mechanisms
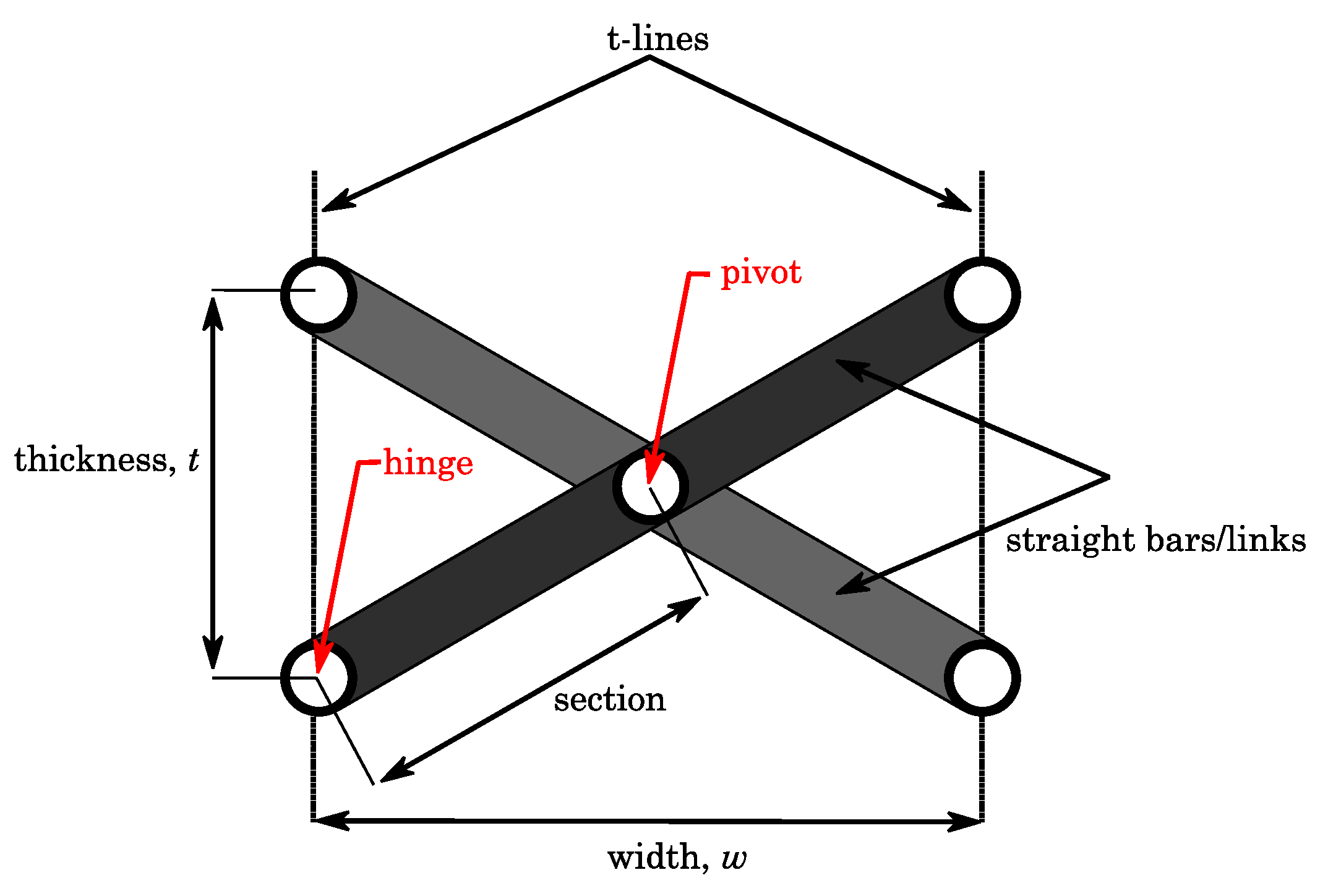
2.1.1. Terms and Definitions
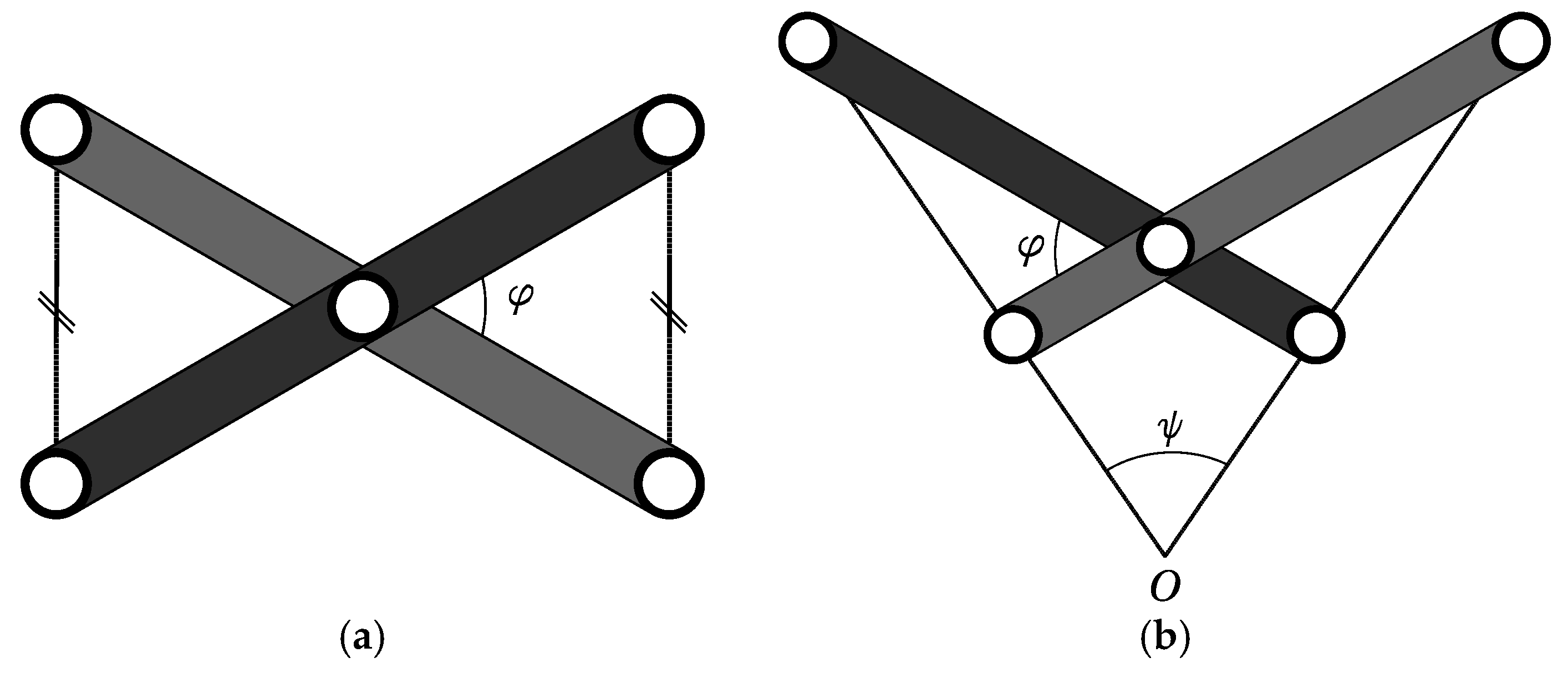
2.1.2. Typology of Scissor-Like Elements
2.2. Kinematic Analysis of Scissor-Structural Mechanisms
2.2.1. Mobility of Scissor-Structural Mechanisms
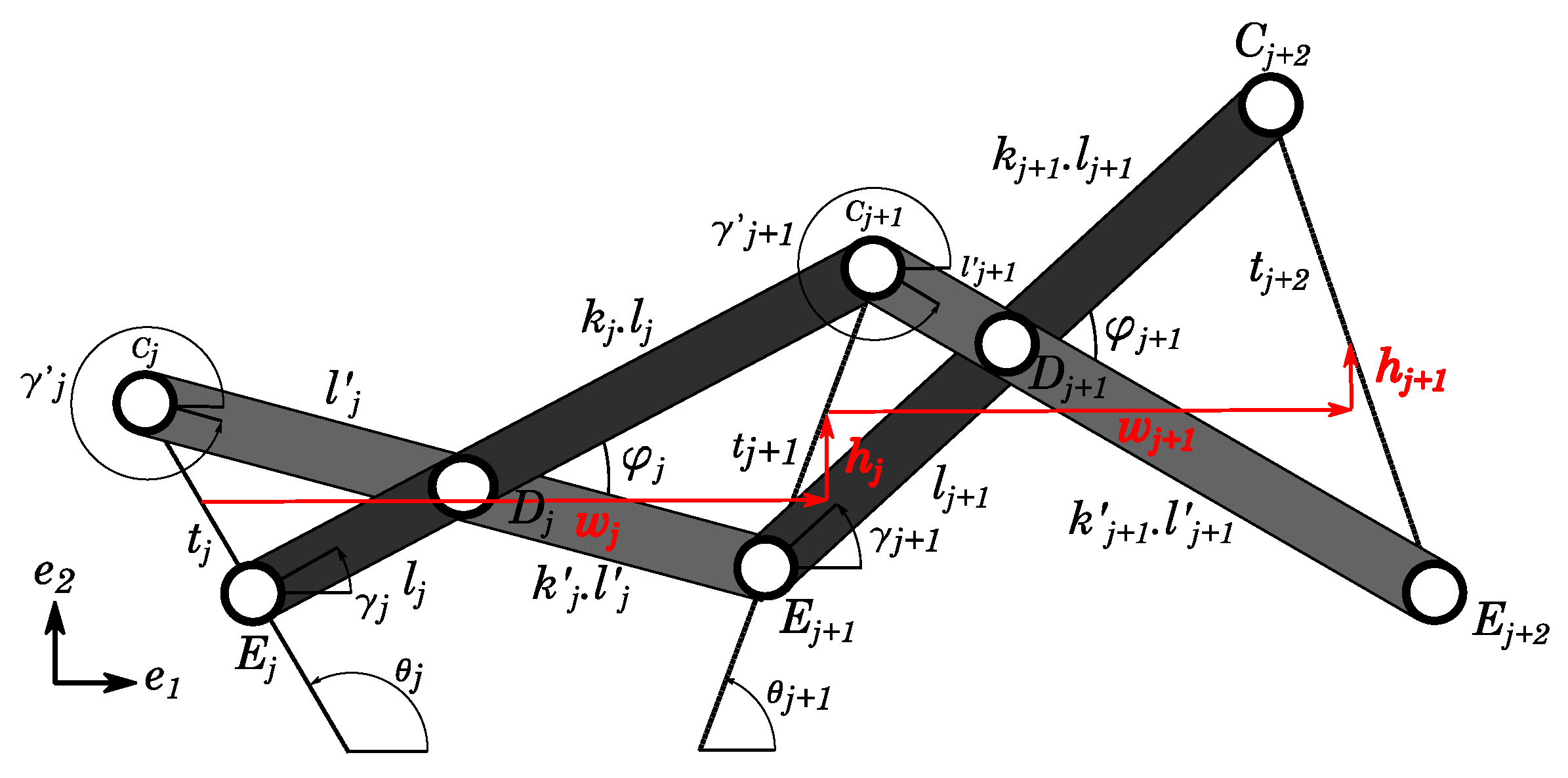
2.2.2. Position Analysis of Scissor-Structural Mechanisms
2.2.3. Velocity and Acceleration Analysis of Scissor-Structural Mechanisms
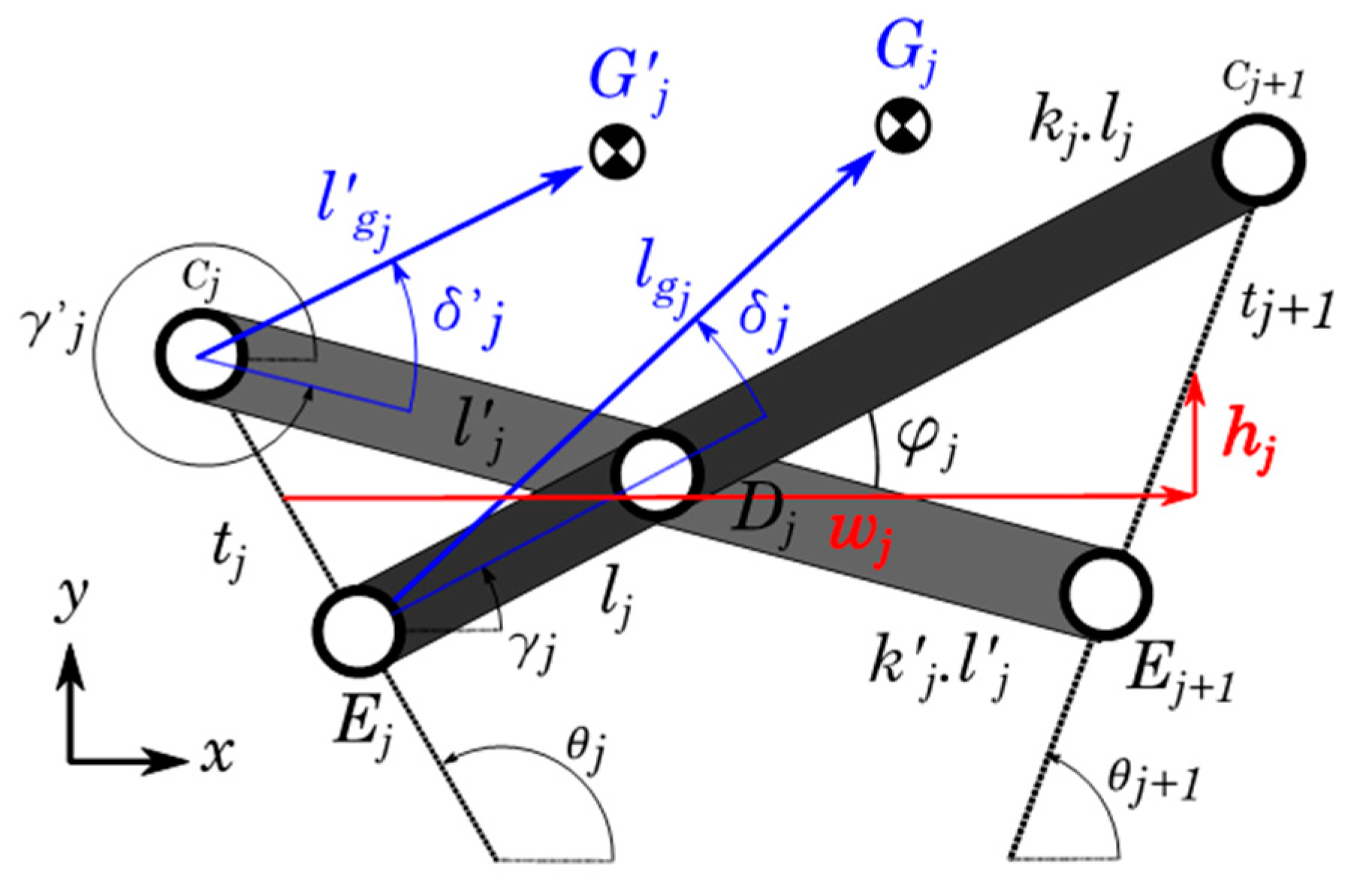
2.3. Aerodynamic Analysis of the Surfaces Formed by Scissor-Structural Mechanisms
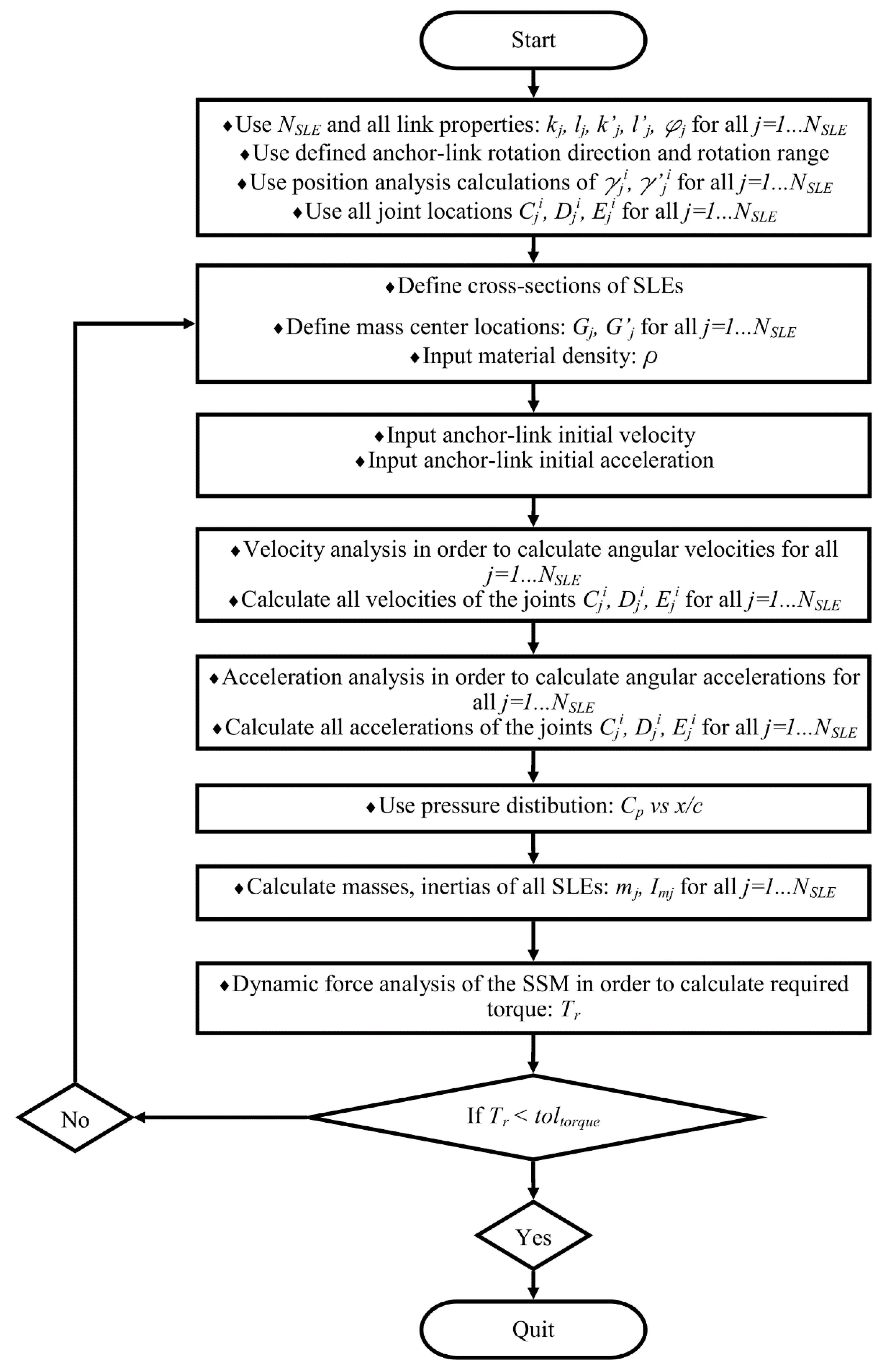
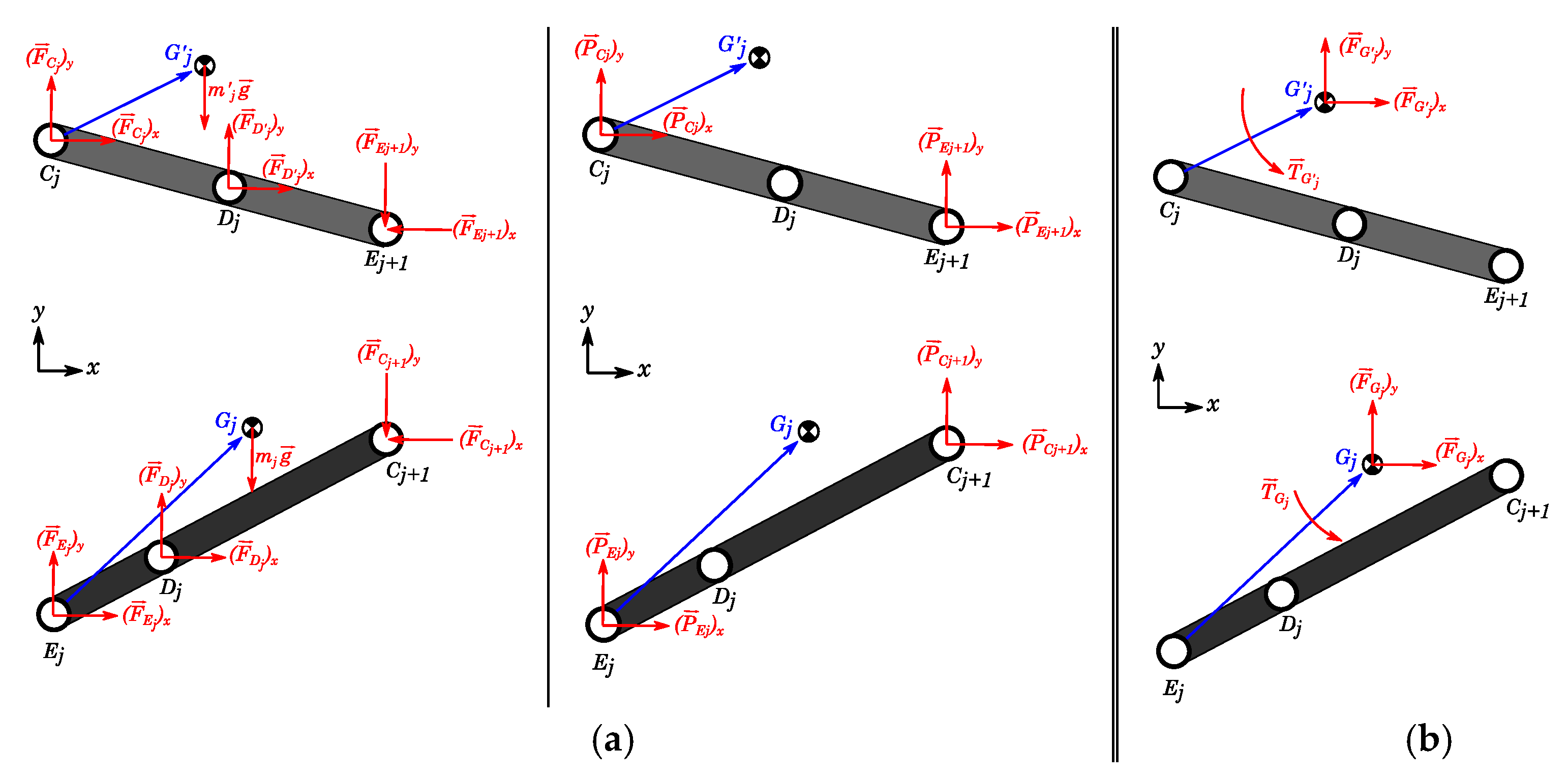
2.4. Dynamic Force Analysis of Scissor-Structural Mechanisms
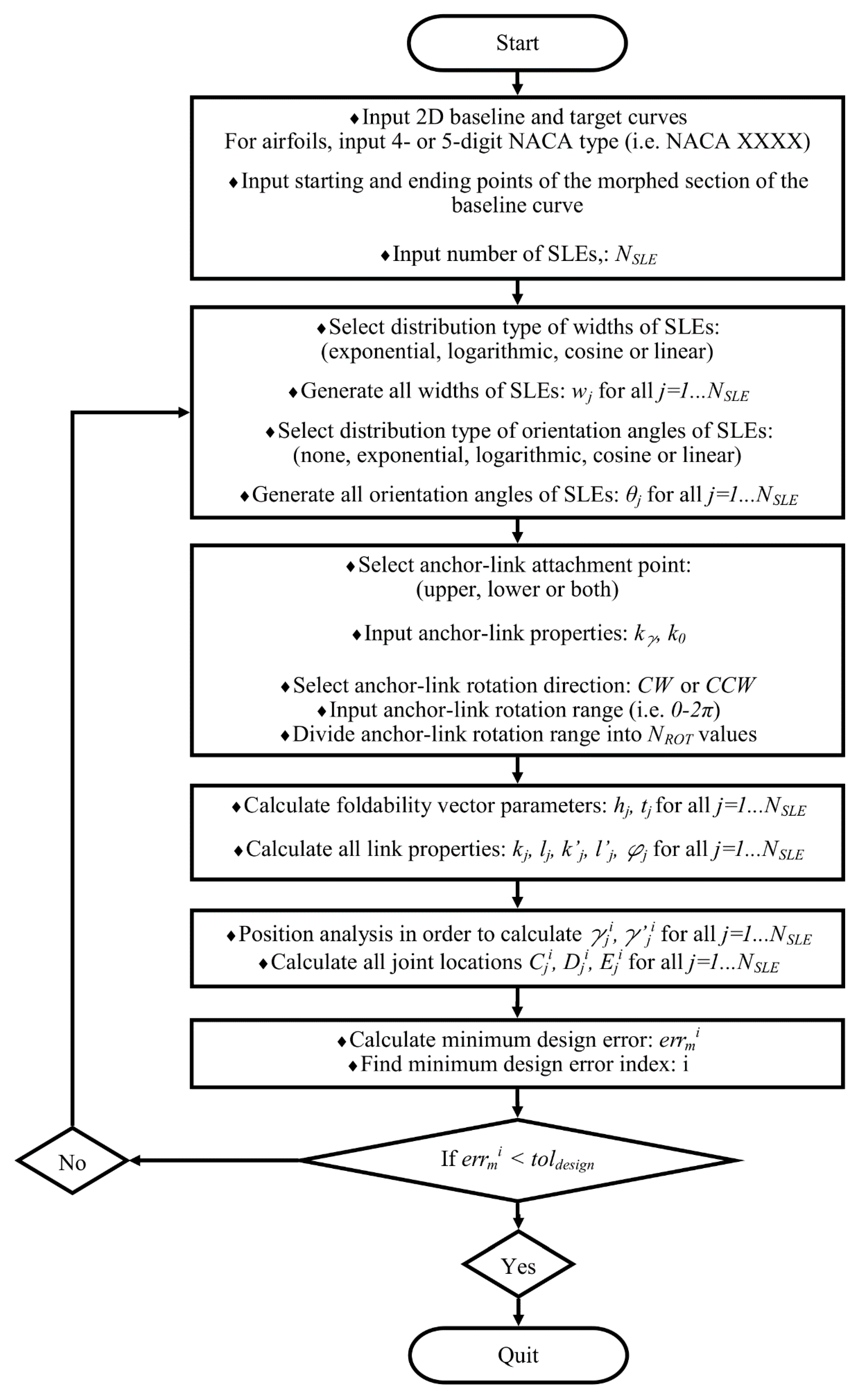
2.5. Synthesis and Design of Scissor-Structural Mechanisms
3. Results
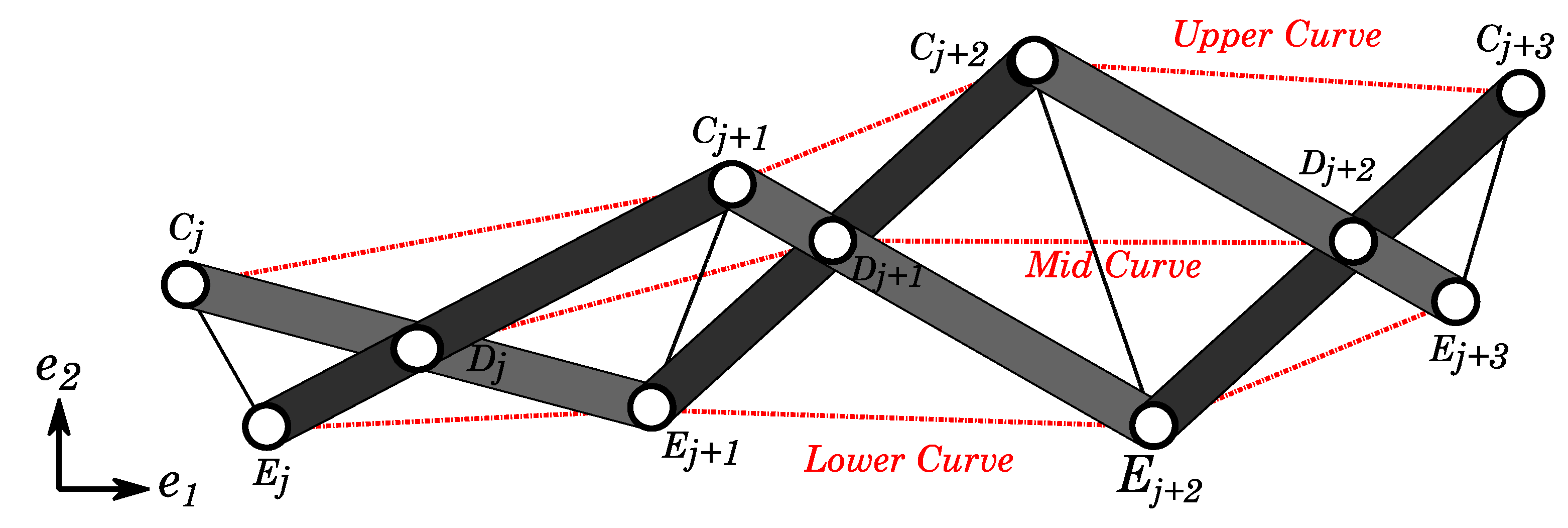
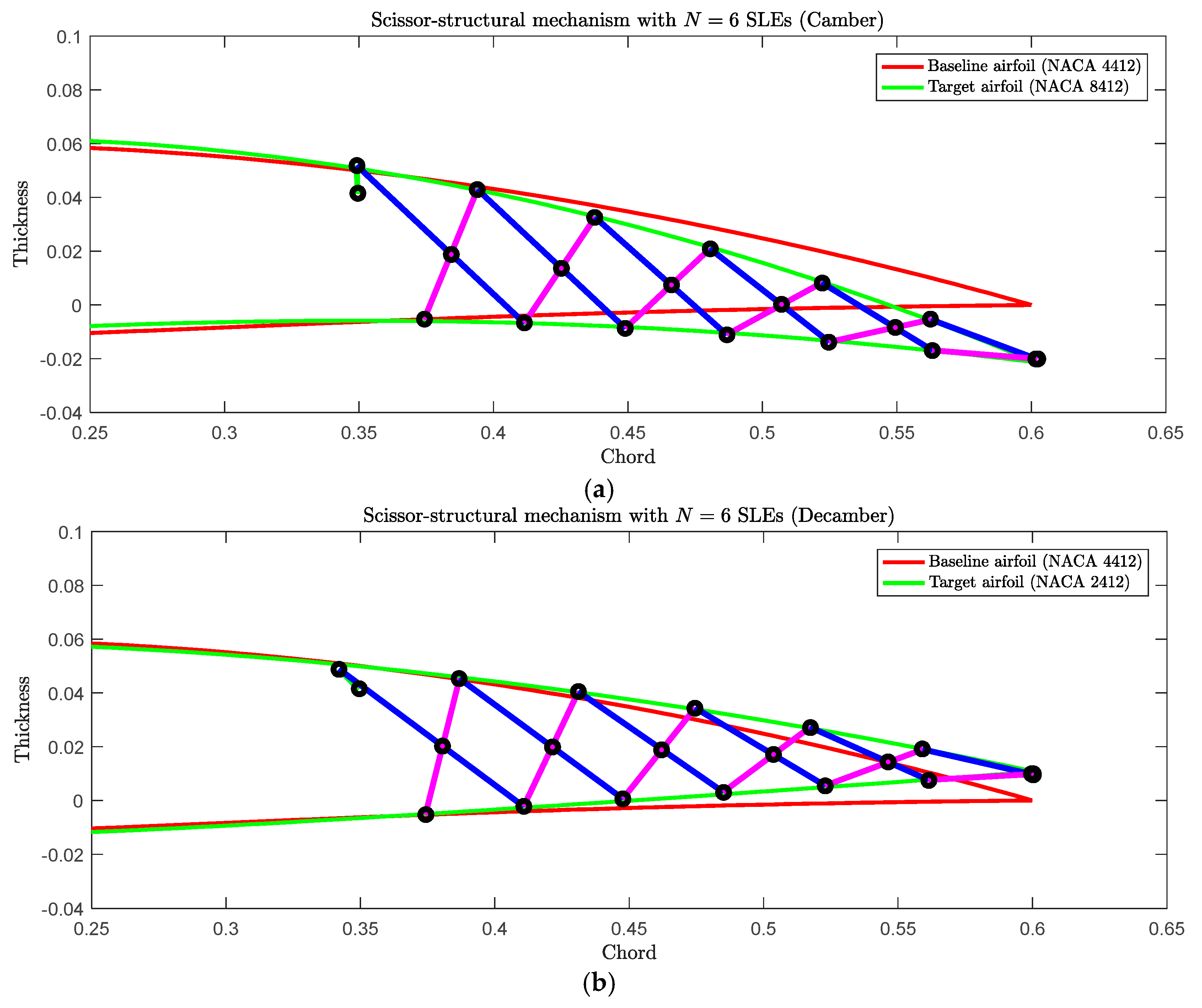
3.1. Scissor-Structural Mechanism for the Trailing Edge of a Morphing Wing
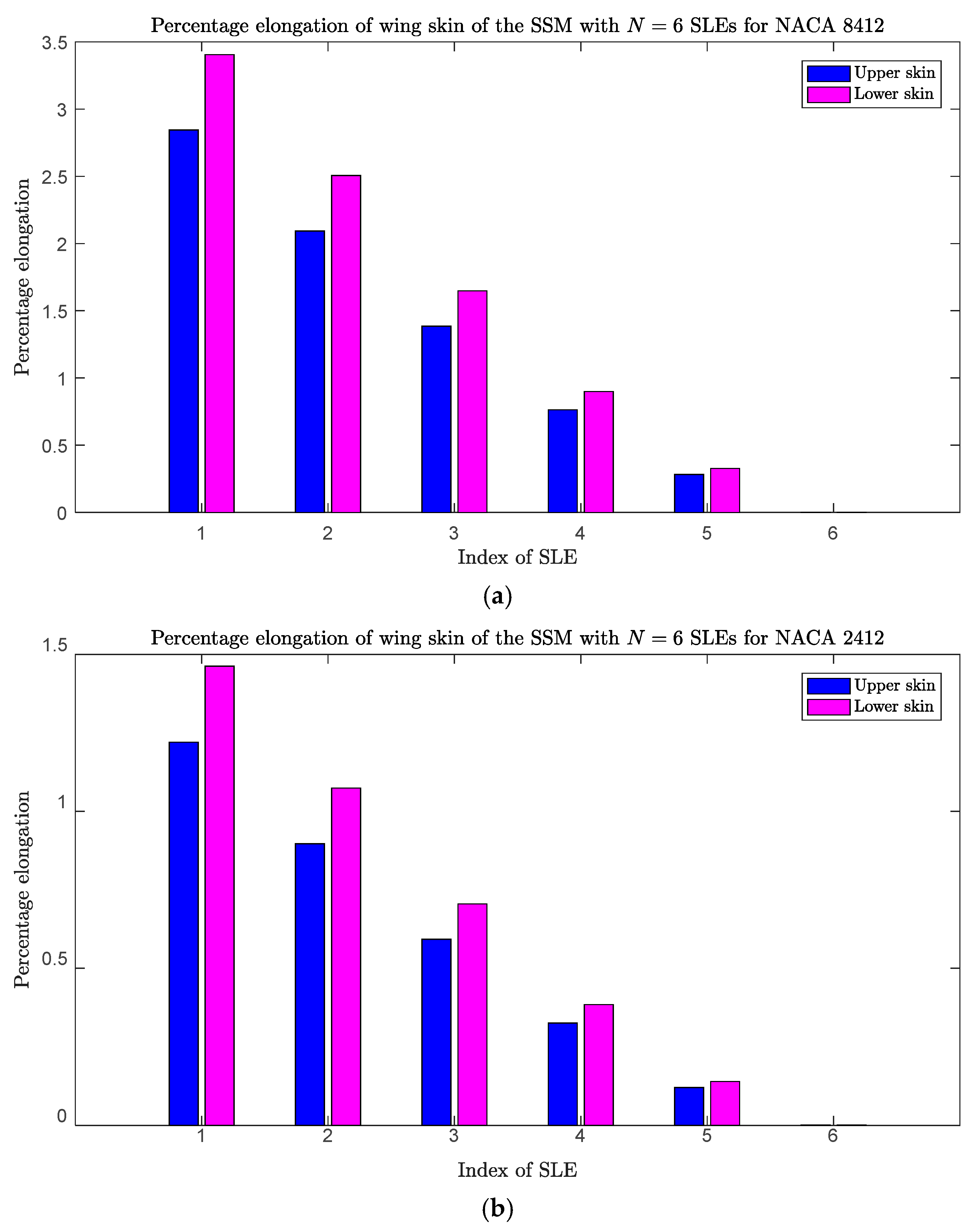
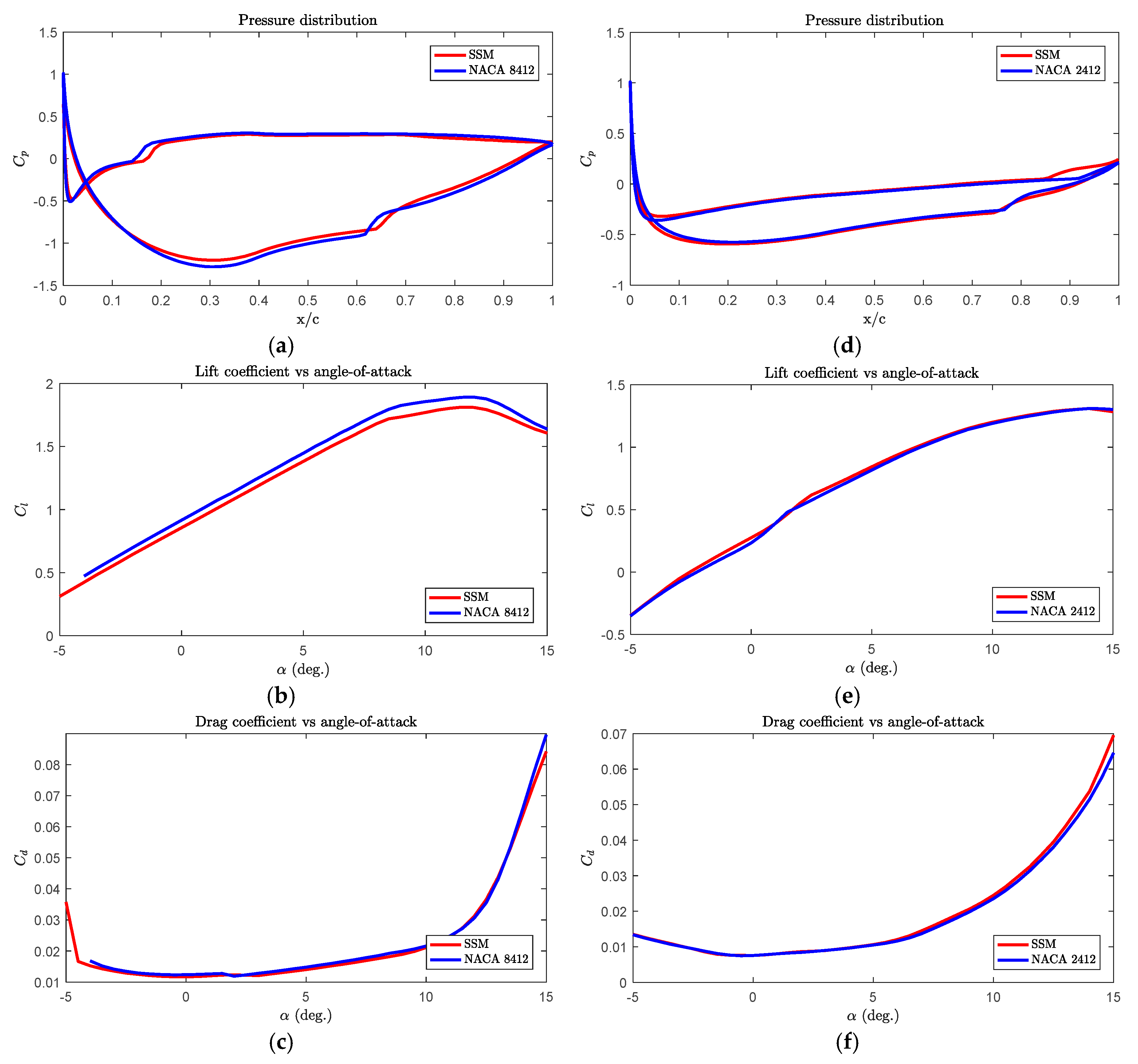
3.2. Aerodynamic Analysis of the Surfaces Formed by Scissor-Structural Mechanisms for the Trailing Edge of a Morphing Wing
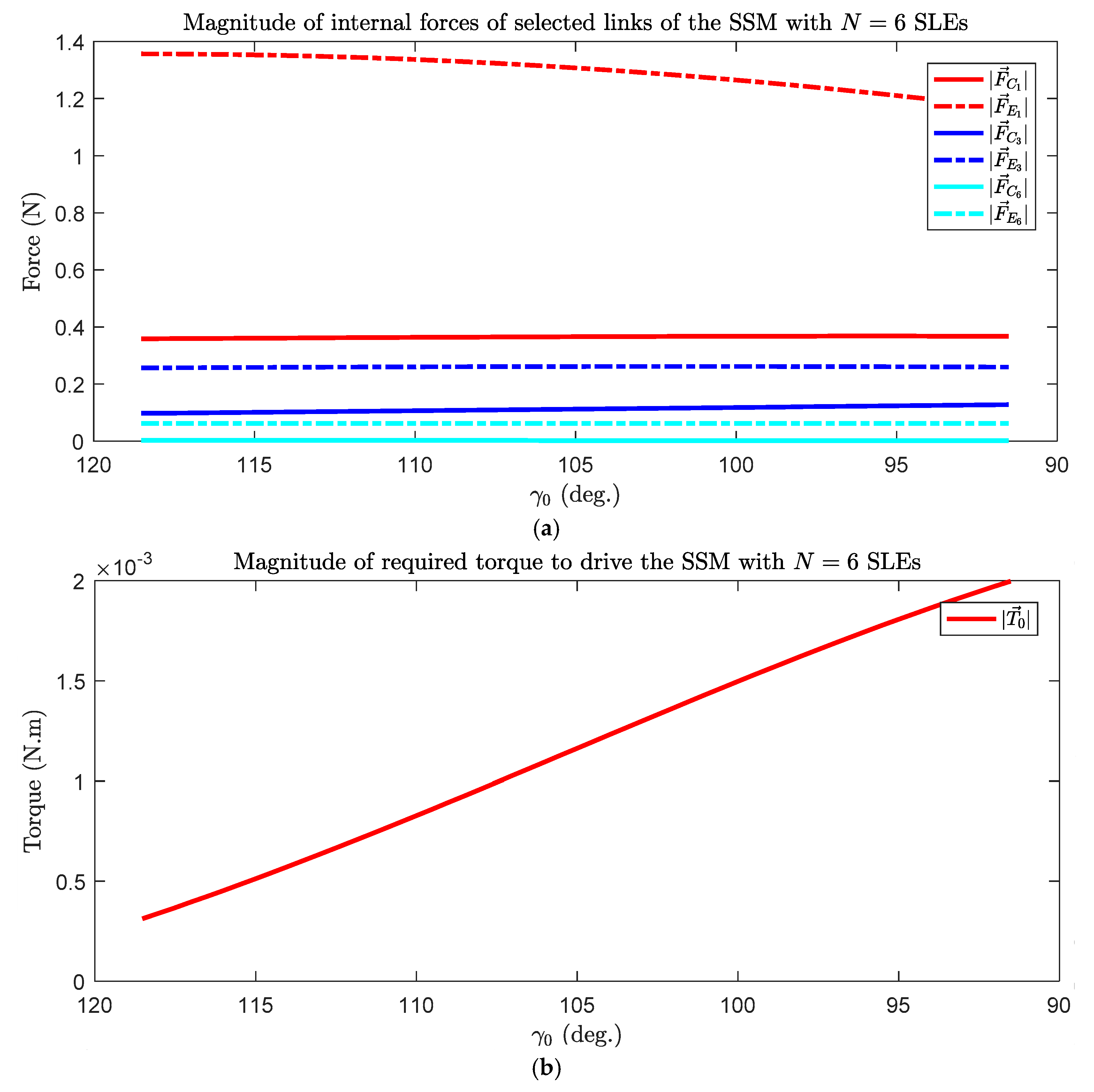
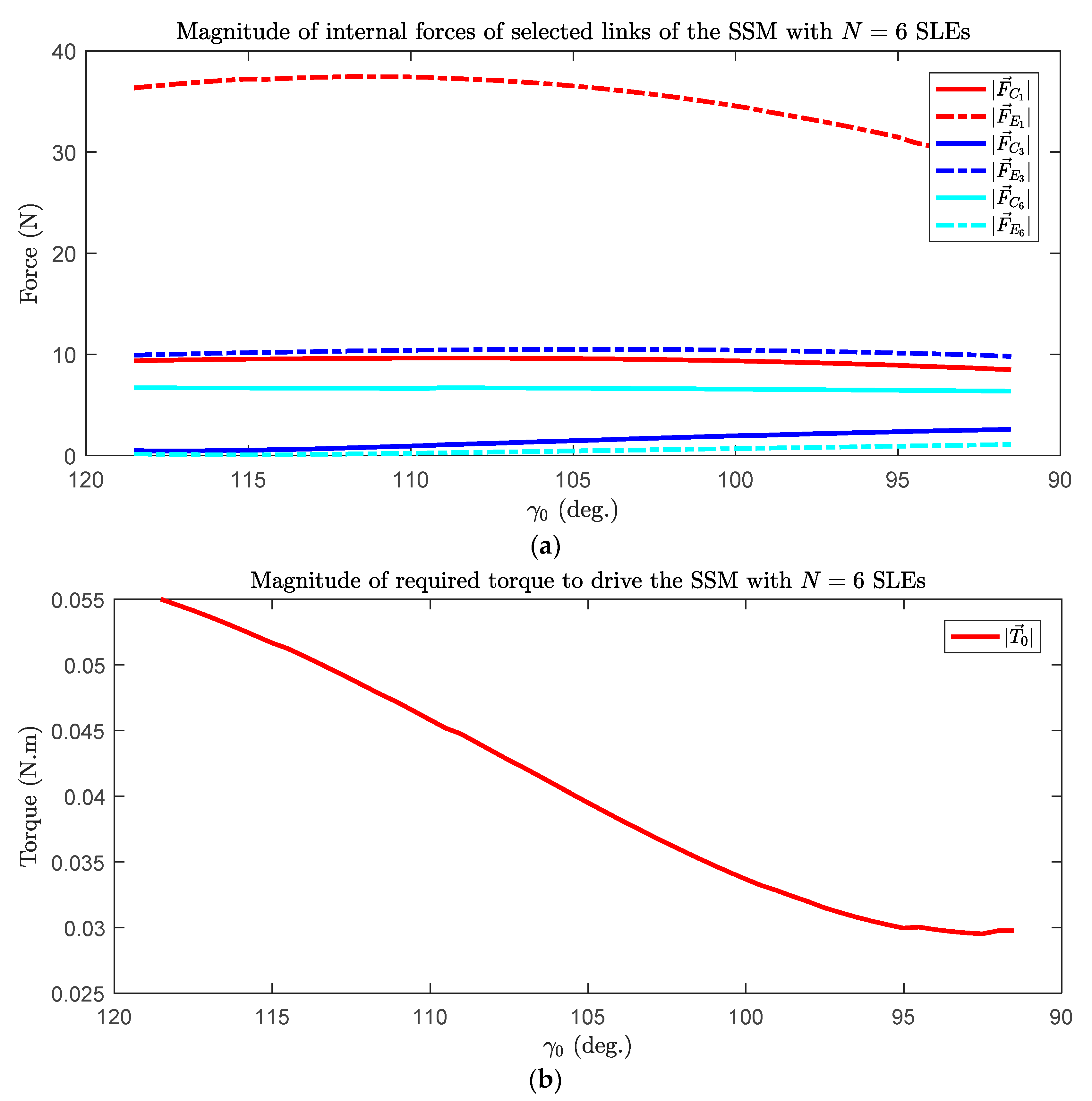
3.3. Dynamic Force Analysis of the Scissor-Structural Mechanisms for the Trailing Edge of a Morphing Wing
3.3.1. In Vacuo Condition
3.3.2. Under Aerodynamic Loading
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ghommem, M.; Hajj, M.R.; Beran, P.S.; Puri, I.K. Role of Wing Morphing in Thrust Generation. Theor. Appl. Mech. 2014, 4, 1–7. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Ninian, D.; Dakka, M.S. Design, Development and Testing of Shape Shifting Wing Model. Aerospace 2017, 4, 52. [Google Scholar] [CrossRef]
- Fincham, J.H.S.; Friswell, M.I. Aerodynamic Optimisation of a Camber Morphing Aerofoil. Aerosp. Sci. Technol. 2015, 43, 245–255. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Flexible Skins for Morphing Aircraft Using Cellular Honeycomb Cores. J. Intell. Mater. Syst. Struct. 2010, 21, 1719–1735. [Google Scholar] [CrossRef]
- Kudva, J.N. Overview of the DARPA Smart Wing Project. J. Intell. Mater. Syst. Struct. 2004, 15, 261–267. [Google Scholar] [CrossRef]
- Thornton, S.V. Reduction of Structural Loads Using Maneuver Load Control on the Advanced Fighter Technology Integration (AFTI)/F-111 Mission Adaptive Wing; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1993. [Google Scholar]
- Smith, K.; Butt, J.; von Spakovsky, M.; Moorhouse, D. A Study of the Benefits of Using Morphing Wing Technology in Fighter Aircraft Systems. In Proceedings of the 39th AIAA Thermophysics Conference, Fluid Dynamics and Co-Located Conferences, Miami, FL, USA, 25–28 June 2007; American Institute of Aeronautics and Astronautics (AIAA): Miami, FL, USA, 2007. [Google Scholar]
- Sofla, A.Y.N.; Meguid, S.A.; Tan, K.T.; Yeo, W.K. Shape Morphing of Aircraft Wing: Status and Challenges. Mater. Des. 2010, 31, 1284–1292. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data, 2nd ed.; Dover Publications Inc.: New York, NY, USA, 1959; Volume 11, ISBN 0486605868. [Google Scholar]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 4th ed.; American Institute of Aeronautics and Astronautics, Inc.: Washington, DC, USA, 2006; ISBN 1563478293. [Google Scholar]
- Murugan, S.; Woods, B.K.S.; Friswell, M.I. Hierarchical Modeling and Optimization of Camber Morphing Airfoil. Aerosp. Sci. Technol. 2015, 42, 31–38. [Google Scholar] [CrossRef]
- Vasista, S.; Tong, L.; Wong, K.C. Realization of Morphing Wings: A Multidisciplinary Challenge. J. Aircr. 2012, 49, 11–28. [Google Scholar] [CrossRef]
- Parker, H.F. Variable-Camber Rib for Aeroplane-Wings. US Patent No. 1341758, 1 June 1920. [Google Scholar]
- Bonney, L.W. Aeroplane Wing or Aerofoil Structure. US Patent No. 1710673, 23 April 1929. [Google Scholar]
- Antoni, U. Construction of Flexible Aeroplane Wings Having a Variable Profile. US Patent No. 1886362, 8 November 1932. [Google Scholar]
- Grant, C.H. Airfoil. US Patent No. 2022806, 3 December 1935. [Google Scholar]
- Cole, J.B. Variable Camber Airfoil. US Patent No. 4053124, 11 October 1977. [Google Scholar]
- Zapel, E.J. Variable Camber Trailing Edge for Airfoil. US Patent No. 4131253, 26 December 1978. [Google Scholar]
- Monner, H.P.; Breitbach, E.; Bein, T.; Hanselka, H. Design Aspects of the Adaptive Wing—The Elastic Trailing Edge and the Local Spoiler Bump. Aeronaut. J. 2000, 104, 89–95. [Google Scholar] [CrossRef]
- Bartley-Cho, J.D.; Wang, D.P.; Martin, C.A.; Kudva, J.N.; West, M.N. Development of High-rate, Adaptive Trailing Edge Control Surface for the Smart Wing Phase 2 Wind Tunnel Model. J. Intell. Mater. Syst. Struct. 2004, 15, 279–291. [Google Scholar] [CrossRef]
- Campanile, L.F.; Anders, S. Aerodynamic and Aeroelastic Amplification in Adaptive Belt-Rib Airfoils. Aerosp. Sci. Technol. 2005, 9, 55–63. [Google Scholar] [CrossRef]
- Marques, M.; Gamboa, P.; Andrade, E. Design of a Variable Camber Flap for Minimum Drag and Improved Energy Efficiency. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Structures, Structural Dynamics, and Materials and Co-Located Conferences, Palm Springs, CA, USA, 4–7 May 2009; American Institute of Aeronautics and Astronautics (AIAA): Palm Springs, CA, USA, 2009. [Google Scholar]
- Barrett, R.V.; Roelof, V. Mechanics of Pressure-Adaptive Honeycomb and Its Application to Wing Morphing. Smart Mater. Struct. 2011, 20, 94010. [Google Scholar]
- Takahashi, H.; Yokozeki, T.; Hirano, Y. Development of Variable Camber Wing with Morphing Leading and Trailing Sections Using Corrugated Structures. J. Intell. Mater. Syst. Struct. 2016, 27, 2827–2836. [Google Scholar] [CrossRef]
- Pecora, R.; Magnifico, M.; Amoroso, F.; Monaco, E. Multi-Parametric Flutter Analysis of a Morphing Wing Trailing Edge. Aeronaut. J. 2014, 118, 1063–1078. [Google Scholar] [CrossRef]
- Wu, R.; Soutis, C.; Zhong, S.; Filippone, A. A Morphing Aerofoil with Highly Controllable Aerodynamic Performance. Aeronaut. J. 2017, 121, 54–72. [Google Scholar] [CrossRef]
- Akgün, Y.; Gantes, C.J.; Sobek, W.; Korkmaz, K.; Kalochairetis, K. A Novel Adaptive Spatial Scissor-Hinge Structural Mechanism for Convertible Roofs. Eng. Struct. 2011, 33, 1365–1376. [Google Scholar] [CrossRef]
- Chen, Y. Design of Structural Mechanisms. Ph.D. Thesis, University of Oxford, Oxford, UK, 2003. [Google Scholar]
- Şahin, H.L.; Yaman, Y. Design and Analysis of a Mechanism for the Chord and Camber Morphing of an Aircraft Wing. In Proceedings of the 7th EASN International Conference on Innovation in European Aeronautics Research, Warsaw, Poland, 26–28 September 2017; The European Aeronautics Science Network (EASN): Warsaw, Poland, 2017. [Google Scholar]
- Zhao, J.S.; Chu, F.; Feng, Z.J. The Mechanism Theory and Application of Deployable Structures Based on SLE. Mech. Mach. Theory 2009, 44, 324–335. [Google Scholar] [CrossRef]
- Chen, W.-J.; Luo, Y.-Z.; Fu, G.-Y.; Gong, J.-H.; Dong, S.-L. A Study on Space Masts Based on Octahedral T russ Family. Int. J. Space Struct. 2001, 16, 75–82. [Google Scholar] [CrossRef]
- Rosenfeld, Y.; Logcher, R.D. New Concepts for Deployable-Collapsable Structures. Int. J. Space Struct. 1988, 3, 20–32. [Google Scholar] [CrossRef]
- Escrig, F.; Perez Valcarcel, J.; Sanchez, J. Deployable Cover on a Swimming Pool in Seville. J. Int. Assoc. Shell Spat. Struct. 1996, 37, 39–70. [Google Scholar]
- Thrall, A.P.; Adriaenssens, S.; Paya-Zaforteza, I.; Zoli, T.P. Linkage-based movable bridges: Design methodology and three novel forms. Eng. Struct. 2012, 37, 214–223. [Google Scholar] [CrossRef]
- You, Z.; Pellegrino, S. Foldable Bar Structures. Int. J. Solids Struct. 1997, 34, 1825–1847. [Google Scholar] [CrossRef]
- Hanaor, A.; Levy, R. Evaluation of Deployable Structures for Space Enclosures. Int. J. Space Struct. 2001. [Google Scholar] [CrossRef]
- Akgün, Y. A Novel Transformation Model for Deployable Scissor-Hinge Structures. Ph.D. Thesis, İzmir Institute of Technology, İzmir, Turkey, 2010. [Google Scholar]
- Roovers, K.; De Temmerman, N. Deployable Scissor Grids Consisting of Translational Units. Int. J. Solids Struct. 2017, 121, 45–61. [Google Scholar] [CrossRef]
- Langbecker, T. Kinematic Analysis of Deployable Scissor Structures. Int. J. Space Struct. 1999, 14, 1–15. [Google Scholar] [CrossRef]
- Şahin, H.L. Synthesis, Analysis and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing. Master’s Thesis, Middle East Technical University (METU), Ankara, Turkey, 2018. [Google Scholar]
- Uicker, J.J., Jr.; Pennock, G.R.; Shigley, J.E. Theory of Machines and Mechanisms, 3rd ed.; Oxford University Press, Inc.: New York, NY, USA, 2003; ISBN 019515598X. [Google Scholar]
- Zhao, J.; Feng, Z.; Ma, N.; Chu, F. Design of Special Planar Linkages, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-662-51353-8. [Google Scholar]
- Şahin, H.L.; Yaman, Y. Design of a Mechanism that Provides Camber and Chord Change for a Fully Morphing Wing. In Proceedings of the 6th National Conference on Aerospace, Kocaeli, Turkey, 28–30 September 2016; UHUK: Kocaeli, Turkey, 2016. (In Turkish). [Google Scholar]
- Russell, K.; Shen, Q.; Sodhi, R.S. Mechanism Design: Visual and Programmable Approaches, 1st ed.; CRC Press, Inc.: Boca Raton, FL, USA, 2013; ISBN 1466570172. [Google Scholar]
- Şahin, H.L.; Yaman, Y. Design and Analysis of a Novel Mechanism for the Morphing of Trailing Edge of an Aircraft Wing. MATEC Web Conf. 2018, 188, 04001. [Google Scholar] [CrossRef]
- Şahin, H.L.; Çakır, B.O.; Yaman, Y. Aerodynamic Modelling and Analysis of a Novel Mechanism for Chord and Camber Morphing Wing. MATEC Web Conf. 2018, 188, 04002. [Google Scholar] [CrossRef]
- Şahin, H.L.; Çakır, B.O.; Yaman, Y. Dynamic Force Analysis of a Novel Mechanism for Chord and Camber Morphing Wing Under Aerodynamic Loading. MATEC Web Conf. 2018, 233, 00006. [Google Scholar] [CrossRef]
- MATLAB®. Available online: https://www.mathworks.com/products/matlab.html (accessed on 9 November 2018).
- Spirlet, G.B. Design of Morphing Leading and Trailing Edge Surfaces for Camber and Twist Control. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- XFLR5. Available online: http://www.xflr5.com/xflr5.htm (accessed on 9 November 2018).
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Şahin, H.L.; Yaman, Y. Synthesis, Analysis, and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing. Aerospace 2018, 5, 127. https://doi.org/10.3390/aerospace5040127
Şahin HL, Yaman Y. Synthesis, Analysis, and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing. Aerospace. 2018; 5(4):127. https://doi.org/10.3390/aerospace5040127
Chicago/Turabian StyleŞahin, Harun Levent, and Yavuz Yaman. 2018. "Synthesis, Analysis, and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing" Aerospace 5, no. 4: 127. https://doi.org/10.3390/aerospace5040127
APA StyleŞahin, H. L., & Yaman, Y. (2018). Synthesis, Analysis, and Design of a Novel Mechanism for the Trailing Edge of a Morphing Wing. Aerospace, 5(4), 127. https://doi.org/10.3390/aerospace5040127




