A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight
Abstract
1. Introduction
2. Computational Methodology
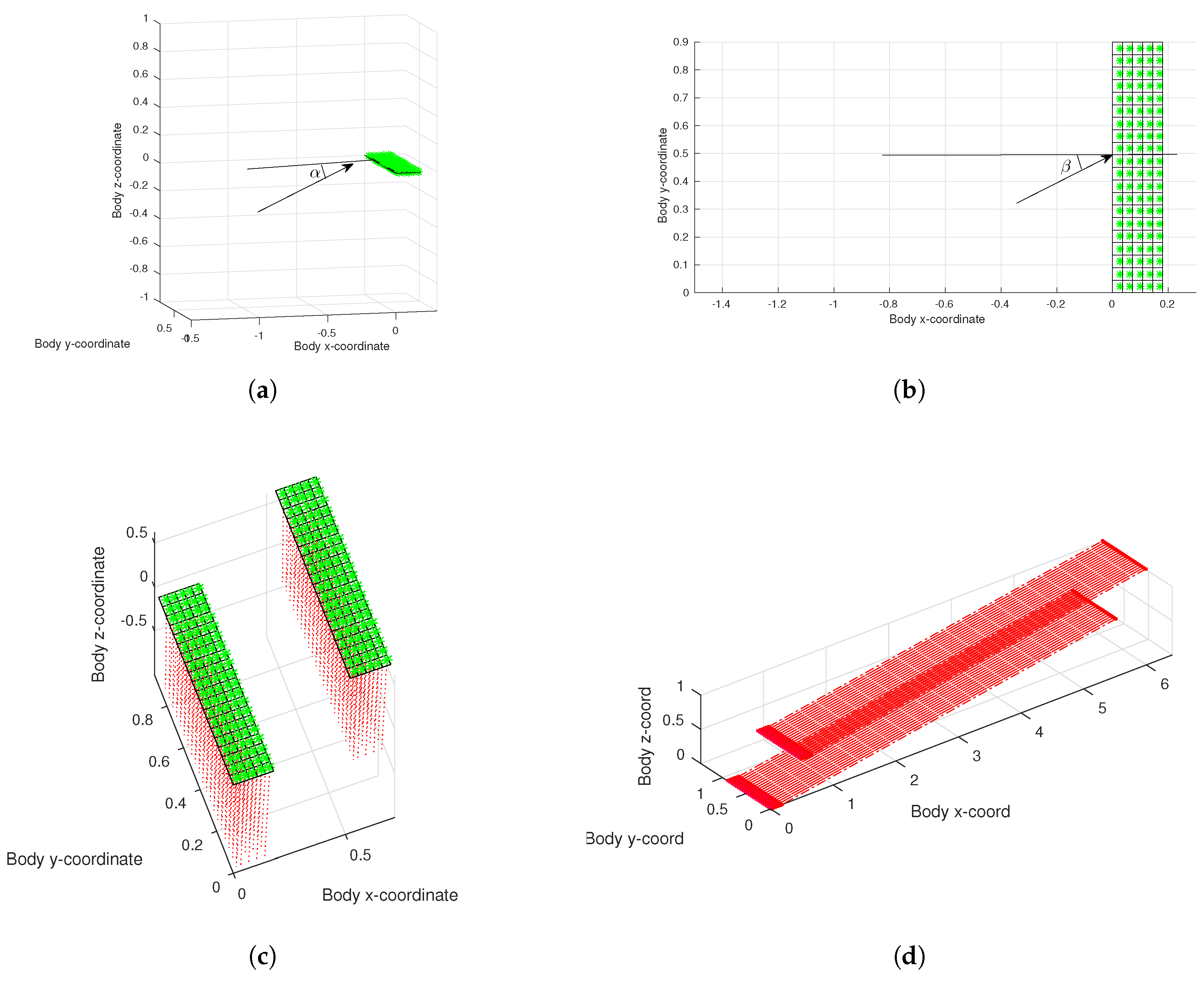
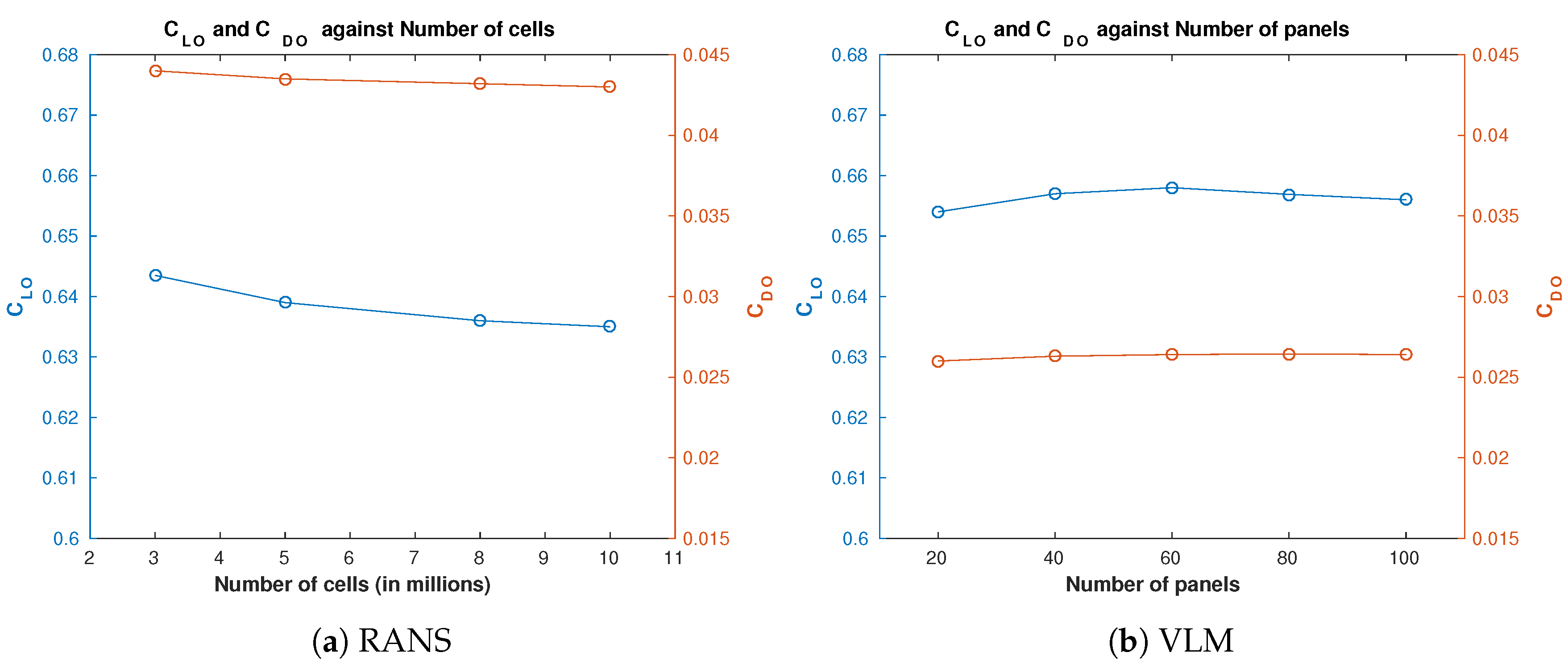
2.1. Low-Fidelity: Vortex Lattice Method
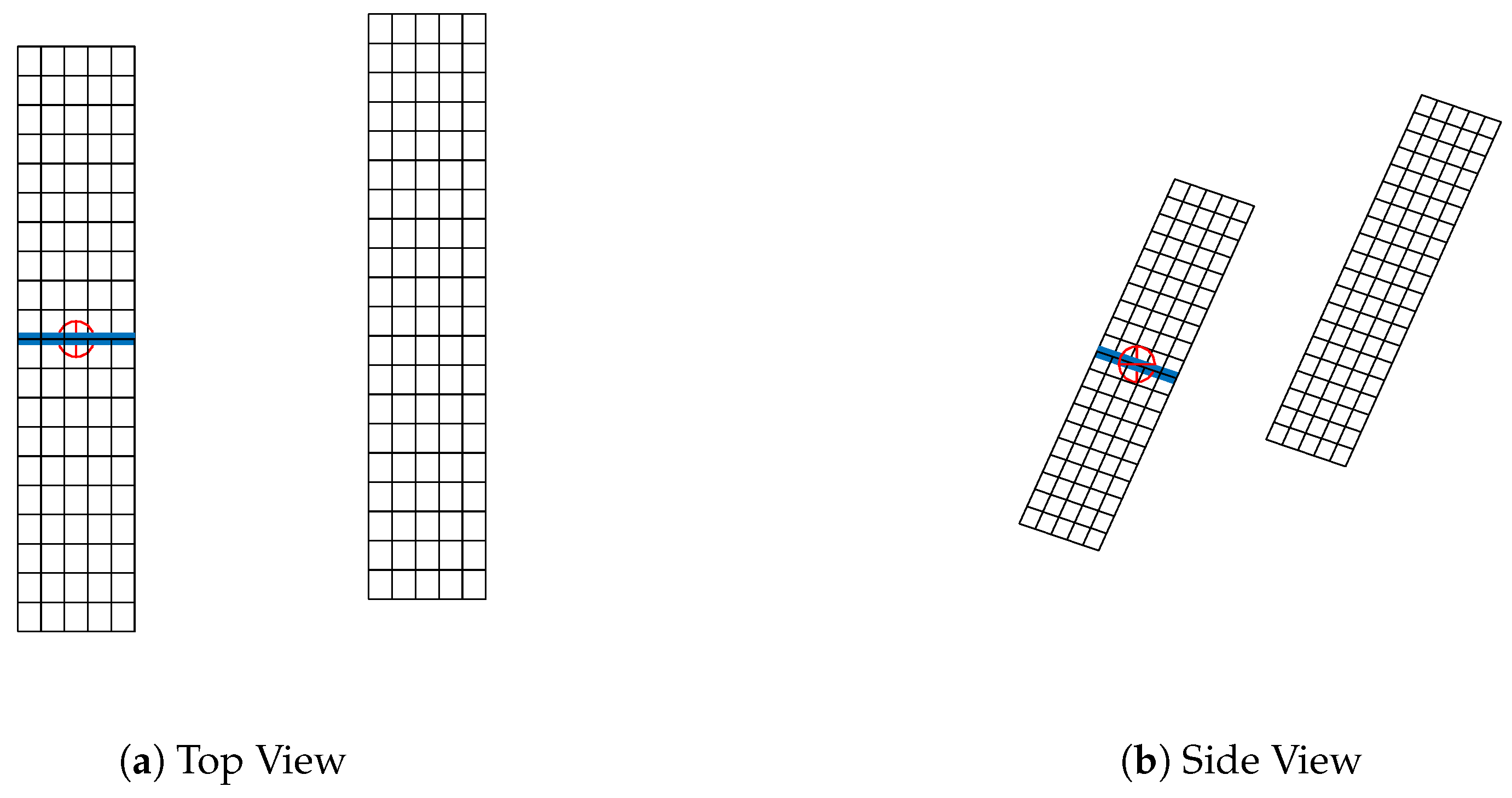
2.2. High-Fidelity: Reynolds Averaged Navier-Stokes
3. Application of the Multi-Fidelity Framework
3.1. Isolated Wing
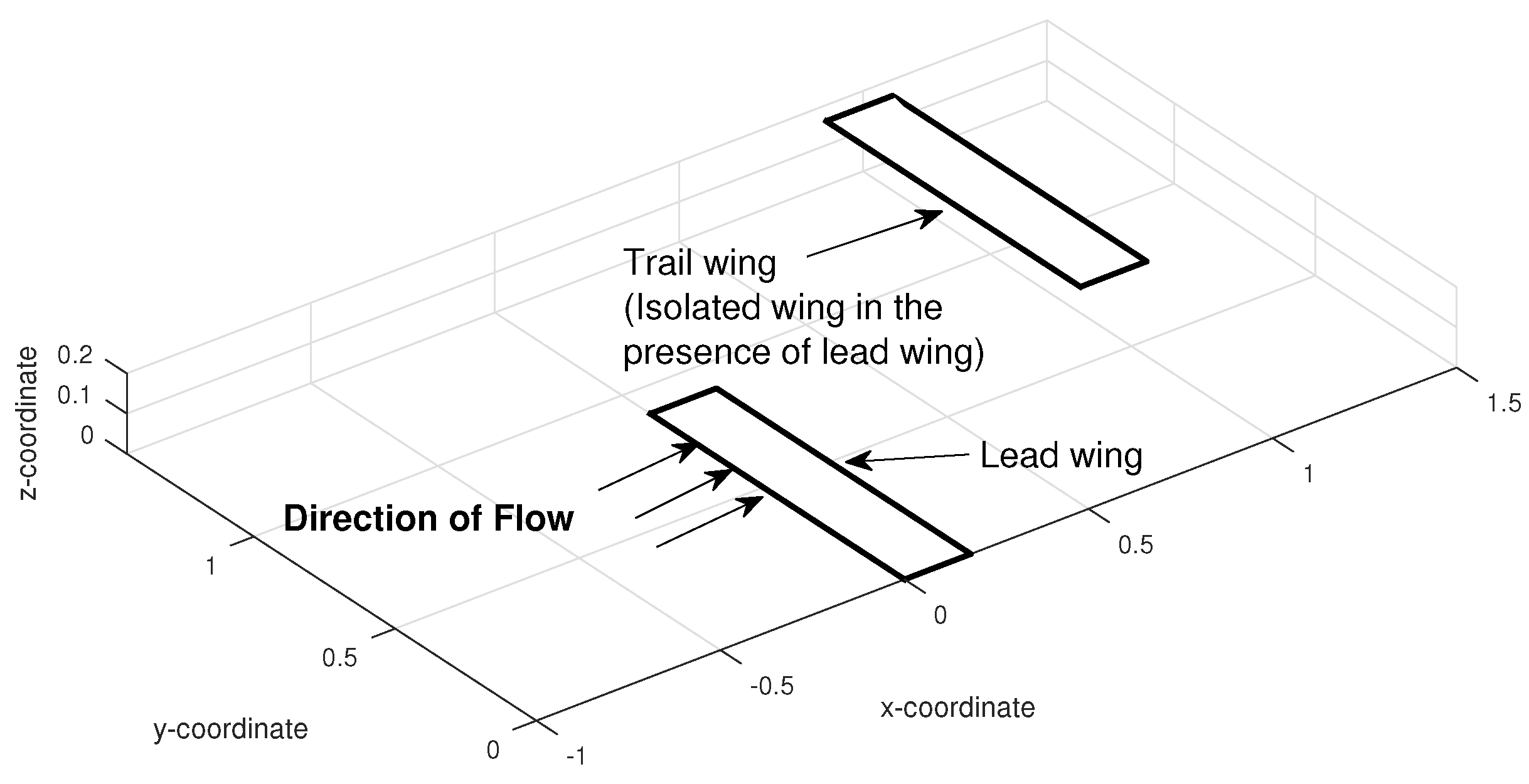
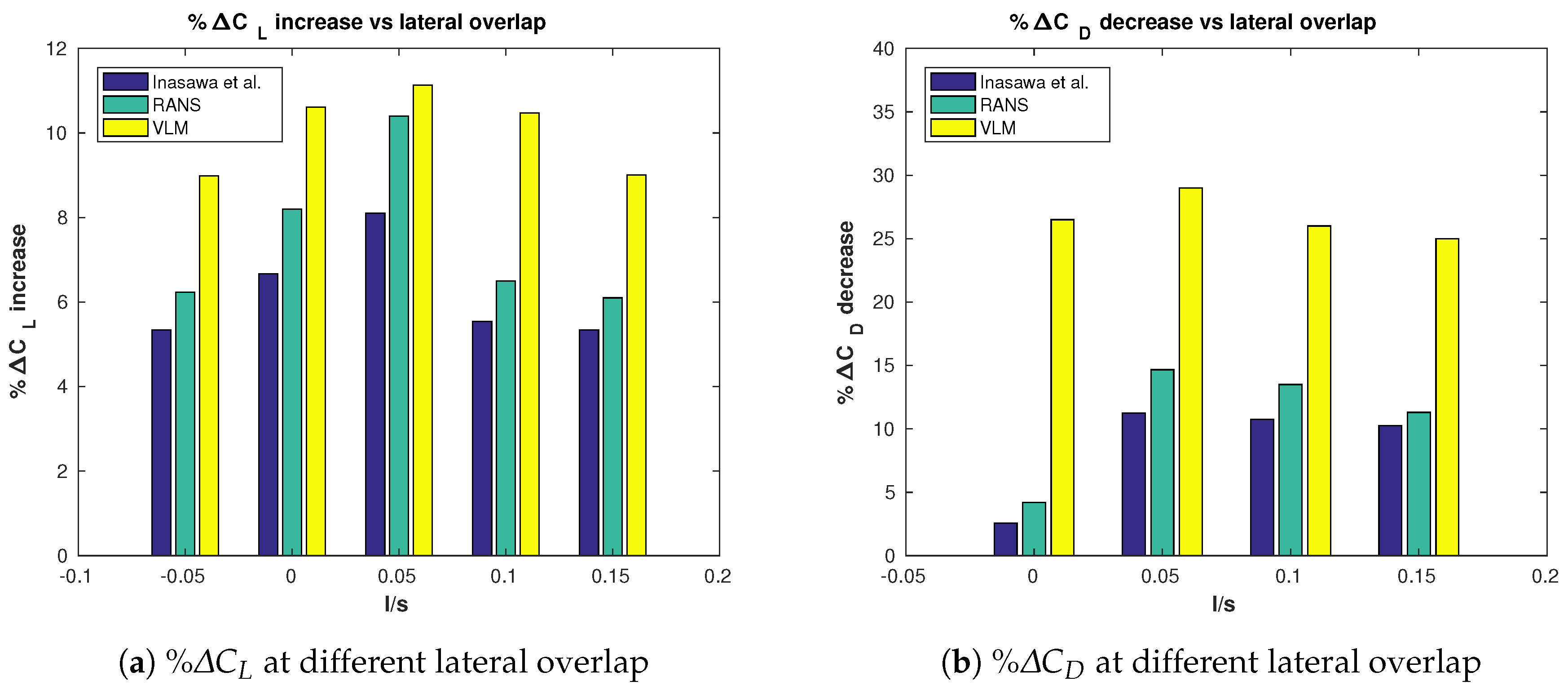
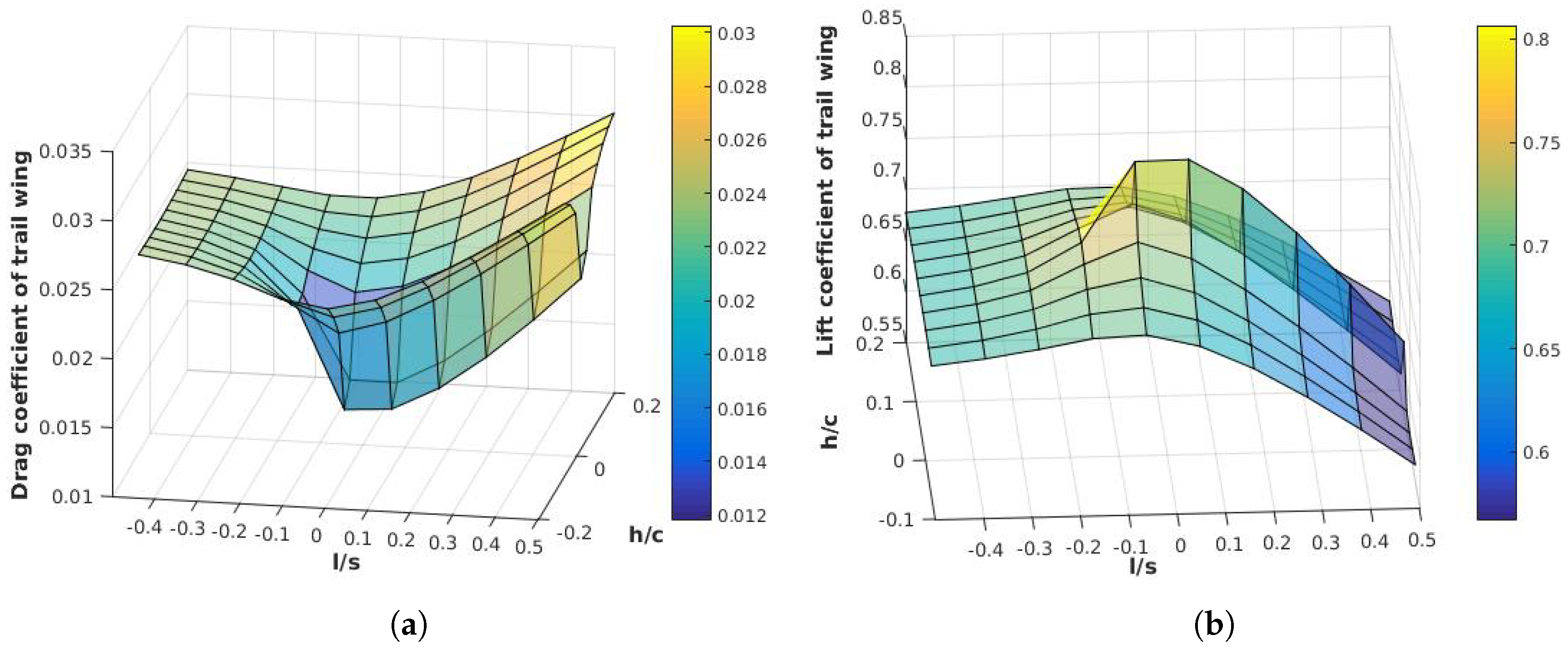
3.2. Two Wings in Tandem Configuration
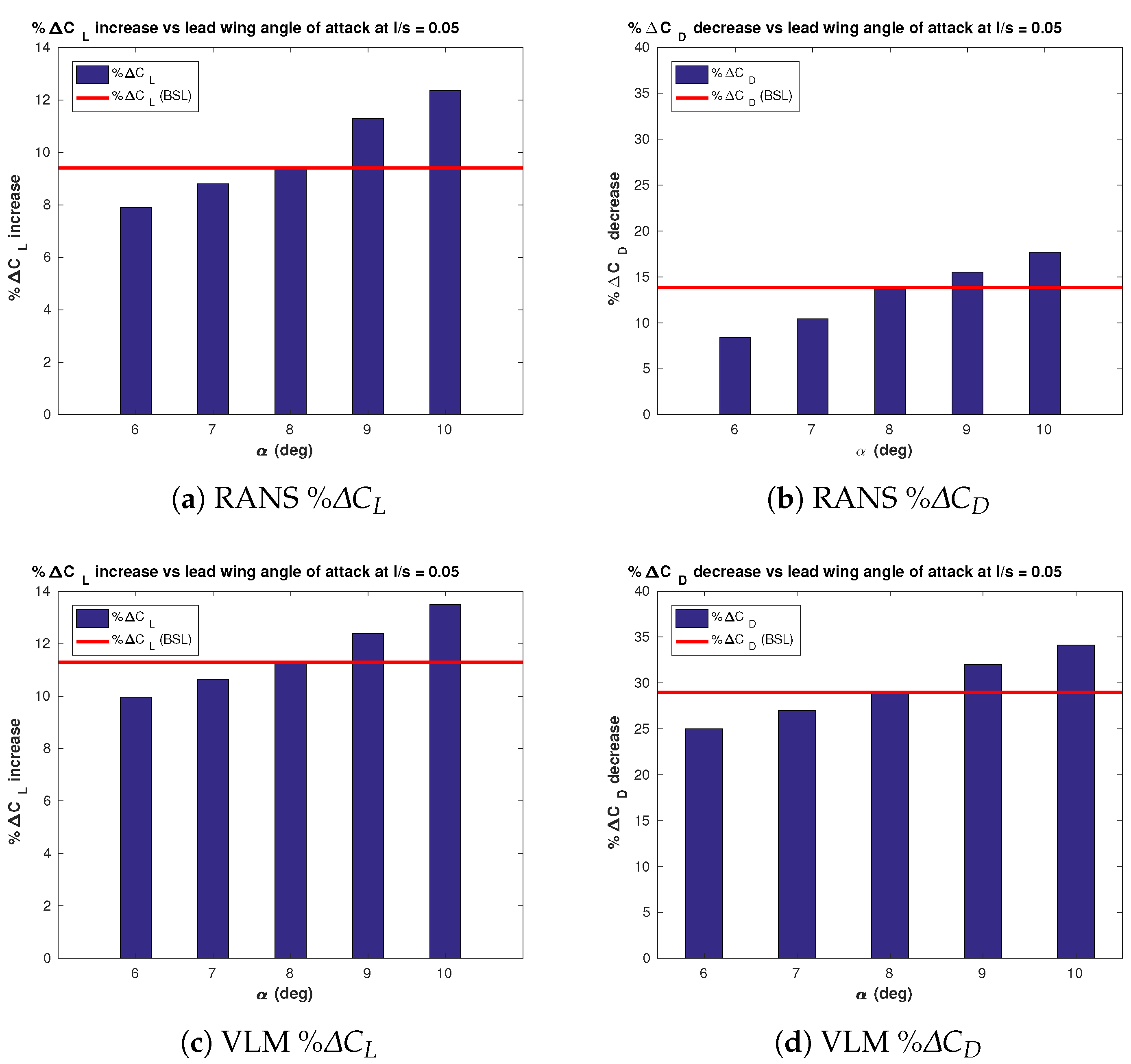
3.3. Effect of the Lead Wing’s AOA
3.4. Blended-Wing-Body Aircraft in Formation
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| RANS | Reynolds Averaged Navier–Stokes |
| VLM | Vortex Lattice Method |
| AOA | Angle of Attack |
| AR | Aspect Ratio |
| Re | Reynolds Number |
| SIMPLE | Semi Implicit Pressure Linked Equations |
References
- Weimerskirch, H.; Martin, J.; Clerquin, Y.; Alexandre, P.; Jiraskova, S. Energy saving in flight formation. Nature 2001, 413, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Bajec, I.; Heppner, F. Organized flight in birds. Anim. Behav. 2009, 78, 777–789. [Google Scholar] [CrossRef]
- Lissaman, P.; Shollenberger, C.A. Formation flight of birds. Science 1970, 168, 1003–1005. [Google Scholar] [CrossRef] [PubMed]
- Hainsworth, F.R. Precision and dynamics of positioning by Canada geese flying in formation. J. Exp. Biol. 1987, 128, 445–462. [Google Scholar]
- Beukenberg, M.; Hummel, D. Aerodynamics, Performance and Control of airplanes in formation flight. In Proceedings of the 17th Congress of the International Council of the Aeronautical Sciences, Stockholm, Sweden, 9–14 September 1990; Volume 2, pp. 1777–1794. [Google Scholar]
- DeVries, L.D.; Paley, D.A. Wake estimation and optimal control for autonomous aircraft in formation flight. In Proceedings of the Conference on AIAA Guidance, Navigation, and Control (GNC), Boston, MA, USA, 19–22 August 2013; p. 4705. [Google Scholar]
- Shin, H.; Antoniadis, A.; Tsourdos, A. Parametric Study on Formation Flying Effectiveness for a Blended-Wing UAV. J. Intell. Robot. Syst. 2018, 10. [Google Scholar] [CrossRef]
- Qiu, H.; Duan, H. Multiple UAV distributed close formation control based on in-flight leadership hierarchies of pigeon flocks. Aerosp. Sci. Technol. 2017, 70, 471–486. [Google Scholar] [CrossRef]
- Pahle, J.; Berger, D.; Venti, M.; Duggan, C.; Faber, J.; Cardinal, K. An initial flight investigation of formation flight for drag reduction on the C-17 aircraft. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012; pp. 13–16. [Google Scholar]
- Ayumu Inasawa, F.M.; Asai, M. Detailed Observation of Interaction of Wingtip Vortices in Close-formation Flight. J. Aircr. 2012, 49, 206–213. [Google Scholar] [CrossRef]
- Blake, W.; Gingras, D.R. Comparison of predicted and measured formation flight interference effects. J. Aircr. 2004, 41, 201–207. [Google Scholar] [CrossRef]
- Slotnick, J.P.; Clark, R.W.; Friedman, D.M.; Yadlin, Y.; Yeh, D.T.; Carr, J.E.; Czech, M.J.; Bieniawski, S.W. Computational aerodynamic analysis for the formation flight for aerodynamic benefit program. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014; AIAA Paper. p. 1458. [Google Scholar]
- Ning, A.; Flanzer, T.C.; Kroo, I.M. Aerodynamic performance of extended formation flight. J. Aircr. 2011, 48, 855–865. [Google Scholar] [CrossRef]
- Blake, W.; Multhopp, D. Design, Performance and Modeling Considerations for Close Formation Fligh. In Proceedings of the 23rd Atmospheric Flight Mechanics Conference, Boston, MA, USA, 10–12 August 1998. AIAA Paper 98-4343. [Google Scholar]
- Maskew, B. Formation Flying Benefits Based on Vortex Lattice Calculations; NASA CR-151974; NASA: Washington, DC, USA, 1977. [Google Scholar]
- Wagner, E.; Jacques, D.; Blake, W.; Pachter, M. Flight test results of close formation flight for fuel saving. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar]
- Wagner, H.E. An Analytical Study of T-38 Drag Reduction in Tight Flight Formation. Air Force Inst of Tech Wright-patterson Afb oh School of Engineering and Management. In Proceedings of the Atmospheric Flight Mechanics Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Korkischko, I.; Konrath, R. Formation Flight of Low-Aspect-Ratio Wings at Low Reynolds Number. J. Aircr. 2016, 54, 1025–1034. [Google Scholar] [CrossRef]
- Thien, H.; Moelyadi, M.; Muhammad, H. Effects of leaders position and shape on aerodynamic performances of V flight formation. arXiv, 2008; arXiv:0804.3879. [Google Scholar]
- Gunasekaran, M.; Mukherjee, R. Behaviour of trailing wing(s) in echelon formation due to wing twist and aspect ratio. Aerosp. Sci. Technol. 2017, 63, 294–303. [Google Scholar]
- Melin, T. A Vortex Lattice MATLAB Implementation for Linear Aerodynamic Wing Applications. Master’s Thesis, Department of Aeronautics, Royal Institute of Technology (KTH), Stockholm, Sweden, 2000. [Google Scholar]
- Wilcox, D. Formulation of the kappa-omega turbulence model revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef]
- Chien, K. Predictions of channel and boundary-layer flows with a low-reynolds-number turbulence model. AIAA J. 1982, 20, 33–38. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Roache, P.J.; Ghia, K.N.; White, F.M. Editorial policy statement on the control of numerical accuracy. J. Fluids Eng. 1986, 108. [Google Scholar] [CrossRef]
- Iglesias, S.; Mason, W. Optimum spanloads in formation flight. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; AIAA Paper. Volume 258. [Google Scholar]
- Ekaterinaris, J.; Platzer, M. Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 1998, 33, 759–846. [Google Scholar] [CrossRef]





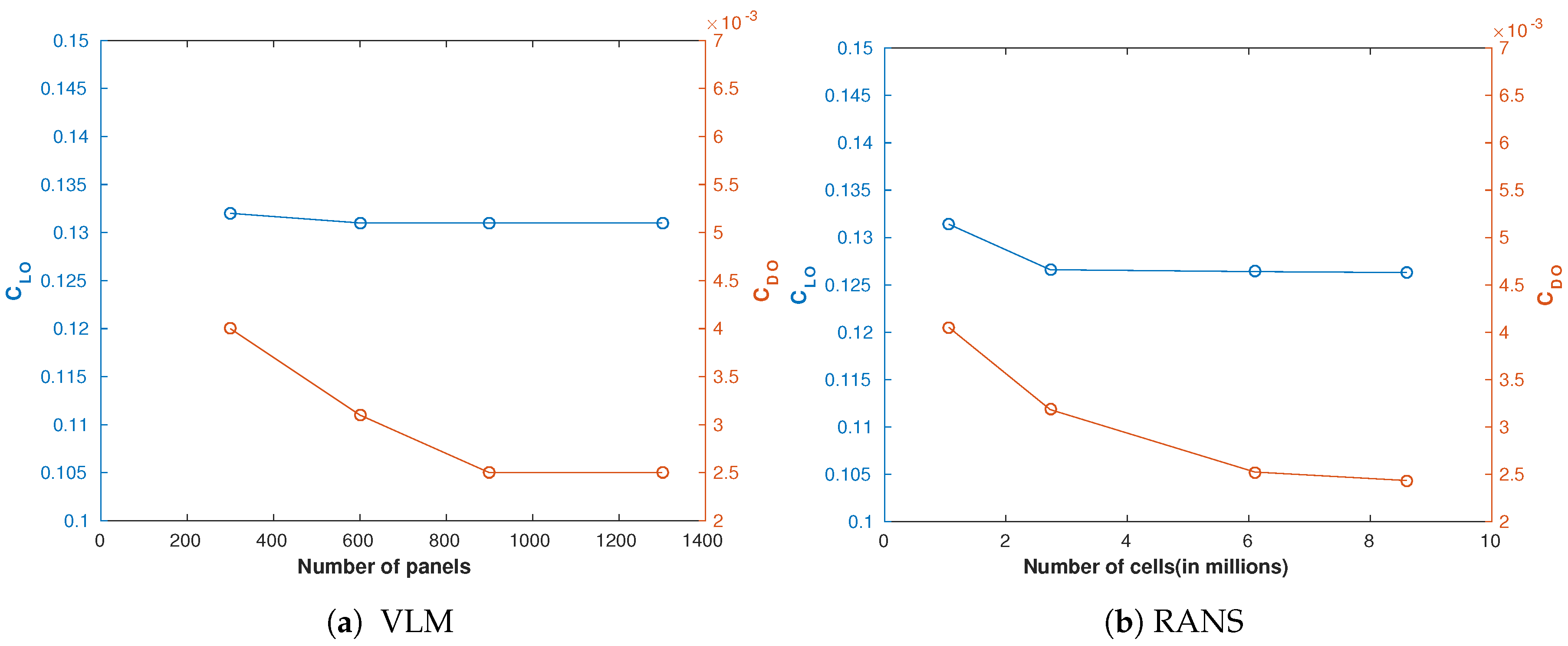



| Configuration | Aerodynamic Coefficients | VLM | RANS |
|---|---|---|---|
| Isolated aircraft | 0.0022 | 0.0028 | |
| 0.1758 | 0.1290 | ||
| Trail aircraft in formation | 0.0016 | 0.0019 | |
| 0.1935 | 0.1450 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, D.; Antoniadis, A.F.; Tsoutsanis, P.; Shin, H.-S.; Tsourdos, A.; Mathekga, S.; Jenkins, K.W. A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight. Aerospace 2018, 5, 66. https://doi.org/10.3390/aerospace5020066
Singh D, Antoniadis AF, Tsoutsanis P, Shin H-S, Tsourdos A, Mathekga S, Jenkins KW. A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight. Aerospace. 2018; 5(2):66. https://doi.org/10.3390/aerospace5020066
Chicago/Turabian StyleSingh, Diwakar, Antonios F. Antoniadis, Panagiotis Tsoutsanis, Hyo-Sang Shin, Antonios Tsourdos, Samuel Mathekga, and Karl W. Jenkins. 2018. "A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight" Aerospace 5, no. 2: 66. https://doi.org/10.3390/aerospace5020066
APA StyleSingh, D., Antoniadis, A. F., Tsoutsanis, P., Shin, H.-S., Tsourdos, A., Mathekga, S., & Jenkins, K. W. (2018). A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight. Aerospace, 5(2), 66. https://doi.org/10.3390/aerospace5020066








