Uncertainty Evaluation in the Design of Structural Health Monitoring Systems for Damage Detection†
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Modeling of SHM Signals
- Built a model of the reduced domain near the rivet hole in ANSYS (ANSYS® Mechanical APDL) with a sensing circle and non-reflecting boundary conditions.
- Evaluated the time-harmonic solutions to the wave scattering problem for frequencies of 2–1000 kHz at 2 kHz intervals, using the finite elements in ANSYS.
- Post-process FEM outputs generated complex scatter-cubes with wave-damage interaction coefficients (WDIC),
- Imported WDIC to Waveform Revealer 2-D (WFR-2D) in order to generate signal data analytically.
Finite Element Modeling
2.2. Experimental Factors and Damage Indices
2.3. Statistical Experimental Design and Analysis Methods
2.3.1. Full Factorial Design
2.3.2. Half-Fraction Factorial Design
3. Results
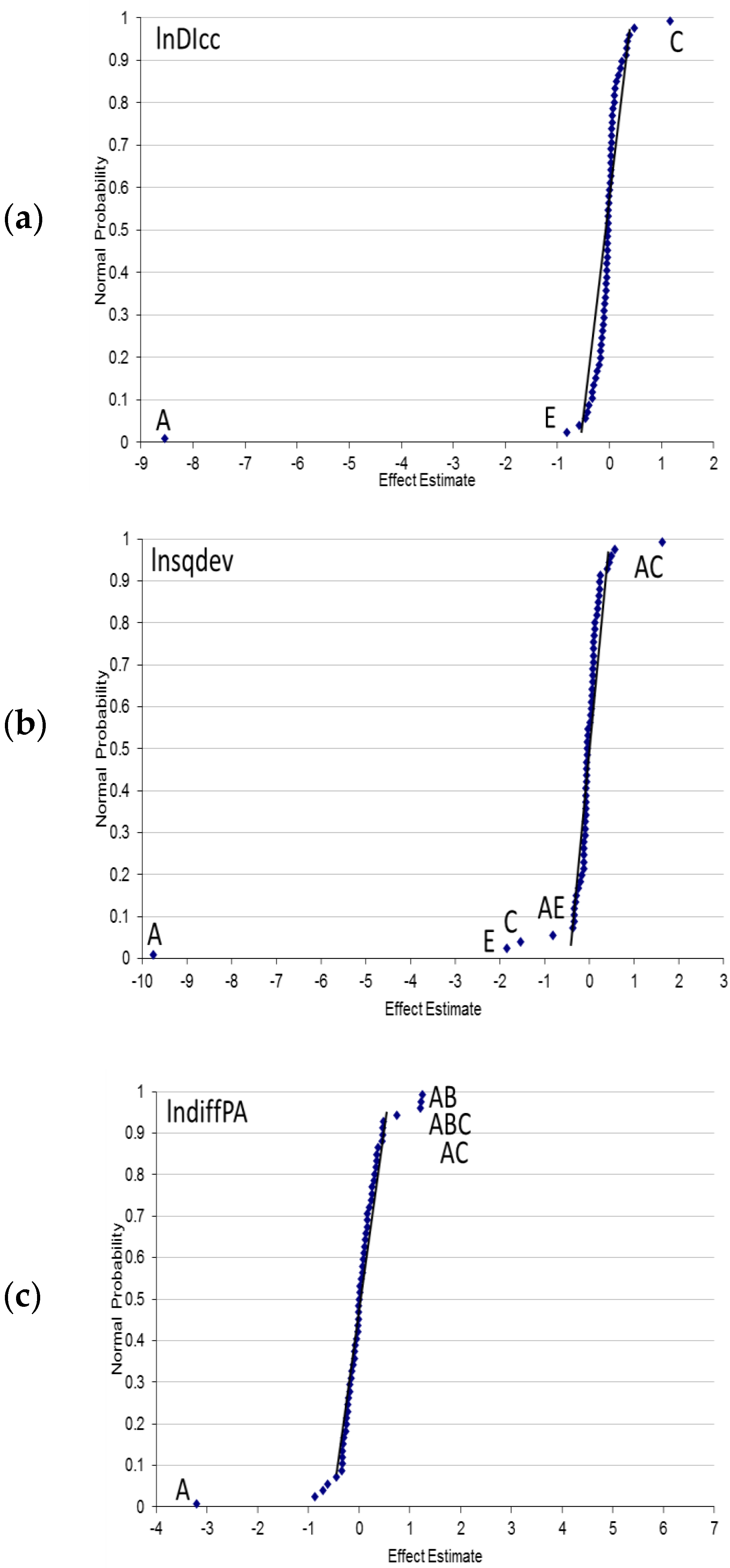
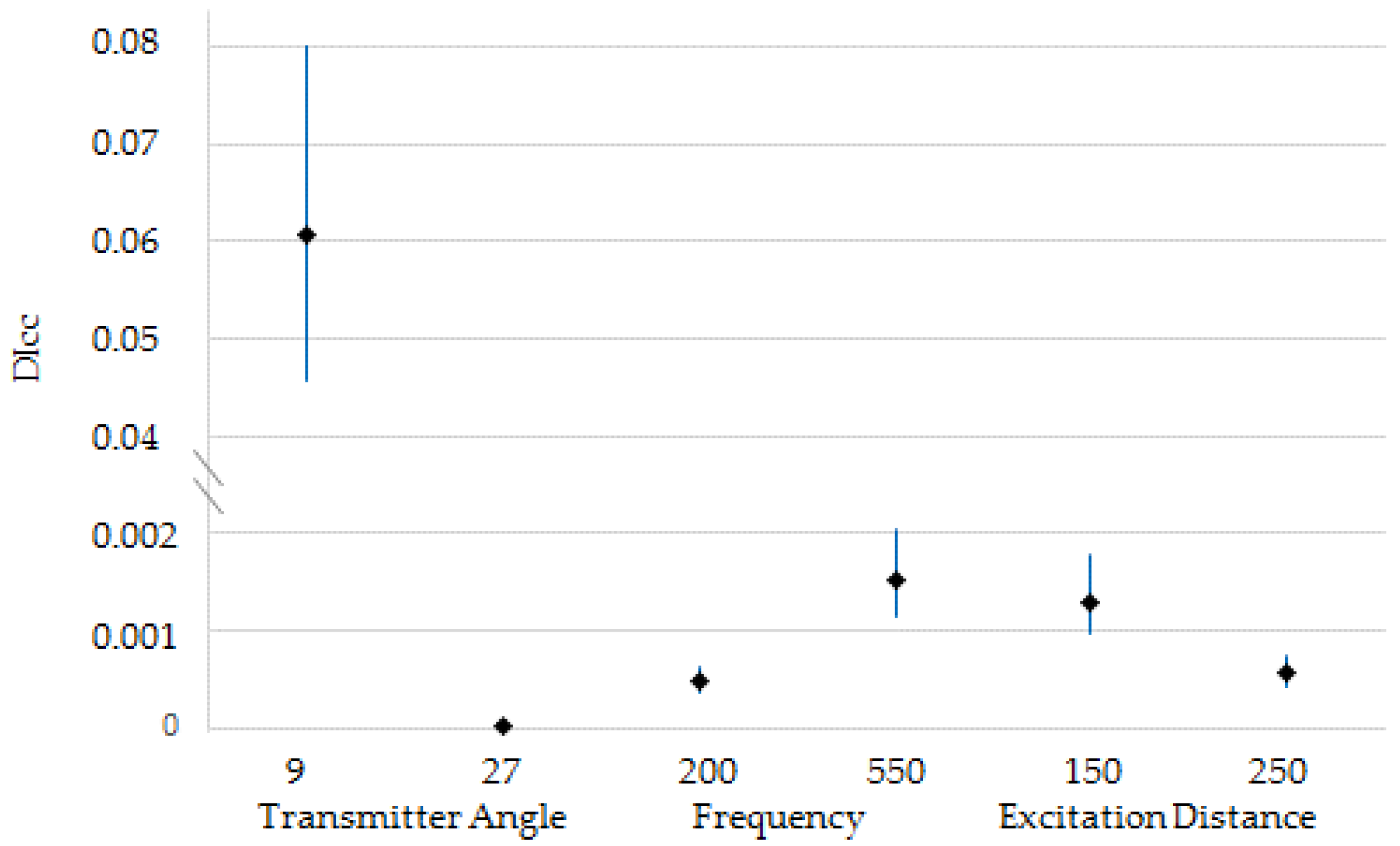
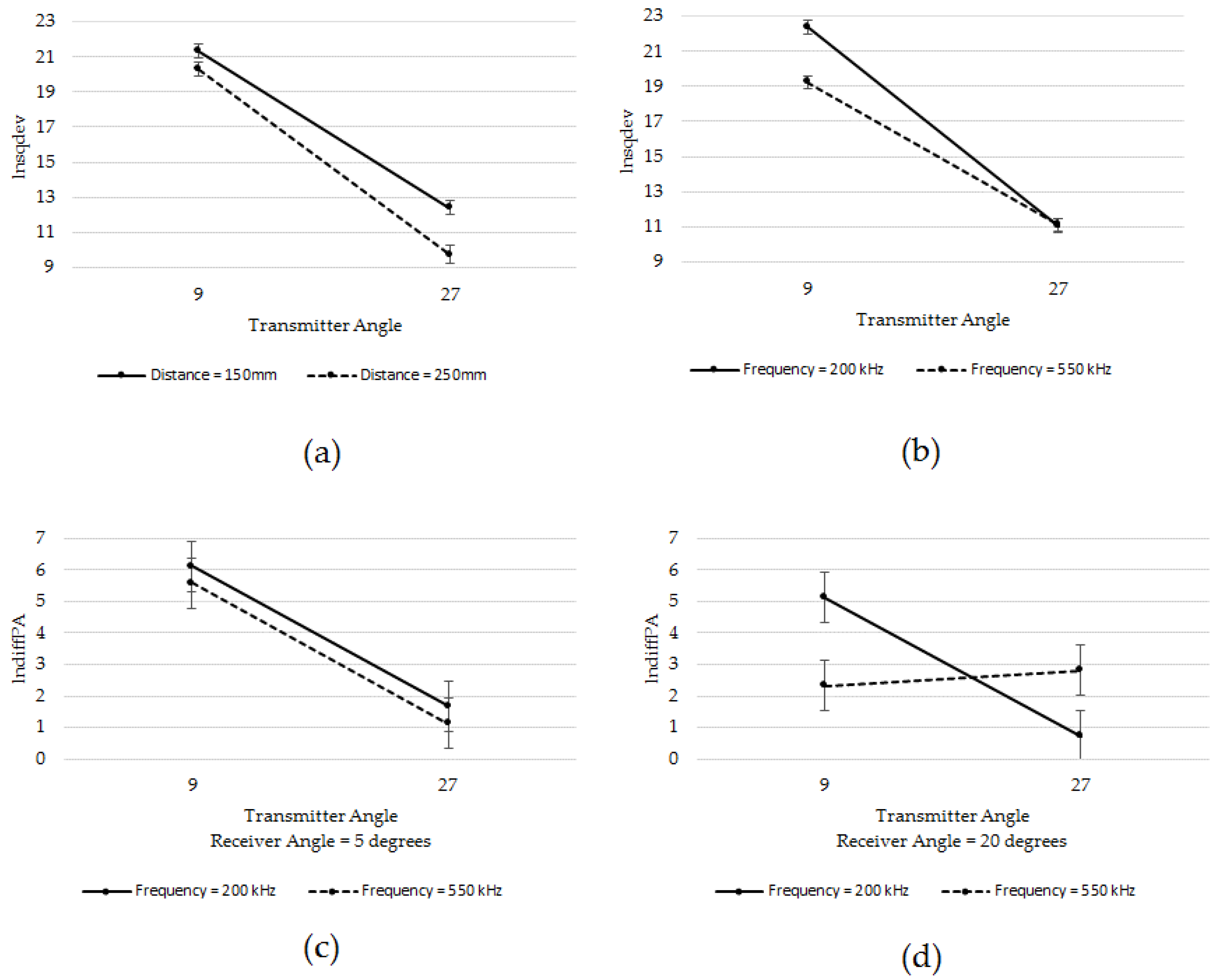
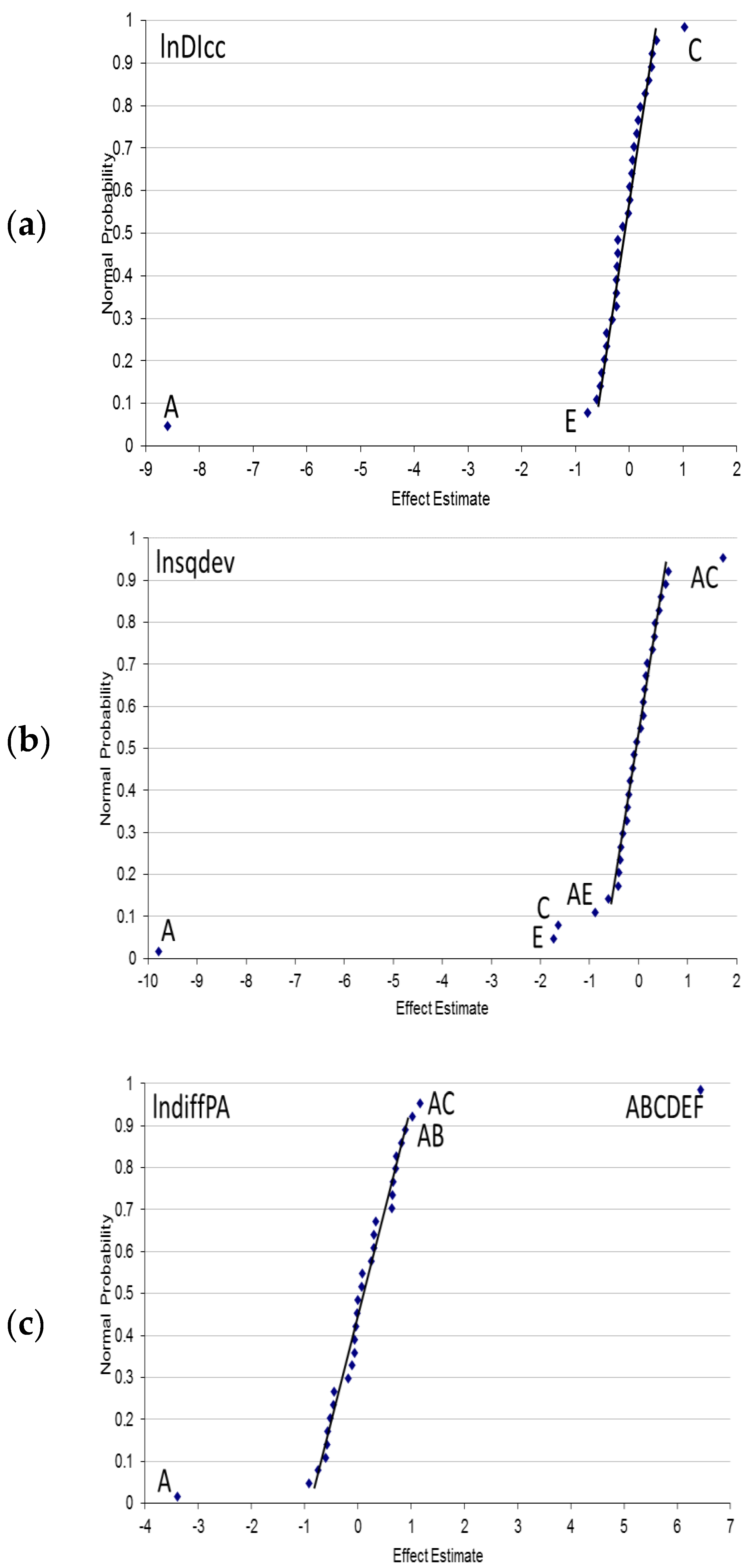
3.1. SHM Configuration Factors Producing the Most Variation in the SHM Response (Damage Index)
3.2. SHM Configuration Factors Identified through the Half-Fraction Factorial Design
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Derriso, M.M.; Olson, E.E.; DeSimio, M.P. Military Aircraft. In Encyclopedia of Structural Health Monitoring; Boller, C., Change, F.-K., Fujino, Y., Eds.; Wiley Blackwell: Hoboken, NJ, USA, 2009; Volume 1. [Google Scholar] [CrossRef]
- Department of Defense. Aircraft Structural Integrity Program General Guidelines; MIL-STD-1530D (USAF); Department of Defense: Arlington County, VA, USA, 2016.
- Condition Based Maintenance Plus (CBM+). CBM+ Plan. 2013. Available online: http://www.acq.osd.mil/log/mpp/.cbm+.html/CBM+_Plan2013v2.pdf (accessed on 12 February 2018).
- Lindgren, E.A.; Knopp, J.S.; Aldrin, J.C.; Steffes, G.J.; Buynak, C.F. Aging aircraft NDE: Capabilities, challenges, and Opportunities. AIP Conf. Proc. 2007, 894, 1731. [Google Scholar] [CrossRef]
- Janapati, V.; Kopsaftopoulos, F.; Li, F.; Lee, S.J.; Chang, F.K. Damage detection sensitivity characterization of acousto-ultrasound-based structural health monitoring techniques. SHM 2016, 15, 143–161. [Google Scholar] [CrossRef]
- Masserey, B.; Fromme, P. Analysis of high frequency guided wave scattering at a fastener hole with a view to fatigue crack detection. Ultrasonics 2017, 76, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Zeng, L.; Lin, J.; Bao, J.; Joseph, R.P.; Huang, L. Spatial resolution improvement for Lamb wave-based damage detection using frequency dependency compensation. J. Sound Vib. 2017, 394, 130–145. [Google Scholar] [CrossRef]
- Stawiarski, A.; Barski, M.; Pajak, P. Fatigue crack detection and identification by the elastic wave propagation method. Mech. Syst. Signal Process. 2017, 89, 119–130. [Google Scholar] [CrossRef]
- Hong, M.; Su, Z.; Lu, Y.; Sohn, H.; Qing, X. Locating fatigue damage using temporal signal features of nonlinear Lamb waves. Mech. Syst. Signal Process. 2015, 60–61, 182–197. [Google Scholar] [CrossRef]
- Ihn, J.B.; Chang, F.K. Pitch-catch active sensing methods in structural health monitoring for aircraft structures. SHM 2008, 7, 5–19. [Google Scholar] [CrossRef]
- Fendzi, C.; Morel, J.; Rebillat, M.; Guskov, M.; Mechbal, N.; Coffignal, G. Optimal sensors placement to enhance damage detection in composite plates. In Proceedings of the 7th European Workshop on Structural Health Monitoring, Nantes, France, 8–11 July 2014; Curran Associates: Red Hook, NY, USA, 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Raghavan, A.; Cesnik, C.E.S. Finite-dimensional piezolelectric transducer modeling for guided wave based structural health monitoring. Smart Mater. Struct. 2005, 14, 1448–1461. [Google Scholar] [CrossRef]
- Lu, Y.; Michaels, J.E. Feature extraction and sensor fusion for ultrasonic structural health monitoring under changing environmental conditions. IEEE Sens. J. 2009, 9, 1462–1471. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.P.; Fassois, S.D. A functional model based statistical time series method for vibration based damage detection, localization, and magnitude estimation. Mech. Syst. Signal Process. 2013, 39, 143–161. [Google Scholar] [CrossRef]
- Kopsaftopoulos, F.P.; Fassois, S.D. Vibration based health monitoring for a lightweight truss structure: Experimental assessment of several statistical time series methods. Mech. Syst. Signal Process. 2010, 24, 1977–1997. [Google Scholar] [CrossRef]
- Roy, S.; Ladpli, P.; Lonkar, K.; Chang, F.K. Structural damage detection using ultrasonic guided waves under varying ambient temperature and loading environments. In Proceedings of the 9th IWSHM, Stanford, CA, USA, 10–12 September 2013; pp. 1284–1293. [Google Scholar]
- Roy, S.; Lonkar, K.; Janapati, V.; Chang, F.K. A novel physics-based temperature compensation model for structural health monitoring using ultrasonic guided waves. SHM 2014, 13, 321–342. [Google Scholar] [CrossRef]
- Moriot, J.; Quaegebeur, N.; Le Duff, A.; Masson, P. A model-based approach for statistical assessment of detection and localization performance of guided wave-based imaging techniques. SHM 2017, 1–13. [Google Scholar] [CrossRef]
- Gianneo, A.; Carboni, M.; Giglio, M. Feasibility study of a multi-parameter probability of detection formulation for a lamb waves-based structural health monitoring approach to light alloy aeronautical plates. SHM 2016, 16, 225–249. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Zagrai, A.; Bao, J.J. Piezoelectric wafer embedded active sensors for aging aircraft structural health monitoring. SHM 2002, 1, 41–61. [Google Scholar] [CrossRef]
- Shen, Y. Structural Health Monitoring Using Linear and Nonlinear Ultrasonic Guided Waves. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 2014. [Google Scholar]
- Bhuiyan, M.Y.; Shen, Y.; Giurgiutiu, V. Interaction of Lamb waves with rivet hole cracks from multiple directions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2974–2987. [Google Scholar] [CrossRef]
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 2nd ed.; Elsevier: Waltham, MA, USA, 2014; ISBN 978-0-12-418691-0. [Google Scholar]
- Shen, Y.; Giurgiutiu, V. WaveFormRevealer 1-D—An Analytical Predictive Tool for the 1-D Simulation of Multimodal Guided Waves Propagation and Interaction with Damage: User’s Guide and Theoretical Foundation; Report # USC-ME-LAMSS-2012-101; University of South Carolina: Columbia, SC, USA, 2012. [Google Scholar]
- Shen, Y.; Giurgiutiu, V. Effective non-reflecting boundary for Lamb waves: Theory, finite element implementation, and applications. Wave Motion 2015, 58, 22–41. [Google Scholar] [CrossRef]
- Bhuiyan, M.Y.; Shen, Y.; Giurgiutiu, V. Guided wave based crack detection in the rivet hole using global analytical with local fem approach. Materials 2016, 9, 602. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1991; ISBN 0-471-52000-4. [Google Scholar]
- Daniel, C. Use of half-normal plots in interpreting factorial two level experiments. Technometrics 1959, 1, 311–342. [Google Scholar] [CrossRef]
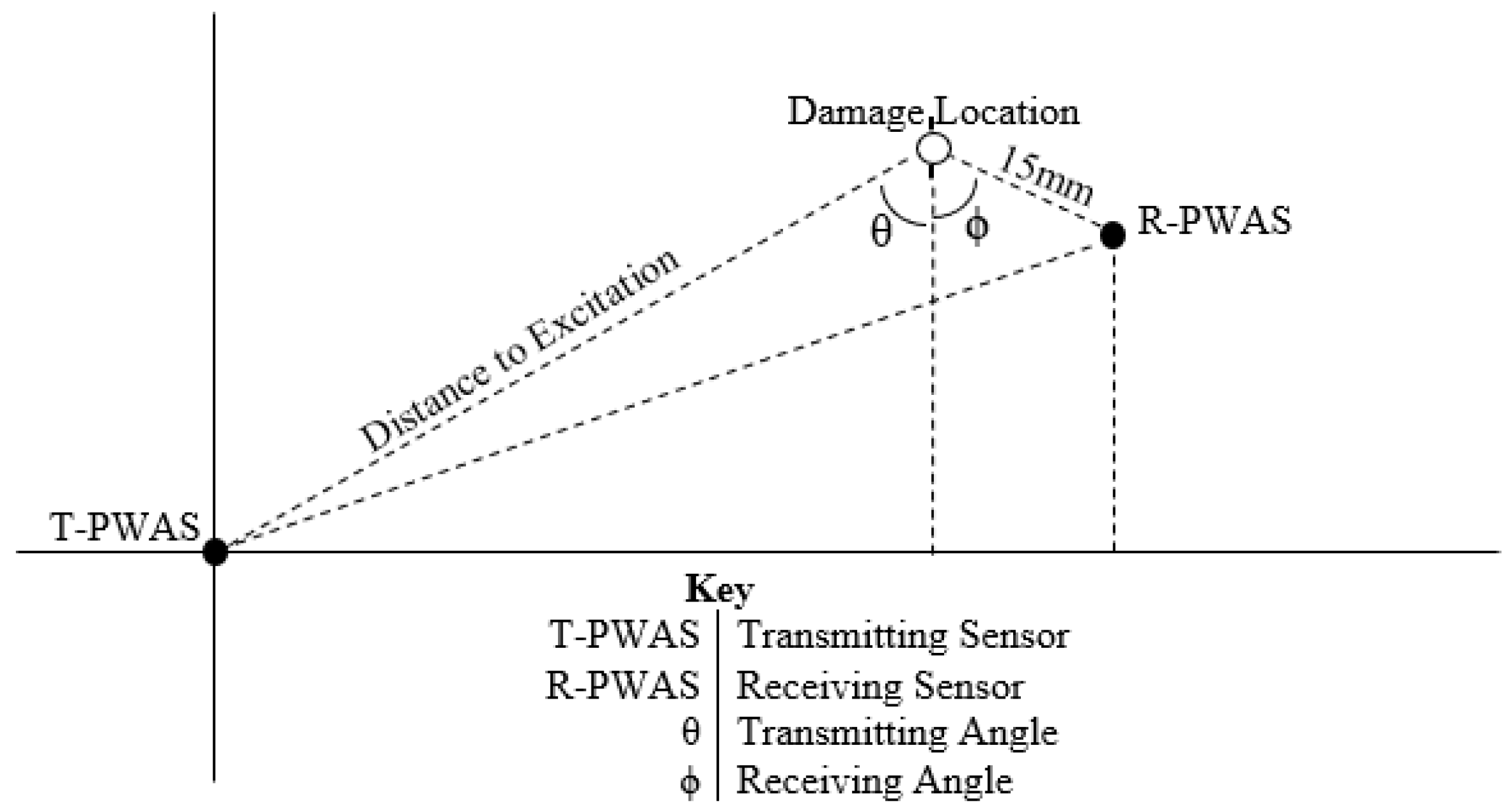
| Label | Factor | Generic Level | Specific Values |
|---|---|---|---|
| A | Transmitter Angle, θ | Low | 9° |
| High | 27° | ||
| B | Receiver Angle, φ | Low | 5° |
| High | 20° | ||
| C | Frequency | Low | 200 kHz |
| High | 550 kHz | ||
| D | Sensor Size | Low | 5 mm |
| High | 7 mm | ||
| E | Distance between Excitation and Damage Site | Low | 150 mm |
| High | 250 mm | ||
| F | Flaw Size | Low | 0.64 mm |
| High | 3.20 mm |
| Run | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| Transmitter Angle | Receiver Angle | Frequency | Sensor Size | Distance to Excitation | Flaw Size | |
| 1 | L | L | L | L | L | L |
| 2 | H | L | L | L | L | L |
| 3 | L | H | L | L | L | L |
| 4 | H | H | L | L | L | L |
| ... | ... | ... | ... | ... | ... | ... |
| 63 | H | H | H | H | H | L |
| 64 | H | H | H | H | H | H |
| Factors for the Half-Fraction Factorial Design (and Associated Aliased Factor) | |||||
|---|---|---|---|---|---|
| A = BCDEF | AB = CDEF | BD = ACEF | DE = ABCF | ABC = DEF | ACF = BDE |
| B = ACDEF | AC = BDEF | BE = ACDF | DF = ABCE | ABD = CEF | ADE = BCF |
| C = ABDEF | AD = BCEF | BF = ACDE | EF = ABCD | ABE = CDF | ADF = BCE |
| D = ABDEF | AE = BCDF | CD = ABEF | ABF = CDE | AEF = BCD | |
| E = ABCDF | AF = BCDE | CE = ABDF | ACD = BEF | ||
| F = ABCDE | BC = ADEF | CF = ABDE | ACE = BDF | ||
| Factor | lnDIcc | lnsqdev | lndiffPA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sums of Squares | df | p-Value | Sums of Squares | df | p-Value | Sums of Squares | df | p-Value | |||
| A | 1166.46 | 1 | <0.0001 | 1518.10 | 1 | <0.0001 | 164.57 | 1 | <0.0001 | ||
| B | - | - | - | - | - | - | 12.18 | 1 | 0.0030 | ||
| C | 21.81 | 1 | <0.0001 | 38.05 | 1 | <0.0001 | 3.22 | 1 | 0.1180 | ||
| E | 10.68 | 1 | 0.0002 | 54.86 | 1 | <0.0001 | - | - | - | ||
| AE | - | - | - | 10.85 | 1 | <0.0001 | - | - | - | ||
| AC | - | - | - | 41.97 | 1 | <0.0001 | 23.58 | 1 | <0.0001 | ||
| AB | - | - | - | - | - | - | 24.96 | 1 | <0.0001 | ||
| BC | - | - | - | - | - | - | 0.14 | 1 | 0.7440 | ||
| ABC | - | - | - | - | - | - | 24.01 | 1 | <0.0001 | ||
| Error | 39.61 | 60 | 36.23 | 58 | 71.66 | 56 | |||||
| Total | 1238.56 | 63 | 1700.07 | 63 | 324.25 | 63 | |||||
| R2 | 0.9680 | 0.9787 | 0.7790 | ||||||||
| RMSE | 0.8125 | 0.7903 | 1.1312 | ||||||||
| Factor | lnDIcc | lnsqdev | lndiffPA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sums of Squares | df | p-Value | Sums of Squares | df | p-Value | Sums of Squares | df | p-Value | |||
| A | 608.68 | 1 | <0.0001 | 834.34 | 1 | <0.0001 | 117.51 | 1 | <0.0001 | ||
| C | 14.80 | 1 | 0.0002 | 15.86 | 1 | 0.0016 | - | - | - | ||
| E | 7.00 | 1 | 0.0065 | 23.45 | 1 | <0.0001 | - | - | - | ||
| AE | - | - | - | 5.96 | 1 | 0.0039 | - | - | - | ||
| AC | - | - | - | 6.37 | 1 | 0.0019 | - | - | - | ||
| Error | 22.64 | 28 | 25.96 | 26 | 64.16 | 30 | |||||
| Total | 653.12 | 31 | 911.93 | 31 | 181.67 | 31 | |||||
| R2 | 0.9653 | 0.9736 | 0.6468 | ||||||||
| RMSE | 0.8993 | 0.9992 | 1.4642 | ||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schubert Kabban, C.; Uber, R.; Lin, K.; Lin, B.; Bhuiyan, M.Y.; Giurgiutiu, V. Uncertainty Evaluation in the Design of Structural Health Monitoring Systems for Damage Detection†. Aerospace 2018, 5, 45. https://doi.org/10.3390/aerospace5020045
Schubert Kabban C, Uber R, Lin K, Lin B, Bhuiyan MY, Giurgiutiu V. Uncertainty Evaluation in the Design of Structural Health Monitoring Systems for Damage Detection†. Aerospace. 2018; 5(2):45. https://doi.org/10.3390/aerospace5020045
Chicago/Turabian StyleSchubert Kabban, Christine, Richard Uber, Kevin Lin, Bin Lin, Md Yeasin Bhuiyan, and Victor Giurgiutiu. 2018. "Uncertainty Evaluation in the Design of Structural Health Monitoring Systems for Damage Detection†" Aerospace 5, no. 2: 45. https://doi.org/10.3390/aerospace5020045
APA StyleSchubert Kabban, C., Uber, R., Lin, K., Lin, B., Bhuiyan, M. Y., & Giurgiutiu, V. (2018). Uncertainty Evaluation in the Design of Structural Health Monitoring Systems for Damage Detection†. Aerospace, 5(2), 45. https://doi.org/10.3390/aerospace5020045






