Design, Development and Testing of Shape Shifting Wing Model
Abstract
:1. Introduction
2. Current Sophisticated Morphing Wing Technology
2.1. Mechanical Monolithic Joint-Less Mechanism
2.2. Rib Based Morphing Trailing Edge
2.3. Dielectric Smart Polymer Morphing Wing
2.4. Transition Regions
3. Concept Analysis
4. Initial Experimental Analysis
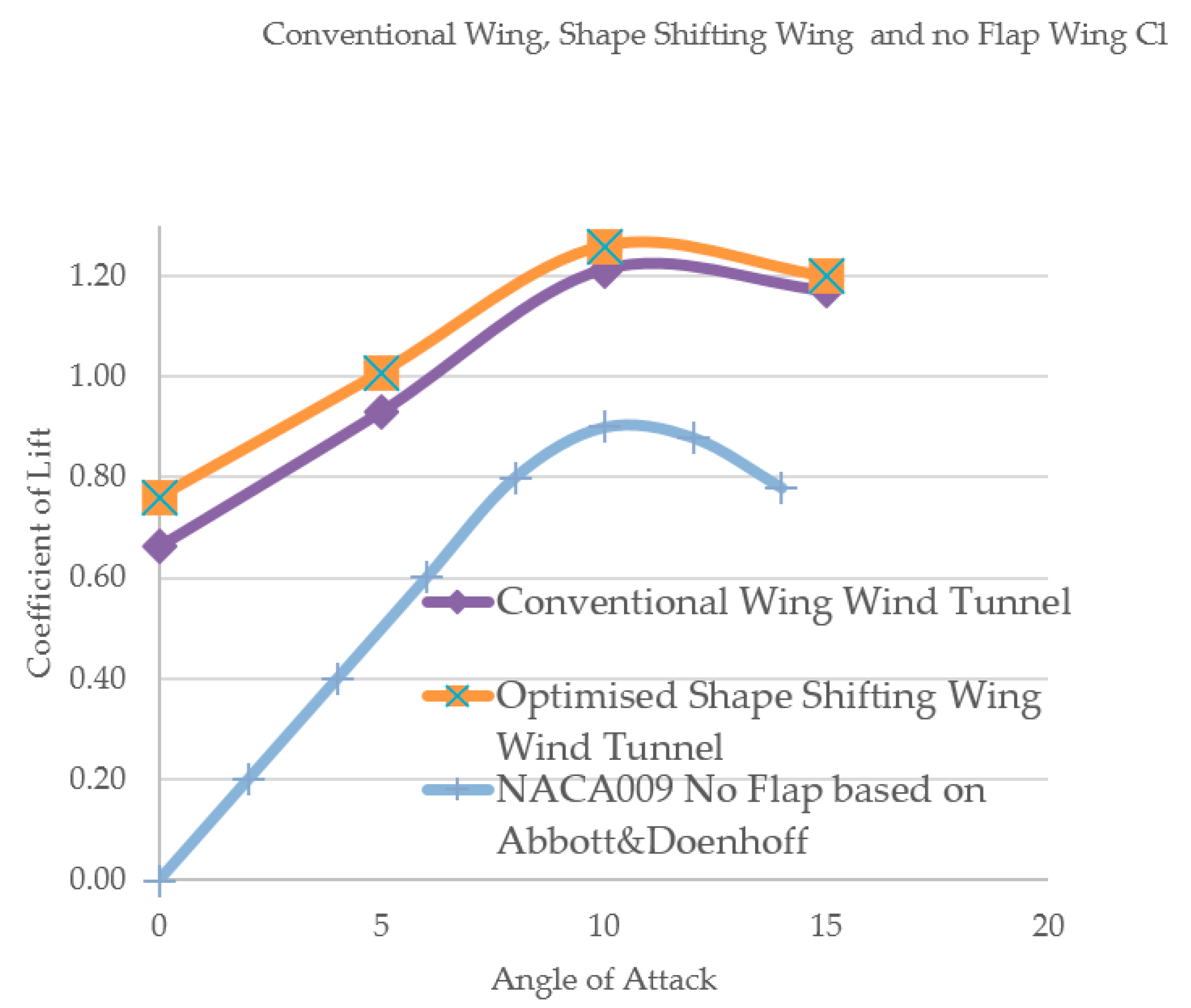
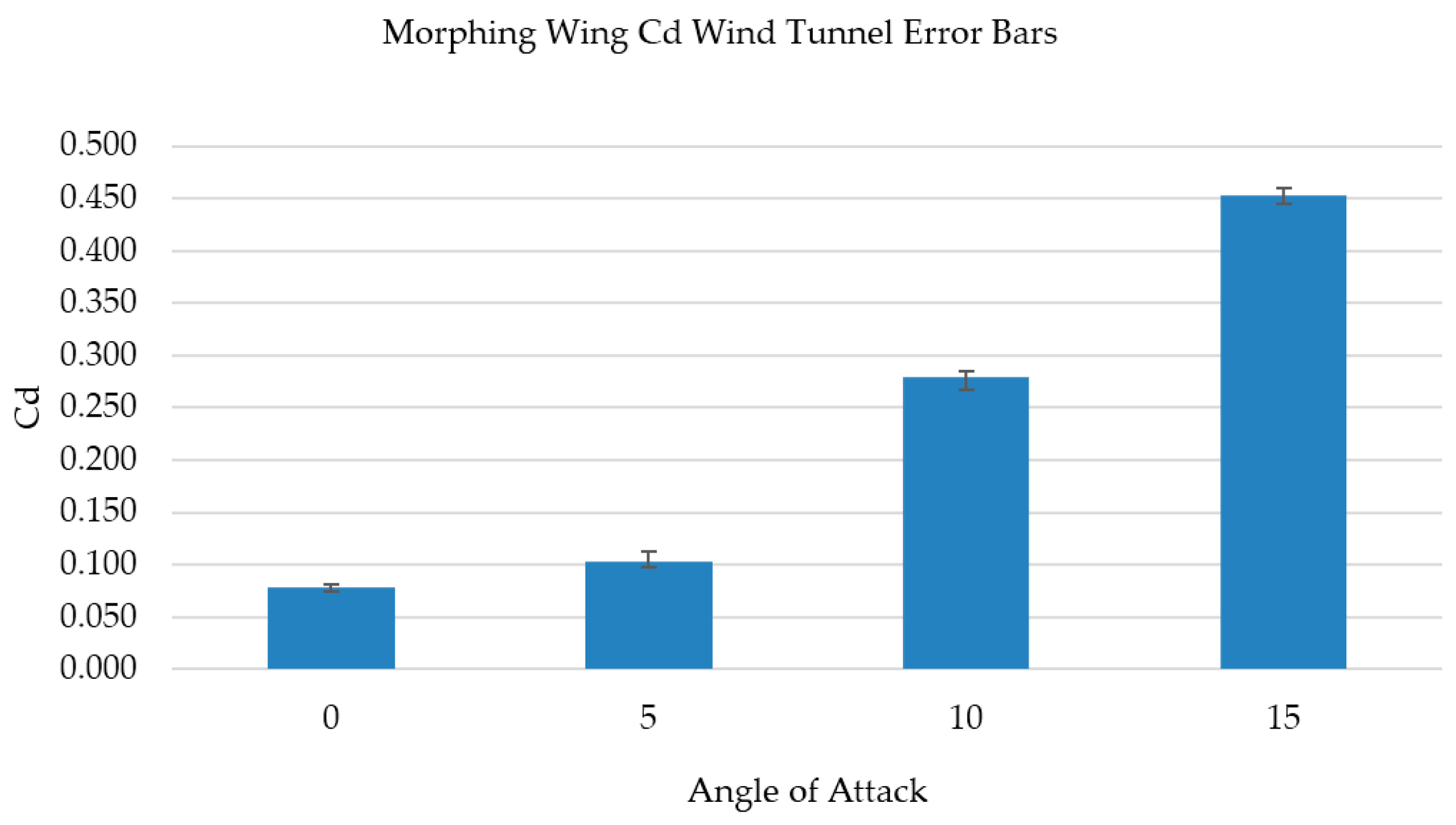
4.1. Wind Tunnel Testing
4.2. Wind Tunnel Results Discussion
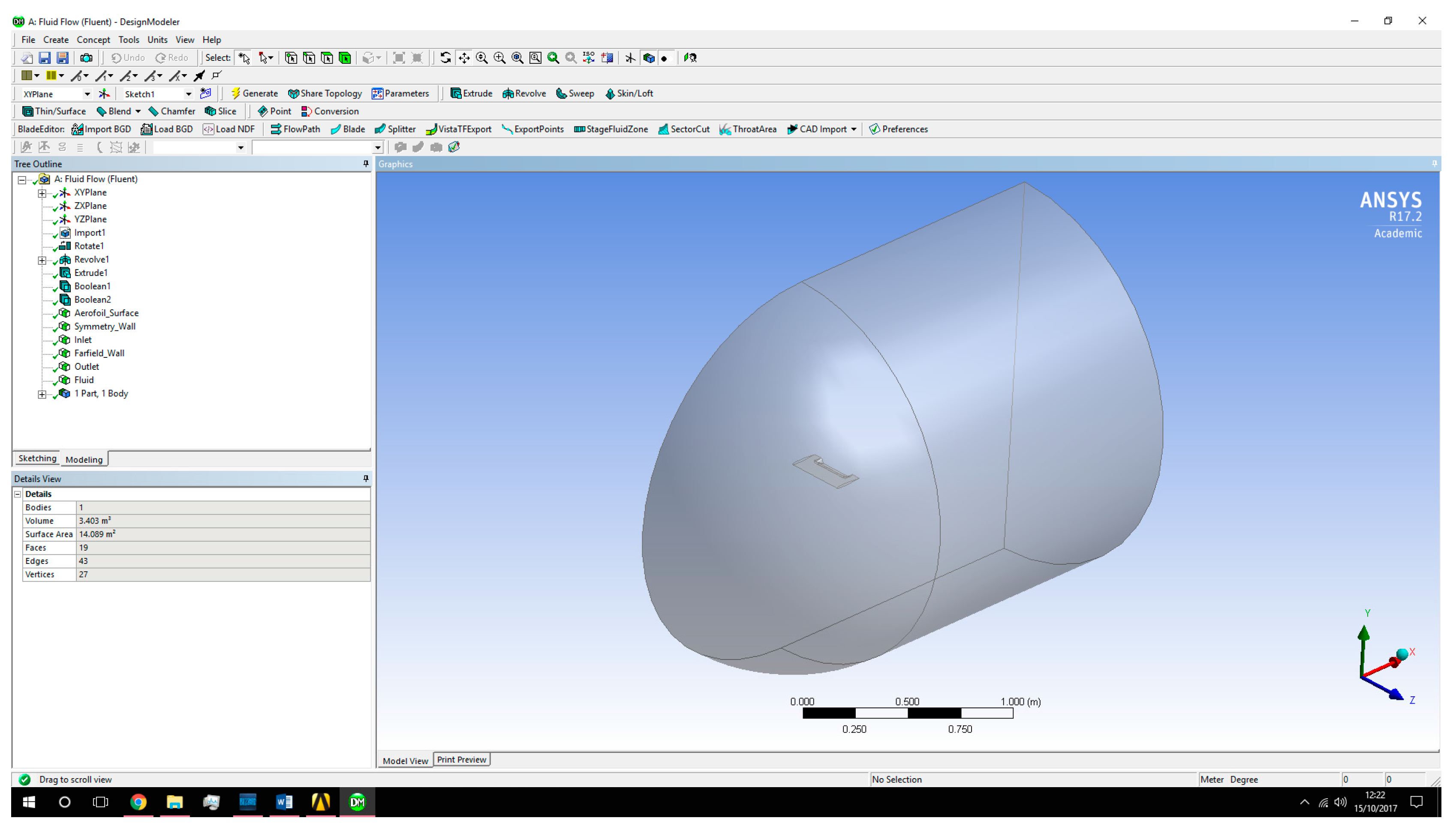
5. Ansys-Fluent Numerical and Experimental Analysis
5.1. Ansys Solver Set-Up
- Energy—On.
- Viscous—K-epsilon, Realizable & Non-equilibrium Wall Functions.
- Boundary Conditions—Turbulent Intensity 5% & Turbulent viscosity ratio 10.
5.2. Conventional Wing Ansys Simulation
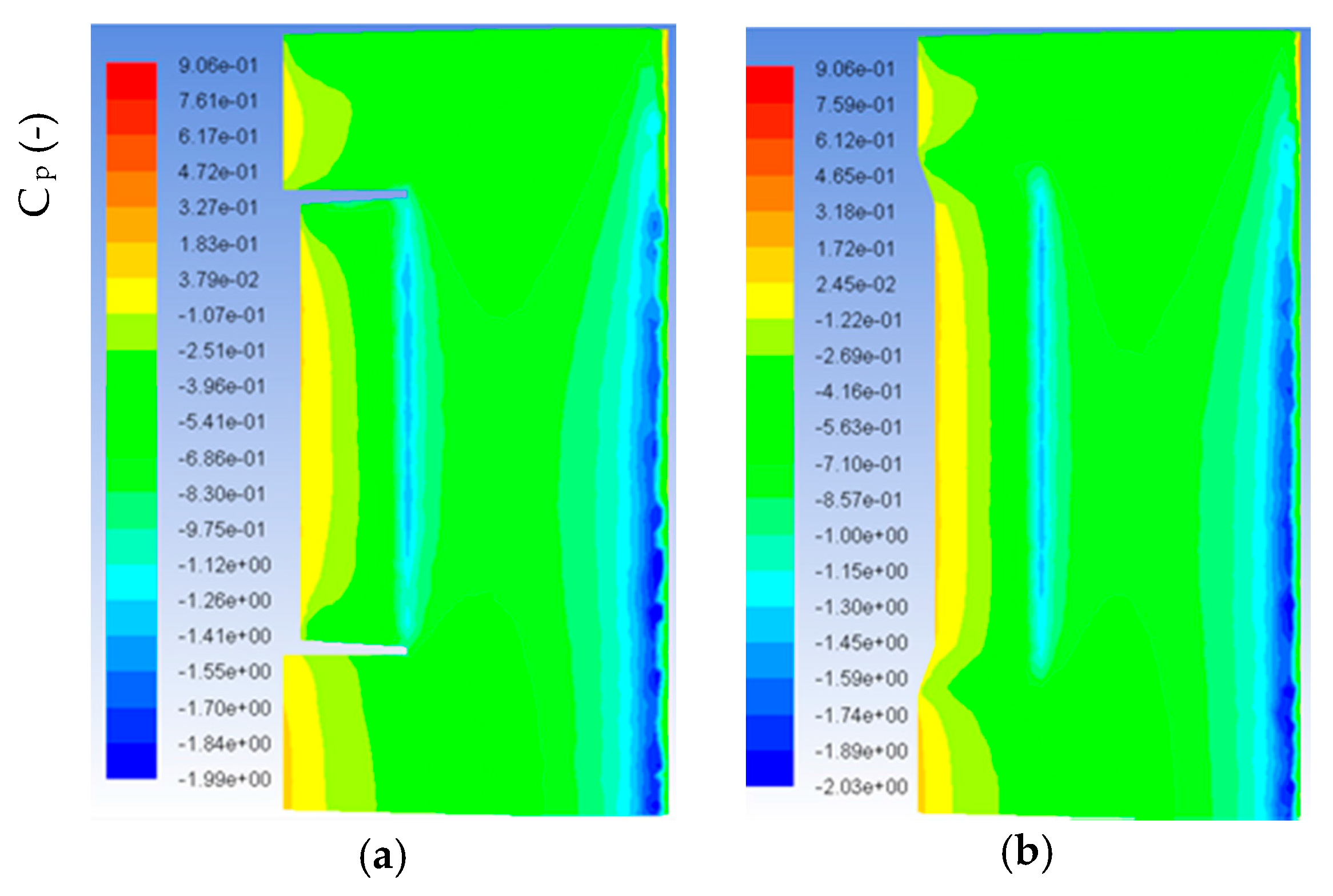
5.3. Initial Morphing Wing Ansys Simulation
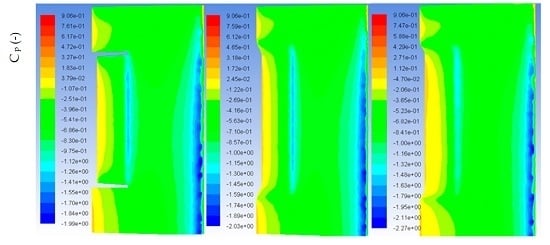
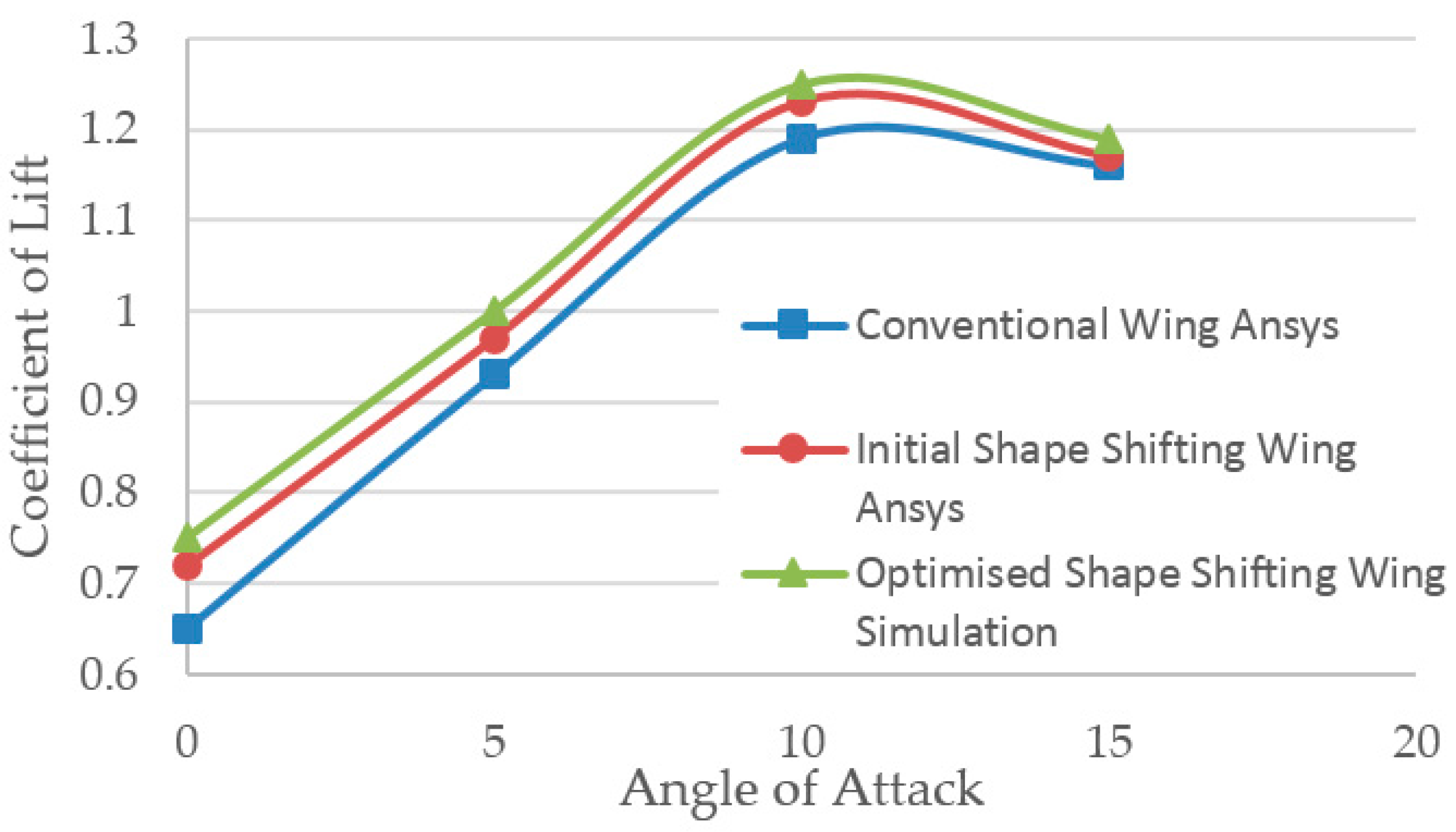
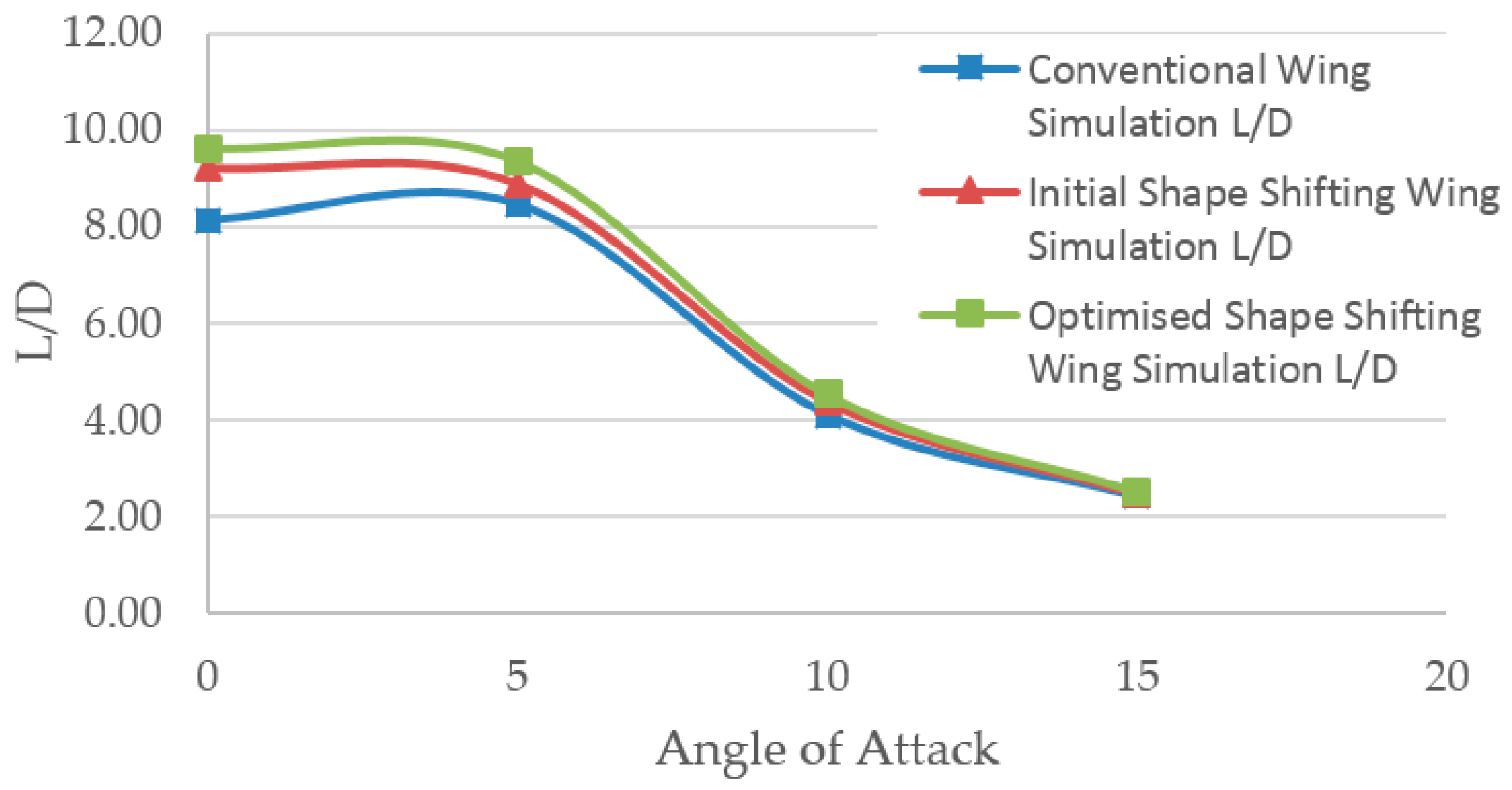
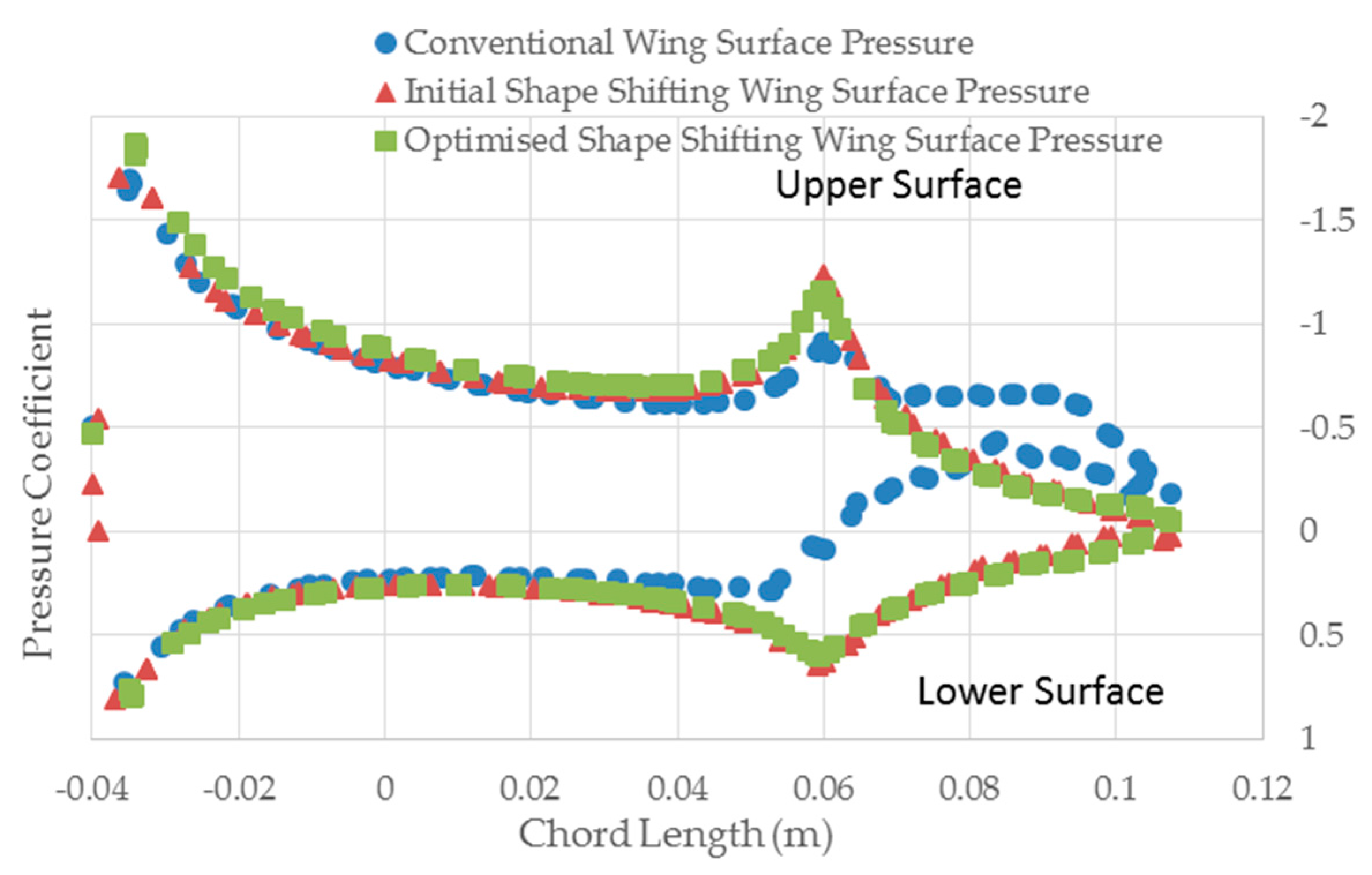
5.4. Optimized Morphing Wing Simulation
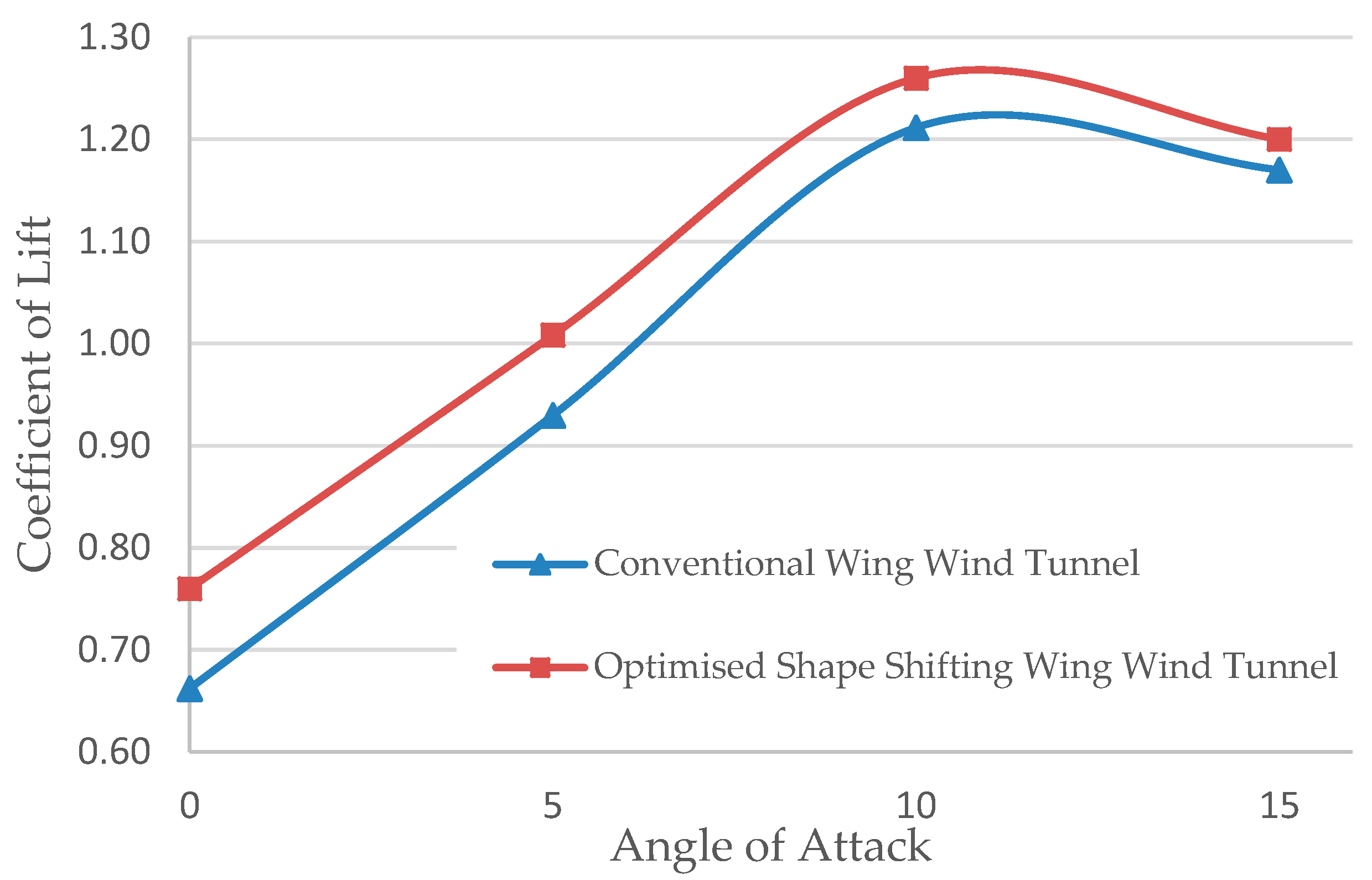
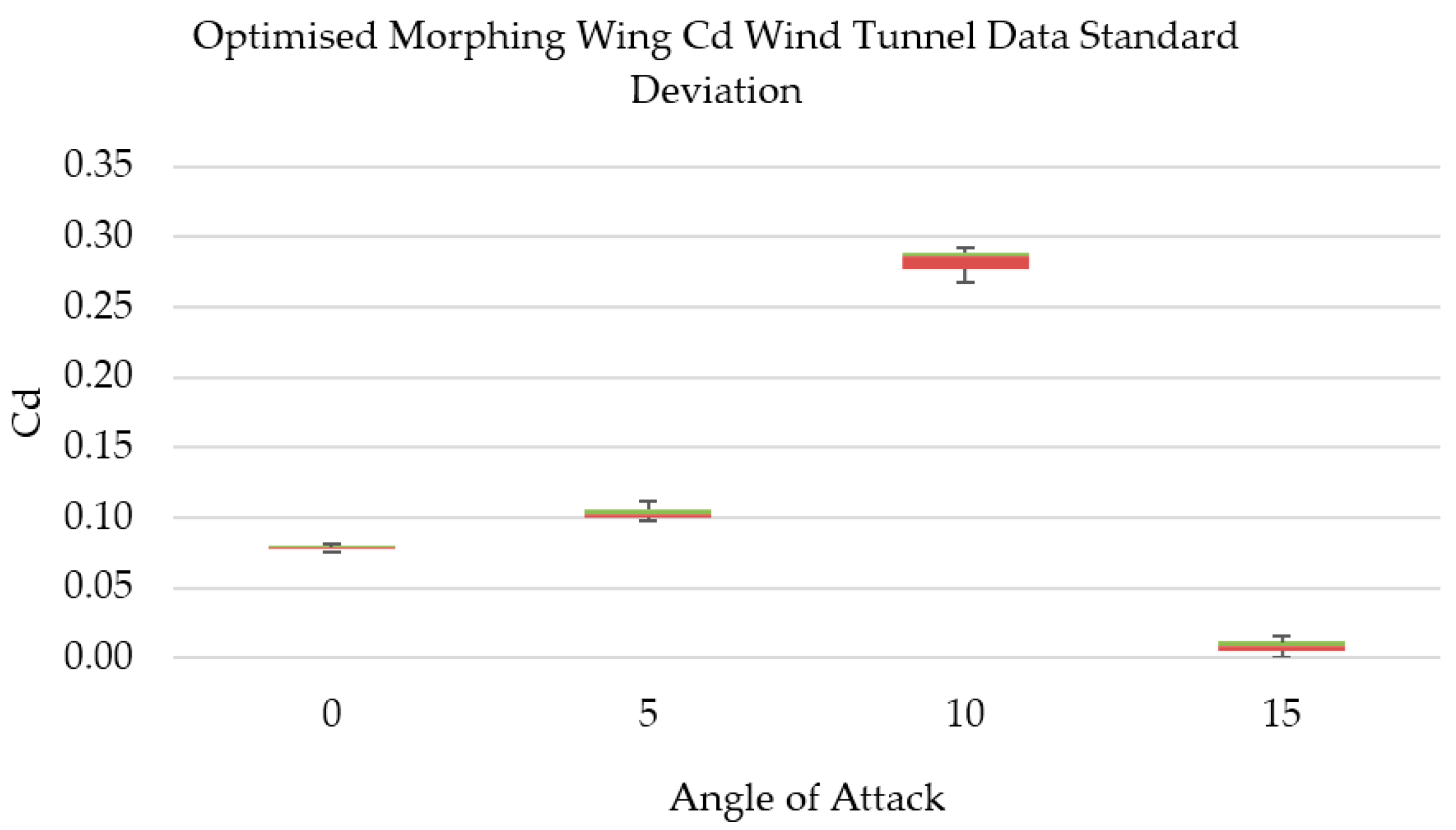
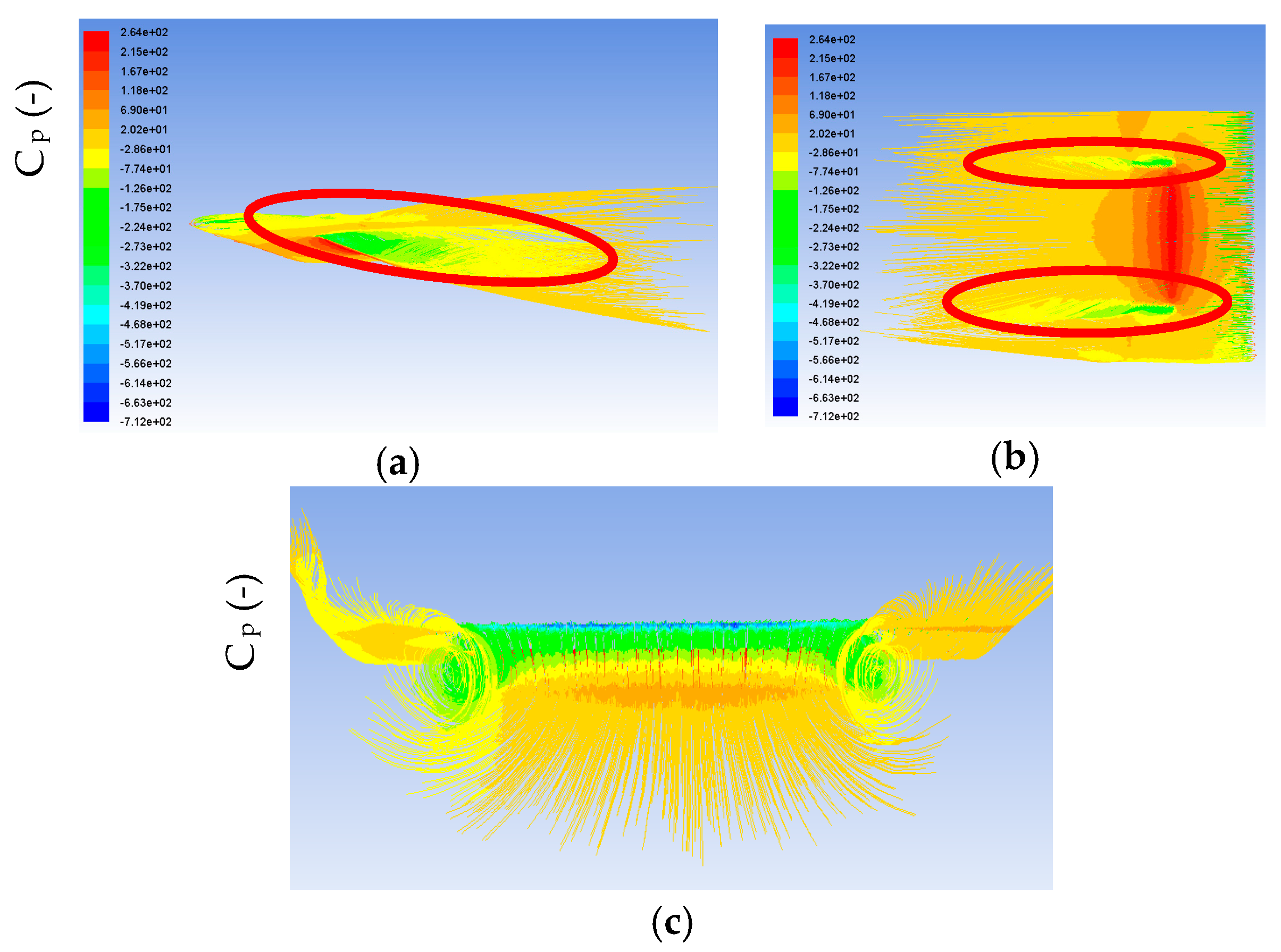
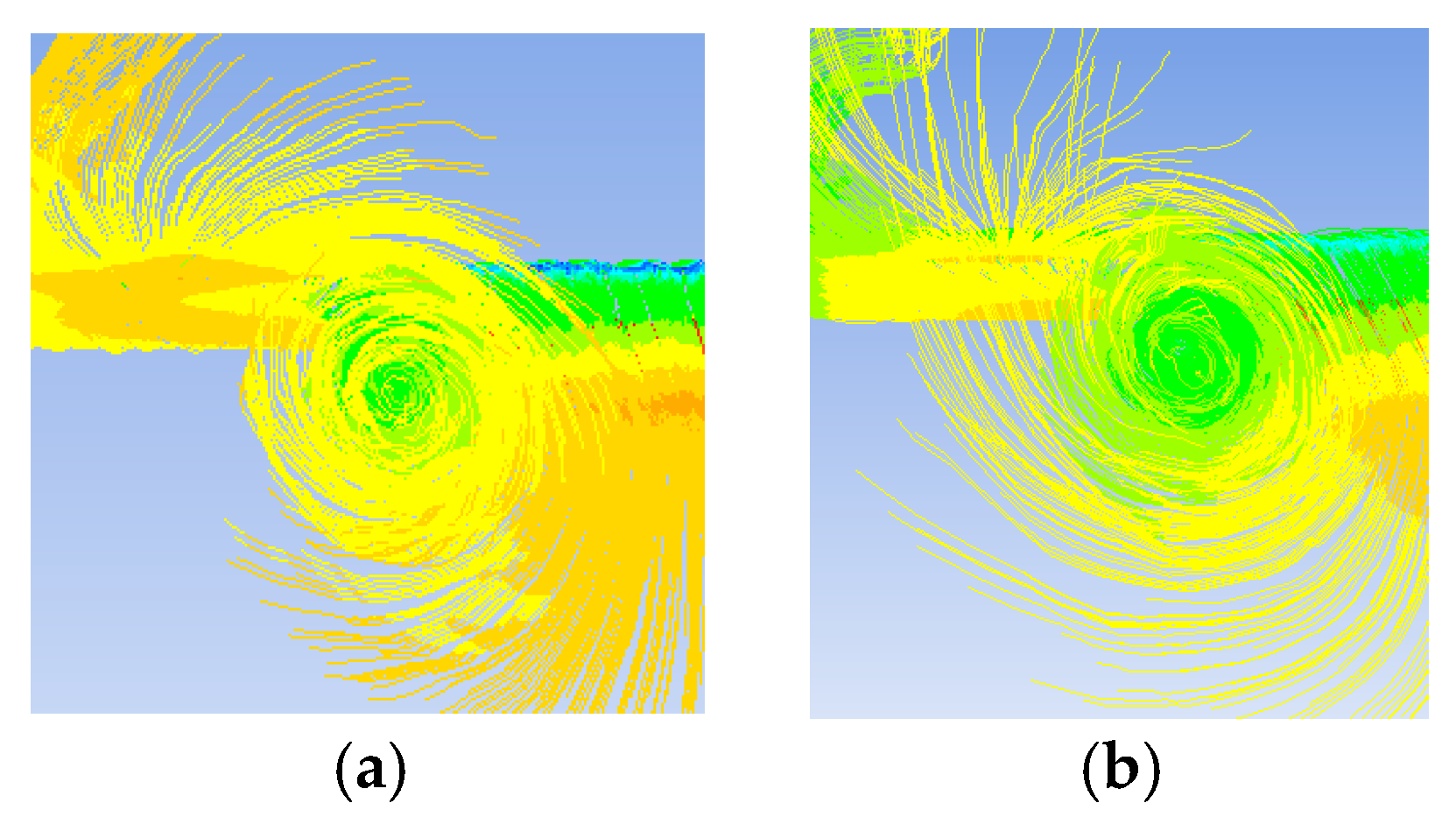
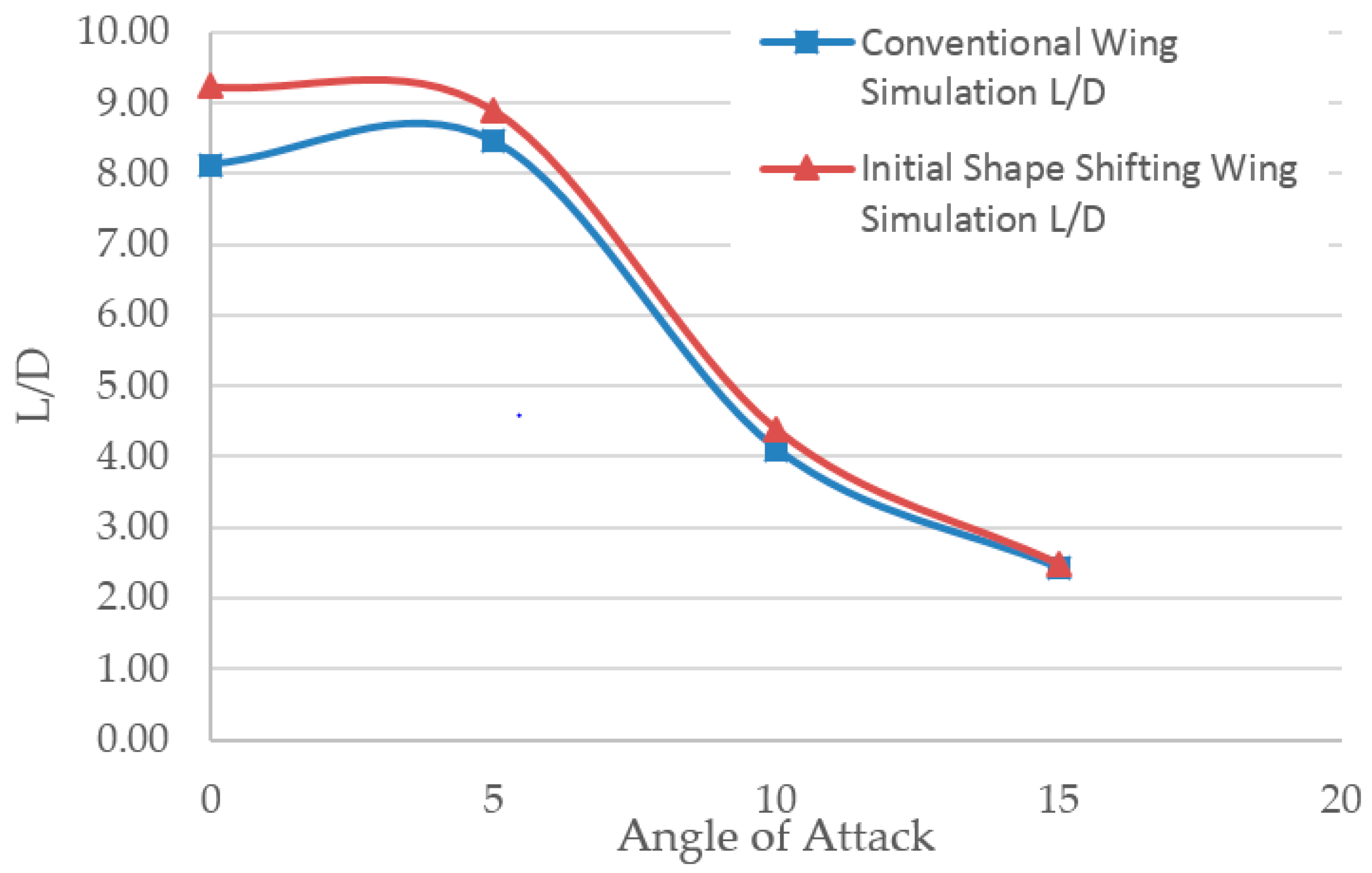
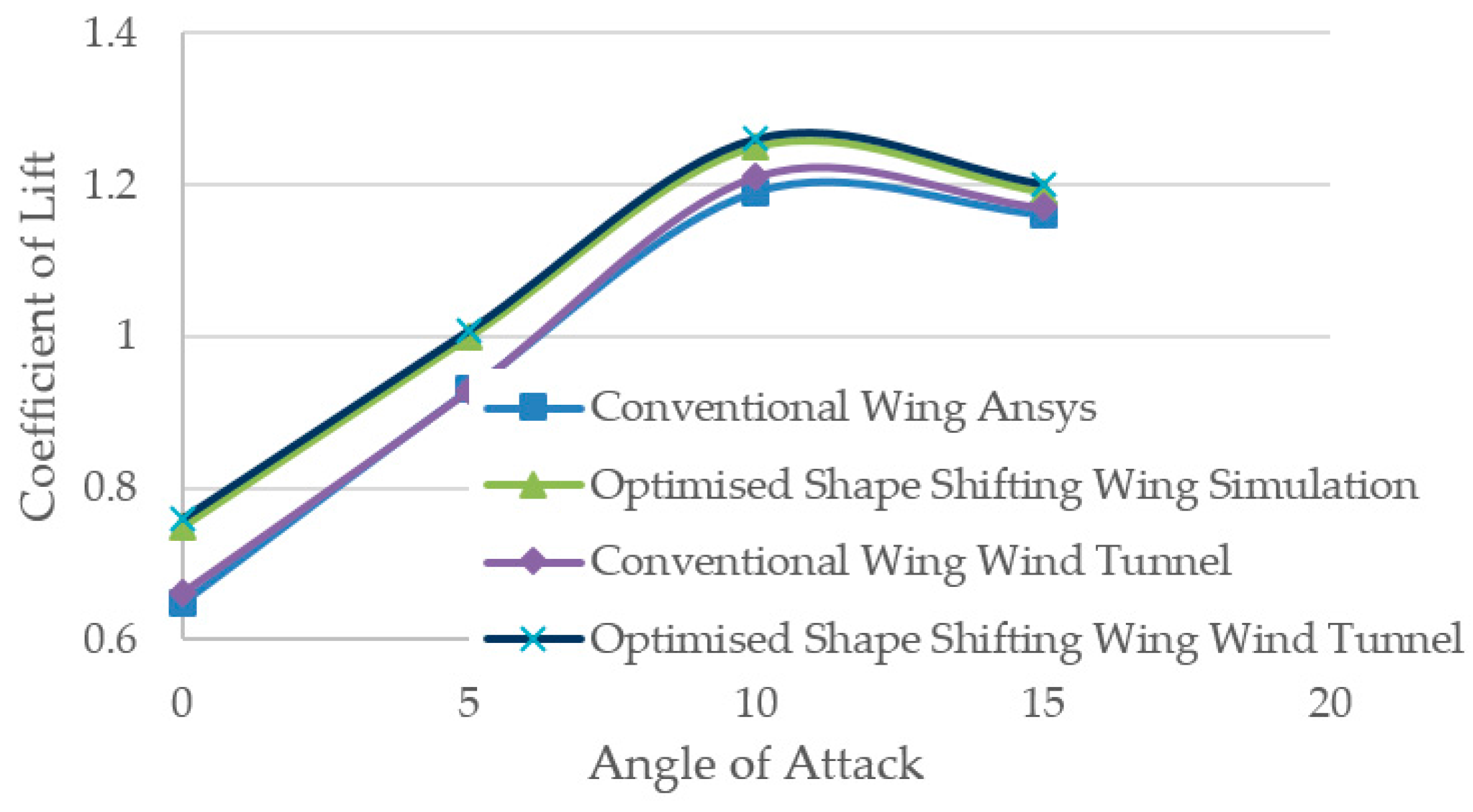
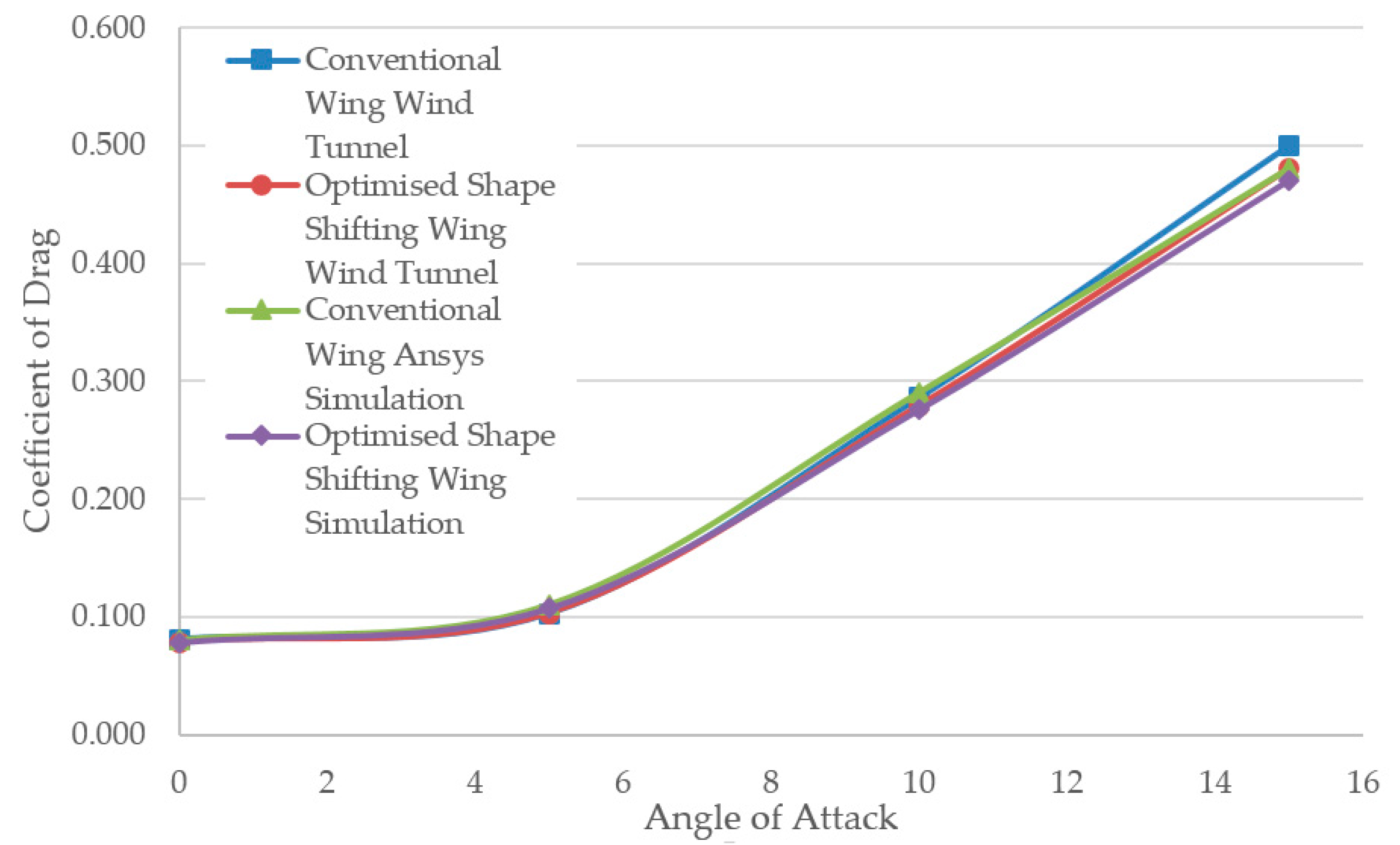
5.5. Wind Tunnel Testing and Simulation Comparison (Validation)
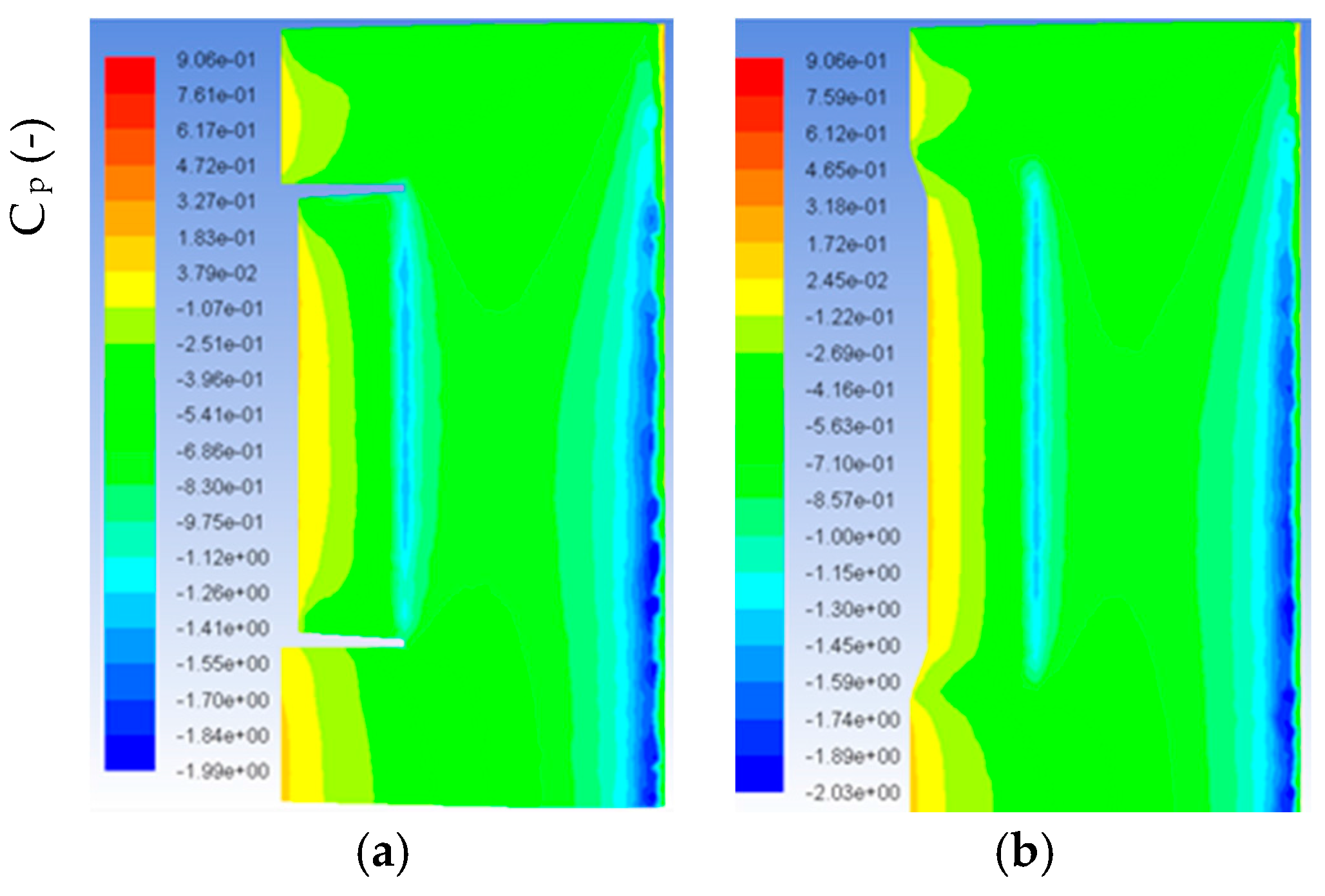
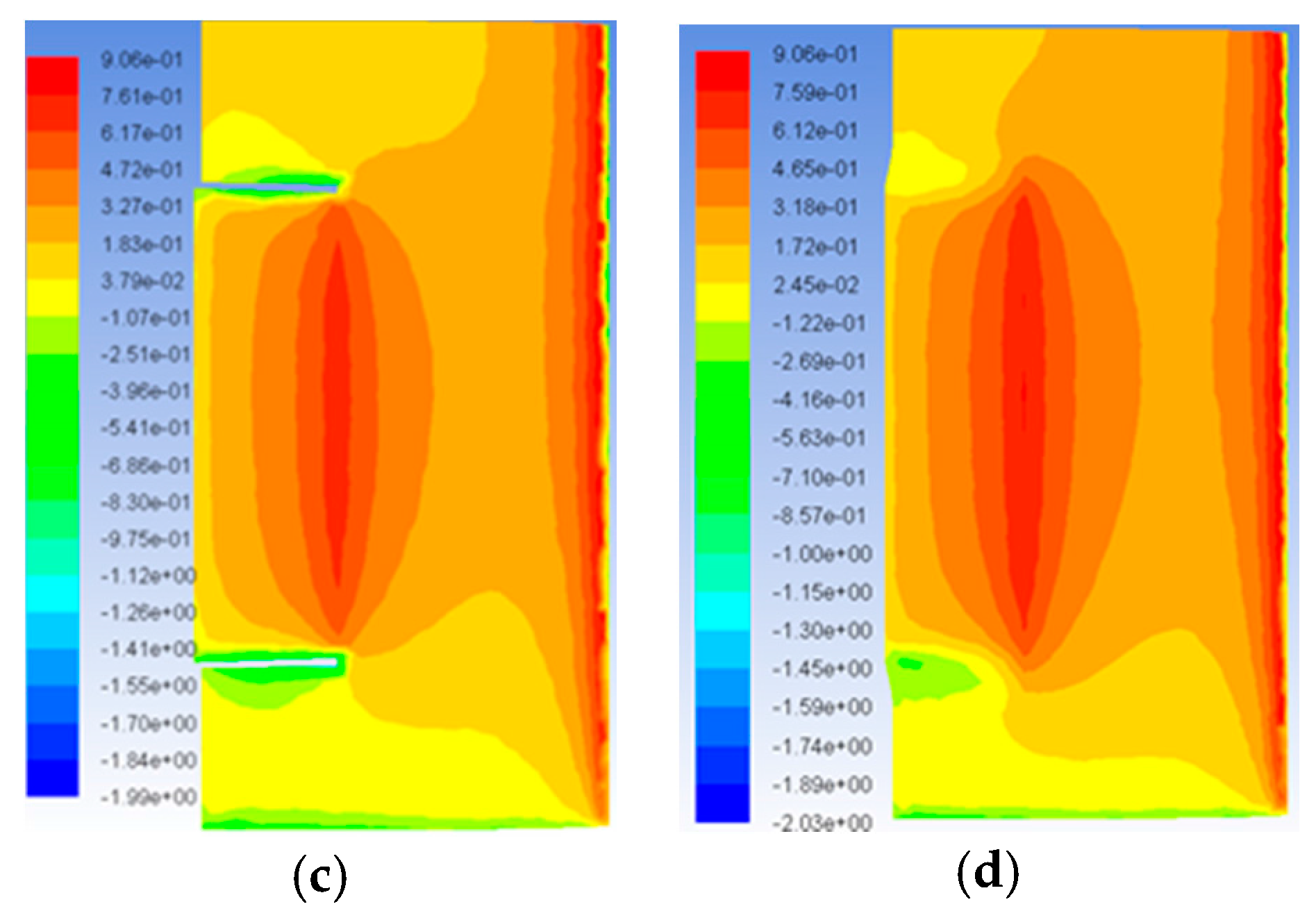
5.6. Ansys and Wind Tunnel Results Discussion
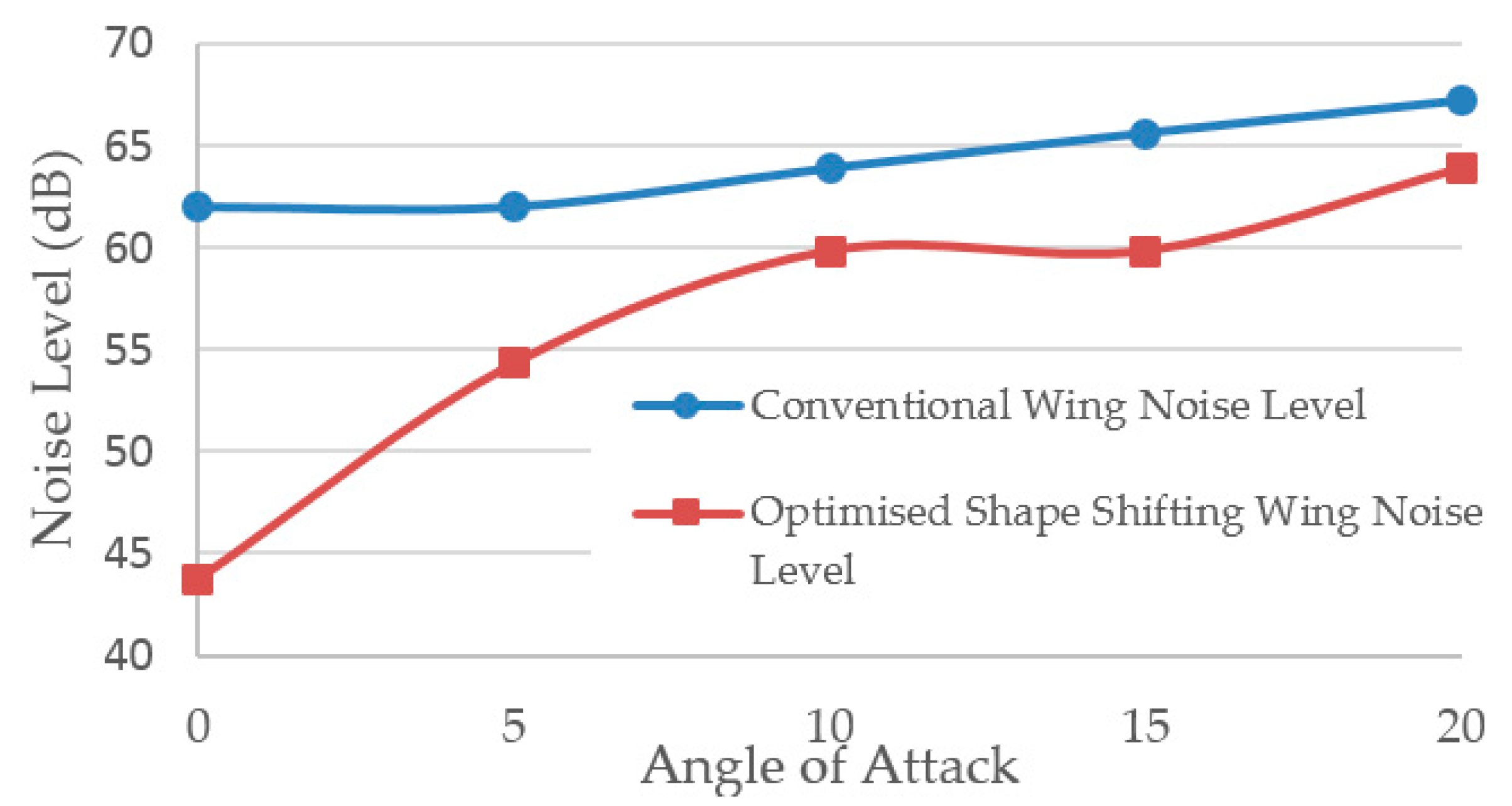
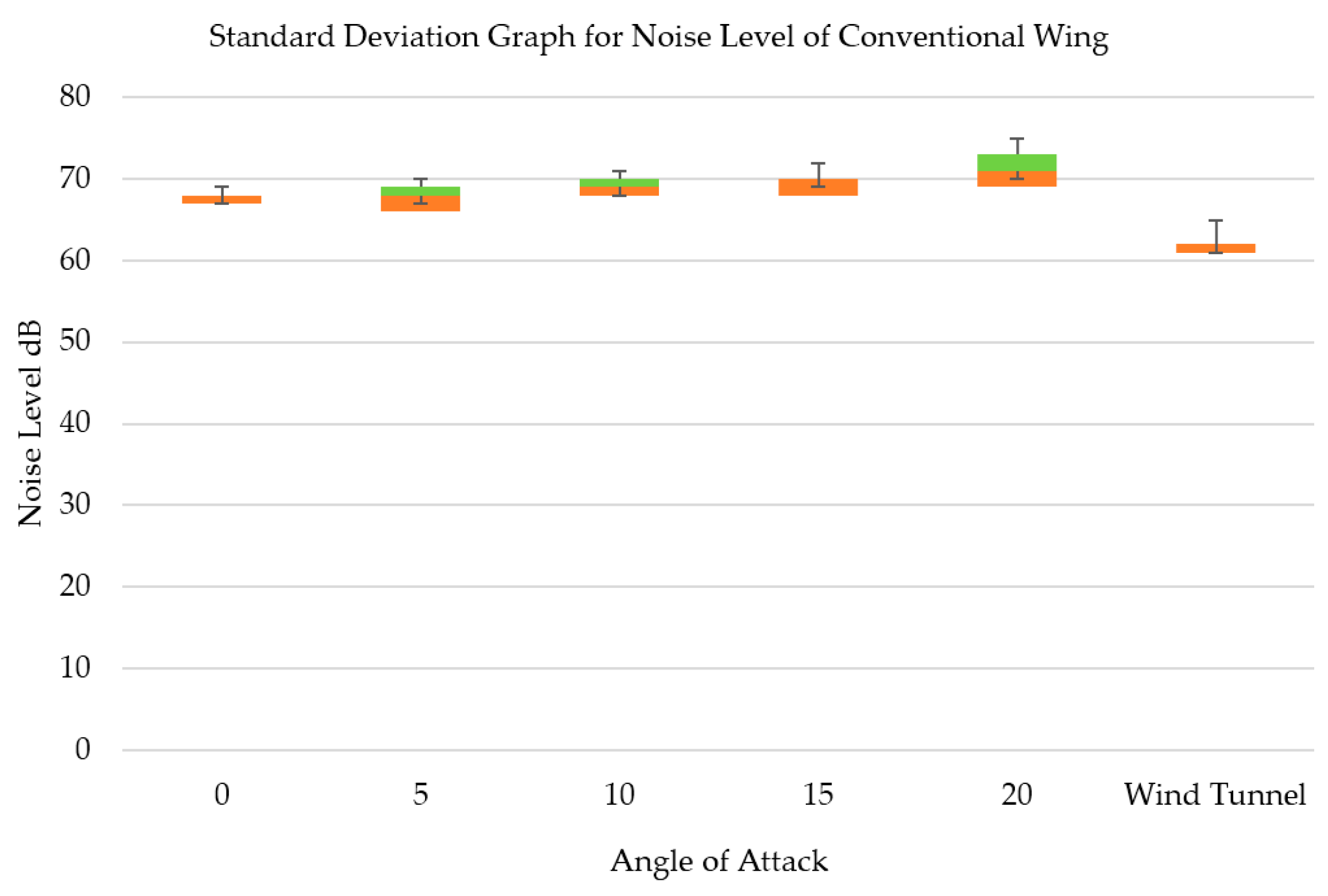
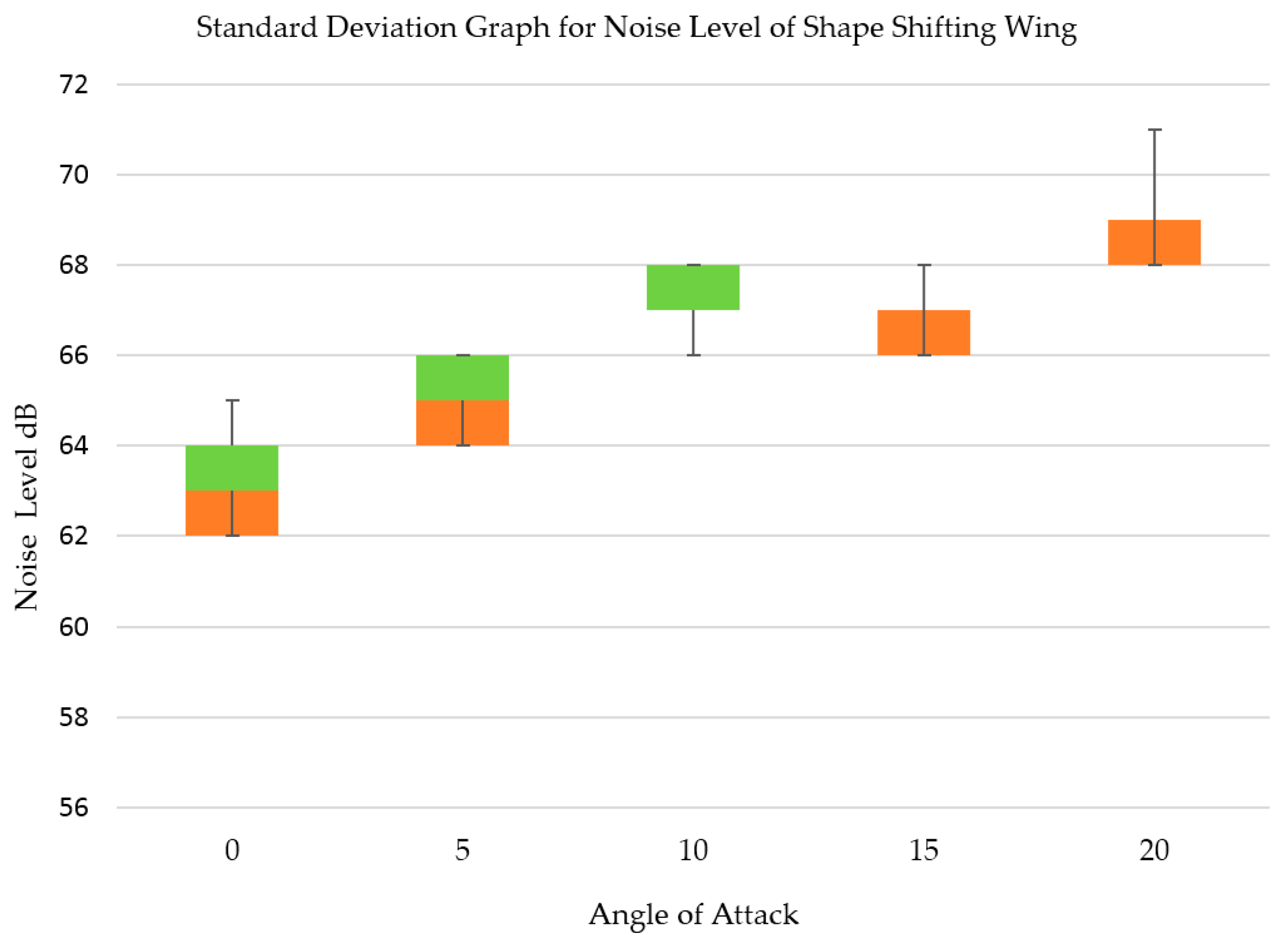
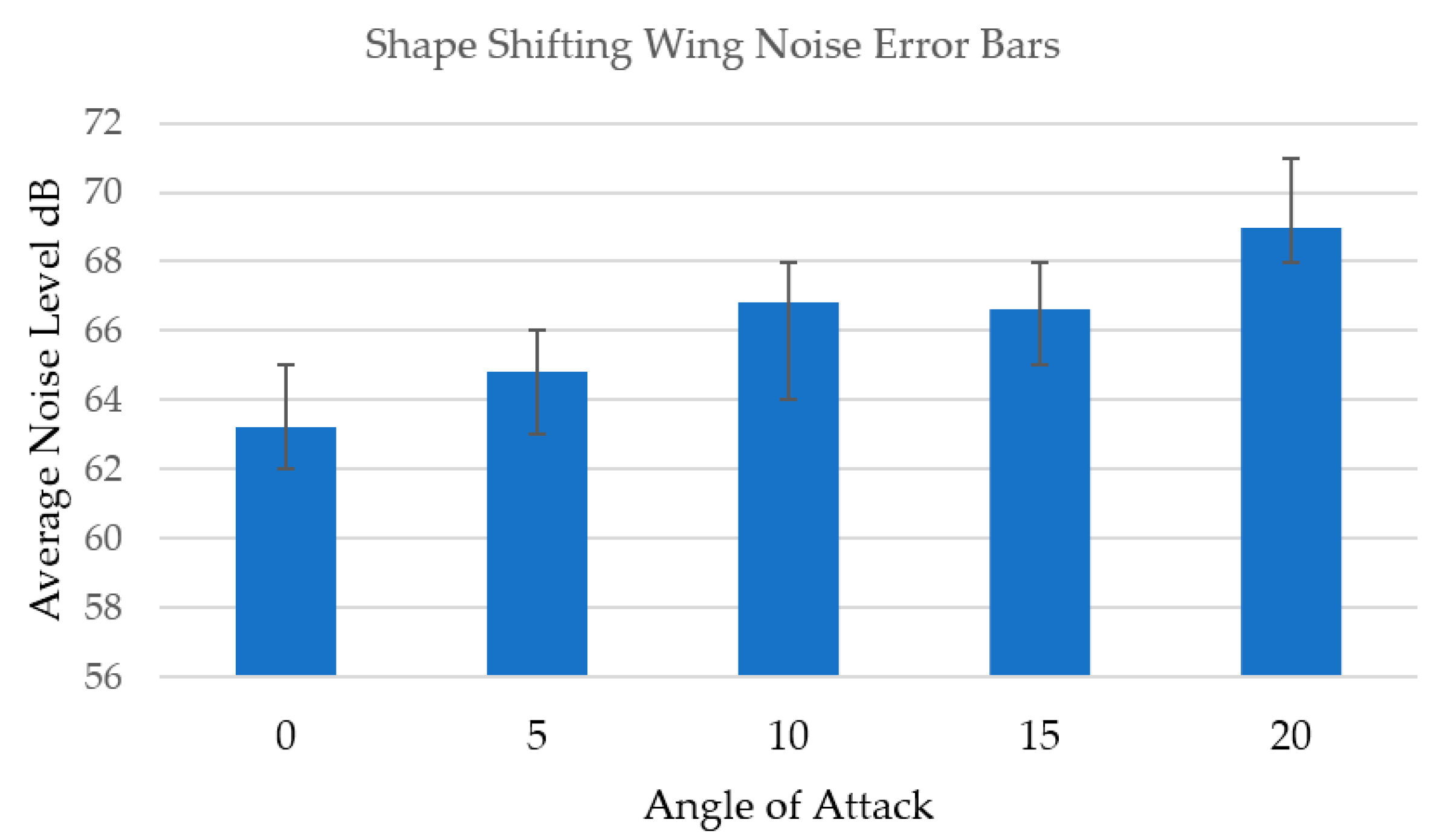
6. Noise
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| P1 | sound pressure, Pa |
| P0 | reference pressure (threshold of hearing 2 × 10−5 Pa), Pa |
| Cp | Pressure Coefficient |
| dB | Noise Level, decibels |
| AOA | Angle of Attack |
| NACA | National Advisory Committee on Aeronautics |
| DARPA | The Defense Advanced Research Projects Agency |
| UAV | Unmanned Air Vehicle |
| SMA | Shape Memory Alloy |
| PZT | Piezoelectric Transducer |
| CFD | Computational Fluid Dynamics |
| RNG | Re-Normalization Group |
Appendix A

References
- Group of Personalities Report; Advisory Council for Aeronautics Research in Europe; Office for Official Publ. of the European Communities. European Aeronautics: A Vision for 2020. In Proceedings of the Society’s Needs and Winning Global Leadership, Luxembourg, 14 January 2001. [Google Scholar]
- Weisshaar, T.A. Morphing Aircraft Systems: Historical Perspectives and Future Challenges. J. Aircr. 2013, 50, 337–353. [Google Scholar] [CrossRef]
- Vasista, S.; Tong, L.; Wong, K.C. Realization of Morphing Wings: A Multidisciplinary Challenge. J. Aircr. 2012, 49, 11–28. [Google Scholar] [CrossRef]
- Rodriguez, A.R. Morphing Aircraft Technology Survey. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2007. [Google Scholar]
- Moorhouse, D.; Sanders, B.; von Spakovsky, M.; Butt, J. Benefits and Design Challenges of Adaptive Structures for Morphing Aircraft. Aeronaut. J. 2006, 110, 157–162. [Google Scholar] [CrossRef]
- Ivanco, T.G.; Scott, R.C.; Love, M.H.; Zink, S.; Weisshaar, T.A. Validation of the Lockheed Martin Morphing Concept with Wind Tunnel testing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Flanagan, J.S.; Strutzenberg, R.C.; Myers, R.B.; Rodrian, J.E. Development and Flight Testing of a Morphing Aircraft, the NextGen MFX-1. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar]
- Samuel, J.B.; Pines, D. Design and Testing of a Pneumatic Telescopic Wing for Unmanned Aerial Vehicles. J. Aircr. 2007, 44, 1088–1099. [Google Scholar] [CrossRef]
- Yokozeki, T.; Sugiura, A.; Hirano, Y. Development of Variable Camber Morphing Airfoil Using Corrugated Structure. J. Aircr. 2014, 51, 1023–1029. [Google Scholar] [CrossRef]
- Beguin, B.; Breitsamter, C.; Adams, N. Aerodynamic Investigations of a Morphing Membrane Wing. AIAA J. 2012, 50, 2588–2599. [Google Scholar] [CrossRef]
- Beguin, B. Development and Analysis of an Elasto-Flexible Morphing Wing. Ph.D. Thesis, Chair of Aerodynamics and Fluid Mechanics, Technische Universität München, Munich, Germany, 2014. [Google Scholar]
- Stanford, B.; Viieru, D.; Albertani, R.; Shyy, W.; Ifju, P. A Numerical and Experimental Investigation of Flexible Micro Air Vehicle Wing Deformation. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Hu, H.; Tamai, M.; Murphy, J.T. Flexible-Membrane Airfoils at Low Reynolds Numbers. J. Aircr. 2008, 45, 1767–1778. [Google Scholar] [CrossRef]
- Ifju, P.; Jenkins, D.; Ettinger, S.; Lian, Y.; Shyy, W.; Waszak, R.M. Flexible-Wing-Based Micro Air Vehicles. In Proceedings of the Confederation of European Aerospace Societies Aerodynamics Conference, Cambridge, UK, 10–12 June 2002. [Google Scholar]
- Kunz, R. Apparatus for Closing an Air Gap between a Flap and an Aircraft. U.S. Patent No. US4471925A, 18 September 1984. [Google Scholar]
- Diller, J.B.; Miller, N.F. Elastomeric Transition for Aircraft Control Surface. U.S. Patent No. US6145791A, 14 November 2000. [Google Scholar]
- Caton, J.H.; Hobey, M.J.; Groeneveld, J.D.; Jacobs, J.H.; Wille, R.H.; Brase, L.O., Jr. Control Surface for an Aircraft. U.S. Patent No. US6349903B2, 26 February 2002. [Google Scholar]
- Etling, K.A. Morphing Control Surface Transition. U.S. Patent No. US8342447B2, 1 January 2013. [Google Scholar]
- Khorrami, M.R.; Lockard, D.P.; Moore, J.B.; Su, J.; Turner, T.L.; Lin, J.C.; Taminger, K.M.; Kahng, S.K.; Verden, S.A. Elastically Deformable Side-Edge Link for Trailing-Edge Flap Aeroacoustic Noise Reduction. U.S. Patent No. US8695925B2, 15 April 2014. [Google Scholar]
- Khorrami, M.R.; Humphreys, W.M.; Lockard, D.P.; Ravetta, P.A. Aeroacoustic evaluation of flap and landing gear noise reduction concepts. In Proceedings of the 20th AIAA Aviation and Aeronautics Forum and Exposition, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Woods, B.K.S.; Friswell, M.I. Preliminary investigation of a fishbone active cam-ber concept. In Proceedings of the ASME 2012 Conference on Smart Mate-Rials, Adaptive Structures and Intelligent Systems, Stone Mountain, GA, USA, 19–21 September 2012; pp. 555–563. [Google Scholar]
- Woods, B.K.S.; Bilgen, O.; Friswell, M.I. Wind tunnel testing of the Fish Bone Active Camber morphing concept. J. Intell. Mater. Syst. Struct. 2014, 25, 722–785. [Google Scholar] [CrossRef]
- Woods, B.K.S.; Parsons, L.; Coles, A.B.; Finchamb, J.H.S.; Friswell, M.I. Morphing elastically lofted transition for active camber control surfaces. Aerosp. Sci. Technol. 2015, 55, 439–448. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswel, M.I.; Inman, D.J. A Review of Aircraft Morphing. J. Intell. Mater. Syst. Struc. 2011, 22, 823–876. [Google Scholar] [CrossRef]
- Norris, G. FlexSys and Aviation Partners Display Morphing Wing. 2016. Available online: http://aviationweek.com/MorphingWing (accessed on 28 July 2017).
- Kota, S.; Osborn, R.; Ervin, G.; Maric, D.; Flick, P.; Paul, D. Mission Adaptive Compliant Wing—Design, Fabrication and Flight Test. NATO OTAN 2006, 1–18. [Google Scholar]
- Shili, L.; Wenjie, G.; Shujun, L. Optimal Design of Compliant Trailing Edge for Shape Changing. Chin. J. Aeronaut. 2008, 21, 187–192. [Google Scholar] [CrossRef]
- Schorsch, O.; Lühring, A.; Nagel, C.; Pecora, R.; Dimino, I. Polymer Based Morphing Skin for Adaptive Wings. In Proceedings of the 7th ECCOMAS Thematic Conference on Smart Structures and Materials, Ponta Delgada, Portugal, 3–6 June 2015; pp. 2–15. [Google Scholar]
- Belluco, P. EAP—ElectroActive Polymers. 2007. Available online: http://home.deib.polimi.it/gini/introEAP.pdf (accessed on 28 October 2016).
- Abbott, I.H.; Doenhoff, A.E. Thoery of Wing Sections: Including a Summary of Airfoil Data; Dover Publictaions: Mineola, NY, USA, 1959. [Google Scholar]

















| Concept Feature | Dielectric Smart Polymer | Elastomer Skin |
|---|---|---|
| Cost | 2 | 5 |
| Maintainability | 5 | 5 |
| Performance | 5 | 3 |
| Installation Ease | 2 | 5 |
| Ease of assembly | 2 | 3 |
| Weight | 5 | 4 |
| Environment Resistance | 5 | 3 |
| Safety | 3 | 3 |
| TOTAL | 29 | 31 |
| Angle of Attack (AOA) | Conventional Wing Noise Level | Shape Shifting Wing Noise Level | Wind Tunnel Noise Level (All AOA) |
|---|---|---|---|
| 0 | 68 dB | 63 dB | 62 dB |
| 5 | 68 dB | 65 dB | |
| 10 | 69 dB | 67 dB | |
| 15 | 70 dB | 67 dB | |
| 20 | 71 dB | 69 dB |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ninian, D.; Dakka, S.M. Design, Development and Testing of Shape Shifting Wing Model. Aerospace 2017, 4, 52. https://doi.org/10.3390/aerospace4040052
Ninian D, Dakka SM. Design, Development and Testing of Shape Shifting Wing Model. Aerospace. 2017; 4(4):52. https://doi.org/10.3390/aerospace4040052
Chicago/Turabian StyleNinian, Dean, and Sam M. Dakka. 2017. "Design, Development and Testing of Shape Shifting Wing Model" Aerospace 4, no. 4: 52. https://doi.org/10.3390/aerospace4040052
APA StyleNinian, D., & Dakka, S. M. (2017). Design, Development and Testing of Shape Shifting Wing Model. Aerospace, 4(4), 52. https://doi.org/10.3390/aerospace4040052