Optimization of Heat Exchangers for Intercooled Recuperated Aero Engines
Abstract
:1. Introduction
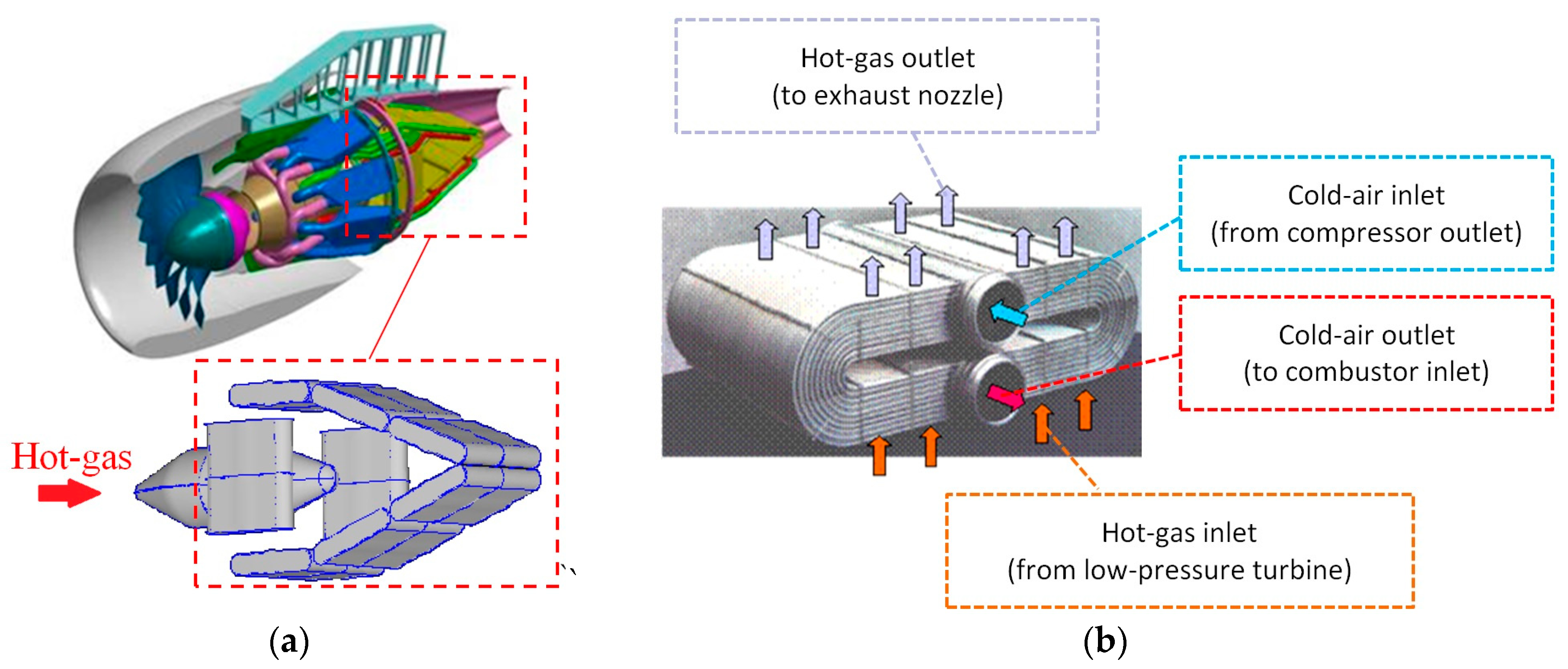
2. Optimization of Heat Exchanger Concepts
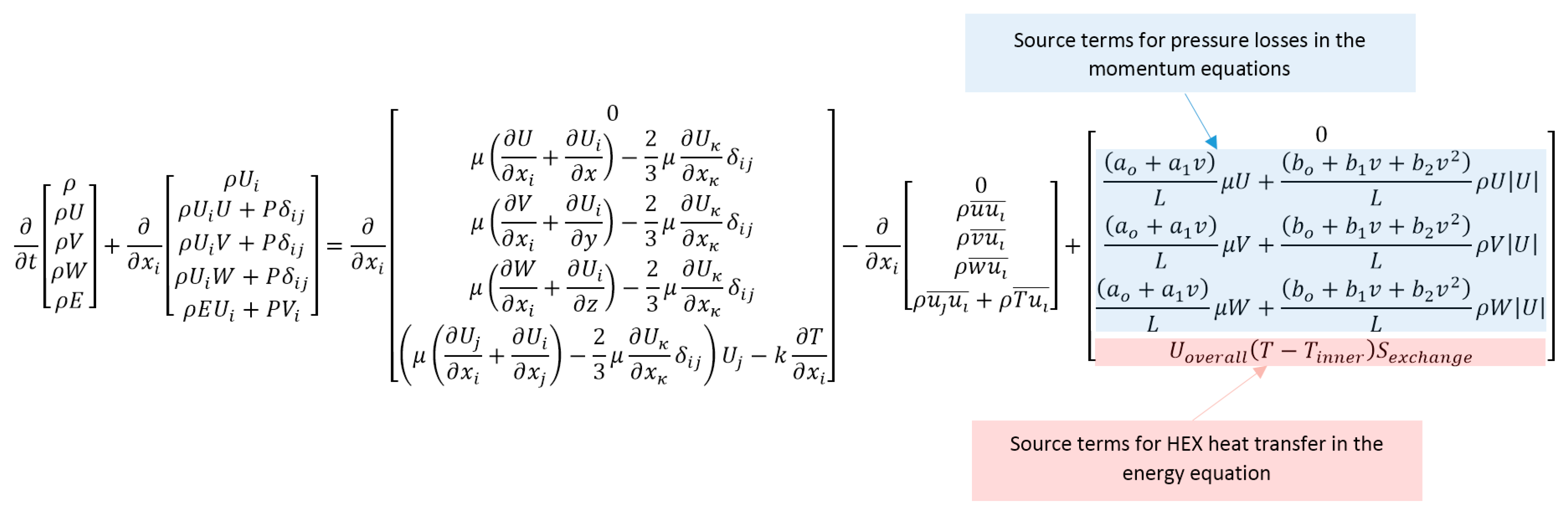
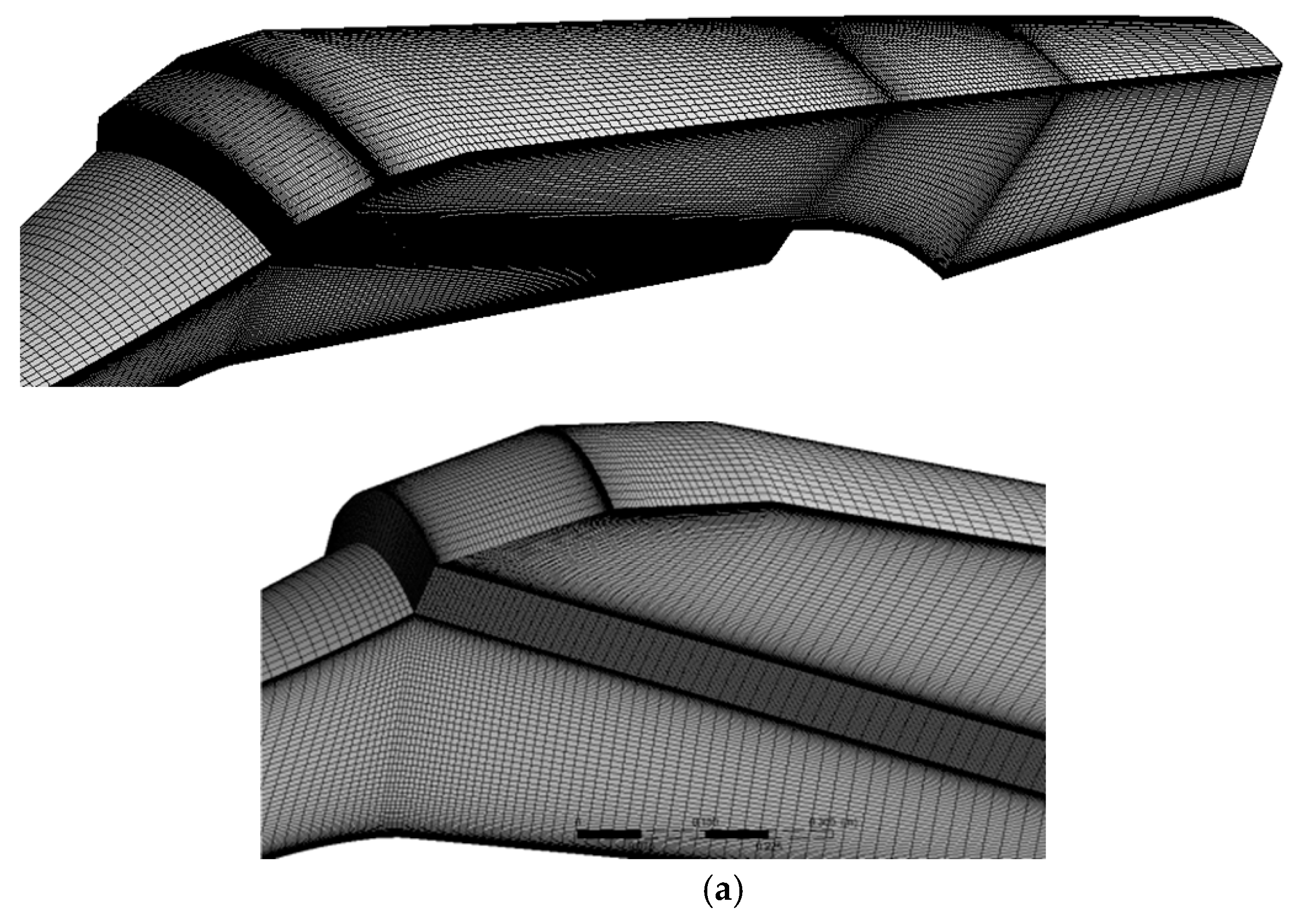
2.1. The Heat Exchanger–Recuperator Porosity Model Approach
2.2. Hot Side Pressure Loss Model
2.3. Cold Side Pressure Loss Model
2.4. Heat Transfer Model
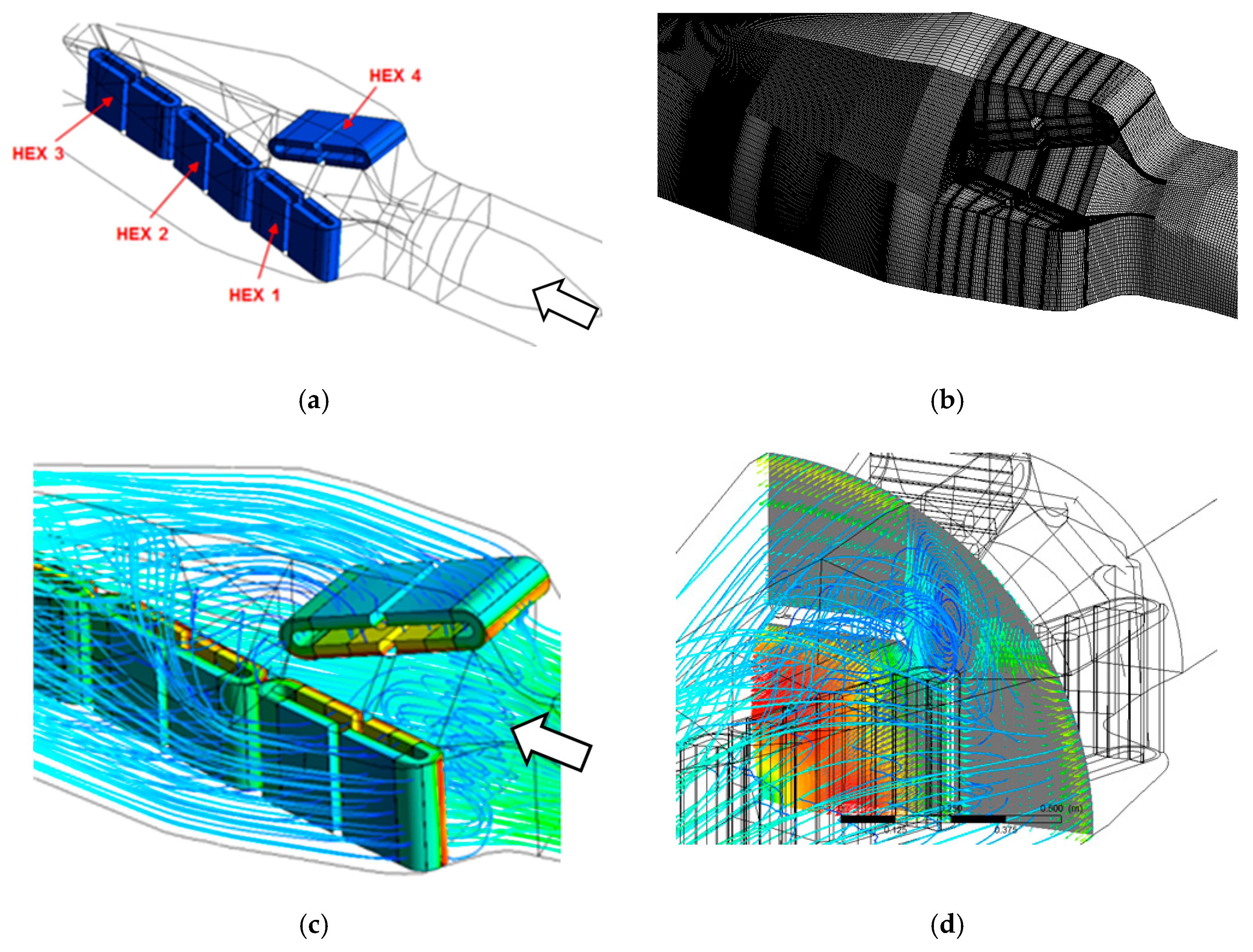
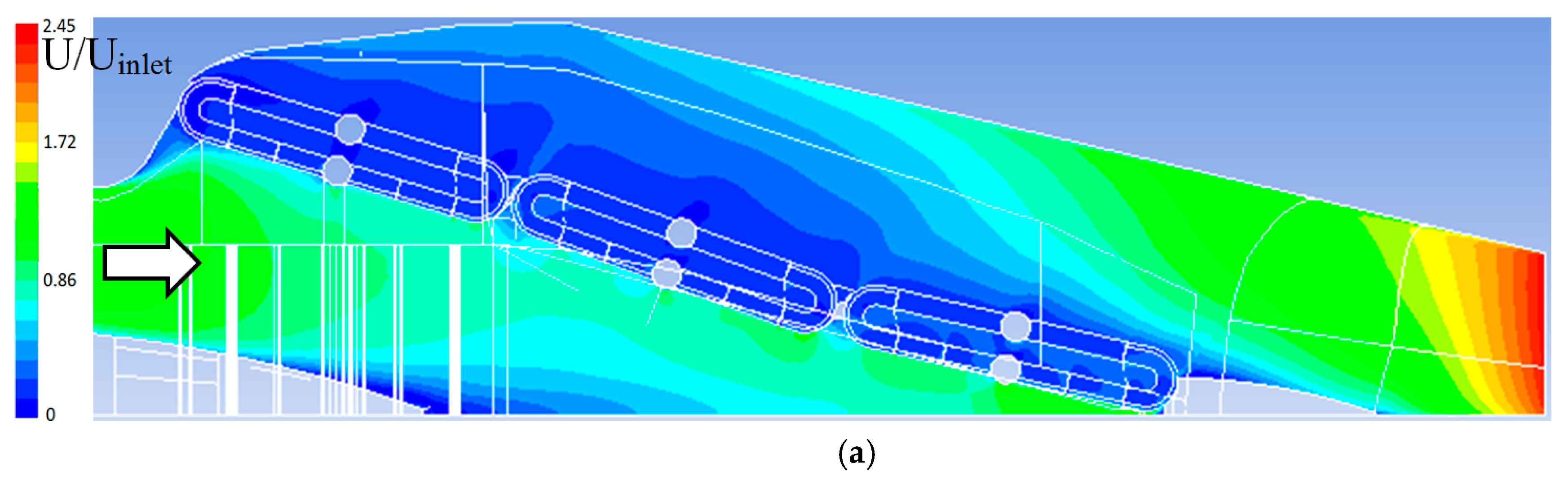
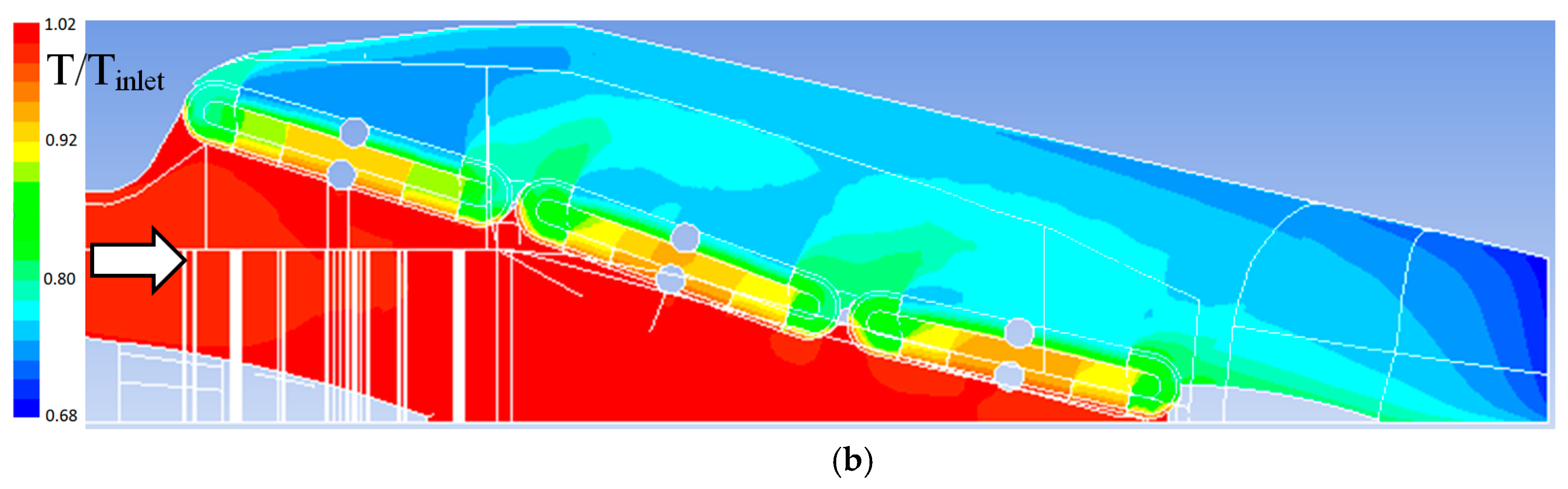
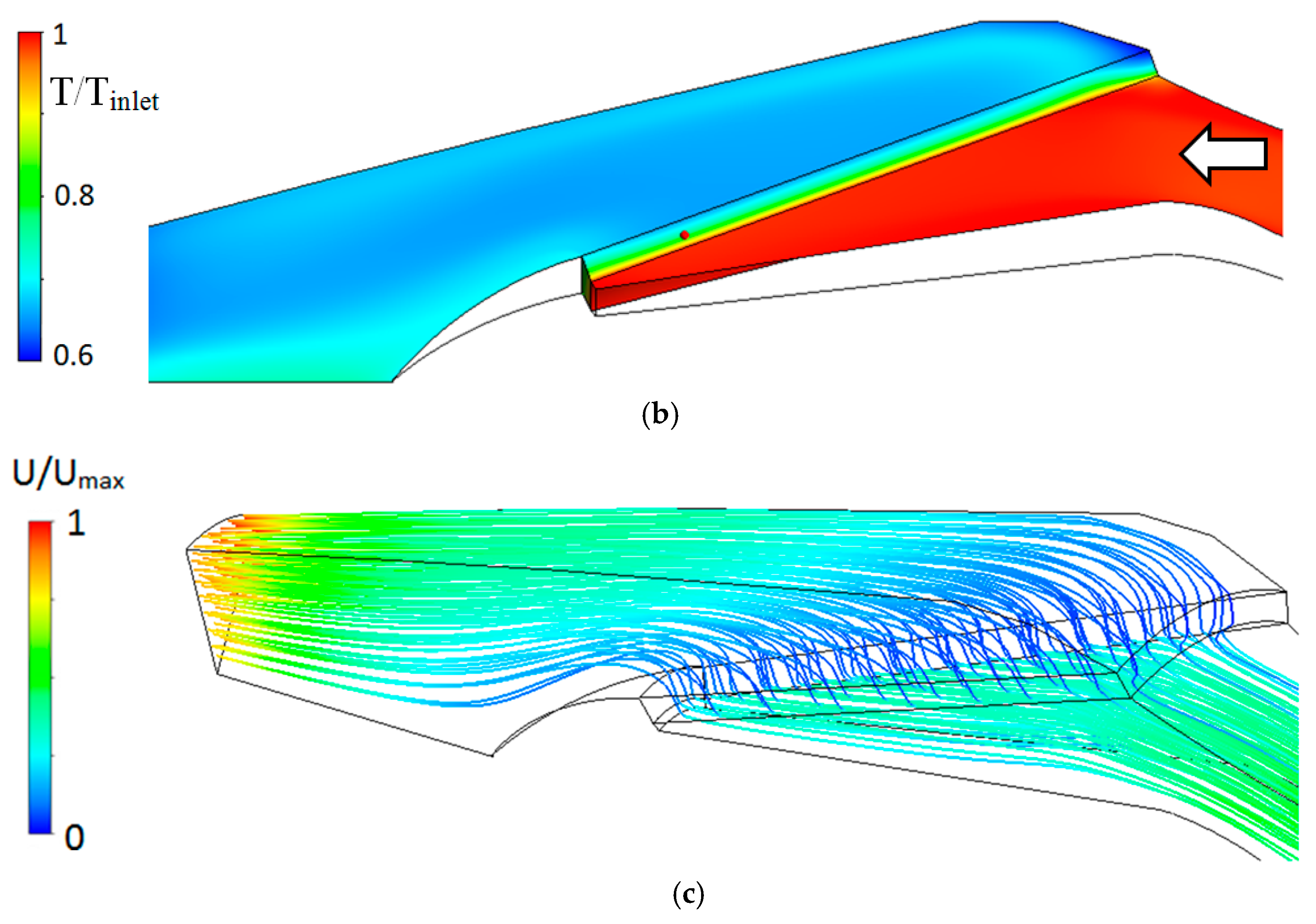
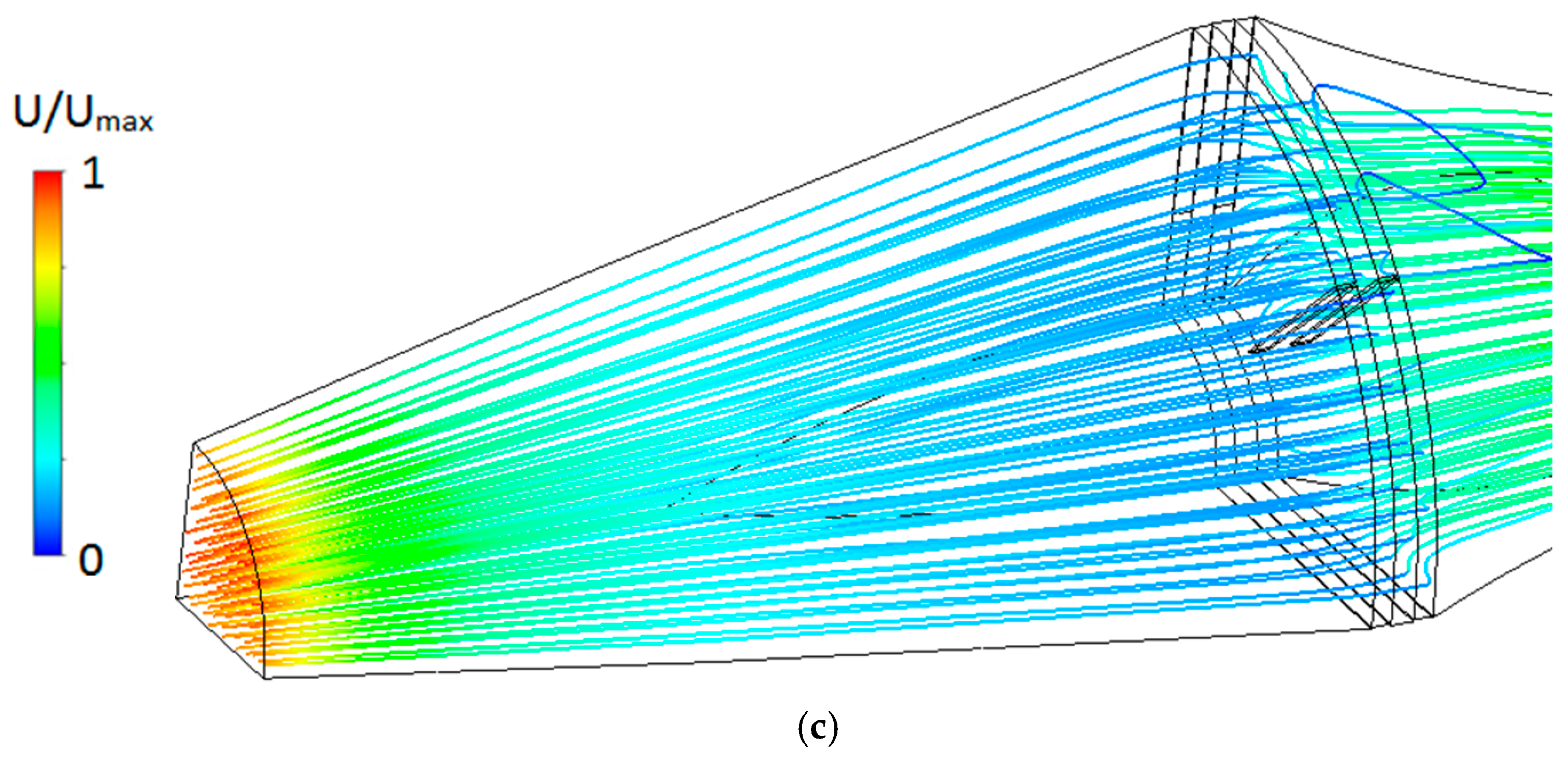
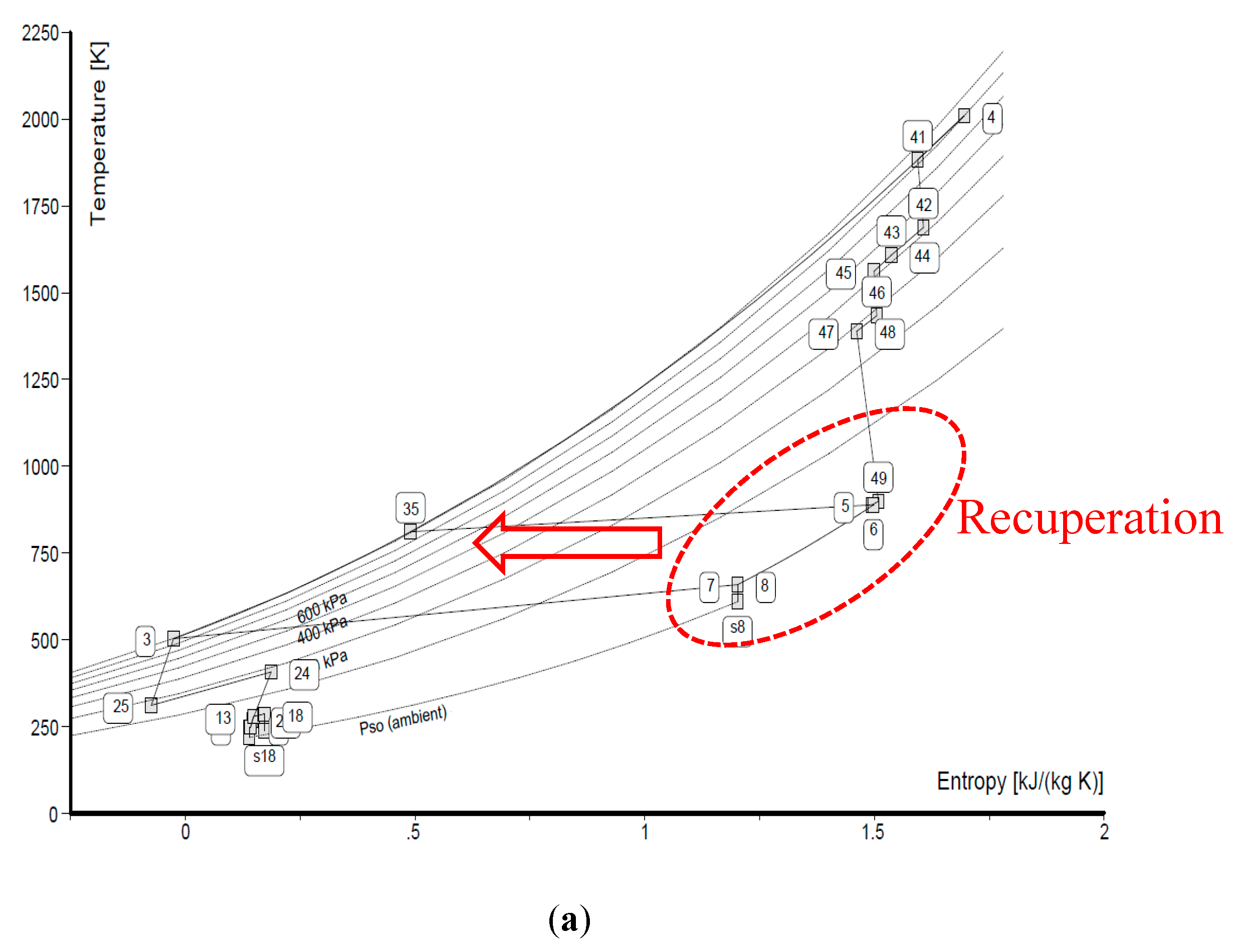
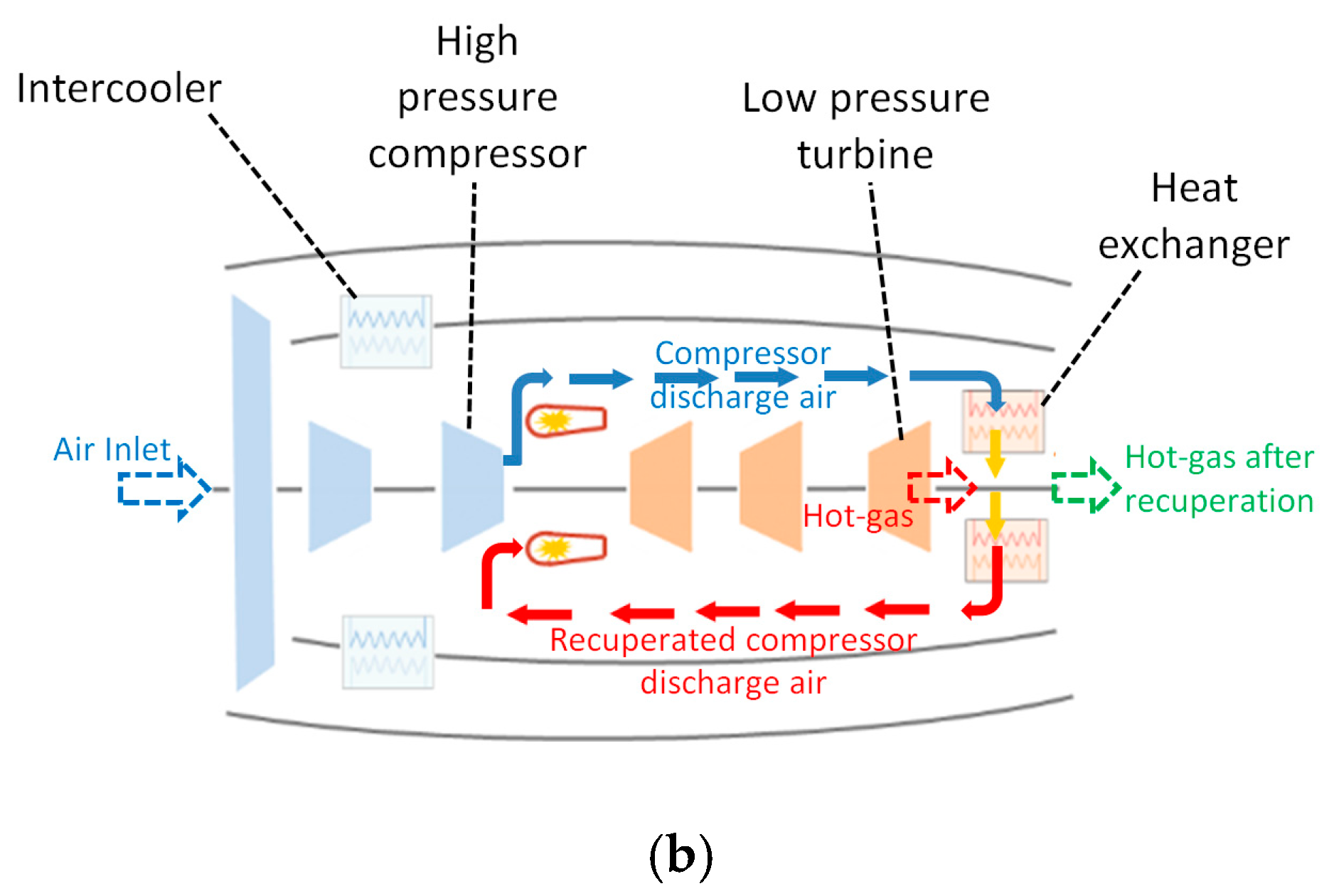
3. Results of the Recuperation Concepts
4. Discussion
5. Conclusions
- The optimization procedure of the reference MTU heat exhcanger was based on the development of a customizable numerical tool which can efficiently model the heat exchanger performance regarding heat transfer enhancement and pressure losses minimization, specially designed for aero engine applications.
- The described numerical tool is based on an advanced porosity model approach where the heat exchanger core is modeled as a porous media of predifined heat transfer and pressure losses behavior. Additionally, the derived porosity model is able to provide accurate results to a wide range of conditions (from laboratory to flight conditions) and to incorporate the major critical recuperator design decisions in the CFD computations, through the coupling of the flow momentum and energy transport equations.
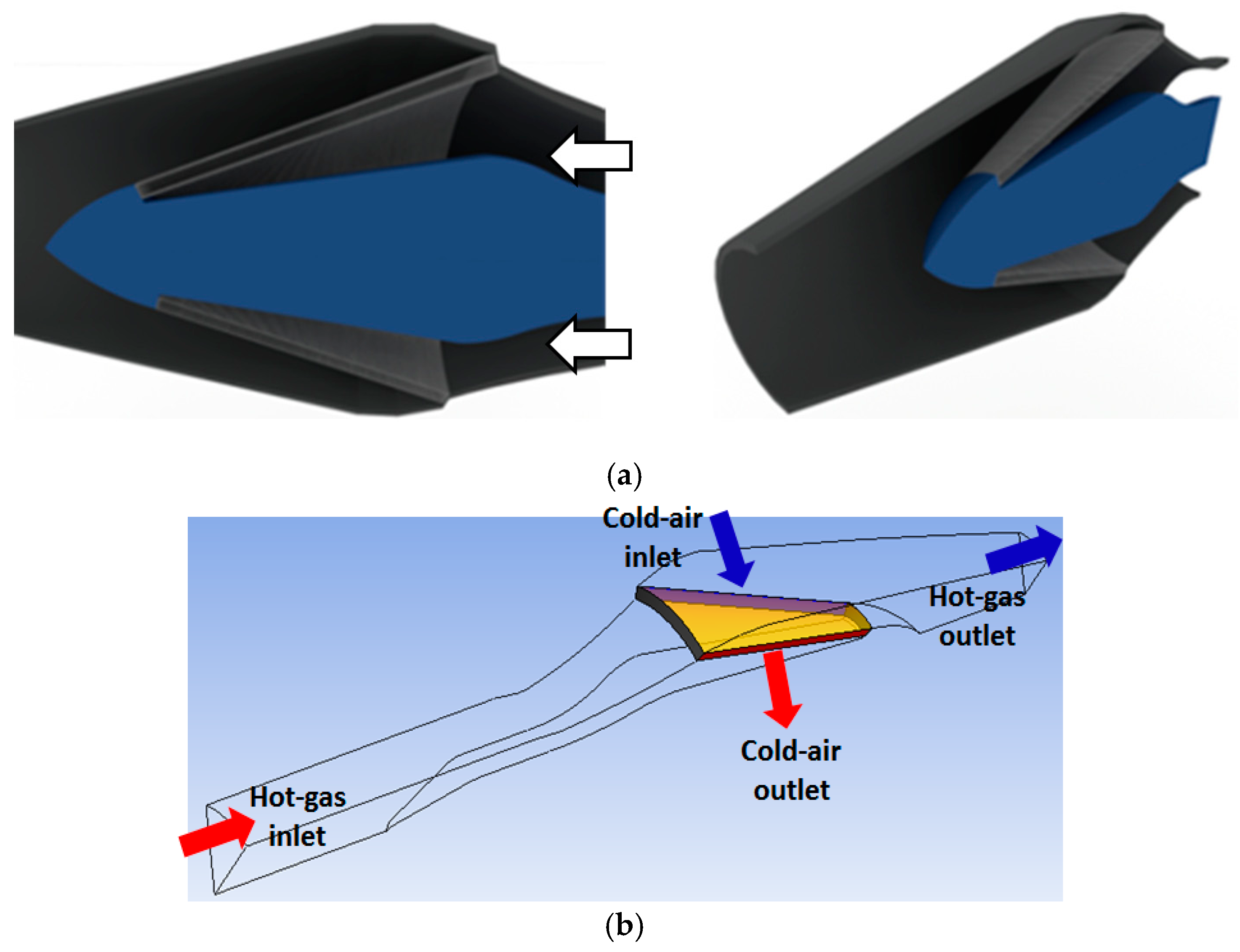
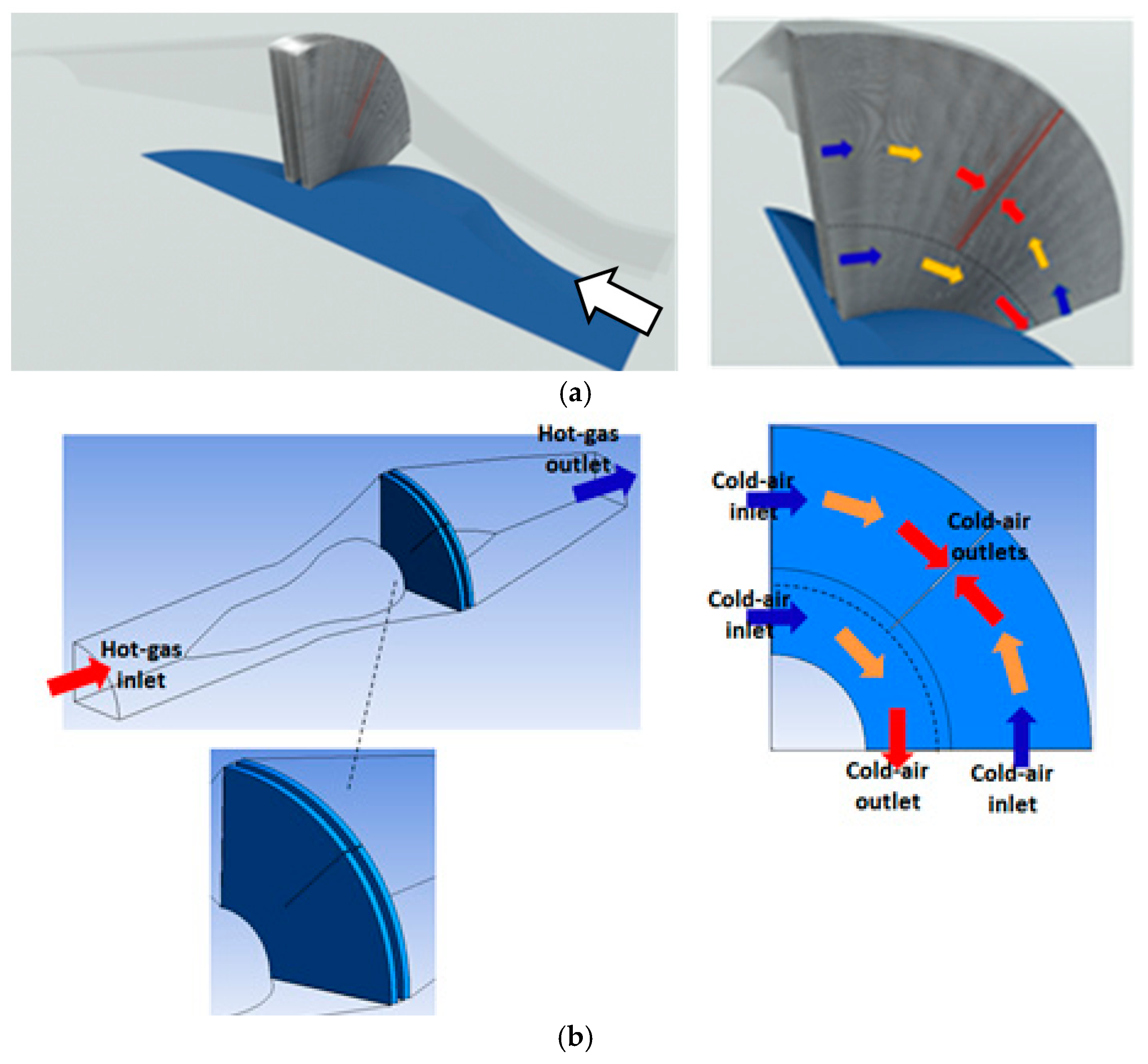
- The optimization efforts resulted in two completely new innovative recuperator design concepts, named as CORN (COnical Recuperative Nozzle) and STARTREC (STraight AnnulaR Thermal RECuperator). These concepts were following an annular tubes recuperator axisymetric core design inside the hot-gas exhaust nozzle.
- The proposed recuperators were assesed in a thermodynamic cycle analysis providing improved SFC and significant benefits in terms of pollutants emission and weight reduction in comparison to the original NEWAC recuperator installation of the IRA engine, thus promoting the fullfillment of ACARE goals towards greener and environmentally friendly aero engines.
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Viscous pressure loss coefficients | |
| Inertial pressure loss coefficients | |
| Nusselt number coefficients | |
| Calibration constants for inner pressure losses | |
| Pressure loss per tube length coefficient | |
| Outer and inner heat transfer coefficients, W·m−2·K−1 | |
| Total and static specific enthalpy, J·kg−1 | |
| Length of the heat exchanger, m | |
| Mass flow of the consumed fuel | |
| Nusselt number | |
| Total pressure of the inner flow, Pa | |
| Prandtl number | |
| Reynolds number | |
| Heat exchange surface per unit volume of the heat exchanger, m2·m−3 | |
| Temperature, K | |
| Temperature of the inner flow, K | |
| Kinematic viscosity, m2·s−1 | |
| Cartesian velocity vector, m·s−1 | |
| Overall heat transfer coefficient, W·m−2·K−1 | |
| Reynolds stresses, m2·s−2 | |
| Inner “cold” air velocity, m·s−1 | |
| Cartesian coordinates | |
| Hot-gas pressure losses, Pa | |
| Molecular viscosity, kg·m−1·s−1 | |
| Fluid density, kg·m−3 | |
| CORN | COnical Recuperative Nozzle |
| HEX | Heat EXchanger |
| IRA | Intercooled Recuperative Aero-engine |
| LEMCOTEC | Low Emissions Core-Engine Technologies |
| NEWAC | NEW Aero engine Core concepts |
| SFC | Specific Fuel Consumption |
| STARTREC | STraight AnnulaR Thermal RECuperator |
| ULTIMATE | Ultra Low emission Technology Innovations for Mid-century Aircraft Turbine Engines |
References
- Bock, S.; Horn, W.; Wilfert, G.; Sieber, J. Active Core Technology within the NEWAC Research Program for Cleaner and More Efficient Aero Engines. In Proceedings of the European Air and Space Conference, Berlin, Germany, 10–13 September 2007. CEAS-2007–055.
- Wilfert, G.; Sieber, J.; Rolt, A.; Baker, N.; Touyeras, A.; Colantuoni, S. New environmental friendly aero engine core concepts. In Proceedings of the ISABE 2007 Conference, Beijing, China, 2–7 September 2007.
- Low Emissions Core-Engine Technologies (LEMCOTEC) Project Web Site. Available online: http://www.lemcotec.eu/ (accessed on 29 December 2016).
- Misirlis, D.; Vlahostergios, Z.; Flouros, M.; Salpingidou, C.; Donnerhack, S.; Goulas, A.; Yakinthos, K. Intercooled Recuperated Aero Engine: Development and Optimization of Innovative Heat Exchanger Concepts. In Proceedings of the 2nd ECATS Conference on Making Aviation Environmentally Sustainable, Athens, Greece, 7–9 November 2016.
- Intercooled Recuperative Core Concept. Available online: http://www.newac.eu/uploads/media/Intercooled_Recuperative_Core_Concept.pdf (accessed on 10 February 2017).
- NEWAC Subproject 2 “Intercooled Recuperative Core”. Available online: http://www.newac.eu/86.0.html (accessed on 10 February 2017).
- Broichhausen, K.; Scheugenpflug, H.; Mari, Ch.; Barbot, A. Clean the European Initiative towards Ultra Low Emission Engines. In Proceedings of the ICAS 2000, Harrogate, UK, 27 August–1 September 2000.
- Wilfert, G.; Masse, B. Technology integration in a low emission heat exchanger engine. In Proceedings of the 8th CEAS European Propulsion Forum, Nottingham, UK, 1 March 2001.
- Boggia, S.; Rüd, K. Intercooled recuperated aero engine. In Proceedings of the Deutscher Luft- und Raumfahrt Kongress, Dresden, Germany, 20–23 September 2004.
- Schonenborn, H.; Simon, B.; Ebert, E.; Storm, P. Thermomechanical design of a heat exchanger for a recuperative aero engine. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea and Air, Vienna, Austria, 14–17 June 2004.
- Goulas, A.; Donnerhack, S.; Flouros, M.; Missirlis, D.; Vlahostergios, Z.; Yakinthos, K. Thermodynamics cycle analysis, Pressure loss and heat transfer assessment of a recuperative system for aero engines. In Proceedings of the ASME Turbo Expo 2014: Power for Land, Sea and Air, Düsseldorf, Germany, 16–20 June 2014.
- Kyprianidis, K.G.; Grönstedt, T.; Ogaji, S.O.T.; Pilidis, P.; Singh, R. Assessment of future aero-engine designs with intercooled and intercooled recuperated cores. J. Eng. Gas Turbines Power 2011, 133, 011701. [Google Scholar] [CrossRef]
- Xu, L.; Kypianidis, K.; Grönstedt, T. Optimization study of an intercooled recuperated aero-engine. J. Propuls. Power 2013, 29, 424–432. [Google Scholar] [CrossRef]
- Missirlis, D.; Yakinthos, K.; Palikaras, A.; Katheder, K.; Goulas, A. Experimental and numerical investigation of the flow field through a heat exchanger for aero-engine applications. Int. J. Heat Fluid Flow 2005, 26, 440–458. [Google Scholar] [CrossRef]
- Yakinthos, K.; Missirlis, D.; Palikaras, A.; Storm, P.; Simon, B.; Goulas, A. Optimization of the design of recuperative heat exchangers in the exhaust nozzle of an aero engine. Appl. Math. Model. 2007, 31, 2524–2541. [Google Scholar] [CrossRef]
- Albanakis, C.; Yakinthos, K.; Kritikos, K.; Missirlis, D.; Goulas, A.; Storm, P. The effect of heat transfer on the pressure drop through a heat exchanger for aero engine applications. Appl. Therm. Eng. 2009, 29, 634–644. [Google Scholar] [CrossRef]
- Albanakis, C.; Missirlis, D.; Storm, P.; Yakinthos, K.; Goulas, A. Experimental investigation of the effect of heat transfer on pressure drop for a heat exchanger for aero engine applications, ExHFT-7. In Proceedings of the 7th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Krakow, Poland, 28 June–3 July 2009.
- ANSYS 15/Fluent CFD Software User’s Guide. Available online: http://148.204.81.206/Ansys/150/ANSYS%20Fluent%20Users%20Guide.pdf (accessed on 10 January 2017).
- Missirlis, D.; Donnerhack, S.; Seite, O.; Albanakis, C.; Sideridis, A.; Yakinthos, K.; Goulas, A. Numerical development of a heat transfer and pressure drop porosity model for a heat exchanger for aero engine applications. Appl. Therm. Eng. 2010, 30, 1341–1350. [Google Scholar] [CrossRef]
- Yakinthos, K.; Missirlis, D.; Sideridis, A.; Vlahostergios, Z.; Seite, O.; Goulas, A. Modelling the operation of a system of recuperative heat exchangers for an aero engine with the combined use of a porosity model and a thermo mechanical model. Eng. Appl. Comput. Fluid Mech. 2012, 6, 608–621. [Google Scholar] [CrossRef]
- Yakinthos, K.; Misirlis, D.; Vlahostergios, Z.; Flouros, M.; Donnerhack, S.; Goulas, A. Best Strategies for the Development of a Holistic Porosity Model of a Heat Exchanger for Aero Engine Applications. In Proceedings of the ASME Turbo Expo 2015: Power for Land, Sea and Air, Montreal, PQ, Canada, 15–19 June 2015.
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- New Aero Engine Core Concepts (NEWAC) Project. Available online: http://www.newac.eu/ (accessed on 29 December 2016).
- Yakinthos, K.; Missirlis, D.; Seite, O.; Vlahostergios, Z.; Goulas, A. Modeling the operation of a heat exchanger for aero engine applications for real engine operating conditions. In Proceedings of the 8th International ERCOFTAC Symposium on Engineering Turbulence Modelling and Measurements, Marseille, France, 9–11 June 2010.
- Missirlis, D.; Yakinthos, K.; Seite, O.; Goulas, A. Modeling an installation of recuperative heat exchangers for an Aero engine. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea and Air, Glasgow, UK, 14–18 June 2010.
- Kurzke, J. Design and Off-Design Performance of Gas Turbines, GasTurb 11; GasTurb GmbH: Aachen, Germany, 2011. [Google Scholar]
- Ultra Low Emission Technology Innovations for Mid-Century Aircraft Turbine Engines (ULTIMATE) Project. Available online: http://www.ultimate.aero/ (accessed on 10 January 2017).

| Case | SFC Reduction (in Relation to a Conventional Aero Engine) | Heat Exchangers‘ Weight Reduction (in Relation to NEWAC) |
|---|---|---|
| NEWAC nozzle | 12.3% | 0 |
| CORN | 13.1% | ~5% |
| STARTREC | 9.1% | ~50% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Misirlis, D.; Vlahostergios, Z.; Flouros, M.; Salpingidou, C.; Donnerhack, S.; Goulas, A.; Yakinthos, K. Optimization of Heat Exchangers for Intercooled Recuperated Aero Engines. Aerospace 2017, 4, 14. https://doi.org/10.3390/aerospace4010014
Misirlis D, Vlahostergios Z, Flouros M, Salpingidou C, Donnerhack S, Goulas A, Yakinthos K. Optimization of Heat Exchangers for Intercooled Recuperated Aero Engines. Aerospace. 2017; 4(1):14. https://doi.org/10.3390/aerospace4010014
Chicago/Turabian StyleMisirlis, Dimitrios, Zinon Vlahostergios, Michael Flouros, Christina Salpingidou, Stefan Donnerhack, Apostolos Goulas, and Kyros Yakinthos. 2017. "Optimization of Heat Exchangers for Intercooled Recuperated Aero Engines" Aerospace 4, no. 1: 14. https://doi.org/10.3390/aerospace4010014
APA StyleMisirlis, D., Vlahostergios, Z., Flouros, M., Salpingidou, C., Donnerhack, S., Goulas, A., & Yakinthos, K. (2017). Optimization of Heat Exchangers for Intercooled Recuperated Aero Engines. Aerospace, 4(1), 14. https://doi.org/10.3390/aerospace4010014







