Intercepting 3I/ATLAS at Its Closest Approach to Jupiter with the Juno Spacecraft

Abstract

The interstellar object 3I/ATLAS is expected to arrive at a distance of $53.56(\pm 0.45)$ million $\mathrm{km}$ ($0.358\pm 0.003$ au) from Jupiter on 16 March 2026. We show that applying a total thrust $\Delta$V of $2.6755\mathrm{km}{\mathrm{s}}^{-1}$ to the lower perijove on 9 September 2025 and then executing a Jupiter Oberth Maneuver can bring the Juno spacecraft from its orbit around Jupiter to intercept the path of 3I/ATLAS on 14 March 2026. We further show that it is possible for Juno to come much closer to 3I/ATLAS (~27 million $\mathrm{km}$) with 110 kg of remaining propellant, merely 5.4% of the initial fuel reservoir. We find that for low available $\Delta$V, there is no particular benefit in the application of a double impulse (for example, to reach ~27 million $\mathrm{km}$ from 3I/ATLAS); however, if Juno has a higher $\Delta$V capability, there is a significant advantage of a second impulse, typically saving propellant by a factor of a half. A close fly-by might allow us to probe the nature of 3I/ATLAS far better than telescopes on Earth.

1. Introduction

The interstellar object 3I/ATLAS (Minor Planet Center (https://www.minorplanetcenter.net/mpec/K25/K25N12.html), accessed on 10 July 2025) was discovered on 1 July 2025 [1,2,3,4,5,6,7]. It is expected (NASA JPL SSD https://ssd.jpl.nasa.gov/tools/sbdb_lookup.html#/?sstr=1004083, accessed on 10 July 2025) to arrive at a distance of $53.56(\pm 0.45)$ million $\mathrm{km}$ ($0.358\pm 0.003$ au) from Jupiter on 16 March 2026.

The ‘3I’ designation indicates this is the third interstellar object to be discovered encountering our solar system. With a heliocentric hyperbolic excess speed, ${\mathrm{V}}_{\infty }$$~58$$\mathrm{km} {\mathrm{s}}^{-1}$, this object is unequivocally extrasolar and joins the first interstellar object, 1I/’Oumuamua [8,9,10,11,12,13], and second, 2I/Borisov [14], initially detected in 2017 and 2019, respectively, as offering the potential of hitherto unparalleled scientific return on stellar systems far beyond our own in our Milky Way galaxy. They have conveniently provided us with an opportunity to study material from outside our solar system, without actually sending an interstellar spacecraft. Such a craft would otherwise take tens of thousands of years to arrive at its destination, using present day chemical rocket technology.

This study focuses on the topic of sending an extant NASA spacecraft currently in orbit around Jupiter to intercept 3I/ATLAS. The concept of sending spacecraft to an interstellar object is not new. Refer, for example, to the ‘Project Lyra’ research for missions to 1I/$\prime$ Oumuamua (undertaken largely by the Initiative for Interstellar Studies, i4is [15]), which can be found in [16,17,18,19,20,21], and also refer to [22]. Furthermore, missions to 2I/Borisov have also been investigated by the i4is team [23].

The analysis herein was conducted largely as a consequence of previous research which demonstrated that spacecraft missions to 3I/ATLAS from Earth are currently infeasible [24]. The possibility of exploiting currently operating interplanetary spacecraft to observe 3I/ATLAS near its perihelion, when the Sun will shield it from Earth telescopes, has already been explored comprehensively in [25]. The research expounded in the following is intended to elaborate on the potential capability of the NASA Juno probe, by bringing it closer to the 3I/ATLAS object, when this object approaches Jupiter in March 2026.

This close encounter provides a rare opportunity to shift the spacecraft Juno (NASA Juno Mission https://www.jpl.nasa.gov/missions/juno/, accessed on 10 July 2025) from its current orbit around Jupiter to intercept the path of 3I/ATLAS at its closest approach to Jupiter. The instruments available on Juno, namely a near-infrared spectrometer, magnetometer, microwave radiometer, gravity science instrument, energetic particle detector, radio and plasma wave sensor, UV spectrograph and visible light camera/telescope, can all be used to probe the nature of 3I/ATLAS from a close distance.

Below, we study the thrust required to shift Juno from its current orbit around Jupiter to a path that will intercept 3I/ATLAS in mid-March 2026.

2. Orbit Calculation

There are two main strategies generally adopted for the determination of optimal trajectories (in this case, of spacecraft trajectories): the indirect method and the direct method [26]. The former normally involves expressing the problem in terms of a Hamiltonian and adjoint variables, and then solving the trajectory, normally via trajectory integration, or alternatively through collocation methods, and using iterative steps until the initial adjoint variables are solved and the conditions for optimality, as formulated by Pontyragin in his ‘Pontryagin Maximum Principle’, including the target transversality conditions, are satisfied. This method ensures that the true optimal solution is found to be within the prescribed tolerance. The application of this principle is wide in scope and can also be exploited to solve the problem of optimal N-impulse transfers [27].

The alternative direct method [26] normally involves simplifying the problem significantly by parameterizing the controls (such as assuming they evolve linearly with time) and finding the coefficients/control parameters which result in an extreme of the cost functional (such as minimizing fuel usage) over the course of the trajectory. The method can be used in conjunction with a choice of global optimization paradigms involving iteration methods, such as Non-Linear Problem (NLP) solvers or Genetic Algorithms [28], and so on. Depending on the parameterization adopted, this direct method may not find the precise theoretical solution, but may come sufficiently close to an extent that it becomes indistinguishable from the theoretical solution.

Our analysis exploits the software package known as Optimum Interplanetary Trajectory Software (OITS). Note that OITS employs a ‘direct method’ strategy as explained above. Further information regarding OITS is provided by [23,29,30]. Two possible NLP solver options are available for the work conducted here, namely NOMAD [31] or MIDACO [32,33,34]. This is a modified version of OITS in that the central body of interest is not the Sun but Jupiter. The data for Juno is taken from the SPICE data website [35], using the file juno_pred_orbit.bsp. Furthermore, solar and planetary positions and velocities are derived from the SPICE data file de430.bsp.

OITS solves the Lambert problem for one orbital cycle only: given two times $t_1$ and $t_2$, what are the two orbital arcs that connect them? Assuming that the positions at the beginning of the arc and the end of the arc are known, then there are two solutions, a short way and a long way, equivalent to an angular sweep, $\theta$, and the retrograde angular sweep, $2\pi -\theta$. Here, $\theta$ is found from the dot product of the initial and final position vector. Having determined the short way and long way solutions, the way with the maximum $\Delta$V is rejected, leaving the desired, lowest $\Delta$V solution. This procedure is conducted iteratively with different trial values of $t_1$ and $t_2$ (within user-specified bounds), until OITS has converged on the overall minimum $\Delta$V solution.

In addition, in order to model Oberth Maneuvers (refer [36]), that is applications of $\Delta$V at points other than at an encounter with a celestial body (so normally at the periapsis of the central body), the notion of Intermediate Points [30] is utilized. An Intermediate Point is a point on a spherical surface of user-specified radius from the center of attraction (such as, in this case, Jupiter). The longitude and latitude, $\theta$ and $\varphi$, respectively, of this specified radius are optimized by the NLP in question, along with the aforementioned times $t_1$ and $t_2$. This would normally necessitate a good guess by the user as to the exact value of this radial distance; however, for the version of OITS applied in this research, the user may specify a range of distances, and thus, this radial distance, R, can be optimized by the NLP also. Therefore, this allows full optimization of the point where the Oberth $\Delta$V is applied.

To solve the Lambert problem, the Universal Variable formulation is followed [37]. We focus on an intercept (i.e., a fly-by) since a rendezvous, where the target’s velocity is matched by the spacecraft, is out-of-the-question, owing to the excessively high hyperbolic speed of 3I/ATLAS relative to Jupiter (~65.9 $\mathrm{km} {\mathrm{s}}^{-1}$).

The binary SPICE kernel file for the interstellar object 3I/ATLAS was also extracted from the NASA Horizons service, on 18 July 2025.

The intercept distances derived in this research are around 0.36 au from Jupiter, which is almost precisely the radius of Jupiter’s Hill Sphere. As far as Juno is concerned, it starts deep in Jupiter’s gravitational well, and this is the overwhelming driver governing the magnitude of the probe’s intercept $\Delta$V. Thus, when simulations including the Sun’s influence were conducted, there was no evident difference in the required $\Delta$V, at least discernible within the precision of the NLP software. Furthermore, $\Delta$V budgets are listed WITHOUT the provision for navigational errors and Mid-Course Corrections (MCCs). Such parameters are not within the scope of this research and are rather something that the NASA Juno team should determine with their ‘insider’ knowledge of Juno’s current status.

Note that the precise mass of residual propellant remaining in Juno’s tanks, as well as the current status of the probe’s engine, is known only in full by the NASA Juno project team. Thus, the research herein is intended as a reference for the team to determine which options are the most appropriate given the probe’s current condition. Note also that perturbations other than those mentioned above are not considered, as they are negligible for the trajectories studied (at around 3 Jupiter radii). For instance, the effect of Jupiter’s J2 gravitational harmonic, which falls according to the inverse cube of Jupiter distance, would be insignificant. Additionally, Juno’s orbit is considerably inclined to Jupiter’s equator; thus, the influence of Jupiter’s moons on Juno’s orbit can be effectively discounted.

As this research amounts to a feasibility study, engine-specific parameters are not adopted, and where applicable, estimated propellant requirements are provided with required $\Delta$V to allow NASA to determine itself the appropriate mission options to choose.

Despite the caveats mentioned above, for the REBOUND simulations (refer to later in this section), the trajectories were also integrated with the Sun’s perturbing gravitational force included, and this was found to have no noticeable effect on the trajectory solutions.

Juno is hardened to survive close approaches to Jupiter. Thus, sensitive electronics are inside a radiation-shielded box.

Using the approach outlined above, color contour maps were generated by OITS for a Juno $\Delta$V application window covering the present as at the time of writing (27 July 2025) to the point at which the data in the binary SPICE file for Juno expires (17 September 2025), marking the possible end of the mission which is currently scheduled to occur around that time. Refer to Figure 1 and Figure 2.

The feasibility of intercepting 3I/ATLAS depends on the current amount of fuel available from the propulsion system of Juno. However, some inferences can be drawn from the total $\Delta$V available at the beginning of the Juno mission. On its interplanetary trajectory, Juno conducted two Deep Space Maneuvers (DSMs), and one Jupiter orbital insertion, both of which would have placed a significant demand on the chemical propulsion employed by Juno (Hydrazine and oxidizer nitrogen tetroxide).

Let us assume a total initial wet mass of the spacecraft $M_{tot}$, a dry mass of $M_{dry}$, and a specific impulse given by $I_{sp}$; then, the total $\Delta$V available to Juno is given by

$$\Delta V=I_{sp}gln\left({\displaystyle \frac{M_{tot}}{M_{dry}}}\right)$$

(1)

where $g=9.8$ $\mathrm{m} {\mathrm{s}}^{-2}$.

The data for the above parameters can be sourced from [38].

Thus, we have $M_{tot}=3625$ $\mathrm{kg}$ and $M_{dry}=1593$ $\mathrm{kg}$. For the specific impulse, we assume an optimistic $I_{sp}=340$$\mathrm{s}$, giving an overall initial $\Delta$V available of 2.74 $\mathrm{km} {\mathrm{s}}^{-1}$.

This value is similar to the required $\Delta$V for Juno to intercept 3I/ATLAS, given in

Table 1. Pertinent trajectory data for an intercept of 3I/ATLAS with $\Delta$V applied in mid-August; refer to the middle trough in Figure 2.

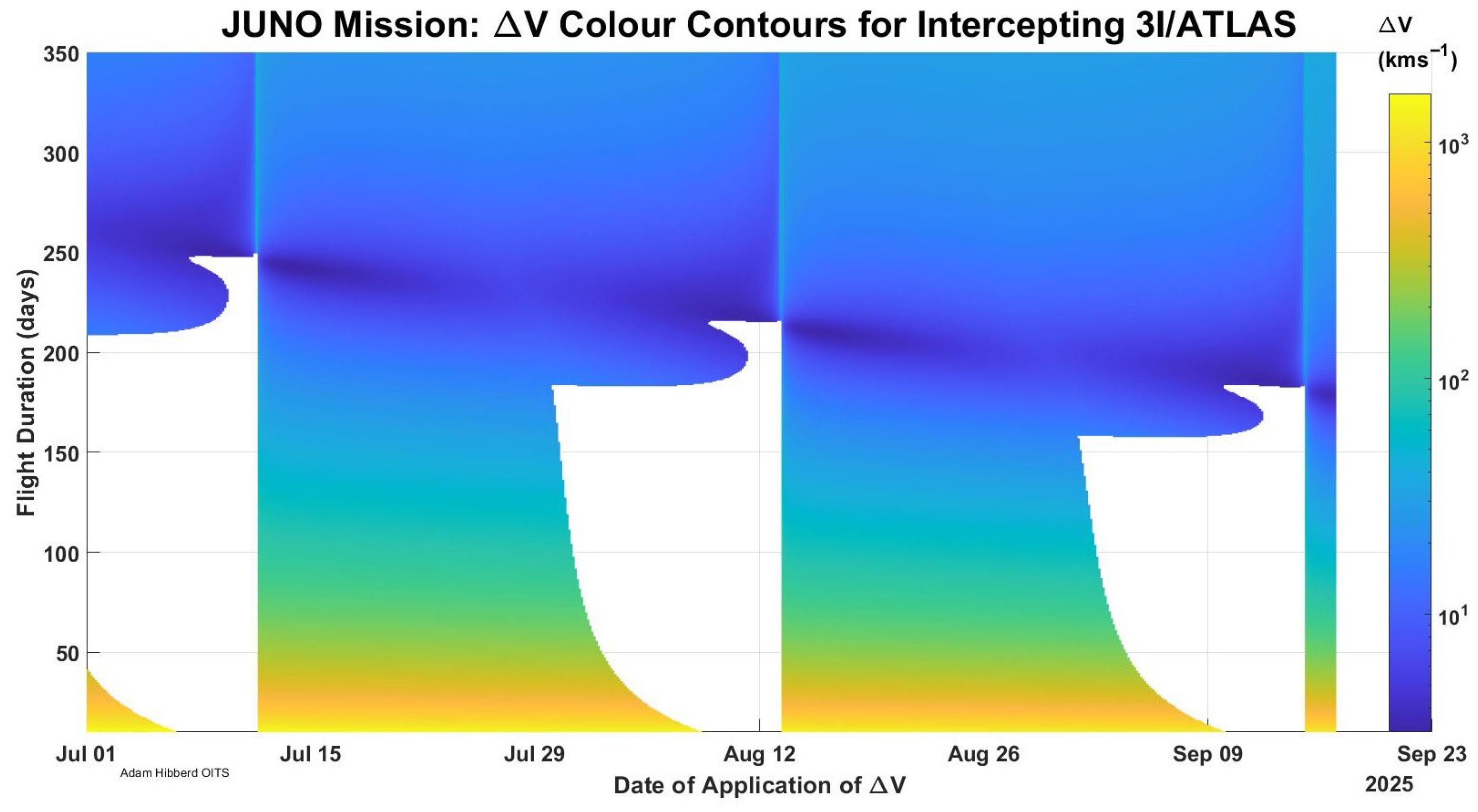
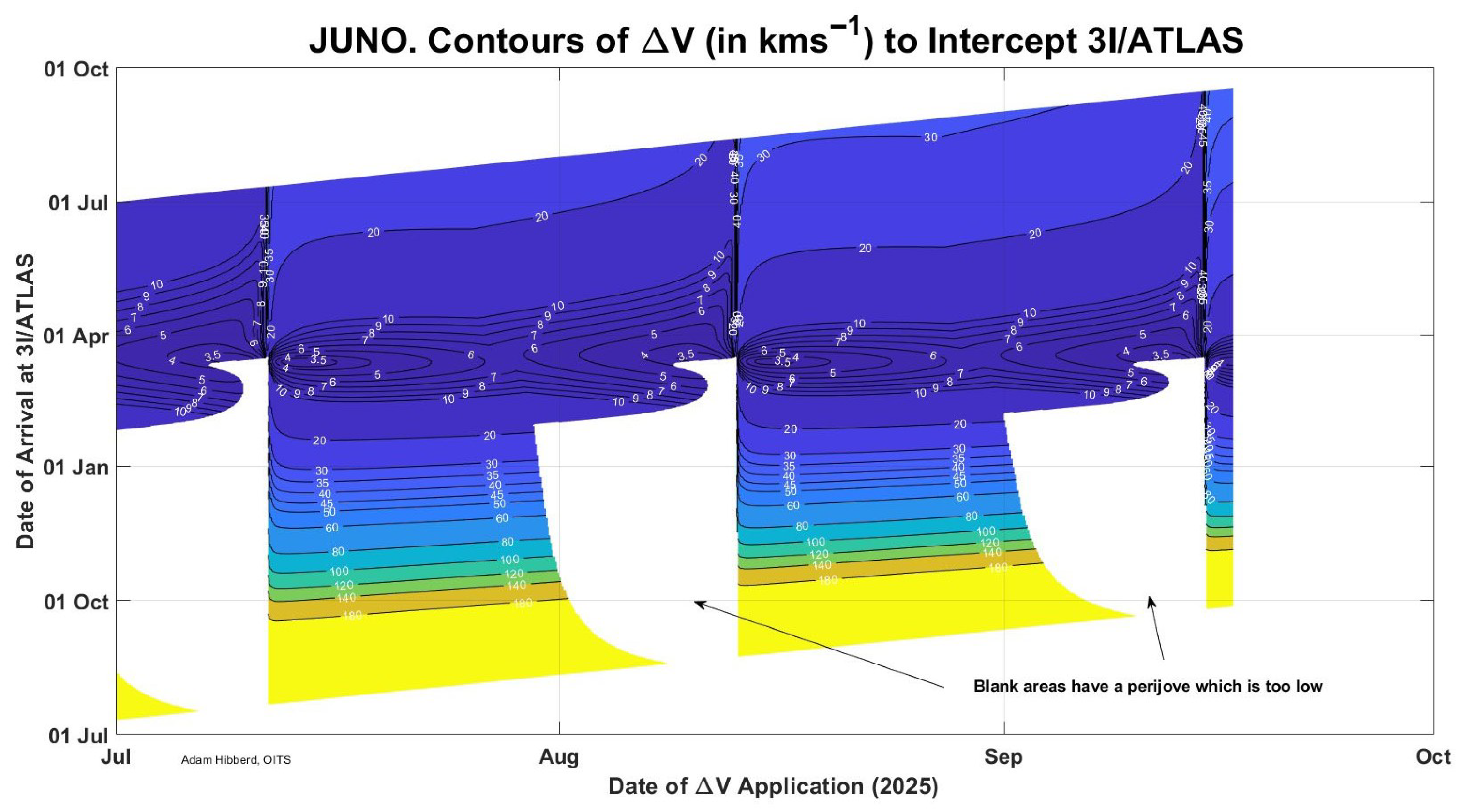
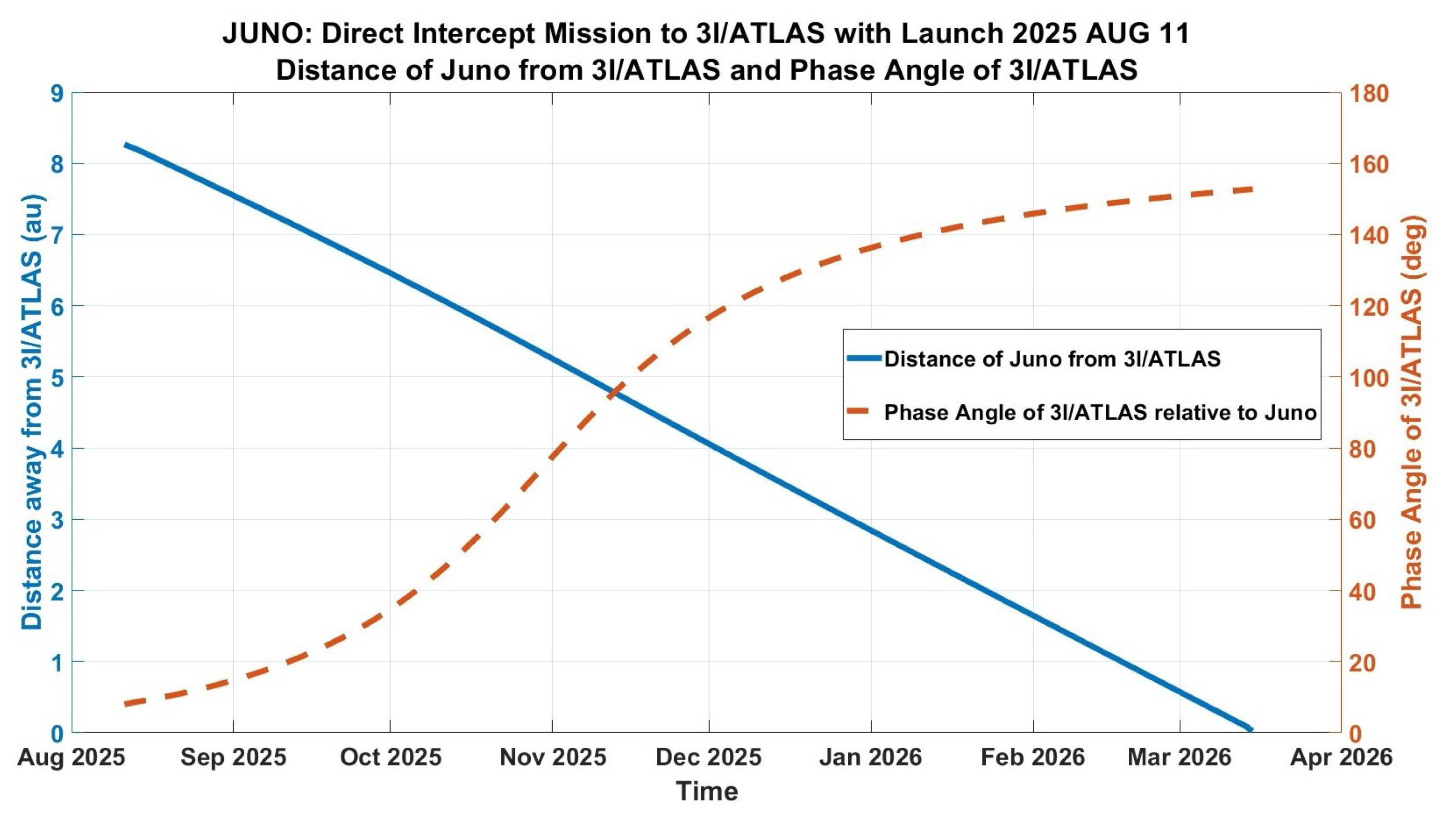
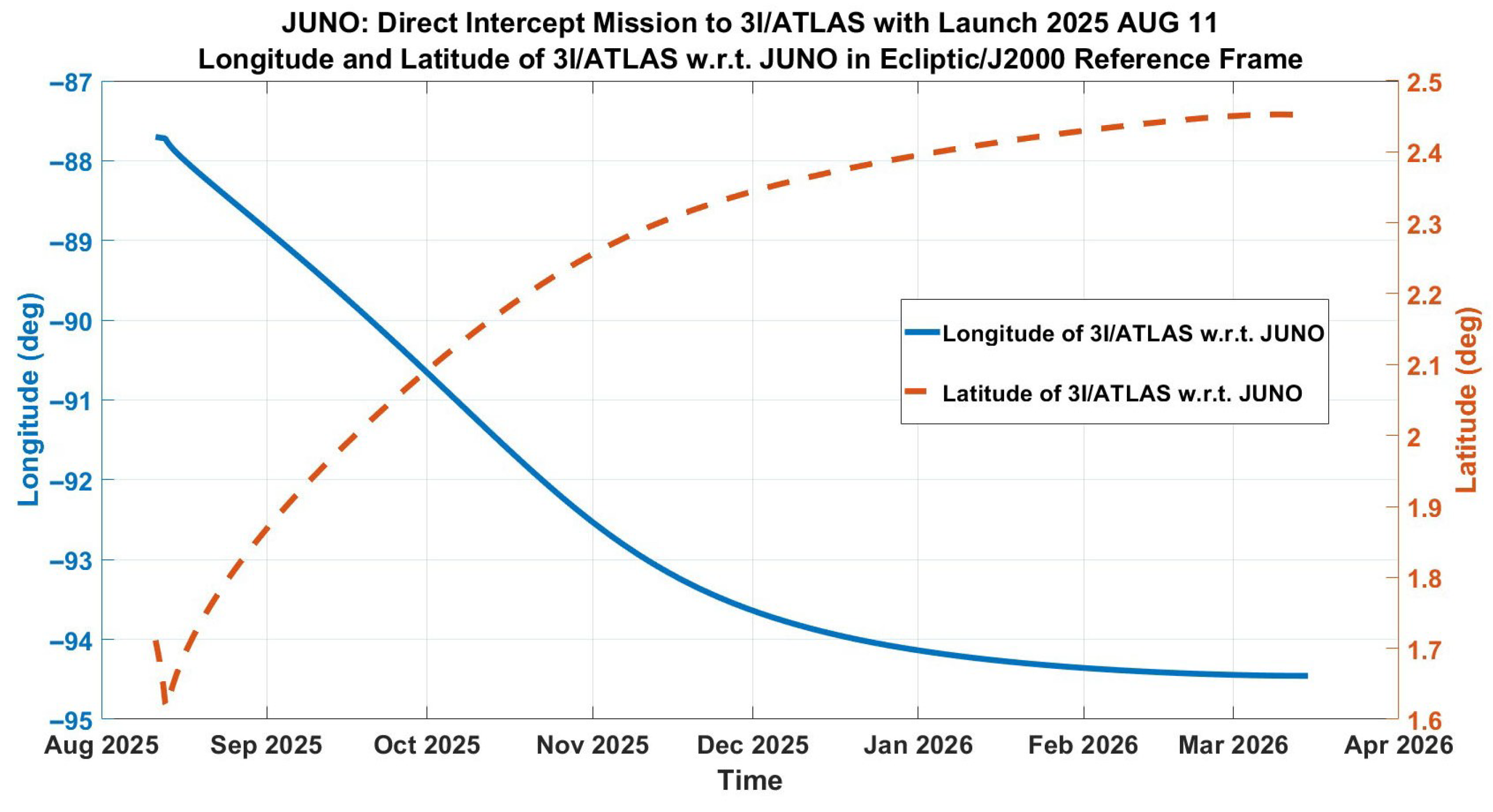
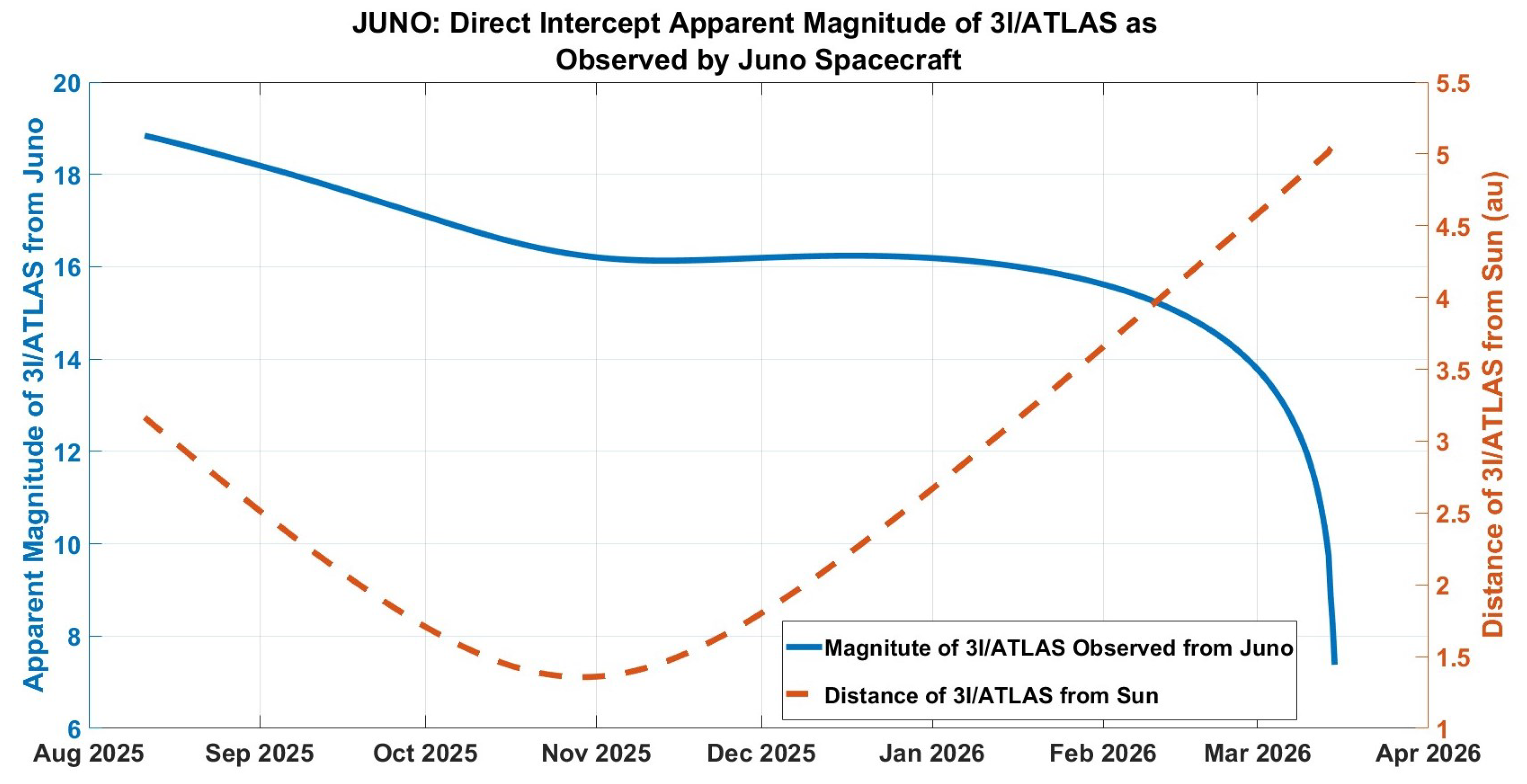
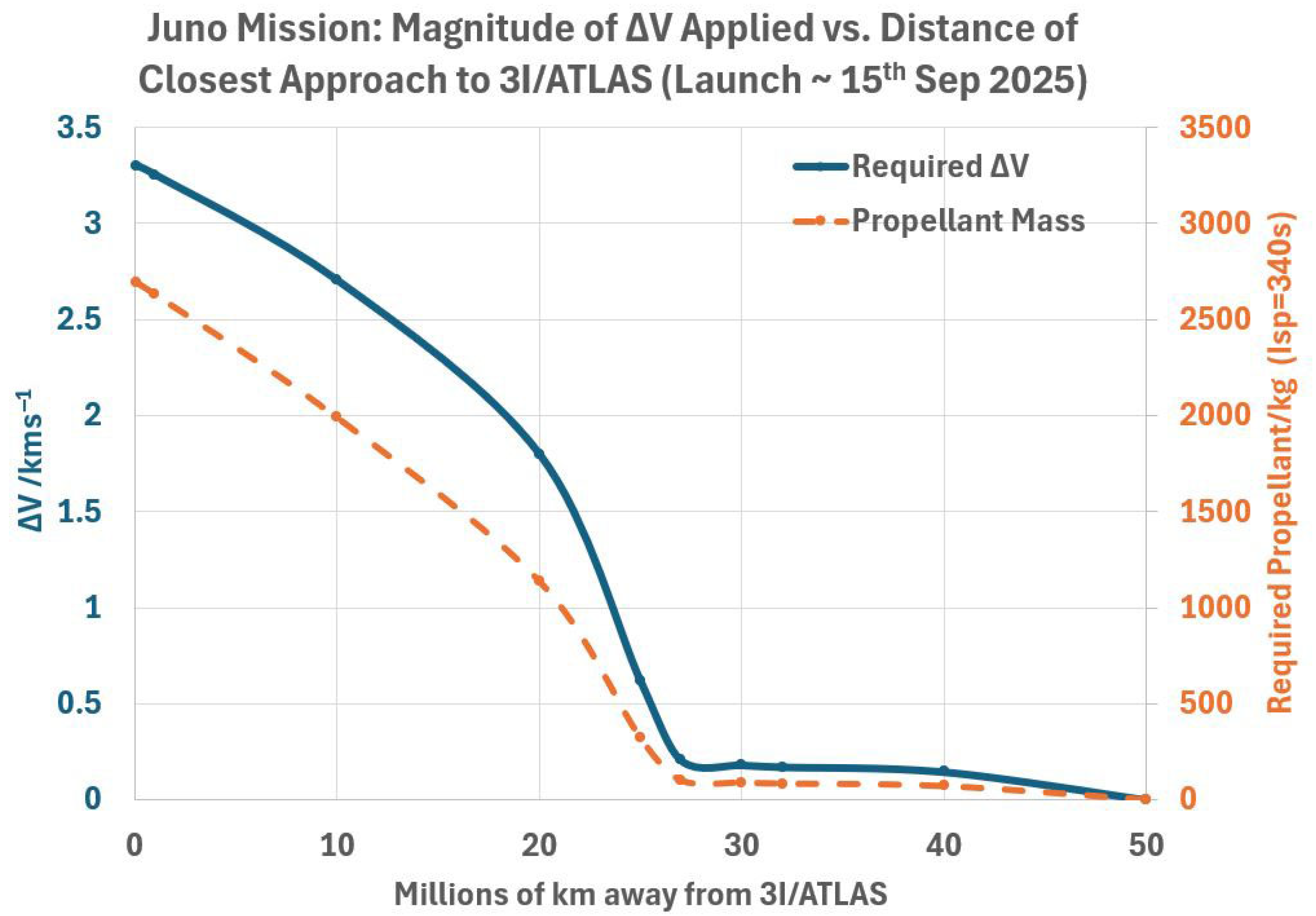
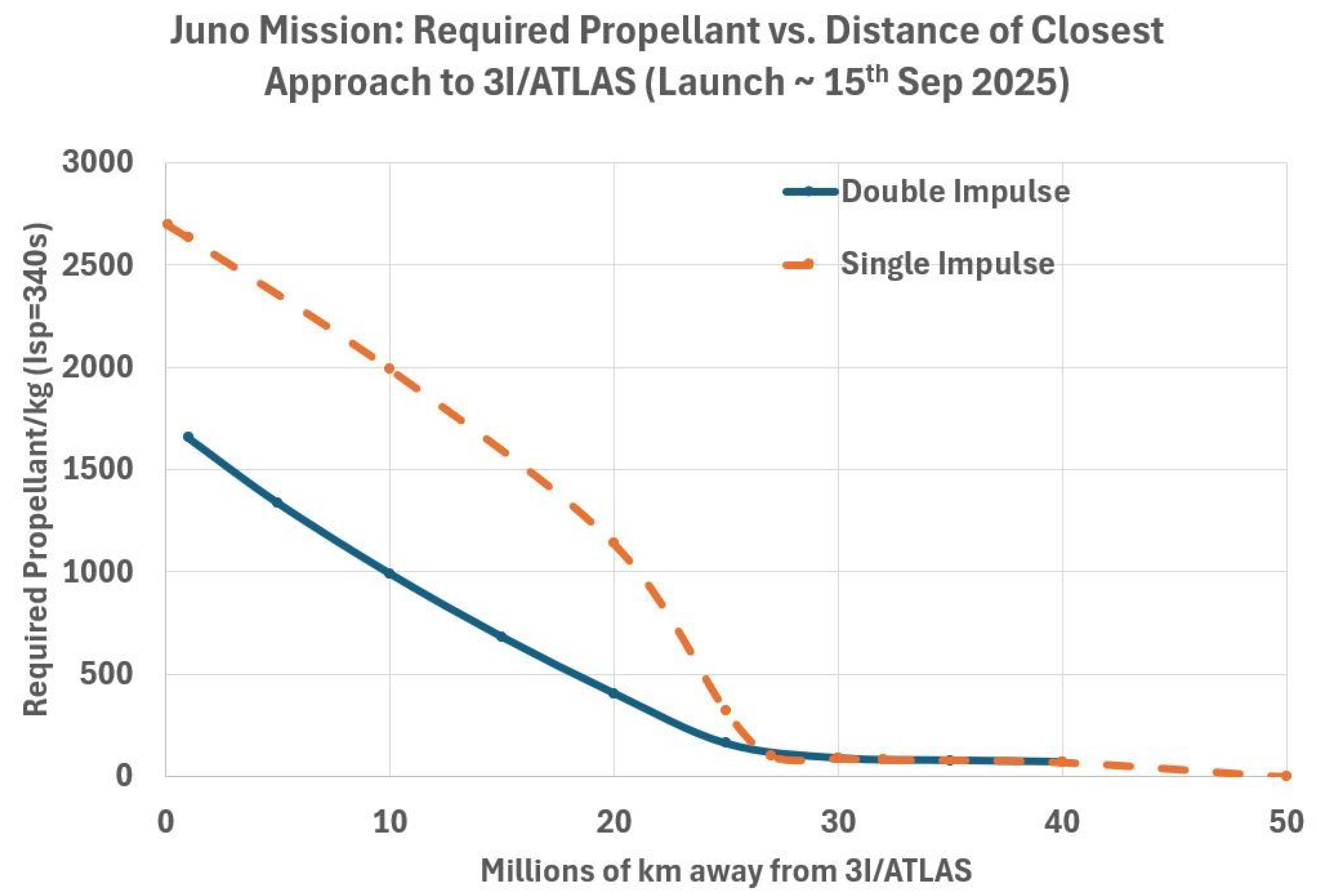
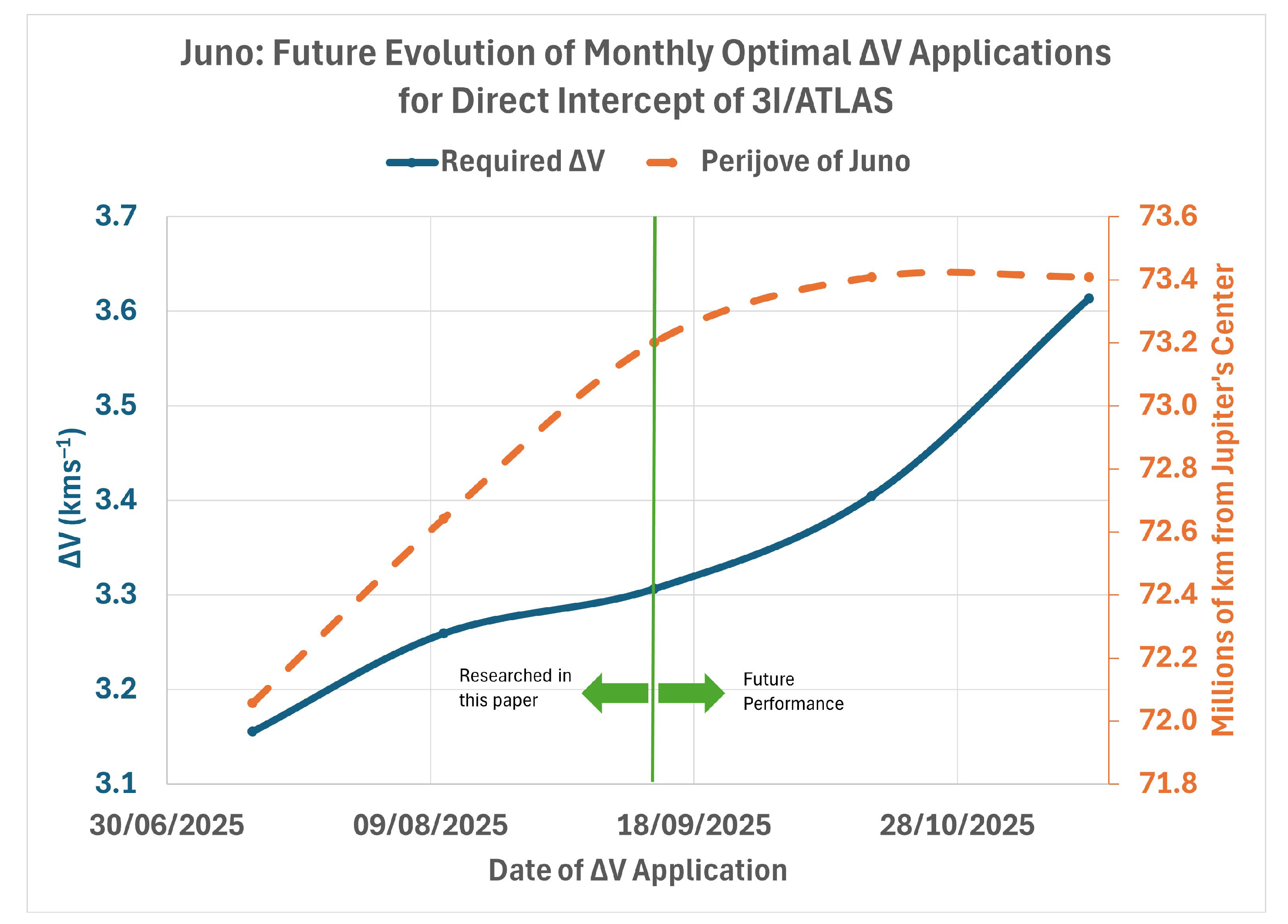
Number	Event	Time	Arrival Speed	Departure Speed	$\mathbf{\Delta }$V	Distance from Jupiter	Perijove Alt.
			m/s	m/s	m/s	km	km
1	Juno	2025 AUG 11 03:19:36	0	3259.3	3259.3	2,303,610	63,276
2	3I/ATLAS	2026 MAR 16 01:32:30	66,129.2	66,129.2	0	53,392,590	63,276
				Contingency Margin	490 (15%)
				Total $\mathbf{\Delta }$V	3749.3

,

Table 2. Trajectory data for an intercept of 3I/ATLAS with $\Delta$V applied in mid-September; refer to the trough on the right in Figure 2.

Number	Event	Time	Arrival Speed	Departure Speed	$\mathbf{\Delta }$V	Distance from Jupiter	Perijove Alt.
			m/s	m/s	m/s	km	km
1	Juno	2025 SEP 12 22:29:49	0	3306.5	3306.5	2,235,639	60,390
2	3I/ATLAS	2026 MAR 16 11:45:48	66,068.9	66,068.9	0	53,331,939	60,390
				Contingency Margin	500 (15%)
				Total $\mathbf{\Delta }$V	3806.5

and

Table 3. Jupiter Oberth Maneuver offers a lower $\Delta$V requirement than the direct option.

Number	Event	Time	Arrival Speed	Departure Speed	$\mathbf{\Delta }$V	Distance from Jupiter	Perijove Alt.
			m/s	m/s	m/s	km	km
1	Juno	2025 SEP 09 22:40:01	0	2157.4	2157.4	3,863,491
2	2.68 Jupiter Radii	2025 SEP 14 18:37:14	35,881.8	36,388.6	518.1	191,595	120,103
3	3I/ATLAS	2026 MAR 14 12:51:04	66,536.8	66,536.8	0	54,576,427	88,660
				Contingency Margin	400 (15%)
				Total $\mathbf{\Delta }$V	3075.5

.

The opportunity shown in Table 1 has a ‘launch’ (henceforth defined as time of initial $\Delta$V application) of 11 August 2025, and in what follows, this will be the reference mission. Refer to Figure 3, Figure 4, Figure 5 and Figure 6, which provide the pertinent trajectory data for this reference mission, including an estimate of the brightness of 3I/ATLAS, as well as the necessary attitude of Juno for tracking the target. Further missions investigated follow similar profiles and so are not provided.

Although the engine of Juno was not operated since 2016, the required $\Delta$V might potentially be within Juno’s performance envelope. In that case, Juno would be able to get close to 3I/ATLAS and use its instruments to probe the nature of the interstellar object and any cloud of gas or dust around it.

The optimal option involves a Jupiter Oberth Maneuver which requires an application of $\Delta$V on 9 September 2025, only 8 days prior to the originally intended termination date for Juno’s plunge into the atmosphere of Jupiter. Having delivered this thrust to diminish Juno’s altitude, a further $\Delta$V is subsequently delivered, constituting a Jupiter Oberth Maneuver and resulting in an eventual intercept of the target 3I/ATLAS on 14 March 2026. Refer to Table 3 for more details. In total, an overall $\Delta$V of $(2.1574+0.5181)=2.6755$$\mathrm{km} {\mathrm{s}}^{-1}$ is utilized.

If doable, this exciting new goal will rejuvenate Juno’s mission and extend its scientific lifespan beyond 14 March 2026.

So far, we have examined a zero distance intercept of Juno with 3I/ATLAS. It is salient at this juncture to ask the question “how close can Juno approach 3I/ATLAS, given that it has a limited remaining propellant mass, and so a restricted $\Delta$V?”.

In order to perform these investigations, a software application using SPICE [35], REBOUND [39,40] and NOMAD [31] was constructed.

We investigate the mid-August 2025 opportunity first. Figure 7 assumes a rocket specific impulse, $I_{sp}=340$ s, and uses Equation (1) to derive the required propellant mass for a given $\Delta$V. We find that a relatively low $\Delta$V is needed (<0.23 $\mathrm{km} {\mathrm{s}}^{-1}$, equivalent to a propellant mass of ~110 $\mathrm{kg}$, which is merely 5.4% of the initial fuel reservoir) to approach 3I/ATLAS within a distance of 27 million km. Below ~27 million km, the required $\Delta$V rises significantly until it reaches 3.3 $\mathrm{km} {\mathrm{s}}^{-1}$ at zero distance as determined in the preceding analysis results, presented in Table 1.

Figure 8 refers to the September 2025 opportunity and shows a similar behavior with similar levels of required $\Delta$V and propellant mass, though the advantage of this option is that it provides a month of extra time to prepare for the maneuver.

There would potentially be a lower overall $\Delta$V requirement with more than one impulse application. For simplicity, we investigate here only the double impulse case and focus on the mid-September 2025 launch. Figure 9 compares the $\Delta$Vs of the double impulse with the single impulse option. There is a significant drop in the required $\Delta$V for the double impulse scenario. Figure 10 shows how this $\Delta$V translates to required propellant, implying a factor of a half reduction in the propellant mass needed in order to get to a distance of 10 million km from 3I/ATLAS.

Figure 11 shows the distribution of $\Delta$V between the 1st impulse (blue section) and 2nd impulse (red section), indicating that for the situation where only small $\Delta$Vs are available (i.e., closest approach to 3I/ATLAS > 25 million $\mathrm{km}$), there is no benefit at all to choosing the additional impulse. We note that the double impulse is more challenging to realize given the limited time remaining for preparation.

3. Future Opportunities

The investigations in the preceding section were conducted up to the end of the NASA SPICE kernel file for Juno, which is in late September 2025, and so they ignore any opportunities which may arise after this cut-off point. Since more up-to-date data is now available from NAIF, extending the Juno ephemerides to late November 2025, this offers the opportunity to characterize the future evolution of the performance of a Juno mission to 3I/ATLAS.

Thus, refer to Figure 12, which extends the level of $\Delta$V needed for a direct intercept beyond August and September (refer to Table 1 and Table 2, respectively) and up to the end of November. This provides a good idea of how the other trajectory scenarios investigated in Section 2 will perform in the future.

Evidently, there are two key factors which govern the level of $\Delta$V required to intercept 3I/ATLAS:

1.

The time available from application of the initial $\Delta$V to reach and intercept the target, 3I/ATLAS.

2.

The precise perijove of Juno, since the lower this value, the greater the kick which can be delivered from the Oberth effect using the same magnitude $\Delta$V.

As can be observed in Figure 12, the perijove of Juno ascended from July onwards and then plateaued in October/November. This implies that in the future, from November onwards, there will be no obvious benefit from Juno’s orbit in terms of reducing the applied $\Delta$V to arrive at 3I/ATLAS. In fact, if one refers to the plot of required $\Delta$V in this Figure, we find that this important metric of feasibility continues quite steeply upwards despite this plateau in perijove, implying that it is indeed the first of the items above (lower flight durations due to the more imminent arrival of 3I/ATLAS) that is the overriding factor governing the viability of a mission to 3I/ATLAS. In short, the sooner Juno is ‘launched’ the better.

4. Discussion

The amount of fuel left in Juno’s engine is not publicly available. As a result, our paper provided the distance of the closest approach that Juno can reach relative to 3I/ATLAS as a function of that unknown fuel reservoir. This is the best that can be done at this time, following email exchanges we had with the Juno team.

We have found that the application of a thrust of $2.6755\mathrm{km}{\mathrm{s}}^{-1}$ on 9 September 2025 can potentially shift the Juno spacecraft from its orbit around Jupiter to intercept the path of 3I/ATLAS on 14 March 2026.

With Juno’s many instruments, a fly-by can probe the nature of 3I/ATLAS far better than telescopes on Earth.

We have further shown that much closer distances to 3I/ATLAS (~27 million $\mathrm{km}$) can be achieved with smaller $\Delta$V requirements should Juno have a relatively low level of propellant mass remaining.

Small corrections to Juno’s path might be needed if cometary activity of 3I/ATLAS will be intensified as it comes closer to the Sun and its non-gravitational acceleration will change its expected trajectory.