Phase-Adaptive Reinforcement Learning for Self-Tuning PID Control of Cruise Missiles

Abstract

Conventional fixed-gain PID controllers face inherent limitations in maintaining optimal performance across the diverse and dynamic flight phases of cruise missiles. To overcome these challenges, we propose Time-Fusion Proximal Policy Optimization (TF-PPO), a novel adaptive reinforcement learning framework designed specifically for cruise missile control. TF-PPO synergistically integrates Long Short-Term Memory (LSTM) networks for enhanced temporal state perception and phase-specific reward engineering enabling self-evolution of PID parameters. Extensive hardware-in-the-loop experiments tailored to cruise missile dynamics demonstrate that TF-PPO achieves a 36.3% improvement in control accuracy over conventional PID methods. The proposed framework provides a robust, high-precision adaptive control solution capable of enhancing the performance of cruise missile systems under varying operational.

1. Introduction

Cruise missiles are missiles that fly within the atmosphere in a cruising state, and their flight process can be divided into multiple stages such as altitude adjustment, cruise, and dive, each with different aerodynamic characteristics and control requirements [1]. The control system must ensure that the missile maintains a stable attitude and precise trajectory tracking in complex and variable flight environments. Cruise missile controllers commonly use PID controllers for attitude control [2,3]. However, the traditional proportional–integral–derivative (PID) control method, due to its static design [4,5,6], exhibits significant limitations in addressing nonlinear systems and external disturbances [7]. Studies indicate that traditional PID control struggles to accurately model the dynamic characteristics of missiles, and parameter tuning requires iterative adjustments, which is a cumbersome process [8,9]. Furthermore, the multi-stage flight requirements of cruise missiles necessitate compromises in control parameters across different phases, making it impossible to achieve optimal control across the full speed range, full airspace, and under large maneuver conditions [10].

In order to improve the adaptability and tedious parameter adjustment problems caused by fixed-gain PID, real-time adaptive control schemes with dynamic parameter adjustment functions have received widespread attention. Adaptive PID control typically encompasses rule-based [11,12], and model-based approaches [13,14]. Rule-based methods, such as Ziegler–Nichols tuning [15] and fuzzy logic adaptive PID control, adaptively adjust gains by leveraging control signal characteristics like overshoot and PID error. Model-based techniques, like Model Reference Adaptive Control [16], neural adaptive sliding mode guidance for UAV piloting [17] and three-dimensional sliding pursuit guidance for surface-to-air missiles [18], utilize mathematical models to adjust PID parameters, accommodating changes in system dynamics or external disturbances, thereby improving tracking performance and stability. Although many methods [19,20] have made significant progress in their respective fields, they still have shortcomings for missile attitude control with strong nonlinearity. Rule-based methods rely heavily on predefined rules or expert knowledge, limiting their adaptability to unforeseen conditions in highly dynamic missile flight scenarios. Model-based approaches face challenges in highly nonlinear systems where design complexity increases significantly, and unmodeled dynamics or model errors lead to performance degradation. These challenges are particularly pronounced in the rapidly evolving field of cruise missile control. A novel approach is needed to enhance adaptability to dynamic systems and environments.

With advancements in artificial intelligence, reinforcement learning (RL) [21,22,23] offers a promising direction for missile attitude control [24,25,26,27]. Especially for unmanned aerial vehicle attitude control, RL performs better than traditional control methods. By leveraging deep reinforcement learning techniques combined with PID controllers [28] and designing a reinforcement learning framework [29], they achieved online optimization of network parameters, enhanced the control performance of the aircraft, and attained satisfactory tracking accuracy and robustness. Similarly, Zhao [30] designed a PPO based attitude control framework for unmanned aerial vehicles in a simulation environment demonstrating superior sample efficiency and stability in attitude control. The integration of RL with missiles has primarily focused on guidance law design for autonomous obstacle avoidance [31] and target tracking [32]. For missile attitude control, Zhang [33] developed a DDPG-based longitudinal controller for missile attitude control. Through longitudinal plane simulations, the study demonstrated the feasibility of this data-driven control method in stabilizing the nonlinear angle of attack dynamics in the missile’s longitudinal motion. Lee [34] designed an RL-based PID control strategy for large angle-of-attack commands, achieving improved tracking performance.

Despite these developments, current research has certain limitations: existing methods often train in specific scenarios, limiting validation across diverse flight conditions. Simultaneously, they overlook the inherent non-Markovian nature of PID controllers—existing RL controller designs discard crucial historical state information. Additionally, as RL-based AI systems become more general and autonomous, designing reward mechanisms to elicit desired behaviors becomes increasingly important and challenging. Current researchers often focus solely on system design and straightforward objectives, thereby neglecting the design of reward engineering [35], which results in inadequate adaptability of algorithms in multi-stage tasks [32].

To address these limitations, we developed an adaptive PID tuning framework utilizing the Time-Fusion Proximal Policy Optimization (TF-PPO) algorithm. TF-PPO is an enhancement of the established Proximal Policy Optimization (PPO) [22] algorithm, whose stability and efficiency have been demonstrated in adaptive PID tuning applications [36]. Our approach integrates long short-term memory (LSTM) [37] network, robust training method, and adaptive reward function, which can effectively perceive historical states and adaptively adjust parameters to cope with changes in flight states in different scenarios. Specifically, we construct a PPO-based adaptive PID parameter tuning algorithm for missile attitude control, incorporating LSTM networks to capture historical state dependencies and achieve precise attitude regulation. This approach employs a full six-degree-of-freedom aerodynamic model, trained through interactions with a game-based adversarial simulation system. This approach utilizes a full six-degree-of-freedom aerodynamic model and trains through adversarial interactions within a simulation environment. During optimization, PID controller gains function as policy parameters in the RL actor network, updated through online environment interactions. For characterizing flight-phase dynamics, we implement reward engineering with specialized functions for altitude adjustment, cruise, descent and terminal guidance phases. Through these designs, optimal parameters for each phase can be automatically identified without relying on initial values.

Table 1. Comparative Summary of Controller Performance.

Feature	Traditional PID	Rule-Based Adaptive PID	Model-Based Adaptive PID	RL-PID (e.g., DDPG PPO)	TF-PPO
Nonlinear System Handling	Moderate	Moderate	Limited	Good	Good
Parameter Tuning Complexity	High	Moderate	Moderate	Low	Low
Multi-Phase Adaptability	Poor	Moderate	Moderate	High	High
Historical State Utilization	None	Limited	Limited	None	Good

compares our method with existing approaches.

To experimentally assess the proposed framework, a rapid-prototyping missile control system was engineered. This verification infrastructure integrated step-response testing with full-trajectory simulation, with experimental data confirming robustness under divergent initial conditions and wind disturbances. We designed and constructed a reinforcement learning-based rapid prototyping system for missiles, establishing a verification framework that combines step response testing and full envelope simulation. By evaluating attitude tracking performance under varied initial conditions and different wind disturbances, we demonstrated the robustness and effectiveness of the proposed algorithm. This study advances reinforcement learning applications in missile attitude control, providing robust and adaptive solutions for nonlinear dynamics and multi-phase flight scenarios.

The rest of this paper is organized as follows: Section 2 presents system modeling and missile attitude control architecture. Section 3 details the TF-PPO algorithm, including reward engineering and implementation workflow. In Section 4, all experimental results are presented, including step response tests, offline training, and comparative experiments on the missile rapid prototyping system. Section 5 summarizes contributions and future work.

2. System Modeling and Control System Architecture

For high-fidelity missile dynamics modeling, aerodynamic parameter estimation of a cruise missile was performed. Parameters are assumed representative of a generic subsonic cruise missile, which utilizes aerodynamic controls, scaled for simulation purposes based on typical values from literature [38]. The following key parameters from

Table 2. Missile parameters.

Symbols	Parameter Explanation	Units	Values
$m_{wet}/m_{dry}$	Fully Loaded/Unloaded mass	kg	675/580
$v_{max}$	Maximum cruise speed (3000 m)	Ma	0.7
$R$	Range	km	270
$I_{y,wet}/I_{y,dry}$	Pitch moment of inertia (Fully Loaded/Unloaded)	-	1400/1350
$T_{max}$	Maximum thrust	N	2700
$h_{max}$	Service ceiling	m	8000

are utilized in the missile system model.

This paper conducts numerical modeling and analysis of missile aerodynamic characteristics using ANSYS FLUENT (v2022 R2). Combined with key parameters in Table 1 and six-degree-of-freedom rigid-body equations of motion [39,40,41], a nonlinear dynamic model of the pitch channel is established. Given the similarity in control logic across pitch, roll, and yaw channels, this study focuses exclusively on the self-evolutionary parameter analysis of the pitch loop. Under the assumption of small angles of attack ($\alpha <{15}^{°}$) [42] and symmetric missile configuration, the coupling from yaw and roll channels can be reasonably neglected [43]. Neglecting coupling effects from yaw and roll channels, the nonlinear pitch dynamics can be described by

$$\left\{\begin{array}{l}\dot{\theta }=q\\ \dot{\alpha }=q+{\displaystyle \frac{1}{mV}}\left[\overline{q}S(C_{Z\alpha }\alpha +C_{Z\delta }{\delta }_e)-T\sin \alpha -mg\cos \theta \right]\\ \dot{q}={\displaystyle \frac{1}{I_y}}\left[\overline{q}S\overline{d}(C_{m\alpha }\alpha +C_{m\delta }{\delta }_e+C_{mq}{\displaystyle \frac{\overline{d}q}{2V}})\right]\end{array}\right.$$

(1)

The symbols used in Equation (1) are defined in

Table 3. Symbols used in pitch channel dynamics equations.

Symbols	Parameter Explanation	Units
$\theta$	Pitch angle	rad
$\alpha$	Angle of attack	rad
$q$	Pitch rate	Rad/s
$m$	Missile mass	kg
$V$	Missile velocity	m/s
$\overline{q}$	Dynamic pressure	Pa
$S$	Reference area	m2
$\overline{d}$	Reference length	m
$C_{Z\alpha }$	Normal force coefficient due to angle of attack	-
$C_{Z\delta }$	Normal force coefficient due to elevator defection	-
$C_{m\alpha }$	Pitch moment coefficient due to angle of attack	-
$C_{m\delta }$	Pitch moment coefficient due to elevator defection	-
$C_{mq}$	Pitch moment damping coefficient	-
${\delta }_e$	Elevator defection angle	rad
$T$	Thrust	N
$g$	Gravitational acceleration	m/s2
$I_y$	Pitch moment of inertia	kg$·$m2

.

The trajectory of a cruise missile consists of a planned trajectory and a guided trajectory. Before launch, the missile’s flight plan is predetermined and cannot be altered once launched [1]. The input to the missile’s attitude controller is the desired attitude angle generated by a fixed control law. The task of attitude control is to track the desired angle, minimizing the attitude angle error ${\theta }_e$. The PID controller for the pitch loop attitude can be expressed as

$${\delta }_{e\mathrm{,cmd}}=k_p{\theta }_e+k_i{\displaystyle \int {\theta }_e}dt-k_d{\omega }_z$$

(2)

In the equation, ${\delta }_{e\mathrm{,cmd}}$ represents the elevator command, and the steering gear model is represented by a second-order model [44]:

$${\displaystyle \frac{{\delta }_e}{{\delta }_{e,cmd}}}={\displaystyle \frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}}$$

(3)

To address the attitude control requirements of cruise missiles with complex motion characteristics, this paper designs an RL-PID intelligent control system that integrates deep reinforcement learning with classical PID control. Through an online parameter tuning mechanism, optimal control is achieved under different flight conditions.

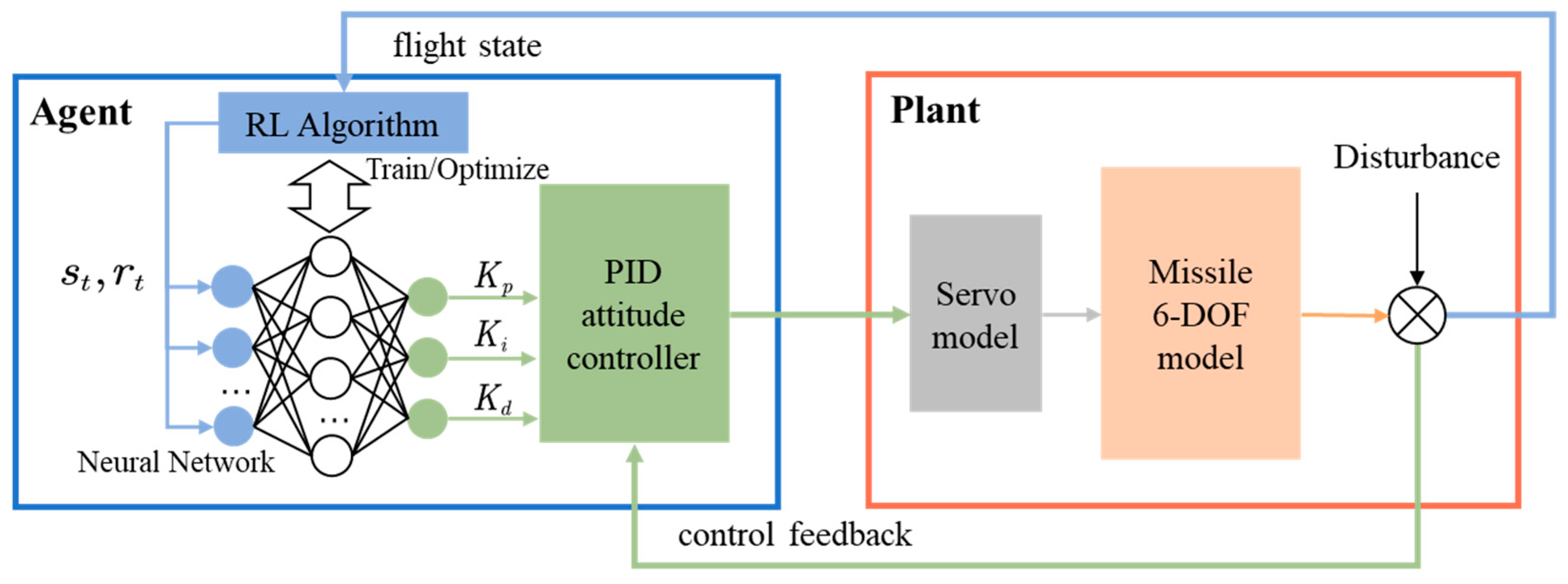
The overall system architecture, as shown in Figure 1, consists of the RL-PID agent and the missile system model. The RL-PID agent utilizes a deep neural network to real-time parse missile state information $s_t$, calculates rewards based on a designed reward function, and dynamically outputs the optimal tuning values $a_t$ for PID parameters. It can be expressed as

$$a_t={\pi }_{\theta }(s_t)={[K_p^t,K_i^t,K_d^t]}^T$$

(4)

The reinforcement learning algorithm is divided into a training phase and an online optimization phase. During the training phase, a maximum reward mechanism drives the agent to learn parameter tuning strategies. In online operation, the network parameters are fixed, and the $K_p$, $K_i$, and $K_d$ coefficients are updated based on real-time flight data, enabling the PID controller to achieve condition awareness and parameter evolution capabilities.

3. Method

TF-PPO algorithm is an optimized framework for missile attitude control, developed on the basis of the Proximal Policy Optimization (PPO) algorithm. Its innovations involve reconstructing the state space, incorporating a temporal network to capture historical state dependencies, tailoring the algorithm workflow specifically for missile autopilot dynamics, and introducing a meticulously designed reward function that accounts for stage-specific characteristics of the cruise missile’s flight.

The complete TF-PPO implementation necessitates comprehensive design specifications for states, rewards, actions, and network architecture. As specified in Section 2, the RL-PID controller’s action outputs are formally defined. Subsequent sections will elaborate on the design methodology for each component.

3.1. State Space Reframing

Missile control system design relies on long-period observable parameters (e.g., Mach number $M_a$, angle of attack $\alpha$, flight altitude $H$) as states tailored to specific flight phases. Given that the attitude controller’s output consists of pitch angle commands, the commanded pitch angle ${\theta }_{\mathrm{des}}$ and the current body pitch angle ${\theta }_{\mathrm{cur}}$ must be incorporated. The state variables selected in this study are

$$s=[\begin{array}{ccccc}H& Ma& \alpha & {\theta }_{\mathrm{cmd}}& {\theta }_{\mathrm{body}}\end{array}]$$

(5)

During missile flight, frequent PID adjustments may induce undesirable oscillations. We select $t=5s$ as the control interval for the RL-PID system. However, since PID response constitutes a dynamic process, the state space design for missile attitude control must satisfy dual constraints: dynamic response representational completeness and computational feasibility. Considering both missile performance characteristics and state information within control intervals, this paper proposes a sliding-window based temporal state space construction method. The complete 13-dimensional state vector is defined as follows:

$$s_t=\left[\begin{array}{c}M{a}_t,H_t,{\alpha }_t,\underset{5-\mathrm{stepdesiredpitch}}{\underbrace{{\theta }_{\mathrm{cmd}}^{t-4},{\theta }_{\mathrm{cmd}}^{t-3},\dots ,{\theta }_{\mathrm{cmd}}^t}},\underset{5-\mathrm{stepactualpitch}}{\underbrace{{\theta }_{\mathrm{body}}^{t-4},{\theta }_{\mathrm{body}}^{t-3},\dots ,{\theta }_{\mathrm{body}}^t}}\end{array}\right]\in {ℝ}^{13}$$

(6)

where ${\theta }_{\mathrm{cmd}}^{t-k}$ and ${\theta }_{\mathrm{body}}^{t-k}$ denote the commanded pitch angle and actual body pitch angle at time $t-k$, respectively, forming a raw temporal sequence spanning a 5 s time window.

3.2. Neural Architecture Design

The TF-PPO algorithm operates on an Actor–Critic [45] framework to collaboratively optimize control policies. Although the Actor–Critic architecture inherently assumes a Markov Decision Process (MDP), the missile PID control system exhibits non-Markovian characteristics due to its integral and derivative components requiring historical signal information prior to the current timestep. To address these non-Markovian properties, we embed a shared LSTM layer within the conventional Actor–Critic structure, thereby constructing a temporal feature fusion network. The detailed architecture is depicted in Figure 2.

The input layer receives a 13-dimensional state vector $s_t$, which undergoes Batch Normalization preprocessing before entering the shared feature extraction layer. The shared LSTM module employs a unidirectional structure. The temporal dependency between commands and responses is formulated as

$$(z_t,c_t)=\mathrm{LSTM}(s,z_{t-1},c_{t-1})$$

(7)

where $z_t$ denotes the hidden state output from the LSTM network, $c_t$ represents the cell state in long-term memory. The hidden state is concurrently fed into both Actor and Critic networks, where two distinct fully connected layers generate the action $a_t$ and state-value function $V_{\varphi }(s_t)$, respectively, achieving historical feature reuse.

3.3. Reward Engineering

Reward engineering in reinforcement learning is the process of designing reward systems. Through deliberate reward structuring, it provides agents with discriminative signals that indicate behavioral correctness [35]. The missile control system represents a highly nonlinear precision engineering system. Prior to reinforcement learning deployment, the identification of reward-shaping metrics critical to optimizing control precision is essential for RL-driven controllers. Addressing distinct dynamic characteristics during altitude adjustment, cruise, and descent phases of cruise missiles, this section proposes an adaptive stage-strength quantified reward function. This framework reconstructs RL rewards through phase-strength quantification, enabling stable optimization trajectories for control policies.

3.3.1. Stage-Strength Quantification

The stage-strength $\Psi \in [0,1]$ parameter characterizes the dominance of the current flight phase, where a higher value indicates greater priority for phase-specific control objectives. This parameter depends solely on instantaneous flight states, eliminating inter-phase coupling complexities while ensuring global adaptability with seamless phase transitions. The quantification mechanism is defined as follows:

$$\Psi =\left\{\begin{array}{c}{\Psi }_{\mathrm{adjust}}\left({\dot{h}}_t\right)={\displaystyle \frac{1}{1+e^{-k_1({\widehat{h}}_t-{\delta }_1)}}}\\ {\Psi }_{\mathrm{descend}}\left({\dot{h}}_t\right)={\displaystyle \frac{1}{1+e^{k_2({\widehat{h}}_t+{\delta }_2)}}}\\ {\Psi }_{\mathrm{cruise}}\left({\dot{h}}_t\right)=1-({\Psi }_{\mathrm{adjust}}+{\Psi }_{\mathrm{descend}})\end{array}\right.$$

(8)

where the shape parameter $k_1,k_2>0$ controls the function slope, ${\delta }_1,{\delta }_2>0$ denotes the phase offset and $\widehat{h}$ represents the rate of change of altitude. To eliminate dimensional disparities and establish probabilistic weight allocation, we apply a softmax normalization, this guarantees ${\displaystyle \sum {\tilde{\alpha }}_i=1}$, thereby ensuring continuous transitions of phase dominance rights.

$$[{\tilde{\Psi }}_c,{\tilde{\Psi }}_r,{\tilde{\Psi }}_d]=\mathrm{softmax}([{\Psi }_{\mathrm{adjust}},{\Psi }_{\mathrm{cruise}},{\Psi }_{\mathrm{descend}}])$$

(9)

The schematic of the stage-strength evolution is shown in Figure 3.

3.3.2. Adaptive Reward Function Formulation

The RL-PID system targets high-precision tracking of guidance-commanded pitch attitudes. Therefore, pitch angle error ${\theta }_e$ and pitch rate error $q_e$ should be considered in the reward function. To mitigate unnecessary oscillations induced by frequent PID adjustments, the elevator deflection angle ${\delta }_e$ is incorporated into the reward function. The global reward function is formulated around three core components: pitch angle error ${\theta }_e$, pitch rate error $q_e$, and elevator deflection ${\delta }_e$. Phase-adaptive optimization is achieved through the weighting matrix $A\in {ℝ}^{3\times 3}$. Its mathematical form is

$$R=\tilde{\Psi }A{\varphi }^T$$

(10)

where $\varphi =[\begin{array}{ccc}{\theta }_e& q_e& {\delta }_e\end{array}]$ denotes the parameters considered for the reward function. Tailored to distinct phase characteristics, the weighting matrix $A$ is architected as

$$A=\left[\begin{array}{ccc}{\eta }_{\theta ,\mathrm{adjust}}& {\eta }_{q,\mathrm{adjust}}& 0\\ {\eta }_{\theta ,\mathrm{cruise}}& 0& {\eta }_{\delta ,\mathrm{cruise}}\\ {\eta }_{\theta ,\mathrm{descent}}& {\eta }_{q,\mathrm{descent}}& {\eta }_{\delta ,\mathrm{descent}}\end{array}\right]$$

(11)

Each column weight must meet the normalization constraint ${\displaystyle \sum {\eta }_{i,j}}=1(\forall i\in \{\theta ,q,\delta \})$, The values of the weight matrix are manually designed based on the characteristics of the flight phase. Through explicit functional coupling between the stage-strength $\Psi$ parameter and weight matrix $A$, adaptive prioritization switching of control objectives is achieved.

3.4. Training Process

The training process of the TF-PPO algorithm introduces an adaptive exploration mechanism to optimize stability within the canonical PPO framework. Parameters of the Actor and Critic networks are initialized orthogonally [46], ensuring the initial policy satisfies Gaussian distribution properties. The agent generates PID parameters $K_p$, $K_i$, $K_d$ through the Actor network, with adaptive Gaussian noise superimposed to maintain exploratory behavior:

$$a_t~\mathcal{N}(\pi (\mu |s_t),{\sigma }^2)$$

(12)

Traditional PPO algorithms typically employ fixed-decay exploration strategies, which cannot guarantee convergence. This paper proposes an adaptive exploration strategy based on advantage functions. When substantial policy advantage exists, it reduces randomness in action sampling to guarantee stable convergence to optimal policies. If the current strategy has strong advantages, reduce the randomness of exploration. This ensures that the algorithm converges to the optimal strategy.

$${\sigma }_{e+1}={\sigma }_e\cdot \left(1-\zeta \cdot {\displaystyle \frac{A\left(s_e,a_e\right)}{\max \left(A\right)}}\right)\cdot \left(1-\beta \cdot {\displaystyle \frac{e}{E}}\right)$$

(13)

In the formula, ${\sigma }_e$ is the standard deviation of action sampling for the current episode, $A\left(s_e,a_e\right)$ is the dominant function value in state $s_e$.$\zeta ,\beta$ is the relevant attenuation coefficient $(0<\zeta ,\beta <1)$, used to control the influence of the number of training episodes on the standard deviation. $E$ is the total number of training episodes or the preset upper limit of training times.

During this process, the interaction between the missile autopilot and the environment forms a closed-loop control loop. The PID parameter increment output by the intelligent agent is applied in real-time to the six degrees of freedom dynamic model of the missile, generating elevator deflection commands ${\delta }_z$ and driving flight trajectory adjustment. The observation includes the attitude angle error ${\theta }_e$, altitude change rate $\widehat{h}$, and other critical state variables at the next moment under environmental feedback. Next, the scalar reward signal will be calculated using the reward function designed in the previous section. After each training round, the system calculates discount returns $G_t={\displaystyle \sum _{.}^{k=0}{\gamma }^k}{r}_{t+k}$ and advantage functions $A_t=G_t-V_{\varphi }(s_t)$ based on accumulated rewards, Where $V_{\varphi }(s_t)$ is the state value estimated by the critic network, ${\gamma }^k$ represents the discount factor and $r_{t+k}$ Instant reward obtained from time step $t$.

For the process of strategy optimization, the objective function of TF-PPO algorithm is designed as:

$${\mathcal{L}}_{\mathrm{actor}}={\mathbb{E}}_t\left[\min \left({\displaystyle \frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\mathrm{old}}}(a|s)}}{A}_t,\mathrm{clip}\left({\displaystyle \frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\mathrm{old}}}(a|s)}},1-\epsilon ,1+\epsilon \right)A_t\right)\right]$$

(14)

The actor network employs a clipped policy ratio mechanism to constrain parameter updates and prevent abrupt policy shifts. Simultaneously, the critic network updates by minimizing value estimation errors:

$${\mathcal{L}}_{\mathrm{critic}}={\mathbb{E}}_t[{\left(V_{\varphi }(s_t)-G_t\right)}^2]$$

(15)

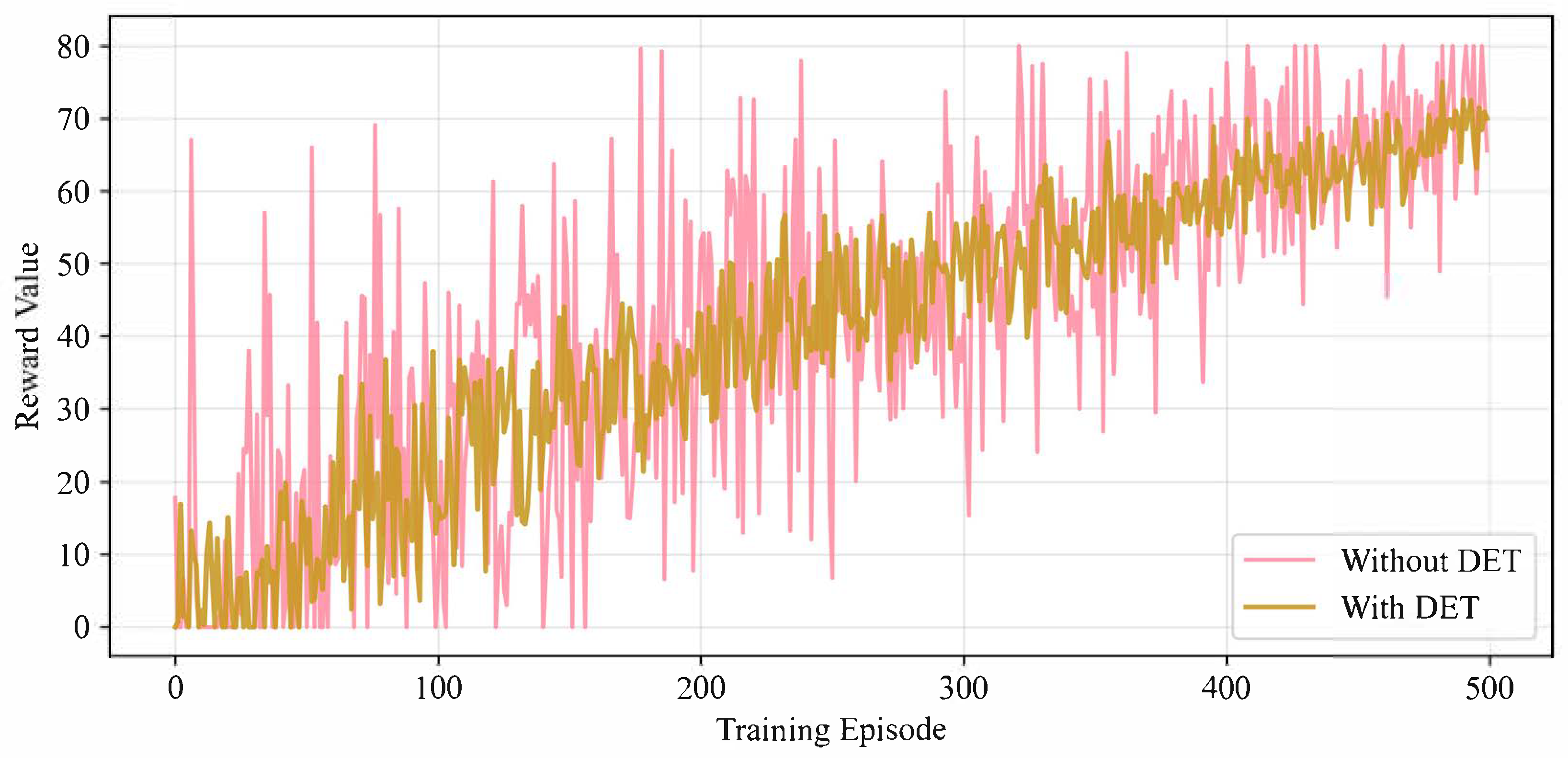
During algorithm training, reinforcement learning agents exhibit high sensitivity to training data quality in their parameter optimization. When suboptimal control trajectories are significantly present in the experience replay buffer, agents risk acquiring detrimental control patterns through policy gradient updates, leading to convergence toward suboptimal solutions or even divergence. This study incorporates dynamic early termination (DET) into the training process, enhancing operational robustness to mitigate this vulnerability.

The early termination criterion is mathematically defined as

$${\mathcal{T}}_{\mathrm{stop}}=\left\{\begin{array}{cc}1,& if\left|{\theta }_e\right|>{\theta }_{th}\wedge {\theta }_e\cdot q_e>0\\ 0,& \mathrm{otherwise}\end{array}\right.$$

(16)

When ${\mathcal{T}}_{\mathrm{stop}}=1$, terminate the current training round and adjust the termination time reward to

$$R_{\mathrm{term}}=R_{\mathrm{base}}-\lambda R_{\mathrm{fixed}}$$

(17)

where $R_{\mathrm{base}}$ denotes the raw reward value at termination, $\lambda >1$ represents the penalty coefficient, and $R_{\mathrm{fixed}}$ is a predefined constant penalty term. This design ensures training stability through policy exploration constraints and bounded reward scaling, achieving a 62% reduction in reward variance, as shown in Figure 4.

The pseudocode for the TF-PPO algorithm procedure is presented in Algorithm 1.

Algorithm 1: TF-PPO

Initialize policy network π and value network V

Set hyperparameters: learning rate α, discount factor γ, clip parameter ε, episodes E, update interval U

$\hspace{1em}\mathbf{for} i\in \{1,\cdots ,N\}$ do

$\hspace{1em}\hspace{1em}\mathbf{for} j\in \{1,\cdots ,M\}$ do

$\hspace{1em}\hspace{1em}\mathrm{Run} \mathrm{policy} {\pi }_{\theta }$$, \mathrm{collecting} \{s_t,a_t,r_t\}$

Check termination condition via DET

$\hspace{1em}\hspace{1em}\mathrm{Estimate} \mathrm{discount}\mathrm{returns} G_t$$\mathrm{and} \mathrm{advantages} A_t=G_t-V_{\varphi }(s_t)$

Decay action selection noise:     ${\sigma }_{e+1}={\sigma }_e\cdot \left(1-\zeta \cdot {\displaystyle \frac{A\left(s_e,a_e\right)}{\max \left(A\right)}}\right)\cdot \left(1-\beta \cdot {\displaystyle \frac{e}{E}}\right)$

$\hspace{1em}\hspace{1em}\mathbf{if} j\%T=0$ then   $\hspace{1em}\mathrm{Update} {\pi }_{\theta }$ according to the objective function         ${\mathcal{L}}_{\mathrm{actor}}={\mathbb{E}}_t\left[\min \left({\displaystyle \frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\mathrm{old}}}(a|s)}}{A}_t,\mathrm{clip}\left({\displaystyle \frac{{\pi }_{\theta }(a|s)}{{\pi }_{{\theta }_{\mathrm{old}}}(a|s)}},1-\epsilon ,1+\epsilon \right)A_t\right)\right]$

end if

end for

end for

4. Experimentation and Evaluation

To validate the performance of the proposed TF-PPO algorithm, this section presents comprehensive mathematical simulations and hardware-in-the-loop (HIL) experiments. The validation is conducted in two parts: First, mathematical simulations using step response prove that the TF-PPO algorithm offers faster convergence and better performance than other RL algorithms under large step signal excitation. Second, a missile control rapid prototyping system is designed. The attitude tracking performance of TF-PPO and traditional PID methods is evaluated under different initial conditions and wind disturbances. This verifies the robustness and self-evolution capability of parameters of the proposed method.

4.1. Step Response Experiment

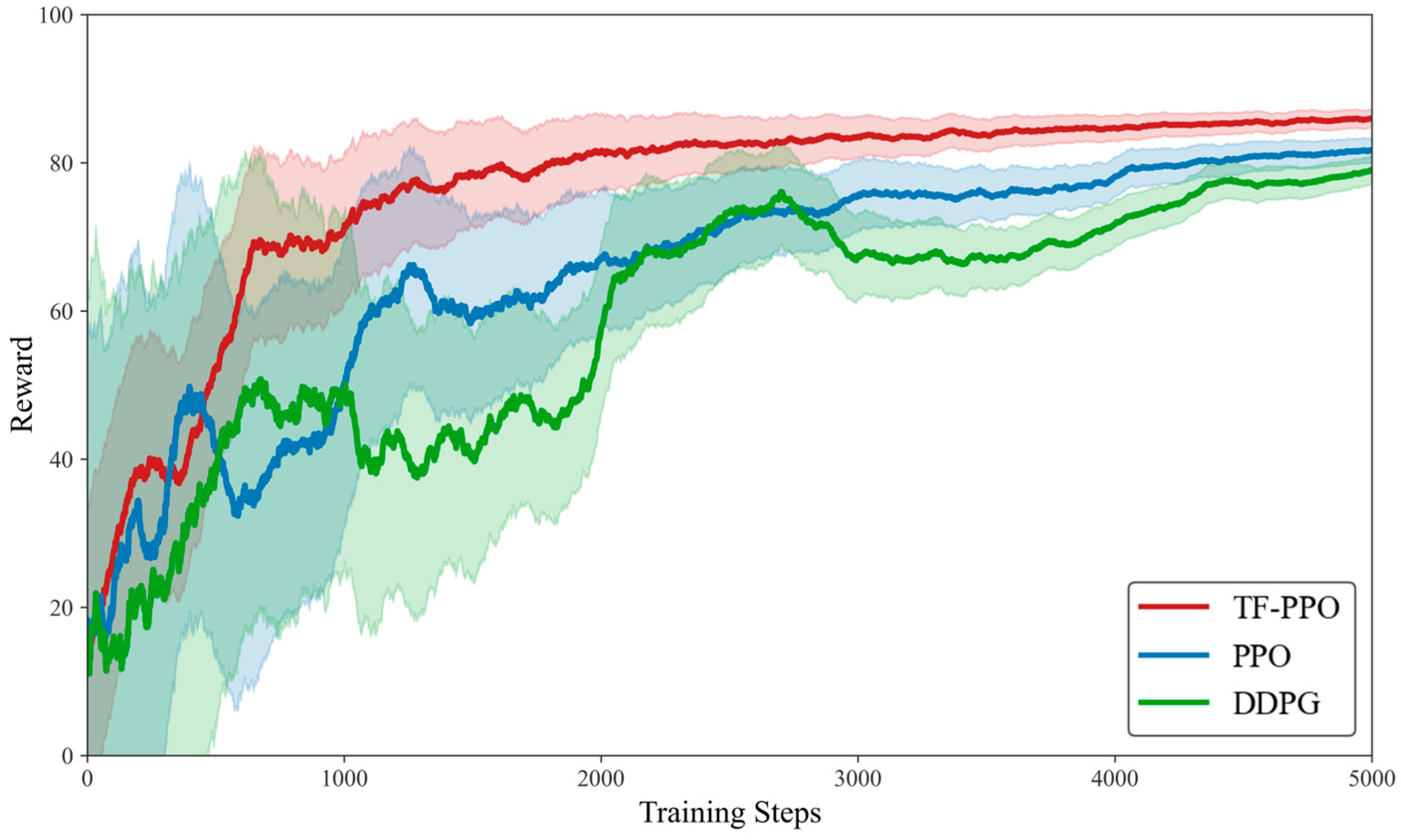
To evaluate the core contribution of the Temporal Feature Fusion mechanism, this part of the experiment uses a simplified reward function $r_t=-{\theta }_e$ to compare TF-PPO with other algorithms. First, a 6-DOF mathematical simulation model of the missile is constructed. Then, different RL algorithms are connected to this mathematical model. We designed a fixed scenario where a large step command is given to the control system every 15 s. Using this scenario, each algorithm is trained for 5000 episodes. The convergence effectiveness of the different algorithms is assessed.

This paper uses three algorithms, TF-PPO, PPO, and DDPG, for comparative step response experiments.

Table 4. TF-PPO hyperparameter settings.

Symbols	Parameter Explanation	Reference Range	Selected Value
$\epsilon$	Clip ratio (limits policy update magnitude)	0.1~0.3	0.1
${\eta }_{\mathrm{action}}$	Actor learning rate	0.00001~0.001	0.00005
${\eta }_{\mathrm{critic}}$	Critic learning rate	0.00001~0.001	0.0001
$\gamma$	Discount factor	0.8~0.999	0.99
N	Sample size per training step	64~512	128
K	Optimization passes per batch	1~100	10
T	Update interval steps	10~10,000	500

describes the relevant algorithm training parameters. The PPO algorithm uses the same training parameters. For DDPG, the parameter $\tau$ is set to 0.005, while other parameters remain consistent. The training results are shown in Figure 5, where a moving average is applied to the results. The shaded area represents the variance of the reward.

From the results, it can be seen that the TF-PPO and PPO algorithms, due to the existence of the clip method, avoid drastic changes in strategy and have relatively stable training processes. Compared to the classical PPO algorithm, TF-PPO exhibits faster convergence speed and learns better results. The trained models are reconnected to the simulation system to compare the effects of the different algorithms.

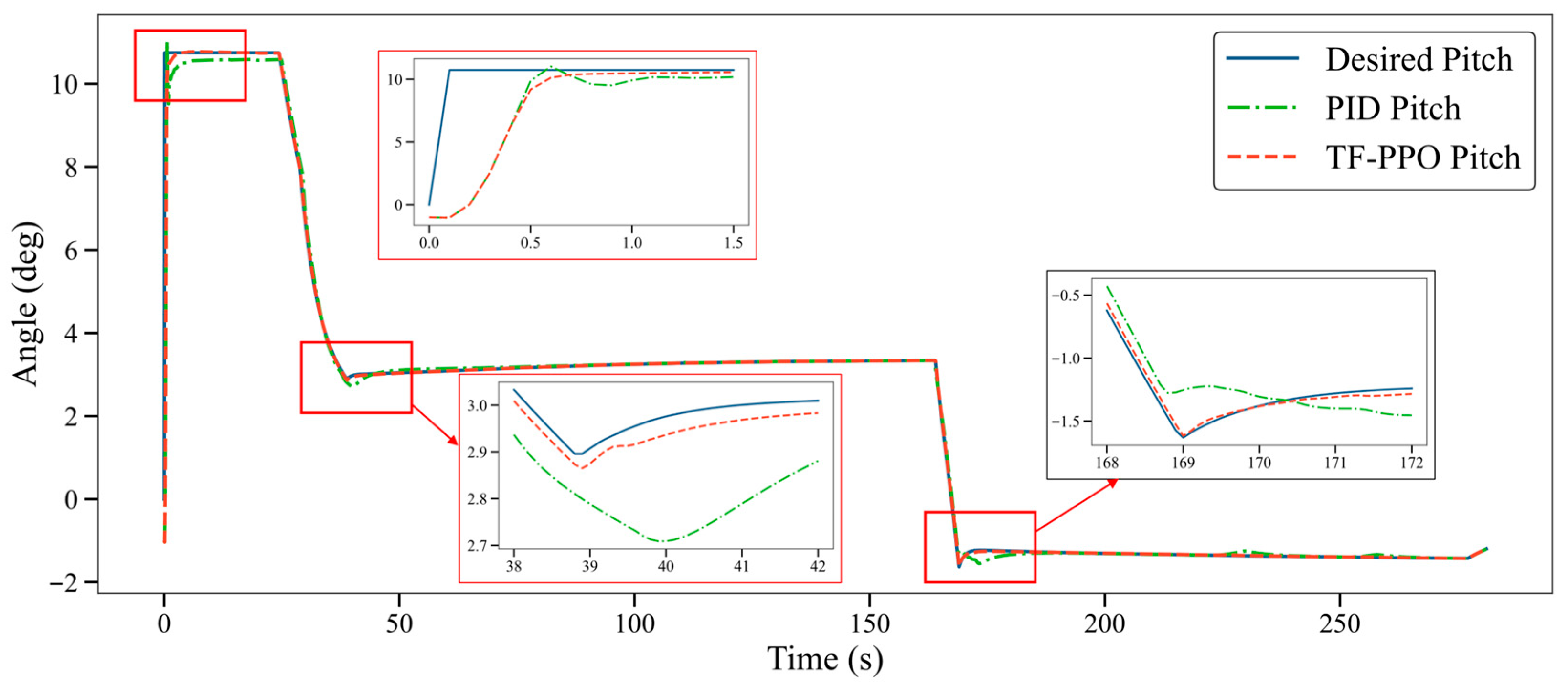
The specific effects are shown in Figure 6. The control accuracy of the TF-PPO algorithm is superior to the other algorithms. Compared with the traditional PPO algorithm, TF-PPO achieves an average control accuracy improvement of 14.3% with similar settling time, as summarized in

Table 5. Numerical simulation results.

Algorithm	$\overline{\mathit{e}}$	${\mathit{\sigma }}_{\mathit{e}}^2$	${\overline{\mathit{t}}}_{\mathit{s}}$
PPO	0.1487	0.5297	0.6627
DDPG	0.2091	0.5675	1.5323
TF-PPO	0.1274	0.4998	0.6250

. This demonstrates that the proposed algorithm has better training effectiveness for the missile guidance and control system.

4.2. Offline Training

The online optimization of the TF-PPO algorithm relies on high-quality offline training. Although TF-PPO is an on-policy algorithm, its missile-borne deployment on cruise missiles requires training the network parameters within the ground segment beforehand. Therefore, constructing a training environment that approximates real missile application conditions is essential. We use the AFSIM simulation platform as the training environment, deploy our six degrees of freedom missile model in AFSIM, and train the missile reinforcement learning control system by designing different initial conditions and flight plans.

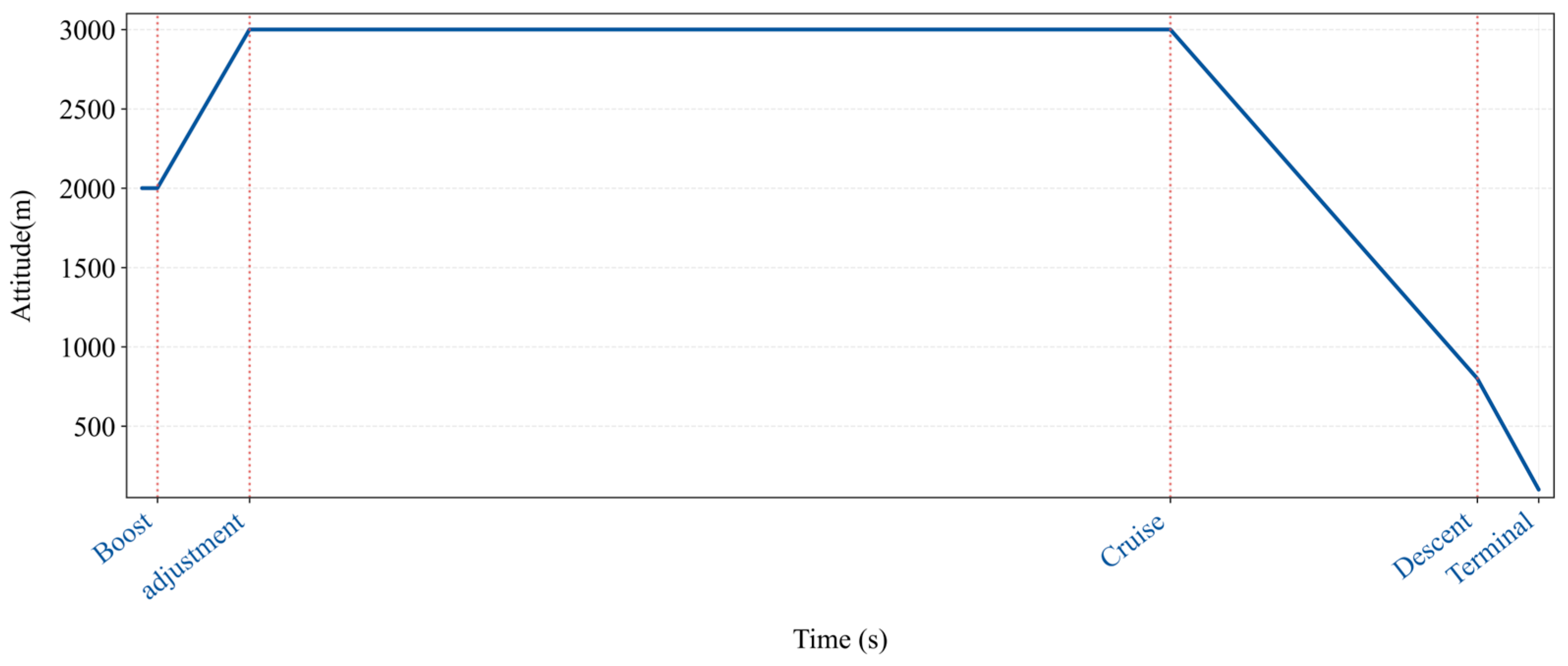
This experiment constructed a cruise trajectory plan based on a simulation platform, which includes an acceleration phase, an altitude adjustment phase, a cruise phase, a descent phase, and a terminal guidance phase. The missile was launched by air launch, and Figure 7 shows a typical trajectory plan for missile flight. Based on typical trajectory schemes, the initial launch conditions and cruising altitude for each training round are determined through uniformly distributed random sampling, and the missile control system network is trained accordingly.

Table 6. Random Sampling Parameters for Offline Training.

Names	Values	Units
Training epochs	5000	-
Launch height	1000–5000	m
Launch elevation angle	−5~5	°
Initial Mach number	0.5~0.7	-
Cruising altitude	3000~5000	m

describes the specific parameter design of offline training parameters. The TF-PPO algorithm was trained using an adaptive reward function, and the model training hyperparameters were consistent with Table 4. After completing offline training of the algorithm, the trained algorithm was reconnected to a typical trajectory through a simulation system for full trajectory flight simulation. The simulation results are shown in Figure 8.

The TF-PPO algorithm trained offline can automatically adjust the PID parameters of the pitch loop without prior knowledge. The results show that the missile pitch loop attitude control system under the TF-PPO algorithm exhibits good tracking performance, and in the stage transition stage, the algorithm outperforms the PID control system based on static design. Figure 9 illustrates the dynamic adjustment of PID parameters by RL-PID during missile flight. The PID parameters will be adaptively adjusted according to the stage characteristics.

4.3. Rapid Prototyping System

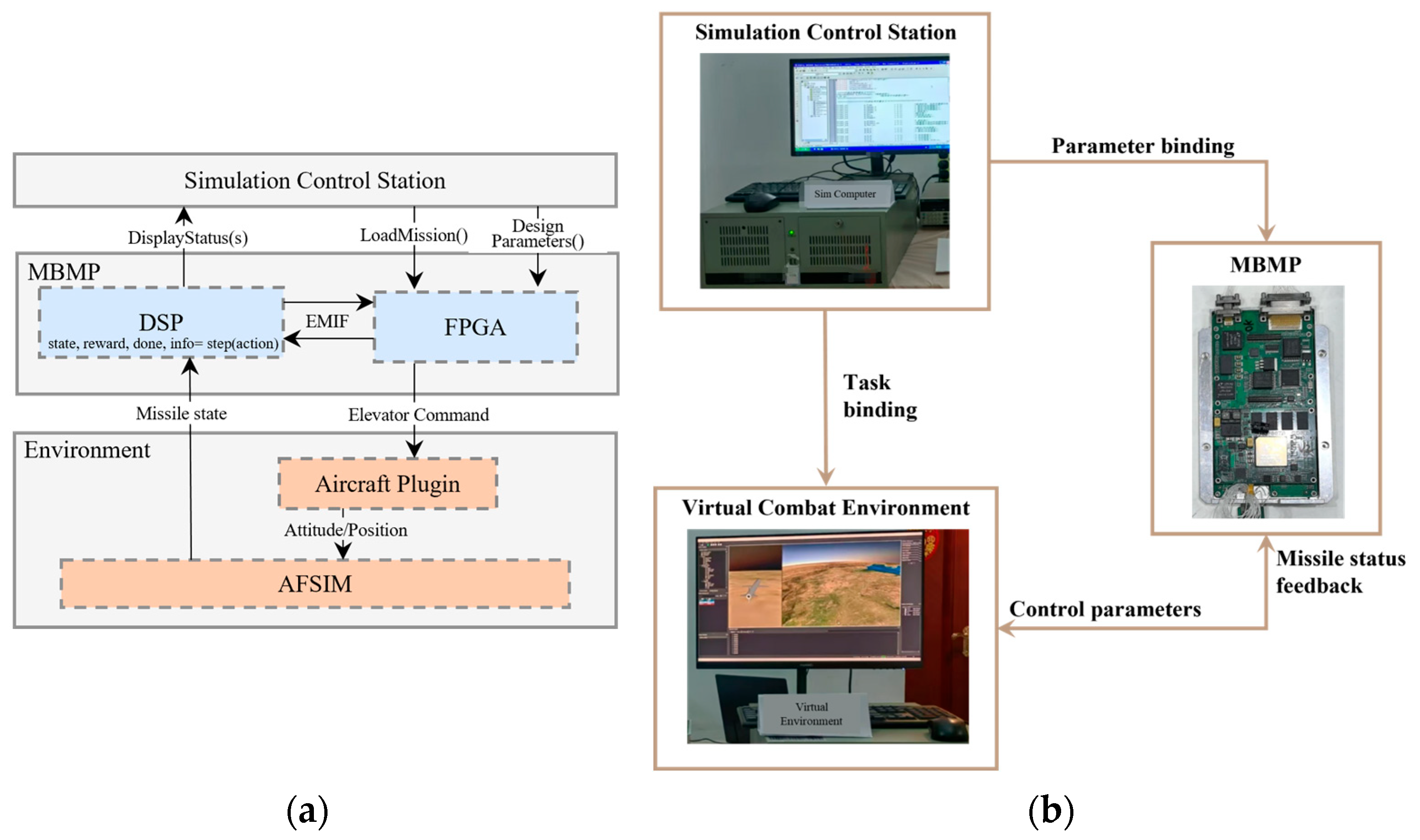
To validate the performance of the RL-PID algorithm in practical control, this study constructed a missile rapid prototyping system consisting of a simulation computer, missile-borne mission computer, and simulation platform, as shown in Figure 10. Hardware-in-the-loop (HIL) simulation was implemented to achieve closed-loop verification of multi-phase trajectories.

Rapid prototyping is a prototype development methodology that focuses on creating prototypes early in the development cycle [47]. This enables early feedback and analysis to support the development process. The rapid prototyping system described in this paper integrates three components: a Simulation Control Station for initial parameter configuration and mission programming that exchanges data bidirectionally with the core systems; a Missile-Borne Mission Processor (MBMP) implementing DSP + FPGA architecture to emulate physical missile control hardware, where this embedded processor executes the full missile control algorithm suite by receiving real-time missile states, computing aerodynamic surface commands, and transmitting control signals; and a Virtual Combat Environment leveraging the U.S. Air Force Research Laboratory’s AFSIM [48] platform, within which our six-degree-of-freedom missile model operates to execute received control commands, simulate adversarial engagements, and provide continuous state feedback.

Table 7. Hardware configuration of MBMP.

Component	Values
DSP (TMS320C6678)	8-core, 1.25 GHz clock speed, 4 GB DDR3
FPGA (Xilinx Kintex-7 XC7K325T)	326 K logic cells, 1.4 Gb/s transceiver speeds
Gigabit Ethernet	100 Mb/s bidirectional data exchange
LVDS Serial Links	End-to-end latency < 0.5 ms

describes the hardware configuration of MBMP.

To validate the control algorithm’s adaptability to various flight profiles, multiple distinct planned trajectories were randomly generated within the parameter boundaries specified in Table 6 for simulation. Concurrently implemented two control groups demonstrate algorithm and reward engineering advantages: the first group utilizes a manually tuned PID controller with fixed gains for standard flight profiles, and the second group employs a TF-PPO algorithm with $r_t=-{\theta }_e$ as its reward function (also trained offline for 5000 iterations under identical conditions; no reward engineering, labeled no RE in figures). Both groups were validated under identical randomized initial condition configurations as the experimental group.

The experimental framework was designed around a simulated test scenario featuring an air-launched cruise missile deployed by a fighter aircraft. The missile’s objective is to strike a designated maritime target in a simulated maritime environment.

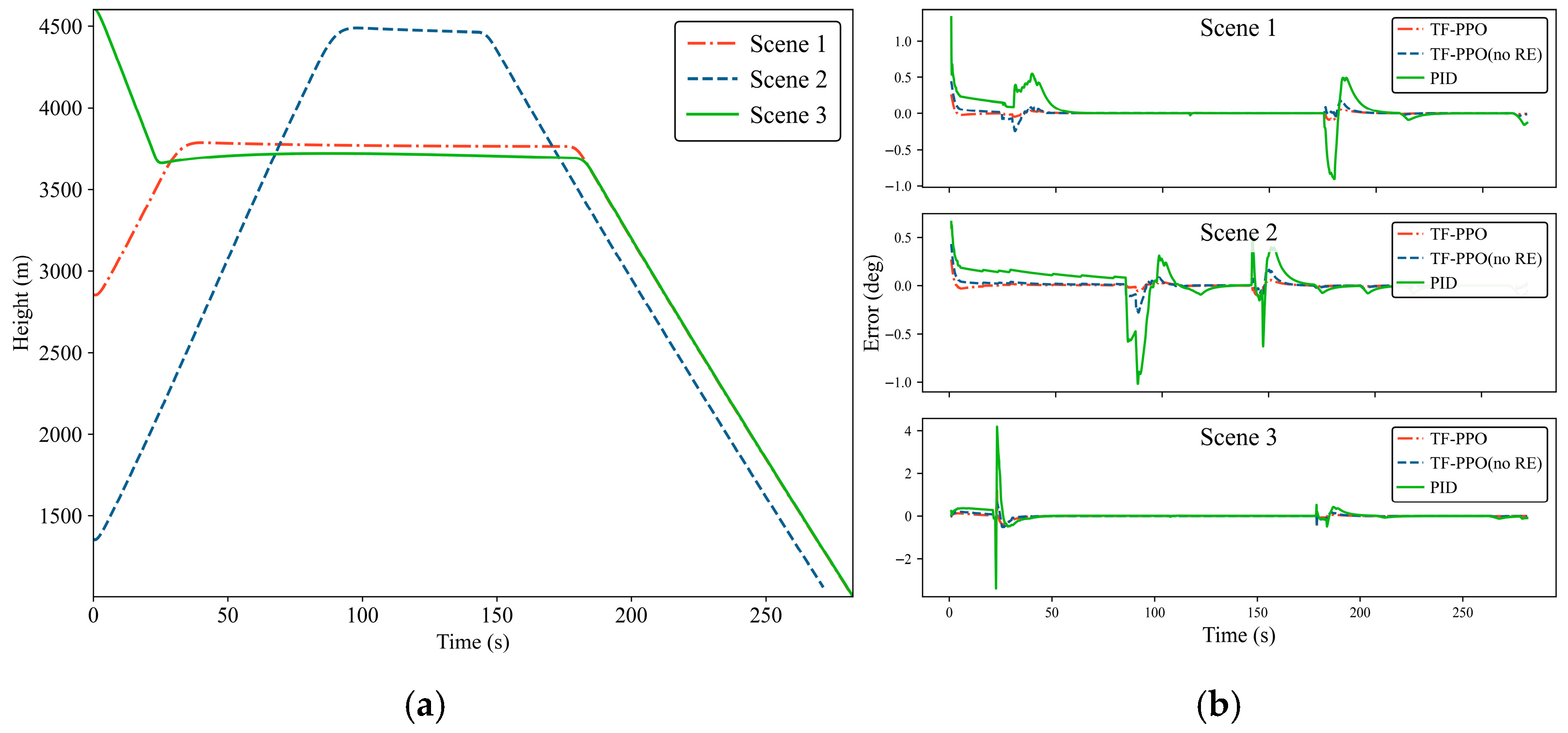
Due to different control strategies employed in the terminal guidance phase, data collection was limited to the launch-to-descent phase. Statistical results from all experiments are shown in

Table 8. Pitch Angle Error Statistics.

Evaluation Scope	Control Method	Mean (95% CI) (°)	Std (°)	Max (°)
Entire trajectory	PID	0.0212 (0.0186–0.0234)	0.1215	4.9703
	TF-PPO (no RE)	0.0144 (0.0131–0.0162)	0.0494	2.9721
	TF-PPO	0.0135 (0.0126–0.0151)	0.0235	1.4233
Transition phase	PID	0.1204 (0.0913–0.1495)	0.1701	4.9703
	TF-PPO (no RE)	0.0667 (0.0561–0.0783)	0.0853	2.9721
	TF-PPO	0.0528 (0.0421–0.0615)	0.0690	1.4233

. Representative experimental runs are depicted in Figure 11, which illustrates the missile flight altitude and attitude angle error.

Figure 12 shows simulation snapshots capturing key moments of the engagement scenario within the AFSIM environment. The results indicate that the TF-PPO algorithm demonstrates significant improvement over the empirically tuned PID controller, achieving a 36.3% increase in pitch angle control accuracy across the entire trajectory. Analysis of maximum values reveals that control errors predominantly concentrate during transitional phases. During these transitional phases, compared to TF-PPO without DET, the TF-PPO algorithm reduced the maximum attitude tracking error by 52.1%.

Furthermore, reward engineering constraints on elevator deflection prevent excessive PID adjustments, reducing control error variance by 54% throughout the flight. These findings demonstrate the practical utility and robustness of the reward engineering-based TF-PPO algorithm.

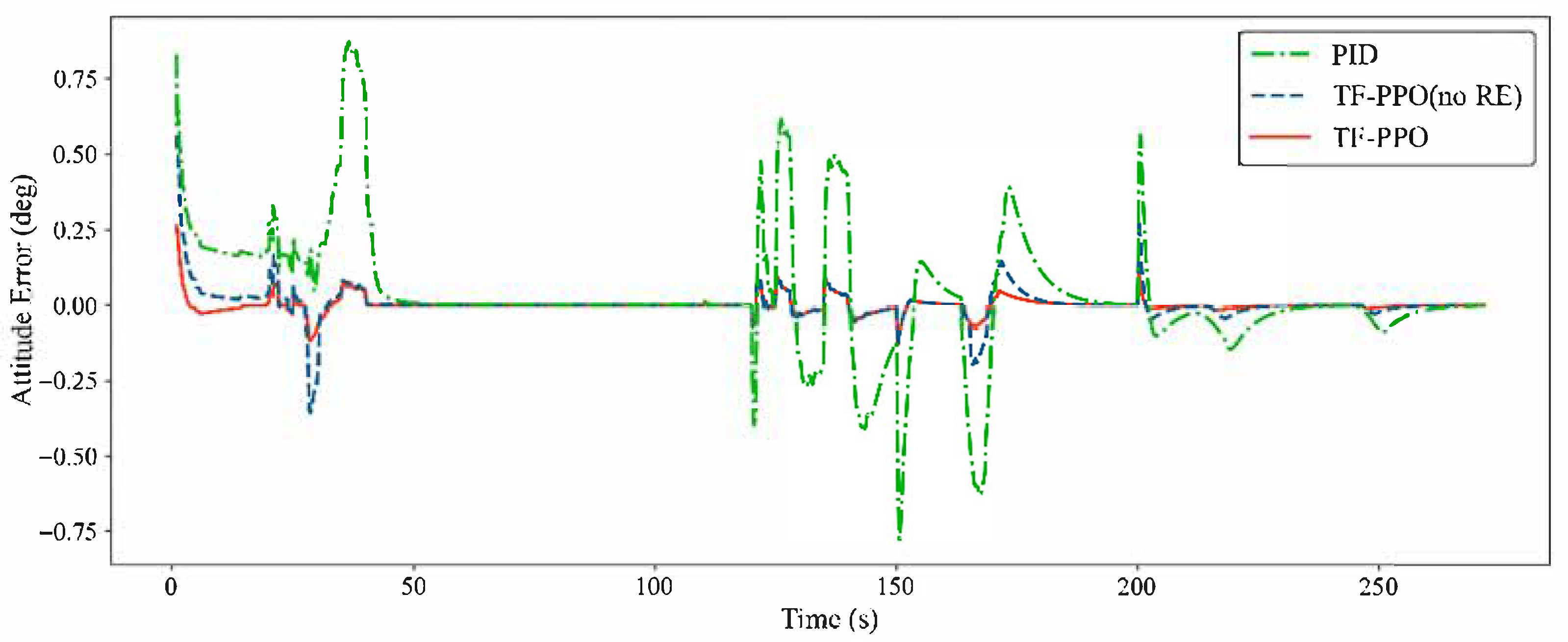
To further validate the disturbance rejection capability of the TF-PPO-controlled longitudinal channel, wind disturbance profiles were applied during altitude adjustment, cruise, and descent phases in typical simulation scenarios, verifying the algorithm’s attitude stabilization performance under external disturbances.

Table 9. Wind Disturbance Variation Matrix.

Duration (s)	Steady-State Wind Bias (East, North, Up; m/s)	Gust Wind Bias (East, North; m/s)
20~40	(-, -, -)	(20, -)
20~60	(-, -, −6)	(-, -)
120~140	(-, -, -)	(20, 20)
150~200	(-, -, 10)	(-, -)
370~390	(-, -, -)	(-, 20)
390~430	(-, -, 8)	(-, -)

details the design matrix for wind disturbance variations.

The results demonstrate that TF-PPO’s adaptable reward mechanism effectively mitigates attitude fluctuations induced by external disturbances. Under wind disturbances, the TF-PPO algorithm exhibits significantly lower average error than conventional PID control, as quantitatively compared in

Table 10. Error Statistics Comparison Under Wind Disturbance Variation Tests.

Evaluation Scope	Control Method	Mean	Std	Max
Wind disturbance period	PID	0.2489	0.2202	0.8249
disturbance	TF-PPO (no RE)	0.0569	0.0474	0.5622
period	TF-PPO	0.0389	0.0359	0.2628

and Figure 13. Compared to the version without reward engineering, the complete TF-PPO algorithm achieves 31.6% higher comprehensive accuracy, confirming its practical value for engineering implementation in complex battlefield environments.

5. Conclusions

(1)

An expert-free RL-PID architecture is proposed for missile control parameter self-evolution through autonomous online optimization, eliminating manual tuning dependency during complex flight maneuvers while ensuring real-time adaptation across all mission phases.

(2)

The TF-PPO framework incorporating LSTM networks to enhance reinforcement learning adaptability for PID parameter tuning, where strategic reward engineering and adaptive exploration strategies effectively identify optimal parameters across distinct missile flight phases.

(3)

A modular rapid-prototyping missile control platform integrates hardware-in-loop simulation with combat-realistic environments, enabling direct validation of controller performance under stochastic disturbances through rapid iteration capability.

(4)

Established quantifiable verification methodology combining step-response analysis and rapid prototyping experiments objectively evaluates transient response improvement and disturbance rejection superiority over conventional methods.

6. Limitations and Future Work

Our study has several limitations: the system modeling overlooks the coupling effects between different attitude channels, potentially leading to deviations from actual missile dynamics; the application of reinforcement learning in missile control requires stronger interpretability to meet the high safety standards of the field; and the proposed method lacks comprehensive comparisons with state-of-the-art algorithms. To develop more reliable and practical solutions, our future research will prioritize creating a unified framework for the simultaneous and coordinated optimization of all three attitude channels.