A Unified Scheduling Model for Agile Earth Observation Satellites Based on DQG and PPO

Abstract

Agile Earth Observation Satellites (AEOSs), with their maneuverability, can flexibly observe point, line and region targets. However, existing research typically requires distinct algorithms for each target type, lacking a unified modeling and solution framework, which hinders the ability to meet the demands of rapid and coordinated observation of multiple target types in complex scenarios. To address these issues, this paper proposes a unified scheduling model for agile Earth observation satellites based on the Degenerate Quadtree Grid (DQG) and Proximal Policy Optimization (PPO), termed AEOSSP-USM. Firstly, the DQG is first employed to enable unified management and integrated modeling of point, line, and area targets; Secondly, traditional time window calculations based on longitude and latitude are replaced with grid code-based computations using DQG; Finally, the PPO algorithm, a deep reinforcement learning method, is introduced to formulate AEOSSP-USM as a Markov Decision Process (MDP), enabling efficient problem solving. Experimental results demonstrate that the proposed method effectively realizes unified scheduling of heterogeneous targets, improving imaging quality about 3 times, reducing energy consumption by 10%, decreasing memory usage more than 90%, and enhancing computational efficiency by 35 times compared to conventional longitude-latitude strip algorithm.

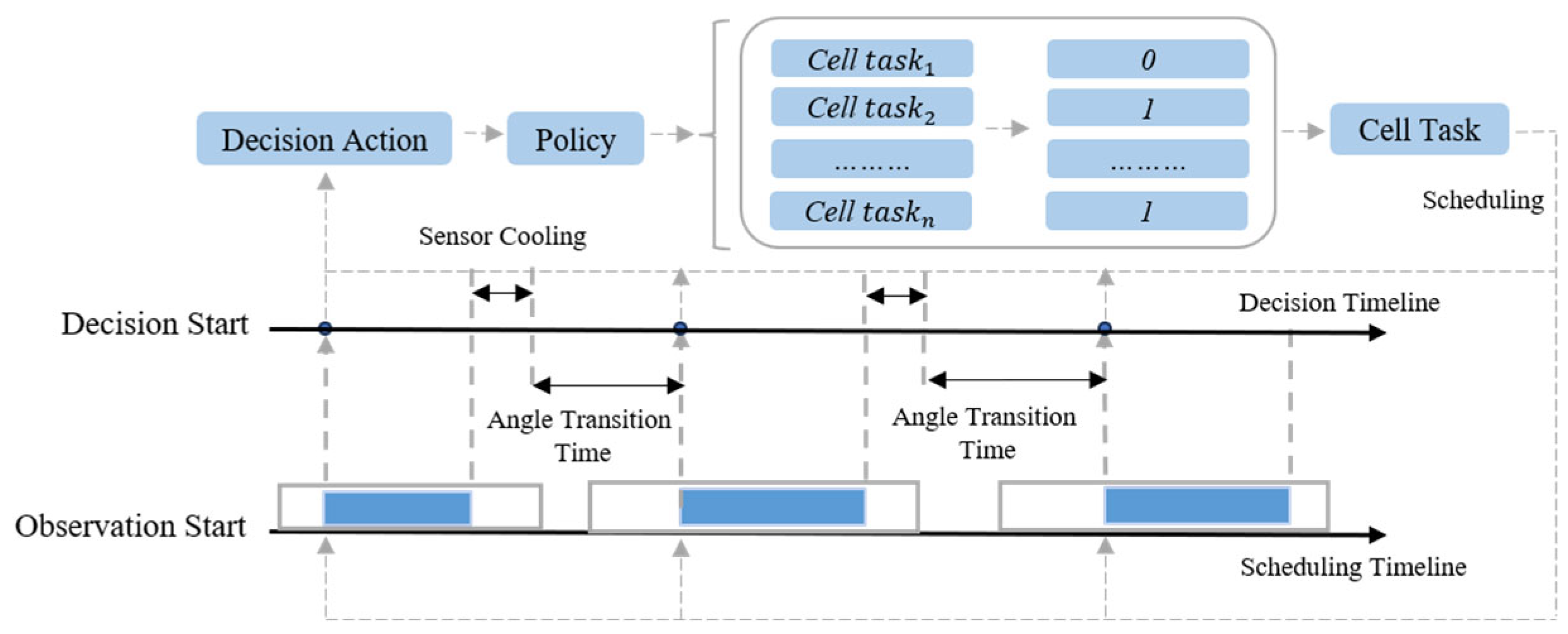
1. Introduction

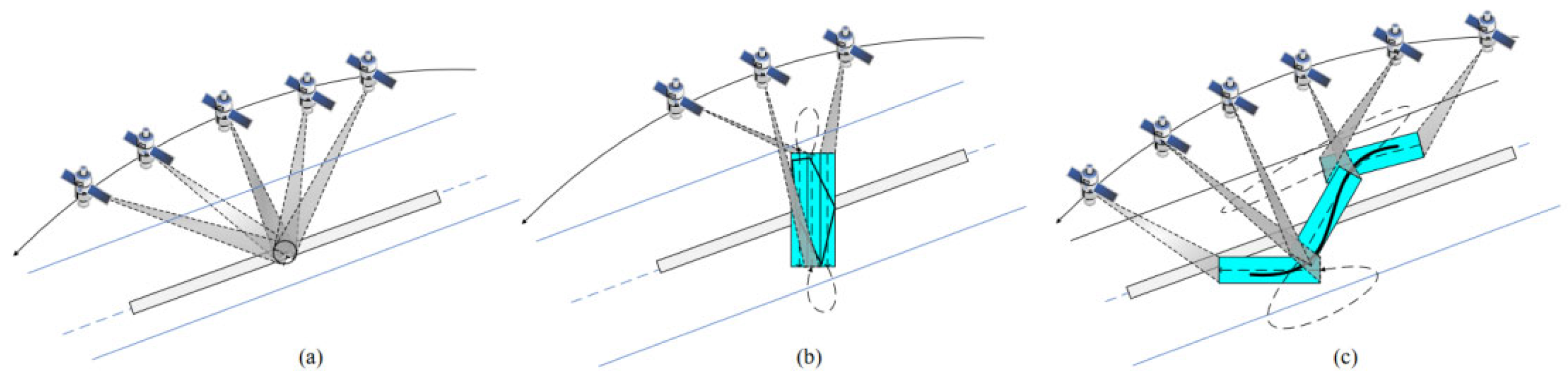
With the rapid development of imaging payload technology, agile Earth observation satellites have significantly extended the observable time window for targets through their high-precision pitch and yaw control systems, enabling the acquisition of high-resolution images and supporting multi-angle stereoscopic imaging (Figure 1a), regional target mosaic imaging Figure 1b, and line target non-adjacent imaging Figure 1c) and other diverse mission requirements. The related capabilities have been widely applied in key fields such as intelligent transportation systems, emergency response, and military operations. However, current Earth observation tasks often require the simultaneous acquisition of image data of three heterogeneous targets: point targets that need precise positioning, line targets that require continuous trajectory coverage, and region targets that need large-scale monitoring. To support comprehensive situational awareness, existing studies have independently designed algorithms for point targets, line targets, and region targets. Due to the characteristic differences in the need for precise positioning of point targets, continuous path coverage of line targets, and multi-view data stitching of region targets, a unified representation framework is missing, which leads to threefold complex scheduling challenges: under the strong constraints of limited resources such as satellite maneuverability, energy supply, and observation window, it is necessary to coordinate the priority conflicts between high-urgency point target monitoring tasks such as disaster response and large-scale environmental assessment tasks such as region monitoring; it is necessary to integrate diverse constraints such as coordinate accuracy, continuous coverage path, and multi-temporal data requirements into a unified modeling framework; and it is necessary to simultaneously optimize the observation efficiency and resource allocation of dynamic arriving heterogeneous targets such as sudden disaster point targets and continuous monitoring surface targets through a single scheduling decision. These challenges jointly restrict the collaborative observation capability of agile Earth observation satellites for heterogeneous targets, highlighting the necessity of developing a unified scheduling method to improve operational efficiency and ensure the timely execution of key tasks.

Over the past few decades, research on the Agile Earth Observation Satellite Scheduling Problem (AEOSSP) has been conducted separately for three types of task objectives: point, line, and region targets. In point target planning, ref. [1] first modeled the task as a joint optimization problem of task selection and planning. Early studies predominantly employed exact algorithms such as CPLEX [2,3,4], yet encountered bottlenecks in solving efficiency within large-scale task scenarios, which spurred the development of heuristic and meta-heuristic algorithms. Representative approaches include: tabu search [5], iterative local search [6], improved genetic algorithms [7,8,9], greedy algorithms, dynamic programming [10], hybrid differential evolution [11], and adaptive large neighborhood search [4,12], among others. For line target planning, research has primarily focused on the observation of low-speed moving line targets. Refs. [13,14,15] and colleagues established a three-stage scheduling framework “search-positioning-tracking” based on Bayesian estimation and Gaussian Markov motion prediction. Regarding region target planning, ref. [16] first decomposed the original problem into the region target decomposition problem and the Set Cover Problem (SCP). Since region targets are typically discretized into a large number of point targets, the task scale expands dramatically while computational complexity increases substantially. To address this challenge, scholars have proposed two methods: the strip method and the grid method. The strip method generates satellite coverage rectangular strips through parallel or dynamic segmentation [17,18], focusing on orbital characteristics and task sequence optimization. The grid method discretizes the region into point sets and enhances coverage efficiency through Gaussian projection or equal-latitude division [19,20]. In summary, current research independently designs algorithms for heterogeneous point, line, and region targets, facing the dilemma of fragmented paradigms for multi-objective collaborative modeling. Moreover, these methods generally rely on specific heuristic strategies, which exhibit insufficient robustness—leading to high risks of model tuning failures—and their computational complexity increases exponentially with task scale, rendering them inadequate for meeting the real-time observation demands of multiple target types.

Deep reinforcement learning (DRL), leveraging its robust generalization capabilities and online learning features exemplified by breakthroughs such as the AlphaGo series, has demonstrated remarkable advantages in addressing the AEOSSP. Specifically, ref. [21] approached the real-time scheduling of a single satellite by formulating dynamic task allocation as a dynamic knapsack problem and applied the A3C algorithm to enable online decision-making for stochastic tasks. While the method benefits from efficient parallel sampling, the synchronization challenges inherent in the actor-critic architecture may result in training instability, thereby limiting its effectiveness in environments with stringent real-time requirements; ref. [22] developed an end-to-end deep learning framework; however, their model was confined to fixed scenarios, which constrained the generalization capability of the learned policy; ref. [23] introduced a two-stage neural network-based combinatorial optimization approach that enhanced decision-making efficiency in complex environments. However, the separation into two distinct stages may lead to conflicting objectives between the sub-problems; ref. [24] proposed the RLPT method to achieve non-iterative multi-objective optimization, effectively reducing the number of computational iterations. Nevertheless, the approach exhibited limited responsiveness to high-priority dynamic tasks; ref. [25] integrated graph clustering with the Deep Deterministic Policy Gradient (DDPG) algorithm to manage continuous-time planning, leveraging graph structures to reduce state space complexity. However, DDPG is sensitive to sparse reward signals in continuous action spaces (e.g., attitude angle adjustments), necessitating the use of reward shaping techniques for performance improvement; ref. [26] modified the DQN architecture to better accommodate task sequencing and temporal constraints by simplifying decision logic through a discrete action space. However, this discretization may compromise the precision of continuous attitude adjustments; ref. [27] designed the GDNN framework to improve decision-making efficiency by accelerating inference through neural network compression. However, such model compression may reduce adaptability in scenarios involving small sample sizes; and ref. [28] applied supervised Monte Carlo Tree Search (MCTS) to address collaborative scheduling of imaging and data transmission under multiple constraints. While this method excels in explicitly handling complex constraints, its computational complexity increases exponentially with the number of constraints due to the expansion of the search space. However, despite surpassing traditional heuristic methods in efficiency, DRL remains constrained by repetitive floating-point operations inherent in latitude–longitude-based time window calculations, creating a structural contradiction between computational power and timeliness requirements. Consequently, there is an urgent need to develop innovative space computing paradigms and dynamic resource scheduling mechanisms to overcome the real-time response bottlenecks in agile satellite multi-target collaborative observation.

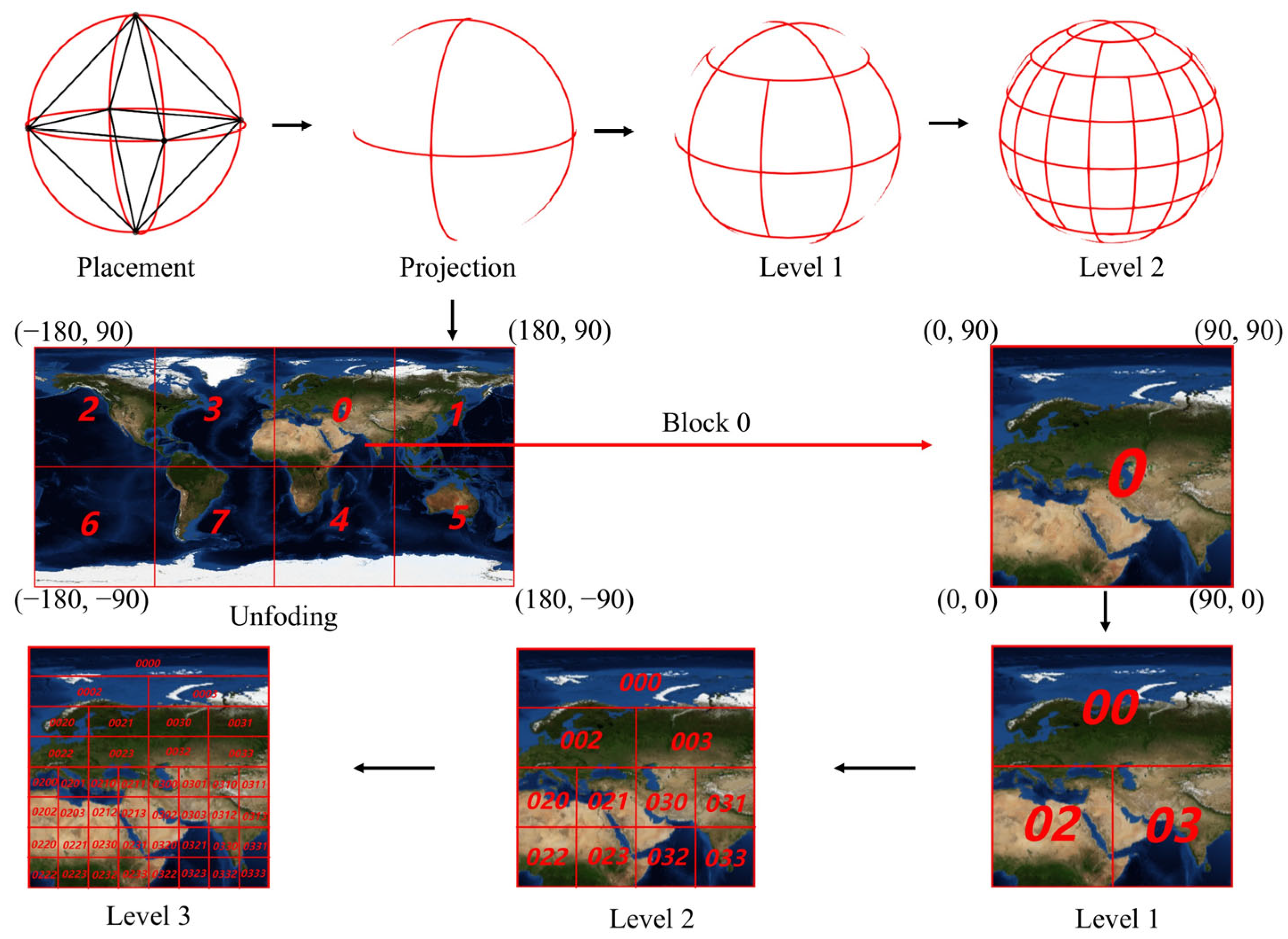
The Discrete Global Grid System (DGGS) a multi-scale earth-fitting grid constructed on a spherical surface with infinite subdivision capability while preserving its geometric integrity, enables uniform modeling of point, line, and region targets through its globally unique encoded indexing system [29]. This system effectively addresses the computational inefficiency of traditional latitude–longitude models and has been applied in diverse satellite observation tasks [30,31,32,33,34,35]. However, its application remains unexplored in the AEOSSP. 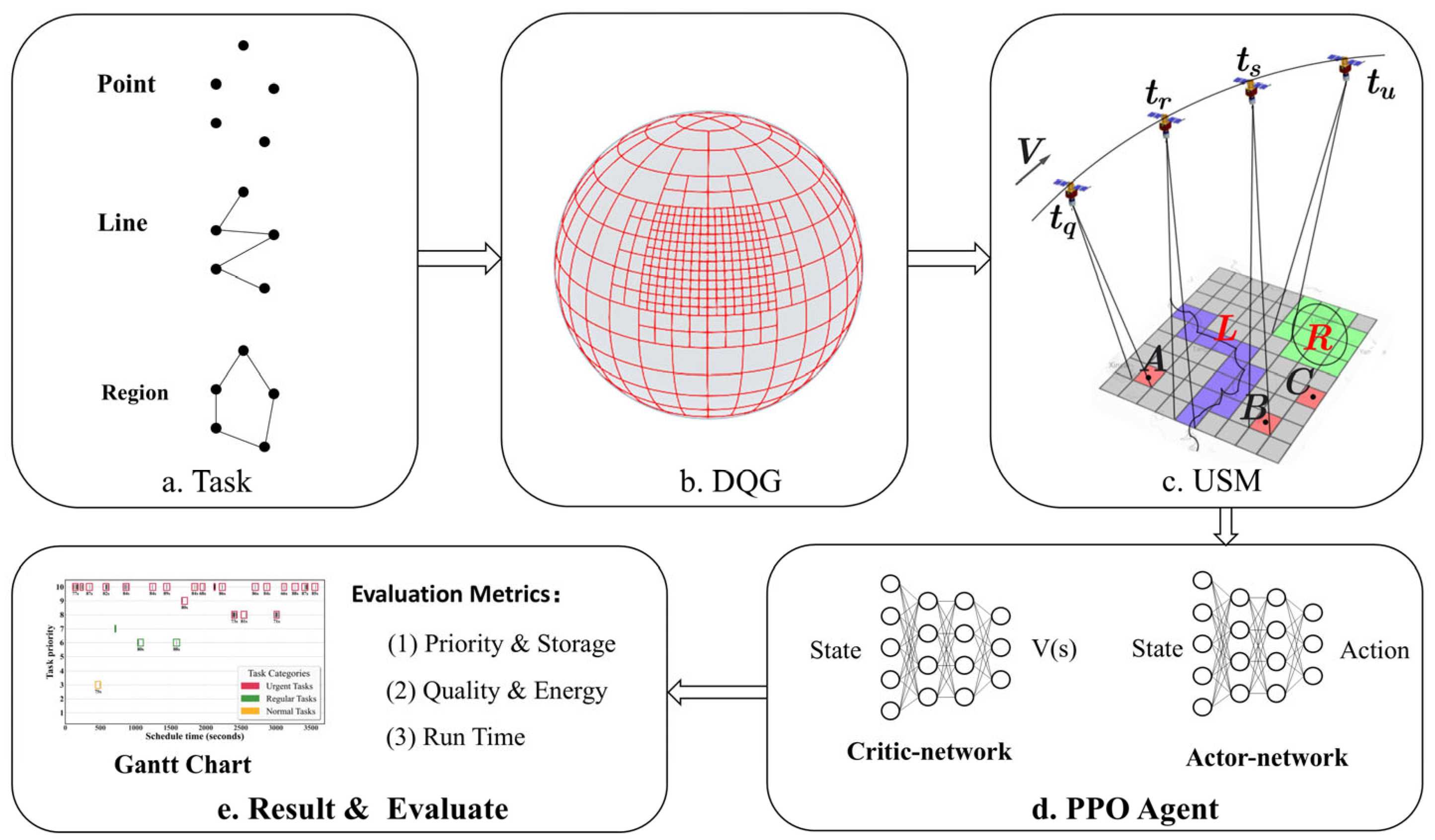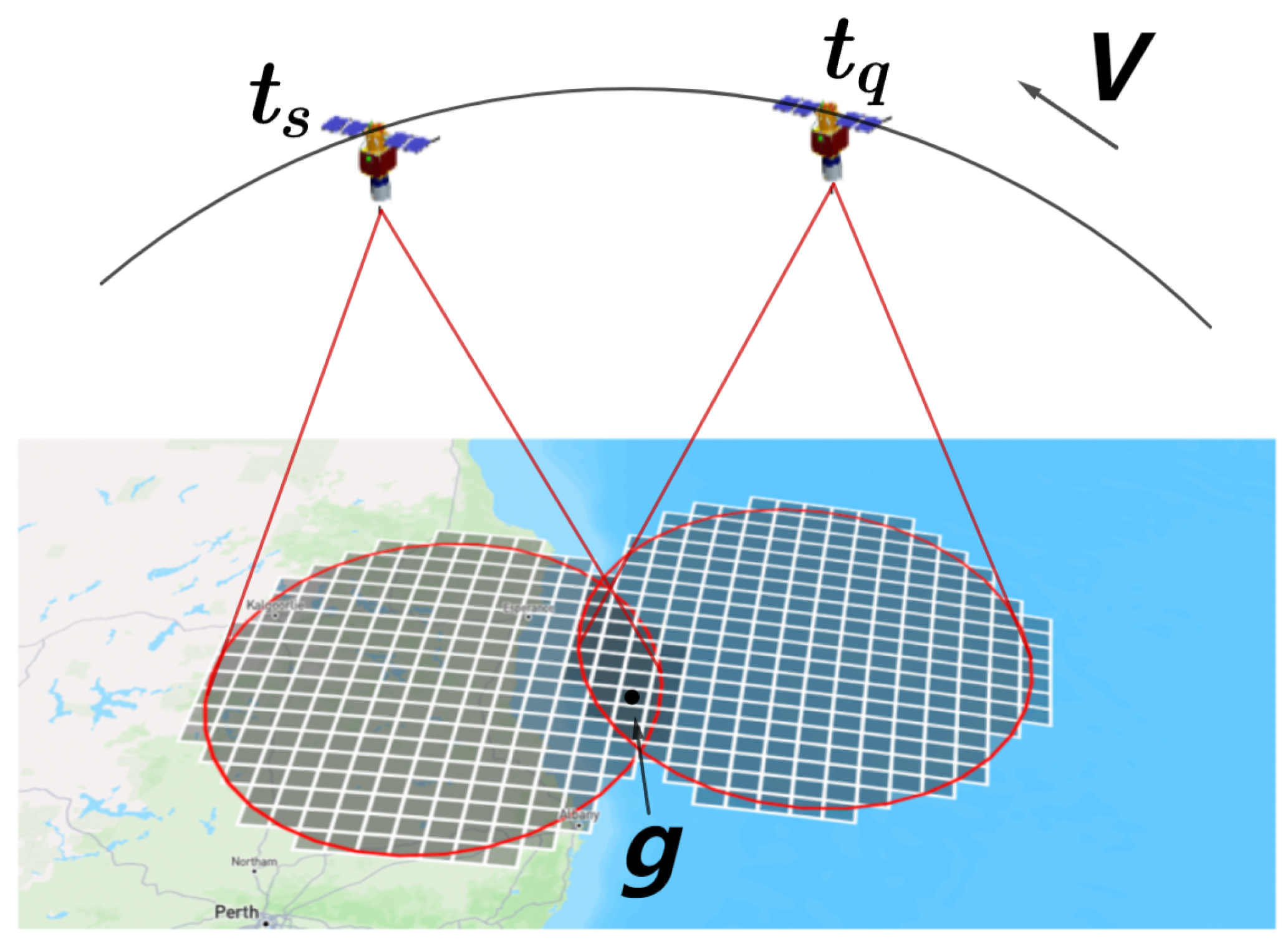To address this gap, this study proposes a unified scheduling model for agile Earth observation satellites based on the DQG [36] and PPO. The proposed model enhances rapid response capabilities and planning efficiency for multi-type target scheduling through two key innovations: (1) leveraging DQG’s global seamless coverage and multi-scale characteristics to establish a unified management framework for point, line, and region targets, thereby constructing a collaborative scheduling paradigm; and (2) replacing traditional latitude–longitude-based time window calculations with grid encoding computation to significantly improve computational efficiency. The main contributions are as follows:

(1)

An integrated solution framework for AEOSSP that combines the DQG unified scheduling model with the PPO deep reinforcement learning algorithm, improving real-time response capabilities and system generalization performance.

(2)

A unified scheduling model grounded in the DQG discrete grid system, establishing the grid as the fundamental computational unit to enable integrated management and modeling of heterogeneous targets (points, lines, and regions).

(3)

A novel time window calculation paradigm utilizing DQG encoding to replace traditional latitude–longitude-based computations, significantly enhancing task scheduling efficiency with PPO.

The study is structured as follows: The second part systematically elaborates on the research model and methodology; the third part details the experimental design and analysis, including the datasets, performance evaluation of task scheduling, comparative experiments, and generalization capability verification; the fourth part explores the intrinsic mechanisms underlying the model’s effectiveness; the fifth part summarizes the algorithm’s core value, application scenarios, theoretical contributions, and prospects for future research.

2. Model and Method

To address the limitations of existing satellite scheduling algorithms, which require separate design approaches for point, line, and region targets and depend heavily on floating-point computations based on geographic coordinates, this study proposes a unified agile Earth observation satellite scheduling model based on DQG and PPO. The technical approach is illustrated in Figure 2. First, the DQG-based global multi-scale grid is employed to uniformly manage point, line, and area targets, thereby establishing a Unified Scheduling Model (USM) and constructing a homogenized mapping mechanism for heterogeneous tasks. Second, grid encoding is implemented as an alternative to floating-point operations, overcoming the spatial computational bottlenecks inherent in traditional longitude-latitude models and enabling rapid topological analysis of the spatiotemporal relationships among task allocations. Furthermore, an MDP-based resource scheduling decision model is developed, and a reinforcement learning framework incorporating the PPO algorithm is designed to support online autonomous decision-making for collaborative observation of multiple target types within a globally discrete space. Finally, a multidimensional verification system encompassing computational efficiency, observational effectiveness, and dynamic response capability is established to comprehensively evaluate the performance of the proposed method.

2.1. Unified Scheduling Model

2.1.1. Principle of USM

To achieve unified management of point, line, and region task objectives, this study introduces DQG. Compared with other discrete global grid systems such as Uber H3 and Google S2, DQG achieves comparable area uniformity. Regarding hierarchical nesting defined as a parent cell fully containing all child cells, H3 is categorized as a non-nesting grid system because it fails to satisfy this property, while DQG maintains strict hierarchical nesting. Unlike S2 and H3, whose grid edges deviate from cardinal geographic directions, DQG aligns its grid edges precisely with latitude and longitude lines, ensuring seamless integration with geographic coordinate systems. Furthermore, while S2 and H3 rely on the subdivision of regular polyhedra followed by projection onto the Earth’s surface, a process that introduces geometric distortions, DQG directly partitions the latitude–longitude space at all levels except the base layer, eliminating projection requirements and reducing computational complexity. As a result, DQG enables faster and more accurate bidirectional coordinate-to-grid conversions. These features collectively demonstrate DQG’s superior performance in area uniformity, hierarchical nesting fidelity, geographic alignment precision, and computational efficiency compared to existing grid systems.

As illustrated in Figure 3, DQG employs a two-pole degeneration algorithm based on the octahedral topological structure: during the hierarchical subdivision process, triangular elements in polar regions gradually degenerate into quadrilateral structures, ensuring that grid cells at the same level maintain the area convergence characteristic. This effectively addresses the area distortion and polar grid convergence issues inherent in traditional latitude–longitude grids on spherical surfaces. After the initial subdivision, the generated octahedrons are encoded (0–7) based on their spatial locations. Each octahedron can be represented using a degenerate quadtree structure by storing only the positions of its leaf nodes. When the structure is further subdivided into smaller grids, the positions of the leaf nodes are uniquely encoded using quaternary Morton codes. This approach ultimately maps each location on Earth to a unique one-dimensional indexed code. Compared with traditional two-dimensional floating-point latitude and longitude representations, the proposed hierarchical encoding method achieves higher indexing efficiency while reducing memory consumption. Thus, DQG is a uniformly multi-scale earth-fitting grid based on a spherical surface that supports infinite subdivision without shape alteration.

Based on the aforementioned partitioning and encoding methodologies, we have developed a global discrete grid system grounded in DQG, integrated with a suite of spatial operation algorithms aimed at enhancing the performance of AEOSSP. Initially, the DQG enables the unified representation of point, line, and region targets, thereby reducing the computational complexity associated with vector-based tasks. By employing bidirectional conversion algorithms between geographic coordinates and grid identifiers, along with polygon-to-grid mapping techniques, diverse target types can be transformed into corresponding grid cells. Subsequent aggregation operations facilitate target clustering and the resolution of priority conflicts. The DQG exhibits multi-resolution capabilities, allowing for the representation of space–ground resources across multiple spatial scales. In practical deployment, high-resolution grid cells are utilized to model task targets, whereas grid cells approximating the satellite’s imaging swath width are employed to characterize its ground coverage capacity. This strategy effectively limits the total number of grid cells while preserving accuracy, thereby achieving a balanced trade-off between computational efficiency and spatial precision. Furthermore, the DQG coding structure possesses a globally unique one-dimensional integer identifier, which facilitates the implementation of hash-based indexing mechanisms. This feature significantly accelerates the time window calculation between target grids and satellite coverage grids, thereby enhancing the overall efficiency of task matching processes.

Building upon this foundation, we propose the Unified Scheduling Model (USM) based on the DQG (as shown in Figure 2c). USM consists of fine-resolution minimum task grids and coarse-resolution basic task unit grids: satellites utilize the coarse-resolution grids as decision units for task planning, leveraging their flexible maneuverability to observe and image internal fine grids. Specifically, the fine minimum task grid uniformly manages point targets (e.g., A, B, C), line targets (L), and area targets (R). Given that satellite point target coverage ranges from approximately 0–10 km, line target widths generally do not exceed several kilometers, and satellite speeds average around 7.8 km per second, the scale of fine minimum task grids is set within 1–10 km. The basic task unit grid fully encompasses all minimum task grids as their parent grid, ensuring that satellites can complete imaging of all point, line, and area targets within a single pass (as illustrated by the boundary range of the USM coarse-resolution grid in Figure 2c).

In summary, USM simultaneously satisfies the requirements for unified spatial task management and efficient satellite-based spatial computation. The following sections will detail the formal representation, imaging quality, energy consumption, and time window calculation methods of USM.

2.1.2. Formalization of USM

The satellite uses a coarse-resolution grid as a task decision unit for the USM. Therefore, any feasible solution (S) of the USM can be formally expressed as:

$$S=\{Sat, ST,ET,SVT,\mathrm{S}GT\}$$

(1)

among them, the symbols included in the feasible solution are defined as follows:

$Sat=\left\{sa{t}_i|1\le i\le n_s\right\}$ denote the set of all Earth observation satellites in the unified scheduling model, where $n_s$ represents the number of satellites.

$ST=\left\{s_c^{sa{t}_i}\right|1\le i\le n_s\}$ denotes the start time of the overall observable time window for each satellite with respect to every coarse-resolution basic grid cell in the unified scheduling model.

$ET=\left\{e_c^{sa{t}_i}\right|1\le i\le n_s\}$ denotes the end time of the overall observable time window for each satellite with respect to every coarse-resolution basic grid cell in the unified scheduling model.

$SVT=\left\{v{t}_i\right|1\le i\le n_{vt}\}$ represents the set of all vector-based ground targets within the effective time window of the unified scheduling model, where $n_{vt}$ is the total number of ground targets. Each ground target is expressed as:

$${vt}_i=\left\{id,p,t\right\}$$

(2)

where $id$ is the target identifier, serving as the unique identity of ${vt}_i$. $p$ denotes the task priority of ${vt}_i$. $t$ indicates the target type (0 for point targets, 1 for line targets, and 2 for region target).

$SGT=\left\{{gt}_i\right|1\le i\le n_{gt}\}$ the set of all grid-based ground targets within the effective time window of the unified scheduling model, where $n_{gt}$ is the total number of ground grid targets. Each ground grid target is represented as:

$${gt}_i=\left\{code,p_i,b_0,d_i,b_i,{\omega }_i,{\phi }_i,{\gamma }_i,w_i\right\}$$

(3)

where $code$ is the grid target encoding, globally unique and associated with geographic information, serving as the unique identity of ${gt}_i$. $p_i$ is the task priority of ${gt}_i$, calculated as the cumulative priority of all vector targets within the grid. $b_0$ denotes the optimal observation time. $d_i$ represents the observation duration. $b_i$ corresponds to the start time of the actual imaging time window. ${\omega }_i$, ${\phi }_i$ and ${\gamma }_i$ respectively denote the pitch angle, roll angle, and yaw angle at the actual start time. $w_i$ represents the visible time window (VTW) of ${gt}_i$, which is described as:

$$w_i=\left\{id,s,e,\omega List,\phi List,\gamma List\right\}$$

(4)

where $id$ is the unique identifier of $w_i$, used to represent multiple visible time windows for each ground target. $s$ and $e$ correspond to the start and end times of $w_i$, respectively. $\omega List$, $\phi List$ and $\gamma List$ respectively represent all the satellite pitch angles, roll angles and yaw angles within the entire visible time window $w_i$. In this study, the time window is discretized into whole-second units, with each discrete time point corresponding to a specific set of attitude angles.

2.1.3. Image Quality of USM

The imaging quality of satellite observation targets directly determines data usability. Traditional satellite planning allocates fixed rewards for observation targets. In contrast, the imaging quality of agile satellites depends on attitude angles. As the observation angle deviates from the nadir point, imaging quality progressively degrades, leading to distortion. To address this issue, this study proposes a dynamic reward mechanism that reflects real-time changes in imaging angles and prioritizes observations near the nadir point to acquire higher-quality data.

Previous studies [4,37] confirm that satellite imaging quality achieves its optimal level during the mid-phase of the visible time window. They model the imaging quality (q) as a function, taking integer values from 1 to 10, which depends on the observation time point (u). The defined as follows:

$$q\left(u\right)=10 -9{\displaystyle \frac{|u-\widehat{u}|}{\widehat{u}-b}}$$

(5)

where $\widehat{u}$ corresponds to the midpoint of the visible time window and is referred to as the optimal imaging time point. b represents the start time of the visible time window.

Building on the prior research of [4,37], refs. [38,39] formalize the satellite imaging quality as a continuous variable ranging from 0 to 1, with its value contingent on the pitch angle during observation. The definition is as follows:

$$q\left(u\right)=1 -{\displaystyle \frac{\left|\omega \left(u\right)\right|}{90°}}$$

(6)

where $\omega \left(u\right)$ represents the pitch angle of the satellite when observing the ground target at the time point $u$.

Equations (5) and (6) only consider the impact of pitch angle variation on imaging quality, based on the assumption that each ground target is observed individually. However, this calculation paradigm cannot be applied to the unified observation of multiple types of targets via satellite imaging. To address this limitation, this study proposes a comprehensive imaging quality calculation method that simultaneously incorporates the pitch angle and roll angle at the observation moment. The definition is as follows:

$$q\left(u\right)=(1-{\displaystyle \frac{1}{k}}·{\displaystyle \frac{\left|\omega \left(u\right)\right|}{90°}})·(1-{\displaystyle \frac{1}{k}}·{\displaystyle \frac{\left|\phi \left(u\right)\right|}{90°}})$$

(7)

where $\omega \left(u\right)$ and $\phi \left(u\right)$ represent the pitch angle and roll angle of the satellite at the observation moment $u$. The parameter $k$ characterizes the ability of different sensors to resist angle distortion, with $k\ge 1$, and higher-resolution task sensors exhibit stronger anti-distortion capabilities. Furthermore, the imaging quality $q\left(u\right)$ is a continuous real number defined on the interval [0, 1], where a larger $q\left(u\right)$ value indicates higher imaging quality for satellite observations of ground grid targets.

2.1.4. Energy Consumption of USM

Satellites typically encounter significant energy ceilings. Even with real-time solar charging capabilities, prolonged high-load operations accelerate the performance degradation of sensors and other onboard components. Therefore, it is essential to ensure that observation tasks are completed efficiently under limited energy conditions. The satellite imaging observation process within the unified scheduling model primarily involves four fundamental energy-consuming activities: sensor activation, power-saving mode maintenance, ground target observation, and attitude maneuvering. The energy consumption of these activities collectively constitutes the total energy expenditure for a single observation task. To accurately quantify the energy consumption of these four activities, this study defines a series of variables, as shown in

Table 1. Details of these indicators.

Variables	Meaning
$E_i$	The total energy consumption for $t_i$
$s{t}_i$	The total time for executing task $t_i$ while keeping the camera in power-saving mode
$o{t}_i$	The total time for executing task $t_i$, including all grid targets
$c{t}_i$	The time consumed by satellite attitude maneuver for task $t_i$
$et$	Starting the camera consumes energy.
$es$	The energy consumption of the satellite in the power-saving mode.
$eo$	The energy consumption for the satellite to observe ground targets.
$ec$	The energy consumption for the satellite to adjust its posture.

.

The total energy consumption of a satellite for executing a single observation task can be defined as

$$E_i=et+s{t}_i\times es+{ot}_i\times eo+c{t}_i\times ec$$

(8)

where et, es, eo and ec are constant parameters. Given that according to [40], we take et = 1 J, es = 0.01 W, eo = 0.03 W and ec = 0.05 W. Furthermore, the calculation methods for $o{t}_i$, $s{t}_i$ and $c{t}_i$ are as shown in Equations (9), (10) and (14), respectively:

$$o{t}_i={\sum }_{j=1}^{n_{gt}}{d}_j$$

(9)

where $n_{gt}$ represents the number of ground targets included in the observation task (t). $d_j$ indicates the imaging duration of the ground target $g{t}_j$.

$$s{t}_i={\sum }_{j=1}^{n_{gt}-1}(b_{j+1}-(b_j+d_j\left)\right)$$

(10)

where $b_{j+1}$ represents the observation start time of the ground target $g{t}_{j+1}$. And $b_j+d_j$ represents the observation end time of the ground target $g{t}_j$.

The satellite employed in this study exhibits high compatibility with the AS-01 satellite used in [37] in terms of key performance parameters. Thus, the attitude maneuvering calculation method proposed in that study is directly adopted.

$$trans\left(\Delta g\right)=\left\{\begin{array}{c}35/3 \Delta g\le 10\\ 5+{\displaystyle \frac{\Delta g}{v_1}} 10<\Delta g\le 30\\ \begin{array}{c}10+{\displaystyle \frac{\Delta g}{v_2}} 30<\Delta g\le 60\\ 16+{\displaystyle \frac{\Delta g}{v_3}} 60<\Delta g\le 90\\ 22+{\displaystyle \frac{\Delta g}{v_4}} \Delta g>90\end{array}\end{array}\right.$$

(11)

where $trans\left(\Delta g\right)$ represents the time consumed by the attitude maneuver $\Delta g$, measured in seconds. The values $v_1$ = 1.5°/s, $v_2$ = 2°/s, $v_3$ = 2.5°/s, and $v_4$ = 3°/s correspond to four different types of attitude angle maneuver speeds. $\Delta g$ represents the change in attitude angle, defined as follows:

$$\Delta g=\Delta \omega +\Delta \phi +\Delta \gamma$$

(12)

where $\Delta \omega$, $\Delta \phi$ and $\Delta \gamma$ = 0 (not considered in practical applications), respectively, represent the change amounts of the pitch angle, roll angle and yaw angle.

Take $g{t}_j$ and $g{t}_{j+1}\in SGT$ as an example. They are two adjacent ground targets within the same observation task (t) and $g{t}_j$ precedes $g{t}_{j+1}$. Therefore, the attitude angle change (Δg) of the satellite when rotating from $g{t}_j$ to $g{t}_{j+1}$ can be expressed as

$$\Delta g_{g{t}_j\to g{t}_{j+1}}=\left|{\omega }_{j+1}-{\omega }_j\right|+\left|{\phi }_{j+1}-{\phi }_j\right|$$

(13)

therefore, the time consumed by the attitude maneuver within the observation task (t) can be expressed as:

$$c{t}_i={\sum }_{j=1}^{n_{gt}-1}trans(\Delta g_{g{t}_j\to g{t}_{j+1}})$$

(14)

2.1.5. Time Window of USM

During satellite scheduling, it is necessary to repeatedly calculate the time windows for satellite access to targets in real time. Traditional methods (e.g., spatial sampling point method and boundary line segment matching method) can achieve high computational accuracy but incur significant time consumption, rendering them inadequate for real-time satellite observation requirements. To address this issue, this study leverages the advantages of USM grid coding and proposes a hash-accelerated time window calculation method. As illustrated in Figure 4, the ground target grid is formally defined as $G_{codes}=\left\{g|g\in codes\right\},\left|G_{codes}\right|=n_g\}$. For a given satellite, at time $t_q$, its position is computed using the SGP4 satellite orbit prediction model. Based on the maximum maneuvering capability, the satellite’s visible coverage area at time $t_q$ is determined, which extends beyond the sensor’s field of view to include all possible maneuver-induced visibility ranges. The grids falling within this coverage area are referred to as instantaneous coverage grids and are denoted as $S_{codes}\left(t_q\right)$. Subsequently, similar computations are carried out for the next time instance $t_s$, and this process is iteratively repeated. Finally, a hash-based algorithm is employed to efficiently compute the intersection between $G_{codes}$ and $S_{codes}$, thereby identifying the start and end times for each ground target $g$. These time intervals are recorded as $T_{codes}(g,t_{start},t_{end})$, representing the available observation time windows for each corresponding ground target.

2.2. AEOSSP-USM Method

Satellite real-time task scheduling refers to the process of dynamically formulating and adjusting task plans during mission execution, based on continuously changing task requirements and environmental conditions. This process requires efficient management of limited resources, rapid adaptation to environmental changes, and optimization of task scheduling strategies to enhance task benefits and execution efficiency. Building upon the USM framework for unified spatial management of tasks and efficient space–ground computation, this study integrates DRL to solve the AEOSSP. Specifically, it first constructs an agile satellite scheduling model based on USM, defining the decision variables, objective function, and constraints of the model; subsequently establishes the MDP for this scheduling problem; and finally employs the PPO algorithm to train the AEOSSP-USM, achieving unified real-time scheduling for multiple types of observation targets.

2.2.1. Problem Description of AEOSSP-USM

Deep reinforcement learning trains and solves the model by calculating the rewards of the objective function. Upon successful task execution, the system obtains corresponding rewards, with the ultimate goal of maximizing the total rewards of all accepted tasks within a specified time period. To conduct scheduling analysis, this study proposes the following basic assumptions:

(1)

Satellite attributes exhibit significant differences. This study focuses on agile Earth observation satellites, assuming they possess active imaging capabilities and can perform pitch and roll attitude maneuvers;

(2)

It is assumed that agile Earth observation satellites can efficiently complete imaging data playback, ensuring sufficient and effective onboard storage resources throughout the scheduling process;

(3)

Referring to the maximum single imaging area of existing satellites, a coarse-resolution grid not exceeding this limit is adopted as the basic unit of USM, guaranteeing that all point, line, and area targets within the unit can be observed during a single satellite pass;

(4)

Given that ground target demands far exceed satellite observation capacity, each ground target is assumed to be observable at most once.

This study employs $D_{code}^{\pi }$ to denote the decision variable, which is defined as follows: under policy π, this variable represents the decision outcome for task code. A value of 0 indicates rejection of the current task’s imaging request, and a value of 1 signifies acceptance of the task and execution of the imaging operation.

$$D_{code}^{\pi }=\left\{\begin{array}{c}0\\ 1\end{array}\begin{array}{c}, reject\\ , accept\end{array}\right.$$

(15)

Consequently, the objective function of AEOSSP-USM is defined as Equation (16), which encompasses four interrelated optimization objectives: maximizing total reward R′, maximizing imaging quality Q′, minimizing energy consumption E′, and minimizing memory usage S′.

$$maxG=w_R·R^{\prime }+w_Q·Q^{\prime }-w_E·E^{\prime }-w_S·S^{\prime }$$

(16)

$$\forall \mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\in C_{order}^T, {et}_{code-1}+2t_{trans} \le {st}_{code}$$

(17)

$$\forall \mathrm{c}\mathrm{o}\mathrm{d}\mathrm{e}\in C_{order}^T, {st}_{code}+{tt}_{code}\le T-{et}_{code}$$

(18)

$$count \le Coun{t}_{max}$$

(19)

where $maxG$ represents the total reward obtained by scheduling the task $C_{order}^T$ within the current simulation period $T$, serving as the primary optimization objective of this study. $Q$ denotes the imaging quality of a single satellite task execution. As defined in Section 2.1.3, for any task code $\forall code \in C_{order}^T$ there exists a corresponding $q_{code}\left(t_i\right)$, which represents the grid-based imaging quality at time $t_i$. $R$ signifies the reward gained after completing a single satellite task. Notably, although imaging satellites operate on fixed orbits and typically do not perform orbital maneuvers, the reward $R$ varies dynamically with the spatial relationship between the satellite and target due to the USM framework’s consideration of imaging quality. For $\forall code \in C_{order}^T$ the time-dependent reward function $R_{code}\left(t_i\right)=p_{code} \ast q_{code}\left(t_i\right)$ is defined to quantify the task’s reward at time $t_i$. $E$ indicates the energy consumption of a single satellite task execution. As specified in Section 2.1.4, each task code $\forall code \in C_{order}^T$ has a corresponding energy consumption value $E_{code}$. $S$ represents the memory usage during task execution. Given the globally uniform distribution characteristic of DQGs, it is assumed that all task codes $\forall code \in C_{order}^T$ consume memory equivalent to the number of fine-grained task grids s in USM, i.e., $S=count\left(Code\right)$. Here, Q′, R′, E′, and S′ denote the L2-normalized values of Q, R, E, and S, respectively.

In the USM, agile satellites possess enhanced maneuverability for multi-angle imaging (including side-swing and pitch maneuvers), yet must adhere to the following constraints:

(1)

The attitude transition time shall comply with the requirements of Equation (17) for inter-task attitude adjustment.

(2)

Equation (18) must be satisfied to ensure sufficient time for the satellite to receive the next task and complete the final task within the simulation cycle. Specifically, ${st}_{code}$ denotes the start time of the current task, ${et}_{code-1}$ represents the end time of the preceding task, and ${tt}_{code}$ indicates the duration required for single-task execution.

(3)

To guarantee stable sensor operation, the number of imaging operations within the simulation cycle T is subject to an upper limit constraint, denoted as $Coun{t}_{max.}$

2.2.2. MDP of AEOSSP-USM

Deep reinforcement learning serves as a core approach for real-time scheduling of AEOSSP, wherein MDP constitutes a critical step in modeling deep reinforcement learning systems. Given that the subsequent state of satellite task scheduling depends solely on the current state and is independent of historical trajectories, AEOSSP-USM the satellite as an MDP agent represented by the quintuple $G = <S, A, P, R, \gamma >$. Specifically:

State $S$: The satellite is the agent, and the state composition is $S= <t_{start}, p_{code}\left(t_i\right), e, q, s,t_{remain}>$, where $t_{start}$ represents the imaging time of the task; $p_{code}\left(t_i\right)$ indicates the benefit of the task at the current time, reflecting the value of the task at that time point. e, q, and s represent the current energy consumption, imaging quality, and memory consumption, respectively. $t_{remain}$ represents the remaining simulation time.

Action $A$: A binary decision mechanism for executing or skipping a task, which is consistent with the decision variables defined in Equation (15), is optimized based on urgency, resource constraints, and potential reward.

State transition probability $P$: Determined by satellite orbit, task attributes, and decision outcomes.

Reward function $R$: Immediate benefit from completing a task $r_i=w_R·p_{code}\left(t_i\right)+w_Q·q-w_E·e-w_S·s$.

Discount factor $\gamma$: Balances short- and long-term rewards (0 ≤ γ < 1).

The agent operates within MDP framework through cyclical execution: initiating from an initial state, selecting actions to obtain rewards and transitioning to new states, thereby iteratively refining its policy (as illustrated in Figure 5). At each decision step, the satellite dynamically selects a task from the observable set, schedules it to the earliest available time window, and updates the decision horizon to the task’s completion time. This cycle repeats until all tasks are scheduled or system resources are exhausted. The policy $\pi$ generates a feasible observation sequence $\{o_1,o_2,\dots ,o_N\}$, whose joint probability distribution is defined as $P\left(\tau |\pi \right)=\prod _{i=1}^{N}P\left(o_i\right|o_1,o_2,\dots ,o_{i-1},\pi )$. Here, the conditional probability $P\left(o_i\right|o_1,o_2,\dots ,o_{i-1},\pi )$ quantifies the likelihood of selecting task $o_i$ based on historical task information and the current policy $\pi$. This mechanism embodies the sequential decision-making nature of task scheduling each decision depends on prior states and the prevailing policy. By optimizing the strategy $\pi$, the overall efficiency of the scheduling plan or the satisfaction of key performance metrics can be maximized, ultimately achieving efficient execution of satellite missions.

2.2.3. Training of AEOSSP-USM

After constructing the MDP, the training methodology for AEOSSP-USM is introduced. Ref. [41] proposed the Proximal Policy Optimization (PPO) algorithm within the Actor-Critic framework, building upon the Policy Gradient approach. By introducing a surrogate objective function and adopting a mini-batch parameter update mechanism, PPO significantly enhances the training efficiency of Policy Gradient algorithms, addressing their slow parameter update issue. Owing to its stability and efficient update mechanism in complex sequential decision-making tasks, PPO has emerged as the optimal algorithm for solving AEOSSP. PPO features two variants: (1) The variant based on adaptive KL penalty; (2) The variant employing clipped objective functions. The clipped objective function variant, distinguished by its superior performance and simplicity, has gained wider adoption compared to the KL-modified surrogate objective variant. The policy update equation of PPO is as follows:

$$L\left(\theta \right)={\widehat{E}}_t[\mathit{min}\left(r_t\left(\theta \right){\widehat{A}}_t,clip(r_t\left(\theta \right),1-\epsilon ,1+\epsilon \right){\widehat{A}}_t)]$$

(20)

where

$$r_t\left(\theta \right)={\displaystyle \frac{{\pi }_{\theta }\left(a_t\right|s_t)}{{\pi }_{{\theta }_{old}}\left(a_t\right|s_t)}}$$

(21)

By bounding the probability ratio $r\left(\theta \right)$ of action outputs between the old and new networks within a fixed range through Equation (21), the specific policy update process of PPO-clip is formulated as follows:

$${\theta }_{k+1}=\mathit{arg}max{\displaystyle \frac{1}{\left|D_k\right|T}}\sum _{\tau \in D_k}\sum _{t=0}^T\mathit{min}\left({\displaystyle \frac{{\pi }_{\theta }\left(a_t|s_t\right)}{{\pi }_{{\theta }_{old}}\left(a_t|s_t\right)}}{A}^{{\pi }_{{\theta }_k}}\left(s_t,a_t\right),g\left(\epsilon ,A^{{\pi }_{{\theta }_k}}\left(s_t,a_t\right)\right)\right)$$

(22)

Value update equation is as follows:

$${\phi }_{k+1}=\mathit{arg}min{\displaystyle \frac{1}{\left|D_k\right|T}}\sum _{\tau \in D_k}\sum _{t=0}^T{\left(V_{\phi }\left(s_t\right)-R_t\right)}^2$$

(23)

In summary, this study develops a PPO variant algorithm based on the clipped objective function, integrates it with the satellite scheduling model, and ultimately establishes the AEOSSP-USM intelligent decision-making algorithm. This algorithm aims to enhance the efficiency of satellite resource allocation strategies through optimized decision-making processes. The pseudocode of Algorithm 1 is presented as follows:

Algorithm 1 AEOSSP-USM

1: Input: Task dataset and satellite reinforcement learning environment, total training rounds N, batch processing size B

2: Output: The trained model and the parameters ${\theta }^{\mathrm{*}}$ and ${\phi }^{\mathrm{*}}$

3: Initialize the policy parameter $\mathsf{\theta }$ and the value function parameter φ Set ${\theta }^{\mathrm{*}}=\theta$ and ${\phi }^{\mathrm{*}}=\phi$

4: Initialize the ${\theta }_{Adam}$ and ${\phi }_{Adam}$ optimizers.

5: for episode ← 1 : N do

6:    Initialize environment

7:    while not done do

8:         Using the strategy ${\pi }_k=\pi \left({\theta }_k\right)$, explore and calculate the reward $R_t$ of the trajectory $D_k$.

9:         Util done

10:       The value function $V_{\phi k}$ is calculated through $D_k$.

11:       Update the parameters ${\theta }_{k+1}$ using Equation (22) and the ${\theta }_{k+1}$ update strategy.

12:       Equation (23) and the function for updating the parameter ${\phi }_{k+1}$ of the ${\phi }_{Adam}$

13:       Soft Update Network:

14:         ${\theta }^{\mathrm{*}}\leftarrow \tau ·\theta +\left(1-\tau \right)·{\theta }^{\mathrm{*}}$

15:         ${\phi }^{\mathrm{*}}\leftarrow \tau ·\phi +\left(1-\tau \right)·{\phi }^{\mathrm{*}}$

16: end for

3. Results and Analysis

This experiment aims to evaluate the performance of the AEOSSP-USM algorithm under multi-constraint conditions, with a focus on analyzing the USM framework’s capabilities in priority reward, imaging quality, energy consumption control, resource utilization efficiency, and real-time response. The experimental setup is based on simulated satellite parameters and remote sensing task requirements. By integrating WRS-2 grids and DQGs, a composite task set comprising point targets, linear targets, and area targets is generated to construct an experimental dataset that reflects realistic satellite mission characteristics. Priority weight simulation is employed to mimic practical application scenarios. The experiments were carried out on a system running the Ubuntu 22.04 operating system, equipped with an NVIDIA GeForce RTX 4090 GPU, an Intel Core i9-14900K CPU, and 64 GB of RAM.

3.1. Dataset Construction

The core objective of AEOSSP is to enable efficient imaging of ground targets using limited satellite resources. Consequently, the dataset construction focuses on two key components: satellite parameters and task data.

Satellite Parameters: A typical low-Earth-orbit agile satellite (orbital altitude: 500 km, velocity: 7.8 km/s) was selected as the research subject, with technical specifications referencing China’s GaoJing-1 satellite. This satellite supports continuous imaging, multi-target observation, and stereoscopic imaging modes, with a maximum single imaging area of 60 × 70 km. It employs three-axis attitude control technology (maximum maneuverability: 120°/47 s, attitude stability: <0.0005°/s), enabling large-scale precision observation. The simulation parameters are configured as follows: orbital inclination of 75°, bidirectional (cross-track/pitch) attitude adjustment range of 30°, and single-orbit coverage width of 15 km.

Task Data: Task data were managed using a grid-based approach, following the Landsat WRS-2 grid standard for generation. WRS-2 grid divides the observation area into 57,784 globally uniform cells (each 185 × 185 km), with unique spatial mapping achieved through path/row identifiers. In this study, 2000 point targets, 500 linear targets, and 500 area targets were randomly sampled from the WRS-2 grid, with each target assigned a priority weight ranging from 1 to 10. Based on priority distribution, tasks with priorities 8–10, 6–7, and 1–5 were classified as Urgent Tasks, Regular Tasks, and Normal Tasks, respectively. The USM was employed to uniformly organize multi-type targets, generating a standardized ground task dataset for scheduling experiments.

3.2. Experimental Results

To enhance the realism and comprehensiveness of the simulation experiments, the initial states of the satellite (including position, velocity, and other parameters) are initialized using a random strategy. The simulation cycle is set to 3600 s, and the SGP4 satellite trajectory calculation library is employed to compute the satellite’s observable time windows for targets with a time step of 1 s. Based on the PPO algorithm, the performance of the USM unified scheduling model is compared with the latitude–longitude strip (LLS) direct coverage method to verify the advantages of USM in unified task scheduling.

To ensure training stability and optimize algorithmic performance, the hyperparameters of PPO are configured as follows: learning rate η = 0.0004, discount factor γ = 0.99995, clipping factor ϵ = 0.2, and 10 policy network updates per training step.

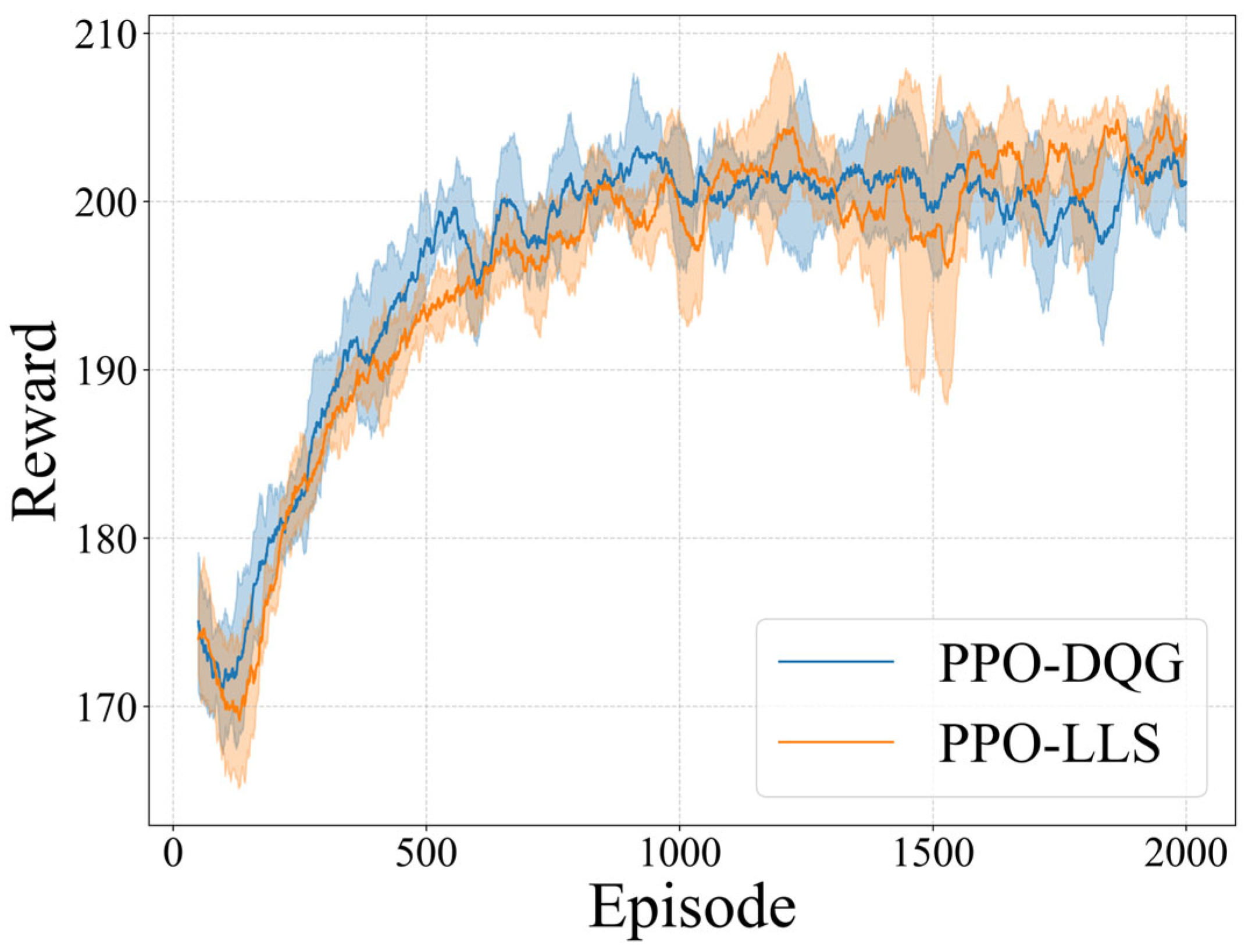
The experimental results are presented in Figure 6, where PPO-DQG represents the USM method implemented based on the DQG, and PPO-LLS denotes the traditional latitude–longitude strip (LLS) direct coverage approach. As shown, after 2000 training epochs, both algorithms achieve stable convergence to the optimal target values without exhibiting training failure or value oscillation. Under identical training configurations, the task rewards of the two algorithms exhibit comparable performance, demonstrating that USM can effectively replace the LLS method for rational task allocation and scheduling.

To comprehensively evaluate the overall performance of both methods, a comparative analysis was conducted across five key metrics: Image Quality (IQ), Storage Occupy (SO), Energy Consume (EC), Task Reward (TR), and Time Waste (TW). Statistical measures including mean and standard deviation were employed to quantify performance disparities, with detailed results summarized in

Table 2. Performance statistics table of PPO-DQG and PPO-LLS.

Model	TR		EC		IQ		SO		TW (s)
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
PPO-LLS	198.28	15.62	102.34	5.21	18.63	0.73	1352.56	41.11	13.956	0.00131
PPO-DQG	199.61	14.2	89.58	6.05	65.5	12.97	91.04	17.78	0.4063	0.00528

.

The experimental results demonstrate that, under comparable task reward conditions, the proposed algorithm exhibits significant advantages over the traditional latitude–longitude strip method: imaging quality is improved by approximately 3 times, energy consumption is reduced by approximately 10%, memory usage is decreased by over 90%, and task scheduling computational efficiency is enhanced by up to 35 times.

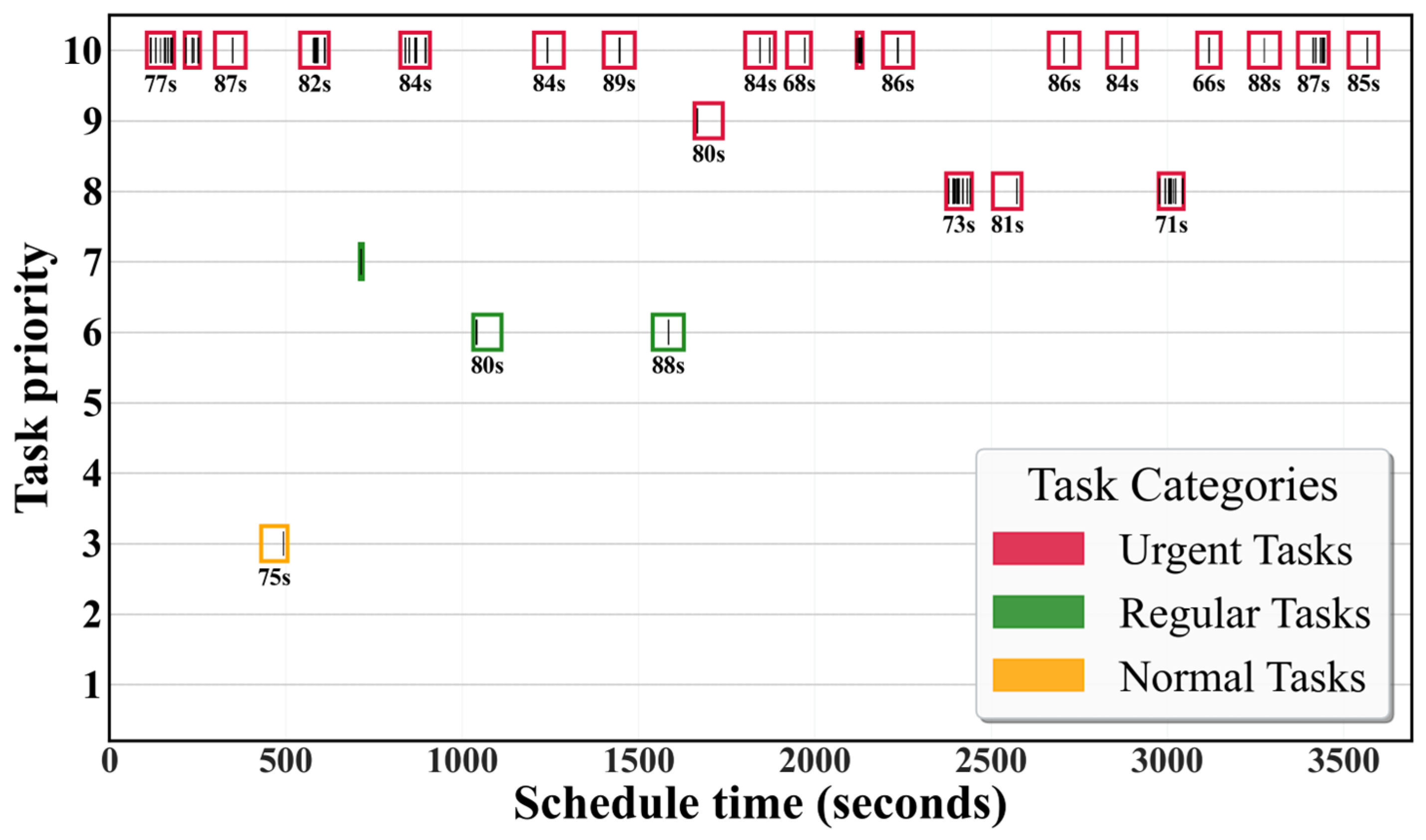
Furthermore, scheduling results are categorized by priority into urgent, regular, and normal tasks for grouped visualization. As shown in Figure 7, the vertical axis represents the task priority (1–10), while the horizontal axis denotes the simulation time. Different colored rectangular boxes represent the observable time windows of the USM basic units, and the black stripes within these boxes indicate the scheduling time of fine-resolution points, lines, and region targets within the corresponding USM. Results show all tasks meet timing and attitude constraints, with over 80% classified as urgent, validating priority optimization. Meanwhile, execution of regular and normal tasks demonstrates efficient satellite resource utilization.

3.3. Comparative Analysis

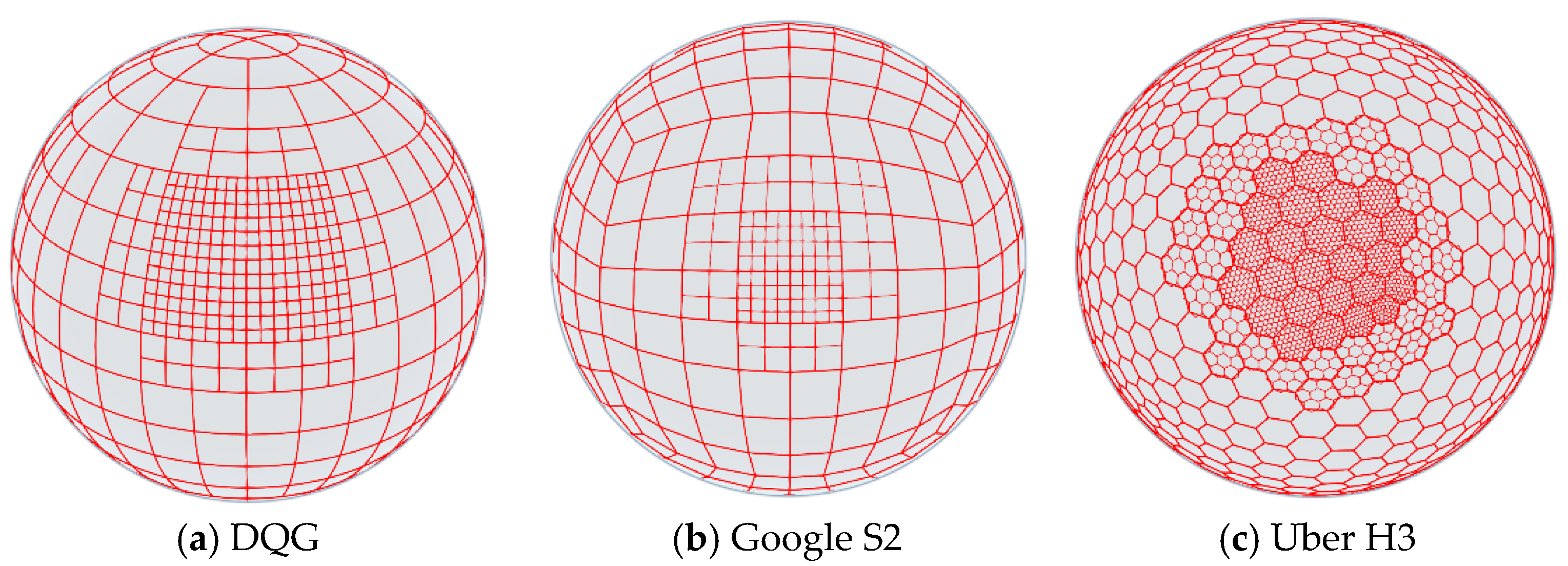
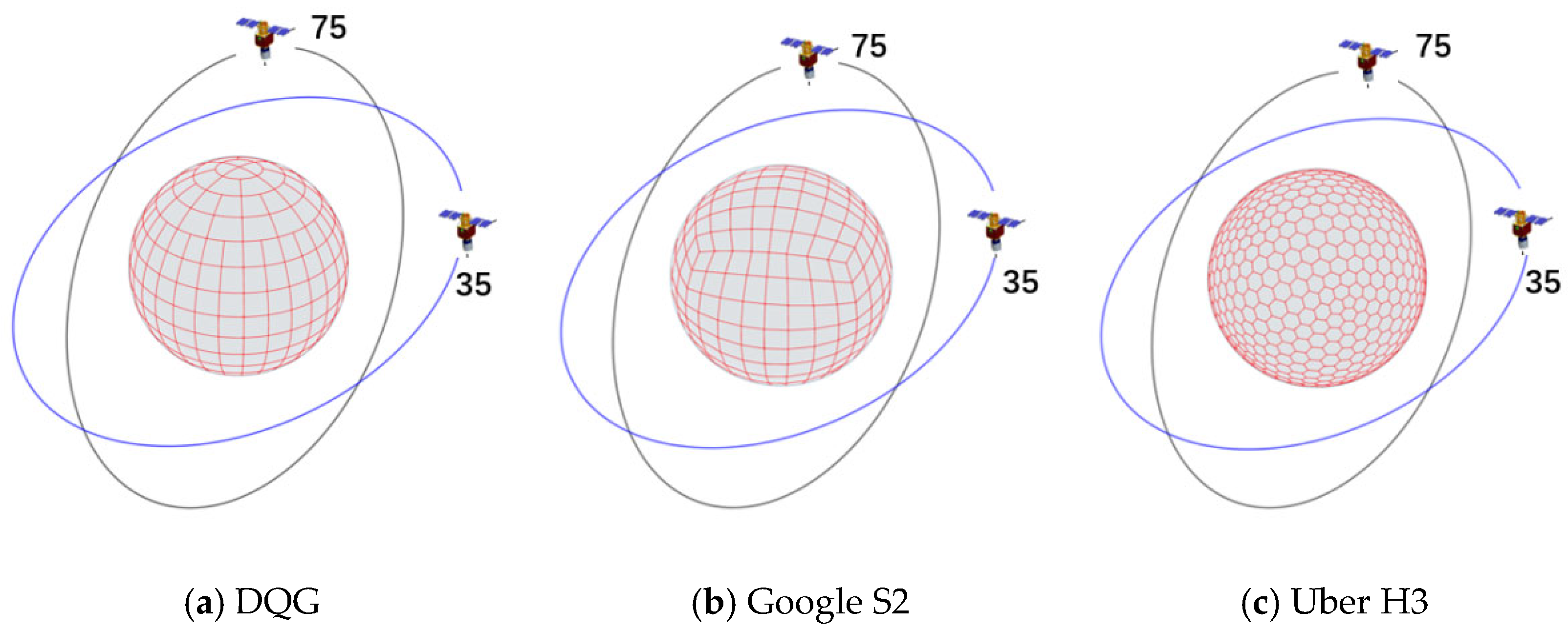
Different discrete grid systems employ distinct base partitioning units and encoding methods. As shown in Figure 8, these grid systems exhibit significant differences in surface partitioning approaches, spatial coverage capacity, computational complexity, and scalability, thereby impacting satellite scheduling performance to varying degrees. Consequently, in addition to the DQG adopted in this study, we selected Google’s S2 grid and Uber’s H3 grid for comparative performance analysis in satellite scheduling. Specifically, the S2 grid is a probability-equalized projection grid based on spherical segmentation, featuring superior spatial uniformity and computational efficiency. The H3 grid adopts a hexagonal lattice structure and has been widely utilized in domains such as ride-hailing service scheduling.

This study implements the USM on three global discrete grids (S2, H3, DQG), trains the model using the PPO algorithm, and conducts comparative experiments with the latitude–longitude strip method. Five key performance metrics, namely Image Quality (IQ), Storage Occupy (SO), Energy Consume (EC), Task Reward (TR), and Time Waste (TW), are used to systematically evaluate the four models (PPO-LLS, PPO-S2, PPO-H3, PPO-DQG). Statistical indicators such as mean and standard deviation are employed to quantify performance disparities, with detailed results presented in

Table 3. Comparative statistics table of different discrete grid systems.

Model	TR		EC		IQ		SO		TW (s)
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
PPO-LLS	198.28	15.62	102.34	5.21	18.63	0.73	1352.56	41.11	13.956	0.00131
PPO-S2	203.56	13.44	92.17	5.52	58.05	10.89	81.07	14.89	1.3770	0.00138
PPO-H3	199.48	14.06	85.31	5.28	54.57	11.75	74.01	15.7	1.1182	0.00382
PPO-DQG	199.61	14.2	89.58	6.05	65.5	12.97	91.04	17.78	0.4063	0.00528

.

The experimental data show that there is a significant difference in task reward (TR) and memory usage among the four models: PPO-S2 has the highest TR mean of 203.56 ± 13.44, which is 2.0% higher than PPO-DQG (199.61 ± 14.2), 2.1% higher than PPO-H3 (199.48 ± 14.06), and 2.7% higher than PPO-LL (198.28 ± 15.62). However, the high TR of S2 is accompanied by a significant increase in memory overhead (SO), with an SO mean of 58.05 ± 10.89 units, which is 6.4% higher than H3 (54.57 ± 11.75) and 36.2% lower than DQG (91.04 ± 17.78). Further analysis reveals that for every 1% increase in TR of S2, approximately 3.6% of additional memory resources are consumed, while PPO-LL has an SO mean of 1352.56 ± 41.11 units due to its fixed strip coverage strategy, resulting in an insufficient memory utilization rate of less than 5% and being suitable only for static offline scenarios.

Energy consumption (EC) and imaging quality (IQ) show a significant negative correlation: PPO-H3 achieves the optimal energy efficiency with an EC mean of 85.31 ± 5.28 units, which is 16.6% lower than PPO-LL (102.34 ± 5.21), but its IQ mean (32.39 ± 9.04) is 50.6% lower than PPO-DQG (65.5 ± 12.97). PPO-DQG increases its IQ by 100.6% by increasing energy consumption by 4.8% (89.58 ± 6.05 vs. 85.31 ± 5.28), while controlling the quality variability (Δσ = 0.58) at a lower level. The experiment further reveals that models with EC below 90 units (such as PPO-H3) generally have an IQ drop of more than 50%, indicating that energy efficiency optimization comes at the cost of significant image quality loss. For example, although PPO-LL has the highest EC mean (102.34), its IQ is only 32.39 ± 9.04, reflecting that low energy efficiency models are difficult to balance quality stability.

The processing time (TW) metric reveals the differences in real-time performance among the models: PPO-DQG has the absolute advantage with a TW mean of 0.4063 ± 0.0015 s, which is 63.6% faster than PPO-H3 (1.1182 ± 0.00382 s) and 70.5% faster than PPO-S2 (1.3770 ± 0.00138 s), and its 99th percentile delay is stable at 0.4256 s, meeting the strict requirements of real-time systems. However, the SO standard deviation of DQG reaches 17.78 units, which is 236.4% and 63.3% higher than H3 (5.28) and S2 (10.89), indicating that efficient processing is accompanied by memory fluctuation risks. In contrast, PPO-LL has an TW mean of 13.956 ± 0.00131 s, with a delay level 10 times higher than other models, and its distribution is significantly skewed, only suitable for non-real-time offline tasks (such as historical data analysis).

Overall, models based on discrete grid systems demonstrate significant performance improvements over the latitude–longitude strip method in terms of energy consumption, imaging quality, memory usage, and response time. These results further validate the feasibility of replacing traditional latitude–longitude models with discrete grid systems, enabling more efficient execution of AEOSSP task scheduling.

3.4. Generalization Analysis

In on-board deployment scenarios, satellite agents must exhibit robust adaptability and generalization capabilities due to the highly dynamic and uncertain operational environment, as well as limited computational resources. The agent is required not only to stably execute tasks in the training environment but also to rapidly adapt its strategies and make decisions in complex, real-world situations (e.g., sudden changes in imaging resource availability). To this end, we designed a comparative experiment: transferring the policy trained in a 25-imaging-capability environment to a new environment with 15-imaging-capability, evaluating its environmental adaptability. The results are presented in

Table 4. Generalization statistics table of different discrete grid systems.

Model	TR		EC		IQ		SO		TW (s)
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
PPO-LLS	118.68	11.66	62.27	3.41	11.37	0.37	825	0	14.319	0.1670
PPO-S2	121.75	10.94	54.89	4.55	34.59	8.38	48.29	11.41	1.4209	0.0060
PPO-H3	120.60	10.65	51.36	3.57	32.39	9.04	44.03	12.18	1.2367	0.0012
PPO-DQG	119.50	10.97	53.96	4.14	40.11	9.62	55.84	13.31	0.4211	0.0015

.

When the resources in Table 4 were reduced to 60% of those in Table 3, all models exhibited linear performance degradation: the mean values of Task Reward (TR), Energy Consume (EC), and Image Quality (IQ) decreased proportionally by approximately 60% (e.g., PPO-LL’s TR dropped from 198.28 to 118.68). Although the variance reduction to zero led to a sharp decline in performance fluctuations, this indicates more stable scheduling under resource constraints. Notably, the PPO-DQG model maintained the fastest computation speed (TW = 0.42 s). Overall, agents based on discrete grid systems demonstrated superior generalization capabilities, potentially attributed to their enhanced ability to capture spatial environmental information through discrete grid structures.

4. Discussions

4.1. Feasibility

(1) Performance: The proposed AEOSSP-USM achieves synergistic optimization for heterogeneous point, line, and region tasks in scheduling efficiency, imaging precision, and resource management via innovative spatial computing paradigms (Figure 9). Its core mechanisms include: encoding-driven spatial relationship determination, grid-anchored imaging precision enhancement, and target-level resource management for memory optimization.

Compared to traditional latitude–longitude algorithms’ continuous spatial computation (time complexity O(n²)), discrete grids replace spherical trigonometric calculations with hash retrieval, reconstructing spatial relationship determination as encoding matching (time complexity O(n)). However, the algorithm faces an energy trade-off: fine-grained grids reduce per-task energy consumption but increase total energy due to frequent inter-grid attitude maneuvers, necessitating further optimization of the energy weight model and on-board validation. Additionally, grid granularity conflicts with computational precision—finer grids improve accuracy at higher computational costs. To address this, hybrid hierarchical indexing is proposed: deploying high-resolution grids in hotspot regions while applying low-resolution grids to other areas for balancing resource efficiency and imaging quality.

(2) Resource generalization adaptability: Algorithms based on different grids demonstrate comparable generalization capabilities in imaging resource management. As shown in Figure 10, when deployed on satellite platforms with 40% resource capacity variation, the DQG model maintains performance metrics consistent with its original configuration. This resource robustness provides feasible technical support for collaborative scheduling in heterogeneous resource satellite clusters.

4.2. USM Performance Across Diverse Scenarios

The impact of different DGGS methods on model performance varies significantly across AEOSSP scenarios, and their specific advantages and limitations require further in-depth analysis. This study employs an expert scoring-based comprehensive evaluation method to systematically assess the scenario adaptability of PPO-LLS, PPO-S2, PPO-H3, and PPO-DQG. As shown in

Table 5. Diverse Scenarios statistics table of different discrete grid systems.

Model	Reward	Quality	Energy	Storage	Time	Total
PPO-LLS	0.9737	0.2846	0.83	0.0547	0.0291	44.623
PPO-S2	1	0.8861	0.93	0.9125	0.2953	75.006
PPO-H3	0.9801	0.8329	1	1	0.3631	76.954
PPO-DQG	0.9804	1	0.95	0.8131	1	97.043

, taking emergency scheduling scenarios as an example, five key performance metrics imaging quality, memory overhead, energy consumption, task reward, and processing time are classified into positive and negative indicators to calculate the relative benefits of the four algorithms. Based on empirical weighting, the weights for reward, quality, energy, storage, and time are set to (0.3, 0.2, 0.1, 0.1, 0.3), and the overall benefit of each model is computed accordingly.

PPO-DQG demonstrates the best overall performance in this emergency scheduling scenario, where its advantages in imaging quality and processing time effectively meet the dual requirements of rapid response and high-quality imaging for emergency tasks. Although H3 exhibits outstanding energy consumption performance, the time-sensitive nature of emergency scenarios necessitates prioritizing DQG as the preferred solution for urgent cases. For non-time-sensitive tasks, H3 or S2 models can be considered to balance task rewards and resource consumption. In contrast, PPO-LLS shows the lowest comprehensive benefit, as its suboptimal imaging quality and processing time fail to meet the demands of high-tempo, high-quality missions.

4.3. Generalization Capability for Orbital Inclination

In USM-based satellite scheduling algorithm research, the generalization capability of USM for orbital inclination is a key scientific issue determining algorithmic universality. This study systematically investigates the generalization performance of discrete grid systems in inclined orbit scenarios by migrating satellite agents trained on a 75° orbital inclination to a 35° orbital environment, aiming to uncover the path-dependent characteristics of existing grid frameworks for specific orbital patterns. The experimental results are presented in

Table 6. Orbital inclination statistics table of different discrete grid systems.

Model	TR		EC		IQ		SO		TW (s)
	Mean	Std	Mean	Std	Mean	Std	Mean	Std	Mean	Std
PPO-LL	157.69	21.23	81.17	9.57	14.66	1.68	1062.49	120.57	13.796	0.0510
PPO-S2	201.10	13.82	92.55	5.81	58.55	11.11	81.33	15.15	1.3539	0.00413
PPO-H3	172.48	23.13	73.86	8.67	46.39	11.71	62.97	15.92	1.1799	0.00558
PPO-DQG	156.06	24.47	71.12	10.23	56.33	14.27	77.72	19.47	0.3861	0.00166

.

As shown in Table 6, the S2 grid demonstrates significant advantages over the H3 grid in task reward and imaging quality. The synergistic optimization of memory usage and processing time highlights the robust representation capability of polyhedral geometric structures under resource constraints. In contrast, traditional latitude–longitude models (LL) and DQG-based latitude–longitude grids exhibit significant randomness in task reward, indicating systemic failure risks in high/low inclination scenarios. In conclusion, scheduling models based on polyhedral discrete grids (S2, H3) show remarkable generalization advantages across varying orbital inclinations, whereas traditional latitude–longitude strip grids demonstrate pronounced random planning characteristics.

The advantage of polyhedral grids in inclination generalization stems from their geometric uniformity optimizing spatial relationship modeling. The equal-area property and angular consistency of polyhedral grids (S2/H3) enable stable spatial mapping between grid cells and subsatellite point trajectories despite variations in orbital inclination (Figure 11). This geometric invariance ensures that state features extracted by agents remain inclination-invariant, allowing the policy network to adapt to new orbital environments without retraining and thereby guaranteeing policy generalization. In contrast, LLS exhibit high-latitude redundancy, while DQGs present special degeneration zones, leading to significant distortions in grid cell area and shape. These distortions disrupt state space continuity and undermine the generalization foundation of the policy network. Future research should establish a quantitative model linking grid deformation gradients to policy decay rates to elucidate the regulatory mechanisms of geometric attributes on inclination generalization.

5. Conclusions

This study proposes a novel AEOSSP-USM framework that simultaneously achieves unified task-space management and efficient space–ground computation, featuring a rigorous formalized expression system, imaging quality optimization mechanism, system energy consumption control method, and time window calculation model. Through experimental comparative analysis, we systematically evaluated the accuracy and efficiency differences between the DQG discrete grid method and traditional latitude–longitude methods, and deeply investigated the performance and generalization capabilities of different grids. The main conclusions are as follows:

(1)

Unified Scheduling and Complexity Optimization: The DQG discrete grid system enables unified management of multi-target tasks by leveraging its unique encoding properties to replace traditional latitude–longitude calculation models and integrate hash algorithms, reducing the spatiotemporal matching complexity and significantly improving AEOSSP solution efficiency.

(2)

Comprehensive Performance Improvement: Under equivalent task reward conditions, the proposed method improves imaging quality by approximately 3 times, reduces energy consumption by approximately 10%, decreases memory usage by over 90%, and enhances scheduling computational efficiency by 35 times.

(3)

Scenario Generalization: Experimental results demonstrate that the proposed method achieves both performance and resource generalization advantages in emergency tasks, with orbital generalization capabilities significantly correlated to the geometric structure of the grid system.

In conclusion, the research indicates that the proposed USM framework provides an innovative formalized modeling approach for AEOSSP. However, further improvements are needed: a single-grid architecture struggles to meet the generalization demands of diverse scenarios. Future work should develop hybrid grid strategies to enhance model robustness, expand application scope, and promote deeper integration of global discrete grid systems in AEOSSP.