The BO-FCNN Inter-Satellite Link Prediction Method for Space Information Networks
Abstract
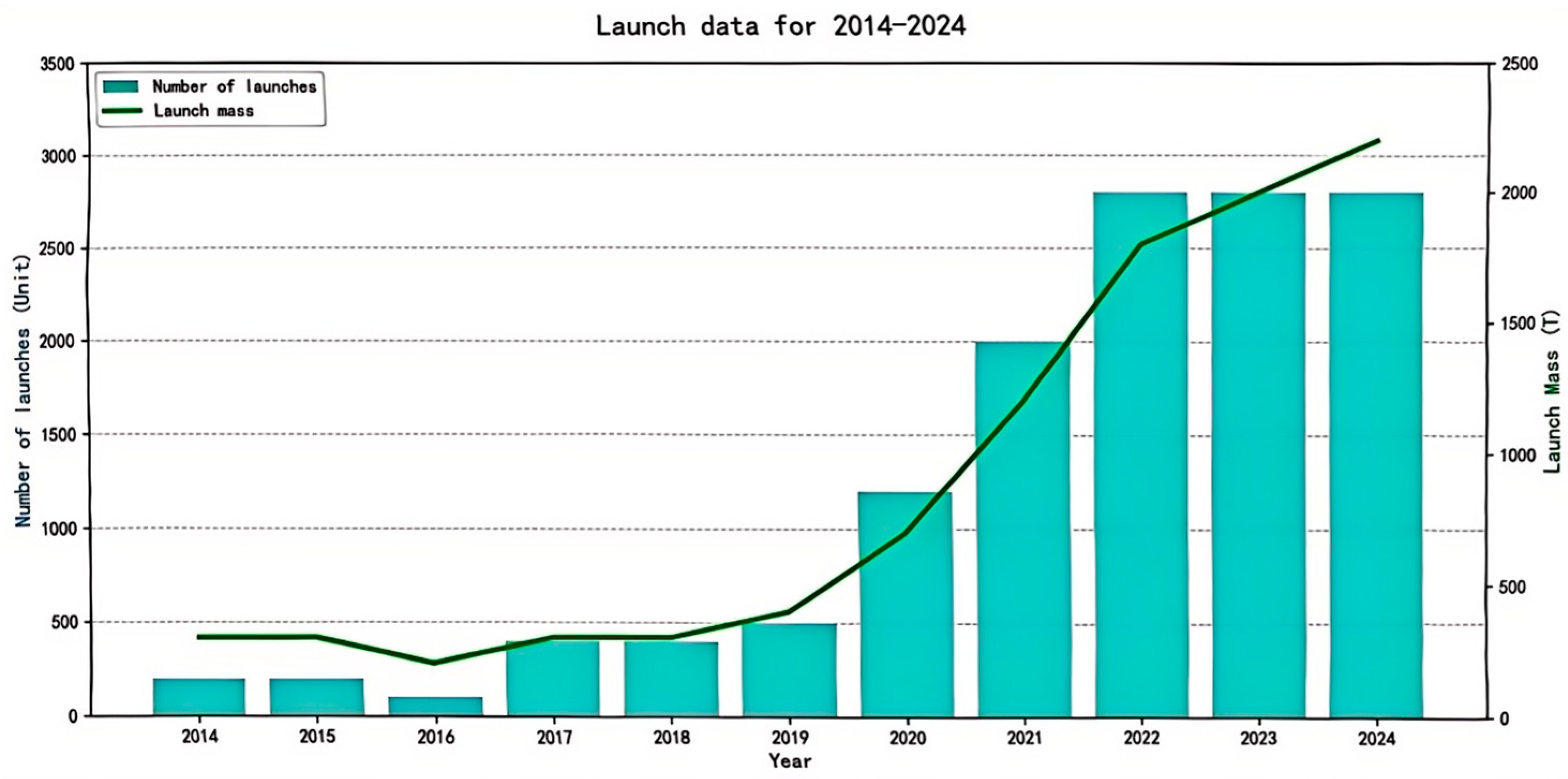
1. Introduction
2. Inter-Satellite Link Prediction and Problem Analysis of Space Information Networks
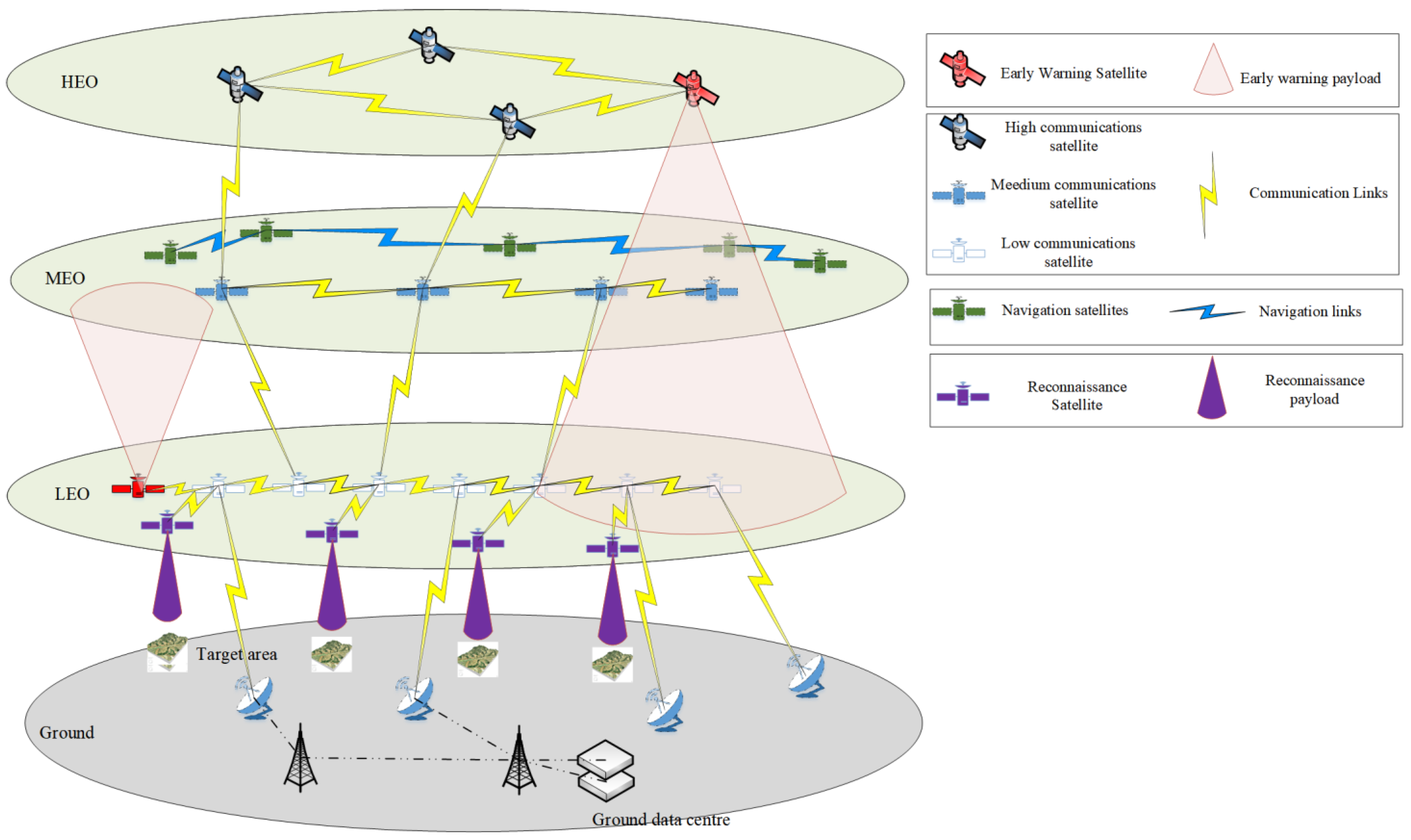
2.1. Overview and Analysis of Space Information Networks
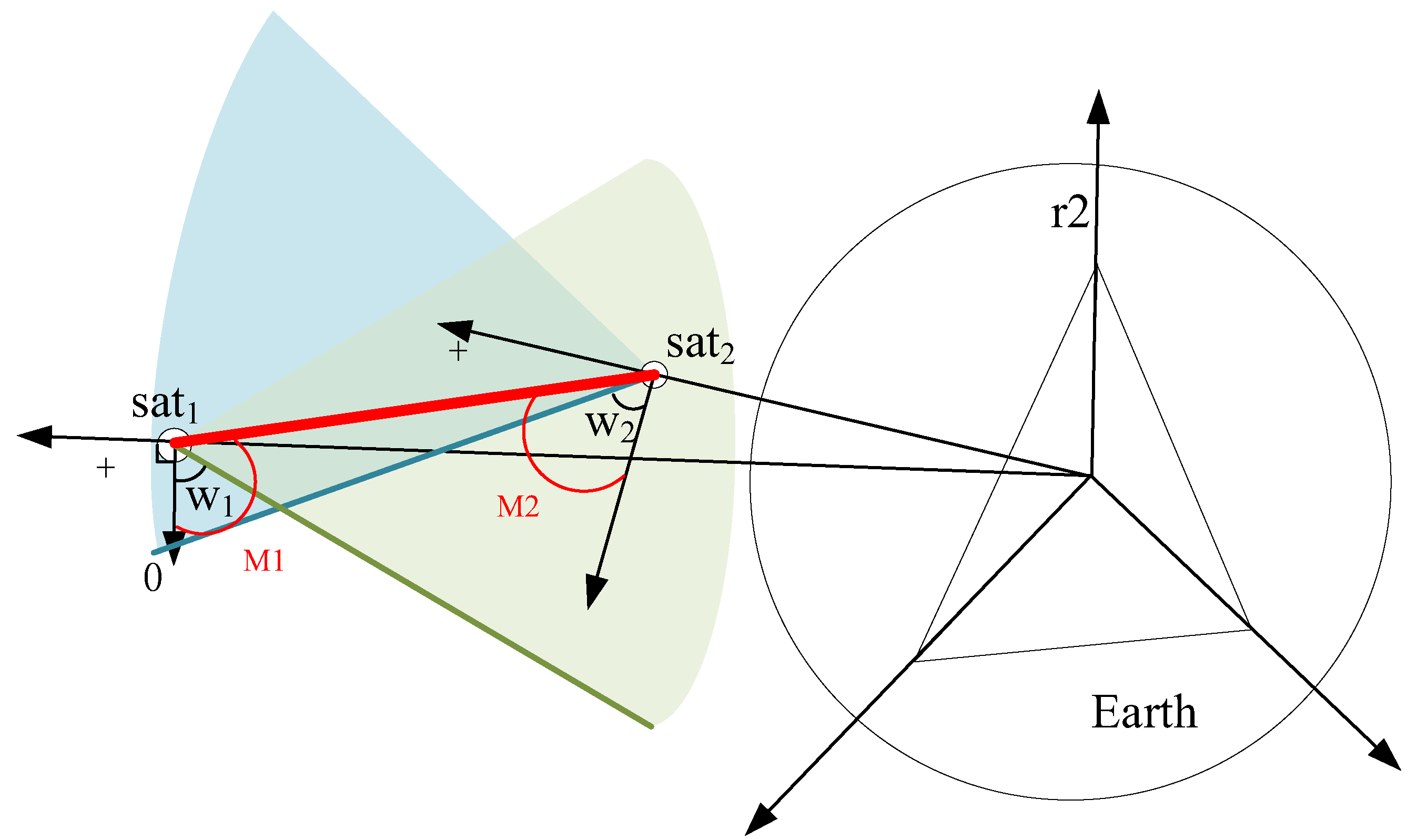
2.2. Inter-Satellite Links
2.3. Summary
3. Inter-Satellite Link Prediction Model Based on Bayesian Optimization
3.1. Theory
3.1.1. Bayesian Optimization
3.1.2. FCNN Model
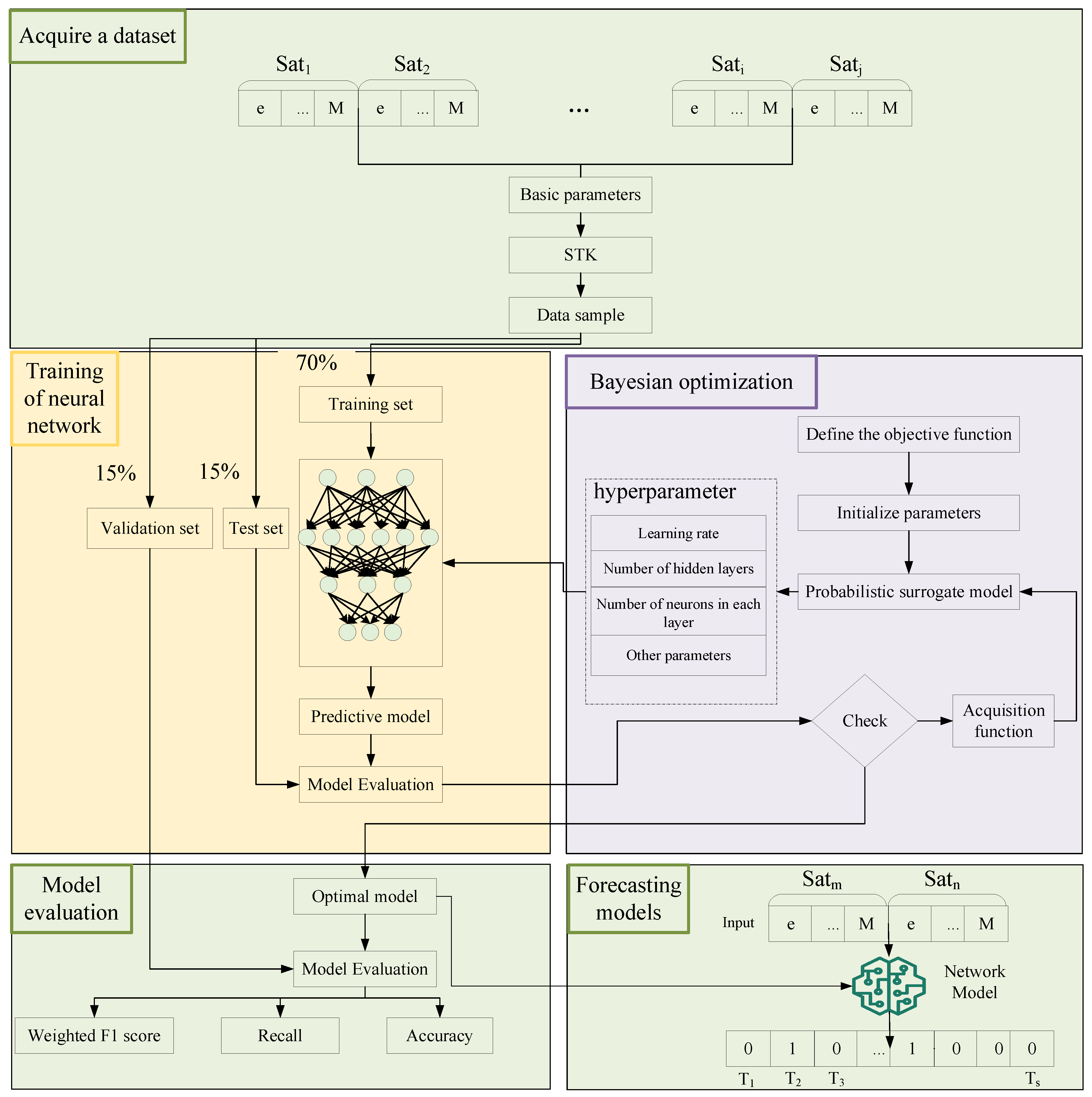
3.2. Inter-Satellite Link Prediction Model Framework
3.2.1. Data Partitioning and Pretreatment
3.2.2. Definition of the Loss Function
3.2.3. Model Parameter Settings
3.2.4. Model Training
3.2.5. Performance Evaluation
4. Results
4.1. Parameter Optimization
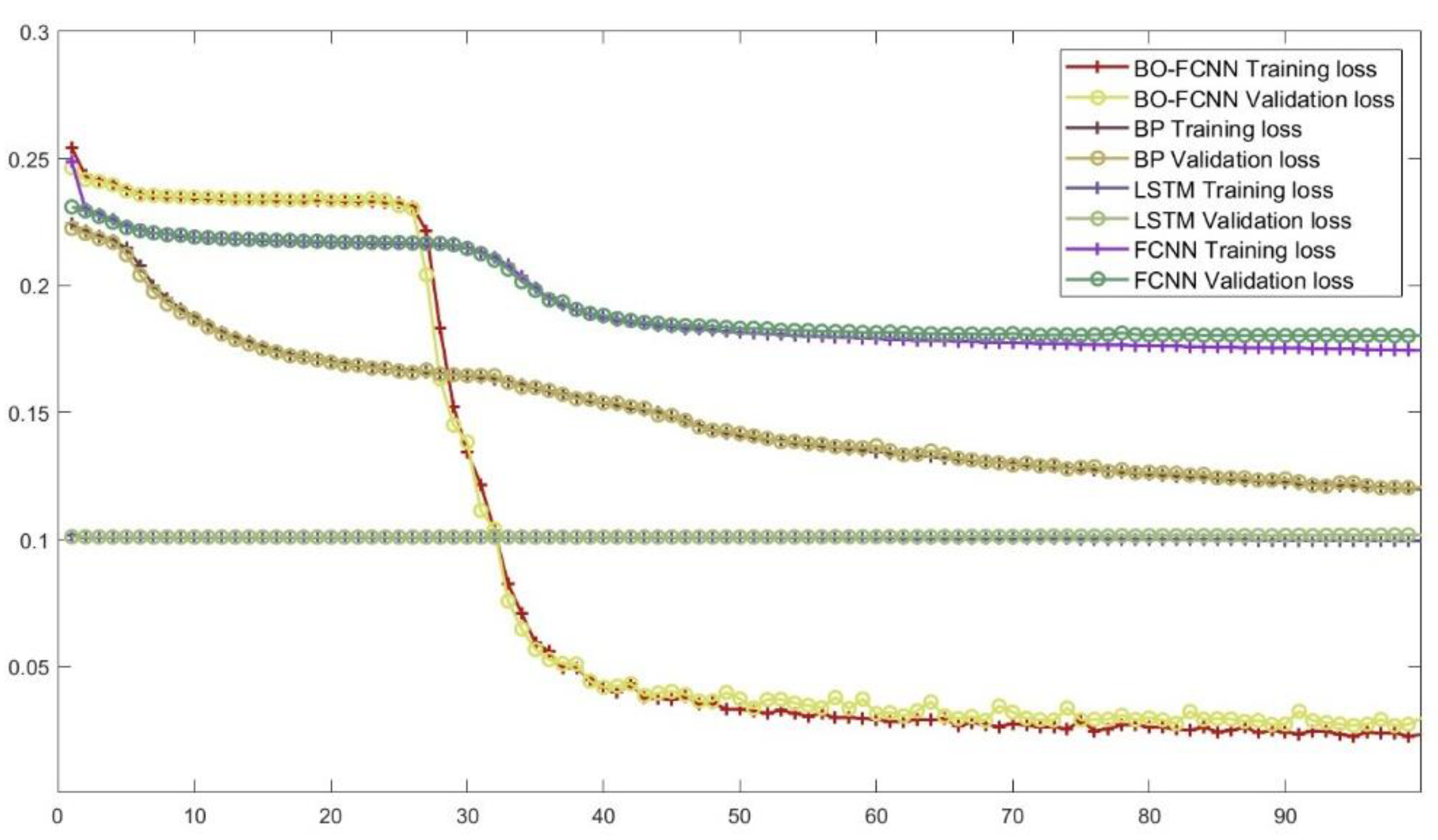
4.2. Control Trial
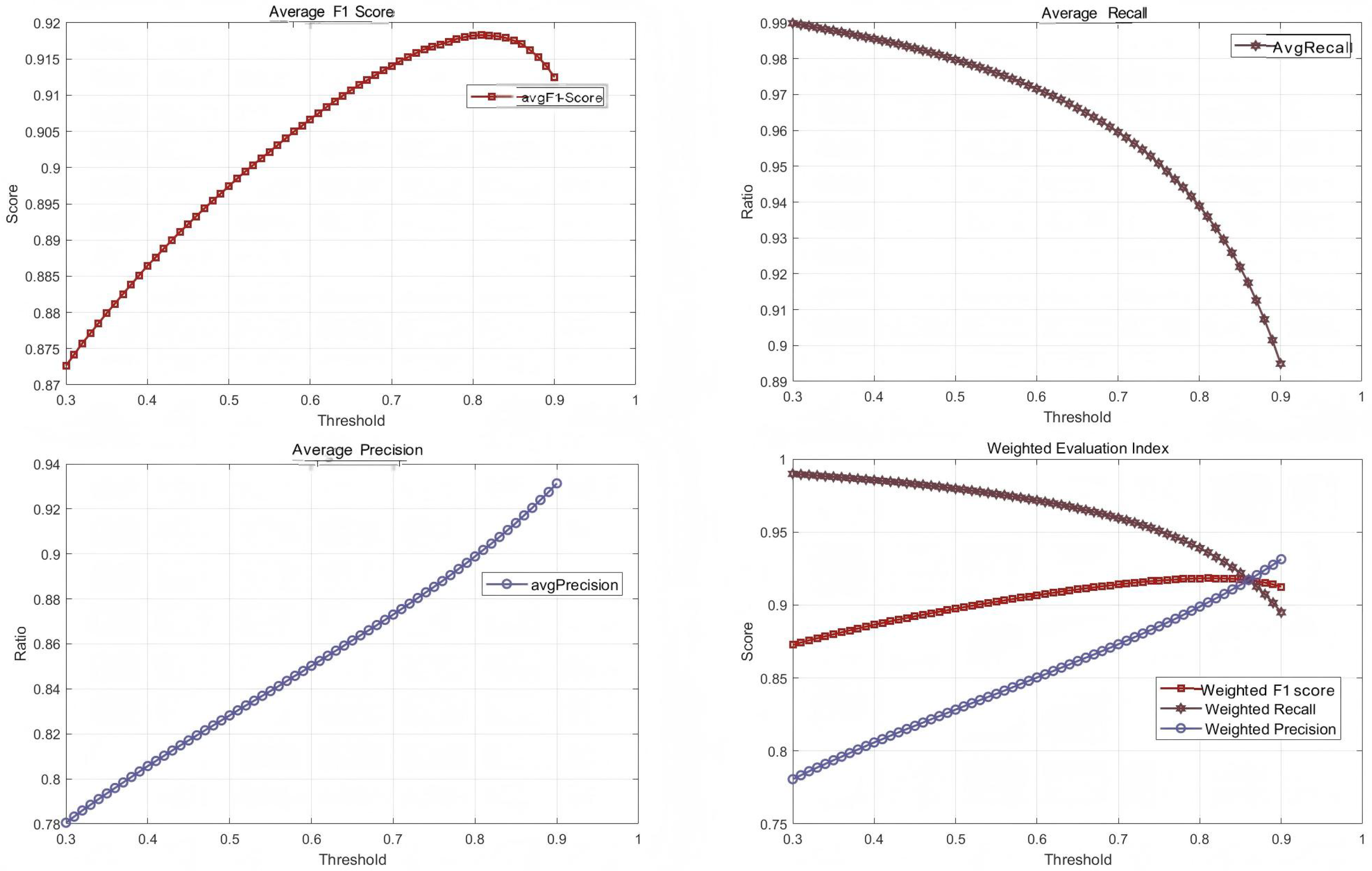
4.3. Threshold Analysis for Classification
4.4. Case Studies
5. Discussion and Analysis
5.1. Model and Parameter Analysis
5.1.1. Model Analysis
5.1.2. Parametric Analysis
5.2. Analysis of Dataset Imbalance
5.3. Analysis of Computational Cost
6. Conclusions and Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LEO | Low-Earth orbit |
| MEO | Medium-Earth orbit |
| HEO | High-Earth orbit |
| SGP4 | Simplified General Perturbation 4 |
| BO | Bayesian optimization |
| FCNN | Fully connected neural network |
| BO-FCNN | Bayesian-optimized fully connected neural network |
| TLE | Two-line element |
| TP | True positive |
| FP | False positive |
| FN | False negative |
| TN | True negative |
References
- Fossa, C.E.; Raines, R.A.; Gunsch, G.H.; Temple, M.A. An overview of the IRIDIUM (R) low Earth orbit (LEO) satellite system. In Proceedings of the IEEE 1998 National Aerospace and Electronics Conference. NAECON 1998. Celebrating 50 Years (Cat. No. 98CH36185), Dayton, OH, USA, 17 July 1998; IEEE: Piscataway, NJ, USA, 1998; pp. 152–159. [Google Scholar]
- Walker, J.G. Satellite constellations. J. Br. Interplanet. Soc. 1984, 37, 559. [Google Scholar]
- Wang, X.; Zhao, F.; Shi, Z.; Jin, Z. Visualization Simulation of Mission Planning Schemes for Remote Sensing Satellites. In Proceedings of the 2022 4th International Conference on System Reliability and Safety Engineering (SRSE), Guangzhou, China, 15–18 December 2022; pp. 394–398. [Google Scholar] [CrossRef]
- Belbachir, R.; Kies, A.; Benbouzid, A.B.; Maaza, Z.M.; Boumedjout, A. Towards Deep Simulations of LEO Satellite Links Based-on Saratoga. Wirel. Pers. Commun. 2021, 119, 1387–1404. [Google Scholar] [CrossRef]
- Shen, D.; Jia, B.; Chen, G.; Pham, K.; Blasch, E. Pursuit-evasion game theoretic uncertainty oriented sensor management for elusive space objects. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 25–29 July 2016; pp. 156–163. [Google Scholar] [CrossRef]
- Ruiz-De-Azua, J.A.; Ramírez, V.; Park, H.; AUG, A.C.; Camps, A. Assessment of Satellite Contacts Using Predictive Algorithms for Autonomous Satellite Networks. IEEE Access 2020, 8, 100732–100748. [Google Scholar] [CrossRef]
- Ferrer, E.; Ruiz-De-Azua, J.A.; Betorz, F.; Escrig, J. Inter-Satellite Link Prediction with Supervised Learning: An Application in Polar Orbits. Aerospace 2024, 11, 551. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, X.; Du, T.; Yuan, S. Multi-objective optimization of aviation dry friction clutch based on neural network and genetic algorithm. Forsch. Ingenieurwes 2025, 89, 66. [Google Scholar] [CrossRef]
- Cui, T.; Yang, X.; Jia, F.; Jin, J.; Ye, Y.; Bai, R. Mobile robot sequential decision making using a deep reinforcement learning hyper-heuristic approach. Expert Syst. Appl. 2024, 257, 124959. [Google Scholar] [CrossRef]
- Alvi, A. Practical Bayesian Optimisation for Hyperparameter Tuning. Ph.D. Thesis, University of Oxford, Oxford, UK, 2020. [Google Scholar]
- Paparusso, L.; Melzi, S.; Braghin, F. Real-time forecasting of driver-vehicle dynamics on 3D roads: A deep-learning framework leveraging Bayesian optimisation. Transp. Res. Part C-Emerg. Technol. 2023, 156, 104329. [Google Scholar] [CrossRef]
- Vien, B.S.; Kuen, T.; Rose, L.R.F.; Chiu, W.K. Optimisation and Calibration of Bayesian Neural Network for Probabilistic Prediction of Biogas Performance in an Anaerobic Lagoon. Sensors 2024, 24, 2537. [Google Scholar] [CrossRef] [PubMed]
- Hoy, Z.X.; Woon, K.S.; Chin, W.C.; Hashim, H.; Van Fan, Y. Forecasting heterogeneous municipal solid waste generation via Bayesian-optimised neural network with ensemble learning for improved generalisation. Comput. Chem. Eng. 2022, 166, 107946. [Google Scholar] [CrossRef]
- Lotfipoor, A.; Patidar, S.; Jenkins, D.P. Deep neural network with empirical mode decomposition and Bayesian optimisation for residential load forecasting. Expert Syst. Appl. 2024, 237, 121355. [Google Scholar] [CrossRef]
- Wang, Y. Unbalanced data identification based on Bayesian optimisation convolutional neural network. Int. J. Inf. Commun. Technol. 2025, 26, 96–111. [Google Scholar] [CrossRef]
- Xiao, W. Statistical analysis of 2024 global space launches. Int. Space 2025, 4–7. Available online: https://qikan.cqvip.com/Qikan/Article/Detail?id=7200404790 (accessed on 4 September 2025).
- Locatelli, M.; Schoen, F. (Global) optimization: Historical notes and recent developments. EURO J. Comput. Optim. 2021, 9, 100012. [Google Scholar] [CrossRef]
- Yu, L.; Hu, Y.; Xie, X.; Lin, Y.; Hong, W. Complex-Valued Full Convolutional Neural Network for SAR Target Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1752–1756. [Google Scholar] [CrossRef]
- Li, B.; Peng, X.; Yang, H.; Liu, G. Modeling and Performance Analysis of Multi-layer Satellite Networks Based on STK. Mach. Learn. Intell. Commun. 2018, 226, 382–393. [Google Scholar]
- Zhang, Y.; Guo, Y.; Hong, J. Analysis of Distributed Inter-satellite Link Network Coverage Based on STK and Matlab. IOP Conf. Ser. Mater. Sci. Eng. 2019, 563, 052003. [Google Scholar]
- Miao, J.; Wang, P.; Yin, H.; Chen, N.; Wang, X. A Multi-attribute Decision Handover Scheme for LEO Mobile Satellite Networks. In Proceedings of the 2019 IEEE 5th International Conference on Computer and Communications (ICCC), Chengdu, China, 6–9 December 2019; pp. 938–942. [Google Scholar]
- Wang, Z.; Bovik, A.C. Mean squared error: Love it or leave it? A new look at signal fidelity measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE). Geosci. Model. Dev. Discuss. 2014, 7, 1525–1534. [Google Scholar]
- Mannor, S.; Peleg, D.; Rubinstein, R. The cross entropy method for classification. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; pp. 561–568. [Google Scholar]








| Parameter | /° | /° | /° | /° |
|---|---|---|---|---|
| Min. | 0 | 0 | 0 | 0 |
| Max. | 360 | 180 | 360 | 360 |
| Type of Orbit | Pair ID | a/km | M/° | i/° | /° | /° | |
|---|---|---|---|---|---|---|---|
| MEO | OMNI-M1 | 11,637.8 | 0 | 34.24 | 44.99 | 329.51 | 325.78 |
| O3B FM4 | 11,637.8 | 0 | 32.13 | 147.43 | 353.90 | 6.14 | |
| … | … | … | … | … | … | … | |
| O3B MPOWER F7 | 11,637.8 | 0 | 178.76 | 86.49 | 138.61 | 181.34 | |
| LEO | CALSPHERE 1 | 7378.1 | 0 | 120.80 | 90.21 | 63.38 | 324.75 |
| CALSPHERE 2 | 7378.1 | 0 | 1170.34 | 90.23 | 67.23 | 202.11 | |
| … | … | … | … | … | … | … | |
| DIGUI-32 | 7378.1 | 0 | 91.53 | 0.02 | 8.93 | 259.53 |
| Pair ID | /° | i/° | /° | /° | /° | i/° | /° | /° |
|---|---|---|---|---|---|---|---|---|
| SO1–ST1 | 180.00 | 1139.88 | 233.55 | 249.01 | 290.34 | 90.26 | 324.80 | 190.70 |
| SO2–ST2 | 357.71 | 103.11 | 5.95 | 225.84 | 274.60 | 155.73 | 346.31 | 274.15 |
| … | … | … | … | … | … | |||
| SOi–STi | 318.39 | 154.96 | 196.14 | 283.96 | 55.10 | 67.35 | 92.99 | 341.59 |
| Pair ID | /° | i/° | /° | /° | /° | i/° | /° | /° |
|---|---|---|---|---|---|---|---|---|
| SO1–ST1 | 0.50 | 0.77 | 0.64 | 0.69 | 0.80 | 0.50 | 0.90 | 0.52 |
| SO2–ST2 | 0.99 | 0.57 | 0.01 | 0.62 | 0.76 | 0.86 | 0.96 | 0.76 |
| … | … | … | … | … | … | |||
| SOi–STi | 0.88 | 0.86 | 0.54 | 0.78 | 0.15 | 0.37 | 0.25 | 0.94 |
| Pair ID | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … | 287 |
|---|---|---|---|---|---|---|---|---|---|---|
| SO1–ST1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 |
| SO2–ST2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | … | 0 |
| … | … | … | … | … | … | … | … | … | … | … |
| SOi–STi | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | … | 0 |
| Hyperparameter | Meaning | Default | Optimization Range |
|---|---|---|---|
| m | Number of hidden layers | 2 | (2, 6) |
| n | Number of neurons in each layer | 32 | (32, 256) |
| e | Learning rate | ||
| A | Coefficient a in the weighted loss function | 0.1 | (0.1, 5) |
| All Categories | True Value | ||
|---|---|---|---|
| True | False | ||
| Predicted value | True | TP | FP |
| False | FN | TN | |
| A_Value | Hidden_Layers | Learning_Rate | Neurons_per_Layer |
|---|---|---|---|
| 2.443257049 | 6 | 0.001749911 | 223 |
| Algorithm | Average F1 Score | Average Recall | Average Precision | Time |
|---|---|---|---|---|
| BO-FCNN | 0.91 | 0.93 | 0.89 | 2235.21 |
| FCNN | 0.25 | 0.31 | 0.29 | 896.08 |
| BP | 0.44 | 0.61 | 0.34 | 101.23 |
| Random Forest | 0.05 | 0.02 | 0.25 | 774.35 |
| LSTM | 0.05 | 0.03 | 0.21 | 4716.01 |
| Metric | Value |
|---|---|
| Average F1 Score | 0.91 |
| Average Recall | 0.93 |
| Average Precision | 0.89 |
| Optimal Threshold | 0.80 |
| Metric | Value |
|---|---|
| Average F1 Score | 0.87 |
| Average Recall | 0.90 |
| Average Precision | 0.84 |
| Optimal Threshold | 0.80 |
| Experimental Group ID | Model Structure | Core Verification Objectives | Key Configurations |
|---|---|---|---|
| F0 | FCNN | Performance bottlenecks in validating empirical hyperparameters | Three-layer full connection (128→128→128) |
| F1 | FCNN + Random Search (RS-FCNN) | To verify the strengths of random search vs. empirical settings | 30-round random sampling hyperparameters (same search space as BO) |
| F2 | FCNN + Grid Search (GS-FCNN) | To verify the difference in the efficiency and performance of grid search vs. random search | 30-round fixed-step grid sampling (same search space as BO) |
| F3 | FCNN + Bayesian Optimization (BO-FCNN) | To verify the hyperparametric optimization advantage of Bayesian optimization | Surrogate model = GP-RBF; collection function = EI; 30 rounds of optimization (initial five random samples) |
| F4 | BO-FCNN-LSTM | To explore BO’s suitability in the temporal dimension (time series modeling + hyperparameter optimization synergy) | Bo optimizes LSTM hyperparameters |
| F5 | LSTM | To verify the advantages of the BO-FCNN in the temporal dimension |
| Experimental Group ID | Model Structure | Average F1 Score | Average Recall | Average Precision | Time | Combination of Parameters |
|---|---|---|---|---|---|---|
| F0 | FCNN | 0.53 | 0.53 | 0.54 | 0 | {3-128-1} |
| F1 | RS-FCNN | 0.79 | 0.94 | 0.68 | 1399.43 | {5-128-4.46} |
| F2 | GS-FCNN | 0.73 | 0.94 | 0.59 | 7968 | {5-256-5} |
| F3 | BO-FCNN | 0.87 | 0.93 | 0.89 | 2935.21 | {5-249-4.76} |
| F4 | BO-FCNN-LSTM | 0.66 | 0.90 | 0.52 | 6313.94 | {2-82-4.98} |
| F5 | LSTM | 0.05 | 0.03 | 0.21 | 4716.01 |
| Model | Average F1 Score | CV (Average F1 Score) | RMSE | CV(RMSE) |
|---|---|---|---|---|
| BO-FCNN | 0.8652 + 0.0115 | 13% | 0.1451 + 0.0075 | 5.7% |
| Dataset | Avg. F1 Score | m | n | e | A |
|---|---|---|---|---|---|
| Dataset A | 0.98 | 6 | 0.003 | 253 | 1.43 |
| Dataset B | 0.91 | 6 | 0.003 | 146 | 4.25 |
| Communication Distance | m | N | E | a | Optimal Threshold | Avg. F1 Score | Avg. Recall | Avg. Precision |
|---|---|---|---|---|---|---|---|---|
| 11,000 | 6 | 246 | 0.0038 | 4.25 | 0.81 | 0.918 | 0.93 | 0.90 |
| 10,500 | 5 | 245 | 0.0022 | 4.27 | 0.82 | 0.932 | 0.94 | 0.91 |
| 10,000 | 6 | 197 | 0.0024 | 4.69 | 0.82 | 0.89 | 0.91 | 0.87 |
| 9750 | 4 | 201 | 0.0024 | 4.60 | 0.81 | 0.82 | 0.87 | 0.78 |
| 9500 | 2 | 139 | 0.0035 | 4.71 | 0.55 | 0.413 | 0.59 | 0.32 |
| 9250 | 3 | 46 | 0.0035 | 4.85 | 0.30 | 0.04 | 0.02 | 0.09 |
| 9000 | 3 | 232 | 0.0092 | 1.57 | 0.30 | 0 | 0.07 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Xiong, W.; Liu, Y. The BO-FCNN Inter-Satellite Link Prediction Method for Space Information Networks. Aerospace 2025, 12, 841. https://doi.org/10.3390/aerospace12090841
Yu X, Xiong W, Liu Y. The BO-FCNN Inter-Satellite Link Prediction Method for Space Information Networks. Aerospace. 2025; 12(9):841. https://doi.org/10.3390/aerospace12090841
Chicago/Turabian StyleYu, Xiaolan, Wei Xiong, and Yali Liu. 2025. "The BO-FCNN Inter-Satellite Link Prediction Method for Space Information Networks" Aerospace 12, no. 9: 841. https://doi.org/10.3390/aerospace12090841
APA StyleYu, X., Xiong, W., & Liu, Y. (2025). The BO-FCNN Inter-Satellite Link Prediction Method for Space Information Networks. Aerospace, 12(9), 841. https://doi.org/10.3390/aerospace12090841






