Reinforced Model Predictive Guidance and Control for Spacecraft Proximity Operations
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Points of Innovation
- The coupling of DRL and MPC for uncooperative target mapping in a relative dynamics scenario;
- A PIL evaluation campaign to validate the methodology’s performance;
2. Problem Statement
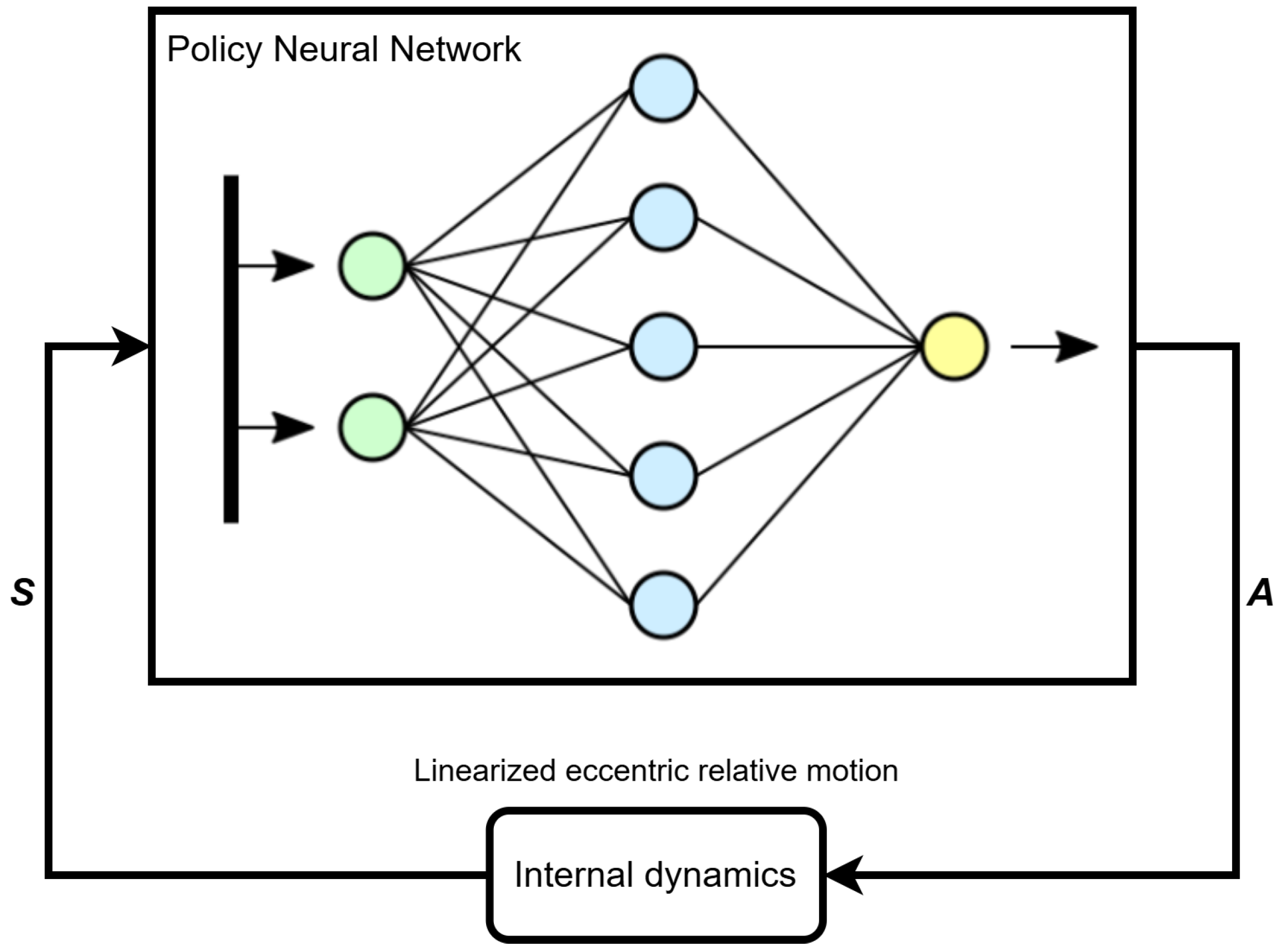
2.1. DRL Guidance
State space
Action space
Reward function
- Map level score. The faces that have both optimal Sun and camera exposure are the ones that generate an improvement in the level of the map. The maximum level defined for the map consists of having each face photographed times. Therefore, at each time step the map level, , can be computed considering how many good photos of each face have been taken until that moment. The corresponding reward score is defined in Equation (6), and at each time step k the agent is rewarded for increasing the map level over the current value, .The improvement in the map depends on two different incidence angles between the target object faces and the Sun and camera directions:
- -
- Sun incidence score. The Sun incidence angle is the angle between the Sun direction relative to the target object and the normal to the face considered. The Sun incidence angle should be between 0° and 70° to avoid shadows or excessive brightness. Values outside this interval may correspond to conditions that degrade the quality of the image. If the angle exceeds this range, the photo can not be considered good enough to make a real improvement in the map.
- -
- Camera incidence score. The camera incidence angle is defined as the angle between the normal to the face and the camera direction. This angle should be maintained between 5° and 60°. Also in this case, if the angle exceeds this range, the photo can not be considered good enough to make a real improvement in the map.
- Position score. Negative scores are given when the spacecraft escapes from the region defined by a minimum and maximum distance from the target object, and .
2.2. MPC Optimization
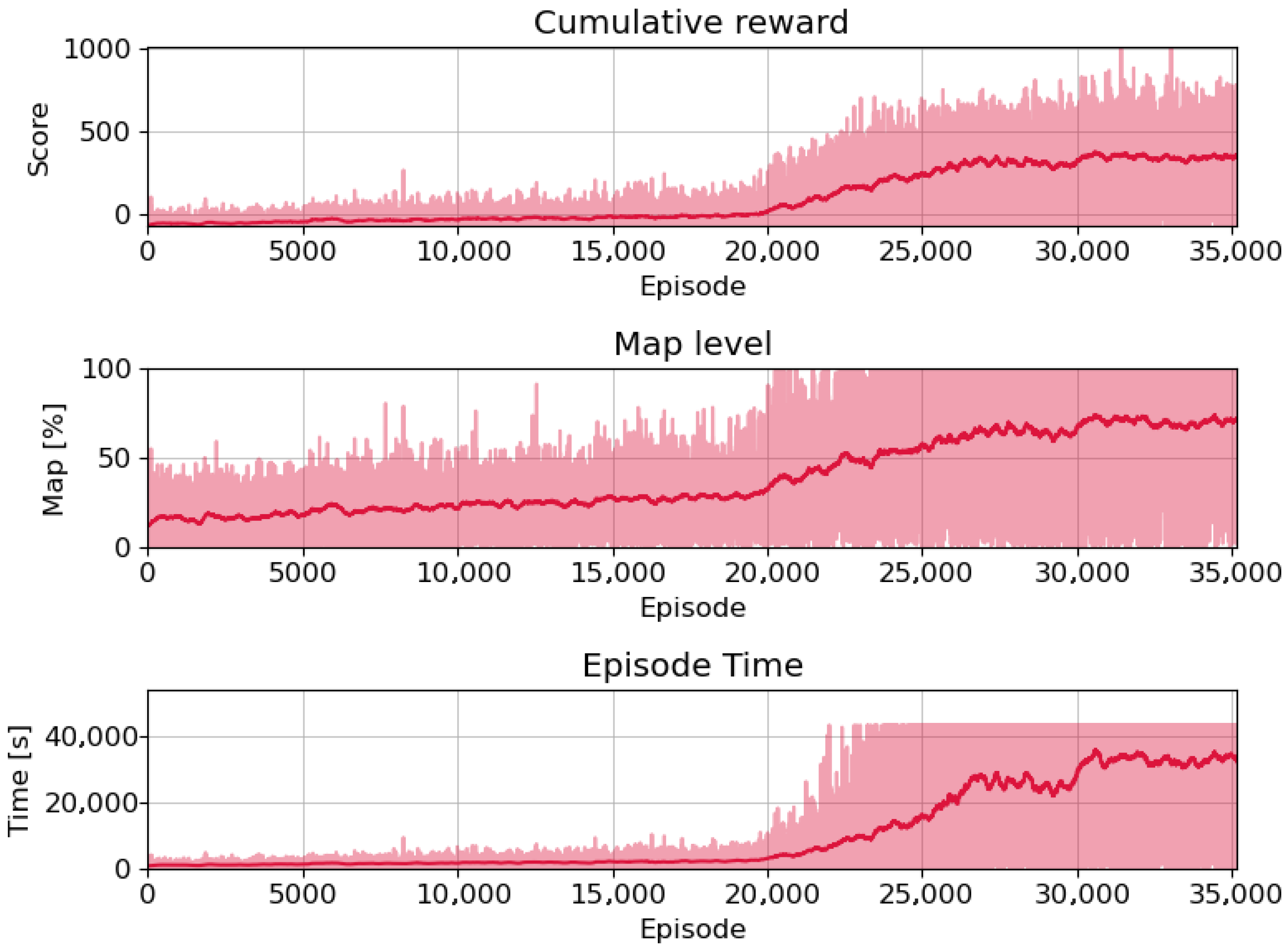
3. Training Results
- At first, a recurrent neural network architecture is selected because of its improved stability when dealing with evolving dynamics with respect to simple feed-forward networks, as already analyzed in [8]. Among the different types of RNNs, here the Long Short-Term Memory (LSTM) recurrent layer is exploited. The definition of the network is presented in Table 2.
- Secondly, a transformer network formulation, the state-of-the-art network for this complex problem, is investigated. The transformer architecture consists of self-attention mechanisms and feed-forward neural networks, as introduced in [13]. This kind of architecture was originally developed for natural language processing (NLP), excelling at capturing dependencies and relationships across sequences, making it suitable for tasks where understanding context and long-range dependencies is crucial. Overall, transformer architectures also offer a promising direction in deep reinforcement learning for continuous action spaces, especially when the problem involves learning complex dependencies and patterns. The architecture defined for the transformer agent is presented in Table 3.
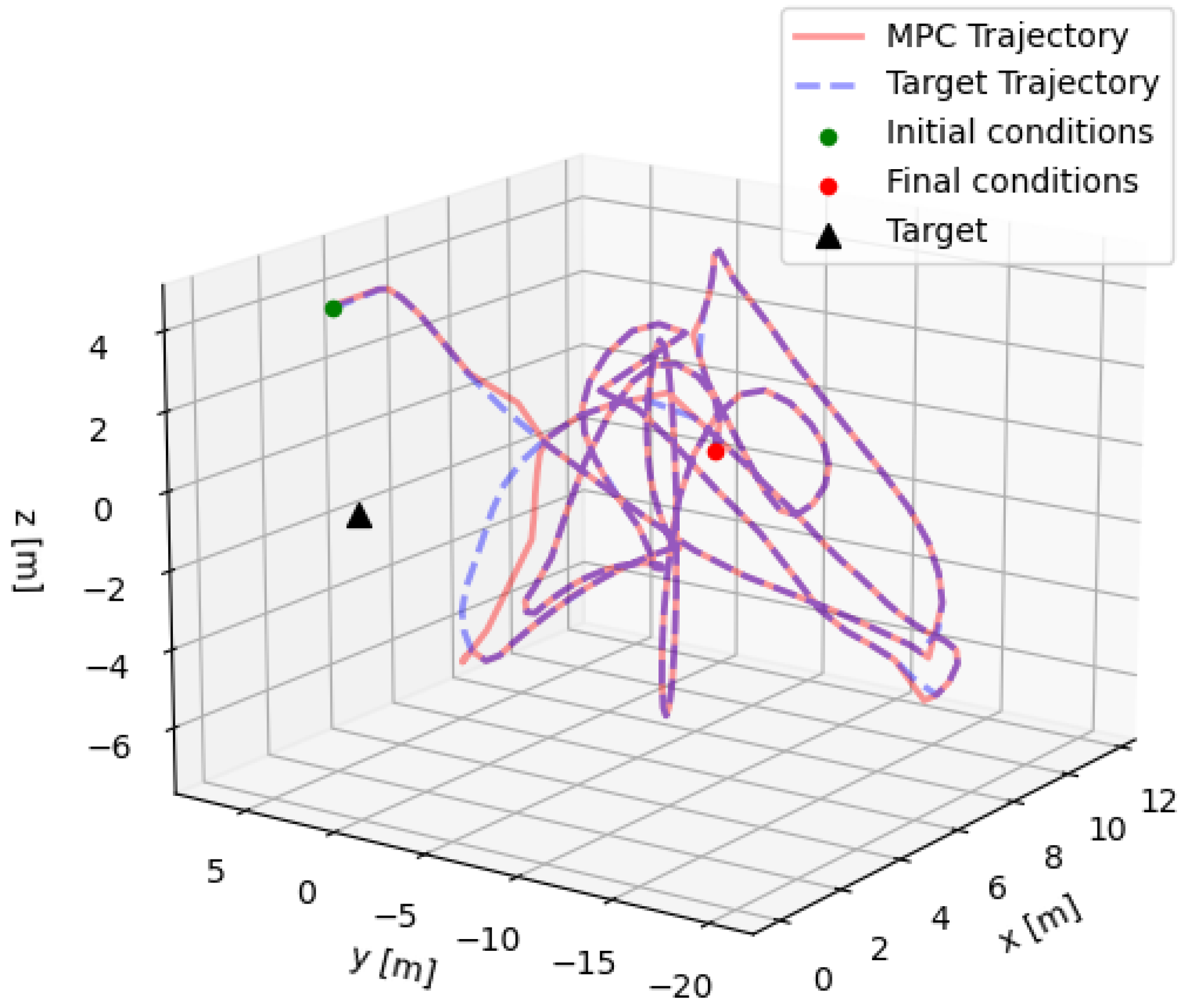
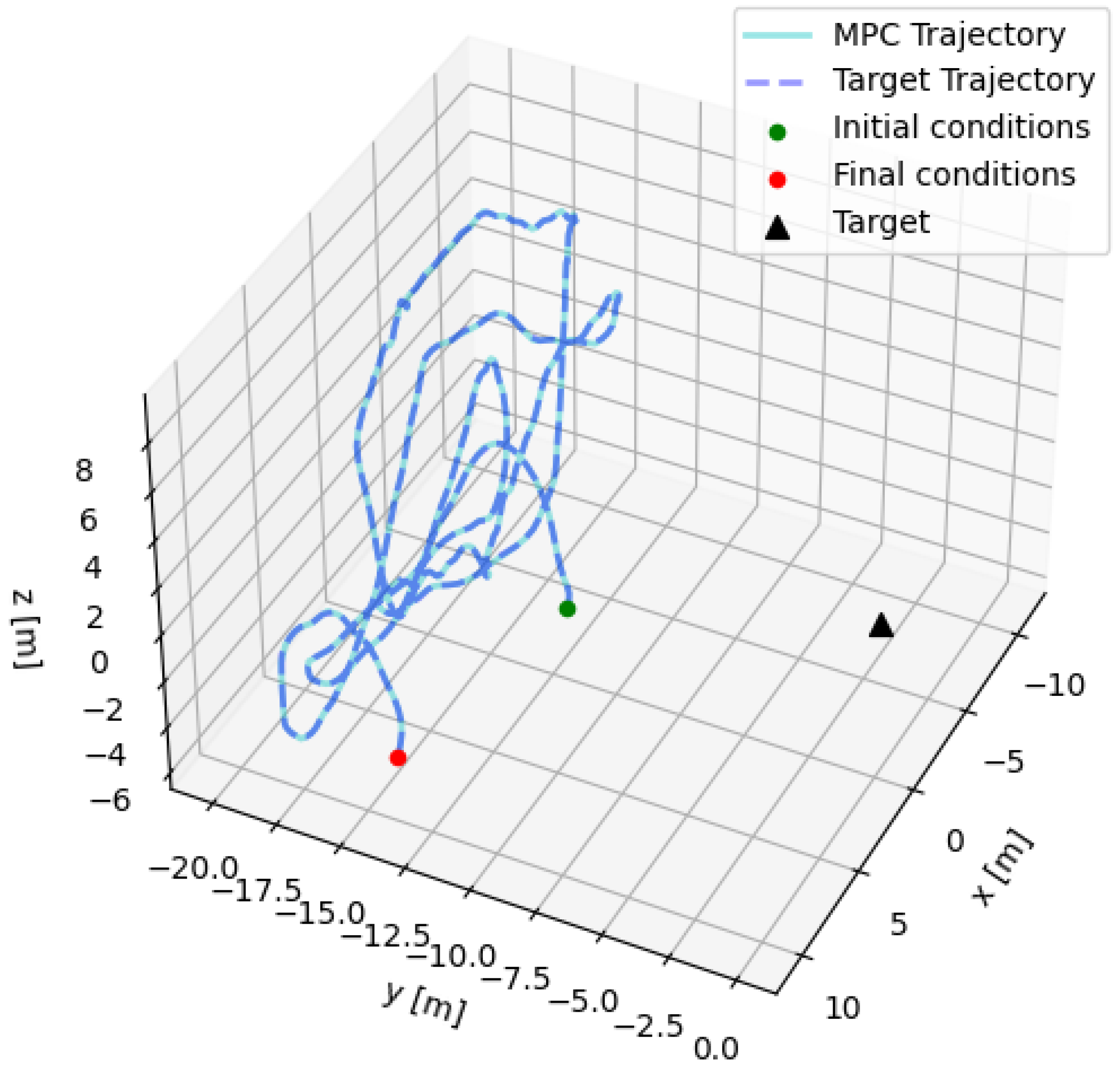
4. Testing Campaign
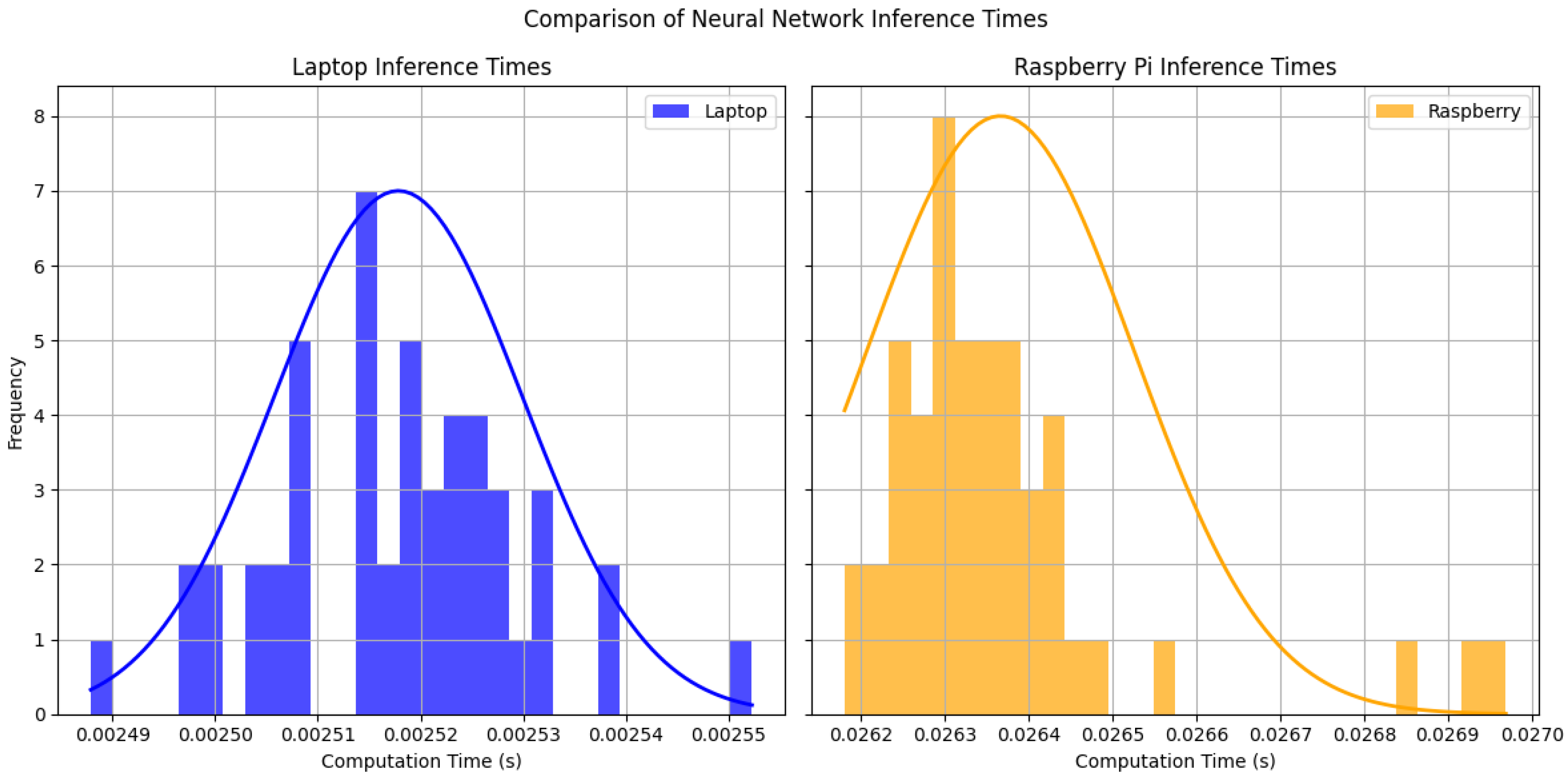
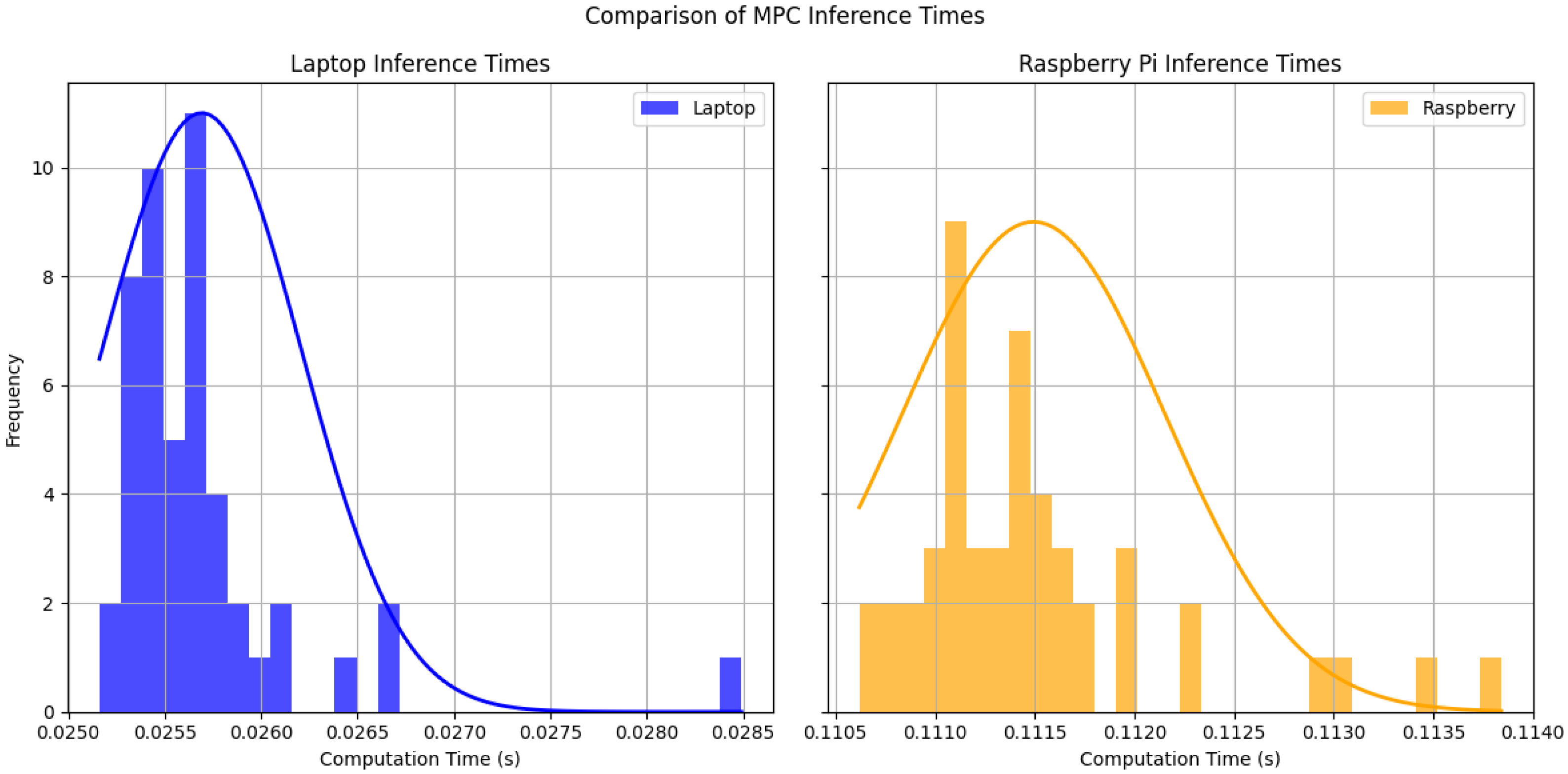
5. Processor-in-the-Loop Validation
- Laptop: Dell Precision 5680-Intel Core i9 13900H, 2.6 GHz (Intel, Santa Clara, CA, USA)
- Raspberry Pi 4: Quad-core Cortex-A72 (ARM v8) 64-bit SoC @ 1.8GHz
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Izzo, D.; Märtens, M.; Pan, B. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Silvestrini, S.; Lavagna, M. Deep Learning and Artificial Neural Networks for Spacecraft Dynamics, Navigation and Control. Drones 2022, 6, 270. [Google Scholar] [CrossRef]
- Linares, R.; Campbell, T.; Furfaro, R.; Gaylor, D. A Deep Learning Approach for Optical Autonomous Planetary Relative Terrain Navigation. Spacefl. Mech. 2017, 160, 3293–3302. [Google Scholar]
- Gaudet, B.; Linares, R.; Furfaro, R. Adaptive Guidance and Integrated Navigation with Reinforcement Meta-Learning. Acta Astronaut. 2020, 169, 180–190. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Deep reinforcement learning for six degree-of-freedom planetary landing. Adv. Space Res. 2020, 65, 1723–1741. [Google Scholar] [CrossRef]
- Brandonisio, A.; Lavagna, M.; Guzzetti, D. Reinforcement Learning for Uncooperative Space Objects Smart Imaging Path-Planning. J. Astronaut. Sci. 2021, 68, 1145–1169. [Google Scholar] [CrossRef]
- Capra, L.; Brandonisio, A.; Lavagna, M. Network architecture and action space analysis for deep reinforcement learning towards spacecraft autonomous guidance. Adv. Space Res. 2022, 71, 3787–3802. [Google Scholar] [CrossRef]
- Brandonisio, A.; Bechini, M.; Civardi, G.L.; Capra, L.; Lavagna, M. Closed-loop AI-aided image-based GNC for autonomous inspection of uncooperative space objects. Aerosp. Sci. Technol. 2024, 155, 109700. [Google Scholar] [CrossRef]
- Izzo, D.; Tailor, D.; Vasileiou, T. On the Stability Analysis of Deep Neural Network Representations of an Optimal State Feedback. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 145–154. [Google Scholar] [CrossRef]
- Korda, M. Stability and Performance Verification of Dynamical Systems Controlled by Neural Networks: Algorithms and Complexity. IEEE Control Syst. Lett. 2022, 6, 3265–3270. [Google Scholar] [CrossRef]
- Romero, A.; Song, Y.; Scaramuzza, D. Actor-Critic Model Predictive Control. arXiv 2024, arXiv:2306.09852. [Google Scholar] [CrossRef]
- Smith, T.K.; Akagi, J.; Droge, G. Model predictive control for formation flying based on D’Amico relative orbital elements. Astrodynamics 2025, 9, 143–163. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2023, arXiv:1706.03762. [Google Scholar] [PubMed]
- Inalhan, G.; Tillerson, M.; How, J. Relative Dynamics and Control of Spacecraft Formations in Eccentric Orbits. J. Guid. Control. Dyn. 2002, 25, 48–59. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; The MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning. arXiv 2016, arXiv:1602.01783. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Morgan, D.; Chung, S.J.; Hadaegh, F. Model Predictive Control of Swarms of Spacecraft Using Sequential Convex Programming. J. Guid. Control Dyn. 2014, 37, 1–16. [Google Scholar] [CrossRef]
- Belloni, E.; Silvestrini, S.; Prinetto, J.; Lavagna, M. Relative and absolute on-board optimal formation acquisition and keeping for scientific activities in high-drag low-orbit environment. Adv. Space Res. 2023, 73, 5595–5613. [Google Scholar] [CrossRef]
- Sarno, S.; Guo, J.; D’Errico, M.; Gill, E. A guidance approach to satellite formation reconfiguration based on convex optimization and genetic algorithms. Adv. Space Res. 2020, 65, 2003–2017. [Google Scholar] [CrossRef]
- Agrawal, A.; Verschueren, R.; Diamond, S.; Boyd, S. A rewriting system for convex optimization problems. J. Control Decis. 2018, 5, 42–60. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Prediction Horizon | 400 s |
| Sampling Time | 10 s |
| Control Horizon | |
| m/s | |
| S | 1000 |
| R | 10 |
| Layer | Elements | Activation |
|---|---|---|
| LSTM Layers | 24 | - |
| 1st Hidden Layer | 64 | ReLU |
| 2nd Hidden Layer | 32 | ReLU |
| Learning rate | - |
| Layer | Elements |
|---|---|
| Embedding Layer | 128 |
| Encoder | 128, head = 4, layers = 2 |
| Output Layer | 128 |
| Learning rate |
| Variable | Range |
|---|---|
| d | |
| v | 0 m/s |
| rad/s rad/s |
| Variable | Value |
|---|---|
| Reward Discount Factor | 0.99 |
| Terminal Reward Discount Factor | 0.95 |
| Clipping Factor | 0.2 |
| Entropy Factor | 0.02 |
| Optimizer | ADAM |
| Optimization Step Frequency | 10 episodes |
| Training Episodes | 18,000 |
| Recurrent | Transformer | |
|---|---|---|
| Average Map | 84.3% | 79.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capra, L.; Brandonisio, A.; Lavagna, M.R. Reinforced Model Predictive Guidance and Control for Spacecraft Proximity Operations. Aerospace 2025, 12, 837. https://doi.org/10.3390/aerospace12090837
Capra L, Brandonisio A, Lavagna MR. Reinforced Model Predictive Guidance and Control for Spacecraft Proximity Operations. Aerospace. 2025; 12(9):837. https://doi.org/10.3390/aerospace12090837
Chicago/Turabian StyleCapra, Lorenzo, Andrea Brandonisio, and Michèle Roberta Lavagna. 2025. "Reinforced Model Predictive Guidance and Control for Spacecraft Proximity Operations" Aerospace 12, no. 9: 837. https://doi.org/10.3390/aerospace12090837
APA StyleCapra, L., Brandonisio, A., & Lavagna, M. R. (2025). Reinforced Model Predictive Guidance and Control for Spacecraft Proximity Operations. Aerospace, 12(9), 837. https://doi.org/10.3390/aerospace12090837








