Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants and Master Curve of Relaxation Modulus
Abstract
1. Introduction
2. Materials and Methods
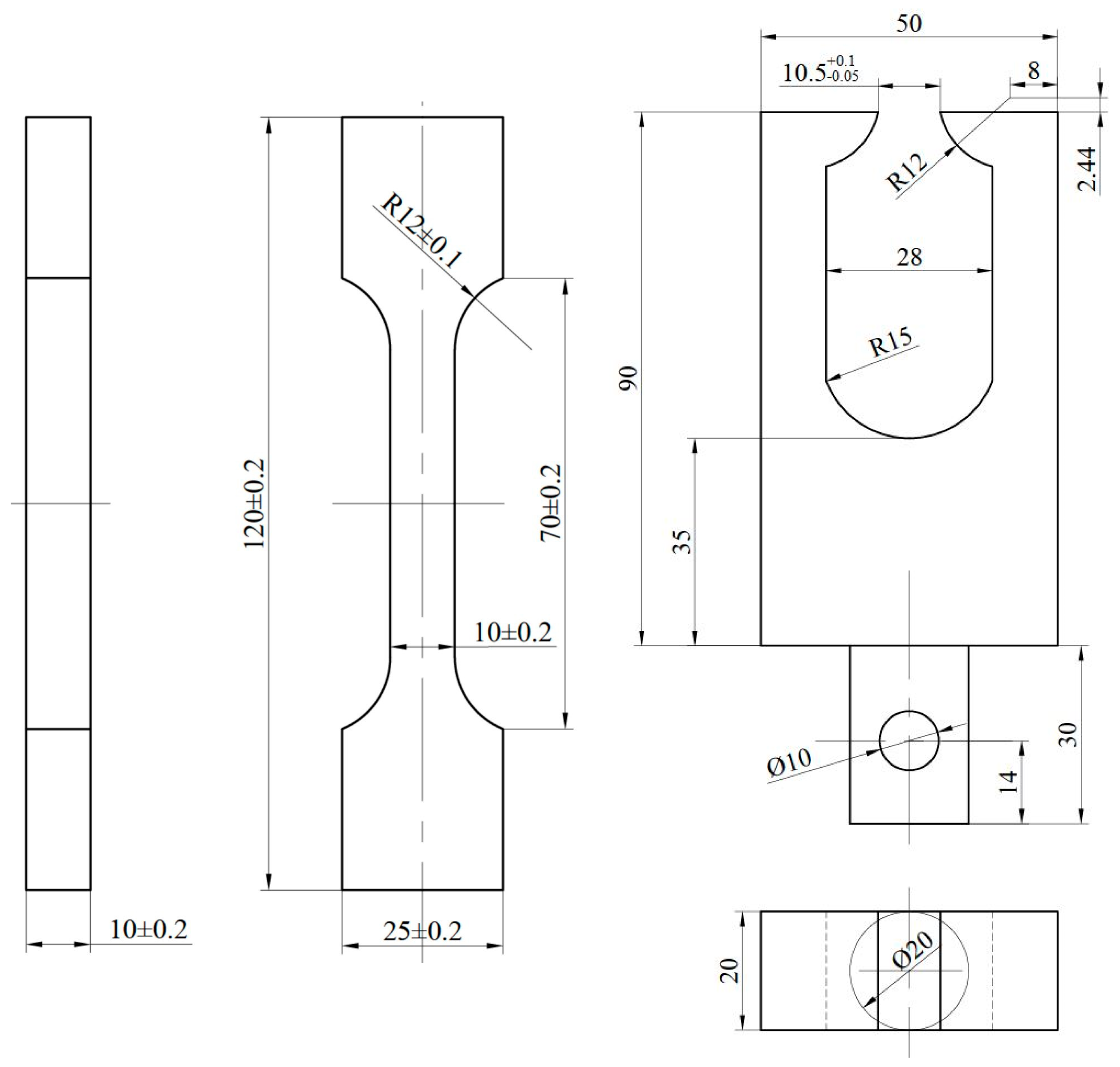
2.1. Test Materials and Specimens
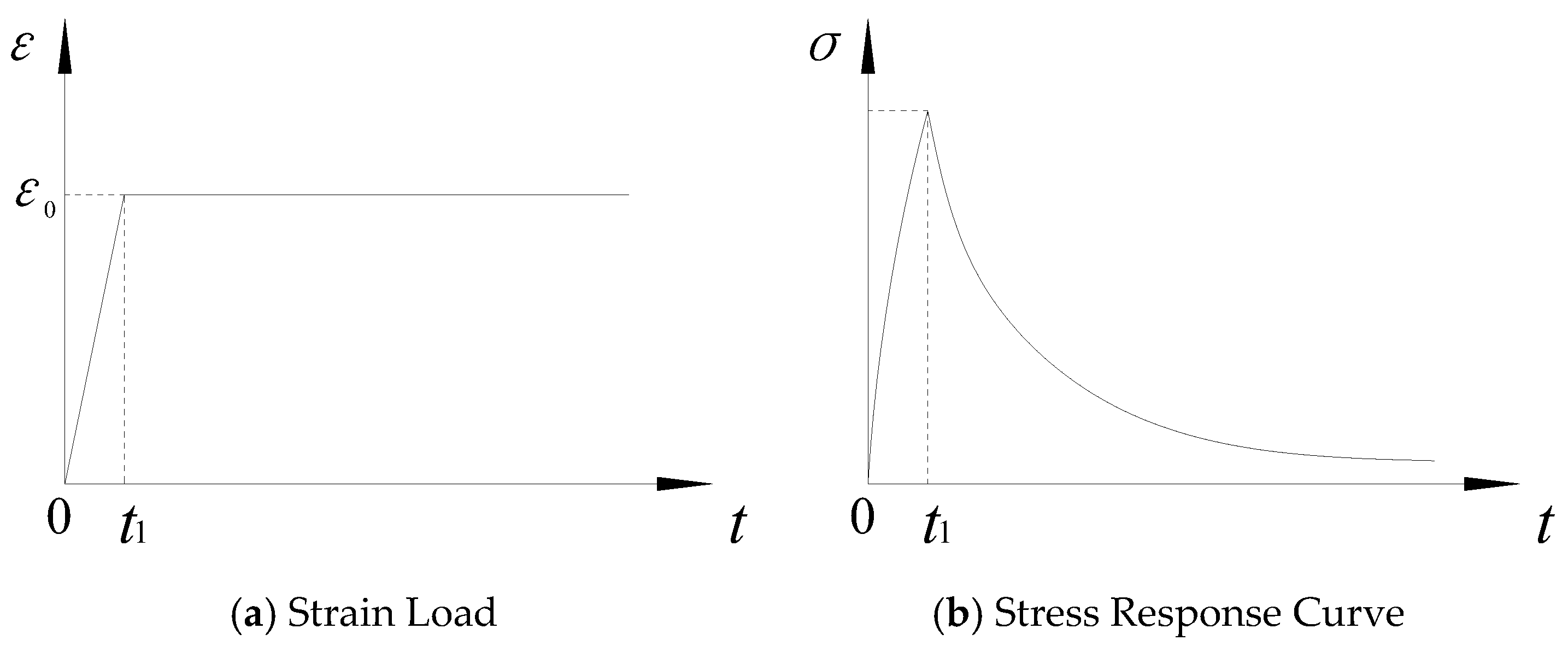
2.2. Test Methods
3. Results and Discussion
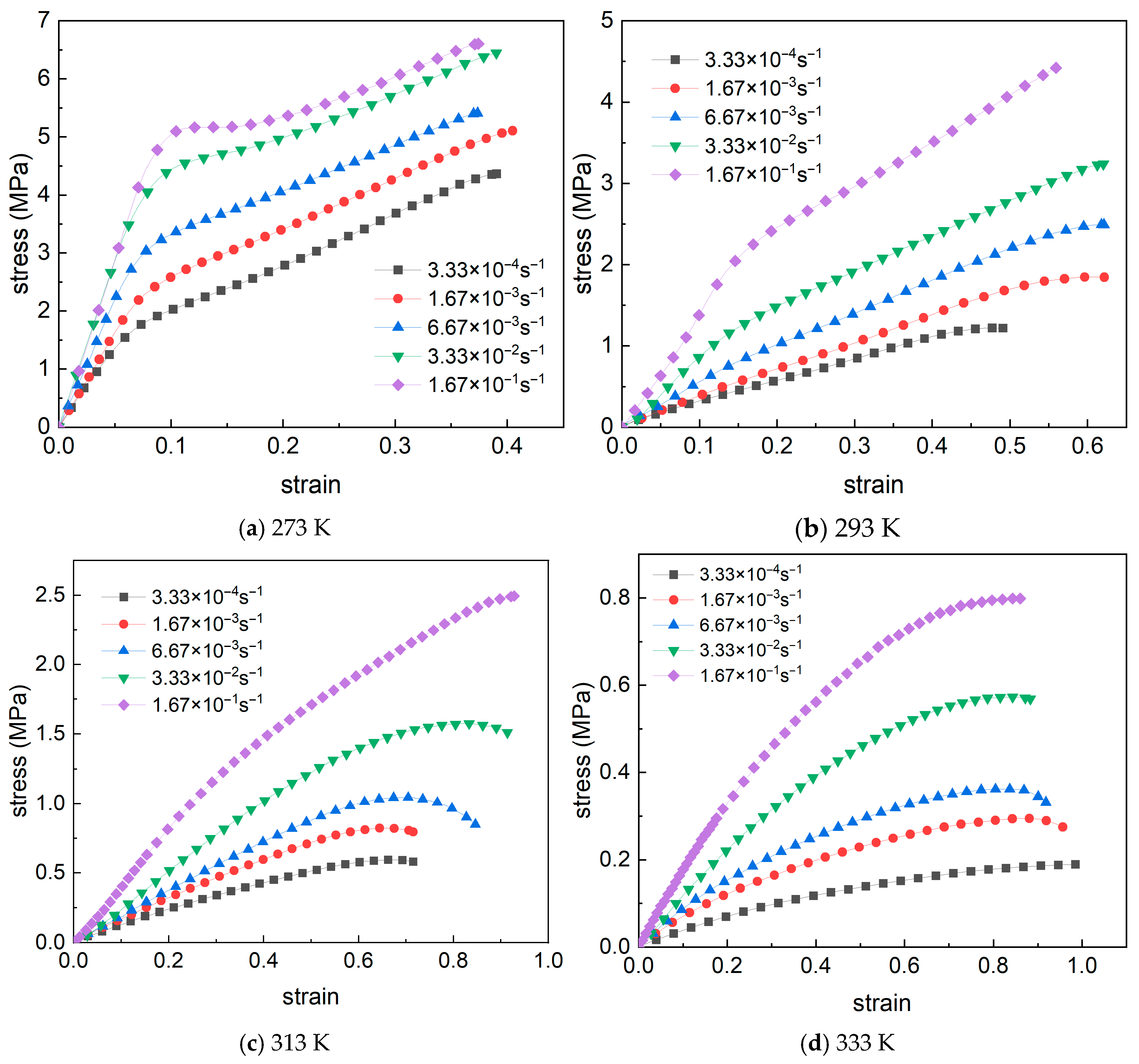
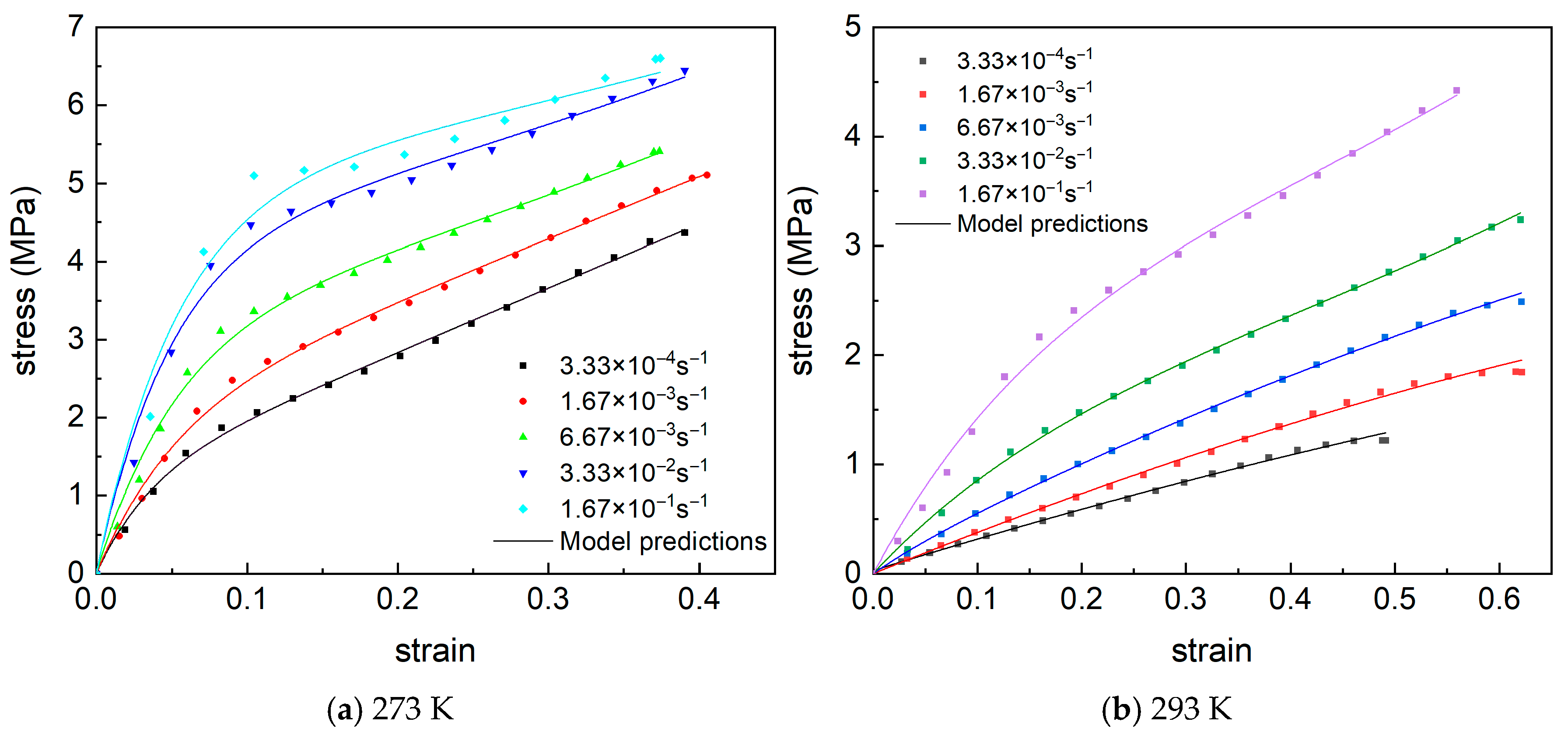
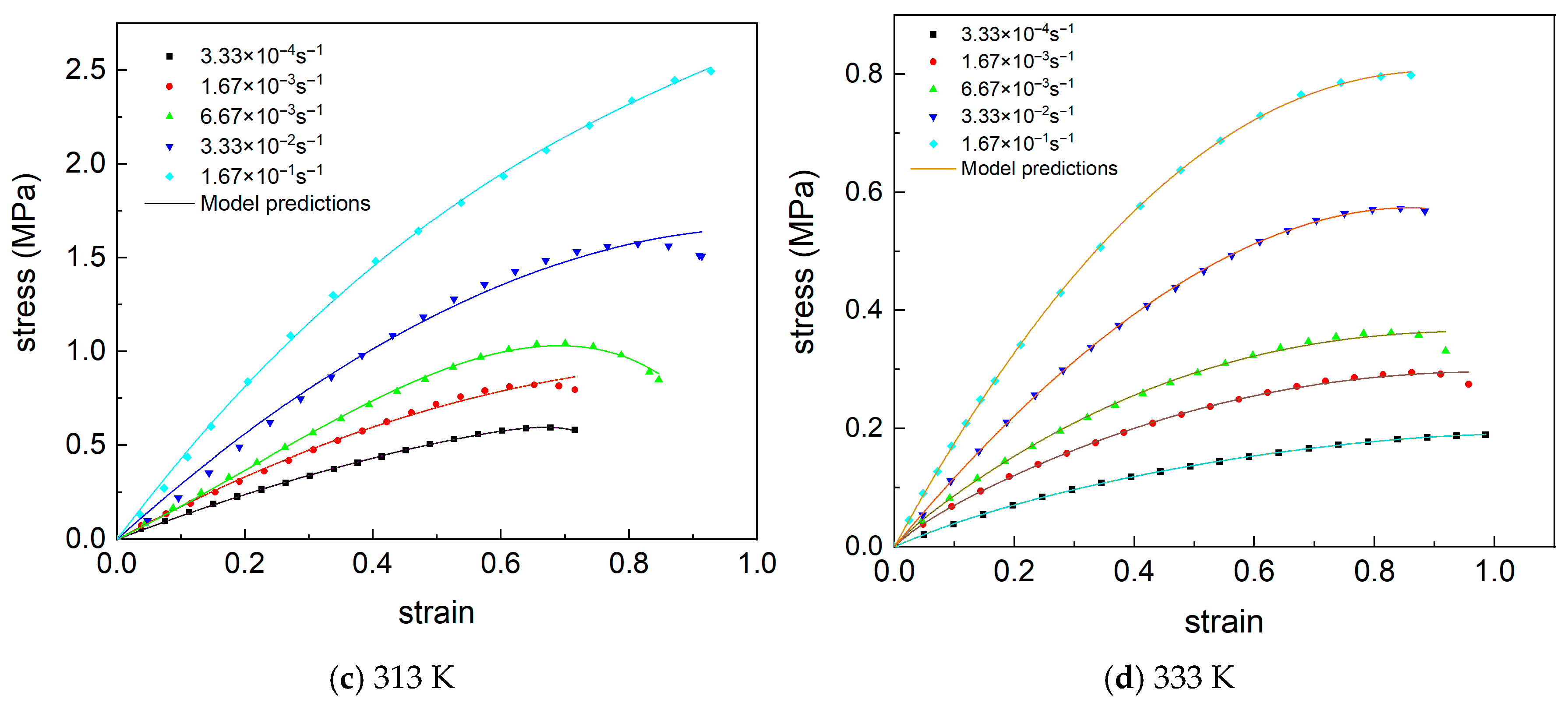
3.1. Uniaxial Tensile Test Results
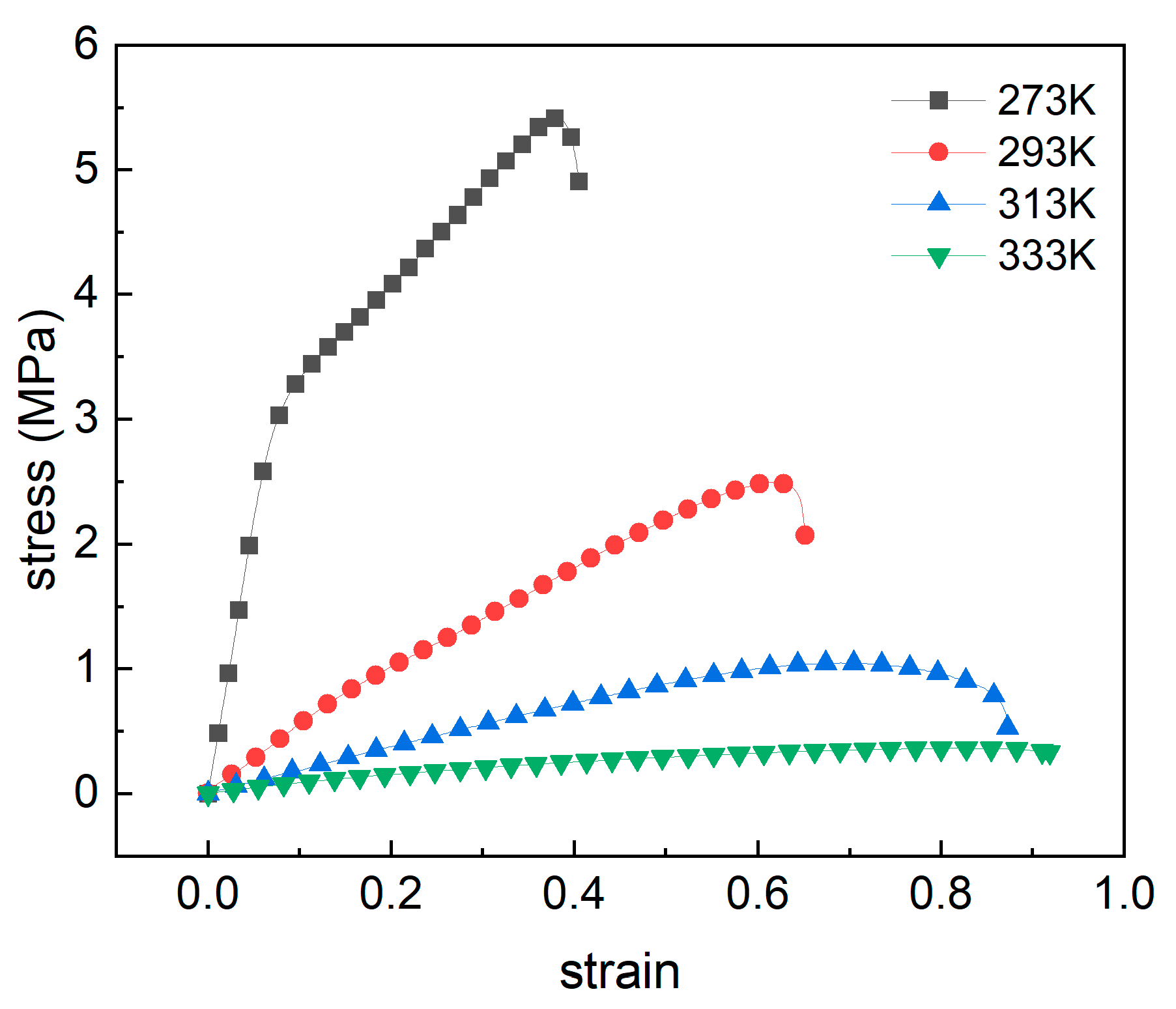
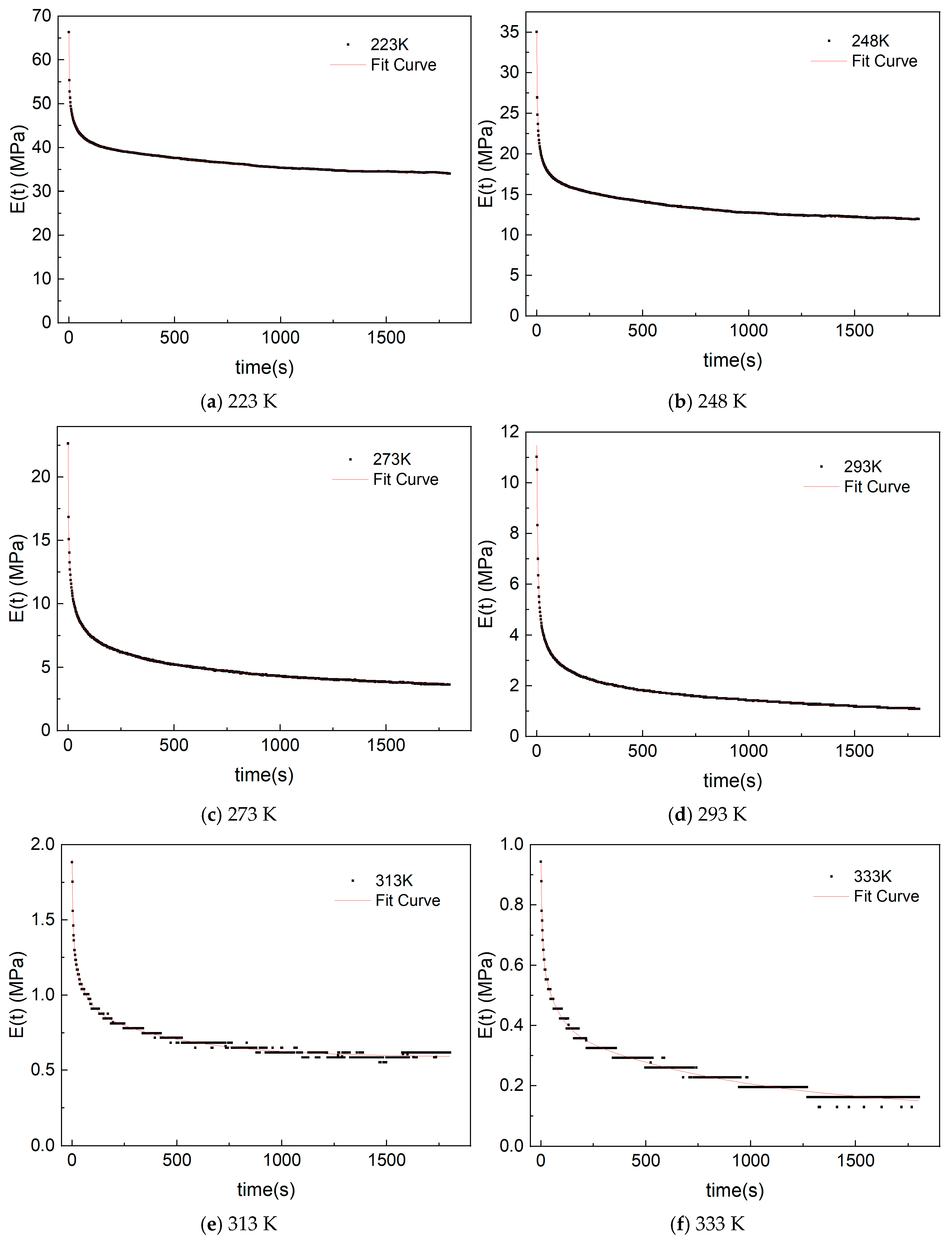
3.2. Relaxation Test Results
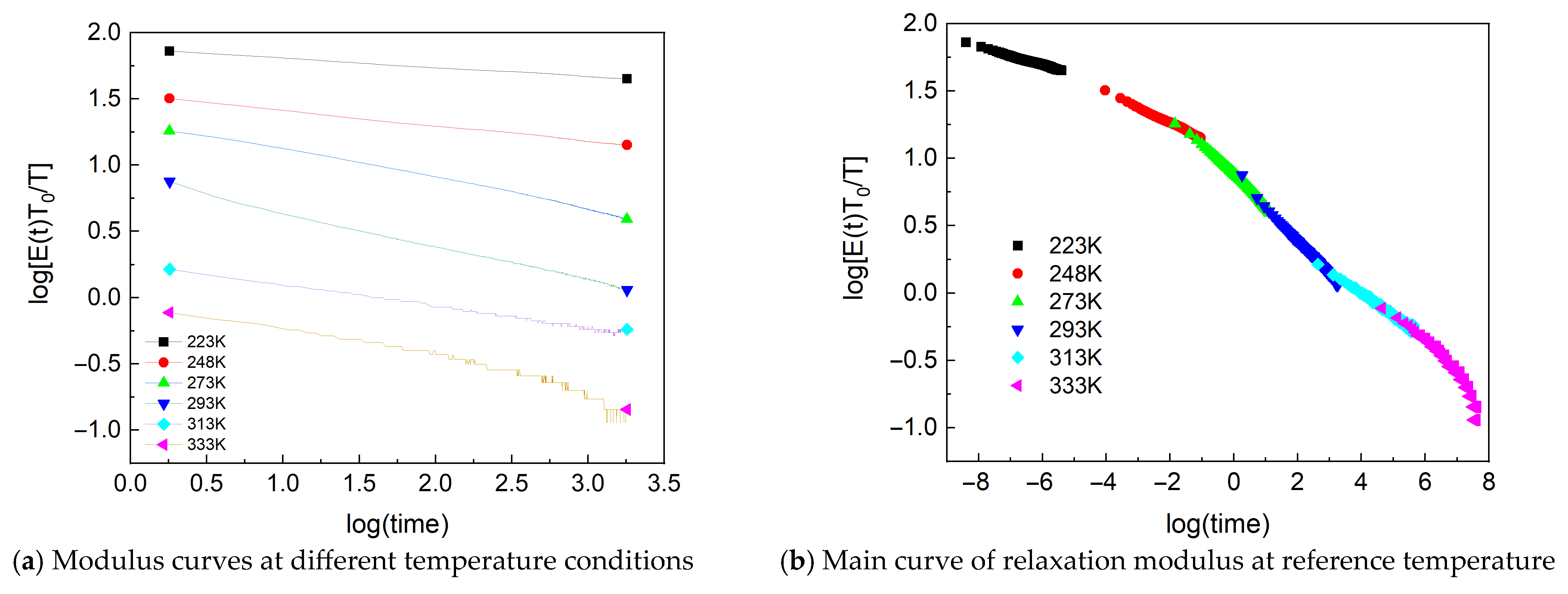
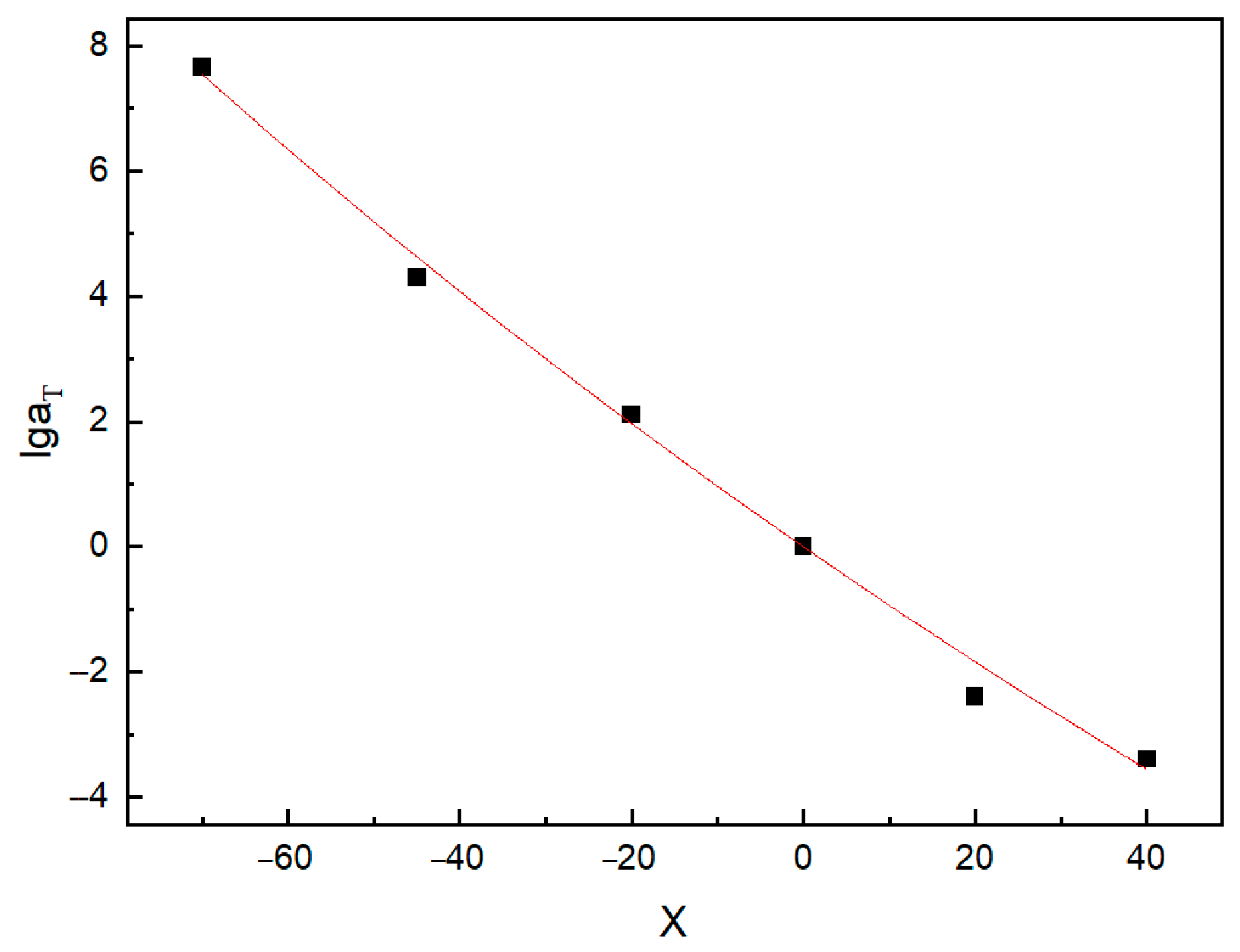
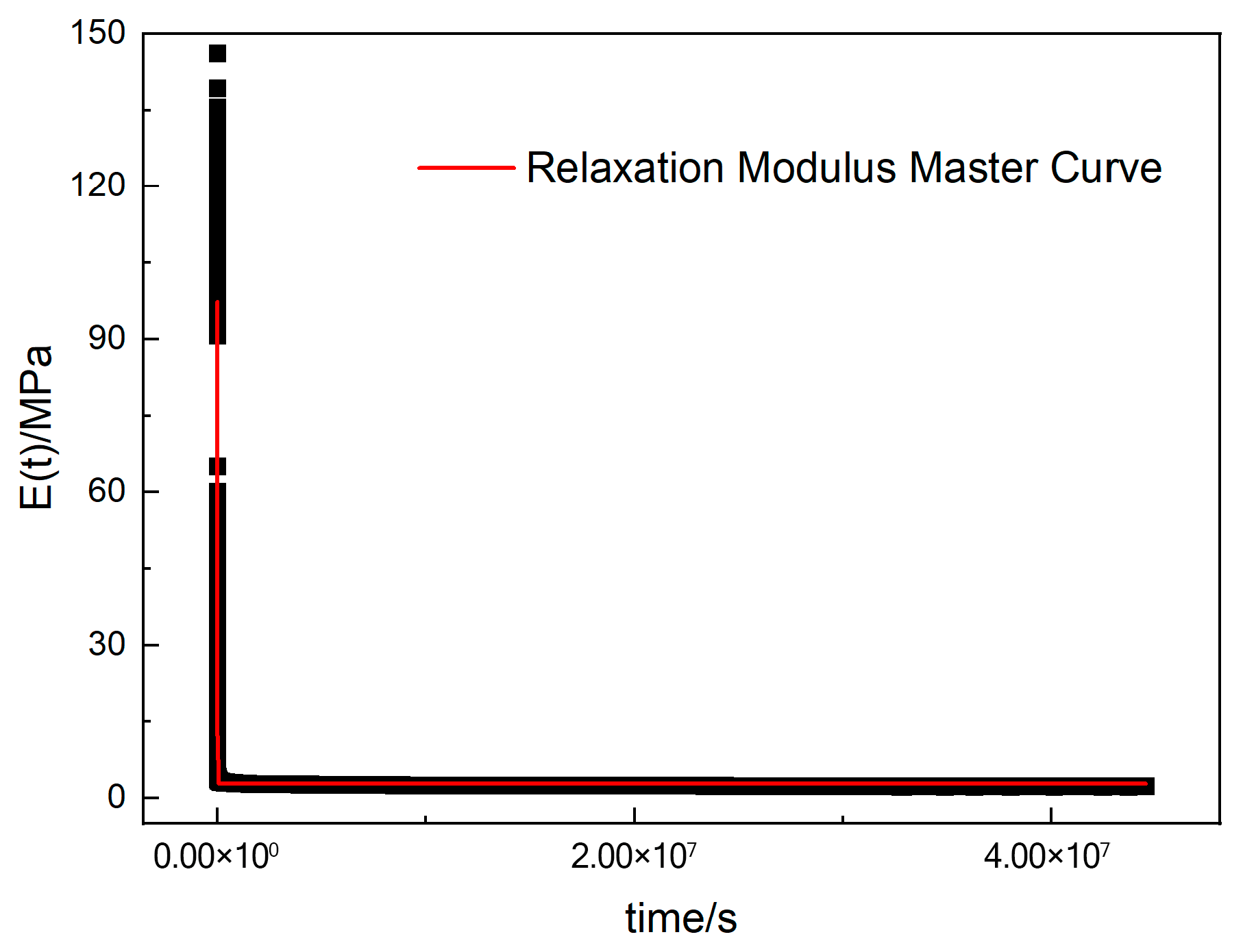
3.3. Master Curve of Relaxation Modulus
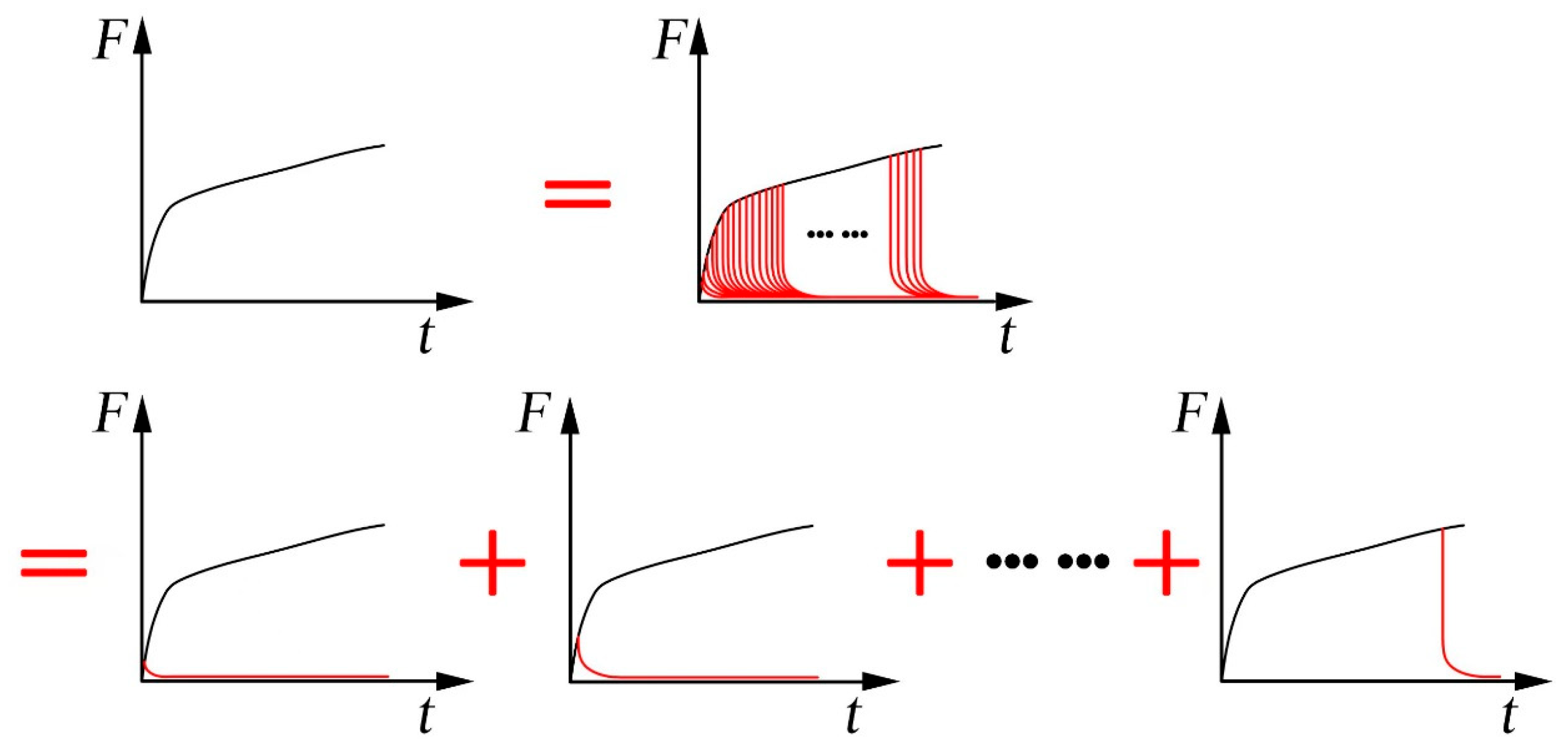
3.4. Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, J.L.; Li, P.; Zhang, Z.Z.; Gong, W.J.; Li, W.F. Research progress on structural integrity of solid rocket motor grains. Sci. Technol. Eng. 2021, 21, 434–441. [Google Scholar]
- Wei, X.L.; Zhou, J.H.; Li, H.Y.; Shu, H.M. Advances in structural integrity analysis of solid propellant grains. J. Ordn. Equip. Eng. 2022, 43, 19–26. [Google Scholar]
- Godai, T. Flame propagation into the crack of solid-propellant grain. AIAA J. 1970, 8, 1322–1327. [Google Scholar] [CrossRef]
- Kumar, M.; Kovacic, S.M.; Kuo, K.K. Flame propagation and combustion processes in solid propellant cracks. AIAA J. 1981, 19, 610–618. [Google Scholar] [CrossRef]
- Lemaitre, J.; Desmorat, R.; Sauzay, M. Anisotropic damage law of evolution. Eur. J. Mech.-A Solids 2000, 19, 187–208. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Park, T. Anisotropic damage effect tensors for the symmetrization of the effective stress tensor. J. Appl. Mech. 1997, 64, 106–110. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Abu Al-Rub, R.K. A finite strain plastic-damage model for high velocity impacts using combined viscosity and gradient localization limiters: Part II-numerical aspects and simulations. Int. J. Damage Mech. 2006, 15, 335–373. [Google Scholar] [CrossRef]
- Manu, H.; Shantanu, M. Evolving structural tensor approach to model the damage induced anisotropy in viscoelastic solids. Int. J. Solids Struct. 2022, 248, 111655. [Google Scholar] [CrossRef]
- Zhao, G.M.; Xie, L.X.; Meng, X.R. A damage-based constitutive model for rock under impacting load. Int. J. Min. Sci. Technol. 2014, 24, 505–511. [Google Scholar] [CrossRef]
- Park, S.W.; Richard, K.Y.; Schapery, R.A. A viscoelastic continuum damage model and its application to uniaxial behavior of asphalt concrete. Mech. Mater. 1996, 24, 241–255. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Taqieddin, Z.N.; Kattan, P.I. Micromechanical approach to damage mechanics of composite materials with fabric tensors. Compos. Part B Eng. 2007, 38, 862–877. [Google Scholar] [CrossRef]
- Schapery, R.A. A theory of mechanical behavior of elastic media with growing damage and other changes in structure. J. Mech. Phys. Solids 1990, 38, 215–253. [Google Scholar] [CrossRef]
- Gibson, N.; Schwartz, C.; Schapery, R.; Witczak, M. Viscoelastic, viscoplastic, and damage modeling of asphalt concrete in unconfined compression. Transp. Res. Rec. J. Transp. Res. Board 2003, 1860, 3–15. [Google Scholar] [CrossRef]
- Kim, Y.R.; Daniel, J.S.; Wen, H. Fatigue Performance Evaluation of WesTrack Asphalt Mixtures Using Viscoelastic Continuum Damage Approach; North Carolina Department of Transportation: Raleigh, NC, USA, 2002. [Google Scholar]
- Lee, H.; Daniel, J.; Kim, Y. Continuum damage mechanics-based fatigue model of asphalt concrete. J. Mater. Civ. Eng. 2000, 12, 105–112. [Google Scholar] [CrossRef]
- Lee, H.; Kim, Y. Viscoelastic continuum damage model of asphalt concrete with healing. J. Eng. Mech. 1998, 124, 1224–1232. [Google Scholar] [CrossRef]
- Sullivan, R.W. Development of a viscoelastic continuum damage model for cyclic loading. Mech. Time-Depend. Mater. 2008, 12, 329–342. [Google Scholar] [CrossRef]
- Underwood, B.; Baek, C.; Kim, Y. Simplified viscoelastic continuum damage model as platform for asphalt concrete fatigue analysis. Transp. Res. Rec. J. Transp. Res. Board 2012, 2296, 36–45. [Google Scholar] [CrossRef]
- Underwood, B.S.; Kim, Y.R.; Guddati, M.N. Characterization and Performance Prediction of ALF mixtures using a viscoelastoplastic continuum damage model (with discussion). In Proceedings of the Association of Asphalt Paving Technologists-Proceedings of the Technical Sessions 2006 Annual Meeting, Savannah, GA, USA, 27–29 March 2006. [Google Scholar]
- Dai, Q.; Sadd, M.H.; You, Z. A micromechanical finite element model for linear and damage-coupled viscoelastic behaviour of asphalt mixture. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1135–1158. [Google Scholar] [CrossRef]
- Guddati, M.; Feng, Z.; Kim, Y. Toward a micromechanics-based procedure to characterize fatigue performance of asphalt concrete. Transp. Res. Rec. J. Transp. Res. Board 2002, 1789, 121–128. [Google Scholar] [CrossRef]
- Kim, Y.; Allen, D.; Little, D. Damage-induced modeling of asphalt mixtures through computational micromechanics and cohesive zone fracture. J. Mater. Civ. Eng. 2005, 17, 477–484. [Google Scholar] [CrossRef]
- Lytton, R.L.; Chen, C.W.; Little, D.N. Microdamage Healing in Asphalt and Asphalt Concrete, Volume III: A Micromechanics Fracture and Healing Model for Asphalt Concrete; Turner-Fairbank Highway Research Center: McLean, VA, USA, 2001. [Google Scholar]
- Onifade, I.; Jelagin, D.; Guarin, A.; Birgisson, B.; Kringos, N. Effect of micro-scale morphological parameters on meso-scale response of Asphalt Concrete. In Asphalt Pavements; CRC Press: Boca Raton, FL, USA, 2014; pp. 1775–1784. [Google Scholar]
- Sadd, M.; Dai, Q.; Parameswaran, V.; Shukla, A. Simulation of asphalt materials using finite element micromechanical model with damage mechanics. Transp. Res. Rec. J. Transp. Res. Board 2003, 1832, 86–95. [Google Scholar] [CrossRef]
- Tashman, L.; Masad, E.; Zbib, H.; Little, D.; Kaloush, K. Microstructural viscoplastic continuum model for permanent deformation in asphalt pavements. J. Eng. Mech. 2005, 131, 48–57. [Google Scholar] [CrossRef]
- Kachanov, L.M. Rupture time under creep conditions. Izviestia Akad. Nauk. SSSR Otd. Tekh. Nauk. 1958, 8, 26–31. [Google Scholar] [CrossRef]
- Lemaitre, J.; Dufailiy, J. Damage measurements. Eng. Fract. Mech. 1987, 28, 643–661. [Google Scholar] [CrossRef]
- Voyiadjis, G.Z.; Kattan, P.I. A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 2008, 18, 315–340. [Google Scholar] [CrossRef]
- Miller, T.C. Damage and dilatometry for solid propellants with digital image correlation. Propellants Explos. Pyrotech. 2018, 44, 234–245. [Google Scholar] [CrossRef]
- Yang, J.H.; Wang, F.W.; Qin, S.Y. Experimental and theoretical study on acoustic emission characteristics and damage modeling of HTPB composite solid propellants. J. Solid Rocket Technol. 2000, 23, 37–40. [Google Scholar]
- Liu, C.W.; Yang, J.H.; Zhang, H. Acoustic emission monitoring of damage evolution in composite solid propellants. Aerosp. Shanghai 2011, 28, 69–72. [Google Scholar]
- Liu, X.G.; Liu, P.J.; Qiang, H.F.; Zhang, Y. Quantitative characterization of dewetting in HTPB propellant via micro-CT. J. Propul. Technol. 2019, 40, 1162–1180. [Google Scholar]
- Yang, Q.Q.; Xu, S.L.; Cai, R.L.; Zhang, J.; Qiang, F.Z.; Huang, Z.P. Mesoscopic damage behavior of composite propellants through digital image processing. J. Solid Rocket Technol. 2022, 45, 83–91. [Google Scholar]
- Li, S.Q.; Qiang, H.F.; Wang, G.; Wang, X.R.; Liu, X.G.; Wang, J.X. Experimental investigation on meso-damage evolution of HTPB propellant under uniaxial tension. J. Propul. Technol. 2022, 43, 411–417. [Google Scholar]
- Chen, S.; Wang, C.; Zhang, K.; Lu, X.; Li, Q. A nonlinear viscoelastic constitutive model for solid propellant with rate-dependent cumulative damage. Materials 2022, 15, 5834. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, X.; Wang, Z.Z.; Li, H.Y. An experimental and modeling investigation on the effects of temperature and strain rate on the tensile-deformation behavior of TB991 weld sealant. Mech. Time-Depend. Mater. 2023, 27, 119–138. [Google Scholar] [CrossRef]
- Li, H.; Xu, J.S.; Chen, X.; Zhang, J.F.; Li, J. A nonlinear viscoelastic constitutive model with damage and experimental validation for composite solid propellant. Sci. Rep. 2023, 13, 2049. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Ju, Y.; Zheng, J.; Han, B. Acquiring the Relaxation Modulus of Composite Solid Propellant. Chin. J. Explos. Propellant 2011, 34, 58–62. [Google Scholar]
- Honglei, M.; Yutao, J.; Changsheng, Z. Determination Way of Relaxation Modulus of Modified DB Propellant. Eng. Mech. 2012, 29, 359–362. [Google Scholar]
- Quanxing, H.; Yudong, J.; Jian, L. Fitting of Relaxation Modulus Master Curve for Solid Propellant and W.L.F Equation Parameters. J. Solid Rocket. Technol. 2003, 26, 46–48. [Google Scholar]
- Junhu, L.; Zheng, W. Evaluation for Relaxation Modulus and Creep Compliance from Stress Relaxation Test Data. J. Solid Rocket. Technol. 1995, 18, 73–78. [Google Scholar]
- QJ 2487-1993; Uniaxial Tensile Stress Relaxation Modulus and Main Curve Determination Methods for Composite Propellant. Aeronautics and Astronautics, Ministry of Industry in the People’s Republic of China: Beijing, China, 1993.
- GJB 770B-2005; Test Method of Propellant. Commission of Science, Technology and Industry for National Defence Publish: Beijing, China, 2005; pp. 200–204+262–266.
- Yang, T.Q.; Luo, W.B.; Xu, P.; Wei, Y.T. Viscoelasticity: Theory and Applications; Science Press: Beijing, China, 2004. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Li, R. Time-temperature superposition method for glass transition temperature of plastic materials. Mater. Sci. Eng. A 2000, 278, 36–45. [Google Scholar] [CrossRef]
- Bueche, F. Rate and pressure effects in polymers and other glass-forming substances. J. Chem. Phys. 1962, 36, 2940–2946. [Google Scholar] [CrossRef]
- Sudarsanan, N.; Fonte, B.R.; Kim, Y.R. Application of time-temperature superposition principle to pull-off tensile strength of asphalt tack coats. Constr. Build. Mater. 2020, 262, 120798. [Google Scholar] [CrossRef]

| Tensile Strain Rate | ||||
|---|---|---|---|---|
| 3.33 × 10−4 s−1 | 261.020 | 0.032 | 1.181 | 28.796 |
| 1.67 × 10−3 s−1 | 227.406 | 0.035 | 1.897 | 20.010 |
| 6.67 × 10−3 s−1 | 3.146 | 18.796 | 315.921 | 0.015 |
| 3.33 × 10−2 s−1 | 4.223 | 20.720 | 630.784 | 0.007 |
| 1.67 × 10−1 s−1 | 4.975 | 18.653 | 741.932 | 0.004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Xu, J.; Zhou, C.; Chen, X.; Yang, X. Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants and Master Curve of Relaxation Modulus. Aerospace 2025, 12, 817. https://doi.org/10.3390/aerospace12090817
Li Y, Xu J, Zhou C, Chen X, Yang X. Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants and Master Curve of Relaxation Modulus. Aerospace. 2025; 12(9):817. https://doi.org/10.3390/aerospace12090817
Chicago/Turabian StyleLi, Yao, Jinsheng Xu, Changsheng Zhou, Xiong Chen, and Xiumin Yang. 2025. "Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants and Master Curve of Relaxation Modulus" Aerospace 12, no. 9: 817. https://doi.org/10.3390/aerospace12090817
APA StyleLi, Y., Xu, J., Zhou, C., Chen, X., & Yang, X. (2025). Constitutive Model Based on Stress Relaxation for Composite Modified Double-Base Propellants and Master Curve of Relaxation Modulus. Aerospace, 12(9), 817. https://doi.org/10.3390/aerospace12090817





