Abstract
The warmer air resulting from climate change reduces the lift force on a departing aircraft, potentially reducing its climb angle and causing more engine noise near the airport. Here, we study this phenomenon at a selection of 30 European airports in northern hemisphere summer (June–July–August). We first formulate and verify a low-complexity model of noise propagation around airports, although we emphasise that our high-level results do not explicitly depend on this agreement. The model includes anisotropic noise propagation, atmospheric absorption, and the ability to model the noise emissions from multiple engines. We study the Airbus A320, but the method could be straightforwardly generalised to other aircraft. We refer to the model as an emulator since (using Latin hypercube parameter sampling) it mimics a more comprehensive model against which it is verified. The model is used to calculate the area enclosed by the 50 dB SPL (sound pressure level) contour, , which agrees well with a similar metric (using the day–evening–night sound level, ) from the verification target, . Using temperature and pressure data from IPCC simulations of future climate, and using a straightforward relation between climb angle and air density, we assess how climate change could affect climb angles by mid-century (2035–2064). The value of is obtained by efficiently covarying (1) the engine noise at 10 m from the engines and (2) the climb angle under ‘historical’ conditions (1985–2014). The median values (across 10 climate models) of climb angle reduction in the future warmer climate are around 1–3% (depending on the airport and climate model used), but individual days can show values as high as 7.5% for the most extreme warming scenarios. By considering the variation in the absorption coefficient of the air with frequency, we find that the number of people affected by noise pollution could increase by up to 4%—as much as 2500 people for the most highly populated areas—by mid-century and that these changes are maximised for the most damaging and psychologically ‘annoying’ (low) frequencies.
1. Introduction
In this work, we examine the effect of climate change on the area enclosed by the 50 dB SPL (decibel sound pressure level) contour around an ensemble of 30 European airports by considering ‘historical’ (1985–2014) and future projection (2035–2064) timescales.
This is a follow-up study to previous work which examined how take-off distance and maximum take-off mass are projected to change in the future [1]. This work uses the same sites as the basis for studying how climb angles may change (disregarding engineering advances) and how neighbouring populations could be affected.
The Williams et al. [1] study in fact is one of a growing number of studies regarding the perturbation of take-off performance as the world warms (see references therein). However, literature on the effect of climate change on noise around airports is only recently starting to appear.
In 2022 [2], in a model study of Chios airport using observed temperature and wind values, it was postulated that climate change could potentially have caused an increase in the area of the of the 60 dB contour (day–evening–night; discussed below in Section 4) of almost 5% in the 25-year period up to 2022 [2]. This was attributed to worsened take-off performance due to climate change-induced temperature and headwind perturbations reducing climb angles. Climate change can also influence atmospheric boundary layer stability [3], which in turn can affect sound propagation [4]. This previous study used the IMPACT model (discussed below) throughout, whereas, in the present study, IMPACT is used as a first-order comparator of noise contour area.
The aim of the present study is to isolate the projected changes to noise pollution solely due to climate change. As discussed in Padhra et al. [2], engines are undoubtedly becoming quieter due to technological advances, but this will not form part of this study.
Commerical airports are a major source of noise pollution. For example, in 2023, the EASA—the European Union Aviation Safety Agency—estimated that almost 3.5 million people in Europe experienced ‘highly annoying’ aircraft-related sound exposure [5]. The EASA defines this as an level of at least 55 dB, which is a weighted average of exposure at different times of the day (i.e., night flights are more disruptive).
Disruption is not limited to the immediately noticeable auditory impacts on humans, however. Indeed, increased airport noise has been identified as a contributor to cardiovascular disease [6] and increased blood pressure [7] in local populations. Wildlife can also experience negative impacts through induced environmental changes affecting birds, whales, and insects, amongst others (see, for example, Alquezar and Macedo [8] and Dominoni et al. [9]).
A good approximation is that, for a given point in the vicinity of an aircraft taking off, the noise experienced by a stationary observer is a function of the distance from the source; the source sound intensity, which is in turn a function of the aircraft’s thrust setting; and the air’s coefficient of absorption. However, in reality, there are many other factors which affect the overall level of sound transmission such as climb angle and surrounding vegetation and/or buildings.
Methods for reducing the exposure to noise pollution include the Noise Abatement Departure Procedures (NADPs) published by the International Civil Aviation Organisation, the ICAO [10]. For example, procedures exist for reducing exposure closer to and farther away from the airport, respectively, by changing thrust levels, acceleration profiles, and climb angles appropriately [11].
In this study, however, the thrust level and the historical climb angle are—post-optimisation—assumed to be constant, whilst the future climb angles change with air density. Work to understand the effects of climate change on more complex take-off procedures, as well as the economic impacts of climate change on take-off fuel usage, is ongoing.
Previously documented comprehensive or ‘consolidated’ tools for conducting quantitative studies of airport noise—i.e., involving the explicit calculation of noise propagation and resulting contours—include those from the following:
- 1.
- The UK Civil Aviation Authority; Aircraft Noise Contour (‘ANCON’) Model [12].
- 2.
- The USA Federal Aviation Administration:
- (a)
- The Integrated Noise Model, ‘INM’ [13].
- (b)
- The Aviation Environmental Design Tool, AEDT, [14].
- 3.
- The European Organisation for the Safety of Air Navigation (EUROCONTROL)’s Integrated Aircraft Noise and Emissions Modelling Platform, or ‘IMPACT’ [15].
In addition to these consolidated tools, there is rich literature studying aircraft noise impacts. This ranges from comparisons of simple noise models and their associativity with environmental impact analyses [16], to studies examining passenger and flight number growth [17] and comparisons of various methods of obtaining thrust values—and hence noise spectra—from the rate of the rotation of the engine [18]. An expansive review is beyond the scope of this study, however.
The present study differs from these tools in that its purpose is to present initial analysis from a new, free, and open-source software tool—available at https://github.com/jonnyhtw/noyse (accessed on 28 August 2025)—and encourage future development and research work with it. It uses projected (future) temperature and pressure data from a previous take-off performance study [1] to quantify potential changes in climb angle and hence impacts on local populations. In this initial, idealised study, we do not consider changes to fleet, engine type, or thrust, therefore isolating the effects which may be expected from climate change. These assumptions could be lifted in follow-up studies, however.
Many of the metrics presented below do not explicitly rely on the ability of the model to reproduce the precise shape of the decibel contours around the airports in question. However, motivated by the previous take-off performance study, we have developed a spatially resolved methodology which not only can show plausible ‘emulated’ contours for the airports in question, but could also be straightforwardly extended to arbitrary sites.
Emulation techniques are widely used in modelling studies of climate-relevant parameters and tools. For example, the FAMOUS climate model [19] simulates (synonymous with ‘emulates’ in this context) the 3D climate response of the higher-resolution HadCM3 model [20], meaning that it can produce results faster. In essence, it largely uses another model as its ‘ground truth’ target.
Another example of emulation is the use of statistical techniques which use large ensembles of climate model results to explore parts of parameter space which are not explicitly resolved in the individual model results themselves. The interested reader is referred to the review article of Castruccio et al. [21] for further information.
We use the area enclosed by a particular decibel contour from IMPACT as our emulation target and use a 20-member Latin hypercube sampling technique—see, for example, Gregoire et al. [22]—to minimise the difference in the values obtained from the two models. We also ensure that the salient features of previously published noise contours are reproduced, although non-trivial differences remain due to the different levels of model complexity.
The choice of emulation target model does not materially affect any of the results or conclusions presented here. IMPACT was chosen due to its availability and to maintain traceability with its use in the previous study of Padhra et al. [2], which motivated this work.
After the establishment of reasonable model parameters for present-day conditions, we proceed to apply them to future conditions at 30 European airports using a simple relation connecting climb angle and air density. In these future conditions—see Williams et al. [1] for details—air density shows an overall decrease, largely due to increased temperatures. This then leads to smaller climb angles and an increased noise pollution footprint.
The effect of changing population density around the sites is also taken into account to provide estimates of changes to the number of people affected by noise pollution under different future climate and land-use change scenarios.
2. Materials and Methods
2.1. Sound Propagation Model
The coordinate system used for noise intensity calculations at ground level is two-dimensional () and centred on the aircraft’s take-off location and extends a set number of multiples of the runway length, , in and . To simplify the calculations, the runway is assumed to run perfectly north–south (the y direction) and the true runway orientation is applied later by rotating the entire grid using third-order spline interpolation [23].
To account for the vertical, z, coordinate, after take-off, the aircraft is assumed to climb with a constant angle, . The Euclidean distance from the aircraft to each point in the grid is then calculated for every in the trajectory. The resulting example noise level presented below for London Heathrow in Figure 1 is then simply the maximum value at each in the aircraft’s path.
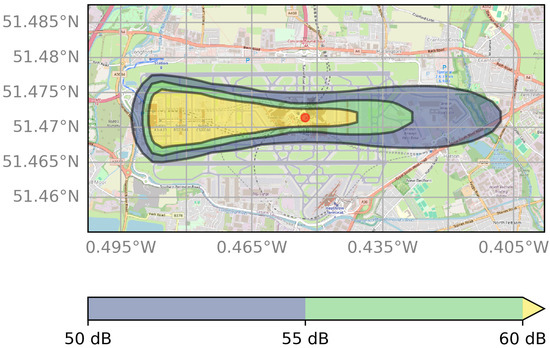
Figure 1.
The extent of the 50, 55, and 60 dB contours around London Heathrow Airport calculated using the present emulator framework. The take-off direction is from west to east.
Assuming that sound radiation is isotropic, its intensity, I, is assumed to reduce with the distance, r, from the source with an inverse square law,
where is the sound (power) intensity at a reference distance, , from the source, taken here to be 10 m. This value is discussed in detail in Section 4. In general, the exponent of r may differ from 2, especially very close to the source, but we do not consider this further here.
The power intensity at some arbitrary distance from the aircraft, I, has units of , but usually, it is the intensity of the sound in decibels, , which is used, where
Combining the relations for I and gives
As well as the geometric factor, the sound intensity (in dB) is also reduced due to absorption processes, and this is included using a coefficient of absorption, (units dB
), which is a complex function of temperature and frequency (we assume 50% relative humidity and International Standard atmosphere pressure). The full expression is given in Bass et al. [24] and Figure 2 shows its variation between 0 and 50 °C for three frequencies: 50, 1000, and 1700 Hz. The highest of these is the ‘peak tonal frequency’ of A320 engines as reported in Figure 9 of Merino-Martinez et al. [25].
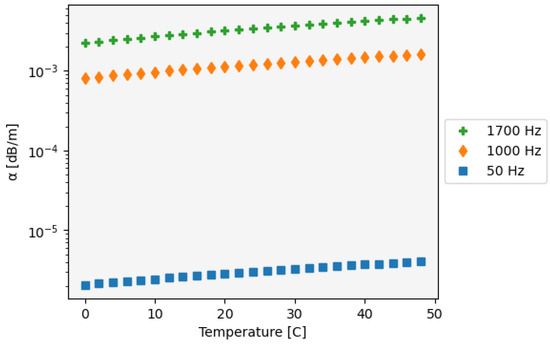
Figure 2.
Absorption coefficient, , as a function of temperature for three different frequencies. The full equation is described in Bass et al. [24].
We do not present results for values between 50 and ≈1000 Hz since the respective changes to the affected populations are uniform across this range. We do not consider higher frequencies in this study since it is the lower frequency range which—in general—causes more annoyance and deleterious health impacts [26].
This gives our final equation for sound fall-off with distance:
For the explicit consideration of multiple, n, engines (two here), the following expression is used:
where each of the is described by Equation (4).
In the earlier companion study [1], a force balance model was used to estimate the changes to take-off distance required and maximum take-off mass for aircraft at the same set of sites considered here. In this work, the acceleration (thrust) force is not a function of temperature. What this tacitly assumes is that any decreases in the density of the air—which, in reality, would cause a reduction in the resultant forward force—are precisely balanced out by changes in the engines’ thrust settings. A full treatment of these scaling relations can be found in, for example, Kandula and Vu [27].
On the other hand, fan noise is an even more complex function of the air’s ambient properties, and we make the further assertion that the fan noise decreases with increasing temperature due to changes in tip Mach number [28].
In reality, entirely separating the contributions of changing jet and fan noise is not possible due to the increase in fan rotation speed which results from a higher thrust setting. However it is pertinent to show a calculation of how these components’ magnitudes change given an illustrative temperature range of 0–40 °C and put them in context of the wider uncertainties present.
The temperature increase (assuming constant pressure) causes a decrease in density and a concomitant decrease in thrust due to mass continuity. For a temperature difference of 40 °C and assuming ISA conditions, this is a decrease of , where is zero Celsius measured in Kelvin.
Now, we require an estimate of the increase in sound power (in dB) for an increase in thrust of 15%.
Empirically, the sound power increases with the thrust raised to a power [29], and and , which gives an estimate of the change in jet noise, , of dB due to the increasing thrust setting of the engines to maintain constant ground acceleration.
For an estimate of the change to the fan noise, , over the same interval, we can examine Figure 4 of Malbéqui et al. [30], which shows that sound pressure from fan noise is a function of the tip Mach number, M. We convert the temperature change to a tip Mach number change estimate by assuming a representative tip speed of 340 (e.g., Sjögren et al. [31]) and calculate the speed of sound in air, , as
where are the specific heat capacities at constant pressure and volume, and . This gives a difference in tip Mach number, , of
and from Figure 4 in Malbéqui et al. [30], we obtain a value of dB.
Bearing in mind the non-trivial uncertainties in the above calculations, as well as the exceptionally complex reality of the noise landscape around a turbofan engine, the fact that justifies our assumption of the constancy of , assuming negligible airframe noise at take-off [32] and . It also, crucially, allows traceability with our previous take-off performance study [1]. The assumption of will not be true under all operating conditions, and this should be borne in mind when considering the validity of the data and conclusions discussed below.
Specific data, from either models or test rigs, on how total (at source) jet noise varies as a controlled function of ambient air density is strikingly absent in the literature. This is partly due to the standardised nature of many noise assessment tools, imposing simple thermodynamic corrections to a ‘standard day’ of, for example, 25 °C (e.g., https://www.legislation.gov.uk/uksi/1990/1514/made, accessed on 28 August 2025), as well as their almost-universal concentration on far-field effects, i.e., those of relevance to urban and peri-urban planners.
McAninch and Shepherd [33] even state—and show in their Figure 1—that, for the INM model discussed above, ‘the aircraft noise measured for one set of atmospheric and aircraft operating conditions is assumed to be applicable to all other conditions as long as the corrected net thrust remains constant’, which is indeed the case assumed here.
One of the only studies which explicitly considers observational campaign data with that from the semi-empirical models of, for example, Heidmann for and Stone for is the 2022 study of Vieira et al. [34]. This work compares the measured and modelled noise levels of various aircraft types (including the A320) at Amsterdam Schiphol Airport, and considers airframe, combustion, fan, and jet noise for a representative range of conditions in June, July, and September 2019. There are two key conclusions which are of specific interest to our work:
- 1.
- The overall sound pressure level (OPSL) range reported for the A320 is the smallest of any of the aircraft types considered, with an interquartile range (itself larger than the standard deviation of a normal distribution) of just ≃1 dB.
- 2.
- The only frequency range in which a good agreement between total (modelled) and measured noise occurs is above the frequency range considered by this study in the regime where fan noise dominates. For lower frequencies, the disparity can be as large as ≈20 dB, depending on the take-off speed, which is itself yet another uncertainty contributor.
In summary, we are aware that the assumed constancy of represents a significant simplification of the real-world physics. However, even state-of-the-art noise-component models fail to reproduce observed values, and so we posit that our assumption is an unavoidable one given its use in previous published work using this input climate model dataset, as well as the lack of explicit data to the contrary from, for example, temperature–noise regression models.
Further work to examine the effect of varying values in line with the Vieira et al. [34] study is ongoing.
In practice, the sound emission from a standard turbofan engine is anisotropic and highly complex—e.g., [35,36]—and is parameterised here by increasing the sound levels both behind and in front of the engine’s intake axis (the y direction, i.e., before taking the runway bearing into account) compared to the lateral, x, direction. This weighting, W, is shown diagrammatically in Figure 3 and described mathematically by
where is the angle over which multiple take-off paths are run in order to represent the enhanced power intensity in the direction parallel to the direction of travel and is an empirically determined scaling parameter. Each path is rotated around the centre of the grid, which is defined as the starting position of travel (for the central estimate, ), where and .
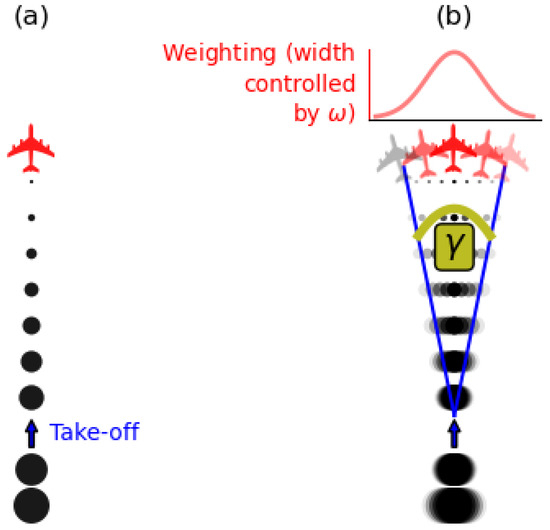
Figure 3.
(a) Spherically isotropic sound propagation and (b) image modified to include a preferentially amplified sound intensity in the forward () and reverse () directions. Also shown in (b) are the angle over which the sound is amplified, as well as their respective weightings, parameterised by .
Equation (8) illustrates Gaussian directional weighting—see, for example, Lyu et al. [37]. Other parameterisations of this angular dependence (exponential; cosine) could be straightforwardly included in extensions to the model described here. However, for the A320’s engines at take-off, a normal distribution is often used; see, for example, Clark et al. [38].
The parameter’s value of 20° (see Table 1) is gleaned from Figure 2a from the previous study of Padhra et al. [2], and was obtained heuristically to fit with IMPACT’s results. The value of fits well within the expected range of ≈25–40° (e.g., from Khavaran and Bridges [39]).

Table 1.
Parameters used for the generation of Figure 1. The mx2t24 and values are means of 30 years of historical data from the ACCESS-ESM1-5 climate model. The mx2t24 variable is the maximum temperature recorded at a site in the preceding 24 h and is the metric used for daily temperature variation, as in [1].
2.2. Motivation and Utility of the Current Model
As mentioned above, there are multiple models available which are capable of modelling noise contours based on assumptions of atmospheric conditions and aircraft type, etc. However, common properties which reduce their utility and uptake include closed-source code bases, licencing restrictions, a lack of in-built version control, and the need to be run on remote servers. The software presented here is not subject to any of these limitations.
This is not just a matter of convenience and transparency; for many research funding bodies, openness and adherence to the FAIR principles of software development (Findable, Accessible, Interoperable, and Reusable) are a priori requirements.
For example, research outputs and software developed by projects funded by the European Union (https://commission.europa.eu/funding-tenders/find-funding/eu-funding-programmes/horizon-europe_en, accessed on 28 August 2025) are required to be open access, and the UK government is also currently consulting on its new Research Data Policy with the requirement that ‘publicly funded research data is made as open as possible’ [41].
Whilst these policies do not, yet, explicitly mandate the use of pre-existing open source software, there is a clear and ongoing trend in this direction.
Our software also has a built-in ‘batch’ mode. Because of this, even though the code runs serially (on one processor), arbitrary numbers of simulations can be run concurrently on a remote cluster of, crucially, the user’s choosing. In the current work, the Reading Academic Computing Cluster (RACC) was used to submit hundreds of simulations at the same time to the Slurm Workload Manager (https://slurm.schedmd.com/, accessed on 28 August 2025) and a standard run of 300 jobs (30 airports × 10 climate models) can take as little as ∼10 min, or just 2 s per model integration on average.
3. Effect of Climate Change on Climb Angle
As greenhouse gases accumulate in the atmosphere and the air warms, the air density tends to decrease in line with the ideal gas law,
where P is the air pressure (which also varies in the models), is the air density, is the specific gas constant for air (287.05 J ·
·
), and T is the temperature.
Using 10 state-of-the-art climate models forced with three different scenarios of (summer only) 2035–2064 greenhouse gas forcing compared to 1985–2014, daily time series of temperature and air pressure were obtained, and from these values, the predicted air density was calculated using Equation (9). The future scenarios used (Shared Socioeconomic Pathways, SSPs) are SSP1-2.6, SSP3-7.0, and SSP5-8.5. The format SSPX-Y refers to the SSP ‘family’, X, and the net radiative forcing per
at 2100, Y. These can be considered as low-, medium-, and high-magnitude climate change amounts, respectively [42].
The historical period does not extend beyond 2014 since this is when the relevant simulations in the 6th Coupled Model Intercomparison Project end [43]. This also removes the influence from the unprecedentedly warm years since 2014 [44], thereby increasing the signal-to-noise ratio in our conclusions.
The dependence of aircraft climb angle is a highly complex function of many variables such as atmospheric conditions, thrust level, aircraft variant, and altitude (see Takahashi and Sóbester [45] and references therein). However, in order to provide a straightforward and accessible presentation of this in software, we assume the following force balance at take-off:
where , D, and W are the thrust, drag, and weight, respectively, and is the climb angle (see, for example, [46], Supplementary Material Part 2).
We assume that the variables in Equation (10) maintain their respective relationships with air density as the climate changes. There are many reasons why, in practical engineering terms, this assumption will not hold (e.g., fleet renewal) but it is an important assumption in order for us to isolate the effect of climate change on the parameters of interest in this study. This could of course change in future studies.
We further make the assumption that both and D are proportional to air density, which is a good approximation assuming incompressible flow in International Standard Atmosphere conditions [47]. This leads to the proportionality relation
or, equivalently,
and
Therefore, we now have an equation for describing how the climate change-affected climb angle can be calculated as a function of the historical and future air densities. The climb angle in the historical situations considered is assumed constant in this work, and its range of validity is discussed in Section 4.
4. Parameter Uncertainty and Latin Hypercube Parameter Sampling
In the model described above—indeed, as is the case for any model—there are many approximations and parameterisations. For example, the sound intensity near the source and the initial climb angle are both assumed constant, neither of which is strictly adhered to in real flight operations. Additionally, the inverse square relation and absorption coefficient described in Equation (4) deviate from these idealised mathematical formulations due to, for example, ground reflection and humidity dependence, respectively [36,48].
To account for these uncertainties, we have established plausible ranges of and and then used Latin hypercube sampling (LHS) to establish parameter values which enable a meaningful comparison with IMPACT, noting again that, in practice, the choice of comparator model for this initial model description would not affect our present conclusions.
LHS efficiently samples the parameter space defined by the input variables () to avoid having to exhaustively sample the full two-dimensional landscape of possible combinations [22]. It is also straightforwardly extensible to much larger sets of parameters which may be explored in future studies with this software.
We used the area enclosed by the 50 dB noise contour around London Heathrow airport from the IMPACT model (https://www.eurocontrol.int/platform/integrated-aircraft-noise-and-emissions-modelling-platform, accessed on 28 August 2025), , as our verification target. The 50 dB level is a commonly used baseline for aircraft-related noise disturbance [49,50] and is broadly representative of a residential, suburban environment [51]. IMPACT is formulated using guidelines from the Report on Standard Method of Computing Noise Contours around Civil Airports from ECAC [52]. This documents, in detail, the different types of noise which are generated by an aircraft.
The output for the model presented here represents one take-off procedure and is ‘unadjusted’; that is, we do not perform any weighting based on frequency, and this is compared against the ‘day–evening–night’ level output from IMPACT. This represents the average noise exposure over a 24 h period [53], includes adjustments for the sensitivity of human hearing, and is given by
which shows the 5 and 10 dB ‘penalties’ which are applied to evening and night flights, respectively. Using alleviates some of the inherent issues in the comparison with IMPACT’s greater complexity and capability (see the Discussion on page 11).
To obtain initial estimates of the bounds for and , we first calculated the area enclosed by the 50 dB SPL contour () using , which is given as a typical value in Gratton et al. [46] and dB for each engine at 1700 Hz.
The choice of 100 dB is the value at 10 m from an engine with a source intensity of 120 dB, assuming isotropic transmission from 1 m away (e.g., Huang and Zheng [54]). This 10 m ‘buffer’, as well as being of the order of the inter-engine distance, , also allows for some amelioration of the reflection effects referred to above. Therefore—and since our model is intended as an emulator rather than a simulator—the precise values used are not crucial as long as they emulate the assumed-equivalent value from IMPACT, or indeed any other target model.
Using dB and , we obtain , compared to , an overestimate of ≈11%. Considering the assumptions and simplifications in the present model, this is an encouragingly small discrepancy. However, it is important to perturb the parameter assumptions to make sure that this is not entirely serendipitous.
The climb angle used in the calculation in IMPACT, when averaged over its first 10,000 ft, is approximately 7.2°. For , from its maximum at ‘take-off roll’, the power setting is reduced by up to ≈40% over the course of the first few nautical miles of its trajectory. A 40% decrease is equivalent to roughly 2 dB since, from Equation (2), , and so we use dB and . The results of this sampling are shown in Figure 4 for a sample size, N, of 20. In LHS studies, the recommended sample size is times the number of free parameters () [22].
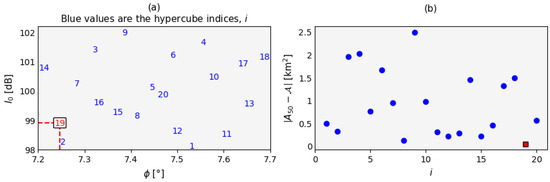
Figure 4.
(a) Scatter plot of the values of and climb angle, (), directly from the Latin hypercube sampling. The respective optimum values of and are shown by the ordinate and abscissa values corresponding to the lowest shown value in (b), i.e., where the value of is closest to . (b) Values of , blue circles, for each value, i, in the sampling distribution. The lowest value is marked with a red square.
Figure 4 shows that the 19th member of the LHS distribution gives the best agreement between and : a difference of 0.11
. This corresponds to dB and , and these values are used for the remainder of this study.
We justify our usage of single frequencies in our model output since the metric from IMPACT is only used in the generation of the and parameters for the peak tonal frequency of 1700 Hz discussed above. Additionally, using the IMPACT model for the generation of a single take-off operation’s noise level at a single frequency results in a noise distribution which is not well resolved by the current model’s grid without significantly increasing its run time by enhancing grid resolution. Further work with this nascent framework to explicitly calculate is encouraged.
5. Results
5.1. Example Noise Contours
Figure 1 shows the results of the verification procedure described above using London Heathrow airport for the parameters shown in Table 1.
Figure 1 shows the 50, 55, and 60 dB noise contours around London Heathrow airport and shows the effect of the anisotropic power intensity, amplified in the direction of travel (to the east in this case), and the tapering-off of the sound as the aircraft climbs.
In addition to the IMPACT comparison detailed above, the overall shape of the contours is in good empirical agreement with previous work by, for example, Tlałka and Rzucidło [55], and Sahai et al. [56] and with policy documentation from the US Federal Aviation Administration [57]. Indeed, considering the relative simplicity of our model, the agreement with previous results is encouraging. In any case, the precise shape does not change any of the conclusions drawn below since we are examining changes to the noise contour area (and affected populations) rather than absolute values.
5.2. Effect of Atmospheric Conditions on
Figure 5 shows the projected increase in around each site as a function of the climate change scenario used in the future modelling at 50 Hz. For higher frequencies, absorption is increased and reduces the magnitude of the changes. This is discussed in Section 5.3 when population changes are also taken into consideration. The format of this figure uses box-and-whisker plots which show the distributions’ median and interquartile range and 1.5× this range either side of the first and third quartiles. Each sub-figure illustrates the effects of the varying air density changes across the sample sites as discussed in detail in Williams et al. [1]. It also takes into account the varying runway lengths by assuming that the take-off distance used is equal to either that at maximum take-off mass (2362 m [2]) or the respective runway length, whichever is shorter. This additional site-dependent assumption tacitly means that we are assuming that the aircraft in question are operating at the maximum allowed mass.

Figure 5.
Percentage change to the area enclosed by the 50 dB SPL contour () at 50 Hz for each of the study sites and climate change scenarios studied (a–z,A–D).
The effect on shown in Figure 5 is broadly uniform across the locations considered. This, however, is important to emphasise given the significantly differing climates of the sites considered (e.g., Oslo, Madrid, and London) and the novelty of the method of the calculation of climb angle change. In addition, when we come to consider the effects of their differing (and temporally changing) population densities, this uniformity disappears.
There is significant inter-model spread within the individual scenarios’ results in Figure 5, and the most extreme warming scenario considered, SSP5-8.5, shows the largest variability. This is the expected behaviour—as previously noted in Williams et al. [1]—because of the range of equilibrium climate sensitivity responses from the models in the ensemble; that is, the susceptibility of temperature change to changing greenhouse gas concentrations.
The values shown in Figure 5 show the response of for each climate model to the mean change in air density in each of the scenarios compared to the historical period. This averaging masks the day-to-day variability in the summer temperatures and pressures. To investigate the full distribution of these values, Figure 6 shows the (daily maximum) temperature, daily mean pressure, and resulting values for UKESM1-0-LL and SSP5-8.5 at another of our study sites, San Sebastián in Spain.
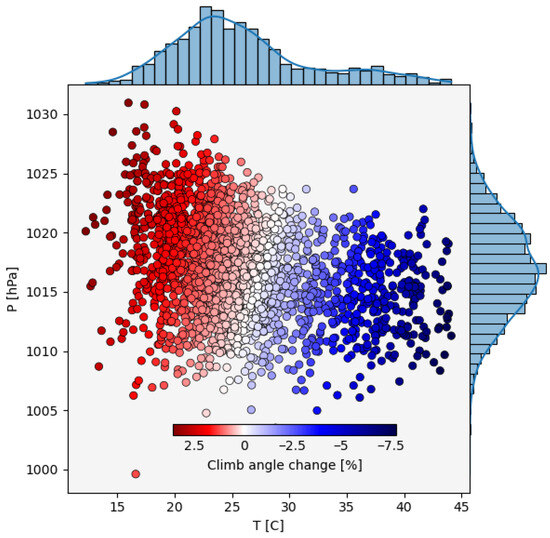
Figure 6.
Scatter plot of climb angles (compared to the assumed historical constant value in Table 1) calculated for San Sebastián airport under SSP5-8.5 conditions using the UKESM1-0-LL climate model [1]. The marginal plots on the top and right show the relative frequency of occurrence of the daily maximum temperature and daily mean pressure values, respectively. Note that the distribution shown here is independent of frequency since this only reflects climb angles and not the impact of any resulting changes to .
Figure 6 shows the individual values for each day in the period 2035–2064 for SSP5-8.5 and clearly shows the expected decrease in with increasing temperature as discussed above. It also shows decreases in as high as 7.5% (blue values), which is significantly higher than the values of 1–3 % obtained in the calculation of the data in Figure 5, which only use the mean value.
In the next section, we examine how these geometric variables can be translated into quantified impacts on populations.
5.3. Climate Change Impacts on Residential Populations near Airports
Although the changes to shown in Figure 5 may appear small, we shall see below that, once the population density around airports is taken into account (which can exceed people per square km), the number of additional people, compared to historical values, potentially affected by these changes can be significant, even without considering extreme values (i.e., Figure 6).
With this in mind, we use the Olén and Lehsten [58] dataset at a 30-arc-second (≈1 km) resolution, which gives population densities in a manner corresponding to the future climate model scenarios used here. Figure 7 shows the population densities around our 30 study sites for each SSP scenario.
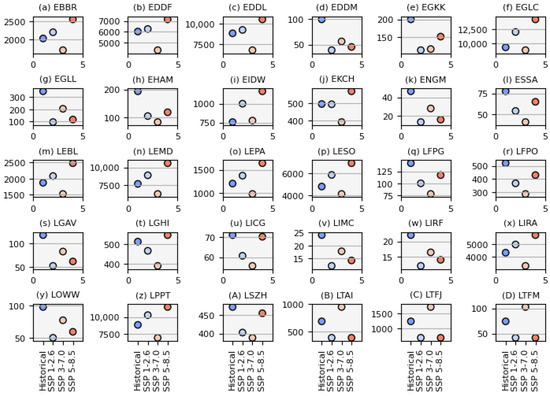
Figure 7.
Population densities (people per square kilometre) at a 30-arc-second ( km) resolution for each of the study sites calculated using data from Olén and Lehsten [58]. The titles of each sub-figure (a–z,A–D) show the ICAO airport code, and the population density is averaged over a km area around each location.
The metric of primary interest in this study is the change to the number of people—relative to the historical baseline—affected by perturbations to the area enclosed by a given decibel contour.
Figure 8 shows the change in the number of people affected by noise pollution for each climate change scenario and for the three frequencies considered. This is found by taking the population density (Figure 7) and the change in the area of the 50 dB contour (Figure 5) into account.
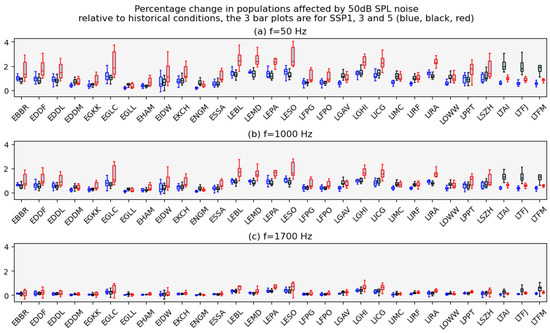
Figure 8.
As for Figure 5 but showing the population changes taking into account the historical average area for each site and the population densities in Figure 7. Each panel shows the results of the simulations described above for each frequency given in the respective titles. Figure A1 in Appendix B shows the same data in absolute terms and without common y-axis limits.
Figure 8 shows that the fractional changes are the highest for low frequencies, and that, for frequencies around the peak tonal frequency of 1700 Hz, the expected changes are negligible. The values for 50 Hz lie between ≈1 and 4% and for, say, London City airport (airport code EGLC), this corresponds to values of up to 500 people per square kilometre, or 2500 when taking into account the area of the 50 dB contour of ≈5
. These values are reduced slightly for 1000 Hz and are negligible for 1700 Hz. This can be attributed to the increased attenuation at higher frequencies as shown in Figure 2, which will also reduce the values shown above for 50 Hz in Figure 5. In general, exposure to low (compared to high) frequency noise causes more health disbenefits [26] and indeed is known to cause more ‘annoyance’, especially in the 20–60 Hz range [59]. Therefore, in summary, our results indicate that climate change has the potential to increase the number of people affected psychologically and physically by noise pollution in the future. In this preliminary analysis, we have not taken the different relative frequency weightings into account, but this should be performed in future studies with this model.
As the frequency is increased, some values of the changes in Figure 8c become negative. This is because the increase in sound attenuation—Figure 2—outweighs the increase in due to the climb angle decrease. Figure A1 in Appendix B shows the same data as in Figure 8 but in absolute terms rather than fractional ones. It also shows outliers in the model ensemble which are more than 1.5 times the interquartile range away from the first or third quartiles, respectively. We do not consider this reduction effect further here, but it should be borne in mind in future work.
6. Recommendations for Future Model Development
There are several key aspects which should be considered in future use of the model; either as presented here or as part of future development.
Firstly, the present model assumes a simple force balance leading to a linear, analytical relation between air density and climb angle. In practice, this will be complicated by factors such as variations in thrust level, headwind, and aircraft type. Because of these uncertainties, and the flexibility and relative simplicity of the model, future studies using different functional relationships are encouraged.
A related ‘upgrade’ to the current model could include more detailed verification metrics. The present study uses the area enclosed by the 50 dB SPL noise contour, and compares this to an assumed-equivalent value from the IMPACT model. Future work could include using a range of decibel values, a larger number of evaluation target models, and an explicit calculation of .
From a geographical perspective, this study—by design—is limited to European airports, and so a further extension to this work could include a larger, ideally global, domain. To enable this, the site specificity and raw climate model data bias correction steps—see Williams et al. [1] and references therein—could be embedded within a common software framework. This would have the distinct advantage of being able to address the intimately related issues of noise pollution and take-off performance restrictions in a unified manner.
The horizontal resolution of the raw climate model input data itself (∼100 km) is an aspect which will lead unavoidably to increased similarity between the results obtained from closely neighbouring sites. For example, although the model data used in this study has undergone data processing and bias correction, the three airports studied in the London region, for example, are close enough for their overall climate response to be essentially the same. This of course has the distinct advantage of making the datasets small enough to be easily distributable and processable on standard PCs and data connections; however, it would be of great interest to consider higher-resolution (raw) input datasets, especially with the advent of new, ultra-high-resolution regional climate projections [60].
Finally, extensions to this modelling framework to include more realistic noise spectrum components, e.g. airframe, as well as the explicit inclusion of atmospheric property-dependence on jet and fan noise, and a non-constant value are encouraged.
7. Conclusions
In this work, we have presented the results of a new, open-source model which has been used to project the climate change-induced changes to populations affected by noise pollution at 30 European airports.
The model was optimised using the Latin hypercube sampling of two key parameters—near-engine sound intensity, and climb angle—to emulate the area enclosed by the 50 dB day–evening–night averaged sound level () contour produced by the IMPACT model.
After this verification step, we used results from 10 state-of-the-art climate models to project how climb angle may change by mid-century compared to a historical baseline. This is based on three possible future scenarios of greenhouse gas emissions which cause varying degrees of perturbation to air temperature; pressure; and, ultimately, air density, which is the input parameter in the climb angle calculation method used.
By combining the projections of the changes to the 50 dB SPL contour area () and local population densities, changes to the number of noise-impacted residents have been estimated. This has been performed for all 30 airports and each climate change scenario with the differing warming responses of the climate models providing a robust uncertainty estimate.
Although the fractional changes to values are broadly uniform across sites, ranging from approximately 1 to 2% at 50 Hz, the population density may change significantly in the future. By considering fractional changes to populations affected by noise pollution over three distinct frequencies, we have shown that low-frequency noise is expected to affect as many as 4% more people in the future. This increase in the number of people affected could be as many as 2500 in the most densely populated areas, such as central London. This does not take engineering advances into account, such as quieter engines, but it should be considered as part of the package of measures taken into account by stakeholders going forward. The consistent relative response uses values of input variables averaged across the respective 30-year periods. By considering the day-to-day distributions of temperature and pressure (with insights into how extreme values may change in the most pessimistic climate change scenario considered), values of as high as 7.5% could result, with concomitant increases to affected populations.
Although this study ultimately focuses on the atmospheric physics of climate change, the results related to the number of people affected by noise pollution are of clear socioeconomic importance. The 2020 study of Mashhoodi and van Timmeren [61] examined 76 European airports, subsetting them into five categories based on their population density, road network connectivity, and other factors. Of these five, the most relevant to this study are those designated as ‘urban’ or ‘urban periphery’ sites. Relatedly, the European Commission estimates that, by 2050, over 83.7% of Europe’s population will be living in ‘urbanised’ areas, up from 76.5% in 2015 [62,63]. A more fine-grained analysis taking these data into account in an expanded future study could provide more general recommendations for planners and airport operations professionals. A pertinent study is that of Wolfe et al. [64], which estimates the populations impacted by the combined operations of London Gatwick and Heathrow airports, monetises the environmental damage caused, and discusses the effects of operational and technological improvements in the sector.
It is hoped that this study, and others in the same vein, will help to assist in alleviating uncertainties in—and improve the co-development and sustainable planning of—near-airport developments.
Author Contributions
Conceptualization, J.W., P.D.W., M.V., A.P., G.G., and S.R.; methodology, J.W., P.D.W., A.P., G.G., and S.R.; software, J.W. and M.V.; validation, J.W., M.V., and P.D.W.; formal analysis, J.W., P.D.W., and M.V.; investigation, J.W., P.D.W., and M.V.; resources, J.W., P.D.W., and M.V.; data curation, J.W. and M.V.; writing, J.W. and P.D.W.; visualization, J.W.; supervision, P.D.W.; project administration, P.D.W.; funding acquisition, P.D.W. All authors have read and agreed to the publication of the current version of the manuscript.
Funding
The work of J.W., P.D.W., and M.V. for this article is part of the AEROPLANE project, which is supported by the SESAR 3 Joint Undertaking and its founding members, Grant Agreement ID 101114682, https://cordis.europa.eu/project/id/101114682, accessed on 10 June 2025. S.R. was funded by the Environmental and Networking Technologies and Applications Unit (ENTA) of the Athena Research Center.
Data Availability Statement
The raw data presented in the study are openly available in the Earth System grid Federation—ESGF—repository [43].
Acknowledgments
We thank the World Climate Research Programme (WCRP), which, through its Working Group on Coupled Modelling, coordinated and promoted CMIP6. We acknowledge the climate modelling groups for generating and making available their model output, the Earth System Grid Federation (ESGF) for archiving the data and providing access, and the many funding agencies who support the vital work of CMIP and the ESGF. We also acknowledge the computational services provided by the University of Reading’s Academic Computing Cluster (RACC) and associated research software engineering staff. Licencing and technical support for the IMPACT model was provided by EUROCONTROL.
Conflicts of Interest
Author Marco Venturini was employed by the company Amigo s.r.l. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AEDT | Aviation Environmental Design Tool |
| ANCON | Aircraft Noise Contour (model) |
| CMIP6 | 6th Coupled Model Intercomparison Project |
| EASA | European Union Aviation Safety Agency |
| FAMOUS | Fast Met Office/UK Universities Simulator |
| HadCM3 | Hadley Centre Coupled Model version 3 |
| ICAO | International Civil Aviation Organisation |
| IMPACT | Integrated Aircraft Noise and Emissions Modelling Platform |
| INM | Integrated Noise Model |
| IPCC | Intergovernmental Panel on Climate Change |
| ISA | International Standard Atmosphere |
| LHS | Latin hypercube Sampling |
| SSP | Shared Socioeconomic Pathway |
Appendix A. Mathematical Symbols Used

Table A1.
Mathematical symbols used.
Table A1.
Mathematical symbols used.
| Symbol | Definition |
|---|---|
| I | Sound intensity |
| r | Distance from sound source |
| Air density | |
| Air density under International Standard Atmosphere conditions at sea level | |
| P | Pressure |
| Coefficient of sound absorption | |
| Heat capacity at constant pressure and density respectively. | |
| Angle over which noise anisotropy is calculated | |
| Empirical scaling parameter controlling the shape of the noise anisotropy | |
| Specific gas constant for air | |
| Climb angle | |
| Thrust | |
| Temperature in Kelvin at 0 °C | |
| D | Drag |
| W | Weight |
| Day–evening–night noise level from IMPACT | |
| Area enclosed by the 50 dB SPL contour in the emulator | |
| Area enclosed by the 50 dB contour in the IMPACT model |
Appendix B. Absolute Population Changes
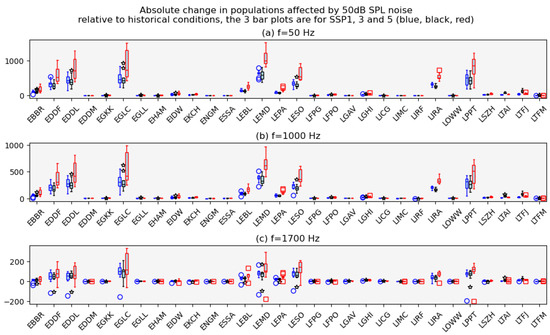
Figure A1.
As for Figure 8 but showing absolute population changes and outlying values which are greater than 1.5 times the interquartile range from the first or third quartiles, respectively. SSP1-2.6 outliers are circles, SSP3-7.0 are stars, and SSP5-8.5 are squares.
References
- Williams, J.; Williams, P.D.; Guerrini, F.; Venturini, M. Quantifying the Effects of Climate Change on Aircraft Take-Off Performance at European Airports. Aerospace 2025, 12, 165. [Google Scholar] [CrossRef]
- Padhra, A.; Rapsomanikis, S.; Gratton, G.; Williams, P.D. The Impacts of Climate Change on Aircraft Noise Near Airports. In Proceedings of the 4th International Aviation Management Conference (IAMC 2022), Dubai, United Arab Emirates, 21–22 November 2022; Available online: https://repository.uwl.ac.uk/id/eprint/9425/3/Manuscript%20-%20IAMC-SP408%20-%20Final%20Version.pdf (accessed on 28 August 2025).
- Caserini, S.; Giani, P.; Cacciamani, C.; Ozgen, S.; Lonati, G. Influence of climate change on the frequency of daytime temperature inversions and stagnation events in the Po Valley: Historical trend and future projections. Atmos. Res. 2017, 184, 15–23. [Google Scholar] [CrossRef]
- Hole, L.R.; Hauge, G. Simulation of a morning air temperature inversion break-up in complex terrain and the influence on sound propagation on a local scale. Appl. Acoust. 2003, 64, 401–414. [Google Scholar] [CrossRef]
- European Union Aviation Safety Agency (EASA). European Aviation Environmental Report. Available online: https://www.easa.europa.eu/en/domains/environment/eaer (accessed on 19 May 2025).
- Stansfeld, S. Airport noise and cardiovascular disease. Br. Med J. 2013, 347, f5752. [Google Scholar] [CrossRef]
- Black, D.A.; Black, J.A.; Issarayangyun, T.; Samuels, S.E. Aircraft noise exposure and resident’s stress and hypertension: A public health perspective for airport environmental management. J. Air Transp. Manag. 2007, 13, 264–276. [Google Scholar] [CrossRef]
- Alquezar, R.D.; Macedo, R.H. Airport noise and wildlife conservation: What are we missing? Perspect. Ecol. Conserv. 2019, 17, 163–171. [Google Scholar] [CrossRef]
- Dominoni, D.M.; Greif, S.; Nemeth, E.; Brumm, H. Airport noise predicts song timing of European birds. Ecol. Evol. 2016, 6, 6151–6159. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Review of Noise Abatement Procedure Research & Development and Implementation Results. 2007. Available online: https://www.icao.int/sites/default/files/sp-files/environmental-protection/Documents/ReviewNADRD.pdf (accessed on 10 February 2025).
- Bhanpato, J.; Puranik, T.G.; Mavris, D.N. Data-Driven Analysis of Departure Procedures for Aviation Noise Mitigation. Eng. Proc. 2021, 13, 2. [Google Scholar] [CrossRef]
- Ollerhead, J. The CAA Aircraft Noise Contour Model: ANCON Version 1; UK Civil Aviation Authority: West Sussex, UK, 1992; Available online: https://www.caa.co.uk/publication/download/12410 (accessed on 28 August 2025).
- Boeker, E.R.; Dinges, E.; He, B.; Fleming, G.; Roof, C.J.; Gerbi, P.J.; Rapoza, A.S.; Hermann, J. Integrated Noise Model (INM) Version 7.0 Technical Manual. Federal Aviation Administration, Office of Environment and Energy. 2008. Available online: https://rosap.ntl.bts.gov/view/dot/12188 (accessed on 28 August 2025).
- Aviation Environmental Design Tool (AEDT) Version 3g Technical Manual. Technical Report. U.S. Department of Transportation; Federal Aviation Administration, Office of Environment and Energy. 2024. Available online: https://aedt.faa.gov/Documents/AEDT3g_UserManual.pdf (accessed on 28 August 2025).
- EUROCONTROL. Integrated Aircraft Noise and Emissions Modelling Platform (IMPACT). 2025. Available online: https://www.eurocontrol.int/platform/integrated-aircraft-noise-and-emissions-modelling-platform (accessed on 20 May 2025).
- Torija, A.J.; Self, R.H.; Flindell, I.H. Airport noise modelling for strategic environmental impact assessment of aviation. Appl. Acoust. 2018, 132, 49–57. [Google Scholar] [CrossRef]
- Pretto, M.; Giannattasio, P.; Gennaro, M.D.; Zanon, A.; Kuehnelt, H. Forecasts of future scenarios for airport noise based on collection and processing of web data. Eur. Transp. Res. Rev. 2020, 12, 4. [Google Scholar] [CrossRef]
- van der Grift, R.C.; Snellen, M.; Amiri-Simkooei, A. The effect of using N1% as input for aircraft noise modelling. Transp. Res. Part D Transp. Environ. 2025, 142, 104710. [Google Scholar] [CrossRef]
- Jones, C.; Gregory, J.; Thorpe, R.; Cox, P.; Murphy, J.; Sexton, D.; Valdes, P. Systematic optimisation and climate simulation of FAMOUS, a fast version of HadCM3. Clim. Dyn. 2005, 25, 189–204. [Google Scholar] [CrossRef]
- Gordon, C.; Cooper, C.; Senior, C.A.; Banks, H.; Gregory, J.M.; Johns, T.C.; Mitchell, J.F.; Wood, R.A. The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim. Dyn. 2000, 16, 147–168. [Google Scholar] [CrossRef]
- Castruccio, S.; McInerney, D.J.; Stein, M.L.; Crouch, F.L.; Jacob, R.L.; Moyer, E.J. Statistical Emulation of Climate Model Projections Based on Precomputed GCM Runs. J. Clim. 2014, 27, 1829–1844. [Google Scholar] [CrossRef]
- Gregoire, L.J.; Valdes, P.J.; Payne, A.J.; Kahana, R. Optimal tuning of a GCM using modern and glacial constraints. Clim. Dyn. 2011, 37, 705–719. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Bass, H.E.; Sutherland, L.C.; Zuckerwar, A.J.; Blackstock, D.T.; Hester, D.M. Atmospheric absorption of sound: Further developments. J. Acoust. Soc. Am. 1995, 97, 680–683. [Google Scholar] [CrossRef]
- Merino-Martinez, R.; Besnea, I.; von den Hoff, B.; Snellen, M. Psychoacoustic Analysis of the Noise Emissions from the Airbus A320 Aircraft Family and its Nose Landing Gear System. In Proceedings of the 30th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 4–7 June 2024; pp. 1–16. [Google Scholar] [CrossRef]
- Alves, J.A.; Paiva, F.N.; Silva, L.T.; Remoaldo, P. Low-Frequency Noise and Its Main Effects on Human Health—A Review of the Literature between 2016 and 2019. Appl. Sci. 2020, 10, 5205. [Google Scholar] [CrossRef]
- Kandula, M.; Vu, B. On the Scaling Laws for Jet Noise in Subsonic and Supersonic Flow. In Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference and Exhibit, American Institute of Aeronautics and Astronautics, Hilton Head, SC, USA, 12–14 May 2003. [Google Scholar] [CrossRef]
- Bozak, R.F.J. Advanced Noise Control Fan Aerodynamic Performance; Technical Memorandum NASA/TM-2009-215807; NASA Glenn Research Center: Cleveland, OH, USA, 2009. Available online: https://ntrs.nasa.gov/api/citations/20090042818/downloads/20090042818.pdf (accessed on 28 August 2025).
- Morris, P.J.; Viswanathan, K. Jet Noise. In Noise Sources in Turbulent Shear Flows: Fundamentals and Applications; CISM International Centre for Mechanical Sciences, Courses and Lectures; Springer International Publishing: Berlin/Heidelberg, Germany, 2013; Volume 545, pp. 119–196. [Google Scholar] [CrossRef]
- Malbéqui, P.; Rozenberg, Y.; Bulté, J. Aircraft Noise Prediction in the IESTA Program. In Proceedings of the European Conference for Aerospace Sciences (EUCASS), ONERA, Châtillon Cedex, France, 6–9 July 2009. [Google Scholar]
- Sjögren, O.; Grönstedt, T.; Lundbladh, A.; Xisto, C. Fan Stage Design and Performance Optimization for Low Specific Thrust Turbofans. Int. J. Turbomach. Propuls. Power 2023, 8, 53. [Google Scholar] [CrossRef]
- Spakovszky, Z.S. Advanced low-noise aircraft configurations and their assessment: Past, present, and future. CEAS Aeronaut. J. 2019, 10, 137–157. [Google Scholar] [CrossRef]
- McAninch, G.L.; Shepherd, K.P. On INM’s Use of Corrected Net Thrust for the Prediction of Jet Aircraft Noise; Technical Memorandum NASA/TM–2011-217177; NASA Langley Research Center: Hampton, VA, USA, 2011. [Google Scholar]
- Vieira, A.; von den Hoff, B.; Snellen, M.; Simons, D. Comparison of Semi-Empirical Noise Models with Flyover Measurements of Operating Aircraft. J. Aircr. 2022, 59, 1574–1587. [Google Scholar] [CrossRef]
- Xue, R.; Jiang, J.; Zheng, X.; Gong, J.l.; Jackson, A. Study of Noise Reduction Based on Optimal Fan Outer Pressure Ratio and Thermodynamic Performance for Turbofan Engines at Conceptual Design Stage. Int. J. Aeronaut. Space Sci. 2019, 21, 439–450. [Google Scholar] [CrossRef]
- Zaporozhets, O.; Tokarev, V.; Attenborough, K. Aircraft noise characteristics on the ground and in the atmosphere. J. Sound Vib. 2014, 333, 1043–1064. [Google Scholar] [CrossRef]
- Lyu, B.; Dowling, A.P.; Naqavi, I. Prediction of installed jet noise. J. Fluid Mech. 2017, 811, 234–268. [Google Scholar] [CrossRef]
- Clark, I.A.; Nesbitt, E.H.; Thomas, R.H.; Guo, Y. Turbofan Inlet-Radiated Broadband Acoustic Flight Effects. In Proceedings of the AIAA Aviation Forum, Las Vegas, NV, USA, 21–25 July 2025. [Google Scholar] [CrossRef]
- Khavaran, A.; Bridges, J. Modeling of Turbulence Generated Noise in Jets; Technical Memorandum NASA/TM—2004-213105; NASA Glenn Research Center: Cleveland, OH, USA, 2004. Available online: https://ntrs.nasa.gov/api/citations/20040086533/downloads/20040086533.pdf (accessed on 28 August 2025).
- Airbus, S.A.S. A320 Aircraft Characteristics—Airport and Maintenance Planning, 44th ed.; Airbus S.A.S.: Blagnac Cedex, France, 2024; Available online: https://aircraft.airbus.com/sites/g/files/jlcbta126/files/2025-01/AC_A320_0624.pdf (accessed on 10 June 2025).
- UK Research and Innovation, Swindon, UK. Draft UKRI Research Data Policy. Draft Policy for Consultation. 2025. Available online: https://engagementhub.ukri.org/ukri-openresearch/developing-ukris-research-data-policy/user_uploads/draft-ukri-research-data-policy-for-consultation_published-09-april-2025.pdf (accessed on 28 August 2025).
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- World Meteorological Organization, Geneva, Switzerland. WMO Confirms 2024 as Warmest Year on Record at About 1.55 °C Above Pre-Industrial Level. 2025. Available online: https://wmo.int/news/media-centre/wmo-confirms-2024-warmest-year-record-about-155degc-above-pre-industrial-level (accessed on 22 July 2025).
- Takahashi, T.T.; Sóbester, A. Climb Performance Anomalies in ‘Real’ Atmospheric Conditions. In Proceedings of the AIAA, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Gratton, G.; Padhra, A.; Rapsomanikis, S.; Williams, P.D. The impacts of climate change on Greek airports. Clim. Chang. 2020, 160, 219–231. [Google Scholar] [CrossRef]
- Marchman, J.F., III. Aerodynamics and Aircraft Performance, 3rd ed.; University Libraries at Virginia Tech.: Blacksburg, VA, USA, 2021; Chapter 4; Available online: https://pressbooks.lib.vt.edu/aerodynamics/ (accessed on 28 August 2025).
- Filippone, A. Aircraft noise prediction. Prog. Aerosp. Sci. 2014, 68, 27–63. [Google Scholar] [CrossRef]
- Roca-Barceló, A.; Nardocci, A.; de Aguiar, B.S.; Ribeiro, A.G.; Failla, M.A.; Hansell, A.L.; Cardoso, M.R.; Piel, F.B. Risk of cardiovascular mortality, stroke and coronary heart mortality associated with aircraft noise around Congonhas airport, São Paulo, Brazil: A small-area study. Environ. Health 2021, 20, 59. [Google Scholar] [CrossRef]
- Baudin, C.; Lefèvre, M.; Champelovier, P.; Lambert, J.; Laumon, B.; Evrard, A.S. Self-rated health status in relation to aircraft noise exposure, noise annoyance or noise sensitivity: The results of a cross-sectional study in France. BMC Public Health 2021, 21, 116. [Google Scholar] [CrossRef]
- Purdue University Department of Chemistry. Noise Sources and Their Effects. 2000. Available online: https://www.chem.purdue.edu/chemsafety/Training/PPETrain/dblevels.htm (accessed on 16 May 2025).
- European Civil Aviation Conference (ECAC). Report on Standard Method of Computing Noise Contours Around Civil Airports. 2016. Volume 2: Technical Guide; ECAC.CEAC Doc 29. Available online: https://www.ecac-ceac.org/images/documents/ECAC-Doc_29_4th_edition_Dec_2016_Volume_2.pdf (accessed on 28 August 2025).
- Directive 2002/49/EC of the European Parliament and of the Council of 25 June 2002 relating to the assessment and management of environmental noise. Off. J. Eur. Communities 2002, L 189, 12–25. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32002L0049 (accessed on 28 August 2025).
- Huang, J.; Zheng, L. Noise analysis of the turbojet and turbofan engine tests. Proc. Inst. Mech. Eng. Part G 2014, 228, 2414–2423. [Google Scholar] [CrossRef]
- Tlałka, F.; Rzucidło, P. Modeling and Analysis of Noise Emission Using Data from Flight Simulators. Appl. Sci. 2023, 13, 10324. [Google Scholar] [CrossRef]
- Sahai, A.K.; Snellen, M.; Simons, D.G.; Stumpf, E. Aircraft Design Optimization for Lowering Community Noise Exposure Based on Annoyance Metrics. J. Aircr. 2017, 54, 3421–3432. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Basics of Aircraft Noise. 2022. Available online: https://www.faa.gov/regulations_policies/policy_guidance/noise/basics (accessed on 11 June 2025).
- Olén, N.B.; Lehsten, V. High-resolution global population projections dataset developed with CMIP6 RCP and SSP scenarios for year 2010–2100. Data Brief 2022, 40, 107804. [Google Scholar] [CrossRef]
- Reybrouck, M.; Podlipniak, P.; Welch, D. Music and Noise: Same or Different? What Our Body Tells Us. Front. Psychol. 2019, 10, 1153. [Google Scholar] [CrossRef]
- Ban, N.; Caillaud, C.; Coppola, E.; Pichelli, E.; Sobolowski, S.; Adinolfi, M.; Ahrens, B.; Alias, A.; Anders, I.; Bastin, S.; et al. The first multi-model ensemble of regional climate simulations at kilometer-scale resolution, part I: Evaluation of precipitation. Clim. Dyn. 2021, 57, 275–302. [Google Scholar] [CrossRef]
- Mashhoodi, B.; van Timmeren, A. Airport location in European airport regions: Five typologies based on the regional road network and land use data. Data Brief 2020, 33, 105317. [Google Scholar] [CrossRef]
- European Commission. Urbanisation in Europe. 2020. Available online: https://knowledge4policy.ec.europa.eu/foresight/topic/continuing-urbanisation/urbanisation-europe_en (accessed on 24 July 2025).
- European Commission. Continuing Urbanisation. 2023. Available online: https://knowledge4policy.ec.europa.eu/continuing-urbanisation_en (accessed on 24 July 2025).
- Wolfe, P.J.; Kramer, J.L.; Barrett, S.R. Current and future noise impacts of the UK hub airport. J. Air Transp. Manag. 2017, 58, 91–99. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).