Fuzzy Multi-Criteria Decision Framework for Asteroid Selection in Boulder Capture Missions

Abstract

A systematic fuzzy multi-criteria decision making (MCDM) framework is proposed to prioritize near-Earth asteroids (NEAs) for a boulder capture mission, addressing the requirement for rigorous prioritization of asteroid candidates under conditions of data uncertainty. Twenty-eight NEA candidates were first selected through filtering based on physical and orbital properties. Then, objective fuzzy weighting MCDM methods (statistical variance, CRITIC, and MEREC) were applied to determine the importance of criteria such as capture cost, synodic period, rotation rate, orbit determination accuracy, and similarity to other candidates. Subsequent fuzzy ranking MCDM techniques (WASPAS, TOPSIS, MARCOS) generated nine prioritization schemes whose coherence was assessed via correlation analysis. An innovative sensitivity analysis employing Dirichlet-distributed random sampling around reference weights quantified ranking robustness. All methodologies combinations consistently identified the same top four asteroids, with 2013 NJ ranked first in every scenario, and stability metrics confirmed resilience to plausible weight variations. The modular MCDM methodology proposed provides mission planners with a reliable, adaptable decision support tool for asteroid selection, demonstrably narrowing broad candidate pools to robust targets while accommodating future data updates.

1. Introduction

Asteroids are remnants of early Solar System formation; they are small bodies larger than one meter in size composed of rocky, icy, or metallic materials that orbit the Sun without qualifying as planets or satellites [1]. A particular subset of them, near-Earth asteroids (NEAs), follow trajectories that bring them into Earth’s neighborhood—by definition, their perihelion is less than 1.3 AU—, making them especially important for scientific investigation, resource prospecting, and planetary defense (PD) [2,3,4]. NEAs preserve primitive materials and record processes from the protoplanetary disk, offering windows into planetary origins and Solar System evolution [5]. At the same time, NEAs hold dual significance: many contain water, volatiles, and metals suitable for in situ resource utilization (ISRU) in future missions, while others pose impact hazards that drive PD mitigation efforts [6,7,8,9,10].

Several space missions have been carried out over the past decades to investigate asteroids and advance scientific understanding of their composition, geology, and potential as strategic resources. One of the most ambitious initiatives in this context was NASA’s Asteroid Redirect Mission (ARM), which proposed capturing an asteroid and relocating it to a stable orbit within the Earth–Moon system. Although ARM was ultimately canceled, it marked a significant shift in the objectives of asteroid missions by emphasizing the demonstration of capture and redirection technologies. Unlike previous sample return missions—such as NEAR Shoemaker, Hayabusa, Hayabusa2, and OSIRIS-REx—ARM aimed not only to collect small surface samples but also to enable the retrieval of a substantial mass of asteroid material for in-depth, direct analysis.

In the beginning of the ARM program, two mission concepts were considered: capturing an entire small asteroid or extracting a large boulder from the surface of the asteroid [11]. The present work focuses on the latter—a boulder capture mission—which was found to be more relevant from the perspective of planetary defense system development and the advancement of proximity operation techniques [12]. While ARM defined a reference mission targeting a specific asteroid with predetermined physical and orbital parameters, the present study generalizes the problem by identifying and prioritizing all viable NEAs from an extended catalog that meet a defined set of requirements.

Despite extensive surveys cataloging thousands of NEAs, only one subset meets the combination of requirements related to size, orbit geometry, and capture viability needed for a boulder capture mission [13]. As detailed in this study, an initial screening process illustrates how proper filtering yields a manageable candidate pool yet still requires rigorous prioritization to guide mission planning. To address this, a structured decision framework is essential.

Building on this motivation, multi-criteria decision making (MCDM) methodologies provide systematic means with which to evaluate alternatives across different criteria [14]. These criteria may include quantitative parameters—such as capture cost estimates, synodic periods, or rotation rates—and others exhibiting high uncertainty—such as orbit determination accuracy under limited observations or the number of similar candidates based on orbital similarity. For this reason, fuzzy logic, as a branch of artificial intelligence, is applied here to rigorously model parameters with elevated uncertainty through triangular fuzzy numbers (TFNs), enabling the decision process to incorporate uncertain or imprecise data in a principled way [15].

It is important to note that the application of artificial intelligence techniques to MCDM extends beyond fuzzy logic for representing vague or uncertain information. Machine learning methodologies such as the adaptive-network-based fuzzy inference system (ANFIS) [16,17] have been implemented successfully in MCDM problems [18,19,20,21,22,23,24]. This kind of system automatically derives appropriate rules from input–output data and leverages neural learning to optimize criterion combinations with minimal error [25]. Additionally, machine learning techniques also allow the evaluation of new alternatives without re-executing the original ranking algorithm [26], and they eliminate the need for experts to specify exact criterion weights [27], which is an advantage already offered by the objective weight determination methods proposed in this work. However, neuro-fuzzy methods require historical data for model training and depend critically on selecting an optimal network architecture—input variables, hidden layers and nodes, transfer functions, learning rules, initialization, stopping criteria, and more—without which models could not converge or generalize effectively [28,29]. The training process can be slow, may fail to converge without sufficient data, and becomes increasingly complex as criteria and decision rules proliferate, leading to exponential growth in rule sets that undermines interpretability and incurs costly rule codification efforts [26,29]. Moreover, reliance on historical data reduces flexibility when criterion structures evolve, and studies have shown that limited sample sizes further constrain generalization [29].

For these reasons, for the purposes of this analysis, a deterministic fuzzy MCDM framework is preferred: it is simple, quick, and cost-effective to construct; it requires neither extensive data collection nor expert-driven weight assignment; and its outputs are transparent, observable, and easily audited, avoiding the “grey-box” limitations of trained neuro-fuzzy systems [25,28]. The proposed framework provides alternative rankings without historical data requirements or architectural overhead. Importantly, the resulting framework establishes a transparent foundation for future machine-learning integration, as clearly defined criteria weights and outcomes will facilitate machine learning adoption once new data becomes available [25,27].

Therefore, the aim of this study is to analyze in detail potential asteroid candidates for an asteroid boulder capture mission and to compare outcomes obtained through combinations of both classical and innovative fuzzy MCDM techniques. By examining how different weighting and ranking methods handle uncertain criteria, decision makers can gain insight into robust top candidates and understand the influence of weight assumptions on final priorities.

This paper is organized as follows. Section 2 details the materials and methods; it introduces the fundamentals of fuzzy logic and presents the MCDM methodologies including the fuzzy weighting methods and fuzzy ranking. Section 3 introduces the decision problem of prioritization of NEAs for boulder capture missions; it describes the initial requirements for candidate selection, outlines the evaluation criteria, and assesses the potential candidates. Section 4 presents the results and discussion, including the weight sets from the three methods, the alternative rankings from the nine MCDM combinations, a comparative analysis of rankings, and the sensitivity analysis findings that quantify ranking robustness. Finally, Section 5 provides the conclusions, discussing implications for future asteroid mission planning, lessons on decision support under uncertainty, and potential extensions as observational data improve.

2. Materials and Methods

This study implements three fuzzy weighting MCDM methods, i.e., fuzzy statistical variance (Section 2.2.1), fuzzy CRITIC (Section 2.2.2), and fuzzy MEREC (Section 2.2.3), to derive criterion importance from a decision matrix constructed from filtered NEA parameters obtained from NASA JPL’s Small-Body Database System (SBDS) [30]. Alternatives are then ranked using three fuzzy MCDM techniques: fuzzy WASPAS (Section 2.3.1), fuzzy TOPSIS (Section 2.3.2), and fuzzy MARCOS (Section 2.3.3), facilitating a comparative analysis of classical and innovative fuzzy-based MCDM approaches. In addition, an innovative sensitivity analysis system based on random sampling of weight assignments using a Dirichlet distribution centered on reference weights is introduced to rigorously analyze the results.

It is worth noting that the modular structure of this MCDM framework allows seamless incorporation of new data or criteria, ensuring that prioritization remains scientifically rigorous, transparent, and adaptable as mission requirements or observational inputs evolve. A high-level overview of the workflow adopted in this study to address the asteroid selection decision problem is presented in Figure 1.

2.1. Fuzzy Logic and Fuzzy Sets

Fuzzy logic is an artificial intelligence technique that enables rigorous handling of variables whose values involve uncertainty or are vaguely defined [31]. This capability has made the application of fuzzy logic to MCDM problems a growing research topic [32].

Fuzzy sets provide the foundational concept for fuzzy logic [33]. Formally, given a universe of discourse X, a fuzzy set A is defined by a membership function $f_A:X\to [0,1]$, where $f_A$ indicates the degree to which x belongs to A. In other words, as $f_A\left(x\right)$ approaches 1, the degree to which x belongs to A increases. Thus, A can be expressed as $A=\left\{f_A\left(x\right)\right|x\in X\}$ [34]. This mechanism allows gradual boundaries and a formal representation of uncertainty or vagueness. Building on this concept, fuzzy variables are defined by associating each possible value of a quantity with a corresponding fuzzy set, so that an uncertain parameter is represented not by a single crisp value but by a membership distribution over a range.

Fuzzy sets can be defined by different membership functions [32,35]: triangular, trapezoidal, sigmoid, gaussian, etc. Among the multiple ways to represent fuzzy sets, triangular fuzzy numbers are particularly popular in MCDM. A TFN $\tilde{z}$ is represented by the tuple $\tilde{z}=(z^l,z^m,z^u)$, where $z^l\le z^m\le z^u$ correspond to the minimum, modal, and maximum values of the variable, respectively. This representation is notably advantageous: it captures uncertainty rigorously while allowing direct and efficient computation, given that all fuzzy arithmetic operations (addition, subtraction, multiplication, division) can be performed via simple formulae on the three parameters (for details on TFNs and their arithmetic operations, see [36]). In addition, numerous empirical MCDM applications [32,34,35,37,38,39] demonstrate that TFNs deliver robust decision outcomes without excessive modeling burden [15,40]. The consensus in the literature is that TFNs offer the most practical trade-off between interpretability, computational complexity, and fidelity in representing uncertainty [41,42]. In this study, a combination of real (crisp) variables and fuzzy variables represented as TFNs is considered. This combination has proven to be an effective approach for handling MCDM problems involving heterogeneous data types [34,37,43,44]. Consequently, the mathematical fundaments of the MCDM algorithms for the determination of the weights of the criteria and the assessment of the alternatives must be adapted to their fuzzy counterparts.

Finally, it is worth noting that fuzzy variables sometimes need to be converted into a representative crisp value z. Although this process, called defuzzification, can be performed using various methods, this study employs the formula proposed in [45]:

$$z={\displaystyle \frac{z^l+4z^m+z^u}{6}}$$

(1)

Although the defuzzification method presented in Equation (1) is well established in the literature, an alternative method based on the best non-fuzzy performance approach [44] has been implemented to ensure the robustness of the results. In this way, the influence of the defuzzification method on the final outcomes will be analyzed in Section 4.2.

2.2. Weight Determination for Fuzzy MCDM

Weighting methods can be classified as objective, subjective, or hybrid approaches [46]. Objective methods determine the weight of each criterion by mathematically analyzing the intrinsic information contained within the decision matrix, which represents the evaluation of each alternative with respect to each criterion. Subjective methods derive the weights based on expert judgments regarding the relative importance of the criteria. Hybrid methods combine elements of both objective and subjective approaches to establish weights.

Although subjective methods are widely used in MCDM problems, they are not well suited to scenarios involving large volumes of data or situations in which experts lack sufficient information to make reliable experience-based judgments. In such contexts, objective weighting methods are becoming increasingly popular [47].

It should be emphasized that when fuzzy values are used in the decision matrix, either modifications to the traditional weighting methods or the use of their fuzzy versions are required in order to handle the data appropriately.

For these reasons, this study implements and analyzes several fuzzy objective weighting methods to enable comparison of the results produced by each approach.

2.2.1. Fuzzy Statistical Variance Method

The first method considered is the statistical variance method [48,49]. This straightforward technique prioritizes criteria exhibiting greater performance variance across alternatives, under the principle that higher dispersion implies greater discriminative power.

The application of this method involves several steps.

• The elements of the decision matrix ${\tilde{x}}_{ij}=(x_{ij}^l,x_{ij}^m,x_{ij}^u)$, where $i\in [1,n]$ indicates the ith alternative and $j\in [1,m]$ indicates the jth criterion, which are first normalized using Equation (2) for benefit-type criteria—where higher values are preferred—and Equation (3) for cost-type criteria—where lower values are more desirable:

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_{ij}^l}{x_j^{*u}}},{\displaystyle \frac{x_{ij}^m}{x_j^{*u}}},{\displaystyle \frac{x_{ij}^u}{x_j^{*u}}}\right),\mathrm{where}{x}_j^{*u}=\underset{i}{max}\left\{x_{ij}^u\right\},$$

  (2)

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_j^{-l}}{x_{ij}^u}},{\displaystyle \frac{x_j^{-l}}{x_{ij}^m}},{\displaystyle \frac{x_j^{-l}}{x_{ij}^l}}\right),\mathrm{where}{x}_j^{-l}=\underset{i}{min}\left\{x_{ij}^l\right\}.$$

  (3)
• Next, the statistical variance of each normalized criterion is calculated using the mean value of each component ${\overline{r}}_j^k$ and Equation (4):

  $$V_j^k=\left({\displaystyle \frac{1}{n}}\right)\sum _{i=1}^n{\left(r_{ij}^k-{\overline{r}}_j^k\right)}^2,\mathrm{for}k=l,m,u.$$

  (4)
• Finally, the fuzzy weight of each criterion is obtained through

  $${\tilde{w}}_j=(w_j^l,w_j^m,w_j^u),\mathrm{where}{w}_j^k={\displaystyle \frac{V_j^k}{{\sum }_{j=1}^m{V}_j^k}}\mathrm{for}k=l,m,u.$$

  (5)

2.2.2. Fuzzy CRITIC Method

The CRITIC (Criteria Importance Through Intercriteria Correlation) method is a robust and well-established approach for determining weights that expands upon the statistical deviation concept by incorporating inter-criteria correlation analysis [50,51]. This method assigns greater information content—and consequently higher weight—to criteria exhibiting larger standard deviations in alternative performance scores. Conversely, when two criteria show strong performance correlation, they likely contain redundant information, and thus each should receive reduced weight to account for their diminished unique informational contribution.

The application of this method involves several steps [51]:

• The decision matrix is first normalized using the normalizing method determined by Equation (6) for benefit-type criteria and Equation (7) for cost-type criteria:

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_{ij}^l-x_j^{-l}}{x_j^{*u}-x_j^{-l}}},{\displaystyle \frac{x_{ij}^m-x_j^{-l}}{x_j^{*u}-x_j^{-l}}},{\displaystyle \frac{x_{ij}^u-x_j^{-l}}{x_j^{*u}-x_j^{-l}}}\right),$$

  (6)

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_j^{*u}-x_{ij}^u}{x_j^{*u}-x_j^{-l}}},{\displaystyle \frac{x_j^{*u}-x_{ij}^m}{x_j^{*u}-x_j^{-l}}},{\displaystyle \frac{x_j^{*u}-x_{ij}^l}{x_j^{*u}-x_j^{-l}}}\right),$$

  (7)

  where

  $$x_j^{-l}=\underset{i}{min}\left\{x_{ij}^l\right\},x_j^{*u}=\underset{i}{max}\left\{x_{ij}^u\right\}.$$

  (8)
• The correlation coefficient between all the criteria ${\rho }_{j{j}^{\prime }}^k$ and the standard deviation of each criterion, ${\sigma }_j^k$, are computed.
• The weights of the criteria are calculated based on the standard deviation and its correlation with the remaining criteria. The objective fuzzy weights are determined as follows:

  $${\tilde{w}}_j=(w_j^l,w_j^m,w_j^u),\mathrm{where}{w}_j^k={\displaystyle \frac{C_j^k}{{\sum }_{j=1}^m{C}_j^k}}\mathrm{for}k=l,m,u,$$

  (9)

  and

  $$C_j^k={\sigma }_j^k·\sum _{j^{\prime }=1}^m(1-{\rho }_{j{j}^{\prime }}^k).$$

  (10)

2.2.3. Fuzzy MEREC Method

The MEREC (Method based on the Removal Effects of Criteria) [52] is an innovative approach gaining recognition in the MCDM literature [46]. This method determines weights by analyzing how the removal of each criterion affects the alternatives’ overall performance. Criteria whose removal causes significant performance changes receive higher weights, while those with minimal impact receive lower weights.

The application of this method involves several steps:

• Normalization of the decision matrix using Equation (11) for benefit-type criteria and Equation (12) for cost-type criteria [53]:

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_j^{-l}}{x_{ij}^u}},{\displaystyle \frac{x_j^{-l}}{x_{ij}^m}},{\displaystyle \frac{x_j^{-l}}{x_{ij}^l}}\right),\mathrm{where}{x}_j^{-l}=\underset{i}{min}\left\{x_{ij}^l\right\},$$

  (11)

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_{ij}^l}{x_j^{*u}}},{\displaystyle \frac{x_{ij}^m}{x_j^{*u}}},{\displaystyle \frac{x_{ij}^u}{x_j^{*u}}}\right),\mathrm{where}{x}_j^{*u}=\underset{i}{max}\left\{x_{ij}^u\right\}$$

  (12)
• We calculate the overall performance $S_i^k$ of each component of the alternatives using

  $$S_i^k=ln\left(1+{\displaystyle \frac{1}{m}}\sum _{j=1}^m\left(\left|ln\left(r_{ij}^k\right)\right|\right)\right),\mathrm{for}k=l,m,u.$$

  (13)
• We then compute the performance of each alternative, $S_i^{*k}$ when removing each criterion:

  $$S_i^{*k}=ln\left(1+{\displaystyle \frac{1}{m}}\sum _{j^{\prime }\ne j}\left(\left|ln\left(r_{i{j}^{\prime }}^k\right)\right|\right)\right),\mathrm{for}k=l,m,u.$$

  (14)
• We compute the effect of removing the jth criterion by computing the summation of absolute deviations using

  $$E_j^k=\sum _{i=1}^n|S_i^{*k}-S_i^k|,\mathrm{for}k=l,m,u.$$

  (15)
• Finally, the fuzzy weight of each criterion is obtained through

  $${\tilde{w}}_j=(w_j^l,w_j^m,w_j^u),\mathrm{where}{w}_j^k={\displaystyle \frac{E_j^k}{{\sum }_{j=1}^m{E}_j^k}}\mathrm{for}k=l,m,u.$$

  (16)

It is important to note that, while some of the normalization techniques discussed earlier are linked to the weight determination procedure—such as in the case of MEREC [54]—for methods like fuzzy statistical variance and fuzzy CRITIC, normalization techniques are interchangeable [55]. In order to ensure independence and a more transparent assessment of the objective weighting methods implemented in this study, the normalization techniques commonly associated with each method have been retained. Nonetheless, Section 4.2 provides an analysis of how alternative normalization choices may affect the results.

2.3. MCDM Fuzzy Ranking Methods

Once the decision matrix and criterion weights are computed, ranking methods must be employed to prioritize the proposed alternatives. Although numerous ranking methods exist in the MCDM literature [15], this study applies three distinct approaches: Fuzzy-WASPAS, Fuzzy-TOPSIS, and Fuzzy-MARCOS.

The selection of these ranking methods is primarily based on the fact that each employs a fundamentally different prioritization strategy, ensuring independence among the resulting solutions. Additionally, the chosen methods represent a balanced and representative sample, allowing for comparison between classical and straightforward approaches such as WASPAS, widely recognized and established techniques like TOPSIS, and more recent and innovative methods such as MARCOS. Furthermore, all selected methods have well-tested fuzzy extensions, enabling efficient and rigorous handling of uncertainty expressed through triangular fuzzy numbers.

In conclusion, this multi-method implementation will enable a robust solution analysis through comparative ranking evaluation.

2.3.1. Fuzzy WASPAS

WASPAS (Weighted Aggregated Sum Product Assessment) is an efficient yet straightforward MCDM technique widely used for alternative ranking. This method prioritizes candidates through a weighted combination of their performance scores calculated via two approaches: the Weighted Sum Method (WSM) and Weighted Product Method (WPM).

The WASPAS implementation procedure consists of five sequential steps [51,56].

• The decision matrix is normalized using Equations (2) and (3), following the same normalization scheme as in the fuzzy statistical variance weighting method.
• The global performance of each alternative is computed through WSM, ${\tilde{Q}}_i$, and WPM, ${\tilde{G}}_i$ aggregations:

  $${\tilde{Q}}_i=\sum _{j=1}^m{\tilde{r}}_{ij}{\tilde{w}}_j\mathrm{and}{\tilde{G}}_i=\prod _{j=1}^m{\left({\tilde{r}}_{ij}\right)}^{{\tilde{w}}_j}.$$

  (17)
• Then, WSM and WPM performance scores are defuzzified using Equation (1).
• The performance measures are combined using a weighting parameter $\lambda$:

  $$K_i=\lambda Q_i+(1-\lambda )G_i\mathrm{where}\lambda ={\displaystyle \frac{{\sum }_{i=1}^n{G}_i}{{\sum }_{i=1}^n{Q}_i+{\sum }_{i=1}^n{G}_i}}.$$

  (18)
• Finally, alternatives are ranked in descending order of their combined performance values, with the highest scoring alternative representing the best choice.

2.3.2. Fuzzy TOPSIS

TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) is a widely used MCDM ranking method valued for its versatility and robustness [57]. TOPSIS ranks the alternatives by simultaneously evaluating their distance to a theoretically ideal and anti-ideal solution. The best alternatives demonstrate geometric closeness to the ideal reference point while remaining distant from the anti-ideal solution.

The application of this method involves several steps [58]:

• The decision matrix is normalized following the same procedure as in the WASPAS method.
• The elements ${\tilde{l}}_{ij}$ of the weighted normalized fuzzy decision matrix are computed:

  $${\tilde{l}}_{ij}={\tilde{r}}_{ij}{\tilde{w}}_j.$$

  (19)
• The ideal solution, $A^{*}$, and anti-ideal solution, $A^{-}$, are identified by selecting the most extreme values across all alternatives for each criterion:

  $$A^{*}=({\tilde{l}}_1^{*},{\tilde{l}}_2^{*},\dots ,{\tilde{l}}_m^{*}),\mathrm{where}{\tilde{l}}_j^{*}=\underset{i}{max}\left\{l_{ij}^u\right\},$$

  (20)

  $$A^{-}=({\tilde{l}}_1^{-},{\tilde{l}}_2^{-},\dots ,{\tilde{l}}_m^{-}),\mathrm{where}{\tilde{l}}_j^{-}=\underset{i}{min}\left\{l_{ij}^l\right\}.$$

  (21)
• The distance between each alternative and ideal solution, $d_i^{*}$, and the anti-ideal solution, $d_i^l$, is computed.

  $$d_i^{*}=\sum _{j=1}^{m}d({\tilde{l}}_{ij},{\tilde{l}}_j^{*}),d_i^{-}=\sum _{j=1}^{m}d({\tilde{l}}_{ij},{\tilde{l}}_j^{-}),$$

  (22)

  where the distance between two TFN $\tilde{y}$ and $\tilde{z}$ can be calculated by

  $$d(\tilde{y},\tilde{z})=\sqrt{{\displaystyle \frac{1}{3}}\left[{\left(y^l-z^l\right)}^2+{\left(y^m-z^m\right)}^2+{\left(y^u-z^u\right)}^2\right]}.$$

  (23)
  It is worth noting that this distance metric is the most commonly applied in TOPSIS [59]; however, alternative metrics, such as the one proposed by Tran and Duckstein [60], can also be used. The effect of changing the distance metric on the obtained results will be analyzed in Section 4.2.
• A closeness coefficient, $CC$, is calculated for each alternative using

  $$CC={\displaystyle \frac{d_i^{-}}{d_i^{-}+d_i^{*}}}.$$

  (24)
• Alternatives are ranked in descending order of their $CC$ values, with higher values indicating better performance.

2.3.3. Fuzzy MARCOS

MARCOS (Measurement of Alternatives and Ranking according to Compromise Solution) is a state-of-the-art ranking methodology that addresses two critical aspects of MCDM problems: the need for robust reference-based evaluation and the requirement for balanced compromise solutions [61]. This technique evaluates alternatives by establishing their utility functions relative to both reference solutions—that is, ideal and anti-ideal—ultimately generating a compromise ranking that balances these benchmarks.

The application of this method involves several steps [62].

• We determine the ideal $\tilde{A}\left(ID\right)$, and anti-ideal, $\tilde{A}\left(AI\right)$ values from the decision matrix for each criterion according to whether it is a cost, C, or benefit, B, criterion:

  $$\tilde{A}\left(AI\right)=\underset{i}{min}\left\{{\tilde{x}}_{ij}^k\right\}\mathrm{if}j\in B\mathrm{and}\underset{i}{max}\left\{{\tilde{x}}_{ij}^k\right\}\mathrm{if}j\in C,\mathrm{for}k=l,m,u,$$

  (25)

  $$\tilde{A}\left(ID\right)=\underset{i}{max}\left\{{\tilde{x}}_{ij}^k\right\}\mathrm{if}j\in B\mathrm{and}\underset{i}{min}\left\{{\tilde{x}}_{ij}^k\right\}\mathrm{if}j\in C,\mathrm{for}k=l,m,u.$$

  (26)
• We then normalize the decision matrix using Equations (27) and (28):

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_{ID}^l}{x_{ij}^u}},{\displaystyle \frac{x_{ID}^l}{x_{ij}^m}},{\displaystyle \frac{x_{ID}^l}{x_{ij}^l}}\right)\mathrm{if}j\in C,$$

  (27)

  $${\tilde{r}}_{ij}=\left({\displaystyle \frac{x_{ij}^l}{x_{ID}^u}},{\displaystyle \frac{x_{ij}^m}{x_{ID}^u}},{\displaystyle \frac{x_{ij}^u}{x_{ID}^u}}\right)\mathrm{if}j\in B.$$

  (28)
• We compute the elements, ${\tilde{l}}_{ij}$, of the weighted decision matrix following the same procedure as in the TOPSIS method.
• The ideal, ${\tilde{K}}_i^{+}$, and anti-ideal, ${\tilde{K}}_i^{-}$, utility degrees for each alternative are determined:

  $${\tilde{K}}_i^{+}={\displaystyle \frac{{\tilde{S}}_i}{{\tilde{S}}_{ID}}}=\left({\displaystyle \frac{s_i^l}{s_{ID}^u}},{\displaystyle \frac{s_i^m}{s_{ID}^m}},{\displaystyle \frac{s_i^u}{s_{ID}^l}}\right),$$

  (29)

  $${\tilde{K}}_i^{-}={\displaystyle \frac{{\tilde{S}}_i}{{\tilde{S}}_{AI}}}=\left({\displaystyle \frac{s_i^l}{s_{AI}^u}},{\displaystyle \frac{s_i^m}{s_{AI}^m}},{\displaystyle \frac{s_i^u}{s_{AI}^l}}\right),$$

  (30)

  where

  $${\tilde{S}}_i=\sum _{j=1}^m{\tilde{l}}_{ij}.$$

  (31)
• We compute the elements ${\tilde{t}}_i$ of the aggregated utility matrix:

  $${\tilde{t}}_i={\tilde{K}}_i^{+}+{\tilde{K}}_i^{-}.$$

  (32)
• We then compute the fuzzy number $\tilde{H}$ and its defuzzied value, $h_{crisp}$ using Equation (1):

  $$\tilde{H}=(h^l,h^m,h^u)=max\left\{{\tilde{t}}_i^k\right\}\mathrm{for}k=l,m,u.$$

  (33)
• Then, the utility function of each alternative in relation to the ideal, $f\left({\tilde{K}}_i^{+}\right)$, and anti-ideal, $f\left({\tilde{K}}_i^{-}\right)$, solutions is determined:

  $$\tilde{f}\left({\tilde{K}}_i^{+}\right)={\displaystyle \frac{{\tilde{K}}_i^{-}}{h_{crisp}}}=\left({\displaystyle \frac{k_i^{-l}}{h_{crisp}}},{\displaystyle \frac{k_i^{-m}}{h_{crisp}}},{\displaystyle \frac{k_i^{-u}}{h_{crisp}}}\right),$$

  (34)

  $$\tilde{f}\left({\tilde{K}}_i^{-}\right)={\displaystyle \frac{{\tilde{K}}_i^{+}}{h_{crisp}}}=\left({\displaystyle \frac{k_i^{+l}}{h_{crisp}}},{\displaystyle \frac{k_i^{+m}}{h_{crisp}}},{\displaystyle \frac{k_i^{+u}}{h_{crisp}}}\right).$$

  (35)
• We compute the crisp value of ${\tilde{K}}_i^{+}$, ${\tilde{K}}_i^{-}$, $\tilde{f}\left({\tilde{K}}_i^{+}\right)$ and $\tilde{f}\left({\tilde{K}}_i^{-}\right)$ using Equation (1).
• We then calculate the utility function value for each alternative by applying Equation (36):

  $$f\left(K_i\right)={\displaystyle \frac{K_i^{+}+K_i^{-}}{1+\frac{1-f\left(K_i^{+}\right)}{f\left(K_i^{+}\right)}+\frac{1-f\left(K_i^{-}\right)}{f\left(K_i^{-}\right)}}},$$

  (36)
• The alternatives are then ranked such that the highest utility function value corresponds to the best choice.

3. Decision Problem: Prioritization of NEAs for a Boulder Capture Mission

3.1. Statement of the Decision Problem

In this study, the decision making problem to be addressed involves prioritizing a number of NEAs that could potentially serve as targets for a space mission dedicated to the scientific study of asteroids and the technological development of PD systems and ISRU techniques [6].

To achieve this, certain initial requirements that all candidate asteroids must meet will be established. First, NEAs with a diameter between 100 and 350 m will be selected. This size range is considered interesting because such asteroids are massive enough to cause significant damage if they impact Earth, yet they remain small enough that current observation campaigns have only detected a small fraction of their estimated population. This combination makes them a greater impact threat than larger asteroids; while the latter are more destructive, their population is both more limited and nearly completely catalogued [63]. Additionally, asteroids within this size range often exhibit surface boulders suitable for collection and further analysis [12].

Furthermore, to ensure the mission can be executed within a reasonable time frame using available technological capabilities and $\Delta V$ constraints, only asteroids that have at least one natural close approach to Earth between 2030 and 2045 are considered [13,64].

3.2. Criteria Selection

Following the establishment of initial requirements, a set of evaluation criteria must be proposed to prioritize the list of candidates. These criteria are classified as either benefit criteria, where higher performance of an alternative in the criterion improves its overall ranking, or cost criteria, where higher performance worsens its ranking. In addition, the criteria may be classified as crisp when their values are well defined or fuzzy when their values fluctuate within a reference interval or when it becomes necessary to represent the uncertainty associated with a particular value.

Therefore, to establish a suitable set of evaluation criteria for the decision making problem, it is necessary to analyze the key parameters that govern the design of asteroid mission architectures. The first of these is the $\Delta V$ required to perform the mission [64,65], which has a direct impact on the trajectory design as well as on the propulsion system requirements and fuel consumption. This parameter is represented in the model by the capture cost evaluation criterion.

Another desirable characteristic in mission design relates to operational flexibility. Targets with a very high synodic period present the disadvantage of offering infrequent opportunities to conduct missions and gather Earth-based observational data [65]. This feature is addressed in the model through the synodic period evaluation criterion.

The asteroid’s rotational dynamic, spin rate, and spin axis also constitute an important factor in the mission design [66]. The spin rate is incorporated as an evaluation criterion due to its strong influence on the operational cost of synchronizing spacecraft maneuvers during proximity operations. On the other hand, although most asteroids exhibit a stable spin axis, tumbling bodies should be avoided. Since tumbling motion cannot be reliably assessed without detailed observation, it is considered a constraint to be verified in a prior observational campaign before progressing to subsequent phases of mission development [6].

From a preliminary mission design perspective, another relevant aspect is the quality of orbital knowledge of the target, as it affects the possibility of defining precise and robust mission trajectories [65,67]. This characteristic is considered through the orbit determination accuracy criterion.

Additionally, it is advantageous for the selected target to have a group of asteroids with similar orbits [67], as this enables the preliminary trajectory design to be adapted for future missions or backup targets [68]. This feature is reflected in the number of similar candidates criterion.

From a scientific interest point of view, asteroid composition is also a relevant feature. However, current Earth-based observations provide taxonomic classification for only 0.29% of the asteroids within the studied size range [30]. This limitation, combined with the fact that asteroid boulder capture and redirection missions were primarily designed as technology demonstrators rather than for scientific exploration purposes [13], has led to the exclusion of composition as an evaluation criterion.

Therefore, although this study focuses on the analysis of the criteria capture cost, synodic period, rotation rate, orbit determination accuracy, and number of similar candidates, the preliminary results obtained may serve as a basis for organizing follow-up observation campaigns for the most promising candidates. These campaigns would aim to gather additional information on other relevant characteristics, such as taxonomic classification, approximate shape models, or thermal properties, which could be incorporated in a more detailed assessment using the MCDM framework proposed here.

• Capture Cost: This cost-type, crisp criterion estimates the $\Delta V$ required to capture the asteroid or a portion of it into a closed Earth orbit. It is directly derived from the relative orbital geometry of the asteroid and Earth. For each candidate, the capture cost is computed following the methodology developed in [69,70] with orbital data extracted from the SBDS [30].
• Synodic Period: This cost-type, crisp criterion defines the time required for the asteroid to return to the same relative position with respect to Earth. A low synodic period enables multiple observation and launch windows under similar conditions, whereas a high synodic period implies low repeatability of favorable conditions. The value of synodic period of an asteroid $P_{syn}$ can be calculated from the orbital periods of Earth, $P_{Earth}$, and the NEA, $P_{NEA}$ using the following formula:

  $$P_{syn}={\displaystyle \frac{P_{Earth}·P_{NEA}}{|P_{Earth}-P_{NEA}|}}.$$

  (37)
• Rotation Rate: This criterion significantly affects mission operational costs, as higher rotation rates increase both mission complexity and propellant requirements for spacecraft–NEA synchronization during proximity operations. Consequently, rotation rate is classified as a cost-type criterion. When available, crisp rotation rate values for candidate asteroids may be retrieved from SBDS. To ensure reasonable operational costs for spacecraft–asteroid synchronization, only asteroids with known rotation rates below 0.5 revolutions per hour will be considered [6]. It is important to note that applying this filter will significantly reduce the number of potential candidates. One possible way to incorporate this evaluation criterion without excluding candidates would be to estimate the rotation rate using models that relate rotation rate to asteroid’s size [71,72]. However, available data [73] show variations of up to two orders of magnitude in the observed rotation periods for asteroids of the same size within the studied range. Hence, applying such estimations could result in inaccurate performance assessments and, consequently, distort the ranking outcomes. For this reason, this study has opted to exclude candidates with unknown rotation rates, allowing their inclusion in the proposed MCDM framework once reliable data become available.
• Orbit Determination Accuracy: This benefit-type criterion evaluates the quality of the NEA’s orbital determination and its evolution. It is derived from the condition code parameter in SBDS, which quantifies orbital uncertainty on a scale from 0 (low uncertainty) to 9 (very high uncertainty). In practice, orbits of NEAs with condition codes exceeding 6 are considered too uncertain for mission targeting and are excluded as potential candidates unless additional observations improve their orbital determination [67,74]. It is important to note that condition code does not represent an exact and unambiguous value for orbital uncertainty but rather defines an interval containing the potential uncertainty range. Such uncertainty-bearing data can be rigorously handled through fuzzy logic.
  The fuzzy orbit determination accuracy parameter will be calculated through a linear transformation of the condition code. This transformation assigns maximum scores to asteroids with condition code 0, decreasing linearly until reaching null values for condition codes above 6 (see Table 1). This transformation simultaneously accomplishes two critical functions: it enables rigorous uncertainty quantification through fuzzy logic while preventing potential distortions in MCDM outcomes that may arise from zero-value criterion assignments [46,52].

  Table 1. Correspondence between the fuzzy orbit determination accuracy criterion and condition code.

  Orbit Determination Accuracy	Condition Code
  (0.000, 0.143, 0.286)	6
  (0.143, 0.286, 0.429)	5
  (0.286, 0.429, 0.571)	4
  (0.429, 0.571, 0.714)	3
  (0.571, 0.714, 0.857)	2
  (0.714, 0.857, 1)	1
  (0.857, 1, 1)	0

  Table 1. Correspondence between the fuzzy orbit determination accuracy criterion and condition code.

  Orbit Determination Accuracy	Condition Code
  (0.000, 0.143, 0.286)	6
  (0.143, 0.286, 0.429)	5
  (0.286, 0.429, 0.571)	4
  (0.429, 0.571, 0.714)	3
  (0.571, 0.714, 0.857)	2
  (0.714, 0.857, 1)	1
  (0.857, 1, 1)	0

• Number of Similar Candidates: This benefit-type criterion quantifies the number of potential candidates (those meeting all previous requirements) with orbits similar to the NEA under evaluation. The existence of a number of NEAs with similar orbital parameters enables the development of versatile mission architectures. In such scenarios, navigation systems, propulsion profiles, and design strategies can be adapted to analogous targets with minimal modifications. This approach not only optimizes development resources but also expands the range of potential destinations for a single mission, thereby enhancing both technical feasibility and scientific return. For this reason, NEAs lacking any similar orbital candidates will be excluded from further consideration.
  Orbital similarity between two asteroids could be determined through their semimajor axis, a, semi-latus rectum, p, eccentricity, e, inclination, i, argument of the perihelion $\omega$, and longitude of the ascending node $\Omega$ using the metric ${\varrho }_2$ [75]:

  $${\varrho }_2^2=(1+e_1^2)p_1+(1+e_2^2)p_2-2\sqrt{p_1{p}_2}(cosI+e_1{e}_{2}cosP),$$

  (38)

  where subscripts 1 and 2 denote the orbital elements of the first and second NEA being compared, respectively, and

  $$cosI=c_1{c}_2+s_1{s}_{2}cos({\Omega }_1-{\Omega }_2),$$

  (39)

  $$\begin{array}{cc}\hfill cosP=& s_1{s}_{2}sin{\omega }_{1}sin{\omega }_2\hfill \\ \hfill & +(cos{\omega }_{1}cos{\omega }_2+c_1{c}_{2}sin{\omega }_{1}sin{\omega }_2)cos({\Omega }_1-{\Omega }_2)\hfill \\ \hfill & +(c_{2}cos{\omega }_{1}sin{\omega }_2-c_{1}sin{\omega }_{1}cos{\omega }_2)sin({\Omega }_1-{\Omega }_2),\hfill \end{array}$$

  (40)

  where

  $$c=cosi,s=sini.$$

  (41)
  It should be emphasized that no exact threshold exists for the maximum ${\varrho }_2$ value that defines sufficient orbital similarity between two bodies [76]. To address this uncertainty rigorously, fuzzy logic is employed by representing the number of similar candidates by a TFN bounded between two characteristic ${\varrho }_2$ values, ${\varrho }_2=0.16$ and ${\varrho }_2=0.2$. The number ${\tilde{N}}_{sim}$ of similar candidates for a given NEA is then computed as follows:

  $${\tilde{N}}_{sim}=(N_{sim}{|}_{{\varrho }_2=0.16},{\displaystyle \frac{N_{sim}{{|}_{{\varrho }_2=0.16}+N_{sim}|}_{{\varrho }_2=0.2}}{2}},N_{sim}{|}_{{\varrho }_2=0.2}),$$

  (42)

  where $N_{sim}{|}_{{\varrho }_2=0.16}$ and $N_{sim}{|}_{{\varrho }_2=0.2}$ represent the number of similar candidates when applying the threshold conditions ${\varrho }_2=0.16$ and ${\varrho }_2=0.2$, respectively.

Once these criteria and their limitations have been defined, the available data from the SBDS will be analyzed by performing a screening of the potential candidates.

Table 2. Screening criteria applied to the SBDS and their mission design implications.

Filter Criterion	Mission Design Rationale
Asteroid size [100–350 m]	– Represents objects of significant planetary defense interest due to their impact threat [63]. – Implies high likelihood of surface boulder presence [77].
Natural Earth close approach [2030–2045]	– Mission feasibility within practical $\Delta V$ budget constraints [13,69,78]. – Provides lead time to gather additional Earth-based observational data and develop mission design maturation [72,73].
Rotation rate < 0.5 r.p.h	– Minimizes spacecraft synchronization complexity and propellant consumption during proximity operations [6].
Condition code ≤ 6	– Guarantees adequate orbital knowledge for precise and robust trajectory planning [65,67].

provides a summary of the filters applied to the database, along with the corresponding implications for mission design.

It is important to emphasize that this criterion list could potentially be expanded by incorporating additional factors such as an asteroid’s scientific interest based on spectral composition or taxonomic classification [79]. However, current observational data reveals that only 0.29% of NEAs within the target size range have confirmed taxonomic classifications, which would severely constrain the candidate pool if such a criterion was implemented.

Consequently, this study should be interpreted as a foundational framework for prioritizing boulder capture mission candidates. The methodology permits future expansion as observational campaigns yield additional data on candidate asteroids, particularly regarding their compositional properties.

3.3. Proposal and Assessment of Alternatives

Once the requirements and evaluation criteria were established for the asteroid population under study, candidate asteroid data were systematically extracted and filtered using a custom script interfacing with the SBDS API. This screening process yielded a refined set of 28 asteroids meeting all mission constraints as potential targets.

The orbital and physical parameters of these candidates were processed to evaluate their performance across each defined criterion. These results were structured into a comprehensive decision matrix (see

Table 3. Decision matrix for the filtered asteroid candidate list. Alternative assessments with respect to fuzzy criteria are expressed as triangular fuzzy numbers.

Asteroid	Capture Cost [m/s]	Synodic Period [y]	Rotation Rate [rph]	Orbit Det. Accuracy	No. of Similar Candidates
1998 FG2	2754.678	3.091	0.0862	(0.857, 1, 1)	(1, 1, 1)
2000 EW70	1857.441	9.85	0.0303	(0.857, 1, 1)	(2, 3, 4)
2002 TC70	786.246	2.664	0.0381	(0.857, 1, 1)	(1, 1.5, 2)
2005 EE	3106.648	6.026	0.3769	(0.857, 1, 1)	(2, 2.5, 3)
2005 YU55	1542.138	5.093	0.0556	(0.857, 1, 1)	(1, 1.5, 2)
2000 AC6	2387.101	3.736	0.4092	(0.857, 1, 1)	(1, 1.5, 2)
2010 LN14	2209.589	5.176	0.2603	(0.857, 1, 1)	(1, 1, 1)
2003 GA	1598.294	3.218	0.173	(0.857, 1, 1)	(1, 2.5, 4)
2011 DU	1963.789	4.724	0.0972	(0.857, 1, 1)	(2, 3, 4)
2002 UK11	4474.08	2.913	0.125	(0.857, 1, 1)	(1, 1.5, 2)
2010 XC15	1456.013	1.679	0.3741	(0.857, 1, 1)	(1, 1, 1)
2018 DH1	2463.14	1.492	0.2	(0.857, 1, 1)	(1, 1.5, 2)
1994 CJ1	1976.091	2.22	0.0333	(0.857, 1, 1)	(4, 4.5, 5)
1999 FN19	842.875	1.898	0.0373	(0.857, 1, 1)	(2, 3.5, 5)
2000 KA	1675.282	2.861	0.0873	(0.857, 1, 1)	(2, 2.5, 3)
2001 EC16	2100.837	2.783	0.005	(0.857, 1, 1)	(1, 3, 5)
2002 LY1	2307.202	14.163	0.3121	(0.857, 1, 1)	(1, 3, 5)
2006 CT	645.828	7.738	0.0599	(0.857, 1, 1)	(1, 1.5, 2)
2010 AF30	1727.076	2.903	0.3846	(0.857, 1, 1)	(2, 3, 4)
2012 XS111	3986.225	2.127	0.4673	(0.714, 0.857, 1.0)	(1, 1, 1)
2013 NJ	1757.751	3.181	0.004	(0.857, 1, 1)	(1, 2.5, 4)
2014 HK129	2789.751	1.822	0.0661	(0.857, 1, 1)	(1, 1.5, 2)
2015 FO124	3280.651	2.784	0.1278	(0.857, 1, 1)	(2, 2.5, 3)
2017 AG5	1233.459	2.775	0.1361	(0.571, 0.714, 0.857)	(2, 2.5, 3)
2019 CD5	2707.153	1.395	0.033	(0.571, 0.714, 0.857)	(1, 1, 1)
2022 BX1	1512.455	2.163	0.3923	(0.857, 1, 1)	(3, 4, 5)
2022 HB	4161.51	11.21	0.0115	(0.857, 1, 1)	(1, 1, 1)
2022 UD9	2533.317	2.309	0.0797	(0.429, 0.571, 0.714)	(2, 2, 2)

), which serves as the foundation for the subsequent multi-criteria analysis.

4. Results and Discussion

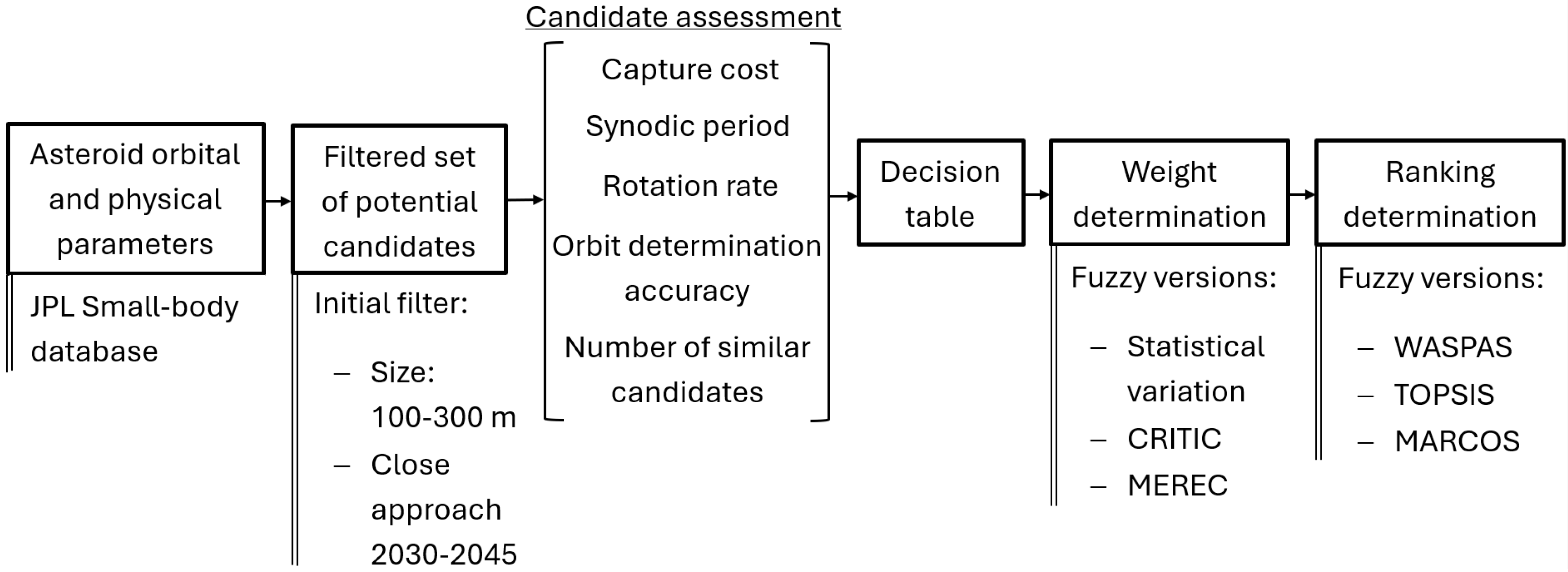
Once the methodological framework is established, the MCDM problem can be addressed. Following alternative evaluation, a set of fuzzy weights will be generated for each weighting mechanism. These weight sets, along with the decision matrix, will serve as inputs to the proposed ranking algorithms. The combination of different weighting methods and ranking techniques will produce a total of nine distinct alternative prioritization rankings, which will require comprehensive comparative analysis.

Upon obtaining the MCDM-derived rankings, an independent sensitivity analysis will be performed to assess how potential deviations in the determined weights could affect the resulting prioritized lists. This sensitivity analysis will serve two critical purposes: verifying the stability of top-ranked asteroid positions and validating that the results derived from both classical and innovative MCDM algorithm combinations are robust and reliable.

4.1. Weight Determination

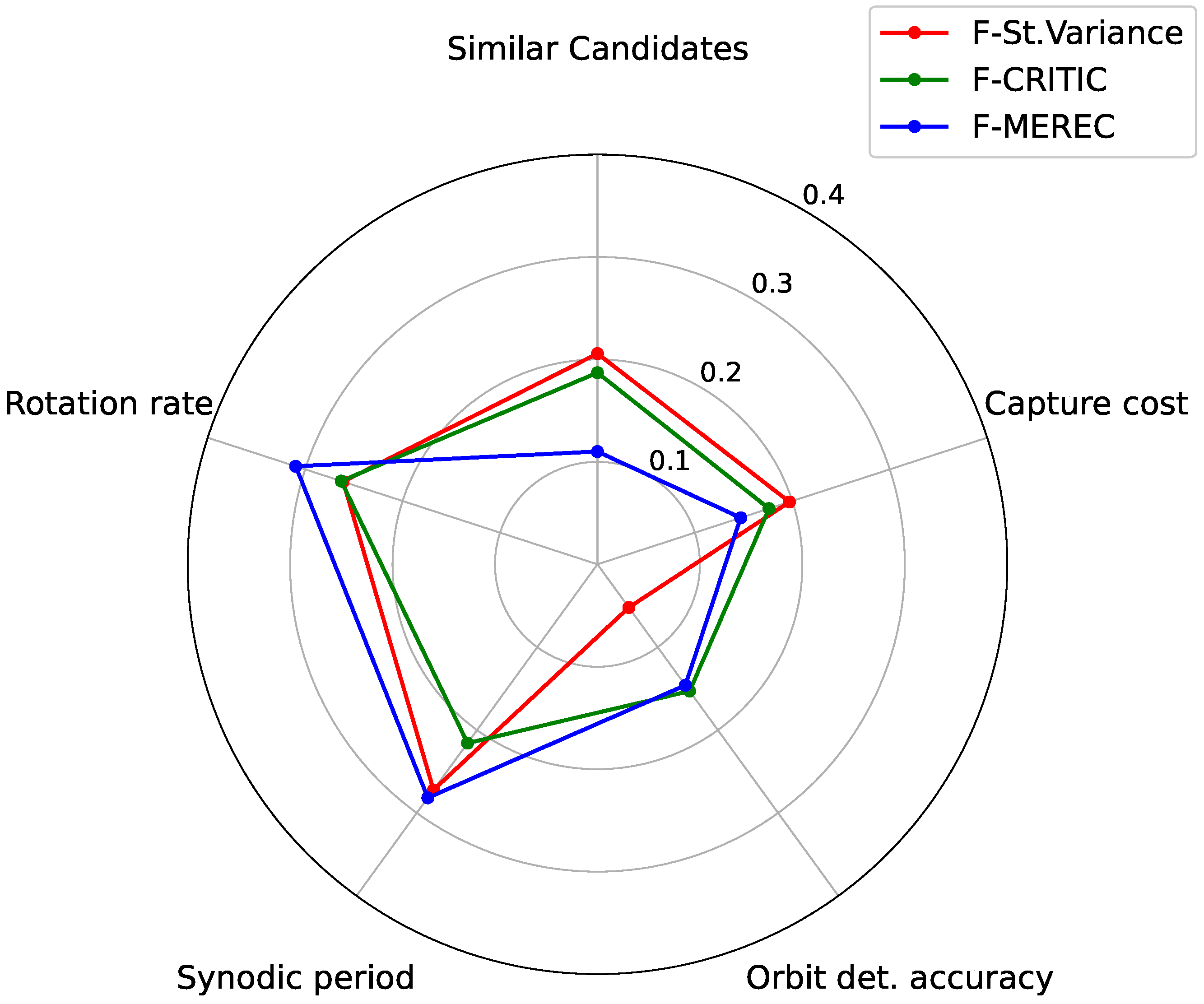
The proposed evaluation methods, fuzzy statistical variance, fuzzy CRITIC, and fuzzy MEREC, were applied to the decision matrix presented in Table 3. Since each weighting method assesses criterion importance through distinct normalization and information processing techniques, the resulting fuzzy weight sets are expected to differ from one another.

Consequently,

Table 4. Fuzzy weights calculated by the F-statistical variance, F-CRITIC and F-MEREC methods.

Criterion	F-Statistical Variance	F-CRITIC	F-MEREC
Capture cost	(0.171, 0.202, 0.202)	(0.174, 0.176, 0.176)	(0.139, 0.145, 0.161)
Synodic period	(0.236, 0.279, 0.279)	(0.211, 0.217, 0.217)	(0.267, 0.279, 0.307)
Rotation rate	(0.226, 0.268, 0.268)	(0.261, 0.263, 0.263)	(0.292, 0.306, 0.340)
Orbit det. accuracy	(0.017, 0.059, 0.059)	(0.096, 0.164, 0.164)	(0.130, 0.149, 0.149)
Similar candidates	(0.120, 0.191, 0.349)	(0.150, 0.179, 0.256)	(0.061, 0.120, 0.120)

presents the fuzzy weight evaluation results for each criterion, while

Table 5. Defuzzified weights calculated by the F-statistical variance, F-CRITIC and F-MEREC methods and Equation (1).

Criterion	F-Statistical Variance	F-CRITIC	F-MEREC	Average
Capture cost	0.197	0.176	0.147	0.175
Synodic period	0.272	0.216	0.282	0.259
Rotation rate	0.261	0.263	0.310	0.280
Orbit det. acc.	0.052	0.153	0.146	0.118
Sim. Candidates	0.206	0.187	0.110	0.169

and Figure 2 display the defuzzified weight values using Equation (1).

It is worth highlighting that although the CRITIC method already incorporates correlation control within its weighting algorithm, it is important to assess the correlation among criteria to ensure the robustness of the results. A straightforward way to do so is through the calculation of the Variance Inflation Factor (VIF) [80]. A high VIF value for a given criterion indicates that its behavior may be explained by the remaining criteria. Accordingly, the VIF was calculated for all criteria, and in all cases, the values were found to be below 1.2, which is under the commonly accepted threshold of 5 used in the literature [81]. This fact confirms that the correlation among criteria in this problem is adequately controlled.

To compare the results calculated by different weighting MCDM methods, a common approach involves computing the Pearson correlation coefficient and constructing a correlation matrix. Each entry in this matrix represents the Pearson correlation coefficient between the weights obtained from two different methods. A coefficient close to unity indicates a strong positive correlation, meaning that if a criterion’s weight is high in one method, it tends to be high in the other as well. A negative coefficient suggests an inverse relationship, where a relatively high weight in one method corresponds to a low weight in the other. Finally, a coefficient near zero implies no clear relationship between the weight tendencies of the two methods.

The correlation matrix comparing the three weighting methods is shown in Figure 3.

As observed, all correlation indices are positive and close to 1. The lowest correlation occurs between fuzzy statistical variance and fuzzy MEREC, which can be attributed to their fundamentally different weighting procedures [49]. Notably, the largest discrepancy lies in the orbit determination accuracy criterion, where MEREC assigns a weight of 0.153 compared to statistical variance’s 0.0521, and there are a number of similar candidates for which the distribution is the opposite (0.11 according to MEREC and 0.206 according to the statistical variance method).Such discrepancies are inherent to MCDM weighting techniques, yet the correlation coefficient value of 0.638 between fuzzy statistical variance and fuzzy MEREC remains sufficiently high to confirm that all methods produce highly correlated, coherent results [82].

Finally, it is important to note that while the defuzzified weights in Table 5 and Figure 3 were used for comparison purposes, fuzzy weights will be employed for calculations of alternative rankings.

4.2. Alternative Rankings

Each of the three fuzzy weight sets calculated in the previous section will be used, along with the decision matrix, as input for the different fuzzy ranking methods of F-WASPAS, F-TOPSIS, and F-MARCOS, resulting in a total of nine alternative rankings. As discussed in Section 2.3, the diverse normalization approaches and data-processing techniques will naturally lead to variations between the different rankings, which is a common outcome when applying MCDM methods [14,34], though these differences must be systematically analyzed and controlled.

Following this approach,

Table 6. Asteroid rankings according to nine different combinations of MCDM weighting and sorting methods.

Rank	St.Variance WASPAS	CRITIC WASPAS	MEREC WASPAS	St.Variance TOPSIS	CRITIC TOPSIS	MEREC TOPSIS	St.Variance MARCOS	CRITIC MARCOS	MEREC MARCOS
2013 NJ	1	1	1	1	1	1	1	1	1
2001 EC16	2	2	2	2	2	2	2	2	2
1999FN19	3	3	3	3	3	3	3	3	3
1994 CJ1	4	4	4	4	4	4	4	4	4
2002 TC70	5	5	5	6	6	7	6	6	8
2019 CD5	6	6	6	8	9	5	8	11	7
2022 BX1	7	8	10	5	5	8	5	5	6
2014HK129	8	9	7	13	14	10	12	13	10
2000 KA	9	7	9	14	13	11	13	12	11
2017 AG5	10	12	12	10	15	14	11	15	15
2018 DH1	11	13	8	7	7	6	7	7	5
2006 CT	12	10	11	15	10	13	14	10	13
2022 UD9	13	19	16	19	21	18	18	20	19
2000EW70	14	11	14	18	17	21	19	18	20
2003 GA	15	15	19	12	12	15	15	14	14
2010XC15	16	20	13	11	11	9	9	8	9
2011 DU	17	14	20	16	16	19	16	16	18
2010 AF30	18	18	22	9	8	12	10	9	12
2015FO124	19	17	18	17	18	16	17	17	16
2005YU55	20	16	17	21	20	23	21	19	23
2022 HB	21	21	15	27	27	24	27	27	24
1998 FG2	22	22	21	26	26	22	25	25	22
2002UK11	23	23	23	23	22	20	23	22	21
2012XS111	24	27	24	22	23	17	20	23	17
2000 AC6	25	24	25	24	24	25	24	24	25
2005 EE	26	25	27	25	25	26	26	26	26
2002 LY1	27	26	28	20	19	27	22	21	28
2010LN14	28	28	26	28	28	28	28	28	27

presents the alternative rankings in descending order for all nine combinations of weighting and ranking methods.

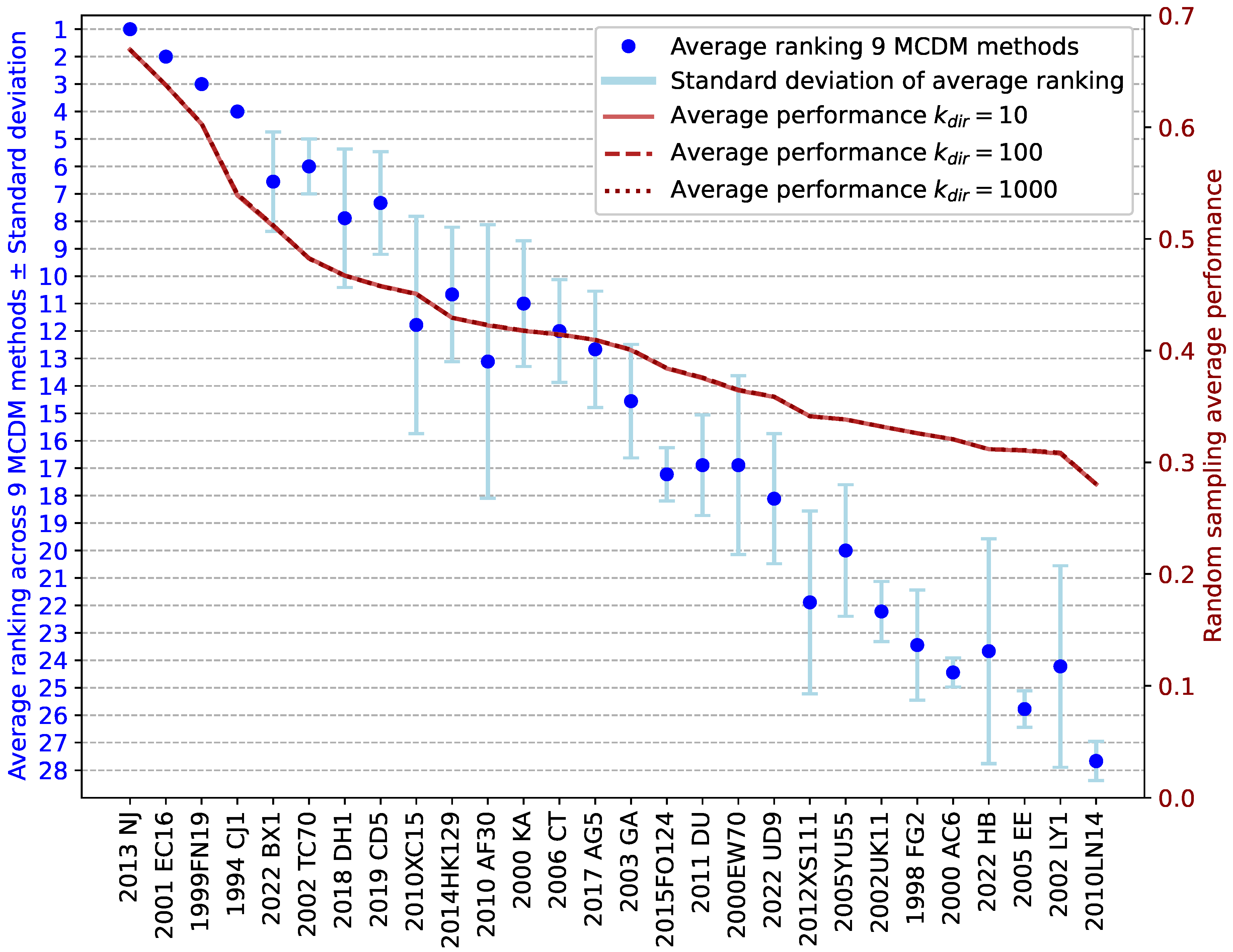
As evidenced by the results, while the rankings differ, a consistent trend emerges where the top performing asteroids in one ranking maintain strong positions across all others and vice versa. Notably, the four highest-ranked candidates remain identical in all rankings, with 2013 NJ consistently outperforming all other alternatives.

Interestingly, 2013 NJ is a small Apollo-class NEO with an estimated diameter on the order of 0.1–0.2 km. Its orbit—semimajor axis $a\approx 1.286AU$, eccentricity $e\approx 0.283$, inclination $i\approx 3.{941}^{\circ }$, longitude of the ascending node $\Omega \approx 238.{54}^{\circ }$ and argument of perihelion $\omega \approx 140.4^{\circ }$—has been well determined over multiple apparitions and radar astrometry techniques. Photometric and spectroscopic observations show it has a relative low rotation rate (0.004 revolutions per hour) with a Q-type (high-albedo, olivine/pyroxene–rich) surface [83] analogous to ordinary chondritic or ureilite meteorites with minimal space weathering.

It is worth noting that the four main candidates for the boulder capture option of the ARM mission—Itokawa (1998 SF36), Bennu (1999 RQ36), 1999 JU3, and 2008 EV5—do not appear in the rankings, as their sizes exceed the limits defined in this study and were therefore excluded during the preliminary screening phase. However, other asteroids proposed by ARM as potential targets are included, such as 2006 CT, which was ranked between positions 10 and 15 across the different methods, and 2000 AC6, which was ranked between positions 24 and 25 due to its higher rotation rate and capture cost.

Although the agreement in the top four ranking position suggests robust and coherent solutions across methodologies, a correlation analysis was conducted to quantitatively validate this observed consistency. As a result, Figure 4 presents the ranking correlation matrix for all method combinations proposed.

As shown in Figure 4, all correlation coefficients are positive and close to one, indicating strong relationships between the rankings. The lowest value, 0.814, corresponds to the MEREC–WASPAS and CRITIC–TOPSIS combinations, which still reflects a strong correlation. It is worth noting that the high correlation values observed among the rankings suggest a notable robustness of the obtained solutions. On average, these correlations exceed those observed between the weight distributions, indicating that the resulting rankings remain stable under small variations in the weighting of criteria.

To provide preliminary evidence on robustness prior to the dedicated sensitivity study, a set of targeted methodological tests addressing three key choices—defuzzification, normalization, and the TOPSIS distance metric—were performed. First, the defuzzification method proposed in Equation (1) was replaced by the best non-fuzzy performance-based defuzzification approach [44]. After conducting the simulations, it was found that the resulting rankings are robust, with correlation coefficients between the rankings obtained through the different defuzzification methods exceeding 0.99 in all cases. Second, to test sensitivity to normalization, the original procedures for fuzzy statistical variance and fuzzy CRITIC were subsequently replaced by linear max–min normalization and simple linear normalization [55], respectively, to test the robustness of the prioritization results. The simulation results using these alternative procedures yield correlation coefficients greater than 0.97 in all cases when compared to those obtained with the original normalization techniques. Third, to assess the sensitivity of the results to distance metric selection, the standard TOPSIS implementation using Euclidean distance [59] was compared with an alternative formulation proposed by Tran and Duckstein [60]. The resulting rankings demonstrated remarkable consistency, with correlation coefficients between the rankings obtained using the original TOPSIS implementation and those obtained with the alternative metric across the different weighting methods exceeding 0.99, confirming the robustness of the implementation to this methodological variation. In addition, the ranking of the top performing candidates remained invariant across all tested methodological variations.

4.3. Sensitivity Analysis

To conclude the analysis of the prioritized results obtained through the combination of MCDM methods, it is advisable to perform a sensitivity analysis to evaluate how slight deviations in the calculated weights may affect the ranking of alternatives. Traditionally, such analyses involve a series of simulations in which the weight of the most influential criterion is modified while adjusting the remaining weights proportionally [84]. However, this approach leads to a constrained weight distribution that does not comprehensively explore the space of possible weight combinations. To address this limitation, this study introduces a novel sensitivity analysis technique based on random sampling of weight combinations in the vicinity of a reference weight vector. This sampling is conducted using a Dirichlet distribution centered on the defuzzified average weights of each criterion shown in Table 5.

Although readers interested in the mathematical formulation of the Dirichlet distribution can refer to the specialized literature [85], in essence, the Dirichlet distribution generates the components of the weight vector, $(w_{dir-1},w_{dir-2},\dots ,w_{dir-m})$ according to a set of parameters $({\alpha }_{dir-1},{\alpha }_{dir-2},\dots ,{\alpha }_{dir-m})$. By expressing ${\alpha }_{dir-j}$, where $j\in \left[1,m\right]$, as ${\alpha }_j=k_{dir}{w}_{ref-j}$, a distribution centered around the reference weights $(w_{ref-1},w_{ref-2},\dots ,w_{ref-m})$ with the dispersion controlled by the parameter $k_{dir}$ is obtained.

It should be emphasized that this approach not only ensures that the sampled weight vectors remain focused within the region of interest defined by the reference weights but also guarantees that the sum of the weights in each simulation equals one, maintaining consistency in the decision making framework.

Thus, to conduct a robust sensitivity analysis, different values of the dispersion parameter $k_{dir}$ were evaluated. For each value, a set of 10,000 simulations were performed, generating different weight combinations, around the reference weight vector. The distribution of simulated weights around the reference values for each $k_{dir}$ is shown in

Table 7. Simulation’s random weight distribution parameters for different $k_{dir}$ values.

Criterion	Sim. Parameter	${\mathit{k}}_{\mathit{dir}}=10$	${\mathit{k}}_{\mathit{dir}}=100$	${\mathit{k}}_{\mathit{dir}}=1000$
Capture cost	Ref. Weight	0.1747	0.1747	0.1747
	Full range	[0.0002, 0.7235]	[0.0662, 0.3417]	[0.1353, 0.2242]
	75% range	[0.0540, 0.3162]	[0.1318, 0.2193]	[0.1610, 0.1889]
	Mean % dev.	52.98%	17.30%	5.56%
Synodic Period	Ref. Weight	0.2585	0.2585	0.2585
	Full range	[0.0057, 0.8386]	[0.1137, 0.4514]	[0.2068, 0.3126]
	75% range	[0.1102, 0.4175]	[0.2084, 0.3099]	[0.2427, 0.2740]
	Mean % dev.	41.17%	13.56%	4.23%
Rotation Rate	Ref. Weight	0.2800	0.2800	0.2800
	Full range	[0.0100, 0.8666]	[0.1406, 0.4656]	[0.2322, 0.3434]
	75% range	[0.1248, 0.4449]	[0.2289, 0.3322]	[0.2637, 0.2964]
	Mean % dev.	39.39%	12.85%	4.07%
Orbit det. accuracy	Ref. Weight	0.1179	0.1179	0.1179
	Full range	[0.0000, 0.6909]	[0.0256, 0.2521]	[0.0785, 0.1582]
	75% range	[0.0226, 0.2304]	[0.0820, 0.1557]	[0.1064, 0.1299]
	Mean % dev.	63.90%	21.56%	6.89%
Sim. Candidates	Ref. Weight	0.1689	0.1689	0.1689
	Full range	[0.0008, 0.7177]	[0.0575, 0.3434]	[0.1253, 0.2134]
	75% range	[0.0504, 0.3032]	[0.1263, 0.2123]	[0.1551, 0.1826]
	Mean % dev.	52.71%	17.62%	5.64%

.

In each simulation, the sampled weight vector was combined with the defuzzified decision matrix using a normalized additive weighting model. Based on the outcomes of all simulations for each $k_{dir}$, two metrics were derived: the random sampling average performance and the dominance percentage [86].

The first metric, the random sampling average global performance across the simulations, serves as a validation measure for the rankings produced by the different MCDM method combinations. Candidates exhibiting high average performance values across simulations should correspond to those achieving top rankings in the method evaluations, while low average performance values align with poorly ranked alternatives. Figure 5 presents these results for the various $k_{dir}$ parameter values tested.

The results presented in Figure 5 yield several key observations. First, the trend in random sampling average performance closely aligns with the average results from the proposed MCDM methods, confirming the robustness of the MCDM-derived rankings. Second, the slope of the random sampling average performance curve flattens for lower-ranked asteroids, indicating that the top performing candidates demonstrate markedly superior performance compared to the remainder. Third, as expected, the dispersion parameter $k_{dir}$ shows no significant influence on the random sampling average performance metric.

The second metric, the dominance percentage, quantifies the frequency with which each alternative attained the top ranking position across all simulated scenarios. A higher dominance percentage directly correlates with greater ranking stability for the top performing candidate around the reference weights, indicating stronger robustness to weight variations.

Table 8. Percentage of simulations for 10,000 Dirichlet-sampled weight vectors centered on reference values where top five candidates achieved the highest rank, evaluated for dispersion parameters $k_{dir}$ = 10, 100, and 1000. Larger $k_{dir}$ values indicate tighter sampling distributions around reference weights.

Asteroid	Av. Random Sampling Performance	% Dominance ${\mathit{k}}_{\mathit{dir}}=10$	% Dominance ${\mathit{k}}_{\mathit{dir}}=100$	% Dominance ${\mathit{k}}_{\mathit{dir}}=1000$
2013 NJ	0.671	60.44	89.87	100
2001 EC16	0.640	1.06	0	0
1999 FN19	0.602	29.07	10.13	0
1994 CJ1	0.540	4.85	0	0
2022 BX1	0.512	0	0	0

presents this metric for the five asteroids exhibiting the highest average performance values.

Based on the data presented in Table 8, the following conclusions can be drawn. First, the dispersion parameter $k_{dir}$ has a significant influence on the dominance percentage metric. For small values of $k_{dir}$, there is a certain proportion of weight combinations under which alternatives with a lower random sampling average performance than 2013 NJ are able to dominate the ranking. As expected, as $k_{dir}$ increases, the weights become more concentrated around the reference weights, and dominance tends to converge toward the best performing candidate. However, it is worth noting that the leading position of the candidate 2013 NJ is remarkably stable, as it consistently ranks highest in both average performance and dominance percentage across the different values of $k_{dir}$.

Second, it is noteworthy that asteroids such as 1999 FN19 and 1994 CJ1 exhibit a higher dominance percentage than 2001 EC16, despite receiving a lower overall ranking based on the combined results of the MCDM methods and the random sampling average performance. This phenomenon should not be interpreted as a lack of robustness in the ranking obtained, but rather as an indication that if decision makers were to shift the weight allocation in specific directions, the ranking would change in favor of the candidates with higher dominance percentages.

Thus, although 2001 EC16 shows high overall performance on average, the individual criterion-specific performances of other candidates tend to be stronger, often relegating 2001 EC16 to second place. For instance, if decision makers were to assign greater importance to the capture cost criterion, the ranking would likely be dominated by 1999 FN19. Conversely, if more weight were placed on the number of similar candidates, 1994 CJ1 would tend to dominate, overshadowing 2001 EC16 despite its high global performance. However, when 2013 NJ is removed from the ranking and the dominance percentages are recalculated, 2001 EC16 achieves dominance percentages of 65.81%, 95.39%, and 100% for $k_{dir}$ = 10, 100, and 1000, respectively. This reinforces the idea that the random sampling average performance remains a suitable metric for validating the obtained rankings, while the dominance percentage provides a useful indication of which candidates are most likely to take the top position if deviations from the reference weights occur.

Finally, it is worth noting that an alternative way of selecting $k_{dir}$ involves progressively increasing its value and simulating the resulting rankings until they stabilize, particularly with regard to the top performing candidates. Once such a value is identified, it can be accepted by the analyst if the trade-off between the dominance percentage of the top-ranked alternative and the average percentage variation of the simulated weights is deemed satisfactory. As an example, in this study, all integer values of $k_{dir}$ within the interval [1, 1000] were explored, and it was found that the rankings stabilized from $k_{dir}=40$ onwards. For this value, the variation introduced by the simulations was sufficient, as the mean variation of the simulated criterion weights exceeded the average variation observed among the original weighting methods in all cases and, furthermore, 2013 NJ exhibited an acceptably high dominance (77.67%). Therefore, selecting a $k_{dir}$ value around 40 may be considered acceptable for the purpose of sensitivity analysis in this work.

As an additional robustness check, an alternative sensitivity analysis was performed using normal distributions centered on the mean weight [86], with a standard deviation equal to that observed across the three weighting methods. The results of this analysis were consistent with those obtained in the primary evaluation, further reinforcing the stability of the proposed approach.

In conclusion, the sensitivity analysis applied to this problem indicates not only that the ranking trends produced by the proposed combination of MCDM methodologies are coherent and satisfactory but also that the resulting classification is highly robust with respect to deviations around the calculated weights.

4.4. Limitations and Future Work

To conclude this section, it is important to remark that future work should consider extending the framework as new data become available. For example, a key limitation of this study is that rotation rates are currently known for only 4.46% of candidate asteroids, significantly restricting the final candidate selection. As observational campaigns progressively expand this dataset, the methodological framework presented here could be applied to a larger, more comprehensive pool of potential targets.

Furthermore, future research could enhance this decision making framework by integrating spectral or taxonomic classifications as data coverage improves, or by developing hybrid approaches that combine expert elicitation (subjective weights) with existing objective fuzzy methods.

Although the proposed fuzzy multi-criteria decision making approach provides a robust framework for preliminary asteroid prioritization using established accessibility metrics, we acknowledge that the current model’s scope does not fully capture potential mission design constraints that emerge during a more detailed mission planning [87,88]. Specifically, Earth-departure energy limits ($C_3$), launch-window dynamics, mass-return efficiency and rotation axis orientation were not incorporated into this model. The absence of a launch-window criterion may underestimate the importance of time frame in mission design, while payload mass exclusions could mask important trade-offs between sample return mass and trajectory design. Furthermore, while rotation rate provides a useful preliminary metric, it neglects important factors like spin-axis orientation and libration modes that significantly impact proximity operations’ cost and complexity. These omissions stem from the focus on high-level assessment during the initial screening phase but warrant further investigation to enhance practical applicability. For these reasons, in future work, trajectory simulation tools for launch-window and $C_3$ analysis, as well as the development of a mass-return metric will be implemented to support more detailed operational feasibility assessments. By coupling our systematic MCDM framework with these mission-design considerations, it would be possible to deliver a comprehensive selection tool that bridges theoretical accessibility with practical implementation requirements.

Moreover, it is worth highlighting that the ranking methods used in this study belong to the class of compensatory methods [14]. These methods offer the advantage of being more intuitive, as they combine the performance across different criteria into a single representative index used to produce the final ranking. However, they present certain limitations. Specifically, they do not adequately account for situations where a poor result in one evaluation criterion can be offset by an excellent result in another, which may mask critical weaknesses or generate rankings not so influenced by the criteria with greater weights [44]. Moreover, to generate an aggregated metric that produces a final ranking, these methods require a defuzzification procedure in the final stages to obtain a crisp ranking.

These limitations suggest that future work should explore a comparison between the results obtained using compensatory methods and those derived from the implementation of fuzzy outranking methods such as ELECTRE [89] and PROMETHEE [90], which allow the uncertainty contained in the weights and performance values to be preserved until the final stages of the classification process [91]. Nevertheless, the use of such methods also entails a series of disadvantages. First, the results produced by these approaches are not always conclusive, often requiring additional techniques to derive a complete ranking of the candidates. Second, it is necessary to define a set of preference or veto thresholds for each criterion, which would require expert input and add subjectivity to the decision model. Finally, these methods tend to be less interpretable, due to the complex interactions formulated between the criteria [14].

Finally, the modular design of this MCDM system will allow decision makers and designers to expand and adapt this methodology to support broader aerospace decision making under uncertainty or apply this fuzzy MCDM framework to other NEA mission types (e.g., observation campaign target selection, or complete capture missions) or to different small-body populations (e.g., main-belt asteroids and comets). In addition, this modularity also opens up the opportunity for future works to build upon the results obtained within the proposed framework in order to integrate machine learning-based MCDM methods, enabling the development of classification models capable of predicting the evaluation of new candidates as more asteroid data become available.

5. Conclusions

This study has fulfilled its two main objectives; the first was to analyze in detail potential near-Earth asteroid candidates for a boulder capture mission, and the second was to compare the outcomes obtained through combinations of both classical and innovative fuzzy MCDM techniques. The methodology herein involved the application of three objective fuzzy weighting methods—fuzzy statistical variance, fuzzy CRITIC, and fuzzy MEREC—combined with three fuzzy ranking techniques—fuzzy WASPAS, fuzzy TOPSIS, and fuzzy MARCOS—resulting in nine distinct prioritization schemes applied to a filtered set of 28 NEAs.

The results show a high degree of consistency and robustness across methods. Despite small differences in how each weighting approach quantifies criterion importance, the top-ranked asteroids remain largely stable. NEA 2013 NJ was ranked first in all nine method combinations, while the same four asteroids consistently appeared in the top positions. Correlation analysis between weight sets and rankings confirmed strong coherence, reinforcing the reliability of the framework regardless of the weighting method used. From a mission planning perspective, the results confirm that a structured fuzzy MCDM approach can effectively narrow a large NEA candidate pool to a robust set of priorities, guiding resource allocation and reducing risk.

To further assess robustness, a statistical sensitivity analysis based on random sampling of weight assignments was implemented using a Dirichlet distribution centered on the reference weights. This innovative approach confirmed that the rankings are resilient to plausible variations in criterion importance, providing mission planners with confidence in the prioritization outcome.

Beyond ranking stability, the integration of fuzzy logic has proven essential for addressing parameters with high uncertainty, such as orbit determination accuracy or similarity among asteroid orbits. The use of triangular fuzzy numbers enabled rigorous treatment of imprecise data without compromising methodological transparency.

Moreover, the framework’s modularity allows incorporation of additional criteria such as compositional data or updated observational inputs without altering the core methodology. This flexibility ensures that as new measurements become available or mission requirements evolve, the same decision support structure can be readily adapted.

In summary, this work demonstrates the viability and value of combining classical and novel fuzzy MCDM techniques to support asteroid target selection in the presence of uncertainty. The proposed framework not only narrows down a broad set of potential candidates into a scientifically grounded priority list but also offers insights into the influence of each method and the sensitivity of the decision space.

The results herein support further investigation of the highest-ranked targets—particularly 2013 NJ—for mission design studies and offer a flexible toolset that is adaptable to future data updates or additional mission constraints. This methodology may also be extended to other small-body exploration scenarios, promoting robust, data-informed decision making in aerospace applications.