Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle †
Abstract
1. Introduction
1.1. Previous Work
1.2. Current Concept
2. Vehicle Design
2.1. Propeller Arm Folding/Deployment Mechanism
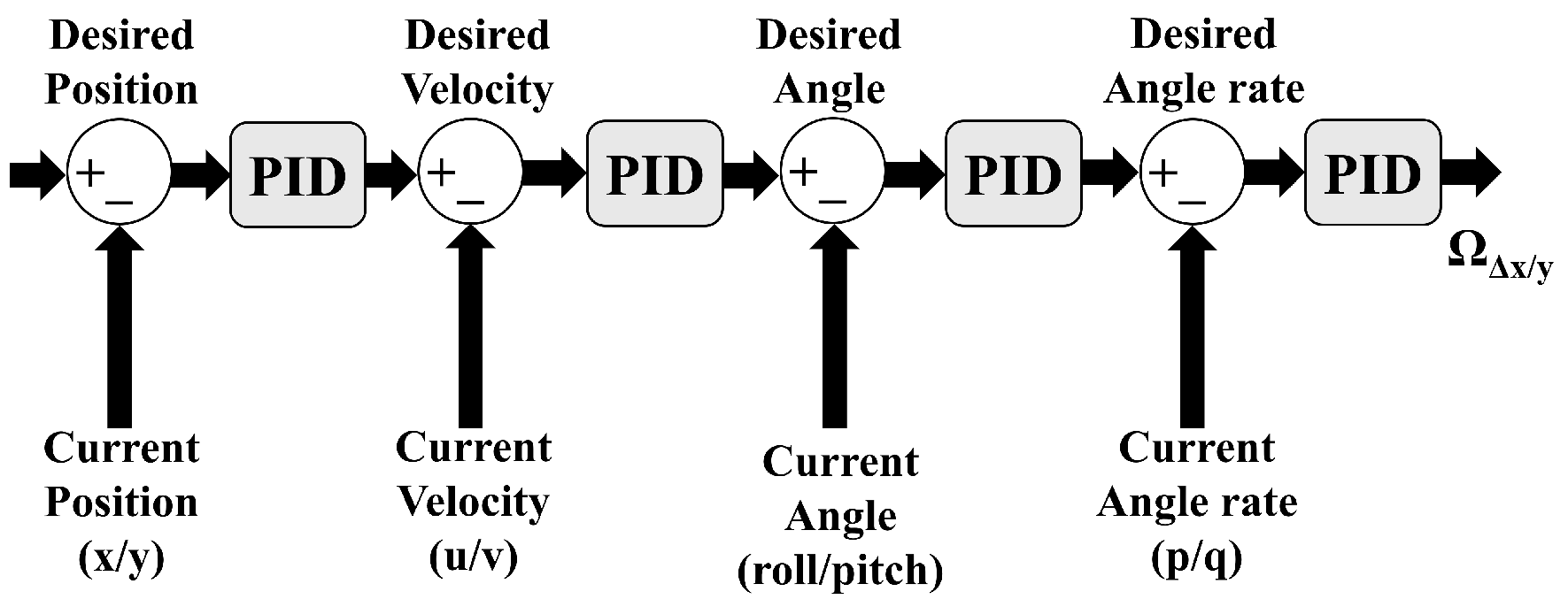
2.2. Control Methodology
3. Testing
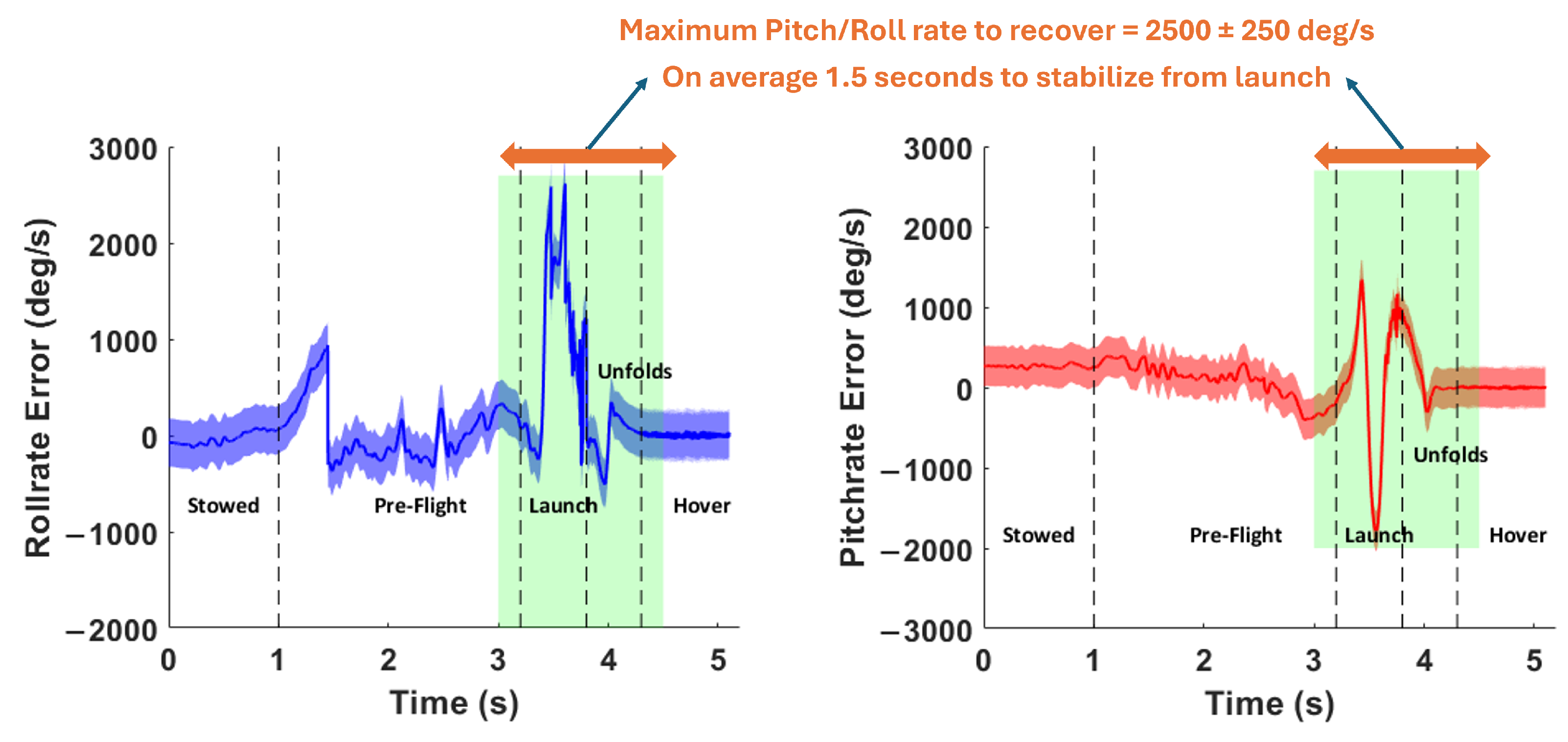
3.1. Proof-of-Concept Testing
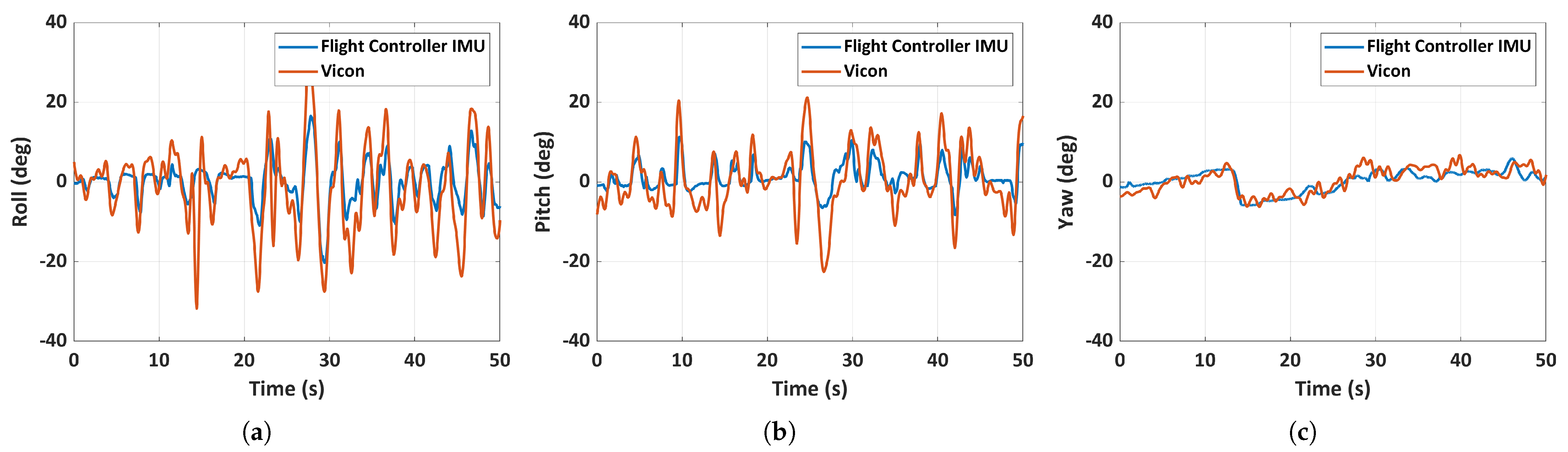
3.2. Flight Testing in Motion Capture System
3.3. Propeller Testing
4. Flight Dynamics Modeling
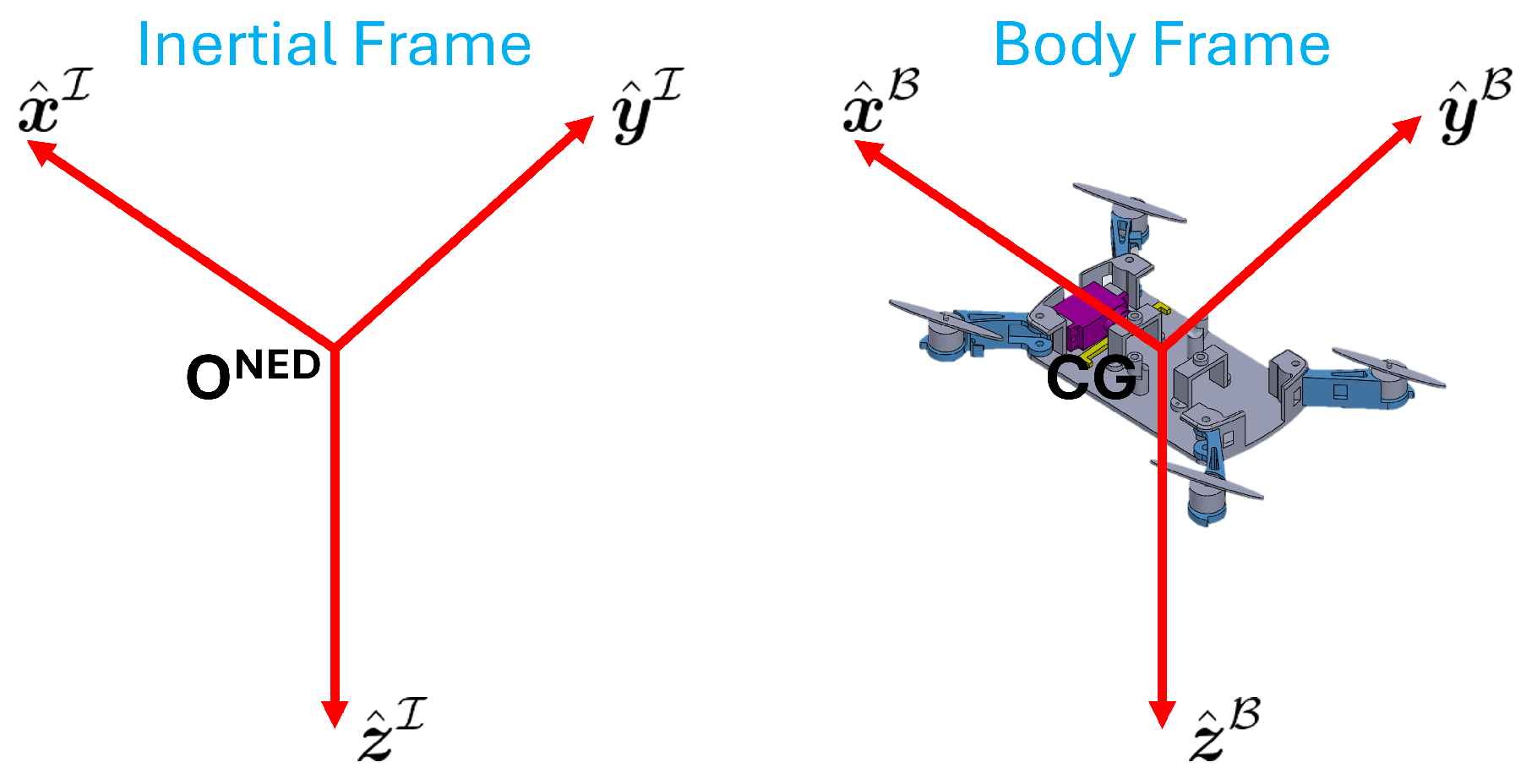
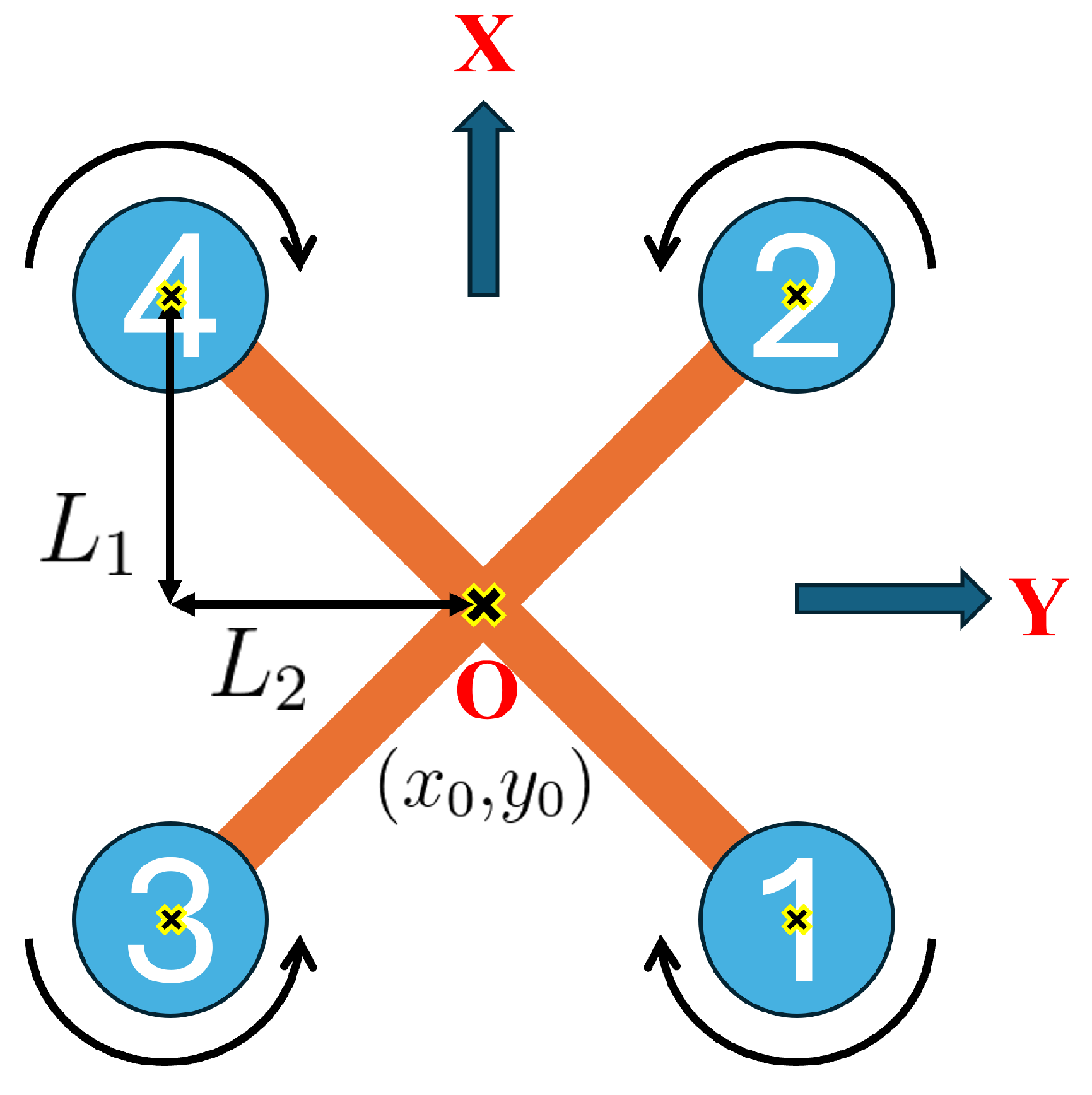
4.1. Equations of Motion
4.2. Aerodynamic Modeling
4.3. Controller Architecture
- : the desired increase in RPM across all motors that facilitates vertical motion along the z-axis.
- : the desired difference in RPM between the motors on either side of the x-axis leads to changes in the roll angle, resulting in lateral motion along the y-direction.
- : the desired difference in RPM between the motors on either side of the y-axis leads to changes in the pitch angle, resulting in longitudinal motion along the x-direction.
- : the desired difference in RPM between the clockwise and counterclockwise motors generates a net torque that rotates the vehicle around the vertical z-axis.
4.3.1. Vertical Motion Controller (Z-Controller)
4.3.2. Lateral Motion Controller (X/Y-Controller)
4.3.3. Heading Controller (Yaw-Controller)
5. Results
5.1. Proof-of-Concept Testing
5.2. Flight Testing in Motion Capture System
5.3. Propeller Testing
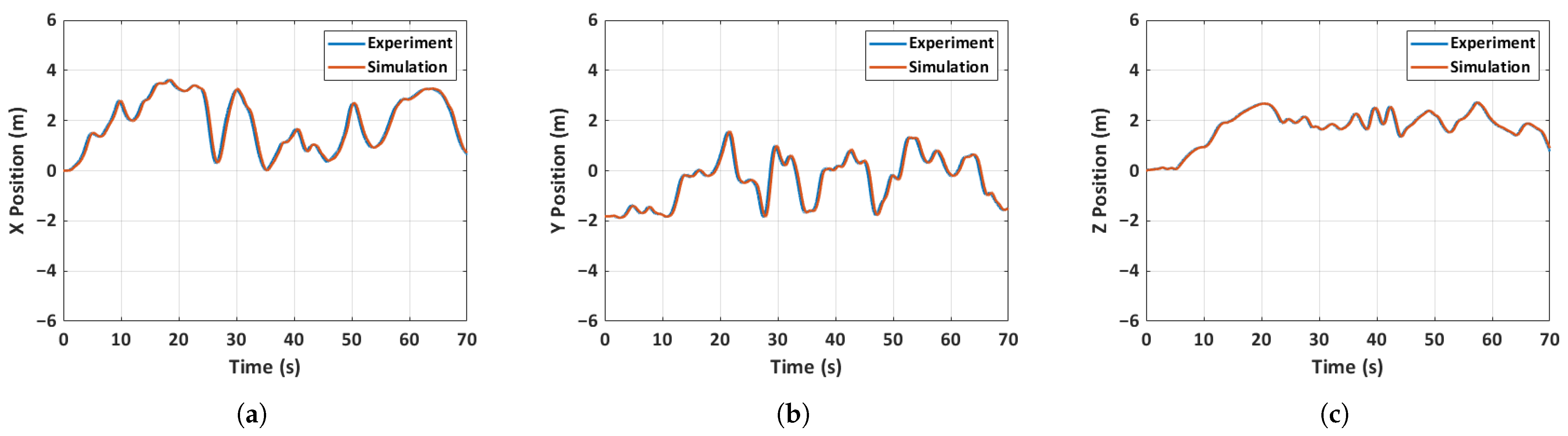
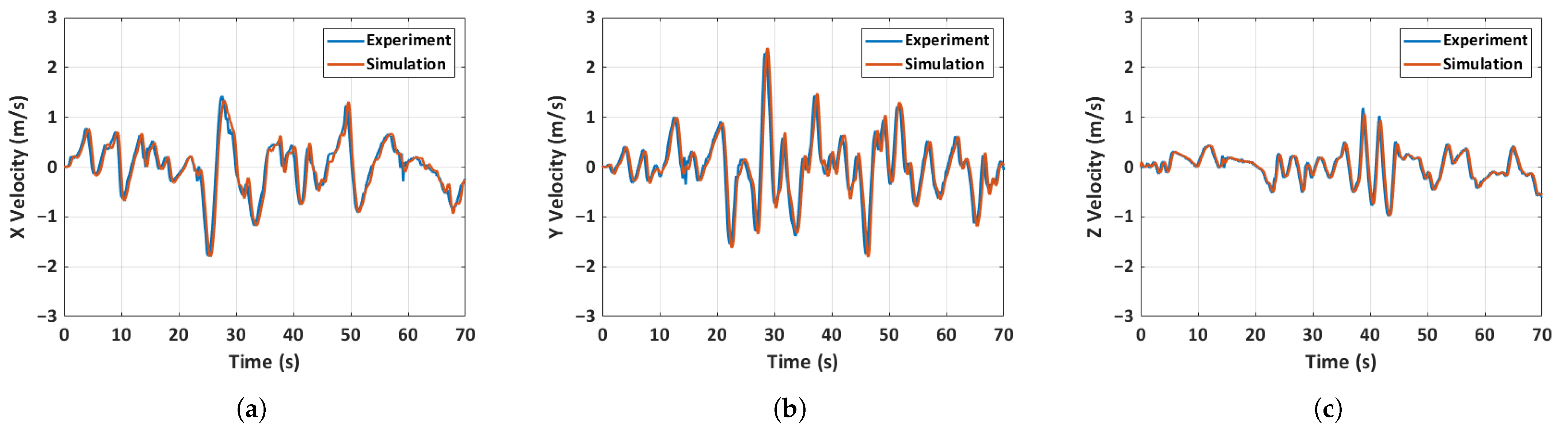
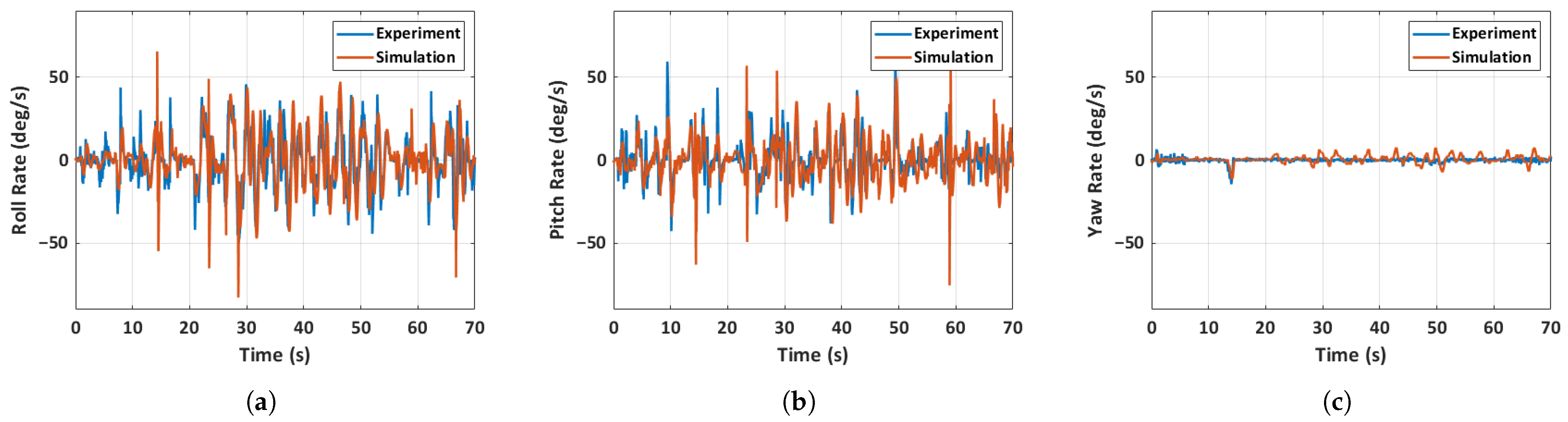
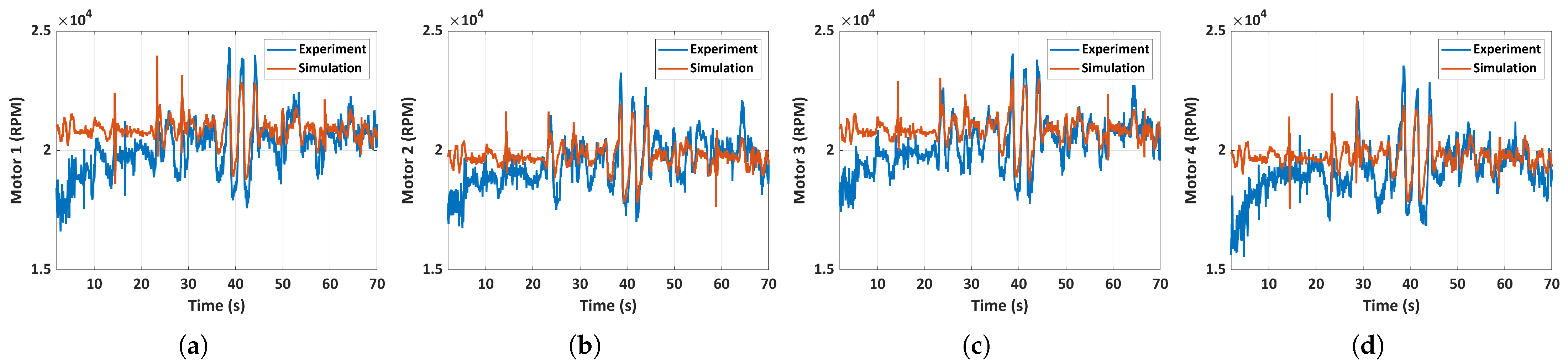
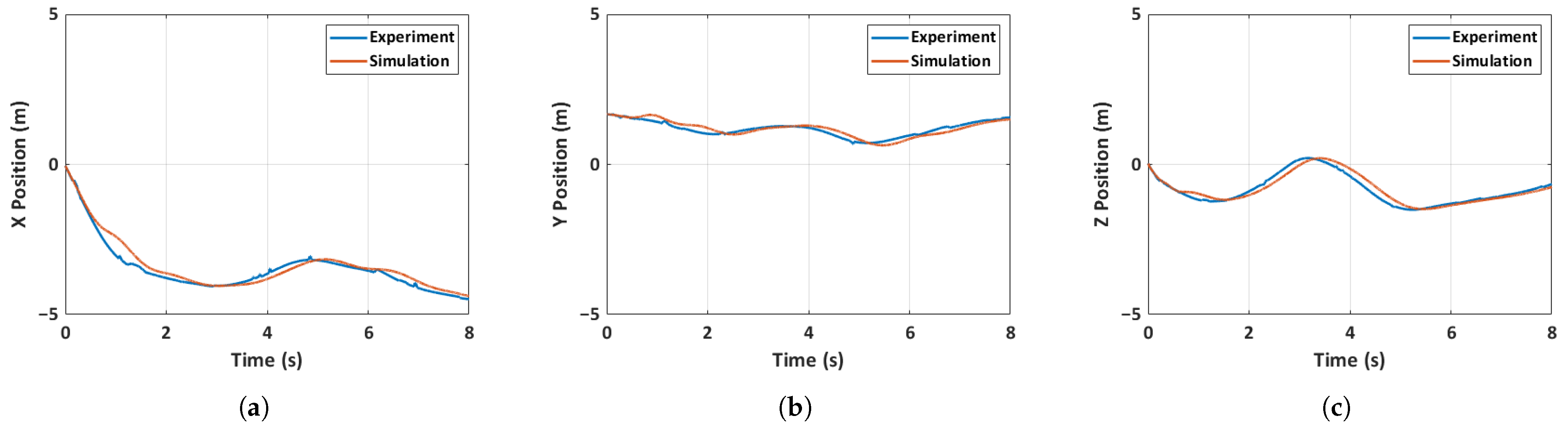
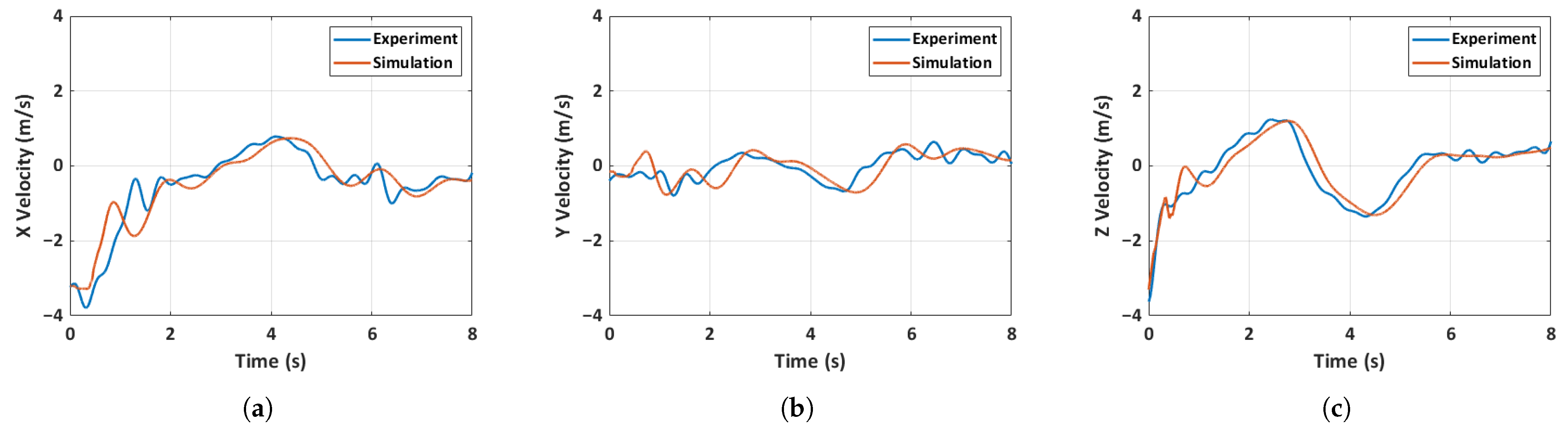
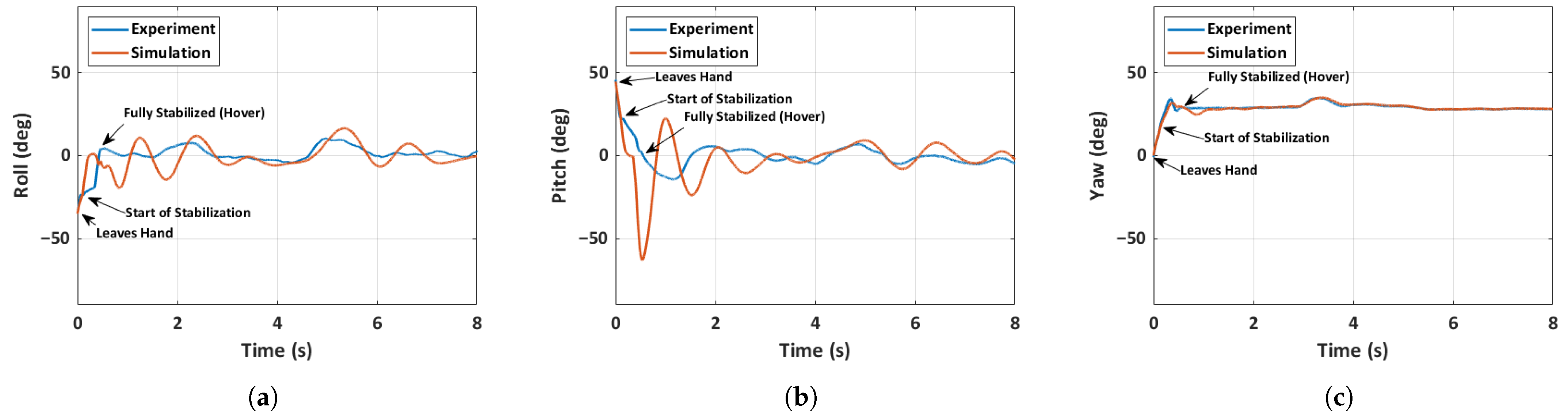
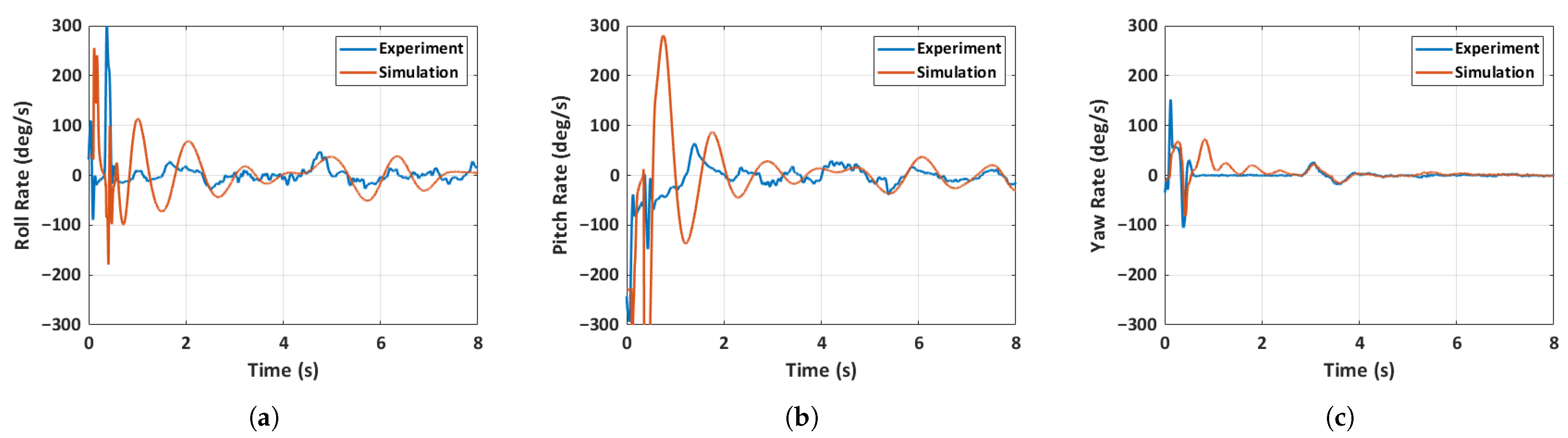
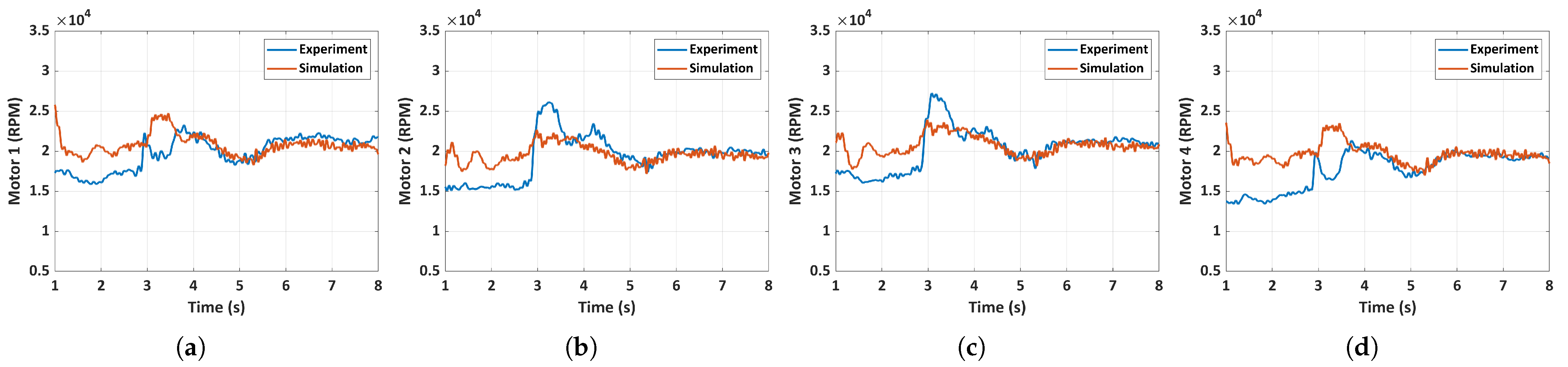
5.4. Flight Dynamics Model Validation
5.4.1. Case 1: General MAV Flight
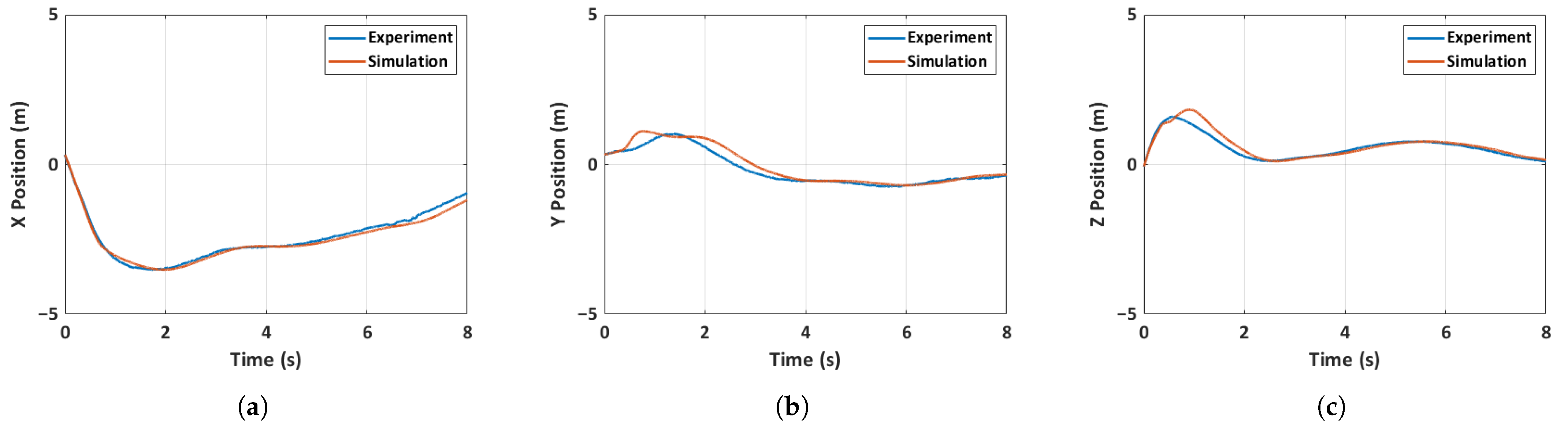
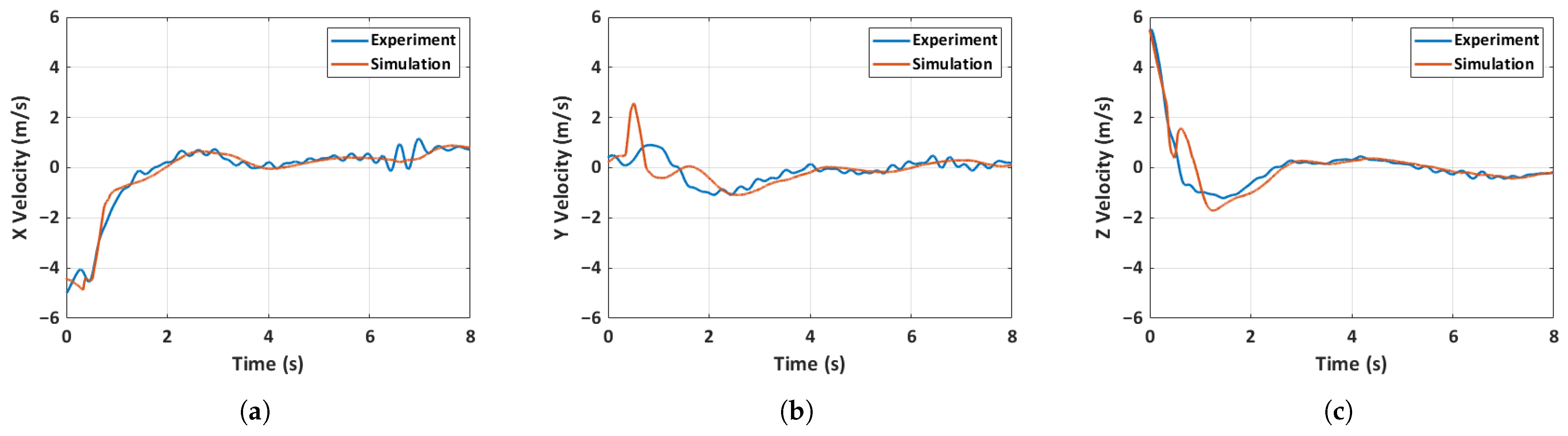
5.4.2. Case 2: Unfolded Hand-Launch
5.4.3. Case 3: Folded Hand-Launch
6. Discussion
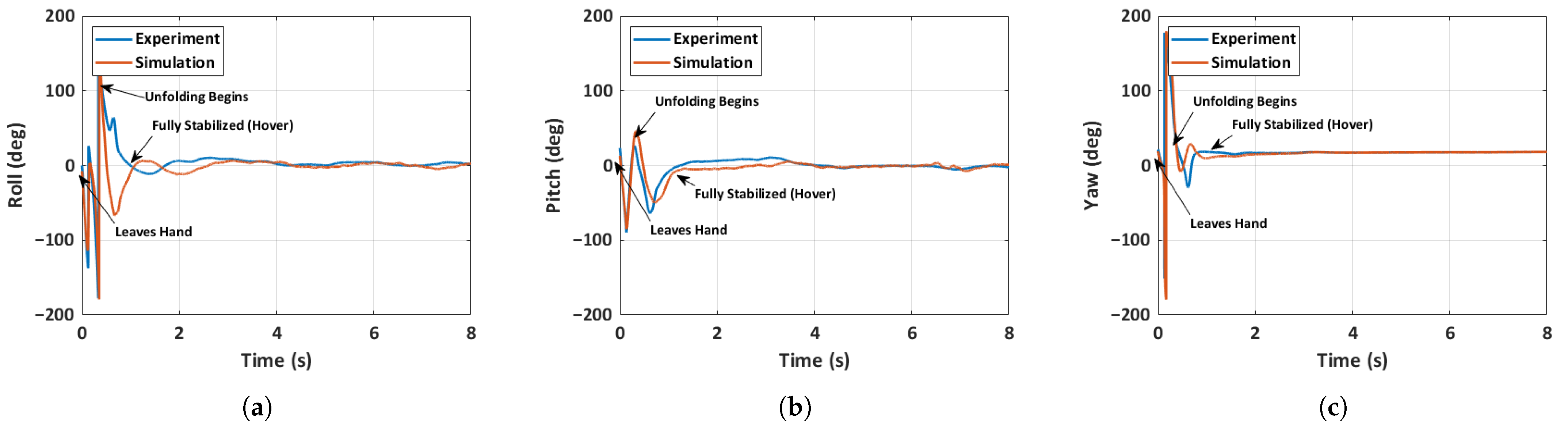
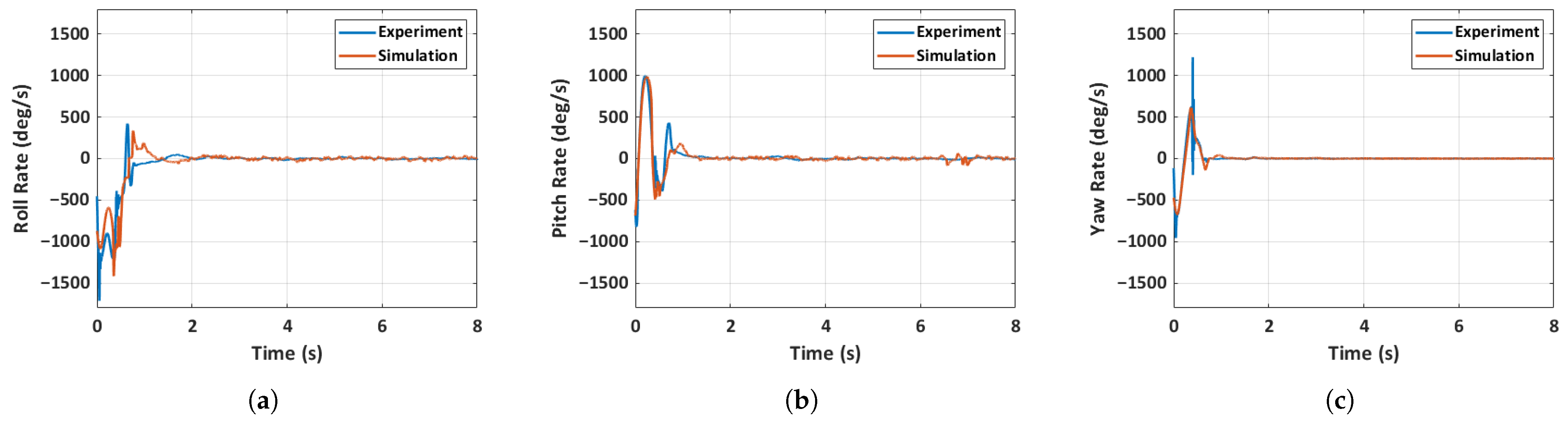
- The locking mechanism designed for the propeller arms exhibited quick unfolding of the propeller arms while in flight. It takes less than 0.05 s to fully unfold the propeller arms. This deployment mechanism can be highly advantageous in emergencies as it does not rely on any standard launch procedure; instead, a simple hand launch suffices.
- The proficiency of the control architecture was demonstrated through numerous indoor and outdoor flight tests. Flight data was collected from the motion capture system and on-board sensors on the flight controller. The analysis reveals that the MAV was able to recover in less than a second even when launched with high linear and angular velocities.
- A 6-DOF simulation model of the quadcopter MAV accurately predicted various aspects of the MAV’s state, including the control inputs. Three distinct flight scenarios, including a general MAV flight, an unfolded throw, and a full hand-launch from a folded position, are simulated and validated. The accuracy of the prediction is heavily dependent on the initial conditions, as evidenced by the results of the general MAV flight scenario, where acquiring initial conditions is relatively straightforward. Despite significant changes in inertia mid-flight due to the deployment of the arms, the simulation predictions remain largely unaffected due to the rapid deployment of the arms and immediate spinning up of the motors.
7. Patents
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| force due to gravity | |
| net forces acting on the MAV | |
| inertias | |
| torque constant | |
| thrust constant | |
| rotor distances from the center | |
| m | mass |
| body frame angular velocities | |
| body frame angular accelerations | |
| Q | torque |
| quaternions | |
| quaternion rates | |
| rotation matrix from body to inertial | |
| rotation matrix from inertial to body | |
| T | thrust |
| body frame velocities | |
| body frame accelerations | |
| inertial positions | |
| inertial velocities | |
| MAV geometric center with respect to C.G | |
| , , | body coordinate frame |
| , , | inertial coordinate frame |
| net moments acting on the MAV | |
| motor RPM | |
| RPM control inputs |
References
- McMichael, J.M.; Francis, M.S. Micro Air Vehicles—Toward a New Dimension in Flight. Unmanned Syst. 1997, 15, 10–15. [Google Scholar]
- Pines, D.J.; Bohorquez, F. Challenges Facing Future Micro-Air-Vehicle Development. J. Aircr. 2006, 43, 290–305. [Google Scholar] [CrossRef]
- Kumar, V.; Michael, N. Opportunities and challenges with autonomous micro aerial vehicles. Int. J. Robot. Res. 2012, 31, 1279–1291. [Google Scholar] [CrossRef]
- Lidor, A.; Weihs, D.; Sher, E. Novel Propulsion Systems for Micro Aerial Vehicles. J. Propuls. Power 2019, 35, 243–267. [Google Scholar] [CrossRef]
- Oleynikova, H.; Lanegger, C.; Taylor, Z.; Pantic, M.; Millane, A.; Siegwart, R.; Nieto, J. An open-source system for vision-based micro-aerial vehicle mapping, planning, and flight in cluttered environments. J. Field Robot. 2020, 37, 642–666. [Google Scholar] [CrossRef]
- Taha, H.; Hajj, M.R.; Nayfeh, A. Flight dynamics and control of flapping-wing MAVs: A review. Nonlinear Dyn. 2012, 70, 907–939. [Google Scholar] [CrossRef]
- Aboelezz, A.; Mohamady, O.; Hassanalian, M.; Elhadidi, B. Nonlinear Flight Dynamics and Control of a Fixed-Wing Micro Air Vehicle: Numerical, System Identification and Experimental Investigations. J. Intell. Robot. Syst. 2021, 101, 64. [Google Scholar] [CrossRef]
- Blösch, M.; Weiss, S.; Scaramuzza, D.; Siegwart, R. Vision based MAV navigation in unknown and unstructured environments. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 21–28. [Google Scholar] [CrossRef]
- Lei, Y.; Wang, H. Aerodynamic Performance of a Quadrotor MAV Considering the Horizontal Wind. IEEE Access 2020, 8, 109421–109428. [Google Scholar] [CrossRef]
- Shyy, W.; Lian, Y.; Tang, J.; Liu, H.; Trizila, P.; Stanford, B.; Bernal, L.; Cesnik, C.; Friedmann, P.; Ifju, P. Computational Aerodynamics of Low Reynolds Number Plunging, Pitching and Flexible Wings for MAV Applications. Acta Mech. Sin. 2008, 24, 351–373. [Google Scholar] [CrossRef]
- Prothin, S.; Escudero, C.F.; Doué, N.; Jardin, T. Aerodynamics of MAV rotors in ground and corner effect. Int. J. Micro Air Veh. 2019, 11, 1756829319861596. [Google Scholar] [CrossRef]
- Benedict, M.; Chopra, I.; Mattaboni, M.; Masarati, P. Aeroelastic Analysis of a MAV-Scale Cycloidal Rotor. In Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010. [Google Scholar]
- Chimakurthi, S.K.; Tang, J.; Palacios, R.; Cesnik, C.E.S.; Shyy, W. Computational Aeroelasticity Framework for Analyzing Flapping Wing Micro Air Vehicles. AIAA J. 2009, 47, 1865–1878. [Google Scholar] [CrossRef][Green Version]
- RQ-11 Raven UAS. Available online: https://perma.cc/P8B3-H4NU (accessed on 15 March 2024).
- Jahner, K. Army Wants Mini-Drones for Its Squads by 2018. Available online: https://perma.cc/4ZAY-S4UU (accessed on 15 March 2024).
- Bouman, A.; Nadan, P.; Anderson, M.; Pastor, D.; Izraelevitz, J.; Burdick, J.; Kennedy, B. Design and Autonomous Stabilization of a Ballistically-Launched Multirotor. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; pp. 8511–8517. [Google Scholar] [CrossRef]
- Denton, H.; Benedict, M.; Kang, H. Design, development, and flight testing of a tube-launched coaxial-rotor based micro air vehicle. Int. J. Micro Air Veh. 2022, 14, 17568293221117189. [Google Scholar] [CrossRef]
- Elliott, C.; Benedict, M. Hand-Launched, Foldable MAV: Proof-of-Concept Flight Test. Uploaded: 20 September 2023. Available online: https://youtu.be/95dgEMVFtIg (accessed on 22 April 2024).
- Elliott, C.; Saj, V.; Denton, H.; Belgum, N.; Benedict, M. Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle. In Proceedings of the Vertical Flight Society 80th Annual Forum & Technology Display, Montreal, QB, Canada, 7–9 May 2004; pp. 1–19. [Google Scholar] [CrossRef]
- Beard, R. Quadrotor Dynamics and Control; Brigham Young University: Provo, UT, USA, 2008; Volume 19. [Google Scholar]
- Saj, V.; Saemi, F.; Kamal, T.; Wang, Y.C.; Sapra, H.; Halder, A.; Benedict, M.; Kokjohn, S.; Mitsingas, C.M. A Model-Based Design Framework for Electric VTOL Aircraft. In Proceedings of the VFS Forum 79, West Palm Beach, FL, USA, 16–18 May 2023. [Google Scholar]
- Schaub, H.; Junkins, J.L. Analytical Mechanics of Space Systems; AIAA: Reston, VA, USA, 2003; pp. 95–110. [Google Scholar]
- Elliott, C.; Benedict, M. Hand-Launched, Foldable MAV: Motion Capture Flight Test. Uploaded: 31 March 2024. Available online: https://youtu.be/X9CWYcDNhu8 (accessed on 22 April 2024).
- Elliott, C.; Benedict, M. Hand-Launched, Foldable MAV: Vicon® Screen Capture of Flight Test. Uploaded: 22 April 2024. Available online: https://youtu.be/Jkjl11dld4A (accessed on 22 April 2024).


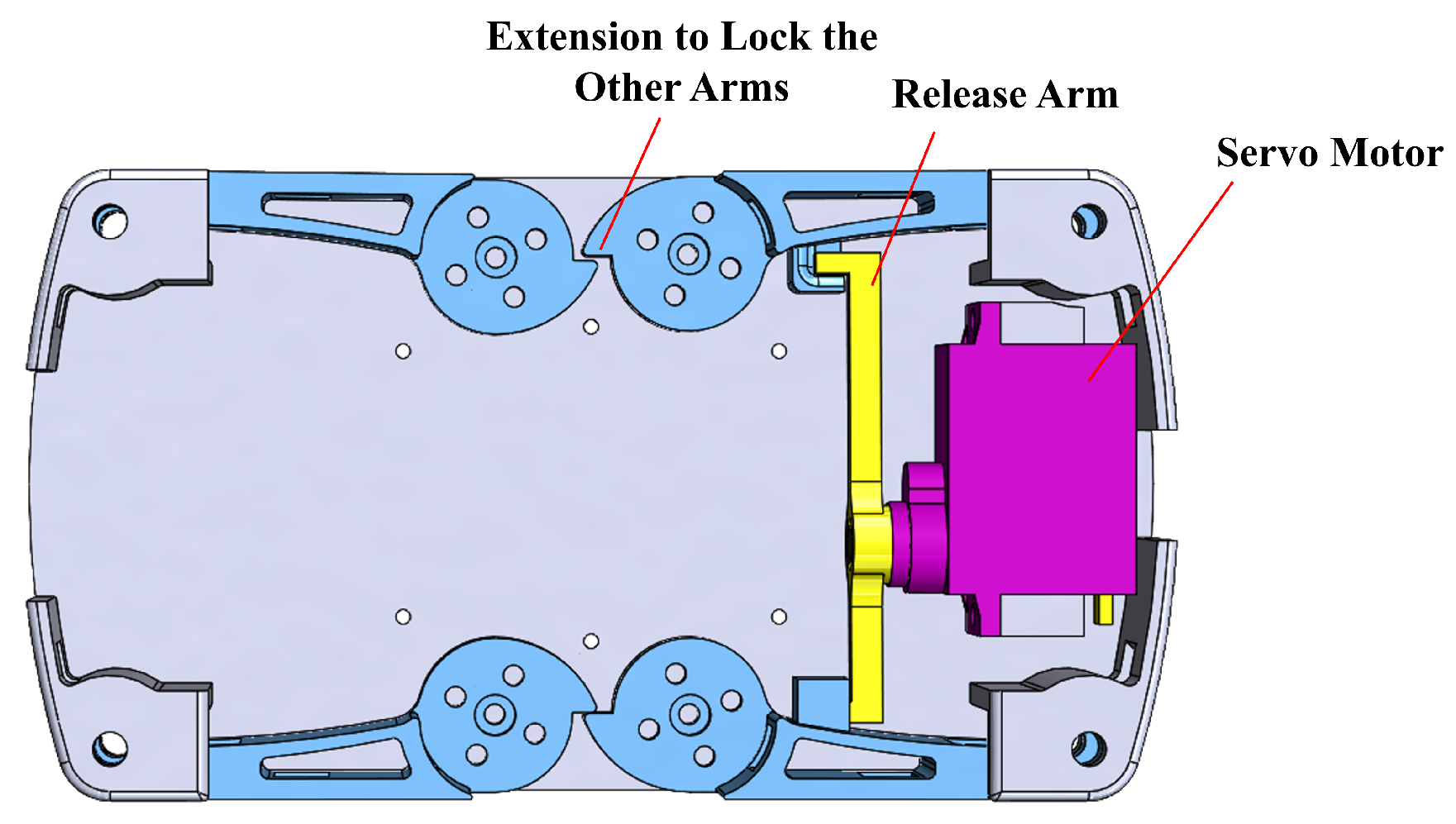
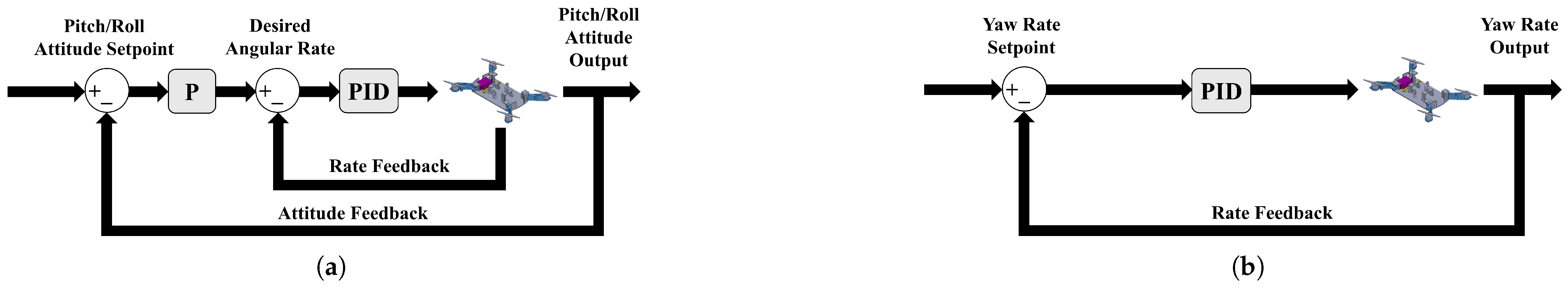











| Components | Mass (g) | % Total |
|---|---|---|
| Propellers | 2.0 | 1.79 |
| Motors | 20.0 | 17.86 |
| Servo Motor | 10.1 | 9.02 |
| Release Arm | 0.5 | 0.45 |
| Propeller Arms | 10.0 | 8.93 |
| Fuselage | 22.9 | 20.45 |
| Flight Controller | 6.6 | 5.89 |
| Battery | 18.2 | 16.25 |
| Receiver | 1.5 | 1.34 |
| Wires and Screws | 15.5 | 13.84 |
| Vicon® Markers | 4.7 | 4.0 |
| Total | 112.0 g | 100.0% |
| P | I | D | |
|---|---|---|---|
| Roll | 45.0 | 60.0 | 20.0 |
| Pitch | 47.0 | 62.0 | 20.0 |
| Yaw | 45.0 | 80.0 | 0.0 |
| Control Loop | Axis | P | I | D |
|---|---|---|---|---|
| Position | X | 3.0 | 0.0 | 0.0 |
| Y | 3.0 | 0.0 | 0.0 | |
| Z | 4.0 | 0.0 | 0.0 | |
| Velocity | VX | 30.0 | 0.0 | 0.0 |
| VY | 30.0 | 0.0 | 0.0 | |
| VZ | 10,000.0 | 3000.0 | 0.0 | |
| Attitude | Roll | 15.0 | 15.0 | 0.0 |
| Pitch | 15.0 | 15.0 | 0.0 | |
| Yaw | 15.0 | 15.0 | 1.0 | |
| Attitude Rate | Roll | 100.0 | 100.0 | 0.0 |
| Pitch | 200.0 | 200.0 | 0.0 | |
| Yaw | 500.0 | 500.0 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elliott, C.; Saj, V.; Denton, H.; Benedict, M. Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle. Aerospace 2025, 12, 754. https://doi.org/10.3390/aerospace12090754
Elliott C, Saj V, Denton H, Benedict M. Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle. Aerospace. 2025; 12(9):754. https://doi.org/10.3390/aerospace12090754
Chicago/Turabian StyleElliott, Connor, Vishnu Saj, Hunter Denton, and Moble Benedict. 2025. "Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle" Aerospace 12, no. 9: 754. https://doi.org/10.3390/aerospace12090754
APA StyleElliott, C., Saj, V., Denton, H., & Benedict, M. (2025). Design and Flight Dynamics of a Hand-Launched Foldable Micro Air Vehicle. Aerospace, 12(9), 754. https://doi.org/10.3390/aerospace12090754







