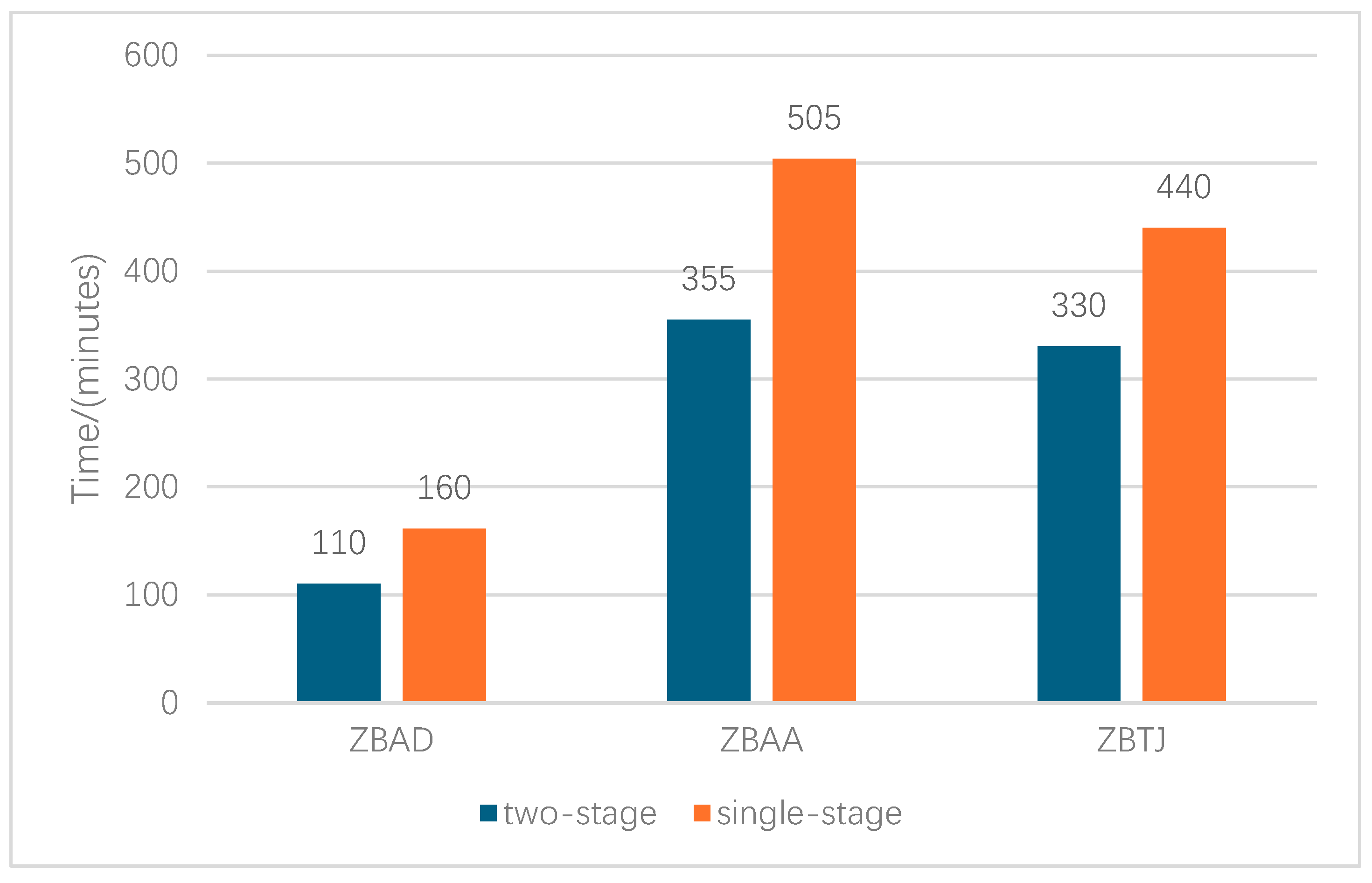Two-Stage Robust Optimization for Collaborative Flight Slot in Airport Group Under Capacity Uncertainty

Abstract

Airport congestion in metropolitan clusters (Metroplex systems) poses significant challenges, particularly when capacity reductions occur due to adverse weather conditions. This study introduces a two-stage robust optimization model aimed at improving the robustness of flight slot allocation in multi-airport systems under such uncertainties. In the first stage, the model minimizes deviations from requested slots while respecting airport and waypoint capacities, turnaround times, and adjustment limits. The second stage dynamically adjusts slot allocations to minimize worst-case displacement costs under potential capacity constraints, ensuring robustness against disruptions. The model is validated using real data from the Beijing–Tianjin–Hebei Metroplex, which includes 468 peak-hour flights. The results demonstrate the model’s effectiveness in eliminating demand–capacity violations, particularly at critical airports such as Beijing Daxing, where initial peak demand exceeded capacity by 36.2%. Post-optimization, the model ensures dynamic capacity adherence and adaptive resource allocation, with varying adjustment intensities across airports (12.7% at Beijing Capital, 28.4% at Daxing, and 39.0% at Tianjin Binhai). Compared to a single-stage robust optimization approach, the two-stage model reduces worst-case displacement by 28.2%, highlighting its superior adaptability. This computationally efficient framework, solved via Gurobi 12.0.2/Python 3.11.9, enhances operational robustness through integrated waypoint modeling and a two-stage decision architecture.

1. Introduction

Air traffic management in multi-airport systems, particularly in densely populated regions like the Beijing–Tianjin–Hebei (BTH) cluster in China, has become increasingly complex. The BTH region is a critical hub in China’s civil aviation industry, comprising major airports, such as Beijing Capital (ZBAA), Beijing Daxing (ZBAD), Tianjin Binhai (ZBTJ), and Shijiazhuang Zhengding (ZBSJ). These airports serve a high volume of both domestic and international traffic. However, rapid growth has led to significant challenges in airspace congestion, resource allocation, and scheduling conflicts, especially during peak traffic periods [1].

The interconnected nature of these airports exacerbates operational interdependencies, with simultaneous demand surges overwhelming runway, waypoint, and airspace capacity. Traditional slot allocation methods, based on fixed priority rules or static fairness principles, fail to address the dynamic and complex nature of these challenges [2,3,4,5,6]. Therefore, there is a need for more adaptive, flexible, and efficient slot allocation methods that can respond to real-time traffic fluctuations and resource constraints.

To address these challenges, in this study, we propose a two-stage robust optimization model designed to optimize flight slot allocation in the face of uncertainty and disruptions across a multi-airport system. In the first stage, the model focuses on strategic planning by pre-allocating flight slots to minimize nominal displacement costs during ideal conditions. The second stage introduces a tactical adjustment phase that dynamically reallocates slots in response to real-time disruptions, such as adverse weather or unexpected traffic congestion, to minimize worst-case delays and system inefficiencies.

The model incorporates a variety of operational constraints, including airport and waypoint capacity limits, aircraft turnaround requirements, and maximum permissible slot adjustments. A key feature of the model is its ability to integrate dynamic weather-induced capacity decay and optimize resource allocation across the system. This makes the model especially suited to real-world applications in complex, high-demand airport clusters such as the BTH region, where uncertainty is a constant operational challenge.

To validate the proposed model, we conduct a case study of the BTH cluster using a real-world flight schedule and airspace data from November 2021. The results demonstrate that the proposed two-stage robust optimization model outperforms conventional methods by reducing schedule displacement and improving the equity and efficiency of flight slot assignments. A comprehensive comparison with a single-stage robust optimization model further underscores the benefits of our two-stage approach in handling uncertain and fluctuating operational conditions.

The remainder of this paper is structured as follows: Section 2 discusses previous related work and describes the contributions of this study. Section 3 outlines the problem formulation, including mathematical definitions of the model, decision variables, and constraints. Section 4 presents the case study setup, data sources, and model validation methodology and discusses the computational results, including comparisons with baseline methods and sensitivity analysis. Finally, Section 5 concludes this study and provides suggestions for future research directions.

2. Literature Review

Research on airport slot allocation has increasingly focused on improving efficiency, fairness, and adaptability in the face of uncertainty. Earlier studies primarily addressed optimization for individual airports [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30], but more recent works have shifted toward multi-airport systems and dynamic models that can adapt to real-time disruptions [31,32,33,34,35,36]. This section reviews key developments in the following areas: efficiency in slot scheduling, fairness in allocation, adaptability under uncertainty, and multi-airport cluster management.

2.1. Efficiency in Slot Scheduling

Optimizing the efficiency of slot allocation has been a primary focus in the literature. Traditional approaches, such as those proposed by Zografos et al. [7,8,9,10], have employed mathematical programming to minimize the gap between requested and allocated slots, leading to enhanced throughput and reduced delays. In a similar vein, Yang et al. introduced a genetic algorithm (GA) with neighborhood search techniques to address single-airport allocation, demonstrating that time-adjustment GAs can provide robust solutions under fluctuating capacities [11]. Furthermore, Zeng et al. proposed a bi-objective model for hub airports, balancing the minimization of delay propagation and maximization of fairness, achieving a significant reduction in average departure delays from 23 min to 3 min [12].

Other algorithms, such as hybrid heuristics and large neighborhood search (LNS), have also been explored to improve computational efficiency in congested airports while preserving solution quality. However, these studies generally assume static capacities and treat the scheduling problem as a localized issue. As airport networks become more interdependent, addressing system-wide inefficiencies and inter-terminal congestion requires models capable of network-level optimization.

2.2. Fairness in Slot Allocation

Fairness in airport slot allocation has garnered increased attention, particularly as air traffic management becomes more competitive. Several studies have sought to incorporate equity constraints into slot allocation models, with a focus on balancing the interests of various stakeholders, including airlines, airports, and air traffic control [13,14,15,16,17,18,19]. For example, Jacquillat and Ribeiro proposed equity-aware optimization frameworks that improve stakeholder satisfaction while maintaining operational efficiency. Their frameworks prioritize fairness without sacrificing operational goals, offering a more balanced approach compared to traditional models [13].

Souza et al. extended the top trading cycles (TTC) mechanism to collaborative decision making (CDM), incorporating preferences from airlines, air traffic controllers (ATC), and airport managers [17]. This multi-stakeholder approach reduces unilateral reallocations by 20% in case studies, though it assumes full preference transparency. This approach aligns with the equity-aware frameworks of Jacquillat and Ribeiro but adds a layer of complexity by considering the bargaining dynamics between stakeholders. Despite these advancements, many fairness-oriented models still employ static thresholds, limiting their adaptability to changing traffic demand and operational context. Dynamic fairness mechanisms remain an active area of research.

2.3. Flexibility and Robustness Under Operational Uncertainty

Given the inherent uncertainty in air traffic operations, several studies have focused on developing robust optimization models to account for variability in demand, capacity, and disruptions [20,21,22,23,24,25,26,27,28,29,30]. Researchers such as Zeng et al. have introduced predictive scheduling models based on historical data to account for delay patterns and ensure stable operations under fluctuating conditions [24]. Meanwhile, Cheung and Wang applied stochastic and robust programming techniques to develop models that adapt to uncertain schedules and changing weather conditions [25,31]. Other studies, Ng et al. and Lui et al., have advanced robust approaches for dynamic airspace configuration and delay management under uncertainty [21,29].

Despite these advances, most existing models overlook multi-airport interactions and fix trade-offs between efficiency and robustness. A key challenge lies in developing models that can simultaneously optimize operational efficiency while maintaining a high degree of flexibility in response to uncertainty. Existing frameworks typically assume static conditions or make oversimplified assumptions about system-wide impacts during disruptions.

2.4. Cluster-Level and Network-Oriented Slot Allocation

A growing body of literature has shifted its focus from single-airport models to multi-airport networks, recognizing the interdependencies among airports that share airspace and routing infrastructure. Corolli and Zhang proposed two-stage and stochastic programming models to optimize scheduling across interconnected airports, capturing the complex interactions that influence air traffic management [20,28]. Similarly, Zografos developed tri-objective models to jointly optimize efficiency, fairness, and displacement metrics across multi-airport systems, although these models typically rely on fixed input parameters and limited real-time adaptability [27].

Other studies, such as those by Wang et al., have focused on minimizing cascading delays by coordinating schedules across multiple terminals. Hybrid algorithms and network-based simulations have been shown to reduce total delays by 30–40% in case studies [33]. However, these models generally do not integrate real-time data or adaptive controls, highlighting the need for more flexible and dynamic approaches that can respond to the challenges posed by real-time traffic fluctuations.

3. Methodology

3.1. Problem Description

Air traffic congestion in the BTH region results from the shared use of finite airspace resources, particularly waypoints that serve as key bottlenecks during peak flight periods. Uncertainties in operational capacity, such as those caused by adverse weather, can propagate delays across multiple airports, exacerbating system inefficiencies and complicating air traffic management. This study formulates the slot allocation problem as a two-stage robust optimization model and aims to address uncertainties in flight slot allocation. Unlike traditional single-stage approaches, our model enhances operational flexibility by incorporating both a strategic planning phase and a tactical adjustment phase.

3.2. Two-Stage Robust Modeling Framework

This study introduces a two-stage robust optimization framework for flight slot allocation in a multi-airport system, accounting for shared airspace resources like waypoints. The goal is to minimize congestion, optimize flow efficiency, and ensure feasibility under uncertain operational conditions.

(i) Stage I—Strategic planning

In this stage, flight slots are pre-allocated based on the requested times, capacities of airports and waypoints, and required minimum turnaround times. No probabilistic assumptions are made about disruptions, and the objective is to minimize the total nominal displacement cost over a 24 h period, which is discretized into 288 5-min intervals. The formula is as follows:

$$\mathrm{T}=\{\mathrm{0,1},\dots ,287\}$$

(ii) Stage I—Tactical adjustment

Once disruptions (e.g., adverse weather) occur, slot assignments are adjusted to account for these real-time changes. The objective of this phase is to hedge against worst-case scenarios by minimizing the maximum delay displacement across all possible disruption scenarios. This ensures that the system remains robust under uncertain conditions.

3.3. Parameter Definitions

Table 1. Model parameters.

Symbol	Description
$F$	Set of flights, $f\in F$
$D$	Set of departure airports, $d\in D$
$A$	Set of arrival airports, $a\in A$
$T$	Set of time slots $t$, $t\in T$
$K$	Set of capacity measurement periods, $k\in K$
$U$	$\mathrm{S}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{w}\mathrm{a}\mathrm{y} \mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s},u_i\in U$
$E_d$	$\mathrm{S}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{s} \mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{f}\mathrm{r}\mathrm{o}\mathrm{m} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} d$
$F_a$	$\mathrm{S}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{s} \mathrm{a}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{i}\mathrm{n}\mathrm{g} \mathrm{a}\mathrm{t} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} a$
$S$	$\mathrm{S}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{o}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{s},\mathrm{s}\in \mathrm{S}$
$\Omega$	$\mathrm{S}\mathrm{e}\mathrm{t} \mathrm{o}\mathrm{f} \mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t} \mathrm{p}\mathrm{i}\mathrm{a}\mathrm{r}\mathrm{s} \left(f^{\prime }, f\right) \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d} \mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}$
$l_{f^{\prime }f}$	$\mathrm{M}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{u}\mathrm{m} \mathrm{t}\mathrm{u}\mathrm{r}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d} \mathrm{t}\mathrm{i}\mathrm{m}\mathrm{e} \mathrm{b}\mathrm{e}\mathrm{t}\mathrm{w}\mathrm{e}\mathrm{e}\mathrm{n} \mathrm{f}\mathrm{l}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{s} \left(f^{\prime }, f\right)\in \Omega$
$t_f^d$	Requested time slot for departure flight $f$
$t_f^a$	Requested time slot for arrival flight $f$
${NC}_d^k$	$\mathrm{N}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} d \mathrm{i}\mathrm{n} \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d} k$
$N{C}_a^k$	$\mathrm{N}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{a}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{l} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} a \mathrm{i}\mathrm{n} \mathrm{p}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{d} k$
$C_{dk}^s$	$\mathrm{C}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{e} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} d \mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r} \mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{o} s$
$C_{ak}^s$	$\mathrm{C}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{a}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{v}\mathrm{a}\mathrm{l} \mathrm{a}\mathrm{i}\mathrm{r}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t} a \mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r} \mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{o} s$
$C_{u_i}^k$	$\mathrm{N}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l} \mathrm{c}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{w}\mathrm{a}\mathrm{y} \mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t} u_i in period k$
$C_{k{u}_i}^s$	$\mathrm{C}\mathrm{a}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{t}\mathrm{y} \mathrm{o}\mathrm{f} \mathrm{w}\mathrm{a}\mathrm{y} \mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t} u_i \mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r} \mathrm{s}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{a}\mathrm{r}\mathrm{i}\mathrm{o} \mathrm{s}$
$n_s$	Number of slots per day
$t_{f_d}^{u_i}$	Time taken by outbound flight from airport to waypoint
$t_{f_a}^{u_i}$	Time taken by inbound flight from waypoint to airport

defines the key parameters used in the model.

3.4. Strategic Phase Model

3.4.1. Decision Variables

$$x_f^t=1 \mathrm{if} \mathrm{flight} f \mathrm{departs} \mathrm{at} \mathrm{time} t, 0 \text{otherwise.}$$

$$y_f^t=1 \mathrm{if} \mathrm{flight} f \mathrm{arrives} \mathrm{at} \mathrm{time} t, 0 \text{otherwise.}$$

3.4.2. Objective Function

The objective of the strategic phase is to minimize the total displacement cost, which is defined as the sum of the displacement of departure and arrival times from their requested times:

$$\mathit{min} \sum _{f\in F}\sum _{t\in T}\left(\left|t-t_f^d\right|\cdot x_f^t+\left|t-t_f^a\right|\cdot y_f^t\right)$$

(1)

To linearize the absolute value, we introduce auxiliary variables $z_f^{t+}$ and $z_f^{t-}$ for positive and negative deviations:

$$\left|t-t_f\right| = z_f^{t+}+z_f^{t-}$$

(2)

where $z_f^{t+}$ ≥ 0 measures tardiness, and $z_f^{t-}$ ≥ 0 measures earliness.

3.4.3. Constraints

(i) Slot uniqueness

Each flight can only be assigned one departure and one arrival slot:

$$\sum _{t\in T}{x}_f^t=1,\forall f\in F$$

(3)

$$\sum _{t\in T}{y}_f^t=1,\forall f\in F$$

(4)

(ii) Minimum turnaround time

The turnaround time between consecutive flights $f$ and $f\prime$ must be at least $l_{f{f}^{\prime }}$:

$$\sum _{t\in T}t\cdot \left(x_{f^{\prime }}^t-y_f^t\right)\ge l_{f{f}^{\prime }},\forall (f,f^{\prime })\in \Omega$$

(5)

(iii) Airport capacity constraints

The total number of flights departing from an airport d or arriving at an airport a at any given time t cannot exceed the airport’s capacity:

$$\sum _{f\in {\mathrm{E}}_d}\sum _{t\in k}{x}_f^t\le N{C}_{dk},\forall d\in D,k\in K$$

(6)

$$\sum _{f\in {\mathrm{F}}_a}\sum _{t\in k}{y}_f^t\le N{C}_{ak},\forall a\in A,k\in K$$

(7)

(iv) Maximum displacement constraints

A flight must not deviate more than 1 h from its original requested departure time:

$$\sum _{t = t_f}^{t_f+12}{x}_f^t = 1,\forall f\in F$$

(8)

(v) Waypoint capacity constraints

The number of flights passing through any waypoint must not exceed its nominal capacity:

$$\sum _{f\in F}\sum _{t\in T}{x}_f^{t+t_{f_d}^{ui}}\le C_{{ku}_i},\forall d\in D,u_i\in U$$

(9)

$$\sum _{f\in F}\sum _{t\in T}{x}_f^{t-t_{f_a}^{ui}}\le C_{{ku}_i},\forall a\in A,u_i\in U$$

(10)

3.5. Tactical Phase Model

3.5.1. Decision Variables

$$u_{fs}^t=1 \mathrm{if} \mathrm{flight} f \mathrm{departs} \mathrm{at} \mathrm{time} t \mathrm{under} \mathrm{scenario} s, 0 \text{otherwise.}$$

$$v_{fs}^t=1 \mathrm{if} \mathrm{flight} f \mathrm{arrives} \mathrm{at} \mathrm{time} t \mathrm{under} \mathrm{scenario} s, 0 \text{otherwise.}$$

3.5.2. Objective Function

The objective of the tactical phase is to minimize the worst-case adjusted displacement across all disruption scenarios, defined as:

$${min}_{(u,v)}\left\{\underset{s\in S}{max}{Q}_s\right\},Q_s = \sum _{f\in F}\sum _{t\in T}\left(\left|u_{fs}^t-x_f^t\right|\cdot t+\left|v_{fs}^t-y_f^t\right|\cdot t\right)$$

(11)

The min–max objective is linearized by introducing auxiliary variable $\eta$ and constraints:

$${min}_{(u,v,\eta )}\left\{\eta \right\}$$

(12)

Subject to:

$$\eta \ge Q_s,{ \forall s\in S, Q}_s = \sum _{f\in F}\sum _{t\in T}\left(\left|u_{fs}^t-x_f^t\right|\cdot t+\left|v_{fs}^t-y_f^t\right|\cdot t\right)$$

3.5.3. Constraints

(i) Slot uniqueness (scenario-specific)

Each flight in each scenario must also be assigned one departure and one arrival slot:

$$\sum _{t\in T}{u}_{fs}^t=1,\forall f\in F,s\in S$$

(13)

$$\sum _{t\in T}{v}_{fs}^t=1,\forall f\in F,s\in S$$

(14)

(ii) Minimum turnaround time (scenario-specific)

The turnaround time between flights $f$ and $f\prime$ in each scenario must also adhere to the same minimum constraints:

$$\sum _{t\in T}t\cdot \left(u_{fs}^t-v_{f^{\prime }s}^t\right)\ge l_{f{f}^{\prime }},\forall (f,f^{\prime })\in \Omega ,s\in S$$

(15)

(iii) Scenario-dependent airport and waypoint capacity constraints

Constraints (6)–(10) are updated to reflect $C_{dk}^s$, $C_{ak}^s$, $C_{k{u}_i}^s$ under each scenario, ensuring the system adapts to potential disruptions.

(iv) No Early Departures

A flight must not deviate more than 1 h from its original requested departure time:

$$\sum _{t\in T}t\cdot \left(u_{fs}^t-x_f^t\right)\ge 0,\forall f\in F,s\in S$$

(16)

This ensures that tactical adjustments do not contradict the strategic schedule by scheduling flights earlier than planned.

This two-stage robust optimization model offers a structured and computationally efficient approach to real-time slot reallocation under uncertainty. By integrating strategic displacement minimization with tactical scenario-based adjustments, the model robustly addresses delay propagation across complex airport networks while respecting dynamic capacity constraints at both airports and waypoints.

4. Computational Experiments

4.1. Data Processing and Selection

4.1.1. Flight Schedule Data Collection

Flight data from 17 November 2021 were selected despite occurring during the COVID-19 pandemic period. This date represents a typical operational weekday during the 2021 winter–spring season with flight volumes comparable to pre-pandemic levels in the BTH cluster. Crucially, the structural interdependencies, capacity constraints, and weather patterns relevant to the model validation remain consistent. Post-pandemic traffic recovery has further validated the persistence of these peak congestion dynamics.

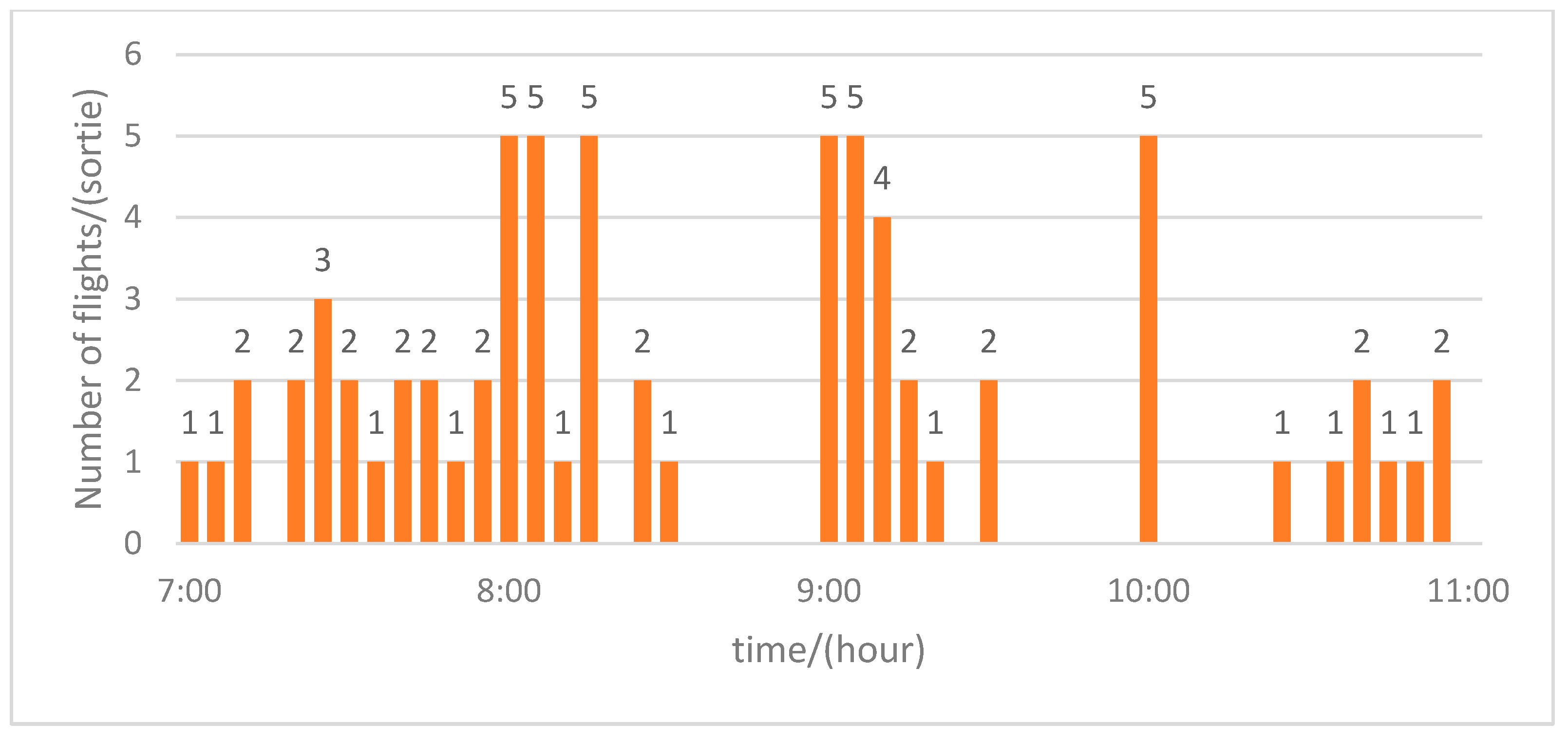
The data were collected from the Advance Flight Planning Management System (AFPMS) for four major airports in the BTH cluster. Flight counts for departures were aggregated by hour, providing insight into the temporal distribution and traffic patterns across these airports. Figure 1 highlights the significant fluctuations in flight activity observed, a key congestion window, and serves as the foundation for our model validation and subsequent analysis.

Notably, ZBSJ, located on the periphery of the BTH cluster, operates with distinct temporal patterns and experiences significantly lower traffic volumes compared to the core airports (ZBAA, ZBAD, and ZBTJ). As shown in Figure 1, ZBSJ’s operational profile results in minimal coordination requirements with the central airports, and, thus, ZBSJ was excluded from the model’s decision-making scope. This ensures that the focus remains on optimizing the flight schedules for the core terminals within the BTH cluster.

4.1.2. Flight Schedule Data for Model Validation

A subset of 468 flight slots, selected from the 24 November 2021 data, was used for model validation. This subset corresponds to the peak traffic window from 07:00 to 11:00, a critical period for testing the model’s performance under high-congestion conditions. During this window, the highest demand–capacity mismatches occur, making it the ideal time to demonstrate the impact of the model’s optimization. While full-day results show similar patterns, the congestion is less pronounced outside the peak period.

Table 2. Sample flight schedule data.

Flight Number	Aircraft Model	Working Day	Departure Airport	Time of Departure	Destination Airport	Time of Arrival
CHH7189	738	3.4.5.6.7	ZBAA	0705	ZUGY	1045
CCA1879	321	1.2.3.4.5.6	ZBAA	0710	ZSYW	0935
CHH7123	738	3.5.7	ZBAA	0710	ZSHZ	0900
CHH7169	738	1.2.3.4.5.6.7	ZBAA	0710	ZLLL	0945
CXA8393	738	1.2.3.4.5.6.7	ZBAD	0655	ZJSY	1105
CXA8395	788	1.2.3.4.5.6.7	ZBAD	0755	ZGGG	1115
CXA8455	738	1.2.3.4.5.6.7	ZBAD	2115	ZUCK	0010
CXA8469	738	1.2.3.4.5.6.7	ZBAD	0745	ZUTF	1045
CBG8854	E90	3.5.7	ZBTJ	1415	ZGCD	1640
CGZ7122	E90	3.5.7	ZBTJ	1855	ZUWX	2135
DKH1136	320	1.2.3.4.5.6.7	ZBTJ	2215	ZSPD	0030
DKH1206	320	1.2.3.4.5.6.7	ZBTJ	1025	ZSPD	1300

presents a sample of these selected flight slots.

4.1.3. Waypoint Capacity Constraints

The BTH airport cluster operates within the highly structured and dense Beijing Terminal Area, encompassing ZBAA, ZBAD, and ZBTJ. The airspace is defined by a set of seven primary departure waypoints, RUSDO, IDKEX, BOTPU, PEGSO, ELKUR, OMDEK, and IGMOR, and six arrival waypoints, DUGEB, GUVBA, AVBOX, BLEAX, ELAPU, and DUMAP. Figure 2 illustrates the configuration of these waypoints and their respective airspace divisions.

Waypoint capacity limits were determined based on operational statistics provided by the North China Air Traffic Management Bureau.

Table 3. Sample flight schedule data.

Airport	Orientation	Waypoint	Capacity/(Sorties/Hour)
ZBAA	Central South	RUSDO	15
	Southwest/northwest	BOTPU/IDKEX	20
	Eastern China	ELKUR	26
ZBAD	Central South	OMDEK	28
	Southwest/northwest	PEGSO	16
	Eastern China	ELKUR	26
ZBTJ	Central South	OMDEK	20
	Southwest/northwest	PEGSO/BOTPU	16
	Eastern China	IGMOR	20

and

Table 4. Sample flight schedule data.

Airport	Orientation	Waypoint	Capacity/(Sorties/Hour)
ZBAA	Central South	DUGEB	18
	Southwest/northwest	GUVBA	7
	Eastern China	AVBOX	35
ZBAD	Central South	BLEAX	24
	Southwest/northwest	ELAPU	6
	Eastern China	AVBOX	35
ZBTJ	Central South	AVBOX	20
	Southwest/northwest	GUVBA	10
	Eastern China	DUMAP	10

summarize the hourly capacity limits for departure and arrival waypoints, which are critical for optimizing air traffic scheduling.

4.1.4. Decision Variables

Airport capacity constraints were derived from 2021 data released by the Civil Aviation Administration of China (CAAC) and the North China Regional Administration.

Table 5. Airport slot capacity constraints in the BTH cluster.

Airport	Capacity/(Sorties/Hour)
ZBAA	70
ZBAD	62
ZBTJ	31

outlines the hourly capacity limits for the BTH cluster’s core airports, focusing on the maximum number of aircraft that can depart or arrive per hour.

4.1.5. Average Flight Time

The average travel time for outbound and inbound flights to reach their respective waypoints was estimated using radar trajectory data collected in November 2021 by the North China Air Traffic Management Bureau. The estimated travel times for both outbound and inbound flights are provided in

Table 6. Average time taken by outbound flights to waypoint.

Airport	Orientation	Waypoint	Time/(Minutes)
ZBAA	Central South	RUSDO	20
	Southwest/northwest	BOTPU/IDKEX	15
	Eastern China	ELKUR	25
ZBAD	Central South	OMDEK	20
	Southwest/northwest	PEGSO	20
	Eastern China	ELKUR	20
ZBTJ	Central South	OMDEK	15
	Southwest/northwest	PEGSO/BOTPU	15
	Eastern China	IGMOR	15

and

Table 7. Average time taken by inbound flights to waypoints.

Airport	Orientation	Waypoint	Time/(Minutes)
ZBAA	Central South	DUGEB	25
	Southwest/northwest	GUVBA	25
	Eastern China	AVBOX	25
ZBAD	Central South	BLEAX	20
	Southwest/northwest	ELAPU	30
	Eastern China	AVBOX	15
ZBTJ	Central South	AVBOX	15
	Southwest/northwest	GUVBA	15
	Eastern China	AVBOX	15

, respectively. These parameters support the modeling of waypoint capacity constraints and ensure that the temporal distribution of flights is accurately reflected in the optimization process.

4.1.6. Capacity for Severe Weather Conditions

Three distinct adverse weather scenarios $(s_1, s_2, s_3\in S)$ were integrated into the model using meteorological data from November 2021:

• Scenario $s_1$: Heavy snowfall (50% nominal capacity).
• Scenario $s_2$: Early snowfall (60% nominal capacity).
• Scenario $s_3$: Intermittent snowfall (70% nominal capacity).

These data provided insights into how snowfall impacted the operational capacity of airports, specifically during the 07:00–11:00 period. The capacity decay parameters, informed by the real-time weather data, reflect significant reductions in departure and arrival throughput at the core airports in the BTH cluster.

As shown in

Table 8. Capacity decay by airport during adverse weather.

Time	ZBAA	ZBAD	ZBTJ	Meteorological Description
7:00	42 (60%)	37 (60%)	19 (60%)	Early snowfall, snow removal required, single runway operation
8:00	42 (60%)	37 (60%)	19 (60%)	Continuing snowfall
9:00	49 (70%)	43 (70%)	22 (70%)	Intermittent snowfall with partial recovery
10:00	35 (50%)	31 (50%)	16 (50%)	Heavy snowfall, low visibility
11:00	35 (50%)	31 (50%)	16 (50%)	Continued heavy snowfall

, ZBAA and ZBTJ experienced severe capacity reductions, particularly due to snowfall and the resulting low visibility. The single runway operation at these airports further contributed to the diminished capacity. This weather-driven capacity decay is crucial for realistic model validation, highlighting how severe weather can affect air traffic management.

4.1.7. Turnaround and Connectivity Parameters

To reflect more realistic operational conditions, the model incorporates turnaround time parameters that account for aircraft type and airline operational characteristics. These parameters impose regulatory and logistical constraints on the minimum and maximum permissible ground times between consecutive flight legs, ensuring that the flight scheduling process aligns with typical airline practices.

Turnaround times were categorized according to aircraft type, including narrow-body, wide-body, and regional aircraft, with the specific values assigned based on empirical data gathered from major airline operators within the BTH cluster. As shown in

Table 9. Turnaround time parameters by aircraft type.

Aircraft Type	Min Turnaround (Minutes)	Max Turnaround (Minutes)	Representative Operators
Narrow-body	45	120	CA, CZ, MU
Wide-body	90	180	CA (long-haul)
Regional	35	75	NS, GJ, BK

,these empirical data serve as the basis for defining realistic turnaround time ranges, which allow flexibility in slot assignments while also maintaining scheduling consistency.

These turnaround time constraints are critical for modeling the sequential flight pairs in a hub-based carrier environment, where airlines operate multiple daily rotations through the BTH cluster. The constraints ensure that the model respects operational realities, such as the ground time required for aircraft turnaround, which is necessary to avoid unrealistic schedule compressions or excessive idle times between flights.

4.2. Computational Experiments and Simulation Results

4.2.1. Simulation Setup and Computational Details

The computational experiments were performed using Gurobi 12.0.2 solver, implemented via Python 3.11.9. Computational times for the peak period (468 flights) averaged 32 min for the two-stage model and 18 min for the single-stage benchmark. Solution times scaled linearly with flight count.

4.2.2. Optimization Results: Pre- and Post-Optimization Distributions

Figure 3, Figure 4 and Figure 5 depict the critical peak congestion window (07:00–11:00), which experiences the highest demand–capacity mismatches and, thus, most clearly demonstrates the model’s optimization impact. Full-day results exhibit similar patterns but with less pronounced congestion.

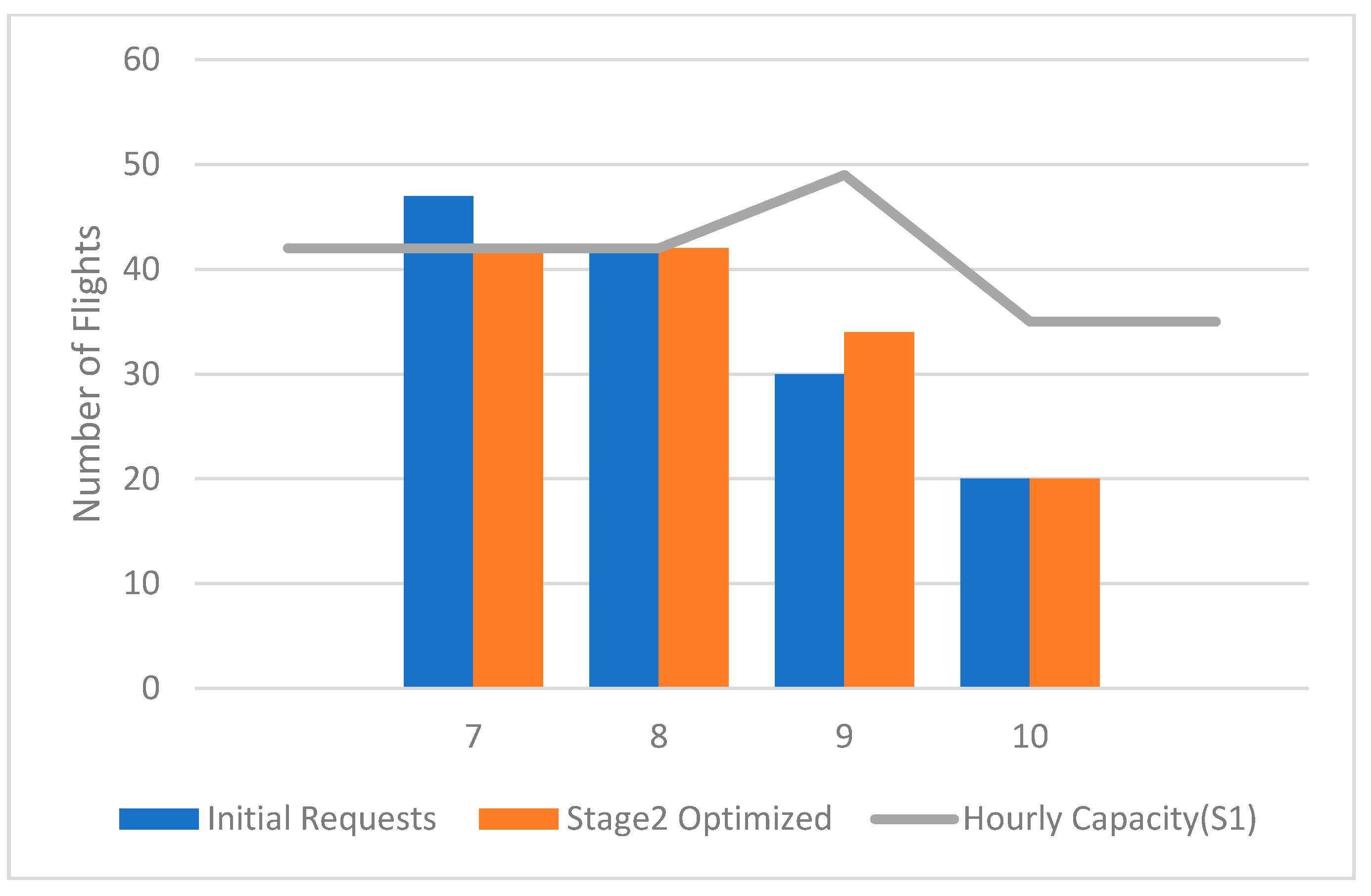
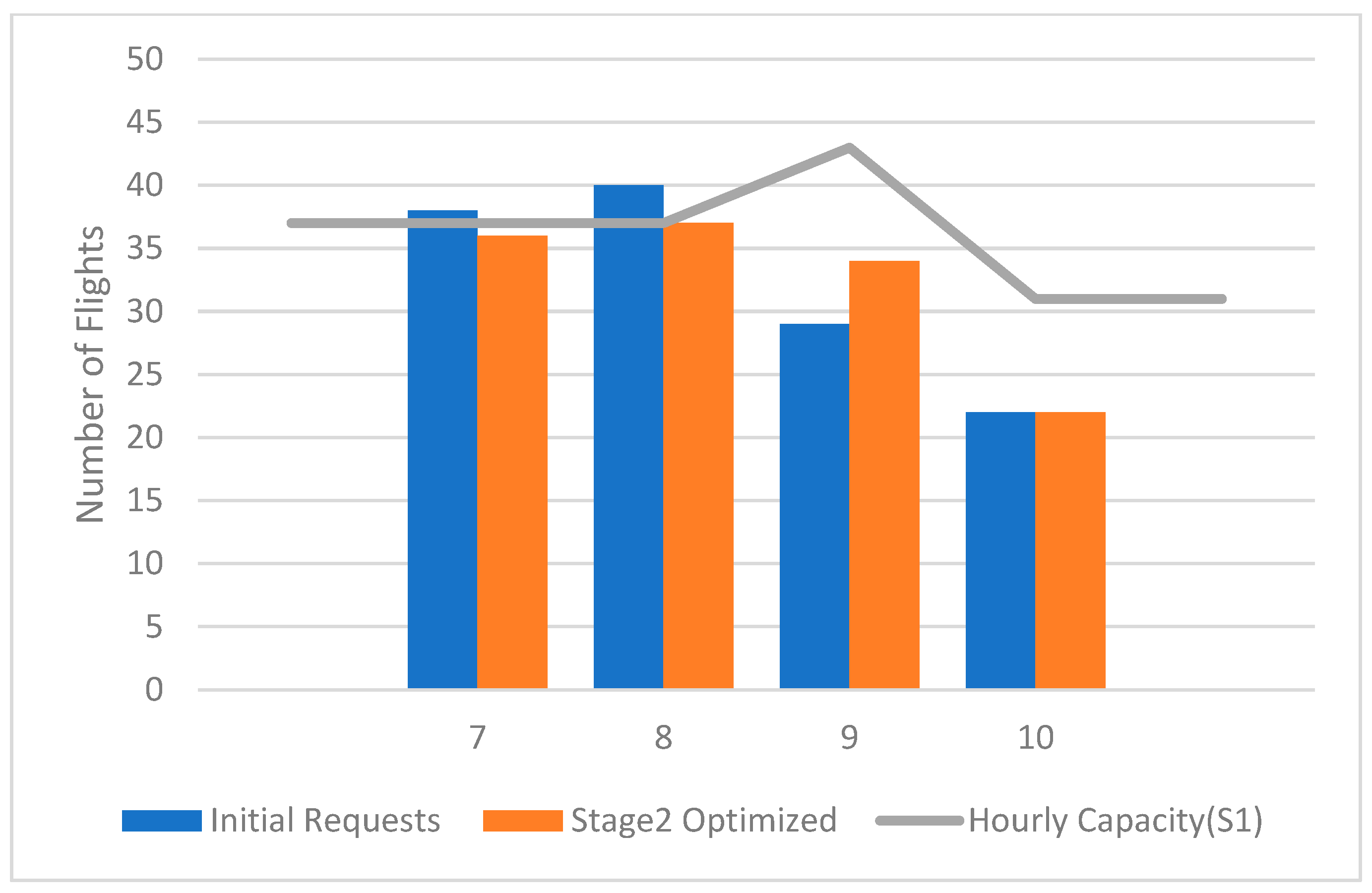
Figure 3, Figure 4 and Figure 5 show the flight distributions before and after optimization at three major airports: ZBAA, ZBAD, and ZBTJ. The horizontal axis represents time (in minutes), and the vertical axis represents the number of flights. ZBAA (Beijing Capital) showed a relatively balanced distribution of flights prior to optimization. The optimization results only required minimal adjustments, as the airport already exhibited a demand–capacity equilibrium. ZBAD (Beijing Daxing) experienced the largest overflow during peak times, with flight requests exceeding capacity by 36.2% from 07:00 to 08:00. After applying the optimization, the schedule was successfully redistributed, maintaining departures within capacity across all time slots. ZBTJ (Tianjin Binhai) also showed a similar congestion pattern, with flight requests exceeding capacity in the early hours. Post-optimization, flights were distributed more evenly, reducing peak congestion. Key observations from optimization are as follows:

(i) ZBAA: The minimal adjustment (12.7%) was required due to the already-balanced demand–capacity relationship.

(ii) ZBAD and ZBTJ: Both airports required higher levels of adjustment, at 28.4% and 39%, respectively, due to their higher congestion and more limited capacity.

This indicates that the model’s optimization mechanism is particularly effective for airports with more severe congestion, helping to balance resources dynamically.

4.2.3. Displacement Metrics

Figure 6 presents the total schedule displacement before and after optimization, highlighting the relationship between displacement and air traffic efficiency. The lower the displacement, the more effectively the system manages its resources, especially under adverse weather conditions.

The results indicate that the optimization process significantly reduced displacement, particularly at ZBAD and ZBTJ, where peak congestion occurred. For example, the total displacement for ZBAD was reduced by 150 min after optimization.

4.2.4. Analysis of Flight Distribution Pre- and Post-Optimization

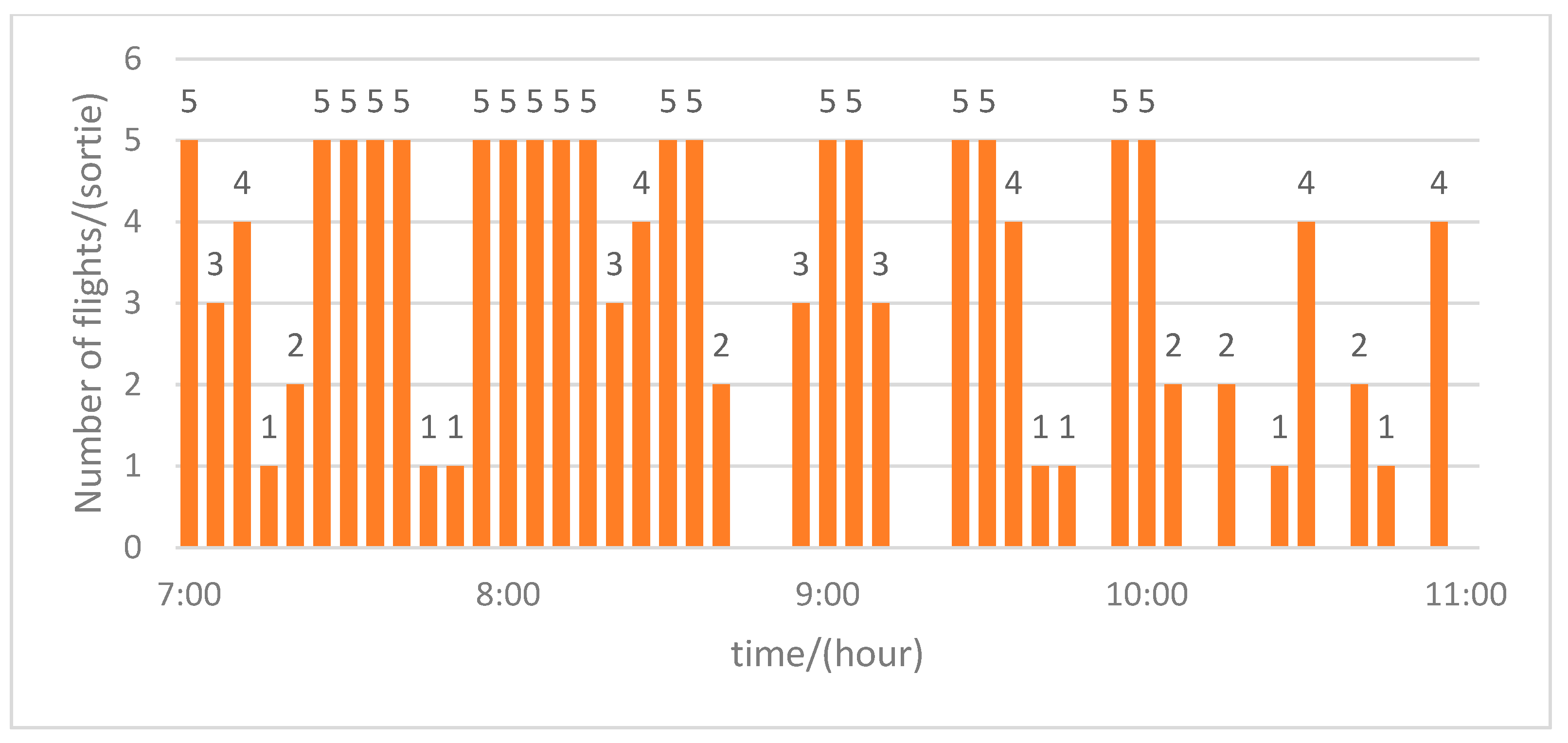
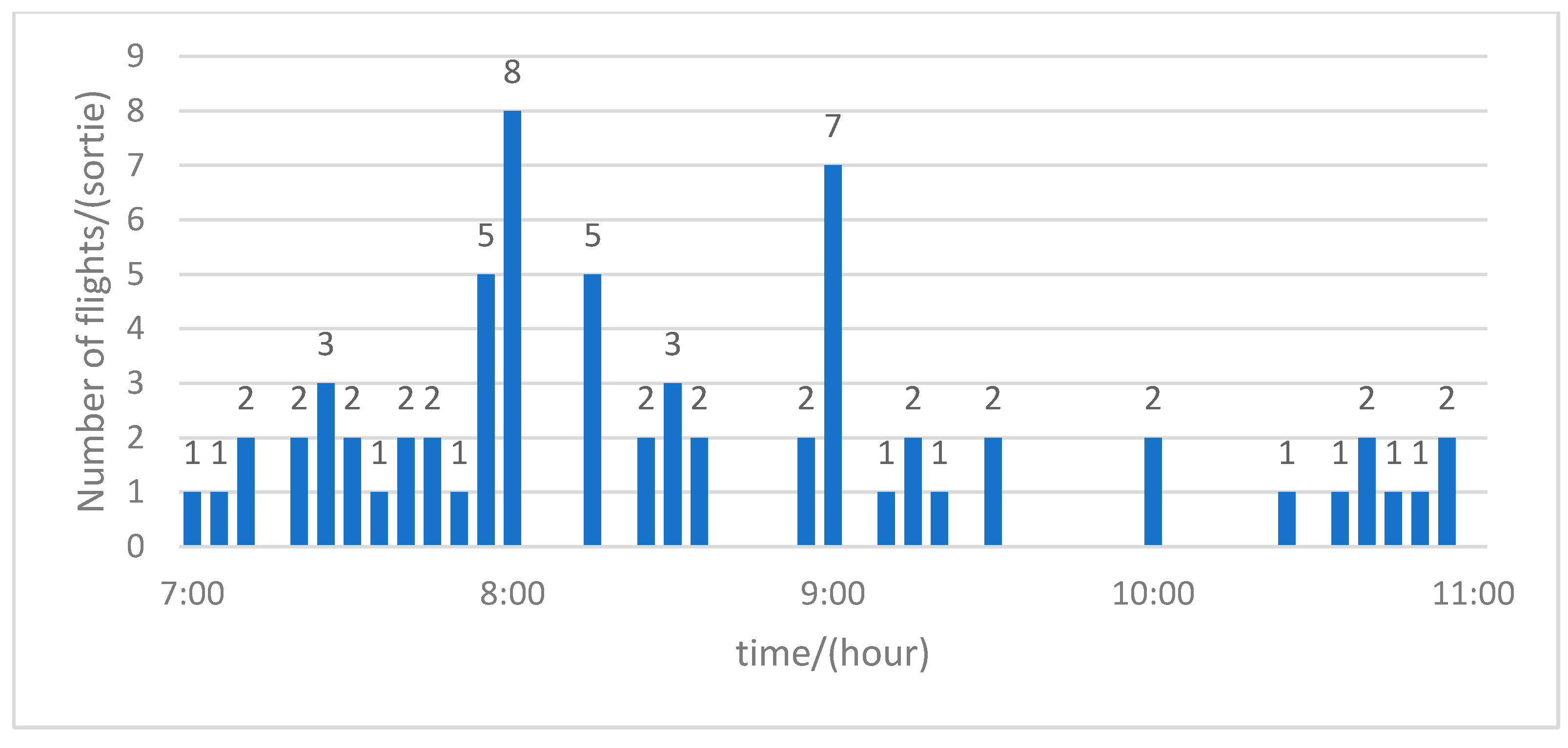
Figure 7, Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12 show the pre- and post-optimization flight distribution at ZBAA, ZBAD, and ZBTJ. These figures emphasize the significant temporal imbalances in slot utilization before optimization and the improvements in post-optimization distribution, as follows:

(i) ZBAA: The pre-optimization distribution revealed a concentration of flights at 07:55 and 08:00, leading to congestion. After optimization, the flight distribution was more uniform, with a 12% adjustment made to balance the schedule.

(ii) ZBAD: Before optimization, ZBAD faced major congestion at 08:30 and 09:00, with flight accumulation during peak hours. Post-optimization, the distribution became more balanced, with over 60% of flights being redistributed effectively.

(iii) ZBTJ: ZBTJ also experienced significant congestion at 08:00. Post-optimization, the adjustments ensured a more balanced utilization of slots across the day, similar to ZBAD.

In conclusion, all three airports exhibited much more uniform slot utilization, which would reduce delays and improve operational efficiency after optimization. The redistribution at ZBAD and ZBTJ resulted in substantial congestion reduction, contributing to smoother operations at these airports during peak hours.

4.2.5. Performance Comparison: Two-Stage vs. Single-Stage Optimization Models

To validate the operational advantages of the proposed slot optimization scheme, which incorporates tactical phase uncertainty, a comparative performance analysis was conducted between the developed two-stage robust optimization model and a traditional single-stage robust planning model.

The single-stage robust optimization (SSRO) benchmark minimizes the worst-case displacement simultaneously under all scenarios $s\in S$. The objective function was framed as:

$$\underset{x,y}{\min }\left\{\underset{s\in S}{\mathit{max}}\sum _{f\in F}\sum _{t\in T}\left(\left|t-t_f^d\right|·x_f^t+\left|t-t_f^a\right|·y_f^t\right)\right\}$$

(17)

subject to Constraints (3)–(10) and scenario-dependent capacities (Section 3.5.3 iii). This approach lacks the strategic–tactical decomposition, leading to overly conservative slot assignments and higher displacement.

The results from two-stage robust optimization demonstrate superior performance in comparison to the single-stage approach. As shown in Figure 13, the schedule displacement durations for each airport were measured. The orange bars represent the displacement duration after single-stage robust optimization, while the blue bars represent the two-stage robust optimization results. For ZBAA, ZBAD, and ZBTJ, the two-stage optimization required 110, 355, and 330 min of adjustment, respectively. In contrast, single-stage optimization required 160, 505, and 440 min for the same airports.

In total, the two-stage optimization reduced the required adjustment time by 310 min, down from 1105 min in single-stage optimization to 795 min. This outcome demonstrates that the two-stage robust optimization model, by accounting for various uncertain factors such as weather during tactical operations, produces more robust and adaptive decisions. In contrast, the single-stage approach required simultaneous satisfaction of all extreme scenario constraints, leading to increased adjustment times and less flexibility.

5. Conclusions

This study presents a two-stage robust optimization model for collaborative flight slot allocation in multi-airport systems under capacity uncertainty. The model effectively addresses the complex issue of air traffic congestion in the Beijing–Tianjin–Hebei (BTH) airport cluster by considering the shared use of limited airspace resources such as waypoints, as well as the dynamic uncertainties introduced by adverse weather conditions.

The strategic phase of the model focuses on minimizing nominal displacement costs during ideal conditions by pre-allocating flight slots based on airport and waypoint capacities, along with turnaround time constraints. The tactical phase then adjusts these allocations in response to real-time disruptions, such as adverse weather, by minimizing the worst-case delays across all possible disruption scenarios. By integrating both phases, the model ensures a robust and flexible scheduling system that can adapt to uncertain conditions without compromising operational efficiency.

Key findings from the computational experiments and simulations include the following:

(i) Improved Resource Utilization

The optimization process successfully redistributes flight schedules to balance slot utilization, especially at ZBAD and ZBTJ, which exhibit more pronounced congestion during peak hours. While ZBAA remained relatively unaffected due to its inherent demand–capacity equilibrium, the model’s flexibility was critical for accommodating capacity fluctuations at more constrained airports.

(ii) Reduction in Schedule Displacement

The two-stage robust optimization model outperformed the traditional single-stage robust planning model. The two-stage approach resulted in a 310 min reduction in total schedule displacement, demonstrating its superior ability to adjust dynamically to adverse conditions and optimize resources more effectively.

(iii) Weather-Adjusted Capacity Constraints

The integration of meteorological data into the model proved essential in accurately reflecting the impact of severe weather, such as snowfall, on airport and waypoint capacities. The capacity decay observed during adverse weather conditions highlighted the importance of including weather-adjusted constraints for real-world applicability.

(iv) Realistic Operational Constraints

By incorporating realistic turnaround time parameters and minimum turnaround time constraints between consecutive flights, the model aligns with operational practices within the BTH airport cluster, ensuring that flight schedules are not only optimized but also feasible from a logistical standpoint.

This study demonstrates that the two-stage robust optimization model is a highly effective tool for managing flight schedules in the face of uncertainties, particularly those introduced by weather disruptions. It provides significant operational advantages over traditional single-stage approaches, offering a more adaptive and flexible solution that ensures the robust performance of the system under dynamic and unpredictable conditions.

Future research could explore the extension of this model to larger airport clusters or consider other types of disruptions, such as airspace restrictions or technical failures. Additionally, further advancements in machine learning algorithms could be explored to predict disruptions more accurately, enabling even more proactive scheduling decisions. Finally, the model’s applicability could be tested in real-time systems, allowing for direct implementation and evaluation in live air traffic management operations.