Parameter Tuning of Detached Eddy Simulation Using Data Assimilation for Enhancing the Simulation Accuracy of Large-Scale Separated Flow Around a Cylinder
Abstract
1. Introduction
2. Methodology
2.1. Simulation Models and Parameters
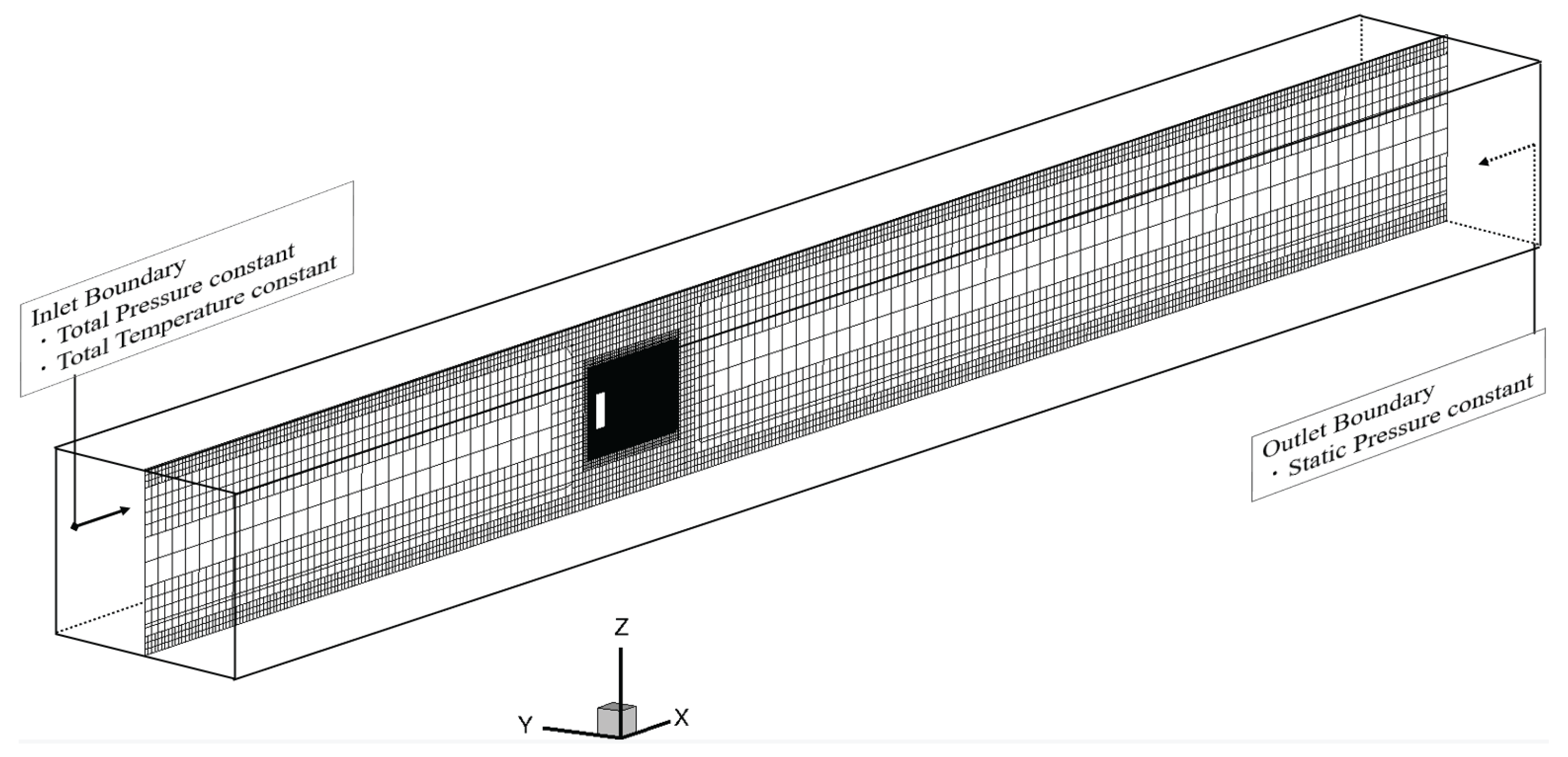
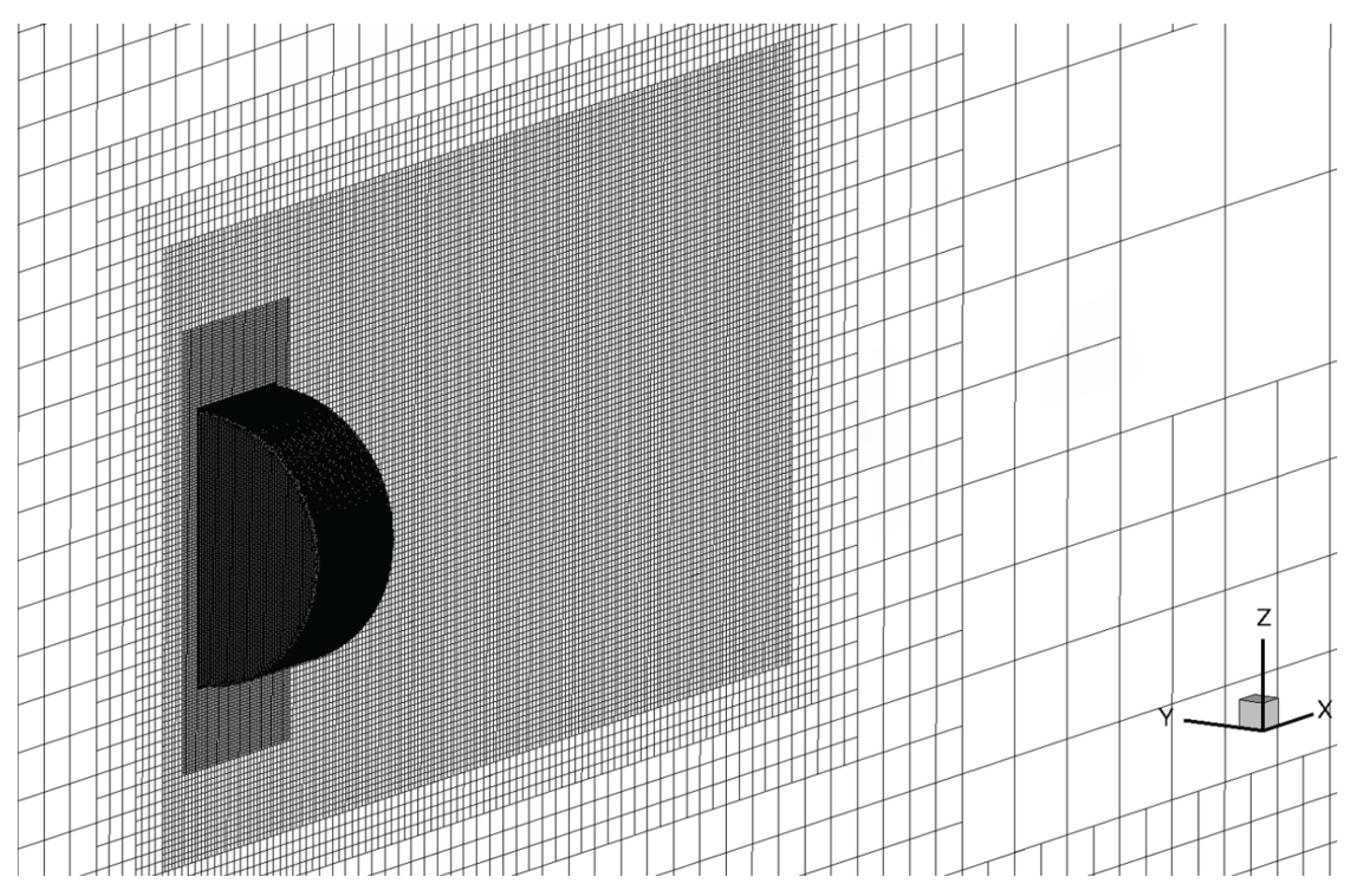
2.2. CFD Code and Simulation Conditions
2.3. Data Assimilation Method
2.4. Data Assimilation Process
- Generation of the Initial Ensemble: Variability is introduced to the parameters targeted for tuning using the Latin hypercube sampling method, and a set of 50 simulation cases (the simulation ensemble) is prepared. Each simulation case (ensemble member) undergoes initial simulation (70,000 time steps).
- Forecasting Step: Each ensemble member performs 400 simulation steps. Next, from the simulation data of each ensemble member, the x-direction velocity u and z-direction velocity w are extracted at the same locations as the PIV measurement coordinates.
- Filtering Step: Data assimilation using EnSRF is performed with the extracted simulation data, the PIV measurement data, and the turbulence model parameters. The parameter values of each ensemble member are updated and returned to the original ensemble members.
- Repetition of Steps 2 and 3: Steps 2 and 3 are repeated. Parameter tuning was terminated after 60 iterations of data assimilation.
- Calculate the ensemble mean of each parameter to obtain the tuned parameters. Then, simulate the flow around the circular cylinder using tuned parameters.
3. Results and Discussions
3.1. Process for Verification of Results
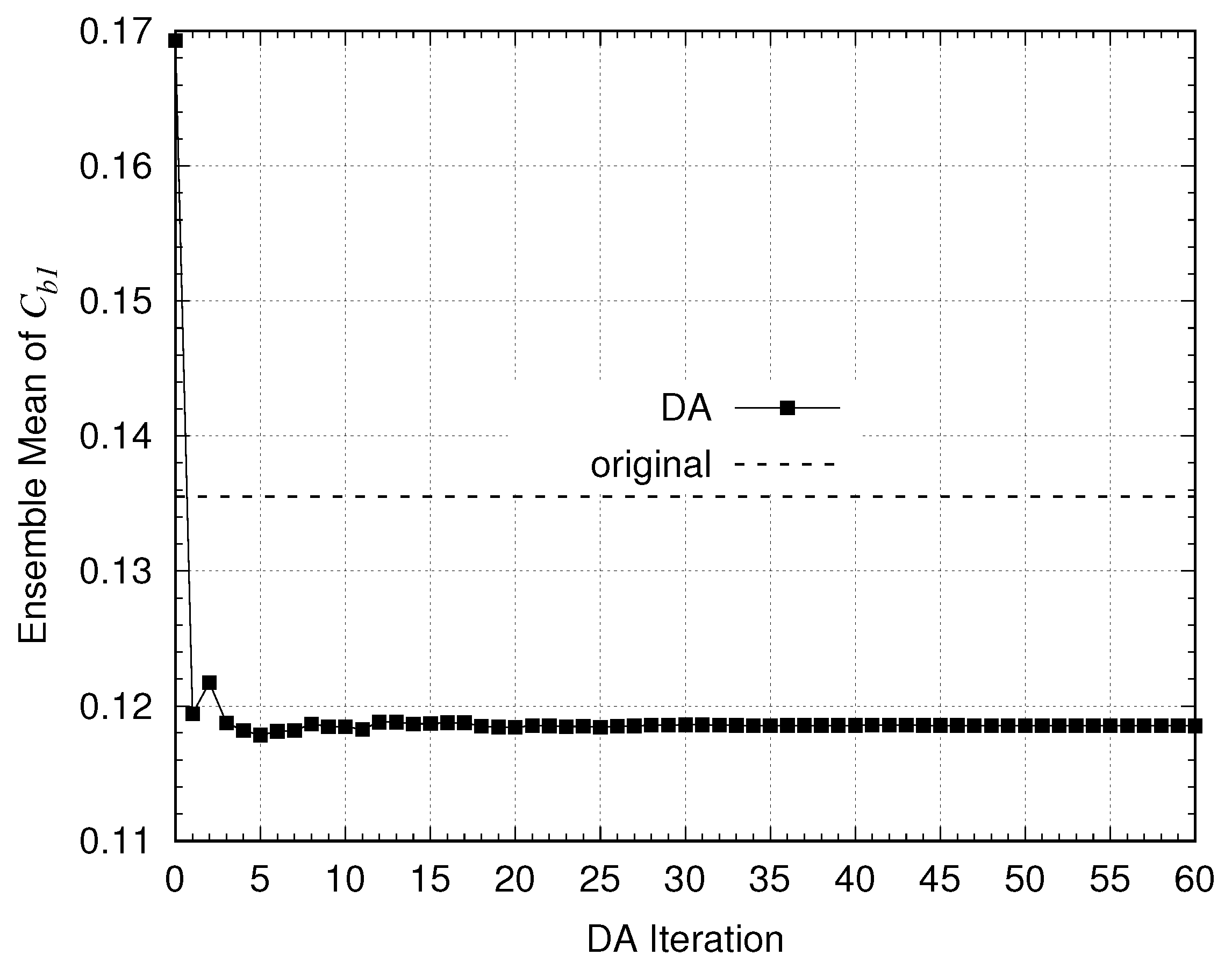
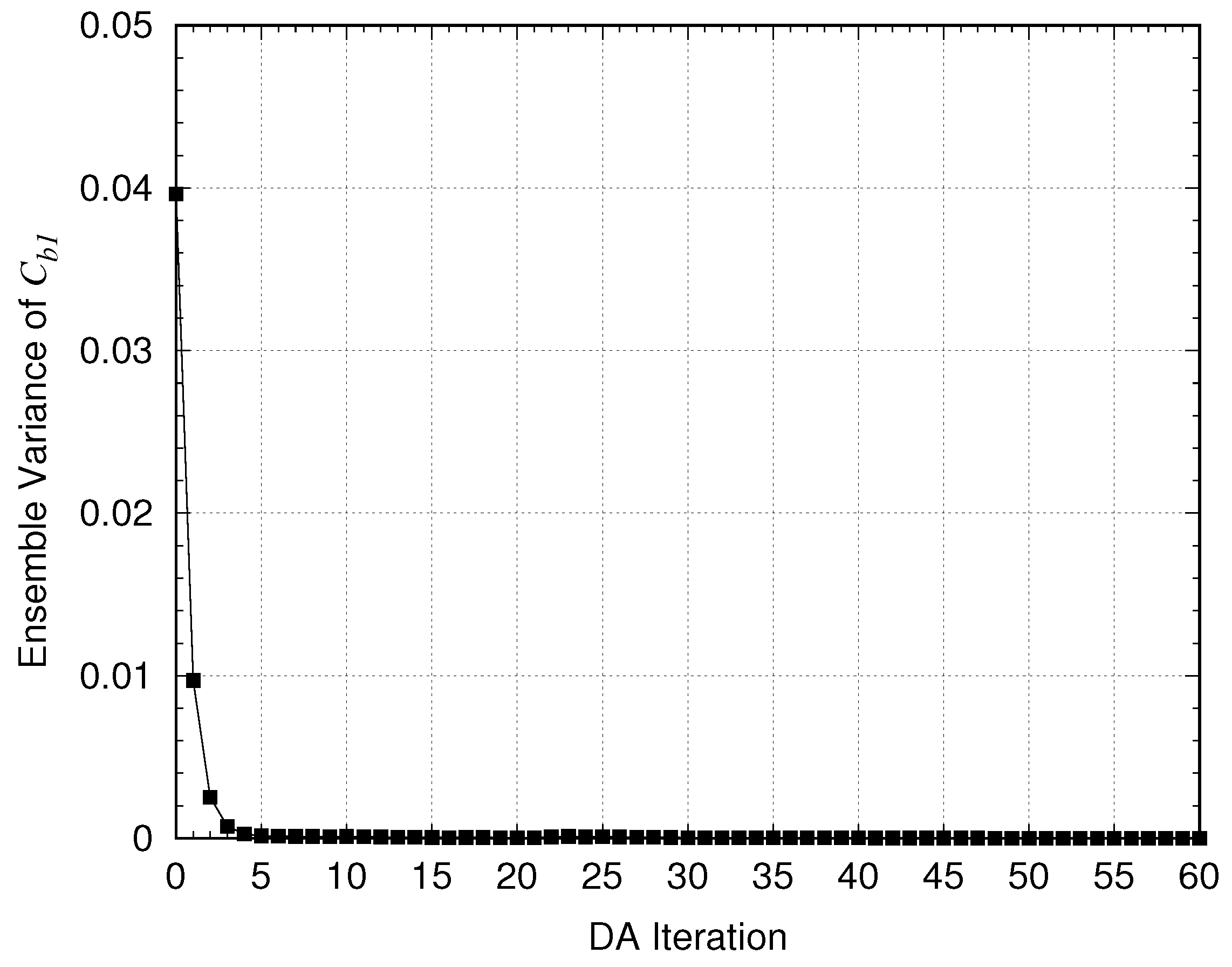
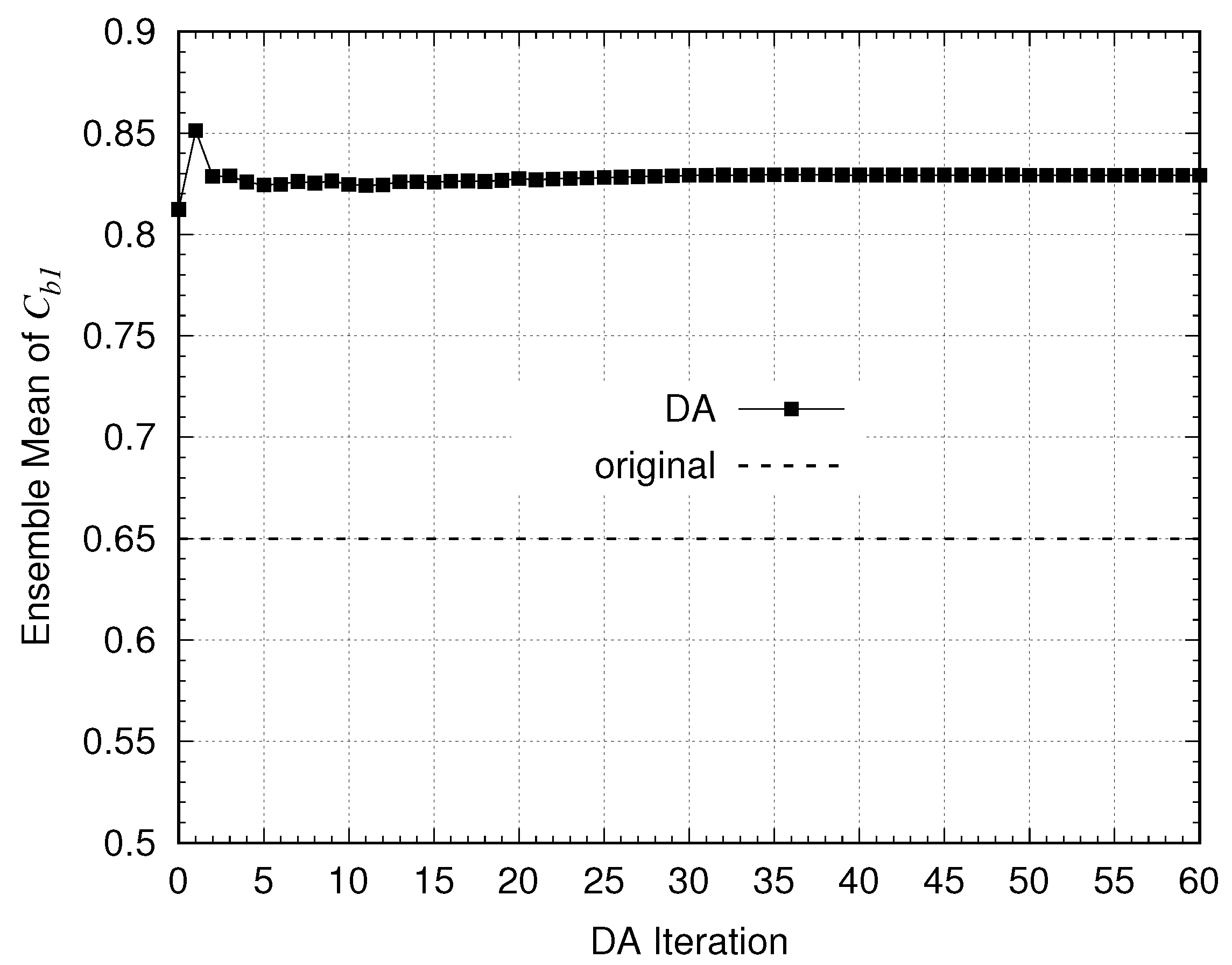
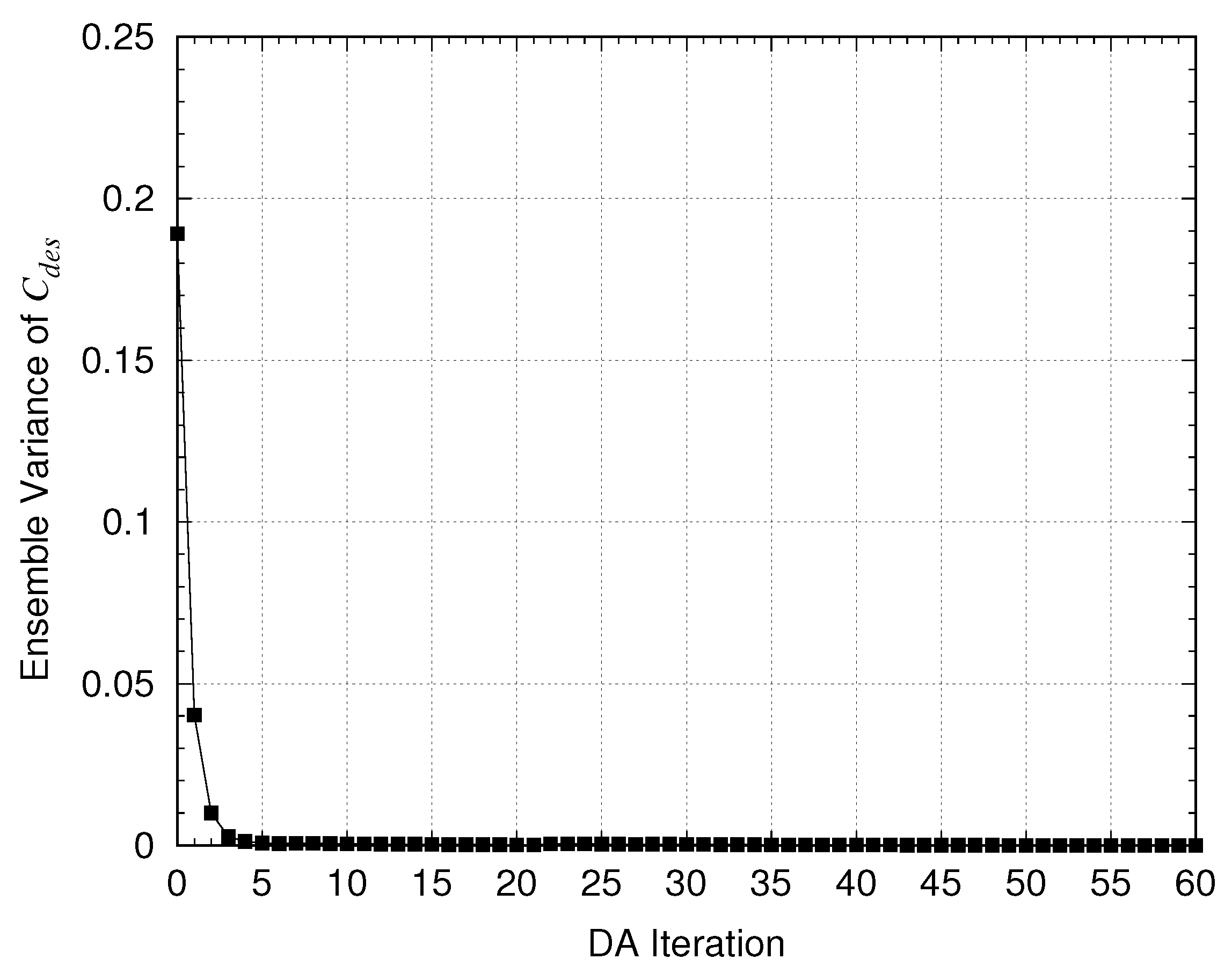
3.2. Results of Parameter Tuning
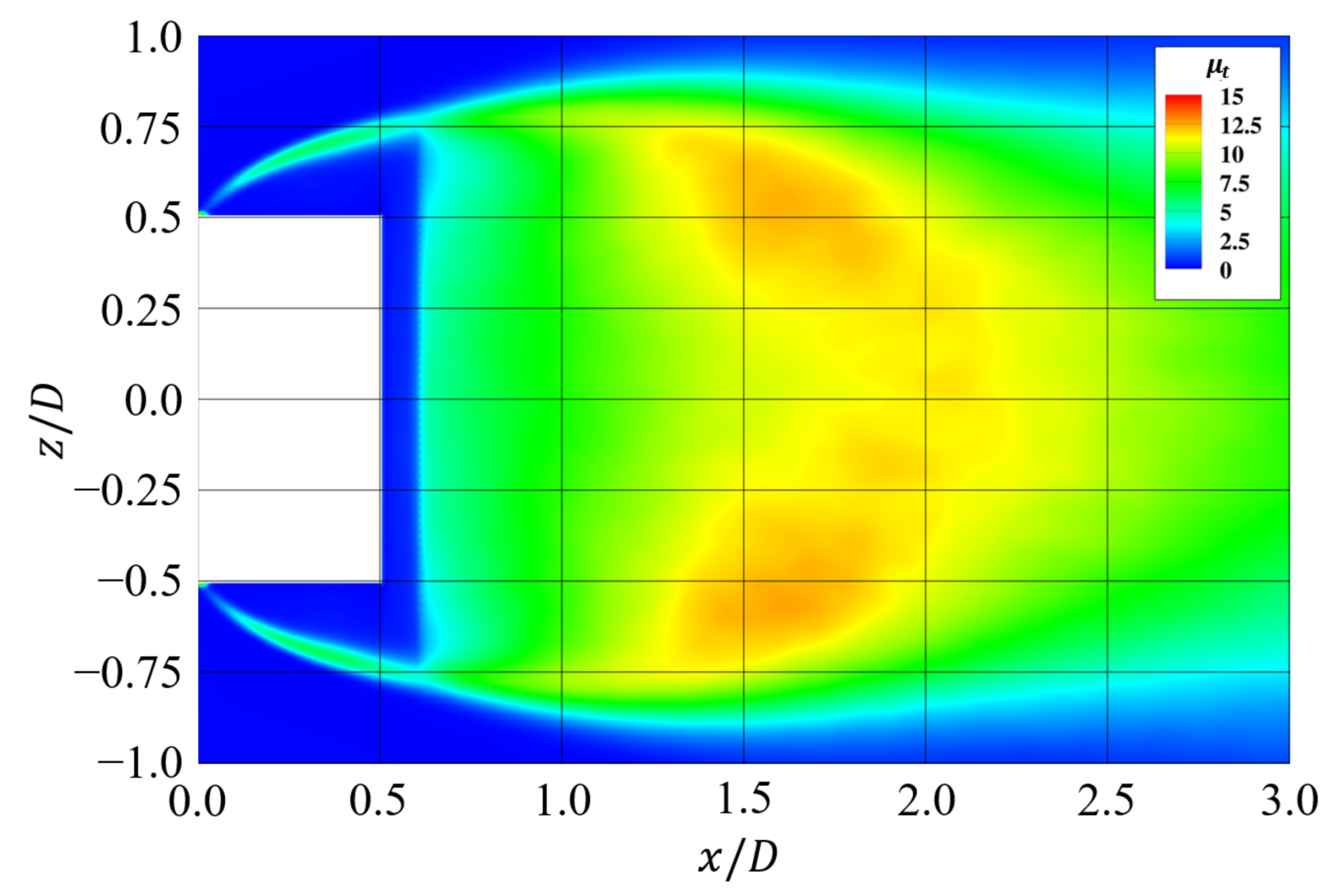
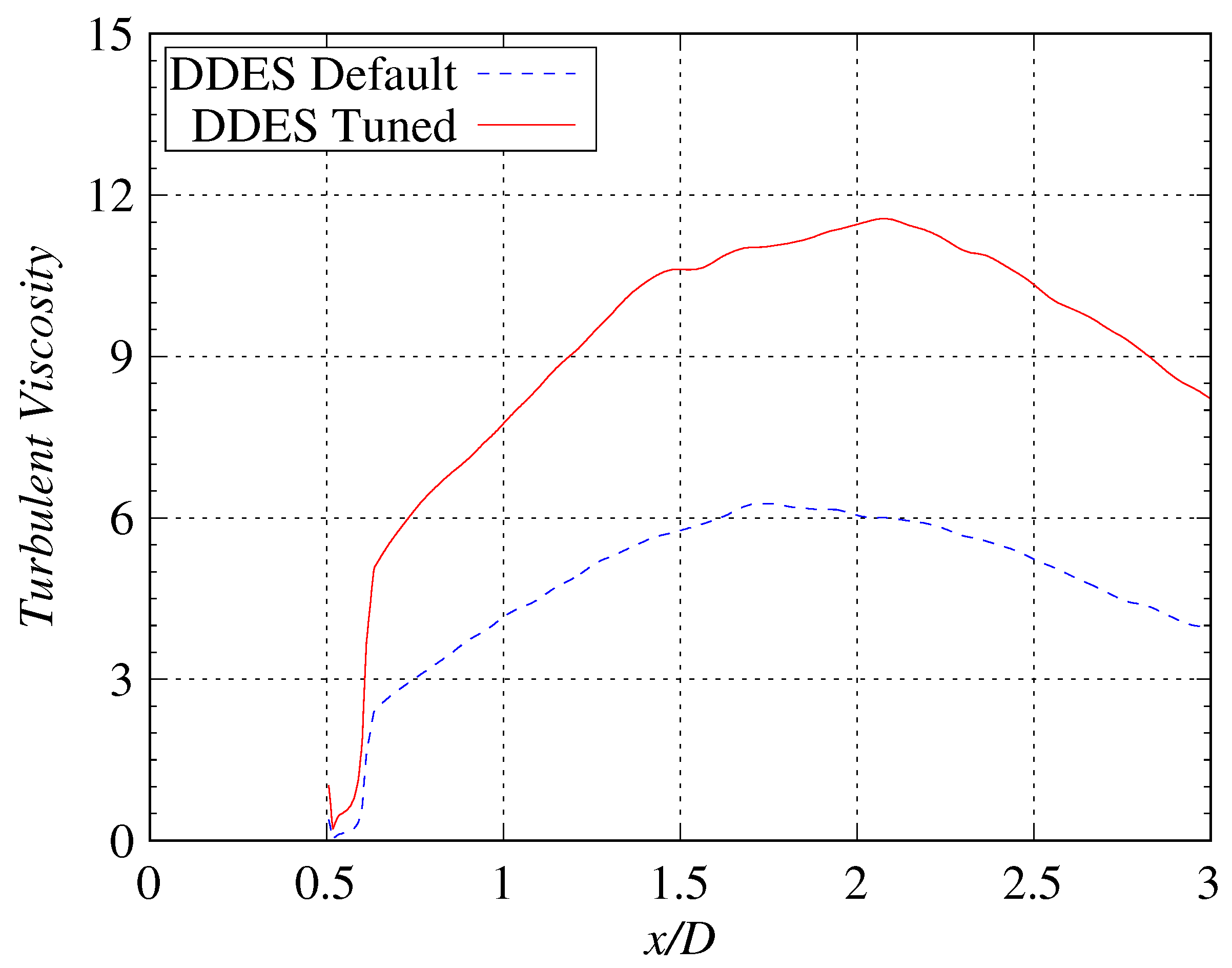
3.3. Comparison of Turbulent Viscosity Coefficients in Flow Fields
3.4. Comparison of Reynolds Stress Components
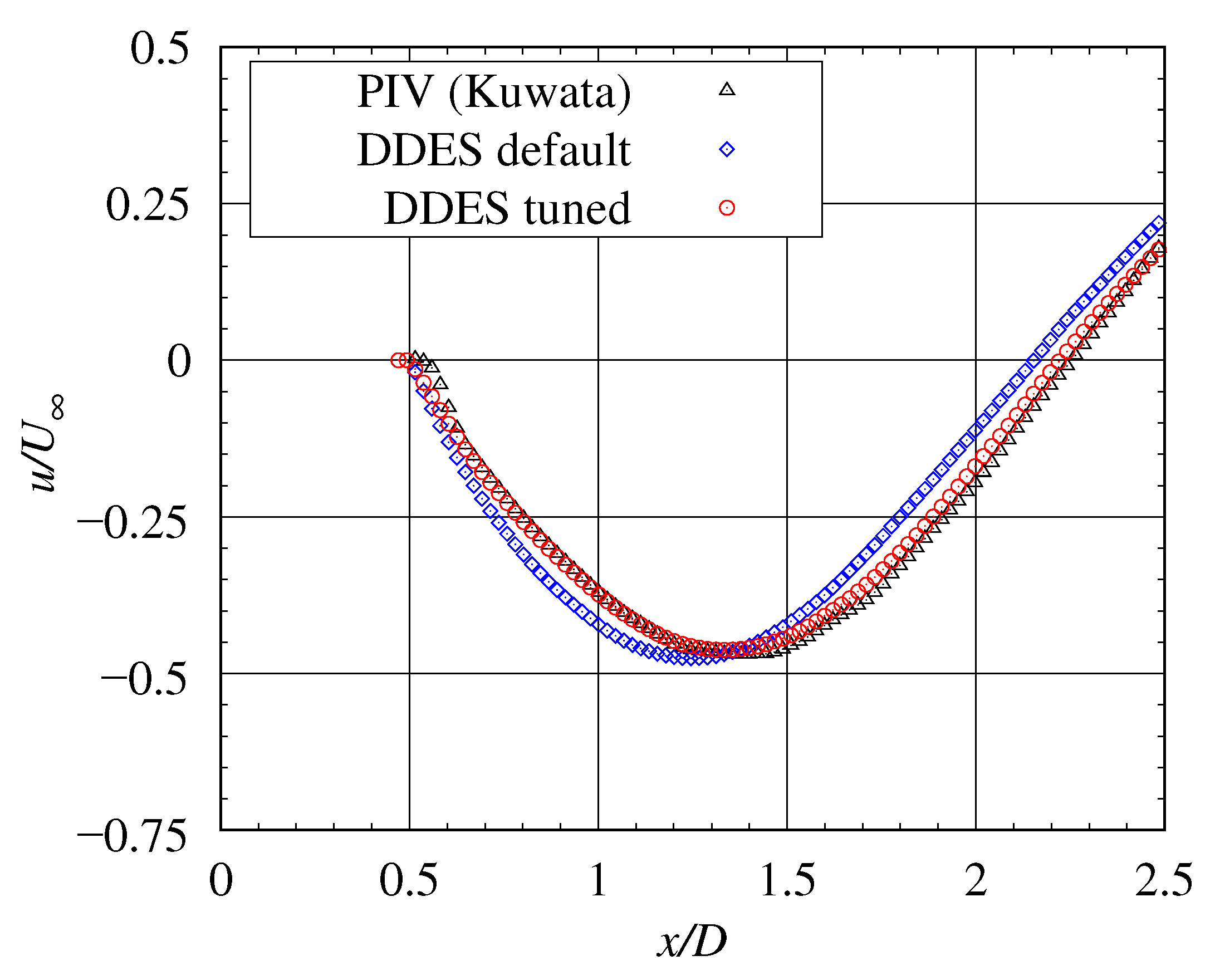
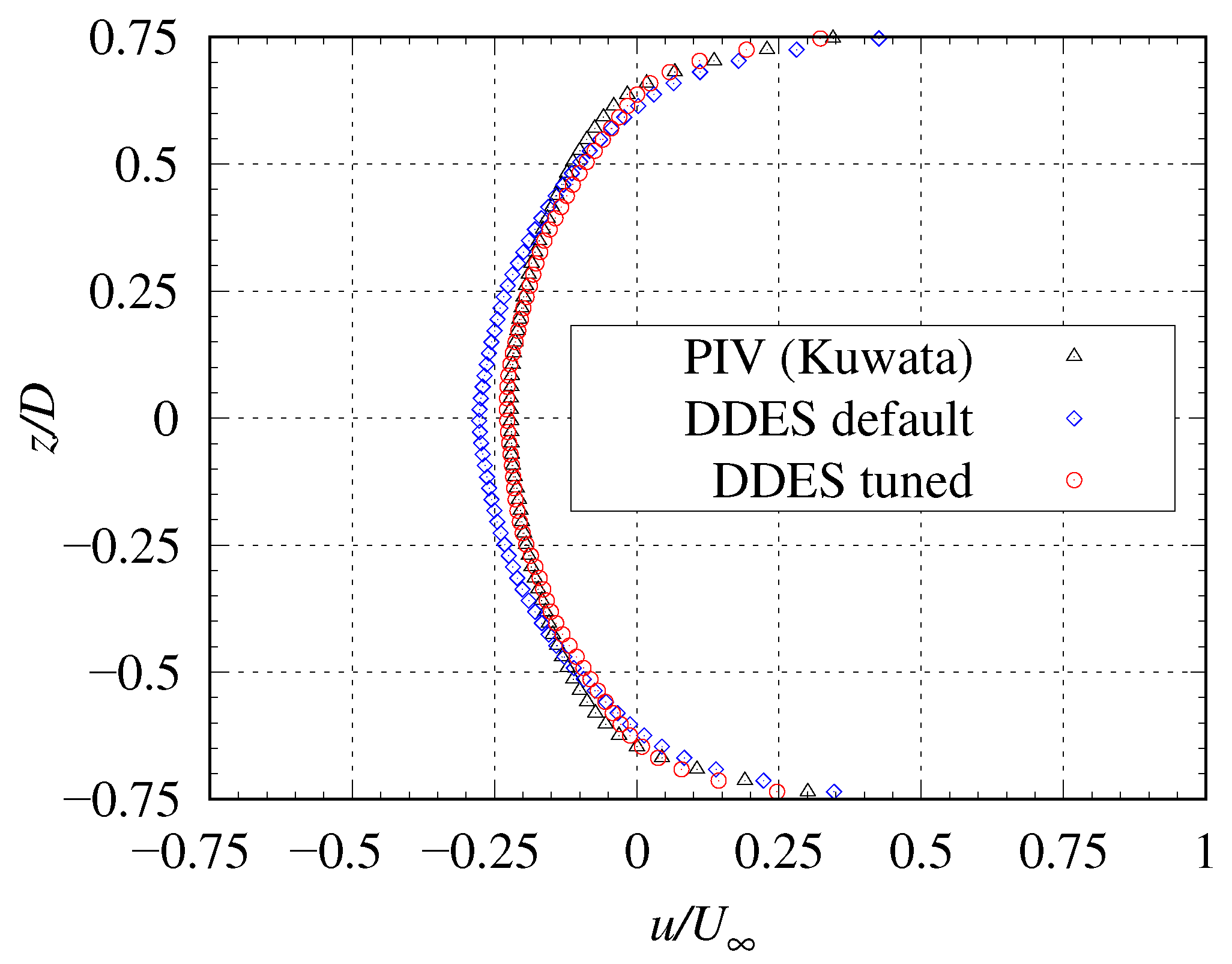
3.5. Comparisons of Velocity Distribution at Wake Flow
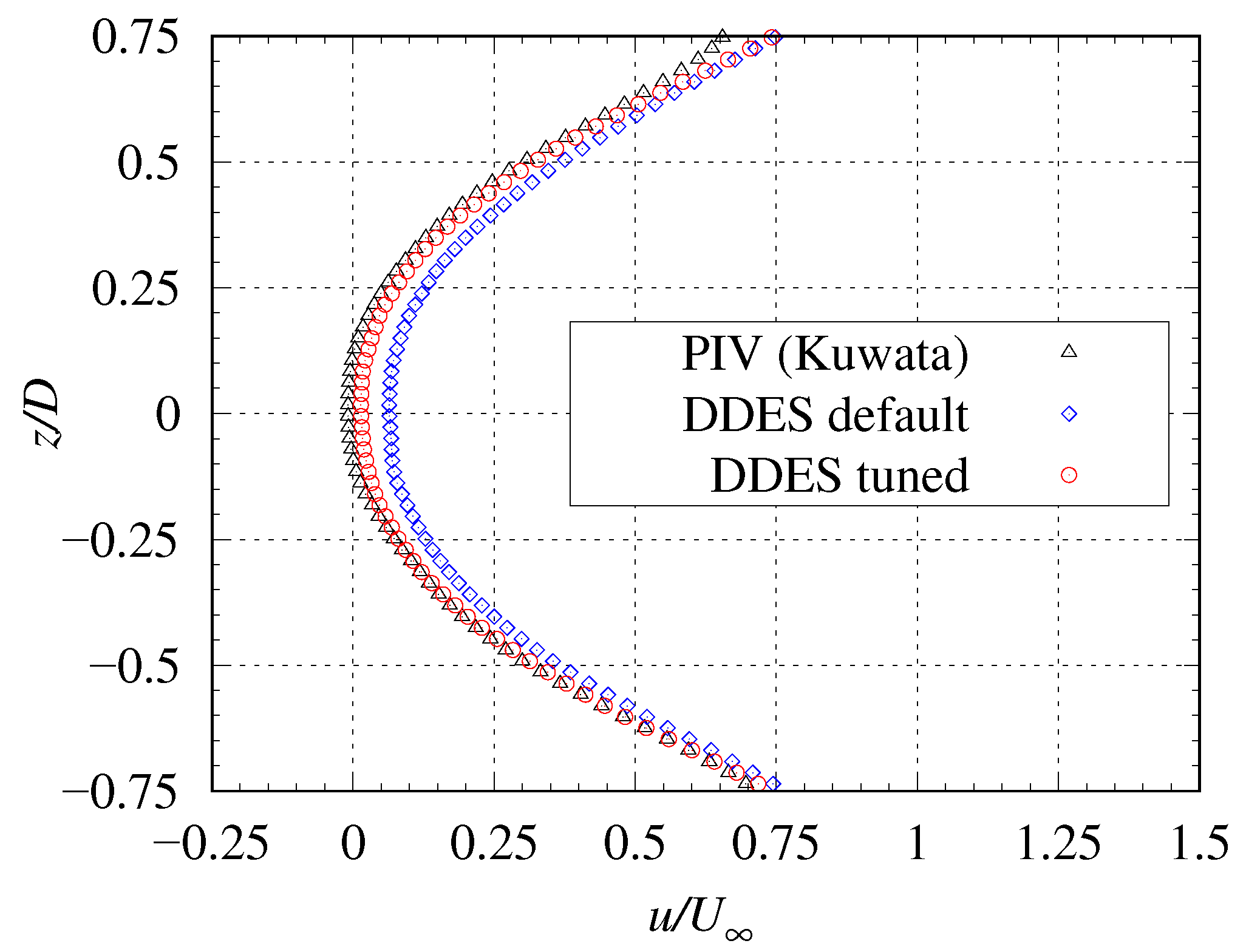
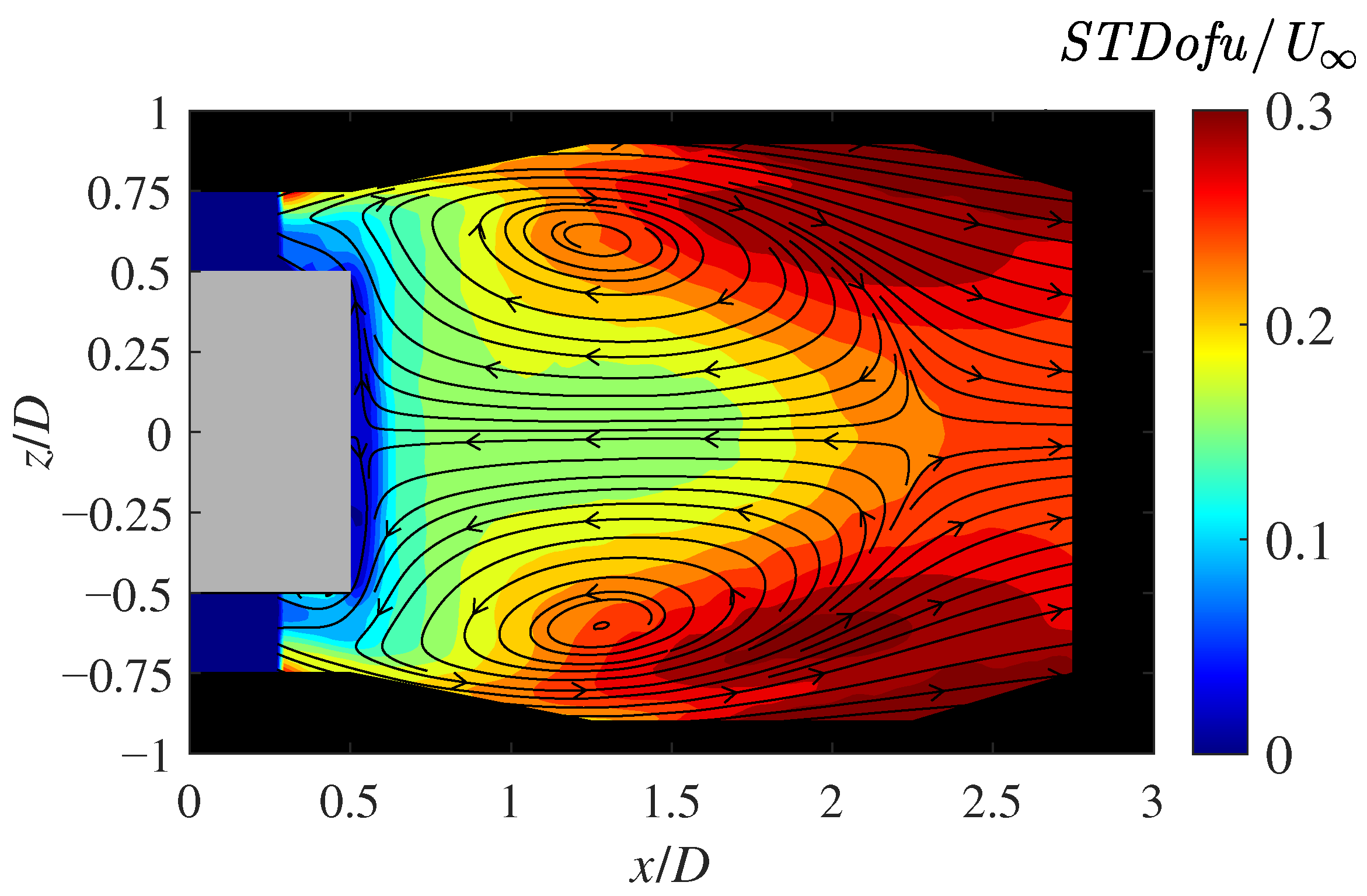
3.6. Velocity Fluctuations in the Wake of the Cylinder
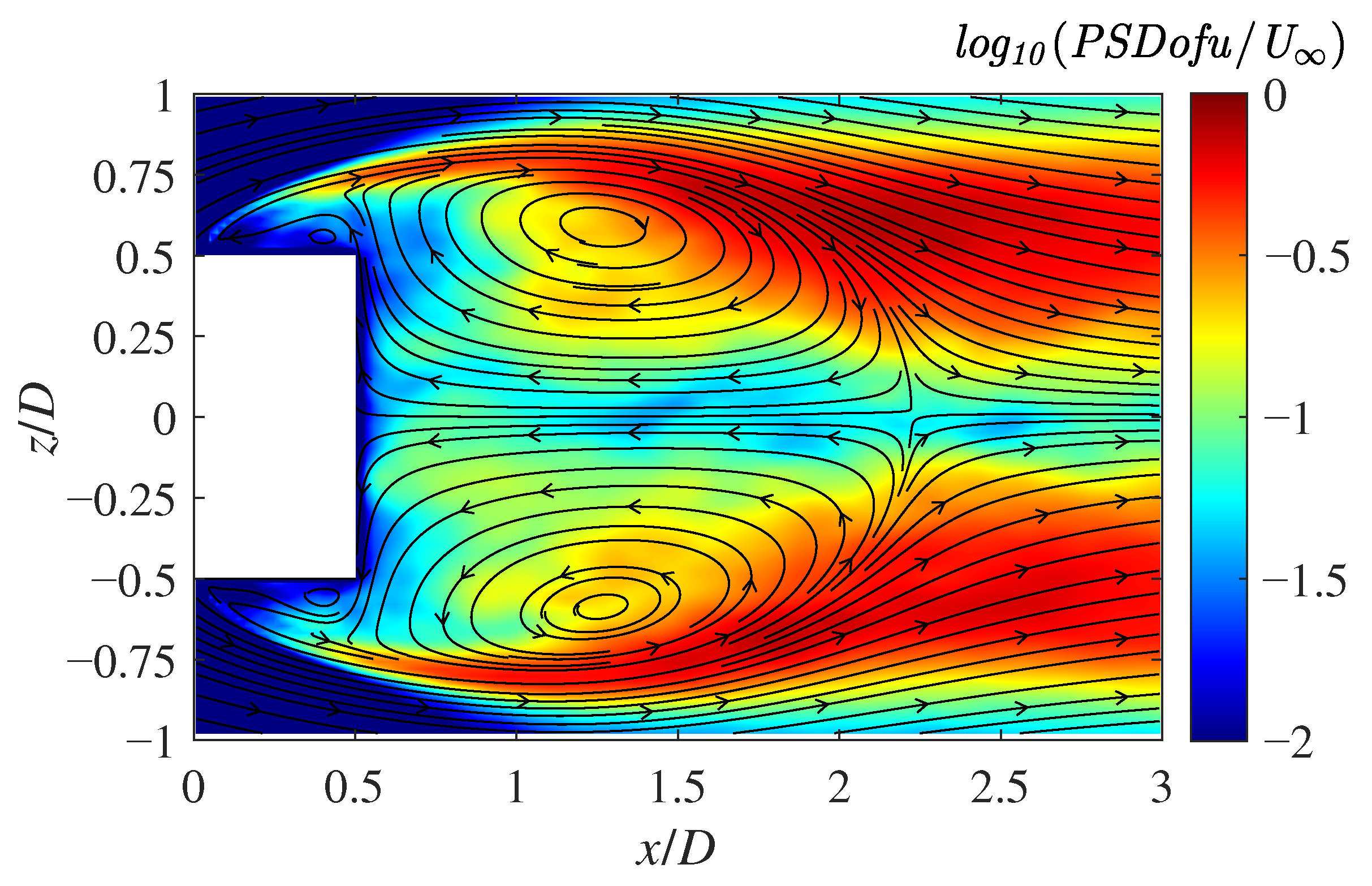
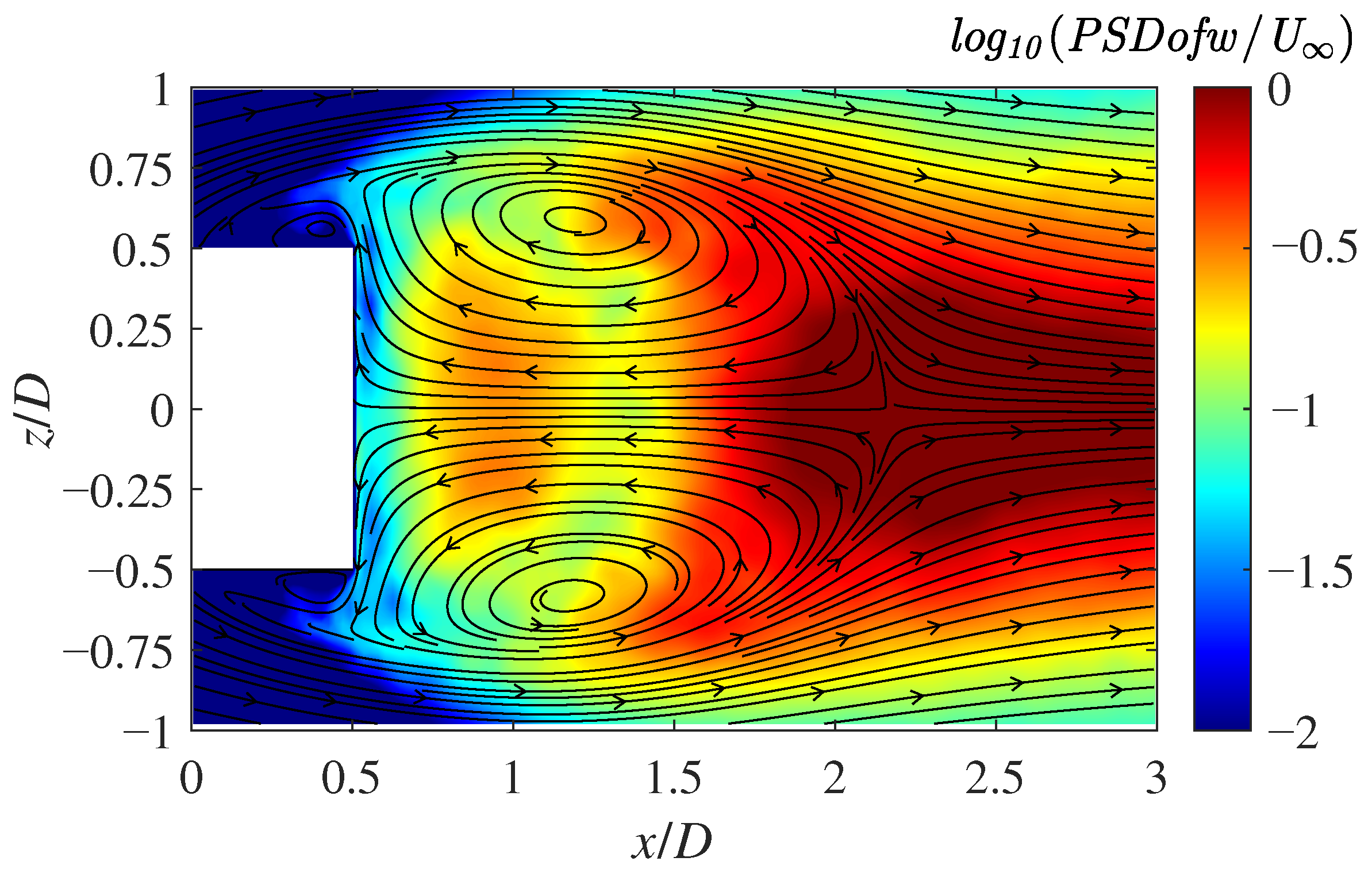
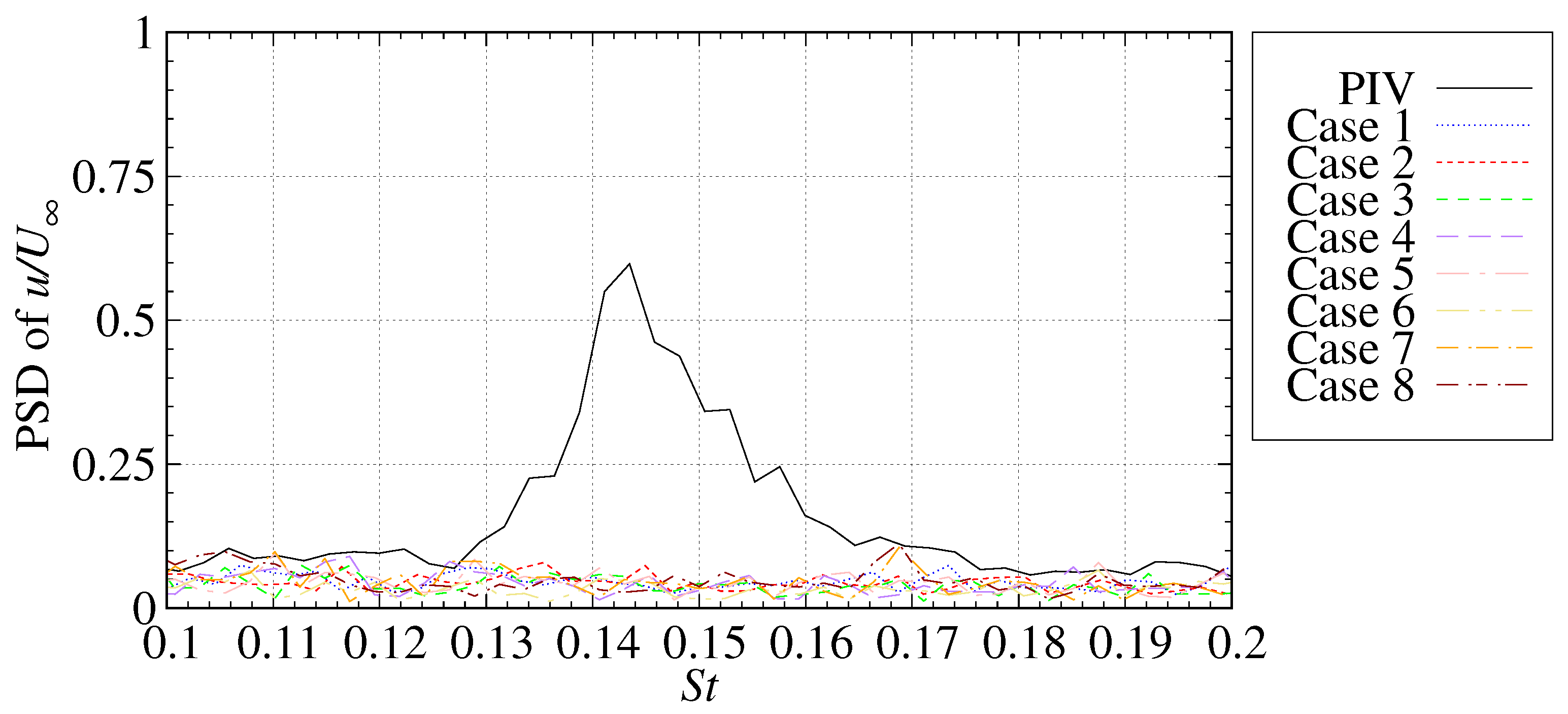
3.7. Time–Frequency Analysis of Velocity Fluctuation
3.8. Relationship Between Parameter Values and Simulation Results of Wake Velocity and Vorticity Components
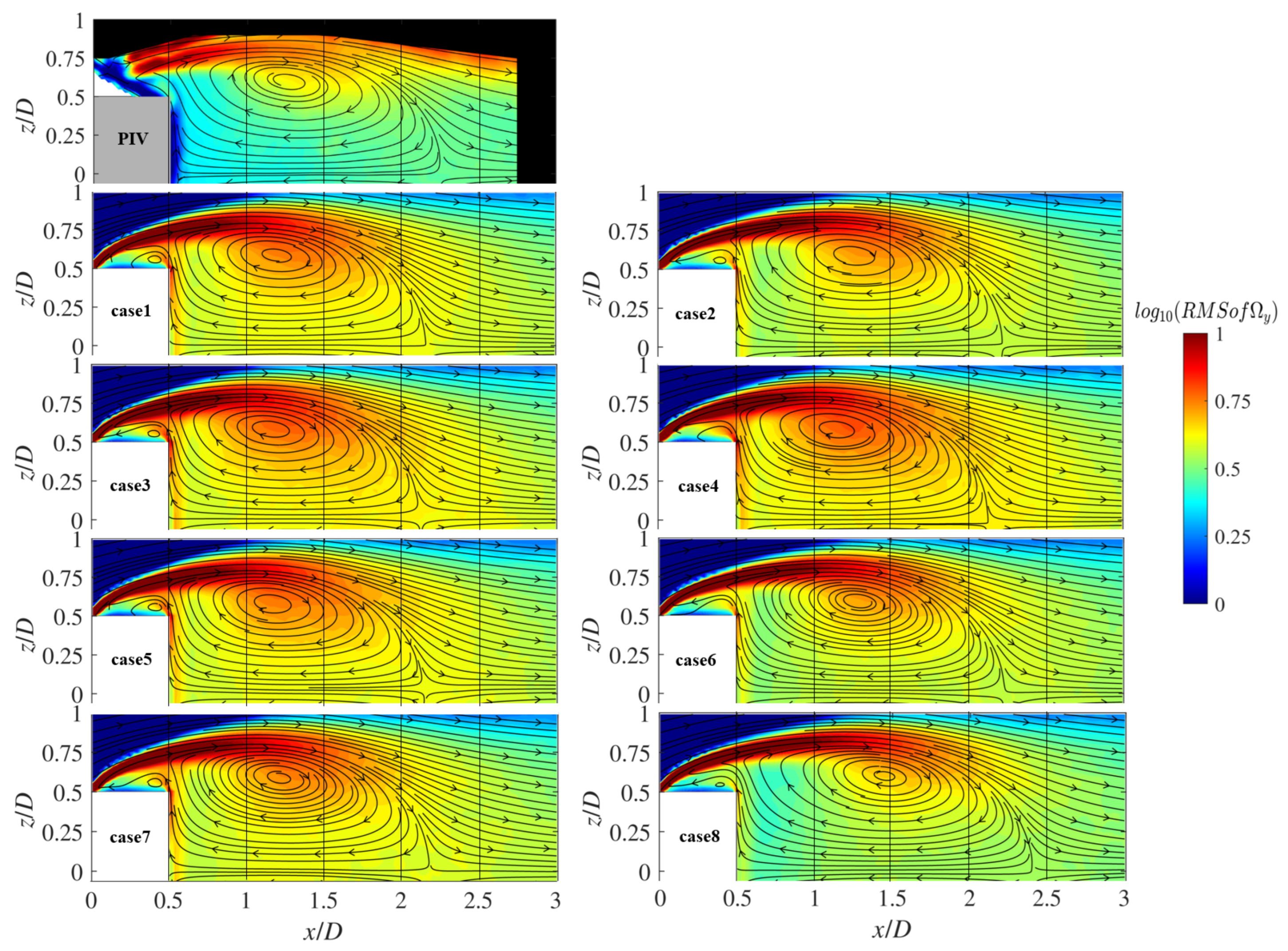
3.8.1. Comparison of the Root Mean Square (RMS) of the Vorticity Component
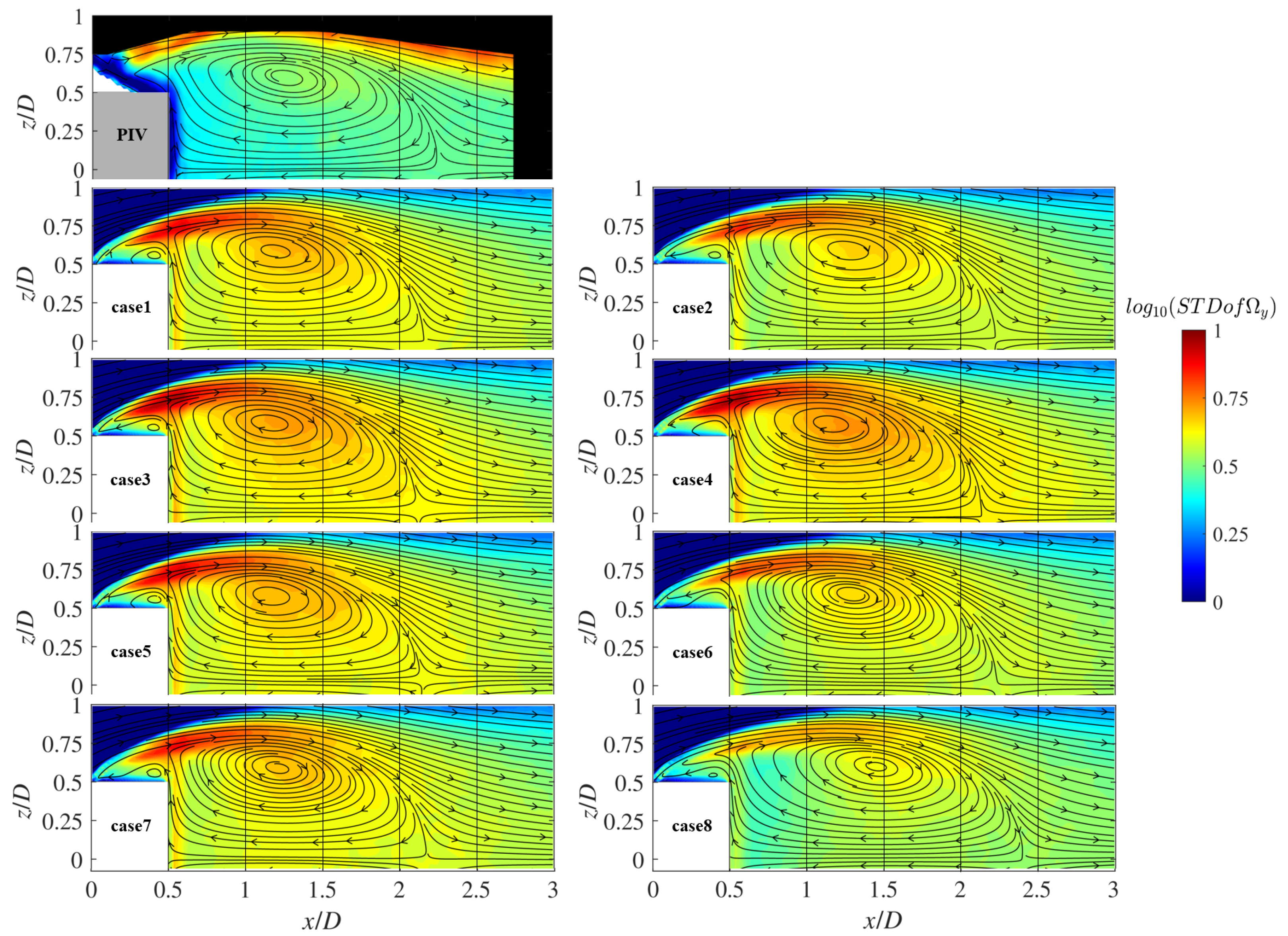
3.8.2. Comparison of the Standard Deviation (STD) of the Vorticity Component
3.8.3. Relationship Between Parameter Tuning and Improvement in Time-Averaged Velocity Distribution
3.8.4. Relationship Between Parameter Tuning and Frequency Analysis Results
3.8.5. Effect of Parameter Tuning in DES Through Comparison with LES and Consideration of Possible Improvements for Simulation Accuracy of DES
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asada, K.; Kawai, S. Large-eddy simulation of airfoil flow near stall condition at Reynolds number 2.1 × 106. Phys. Fluids 2018, 30, 085103-1–085103-22. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Slotnick, J.P. Overview and Summary of the Second AIAA High Lift Prediction Workshop. In Proceedings of the AIAA Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA paper 2014-0747. [Google Scholar]
- Sawada, E.; Aoyama, T.; Hamamoto, S.; Matsushima, K.; Imamura, T.; Yoshimoto, M.; Ueno, Y.; Nakakita, K.; Murayama, M. 6th Aerodynamics Prediction Challenge (APC-6). In Proceedings of the Fluid Dynamics Conference/Aerospace Numerical Simulation Symposium 2020 Online, Online, 28–30 September 2020. JAXA-SP-20-005. [Google Scholar]
- Strelets, M. Detached eddy simulation of massively separated flows. In Proceedings of the 39th Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 8–11 January 2001. AIAA 2001-0879. [Google Scholar]
- Imamura, T.; Tamaki, Y. Unsteady Flow Simulation around Two-wheel Main Landing Gear based on Compressible Navier-Stokes Solver with Immersed Boundary Method. In Proceedings of the AIAA AVIATION 2020 FORUM, Virtual Event, 8 June 2020. AIAA 2020-2579. [Google Scholar]
- Ohmichi, Y.; Kobayashi, K.; Kanazaki, M. Numerical investigation of wake structures of an atmospheric entry capsule by modal analysis. Phys. Fluids 2019, 31, 074105-1-12. [Google Scholar] [CrossRef]
- Caruelle, B.; Ducros, F. Detached-Eddy Simulations of Attached and Detached Boundary Layers. Int. J. Comput. Fluid Dyn. 2003, 17, 433–451. [Google Scholar] [CrossRef]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Kato, H.; Ishiko, K.; Yoshizawa, A. Optimization of Parameter Values in the Turbulence Model Aided by Data Assimilation. AIAA J. 2016, 54, 1512–1523. [Google Scholar] [CrossRef]
- Nakamura, M.; Ozawa, Y.; Nonomura, T. Low-grid-resolution-RANS-based Data Assimilation of Time Averaged Separated Flow Obtained by LES. Int. J. Comput. Fluid Dyn. 2022, 36, 167–185. [Google Scholar] [CrossRef]
- Berger, E.; Scholz, D.; Schumm, M. Coherent Vortex Structures in the Wake of a Sphere and a Circular Disk at Rest and Under Forced Vibrations. J. Fluids Struct. 1990, 4, 231–257. [Google Scholar] [CrossRef]
- Yang, J.; Liu, M.; Wu, G.; Zhong, W.; Zhang, X. Numerical Study on coherent structure behind a circular disk. J. Fluids Struct. 2014, 51, 172–188. [Google Scholar] [CrossRef]
- Camarri, S.; Salvetti, M.V.; Koobus, B.; Dervieux, A. Large-Eddy Simulation of a Bluff-Body Flow on Unstructured Grids. Int. J. Numer. Methods Fluids 2002, 40, 1431–1460. [Google Scholar] [CrossRef]
- Tiras, F.X.; Gorobets, A.; Oliva, A. Turbulent Flow around a Square Cylinder at Reynolds Number 22,000: A DNS Study. Comput. Fluids 2015, 123, 87–98. [Google Scholar] [CrossRef]
- Ito, S.; Furukawa, M.; Yamada, K.; Manabe, K. Applying Ensemble Kalman Filter to Transonic Flows Through a Two-Dimensional Turbine Cascade. J. Fluids Eng. 2021, 143, 121113. [Google Scholar] [CrossRef]
- Okuizumi, H.; Sawada, H.; Nagaike, H.; Konishi, Y.; Obayashi, S. Introduction of 1-m MSBS in Tohoku University, New Device for Aerodynamics Measurements of the Sports Equipment. In Proceedings of the 12th Conference of the International Sports Engineering Association (Proceeding Paper), Brisbane, QLD, Australia, 26–29 March 2018; Volume 2. [Google Scholar]
- Kuwata, M.; Abe, Y.; Sho, Y.; Nonomura, T.; Sawada, H.; Yakeno, A.; Asai, K.; Obayashi, S. Flow Characteristics around Extremely Low Fineness-Ratio Circular Cylinders. Phys. Rev. Fluids 2021, 6, 1–14. [Google Scholar] [CrossRef]
- Spalart, P.A.; Allmaras, S. One-Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, Nevada, 6–9 January 1992. AIAA-92-0439. [Google Scholar]
- Tamaki, Y.; Imamura, T. Turbulent Flow Simulations of the NASA Common Research Model Using the Immersed Boundary Method with a Wall Function. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. AIAA 2017-4235. [Google Scholar]
- Mavriplis, D.J. Revisiting the Least-Squares Procedure for Gradient Reconstruction on Unstructured. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003. AIAA 2003-3986. [Google Scholar]
- van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Shima, E.; Kitamura, K. On New Simple Low-Dissipation Scheme of AUSM-Family for akk Speeds. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. AIAA-2009-136. [Google Scholar]
- Yoon, S.; Jameson, A. Lower-upper Symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations. AIAA J. 1988, 26, 1025–1026. [Google Scholar] [CrossRef]
- Tippett, M.K.; Anderson, J.L.; Bishop, C.H.; Hamill, T.M.; Whitaker, J.S. Ensemble Square Root Filters. Mon. Weather. Rev. 2003, 131, 1485–1490. [Google Scholar] [CrossRef]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-Geostrophic Model using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Fujii, K. Developing an Accurate and Efficient Method for Compressible Flow Simulation—An Example of CFD in Aeronautics. In Proceedings of the 5th International Conference on Numerical Ship Hydrodynamics, Washington, DC, USA, 24–28 September 1990. [Google Scholar]




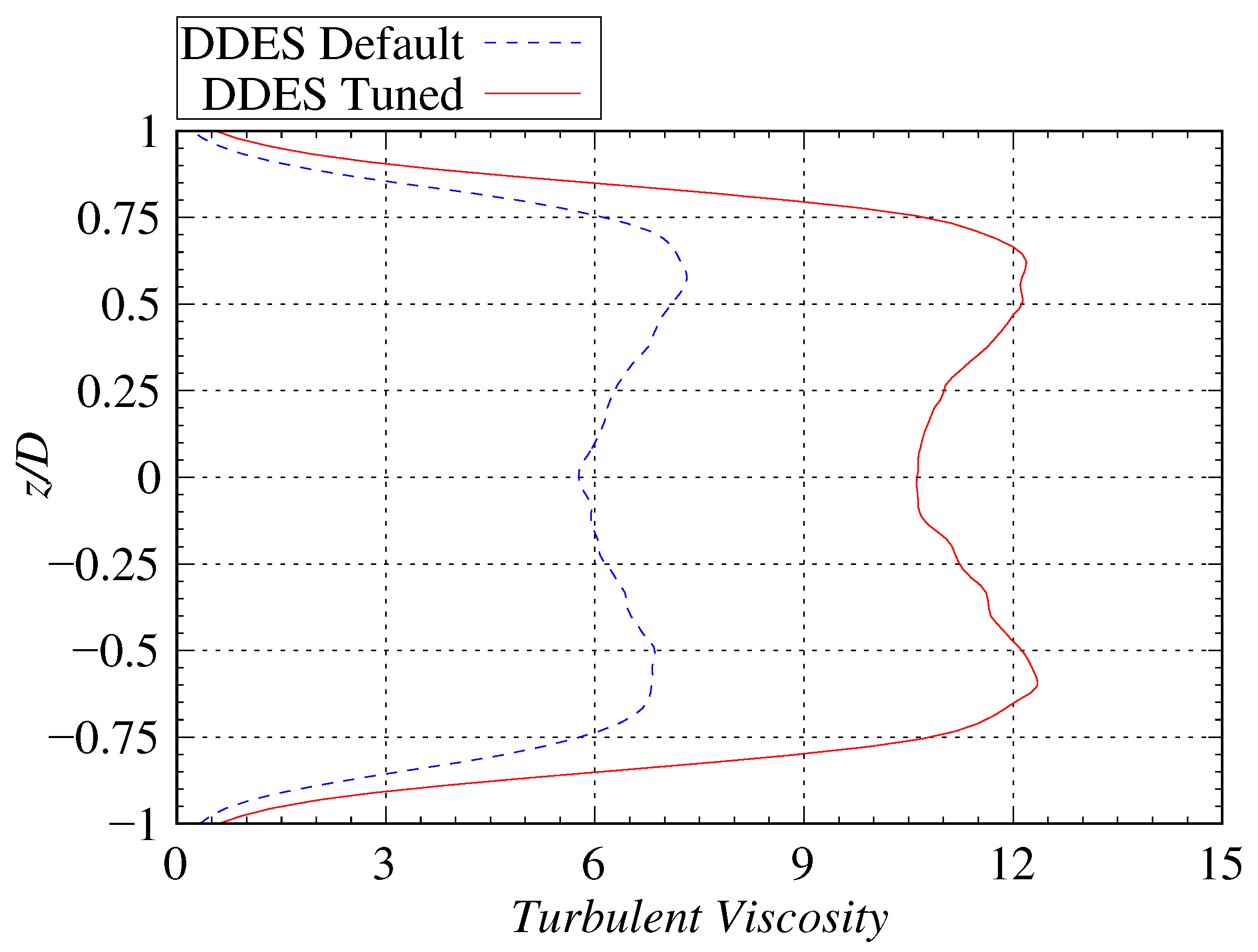
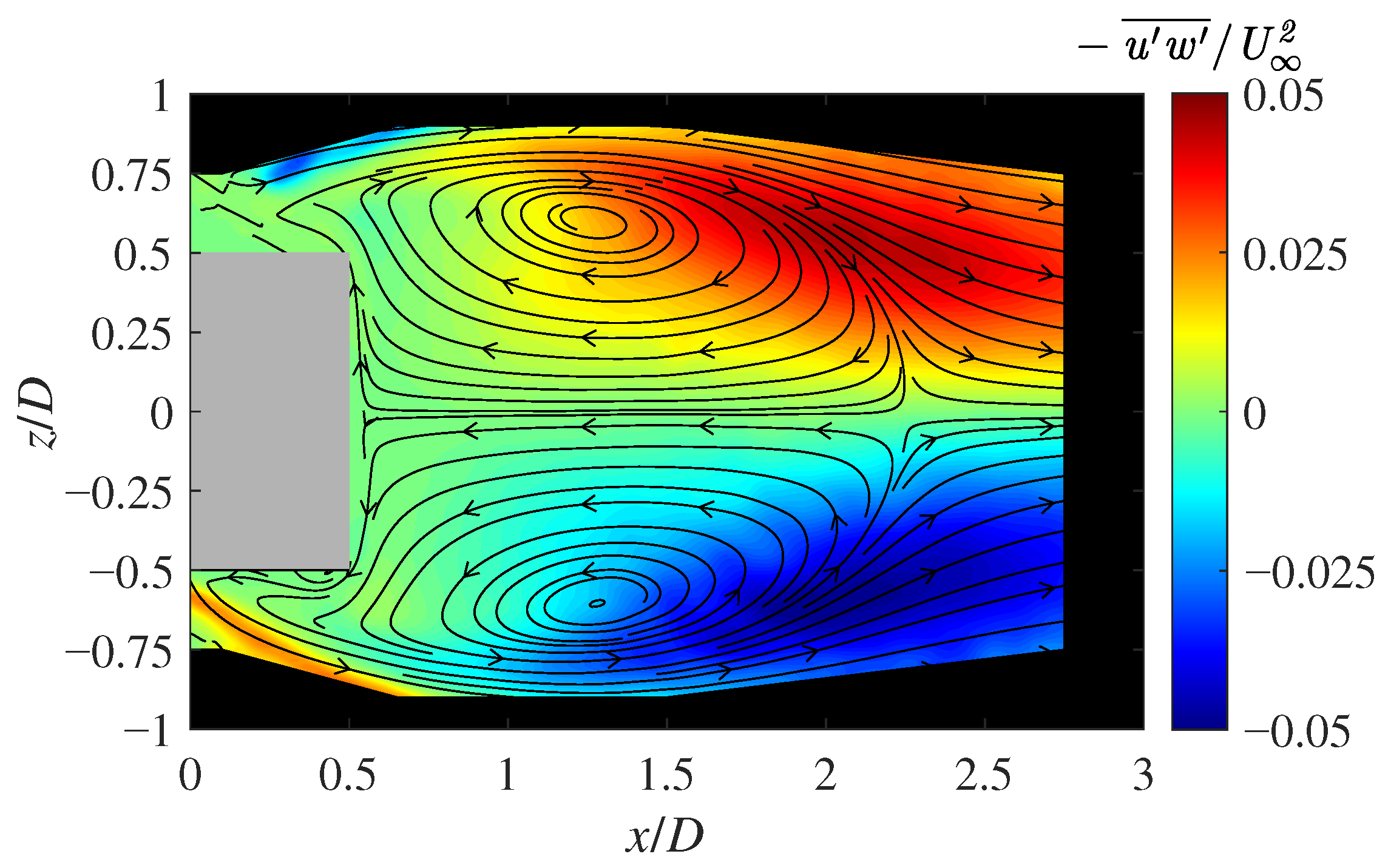
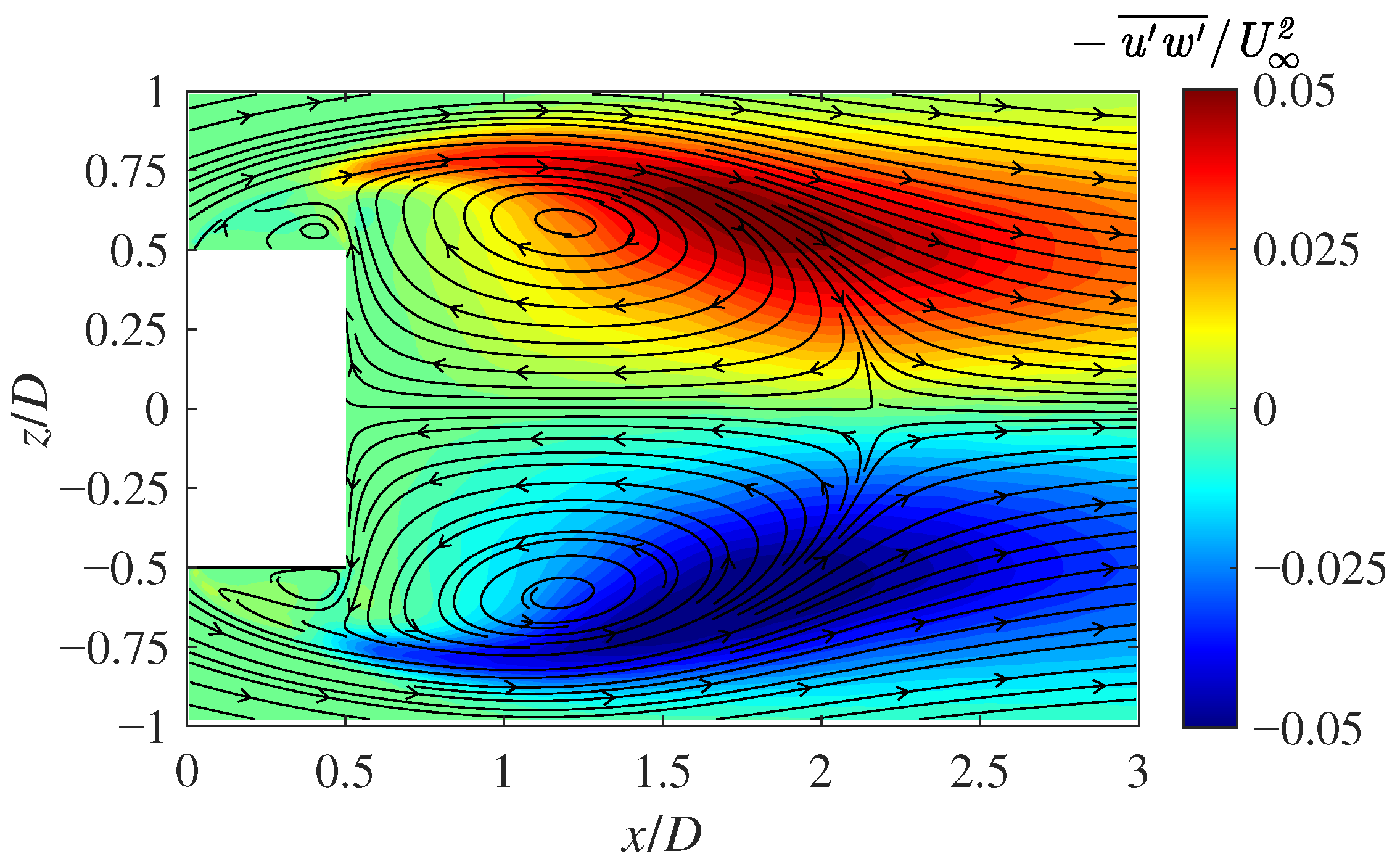

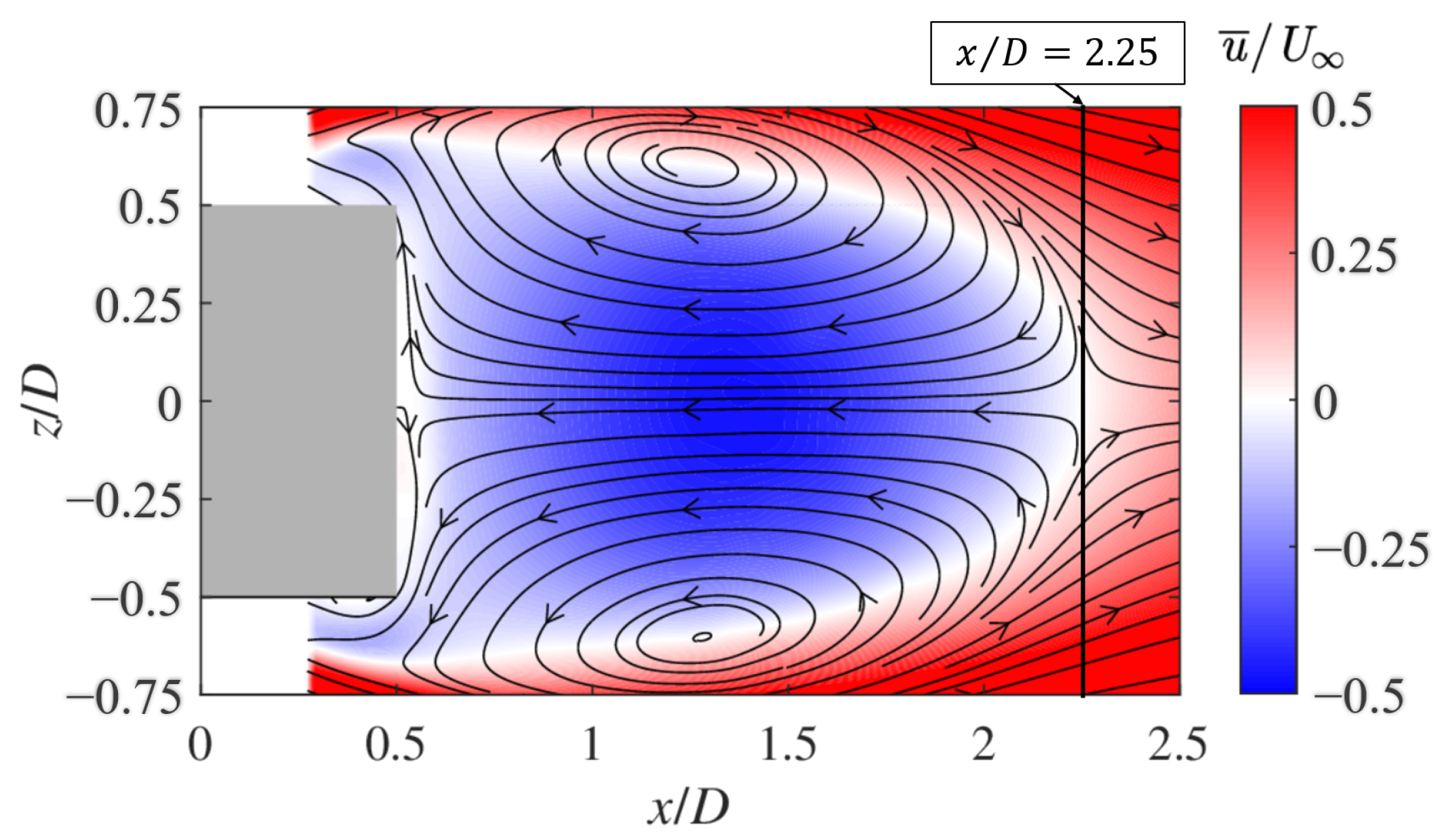





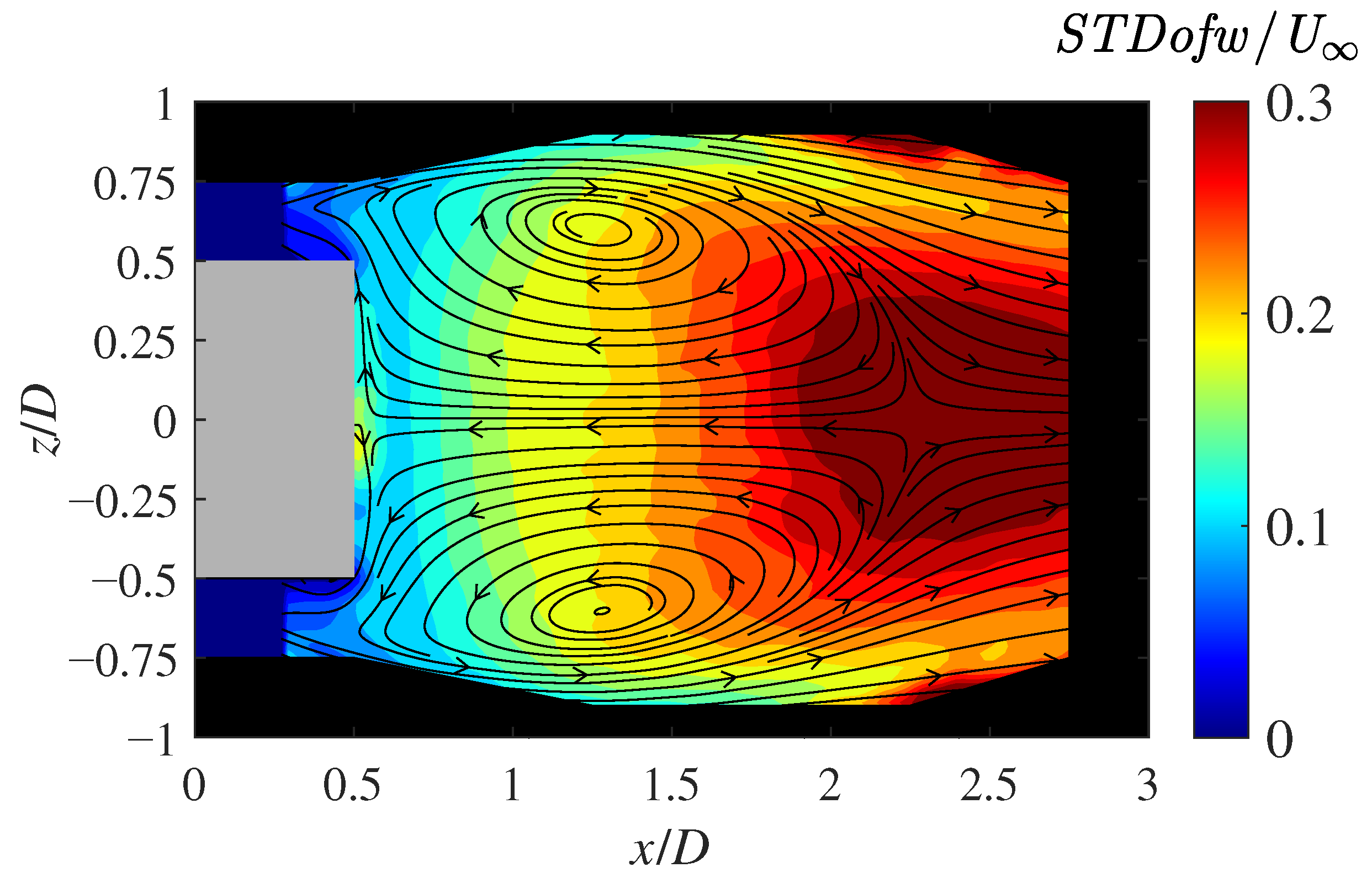

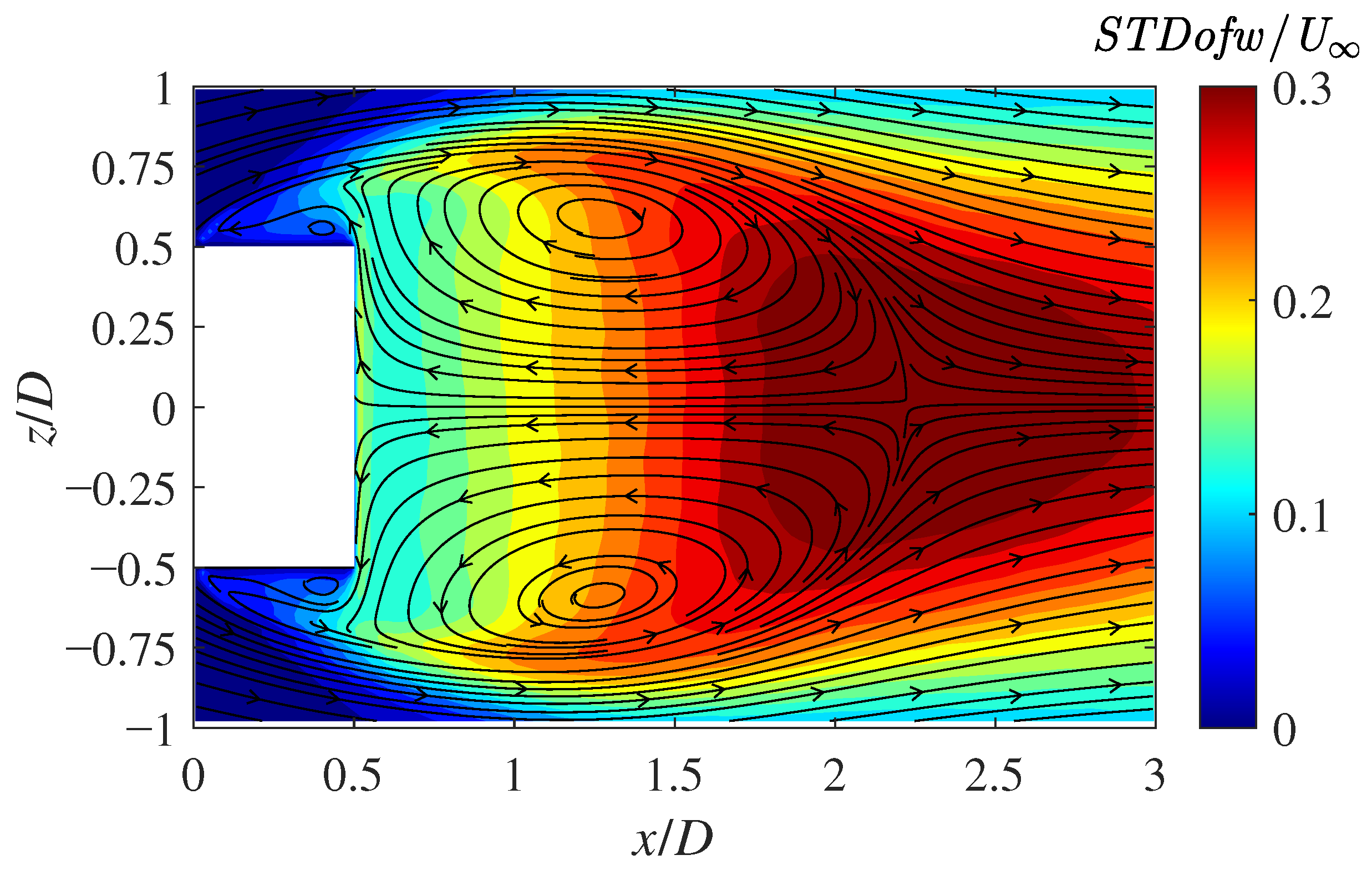
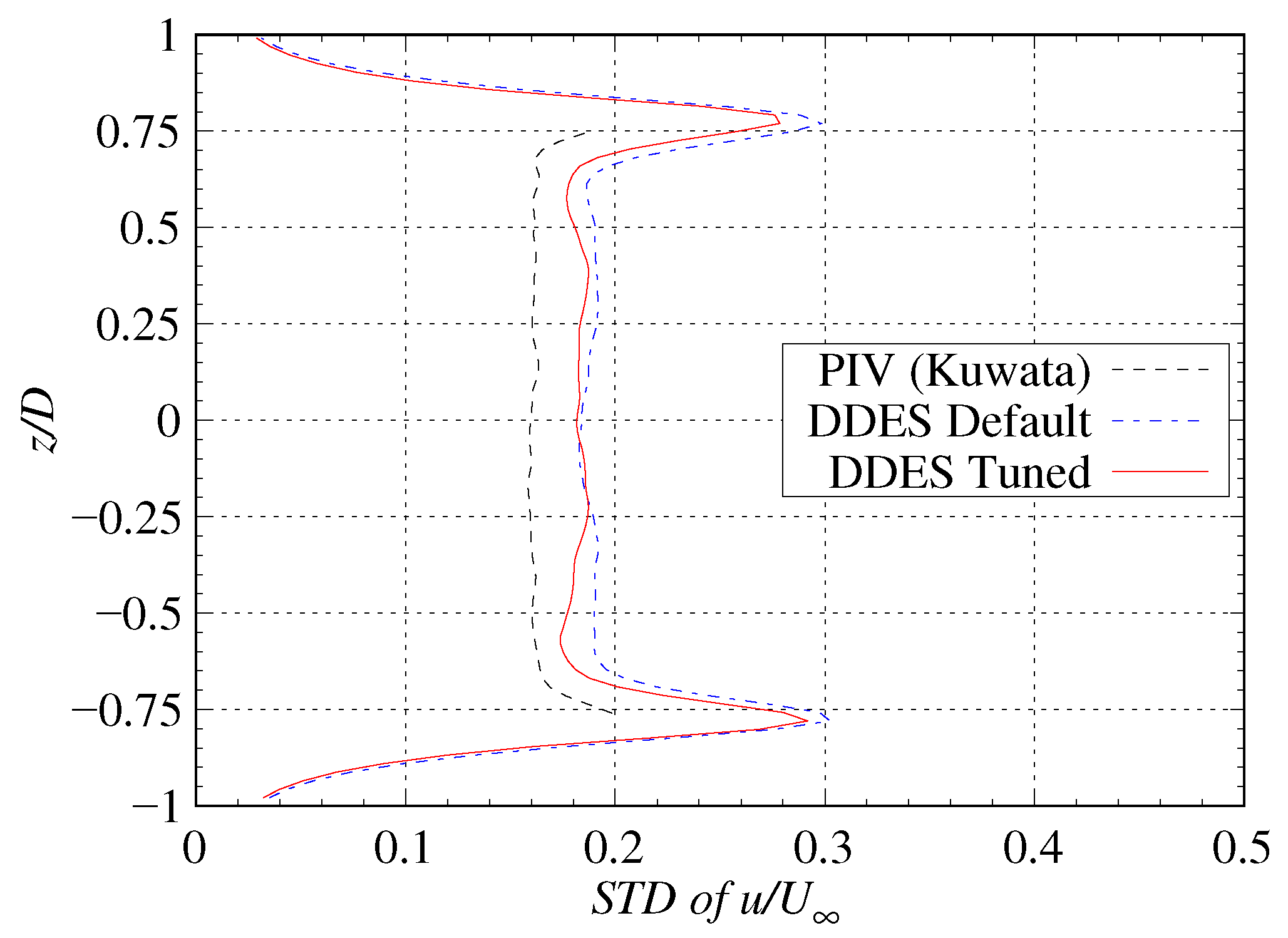
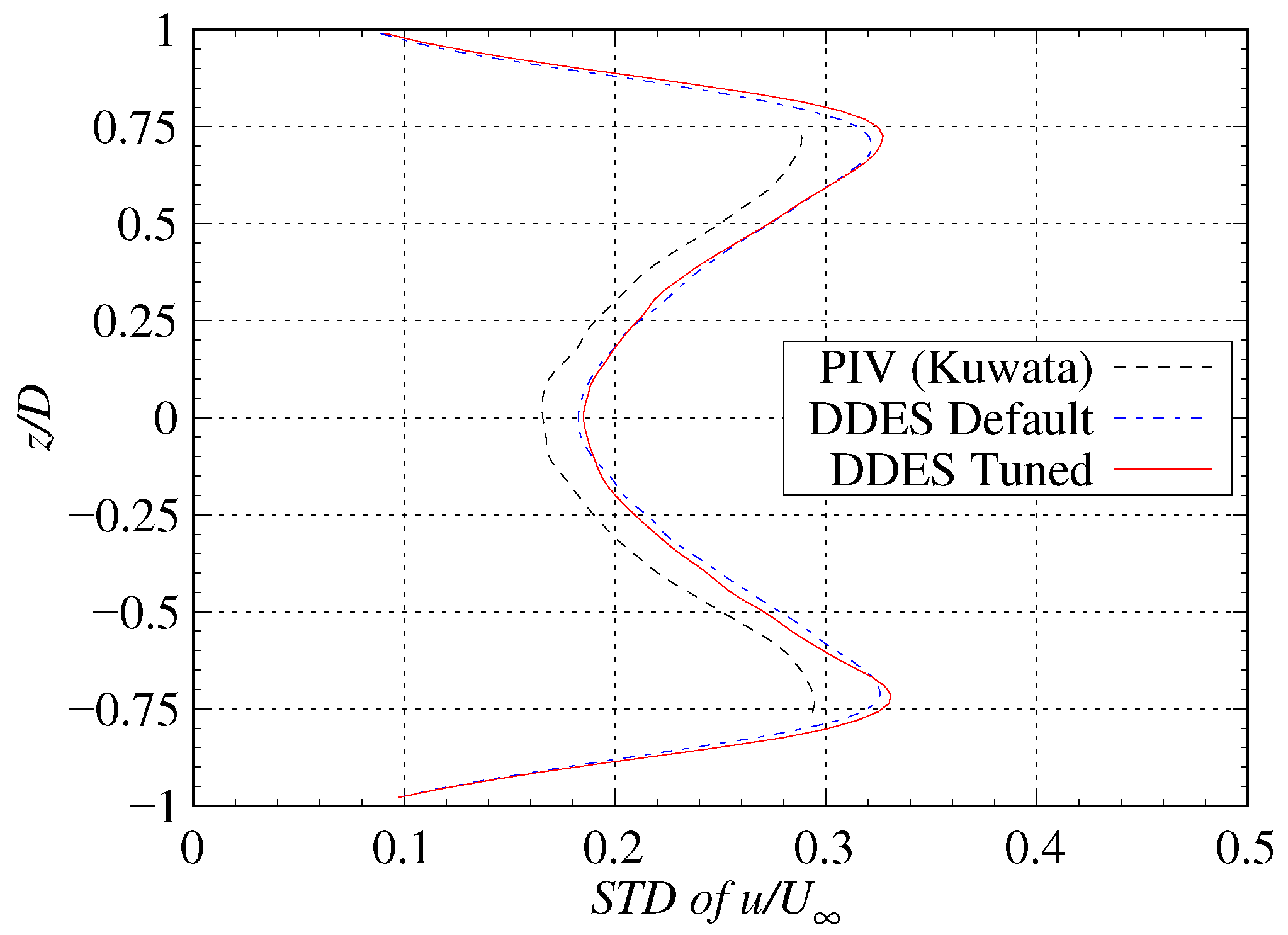
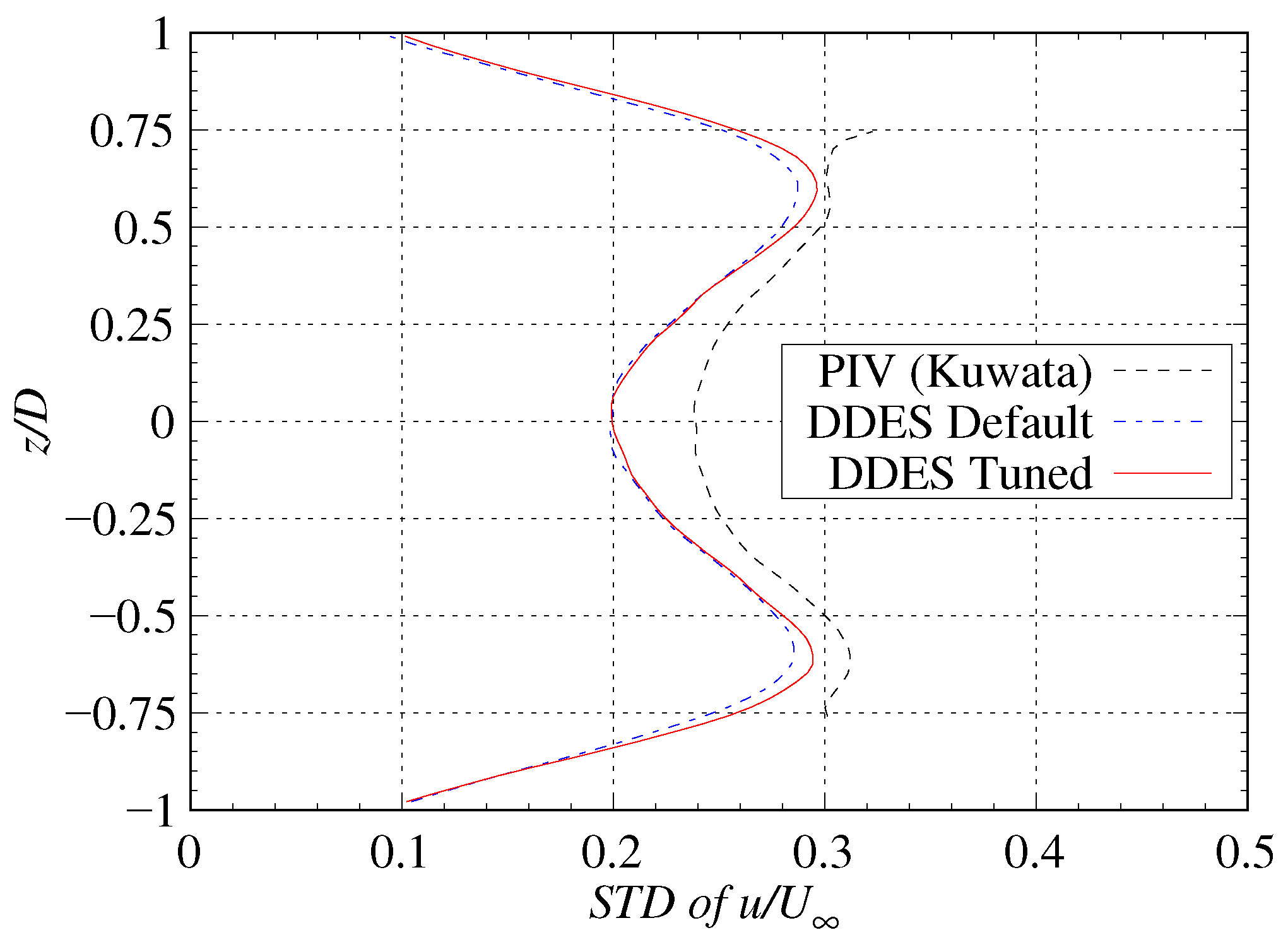
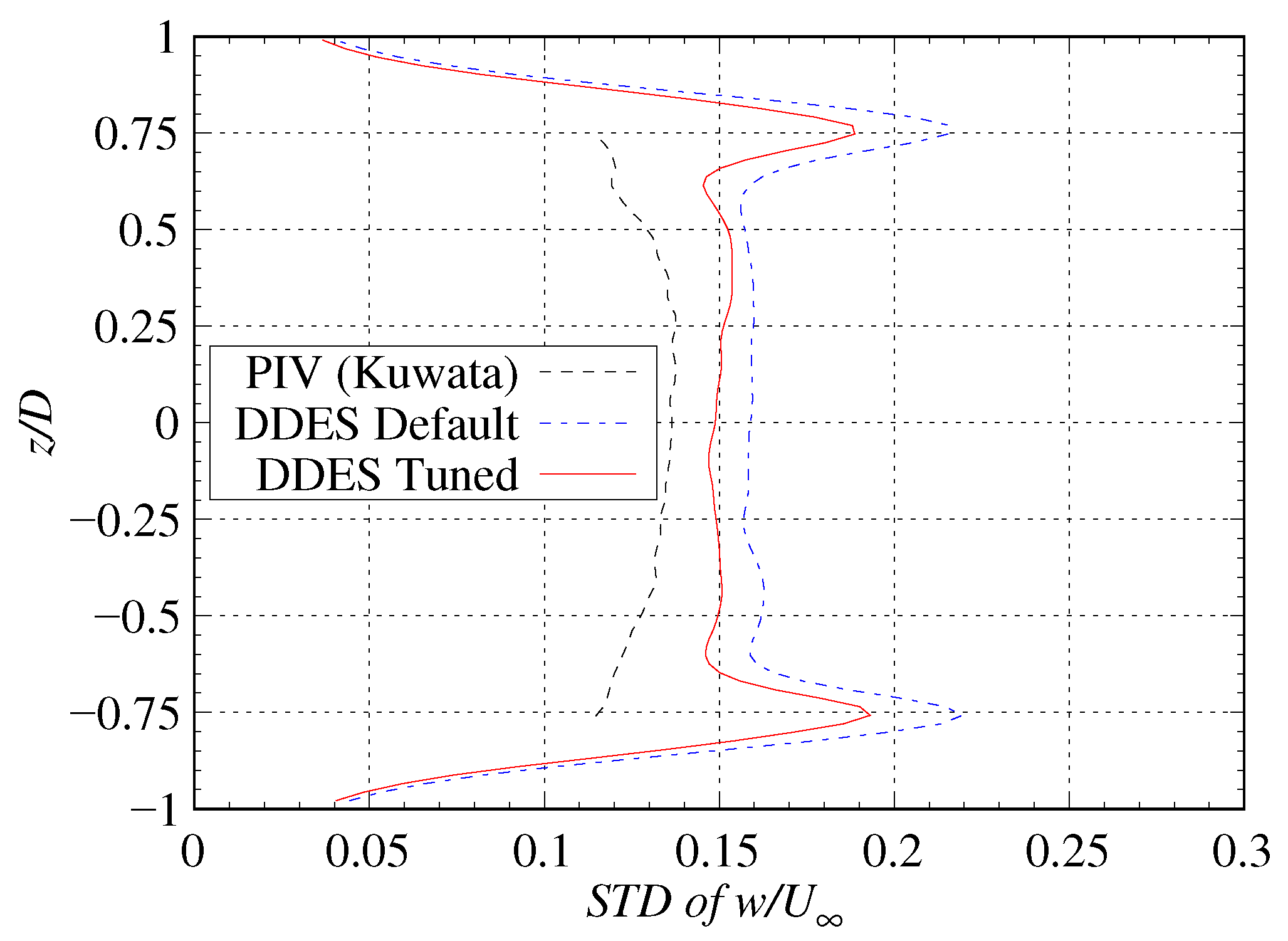

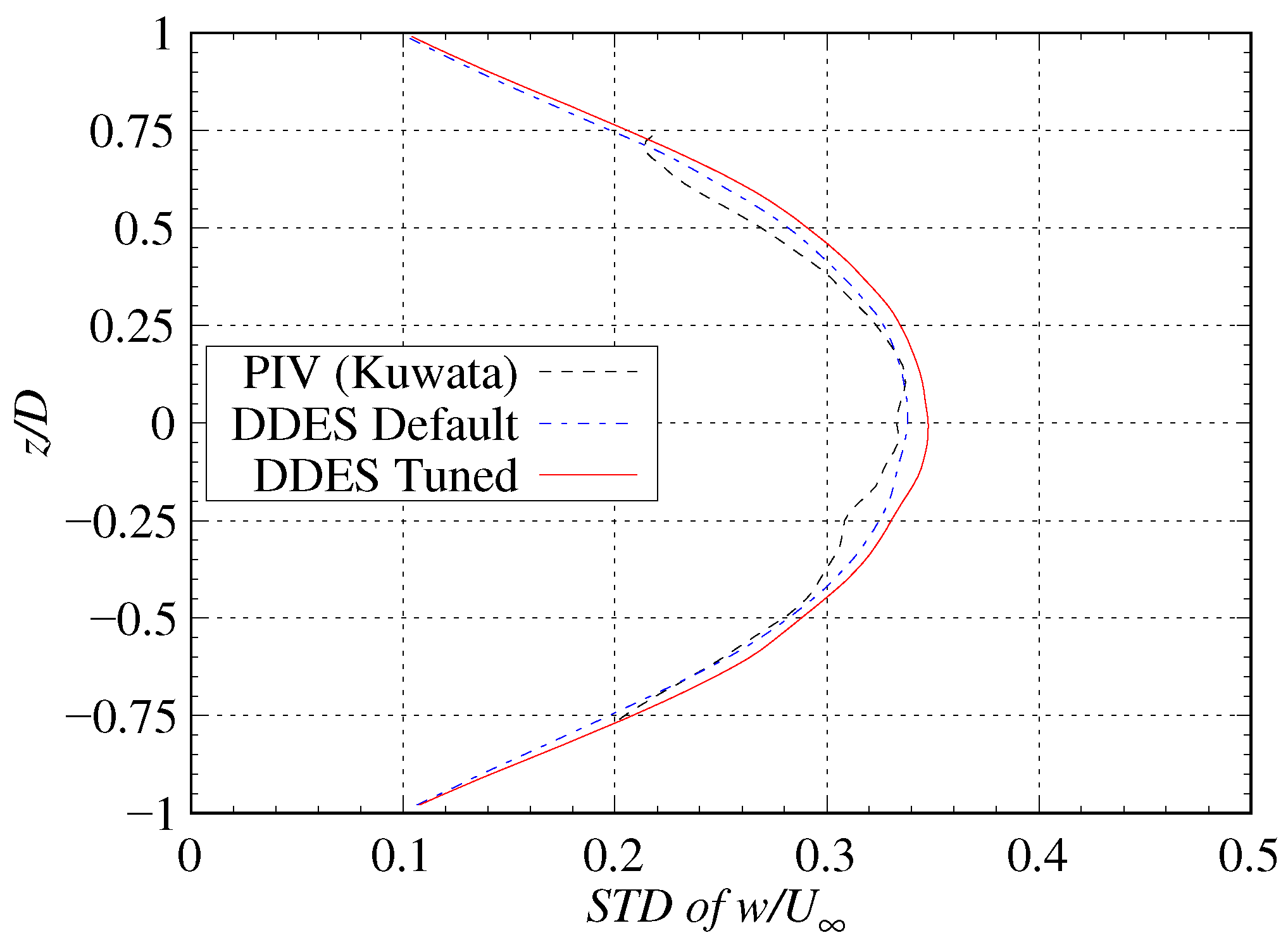
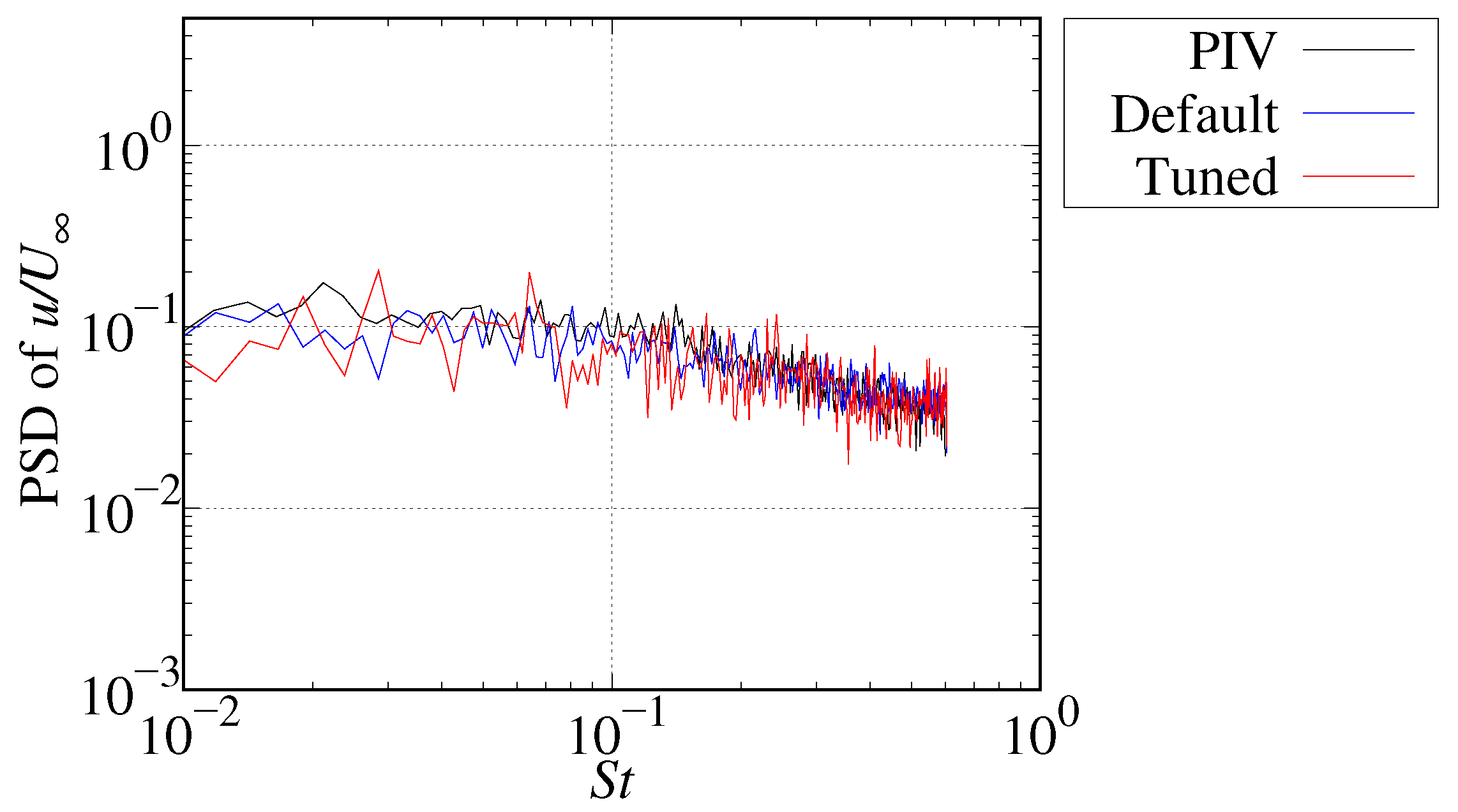
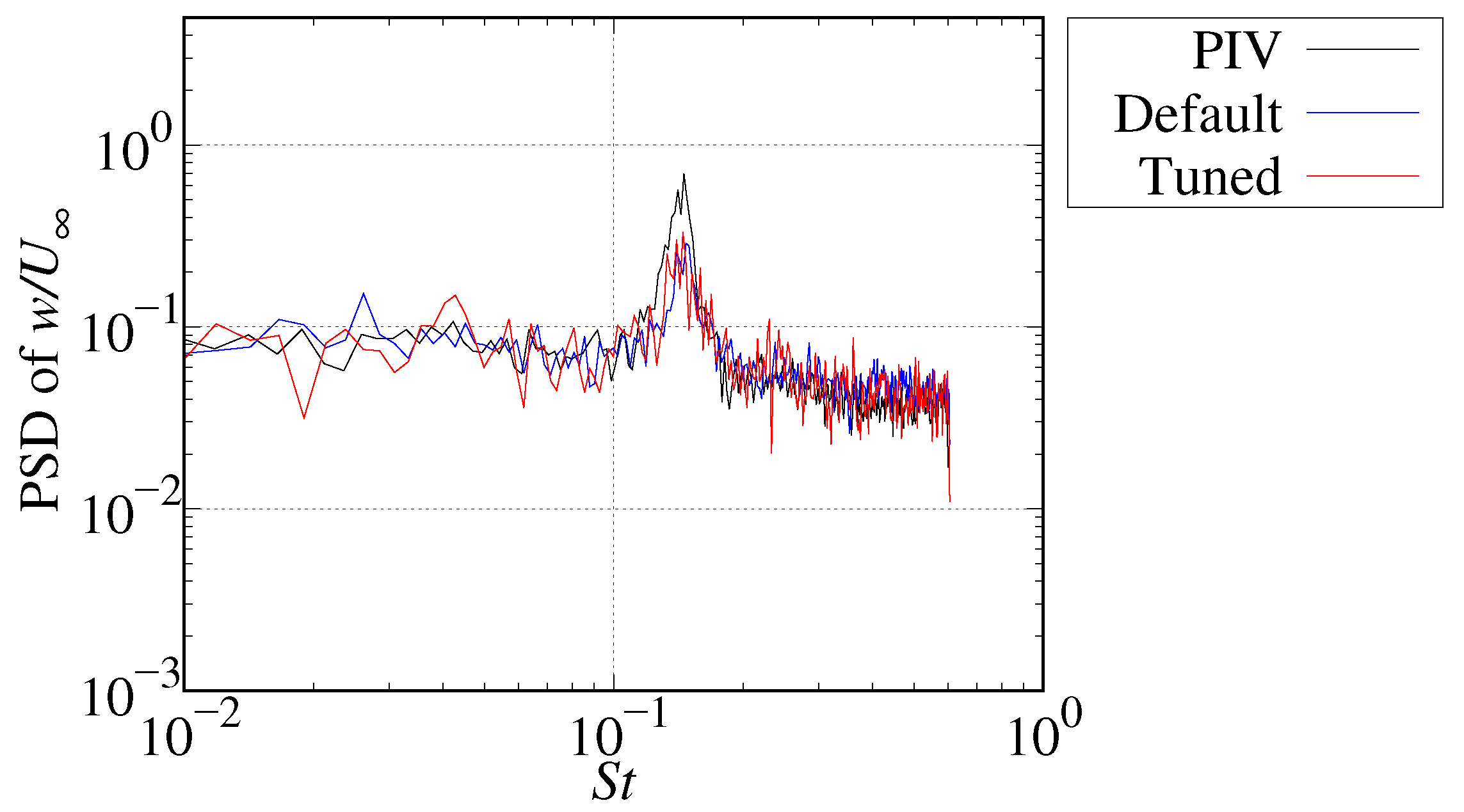

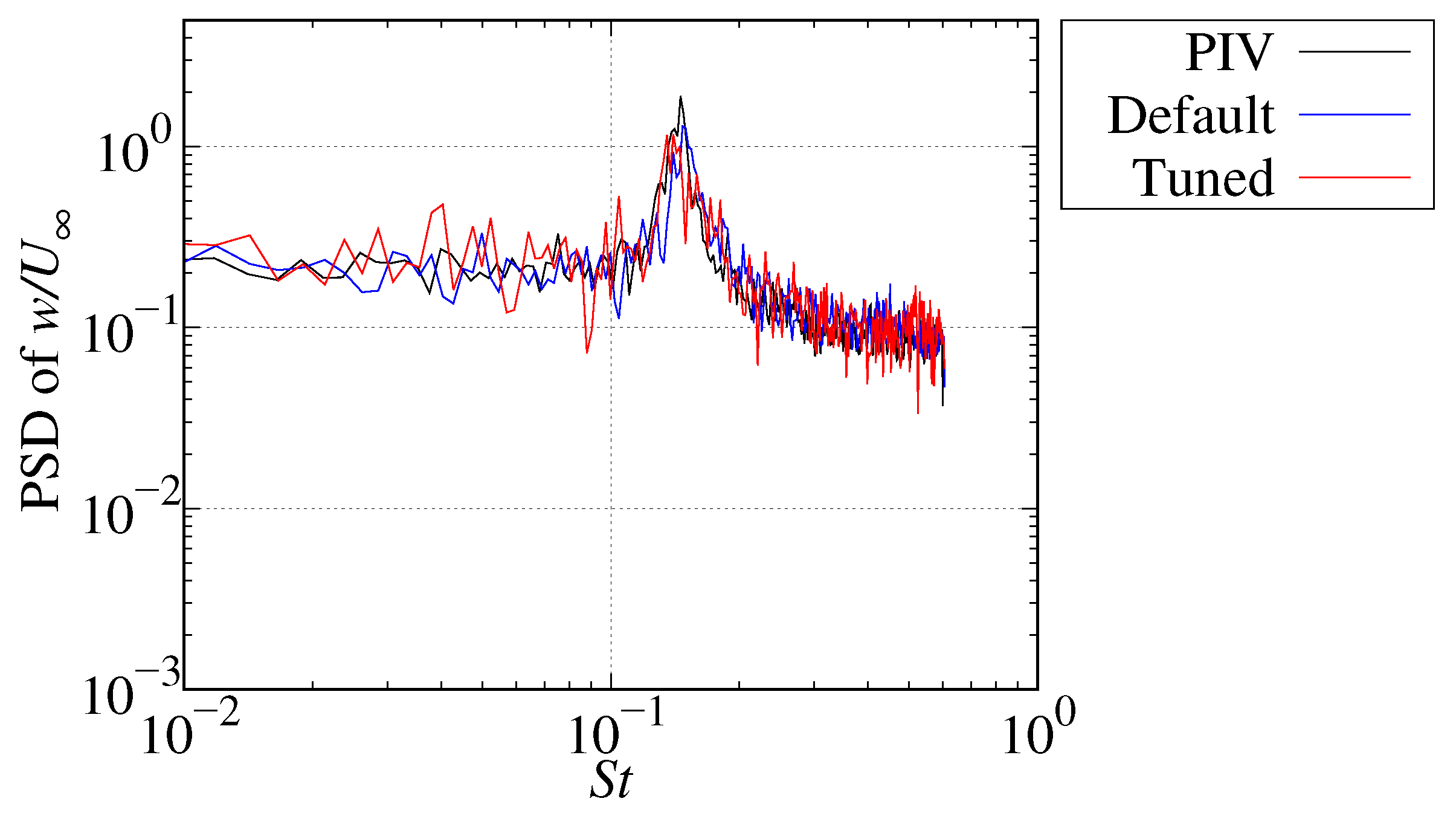


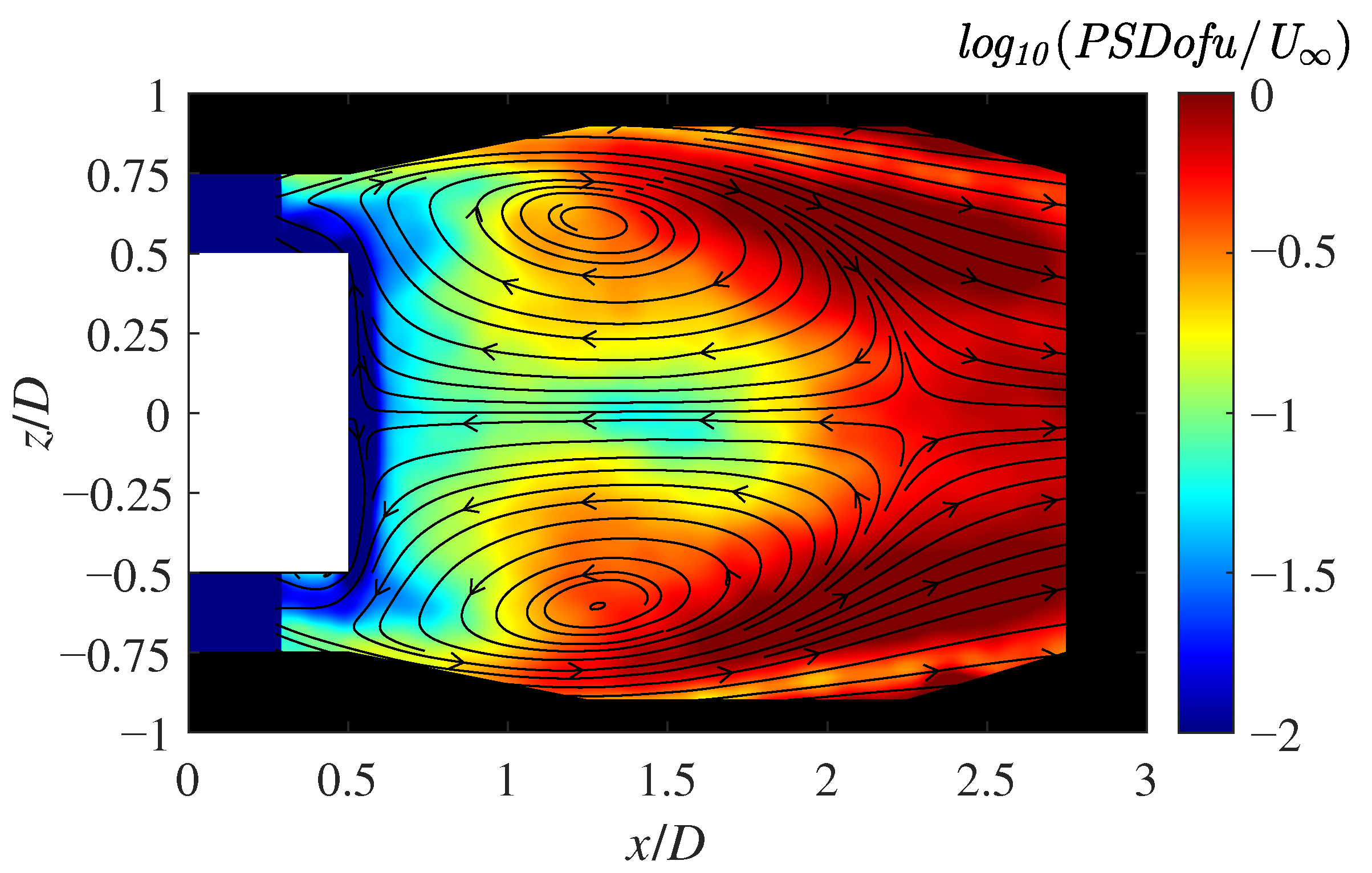
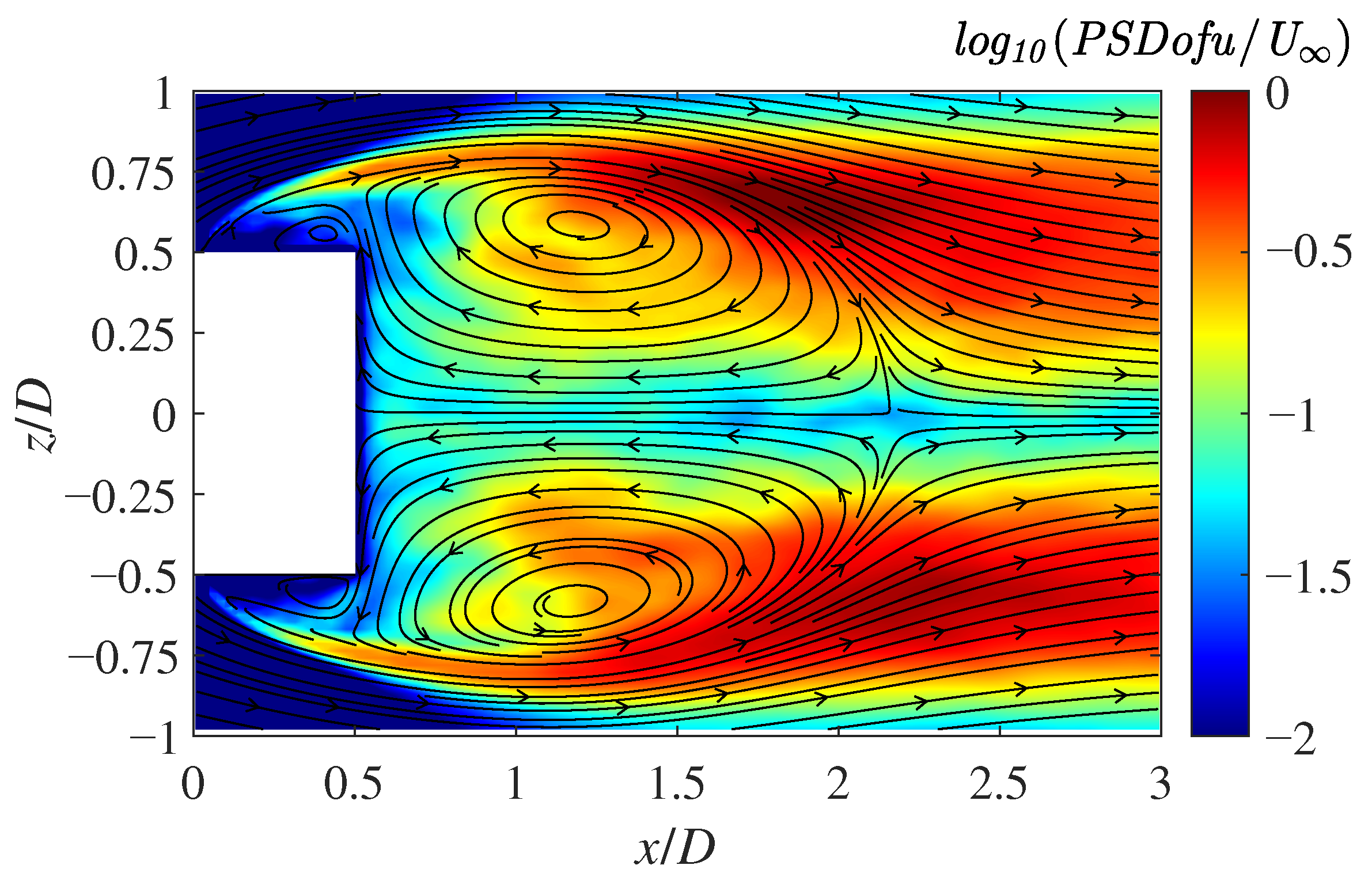







| Parameter | Default | Tuned | Relative Error |
|---|---|---|---|
| 0.1355 | 0.1185 | 12.5% | |
| 0.65 | 0.8292 | 27.5% |
| Location | Value | |
|---|---|---|
| PIV (Kuwata) | 1.40 | −0.471 |
| DDES-Default | 1.23 | −0.483 |
| DDES-Tuned | 1.35 | −0.468 |
| Case 1 | 0.1355 (default) | 0.65 (default) |
| Case 2 | 0.1083 (tuned) | 0.8619 (tuned) |
| Case 3 | 0.06 | 0.65 |
| Case 4 | 0.1083 | 0.65 |
| Case 5 | 0.2 | 0.65 |
| Case 6 | 0.1355 | 0.4 |
| Case 7 | 0.1355 | 0.8619 |
| Case 8 | 0.1355 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nomoto, K.; Obayashi, S. Parameter Tuning of Detached Eddy Simulation Using Data Assimilation for Enhancing the Simulation Accuracy of Large-Scale Separated Flow Around a Cylinder. Aerospace 2025, 12, 736. https://doi.org/10.3390/aerospace12080736
Nomoto K, Obayashi S. Parameter Tuning of Detached Eddy Simulation Using Data Assimilation for Enhancing the Simulation Accuracy of Large-Scale Separated Flow Around a Cylinder. Aerospace. 2025; 12(8):736. https://doi.org/10.3390/aerospace12080736
Chicago/Turabian StyleNomoto, Kyosuke, and Shigeru Obayashi. 2025. "Parameter Tuning of Detached Eddy Simulation Using Data Assimilation for Enhancing the Simulation Accuracy of Large-Scale Separated Flow Around a Cylinder" Aerospace 12, no. 8: 736. https://doi.org/10.3390/aerospace12080736
APA StyleNomoto, K., & Obayashi, S. (2025). Parameter Tuning of Detached Eddy Simulation Using Data Assimilation for Enhancing the Simulation Accuracy of Large-Scale Separated Flow Around a Cylinder. Aerospace, 12(8), 736. https://doi.org/10.3390/aerospace12080736







