Numerical Simulation of Gliding Arc Plasma-Assisted Ignition and Combustion in Afterburner Combustor
Abstract
1. Introduction
2. Numerical Simulation Methods
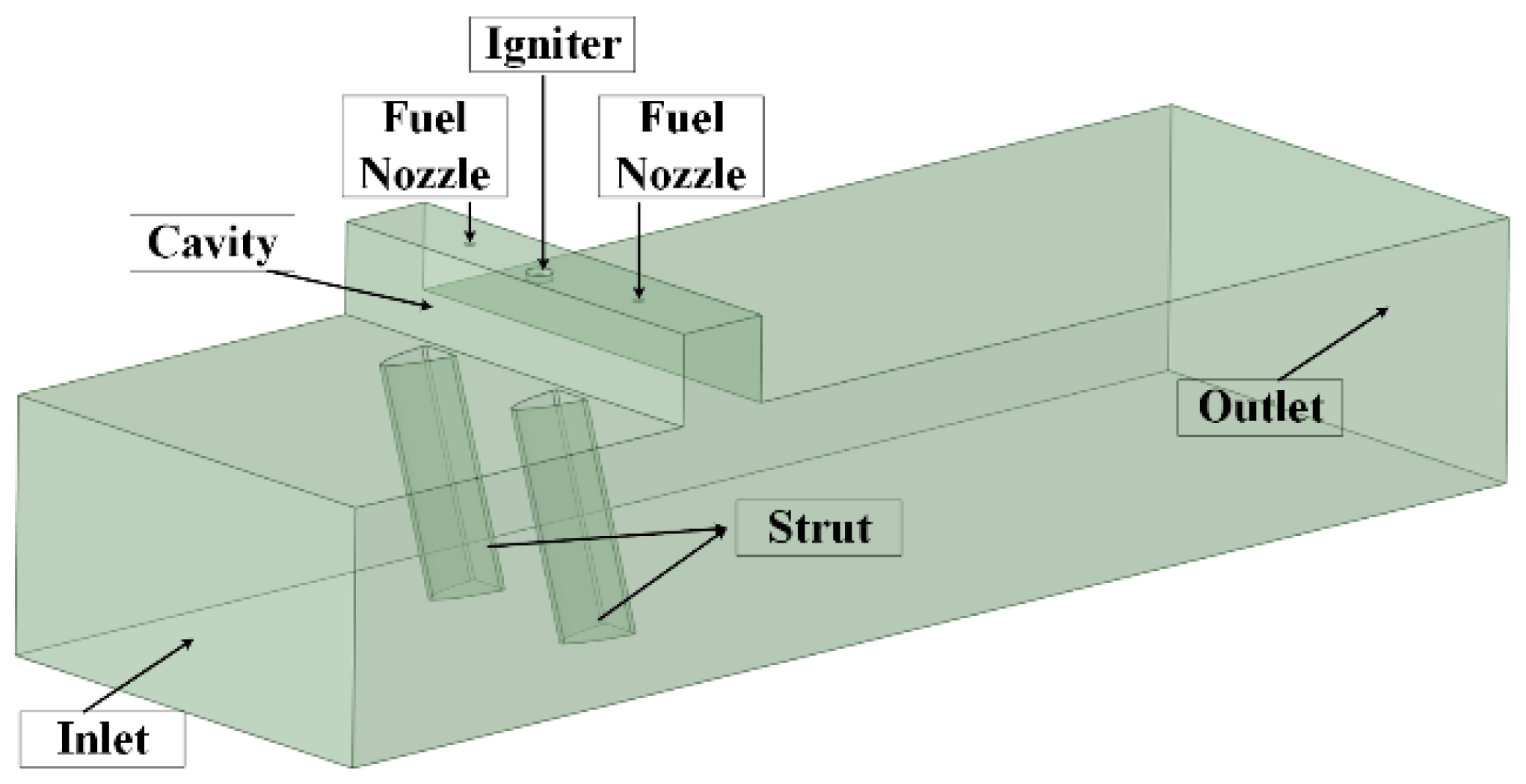
2.1. Geometric Model
2.2. Spark Ignition Model
2.3. Gliding Arc Ignition Model
2.4. Boundary Conditions
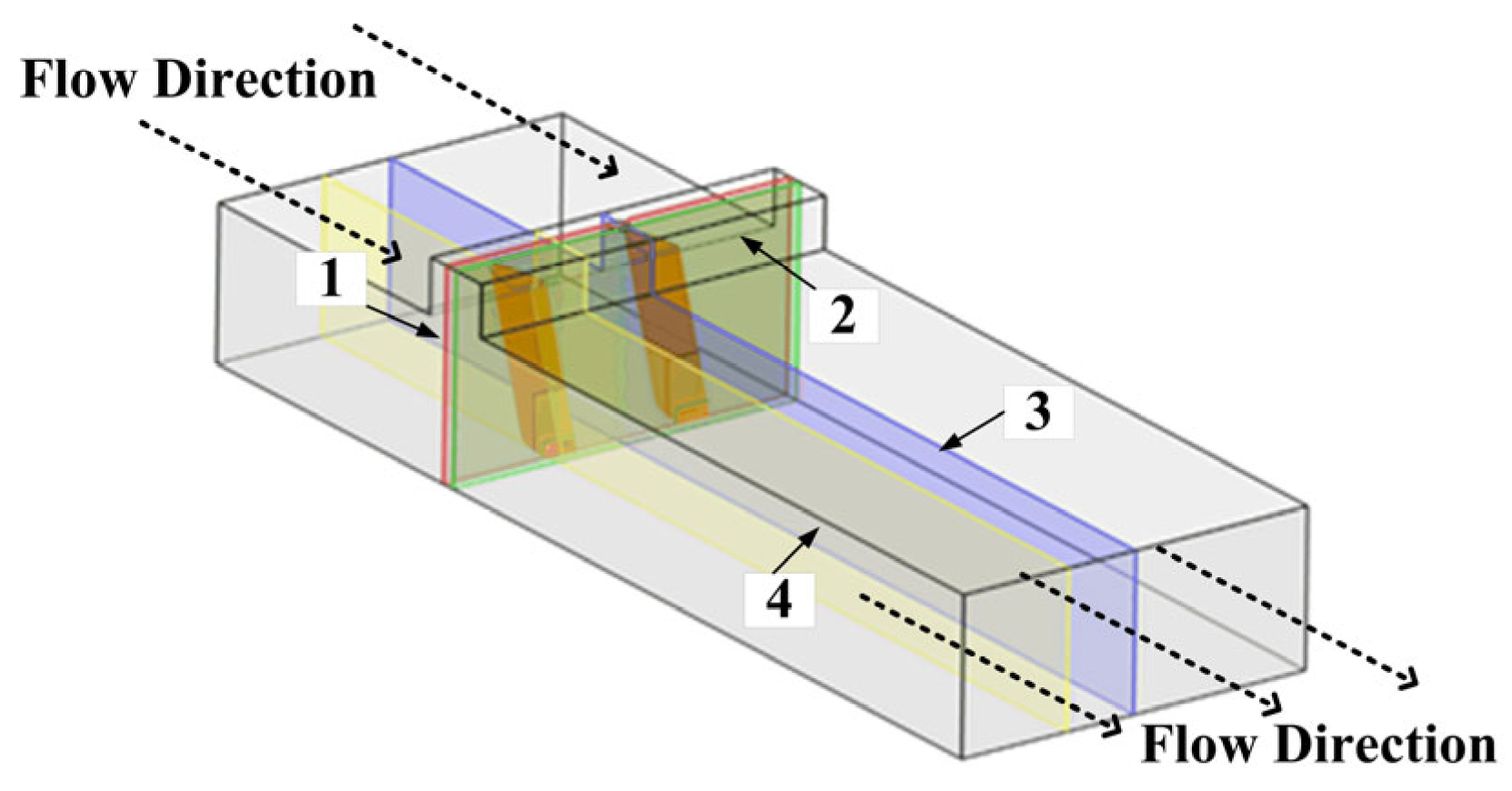
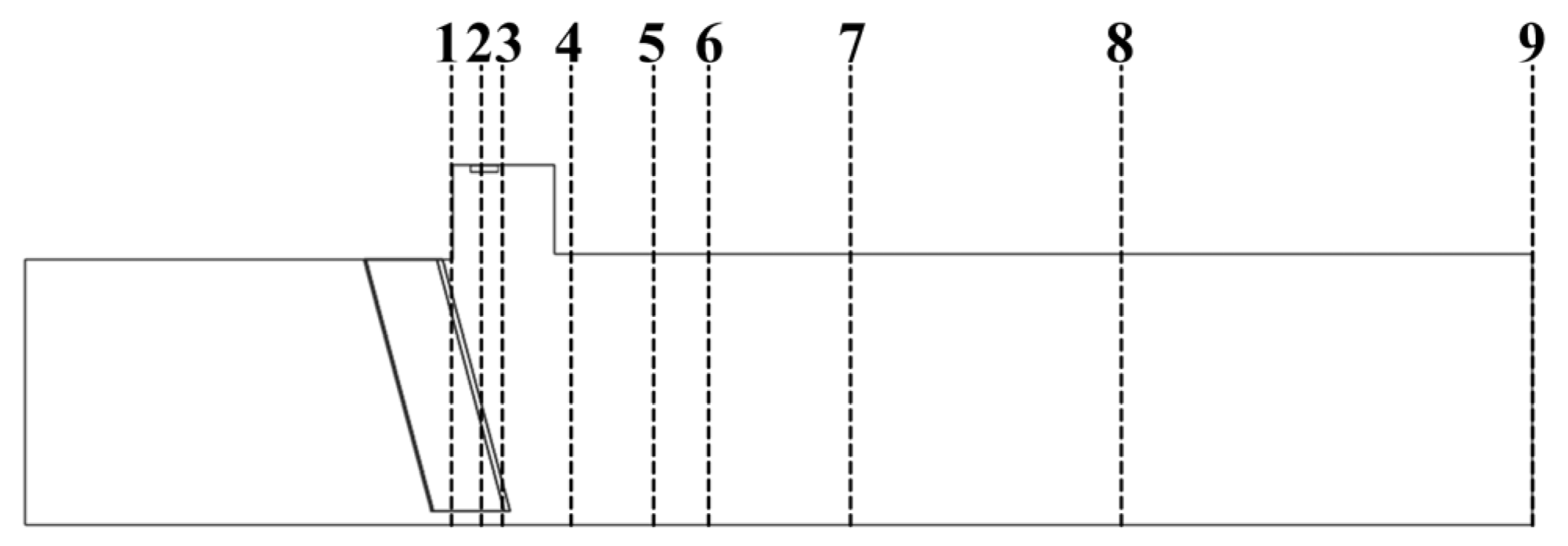
2.5. Cross-Section
2.6. Numerical Setup
2.7. Grid Independence Verification
3. Results Analysis and Discussion
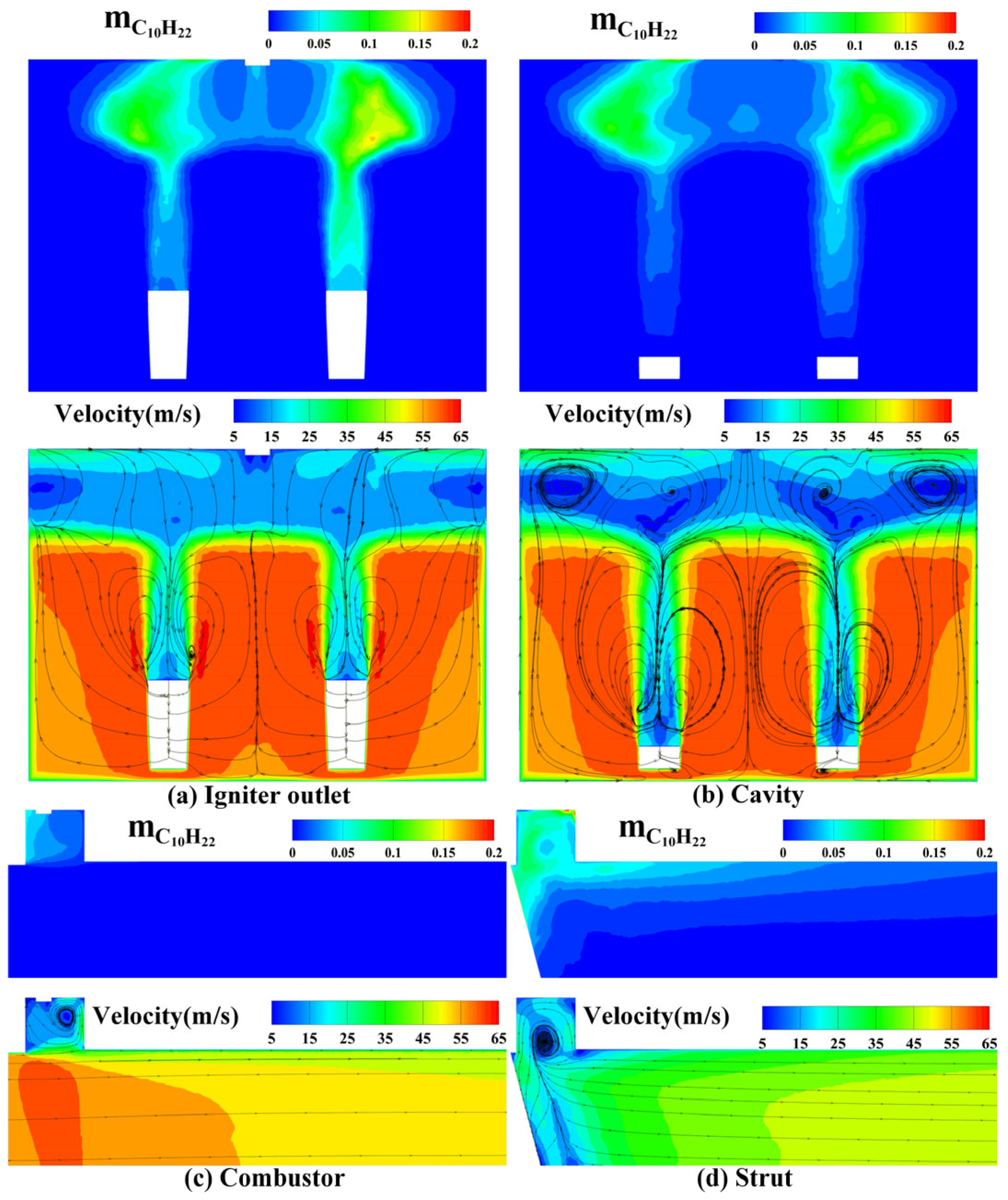
3.1. Distribution of Oil Mist Field and Velocity Field in Cold State
3.2. Ignition Analysis
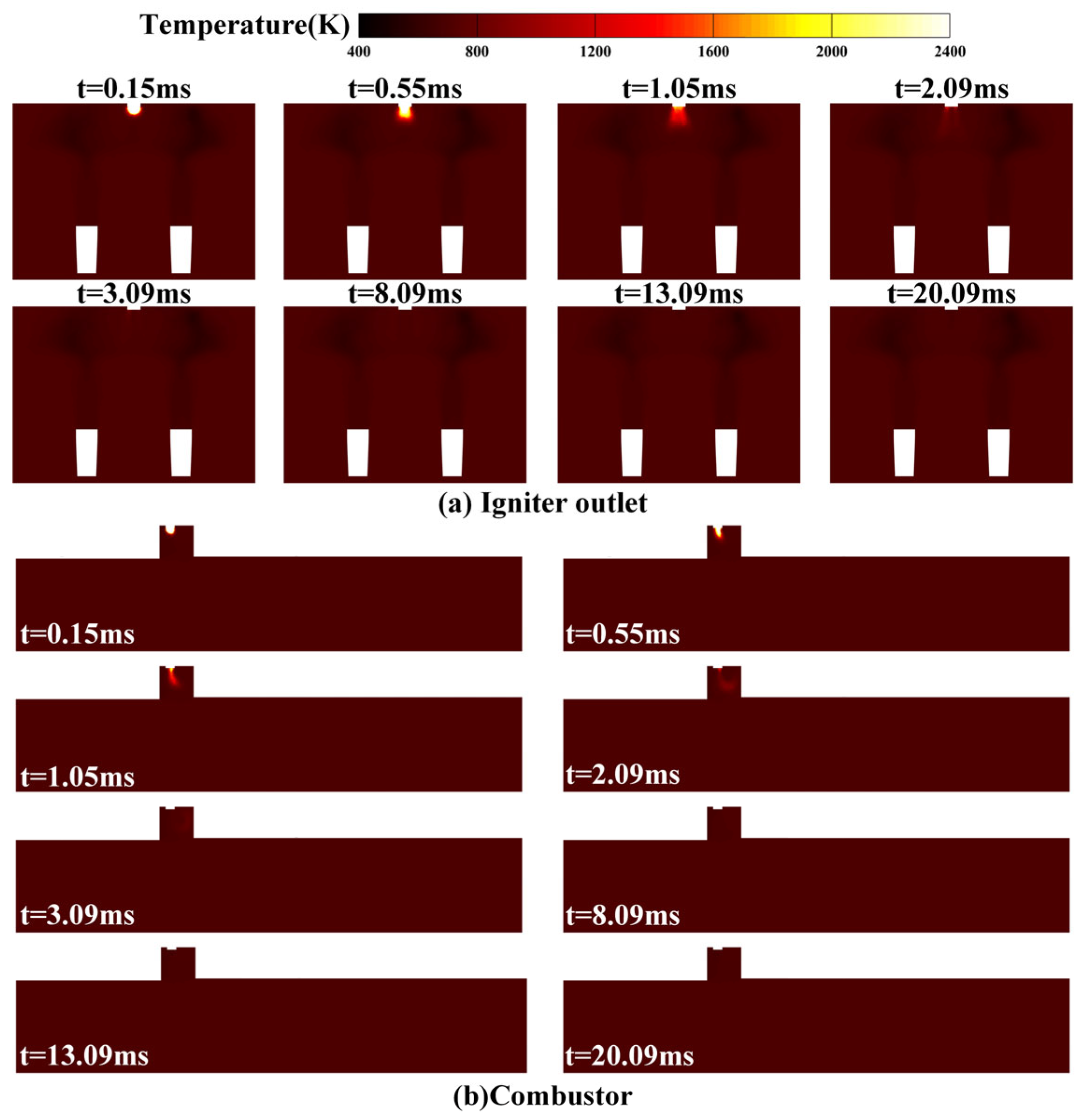
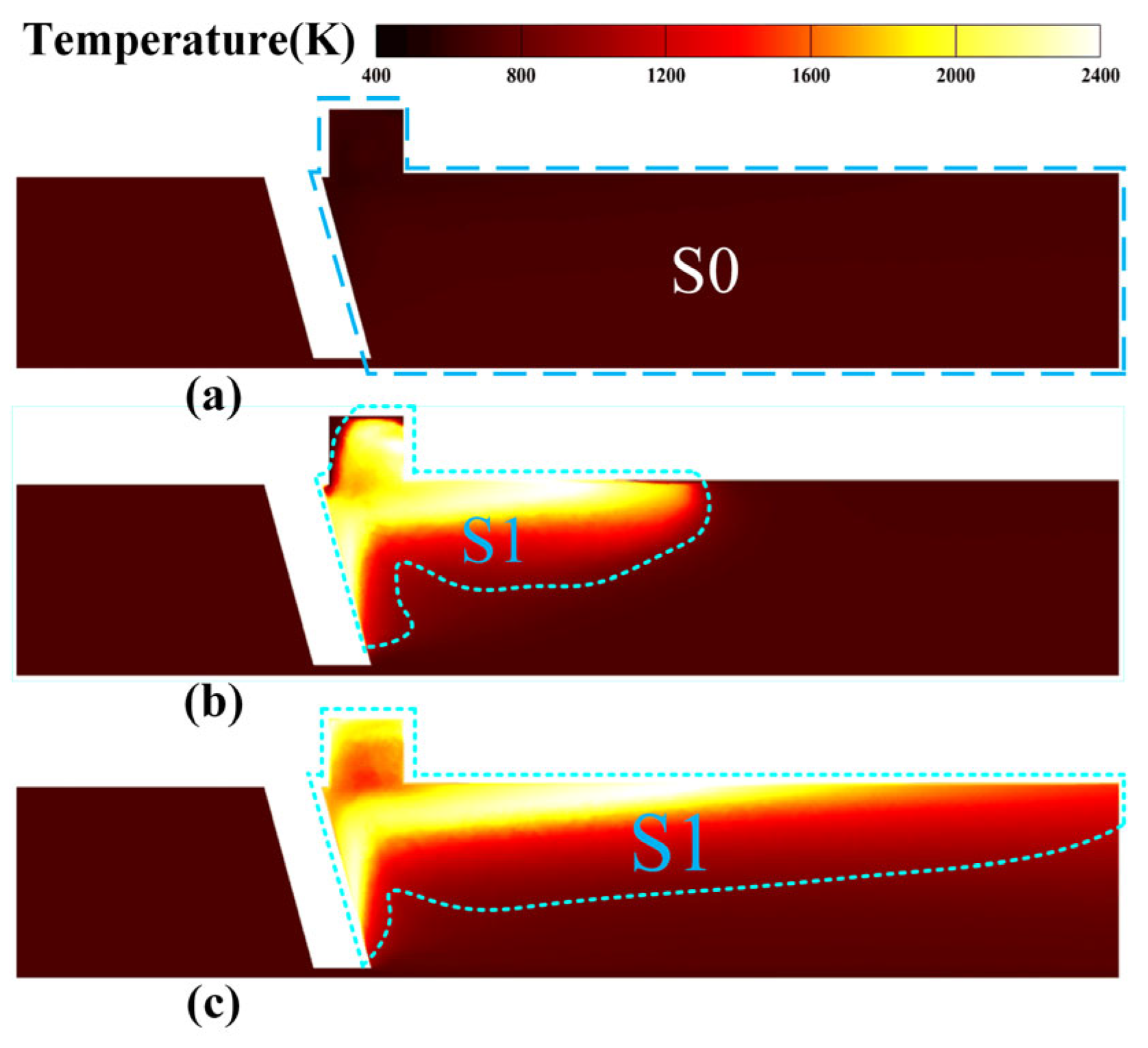
3.2.1. Ignition Results Analysis
3.2.2. Gliding Arc Ignition Analysis
3.2.3. Spark Ignition Analysis
3.2.4. Analysis of Spark Ignition Failure
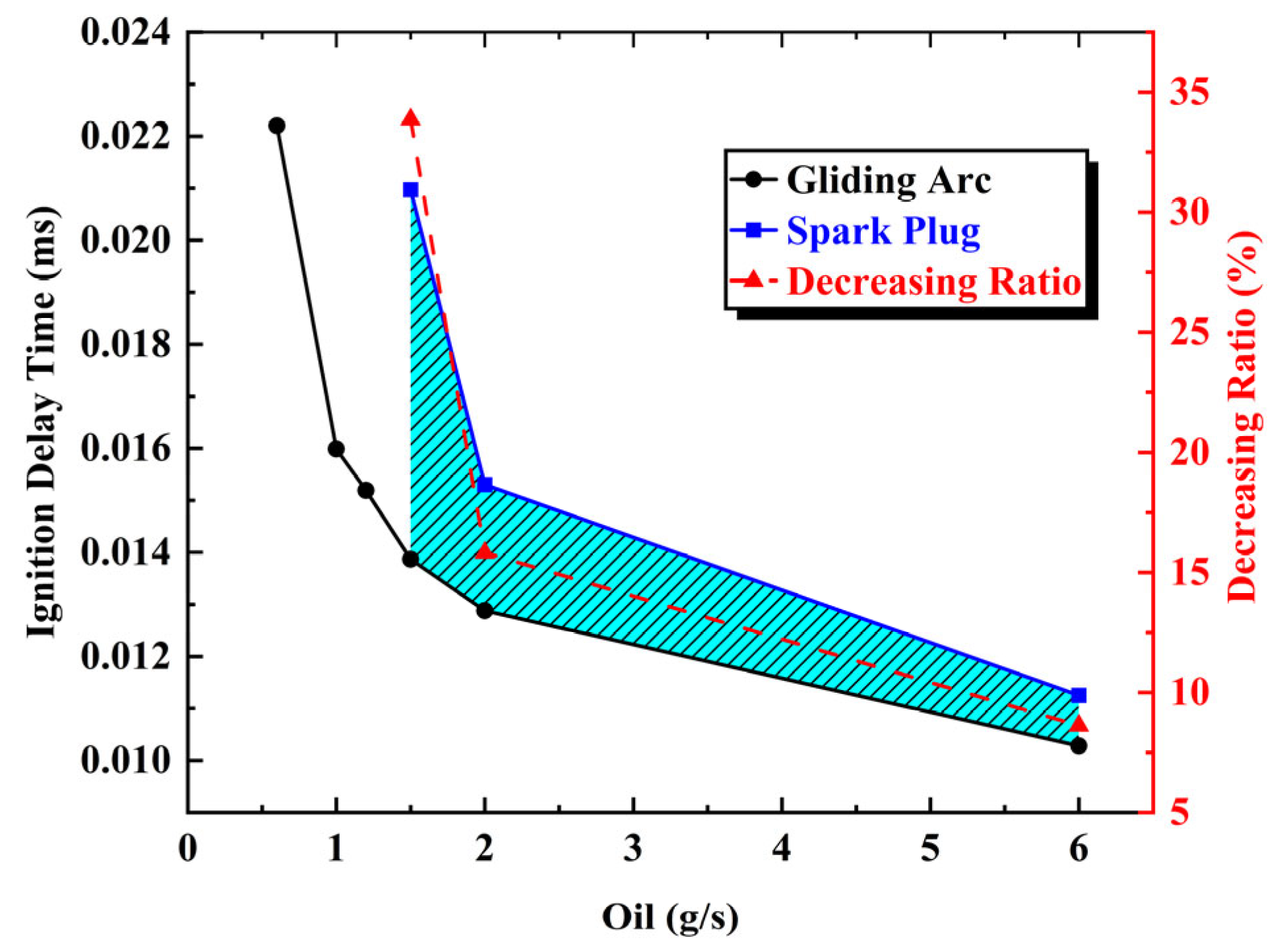
3.2.5. Ignition Delay Time
3.3. Combustion Analysis
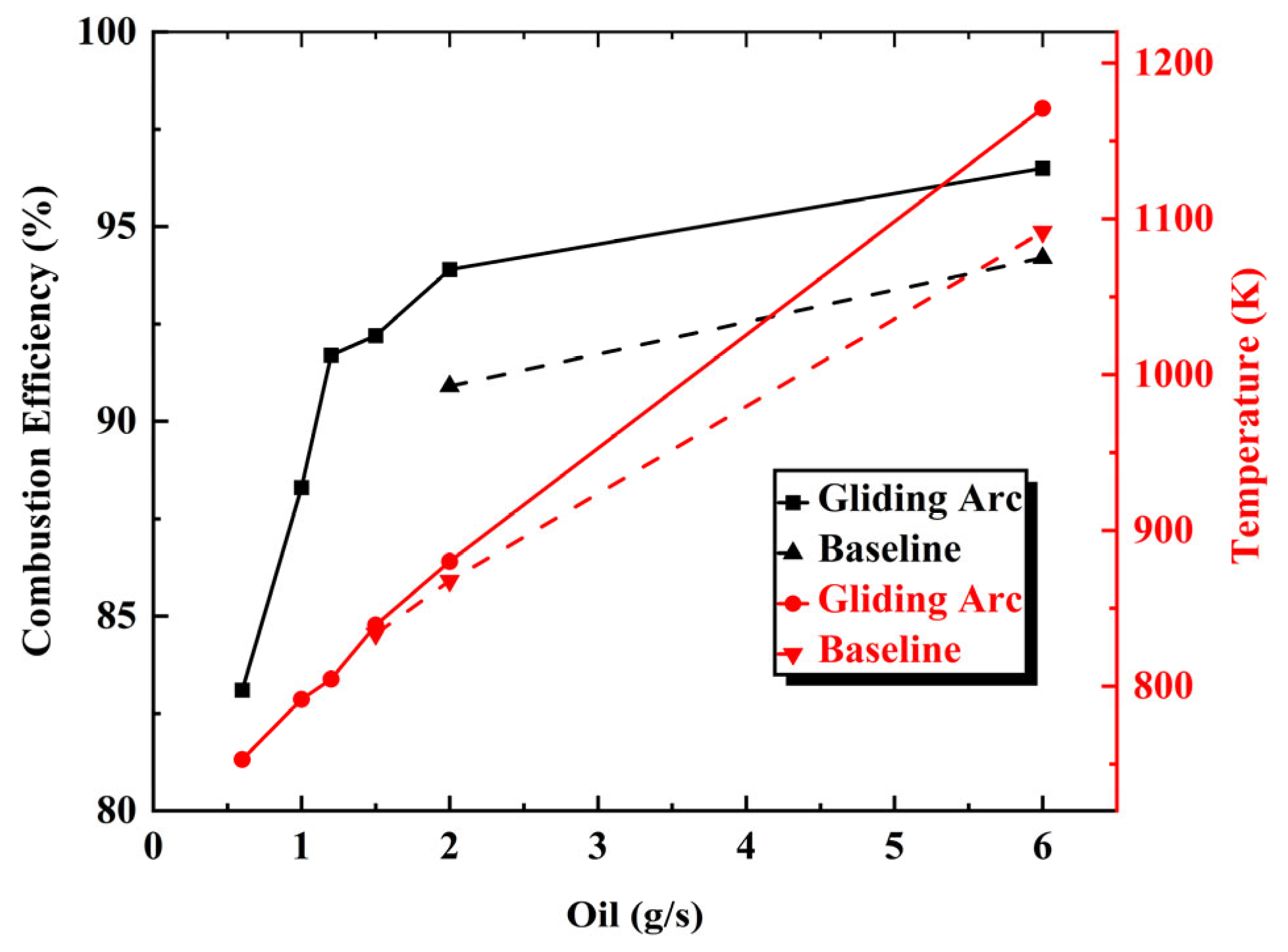
3.3.1. Combustion Efficiency
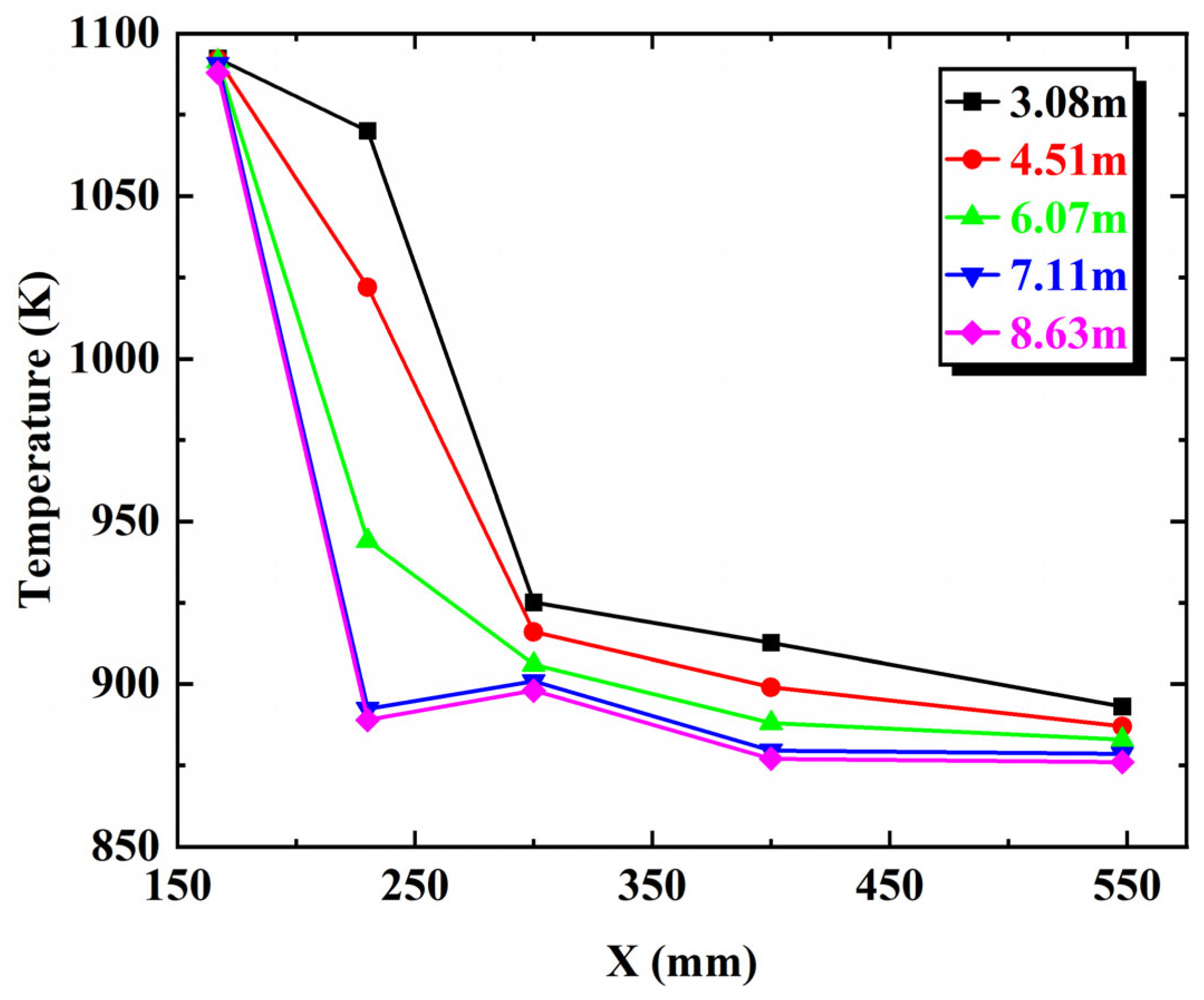
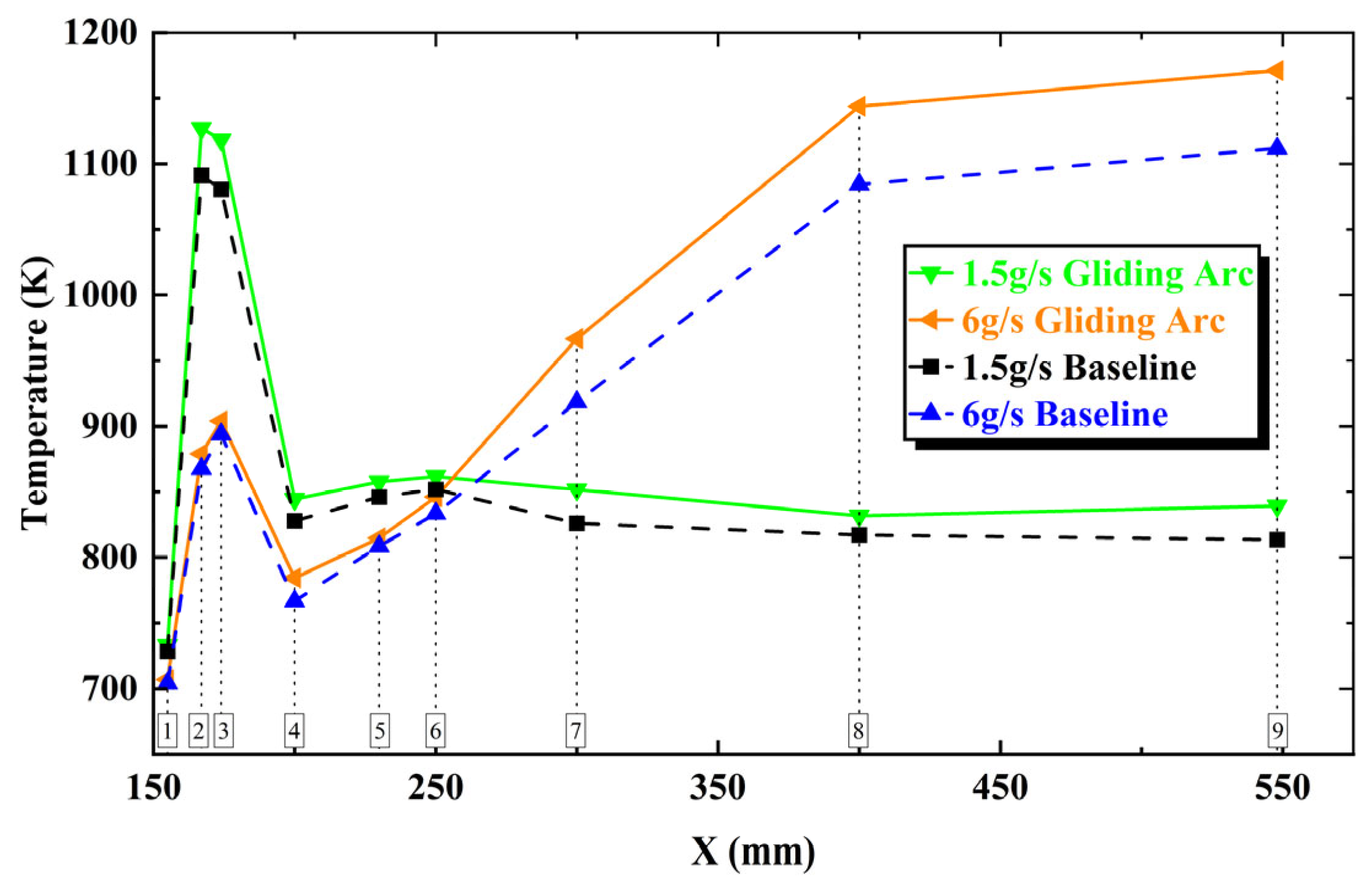
3.3.2. Axial Cross-Section Temperature
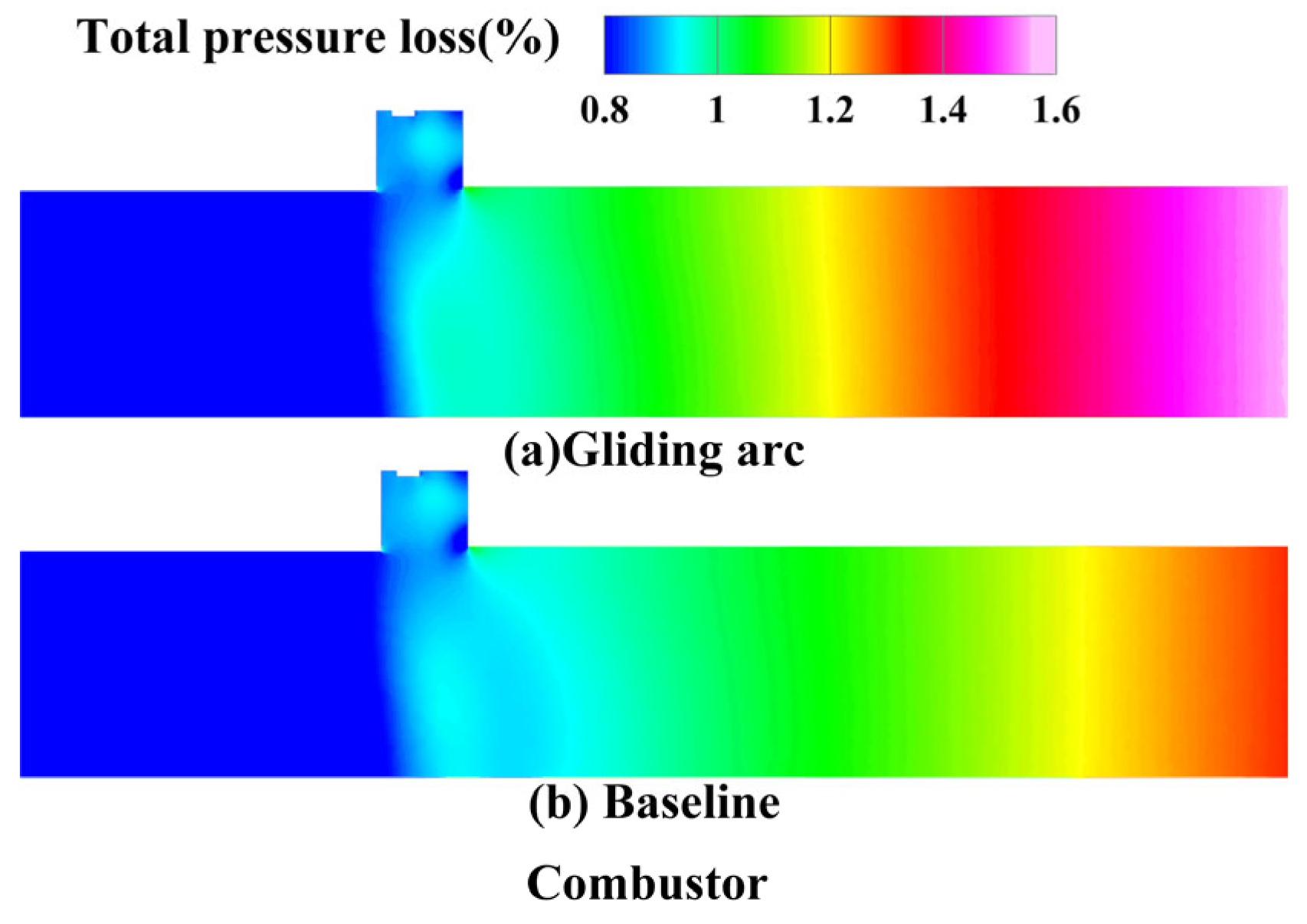
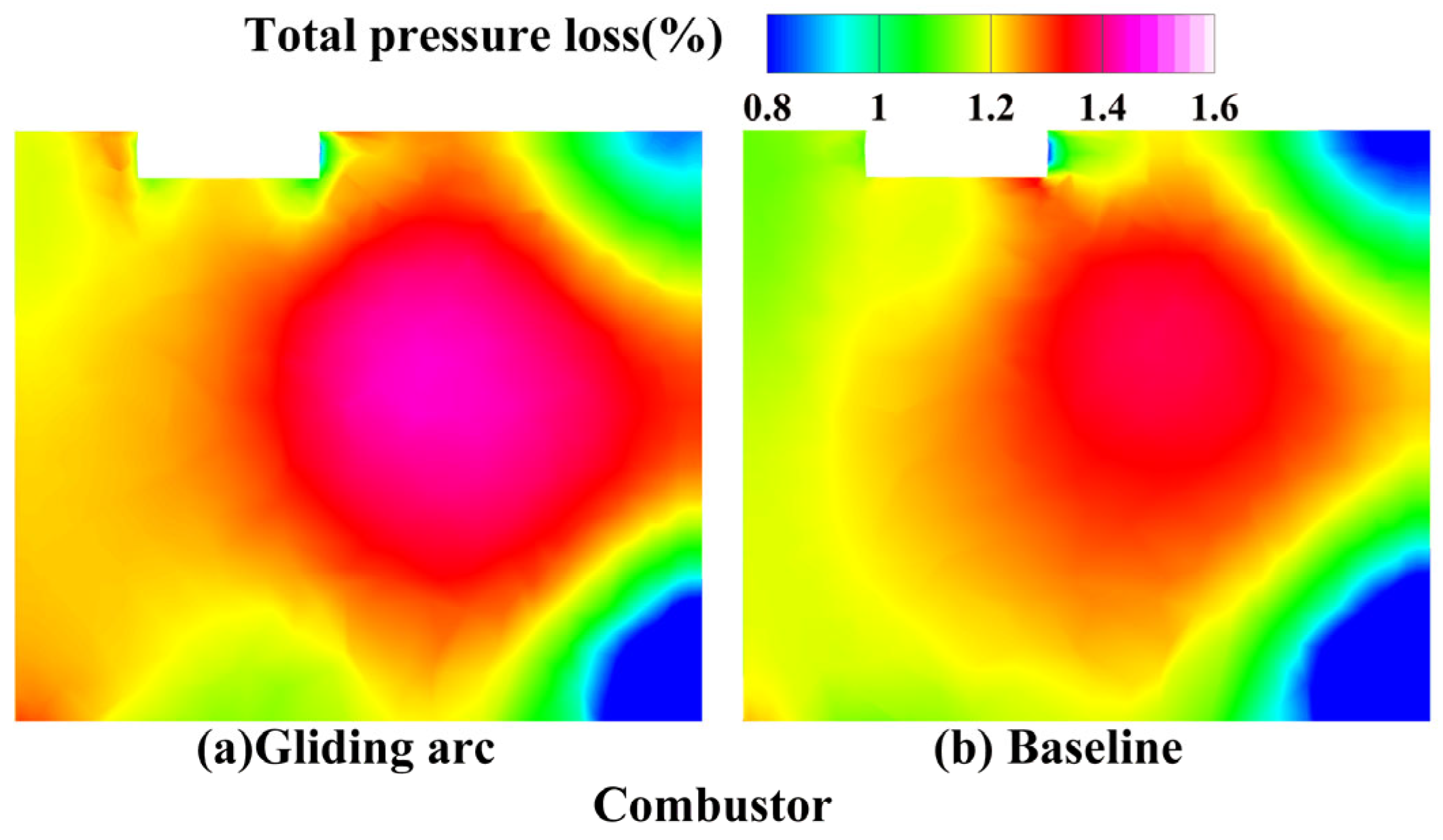
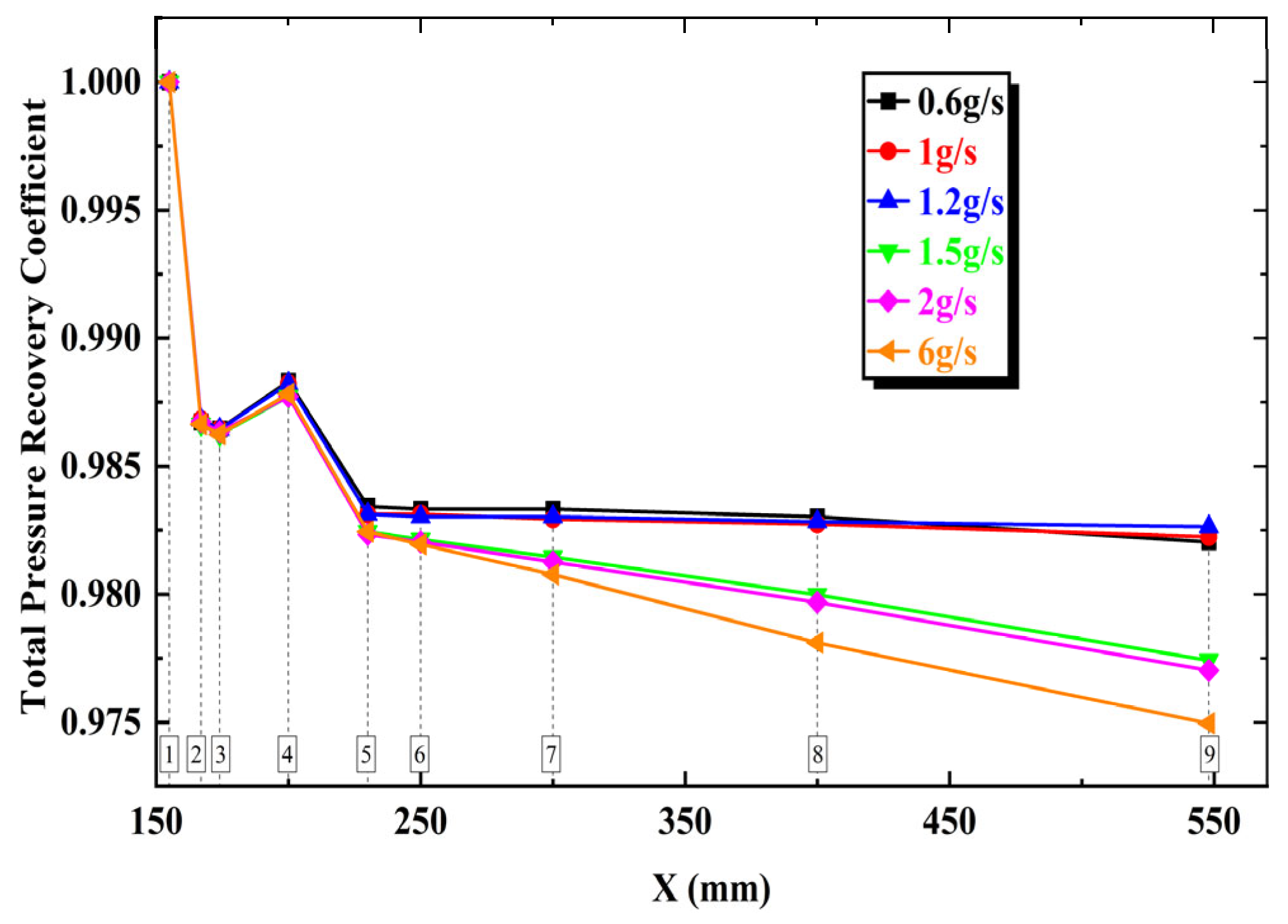
3.3.3. Total Pressure Recovery Coefficient
4. Conclusions
- Under the same oil–gas ratio, compared to the electric spark generated at the outlet of the spark plug igniter, the ignition kernel and initial flame formed by the jet at the outlet of the gliding arc igniter are larger in area, which facilitates successful ignition. At lower fuel flow rate, the spark plug igniter fails to ignite in the cavity due to its inability to form a stable flame. Gliding arc can extend the lean oil ignition limit of the afterburner by a remarkable 50% in this research.
- As the oil–gas ratio decreases, the ignition delay time of both the gliding arc igniter and the spark plug igniter increases. However, the delay time of the spark plug igniter increases more significantly, leading to a growing difference between the two. The decreasing ratio of ignition delay time achieved by the gliding arc (compared to spark plug ignition) progressively increased from 8.6% to 33.85%. Therefore, the gliding arc igniter can effectively reduce the ignition delay time compared to the spark plug igniter.
- The combustion efficiency increases with fuel flow rate but with progressively diminishing growth rates, while the afterburner outlet temperature displays a linear correlation with fuel flow rate. Under this pattern, the gliding arc significantly enhances combustion efficiency under low fuel flow rate, while, under high fuel flow rate, it improves combustion organization to enable the fuel to release more heat.
- The total pressure recovery coefficient of the combustor gradually decreases with increasing oil–gas ratio. Compared to baseline without excitation effects, the gliding arc demonstrates enhanced combustion effects, leading to more intense combustion. Consequently, under identical operating conditions, the gliding arc results in greater total pressure losses, approximately 8% higher than those observed with baseline.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, M.; Dai, X.; Zhang, F.; Liao, G.; E, J. Numerical investigation on film cooling and aerodynamic performance for gas turbine endwalls with upstream vane-type and cascade-type slots. Aerosp. Sci. Technol. 2024, 145, 108857. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Cheng, W.; Jiang, Y.; Jiang, L.; Tian, Y.; Zhang, L. Spatiotemporally resolved characteristics of AC three-dimensional rotating gliding arc at atmospheric pressure. J. Phys. D Appl. Phys. 2021, 54, 225203. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, Y.; Bai, X.S.; Xu, L.; Shan, X.; Bi, Y.; Deng, Y.; Han, Q. Experimental study on combustion and flow resistance characteristics of an afterburner with air-cooled bluff-body flameholder. Aerosp. Sci. Technol. 2022, 123, 107488. [Google Scholar] [CrossRef]
- Lovett, J.; Brogan, T.; Philippona, D.; Kiel, B.V.; Thompson, T. Development needs for advanced afterburner designs. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004; p. 4192. [Google Scholar]
- Safdar, M.M.; Masud, J.; Mufti, B.; Naseer, U.; Farooq, A.; Ullah, A. Numerical modeling and analysis of afterburner combustion of a low bypass ratio turbofan engine. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 628. [Google Scholar]
- Kheirkhah, S.; Maxim, C.J.D.; Saini, P.; Venkatesan, K.; Steinberg, A.M. Dynamics and mechanisms of pressure, heat release rate, and fuel spray coupling during intermittent thermoacoustic oscillations in a model aeronautical combustor at elevated pressure. Combust. Flame 2017, 185, 319–334. [Google Scholar] [CrossRef]
- Stöhr, M.; Yin, Z.; Meier, W. Interaction between velocity fluctuations and equivalence ratio fluctuations during thermoacoustic oscillations in a partially premixed swirl combustor. Proc. Combust. Inst. 2017, 36, 3907–3915. [Google Scholar] [CrossRef]
- Zhang, B. Status and development of aeroengine combustors. Aeroengine 2013, 39, 67–73. [Google Scholar]
- Zhang, X.C.; Sun, Y.C.; Liu, T. Summary of advanced afterburner design technology. Aeroengine 2014, 40, 24–30. [Google Scholar]
- He, L.M.; Yu, J.L.; Zeng, H. The Technology of Plasma Ignition and Assisted Combustion; Aviation Industry Press: Beijing, China, 2019; pp. 1–6. [Google Scholar]
- Wang, H.R.; Jin, J. Overview of lean blowout limit prediction methods for aeroengine combustors. Aeroengine 2014, 40, 72–78. [Google Scholar]
- Li, Y.H.; Wu, Y. Research progress and outlook of flow control and combustion control using plasma actuation. Sci. Sin. Technol. 2020, 50, 1252–1273. [Google Scholar] [CrossRef]
- Weinberg, F.J.; Hom, K.; Oppenheim, A.K.; Teichman, K. Ignition by plasma jet. Nature 1978, 272, 341–343. [Google Scholar] [CrossRef]
- Wermer, L.; Lefkowitz, J.K.; Ombrello, T.; Im, S.-K. Spark and flame kernel interaction with dual-pulse laser-induced spark ignition in a lean premixed methane–air flow. Energy 2021, 215, 119162. [Google Scholar] [CrossRef]
- Ombrello, T.M.; Hammack, S.D.; Carter, C.D.; Busby, K.; Lefkowitz, J.K. Scramjet cavity ignition using nanosecond-pulsed high-frequency discharges. Combust. Flame 2024, 262, 113335. [Google Scholar] [CrossRef]
- Patel, R.; van Oijen, J.; Dam, N.; Nijdam, S. Low-temperature filamentary plasma for ignition-stabilized combustion. Combust. Flame 2023, 247, 112501. [Google Scholar] [CrossRef]
- Kong, C.; Li, Z.; Aldén, M.; Ehn, A. Stabilization of a turbulent premixed flame by a plasma filament. Combust. Flame 2019, 208, 79–85. [Google Scholar] [CrossRef]
- Zhu, J.; Ehn, A.; Gao, J.; Kong, C.; Aldén, M.; Salewski, M.; Leipold, F.; Kusano, Y.; Li, Z. Translational, rotational, vibrational and electron temperatures of a gliding arc discharge. Opt. Express 2017, 25, 20243–20257. [Google Scholar] [CrossRef]
- Zhu, J.; Sun, Z.; Li, Z.; Ehn, A.; Aldén, M.; Salewski, M.; Leipold, F.; Kusano, Y. Dynamics, OH distributions and UV emission of a gliding arc at various flow-rates investigated by optical measurements. J. Phys. D Appl. Phys. 2014, 47, 295203. [Google Scholar] [CrossRef]
- Feng, R.; Huang, Y.; Zhu, J.; Wang, Z.; Sun, M.; Wang, H.; Cai, Z. Ignition and combustion enhancement in a cavity-based supersonic combustor by a multi-channel gliding arc plasma. Exp. Therm. Fluid Sci. 2021, 120, 110248. [Google Scholar] [CrossRef]
- Yu, J.L.; Zhao, B.B.; Guo, H.; Xu, Z.L.; Hu, Y.J.; Fan, W.; Xu, H.S. Research progress of sliding arc plasma assisted combustion technology in aeroengines. Aeroengine 2022, 48, 52–59. [Google Scholar]
- Liu, X.; He, L.M.; Dai, W.F.; Zhao, Z.C.; Chen, G.C.; Zhang, H.L. Experimental study on characteristics of dc gliding arc plasma igniter. J. Propuls. Technol. 2020, 41, 1550–1559. [Google Scholar]
- Tan, Y.C.; Zhong, H.G.; Sum, R.L. Effect of lean blowout performance of trapped vortex combustor of the afterburner. J. Aerosp. Power 2021, 36, 1932–1941. [Google Scholar]
- Liu, R.; Liu, Y.Y.; Gao, Z. Structural parameters effects on lean blowout performance and prediction method for piloted vaporization flameholder. J. Propuls. Technol. 2017, 38, 2753. [Google Scholar]
- Huang, X.; Wang, H.R. Numerical simulation analysis of a cavity strut flame stabilizer cold flow field influence on ignition characteristics. Gas Turbine Exp. Res. 2018, 31, 11–16. [Google Scholar]
- Hsu, K.; Gross, L.; Trump, D.; Roquemore, W. Performance of a trapped-vortex combustor. In Proceedings of the 33rd Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 1995; p. 810. [Google Scholar]
- Davoudzadeh, F.; Buehrle, R.; Liu, N.S.; Ralph, W. Numerical simulation of the RTA combustion rig. In Proceedings of the 40th Combustion, 28th Airbreathing Propulsion, 22nd Propulsion Systems Hazards, 4th Modeling and Simulations Joint Subcommittees Meetings, Charleston, SC, USA, 13–17 June 2005. [Google Scholar]
- Lee, J.H.; Winslow, R.; Buehrle, R.J. The GE-NASA RTA hyperburner design and development. In Proceedings of the 40th Combustion, 28th Airbreathing Propulsion, 22nd Propulsion Systems Hazards and 4th Modeling and Simulation Joint Subcommittee Meetings, Charleston, SC, USA, 13–17 June 2005. [Google Scholar]
- Pascaud, S.; Boileau, M.; Martinez, L.; Cuenot, B.; Poinsot, T. LES of Steady Spray Flame and Ignition Sequences in Aeronautical Combustors. In Proceedings of the 1st Workshop INCA, SNECMA, Villaroche, France. pp. 19–26. 2025. Available online: https://www.cerfacs.fr/~cfdbib/repository/TR_CFD_05_70.pdf (accessed on 1 August 2025).
- Li, Z.; Zhu, Y.; Pan, D.; Cheng, X. Characterization of a Gliding Arc Igniter from an Equilibrium Stage to a Non–Equilibrium Stage Using a Coupled 3D–0D Approach. Processes 2023, 11, 873. [Google Scholar] [CrossRef]
- Gui, T.; Fang, R.L.; Qiu, W.; Zheng, Y.; Fan, W. Experimental investigation on ignition performance of coaxial and divisional high temperature rise combustor. J. Propuls. Technol. 2022, 43, 224–232. [Google Scholar]
- Li, M.; Wang, Z.; Li, J. Numerical study of cold flow characteristics of a new integrated afterburner with strut flame stabilizer. Aerosp. Sci. Technol. 2024, 153, 109476. [Google Scholar] [CrossRef]
- Li, M.; Wang, Z.; Li, J. Numerical study on the performance of a new integrated afterburner under a wide range of bypass ratio conditions. Energy 2024, 313, 133919. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2024. [Google Scholar]
- Qiu, H.; Zhang, J.; Sun, X.; Chang, J.; Bao, W.; Zhang, S. Flowing residence characteristics in a dual-mode scramjet combustor equipped with strut flame holder. Aerosp. Sci. Technol. 2020, 99, 105718. [Google Scholar] [CrossRef]
- Miao, J.; Fan, Y.; Wu, W.; Zhao, S. Influence of air-entraining intensity on the afterburner ignition, flame-holding and combustion characteristics. Aerosp. Sci. Technol. 2020, 106, 106063. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Y.; Wang, Y.; Liu, B.; Qin, F. Optimization method of global reactions kinetic parameters for kerosene combustion. Aerosp. Technol. 2022, 4, 62–72. [Google Scholar]
- Wang, C.; Tian, Y.; Wang, T.; Liu, C.; Wang, K.; Wang, S.; Liu, F.; Mu, Y.; Xu, G. Study on ignition mechanism and flame dynamic characteristics in a strut and cavity integrated bypass combustor. Phys. Fluids 2025, 37, 055110. [Google Scholar] [CrossRef]

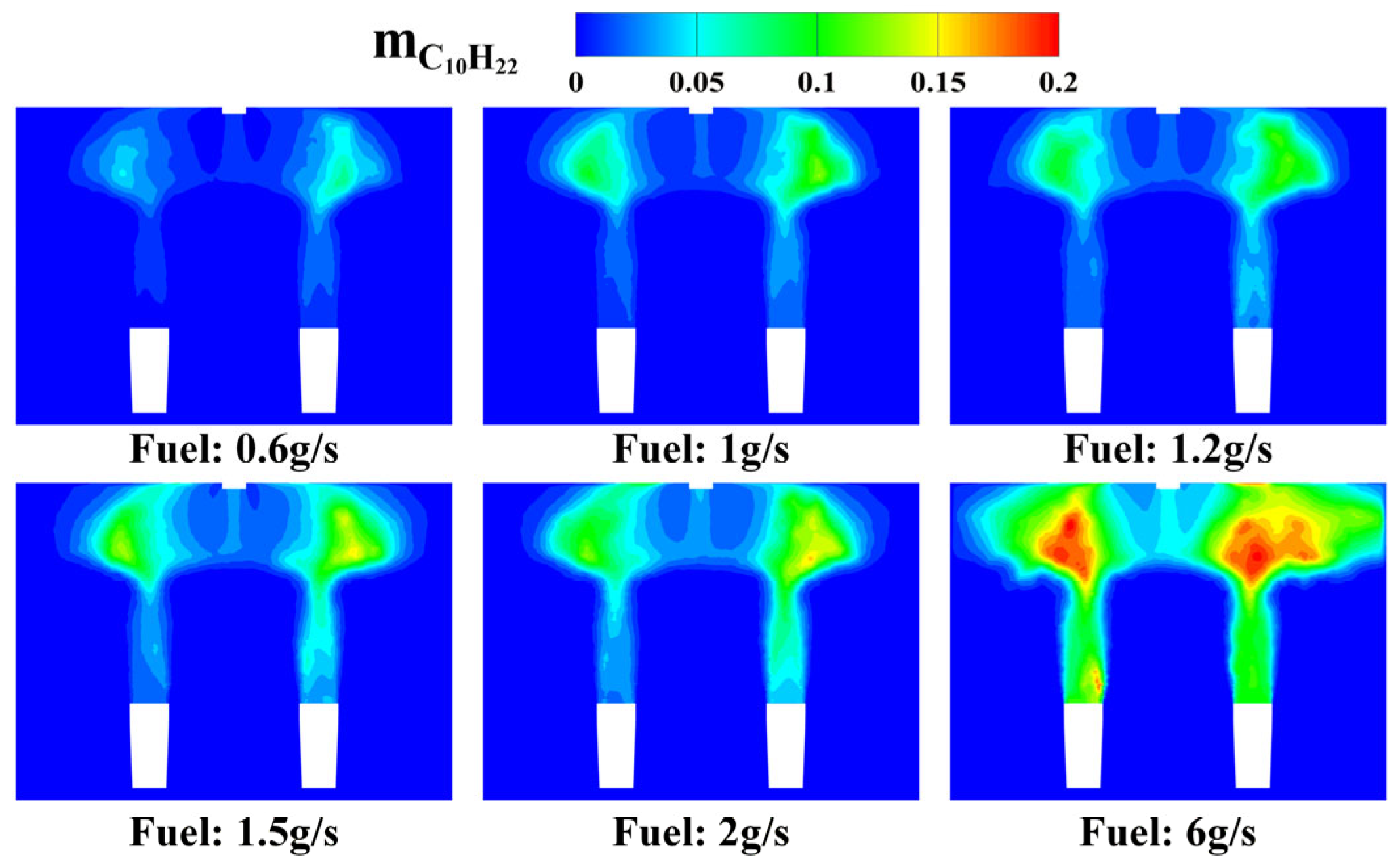
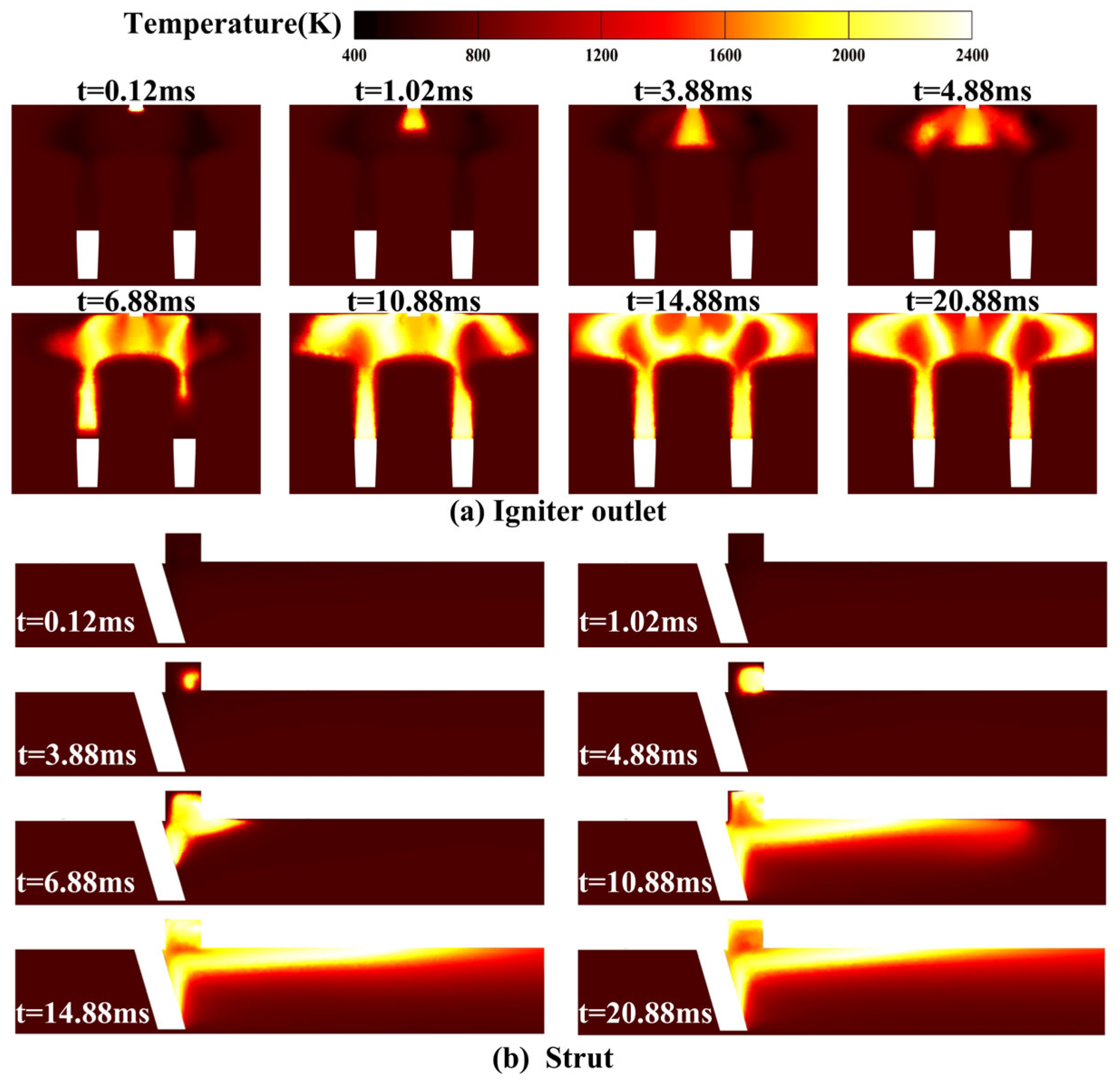
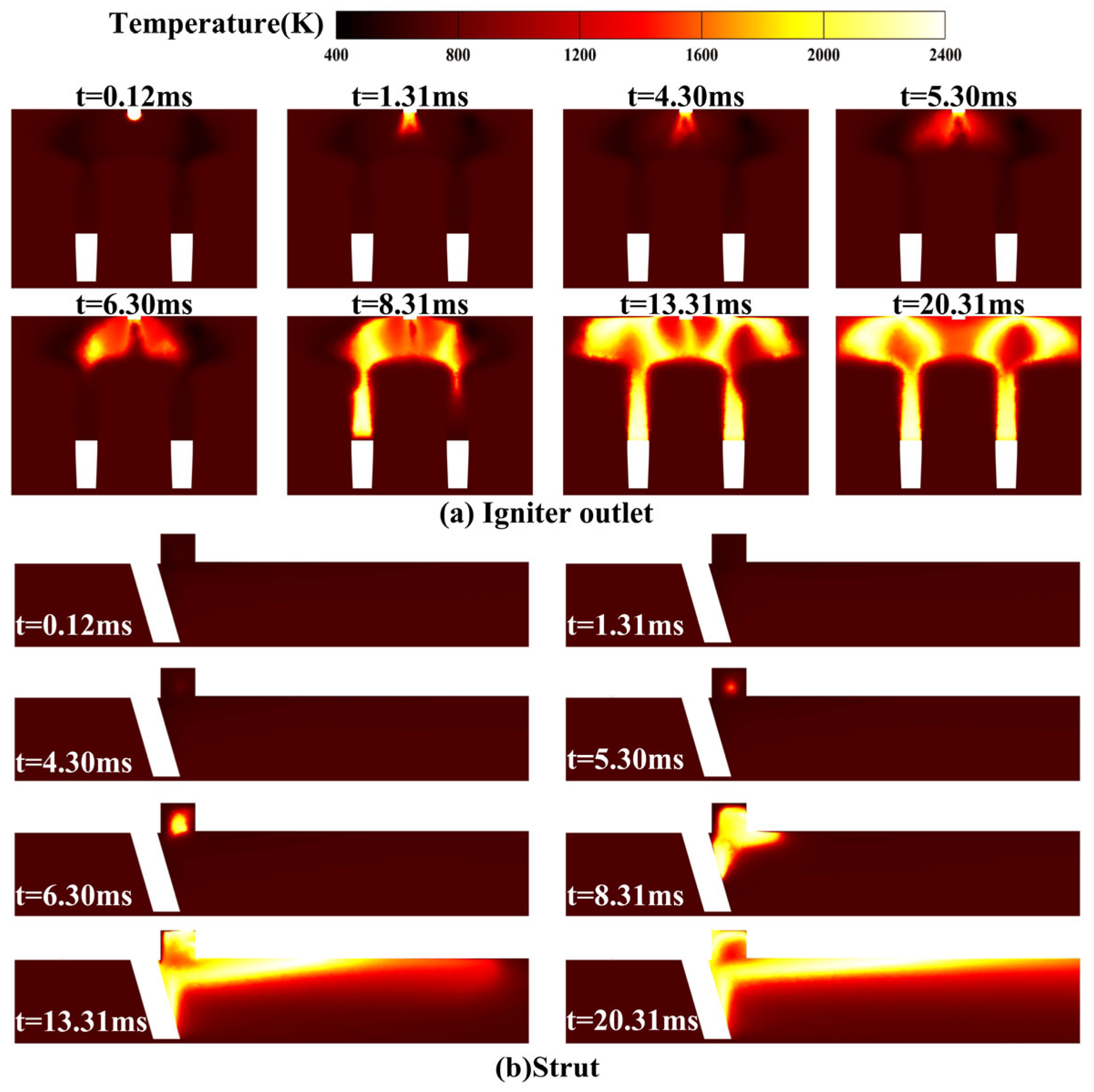
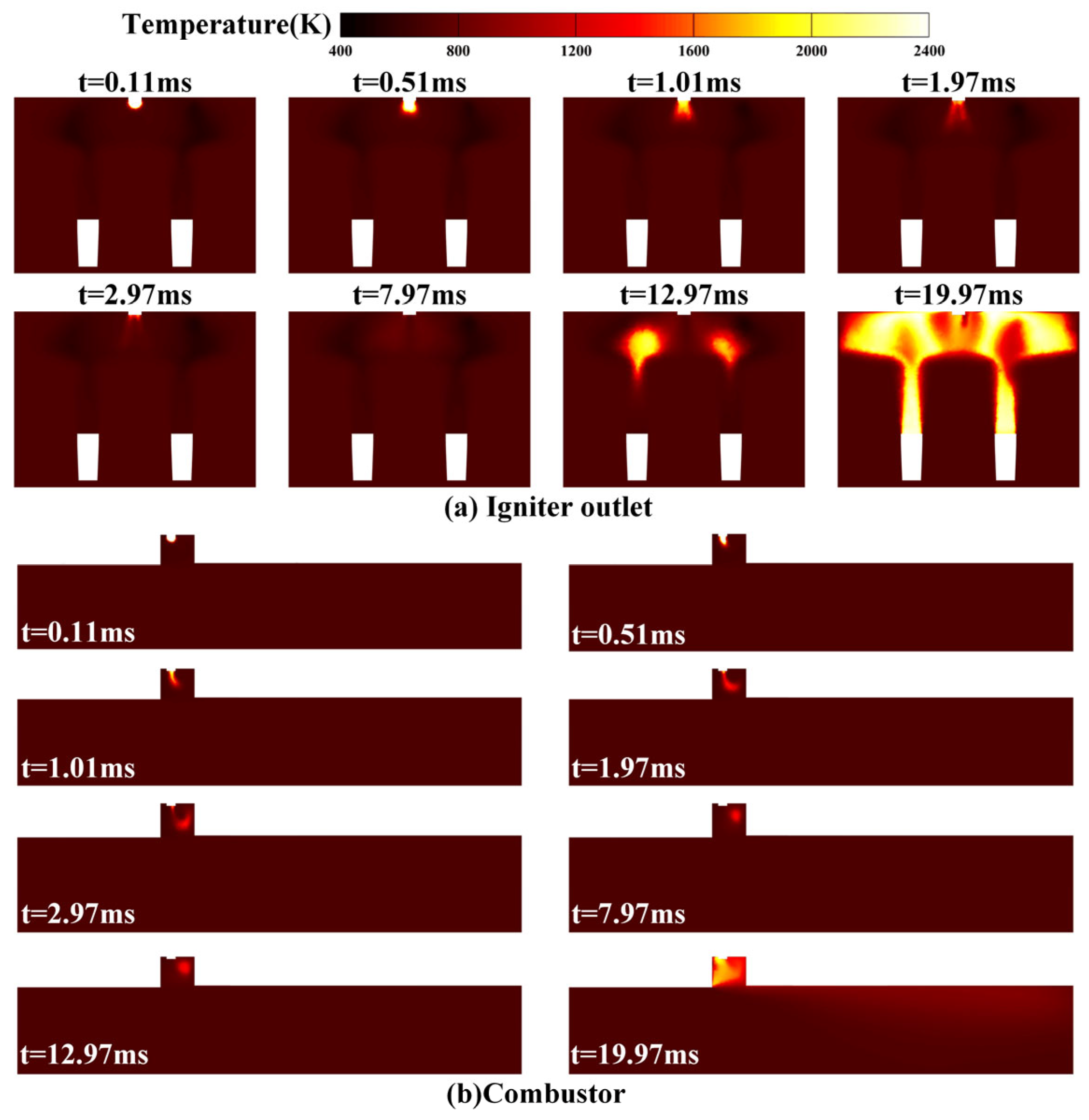


| Inlet O2 Concentration | Inlet CO2 Concentration | Inlet H2O Concentration |
| 18.6% | 2% | 2% |
| Inlet Temperature (K) | Inlet Mass Flow Rate (kg/s) | Inlet Velocity (m/s) |
| 700 | 0.437 | 50 |
| Operating Condition | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 | Case 6 |
|---|---|---|---|---|---|---|
| Fuel Mass Flow Rate (g/s) | 0.6 | 1 | 1.2 | 1.5 | 2 | 6 |
| Oil–Gas Ratio | 0.0014 | 0.0023 | 0.0027 | 0.0034 | 0.0046 | 0.0137 |
| Oil–Gas Ratio | Spark Plugs Ignition | Gliding Arc Ignition |
|---|---|---|
| 0.0014 | Extinguished | Ignited |
| 0.0023 | Extinguished | Ignited |
| 0.0027 | Extinguished | Ignited |
| 0.0034 | Ignited | Ignited |
| 0.0046 | Ignited | Ignited |
| 0.0137 | Ignited | Ignited |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Liang, Y.; Zheng, X.; Zhang, Z.; Wu, Y. Numerical Simulation of Gliding Arc Plasma-Assisted Ignition and Combustion in Afterburner Combustor. Aerospace 2025, 12, 735. https://doi.org/10.3390/aerospace12080735
Li Z, Liang Y, Zheng X, Zhang Z, Wu Y. Numerical Simulation of Gliding Arc Plasma-Assisted Ignition and Combustion in Afterburner Combustor. Aerospace. 2025; 12(8):735. https://doi.org/10.3390/aerospace12080735
Chicago/Turabian StyleLi, Zecheng, Yong Liang, Xing Zheng, Zhibo Zhang, and Yun Wu. 2025. "Numerical Simulation of Gliding Arc Plasma-Assisted Ignition and Combustion in Afterburner Combustor" Aerospace 12, no. 8: 735. https://doi.org/10.3390/aerospace12080735
APA StyleLi, Z., Liang, Y., Zheng, X., Zhang, Z., & Wu, Y. (2025). Numerical Simulation of Gliding Arc Plasma-Assisted Ignition and Combustion in Afterburner Combustor. Aerospace, 12(8), 735. https://doi.org/10.3390/aerospace12080735





