Abstract
Flow separation is a fundamental phenomenon in fluid mechanics governed by the Navier–Stokes equations, which are second-order partial differential equations (PDEs). This phenomenon significantly impacts aerodynamic performance in various applications across the aerospace sector, including micro air vehicles (MAVs), advanced air mobility, and the wind energy industry. Its complexity arises from its nonlinear, multidimensional nature, and is further influenced by operational and geometrical parameters beyond Reynolds number (Re), making accurate prediction a persistent challenge. Traditional models often struggle to capture the intricacies of separated flows, requiring advanced simulation and prediction techniques. This review provides a comprehensive overview of strategies for enhancing aerodynamic design by improving the understanding and prediction of flow separation. It highlights recent advancements in simulation and machine learning (ML) methods, which utilize flow field databases and data assimilation techniques. Future directions, including physics-informed neural networks (PINNs) and hybrid frameworks, are also discussed to improve flow separation prediction and control further.
1. Introduction
Flow transition and separation are important phenomena in fluid dynamics, critically influencing both aeronautical and wind energy systems. Their occurrence crosses a broad spectrum of Re and is influenced by factors such as the geometry and kinematics of the bodies involved, surface roughness, adverse pressure gradients (APGs), and varying environmental conditions [1]. Flow separation around airfoils can significantly impair aerodynamic performance by altering lift and drag—key metrics of wing aerodynamic efficiency [2]. An in-depth study of the dynamic flow field distribution around airfoils is essential for elucidating the mechanisms underlying flow separation, transition, vortex interaction, and wake formation. Such insights are crucial for developing and implementing effective flow control strategies to enhance performance [3,4].
Predicting flow separation is inherently challenging due to its nonlinear dynamic nature. Numerical simulations have become a cornerstone in the design of modern aviation and wind energy systems, providing accurate flow field predictions [5,6]. These simulations often utilise high-fidelity data from solving the Reynolds-averaged Navier–Stokes (RANS) equations, which decompose the instantaneous flow field into mean and fluctuating components to model turbulent flows. RANS modelling is widely used to model attached flows. However, their effectiveness in simulating separated flows remains suboptimal, as the oversimplification of turbulence physics often fails to accurately capture the instantaneous coherent structures of turbulent flows. There is a growing consensus on the need for time-accurate hybrid RANS/Large Eddy Simulation (LES) approaches, alongside the development of faster algorithms and more efficient adaptive grid technologies [7]. Higher accuracy methods, such as LES [8] and Direct Numerical Simulation (DNS) [9], require substantial computational resources and advanced algorithms to resolve complex flows, particularly in three-dimensional contexts. This requirement can be prohibitive in early design and time-sensitive environments. Moreover, experimental research in this domain often faces challenges due to equipment limitations and the difficulty of achieving reproducible results.
The advancement in high-performance computing (HPC) technologies and the refinement of numerical methods have significantly reduced the computational time required for computational fluid dynamics (CFD) simulations. Consequently, there has been an unprecedented surge in the generation of (1) a vast volume of data, (2) a reduction in the costs associated with computation, data storage, and transfer, (3) an abundance of benchmark problems, (4) the availability of open-source software, and (5) substantial industrial investments in data-driving problems [10]. This surge has reignited interest in applying machine learning (ML) techniques in fluid mechanics. However, despite their flexibility, traditional ML models are often criticized for their “black-box” nature, which often leads to less comprehensive model outcomes. To address this, physics-informed neural networks (PINNs) [11] have been introduced to involve governing physical laws, such as the Navier–Stokes (NS) equations, directly in the training process.
Although significant progress has been made in understanding flow separation through numerical simulations and ML, existing reviews often focus on specific methods without providing a comprehensive overview of their integration. There remains a need to systematically assess the strengths and limitations of traditional CFD techniques, hybrid models, and data-driven approaches. This review addresses these gaps by synthesizing recent advancements and identifying key challenges, offering insights into future research directions.
In this review, Section 2 delves into the fundamental mechanisms of both two-dimensional (2D) and three-dimensional (3D) flow separation, establishing a theoretical foundation for understanding the factors that induce separation and the processes involved in flow separation formation. Section 3 examines the evolution of simulation techniques, ranging from traditional CFD methods to contemporary hybrid models, highlighting their roles in visualizing flow separation and validating findings against experimental data. Section 4 explores the burgeoning application of ML technologies in fluid dynamics, emphasizing their contributions to enhancing CFD simulation accuracy, reducing computational costs, and efficiently extracting significant features from extensive datasets.
2. Mechanisms and Impacts of Flow Separation
Flow separation is widely acknowledged as the detachment of the boundary layer from a solid surface. In flow separations, the significantly thickened rotational region and the substantial increase in the velocity component normal to the surface render the traditional boundary layer equations invalid [12]. Flow separation often results in significant aerodynamic losses, including reduced pressure recovery and lift, while also limiting aircraft performance by constraining the maximum lift coefficient and triggering buffet or pitch-up in conventional fixed-wing designs. Effective flow control can harness separation to enhance performance, such as generating maneuvering lift and improving stability through separation-induced leading-edge vortex [2]. Therefore, a fundamental understanding of flow separation is significant to aerodynamics and aeronautical engineering.
2.1. 2D Flow Separation
Flow separation in 2D, axisymmetrical flows typically occurs in the presence of APGs and is influenced by laminar or turbulent viscosity effects. Laminar flow separation occurs when the near-surface fluid decelerates and lacks sufficient momentum to overcome an APG, leading to local flow reversal, as depicted in Figure 1a. This phenomenon results in the formation of laminar separation bubbles, characterized by recirculating flow regions confined between the separation and reattachment points, as shown in Figure 1c,e. The breakdown of these bubbles can potentially lead to a leading edge stall and result in a sudden drop in lift and increased drag. The size of these bubbles varies depending on the flow conditions. Short separation bubbles, typically around 1% of the chord length, have negligible effects on the pressure distribution. Moderate bubbles spanning about 2–3% of the chord length induce a minor change in pressure distribution. In contrast, larger separation bubbles cause the flow to detach further along the airfoil surface and reattach farther downstream [13]. Laminar flow separation generally occurs further upstream compared to turbulent flows due to the lower momentum in the boundary layer, resulting in larger wakes and greater energy losses [13,14].
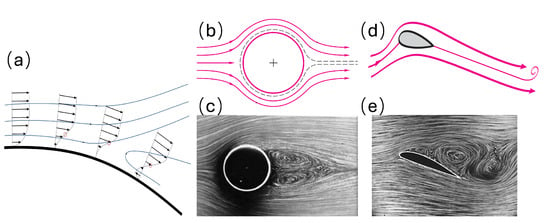
Figure 1.
Illustration of flow attachment and separation: (a) flow progression along a curved surface, showing the transition from attached flow to separation and the formation of a reversed flow region [15]; (b,c) attached flow and separation over a circular cylinder [16]; (d,e) attached flow and separation over an airfoil [17].
Turbulent boundary layers, characterised by chaotic fluctuations and vigorous mixing, enhance momentum transport due to turbulent eddies, increasing the overall exchange of momentum between different layers of flow [18]. This allows turbulent flow to resist the APG and friction more efficiently. The enhanced momentum exchange delays the separation point compared to the laminar flows. The flow separations occur further downstream, resulting in smaller wake regions and reduced drag. The occurrence of turbulent separation is unsteady and often accompanied by periodic vortex shedding, which significantly impacts the induced forces on the body [19]. The Re influences flow separation critically, exhibiting distinct regimes. This has been sufficiently studied for bluff bodies such as cylinders or spheres as shown in Figure 2. At low Re, flows remain predominantly laminar with early separation and large wakes. Vortex shedding and wake formatting occur at a moderate order of 100. As Re increases to the order of , the boundary layer transitions into turbulence, with delayed separation and reduced wake size. The resulting unsteady, three-dimensional, interacting vortical patterns from increasing Re are key contributors to complex flow behaviour [13].
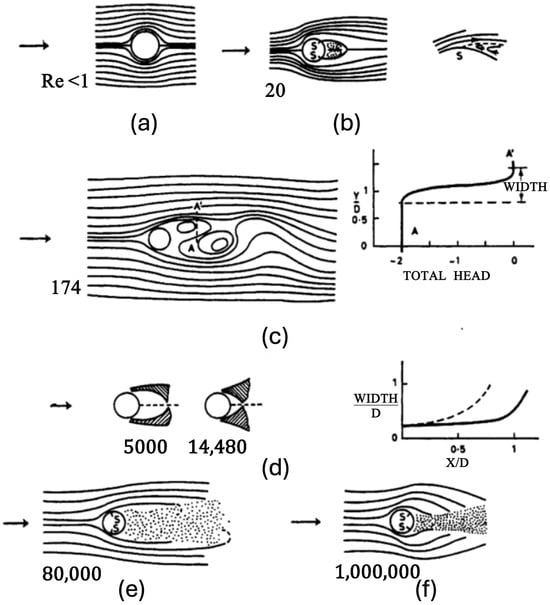
Figure 2.
Illustration of Flows over infinitely long cylinder: (a) at Re less than 1; (b) at Re equals 20; (c) at Re of 174. On the right, transverse with total head tube along AA’, with width of free laminar layer indicated. (d) Boundaries at free layer at Re of 5000 and 14,480, and graphs of the free layer’s width variation with distance X downstream. D is the diameter of the cylinder. Solid curve refers to Re 5000, and the dotted line is for larger Re: (e) at Re of 80,000; (f) at Re of 1,000,000 [13].
2.2. 3D Flow Separation
The classical definition of a separation point as the forward boundary within a separation region is adequate for 2D flows but falls short for 3D flows, which exhibit significantly more complex and nuanced behavior [20,21,22]. In 3D flows, the separated flow is no longer trapped in a closed recirculation bubble as in 2D flows. Instead, flows can laterally escape with a transverse component developed by the velocity as shown in Figure 3a. More often, 3D flow separation does not necessarily involve reverse flow or significant friction variations [13]. Instead, it is characterized by surface streamlines and separation lines that differentiate the deviation between attached and separated flows as shown in Figure 3b–d. The more complex vortical structures in 3D flow separation arise due to the strong cross-flow components introduced by boundary layer interactions. These structures lead to non-uniform separation and the formation of concentrated vortices through the roll-up of shear layers. Kelvin–Helmholtz instabilities often initiate these vortices, which occur when separated shear layers interact with geometric features, such as sharp edges. In contrast, rounded geometries tend to promote flow attachment through mechanisms like the Coanda effect, where the flow adheres to curved surfaces. Such behaviour emphasizes the critical role of geometry in influencing flow separation patterns and vortex formation [3].
The evolution of vortices in 3D flows is dynamic and governed by parameters such as swirl ratio. The swirl ratio is known as the ratio of swirl to axial velocity, which plays a critical role in vortex stability and breakdown. Vortex breakdown, characterized by the sudden deceleration of axial flow and rapid expansion of the vortex core, disrupts the coherence of the flow structure. APG and excessive swirl typically accelerate this breakdown [20]. Control methods, such as swirl reduction or pressure redistribution, can delay breakdown and stabilize the flow. Vortex breakdown can manifest in distinct forms, such as the bubble-like structure in Figure 3b(i), the spiral structure in Figure 3b(ii), and the break of symmetry in Figure 3d. Moreover, 3D vortices are influenced by turbulence ingestion and external flow disturbances, which can alter their coherence and stability. For instance, turbulence introduced through active flow control techniques, such as blowing or suction, can diffuse vortices by weakening their impact or accelerating vortex merging. Secondary flows, such as horseshoe vortices forming around obstacles, are critical in initiating separation. These flows interact with primary separation structures, leading to more complex patterns and enhanced vorticity [23]. The helical instabilities observed in vortices post-breakdown complicate the control further, as these instabilities often induce oscillations or pressure fluctuations on downstream surfaces. In addition, in configurations involving multiple vortices, such as counter-rotating pairs, the interactions between vortices become critical to flow dynamics. These interactions, governed by parameters such as vortex spacing and core radius, can be manipulated to dissipate wake energy or stabilise the flow according to the desired outcome [3].
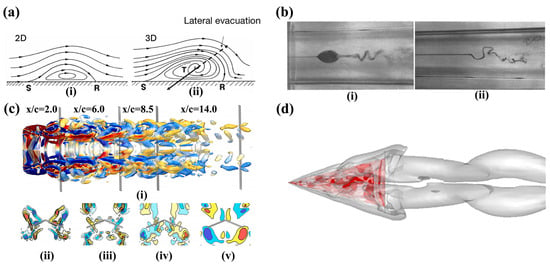
Figure 3.
(a) Comparison of flow separation in 2D and 3D flows, showing the separation point (S), reattachment point (R), and the transverse component (T) unique to 3D flows [24]. (b) Illustration of vortex breakdown, with a flow generally from left to right: (i) bubble form showing axial deceleration and core expansion; (ii) spiral form suggests the development of helical instabilities [20]. (c) Flow structures of the dihedral flapping wing at low Re: (i) top view of the isosurfaces of Q-criteria = 0.2, coloured by the streamwise vorticity ranging from −1 (blue) to 1 (red); and (ii)–(v) streamwise vorticity fields at planes at x/c = 2.0, 6.0, 8.5, and 14.0, respectively [21]. (d) Flow structure of a typical instant for a delta wing at an of —top view of the isosurfaces of Q-criteria = 3 and angle of attack = 60° [22].
Flow separation has long been recognized as a key contributor to high lift generation in flapping flight and delta wings. At low Re, the flow structures around dihedral flapping wings are significantly more complex than those of fixed rectangular wings, involving vortex deformation and interactions with various flow structures [21], as illustrated in Figure 3c. In swept and low-aspect-ratio configurations common in high-speed flight, separation becomes more complex due to interactions with shock waves. Beyond vortex separation in subsonic flows, shock-induced separation and other 3D effects also play a significant role [2]. Jet-propelled fighters and, nowadays, air lifters fly at transonic or supersonic speeds, introducing a new “shock stall” phenomenon. The formation of shock waves interacts with the boundary layer, further intervening in the pressure recovery. Unlike subsonic flow, where the pressure gradient normal to the wall is small enough to assume a static pressure across the boundary, the supersonic flow in a shock region contains that of a significant magnitude. The characteristics of the shock wave–boundary layer interaction state that if laminar flow is involved, Re dominates the pressure coefficient for separation [13]. However, it has little effect when turbulence is incurred. Instead, the Mach number decides on the laminar or the turbulent type of flow. These developments require a more comprehensive understanding of 3D flow separation, where the presence of cross-flows, geometrical interactions, and complex vortical structures further complicates the separation mechanism.
2.3. Discussion
This section discusses the mechanisms of flow separation. While 2D flow separation is well studied due to its relative simplicity, real-life applications often involve inherently 3D flow separation. Fully capturing the phenomenon of flow separation remains challenging with traditional theoretical and experimental approaches. Accurate prediction of flow separation is essential for achieving effective flow control in industrial applications. The complex physics of flow separation plays a critical role in selecting appropriate CFD methods. In Section 3, we explore how these methods are applied to simulate flow separation and the challenges associated with their implementation.
3. Simulations for Flow Separation
CFD was dawning when the last Advisory Group for Aerospace Research and Development (AGARD) conference on separation was held in 1975. Over the intervening decades, advancements in HPC and refined numerical methods have drastically reduced the computational time required for CFD simulations. Early CFD methods, such as transformation or panel methods, primarily solved linear potential equations, focusing on attached flows and inviscid approximations. The introduction of RANS equations marked a significant milestone [2], enabling simulations of turbulent flows and benefiting from the rapid development of computational technologies, including machines and cluster-computing architectures.
Despite its widespread success, RANS modeling has inherent limitations in capturing complex flow phenomena, particularly in transitional, unsteady, and 3D turbulent flows. Advanced approaches such as LES, Detached Eddy Simulation (DES), and DNS have been developed to address these challenges. LES compromises accuracy and computational cost by explicitly resolving large-scale turbulent eddies while modelling smaller, subgrid-scale ones. In contrast, DNS offers the highest level of accuracy by directly resolving all turbulent scales but remains computationally prohibitive for most practical applications. DES, a hybrid approach that applies RANS modelling in near-wall regions and LES in separated flow regions, seeks to optimize the trade-off between computational efficiency and predictive accuracy.
With advanced computational capabilities, hybrid techniques integrating these methods have gained attention, enabling more accurate simulations of flow separation in turbulent and transitional regimes. This section reviews traditional CFD methods, including RANS, LES, and DNS, and explores hybrid modelling approaches, incorporating high-order techniques and reduced-order modelling (ROM). The Lattice Boltzmann Method (LBM) is less commonly used in the aforementioned engineering applications but is more prevalent in low-Re flows, including unsteady separation in microfluidics and multiphase systems. While ML’s role is explored in detail in Section 4, it is briefly mentioned here, alongside suggestions for further enhancing simulation methodologies.
3.1. RANS
Traditional CFD methods like RANS simplify turbulent flow simulations by time-averaging governing equations, capturing mean flow properties (Figure 4a,e), while modelling turbulence effects through closure models like eddy viscosity models (EVMs) or Reynolds stress models (RSMs). EVMs (e.g., k-, k-, shear stress transport (SST)) assume a linear relationship between Reynolds stresses and mean strain rate. RSM (e.g., the Launder–Reece–Rodi Model (LRR) and Speziale–Sarkar–Gatski (SSG)) present case-dependent improvement by capturing anisotropic turbulence. Algebraic Stress Models (ASMs) provide a simplified alternative to RSM by approximating Reynolds stresses [25]. These computationally efficient approaches are widely adopted in industrial applications [26] and well suited for simulating steady flows and flows with minimal large-scale unsteadiness, where turbulence timescales dominate. However, their dependence on turbulence closure models introduces uncertainties and inaccuracies, especially in flow with strong non-equilibrium effects such as separation and shock interaction [27]. Peng et al. [28] evaluate the SST assumption in a low-Re model, demonstrating improved shock location and separation bubble predictions in transonic flows over the RAE2822 airfoil and DLR-F6 wing-body simulations. However, boundary layer recovery remains underpredicted, and grid sensitivity affects separation accuracy.
Most standard RANS models struggle to capture laminar-turbulent transitions, which are often crucial for flow separation phenomena. The RANS SST turbulence model refines the definition of eddy viscosity in the standard model by incorporating turbulence shear stress transport, enhancing its applicability to flow separation. However, it is primarily suited for fully turbulent flows but not for transitional flows. Advanced transitional turbulence models based on the SST framework, such as the low-Reynolds number correction model (LowRe), the correlation-based transition SST model (), the intermittency model (), and the model, have been developed and tested to address this limitation [29] for a Re range of to . The model demonstrates the best overall performance in predicting laminar separation, transition, and reattachment, particularly at higher Re and lower angles of attack (AOAs).
More examples are presented in Table 1. Though transitional models for flow separation analysis have achieved apparent improvements, the models’ accuracy and applicability remain case-dependent and require careful validation. The study highlights the limitations of traditional RANS-based models in capturing massive separation and highly unsteady flows, suggesting that hybrid RANS-LES methods, which combine RANS efficiency with LES resolution of large-scale unsteadiness, may be more appropriate for such cases.

Table 1.
Summary of case studies, methods, and findings in transition modeling for CFD for laminar-turbulent flows in aerodynamic and turbomachinery applications (Tu is turbulence intensity, a dimensionless measure of turbulence level; FSTI is free-stream turbulence intensity, a specific application of Tu to the undisturbed free stream).
Table 1.
Summary of case studies, methods, and findings in transition modeling for CFD for laminar-turbulent flows in aerodynamic and turbomachinery applications (Tu is turbulence intensity, a dimensionless measure of turbulence level; FSTI is free-stream turbulence intensity, a specific application of Tu to the undisturbed free stream).
| Reference | Geometry | Key Parameters | Methods | Key Findings | Limitations |
|---|---|---|---|---|---|
| Langtry et al. [30] | S809 airfoil (21% thickness) | Re = , AoA = 1°– 20°. FSTI = 0.2% | SST with transition model | Improved prediction of separation bubbles and torque; good prediction of lift/drag at moderate AoA | Struggles with massively separated flows; requires empirical correlations |
| Wolgemuth & Walters [31] | NACA0012 airfoil at varying AoA | Re = – , AoA = 0°– 20°, Tu = 0.01–2% | Transition-sensitive | Good prediction of separation bubbles | Overpredicts stall angles at low Re; requires unsteady solvers for convergence |
| Furst et al. [32] | Flat plate; two NACA0012 airfoils in tandem; VKI turbine blade | Re = , Tu = 0.3–9.43% | Algebraic model () with intermittency vs. model | Both predict bypass/natural transition; is better for separated flows | Grid dependency near walls; algebraic model struggles with 3D effects |
| Menter et al. [33] | Flat plates (T3 series); Pak-B turbine blader; T106 cascade; V103 compressor | Re = – , Tu = 0.03–8% | One equation intermittency () model coupled with SST | Galilean invariant; captures the separation bubbles and reattachment | Limited calibration for crossflow transition; requires fine grids for separation bubbles |
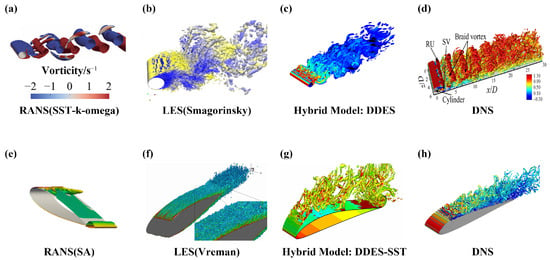
Figure 4.
The instantaneous flow field results over a cylinder (a–d) and an airfoil (e–h) obtained from various CFD models. (a) Isosurfaces of instantaneous vorticity at an Re of 3900 obtained by RANS (SST-k-omega) [34]. (b) Isosurfaces of normalized at an of 3900 by LES (Smagorinsky) [35]. (c) Iso-surface of at by a hybrid model (DDES) [36]. (d) Isosurfaces of , at an of 1000 by DNS [37]. (e) Flow around NACA0018 by RANS (SA) at an of and angle of attack = —isosurface of [38]. (f) The instantaneous vortical structures of the flow around NACA0012 by LES (Vreman) at an of and angle of attack = [39]. (g) The instantaneous vortical structures of the flow around Eppler 387 by a hybrid model (DDES-SST) at an of and an angle of attack = [40]. (h) Flow around SD7003 airfoil by DNS at an Re of and angle of attack = [41]—isosurface of Q-criterion = 500.
3.2. LES
LES emerged as a computationally feasible alternative (Figure 4b,f). LES is effective for unsteady flow separation scenarios, capturing the energy-containing eddies that dominate flow separation and reattachment processes, for instance, in simulating separation bubbles around a circular cylinder across a broad range of Re [8]. The results reveal a sharp drop in drag coefficient within the critical region, the formation and instability of laminar separation bubbles (LSBs), and the transition to turbulent reattachment. These insights enhance the understanding of flow dynamics, which are critical in the context of vortex-induced vibration (VIV) applications and their mitigation through passive and active flow control methods [42]. Other examples include studying flow control strategies in low-speed diffuser cascades with splitter blades [43], predicting separation over curved surfaces [44], and corner separation control in compressor cascades [45]. Despite its reduced computational demands compared to DNS, LES is still computationally expensive, particularly for high-Re flows, and sensitive to grid resolution, especially for near-wall regions. Yet, the reliance on subgrid models introduces inaccuracies, especially near walls. Wall-Modeled LES (WMLES) [46] differs from traditional LES in its treatment of the near-wall region, and employs a wall model to approximate the near-wall flow, avoiding the need for extremely fine grids near the wall. This approach significantly reduces the computational cost but can introduce additional modelling errors, particularly in complex flow regimes where accurate near-wall resolution is critical. The practicality of LES can be limited for high-Re flows and large-scale applications.
3.3. DNS
High-fidelity simulations become more influential in the late 20th century with the development of DNS. DNS resolves all turbulence scales directly by solving the NS equations without modelling approximations, providing a complete representation of flow dynamics (Figure 4d,h). If correct boundary conditions are applied and a high enough resolution is used, DNS generally enables well-compared results to experimental data. The outstanding performance makes DNS indispensable for fundamental turbulence research, such as examining complicated mechanisms of accelerating and decelerating turbulent flows [9,47], and validating turbulence models. DNS provides detailed turbulence statistics for model validation.
Several studies have demonstrated the effectiveness of DNS in analyzing flow separation. Jones et al. [48] applied DNS to investigate LSBs on a NACA 0012 airfoil, examining both forced and unforced transition to turbulence. Shahab et al. [49] utilized DNS with an in-house developed 3D incompressible Navier–Stokes solver (SUSA) to characterize separated low-Re flow around a NACA 65(12)10 cambered airfoil under deeply stalled conditions, effectively capturing unsteady flow features. Spalart and Watmuff [50] investigated separation and reattachment on a flat plate, by simulating a turbulent boundary layer over it with changing pressure gradients. The flow characteristics, such as velocity and turbulence intensity, are provided, and the flow transition was captured. A good agreement with experiments highlights DNS’s ability to improve understanding of turbulent boundary layers. Wu and Moin [51] explored boundary layer separation caused by APG, revealing critical interactions between eddies and shear layers.
DNS has proven invaluable in improving the understanding of flow separation, by providing high-resolved, accurate data on flow structures, turbulence statistics, and dynamic interactions. However, the computational cost of DNS increases exponentially with increasing Re, limiting its practical use to low-to-moderate-Re flows or canonical simple geometries [52]. Furthermore, the accuracy of DNS results is highly dependent on grid resolution and boundary conditions [53].
3.4. Hybrid Modeling Techniques
The strengths and limitations of traditional, widely used CFD methods were just discussed in Section 3.1, Section 3.2 and Section 3.3. This section focuses on hybrid simulation techniques, which combine multiple modelling approaches’ strengths to balance computational efficiency and accuracy. These methods are particularly valuable for addressing complex flow separation phenomena in high-Re flows and geometrically intricate configurations. Recent advancements further enhance hybrid approaches by integrating high-order methods and ROMs to improve predictive accuracy and capabilities.
3.4.1. Hybrid CFD Methods
Hybrid RANS-LES approaches have been developed to balance computational cost and accuracy, enabling simulations of high-Re flows over complex geometries. These methods leverage the efficiency of RANS near walls, where turbulence is typically at fine scales while applying LES in regions with large-scale features. They have demonstrated significant advantages over pure RANS or LES, offering an improved resolution of flow separation, unsteadiness, and other complex flow features [26].
DES has been applied to predict high-Re flows with massive separation [54]. It successfully reproduced abrupt wing stall (AWS) and vortex breakdown in the F-18 aircraft, captured unsteady shock motion, and was validated against experimental data. Adaptive mesh refinement significantly enhanced the resolution of separated flow regions, improving predictions of lift, drag, and pitching moment coefficients. However, further refinement of DES algorithms and grid resolution is needed to accurately model highly complex, dynamic phenomena such as shock oscillation and separation vortex instability.
Recent advancements in Delayed Detached Eddy Simulation (DDES), Stress-Blended Eddy Simulation (SBES), Shielded Detached Eddy Simulation (SDES), and Scale-Adaptive Simulation (SAS v.2024 ) [55,56,57] have introduced different RANS-LES transition criteria and turbulence models to enhance accuracy and efficiency. A key strength of these hybrid approaches is their ability to model laminar-turbulent transition, which significantly influences flow separation. For instance, DDES implemented in German Aerospace Center(DLR)’s TRACER solver and SBES with ANSYS Fluent v.2023 R2 incorporate transition-sensitive turbulence models, such as the transition model, to capture separation-induced transition [58,59]. Similarly, SAS with ANSYS Fluent v.16.1 employs scale-adaptive mechanisms to dynamically resolve transitional structures, while SDES improves shielding functions to better handle transitional boundary layers [60,61].
Despite their strengths, hybrid CFD methods still face challenges in accurately simulating flows with complex geometries and strong interactions between turbulence scales. In addition, the smoothness of transitions between RANS and LES regions remains problematic. For instance, Haering et al. [62] addressed stress depletion in standard hybrid RANS-LES methods with an Active Model Split (AMS) framework. This method effectively captures detailed flow physics. However, it involves significant complexity. The requirements of careful setup and being computationally costly limit its broader applicability. Despite the presence of continuous challenges, the step toward more accurate and efficient hybrid simulations always progresses.
3.4.2. Incorporated High-Order Methods in CFD Simulations
Advancements in numerical techniques, such as high-order methods, have further improved the fidelity of traditional CFD methods. Techniques like the Discontinuous Galerkin (DG) method and Spectral Element Method (SEM) provide superior accuracy and lower numerical dissipation for separation analysis. Compared to conventional low-order methods, they better capture separation bubbles, shear layers, and vortex structures. Furthermore, they have been successfully applied to transitional flows, accurately resolving phenomena like laminar separation, shear layer transition, and turbulent reattachment [63].
For instance, Wang et al. [64] employed high-order Weighted Compact Nonlinear Scheme (WCNS) with SSG/LRR- to enhance flow separation analysis, achieving superior vortex resolution, shock-induced separation, and junction flow prediction compared to the second-order method Monotonic Upstream-centered Scheme for Conservation Laws (MUSCL). While the SST model tends to overdamp unsteady motion, high-order methods more accurately capture flow structures. However, these studies are often limited to simplified configurations and face challenges related to stability and the broader acceptance of Reynolds stress models. Despite these limitations, high-order methods show significant promise for improving separated flow simulations. In a similar manner, Krank et al. [65] incorporated wall function enrichment into the DG framework for RANS simulations, enhancing the resolution of turbulent boundary layers and handling flow separation effectively. However, challenges in predicting reattachment lengths in separated flows suggest the need for hybrid RANS/LES models. DG methods bring high-order accuracy, flexibility for complex geometries, and robust handling of multiscale flow phenomena to CFD simulations. They are particularly well suited for simulations where precise resolution of unsteady flow fields and high-precision schemes for flow separation are significant [66]. Brill et al. [67] introduced an enrichment wall-modeling framework within a high-order SEM CFD solver Nek5000 for LES, incorporating an analytical law-of-the-wall function to improve the resolution of shear stress and turbulent boundary layers. Validated on channel flow cases, it demonstrated improved accuracy in capturing mean velocity profiles and addressing flow separation on under-resolved grids. Ohlsson et al. [9] applied SEM using Nek5000 codes in DNS of separated flow in a 3D diffuser, effectively resolving separation caused by APG and corner vortices, with results closely matching experimental data. While higher-order methods, such as SEM, offer high fidelity in resolving separation dynamics and complex flow features, their effectiveness in turbulence modelling heavily depends on the choice of turbulence model and, consequently, the accuracy of flow separation predictions. Furthermore, reliance on highly structured meshes to achieve high accuracy with fewer elements than traditional low-order methods can be a significant drawback, particularly for complex geometries. Additionally, the need for high-resolution simulations to capture complicated flow details often results in higher computational costs and longer simulation times, limiting their practicality for large-scale or industrial applications [68].
3.4.3. ROM
ROMs have been increasingly utilized in flow separation simulations to model complex flow fields with low computational expense [69]. As discussed in Section 3.1, Section 3.2 and Section 3.3, traditional CFD methods provide high-fidelity results but are too computationally expensive for iterative design and real-time applications like active flow control or adaptive flight systems, where rapid flow prediction is essential [70]. ROMs address this problem by projecting the high-dimensional flow field data onto a lower-dimensional subspace. This effectively reduces the computational cost, as only the dominant flow structures are captured. Among ROMs, Proper Orthogonal Decomposition (POD) and Dynamic Mode Decomposition (DMD) are most commonly used.
As a statistic-based technique, POD extracts data from experiments and simulations. It works by identifying coherent structures that contain the most energy or variance in the data and representing the flow field in terms of these dominant modes. Thus, a high-dimensional problem’s dimensionalities can be effectively reduced [71,72]. Sajadmanesh et al. [72] studied flow separation and reattachment on the suction side of a low-pressure turbine blade using URANS simulations combined with POD. POD identifies dominant flow structures and turbulent kinetic energy (TKE) distribution by analyzing velocity and pressure fields. At higher Re, it presents low-energy, small-scale structures, while at lower Re, it demonstrates high-energy, large-scale vortices that increase turbulence and losses. POD effectively captures phenomena like vortex shedding and shear layer flapping, providing insights beyond conventional simulations. Tong et al. [73] examined shock wave-turbulent boundary layer interactions (STBLIs) over a wavy-wall using DNS with Opencfd-SC and POD. DNS captures detailed flow dynamics, while POD identifies dominant structures and low-frequency unsteadiness in separation bubbles. The wavy-wall splits the separation bubble into smaller bubbles confined to troughs, with distinct low- and high-frequency oscillations displayed by POD. This combined approach improves the understanding of STBLIs and flow separation control strategies.
DMD is a dimensionality reduction and factorisation technique designed for analysing sequential data. It extracts coherent structures, captures dynamic behaviours, and simplifies complex processes into their dominant features. Closely linked to Koopman analysis, DMD has evolved through various extensions and improvements since its introduction. Zhao et al. [74] combined LES with DMD to analyze flow separation on an airfoil with leading-edge protuberances, employing the Smagorinsky-Lilly model in ANSYS Fluent v.19.2. DMD identifies dominant flow structures and frequencies, showing how streamwise vortices delay separation by momentum transfer enhancement. By uncovering shear layer dynamics in separation bubbles, this method provides a detailed understanding of flow separation and offers a robust framework for optimizing control strategies. In general, ROMs have significantly reduced the computational cost of traditional CFD methods while still preserving essential flow physics. However, their accuracy depends on the quality of used data and the chosen modes, which may limit their ability to generalize across different flow conditions or capture highly nonlinear and transient phenomena [75].
3.5. LBM
LBM is a mesoscopic numerical approach that simulates fluid flow by modelling particle distributions on a discrete lattice, recovering macroscopic fluid behaviour through the Boltzmann equation. It has gained attention as an alternative to traditional CFD methods in addressing flow separation problems at low-to-moderate Re due to its efficiency in handling complex geometries, parallelizability, and multiphase flow modeling [76]. While LBM offers high computational efficiency, its simplified boundary treatments and restricted Re range limit its applicability in aerospace, confining its use primarily to MAVs and electric vertical take-off and landing (eVTOL) aircraft. LBM DNS has been employed to study LSBs dynamics on an NACA0012 airfoil, using SIMULIA PowerFLOW v. 6-2022, a LBM-based solver [77], revealing how flow separation induces intermittent vortex shedding, which affects reattachment and turbulence transition. By integrating LES-based hybrid turbulence models, the computational instability and high cost of LBM at high Re have been mitigated [78], with improvements in numerical stability and refined boundary conditions. These enhancements enable better resolution of separation-induced turbulence and reattachment while reducing the need for excessive grid refinement. However, challenges remain in handling high-Re flows and the associated computational costs. Continuous efforts are needed to further enhance LBM’s applicability in broader aerospace applications.
3.6. Further Discussion
Despite its computational expense, DNS can benefit from adaptive meshing and efficient parallelization to extend its applicability to higher Re and more complex geometries. LES, particularly Wall-Modeled LES, requires further refinement of subgrid-scale models to improve near-wall turbulence predictions and reduce dependency on satisfactory grid resolutions. Hybrid DNS-LES methods are considered a wise choice with a counterbalance for DNS and LES to maximise simulation performance. The future of high-fidelity simulations for flow separation lies in overcoming key limitations such as computational expense, wall-region accuracy, and model dependency, while leveraging advancements in computational power and modeling techniques.
The rapid development of ML, such as data-driven turbulence closures and PINN [79], could significantly affect automation and enhance hybrid model performance. Moreover, high-order numerical methods can be made more robust and cost-effective through the development of stable solvers and adaptive grid refinement strategies tailored for shock-induced and complex separation regions. The integration of experimental data into these simulation techniques for validation and uncertainty quantification will further enhance predictive accuracy [80]. Lastly, efforts can be made to combine high-fidelity simulations with emerging technologies like quantum computing and exascale computing infrastructure. These efforts will offer an alternative pathway to target industrial-scale problems and improve aerodynamic designs.
4. ML for Flow Separation
With great potential, ML has gained growing influence in fluid mechanics. It creates a modular and more flexible modelling framework to address complex problems in fluid mechanics, including turbulence closure modelling and control, shape optimization, and flow field reconstruction and completion/prediction [4]. Machine learning algorithms can be classified as supervised, unsupervised, and reinforcement learning.
In supervised learning, training data should contain expert labels. Discrete labels correspond to classification tasks, while continuous labels correspond to regression tasks. Recent advancements in vortex detection have seen CNNs effectively utilized for classification tasks, where they convert the identification of vortices into a binary classification problem. This approach allows for the rapid and robust detection of vortices from flow fields, providing an objective and efficient method compared to traditional techniques [81]. In unsupervised learning, the data are unlabeled, requiring the extraction of patterns or intrinsic structures from the input data. The task involves clustering to identify discrete structures or embedding and dimensionality reduction to capture continuous structures. An example of unsupervised learning is super-resolution, which involves reconstructing a high-resolution image from one or more low-resolution images. It offers an alternative when CFD requires millions of grids in DNS to capture complex turbulent structures or when experimental methods like PIV and Schlieren are constrained by resolution limitations. Generative Adversarial Networks (GANs) are an example of effective methods that generate high-fidelity flow field data from limited or low-fidelity inputs [82,83]. Thus, they are particularly useful for enhancing the resolution of flow field simulations or filling in gaps in data. An autoencoder (AE), a nonlinear mapping method commonly used in unsupervised learning, learns efficient representations to perform dimensionality reduction or extract key features from flow fields. Reinforcement learning plays an increasing role in flow control, such as actively controlling oscillatory laminar flow around the bluff body, as explored by Guéniat et al. [84]. In reinforcement learning, an agent learns to make decisions by acting in an environment to achieve some goals, receiving feedback as rewards or penalties for actions taken [10].
This section reviews the application of ML techniques in advancing flow separation analysis through various approaches. Section 4.1 explores how ML enhances turbulent modeling closures in traditional CFD methods like RANS and LES, which often struggle with the complexity of turbulent flows, especially in separation regions. Section 4.2 focuses on ML-augmented ROMs to accelerate CFD simulations while maintaining accuracy. Section 4.3 highlights the use of Convolutional Neural Networks (CNNs) for reconstructing and predicting flow fields, and Section 4.4 discusses Graph Neural Networks (GNNs) for handling unstructured data in complex geometries. Section 4.5 introduces PINNs, which embed physical laws into ML models for accurate and interpretable predictions in flow separation. Finally, Section 4.6 examines the role of data assimilation in enhancing the scale and fidelity of datasets used for ML applications, further improving prediction accuracy.
4.1. ML Enhancement of Turbulent Modelling Closure
Hybrid models integrating ML with CFD have emerged as powerful tools for improving flow separation predictions. By applying the strengths of both data-driven and physics-based approaches, these methods aim to enhance turbulence modelling, accelerate simulations, and improve the accuracy of flow field predictions. Figure 5a shows a schematic of applying neural networks within an ML model to turbulence models. One prominent application of hybrid models is turbulence modelling, where ML assists in refining subgrid-scale models. Turbulence modelling closure is essential for approximating turbulent flows since directly solving the NS equations is computationally expensive. Traditional methods like RANS, LES, and hybrid approaches are widely used, as discussed in Section 3. Nevertheless, they often face challenges in capturing the complex and chaotic nature of turbulence, which extends across vast spatial and temporal scales. Zhu et al. [85] propose a Radial Basis Function Neural Network (RBFNN) to predict turbulent eddy viscosity for turbulence modelling. This method achieves accurate predictions of flows around the airfoil and exhibits good generalization across interpolation and extrapolation cases for various airfoils such as NACA0014 and RAE2822. However, it is still a preliminary work and does not investigate separated flows and other more complex turbulent flows.
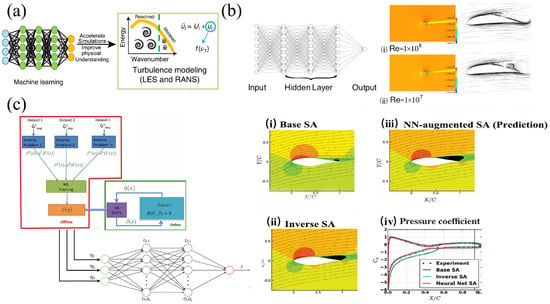
Figure 5.
(a) Applying neural networks within the ML model (left) to turbulence models (LES and RANS) (right) to accelerate computation and improve accuracy [86]. (b) The application of machine learning methods in the analysis and optimization of airfoils [87]. The structure of an 8−input deep neural network (DNN) used for airfoil optimization (left); the velocity field of the optimized airfoil at Re (i) and Re (ii), with an angle of attack of 5 degrees (right). (c) Left: Schematic of the field inversion process and feedforward neural network (NN) architecture for data-augmented turbulence modelling applicable to flow separation. Right: Comparison of streamlines, X-velocity contours, and pressure coefficient distributions around an S809 airfoil at a angle of attack and Re of , showing results from Base SA, Inverse SA, NN-augmented SA, and experimental data [88].
As an emerging approach to enhance turbulence modelling closure, ML techniques are particularly effective in quantifying RANS uncertainty and improving Reynolds stress closures in RANS, as well as the subgrid-scale (SGS) stress closures in LES. By leveraging large datasets, ML models can capture complicated flow dynamics and predict turbulence behaviour with higher fidelity. For example, neural networks have been employed to refine turbulence models by learning non-linear relationships in flow fields, enabling more accurate simulations of separation and collision flows. Ling et al. [89] integrated ML, specifically Tensor Basis Neural Networks (TBNNs), into RANS to improve predictions of Reynolds stress anisotropy. The TBNN enhances CFD simulations by embedding Galilean invariance. It successfully captures flow separation in the wavy walls case, and secondary flows in the duct corners case, where traditional RANS models fail. Figure 5b illustrates the application of ML methods in the analysis and optimization of airfoils [87]. An 8-input deep neural network (DNN) was used for airfoil optimization and the velocity contour and streamlines of the optimized airfoil at different Re values—Re and —with an angle of attack of 5 degrees are demonstrated. Anand et al. [88] proposed a feedforward neural network (NN)-enhanced framework to augment the Spalart–Allmaras (SA) turbulence model using limited experimental data (Figure 5c). Their approach involves reverse modeling to infer the spatial distribution of model discrepancies, demonstrating significant improvements in predictive accuracy for turbulent flow separation over airfoils. While this method enhances the traditional SA model, current research remains largely confined to outcome predictions for trained models, and developing a universally applicable turbulence model continues to be a major challenge.
4.2. ML-Enhanced ROMs
Another advancement in ML is its application in ROMs, where hybrid approaches leverage ML to accelerate flow simulations. By processing large datasets and capturing nonlinear relationships, ML further enhances computational efficiency. For example, Zhang et al. [90] incorporated ML with ROMs to study turbulent flow separation around the NACA 4412 airfoil. Using LES data, a Convolutional Autoencoder (CAE) compresses flow fields, while a multi-head attention-enhanced LSTM predicts latent dynamics, enabling high-accuracy flow field reconstruction. This framework outperforms traditional POD and AE-DMD methods by effectively capturing fine-scale features near trailing edges and wakes. It demonstrates the potential of ML-ROMs for efficient flow separation modelling. Liu et al. [91] integrated ML with ROM to study transonic buffet flows with flow separation. The shock wave motion and flow separation on the OAT15A airfoil are predicted with an enhanced hybrid deep neural network (eHDNN) combining CNN, ConvLSTM, and DeCNN. The model efficiently captures nonlinear spatiotemporal dynamics and achieves higher accuracy compared to traditional methods, particularly in unseen conditions. Furthermore, Jia et al. [92] applied a hybrid reduced-order model (DMD-PODX), a combination of DMD, POD, and Long Short-Term Memory (LSTM) networks, to model and predict unsteady flows (Figure 6). The model predicted flow separation and nonlinear dynamics with higher accuracy than standalone methods in case studies of a 2D circular cylinder at Re and a transonic NACA0012 airfoil. These advancements highlight the potential of ML-ROMs in efficiently capturing complex aerodynamic phenomena, such as vortex shedding and shock wave dynamics.
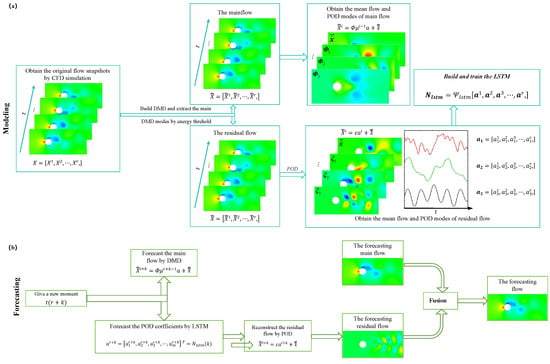
Figure 6.
The architecture of the DMD-PODX for unsteady flow (a) modeling and (b) forecasting [92].
4.3. CNNs
The high-dimensional and nonlinear nature of aeronautical flow problems requires surrogate models capable of handling complex parameter spaces while integrating physical principles and real-time data. In reinforcement learning applied to separated flows, CNNs have shown significant progress in state observation and flow control from structured data inputs without prior knowledge [4].
In supervised learning used for identification and classification of flow fields by mapping input parameters (e.g., Re, geometry, angle of attack) to flow dynamics, CNNs have been widely used. One example is their application in the detection of vortices and cores. Four features—contour area, aspect ratio, area difference, and moment centre—are utilized in the YOLOv5s model, achieving an accuracy of 97.56% in detecting vortex cores across 133 images. This approach not only decreases computational expenses but also ensures high statistical confidence [81]. CNNs have also been applied to cloud classifications (Figure 7b), demonstrating accuracy and robustness with small datasets [93].
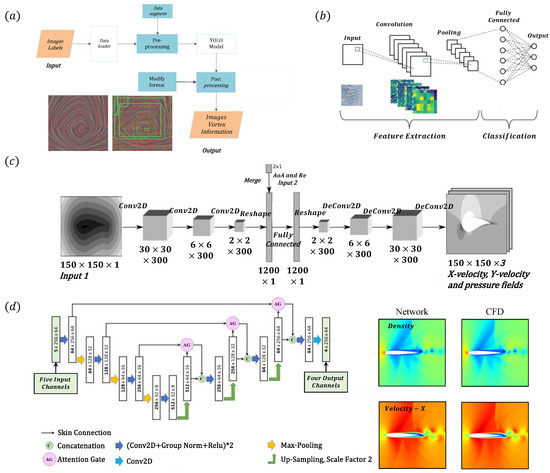
Figure 7.
Application of CNNs in separated flow problems: (a) YOLOv5 model for vortex detection [81]; (b) CNN architecture for cloud feature extraction and classification [93]; (c) CNN encoder–decoder for airfoil flow field prediction [94]; (d) attention U-Net structure for predictive modeling of transonic airfoil flow [95].
For flow field reconstruction and prediction, many researchers utilize CNNs due to their effectiveness in processing images or spatial representations of flow field data. A combination of long short-term memory (LSTM) with a convolution architecture was designed for the fast and accurate prediction of unsteady separating flow around a cylinder and airfoils [96]. CNNs have shown success in modeling steady flow fields, as demonstrated by Sekar et al. [97], where CNNs were used to parameterize airfoil geometries, enabling Multilayer Perceptrons (MLPs) to predict flow fields around airfoils with laminar flow separations. Similarly, Bhatnagar et al. [94] used CNNs to model turbulent transonic airfoil flow fields with separating wakes, achieving robust predictions across a wide range of Re and angles of attack, as shown in Figure 7c. Duru et al. [98] present a CNN-based model for predicting transonic flow fields, including shock waves and flow separation around airfoils. The encoder–decoder architecture efficiently captures complex phenomena like shock wave–boundary layer interaction, offering predictions three orders faster than CFD with minimal accuracy loss. Lee et al. [99] introduce a hybrid framework leveraging GANs for ROM of unsteady flows around a circular cylinder at Re 100. The CNN extracts spatial and temporal features from high-fidelity simulation data, while the GAN generates accurate flow field reconstructions and predicts temporal evolution, including separation and vortex-shedding dynamics. The case study demonstrates that the GAN-based ROM outperforms conventional approaches in accurately capturing nonlinear flow phenomena like separation, associated with high efficiency and robustness in predictive performance.
4.4. GNNs
GNNs are a class of ML models that operate on structured or unstructured data, where relationships between data points are encoded as nodes and edges. Unlike CNNs, which are optimized for structured, grid-like data such as images and struggle with irregular meshes in fluid dynamics simulations, GNNs are designed for unstructured, non-Euclidean domains, making them particularly suitable for predicting complex flow fields, including flow separation and irregular spatial distributions. GNNs employ message-passing mechanisms to aggregate information from neighboring nodes, effectively capturing both local and global relationships within the flow field [100,101].
Ogoke et al. [100] demonstrated the effectiveness of a Graph Convolutional Neural Network (GCNN) framework for predicting aerodynamic properties on unstructured meshes around airfoils with flow separations, using graph-based representations (Figure 8a). The model achieved high accuracy () and outperformed traditional ML approaches. Notably, it can extract meaningful features directly from velocity data without requiring structured inputs, making it highly relevant for flow field prediction in complex geometries and sparse data scenarios. He et al. [101] introduced the Flow Completion Network (FCN), embedding first- and second-order partial derivatives in the NS equations into the loss functions within carefully designed inter-layers of a GNN to predict separating flow fields and forces from incomplete flow field data for the first time (Figure 8b). When tested on data from CFD simulations around a 2D circular cylinder, the FCN outperformed traditional CNNs and DNNs. It integrates spatial gradients and physical principles of the NS equations, achieving high accuracy and robustness even with sparse datasets. This method is highly relevant for flow field prediction, particularly in scenarios with unstructured data and limited measurements.
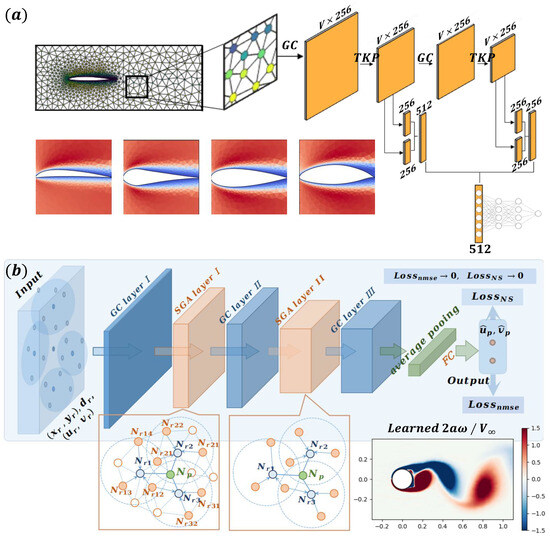
Figure 8.
(a) The architecture of the graph convolution neural network (GCNN). “TKP” refers to Top-K Pooling -adapted from [100]. (b) Flow Completion Network (FCN) for predicting flow fields and forces from incomplete data [101].
David et al. [102] propose a Graph Convolutional Network-based Multi-Mesh Autoencoder (GCN-MM-AE) framework that efficiently predicts aerodynamic loads on aircraft surfaces. This framework significantly reduces computational costs, achieving prediction speeds over 99.9% faster than traditional CFD methods while accurately capturing complex aerodynamic phenomena, including shock waves and flow separation. The framework’s capacity to predict multiple physical quantities, such as pressure and shear-stress distributions, from a single model ensures physical consistency and demonstrates its potential for broader applications beyond aerodynamics, extending to other fields requiring the processing of non-Euclidean data. Hines et al. [103] investigated the use of GNNs for predicting aircraft surface pressure distributions, demonstrating significant improvements in capturing complex aerodynamic phenomena, especially in transonic flows with shocks and flow separation. GNNs outperformed traditional methods like POD coupled with interpolation and MLP in both 2D airfoil and 3D aircraft cases, achieving up to 61% lower error in predicting pressure distributions. The enhanced accuracy and ability to handle localized nonlinearities make GNNs a promising alternative for efficient aerodynamic predictions in industrial applications. Yiren et al. [104] developed a multi-fidelity workflow using a GNN-based surrogate model to enhance low-fidelity vortex lattice method (VLM) predictions of aerodynamic coefficients on delta wings. The workflow achieved a fivefold reduction in prediction error compared to VLM alone, demonstrating significant improvements in capturing nonlinear flow features such as flow separation.
4.5. PINNs
Despite the potential and flexibility offered by ML models, their “black-box” nature poses challenges in terms of transparency and interpretability, especially for nonlinear and complex problems. This opacity hinders understanding the rationale behind models’ decision-making processes. Nevertheless, fluid mechanics researchers remain highly motivated to extract physical insights and uncover the underlying principles driving these models. Broadly, PINNs are a responsive approach that integrates physical laws (e.g., NS equations for fluid flow) directly into the training process, ensuring the model adheres to fundamental principles. In fluid dynamics, this method embeds the NS equations into the neural network’s loss function, reducing reliance on extensive labeled data.
PINNs have been employed in hybrid frameworks to enforce physical laws while incorporating data-driven insights. They have been applied to complex flow fields, such as VIV [105] (Figure 9) and flow separation [11]. In these cases, PINNs effectively capture key separation features, including boundary layer detachment and reattachment, even with sparse or noisy data. This approach offers a cost-effective and accurate alternative to traditional CFD methods for flow separation prediction. Moreover, Ren et al. [106] applied PINNs for a high-Reynolds transonic flows study. Improving boundary layer and shear layer predictions demonstrates its potential in data-driven separation modelling. However, limitations are present with its poor shock–boundary layer handling and steady-state flow focus. There is a need for more work on turbulent and unsteady cases.
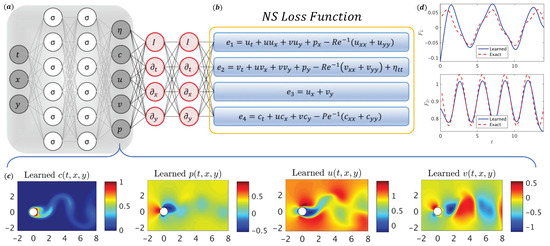
Figure 9.
(a) Schematic of physics-informed neural network (PINN) in DeepVIV. (b) NS Loss Function in DeepVIV. (c) Representative snapshot of flow field of learned and v. (d) Resulting lift force and drag force for CFD and learned flow field [105].
PINNs bridge the gap between data-driven methods and physics-based models, enhancing machine learning applications’ reliability and interpretability. This integration enables the development of more robust and generalizable tools for tackling flow separation and other complex aerodynamic challenges. PINNs outperform traditional methods by achieving faster convergence and lower computational costs. However, challenges remain, such as reduced accuracy due to random sampling. Currently, the integration of PINNs within CNN or GNN models remains underexplored, with limited research focusing on simplified approaches to incorporating physics into the training process [101]. Future work will focus on enhancing dynamic sampling strategies and improving scalability to address complex flow separation problems more effectively.
4.6. Data Assimilation Enhanced ML
Data assimilation can be integrated with traditional CFD methods, ROMs, or ML approaches to enhance flow field prediction and reconstruction by combining computational models with experimental data, thereby improving accuracy and reliability. This section focuses on how ML methods and data assimilation have significantly advanced flow field completion and reconstruction. Traditional techniques, such as ensemble Kalman filters (EnKFs) and variational approaches, have been further refined through ML integration. Mons et al. [107] demonstrated the use of data assimilation to reconstruct turbulent flow fields by combining reduced-order models with experimental data, providing improved predictions of flow separation dynamics. Similarly, Maulik et al. [108] incorporated a data assimilation framework using physics-constrained deep learning to reconstruct separated flow fields using sparse sensor data. These ML-driven approaches provide robust and efficient methods for capturing flow features in both laminar and turbulent regimes.
5. Discussions and Future Trends
This review highlights advancements in simulations and machine learning (ML) for predicting and analyzing flow separation. Table 2 summarizes various methods. Traditional computational approaches, including RANS, LES, and DNS have provided valuable insights into flow dynamics but are hindered by their high computational cost and limited ability to capture complex separated flows accurately. These limitations have driven the exploration of ML techniques as an alternative approach to improving accuracy and efficiency in flow prediction and control. CNNs, Autoencoders, and reinforcement learning have shown promising results in reconstructing and predicting flow fields, reducing computational requirements while maintaining accuracy. Additionally, GNNs have proven effective for handling unstructured data in complex geometries, addressing challenges posed by traditional CFD methods. ROMs augmented with ML further accelerate simulations by simplifying high-dimensional data without compromising performance. These developments enable faster, more efficient analyses of complex flow scenarios, essential for real-time applications. Moreover, advancements in the integration of physical laws into ML frameworks, particularly through PINNs, have been discussed. By embedding governing equations such as the NS equations into neural network architectures, PINNs ensure that models adhere to fundamental physical principles, improving both reliability and interpretability. This approach bridges the gap between purely data-driven models and physics-based simulations, addressing one of the critical challenges in applying ML to fluid mechanics—the lack of transparency and physical consistency. Data assimilation enhances the accuracy of ML-based approaches by integrating computational models with experimental data, improving flow field reconstruction in turbulent and separated flows. This integration boosts the predictive capabilities of reduced-order models and control strategies, providing an effective toolset for tackling flow separation challenges.

Table 2.
Comparison of different methods for flow separation analysis.
Looking ahead, integrating ML with advanced computational tools, experimental data, and emerging technologies like quantum computing will further enhance fluid mechanics research. Addressing challenges such as the “black-box” nature of ML, improving generalizability across flow conditions, and reducing computational costs will drive future advancements, leading to breakthroughs in aerodynamic performance and control with broad applications in the aerospace and renewable energy sectors.
Author Contributions
X.H. (Xueru Hao): Investigation; Analysis; Methodology; Writing—original draft; Writing—review and editing. X.H. (Xiaodong He): Investigation; Analysis; Methodology; Writing—original draft; Writing—review and editing. Z.Z.: Investigation; Analysis; Writing—original draft; Writing—review and editing. J.L.: Conceptualization; Investigation; Supervision; Writing—original draft; Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
King’s College London: Start-up Grant; Daiwa Anglo-Japanese Foundation: Daiwa Foundation Awards (14465/15310).
Data Availability Statement
Not applicable.
Acknowledgments
This work was funded by the Engineering Start-up Grant of King’s College London. The research was also partially funded by the Daiwa Anglo-Japanese Foundation through Daiwa Foundation Awards (14465/15310).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Roshko, A. Perspectives on Bluff Body Aerodynamics. J. Wind. Eng. Ind. Aerodyn. 1992, 49, 79–100. [Google Scholar] [CrossRef]
- Rizzi, A.; Luckring, M.J. Historical Development and Use of CFD for Separated Flow Simulations Relevant to Military Aircraft. Aerosp. Sci. Technol. 2021, 117, 106940. [Google Scholar] [CrossRef]
- Gursul, I.; Wang, Z. Flow Control of Tip/Edge Vortices. AIAA J. 2018, 56, 1731–1749. [Google Scholar] [CrossRef]
- Li, Y.; Chang, J.; Kong, C.; Bao, W. Recent Progress of Machine Learning in Flow Modeling and Active Flow Control. Chin. J. Aeronaut. 2022, 35, 14–44. [Google Scholar] [CrossRef]
- Sun, X.; Xu, Y.; Huang, D. Numerical Simulation and Research on Improving Aerodynamic Performance of Vertical Axis Wind Turbine by Co-flow Jet. J. Renew. Sustain. Energy 2019, 11, 013303. [Google Scholar] [CrossRef]
- Heinz, S. The Potential of Machine Learning Methods for Separated Turbulent Flow Simulations: Classical Versus Dynamic Methods. Fluids 2024, 9, 278. [Google Scholar] [CrossRef]
- Mokhtarpoor, R.; Heinz, S.; Stoellinger, M. Dynamic Unified RANS-LES Simulations of High Re Separated Flows. Phys. Fluids 2016, 28, 095101. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, J.; Gong, Y.; Xu, H. Large Eddy Simulation of Flow and Separation Bubbles Around a Circular Cylinder from Sub-critical to Super-critical Reynolds Numbers. J. Mar. Sci. Appl. 2023, 22, 219–231. [Google Scholar] [CrossRef]
- Ohlsson, J.; Schlatter, P.; Fischer, F.P.; Henningson, S.D. Direct Numerical Simulation of Separated Flow in a Three-dimensional Diffuser. J. Fluid Mech. 2010, 650, 307–318. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Jin, X.; Cai, S.; Li, H.; Karniadakis, G.E. NSFnets (Navier-Stokes flow nets): Physics-Informed Neural Networks for the Incompressible Navier-Stokes Equations. J. Comput. Phys. 2021, 426, 109951. [Google Scholar] [CrossRef]
- Greenblatt, D.; Wygnanski, J.I. The Control of Fow Separation by Periodic Excitation. Prog. Aerosp. Sci. 2000, 36, 487–545. [Google Scholar] [CrossRef]
- Chang, P.K. Introduction to the Problems of Flow Separation. In Separation of Flow; Pergamon Press: Oxford, UK, 1970; pp. 3–35. [Google Scholar]
- Schlichting, H.; Gersten, K. Boundary Layer Theory. In Fundamentals of Boundary—Layer Theory; Springer: Berlin, Germany, 2017; pp. 29–49. [Google Scholar]
- Bezzola, A. Optimal Bass Reflex Loudspeaker Port Design. In Proceedings of the COMSOL Conference 2019, Boston, MA, USA, 2–4 October 2019. [Google Scholar]
- Van Dyke, M. An Album of Fluid Motion; The Parabolic Press: Stanford, CA, USA, 1982. [Google Scholar]
- Wikipedia Contributors. Flow Separation. Available online: https://en.wikipedia.org/wiki/Flow_separation (accessed on 3 March 2025).
- Pope, S.B. Wall Flows. In Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; pp. 264–332. [Google Scholar]
- Graham, M.; Li, J. Vortex Shedding and Induced Forces in Unsteady Flow. Aeronaut. J. 2024, 128, 2149–2190. [Google Scholar] [CrossRef]
- Leibovich, S.; Luckring, J.M. The Structure of Vortex Breakdown. Annu. Rev. Fluid Mech. 1978, 10, 221–246. [Google Scholar] [CrossRef]
- Wang, S.; He, G.; Liu, T. Estimating lift from wake velocity data in flapping flight. J. Fluid Mech. 2019, 868, 501–537. [Google Scholar] [CrossRef]
- Li, J.; Zhao, X.; Graham, M. Vortex force maps for three-dimensional unsteady flows with application to a delta wing. J. Fluid Mech. 2020, 900, A36. [Google Scholar] [CrossRef]
- Simpson, R.L. Junction Flows. Annu. Rev. Fluid Mech. 2001, 33, 415–443. [Google Scholar] [CrossRef]
- Délery, J. Separation in Three-Dimensional Flow: Critical Points, Separation Lines, and Vortices. Onera—The French Aerospace Lab. 2011. Available online: https://www.onera.fr/sites/default/files/ressources_documentaires/cours-exposes-conf/onera-3d-separation-jean-delery-2011-1a.pdf (accessed on 2 January 2025).
- Durbin, P.A. Some Recent Developments in Turbulence Closure Modeling. Annu. Rev. 2018, 50, 77–103. [Google Scholar] [CrossRef]
- Chaouat, B. The State of the Art of Hybrid RANS/LES Modeling for the Simulation of Turbulent Flows. Flow Turbul. Combust 2017, 99, 279–327. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Peng, S.H.; Eliasson, P. Examination of the Shear Stress Transport Assumption with a Low-Reynolds Number k–ω Model for Aerodynamic Flows. In Proceedings of the 37th AIAA Fluid Dynamics Conference and Exhibit, Miami, FL, USA, 25–28 June 2007. AIAA 2007-3864. [Google Scholar]
- Liu, Y.; Li, P.; Jiang, K. Comparative Assessment of Transitional Turbulence Models for Airfoil Aerodynamics in the Low Reynolds Number Range. J. Wind. Eng. Ind. Aerodyn. 2021, 217, 104726. [Google Scholar] [CrossRef]
- Langtry, R.B.; Gola, J.; Menter, F.R. A One-Equation Local Correlation-Based Transition Model. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. AIAA 2006-395. [Google Scholar]
- Wolgemuth, N.M.; Walters, D.K. CFD Prediction of Boundary Layer Transition And Separation on an Airfoil at Varying Angle of Attack. In Proceedings of the EDSM2007 5th Joint ASME/JSME Fluids Engineering Conference, San Diego, CA, USA, 30 July–2 August 2007. FEDSM2007-37111. [Google Scholar]
- Fürst, J.; Příhoda, J.; Straka, P. Numerical Simulation of Transitional Flows. Computing 2013, 95, S163–S182. [Google Scholar] [CrossRef]
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A One-Equation Local Correlation-Based Transition Model. Flow Turbul. Combust 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Xia, X.; You, Z.; Wang, Z. The three types of turbulence models and stability numerical simulation studies for cylindrical flow. Hydro-Sci. Eng. 2024, 5, 84–94. [Google Scholar]
- Lysenko, D.A.; Ertesvåg, I.S.; Rian, K.E. Large-Eddy Simulation of the Flow Over a Circular Cylinder at Reynolds Number 3900 Using the OpenFOAM Toolbox. Flow Turbul. Combust 2012, 89, 491–518. [Google Scholar] [CrossRef]
- Zhang, D.; Cadel, D.R.; Paterson, E.G.; Lowe, K.T. Hybrid RANS/LES Turbulence Model Applied to a Transitional Unsteady Boundary Layer on Wind Turbine Airfoil. Fluids 2019, 4, 128. [Google Scholar] [CrossRef]
- Li, J.; Wang, B.; Qiu, X.; Wu, J.; Zhou, Q.; Fu, S.; Liu, Y. Three-dimensional vortex dynamics and transitional flow induced by a circular cylinder placed near a plane wall with small gap ratios. J. Fluid Mech. 2022, 953, A2. [Google Scholar] [CrossRef]
- Guo, H.; Li, G.; Zou, Z. Numerical Simulation of the Flow around NACA0018 Airfoil at High Incidences by Using RANS and DES Methods. J. Mar. Sci. Eng. 2022, 10, 847. [Google Scholar] [CrossRef]
- Arias-Ramírez, W.; Oberoi, N.; Larsson, J. Multifidelity Approach to Sensitivity Estimation in Large-Eddy Simulation. AIAA J. 2023, 61, 3485–3495. [Google Scholar] [CrossRef]
- Sa, J.H.; Park, S.H.; Kim, C.J.; Park, J.K. Low-Reynolds number flow computation for eppler 387 wing using hybrid DES/transition model. J. Mech. Sci. Technol. 2015, 29, 1837–1847. [Google Scholar] [CrossRef]
- Beck, A.D.; Bolemann, T.; Flad, D.; Frank, H.; Gassner, G.J.; Hindenlang, F.; Munz, C. High-order discontinuous Galerkin spectral element methods for transitional and turbulent flow simulations. J. Int. J. Numer. Meth. Fluids. 2014, 76, 522–548. [Google Scholar] [CrossRef]
- Zhao, M. A Review of Recent Studies on the Control of Vortex-induced Vibration of Circular Cylinders. Ocean. Eng. 2023, 285, 115389. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, J.; Jiang, B.; Zhou, H.; Yang, W.; Ling, J. Large-Eddy Simulation of Flow Separation Control in Low-Speed Diffuser Cascade with Splitter Blades. Processes 2023, 11, 3249. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer Models for Large-Eddy Simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Meng, T.; Li, X.; Zhou, L.; Zhu, H.; Li, J.; Ji, L. Large Eddy Simulation and Combined Control of Corner Separation in a Compressor Cascade. Phys. Fluids 2022, 34, 075113. [Google Scholar] [CrossRef]
- Kawai, S.; Larsson, J. Wall-modeling in Large Eddy Simulation: Length Scales, Grid Resolution, and Accuracy. Phys. Fluids 2012, 24, 015105. [Google Scholar] [CrossRef]
- Malik, R.M.; Uzun, A. DNS of Accelerating and Decelerating Turbulent Flow. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 19 August 2020. [Google Scholar]
- Jones, L.E.; Sandberg, R.D.; Sandham, N.D. Direct Numerical Simulations of Forced and Unforced Separation Bubbles on an Airfoil at Incidence. J. Fluid Mech. 2008, 602, 175–207. [Google Scholar] [CrossRef]
- Shahab, M.F.; Omidyeganeh, M.; Pinelli, A. DNS of Separated Low-Re Flow Around a Cambered Aerofoil. In Direct and Large-Eddy Simulation XI; Springer: Berlin/Heidelberg, Germany, 2019; pp. 373–380. [Google Scholar]
- Spalart, R.P.; Watmuff, H.J. Experimental and Numerical Study of a Turbulent Boundary Layer with Pressure Gradients. J. Fluid Mech. 1993, 249, 337–371. [Google Scholar] [CrossRef]
- Wu, X.; Moin, P. Direct Numerical Simulation of Turbulence in A Nominally Zero-pressure-gradient Flat-plate Boundary Layer. J. Fluid Mech. 2009, 630, 5–41. [Google Scholar] [CrossRef]
- Coleman, G.N.; Sandberg, R.D. A Primer on Direct Numerical Simulation of Turbulence- Methods, Procedures and Guidelines; Technical Report AFM-09/01b; University of Southampton: Southampton, UK, 2010. [Google Scholar]
- Zhang, W.; Samtaney, R. Assessment of Spanwise Domain Size Effect on the Transitional Flow Past an Airfoil. Comput. Fluids 2016, 124, 39–53. [Google Scholar] [CrossRef]
- Cummings, M.R.; Squires, K.; Spalart, P. Multidisciplinary Applications of Detached-Eddy Simulation to Separated Flows at High Reynolds Numbers. In Proceedings of the 2004 Users Group Conference, Williamsburg, VA, USA, 7–11 June 2004; pp. 103–111. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A New Version of Detached-eddy Simulation, Resistant to Ambiguous Grid Densities. Theor. Comput. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Menter, F.R. Stress-Blended Eddy Simulation (SBES)—A New Paradigm in Hybrid RANS-LES Modeling. In Proceedings of the 6th Symposium on Hybrid RANS-LES Methods, Strasbourg, France, 20–21 November 2018; pp. 27–37. [Google Scholar]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Moller, F.M.; Tucker, P.G.; Wang, Z.; Morsbach, C.; Bergmann, M. On the Prediction of Separation-Induced Transition by Coupling Delayed Detached-Eddy Simulation with γ-Transition Model. In Proceedings of the 15th European Conference on Turbomachinery Fluid Dynamics & Thermodynamics, Budapest, Hungary, 24–28 April 2023. [Google Scholar]
- Sandrin, S.; Mazzei, L.; Soghe, R.D.; Fontaneto, F. Computational Fluid Dynamics Prediction of External Thermal Loads on Film-Cooled Gas Turbine Vanes: A Validation of Reynolds-Averaged Navier–Stokes Transition Models and Scale-Resolving Simulations for the VKI LS-94 Test Case. Fluids 2024, 9, 91. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. CFD Analysis of Dynamic Stall on Vertical Axis Wind Turbines using Scale Adaptive Simulation (SAS): Comparison against URANS and Hybrid RANS/ LES. Energy Convers. Manag. 2019, 196, 1281–1298. [Google Scholar] [CrossRef]
- Weihing, P.; Letzgus, T.; Kramer, E. Development of Alternative Shielding Functions for Detached-Eddy Simulations. In Progress in Hybrid RANS-LES Modelling, Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Hoarau, Y., Peng, S.H., Schwamborn, D., Revell, A., Mockett, C., Eds.; Springer: Cham, Switzerland, 2019; pp. 109–118. [Google Scholar]
- Haering, W.S.; Oliver, A.T.; Moser, D.R. Active Model Split Hybrid RANS/LES. Phys. Rev. Fluids 2022, 7, 014603. [Google Scholar] [CrossRef]
- Wang, Z.J.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck, H.; Hartmann, R.; Hillewaert, K.; Huynh, H.T.; et al. High-order CFD Methods: Current Status and Perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar] [CrossRef]
- Wang, S.; Dong, Y.; Deng, X. High-Order Simulation of Aeronautical Separated Flows with a Reynold Stress Model. J. Aircr. 2018, 55, 1177–1190. [Google Scholar] [CrossRef]
- Krank, B.; Kronbichler, M.; Wall, W.A. Wall Modeling via Function Enrichment Within a High-order DG Method for RANS Simulations of Incompressible flow. Int. J. Numer. Methods Fluids, 2024; accepted. [Google Scholar] [CrossRef]
- Ding, Q.; Zhao, M.; Xian, J.; Chen, Y.; Hao, S.; Cheng, C.; Li, X.; Liu, Z. Large Eddy Simulation Based on An Improved High-precision Interior Penalty Discontinuous Galerkin Method: Flow Past Cylinders and Airfoils. Acta Mech. 2024, 235, 6599–6623. [Google Scholar] [CrossRef]
- Brill, S.R.; Pal, P.; Ameen, M.; Xu, C.; Ihme, M. An Enrichment Wall Modeling Framework for Spectral Element Methods. Phys. Fluids 2024, 36, 125169. [Google Scholar] [CrossRef]
- Gassner, G.J.; Beck, A.D. On the Accuracy of High-order Discretizations for Underresolved Turbulence Simulations. Theor. Comput. Fluid Dyn. 2013, 27, 221–237. [Google Scholar] [CrossRef]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order Modelling: New Approaches for Computational Physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef]
- Xu, Z.; Cao, N.Y.; Li, C.; Luo, Y.; Su, E.; Wang, W.; Tang, W.; Yao, Z.; Wang, Z.L.A. Digital Mapping of Surface Turbulence Status and Aerodynamic Stall on Wings of a Flying aircraft. Nat. Commun. 2023, 14, 2792. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Sajadmanesh, S.M.; Mojaddam, M.; Mohseni, A.; Nikparto, A. Numerical Identification of Separation Bubble in an Ultra-high-lift Turbine Cascade Using URANS Simulation and Proper Orthogonal Decomposition. Aerosp. Sci. Technol. 2019, 93, 105329. [Google Scholar] [CrossRef]
- Tong, F.; Sun, D.; Li, X. Direct Numerical Simulation of Impinging Shock Wave and Turbulent Boundary Layer Interaction over a Wavy-wall. Chin. J. Aeronaut. 2021, 34, 350–363. [Google Scholar] [CrossRef]
- Zhao, M.; Zhao, Y.; Liu, Z. Dynamic Mode Decomposition Analysis of Flow Characteristics of an Airfoil with Leading Edge Protuberances. Aerosp. Sci. Technol. 2020, 98, 105684. [Google Scholar] [CrossRef]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.M.; Yeh, C. Modal Analysis of Fluid Flows: Applications and Outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Ribeiro, R.L.; Dantas, C.; Wolf, W. Intermittency of a Transitional Airfoil Flow with Laminar Separation Bubble Solved by the Lattice-Boltzmann Method. Aerosp. Sci. Technol. 2025, 158, 109907. [Google Scholar] [CrossRef]
- Premnath, K.N.; Pattison, M.J.; Banerjee, S. An Investigation of the Lattice Boltzmann Method for Large Eddy Simulation of Complex Turbulent Separated Flow. J. Fluids Eng. 2013, 135, 051401. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhao, S.; Zhou, Y.; Liang, H.; Bian, X. An unstructured adaptive mesh refinement for steady flows based on physics-informed neural networks. arXiv 2024, arXiv:2411.19200. [Google Scholar]
- Wan, Z.; Zhang, W. A unified method of data assimilation and turbulence modeling for separated flows at high Reynolds numbers. Phys. Fluids 2023, 35, 025124. [Google Scholar]
- Xu, Z.; Maria, A.; Chelli, K.; Premare, T.D.; Bilbao, X.; Petit, C.; Zoumboulis-Airey, R.; Moulitsas, I.; Teschner, T.; Asif, S.; et al. Vortex and Core Detection using Computer Vision and Machine Learning Methods. Eur. J. Comput. Mech. 2023, 32, 467–494. [Google Scholar] [CrossRef]
- Hu, L.; Wang, W.; Xiang, Y.; Zhang, J. Flow Field Reconstructions with GANs Based on Radial Basis Functions. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3460–3476. [Google Scholar] [CrossRef]
- Li, N.; Liu, Y.; Gong, G.; Zhao, L.; Yuan, H. A generative deep learning approach for real-time prediction of hypersonic vehicles in fluid-thermo-structural coupling fields. Aerosp. Sci. Technol. 2023, 139, 108398. [Google Scholar] [CrossRef]
- Guéniat, F.; Mathelin, L.; Hussaini, M.Y. A Statistical Learning Strategy for Closed-Loop Control of Fluid Flows. Theor. Comput. Fluid Dyn. 2016, 30, 497–510. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine Learning Methods for Turbulence Modeling in Subsonic Flows Around Airfoils. Phys. Fluids 2019, 31, 015105. [Google Scholar] [CrossRef]
- Vinuesa, R.; Brunton, S.L. Enhancing computational fluid dynamics with machine learning. Nat. Comput. Sci. 2022, 2, 358–366. [Google Scholar] [CrossRef]
- Areias, P.; Correia, R.; Melicio, R. Airfoil Analysis and Optimization Using a Petrov–Galerkin Finite Element and Machine Learning. Aerospace 2023, 10, 638. [Google Scholar] [CrossRef]
- Singh, A.P.; Medida, S.; Duraisamy, K. Machine-Learning-Augmented Predictive Modeling of Turbulent Separated Flows over Airfoils. AIAA J. 2017, 55, 2215–2227. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds Averaged Turbulence Modelling Using Deep Neural Networks with Embedded Invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Zhang, B. Airfoil-based Convolutional Autoencoder and Long Short-term Memory Neural Network for Predicting Coherent Structures Evolution Around an Airfoil. Comput. Fluids 2023, 258, 105883. [Google Scholar] [CrossRef]
- Liu, Z.; Han, R.; Zhang, M.; Zhang, Y.; Zhou, H.; Wang, G.; Chen, G. An Enhanced Hybrid Deep Neural Network Reduced-order Model for Transonic Buffet Flow Prediction. Aerosp. Sci. Technol. 2022, 126, 107636. [Google Scholar] [CrossRef]
- Jia, X.; Li, C.; Ji, W.; Gong, C. A Hybrid Reduced-order Model Combing Deep Learning for Unsteady Flow. Phys. Fluids 2022, 34, 097112. [Google Scholar] [CrossRef]
- Phung, V.H.; Rhee, E.J. A High-Accuracy Model Average Ensemble of Convolutional Neural Networks for Classification of Cloud Image Patches on Small Datasets. Appl. Sci. 2019, 34, 4500. [Google Scholar] [CrossRef]
- Bhatnagar, S.; Afshar, Y.; Pan, S.; Duraisamy, K.; Kaushik, S. Prediction of Aerodynamic Flow Fields Using Convolutional Neural Networks. Comput. Mech. 2019, 64, 525–545. [Google Scholar] [CrossRef]
- Chen, L.; Thuerey, N. Deep learning-based predictive modeling of transonic flow over an airfoil. Phys. Fluids 2024, 36, 127106. [Google Scholar] [CrossRef]
- Han, R.; Wang, Y.; Zhang, Y.; Chen, G. A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network. Phys. Fluids 2019, 31, 127101. [Google Scholar] [CrossRef]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B.C. Fast Flow Field Prediction over Airfoils Using Deep Learning Approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Duru, C.; Alemdar, H.; Baran, O.U. A Deep Learning Approach for the Transonic Flow Field Predictions Around Airfoils. Comput. Fluids 2022, 236, 105312. [Google Scholar] [CrossRef]
- Lee, S.; You, D. Data-Driven Prediction of Unsteady Flow Over a Circular Cylinder Using Deep Learning. J. Fluid Mech. 2019, 879, 217–254. [Google Scholar] [CrossRef]
- Ogoke, F.; Meidani, K.; Hashemi, A.; Farimani, B. Graph Convolutional Networks Applied to Unstructured Flow Field Data. Mach. Learn. Sci. Technol. 2021, 2, 045020. [Google Scholar] [CrossRef]
- He, X.; Wang, Y.; Li, J. Flow Completion Network: Inferring the Fluid Dynamics from Incomplete Flow Information Using Graph Neural Networks. Phys. Fluids 2022, 34, 087114. [Google Scholar] [CrossRef]
- Massegur, D.; Da, R.A. Graph convolutional multi-mesh autoencoder for steady transonic aircraft aerodynamics. Mach. Learn. Sci. Technol. 2024, 5, 025006. [Google Scholar] [CrossRef]
- Hines, D.; Philipp, B. Graph neural networks for the prediction of aircraft surface pressure distributions. Aerosp. Sci. Technol. 2023, 137, 108268. [Google Scholar] [CrossRef]
- Yiren, S.; Alonso, J. Performance Evaluation of a Graph Neural Network-Augmented Multi-Fidelity Workflow for Predicting Aerodynamic Coefficients on Delta Wings at Low Speed. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; pp. 2025–2360. [Google Scholar]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Ren, Z.; Hu, P.; Su, H.; Zhang, F.; Yu, H. Physics-Informed Neural Networks for Transonic Flow Around a Cylinder with High Reynolds Number. Phys. Fluids 2024, 36, 036129. [Google Scholar] [CrossRef]
- Mons, V.; Chassaing, J.C.; Gomez, T.; Sagaut, P. Reconstruction of Unsteady Viscous Flows Using Data Assimilation Schemes. J. Comput. Phys. 2016, 316, 255–280. [Google Scholar] [CrossRef]
- Maulik, R.; Egele, R.; Raghavan, K.; Balaprakash, P. Quantifying Uncertainty for Deep Learning Based Forecasting and Flow-reconstruction Using Neural Architecture Search Ensembles. Phys. D 2023, 454, 133852. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).