Multi-Agent Reinforcement Symbolic Regression for the Fatigue Life Prediction of Aircraft Landing Gear
Abstract
1. Introduction
- (1)
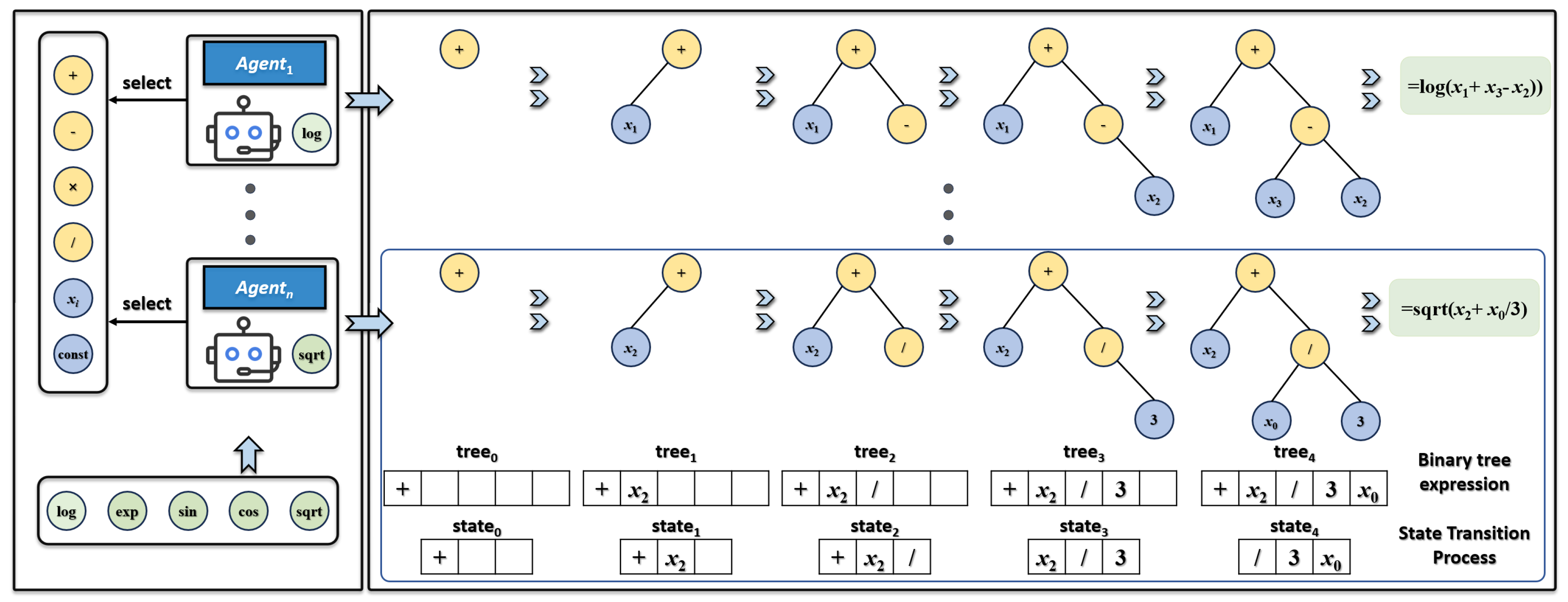
- A multi-agent collaborative mechanism is proposed that decomposes complex expressions into multiple basic components for parallel learning, improving search efficiency and solving the search space explosion and convergence difficulties faced by traditional SR.
- (2)
- A MA-RSR framework is developed that combines SR with Transformer-based reinforcement learning to achieve highly interpretable fatigue life prediction, overcoming the “black box” limitations of machine learning methods.
- (3)
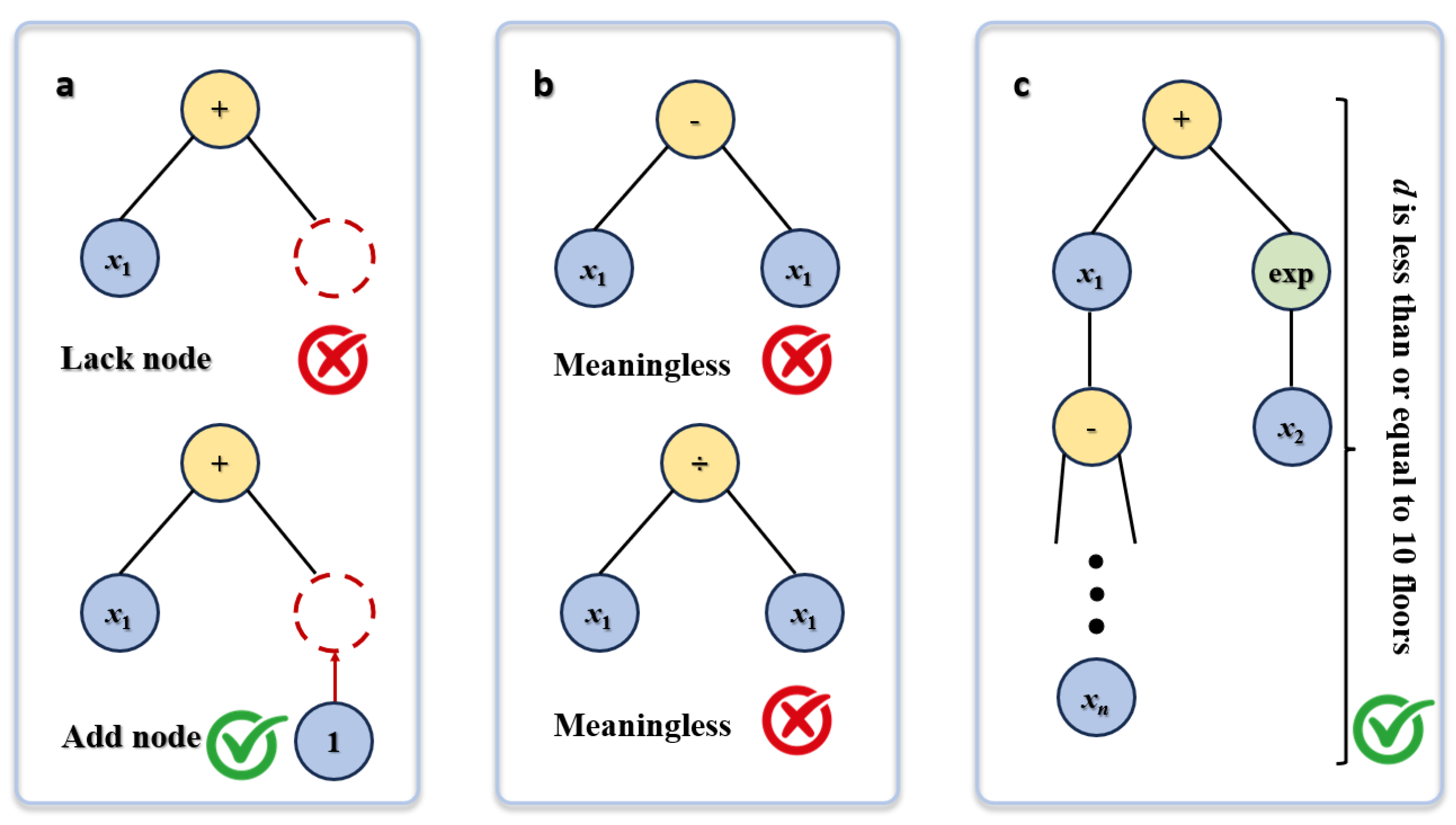
- An intelligent masking mechanism is designed that ensures the mathematical rationality and physical significance of generated expressions through multi-level constraints, avoiding the generation of invalid expressions and improving model reliability.
- (4)
- Based on SAE4340 steel multiaxial fatigue experimental data and landing gear engineering validation, the prediction accuracy and practicality of the MA-RSR method are demonstrated, providing an effective tool for fatigue life assessment of complex engineering structures.
2. Theoretical Foundation
2.1. Traditional Empirical Methods
2.1.1. Coffin–Manson Criterion
2.1.2. Kandil–Brown–Miller (KBM) Criterion
2.1.3. Fatemi–Socie (FS) Criterion
2.1.4. Wu–Hu–Song (WHS) Criterion
2.2. Fundamentals of SR
3. The Proposed Method
3.1. Expression Decomposition Strategy
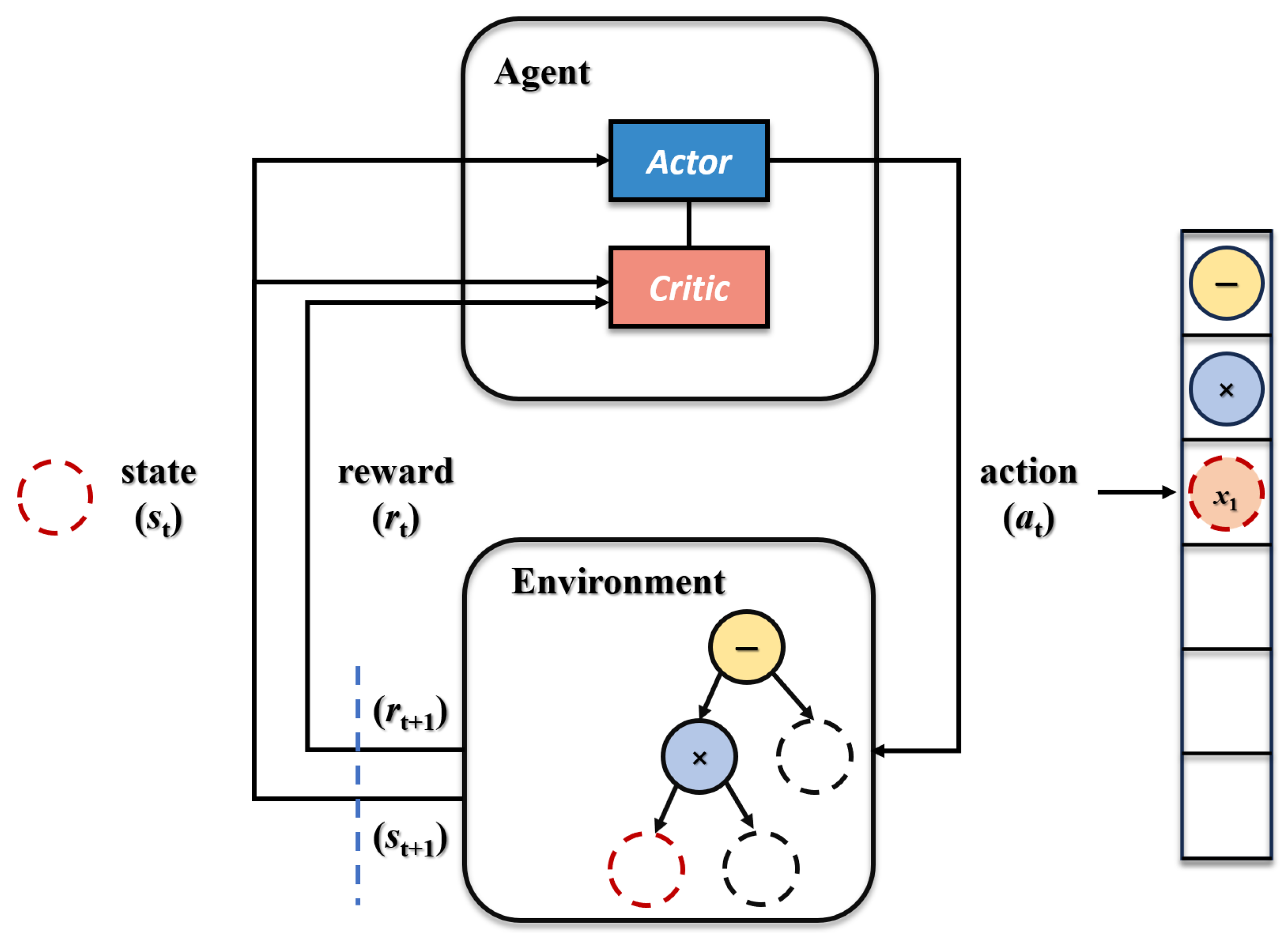
3.2. MA-RSR Framework
3.3. Transformer-Based Agent Design
3.4. Intelligent Constraint Mechanism
4. Numerical Validations
4.1. Experimental Setup
4.2. MA-RSR Modeling and Performance Comparison
4.2.1. Formula Results Obtained from MA-RSR
4.2.2. Comparative Experiments
5. EngineeringValidation for Landing Gear Fatigue Life Prediction
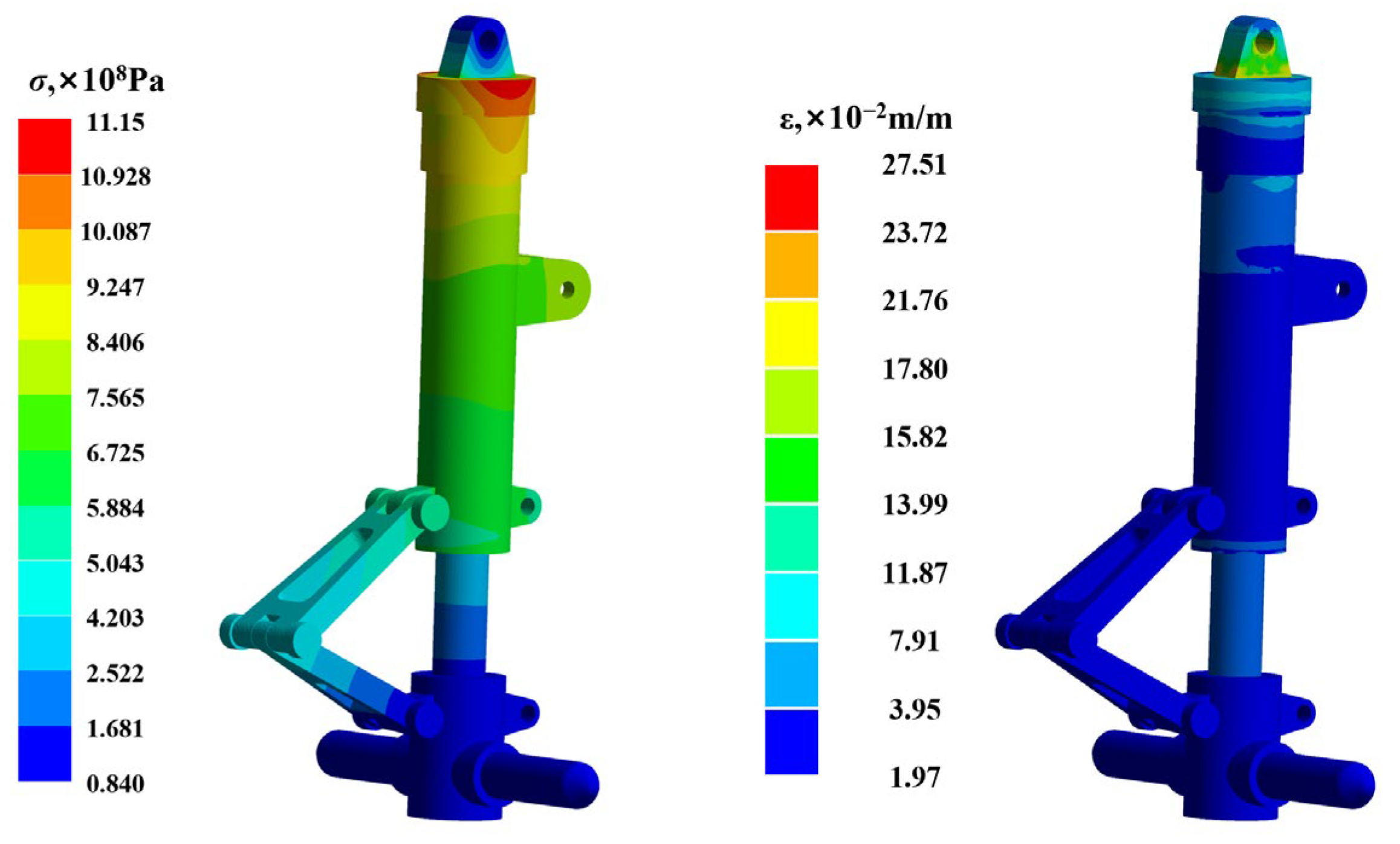
5.1. Landing Gear Finite Element Modeling and Simulation Setup
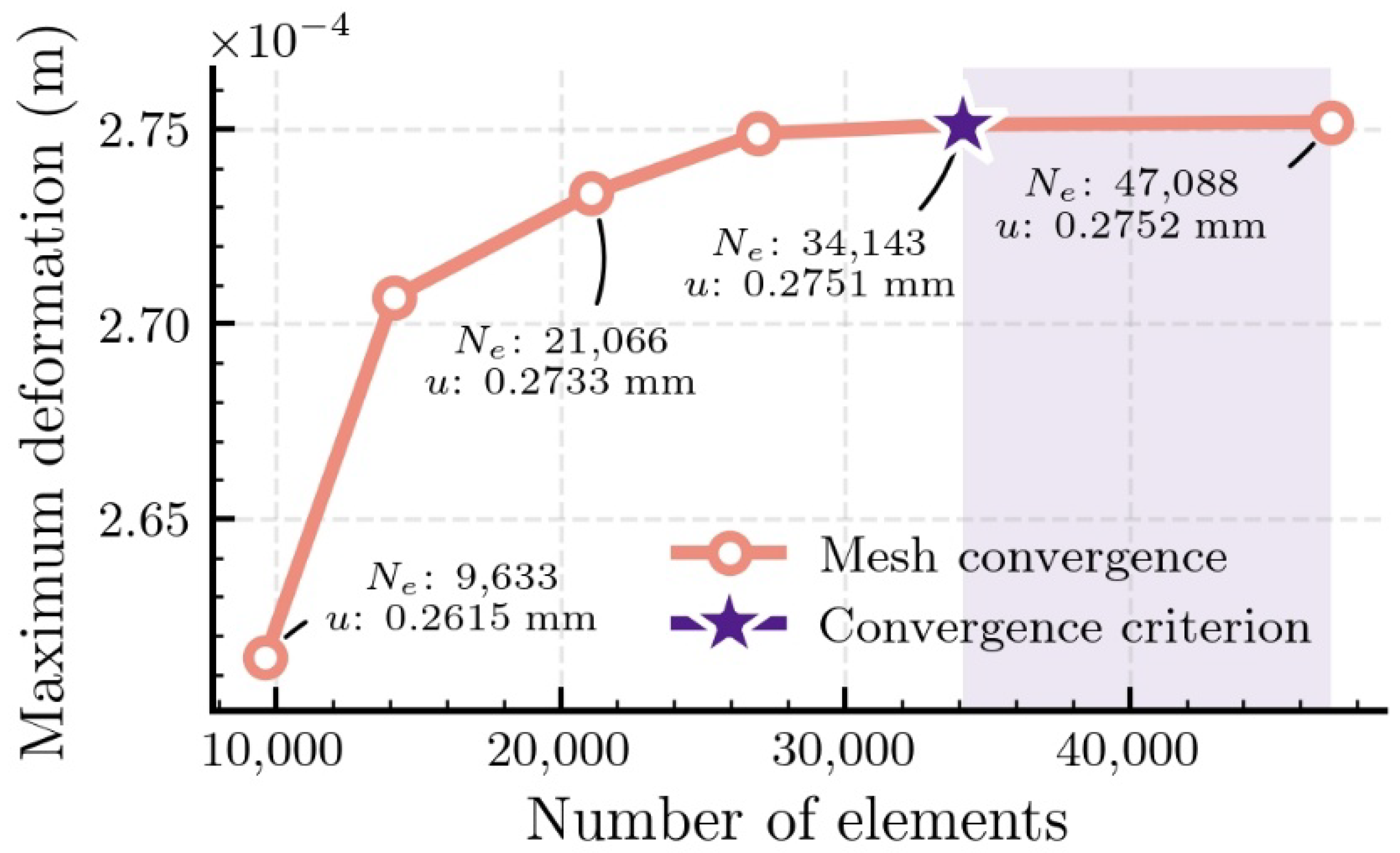
5.2. Mesh Convergence Analysis and Verification
5.3. Fatigue Life Prediction Results and Comparative Analysis
6. Conclusions
- (1)
- Based on 252 sets of SAE4340 steel multiaxial fatigue data, MA-RSR achieves an R2 of 0.96, significantly outperforming traditional empirical formulas (Coffin–Manson, KBM, FS, WHS) and machine learning methods (SVM, ANN), with prediction accuracy improvements exceeding 50% in most cases.
- (2)
- The multi-agent collaborative mechanism effectively addresses search space explosion by decomposing complex expressions into parallel components. Transformer architecture enhances symbolic selection through self-attention mechanisms, while intelligent masking ensures mathematical rationality through multi-level constraints including syntax, semantics, and complexity control.
- (3)
- Generated expressions maintain clear physical interpretability while achieving superior accuracy. Landing gear finite element validation confirms practical applicability under realistic conditions, providing an effective tool for complex engineering structure fatigue analysis.
- (4)
- MA-RSR successfully balances modeling accuracy with interpretability, making it promising for complex engineering reliability analysis. The method provides scientific guidance for critical aircraft component fatigue assessment and advances SR applications in engineering domains.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Liu, P.; Ding, J.; Cheng, J.; Jiang, Y.; Jiang, B. Numerical prediction of fatigue life for landing gear considering the shock absorber travel. Aerospace 2025, 12, 42. [Google Scholar] [CrossRef]
- Deng, K.; Ompusunggu, A.; Xu, Y.; Stoke, M.; Zhao, Y. A review of material-related mechanical failures and load monitoring-based structural health monitoring (SHM) technologies in aircraft landing gear. Aerospace 2025, 12, 266. [Google Scholar] [CrossRef]
- Ni, P. Strength analysis of shock strut of aircraft landing gear based on ANSYS. In Proceedings of the IEEE 10th Conference on Systems, Process & Control (ICSPC), Advanced Materials Reaserch, Malacca, Malaysia, 17 December 2022; pp. 111–116. [Google Scholar]
- Aditya, A.; Sharma, K.; Srinivas, G. A step towards safety: Material failure analysis of landing gear. Mater. Today 2020, 27, 402–409. [Google Scholar]
- Basquin, O. The exponential law of endurance tests. Am. Soc. Test. Mater. 1910, 10, 625–630. [Google Scholar]
- Coffin, L. A study of the effects of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–949. [Google Scholar] [CrossRef]
- Manson, S. Behavior of Materials Under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953; pp. 29–33. [Google Scholar]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals; ASTM International: West Conshohocken, PA, USA, 1965; pp. 45–87. [Google Scholar]
- Ni, X.; Yin, Q.; Wei, X.; Zhong, P.; Nie, H. Research on landing stability of four-legged adaptive landing gear for multirotor UAVs. Aerospace 2022, 9, 776. [Google Scholar] [CrossRef]
- Findley, W. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending. J. Eng. Ind. 1959, 81, 301–305. [Google Scholar] [CrossRef]
- Brown, M.; Miller, K. A theory for fatigue failure under multiaxial stress-strain conditions. Proc. Inst. Mech. Eng. 1973, 187, 745–755. [Google Scholar] [CrossRef]
- Fatemi, A.; Socie, D. A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Wu, Z.; Hu, X.; Song, Y. Multiaxial fatigue life prediction for titanium alloy TC4 under proportional and nonproportional loading. Int. J. Fatigue 2014, 59, 170–175. [Google Scholar] [CrossRef]
- Le, C.; Ferrer, E.; Gibson, S.; Cross, E.; Parente, A.; Vinuesa, R. Improving aircraft performance using machine learning: A review. Aerosp. Sci. Technol. 2023, 138, 108354. [Google Scholar] [CrossRef]
- Sun, Y.; Wen, J.; Li, J.; Cao, A.; Fei, C. Novel integrated model approach for high cycle fatigue life and reliability assessment of helicopter flange structures. Aerospace 2025, 12, 78. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, F.; Shen, M.; Han, D.; Wang, Z.; Yan, N. Ultra-high-cycle fatigue life prediction of metallic materials based on machine learning. Appl. Sci. 2024, 13, 2524. [Google Scholar] [CrossRef]
- Heng, F.; Gao, J.; Xu, R.; Yang, H.; Cheng, Q.; Liu, Y. Multiaxial fatigue life prediction for various metallic materials based on the hybrid CNN-LSTM neural network. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1979–1996. [Google Scholar] [CrossRef]
- Farhadi, S.; Tatullo, S.; Ferrian, F. Comparative analysis of ensemble learning techniques for enhanced fatigue life prediction. Sci. Rep. 2025, 15, 11136. [Google Scholar] [CrossRef]
- Liao, W.; Long, X.; Jiang, C. A physics-informed neural network method for identifying parameters and predicting remaining life of fatigue crack growth. Int. J. Fatigue 2025, 191, 108678. [Google Scholar] [CrossRef]
- Tenachi, W.; Ibata, R.; Diakogiannis, F. Deep symbolic regression for physics guided by units constraints: Toward the automated discovery of physical laws. Astrophys. J. 2023, 959, 99. [Google Scholar] [CrossRef]
- Zhang, P.; Tang, K.; Wang, A.; Wu, H.; Zhong, Z. Neural network integrated with symbolic regression for multiaxial fatigue life prediction. Int. J. Fatigue 2024, 188, 108535. [Google Scholar] [CrossRef]
- Cao, W.; Sun, X.; Chen, X. Estimation and validation for fatigue properties of steels by symbolic regression. Int. J. Fatigue 2024, 186, 108416. [Google Scholar] [CrossRef]
- Feng, S.; Sun, X.; Chen, C.; Wu, H.; Chen, X. LBE corrosion fatigue life prediction of T91 steel and 316 SS using machine learning method assisted by symbol regression. Int. J. Fatigue 2023, 177, 107962. [Google Scholar] [CrossRef]
- Ding, D.; Wang, Q.; Chen, Q.; He, L. Symbolic Regression-Based Modeling for Aerodynamic Ground-to-Flight Deviation Laws of Aerospace Vehicles. Aerospace 2025, 12, 455. [Google Scholar] [CrossRef]
- Li, P.; Choi, J.; Zhang, D.; Zhang, S.; Zhang, Y. Reinforced symbolic learning with logical constraints for predicting turbine blade fatigue life. Aerosp. Sci. Technol. 2025, 158, 109888. [Google Scholar] [CrossRef]
- Fei, C.; Han, Y.; Wen, J.; Li, C.; Han, L.; Choy, Y.S. Deep learning-based modeling method for probabilistic LCF life prediction of turbine blisk. Propuls. Power Res. 2024, 13, 12–25. [Google Scholar] [CrossRef]
- Udrescu, S.; Tegmark, M. AI Feynman: A physics-inspired method for symbolic regression. Sci. Adv. 2020, 6, eaay2631. [Google Scholar] [CrossRef] [PubMed]
- Matchev, K.; Matcheva, K.; Roman, A. Analytical modeling of exoplanet transit spectroscopy with dimensional analysis and symbolic regression. Astrophys. J. 2022, 930, 33. [Google Scholar] [CrossRef]
- Lin, J.; Li, C.; Chao, A.; Fei, C.; Ren, Q. Design and performance evaluation of novel wing-shaped fin radiators for advanced aeroengines. Propuls. Power Res. 2025, 14. [Google Scholar]
- Wen, J.; Zheng, B.; Fei, C. Prioritized Experience Replay-based Adaptive Hybrid Method for Aerospace Structural Reliability Analysis. Aerosp. Sci. Technol. 2025, 163, 110257. [Google Scholar] [CrossRef]
- Milan, M.; Spinelli, D.; Bose, F.; Montezuma, M.; Tita, V. Failure analysis of a SAE 4340 steel locking bolt. Eng. Fail. Anal. 2004, 11, 915–924. [Google Scholar] [CrossRef]
- Fratesi, R.; Roventi, G.; Cavallini, M. Hydrogen-inclusion interaction in tempered martensite embrittled SAE 4340 steels. Mater. Sci. Eng. A 1989, 119, 17–22. [Google Scholar] [CrossRef]



| E/GPa | G/GPa | σ′f/MPa | τ′f/MPa | γ′f | ε′f |
|---|---|---|---|---|---|
| 207 | 80 | 1658 | 957 | 0.845 | 0.563 |
| b | c | b0 | c0 | νe | νp |
| −0.074 | −0.513 | −0.074 | −0.513 | 0.29 | 0.29 |
| Material | σa (MPa) | τa (MPa) | εa (%) | γa (%) | Nf (cycles) | σIn(Nf) | μIn(Nf) | n |
|---|---|---|---|---|---|---|---|---|
| SAE4340 | 993 | 0 | 0.523 | 0 | 2773 | 0.228 | 7.906 | 12 |
| SAE4340 | 786 | 0 | 0.414 | 0 | 9029 | 0.116 | 9.102 | 18 |
| SAE4340 | 676 | 0 | 0.356 | 0 | 22,171 | 0.176 | 9.992 | 18 |
| SAE4340 | 558 | 0 | 0.294 | 0 | 77,977 | 0.154 | 11.253 | 18 |
| SAE4340 | 503 | 0 | 0.265 | 0 | 161,984 | 0.232 | 11.971 | 18 |
| SAE4340 | 1041 | 172 | 0.548 | 0.236 | 1451 | 0.198 | 7.263 | 12 |
| SAE4340 | 793 | 134 | 0.417 | 0.185 | 6203 | 0.157 | 8.721 | 18 |
| SAE4340 | 572 | 93 | 0.301 | 0.128 | 39,608 | 0.207 | 10.545 | 18 |
| SAE4340 | 510 | 86 | 0.269 | 0.119 | 74,212 | 0.274 | 11.18 | 18 |
| SAE4340 | 765 | 507 | 0.403 | 0.698 | 6554 | 0.146 | 8.778 | 12 |
| SAE4340 | 634 | 458 | 0.334 | 0.631 | 20,467 | 0.281 | 9.89 | 18 |
| SAE4340 | 524 | 369 | 0.276 | 0.508 | 61,028 | 0.181 | 11.062 | 18 |
| SAE4340 | 448 | 324 | 0.236 | 0.447 | 127,577 | 0.167 | 11.743 | 18 |
| SAE4340 | 476 | 621 | 0.251 | 0.856 | 53,573 | 0.244 | 10.857 | 18 |
| SAE4340 | 414 | 541 | 0.218 | 0.746 | 142,550 | 0.305 | 11.825 | 18 |
| Formula | Function Type | Mathematical Expression | R2 |
|---|---|---|---|
| 1 | Exp(f1(x)) | 0.9689 | |
| Log(f2(x)) | |||
| Sqrt(f3(x)) | |||
| f4(x) | |||
| 2 | Exp(f1(x)) | 0.9672 | |
| Log(f2(x)) | |||
| Sqrt(f3(x)) | |||
| f4(x) |
| Parameter Type | SVM | ANN | GA-SR | KBM | FS | WHS |
|---|---|---|---|---|---|---|
| Core Parameters | C = 100 γ = 0.1 | Hidden layer = 64 Learning rate = 0.001 | Population = 100 Generations = 500 | S = 0.2 | k = 0.3 | k = 0.4 |
| Algorithm Settings | RBF kernel function | Adam optimizer | Crossover rate = 0.8 | - | - | - |
| Element Size (mm) | Number of Elements | Stress, MPa | Strain, m/m |
|---|---|---|---|
| 15 | 9633 | 874.75 | 0.2615 |
| 12 | 15,127 | 887.70 | 0.2707 |
| 10 | 21,866 | 936.82 | 0.2733 |
| 9 | 26,955 | 1116.44 | 0.2750 |
| 8 | 34,143 | 1115.27 | 0.2751 |
| 7 | 47,088 | 1116.87 | 0.2752 |
| Nf of CM | Nf of KBM | Nf of FS | Nf of WHS | Nf of SVM | Nf of ANN | Nf of GA-SR | Nf of SVM-SR | Nf of MA-RSR | |
|---|---|---|---|---|---|---|---|---|---|
| Life (cycles) | 1247 | 2891 | 8654 | 3429 | 4156 | 4738 | 5892 | 5234 | 6127 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.-P.; Feng, H.; Zheng, B.; Wen, J.-R.; Chao, A.-F.; Fei, C.-W. Multi-Agent Reinforcement Symbolic Regression for the Fatigue Life Prediction of Aircraft Landing Gear. Aerospace 2025, 12, 718. https://doi.org/10.3390/aerospace12080718
Sun Y-P, Feng H, Zheng B, Wen J-R, Chao A-F, Fei C-W. Multi-Agent Reinforcement Symbolic Regression for the Fatigue Life Prediction of Aircraft Landing Gear. Aerospace. 2025; 12(8):718. https://doi.org/10.3390/aerospace12080718
Chicago/Turabian StyleSun, Yi-Pin, Haozhe Feng, Baiyang Zheng, Jiong-Ran Wen, Ai-Fang Chao, and Cheng-Wei Fei. 2025. "Multi-Agent Reinforcement Symbolic Regression for the Fatigue Life Prediction of Aircraft Landing Gear" Aerospace 12, no. 8: 718. https://doi.org/10.3390/aerospace12080718
APA StyleSun, Y.-P., Feng, H., Zheng, B., Wen, J.-R., Chao, A.-F., & Fei, C.-W. (2025). Multi-Agent Reinforcement Symbolic Regression for the Fatigue Life Prediction of Aircraft Landing Gear. Aerospace, 12(8), 718. https://doi.org/10.3390/aerospace12080718







