Numerical Study on Shape Recovery Behaviors of Shape Memory Polymer Composite Hinges Considering Hysteresis Effect
Abstract
1. Introduction
2. Constitutive Equations
2.1. Constitutive Equation for the SMPs
2.2. Constitutive Equation for Shape Memory Behaviors
2.3. Constitutive Equation for the Fabric
3. Validation of the Constitutive Equations
3.1. Coefficients Acquisition Test
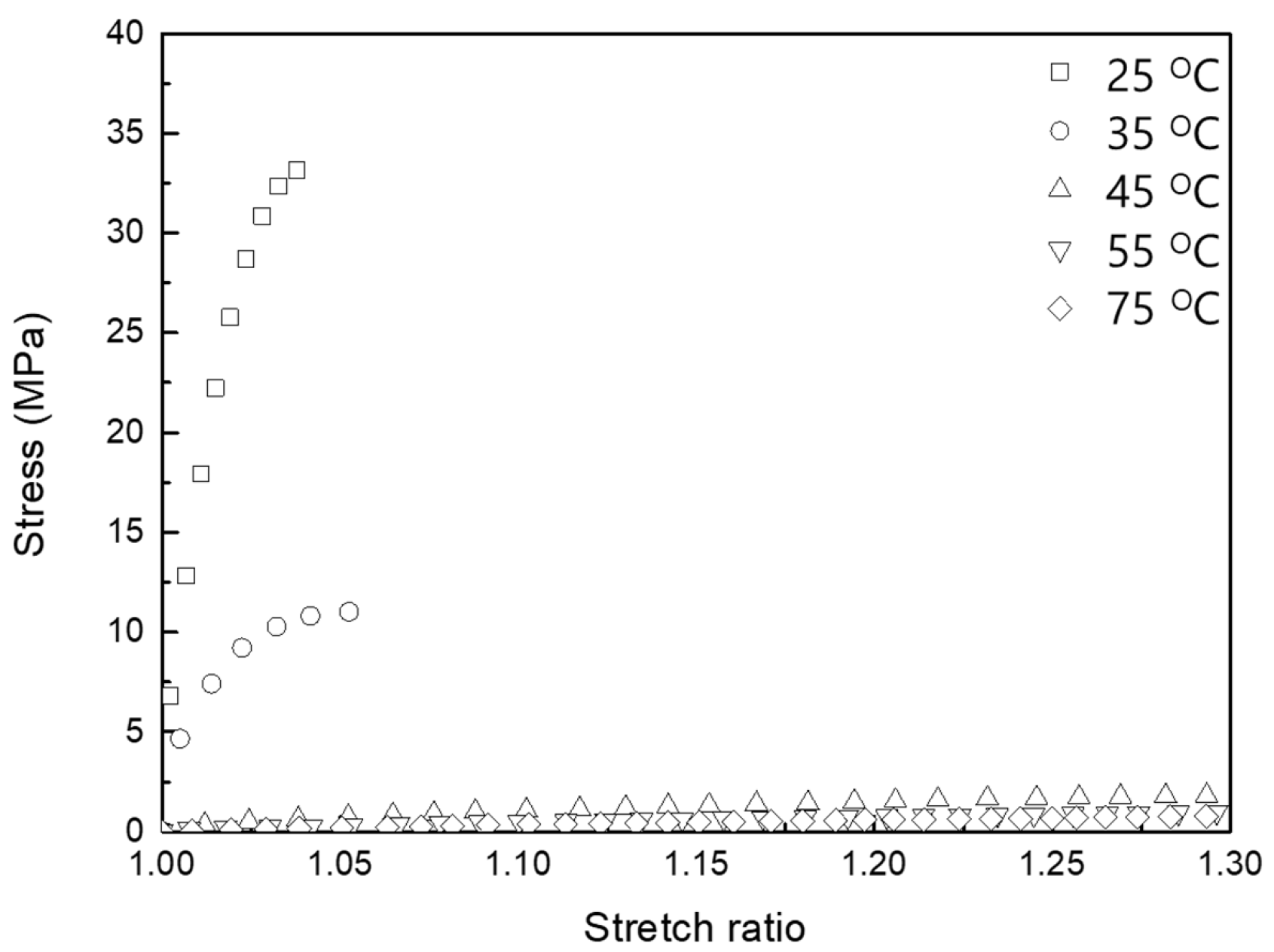
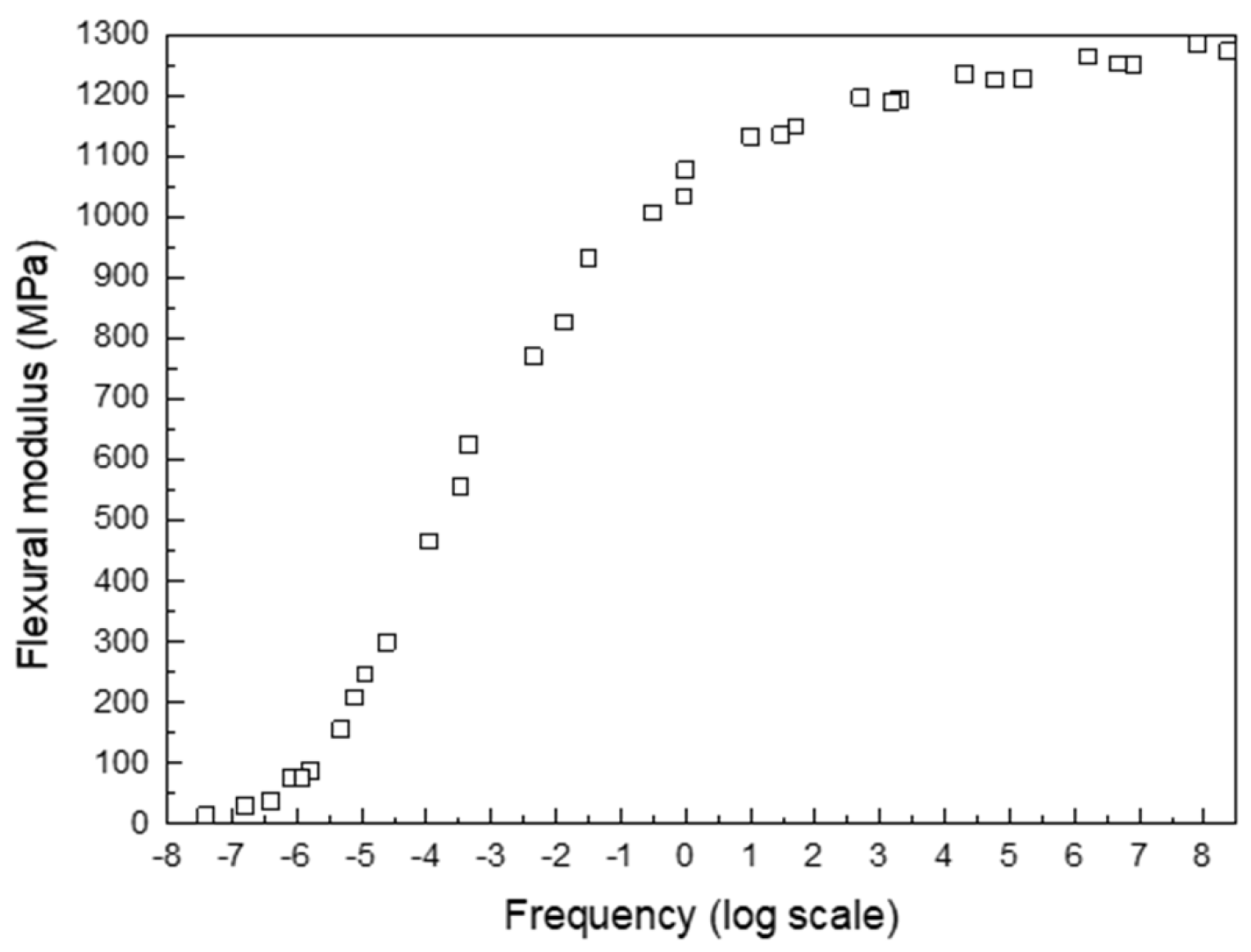
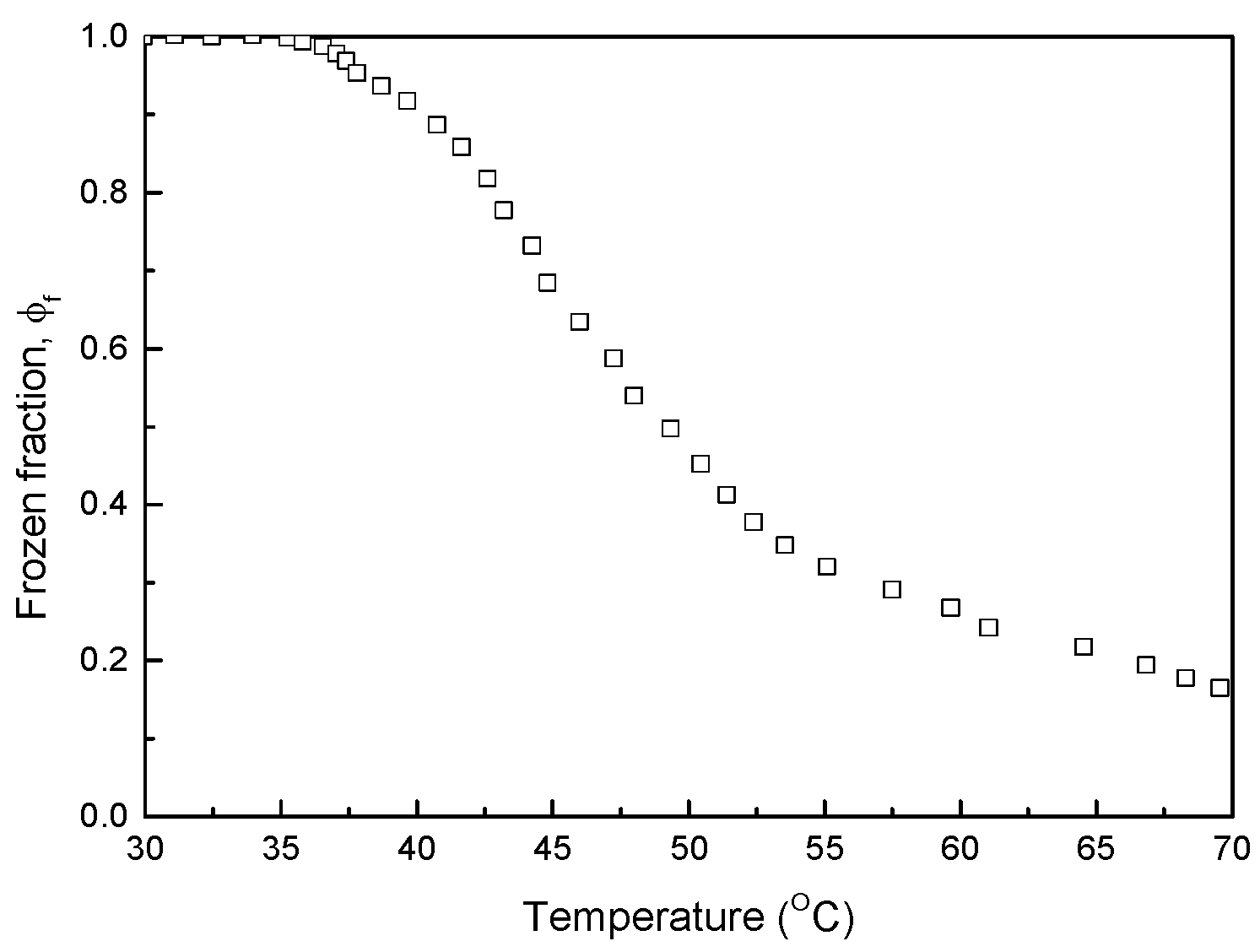
3.1.1. Model Coefficients Associated with SMPs
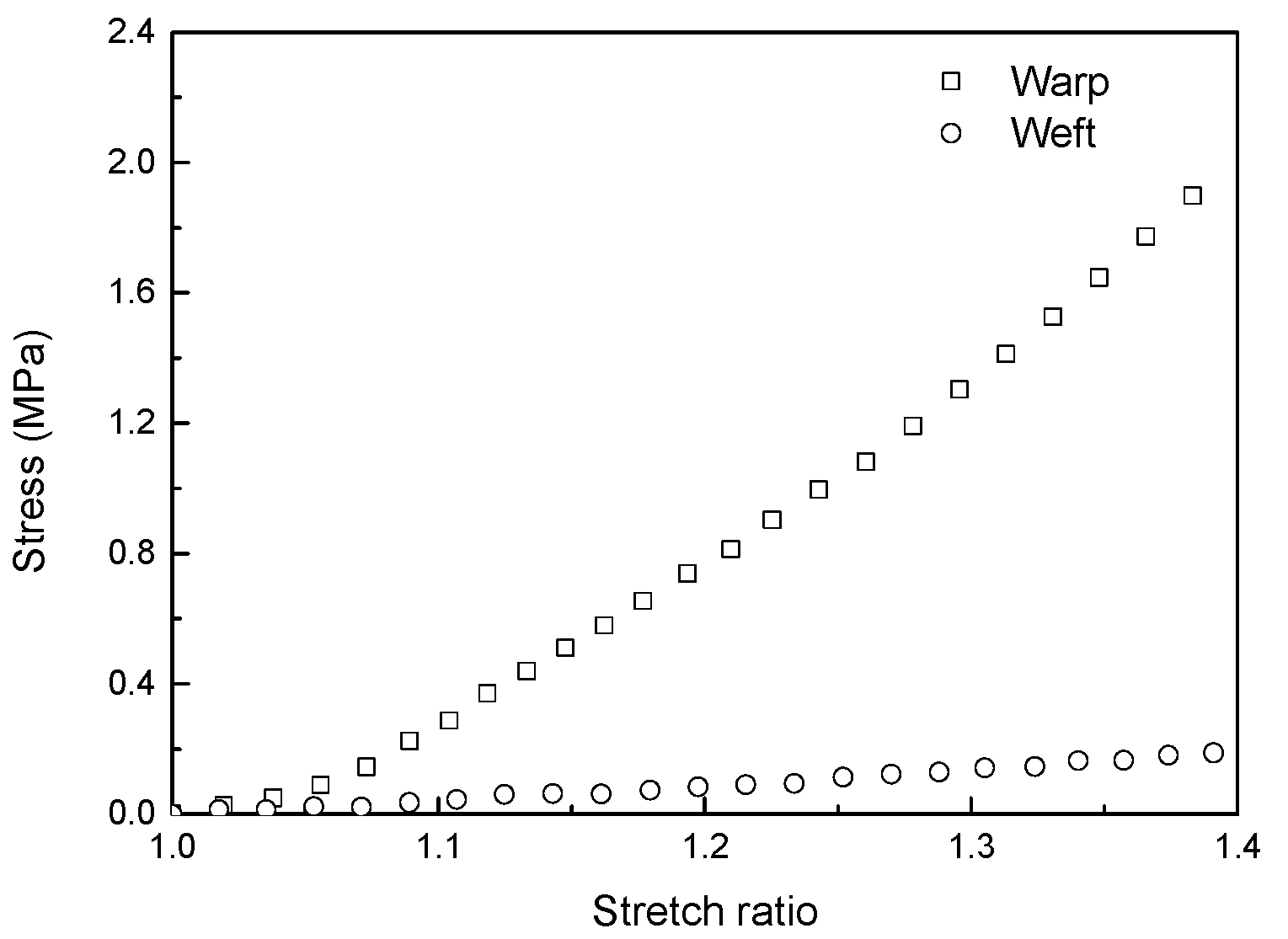
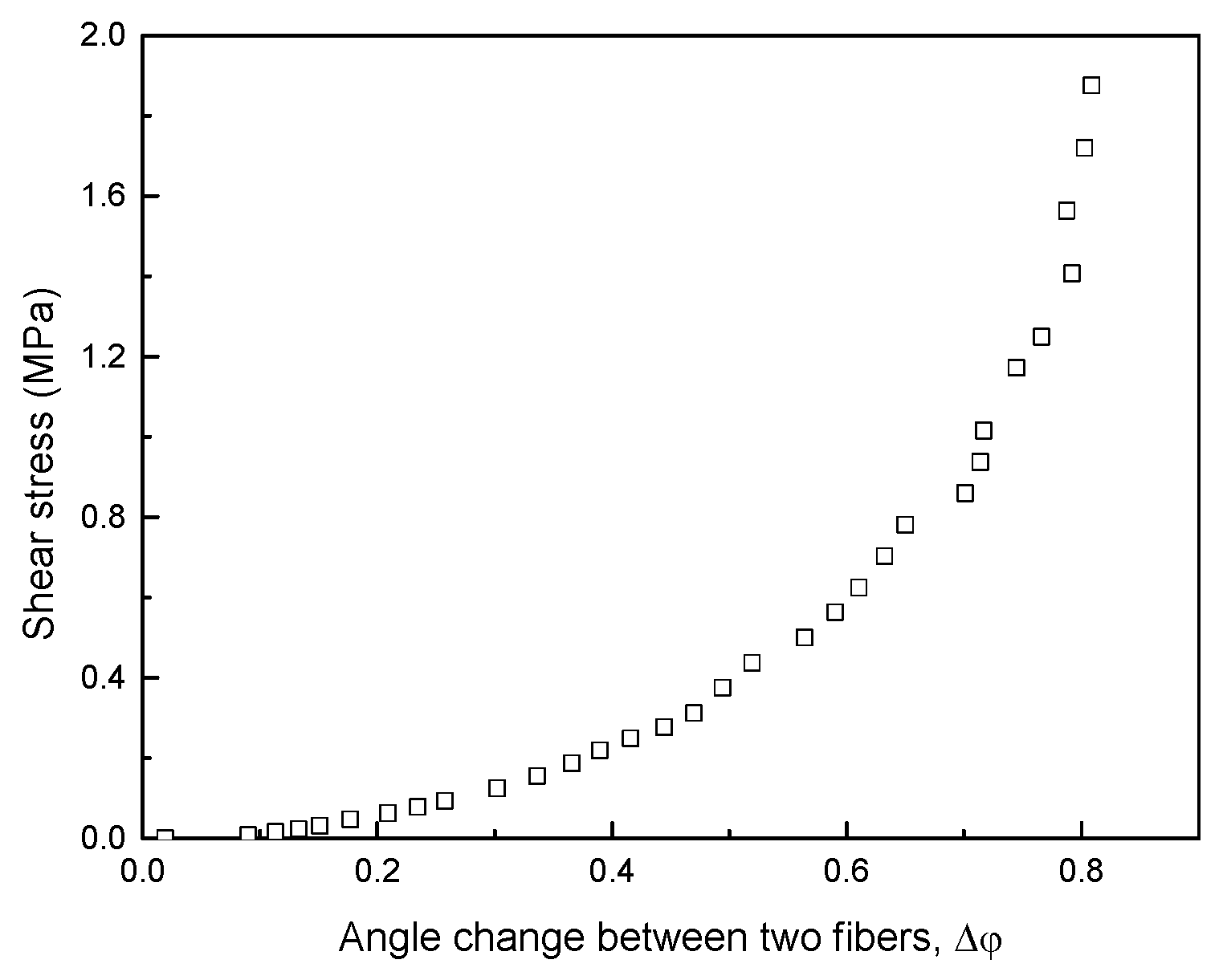
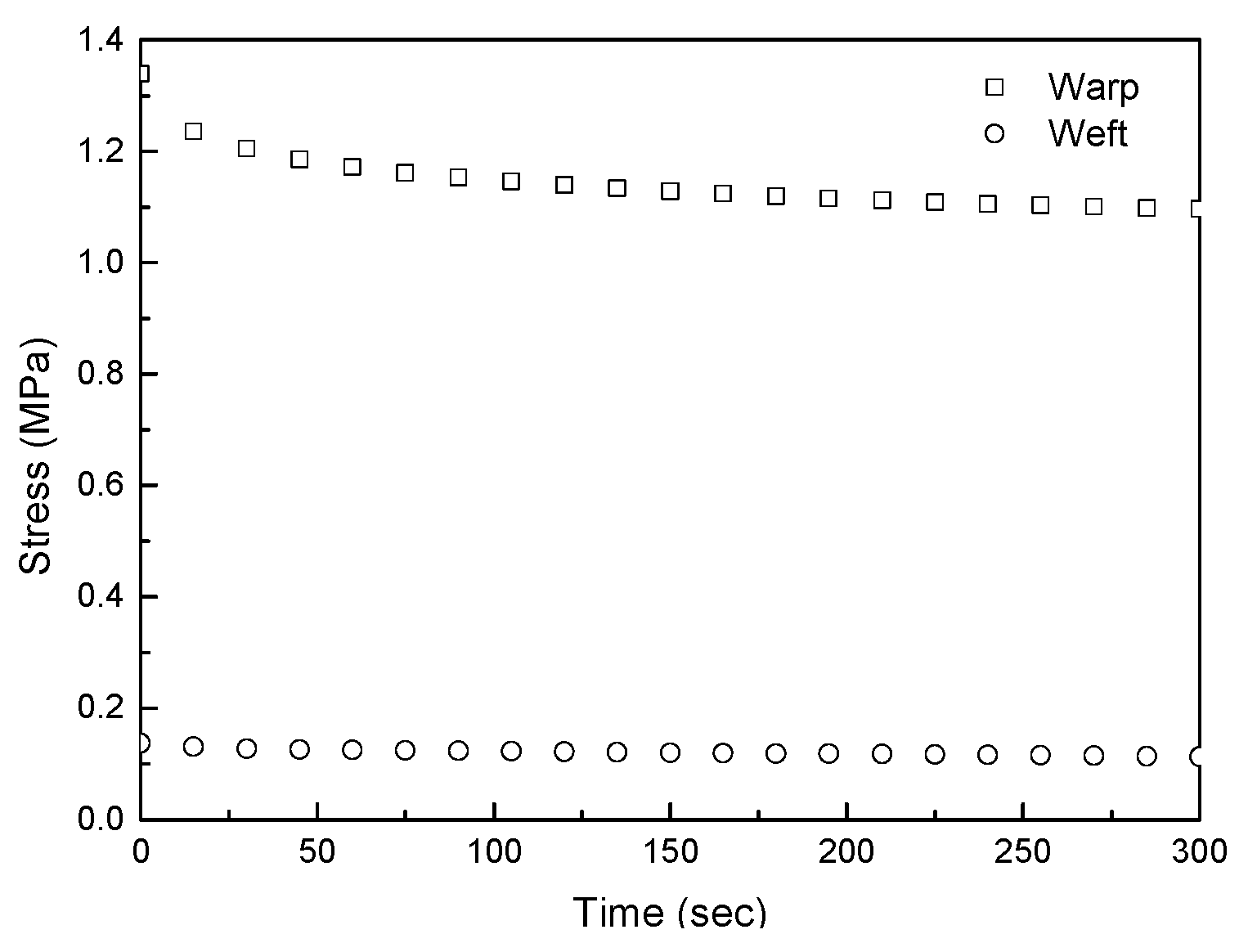
3.1.2. Model Coefficients Associated with Fabrics
3.2. Thermomechanical Characteristics of SMPCs
3.2.1. Fabrication and Experimental Setup for SMPCs
- (1)
- Place the fabric onto a flat mold surface.
- (2)
- Attach copper sheets to both fabric ends using an adhesive film (Loctite 9695) for consistent electrical conductivity across the SMPCs.
- (3)
- Cure the adhesive at 85 °C for 30 min followed by 125 °C for 2 h.
- (4)
- Pour the SMPs onto the fabric and layer it with a release film, caul plate, and breather.
- (5)
- Seal the assembly using vacuum film and sealant tape.
- (6)
- Cure the assembly at 80 °C for 2 h, followed by curing at 125 °C for 2 h.
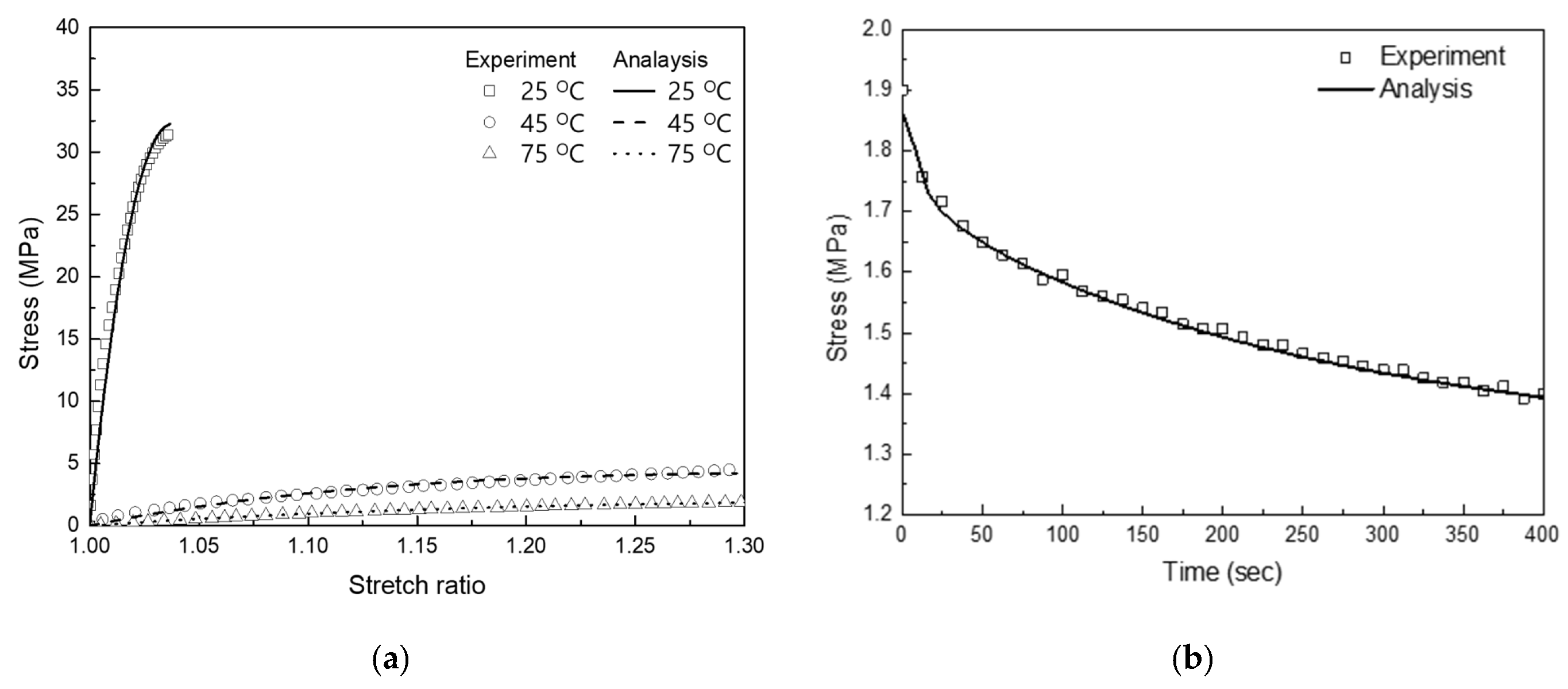
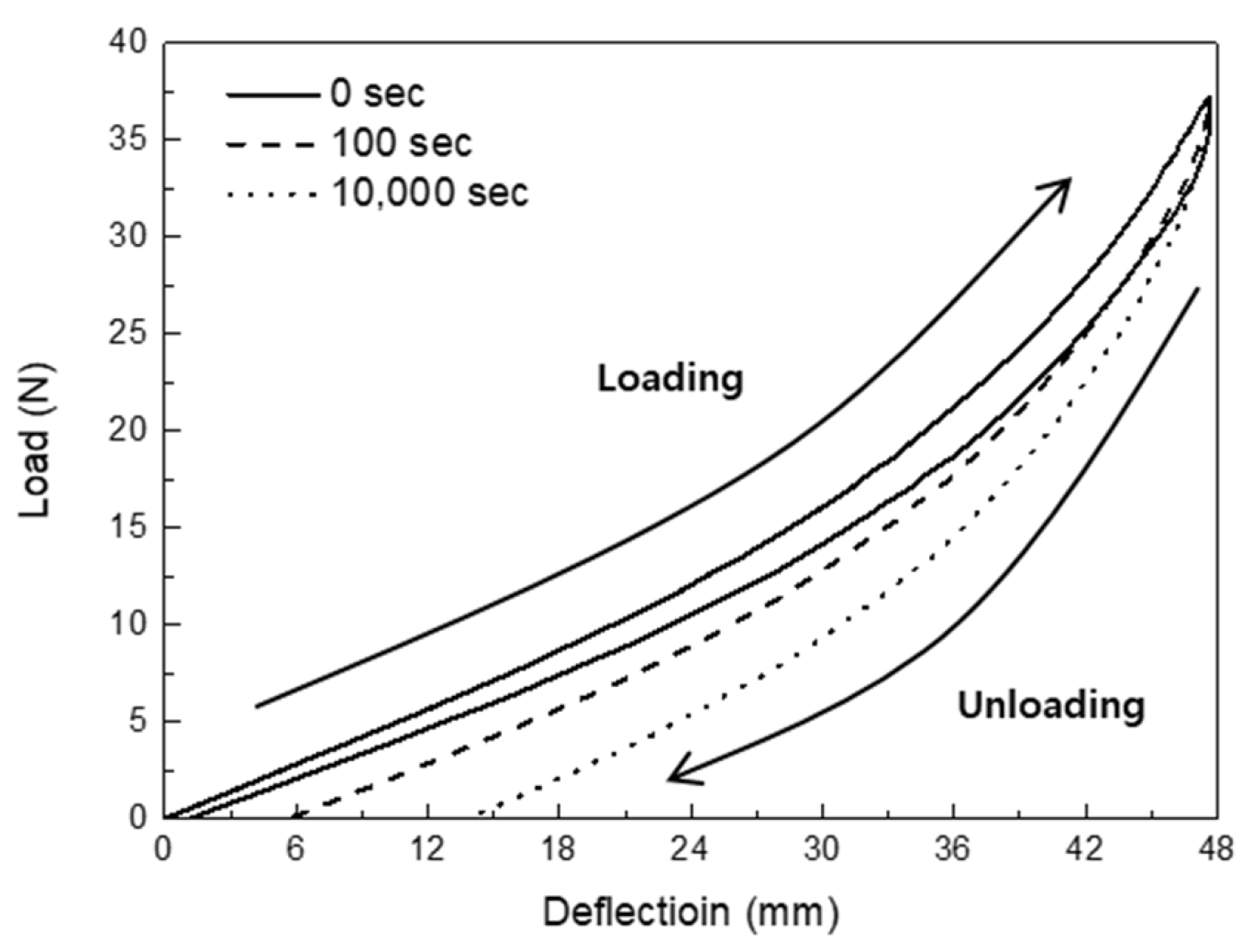
3.2.2. Anisotropic Hyper-Viscoelastic Response
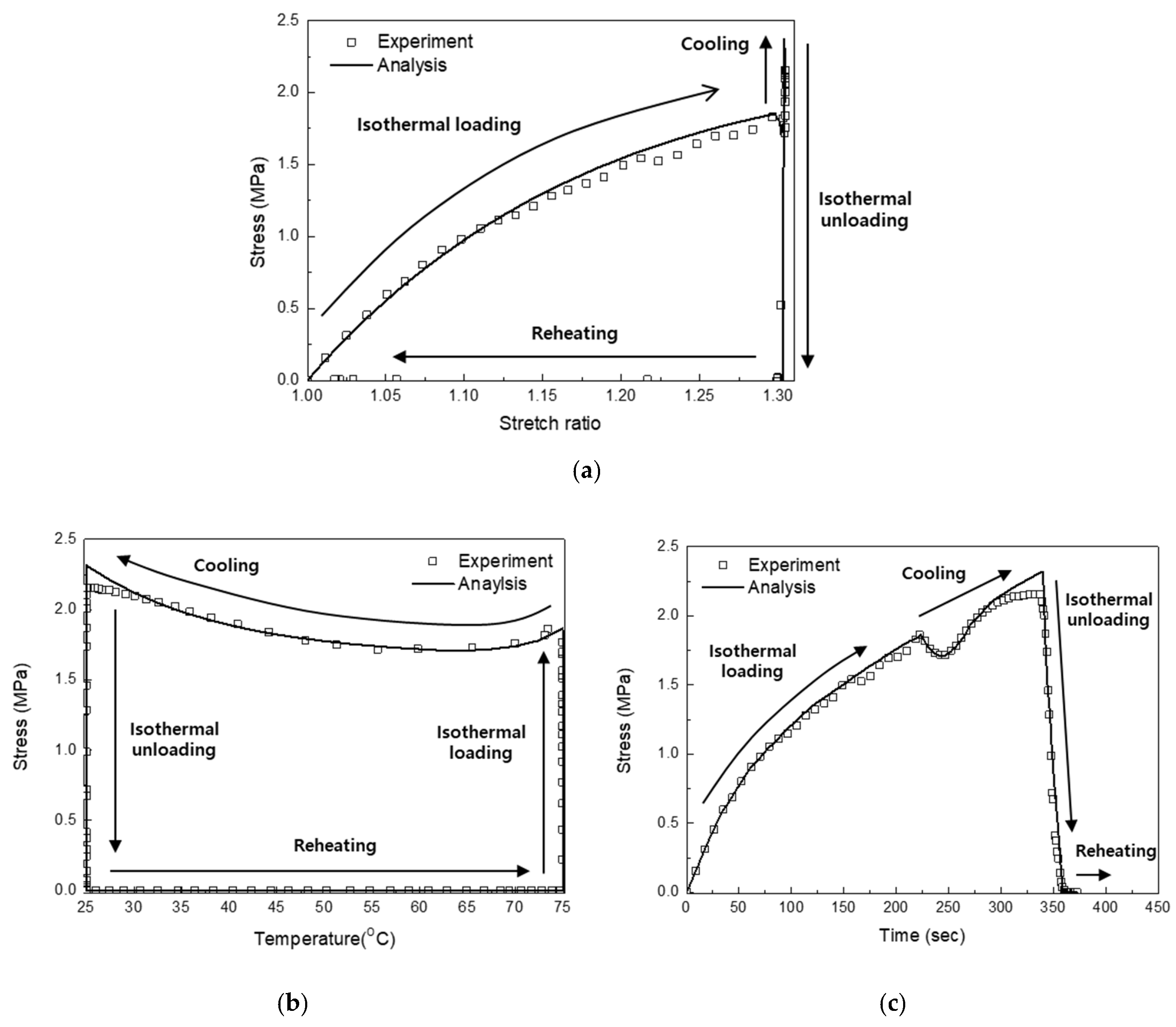
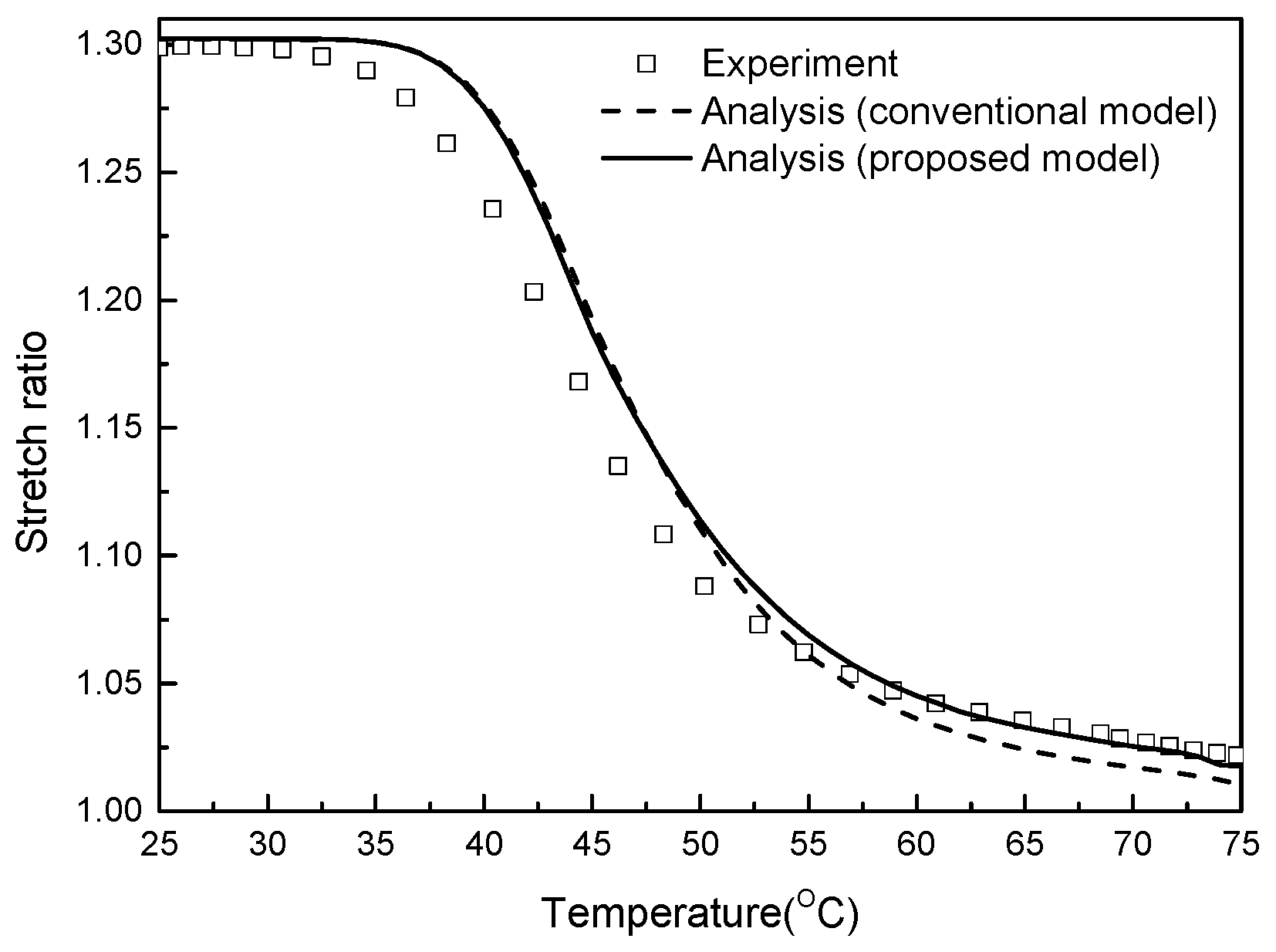
3.2.3. Shape Memory Response
4. Numerical Study on SMPC Hinges
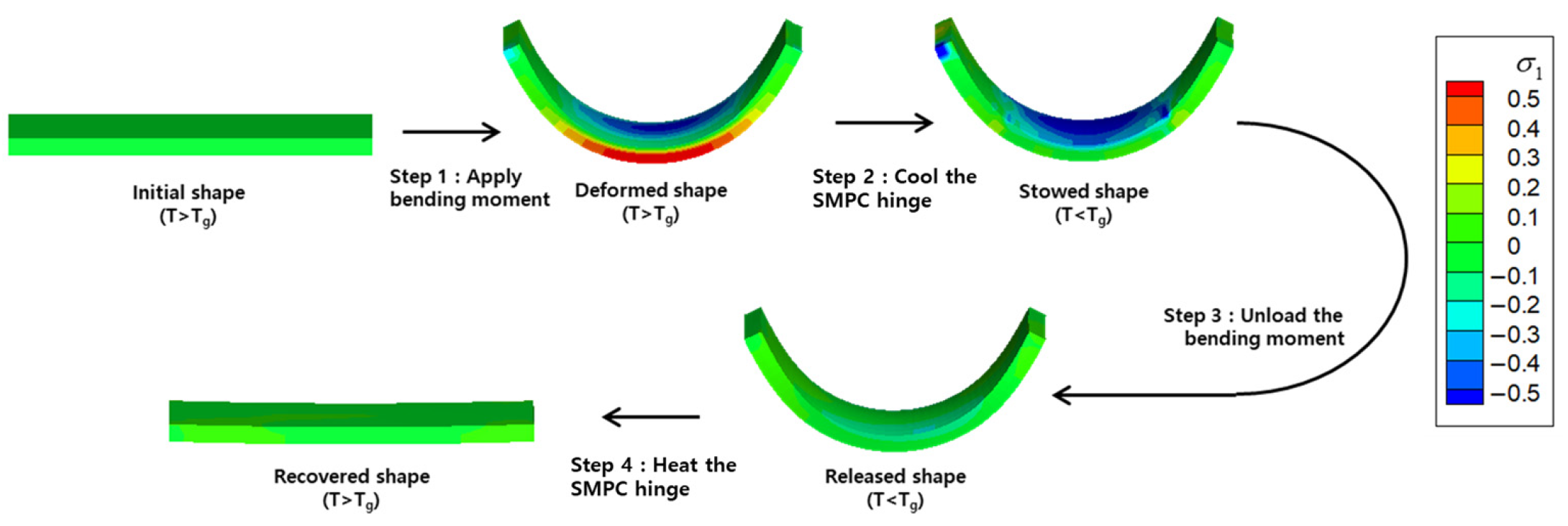
4.1. Numerical Model of SMPC Hinge
4.2. Bending Beahviors with Different Temperatures
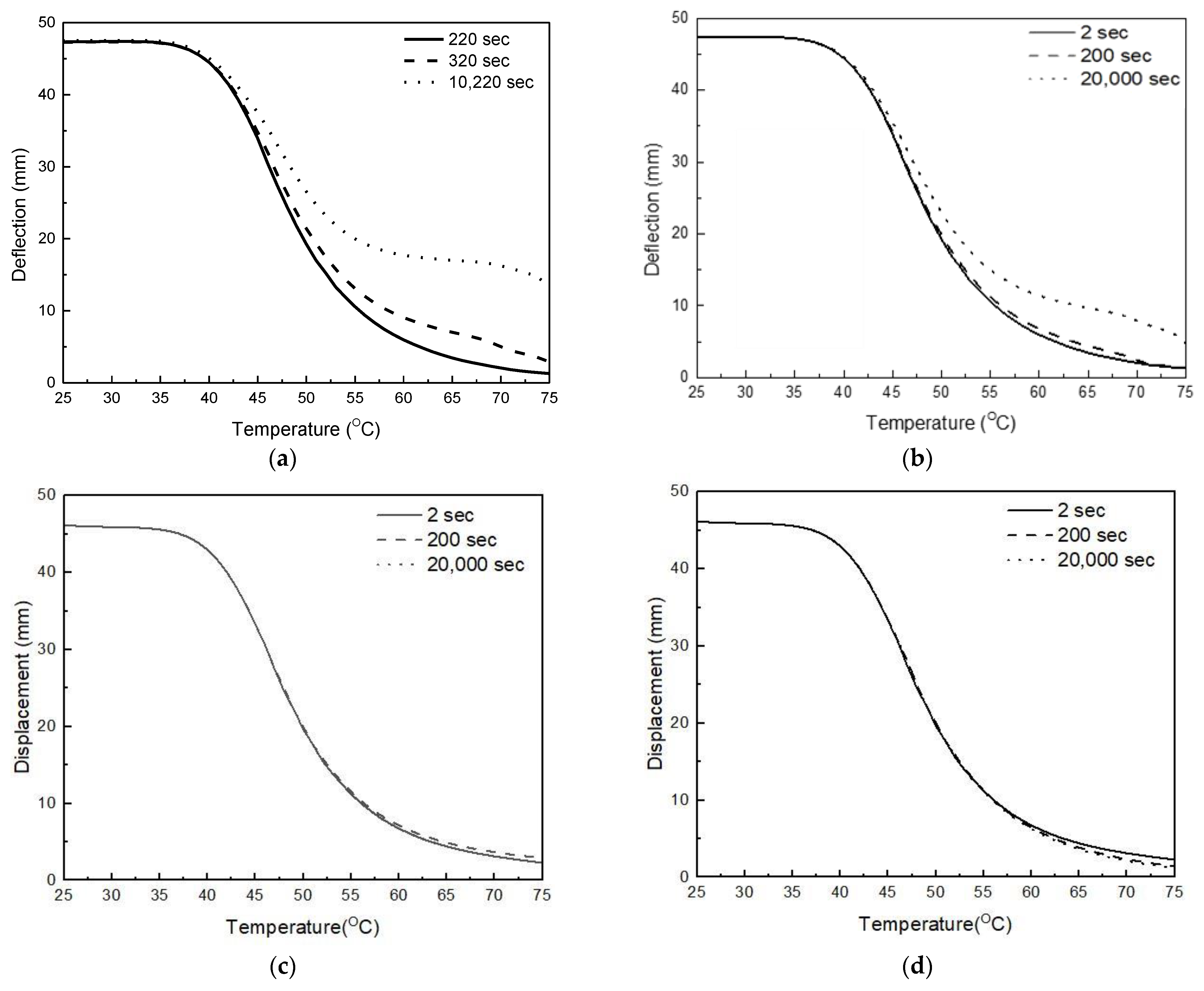
4.3. Shape Recovery Bhaviors with Different Time Variables
5. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DMA | Dynamic Mechanical Analysis |
| FEA | Finite Element Analysis |
| SMP | Shape Memory Polymer |
| SMPC | Shape Memory Polymer Composite |
| TTSP | Time–Temperature Superposition Principal |
| WLF | Williams–Landel–Ferry |
References
- Liu, T.; Liu, L.; Yu, M.; Li, Q.; Zeng, C.; Lan, X.; Liu, Y.; Leng, J. Integrative hinge based on shape memory polymer composites: Materials, design, properties and application. Copmos. Struct. 2018, 206, 164–176. [Google Scholar] [CrossRef]
- Dao, T.D.; Ha, N.S.; Goo, N.S.; Yu, W.R. Design, fabrication, and bending test of shape memory polymer composite hinges for space deployable structures. J. Intell. Mater. Syst. Struct. 2018, 29, 1560–1574. [Google Scholar] [CrossRef]
- Liu, Z.; Lan, X.; Bian, W.; Liu, L.; Li, Q.; Liu, Y.; Leng, J. Design, material properties and performances of a smart hinge based on shape memory polymer composites. Compos. Part B Eng. 2020, 193, 108056. [Google Scholar] [CrossRef]
- Iorio, L.; Quadrini, F.; Santo, L.; Circi, C.; Cavallini, E.; Pellegrini, R.C. Shape memory polymer composite hinges for solar sails. Adv. Space Res. 2024, 74, 3201–3215. [Google Scholar] [CrossRef]
- Zeng, C.; Liu, Z.; Liu, L.; Zhao, W.; Xin, X.; Liu, Y.; Leng, J. Effect of prolonged isothermal exposure and thermal cycling on mechanical properties and shape recovery behavior of shape memory composites. Compos. Part A Appl. Sci. Manuf. 2025, 194, 108921. [Google Scholar] [CrossRef]
- Herath, M.; Epaarachchi, J.; Islam, M.; Fang, L.; Leng, J. Light activated shape memory polymers and composites: A review. Eur. Polym. J. 2020, 136, 109912. [Google Scholar] [CrossRef]
- Boudjellal, A.; Trache, D.; Khimeche, K.; Hafsaoui, S.L.; Bougamra, A.; Tcharkhtchi, A.; Durastanti, J.F. Simulation and reinforcement of shape-memory polymers and their composites: A review. J. Thermoplast. Compos. 2020, 35, 2227–2260. [Google Scholar] [CrossRef]
- Namathoti, S.; Rama Sreekanth, P.S. A review on progress in magnetic, microwave, ultrasonic responsive shape-memory polymer composites. Mater. Today Proc. 2022, 56, 1182–1191. [Google Scholar] [CrossRef]
- Sanaka, R.; Sahu, S.K.; Sreekanth, P.R.; Senthilkumar, K.; Bagdayan, N.D.; Siva, B.V.; Ma, Q. A review of the current state of research and future prospectives on stimulus-responsive shape memory polymer composite and its blends. J. Compos. Sci. 2024, 8, 324. [Google Scholar] [CrossRef]
- Rahman, A.A.; Ikeda, T.; Senba, A. Memory effects performance of polyurethane shape memory polymer composites (SMPC) in the variation of fiber volume fractions. Fibers Polym. 2017, 18, 979–986. [Google Scholar] [CrossRef]
- Herath, M.; Epaarachchi, J.; Islam, M.; Yan, C.; Zhang, F.; Leng, J. Effects of selectively triggered photothermal particles on shape memory polymer composites: An investigation on structural performance, thermomechanical characteristics and photothermal behavior. J. Intell. Mater. Syst. Struct. 2019, 30, 3124–3135. [Google Scholar] [CrossRef]
- Quadrini, F.; Iorio, L.; Bellisario, D.; Santo, L. Shape memory polymer composite unit with embedded heater. Smart Mater. Struct. 2021, 30, 075009. [Google Scholar] [CrossRef]
- Kim, C.L.; Lee, J.J.; Oh, Y.J.; Kim, D.E. Smart wearable heaters with high durability, flexibility, water-repellent and shape memory characteristics. Compos. Sci. Technol. 2017, 152, 173–180. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, H.; Yin, H.; Sun, B.; Gu, B.; Zhang, W. A flexible, high-strength, conductive shape memory composite fabric based on continuous carbon fiber/polyurethane yarn. Smart Mater. Struct. 2020, 29, 085044. [Google Scholar] [CrossRef]
- Yadav, A.; Singh, S.K.; Das, S.; Kumar, S.; Kumar, A. Shape memory polymer and composites for space applications: A review. Polym. Compos. 2025. [Google Scholar] [CrossRef]
- Su, X.; Wang, Y.; Peng, X. An anisotropic visco-hyperelastic model for thermally-actuated shape memory polymer-based woven fabric-reinforced composteis. Int. J. Plast. 2020, 129, 102697. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, H.; Liu, Z.; Peng, X.; Zhou, H. A 3D anisotropic visco-hyperelastic constitutive model for unidirectional continuous fiber reinforced shape memory composites. Polym. Test. 2022, 114, 107712. [Google Scholar] [CrossRef]
- Qi, Y.; Huang, S.; Zhang, H.; Gu, B.; Sun, B.; Zhang, W. Shape memory behaviors of three-dimensional five-directional braided composites with different axial yarns arrangements. Compos. Struct. 2024, 338, 118105. [Google Scholar] [CrossRef]
- Hong, S.B.; Jang, J.H.; Park, H.; Kim, J.G.; Goo, N.S.; Yu, W.R. Three-dimensional constitutive model of woven fabric-reinforced shape memory polymer composites considering thermal residual stress. Smart Mater. Struct. 2019, 28, 035023. [Google Scholar] [CrossRef]
- Al Azzawi, W.; Epaarachchi, J.A.; Islam, M.; Leng, J. Implementation of a finite element analysis procedure for structural analysis of shape memory behavior of fibre reinforced shape memory polymer composites. Smart Mater. Struct. 2017, 26, 125002. [Google Scholar] [CrossRef]
- Gu, J.; Leng, J.; Sun, H.; Zeng, H.; Cai, Z. Thermomechanical constitutive modeling of fiber reinforced shape memory polymer composites based on thermodynamics with internal state variables. Mech. Mater. 2019, 130, 9–19. [Google Scholar] [CrossRef]
- Denis, Y.; Guzman-Maldonado, E.; Hamila, N.; Colmars, J.; Morestin, F. A dissipative constitutive model for woven composite fabric under large strain. Compos. Part A Appl. Sci. Manuf. 2018, 105, 165–179. [Google Scholar] [CrossRef]
- Denis, Y.; Hamila, N.; Itskov, M.; Guzman-Maldonado, E.; Morestin, F. A dissipative model for deep-drawing simulations: Elastic springback prediction and incremental forming strategies. Compos. Part A Appl. Sci. Manuf. 2021, 149, 106547. [Google Scholar] [CrossRef]
- Gupta, M.; Singh, H.; Khan, A.N.; Mahajan, P.; Prabhakaran, R.D.; Alagirusamy, R. An improved orthotropic elasto-plastic damage model for plain woven composites. Thin-Walled Struct. 2021, 162, 107598. [Google Scholar] [CrossRef]
- Dib, W.; Bles, G.; Blaise, A.; Tourabi, A. Modelling of cyclic visco-elasto-plastic behavior of coated woven fabrics under biaxial loading and finite strain. Int. J. Solids Struct. 2018, 154, 147–167. [Google Scholar] [CrossRef]
- Guo, S.; Wang, L.; Shao, G.; Shao, H.; Jiang, J.; Chen, N. Mechanical behavior and energy dissipation of woven and wrap-knitted pvc membrane materials under multistage cyclic loading. Polymers 2022, 14, 1666. [Google Scholar] [CrossRef] [PubMed]
- Spencer, A.J.M. Constitutive theory for strongly anisotropic solids. In Continuum Theory of the Mechanics of Fibre-Reinforced Composites; Springer: Dordrecht, The Netherlands, 1984; pp. 1–32. [Google Scholar]
- Aimenee, Y.; Vidal-Salle, E.; Hagege, B.; Sidoroff, F.; Boisse, P. A hyperelastic approach for composite reinforcement large deformation analysis. J. Copmos. Mater. 2010, 44, 5–26. [Google Scholar] [CrossRef]
- Charmetant, A.; Orliac, J.G.; Vidal-Salle, E.; Boisse, P. Hyperelastic model for large deformation analyses of 3D interlock composite preforms. Compos. Sci. Technol. 2012, 72, 1352–1360. [Google Scholar] [CrossRef]
- Peng, X.; Guo, Z.; Du, T.; Yu, W.R. A simple anisotropic hyperelastic constitutive model for textile fabrics with application to forming simulation. Compos. B Eng. 2013, 52, 275–281. [Google Scholar] [CrossRef]
- Yao, Y.; Huang, X.; Peng, X.; Liu, P.; Youkun, G. An anisotropic hyperelastic constitutive model for plain weave fabric considering biaxial tension coupling. Text. Res. J. 2019, 89, 434–444. [Google Scholar] [CrossRef]
- Gong, Y.; Peng, X.; Yao, Y.; Guo, Z. An anisotropic hyperelastic constitutive model for thermoplastic woven composite prepregs. Compos. Sci. Technol. 2016, 128, 17–24. [Google Scholar] [CrossRef]
- Mansouri, M.R.; Fuchs, P.F.; Criscione, J.C.; Schrittesser, B.; Beter, J. The contribution of mechanical interactions to the constitutive modeling of fiber-reinforced elastomers. Eur. J. Mech. A Solids 2021, 85, 104081. [Google Scholar] [CrossRef]
- Harrison, P.; Clifford, M.F.; Long, A.C. Shear characterization of viscous woven textile composites: A comparison between picture frame and bias extension experiments. Compos. Sci. Technol. 2004, 64, 1453–1465. [Google Scholar] [CrossRef]
- Cao, J.; Akkerman, R.; Boisse, P.; Chen, J.; Cheng, H.S.; De Graaf, E.F.; Gorczyca, J.L.; Harrison, P.; Hivet, G.; Launay, J.; et al. Characterization of mechanical behavior of woven fabrics: Experimental methods and benchmark results. Compos. A Appl. Sci. Manuf. 2008, 39, 1037–1053. [Google Scholar] [CrossRef]
- Bergmann, T.; Heimbs, S.; Maier, M. Mechanical properties and energy absorption capability of woven fabric composites under ±45 off-axis tension. Compos. Struct. 2015, 125, 362–373. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, H.; Wang, Y.; Zhou, H.; Peng, X. Modelling energy dissipation and hysteresis of woven fabrics with large deformation under single loading-unloading cycle. Compos. Struct. 2022, 279, 114781. [Google Scholar] [CrossRef]
- Huang, B.; Zhou, H.; Wang, J.; Yu, T.; Peng, X.; Zhou, H. A mesoscopic constitutive model for woven fabrics with large deformation. Text. Res. J. 2024, 94, 136–151. [Google Scholar] [CrossRef]
- Holzapfel, G.A. Nonlinear Solid Mechanics: A Continuum Approach for Engineering Science; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Mooney, M. A theory of large elastic deformation. J. Appl. Sci. 1940, 11, 582–592. [Google Scholar] [CrossRef]
- Butaud, P.; Ouisse, M.; Jaboviste, K.; Placet, V.; Foltete, E. Dynamical mechanical thermal analysis of shape-memory polymers. In Shape Memory Polymers, Blends and Composites; Springer: Singapore, 2020; pp. 129–515. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1995, 77, 3701–3707. [Google Scholar] [CrossRef]
- Liu, Y.; Grall, K.; Dunn, M.L.; Greenberg, A.R.; Diani, J. Thermomechanics of shape memory polymers: Uniaxial experiments and constitutive modeling. Int. J. Plast. 2006, 22, 279–313. [Google Scholar] [CrossRef]
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. ASTM International: West Conshohocken, PA, USA, 2014.
- ASTM D4065; Standard Practice for Plastics: Dynamic Mechanical Properties: Determination and Report of Procedures. ASTM International: West Conshohocken, PA, USA, 2012.
- ASTM D3039; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM International: West Conshohocken, PA, USA, 2017.














| Characteristics | Test Methods | Coefficients |
|---|---|---|
| Hyperelasticity | Tensile | C10, C01 |
| Viscoelasticity | DMA | βi, τi, c1, c2, Tg |
| Shape recovery | Thermomechanical cycle | T0, h, s |
| Thermal expansion | Increasing temperature | a, b, c |
| Characteristics | Test Methods | Coefficients |
|---|---|---|
| Tensile property | Tensile (0°, 90°) | k1, k2, k3, k4, k5, k6 |
| Hysteresis effect | Loding-unloading | k1, k2, k3, k4, k5, k6 |
| Viscoelasticity | Stress relaxation | βi, τi |
| Shear property | Tensile (±45°) | k7, k8, k9 |
| Characteristics | Temperature (°C) | C10 (MPa) | C01 (MPa) |
|---|---|---|---|
| Hyperelasticity | 25 | −4075 | 4356 |
| 35 | −1145 | 1230 | |
| 45 | −3.017 | 5.263 | |
| 55 | −1.136 | 2.123 | |
| 75 | −0.379 | 1.030 |
| Characteristics | i | βi (-) | τi (s) |
|---|---|---|---|
| Viscoelasticity | 1 | 0.107 | 0.0154 |
| 2 | 0.160 | 2.57 | |
| 3 | 0.235 | 213 | |
| 4 | 0.268 | 9580 | |
| 5 | 0.193 | 202,000 |
| Characteristics | C1 (-) | c2 (°C) | Tg (°C) |
|---|---|---|---|
| Williams–Ladnel–Ferry (WLF) equation | 52.433 | 166.429 | 45 |
| Characteristics | k1 (MPa) | k2 (MPa) | k3 (MPa) | k4 (MPa) | k5 (MPa) | k6 (MPa) |
|---|---|---|---|---|---|---|
| Tensile | 0.0135 | −0.0187 | 0.0545 | −0.0782 | 0.2859 | 0.2618 |
| Characteristics | k7 (MPa) | k8 (MPa) | k9 (MPa) |
|---|---|---|---|
| Shear | 0.7401 | −0.5531 | 0.2107 |
| Characteristics | Weft Direction | Warp Direction | |||
|---|---|---|---|---|---|
| i | βi (-) | τi (s) | βi (-) | τi (s) | |
| Viscoelasticity | 1 | 0.03593 | 2.711 | 0.03257 | 16.31 |
| 2 | 0.12848 | 20.98 | 0.00737 | 16.49 | |
| 3 | 0.05779 | 164.8 | 0.93712 | 3681 | |
| Characteristics | k1 (MPa) | k2 (MPa) | k3 (MPa) | k4 (MPa) | k5 (MPa) | k6 (MPa) |
|---|---|---|---|---|---|---|
| Hysteresis (Unloading) | 0.0537 | 0.0044 | 0.0174 | 1.1946 | −0.7287 | 0.2250 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwon, O.-H.; Roh, J.-H. Numerical Study on Shape Recovery Behaviors of Shape Memory Polymer Composite Hinges Considering Hysteresis Effect. Aerospace 2025, 12, 717. https://doi.org/10.3390/aerospace12080717
Kwon O-H, Roh J-H. Numerical Study on Shape Recovery Behaviors of Shape Memory Polymer Composite Hinges Considering Hysteresis Effect. Aerospace. 2025; 12(8):717. https://doi.org/10.3390/aerospace12080717
Chicago/Turabian StyleKwon, O-Hyun, and Jin-Ho Roh. 2025. "Numerical Study on Shape Recovery Behaviors of Shape Memory Polymer Composite Hinges Considering Hysteresis Effect" Aerospace 12, no. 8: 717. https://doi.org/10.3390/aerospace12080717
APA StyleKwon, O.-H., & Roh, J.-H. (2025). Numerical Study on Shape Recovery Behaviors of Shape Memory Polymer Composite Hinges Considering Hysteresis Effect. Aerospace, 12(8), 717. https://doi.org/10.3390/aerospace12080717





