A Layout Optimization Design Method for Flat-Panel Satellites with In-Orbit Validation

Abstract

Since 2019, Starlink satellites, with their innovative flat-panel design and unprecedented number in orbit, have transformed the traditional satellite industry. Due to their mass production characteristics, flat-panel satellites face a pressing need for satellite layout optimization design (SLOD), particularly for feasible optimization results applicable in engineering. Existing layout optimization algorithms often focus on theoretical optima, computational efficiency, and multi-objective capabilities. Most algorithms are validated exclusively through numerical or CAD-based simulations, leaving their engineering applicability under-reported. This paper establishes a simplified mathematical model of SLOD with consideration for the key features of flat-panel satellites. Furthermore, we propose a differential evolution algorithm that leverages local optima for the layout optimization design of flat-panel satellites. By making targeted and limited improvements to initial human-designed layouts, the algorithm generates practical engineering solutions that significantly enhance the stacking efficiency, mass properties, and thermal distribution of flat-panel satellites. Finally, the effectiveness and engineering feasibility of the algorithm were verified through the design of Longjiang-3, China’s first flat-panel satellite, and the results were also validated in orbit. Compared with the baseline configuration, the optimized layout reduces the principal moment of inertia by 6.6% and the satellite module height by 3.5%. It also achieves a significant improvement in thermal power uniformity across the structure. Overall, the key layout metrics are enhanced by 26%. The present research results provide a theoretical basis and engineering solutions for the SLOD of flat-panel satellites.

1. Introduction

Flat-panel satellites, such as the Starlink constellation, are expected to dominate future low Earth orbit (LEO) communication markets due to their modularity and mass-production capabilities [1]. These platforms have revolutionized the traditional satellite industry by enabling mass production, batch launches, and rapid deployment. Their modular, compact design maximizes space utilization within launch vehicle fairings, reducing launch costs. This modular structure also enables automation and mass production, which reduces manufacturing cycles and costs. In addition, flat-panel platforms adopt a high aspect ratio design, which further maximizes packing efficiency during launches. The expanded surface area accommodates more antennas and payloads, enhancing signal strength and mission flexibility. However, flat-panel satellites pose significant layout optimization challenges. First, limited research on this novel configuration has resulted in a lack of established design guidelines and theoretical foundations. Second, the demands for rapid iteration and large-scale deployment require design solutions that are directly applicable to engineering practice. Thus, studying satellite layout optimization design (SLOD) methods for flat-panel satellites has significant theoretical and practical value.

SLOD is a critical aspect of satellite engineering, influencing performance, cost, and quality [2]. Early studies treated SLOD as a three-dimensional packing problem, widely recognized as NP-hard [3,4]. In an NP-hard problem, a set of boxes must be orthogonally packed into the minimum number of three-dimensional bins [5,6]. Traditional methods often relied on simplified geometric models and basic algorithms to tackle this complexity [7,8]. Taking the layout design of a simplified commercial communication satellite as a background, Huo et al. [9] presented a co-evolutionary method with heuristic rules for the optimal layout design of a satellite module. Sun et al. [10] proposed a basic solution strategy for the optimal layout design of a satellite module, which consists of the centripetal balancing method for global layout design and a quasi-Traveling Salesman Problem model-based Ant Colony Optimization algorithm for layout optimization. However, these studies oversimplified satellite layout as a basic packing problem, neglecting satellite-specific constraints and objectives, creating discrepancies between models and real-world scenarios. The integration of advanced algorithms, such as differential evolution (DE) [11,12] and particle swarm optimization (PSO) [13,14], has further propelled SLOD methodologies. Gao et al. [15] proposed an improved parameter-adaptive differential evolution algorithm to optimize the layout of piezoelectric actuators and sensors and accurately identify the hysteresis nonlinear model of piezoelectric elements. Zhang et al. [16] integrated the Hopfield neural network, genetic algorithm/particle swarm optimization (GA/PSO), and quasi-principal component analysis (QPCA) to deal with the layout design problem of a satellite module. Chen et al. [17] proposed accelerated particle swarm optimization (APSO) to study satellite layout optimization design with complicated performance constraints. These algorithms efficiently handle high-dimensional optimization problems inherent in satellite layout design. Hybrid optimization algorithms based on DE have demonstrated superior performance in generating optimal layouts, offering practical solutions for complex challenges. Zhang et al. [18] proposed a hybrid algorithm consisting of tabu search, DE, and adaptive fine tuning to solve the component assignment and layout optimization problem for multi-module microsatellites considering variable module size. Additionally, multi-objective optimization approaches that account for various factors have enhanced the designer’s toolkit [19,20]. Qin et al. [21] used a multi-objective methodology to find optimized trade-off solutions for the layout of equipment in satellite cabins. Zhang et al. [22] proposed an evolutionary multi-agent framework of the co-operative co-evolutionary multi-objective model, specifically for equipment layout optimization in engineering. These systems provide diverse configurations optimized for criteria such as center of gravity alignment, moments of inertia, debris impact risk, and so on, thereby enhancing the practicality of SLOD for engineering applications.

Despite these advancements, several persistent challenges remain in SLOD research. Firstly, most studies focus on the tank-based structure, neglecting box-panel or flat-panel configurations [23,24,25]. Chen et al. [26] presented a novel tank-shaped satellite layout optimization design approach based on the phi function. Qin et al. [27] presented an optimization tool for the integration of CAD software as well as the optimization algorithms to automatically find solutions for a three-dimensional layout of equipment in a tank-shaped satellite. Such an approach fails to meet the application requirements in real-world engineering. Secondly, most of the works treat components as circles [28], fixed rectangles [29], or prohibit inter-module component migration [30]. Fakoor et al. [31] used the Finite Circle Method to express geometric constraints mathematically, and proposed a hybrid method combining simulated annealing optimization and quasi-Newton methods to optimize satellite layout design. Liu et al. [32] proposed a hybrid method combing with Wang–Landau and local search methods to obtain a final layout scheme and a method for the overlapping depth between two objects (such as two rectangular objects, two circular objects, or a rectangular object and a circular object) embedding each other. Fakoor et al. [33] presented a hybrid optimization algorithm, which globally explores the design search space of satellite using particle swarm optimization and gradient-based Sequential Quadratic Programming to rapidly locate the optimum design point without changing the floor on which the components reside. These simplifications fail to reflect real engineering scenarios [34]. Thirdly, many studies employ only a few constraints, overlooking the complexity of satellite engineering, limiting the applicability of their results [35]. Aiming at the circular packing problem with equilibrium behavioral constraints, Liu et al. [36] put forward a new global search algorithm by combining the improved ELP method, a gradient method based on local search and the heuristic configuration update mechanism. However, real satellite design involves numerous complex engineering constraints. When optimization results are overly focused on meeting the predefined objectives, conflicts with these constraints often arise, rendering the optimized design less applicable to practical engineering scenarios. Finally, some studies prioritize optimization speed at the expense of solution quality [37]. Based on the industrial background of packing objects inside the satellites, Wang et al. [38] proposed a stimulus–response-based allocation (SRA) method. They used three sets of 35 benchmark instances to test the performance of SRA, and found that SRA improved the best-known results on 28 instances, matched 4, and missed 3. In fact, overlooking or proposing incorrect optimization objectives leads to impractical solutions. Achieving optimal solutions, even at the cost of longer but acceptable computation time, is more valuable for engineering applications.

This paper addresses these challenges by proposing a novel approach that integrates engineering realities and utilizes local optimal solutions for layout optimization. The DE-based algorithm improves the layout of the manual designs and generates practical solutions. It retains the engineering details and constraints of manual designs while enhancing the stacking efficiency, mass properties, and thermal distribution of flat-panel satellites. The contributions are organized as follows:

(1)

The complex engineering problem about the layout optimization of flat-panel satellites is simplified, and a mathematical model with design constraints is established.

(2)

Considering that there are many constraints in practical engineering, a DE algorithm using local optimal solutions is proposed. Taking the manual designs as the initial value, the algorithm utilizes local optima and obtains better results than the manual designs.

(3)

The method is validated through a case study of Longjiang-3, China’s first flat-panel satellite. The in-orbit temperature of the satellite meets requirements, and the high-power in-orbit validation of Transmission Antenna 1 and Transmission Antenna 2 is successful.

(4)

This approach aims to improve the practicality and effectiveness of SLOD, particularly for emerging flat-panel satellite platforms. Meanwhile, it provides an engineering solution for SLOD.

2. Mathematical Model for the SLOD of Flat-Panel Satellites

2.1. Key Features of Flat-Panel Satellites

Flat-panel satellite platforms possess several key features that set them apart from traditional satellite configurations and significantly influence their layout and design. These unique characteristics also present specific challenges for layout optimization.

One of the most critical characteristics of flat-panel satellites is that their layout is designed within a two-dimensional plane, rather than in a three-dimensional space. This significantly reduces the complexity of the layout process, as the components are confined to the plane of the satellite’s structural panels. Additionally, both the front and rear surfaces of each panel are used for the layout, typically being identical in shape. These surfaces are usually rectangular but may deviate from perfectly regular shapes.

Another important feature is the integration of thermal management systems, such as heat pipes, which are laid out within the panels. These heat pipes are designed to optimize thermal distribution across the components on both the front and rear surfaces of the panels, ensuring efficient heat dissipation and preventing localized overheating. This ensures that the satellite operates reliably and efficiently in the space environment.

The satellite’s equipment is characterized by several defining features. Most of the onboard components are rectangular or can be enclosed within a rectangular bounding box. Additionally, components must satisfy compatibility, maintainability, and accessibility (CMA) constraints, ensuring proper integration, maintenance ease, and sufficient accessibility for wiring and operations. It is crucial to ensure that there is no interference between the bounding volumes of different satellite components and that all components fit entirely within the envelope of the satellite module without exceeding its boundaries.

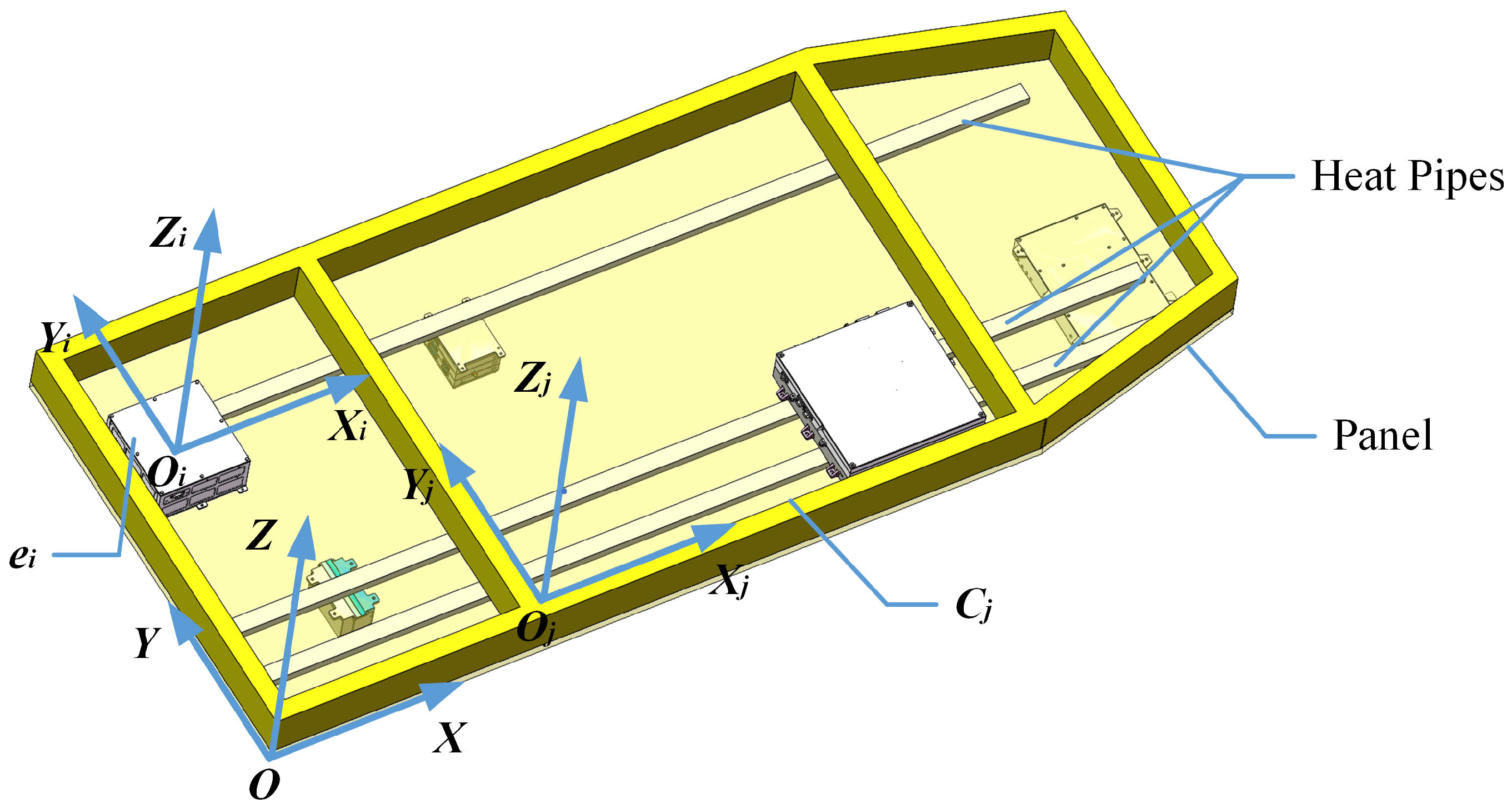
Given these key characteristics, a multi-module model can be used to describe the flat-panel satellite, as shown in Figure 1. The satellite consists of multiple convex quadrilateral panels, each located on the front and rear surfaces of the satellite’s structural panels. The components on the front surface are assigned positive heights, while those on the rear surface are assigned negative heights.

To represent the components’ sizes and positions, a bounding box method is adopted, where each component is described as a rectangular box as presented in Figure 2, accounting for CMA requirements. The edges of these rectangular components can be angled relative to the satellite module’s edges. This provides layout flexibility while ensuring all components stay within the satellite envelope.

These simplifications are particularly suitable for flat-panel satellites and spacecraft dominated by rectangular-shaped equipment, and they may not fully represent detailed geometric complexities or interactions present in structurally complex spacecraft configurations. Constraints related to electromagnetic interference, structural integrity, and subsystem interdependencies are not explicitly modeled in the optimization but are indirectly accounted for through conservative engineering margins and practical design rules.

Although the components are simplified as bounding boxes, this does not compromise engineering accuracy. Most onboard devices are approximately rectangular in shape, and practical layout always leaves sufficient clearance (CMA margin) between components for harness routing and installation. Therefore, the bounding box approach preserves all critical spatial and installation constraints, and the minor geometric details that are omitted do not affect real-world engineering outcomes.

This approach simplifies the complex engineering problem of layout optimization into a mathematical model that can be efficiently solved, while still capturing the critical constraints and characteristics of the flat-panel satellite design.

2.2. Assumption and Objectives

The layout optimization design for flat-panel satellite platforms requires abstraction and simplification of the engineering model. This process necessitates several assumptions to reduce complexity while maintaining essential design constraints. The primary objective of this study focuses on optimizing the structural and thermal control design of flat-panel satellites. However, the proposed mathematical model and algorithm can accommodate additional objectives to support broader optimization tasks.

To generalize the mathematical model without losing applicability, the following assumptions are made. Since the surfaces of panels are quadrangles in flat-panel satellites, all satellite modules are simplified as convex quadrilaterals, and all satellite components are represented as rectangular bounding boxes, including the CMA space. In addition to this geometric simplification, we also ignore cable weight and structural modifications. The weight of cables accounts for less than 5% of the total mass (less than 10 kg for Longjiang-3, a satellite weighing about 230 kg; a NASA assessment report adopts a value of 4.5% for this parameter [39]) and are relatively evenly distributed. In addition, there is a growing trend towards wireless communication to reduce weight and simplify design. As a result, the effects of cable weight on the satellite’s mass properties are ignored. The neglect of structural modifications is due to the consideration that the impact of changes, such as reinforcement modifications, may slightly affect the satellite module structure, but it can be negligible on overall satellite performance.

CMA constraints are mathematically represented within the optimization model by explicitly defining minimum clearance distances between components and ensuring accessibility margins around critical equipment. Specifically, these constraints are modeled as inequality constraints in the optimization formulation:

$$g_{\mathrm{CMA},ij}\left(\mathbf{L}\right)=d_{ij}-d_{\min ,ij}\ge 0,\forall i,j$$

(1)

where $d_{ij}$ denotes the actual distance between components i and j, and $d_{\min ,ij}$ represents the required minimum clearance to satisfy compatibility, maintainability, and accessibility.

The mathematical model aims to assign the given components to the optimal panels and determine their optimal positions while satisfying five requirements: noninterference (R1), improved mass performance (R2), balanced thermal distribution (R3), decreased thickness (R4), and good functional satisfaction (R5). R1, R3, and R5 are three requirements for components of the flat-panel satellite. Noninterference means that all components must be located within the module boundaries without interference with module walls or other components. Additionally, components should be distributed on the limited heat pipes to ensure uniform thermal distribution across the panels. Flat-panel satellites typically carry high-power communication payloads, which demand higher thermal control requirements than traditional satellites. Good functional satisfaction requires that all components must be positioned to meet their functional constraints effectively. For example, antennas operating at different frequency bands need to be placed at a sufficient distance to avoid interference, and some components have fixed orientation requirements. In addition, the SLOD of flat-panel satellites is also required to improve mass performance and decrease thickness. Smaller moments of inertia (MOIs) are more beneficial for the design of the Attitude Determination and Control System (ADCS). The special configuration of flat-panel satellites results in larger MOIs, requiring better control. The overall thickness of the flat-panel satellite should be thin, so that it can be more efficient when stacked within the launch vehicle fairing.

Natural frequency and layout of non-panel-mounted components are excluded in this study due to the specific characteristics of flat-panel satellites. Although natural frequency is critical, particularly for flat-panel satellites, it is more appropriately addressed during the structural design of the satellite’s main frame and its stacked configuration within the launch vehicle fairing. It is not considered a key factor during layout design. In flat-panel satellites, most components are mounted on the primary structural panels. A few exceptions, such as components mounted on external covers, have negligible mass and do not present layout design challenges. Therefore, their layouts are not considered.

By adhering to these assumptions and focusing on these objectives, the mathematical model provides a framework for optimizing the layout design of flat-panel satellites, ensuring practical and effective solutions for engineering applications.

2.3. Mathematical Model

Let $\mathit{E}=\{e_1,e_2,\dots ,e_n\}$ represent the set of components of the satellite, $\mathit{A}=\{{\eta }_1,{\eta }_2,\dots ,{\eta }_n\}$ represent the assignment of all components, and $\mathit{C}=\{C_1,C_2,\dots ,C_N\}$ represent the set of modules. Three coordinate systems are defined as follows. The relationships among these three coordinate systems are shown in Figure 1.

• Reference coordinate system $OXYZ$: The origin O is set at the bottom-left corner of the satellite in the top view. The X-axis corresponds to the satellite’s long side, the Y-axis corresponds to its short side, and the Z-axis corresponds to its thickness direction.
• Module coordinate system $O_j{X}_j{Y}_j{Z}_j$: The origin $O_j$ is set at the bottom-left corner of the satellite module in the top view, and its three axes correspond to the $OXYZ$ coordinate axes.
• Component coordinate system $O_i{X}_i{Y}_i{Z}_i$: The origin $O_i$ is set at the COG of the component, and axis $O_i{Z}_i$ corresponds to the $OZ$ axis, while $O_i{X}_i$ has an angle of ${\theta }_i$ relative to $OX$.

The design variable in the SLOD of flat-panel satellites can be expressed as

$$\mathit{L}=\{{\mathit{L}}_i=(x_i,y_i,z_i,{\theta }_i,{\eta }_i)|i=0,1,\dots ,n-1;{\theta }_i\in [0,\pi /2);{\eta }_i\in \{0,1,\dots ,N-1\}\}$$

(2)

where $(x_i,y_i,z_i)$ is the location of the COG of component $e_i$ in $OXYZ$, ${\eta }_i$ is the number of the module to which component $e_i$ is assigned, and ${\theta }_i$ is the angle between the $OX$ and $O_i{X}_i$ axes.

According to the characteristics of flat-panel satellites, the value of $z_i$ is related to ${\eta }_i$ and can be calculated as

$$z_i=\left({\displaystyle \frac{h_i}{2}}+dp\right)s_i$$

(3)

where $dp$ is the thickness of the satellite’s main panel, $h_i$ is the height of component $e_i$, and $s_i$ is the orientation factor of the module, which equals $+1$ for the $+Z$ side and $-1$ for the $-Z$ side.

According to requirements R1–R3, the objective of this problem is to find $\mathit{L}$ to minimize

$$f_1\left(\mathit{L}\right)=I\left(\mathit{L}\right)$$

(4)

$$f_2\left(\mathit{L}\right)=V\left(\mathit{L}\right)$$

(5)

$$f_3\left(\mathit{L}\right)=T_1\left(\mathit{L}\right)$$

(6)

$$f_4\left(\mathit{L}\right)=T_2\left(\mathit{L}\right)$$

(7)

$$f_5\left(\mathit{L}\right)=T_3\left(\mathit{L}\right)$$

(8)

Subject to

$$g_0\left(\mathit{L}\right)=\sum _{i=0}^{n-1}\sum _{j=i+1}^n\Delta A_{ij}{|}_{{\eta }_i={\eta }_j}=0$$

(9)

$$g_i\left(\mathit{L}\right)=0$$

(10)

where $I\left(\mathit{L}\right)$ represents minimizing the MOI of the satellite, $V\left(\mathit{L}\right)$ represents the total volume of the satellite modules, $T_1\left(\mathit{L}\right)$ represents the total power of devices not located on any heat pipes, $T_2\left(\mathit{L}\right)$ represents the standard deviation of power across all heat pipes, and $T_3\left(\mathit{L}\right)$ represents the standard deviation of power distribution across different regions along the direction of heat pipes. For the thermal distribution objectives, the entire satellite is divided along the X-axis (the direction of the heat pipes) into 10 equal-length regions, based on the total satellite length in the X direction. The standard deviation of power among these regions is then calculated to evaluate axial thermal uniformity. $g_0\left(\mathit{L}\right)$ ensures no interference between components in the same module. $g_i\left(\mathit{L}\right)$ represents the special layout constraints of component $e_i$. For example, certain devices must be installed in specific positions or orientations, while some components require maintaining a specified distance from others.

While the satellite’s overall heat rejection is determined by its external surface area and optical properties, the internal component layout directly affects how heat is distributed among onboard equipment and how efficiently thermal control elements such as heat pipes function. An optimized, balanced layout helps reduce local hot spots and promotes uniform in-orbit temperatures.

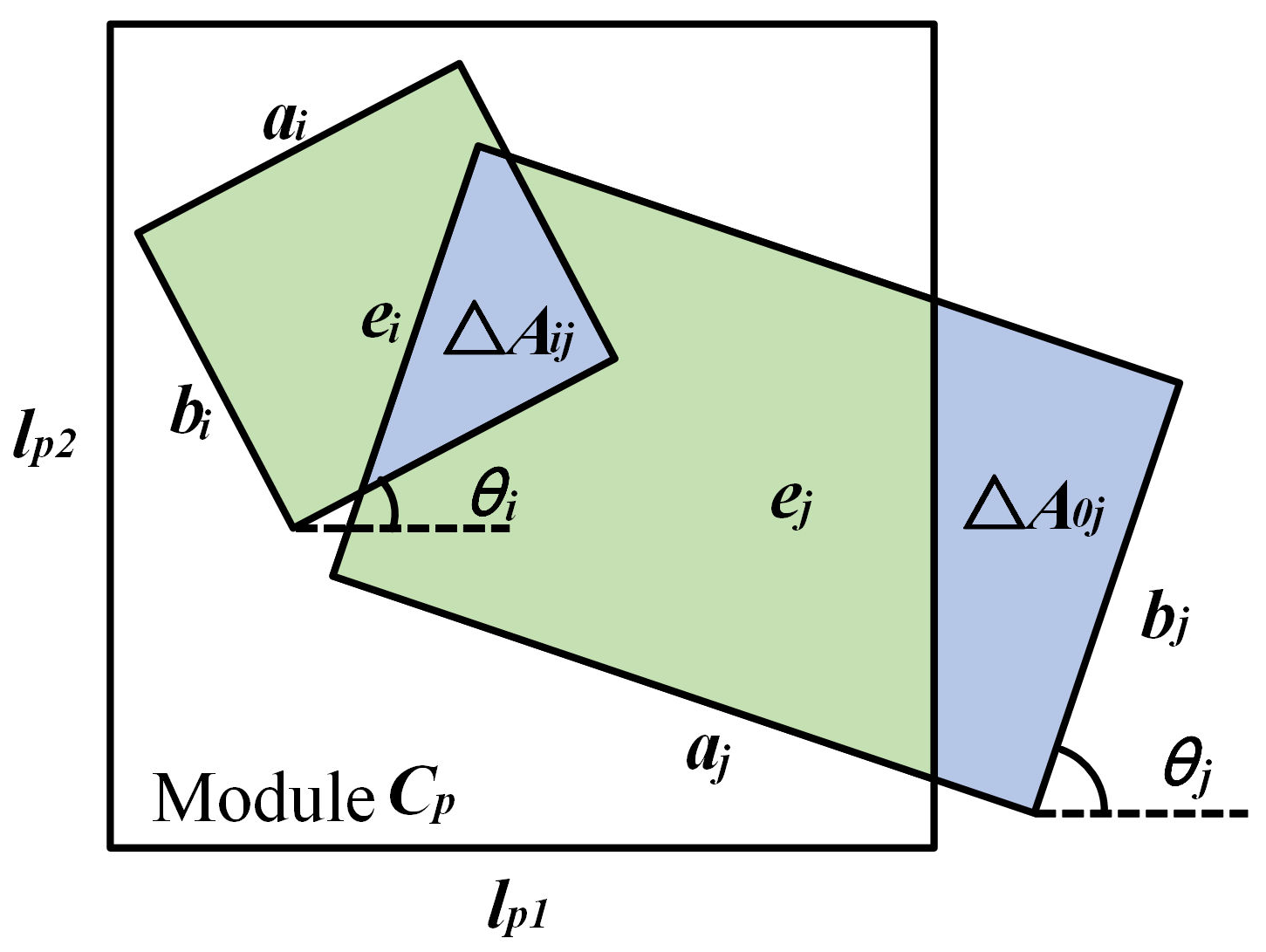
Figure 3 shows the interference area between components and module walls. $\Delta A_{ij}{|}_{{\eta }_i={\eta }_j}$ is the interference area between components $e_i$ and $e_j$ when they are in the same module, where $e_0$ is used to denote the wall of modules.

The satellite’s total MOI $I\left(\mathit{L}\right)$ can be calculated by

$$I\left(\mathit{L}\right)=\sqrt{{I_x}^2\left(\mathit{L}\right)+{I_y}^2\left(\mathit{L}\right)+{I_z}^2\left(\mathit{L}\right)}$$

(11)

where,

$$\begin{array}{cc}\hfill I_x\left(\mathit{L}\right)& =I_{x,0}+\sum _{i=1}^n\left(I_{x^{\prime },i}{cos}^2{\theta }_i+I_{y^{\prime },i}{sin}^2{\theta }_i\right)+\sum _{i=1}^n{m}_i\left(y_i^2+z_i^2\right)-\left(y_m^2+z_m^2\right)\sum _{i=1}^n{m}_i\hfill \\ \hfill I_y\left(\mathit{L}\right)& =I_{y,0}+\sum _{i=1}^n\left(I_{y^{\prime },i}{cos}^2{\theta }_i+I_{x^{\prime },i}{sin}^2{\theta }_i\right)+\sum _{i=1}^n{m}_i\left(x_i^2+z_i^2\right)-\left(x_m^2+z_m^2\right)\sum _{i=1}^n{m}_i\hfill \\ \hfill I_z\left(\mathit{L}\right)& =I_{z,0}+\sum _{i=1}^n{I}_{z^{\prime },i}+\sum _{i=1}^n{m}_i\left(x_i^2+y_i^2\right)-\left(x_m^2+y_m^2\right)\sum _{i=1}^n{m}_i\hfill \end{array}$$

(12)

The total volume of modules $V\left(\mathit{L}\right)$ is defined as

$$V\left(\mathit{L}\right)=\sum _{p=1}^N{A}_p{H}_p$$

(13)

where $A_p=l_{p,1}{l}_{p,2}$ is the area of module $C_p$, and $H_p$ is the height of module $C_p$.

Three thermal control objectives $T_1$(L), $T_2\left(\mathbf{L}\right)$, and $T_3\left(\mathbf{L}\right)$ are expressed as

$$T_1\left(\mathit{L}\right)=\sum _{i\in {\mathcal{E}}_{\mathrm{off}}}{P}_i$$

(14)

$$T_2\left(\mathit{L}\right)=\sqrt{{\displaystyle \frac{1}{n_h}}\sum _{k=1}^{n_h}{(P_k-\overline{P})}^2},\overline{P}={\displaystyle \frac{{\sum }_{k=1}^{n_h}{P}_k}{n_h}}$$

(15)

$$T_3\left(\mathit{L}\right)=\sqrt{{\displaystyle \frac{1}{n_r}}\sum _{r=1}^{n_r}{(P_r-{\overline{P}}_r)}^2},{\overline{P}}_r={\displaystyle \frac{{\sum }_{r=1}^{n_r}{P}_r}{n_r}}$$

(16)

where ${\mathcal{E}}_{\mathrm{off}}$ is the set of components that are not placed on heat pipes, $P_i$ denotes the power consumption of component $e_i$, $n_h$ is the total number of heat pipes, $P_k$ presents the total power load on the k-th heat pipe, $\overline{P}$ is the average power across all heat pipes, $n_r$ denotes the number of regions along the heat pipe direction, $P_r$ is the power in region r, and ${\overline{P}}_r$ is the average power across all regions.

The aggregated objective function is expressed as

$$\phi \left(\mathit{L}\right)=\sum _{i=1}^5{\omega }_i{f}_i\left(\mathit{L}\right)+\sum _{j=1}^n{\lambda }_j{g}_j\left(\mathit{L}\right)$$

(17)

where ${\omega }_i$ and ${\lambda }_j$ are the weight and penalty coefficients, respectively.

In practice, the algorithm is designed to improve upon the manual baseline in all objectives, but the final evaluation is performed using a penalized objective function that includes designer-specified weights for each term. These weights reflect the specific engineering priorities for different satellite missions and are set by the design team based on their experience and project requirements. Allowing designers to tune these weights and penalty factors is a key feature of the proposed method, making it adaptable to a variety of satellite platforms.

3. The DE-Based SLOD

The goal of this study is to propose a new method that utilizes local optima within a DE algorithm to obtain direct engineering solutions for flat-panel satellite layout optimization. The method optimizes key factors while retaining the engineering details and constraints of manual designs.

3.1. Optimization Strategy

In this paper, a differential evolution algorithm leveraging local optima is proposed for the layout optimization design of flat-panel satellites. We selected differential evolution (DE) after systematically evaluating it against genetic algorithms (GAs) and particle swarm optimization (PSO) across the three-stage optimization framework (global exploration, normalization transition, and local refinement). During global exploration, DE effectively maintains population diversity through its differential mutation strategy, reducing the risk of premature convergence compared to GA, which often requires additional mechanisms to maintain diversity, and PSO, which tends to rapidly cluster around the first promising solution. In the normalization transition phase, DE’s ability to simultaneously maintain multiple candidate solutions and perform controlled crossover allows the seamless integration of both manually designed layouts and theoretical optima into the population, an advantage not inherently present in standard GA and PSO methods without substantial modifications. In local refinement, DE’s low mutation factor and direct selection mechanism (trial vs. parent) efficiently fine-tune around the given initial solution without stagnation, overcoming GA’s limited intensification capability and PSO’s rapid but often premature convergence behavior. Furthermore, existing comparative studies [40] consistently indicate that DE exhibits superior robustness and solution quality in various optimization scenarios, particularly in handling complex landscapes and local optima. Therefore, DE was chosen for its balanced search dynamics, fewer required parameter adjustments, and proven effectiveness aligned with the practical constraints and iterative demands of satellite layout optimization.

The optimization process is divided into three phases. In the first phase, the DE algorithm is employed to calculate the theoretical optimal values of the objective functions. The algorithm explores the solution space globally to determine optimal values for key objectives. The DE parameters are set to favor global exploration

$$F_m=0.9,P_c=0.9,r_m=0.5$$

(18)

where $F_m$ is the mutation factor controlling the degree of variation, $P_c$ is the crossover probability determining the exchange of information between solutions, and $r_m$ introduces randomness to avoid premature convergence.

In the second phase, the algorithm incorporates manually designed layouts to calculate normalization factors. For each objective function, the normalization factor is defined as the weighted average of the theoretical optimal value $f_{\mathrm{optimal}}$ and the manual design’s objective function value $f_{\mathrm{manual}}$

$$f_{\mathrm{norm}}=w·{\displaystyle \frac{f_{\mathrm{optimal}}+f_{\mathrm{manual}}}{2}}$$

(19)

where w is the weight coefficient representing the priority of each objective. This step ensures that the optimization process aligns with practical engineering needs while leveraging theoretical benchmarks.

The third phase refines the manual design through local optimization using the DE algorithm. Starting from the manually provided initial layout, the DE parameters are adjusted to prioritize local optimization

$$F_m=0.5,P_c=0.7,r_m=0.1$$

(20)

These settings prioritize rapid convergence and the effective use of local optima.

3.2. Workflow and Implementation

Figure 4 provides a step-by-step flowchart of the global search, normalization, and local refinement phases. The implementation begins with defining the input conditions for global search to obtain the theoretical optimal solution, that is, the initial layout. The input includes the dimensions of the satellite module, thermal pipe positions, and component characteristics

$$L_i=\{x_i,y_i,{\theta }_i,{\eta }_i\},i=0,1,\dots ,N-1$$

(21)

Each component is further characterized by its dimensions ($l,w,h$), mass (m), and power (P). Next, a DE optimization run is performed without relying on the initial layout $L_0$. This step explores the solution space globally to determine the theoretical optimal values $f_{\mathrm{optimal}}$ for each individual objective. These values establish a benchmark for evaluating and refining the manual design.

Simultaneously, the optimization process begins by inputting the parameters of the satellite components and modules, including their dimensions, masses, and heat dissipation characteristics, as well as the structure of the satellite module. Based on this input, a manual layout $L_0$ is designed, which serves as the initial configuration for the optimization.

Then, the multi-objective weight factors are computed. These factors are derived by combining the results of the manual layout and the theoretical optimization. The normalization factor for each objective is calculated as

$$f_{\mathrm{norm},\mathrm{i}}={\displaystyle \frac{f_{\mathrm{manual},\mathrm{i}}+f_{\mathrm{optimal},\mathrm{i}}}{2}}$$

(22)

where $f_{\mathrm{manual}}$ is the value of the objective function for the manual design $L_0$ and $f_{\mathrm{optimal}}$ is the theoretical optimal value.

In the final step, DE optimization is performed using $L_0$ as the starting point. The DE algorithm, with parameters adjusted to exploit local optimal traps, refines the layout to produce an engineering-feasible solution. The optimization minimizes the total normalized objective function

$$F_{\mathrm{total}}=\sum _{i=1}^5{w}_i·{\displaystyle \frac{f_i}{f_{\mathrm{norm},\mathrm{i}}}}$$

(23)

where $f_i$ is the value of the i-th objective function, $f_{\mathrm{norm}}$ is the normalization factor, and $w_i$ is the corresponding weight.

The final output is the optimized layout $L_{\mathrm{best}}$, including the positions, orientations, and module assignments of all components. The results are evaluated to ensure they meet theoretical benchmarks and are practical for engineering applications.

4. Engineering Case Study

To validate the effectiveness of the proposed layout optimization method, this section presents an engineering case study using Longjiang-3, China’s first flat-panel satellite. Successful in-orbit validation is defined as follows: (i) no interference between any satellite components, (ii) no electromagnetic interference observed during in-orbit operation, (iii) all on-board temperatures remained within the qualified range, and (iv) the satellite maintained normal attitude control performance in orbit. The case study demonstrates how to optimize the layout design of a flat-panel satellite using the DE algorithm, starting from the given satellite module and component parameters.

The basic parameters of the Longjiang-3 satellite module are shown in

Table 1. Satellite module parameters (unit: m).

No.	Orientation	Endpoint 1	Endpoint 2	Endpoint 3	Endpoint 4
0	front	(0.04, 0.04)	(0.5645, 0.04)	(0.5645, 0.926)	(0.04, 0.926)
1	front	(0.6045, 0.04)	(1.6685, 0.04)	(1.6685, 0.926)	(0.6045, 0.926)
2	front	(1.7085, 0.04)	(2.176, 0.1652)	(2.176, 0.8008)	(1.7085, 0.926)
3	rear	(0.04, 0.04)	(1.6685, 0.04)	(1.6685, 0.926)	(0.04, 0.926)
4	rear	(1.7085, 0.04)	(2.176, 0.1652)	(2.176, 0.8008)	(1.7085, 0.926)

, which includes the module’s number, orientation, and boundary coordinates. The heat pipe parameters are listed separately in

Table 2. Heat pipe parameters (unit: m).

No.	Start Position (x, y)	End Position (x, y)
0	(0.04, 0.1643)	(2.176, 0.1643)
1	(0.04, 0.2903)	(2.176, 0.2903)
2	(0.04, 0.7555)	(2.176, 0.7555)

, showing the starting and ending positions of each heat pipe. The component parameters are shown in

Table 3. Component parameters.

No.	Name	($\mathit{l},\mathit{w},\mathit{h}$)/m	m/kg	P/W
0	Communication Payload 1	(0.4653, 0.432, 0.0475)	10.13	200
1	Communication Payload 2	(0.4653, 0.432, 0.0475)	10.13	200
2	Communication Payload 3	(0.4653, 0.432, 0.0255)	6.03	100
3	Gyroscope 1	(0.23, 0.18, 0.088)	3.5	13
4	Battery	(0.395, 0.257, 0.0774475)	11.29	0
5	RBF Port	(0.1, 0.085, 0.01)	0.03	0
6	Gyroscope 2	(0.0386, 0.0448, 0.0215)	0.055	3
7	GNSS Receiver	(0.23, 0.177, 0.03)	1.2	2
8	OBC	(0.328, 0.34, 0.075)	5.8	6
9	PCDU	(0.4, 0.366, 0.09)	9	36
10	Gyroscope 3	(0.07, 0.07, 0.0498)	0.45	5.5
11	Magnetometer 1	(0.118, 0.038, 0.038)	0.15	1
12	Magnetometer 2	(0.118, 0.038, 0.038)	0.15	0.4
13	Reaction Wheel 1	(0.175, 0.12, 0.19)	2.35	4
14	Reaction Wheel 2	(0.175, 0.12, 0.19)	2.35	4
15	Reaction Wheel 3	(0.175, 0.12, 0.19)	2.35	4
16	Reaction Wheel 4	(0.175, 0.12, 0.19)	2.35	4
17	Data Processing Module	(0.24, 0.1265, 0.1707)	4	50
18	Hall Thruster Main Tank	(0.224, 0.15, 0.189)	6.5	0
19	Hall Thruster Tank 1	(0.15, 0.046, 0.062)	0.5	0
20	Hall Thruster Tank 2	(0.29, 0.05, 0.05)	0.3	0
21	Reception Antenna 1	(0.184, 0.1035, 0.077)	1.1	20
22	Reception Antenna 2	(0.184, 0.1035, 0.077)	1.1	20
23	Transmission Antenna 1	(0.204, 0.1155, 0.0852)	3.7	210
24	Transmission Antenna 2	(0.204, 0.1155, 0.0852)	3.7	210
25	Reception Antenna 3	(0.4865, 0.344, 0.033)	4.5	15
26	SADA Controller	(0.15, 0.12, 0.077)	1	10
27	Communication Payload 4	(0.18, 0.19, 0.03)	0.5	13
28	Reception Antenna 4	(0.194, 0.175, 0.09)	0.5	0
29	Magnetorquer	(0.5, 0.045, 0.043)	1.246	12
30	Camera	(0.2052, 0.09, 0.0873)	1.4	20
31	Hall Thruster PCU	(0.3, 0.22, 0.052)	2.9	64
32	SADA	(0.144, 0.106, 0.0785)	1.43	0

, which includes the component number, name, dimensions, mass, and power. The special component layout constraints are listed in

Table 4. Component layout constraints.

No.	${\mathit{x}}_{\mathit{i}}$/m	${\mathit{y}}_{\mathit{i}}$/m	${\mathit{\theta }}_{\mathit{i}}$/deg	${\mathit{\eta }}_{\mathit{i}}$	Distance/m
0				≤2
1				≤2
2				≤2
3				≤2
4				≤2
5	0.1667635	0.8570355	0	3
6				≤2
7				≤2
8				≤2
9				≤2
10				≤2
11				≤2	>1 with component 13, 14, 15, 16, 29
12				≤2	>1 with component 13, 14, 15, 16, 29
13			45	≤2
14			135	≤2
15			135	≤2
16			45	≤2
18	>1.98		90	2
19	>1.98		90	2
20	>1.98		90	2
21			90	3	>0.8 with component 23, 24
22			90	3	>0.8 with component 23, 24
23			90	3
24			90	3
25			90	3
28				≥3
29			90
30		<0.3	90	≥3
31	>1.5
32	0.9552368	0.865	0	3

.

The RBF port (No. 5) is mechanically constrained by the launch vehicle interface, requiring its position and orientation to be fixed. Flywheels (13–16) must be mounted at specified angles to control angular momentum along all three axes. Propulsion components (18–20) are positioned opposite to the flight direction and must have clear plume paths. Communication antennas (21–25) are phased arrays, so their installation direction is strictly constrained. The magnetometer (29) is oriented according to the required torque vector alignment. The camera (30) is placed at the satellite edge for unobstructed Earth imaging. The Hall Thruster PCU (31) must be near the propulsion system, and SADA (32) is fixed by the solar panel hinge geometry. Components sensitive to magnetic fields (11, 12) are kept away from sources of strong magnetism (13–16, 29). Receive (21, 22) and transmit antennas (23, 24) must be separated to avoid mutual interference. Additionally, some components are required to be internal (${\eta }_i\le 2$), while others are specified to be external (${\eta }_i\ge 3$).

Antennas, particularly phased-array communication antennas (components 21–25), significantly influence layout optimization due to strict directional and positional constraints required to ensure optimal communication coverage and to minimize electromagnetic interference. The layout optimization algorithm explicitly considers these antenna placement constraints and ensures adequate spatial separation between transmitting and receiving antennas to mitigate mutual interference, directly influencing overall layout decisions.

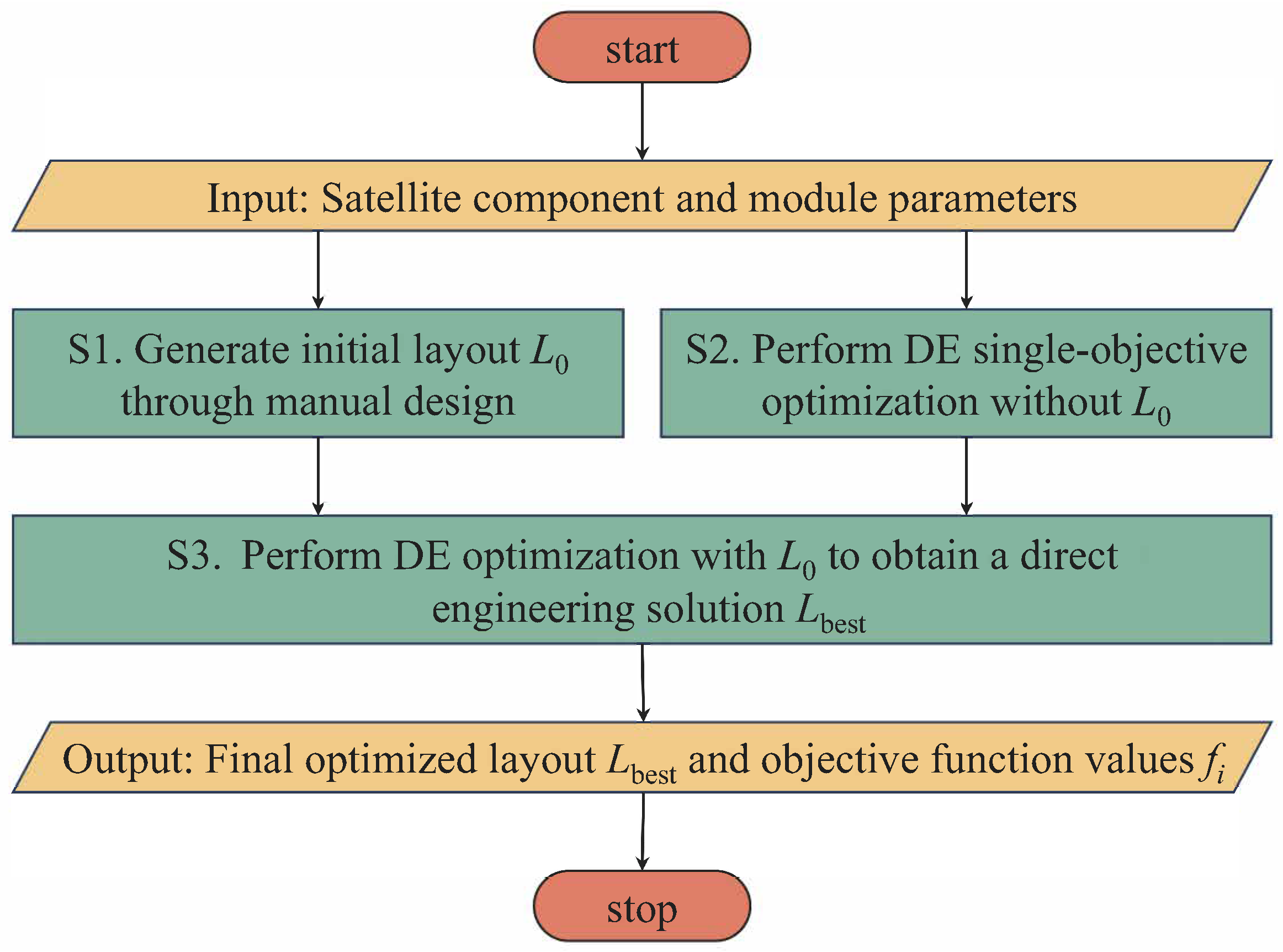
Following the workflow in Figure 4, the algorithm receives the satellite module and component parameters as input. The initial layout $L_0$ is generated manually and shown in

Table 5. Data of initial layout $L_0$.

No.	${\mathit{x}}_{\mathit{i}}$/m	${\mathit{y}}_{\mathit{i}}$/m	${\mathit{\theta }}_{\mathit{i}}$/deg	${\mathit{\eta }}_{\mathit{i}}$	No.	${\mathit{x}}_{\mathit{i}}$/m	${\mathit{y}}_{\mathit{i}}$/m	${\mathit{\theta }}_{\mathit{i}}$/deg	${\mathit{\eta }}_{\mathit{i}}$
1	0.29331	0.26029	0	0	18	1.78755	0.20695	90	2
2	0.99445	0.70281	180	1	19	1.98952	0.3257	90	2
3	0.85505	0.26255	0	1	20	2.064	0.5175	90	2
4	0.16465	0.68194	90	0	21	2.12125	0.43423	90	2
5	0.39086	0.70948	90	0	22	0.1072	0.20783	90	3
6	0.16676	0.85704	0	3	23	0.3172	0.31957	90	3
7	0.64381	0.576	0	1	24	1.28953	0.20657	90	3
8	1.21752	0.22249	90	1	25	1.50903	0.31957	90	3
9	1.47269	0.23	0	1	26	0.93792	0.29728	90	3
10	1.4576	0.74	0	1	27	0.84196	0.72244	90	3
11	0.6988	0.6236	0	1	28	1.01309	0.70038	90	3
12	0.63552	0.78006	90	1	29	1.24222	0.72035	0	3
13	0.67722	0.78354	90	1	30	1.772	0.33843	90	4
14	1.81888	0.44036	45	2	31	1.84859	0.26198	90	4
15	1.88252	0.63633	135	2	32	2.008	0.318	90	4
16	1.98723	0.74104	135	2	33	0.95524	0.865	0	3
17	1.81645	0.78448	45	2

. Figure 5 shows the 2D initial layout and Figure 6 provides a 3D visualization.

By substituting the initial layout design $L_0$, the corresponding objective function values are calculated, as shown in

Table 6. Optimization parameters during the process.

Objective Function	${\mathit{f}}_{\mathbf{manual},\mathit{i}}$	${\mathit{f}}_{\mathbf{optimal},\mathit{i}}$	${\mathit{w}}_{\mathit{i}}$
$f_1\left(L\right)$	59.6668	32.4374	0.3
$f_2\left(L\right)$	0.3542	0.3417	0.4
$f_3\left(L\right)$	16.5	0	0.1
$f_4\left(L\right)$	264.7545	16.91	0.1
$f_5\left(L\right)$	92.8986	77.4867	0.1

. To verify the optimization results, each objective function $f_1\left(L\right)$ to $f_5\left(L\right)$ is optimized as a single objective using the DE algorithm without substituting $L_0$. The population size and iteration parameters of DE are as follows

$$N_p=100,max\_iter=10000,n\_rounds=3$$

(24)

where $N_p$ is the population size, representing the number of individuals (solutions) in each generation; max_iter is the maximum number of iterations per round; and n_rounds is the total number of iterations for the entire DE process. These configurations ensure a comprehensive search of the solution space and establish theoretical benchmarks for the subsequent phases. The optimization results are shown in Table 6. The weights for each objective were determined in consultation with the satellite engineering team, based on the specific mission requirements and priorities of the Longjiang-3 project. The selection reflects practical engineering considerations, such as the relative importance of mass properties, thermal uniformity, and layout compactness for this mission.

Based on the parameters derived from Table 6, the initial layout $L_0$ is substituted and optimized using the following population size and iteration parameters to obtain an engineering-feasible local optimum:

$$N_p=100,max\_iter=5000,n\_rounds=5$$

(25)

The population size is fixed at $N_p=100$ because trial runs showed stable convergence when $80\le N_p\le 120$; larger populations increase runtime with negligible benefit. The global search phase requires max_iter = 10000 to adequately explore the full design space, whereas the subsequent normalization/local phases operate in a reduced space and therefore use max_iter = 5000 without loss of solution quality. For the number of optimization rounds, we use $n_{\mathrm{round}}=5$ in the global phase to ensure robustness against premature convergence, while the later phases use $n_{\mathrm{round}}=3$; additional rounds beyond 3 in the local space showed no appreciable improvement but did extend runtime.

The computational complexity of the proposed DE-based layout optimization algorithm primarily depends on population size ($N_p$), iteration count (max_iter), and the computational cost of evaluating each candidate solution (including interference checking and thermal distribution calculations). On a desktop workstation equipped with an Intel i5-12600 CPU and 64 GB RAM, a full optimization run (encompassing global exploration and local refinement phases) typically completes in approximately 6300 s (about 1 h 45 min). Stable convergence behavior was consistently observed within approximately 3000–5000 generations, with minimal further improvement beyond this point.

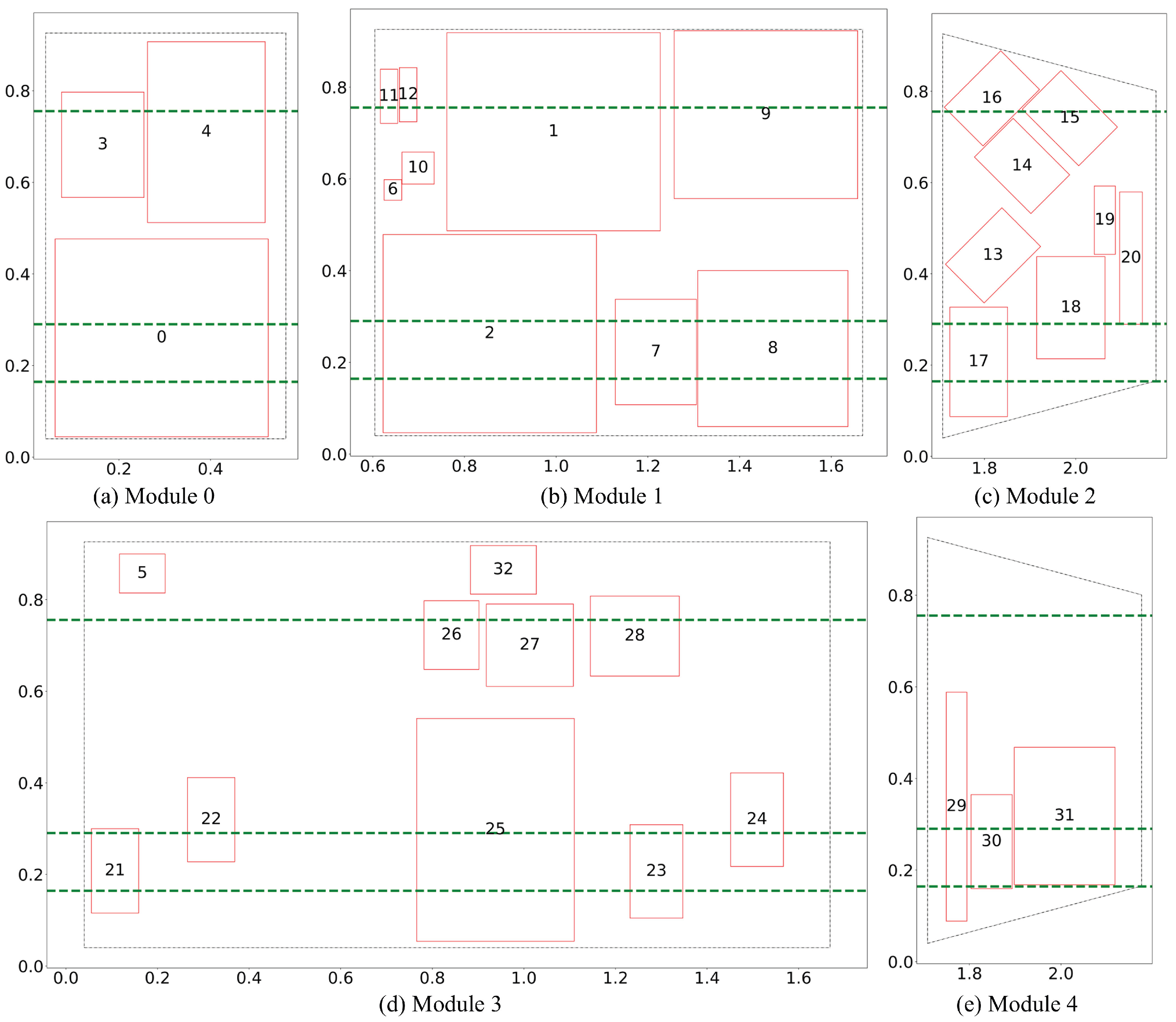
These settings emphasize local optimization and rapid convergence, ensuring the final solution is practically feasible. Through this optimization process, the local optimum $L_{\mathrm{best}}$ is obtained. The layout of the optimization result $L_{\mathrm{best}}$ is shown in

Table 7. Data of optimized layout $L_{\mathrm{best}}$.

No.	${\mathit{x}}_{\mathit{i}}$/m	${\mathit{y}}_{\mathit{i}}$/m	${\mathit{\theta }}_{\mathit{i}}$/deg	${\mathit{\eta }}_{\mathit{i}}$	No.	${\mathit{x}}_{\mathit{i}}$/m	${\mathit{y}}_{\mathit{i}}$/m	${\mathit{\theta }}_{\mathit{i}}$/deg	${\mathit{\eta }}_{\mathit{i}}$
1	0.33154	0.27525	0	0	18	1.83050	0.21602	1.66338	2
2	0.98180	0.69824	0.10463	1	19	2.08058	0.32570	90	2
3	0.86858	0.26426	0	0	20	2.02962	0.51750	90	2
4	0.21464	0.64028	90.29319	0	21	1.98042	0.43423	90	2
5	0.43559	0.68969	90.06927	0	22	0.21567	0.31375	90	3
6	0.16676	0.85704	0	3	23	0.48326	0.19134	90	3
7	1.40761	0.49436	0	1	24	1.52502	0.18800	90	3
8	1.19156	0.36674	89.97112	1	25	1.28913	0.31788	90	3
9	1.44655	0.29929	0	0	26	0.87016	0.53795	90	3
10	1.41622	0.70000	0	1	27	1.31220	0.68927	75.60221	3
11	0.71055	0.73427	0	1	28	0.56741	0.63594	34.95808	3
12	0.63224	0.78596	85.66058	0	29	1.17374	0.52486	0	2
13	0.63235	0.56561	92.29252	0	30	1.63715	0.55847	90	3
14	1.81338	0.38517	45	2	31	1.08768	0.17440	132.30505	3
15	1.81306	0.65196	135	2	32	1.95864	0.58831	74.28278	4
16	1.85758	0.77800	135	2	33	0.95524	0.87000	0	3
17	1.98589	0.69003	45	2

and Figure 7. The optimized result $L_{\mathrm{best}}$ is compared with the initial value $L_0$, as shown in

Table 8. Comparison of optimized layout and initial layout.

Layout Scheme	${\mathit{f}}_1\left(\mathit{L}\right)$	${\mathit{f}}_2\left(\mathit{L}\right)$	${\mathit{f}}_3\left(\mathit{L}\right)$	${\mathit{f}}_4\left(\mathit{L}\right)$	${\mathit{f}}_5\left(\mathit{L}\right)$	${\mathit{F}}_{\mathbf{total}}$
Initial Layout $L_0$	59.6668	0.3542	16.5	264.7545	92.8986	1.3006
Optimized Layout $L_{\mathrm{best}}$	55.7129	0.3417	3.4	94.4319	77.7079	0.9624

. It can be seen that the optimized layout $L_{\mathrm{best}}$ outperforms the initial layout $L_0$ in each objective function and meets the engineering feasibility requirements.

We conducted a comprehensive sensitivity analysis to systematically evaluate the influence of the mutation factor ($F_m$), crossover probability ($P_c$), and randomness factor ($r_m$) on the optimization outcomes. The sensitivity analysis examined multiple parameter combinations across practical ranges commonly adopted in DE-based optimization problems. The complete results of the sensitivity analysis are summarized in

Table 9. Sensitivity analysis of DE parameters.

${\mathit{F}}_{\mathit{m}}$	${\mathit{P}}_{\mathit{c}}$	${\mathit{r}}_{\mathit{m}}$	best_Y	${\mathit{f}}_1\left(\mathit{L}\right)$	${\mathit{f}}_2\left(\mathit{L}\right)$	${\mathit{f}}_3\left(\mathit{L}\right)$	${\mathit{f}}_4\left(\mathit{L}\right)$	${\mathit{f}}_5\left(\mathit{L}\right)$
0.3	0.5	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.3	0.5	0.1	1.2344	58.4470	0.3417	16.5	161.9828	124.2249
0.3	0.5	0.2	1.1758	58.3809	0.3417	12.0	160.5275	122.0665
0.3	0.7	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.3	0.7	0.1	1.3882	59.1133	0.3542	28.5	159.1797	117.0966
0.3	0.7	0.2	1.1777	59.9043	0.3542	13.9	160.7572	83.1266
0.3	0.9	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.3	0.9	0.1	1.2983	61.1751	0.3542	23.4	156.7760	83.1666
0.3	0.9	0.2	no solution	62.3871	0.3542	14.5	166.5350	90.1503
0.5	0.5	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.5	0.5	0.1	1.2248	59.5615	0.3542	16.5	119.5593	123.2392
0.5	0.5	0.2	no solution	63.0504	0.3417	146.9	206.3498	127.7757
0.5	0.7	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.5	0.7	0.1	0.9552	55.7129	0.3417	3.4	94.4319	77.7079
0.5	0.7	0.2	no solution	62.7014	0.4707	152.9	126.0793	104.6938
0.5	0.9	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.5	0.9	0.1	1.2492	59.3403	0.3542	16.5	161.9828	119.6242
0.5	0.9	0.2	1.3973	59.0810	0.3542	28.9	160.5352	120.0429
0.7	0.5	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.7	0.5	0.1	1.3627	62.2882	0.3542	24.4	157.2473	121.2320
0.7	0.5	0.2	no solution	62.9641	0.3417	106.9	231.0368	133.3805
0.7	0.7	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.7	0.7	0.1	1.2315	59.8255	0.3542	16.9	119.4469	123.4676
0.7	0.7	0.2	no solution	64.3975	0.3417	46.9	250.6383	86.1129
0.7	0.9	0	1.4155	64.8678	0.3542	29.9	160.8775	92.8986
0.7	0.9	0.1	1.2498	59.5073	0.3542	16.5	161.9828	119.2172
0.7	0.9	0.2	1.1665	59.3614	0.3417	10.5	162.0075	123.2483

. The analysis clearly demonstrates that the parameter set ($F_m=0.5,P_c=0.7,r_m=0.1$) achieves the optimal performance, delivering the lowest objective function value (best_Y = 0.9552). Accordingly, this parameter combination was adopted for subsequent optimization analyses throughout the manuscript.

As shown in Table 8, the optimized layout outperforms the initial layout in each objective function, with moderate adjustments compared to the manual layout.

Additionally, as shown in

Table 10. Temperature comparison between initial manual layout (simulation) and optimized layout (in orbit).

No.	Name	Initial Layout (Simulation, °C)	Optimized Layout (In Orbit, °C)	Safety Threshold (°C)
0	Communication Payload 1	$-0.7$ to $27.3$	$0.2$ to $26.2$	$-15$ to $+45$
1	Communication Payload 2	$-4.9$ to 23	$-2.1$ to $12.9$	$-15$ to $+45$
2	Communication Payload 3	$-5$ to $22.3$	$-3.3$ to 12	$-15$ to $+45$
3	Gyroscope 1	2 to 28	$18.5$ to $20.4$	$-20$ to $+45$
4	Battery	15 to $26.6$	$15.1$ to $15.6$	$+10$ to $+30$
6	Gyroscope 2	$0.1$ to $26.3$	$7.6$ to $11.4$	$-15$ to $+50$
8	OBC	$-4.7$ to $22.2$	$12.4$ to $16.6$	$-20$ to $+50$
9	PCDU	$0.1$ to $26.7$	22 to $25.1$	$-15$ to $+45$
11	Magnetometer 1	$-1.2$ to $24.1$	$12.6$ to $14.5$	$-10$ to $+50$
13	Reaction Wheel 1	$7.3$ to $29.2$	$11.2$ to $12.7$	$-15$ to $+45$
14	Reaction Wheel 2	$7.8$ to $28.6$	$15.7$ to $22.1$	$-20$ to $+50$
15	Reaction Wheel 3	$8.9$ to $30.5$	12 to $15.1$	$-20$ to $+50$
16	Reaction Wheel 4	4 to $25.7$	$7.2$ to $20.61$	$-20$ to $+50$
21	Reception Antenna 1	$-5$ to 23	$-4.5$ to $14.5$	$-20$ to $+45$
22	Reception Antenna 2	$-5$ to $22.8$	$-2.1$ to $15.2$	$-20$ to $+45$
23	Transmission Antenna 1	$-5.6$ to $28.3$	$-1.4$ to $37.3$	$-20$ to $+45$
24	Transmission Antenna 2	$-5.7$ to $28.7$	$-2.9$ to $13.2$	$-20$ to $+45$
25	Reception Antenna 3	$-5$ to $22.3$	$-2.3$ to $14.5$	$-15$ to $+45$
26	SADA Controller	$-0.4$ to $26.3$	$11.7$ to $16.1$	$-15$ to $+45$
29	Magnetorquer	$-7.4$ to $13.1$	$6.7$ to $11.4$	$-20$ to $+55$
32	SADA	$8.2$ to $38.4$	7 to $16.6$	$-15$ to $+50$

, the satellite’s in-orbit temperature data meet the threshold requirements, with Transmission Antenna 1 and Transmission Antenna 2 successfully undergoing high-power validation in orbit. The comparison shows that after layout optimization, the satellite’s in-orbit temperature distribution is more uniform than with the initial manual layout, supporting the validity of the thermal objectives in the optimization model.

Based on the evaluation metrics and in-orbit test results, it can be concluded that the method proposed in this paper has successfully provided a direct engineering solution.

5. Conclusions

In this paper, the flat-panel satellite layout optimization problem is carefully proposed, studied, and solved by a novel DE-based algorithm with local optima strategy. More specifically, the proposed algorithm takes the engineering realities of flat-panel satellite design into account, focusing on local optima to avoid excessive deviations from manual designs. Based on the engineering case study, we conclude that the proposed method improves design quality by optimizing mass properties, thermal characteristics, and layout efficiency while preserving the initial design’s feasibility. The design and in-orbit results show that the proposed approach effectively meets practical engineering constraints, demonstrating improved engineering applicability through the Longjiang-3 case study. We acknowledge that the current study lacks direct benchmarking comparisons with other published optimization methods. Future research will include comprehensive comparative validation against existing algorithms, specifically evaluating metrics such as runtime efficiency, constraint handling capability, and solution quality across multiple test cases. Currently, the presented optimization method does not include a dedicated graphical user interface or direct integration with existing CAD/CAE software, limiting its immediate practical application in iterative industrial design workflows. Future work will focus on developing software interfaces and integrating the optimization algorithm into mainstream CAD/CAE systems, enabling streamlined iterative design processes and broader industrial applicability. Additionally, more detailed engineering cases involving diverse satellite types, mission profiles, and comprehensive subsystem integration—including a broader and deeper consideration of communication payloads and antennas—are essential to thoroughly validate and extend the practical effectiveness of this optimization method.