Enhanced Conjunction Assessment in LEO: A Hybrid Monte Carlo and Spline-Based Method Using TLE Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Probabilistic Conjunction Screening Using Monte Carlo Simulation
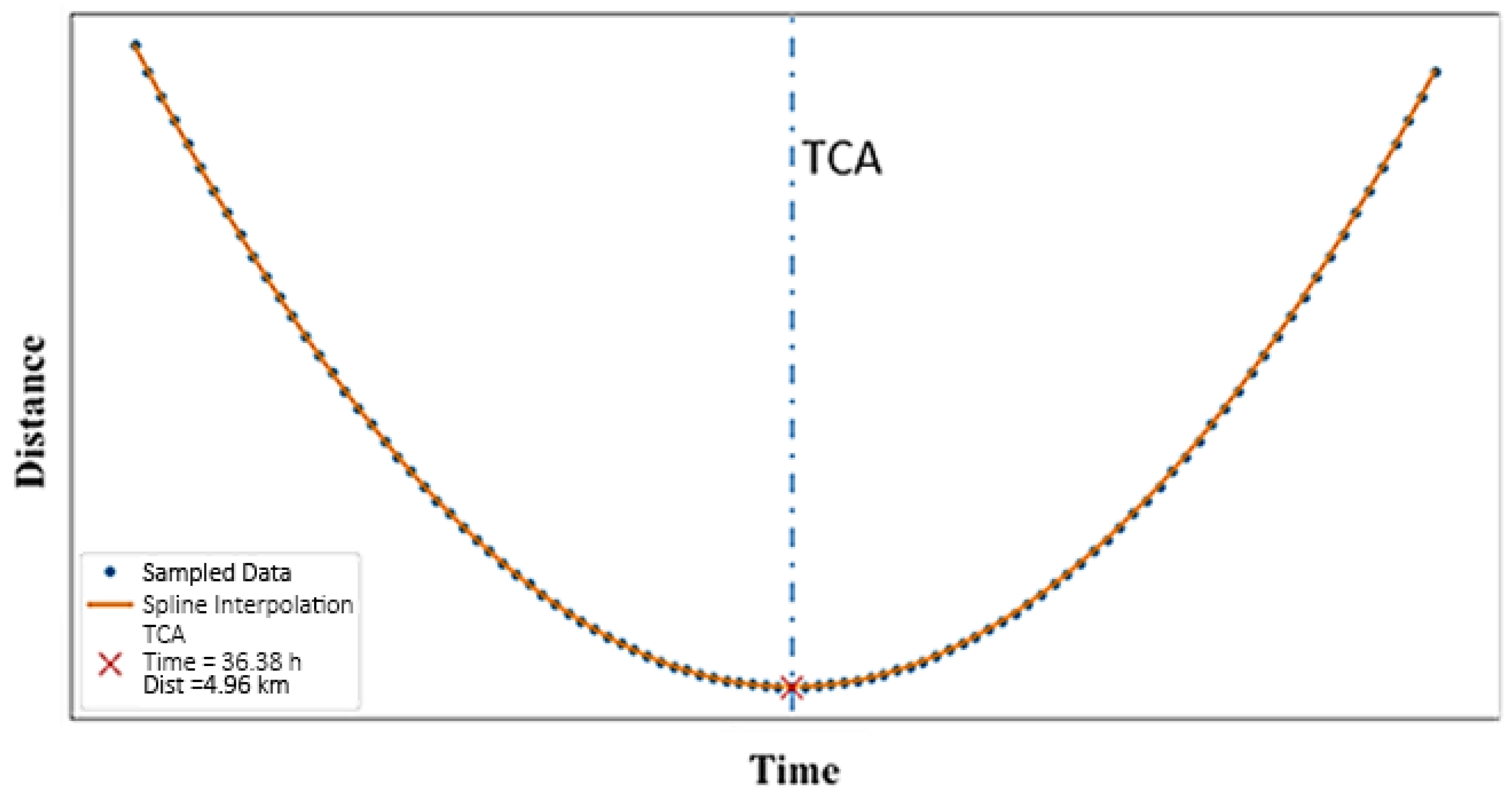
2.2. Spline-Based Deterministic Refinement of TCA
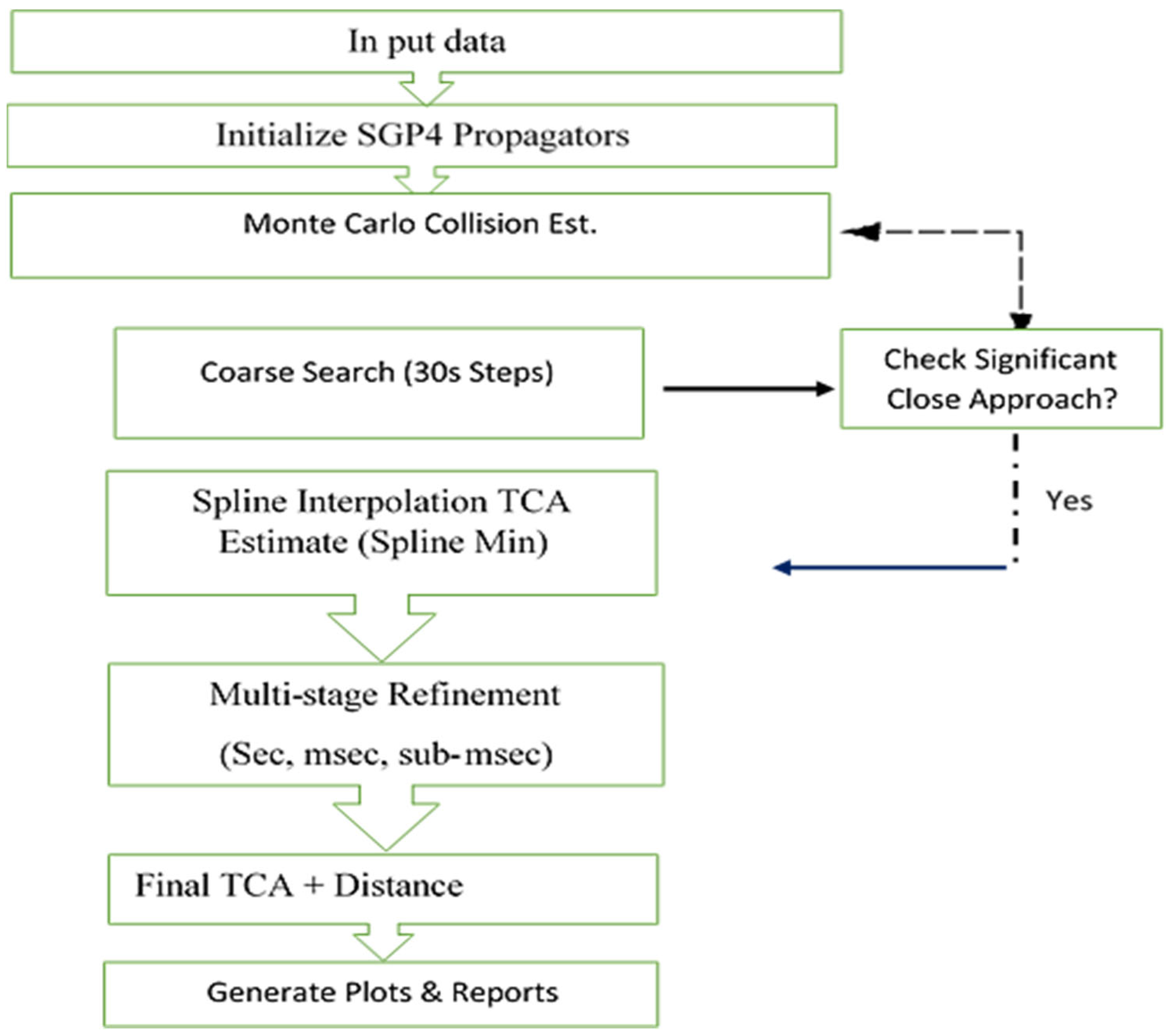
2.3. Multi-Stage Hierarchical Temporal Refinement
2.4. Collision Probability Estimation Model
3. Physical Characterization and Results
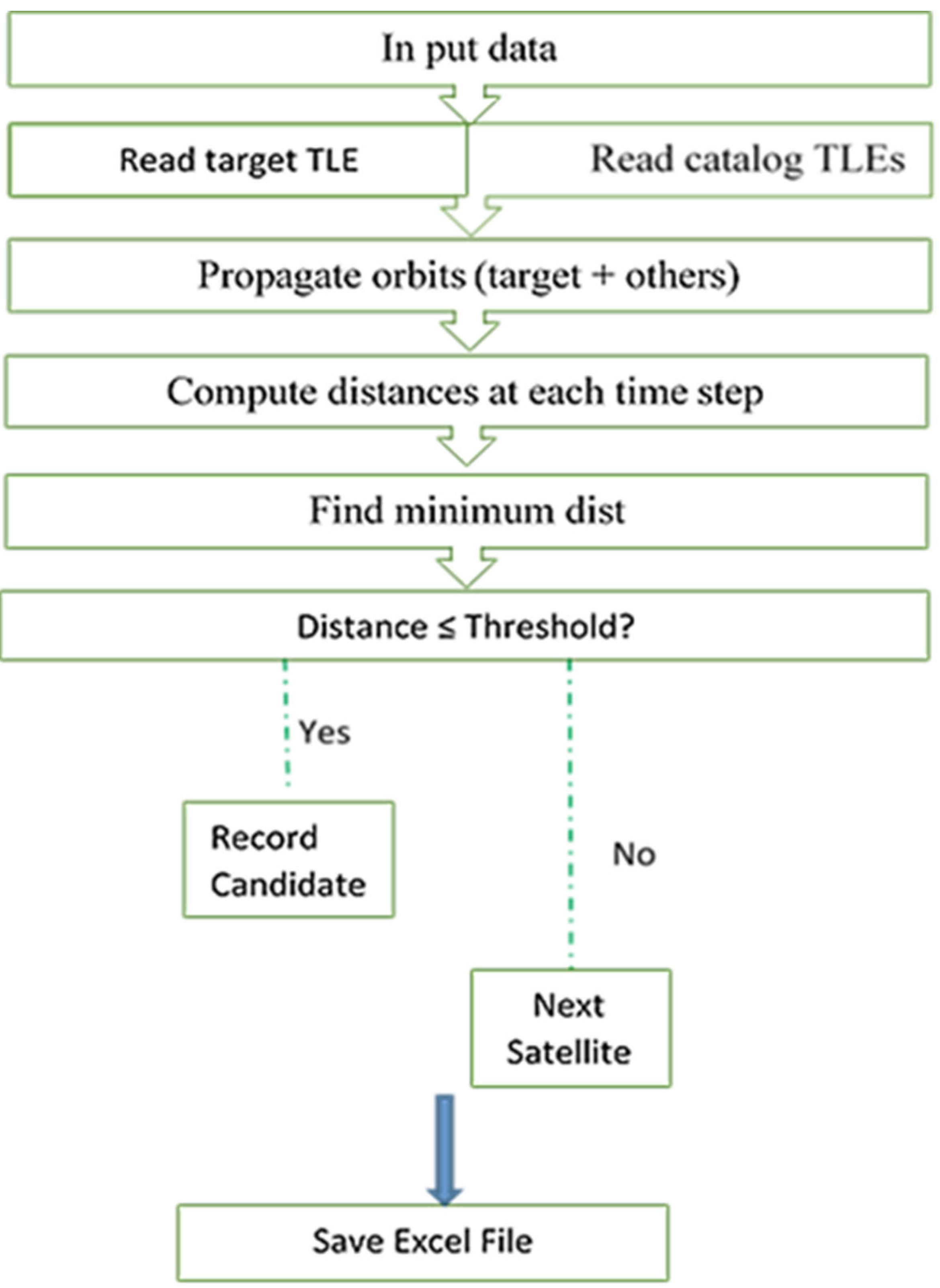
3.1. Initial Conjunction Screening Algorithm
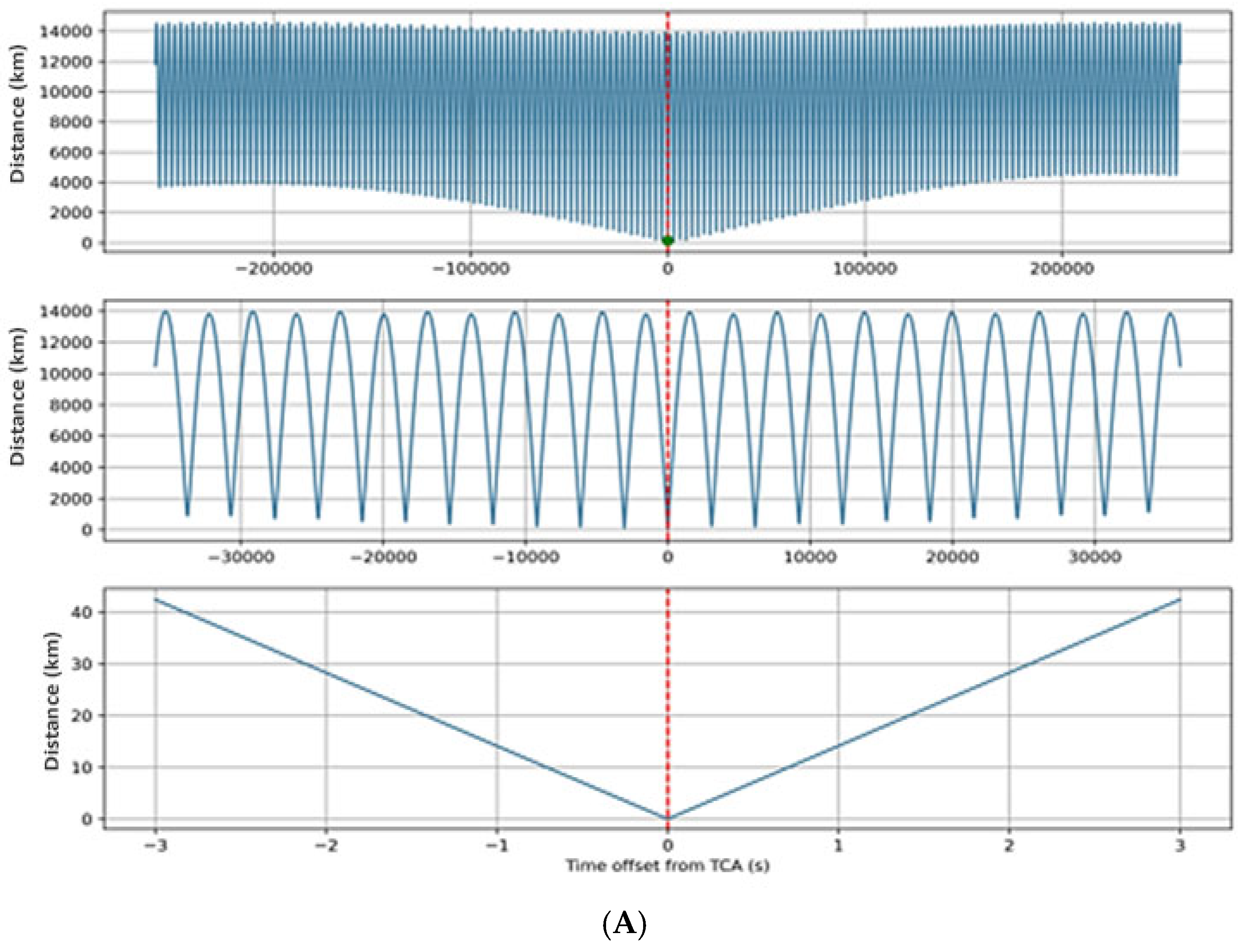
3.2. Case Study Results and Relative Motion Analysis
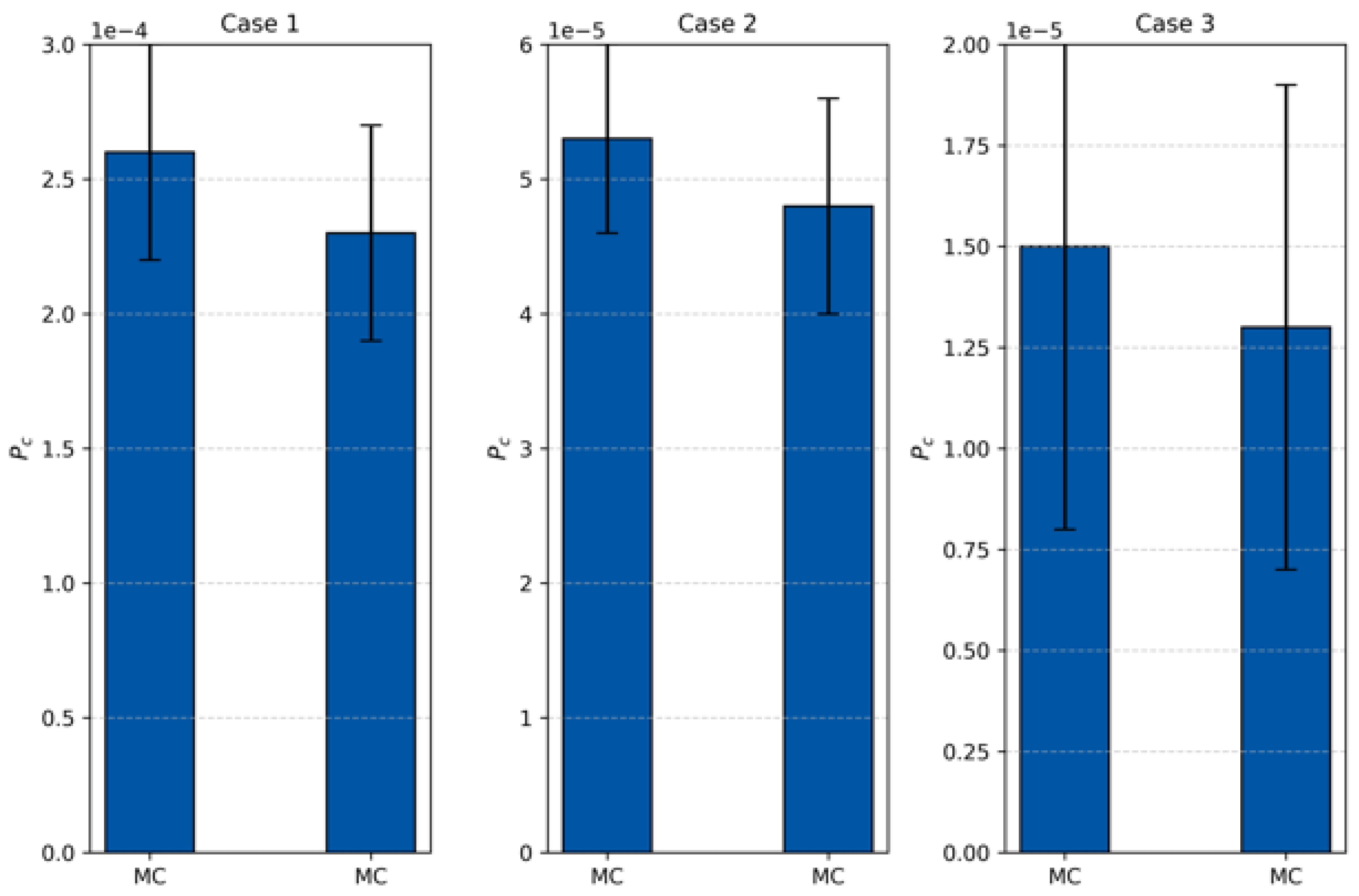
3.3. Collision Probability Estimation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LEO | Low Earth Orbit |
| TLE | Two-Line Element |
| TCA | Time of Closest Approach |
| SGP4 | Simplified General Perturbations Model 4 |
| SSA | Space Situational Awareness |
| SSO | Sun-Synchronous Orbit |
| Probability Density Function | |
| RTN | Radial–Transverse–Normal |
| ROI | Region of Interest |
| ECI | Earth-Centered Inertial |
| DAMC | Differential Algebra Monte Carlo |
| ICRE | Improved Critical Region Estimation |
| MC | Monte Carlo |
References
- Healy, L.M. Close conjunction detection on parallel computer. J. Guid. Control Dyn. 1995, 18, 824–829. [Google Scholar] [CrossRef]
- Letizia, F.; Virgili, B.B.; Lemmens, S. Assessment of orbital capacity thresholds through long-term simulations of the debris environment. Adv. Space Res. 2023, 72, 2552–2569. [Google Scholar] [CrossRef]
- Berger, T.E.; Dominique, M.; Lucas, G.; Pilinski, M.; Ray, V.; Sewell, R.; Sutton, E.K.; Thayer, J.P.; Thiemann, E. The thermosphere is a drag: The 2022 Starlink incident and the threat of geomagnetic storms to low earth orbit space operations. Space Weather 2023, 21, e2022SW003330. [Google Scholar] [CrossRef]
- Kelso, T.S. “Satellite Catalog (SATCAT).” CelesTrak SATCAT Boxscore. Available online: https://celestrak.org/NORAD/documentation/gp-data-formats.php (accessed on 24 May 2025).
- Kessler, D.J.; Cour-Palais, B.G. Collision frequency of artificial satellites: The creation of a debris belt. J. Geophys. Res. Space Phys. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Abdelaziz, A.M.; Molotov, I.E.; Tealib, S.K. Accurate High-Altitude Orbit Determination Method using Electro-Optical Sensors. Int. J. Math. Phys. 2023, 14, 64–76. [Google Scholar] [CrossRef]
- Crawford, D.P.; Vallado, M.D.; Hujsak, D.R.; Kelso, D.T. International best practice for using two line element sets. In Proceedings of the 57th International Astronautical Congress, Valencia, Spain, 2–6 October 2006. [Google Scholar] [CrossRef]
- Liu, W.; Wang, R.; Liu, S.; Shi, L.; Gong, J. TLE Prediction Accuracy Improvement and its Application in Collision Warning. Chin. J. Space Sci. 2014, 34, 449. [Google Scholar] [CrossRef]
- Alfano, S. Relating position uncertainty to maximum conjunction probability. J. Astronaut. Sci. 2005, 53, 193–205. [Google Scholar] [CrossRef]
- Xu, X.-L.; Xiong, Y.-Q. Study on the Orbit Prediction Errors of Space Objects Based on Historical TLE Data. Chin. Astron. Astrophys. 2019, 43, 563–578. [Google Scholar] [CrossRef]
- Hoots, F.R.; Schumacher, P.W., Jr.; PWGlover, R.A. History of analytical orbit modeling in the US space surveillance system. J. Guid. Control. Dyn. 2004, 27, 174–185. [Google Scholar] [CrossRef]
- Morselli, A.; Armellin, R.; Di Lizia PZazzera, F.B. A high order method for orbital conjunctions analysis: Monte Carlo collision probability computation. Adv. Space Res. 2015, 55, 311–333. [Google Scholar] [CrossRef]
- Akella, M.R.; Alfriend, K.T. Probability of collision between space objects. J. Guid. Control Dyn. 2000, 23, 769–772. [Google Scholar] [CrossRef]
- Vallado, D.A. Fundamentals of Astrodynamics and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ghosh, D.; Sabel, M. Spline-based models for predictiveness curves and surfaces. Stat. Its Interface 2010, 3, 445. [Google Scholar] [CrossRef] [PubMed]
- Coffee, B.; Bishop, R.; Cahoy, K. Propagation of CubeSats in LEO using NORAD two line element sets: Accuracy and update frequency. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013; p. 4944. [Google Scholar] [CrossRef]
- Yang, W.Y.; Cao, W.; Kim, J.; Park, K.W.; Park, H.H.; Joung, J.; Ro, J.S.; Lee, H.L.; Hong, C.H.; Im, T. Applied Numerical Methods Using MATLAB; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Li, J.S.; Yang, Z.; Luo, Y.Z. A review of space-object collision probability computation methods. Astrodynamics 2022, 6, 95–120. [Google Scholar] [CrossRef]
- Changé, P.; Mertz, C. Monte Carlo sampling based imminent collision detection algorithm. In Proceedings of the 2017 4th International Conference on Transportation Information and Safety (ICTIS), Banff, AB, Canada, 8–10 August 2017; pp. 368–376. [Google Scholar] [CrossRef]
- Armellin, R.; Di Lizia, P.; Bernelli-Zazzera, F.; Berz, M. Asteroid close encounters characterization using differential algebra: The case of Apophis. Celest. Mech. Dyn. Astronomy 2010, 107, 451–470. [Google Scholar] [CrossRef]
- Swierczewski, C.; Verdier, O. pychebfun-Python Chebyshev Functions. GitHub Repository. 2024. Available online: https://github.com/pychebfun/pychebfun (accessed on 15 March 2025).


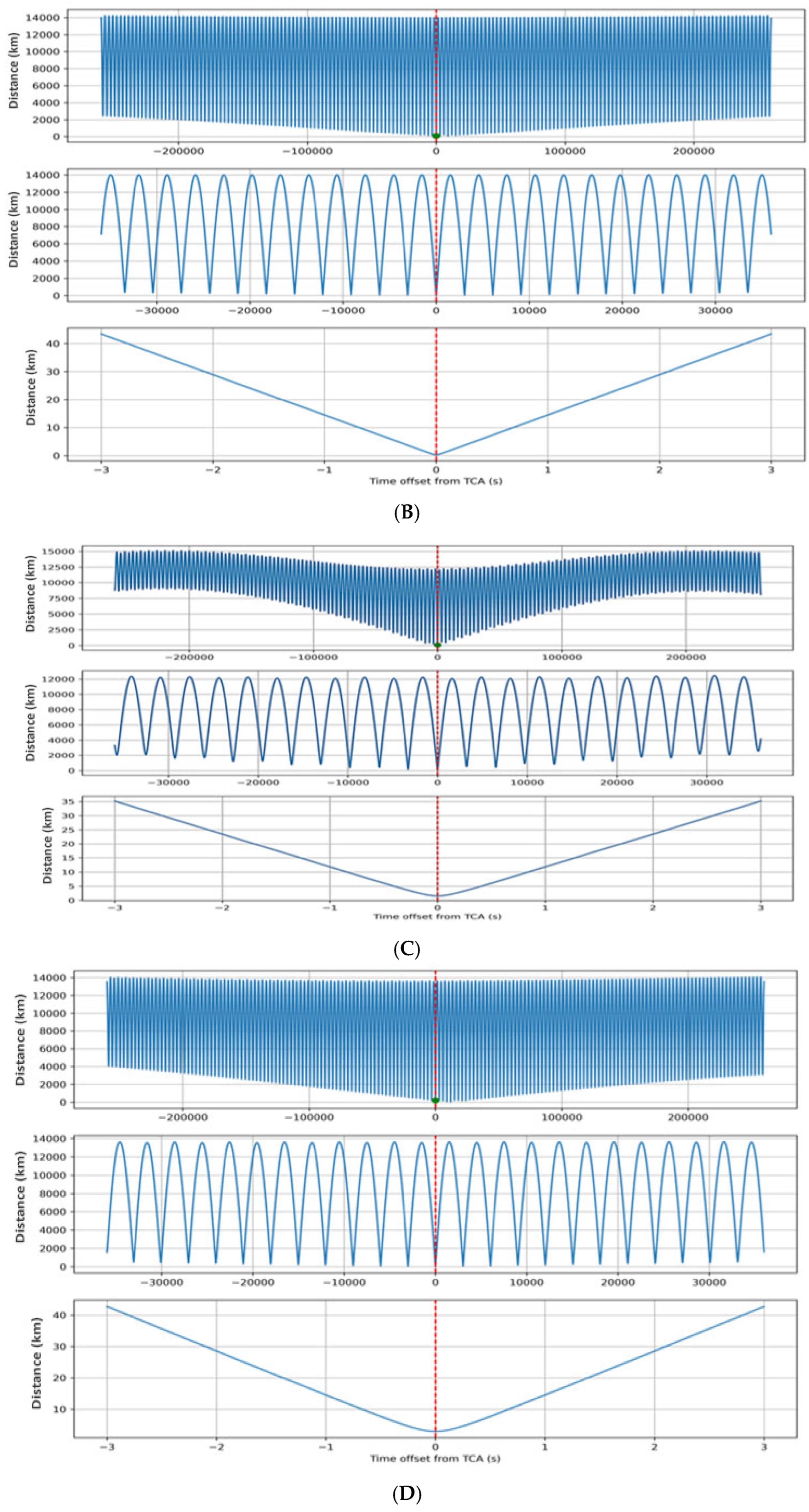
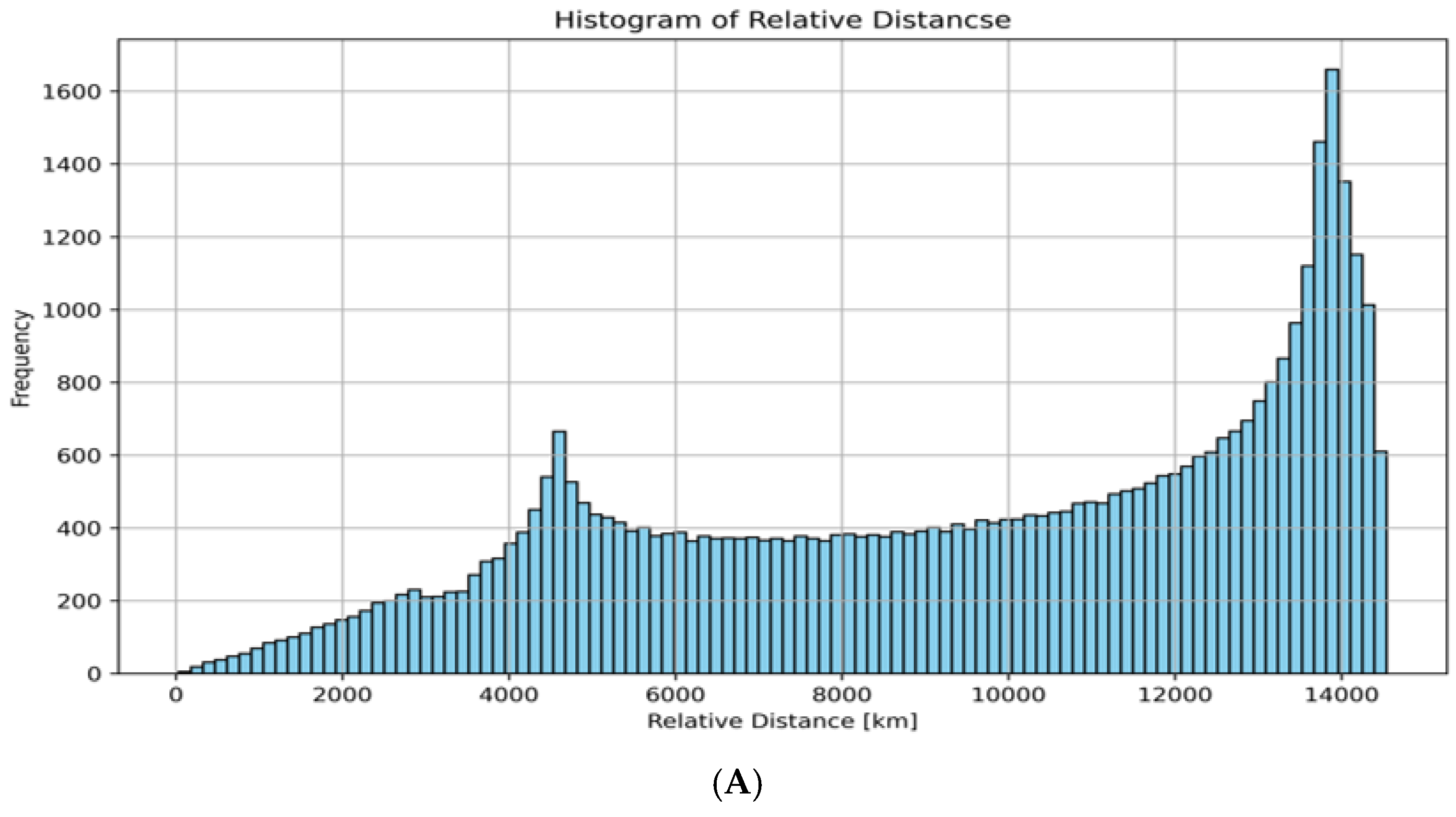
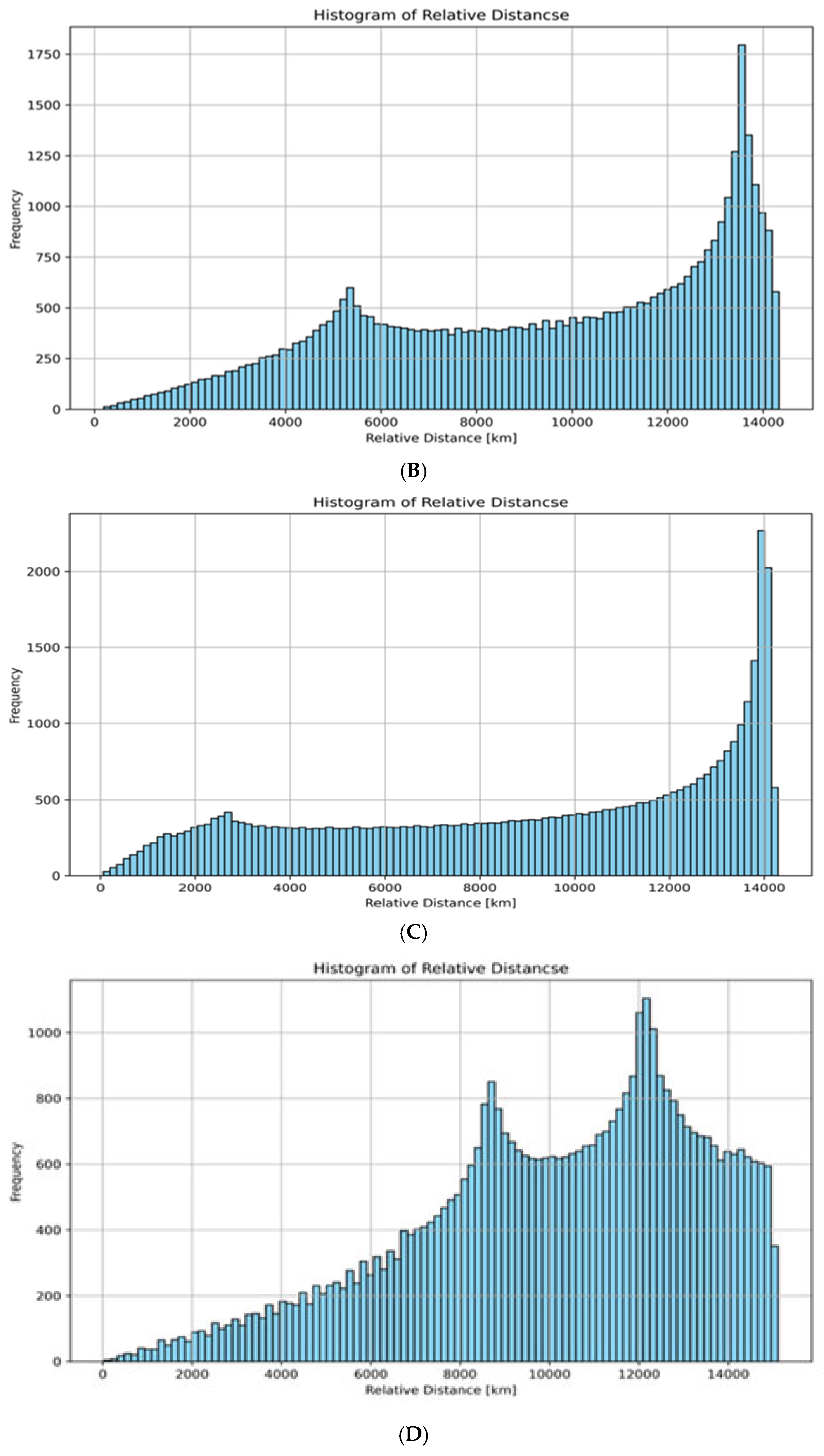
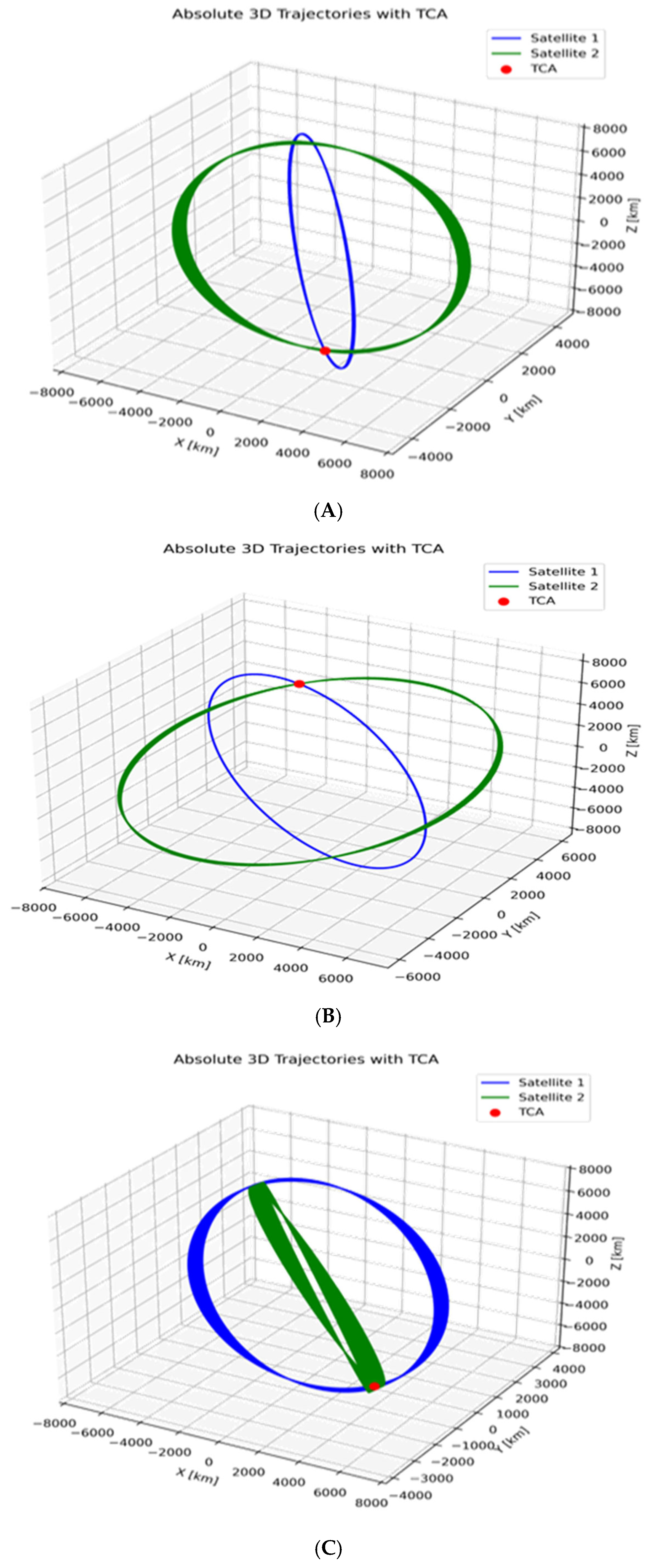
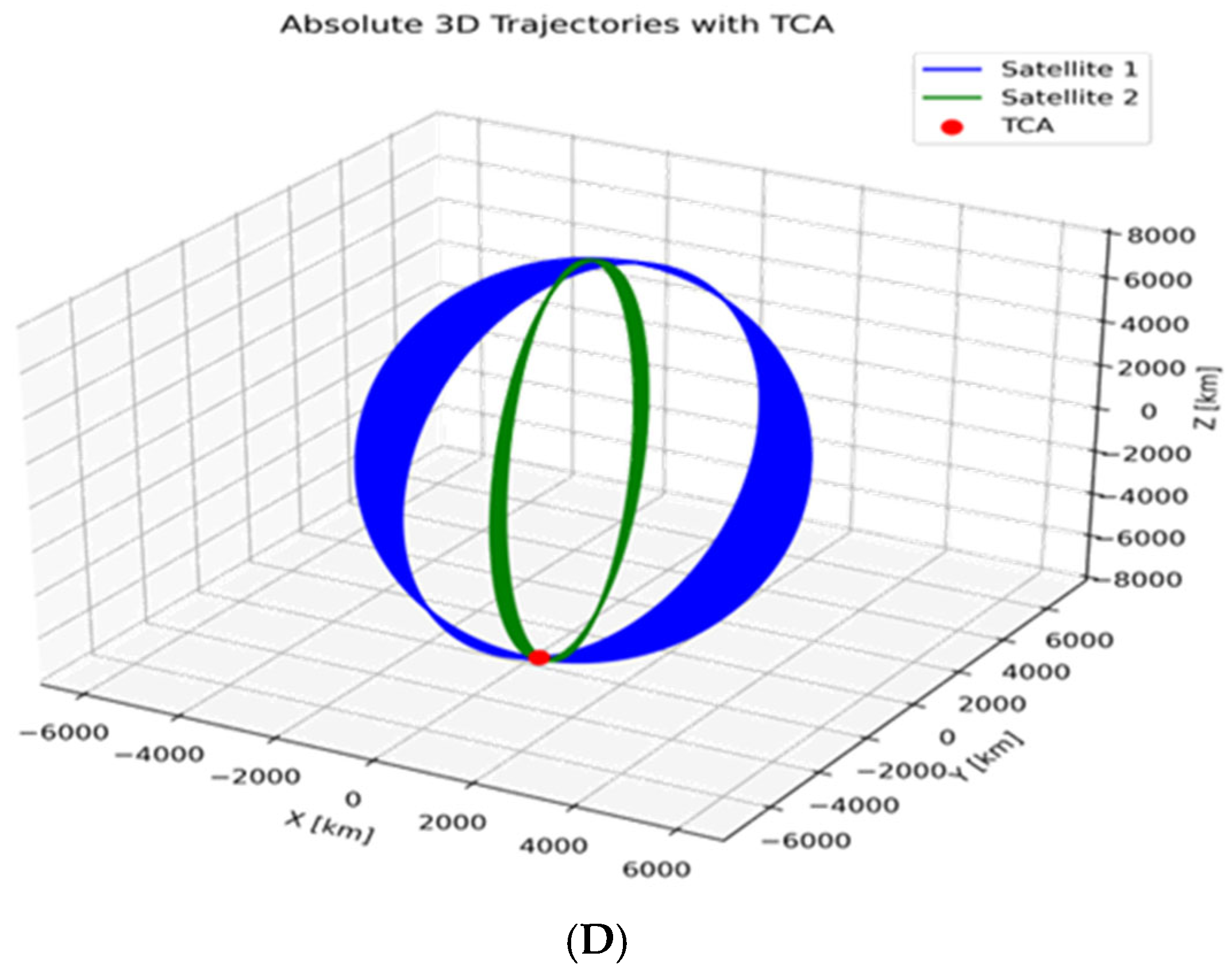
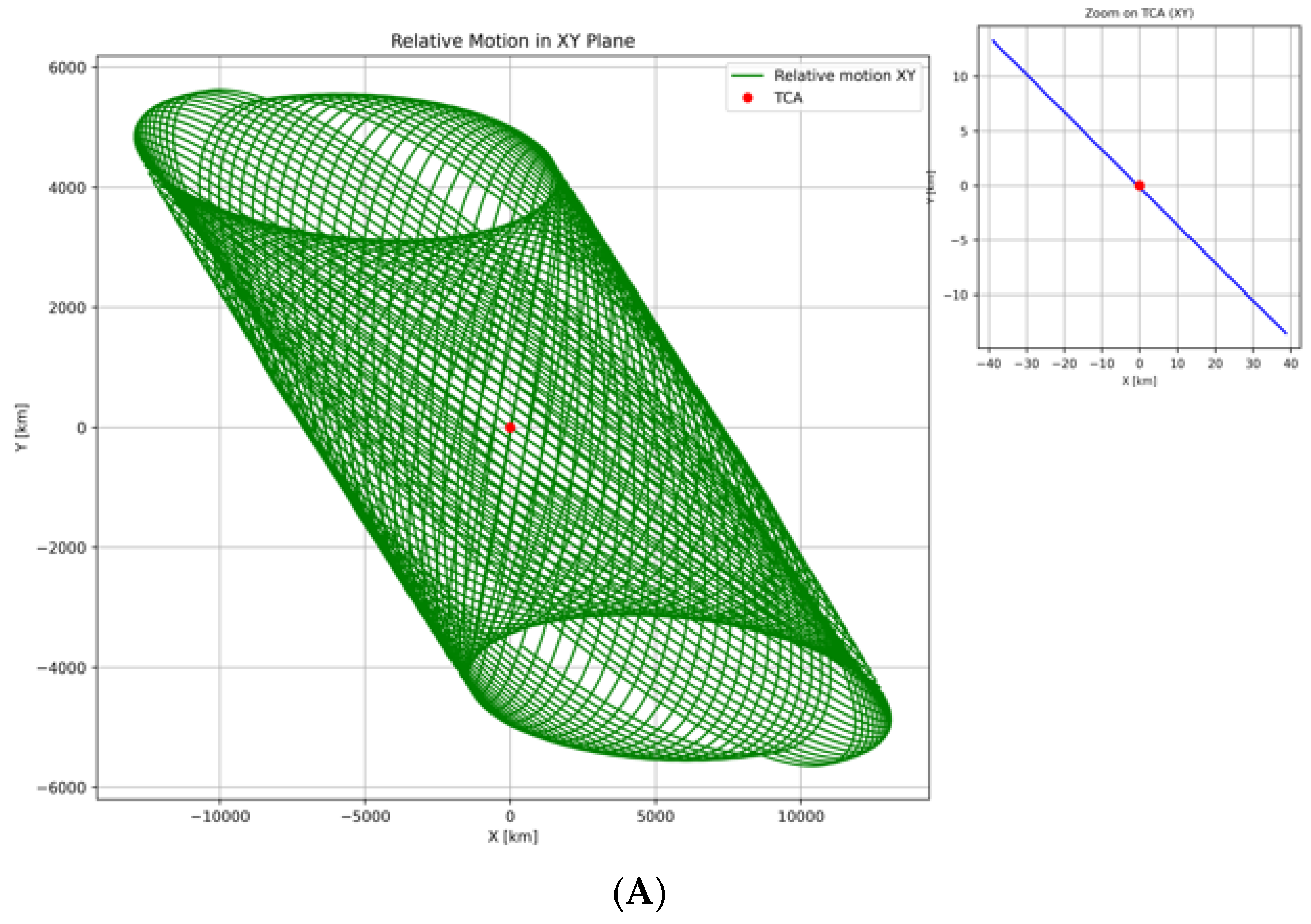
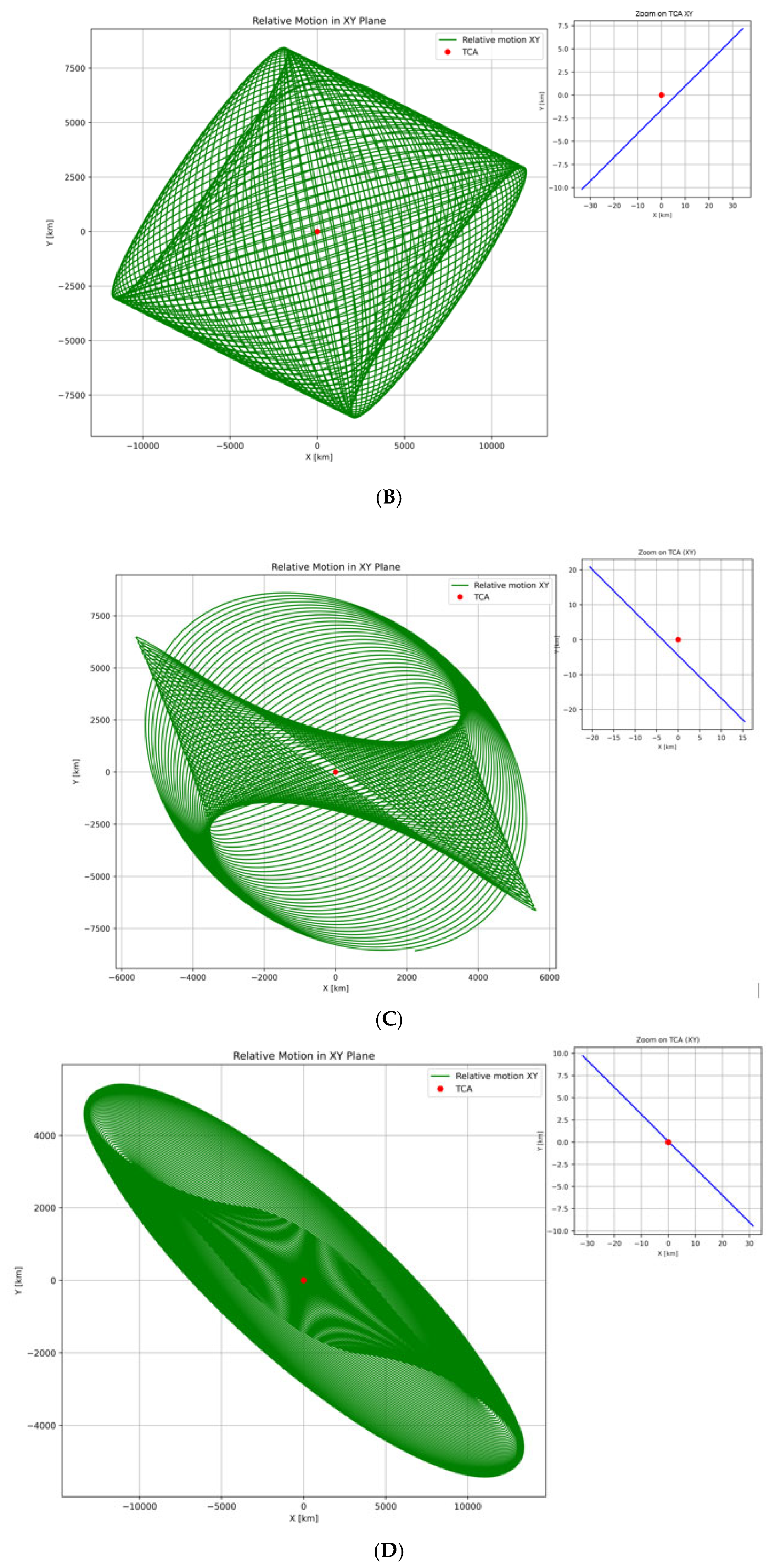
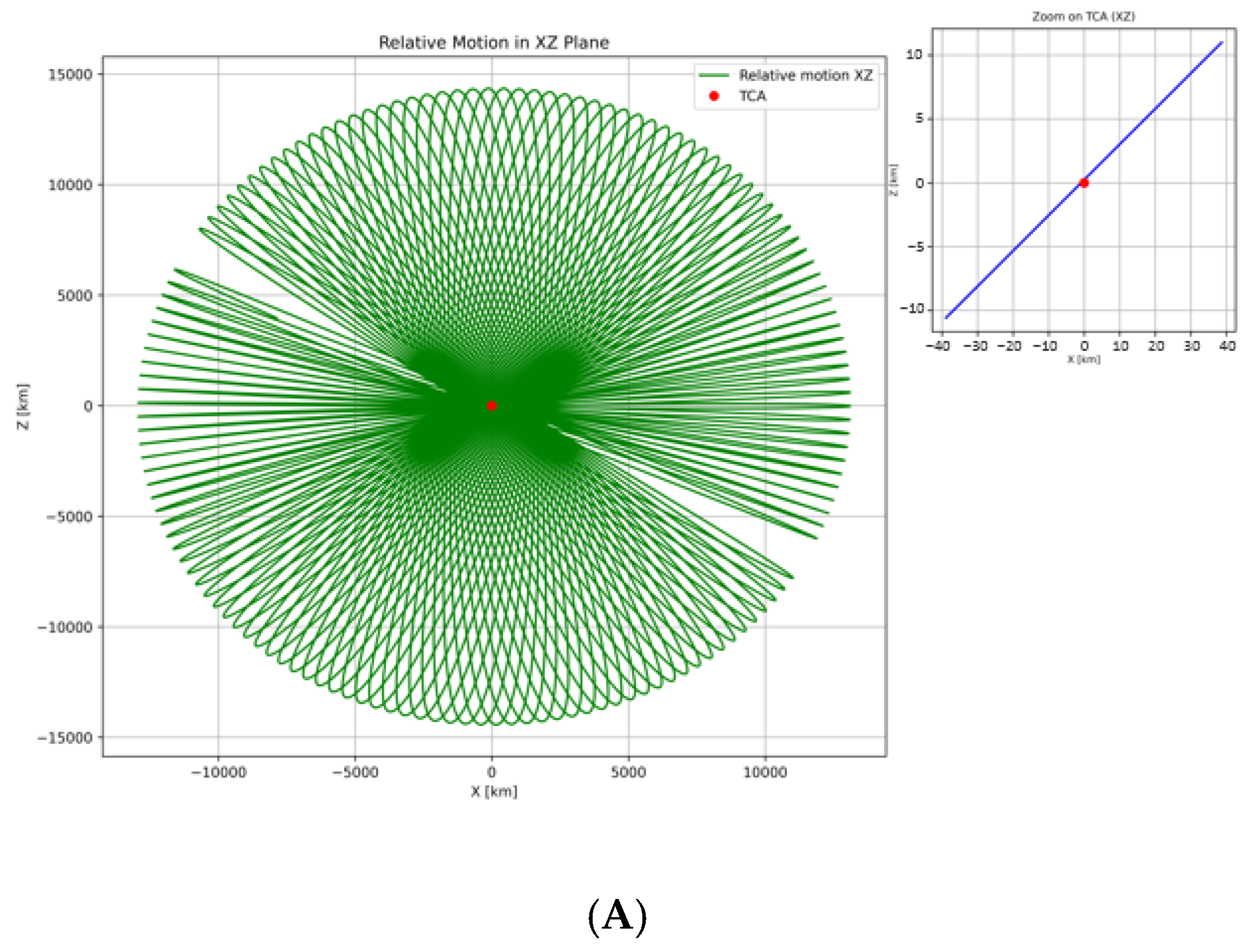
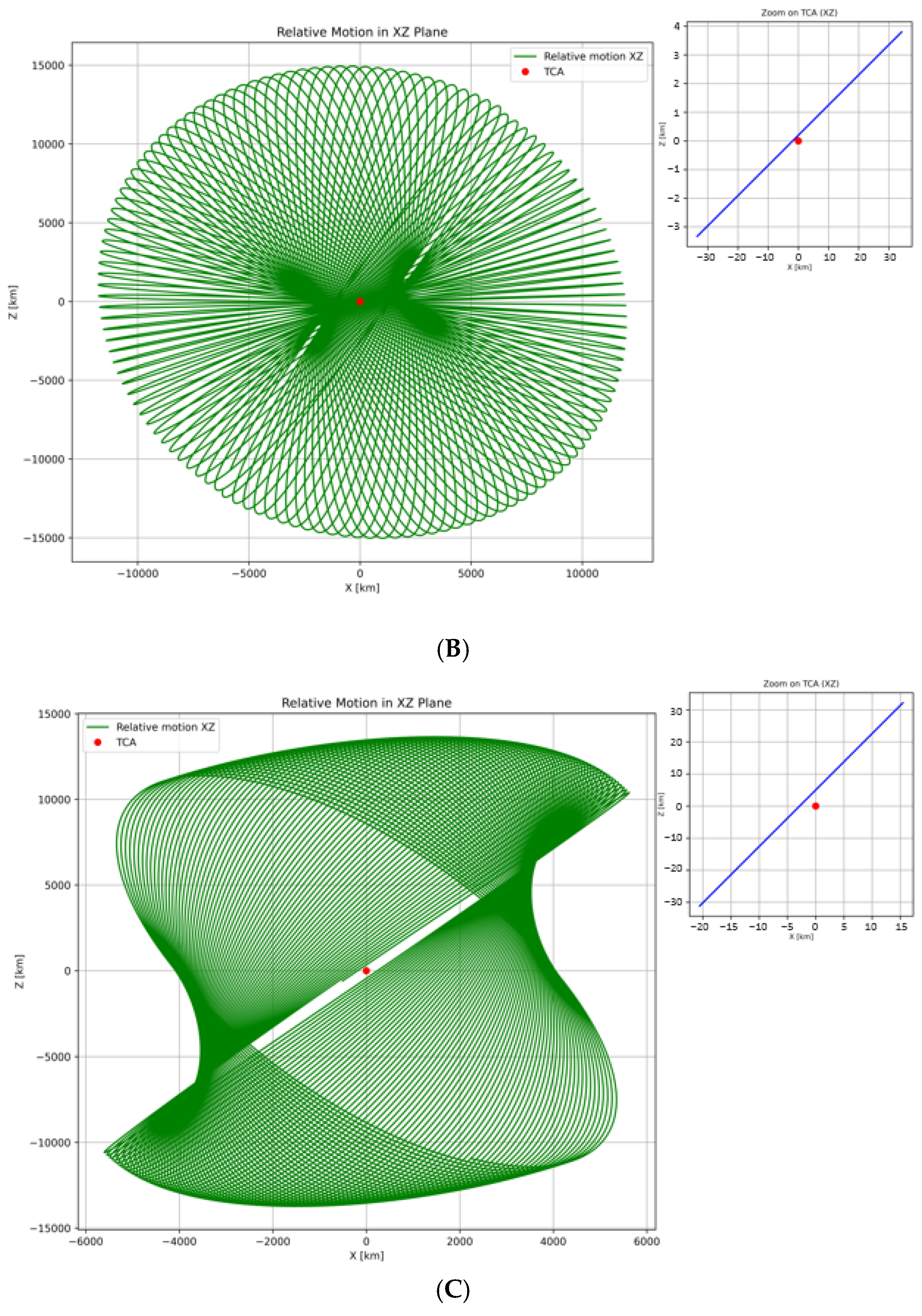


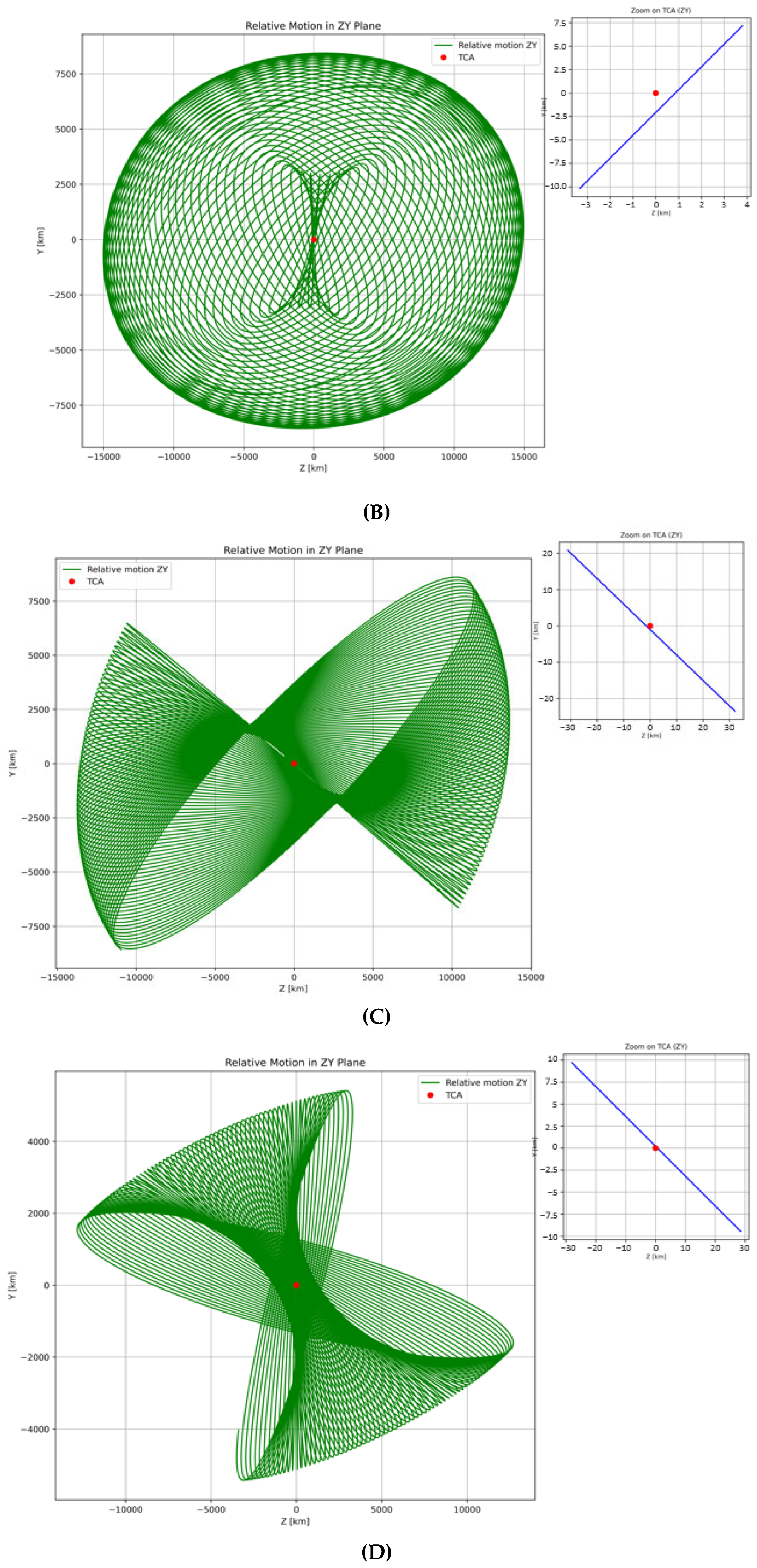
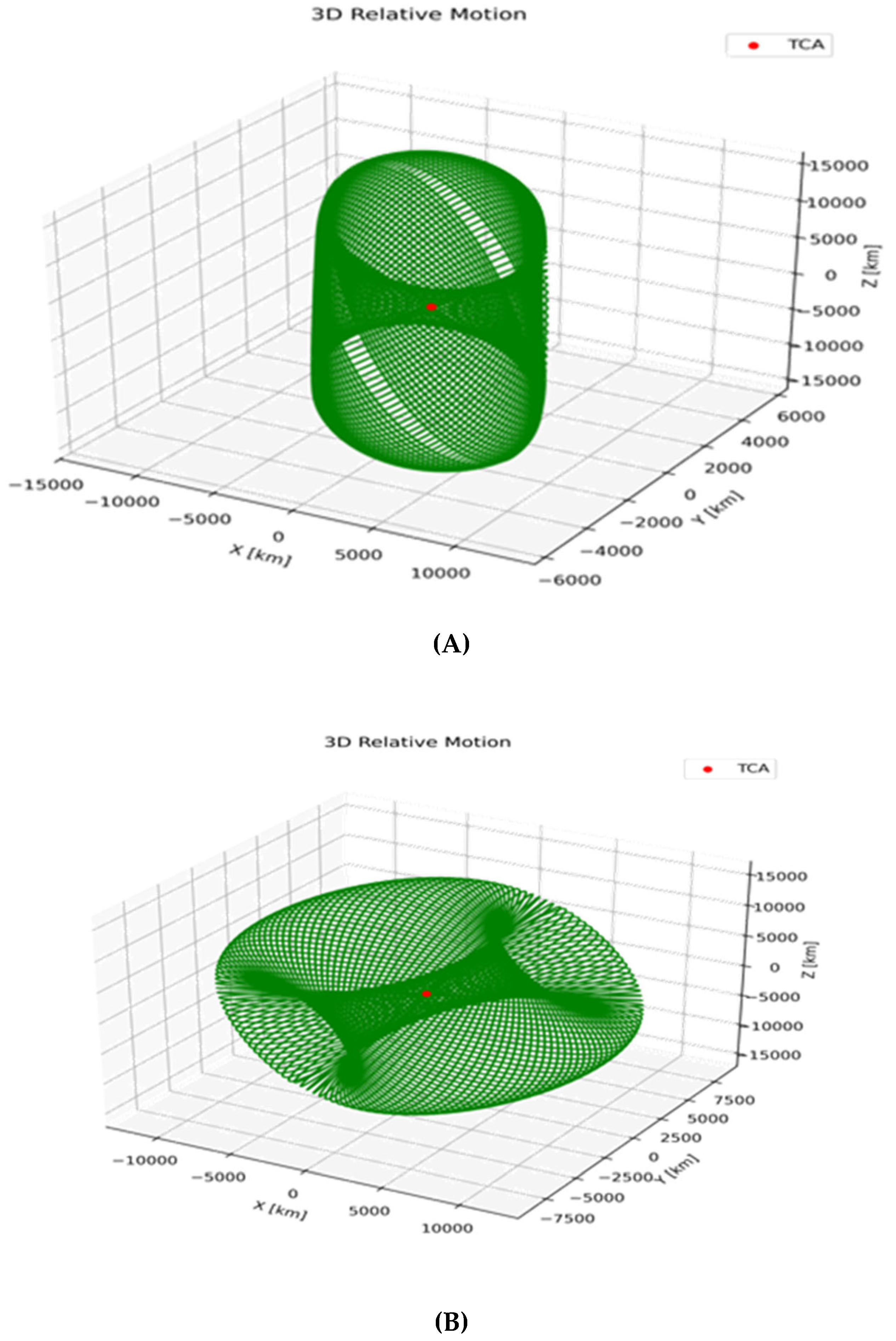
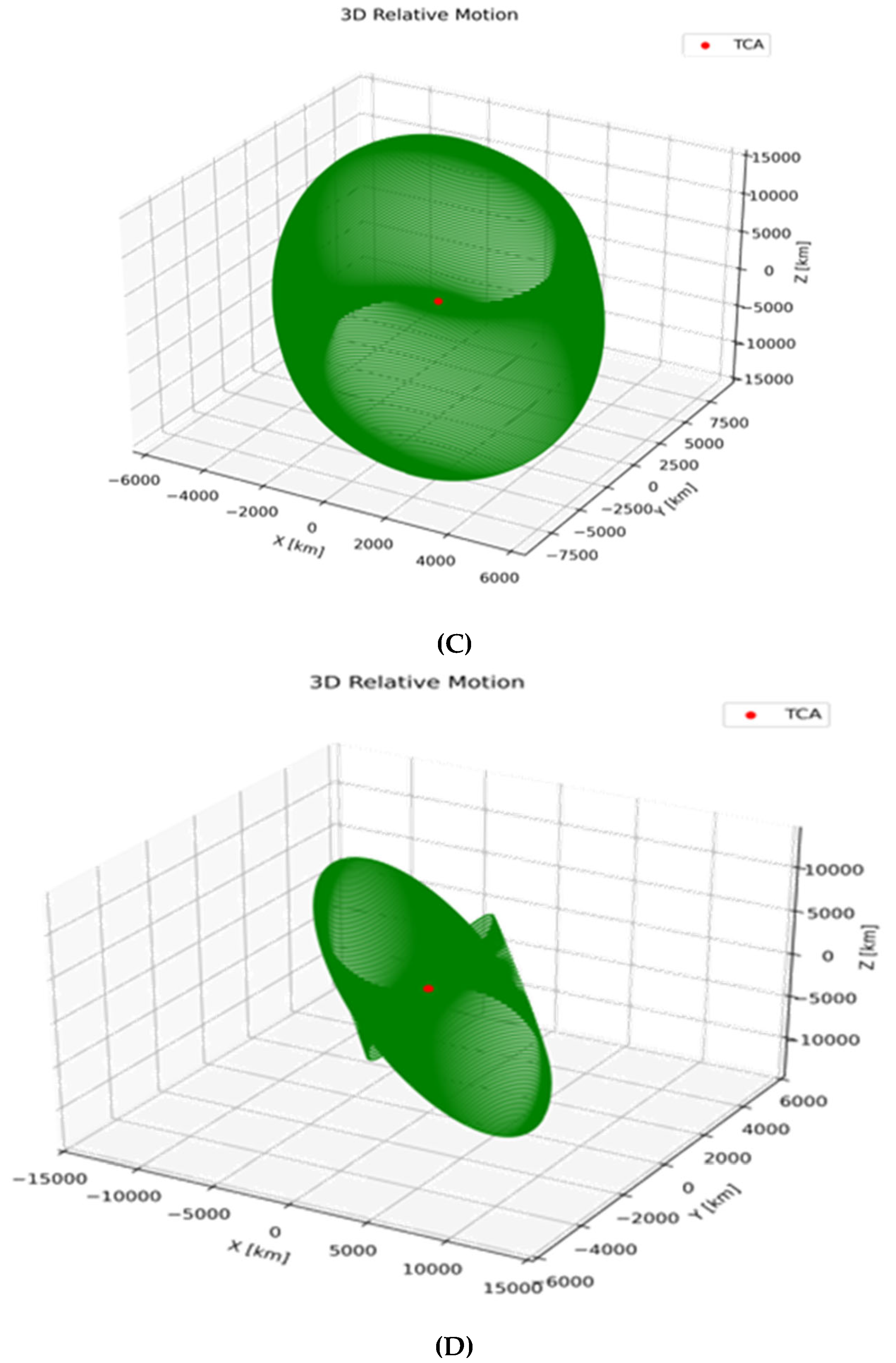
| Object A | Inclination Degree | No of Detected Object | Object B |
|---|---|---|---|
| STARLINK-1008 | 43 | 5 | Debris Catalog (Irdum33—cosmose2551-) |
| STARLINK-5691 | 54 | 6 | |
| STARLINK-5617 | 70 | 12 | |
| STARLINK-4326 | 97 | 4 |
| Algorithm | Time of Epoch | TCA | TCA Deviation from Reference (s) | Min Distance, km | Miss Distance Deviation from Reference (km) | ID |
|---|---|---|---|---|---|---|
| Comparison data | 2025-04-25 15:18:46.0 | 2025-04-25 18:56:38.532 | 0.176 | 0.026 | 29798 & 60876 | |
| Multi-stage | 2025-04-25 18:56:38.501 | 0.202 | ||||
| Comparison data | 2025-05-14 17:06:12.0 | 2025-05-15 22:37:34.909 | 0.424 | 0.161 | 12848 & 32322 | |
| Multi-stage | 2025-05-15 22:37:34.912 | 0.585 | ||||
| Comparison data | 2025-05-20 07:48:45.0 | 2025-05-20 12:00:41.156 | 0.041 | 0.293 | 34159 & 61824 | |
| Multi-stage | 2025-05-20 12:00:41.163 | 0.334 | ||||
| Comparison data | 2025-05-20 07:48:39.0 | 2025-05-20 08:00:03.338 | 0.096 | 0.249 | 37615 & 61291 | |
| Multi-stage | 025-05-20 08:00:03.393 | 0.345 | ||||
| Comparison data | 2025-05-20 07:48:39.0 | 2025-05-22 22:16:14.741 | 0. 146 | 0.588 | 61278 & 54616 | |
| Multi-stage | 2025-05-22 22:16:14.795 | 0.625 | ||||
| Comparison data | 2025-05-20 07:47:41.0 | 2025-05-23 07:18:52.011 | 0.130 | 1.505 | 48826 & 25319 | |
| Multi-stage | 2025-05-23 07:18:51.808 | 1.635 | ||||
| Comparison data | 2025-05-20 14:21:58.0 | 2025-05-23 01:14:15.634 | 0. 103 | 0.072 | 60698 & 22382 | |
| Multi-stage | 2025-05-23 01:14:15.642 | 0.175 | ||||
| Comparison data | 2025-05-22 13:20:18.000 | 2025-05-24 06:32:54.222 | 0. 083 | 0.212 | 41531 & 60251 | |
| Multi-stage | 2025-05-24 06:32:54.169 | 0.295 |
| Case | Method | Collision Probability | Standard Deviation | Real Collision | TAC | Min Distance (km) |
|---|---|---|---|---|---|---|
| 1 | MC | 0.000243 | 0.000016 | 0.0001118305 | 2025-04-25 18:56:38.501680 | 0.203779 |
| DAMC | 0.000219 | 0.000014 | ||||
| 2 | MC | 0.000061 | 0.000008 | |||
| DAMC | 0.000055 | 0.000007 | ||||
| 3 | MC | 0.000015 | 0.000004 | |||
| DAMC | 0.000014 | 0.000003 | ||||
| 1 | MC | 0.000246 | 0.000016 | 0.0001668242 | 2025-05-22 22:16:14.795 | 0.6264654 |
| DAMC | 0.000221 | 0.000014 | ||||
| 2 | MC | 0.000073 | 0.000009 | |||
| DAMC | 0.000066 | 0.000008 | ||||
| 3 | MC | 0.000015 | 0.000004 | |||
| DAMC | 0.000014 | 0.000003 | ||||
| 1 | MC | 0.000245 | 0.000016 | 0.0002276681 | 2025-05-23 07:18:51 | 2.9253064 |
| DAMC | 0.000220 | 0.000014 | ||||
| 2 | MC | 0.000066 | 0.000008 | |||
| DAMC | 0.000059 | 0.000007 | ||||
| 3 | MC | 0.000012 | 0.000003 | |||
| DAMC | 0.000011 | 0.000003 | ||||
| 1 | MC | 0.000244 | 0.000016 | 0.0002734335 | 2025-05-24 06:32:54.169398 | 0.295490267 |
| DAMC | 0.000220 | 0.000014 | ||||
| 2 | MC | 0.000058 | 0.000008 | |||
| DAMC | 0.000052 | 0.000007 | ||||
| 3 | MC | 0.000008 | 0.000003 | |||
| DAMC | 0.000007 | 0.000003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tealib, S.K.; Abdelaziz, A.M.; Molotov, I.E.; Yang, X.; Sun, J.; Liu, J. Enhanced Conjunction Assessment in LEO: A Hybrid Monte Carlo and Spline-Based Method Using TLE Data. Aerospace 2025, 12, 674. https://doi.org/10.3390/aerospace12080674
Tealib SK, Abdelaziz AM, Molotov IE, Yang X, Sun J, Liu J. Enhanced Conjunction Assessment in LEO: A Hybrid Monte Carlo and Spline-Based Method Using TLE Data. Aerospace. 2025; 12(8):674. https://doi.org/10.3390/aerospace12080674
Chicago/Turabian StyleTealib, Shafeeq Koheal, Ahmed Magdy Abdelaziz, Igor E. Molotov, Xu Yang, Jian Sun, and Jing Liu. 2025. "Enhanced Conjunction Assessment in LEO: A Hybrid Monte Carlo and Spline-Based Method Using TLE Data" Aerospace 12, no. 8: 674. https://doi.org/10.3390/aerospace12080674
APA StyleTealib, S. K., Abdelaziz, A. M., Molotov, I. E., Yang, X., Sun, J., & Liu, J. (2025). Enhanced Conjunction Assessment in LEO: A Hybrid Monte Carlo and Spline-Based Method Using TLE Data. Aerospace, 12(8), 674. https://doi.org/10.3390/aerospace12080674


_Zhu.png)





