Optimization of Test Mass Motion State for Enhancing Stiffness Identification Performance in Space Gravitational Wave Detection
Abstract
1. Introduction
2. Principle of Test Mass Stiffness Identification
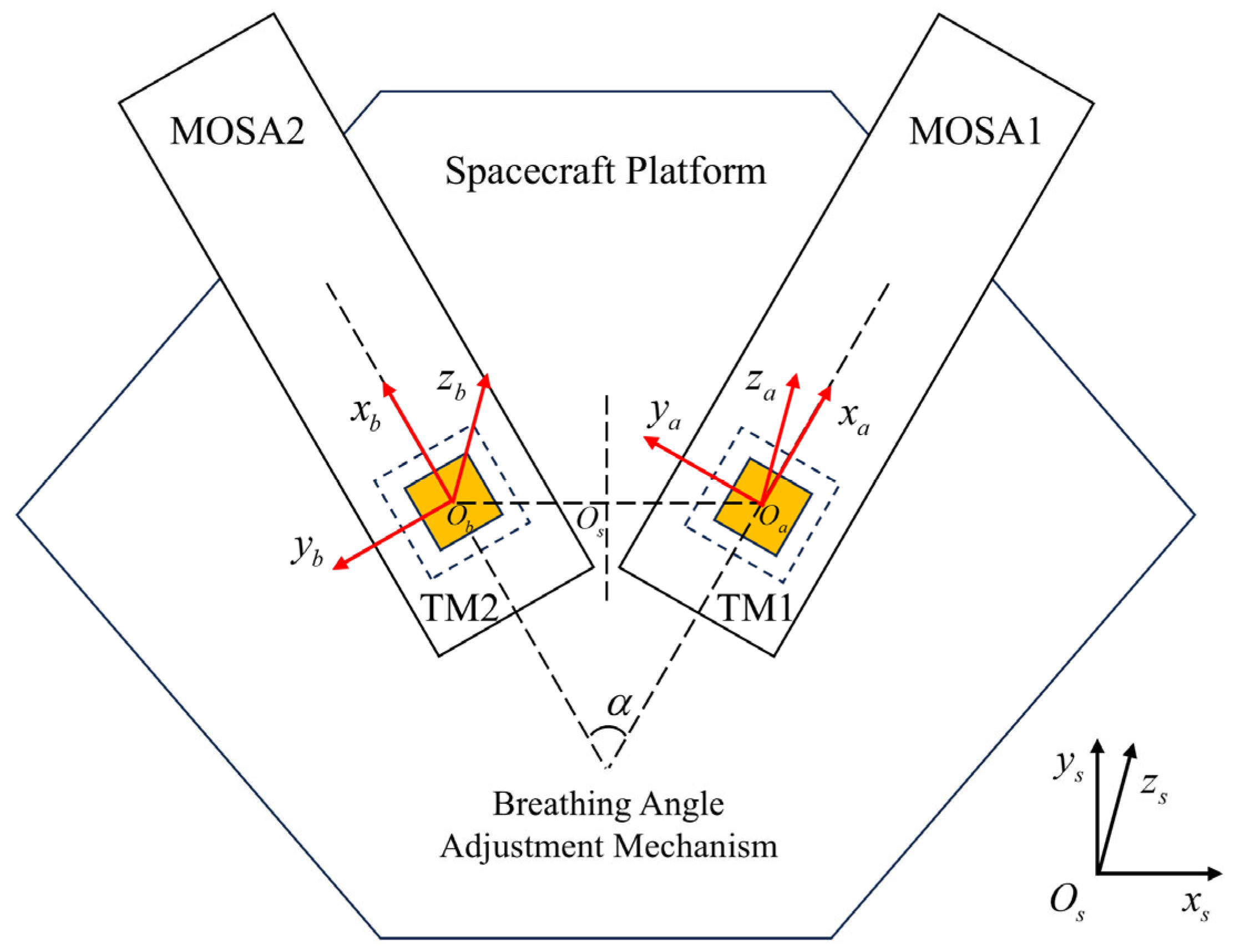
2.1. Coordinate System
- Spacecraft body coordinate system denoted as s: the origin of the coordinate system Os is located at the center of mass of the spacecraft, ys points outward along the axis of symmetry between the two interfering arms, and zs points to the solar panel.
- TM1 coordinate system denoted as a: the origin of the coordinate system Oa is at the center of the nominal position of TM1, xa is outward along the interfering arm, and za is pointing to the solar panel.
- TM2 coordinate system denoted as b: the origin of the coordinate system Ob is at the center of the nominal position of TM2, xb is outward along the interfering arm, and zb is pointing to the solar panel.
2.2. Dynamics for Stiffness Identification
2.3. On-Orbit Stiffness Identification Method
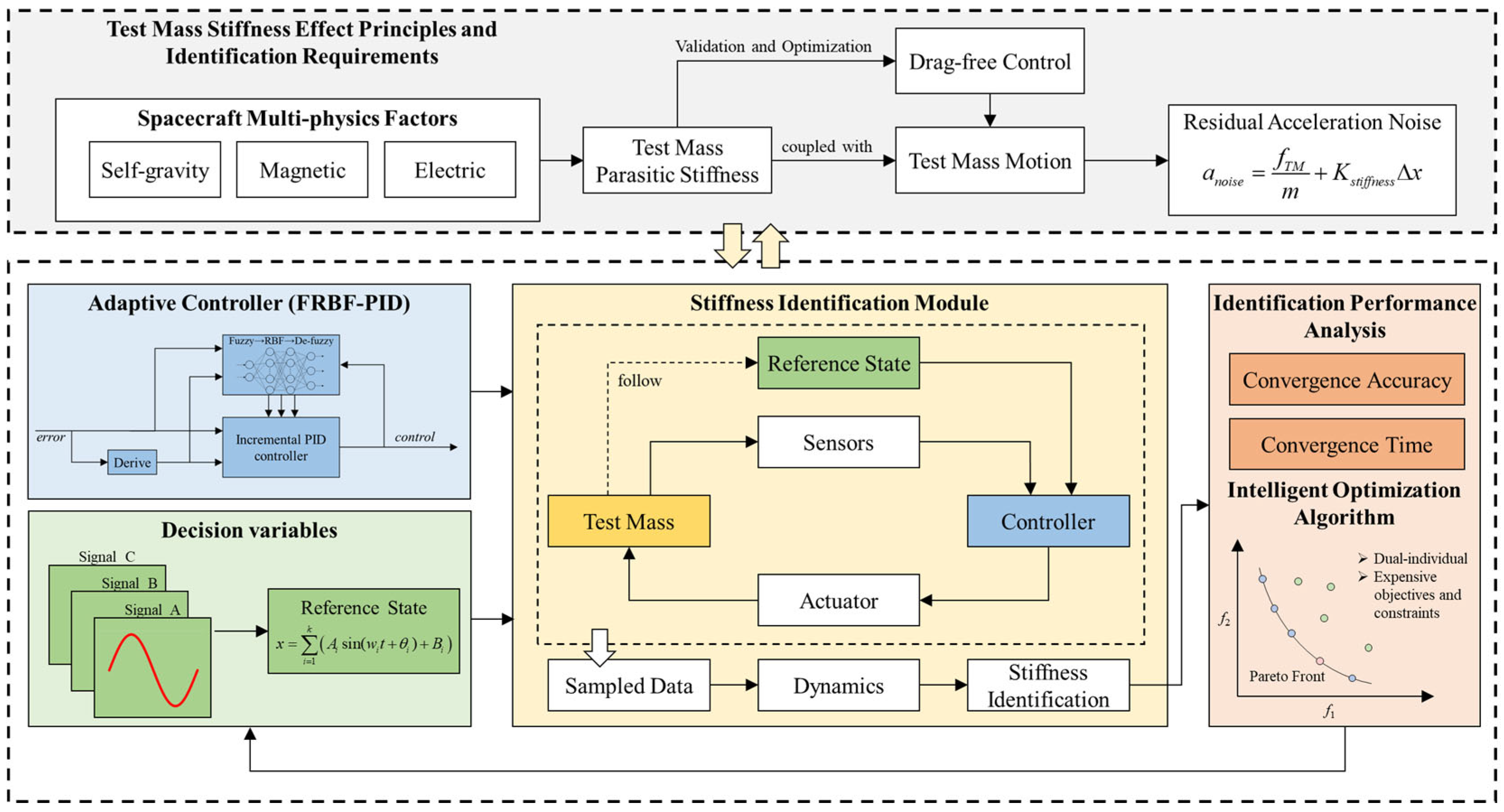
3. Methods for Enhancing Performance of Stiffness Identification
3.1. Research Framework
3.2. Motion State Optimization
3.2.1. Problem Definition
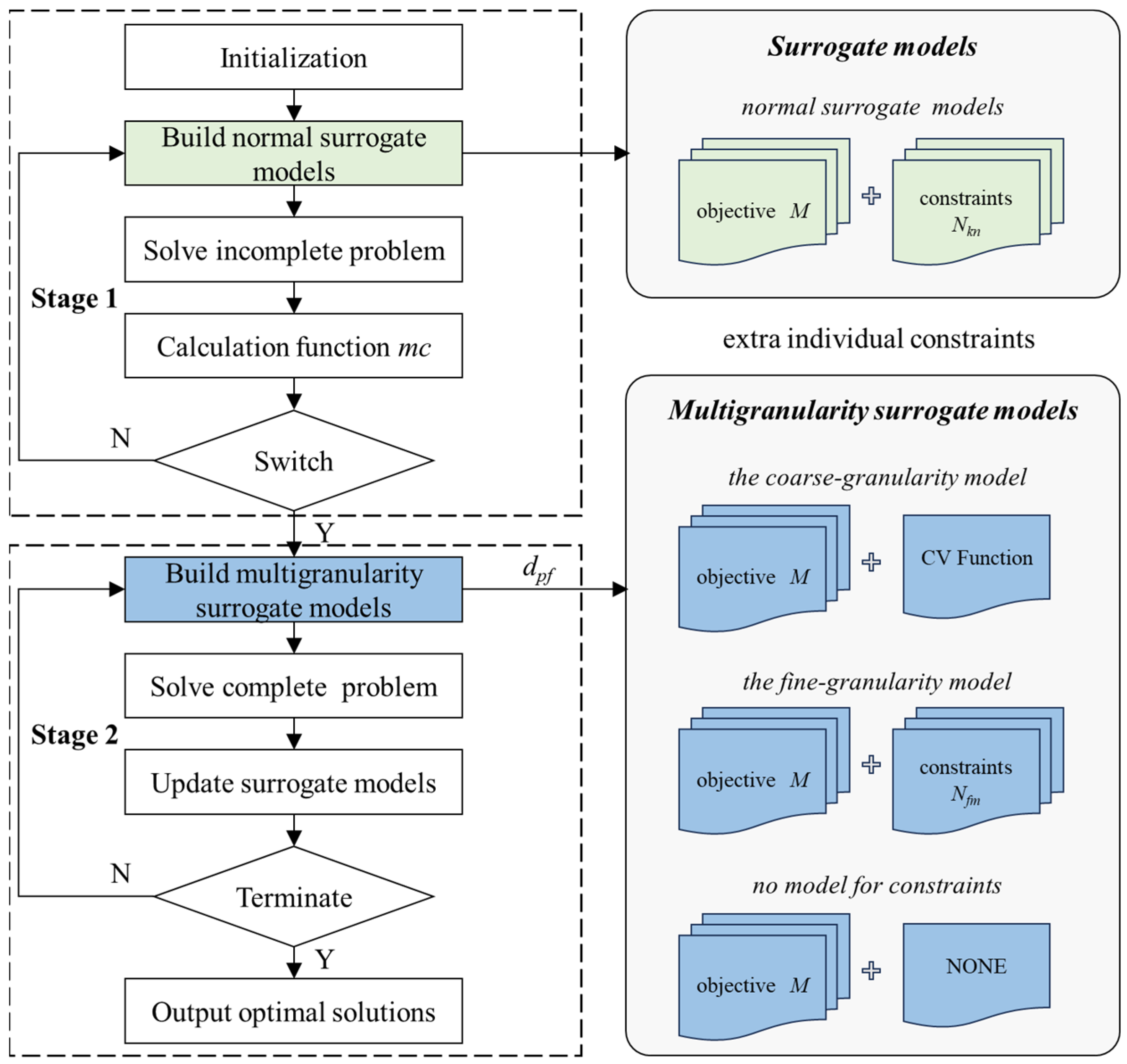
3.2.2. Optimization Algorithm
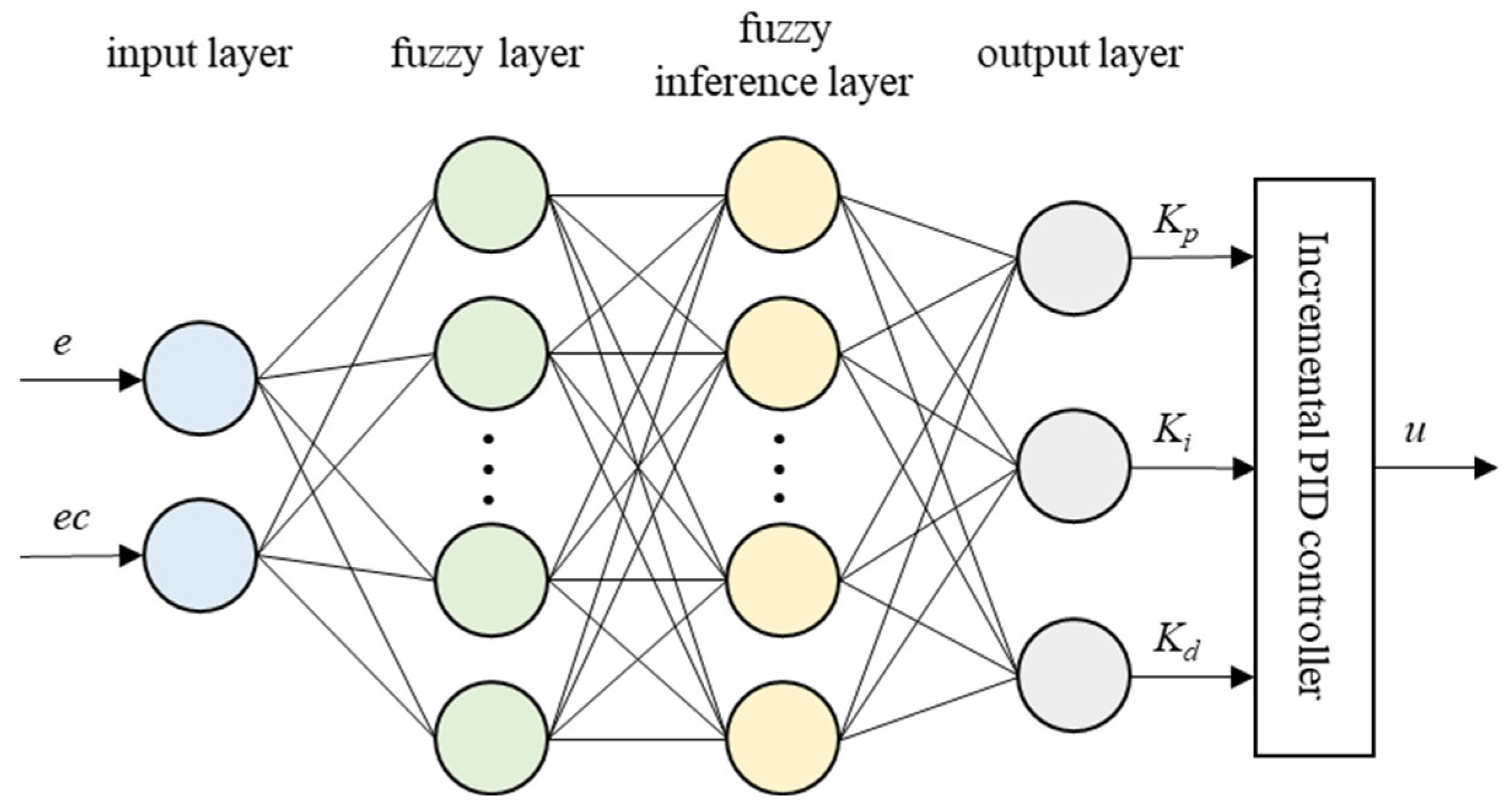
3.3. FRBF-PID Controller
4. Numerical Simulation Experiments
4.1. Basic Simulation Environments
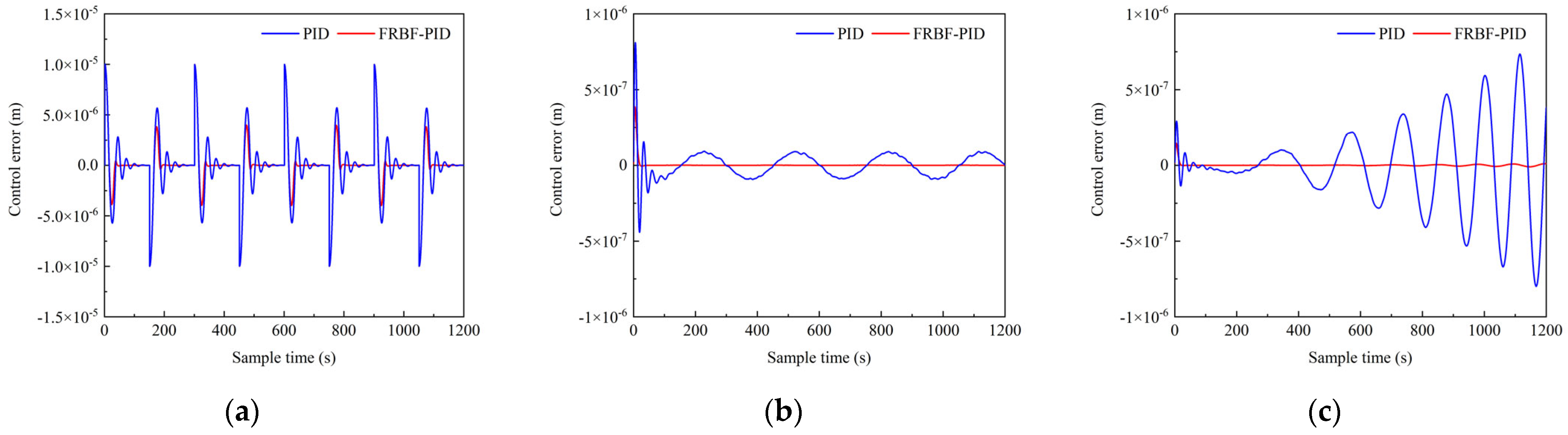
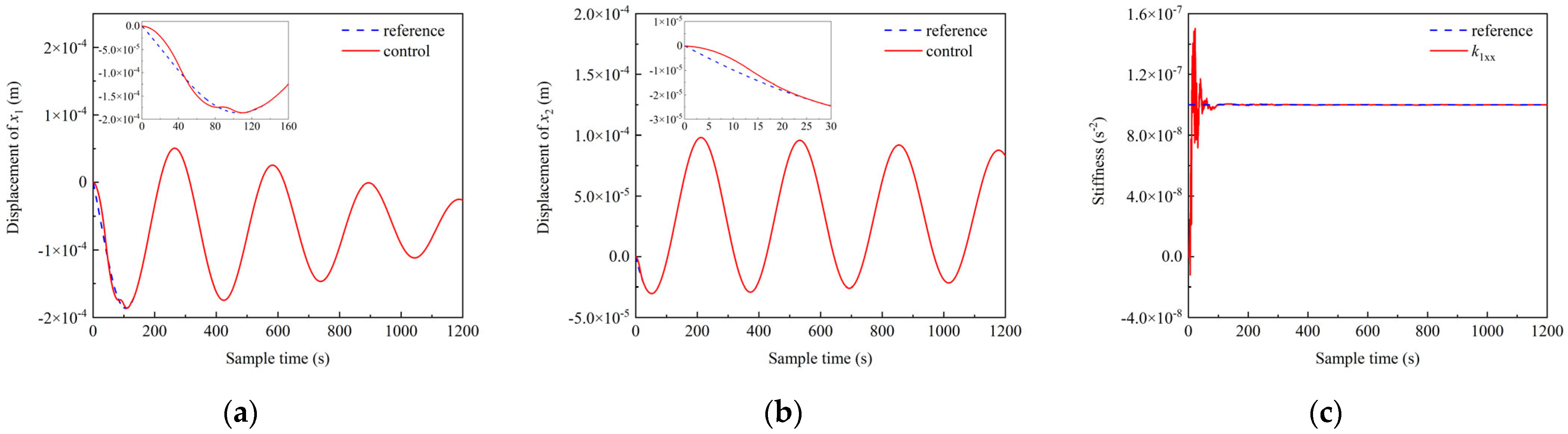
4.2. FRBF-PID Control Performance
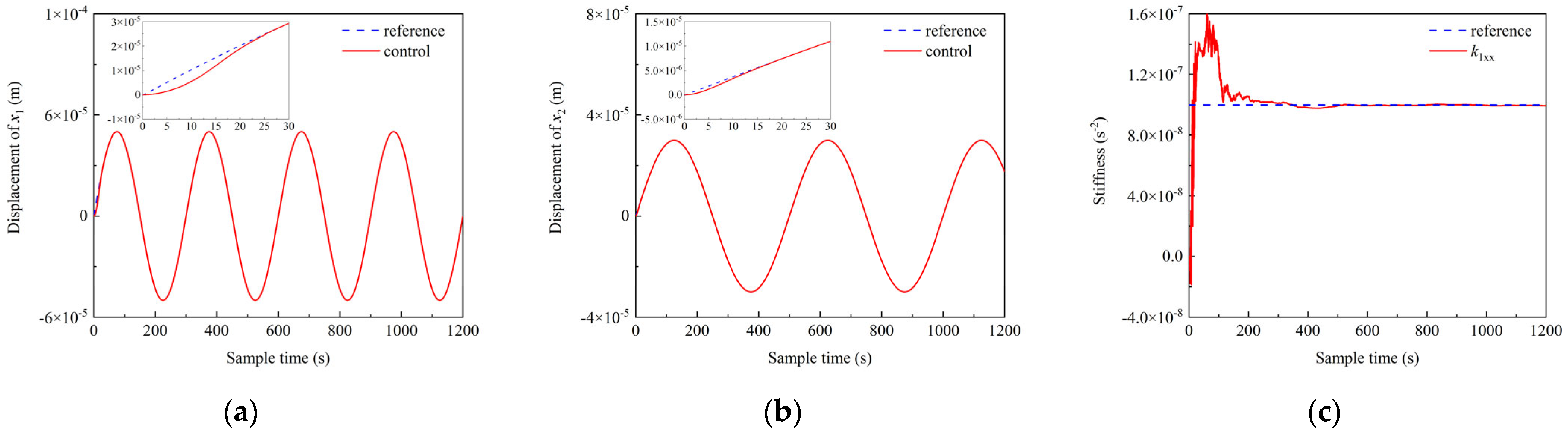
4.3. Stiffness Identification Performance
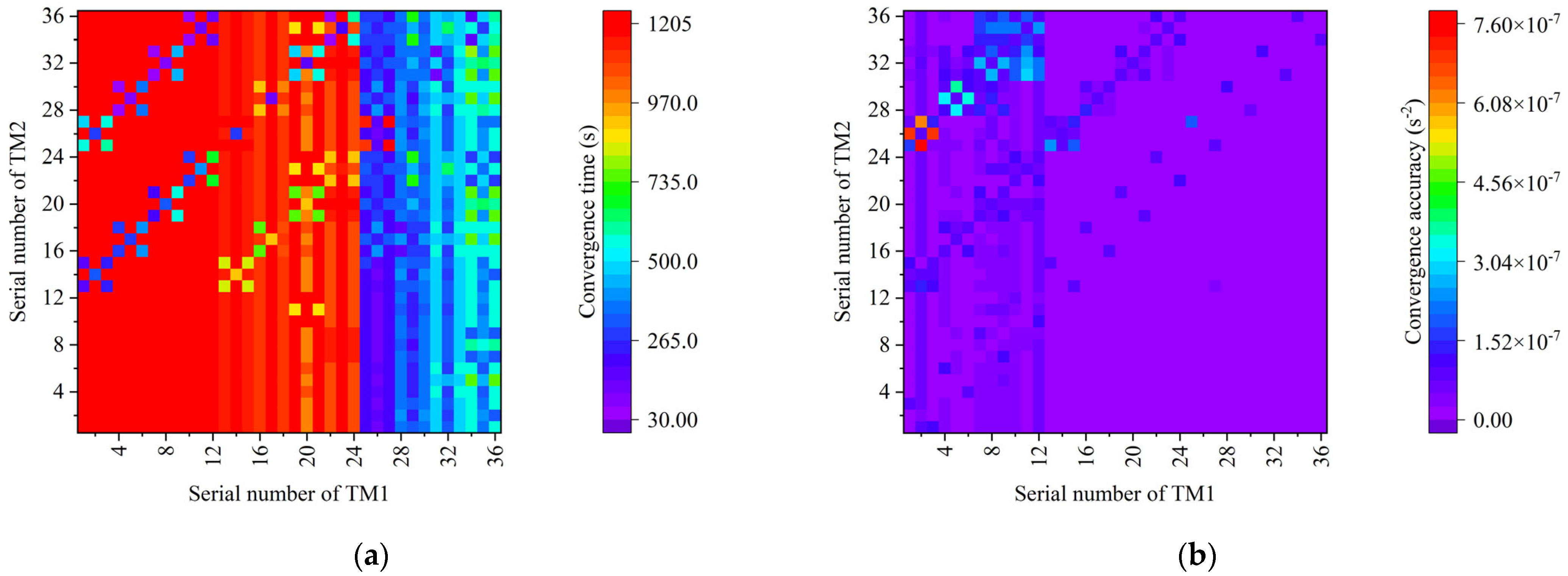
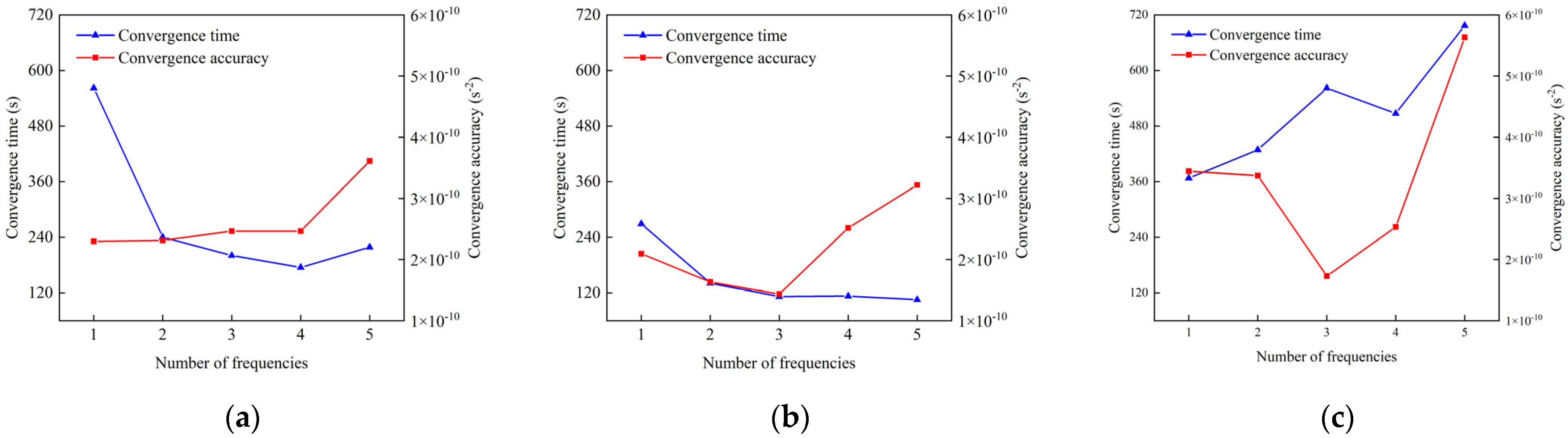
4.4. Stiffness Identification Performance Enhancement by Optimizing the Motion State
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giammarchi, M.; Ricci, F. Gravitational Waves, Event Horizons and Black Hole Observation: A New Frontier in Fundamental Physics. Symmetry 2022, 14, 2276. [Google Scholar] [CrossRef]
- Mastrogiovanni, S.; Karathanasis, C.; Gair, J.; Ashton, G.; Rinaldi, S.; Huang, H.Y.; Dálya, G. Cosmology with gravitational waves: A review. Ann. Phys. 2024, 536, 2200180. [Google Scholar] [CrossRef]
- Wu, Y.L.; Hu, W.R.; Wang, J.Y.; Chang, J.; Cai, R.G.; Zhang, Y.H.; Luo, Z.R.; Lu, Y.J.; Zhou, Y.F.; Guo, Z.K. Review and scientific objectives of spaceborne gravitational wave detection missions. Chin. J. Space Sci. 2023, 43, 589–599. [Google Scholar] [CrossRef]
- Bayle, J.B.; Bonga, B.; Caprini, C.; Doneva, D.; Muratore, M.; Petiteau, A.; Rossi, E.; Shao, L. Overview and progress on the Laser Interferometer Space Antenna mission. Nat. Astron. 2022, 6, 1334–1338. [Google Scholar] [CrossRef]
- Luo, Z.R.; Wang, Y.; Wu, Y.L.; Hu, W.R.; Jin, G. The Taiji program: A concise overview. Prog. Theor. Exp. Phys. 2021, 2021, 05A108. [Google Scholar] [CrossRef]
- Mei, J.; Bai, Y.Z.; Bao, J.; Barausse, E.; Cai, L.; Canuto, E.; Cao, B.; Chen, W.M.; Chen, Y.; Ding, Y.W.; et al. The TianQin project: Current progress on science and technology. Prog. Theor. Exp. Phys. 2021, 2021, 05A107. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Castelli, E.; Cavalleri, A.; Cesarini, A.; Cruise, A.M.; et al. Beyond the required LISA free-fall performance: New LISA pathfinder results down to 20 μHz. Phys. Rev. Lett. 2018, 120, 061101. [Google Scholar] [CrossRef]
- Luo, Z.R.; Zhang, M.; Wu, Y.L. Recent status of Taiji program in China. Chin. J. Space Sci. 2022, 42, 536–538. [Google Scholar] [CrossRef]
- Luo, J.; Bai, Y.Z.; Cai, L.; Cao, B.; Chen, W.M.; Chen, Y.; Cheng, D.C.; Ding, Y.W.; Duan, H.Z.; Gou, X.; et al. The first round result from the Tianqin-1 satellite. Cl. Quantum Grav. 2020, 37, 185013. [Google Scholar] [CrossRef]
- Jennrich, O. LISA technology and instrumentation. Cl. Quantum Grav. 2009, 26, 153001. [Google Scholar] [CrossRef]
- Luo, Z.R.; Bai, S.; Bian, X.; Chen, G.; Dong, P.; Dong, Y. Space laser interferometry gravitational wave detection. Adv. Mech. 2013, 43, 415–447. [Google Scholar]
- Wang, Z.Q.; Gao, D.; Deng, K.N.; Lu, Y.; Ma, S.D.; Zhao, J. Robot base position and spacecraft cabin angle optimization via homogeneous stiffness domain index with nonlinear stiffness characteristics. Robot. Comput. Integr. Manuf. 2024, 90, 102793. [Google Scholar] [CrossRef]
- Piskarev, Y.; Sun, Y.; Righi, M.; Boehler, Q.; Chautems, C.; Fischer, C.; Nelson, B.J.; Shintake, J.; Floreano, D. Fast-Response Variable-Stiffness Magnetic Catheters for Minimally Invasive Surgery. Adv. Sci. 2024, 11, 2305537. [Google Scholar] [CrossRef]
- Li, H.; Bi, K.M.; Hao, H.; Yu, Y.; Xu, L.H. Experimental study of a novel quasi-active negative stiffness damper system for achieving optimal active control performance. Eng. Struct. 2024, 299, 117082. [Google Scholar] [CrossRef]
- Weber, W.J.; Bortoluzzi, D.; Cavalleri, A.; Carbone, L.; Lio, M.D.; Dolesi, R.; Fontana, G.; Hoyle, C.D.; Hueller, M.; Vitale, S. Position sensors for flight testing of LISA drag-free control. Gravitational-Wave Detect. 2003, 4856, 31–42. [Google Scholar]
- Armanoa, M.; Audleyb, H.; Augerc, G.; Bairdn, J.; Binetruyc, P.; Bornb, M.; Bortoluzzid, D.; Brandte, N.; Bursit, A.; Calenof, M.; et al. Constraints on LISA Pathfinder’s self-gravity: Design requirements, estimates and testing procedures. Cl. Quantum Grav. 2016, 33, 235015. [Google Scholar] [CrossRef]
- Gou, X.Y.; Wang, L.J.; Xu, X.M.; Zou, K.; Jiang, Q.H. Study on Dynamic Coordination Condition of Displacement Drag-free Control. J. Astron. 2024, 45, 540–549. [Google Scholar]
- Jiao, B.H.; Liu, Q.F.; Dang, Z.H.; Yue, X.K.; Zhang, Y.H.; Xia, Y.Q.; Duan, L.; Hu, Q.L.; Yue, C.L.; Wang, P.C.; et al. A review on DFACS (I): System design and dynamics modeling. Chin. J. Aeronaut. 2024, 37, 92–119. [Google Scholar] [CrossRef]
- Yue, C.L.; Jiao, B.H.; Dang, Z.H.; Yue, X.K.; Zhang, Y.H.; Xia, Y.Q.; Duan, L.; Hu, Q.L.; Liu, Q.F.; Wang, P.C.; et al. A review on DFACS (II): Modeling and analysis of disturbances and noises. Chin. J. Aeronaut. 2024, 37, 120–147. [Google Scholar] [CrossRef]
- Ziegler, T.; Fichter, W. Test mass stiffness estimation for the LISA Pathfinder drag-free system. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20 August–23 August 2007; Volume 6669. [Google Scholar]
- Nofrarias, M.; Röver, C.; Hewitson, M.; Monsky, A.; Heinzel, G.; Danzmann, K.; Ferraioli, L.; Hueller, M.; Vitale, S. Bayesian parameter estimation in the second LISA Pathfinder mock data challenge. Phys. Rev. D 2010, 82, 122002. [Google Scholar] [CrossRef]
- Congedo, G.; Ferraioli, L.; Hueller, M.; Marchi, F.D.; Vitale, S.; Armano, M.; Hewitson, M.; Nofrarias, M. Time domain maximum likelihood parameter estimation in LISA Pathfinder data analysis. Phys. Rev. D 2012, 85, 122004. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Castelli, E.; Cavalleri, A.; Cesarini, A.; Cruise, A.M.; et al. Calibrating the system dynamics of LISA Pathfinder. Phys. Rev. D 2018, 97, 122002. [Google Scholar] [CrossRef]
- Tang, N.B.; Yang, Z.G.; Cai, Z.M.; Fang, Z.R.; Liu, Y.; Hu, H.Y.; Li, H.W. Identification of test mass stiffness based on dual sensitive axis decomposition. Chin. Opt. 2025, 18, 631–640. [Google Scholar] [CrossRef]
- Tangirala, A.K. Principles of System Identification: Theory and Practice; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Kalaba, R.; Spingarn, K. Control, Identification, and Input Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hao, Z.Q.; Wang, X.Y.; Wei, X.Z.; Dai, H.F. Fast and highly accurate measurement of electrochemical impedance spectra of power batteries based on optimized multi-sine signals. Measurement 2025, 252, 117355. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, S.Y.; Zhang, R.N.; Tian, J.D.; Li, X.Y. State of charge estimation of lithium-ion batteries based on ultrasonic guided waves by chirped signal excitation. J. Energy Storage 2024, 84, 110897. [Google Scholar] [CrossRef]
- Niedermayer, P.; Singh, R. Excitation signal optimization for minimizing fluctuations in knock out slow extraction. Sci. Rep. 2024, 14, 10310. [Google Scholar] [CrossRef] [PubMed]
- Yue, J.K.; Hong, X.B.; Zhang, B. A damage imaging method based on particle swarm optimization for composites nondestructive testing using ultrasonic guided waves. Appl. Acoust. 2024, 218, 109878. [Google Scholar] [CrossRef]
- Xu, J.C.; Fei, Y.M.; Li, J.G.; Li, Y.N. Optimization of Persistent Excitation Level of Training Trajectories in Deterministic Learning. IEEE Trans. Syst. Man. Cybern. 2025, 55, 2924–2936. [Google Scholar] [CrossRef]
- Wang, J.; Qi, K.Q.; Wang, S.X.; Gao, R.H.; Li, P.; Yang, R.; Liu, H.S.; Luo, Z.R. Advance and prospect in the study of laser interferometry technology for space gravitational wave detection. Sci. Sin-Phys. Mech. Astron. 2024, 54, 109–127. [Google Scholar] [CrossRef]
- Wang, S.X.; Guo, W.C.; Zhao, P.A.; Wang, J.; Dong, P.; Xu, P.; Luo, Z.R.; Qi, K.Q. Inertial sensor for space gravitational wave detection and its key technologies. Sci. Sin-Phys. Mech. Astron. 2024, 54, 91–108. [Google Scholar]
- Armano, M.; Benedetti, M.; Bogenstahl, J.; Bortoluzzi, D.; Bosetti, P.; Brandt, N.; Cavalleri, A.; Ciani, G.; Cristofolini, I.; Cruise, A.M.; et al. LISA Pathfinder: The experiment and the route to LISA. Cl. Quantum Grav. 2009, 26, 094001. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Jiang, H.; Tian, Y.; Ma, H.P.; Zhang, X.Y. Multigranularity surrogate modeling for evolutionary multi-objective optimization with expensive constraints. IEEE Trans. Neural Netw. Learn. Syst. 2023, 35, 2956–2968. [Google Scholar] [CrossRef]
- Veldhuizen, D.A.V.; Lamont, G.B. Evolutionary Computation and Convergence to a Pareto Front. In Late Breaking Papers at the Genetic Programming Conference; University of Wisconsin: Madison, WI, USA, 1998; pp. 221–228. [Google Scholar]
- Li, J.Y.; Li, W.D.; Du, X.Y. Research on the characteristics of electro-hydraulic position servo system of RBF neural network under fuzzy rules. Sci. Rep. 2024, 14, 15332. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.P.; Xue, L.T.; Li, Y.; Cao, L.H.; Chen, C.Q. A novel fuzzy controller for Visible-light camera using RBF-ANN: Enhanced positioning and autofocusing. Sensors 2022, 22, 8657. [Google Scholar] [CrossRef] [PubMed]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar] [CrossRef]
- Jain, H.; Deb, K. An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach. IEEE Trans. Evol. Comput. 2013, 18, 602–622. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.Y.; Zhen, H.X.; Li, S.J.; Wang, L.; Liao, Z.W. A simple two-stage evolutionary algorithm for constrained multi-objective optimization. Knowl. Based Syst. 2021, 228, 107263. [Google Scholar] [CrossRef]
- Araújo, A.F.R.; Farias, L.R.C.; Gonçalves, A.R.C. Self-organizing surrogate-assisted non-dominated sorting differential evolution. Swarm Evol. Comput. 2024, 91, 101703. [Google Scholar] [CrossRef]
- Ming, F.; Gong, W.Y.; Jin, Y.C. Even search in a promising region for constrained multi-objective optimization. IEEE/CAA J. Autom. Sin. 2024, 11, 474–486. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| [k1xx, k1yy, k1zz] (s−2) | [1,1,1] × 10−7 |
| [k2xx, k2yy, k2zz] (s−2) | [1,1,1] × 10−7 |
| fD1 (m·s−2) | [1,1,1] × 10−10 |
| fD2 (m·s−2) | [1,1,1] × 10−10 |
| Nm1 (m) | δ = 1×10−11 |
| Nm2 (m) | δ = 1 × 10−8 |
| Nacc (m·s−2) | δ = 1 × 10−12 |
| Nele (m·s−2) | δ = 1 × 10−12 |
| Scheme | Dec | Obj | Configuration |
|---|---|---|---|
| A | TM1 | TM1 | 3 × k & 2 |
| B | TM1 + TM2 | TM1 | 2 × 3 × k & 2 |
| C | TM1 + TM2 | TM1 + TM2 | 2 × 3 × k & 4 |
| Algorithm | Convergence Time (s) | Convergence Accuracy (s−2) | M (Default) | M (7 × 10−11) | M (5 × 10−11) | Final Accuracy (s−2) |
|---|---|---|---|---|---|---|
| NSGA-II [39] | 141.0 | 1.44 × 10−10 | 3.79 | 9.73 | 10.82 | 5.86 × 10−11 |
| NSGA-III [40] | 125.9 | 2.40 × 10−10 | 4.50 | 7.39 | 7.39 | 3.60 × 10−12 |
| C-MOEA/D [41] | 76.2 | 1.13 × 10−09 | 12.55 | 8.83 | 9.52 | 5.90 × 10−11 |
| C-TSEA [42] | 218.8 | 2.44 × 10−10 | 6.08 | 13.53 | 13.64 | 9.10 × 10−12 |
| SSDE [43] | 177.1 | 3.34 × 10−10 | 6.30 | 6.11 | 6.23 | 2.02 × 10−10 |
| CMOES [44] | 175.1 | 1.61 × 10−10 | 4.53 | 6.75 | 6.75 | 1.25 × 10−10 |
| MGSAEA [35] | 103.7 | 4.68 × 10−10 | 6.41 | 8.99 | 8.99 | 1.90 × 10−10 |
| MGSAEA* | 191.9 | 2.31 × 10−10 | 5.51 | 11.36 | 11.53 | 5.50 × 10−11 |
| MGSAEA-IPC | 112.1 | 1.44 × 10−10 | 3.30 | 5.75 | 5.75 | 2.91 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, N.; Fang, Z.; Yang, Z.; Cai, Z.; Hu, H.; Li, H. Optimization of Test Mass Motion State for Enhancing Stiffness Identification Performance in Space Gravitational Wave Detection. Aerospace 2025, 12, 673. https://doi.org/10.3390/aerospace12080673
Tang N, Fang Z, Yang Z, Cai Z, Hu H, Li H. Optimization of Test Mass Motion State for Enhancing Stiffness Identification Performance in Space Gravitational Wave Detection. Aerospace. 2025; 12(8):673. https://doi.org/10.3390/aerospace12080673
Chicago/Turabian StyleTang, Ningbiao, Ziruo Fang, Zhongguang Yang, Zhiming Cai, Haiying Hu, and Huawang Li. 2025. "Optimization of Test Mass Motion State for Enhancing Stiffness Identification Performance in Space Gravitational Wave Detection" Aerospace 12, no. 8: 673. https://doi.org/10.3390/aerospace12080673
APA StyleTang, N., Fang, Z., Yang, Z., Cai, Z., Hu, H., & Li, H. (2025). Optimization of Test Mass Motion State for Enhancing Stiffness Identification Performance in Space Gravitational Wave Detection. Aerospace, 12(8), 673. https://doi.org/10.3390/aerospace12080673





