1. Introduction
Aerodynamic shape optimization has gained increasing attention in complex engineering fields such as aerospace, automotive, and energy industries. Although aerodynamic optimization can be computationally expensive due to the evaluation of cost functions, it is often preferred because it leads to more efficient systems overall. Methods, techniques, and algorithms developed for this purpose are primarily driven by leading research institutes and industrial R&D centers. Today, these approaches are widely adopted and continue to attract interest from a growing number of users, companies, and researchers.
The AIAA Aerodynamic Design Optimization Discussion Group (ADODG) [
1] proposes various benchmark cases with different flow conditions to guide researchers working in aerodynamic optimization. In this study, the results and performance of a surrogate-based optimization framework are investigated for the ADODG’s Test Case 2, which focuses on drag minimization of the RAE 2822 airfoil under transonic flow conditions. One of the main reasons for selecting surrogate-based methods is their high potential for application in aerospace engineering, combined with their flexibility and adaptability.
Table 1 and
Table 2 present literature reviews on the single-point optimization of the RAE 2822 airfoil, focusing based on gradient-based and gradient-free methods, respectively. Similarly,
Table 3 presents a literature review on the multi-point optimization of the RAE 2822 airfoil. In these tables, references that strictly follow the ADODG-defined test case setup are marked as “Yes”, while those adopting different conditions are marked as “No” (i.e., although the conditions of these studies are slightly different than ADODG Test Case 2, they do not reflect the exact conditions as this case). Furthermore, these tables are updated with the corresponding results and the achieved improvements, as will be discussed in the Results section.
Adjoint-based methods have traditionally been the backbone of gradient-based aerodynamic shape optimization due to their ability to compute gradients efficiently, particularly when dealing with a large number of design variables. This capability has made them the preferred approach in several studies focusing on the RAE 2822 airfoil, especially with the ADODG Test Case 2. Numerous studies have utilized the SU2 open-source CFD suite in conjunction with adjoint solvers [
3,
4,
8,
9], while others have applied industrial solvers such as elsA [
5]. Despite their theoretical elegance, these methods are not without limitations. Challenges such as the sensitivity of gradient accuracy to shock-separation interactions [
6], difficulties in optimization convergence due to non-unique flow solutions [
7], and the complexity of robust parameterization [
5] have been frequently reported. For instance, Poole et al. [
2] employed a gradient-based FSQP optimizer with a control point-based deformation strategy and demonstrated reasonable performance with a modest number of design variables. Yang et al. [
3] compared two different geometry parameterization approaches and highlighted their insensitivity to parameterization settings. Abergo [
4] presented a robust adjoint-based optimization in his thesis and acknowledged that while the final result was not the best, it was comparable to existing benchmarks. Other works have echoed similar concerns: Carrier et al. [
5] emphasized that achieving both robustness and efficiency in adjoint methods is nontrivial and often dependent on best-practice consolidation; He et al. [
6] noted sensitivity to shock-induced instabilities, while Lee et al. [
7] demonstrated that mesh resolution and deformation method can significantly impact convergence behavior. These accumulated challenges underscore the growing interest in alternative strategies such as surrogate-based optimization methods. In contrast to adjoint techniques, surrogate models—particularly those embedded in global optimization frameworks—offer robustness against numerical instabilities, flexibility in handling multi-fidelity or multi-point problems, and a natural capacity for global exploration without requiring gradient information. The gradient-free methods require a lot of computational resources when scanning globally. This is indeed a general disadvantage of gradient-free methods. The present study leverages this potential by adopting an EGO [
22] framework enhanced with gradient-informed surrogate models to address the limitations encountered in adjoint-based approaches, especially in transonic, multi-point aerodynamic design.
Surrogate-based optimization strategies have increasingly been explored as robust alternatives to gradient-based methods, especially in aerodynamic shape optimization problems involving costly CFD simulations. These methods aim to reduce computational expenses by approximating the true objective function using inexpensive surrogate models. Notably, Zhang et al. [
10] compared a multi-round surrogate-based optimization strategy with adjoint-based methods for the RAE 2822 airfoil and demonstrated competitive performance. Neural-network-based surrogate approaches have also gained attention: Nagawkar et al. [
11] utilized multifidelity neural networks and further enhanced them through gradient-enriched versions (GENN). While promising, such black-box surrogates often lack interpretability and can suffer from instability in high-gradient regions. A more systematic class of approaches, centered on Kriging and Gaussian Process Regression (GPR), have formed the foundation of many EGO frameworks. For example, Wang et al. [
12], Zhang et al. [
13], and Koratikere et al. [
20] employed EGO variants, often coupled with Expected Improvement (EI) criteria or neural network surrogates. However, standard Kriging models can face challenges when handling high-dimensional (high number of design variables) or ill-conditioned design spaces, and typically lack built-in mechanisms to account for gradient information. To mitigate these issues, more advanced surrogate formulations have been proposed. Xue et al. [
15] incorporated automatic kernel construction to adaptively improve GPR models, while Özkaya and Gauger [
18] proposed a gradient-informed aggregation strategy. Still, many of these methods remain limited in their ability to generalize across multi-point or high-fidelity design requirements, or to effectively integrate gradient data in a stable manner. In contrast, the present study adopts and systematically compares four advanced surrogate models KRG, KPLS, GEK, and GEKPLS within an EGO framework. These models offer complementary strengths: KPLS enhances Kriging’s scalability in high-dimensional spaces through dimensionality reduction; GEK exploits available gradient data to increase local accuracy; and GEKPLS combines both strategies for improved robustness and convergence efficiency. By incorporating these advanced surrogates into a unified optimization framework, this study aims to bridge the gap between global exploration and local refinement, addressing limitations observed in earlier surrogate-based efforts. This structured approach forms the cornerstone of the proposed methodology and highlights the novelty of the current contribution in the aerodynamic shape optimization of transonic airfoils.
While surrogate-based methods have shown promise in single-point aerodynamic optimization, their extension to multi-point scenarios remains relatively underexplored, largely due to increased modeling complexity, conflicting design requirements, and the need for global consistency across multiple operating conditions. Only a limited number of studies have attempted to address the multi-point optimization of the RAE 2822 airfoil. For instance, Koratikere and Leifsson [
20] extended their cEGO-based single-point framework to accommodate three flight regimes by varying the Mach number, representing takeoff, cruise, and landing. Their approach remained confined to a neural-network surrogate and did not explicitly address the scalability and generalizability issues associated with more physically-informed surrogate models. Nagawkar et al. [
14], on the other hand, employed manifold mapping under Euler assumptions to reduce computational costs, but the lack of viscous effects and gradient exploitation limits the practical applicability and local accuracy of the resulting designs. Similarly, Toal and Keane [
21] applied Kriging models to multi-point problems, but scalability with respect to increasing design variables and the integration of gradient information remained unresolved.
The design framework employed in this study incorporates EGO [
23] along with EI as the infill sampling criterion [
23,
24]. Initially, the surrogate model within EGO was integrated with the Kriging method [
25], one of the most frequently encountered surrogate models in literature [
21,
26,
27]. However, there are concerns about the performance limitations of Kriging, and several studies aim to address and improve its capabilities [
28,
29]. Bouhlel et al. [
30] proposed the Kriging with Partial Least Squares (KPLS) method, integrating PLS with Kriging to enable optimization with higher numbers of design variables, although their validation was limited to mathematical analytic functions.
Despite its advantages, Kriging has been reported to suffer from issues such as slow convergence and limited accuracy [
31]. To improve Kriging’s accuracy, GEK [
32] was developed, which incorporates gradient information during surrogate model construction. Finally, Bouhlel et al. [
33] proposed the Gradient-Enhanced Kriging with Partial Least Squares (GEKPLS) method, addressing challenges associated with inverting large gradient-augmented datasets by combining the benefits of KPLS and GEK. Although still relatively new and less widely adopted in the literature, GEKPLS theoretically combines the advantages of PLS in reducing the number of Kriging hyperparameters and the enhanced accuracy of GEK through gradient information, making it particularly effective for high-dimensional optimization problems.
In light of the limitations observed in both adjoint-based and surrogate-based aerodynamic optimization approaches—particularly in the context of multi-point problems—this study aims to advance the state-of-the-art by developing and evaluating a unified surrogate-based optimization framework with gradient-enhancement. The framework is applied to the RAE 2822 airfoil for both single-point and multi-point transonic viscous flow conditions. The proposed approach systematically integrates advanced surrogate models with robust geometry parameterization and CFD-based gradient information, offering a scalable and physically grounded design methodology. The novelty and key contributions of this study can be summarized as follows:
Gradient-informed surrogate modeling: Implementation and comparison of four surrogate types—KRG, KPLS, GEK, and the combined GEKPLS under a single framework—to enable more accurate local approximations and global search.
Multi-point optimization in viscous transonic regime: Extension of the surrogate-based EGO framework to a multi-point setup, addressing multiple operating conditions with viscous CFD, a task rarely attempted in the literature.
Consistent parameterization and FFD-based shape control: Use of a stable and flexible geometry control mechanism compatible with high-fidelity solvers, ensuring robustness across diverse flight regimes.
Systematic evaluation and benchmarking: Direct comparison of surrogate strategies under identical CFD settings and design objectives, offering practical insights into model performance and reliability in realistic aerodynamic scenarios.
These contributions not only address key gaps in previous works but also demonstrate the feasibility of reliable and efficient aerodynamic shape optimization in complex, multi-point design environments.
Extensive comparisons with benchmark literature results are provided to validate the methodology and highlight the competitiveness of the proposed surrogate-assisted strategies in drag reduction.
5. Discussion
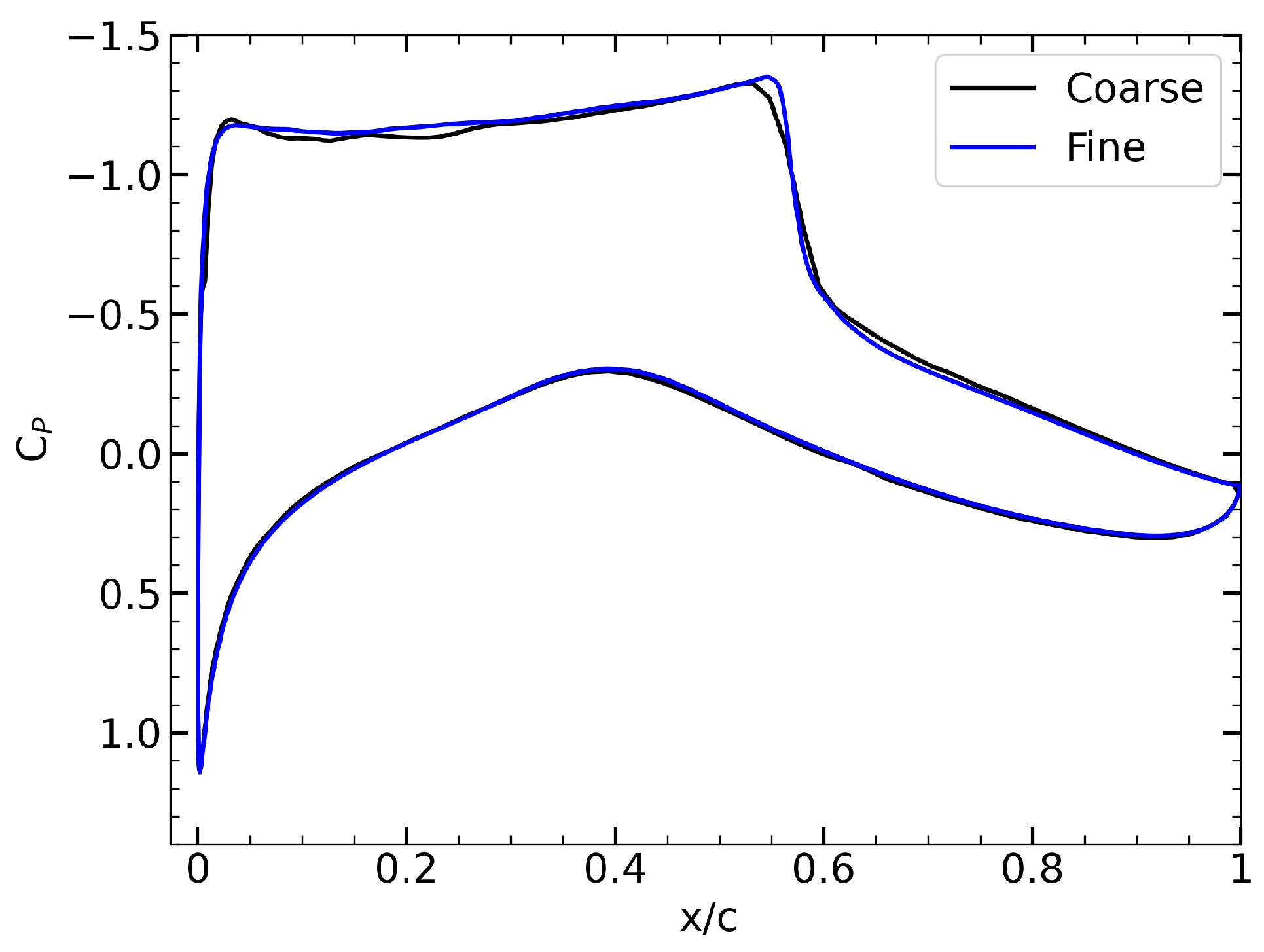
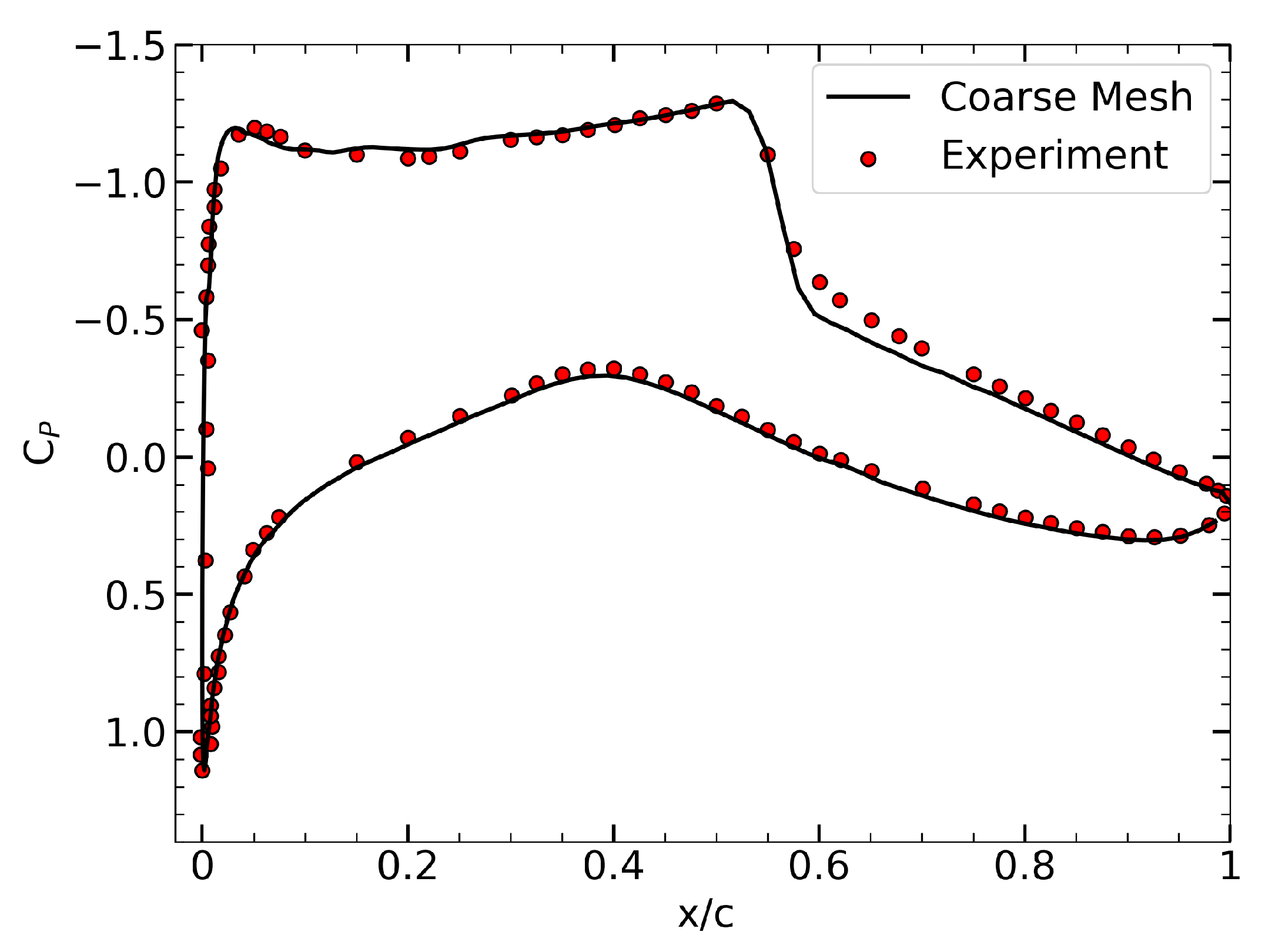
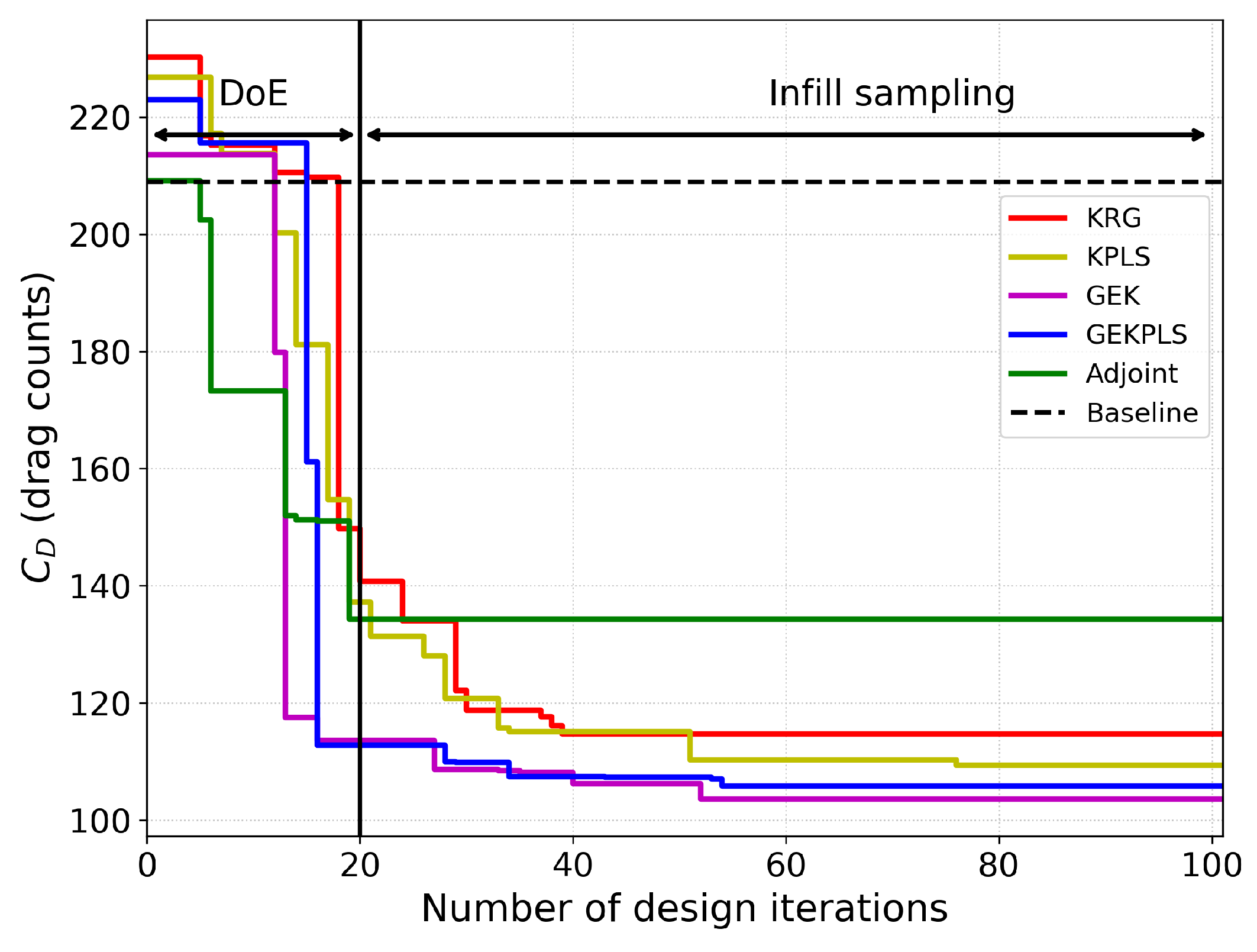
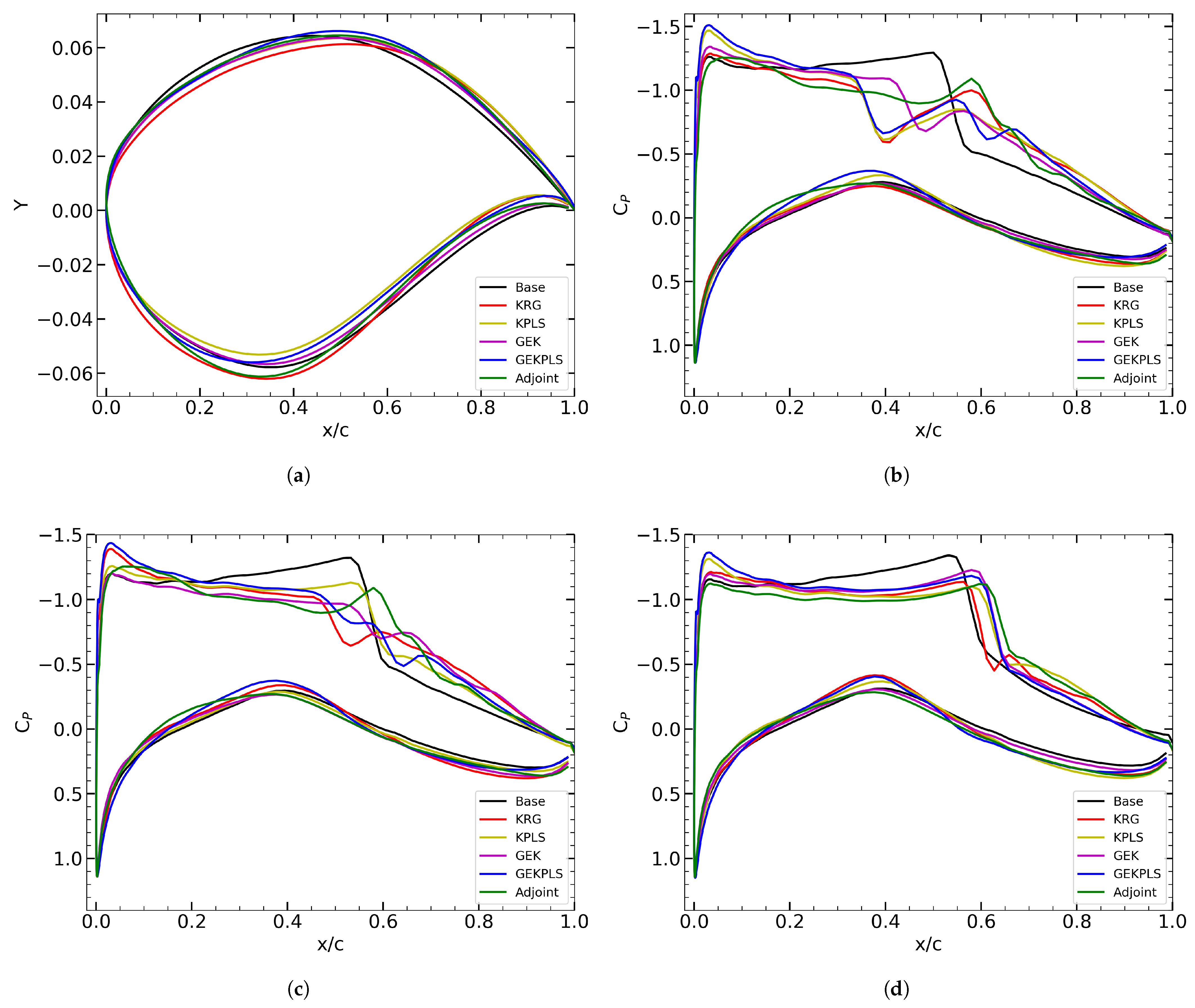
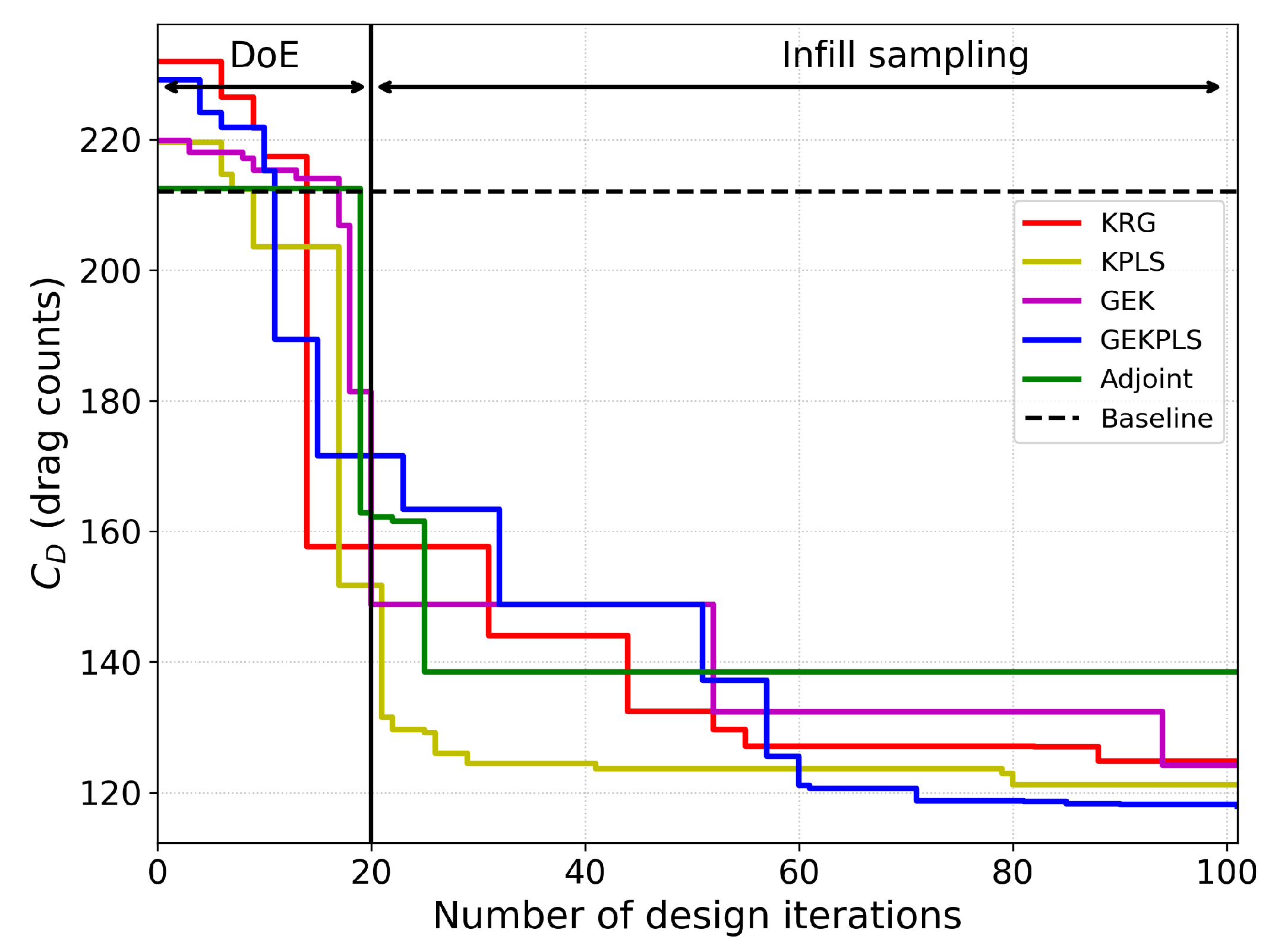
The present study assessed the performance of surrogate-based and gradient-based optimization methods for aerodynamic shape optimization using the RAE 2822 airfoil as a benchmark case. Validation against experimental data confirmed the CFD setup’s ability to capture critical flow features, providing a solid foundation for subsequent optimization. In single-point optimization, surrogate-based methods incorporating gradient information (GEK and GEKPLS) significantly outperformed KRG and KPLS approaches and the adjoint-based method, consistent with prior findings that highlight the advantages of gradient-enriched models. Similarly, in multi-point optimization, the GEKPLS method demonstrated strong performance under transonic, viscous flow conditions, achieving results comparable to or exceeding those reported in the literature.
These results reinforce the hypothesis that incorporating gradient information into surrogate models improves both optimization efficiency and final design quality. The performance gap observed between surrogate-based and gradient-based methods also suggests that, for problems involving complex flow phenomena and multiple operating conditions, surrogate models can provide not only competitive but also more robust solutions with controlled computational resources.
Comparison with literature studies further validated the competitiveness of the present methods, particularly under viscous flow conditions. These results highlight the advantages of incorporating gradient information into surrogate modeling and confirm the robustness of the proposed strategies for both single and multi-point aerodynamic optimizations.
In a broader context, the findings suggest that hybrid frameworks leveraging both surrogate modeling and gradient information can be critical for future high-fidelity aerodynamic optimizations. Future research may explore extensions to three-dimensional configurations, unsteady flows, and the integration of physics-informed machine learning approaches to further enhance surrogate model capabilities and optimization robustness across a wider range of aerodynamic design problems.