A Comparative Study of Unsupervised Deep Learning Methods for Anomaly Detection in Flight Data
Abstract
1. Introduction
- The current occurrence-based system relies on the human operator to establish patterns in exceedances from a particular aircraft or the fleet. It can be an overwhelming exercise for a human operator.
- Such occurrences are identified through set thresholds based on past experience, including incidents or accidents. As a result, the system cannot detect internal vulnerabilities or explore unknown safety issues. For examples, Boeing 737 Max aircraft’s software issues resulting in plane’s nose being pushed down unexpectedly and pilots struggled to regain control.
- Traditional Machine Learning (ML)-based techniques are dependent on quality of flight data, airports, type of aircraft and other various input factors as shown in the scholarly work [2]. The various input factors must be adjusted accordingly, but methods based on deep learning are capable of producing generalized models.
2. Literature Review of Unsupervised Deep Learning Techniques
3. Applications of Deep Learning Techniques
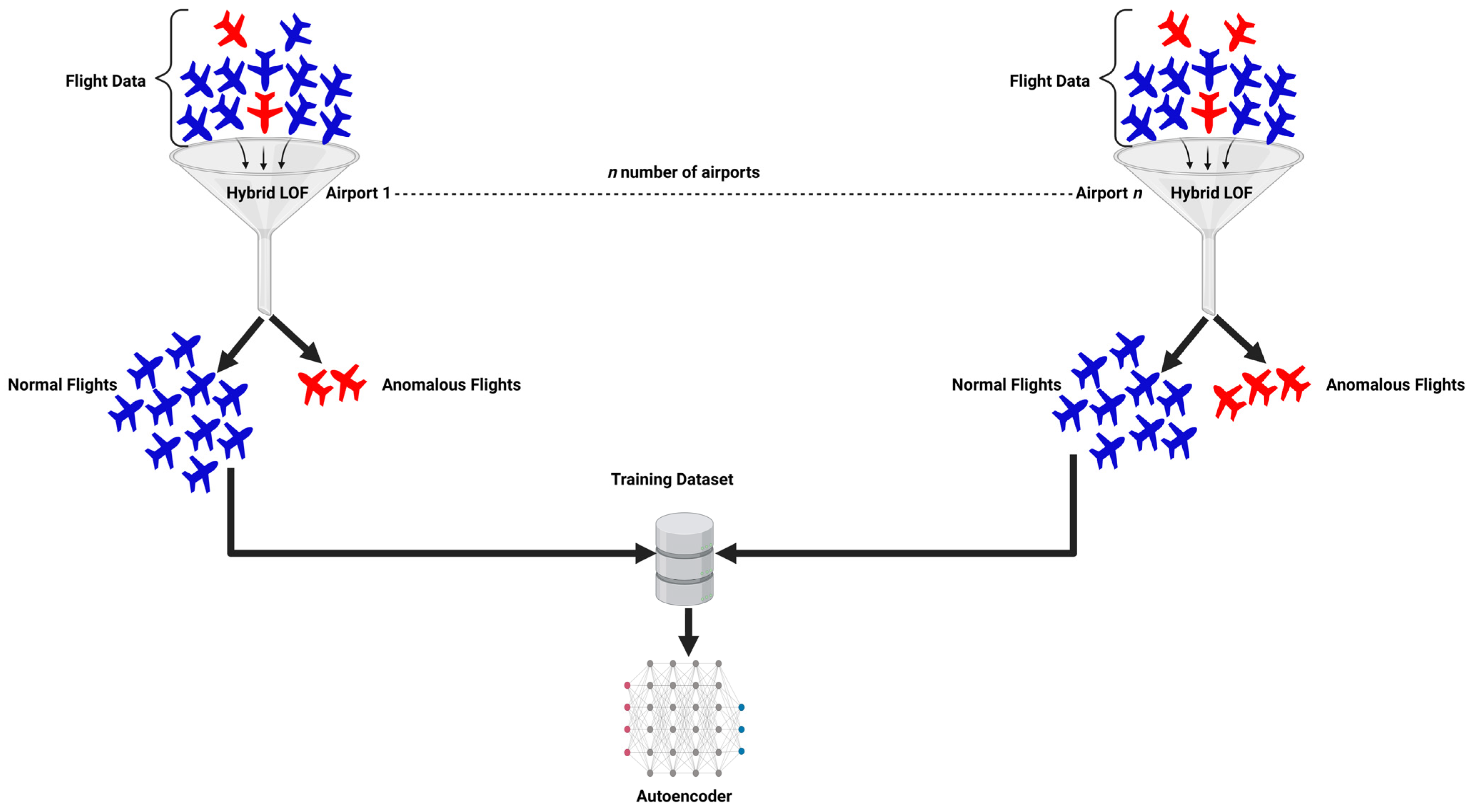
3.1. Flight Dataset
3.2. Selecting Approach and Landing Phase as a Case Study
3.3. Data Pre-Processing
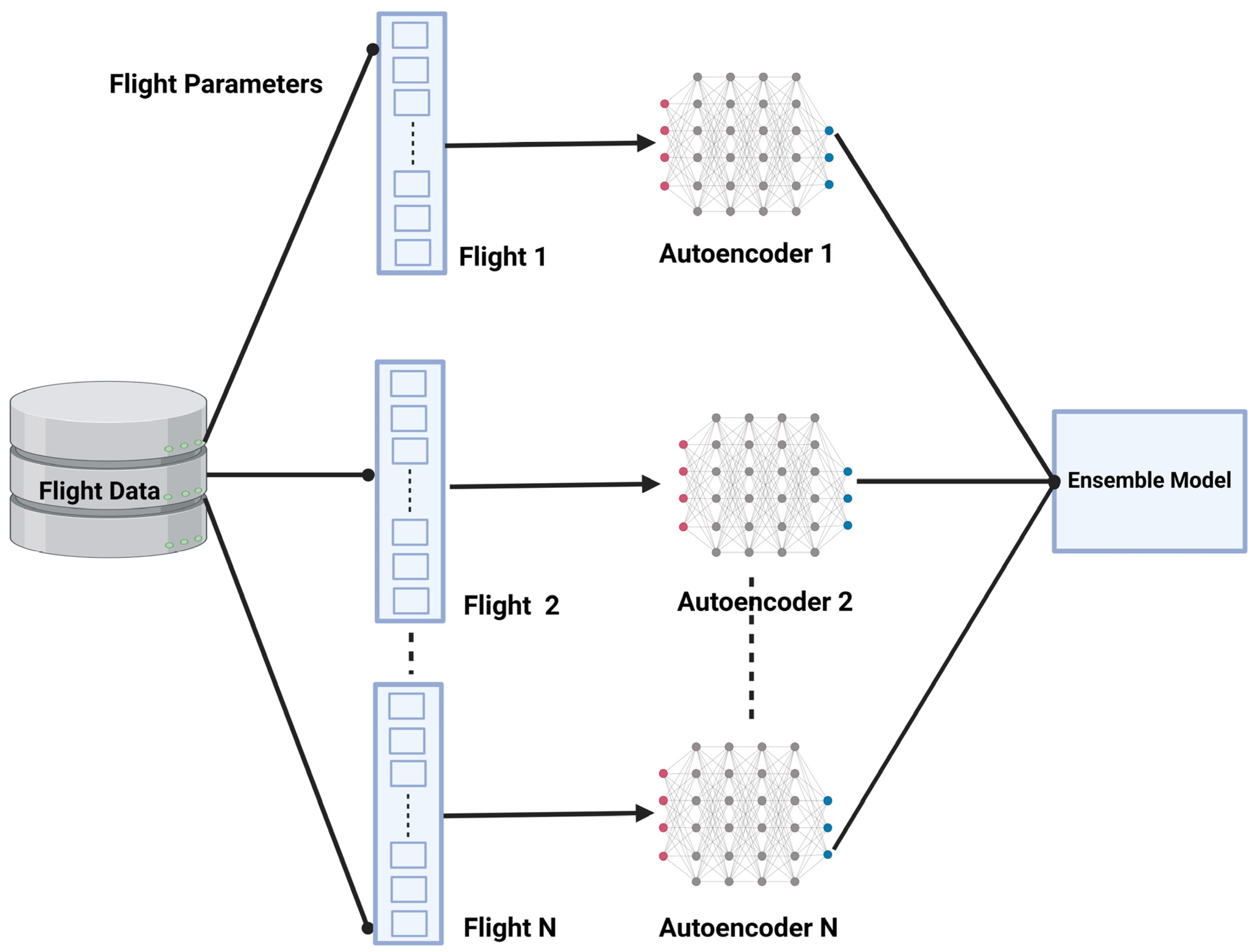
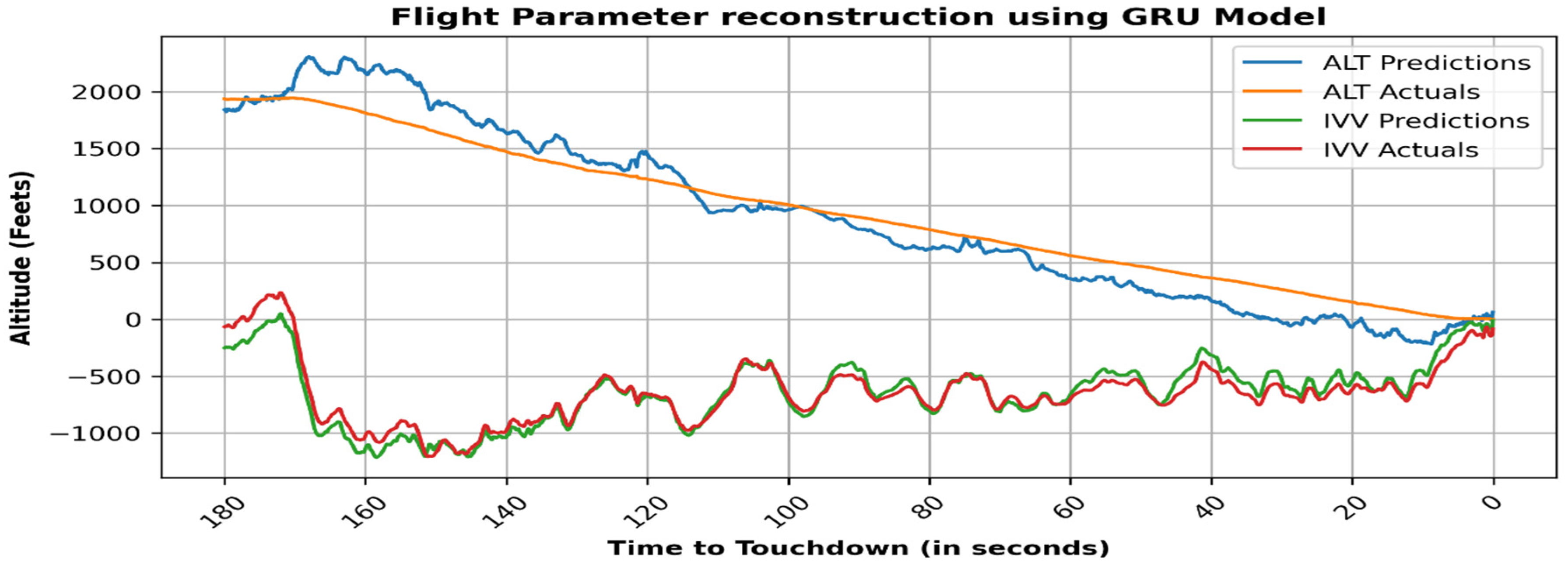
3.4. Unsupervised Deep Learning Techniques for Flight Data Analysis
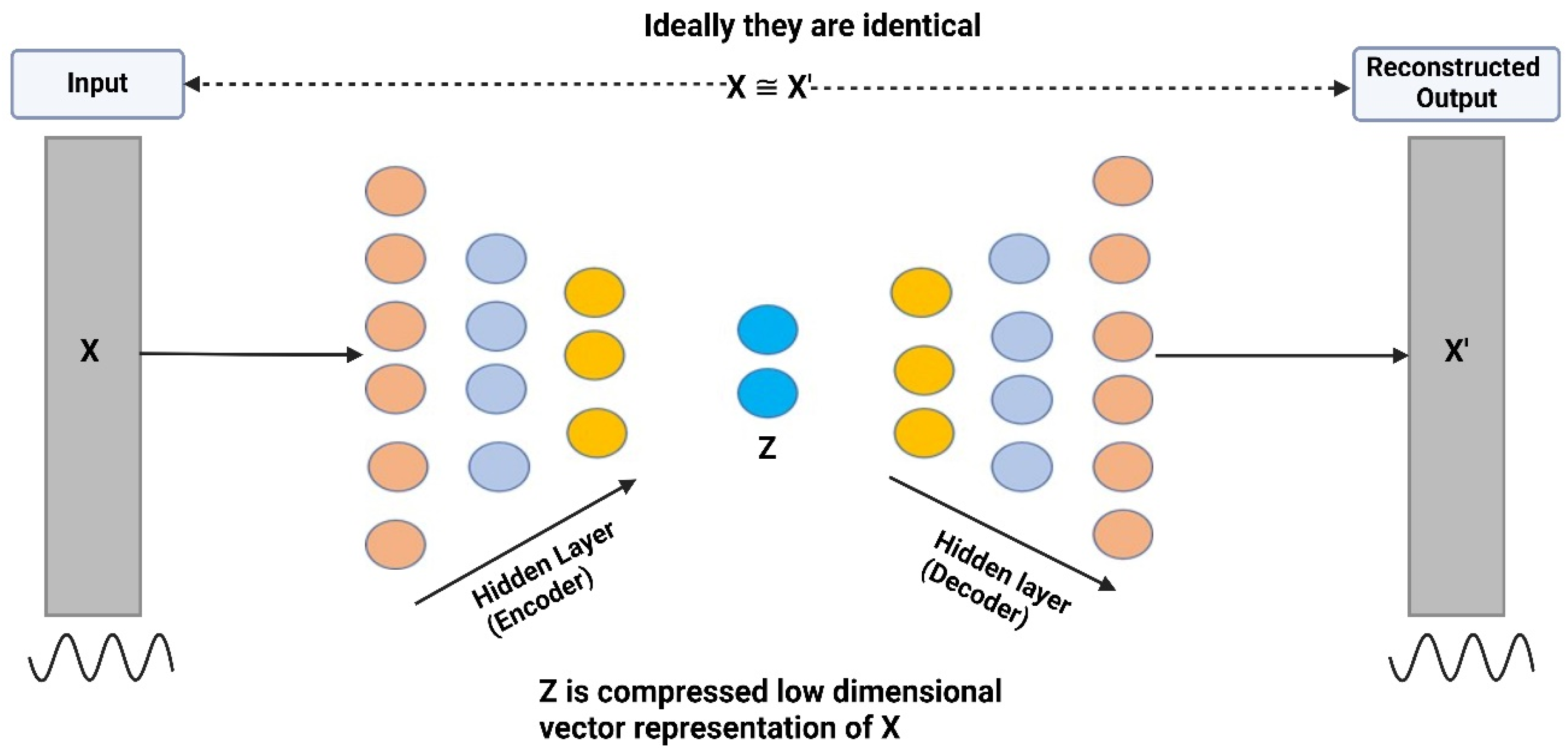
3.4.1. Autoencoder Architecture
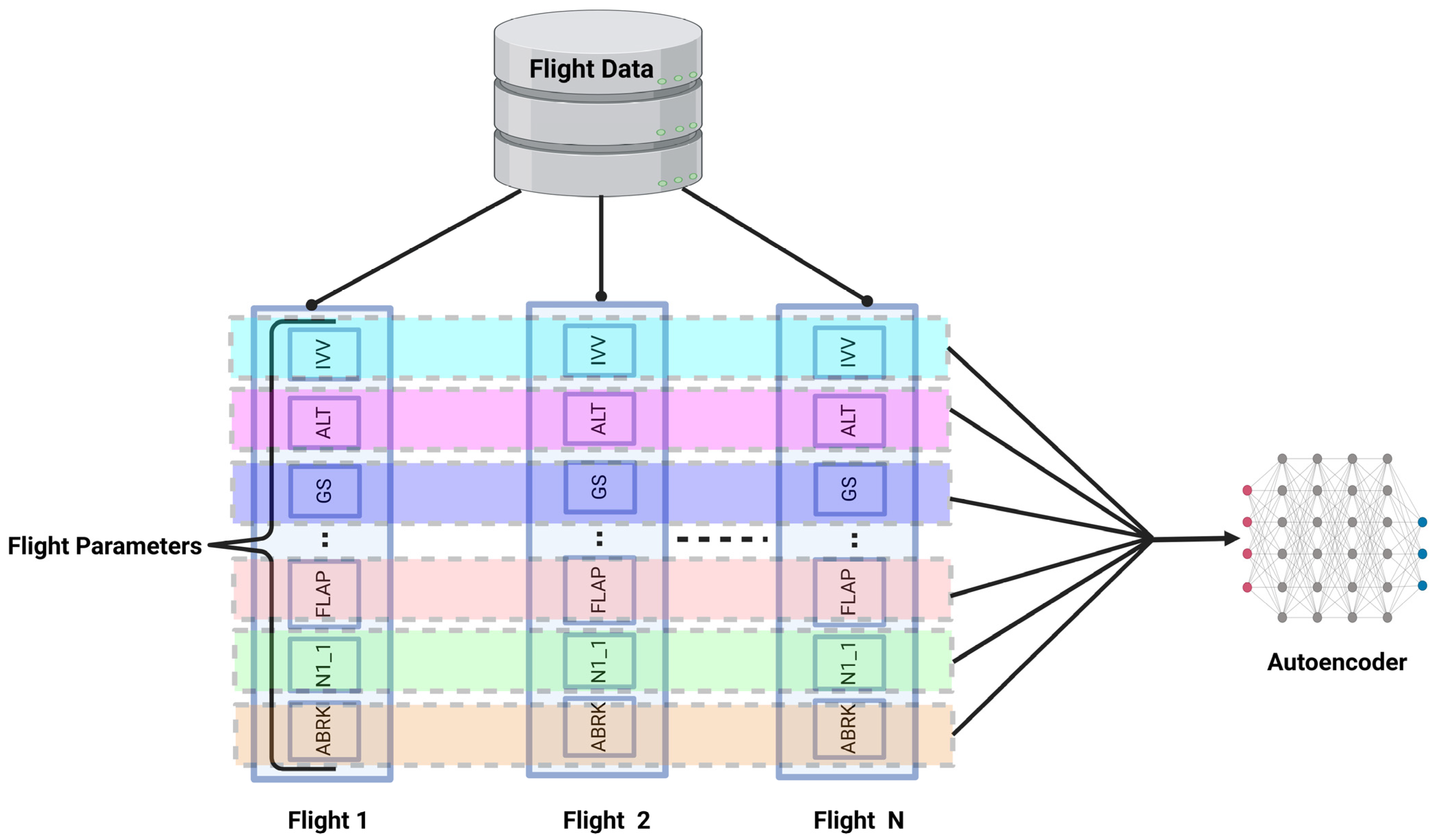
3.4.2. Formatting Flight Data for Autoencoder
3.4.3. Neural Networks
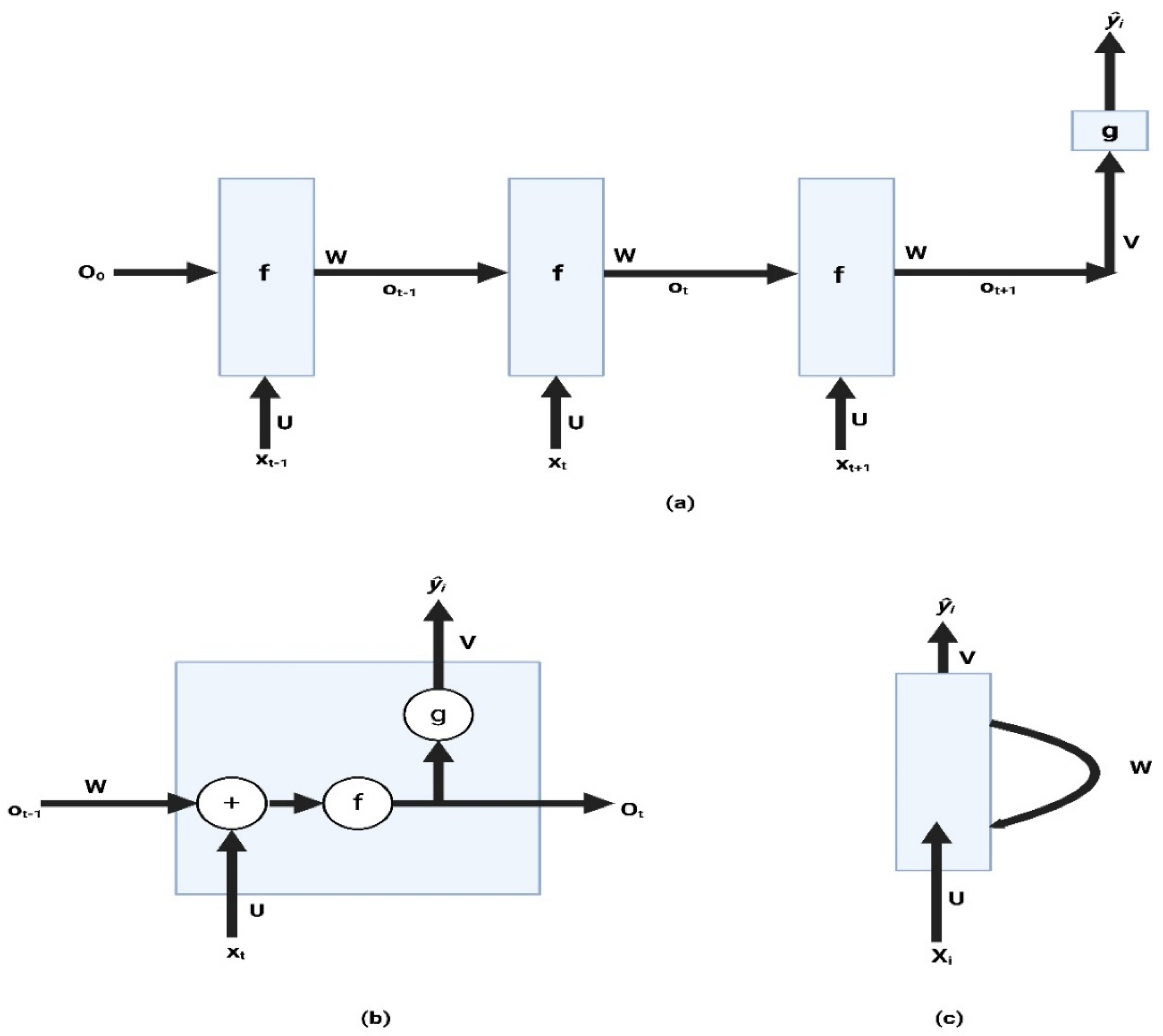
- Recurrent Neural Networks (RNNs)
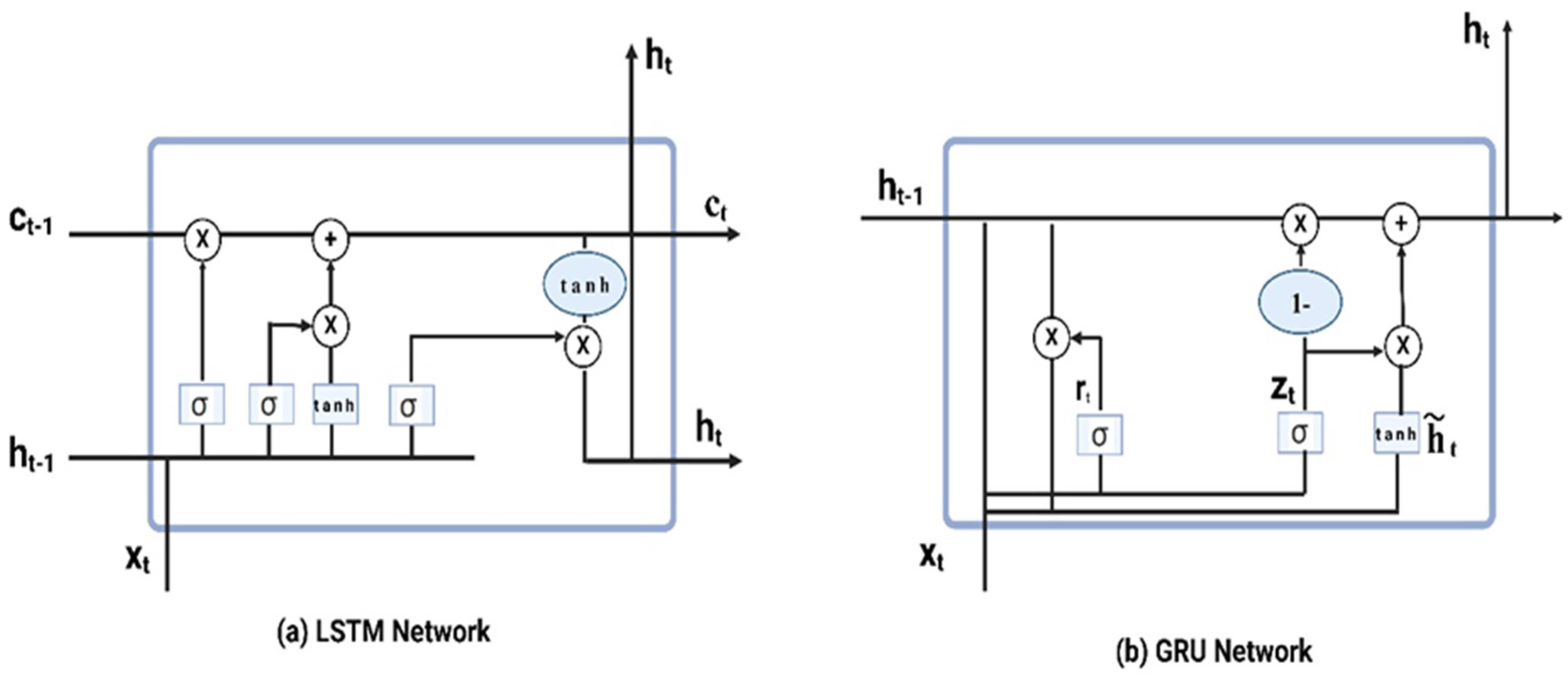
- 2.
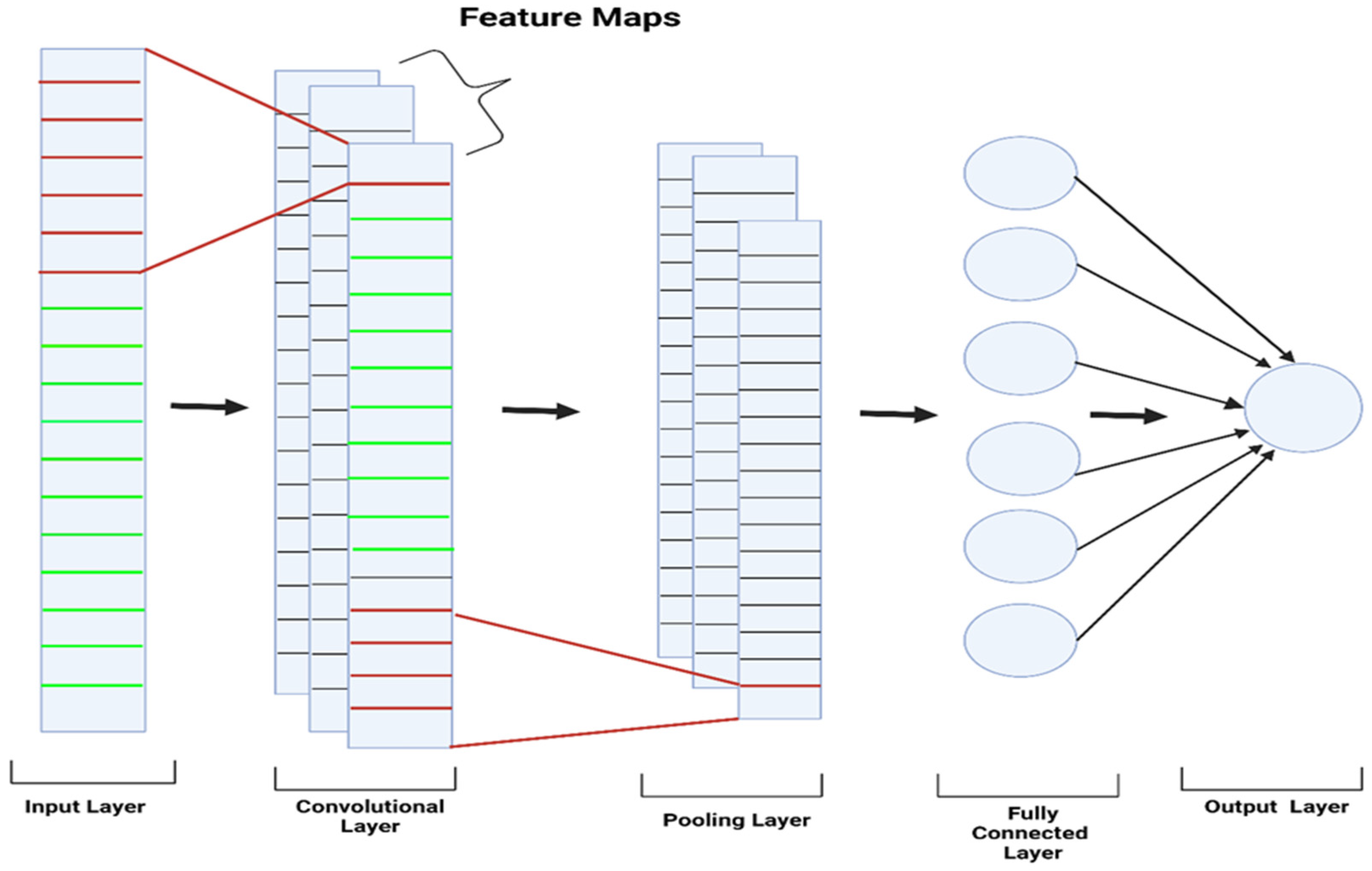
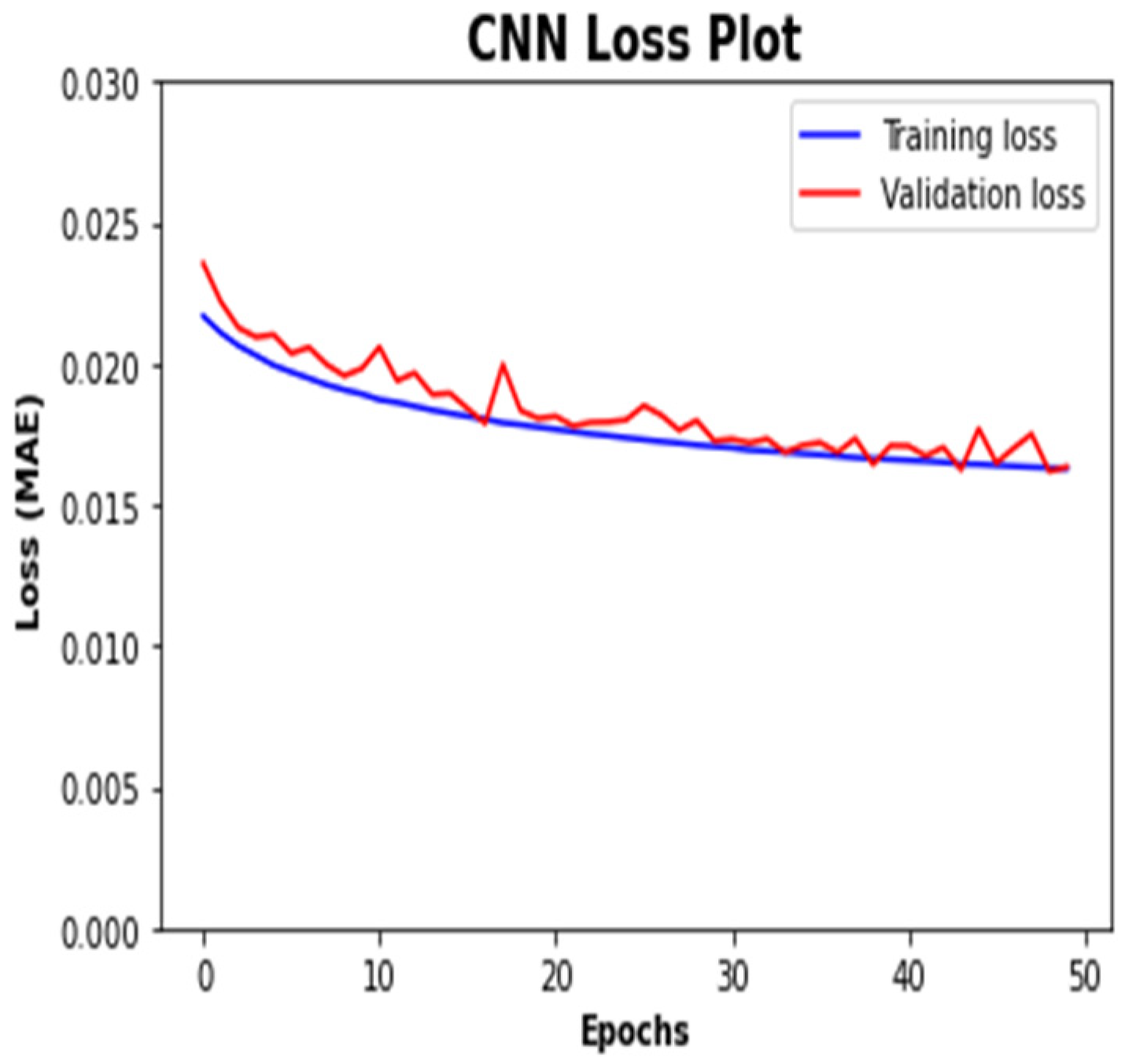
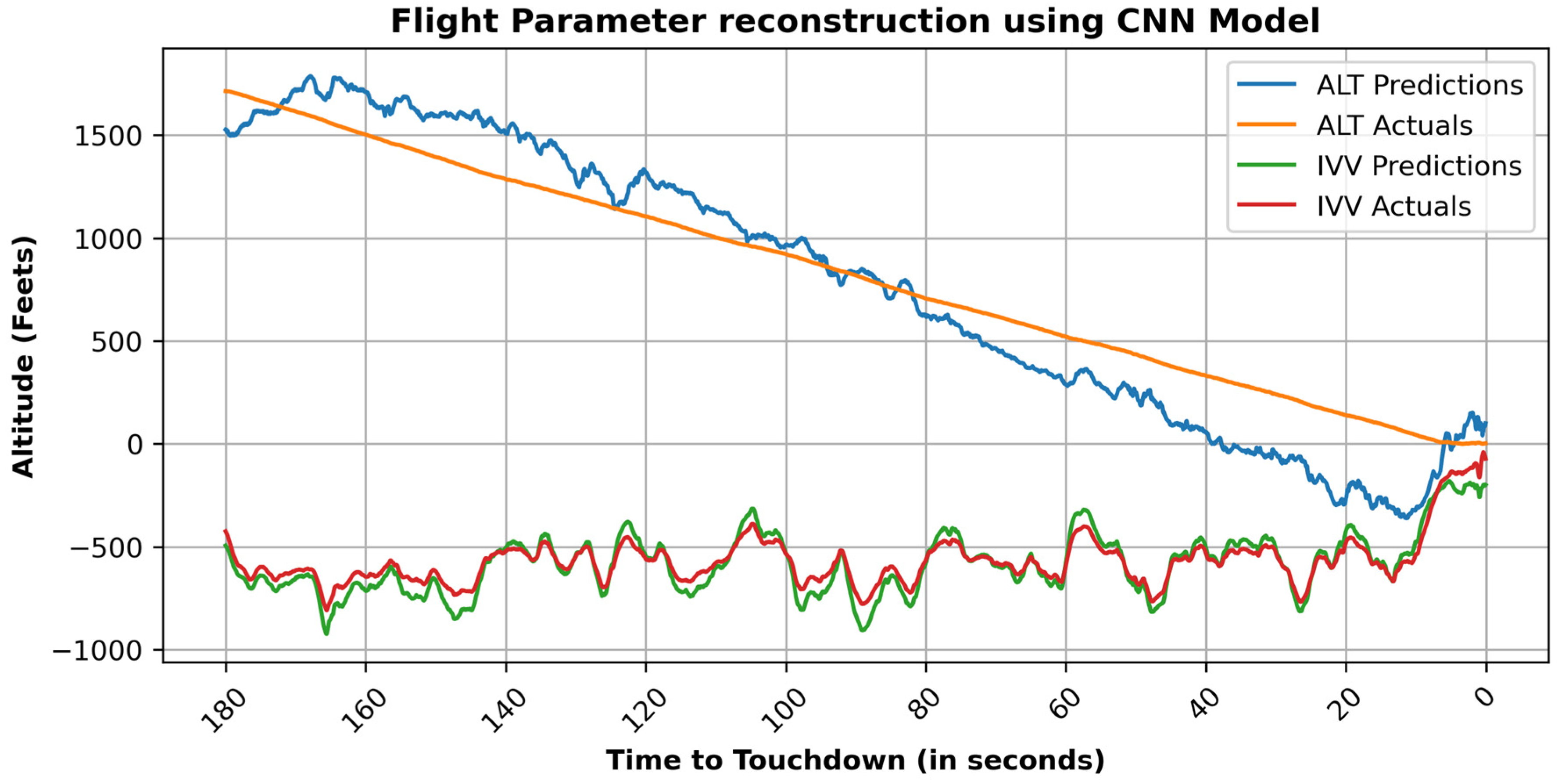
- Convolutional Neural Networks (CNNs)
- 3.
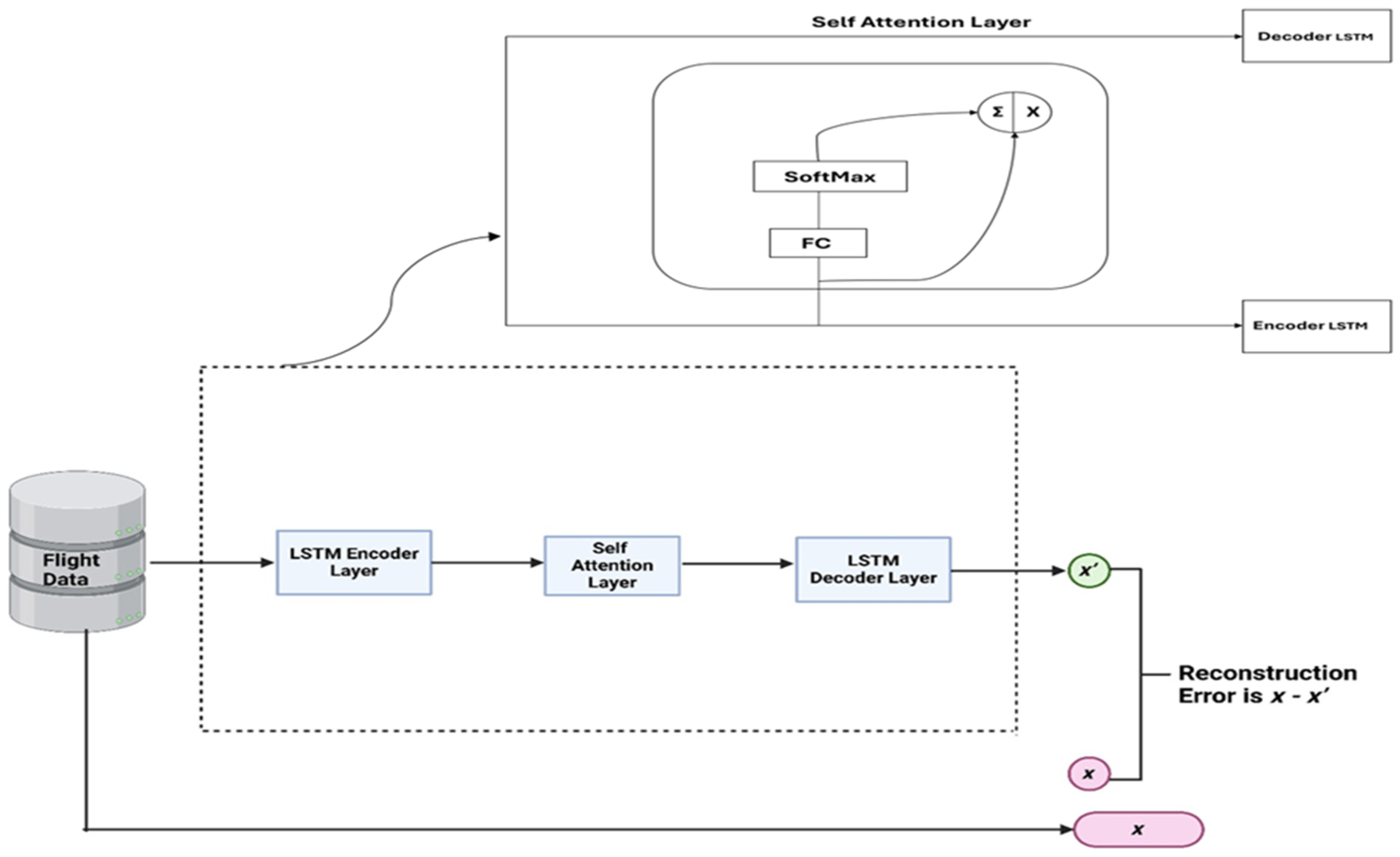
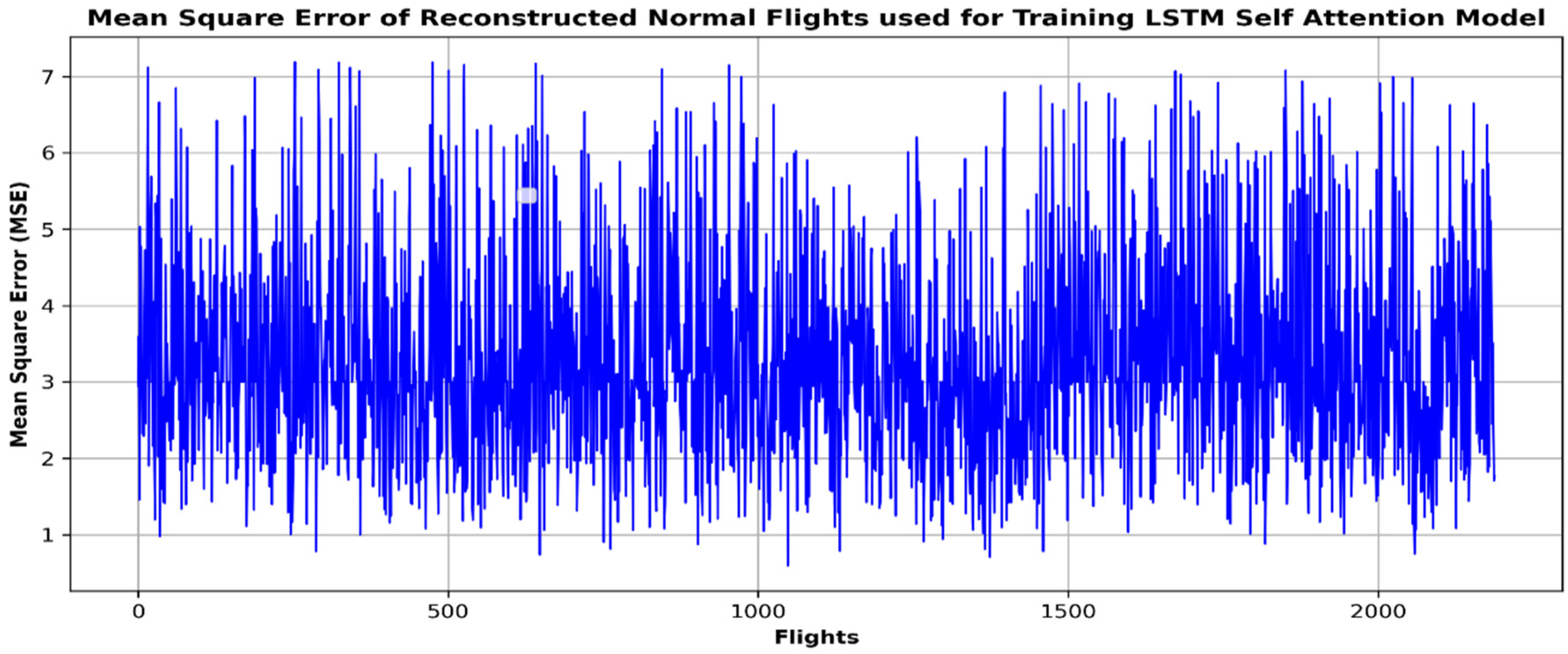
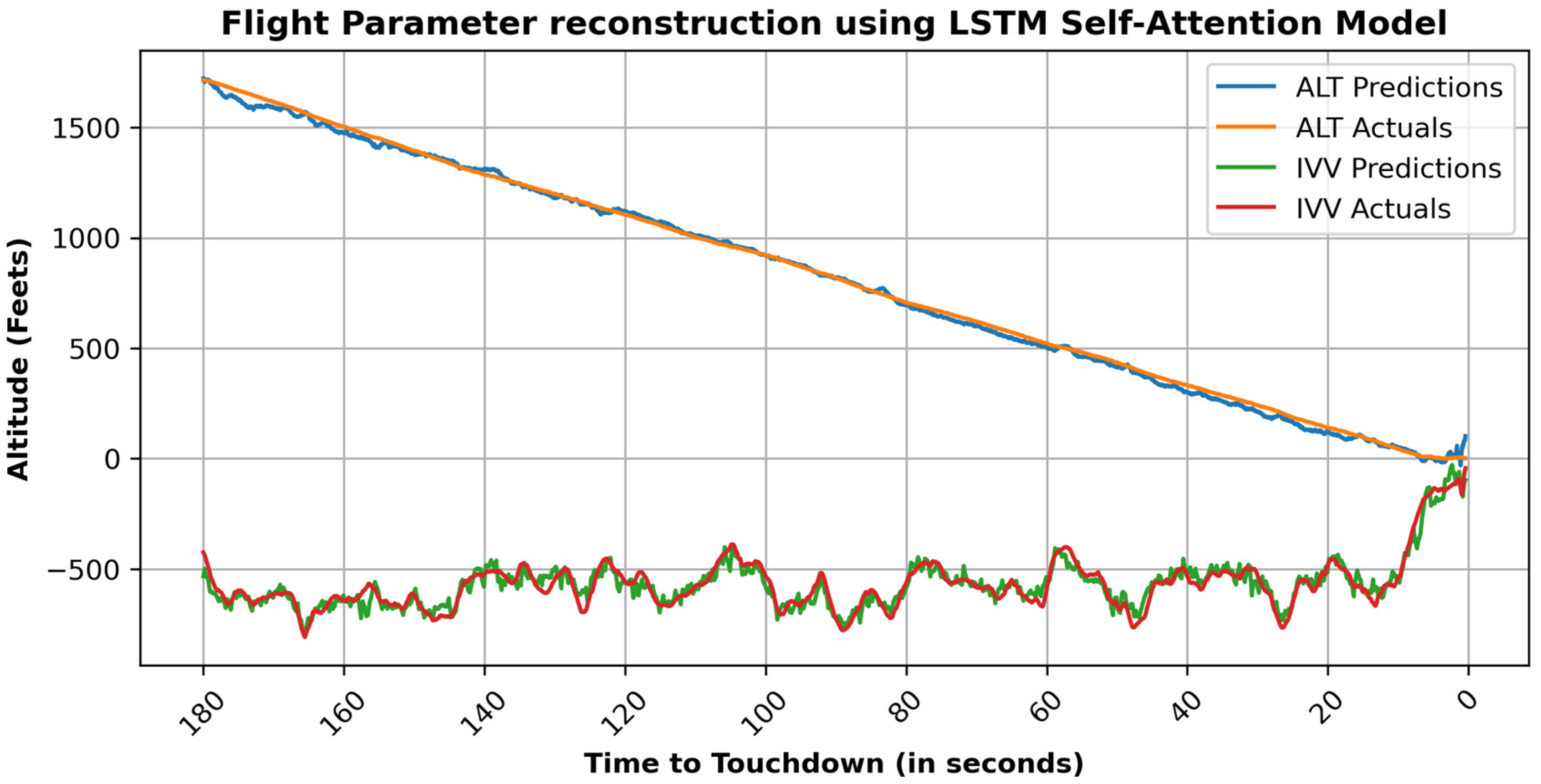
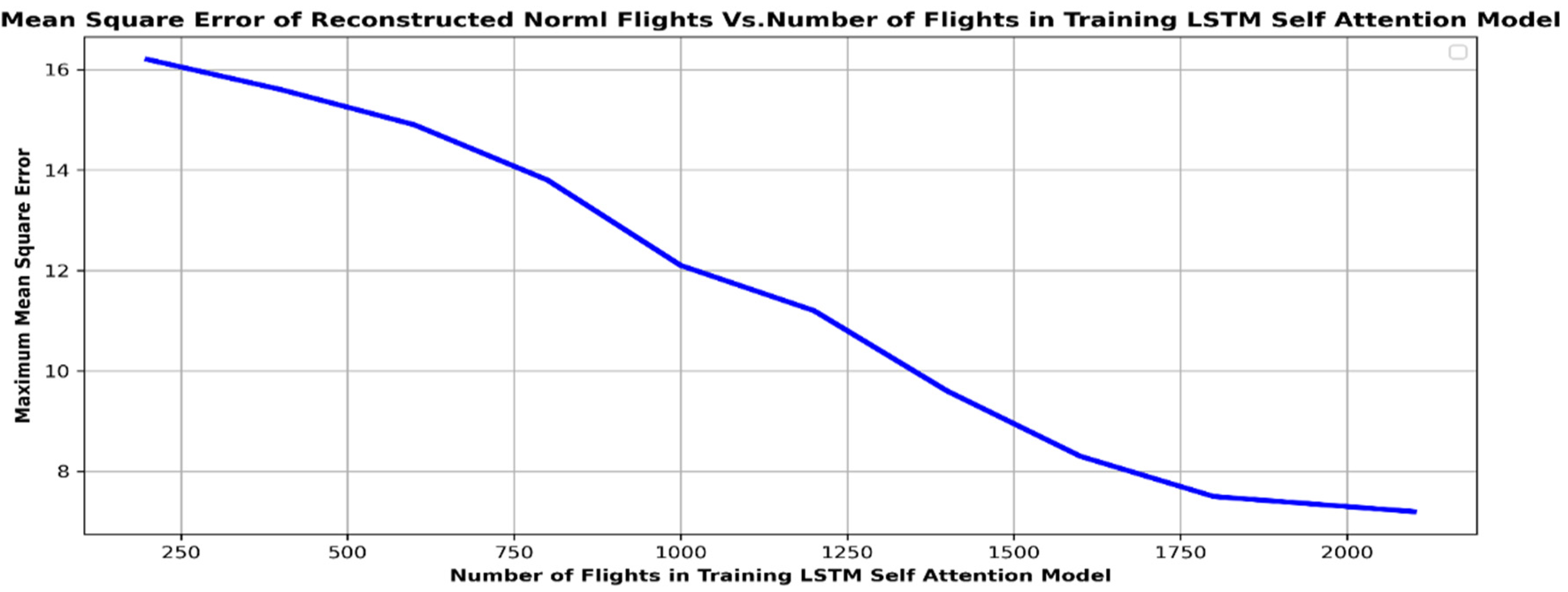
- LSTM Self-Attention Model
- 4.
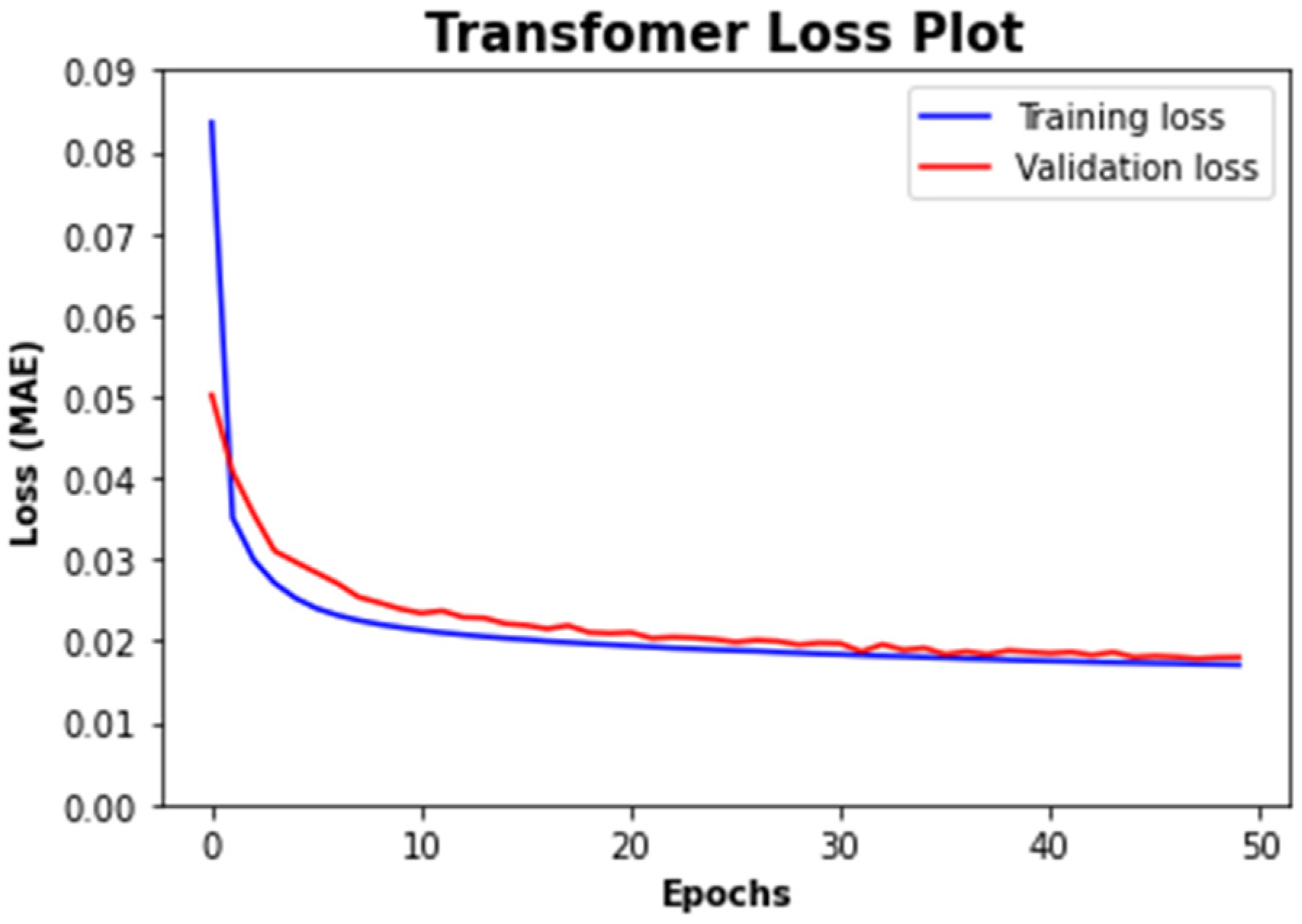
- Transformer
- Input and Output Embeddings: This converts input tokens (time series data) into vector representations (embeddings). Positional Encoding is added to embeddings to retain the positional context of tokens. A fixed (sinusoidal) vector is added to each embedding to inject token order information.
- Encoder (left side): The first layer in encoder block is Multi-Head Attention layer. It computes multiple attention mechanisms in parallel (“heads”) to capture different contexts. Allows each token to attend to all other tokens. For each head, compute
- 3.
- Decoder (right side): It has three layers. The first layer is Masked Multi-Head Attention layer. It allows the model to focus only on previous positions in the output sequence, preventing it from seeing future positions. The second layer is Multi-Head Attention layer. It enables decoder to attend to encoder outputs. The third layer is Feed-Forward Layer. It has a similar function as in the encoder. Similarly to encoder, each sub-layer in decoder is wrapped up with Add & Norm. Decoder layers are also stacked multiple times (N times) for deeper representation learning. It is represented as N×.
- 4.
- Linear Layer and Softmax: Liner layer converts decoder final outputs to the time series dimension. The role of the softmax function is to convert raw attention scores into probability distributions.
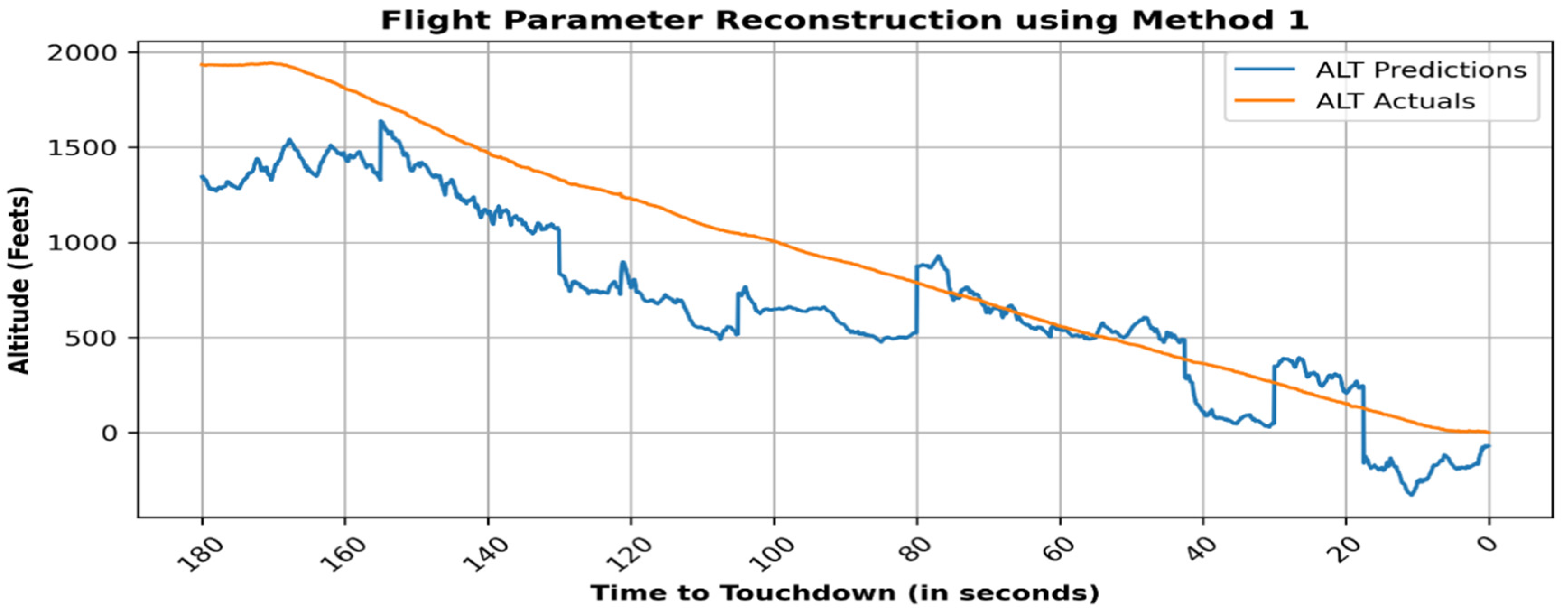
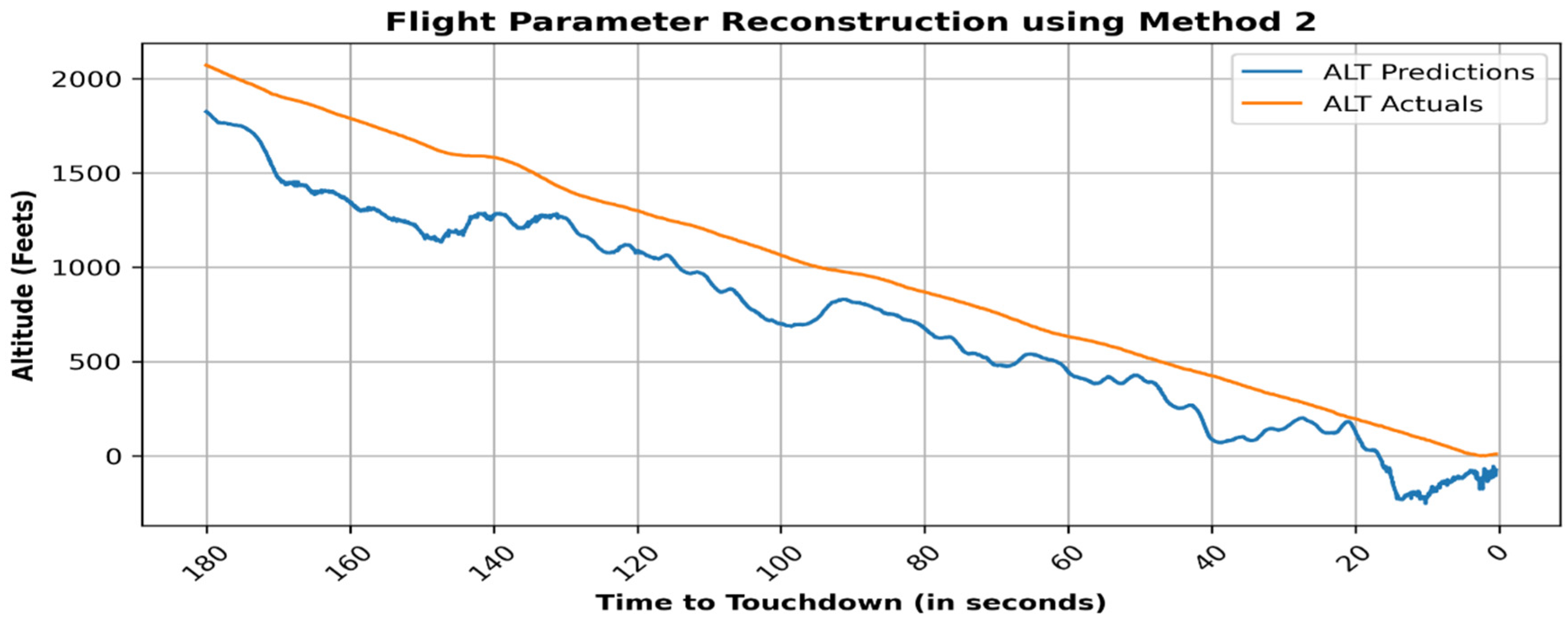
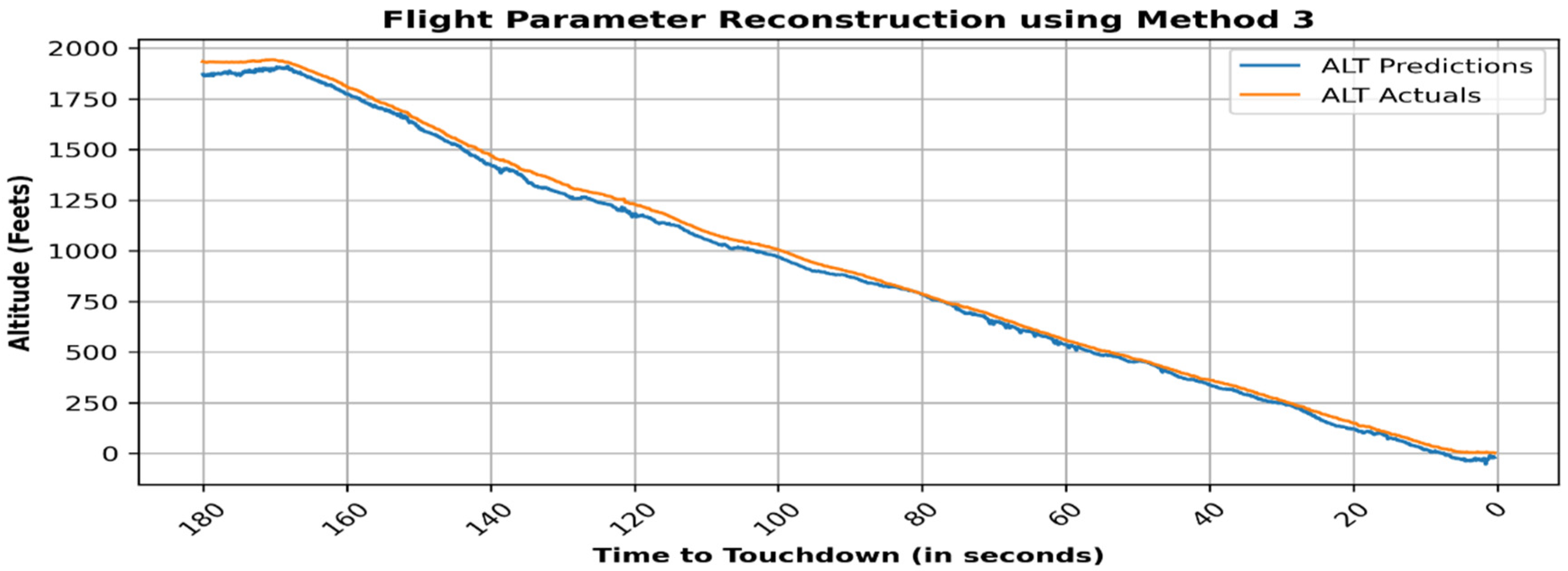
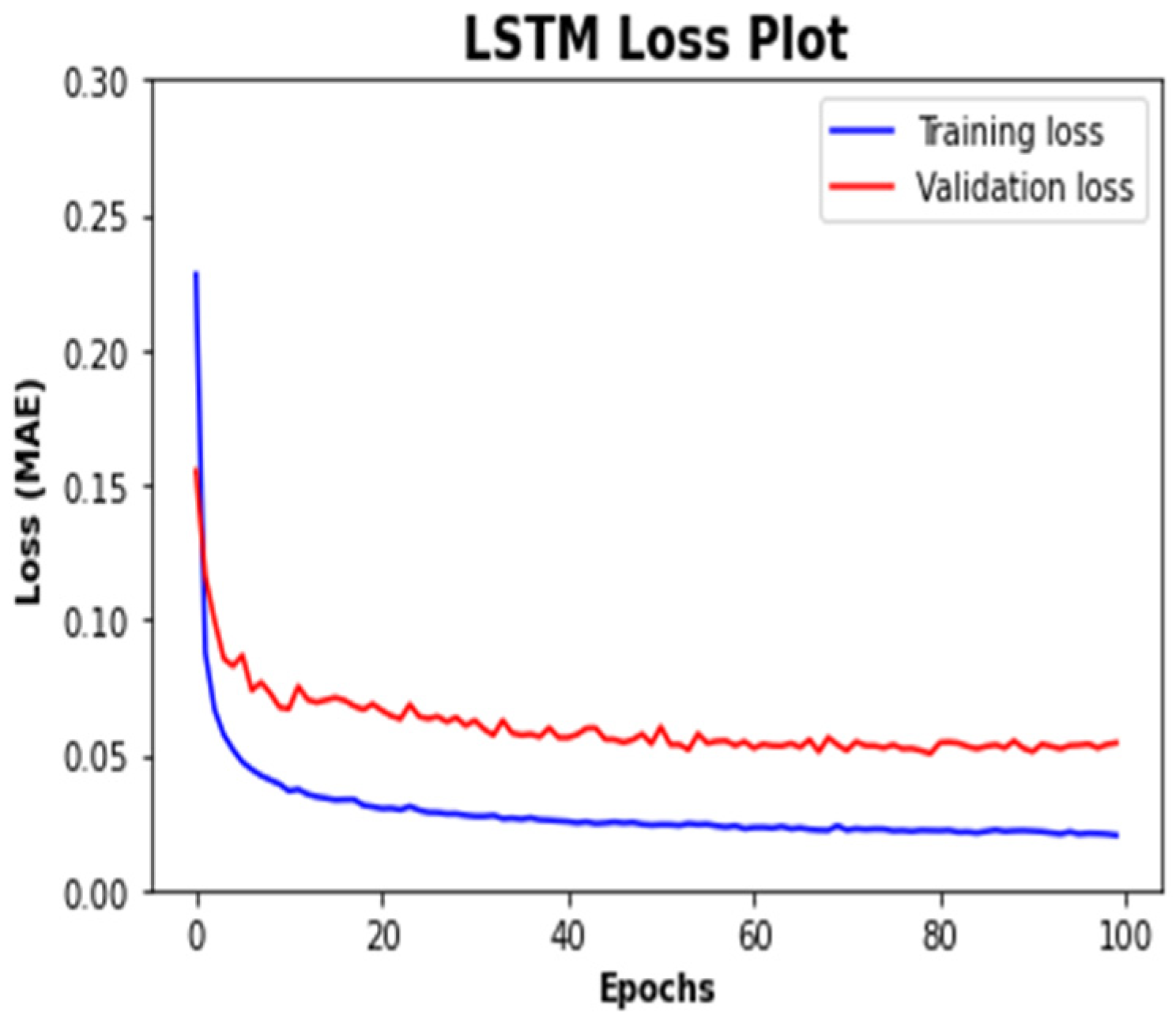
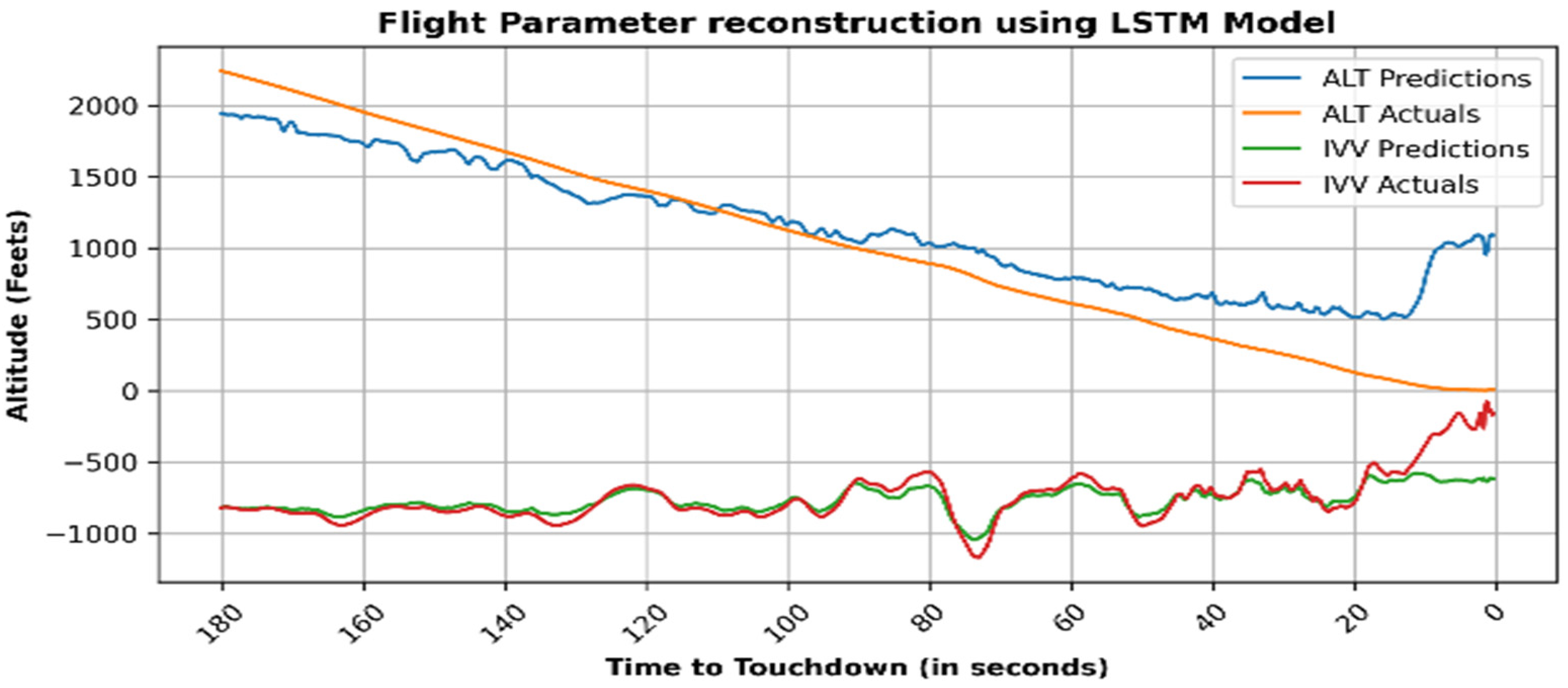
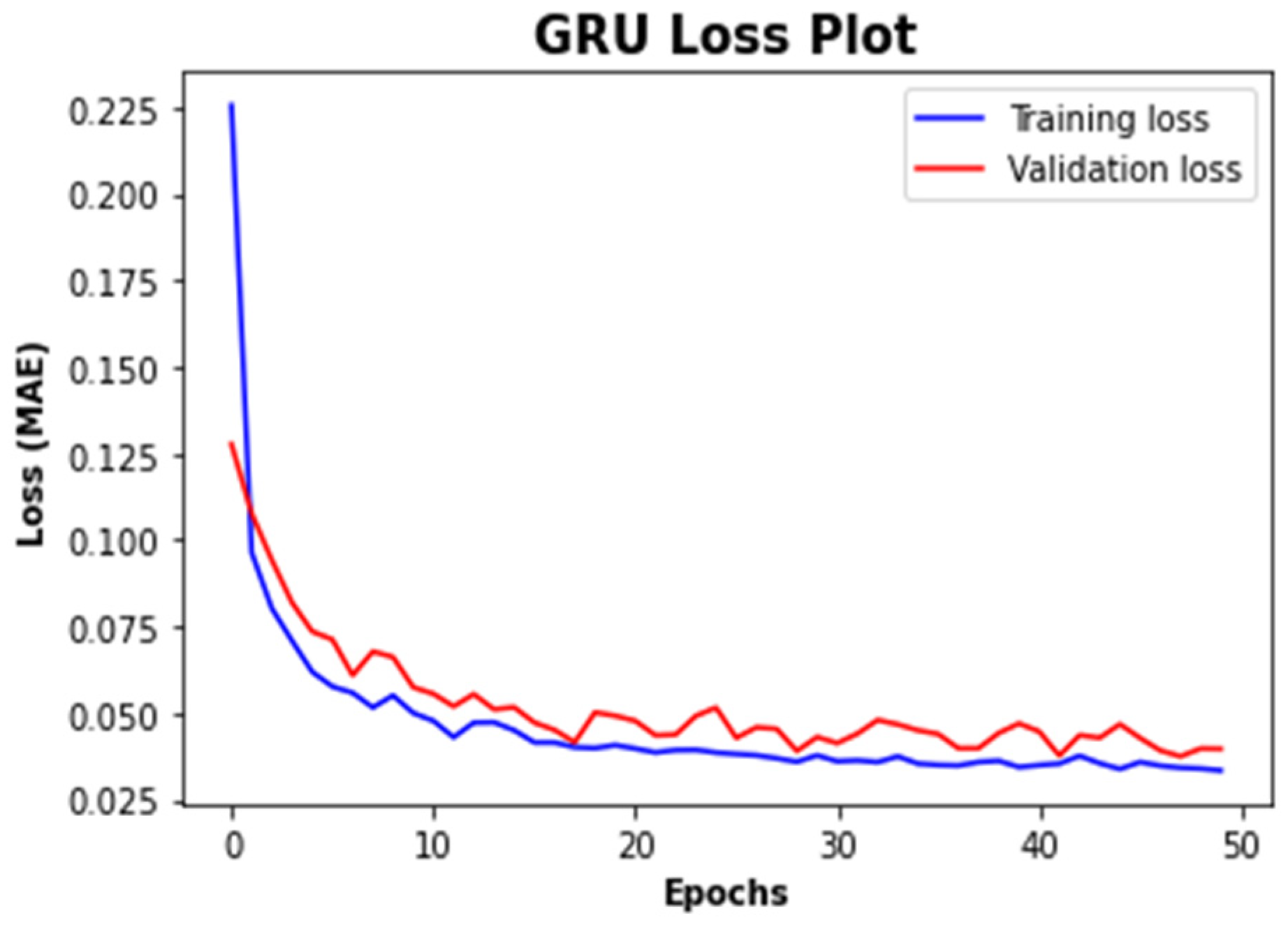
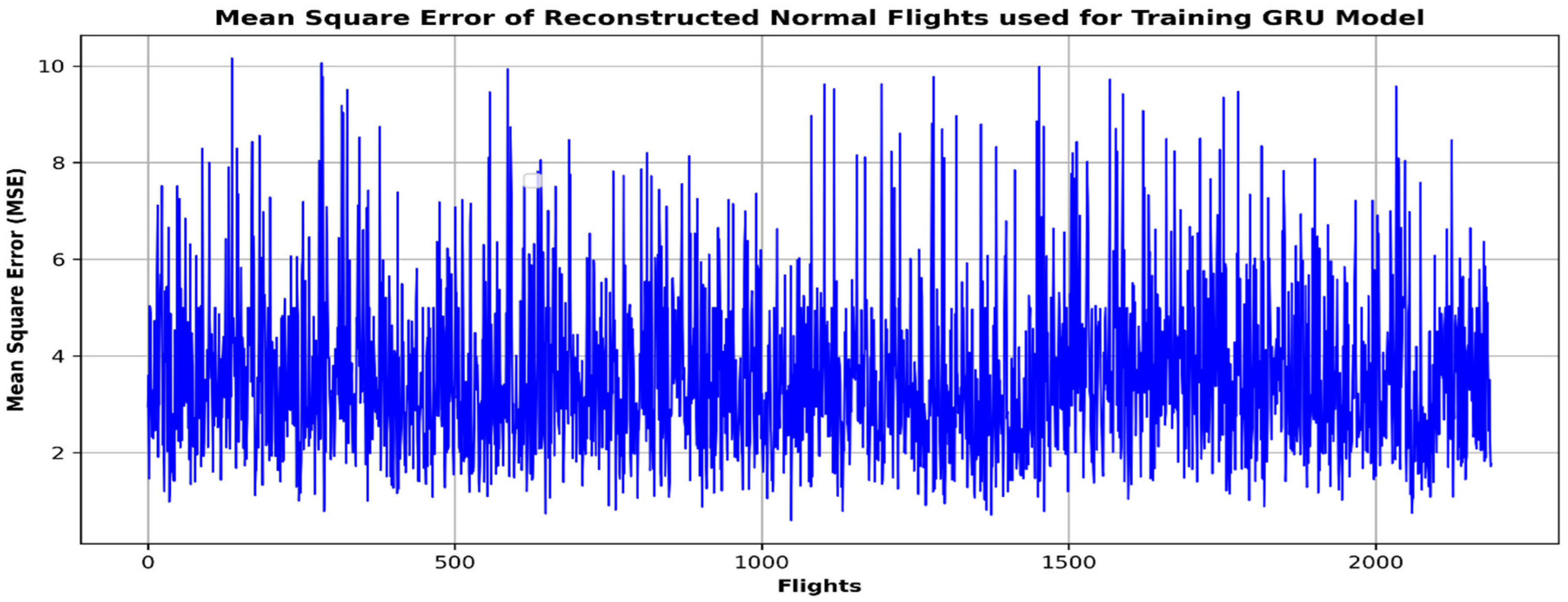
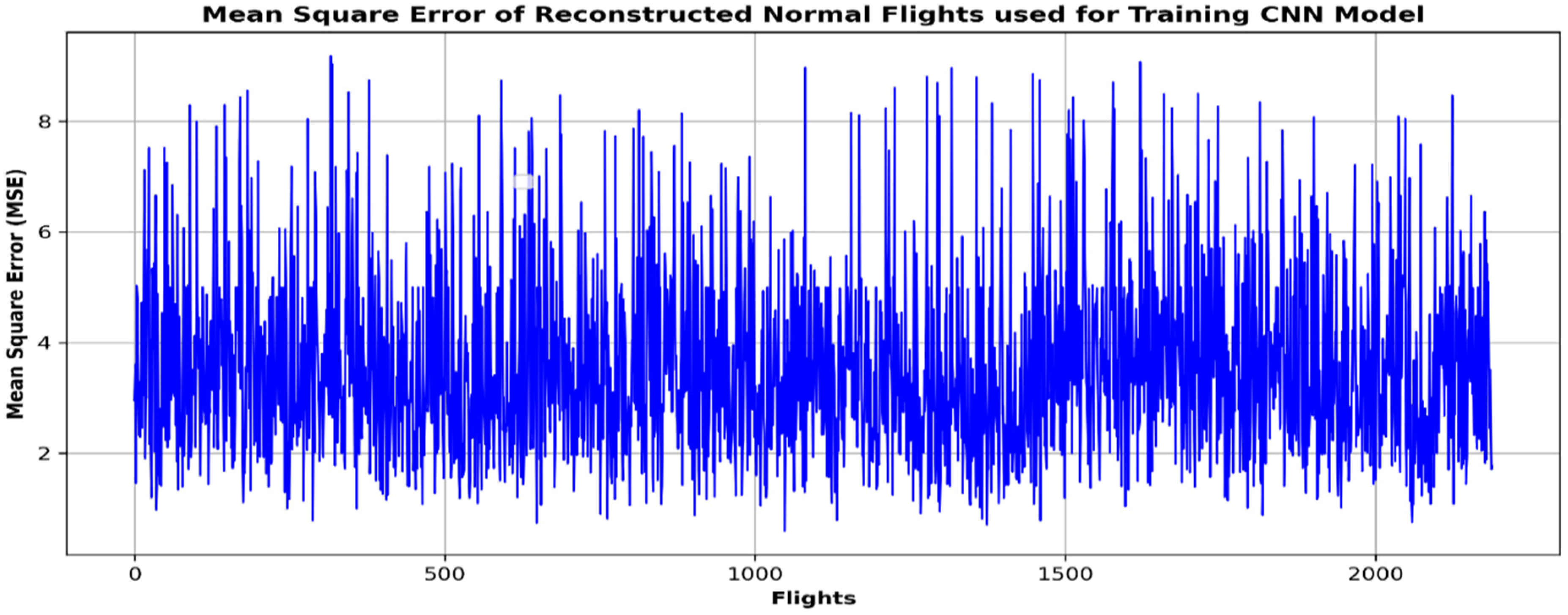
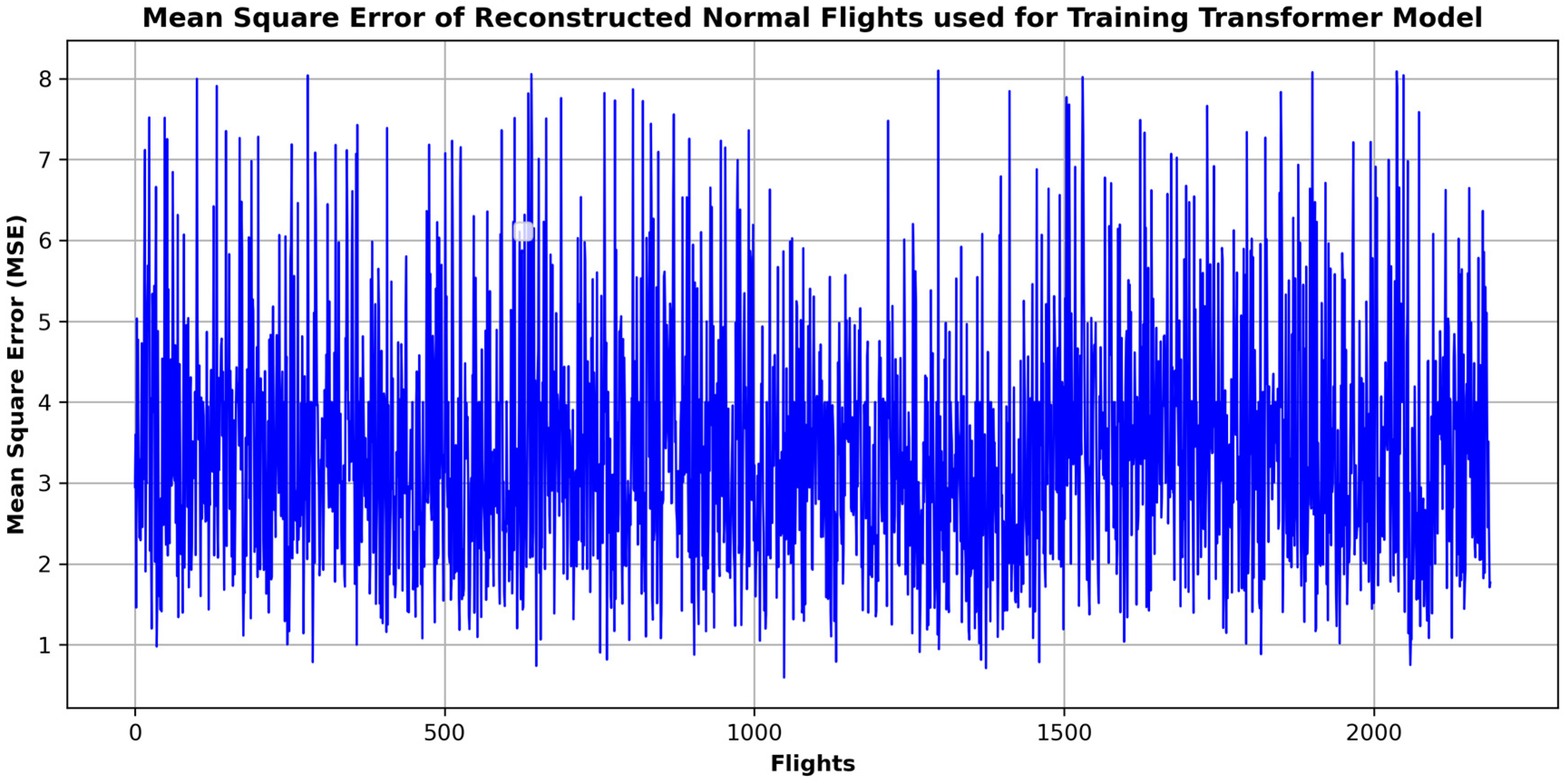
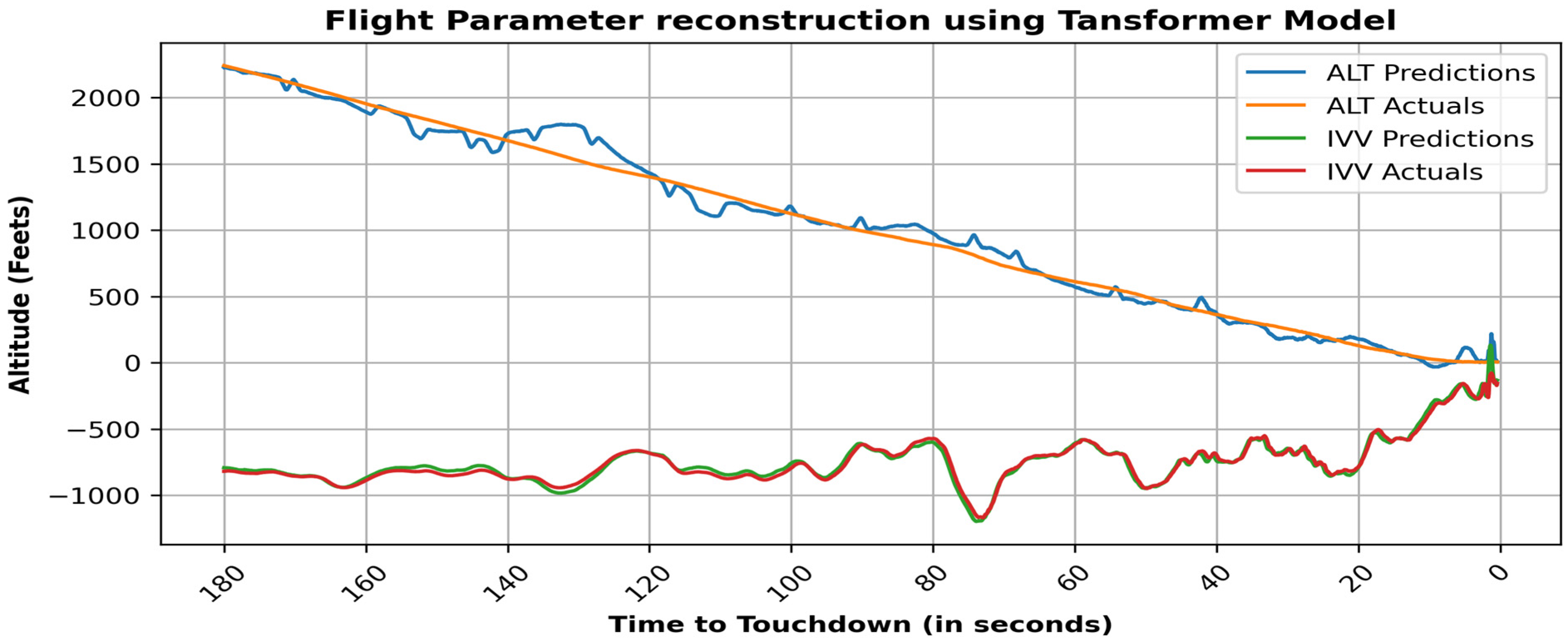
4. Results
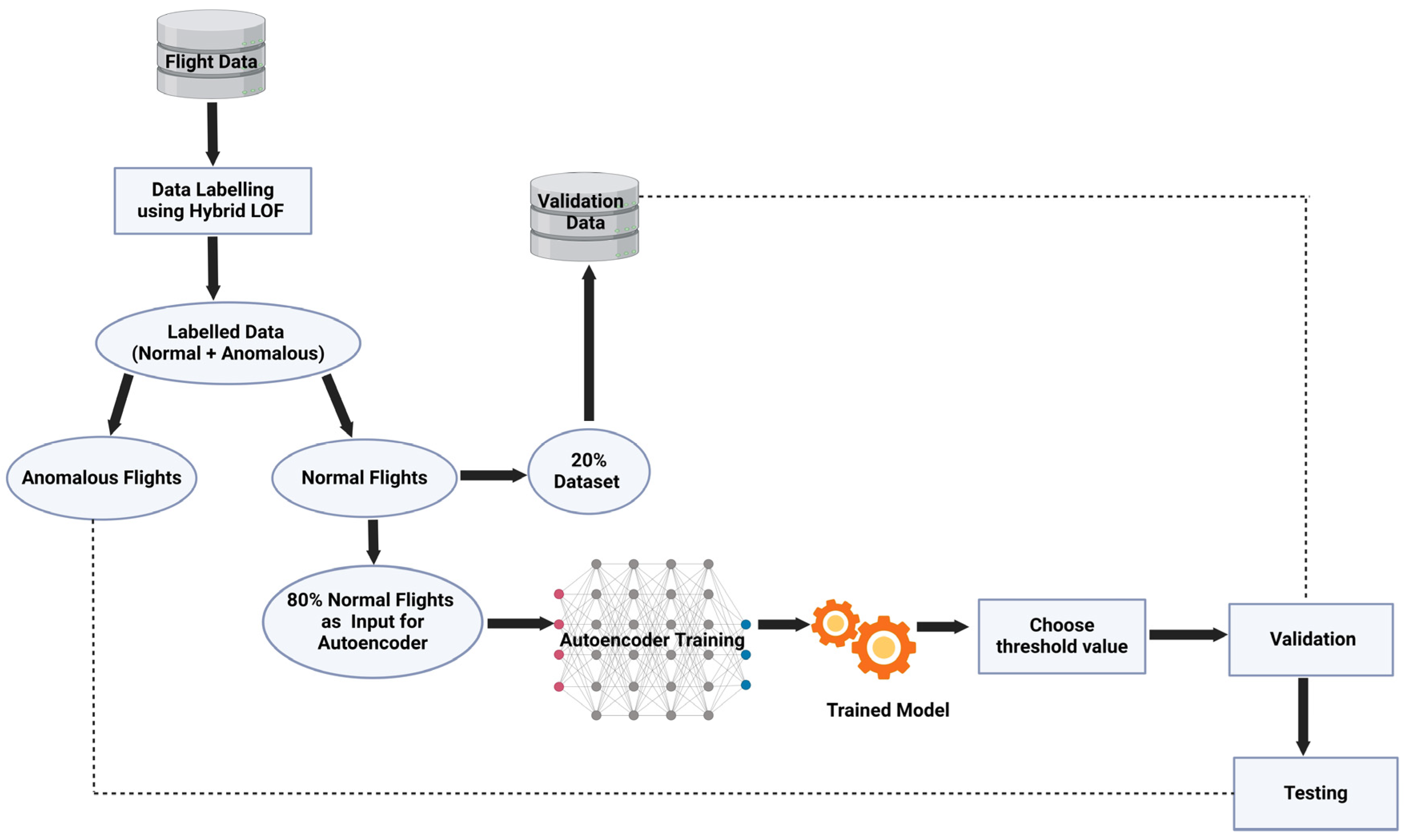
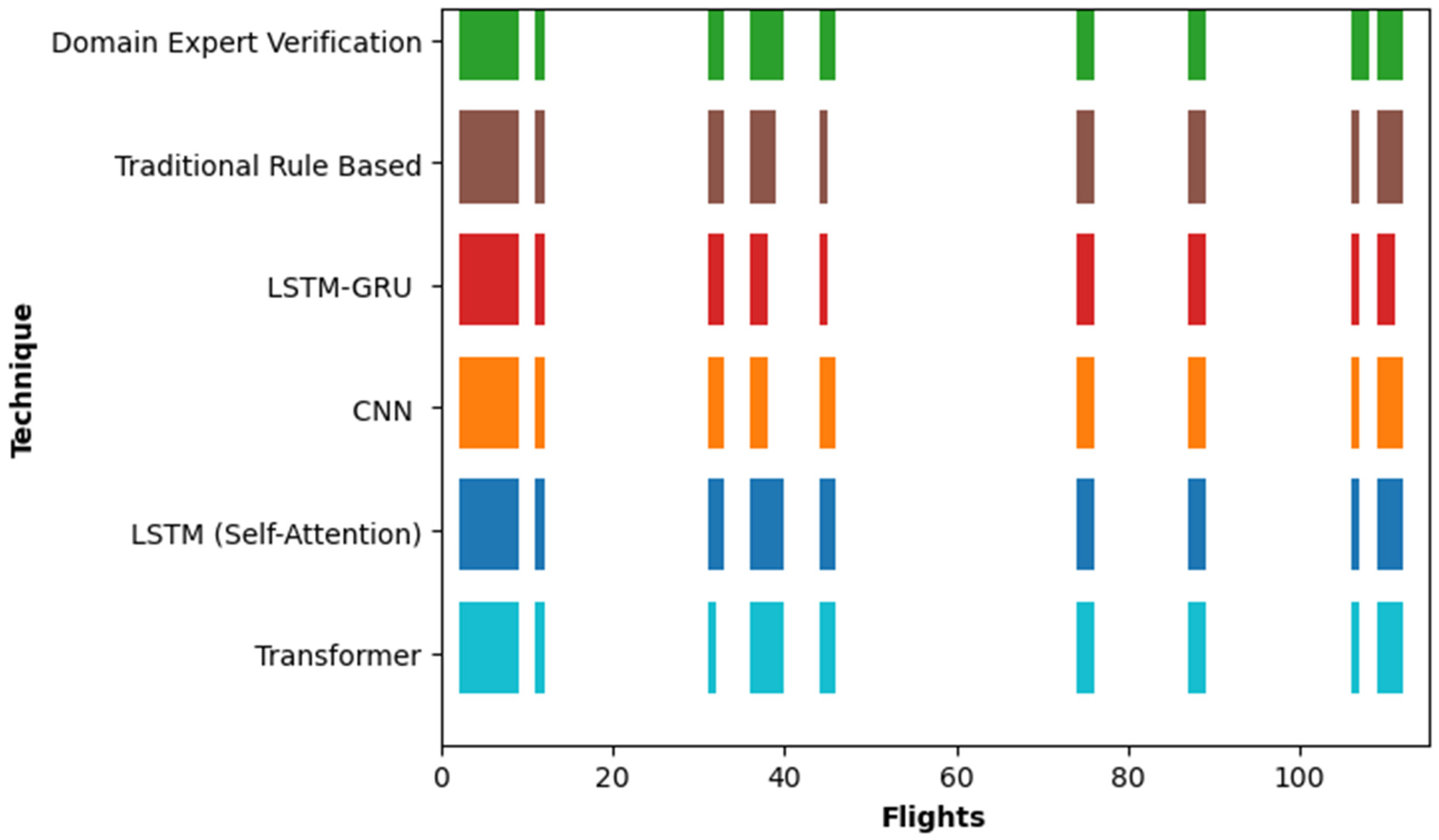
5. Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAA. Airplane Flight Recorder Specifications-14 CFR 121, Appendix M. In Title 14—Aeronautics and Space; Federal Aviation Administration, Ed.; Federal Aviation Administration: Washington, DC, USA, 2011. [Google Scholar]
- Jasra, S.K.; Valentino, G.; Muscat, A.; Camilleri, R. Hybrid Machine Learning–Statistical Method for Anomaly Detection in Flight Data. Appl. Sci. 2022, 12, 10261. [Google Scholar] [CrossRef]
- Walker, G. Redefining the incidents to learn from: Safety science insights acquired on the journey from black boxes to Flight Data Monitoring. Saf. Sci. 2017, 99, 14–22. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection. ACM Comput. Surv. 2009, 41, 1–58. [Google Scholar] [CrossRef]
- Basora, L.; Olive, X.; Dubot, T. Recent Advances in Anomaly Detection Methods Applied to Aviation. Aerospace 2019, 6, 117. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Springer: Cham, Switzerland, 2016; pp. 118–140. [Google Scholar] [CrossRef]
- Pelleg, D.; Moore, A. Active learning for anomaly and rare-category detection. In Proceedings of the 17th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004; pp. 1073–1080. [Google Scholar]
- Megatroika, A.; Galinium, M.; Mahendra, A.; Ruseno, N. Aircraft anomaly detection using algorithmic model and data model trained on FOQA data. In Proceedings of the 2015 International Conference on Data and Software Engineering (ICoDSE), Yogyakarta, Indonesia, 25–26 November 2015. [Google Scholar]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 Integrated Communications Navigation and Surveillance (ICNS), Herndon, VA, USA, 19–21 April 2016. [Google Scholar]
- Li, L.; Das, S.; Hansman, R.; Palacios, R.; Srivastava, A. Analysis of Flight Data Using Clustering Techniques for Detecting Abnormal Operations. J. Aerosp. Inf. Syst. 2015, 12, 587–598. [Google Scholar] [CrossRef]
- Reddy, K.; Sarkar, S.; Venugopalan, V.; Giering, M. Anomaly Detection and Fault Disambiguation in Large Flight Data: A Multi-modal Deep Auto-encoder Approach. In Proceedings of the Annual Conference of the PHM Society, Denver, CO, USA, 3–6 October 2016; Volume 8. [Google Scholar] [CrossRef]
- Memarzadeh, M.; Matthews, B.; Avrekh, I. Unsupervised Anomaly Detection in Flight Data Using Convolutional Variational Auto-Encoder. Aerospace 2020, 7, 115. [Google Scholar] [CrossRef]
- Alhussein, E.; Ali, A. Discovering Anomalous Patterns in Flight Data at Najaf Airport using LSTM Auto Encoders. In Proceedings of the International Iraqi Conference on Engineering Technology and Their Applications (IICETA), Najaf, Iraq, 21–22 September 2021. [Google Scholar] [CrossRef]
- Qin, K.; Wang, Q.; Lu, B.; Sun, H.; Shu, P. Flight Anomaly Detection via a Deep Hybrid Model. Aerospace 2022, 9, 329. [Google Scholar] [CrossRef]
- Campello, R.J.G.B.; Moulavi, D.; Sander, J. Density-Based Clustering Based on Hierarchical Density Estimates. In Advances in Knowledge Discovery and Data Mining, Proceedings of the 17th Pacific-Asia Conference, Gold Coast, Australia, 14–17 April 2013; Springer: Berlin/Heidelberg, Germany; pp. 160–172. [CrossRef]
- Chiu, T.-Y.; Lai, Y.-C. Unstable Approach Detection and Analysis Based on Energy Management and a Deep Neural Network. Aerospace 2023, 10, 565. [Google Scholar] [CrossRef]
- NASA. Sample Flight Data; NASA: Washington, DC, USA, 2012. Available online: https://c3.ndc.nasa.gov/dashlink/projects/85/ (accessed on 12 December 2022).
- Airbus. A Statistical Analysis of Commercial Aviation Accidents 1958–2022. Safety First, (Issue 7 (Reference X00D17008863)), 1–36. February 2023. Available online: https://skybrary.aero/sites/default/files/bookshelf/34689.pdf (accessed on 2 December 2024).
- Boeing. Statistical Summary of Commercial Jet Airplane Accidents 2023. Boeing. Available online: https://www.boeing.com/resources/boeingdotcom/company/about_bca/pdf/statsum.pdf (accessed on 2 October 2024).
- Jasra, S.K.; Valentino, G.; Muscat, A.; Camilleri, R. A Comparative Study of Unsupervised Machine Learning Methods for Anomaly Detection in Flight Data: Case Studies from Real-World Flight Operations. Aerospace 2025, 12, 151. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on SequenceModeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Katrompas, A.; Ntakouris, T.; Metsis, V. Recurrence and Self-attention vs the Transformer for Time-Series Classification: A Comparative Study. In Artificial Intelligence in Medicine, Proceedings of the 20th International Conference on Artificial Intelligence in Medicine, Halifax, NS, Canada, 14–17 June 2022; Springer: Cham, Switzerland; pp. 99–109. [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhao, H.; Jia, J.; Koltun, V. Exploring Self-Attention for Image Recognition. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020. [Google Scholar] [CrossRef]
- Wu, N.; Green, B.; Ben, X.; O’Banion, S. Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. arXiv 2020, arXiv:2001.08317. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Lin, Z.; Feng, M.; Dos Santos, C.; Yu, M.; Xiang, B.; Zhou, B.; Bengio, Y. A Structured Self-attentive Sentence Embedding. arXiv 2017, arXiv:1703.03130. [Google Scholar] [CrossRef]
- Shi, J.; Wang, S.; Qu, P.; Shao, J. Time series prediction model using LSTM-Transformer neural network for mine water inflow. Sci. Rep. 2024, 14, 18284. [Google Scholar] [CrossRef] [PubMed]
- Pang, Y.; Yao, H.; Hu, J.; Liu, Y. A Recurrent Neural Network Approach for Aircraft Trajectory Prediction with Weather Features From Sherlock. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar]
- Pang, Y.; Liu, Y. Conditional generative adversarial networks (CGAN) for aircraft trajectory prediction considering weather effects. In Proceedings of the AIAA Scitech 2020 Forum 1853, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Jia, P.; Chen, H.; Zhang, L.; Han, D. Attention-LSTM based prediction model for aircraft 4-D trajectory. Sci. Rep. 2022, 12, 15533. [Google Scholar] [CrossRef] [PubMed]





| Approach Rule | Flight Parameter | Unit | Optimal Value for Stabilized Approach |
|---|---|---|---|
| Established on the glide path | Glideslope Deviation | degree | 3 |
| Proper air speed | Indicated Airspeed | knots | >VRef & <VRef + 20 knots |
| Stable descent rate | Inertial Vertical Velocity | feet/minute | 750–100 feet/min |
| Stable engine power setting | Engine 1 to Engine 4 Speed (N1 & N2) | % | 30–100% |
| Flaps configuration | Flap Position | degrees/counts | 0–45° |
| Landing Gear Configuration | Landing gear toggle switch | up/down | down |
| Hyperparameter | Selection |
|---|---|
| Loss Function | Mean Square Error (MSE) |
| Dropout | 0.1 |
| Optimizer | Adam |
| Learning rate | 0.001 |
| Weight decay | 0.1 |
| Number of epochs | 50 or 100 |
| Batch size | 32 |
| Layers | Configuration |
| LSTM/GRU Layer | 128 Cells |
| LSTM/GRU Layer | 64 Cells |
| Repeat Vector | Sequence Size = 30 |
| LSTM/GRU Layer | 64 Cells |
| LSTM/GRU Layer | 128 Cells |
| Time Distributed | 132 |
| Layers | Configuration |
|---|---|
| Conv 1D | 64 Filters, Kernel size 30 |
| Conv 1D | 32 Filters, Kernel size 30 |
| Repeat Vector | 30 |
| ConvTranspose1D | 32 Filters Kernel size 30 |
| ConvTranspose1D | 64 Filters, Kernel size 30 |
| Time Distributed | 132 |
| Layers | Configuration |
|---|---|
| LSTM Layer | 128 Cells |
| LSTM Layer | 64 Cells |
| Self-Attention Layer | 64 |
| LSTM Layer | 64 Cells |
| LSTM Layer | 128 Cells |
| Time Distributed | 132 |
| Category | Hyperparameter | Setup Parameter | Meaning |
|---|---|---|---|
| Model Architecture | Number of encoder layers | 6 | Number of transformer encoder layers |
| Number of attention heads | 4 | Number of attention heads in the transformer self-attention mechanism | |
| Model dimension (d_model) | 128 | Size of the vector that represents each time step (or token) as it passes through the network | |
| Feed-forward dimension (d_ff) | 512 | Size of position-wise feed-forward subnetwork | |
| Max input sequence length | 128 | Maximum number of time steps (or tokens) that the Transformer will process in a single forward pass | |
| Positional encoding type | Sinusoidal | Pre-computed using sine and cosine functions of different frequencies: | |
| Loss Function | Mean Square Error (MSE) | The loss function is used to calculate the difference between the real value and the predicted value to evaluate the predictive performance of the model | |
| Regularization | Dropout | 0.1 | Dropout reduces overfitting by randomly zeroing out the outputs of some neurons during training |
| Optimization | Optimizer | Adam | Adam is an extended algorithm for stochastic gradient descent |
| Learning rate | 0.001 | The learning rate is the key hyperparameter used to adjust the rate of gradient descent | |
| Weight decay | 0.1 | Weight decay is to reduce overfitting by adding a penalty term to the loss function | |
| Training | Number of epochs | 50 | Number of iterations |
| Batch size | 32 | Number of independent sequence windows (here, time-series slices) processed together in one pass before updating the model’s weights |
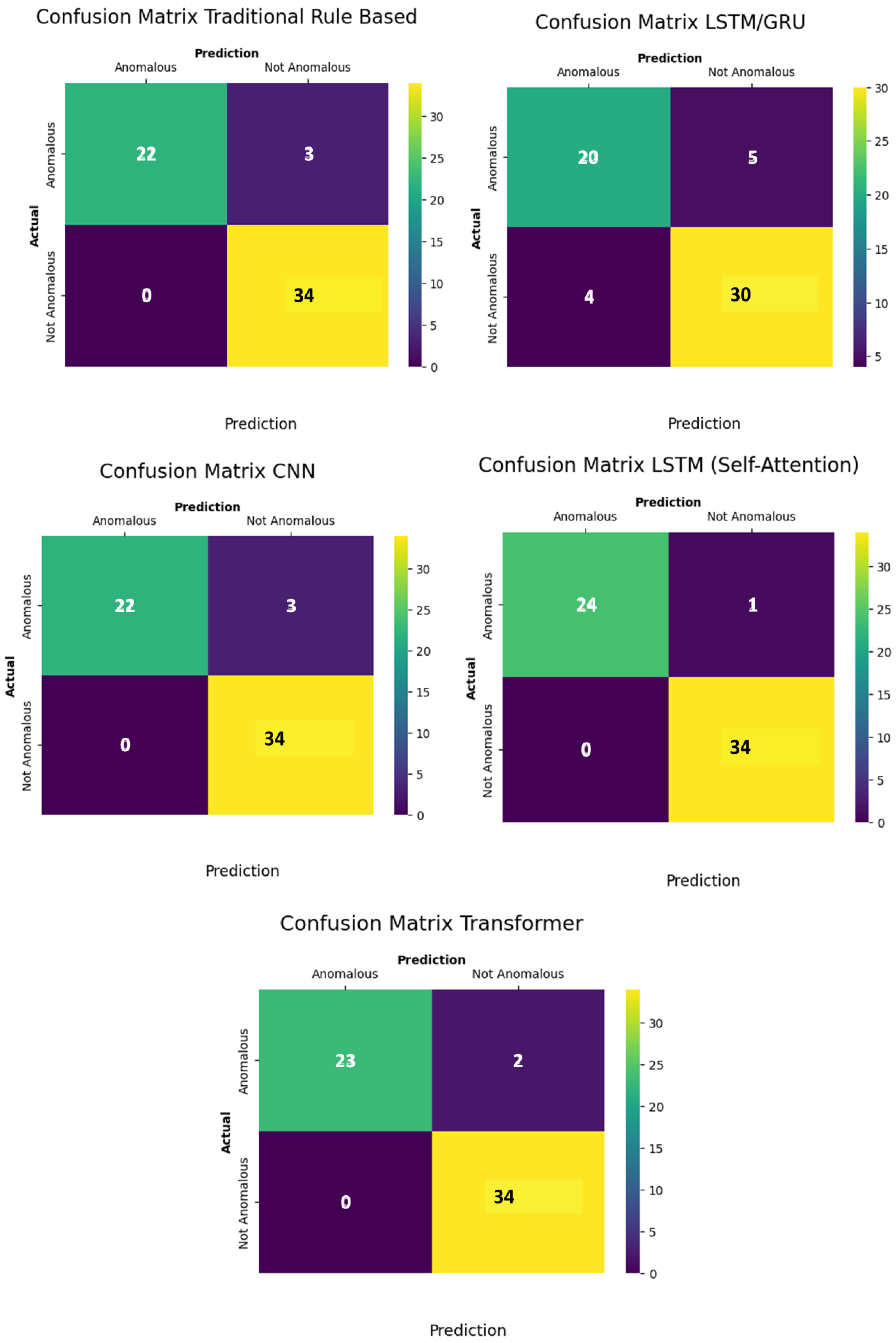
| Method | Precision Rate (PR) | Recall Rate (RR) | F-1 Score |
|---|---|---|---|
| Traditional Rule Based | 1.00 | 0.88 | 0.94 |
| LSTM/GRU | 0.83 | 0.80 | 0.82 |
| CNN | 1.00 | 0.88 | 0.94 |
| LSTM (Self-Attention) | 1.00 | 0.96 | 0.98 |
| Transformer | 1.00 | 0.92 | 0.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jasra, S.K.; Valentino, G.; Muscat, A.; Camilleri, R. A Comparative Study of Unsupervised Deep Learning Methods for Anomaly Detection in Flight Data. Aerospace 2025, 12, 645. https://doi.org/10.3390/aerospace12070645
Jasra SK, Valentino G, Muscat A, Camilleri R. A Comparative Study of Unsupervised Deep Learning Methods for Anomaly Detection in Flight Data. Aerospace. 2025; 12(7):645. https://doi.org/10.3390/aerospace12070645
Chicago/Turabian StyleJasra, Sameer Kumar, Gianluca Valentino, Alan Muscat, and Robert Camilleri. 2025. "A Comparative Study of Unsupervised Deep Learning Methods for Anomaly Detection in Flight Data" Aerospace 12, no. 7: 645. https://doi.org/10.3390/aerospace12070645
APA StyleJasra, S. K., Valentino, G., Muscat, A., & Camilleri, R. (2025). A Comparative Study of Unsupervised Deep Learning Methods for Anomaly Detection in Flight Data. Aerospace, 12(7), 645. https://doi.org/10.3390/aerospace12070645








