Inter-Frequency Aided Acquisition for BeiDou DFMC Receivers: Dual-Frequency Cooperation and Extended Integration

Abstract

With the advancement of the third-generation BeiDou Navigation Satellite System (BDS-3), BeiDou dual-frequency multi-constellation (DFMC) receivers exhibit distinct advantages in accuracy and reliability due to their dual-frequency capabilities. However, the integration time imposes constraints on further improvements in sensitivity. To address this limitation, this study proposes a dual-frequency cooperative acquisition strategy targeting the B1C and B2a signals, with the objective of enhancing acquisition performance in weak signal environments. A dual-channel acquisition architecture was designed, incorporating an inter-frequency Doppler assistance technique to improve acquisition efficiency. Simulation results demonstrate that, compared to conventional fixed short integration time architectures, the proposed cooperative acquisition approach increases the receiver’s acquisition sensitivity by 5.7 dB. Real-world experiments further confirm the effectiveness of this strategy, achieving successful acquisition of the PRN28 signal with 5 ms of coherent integration, thereby highlighting its practical utility. This research offers an innovative solution for high-sensitivity signal acquisition in challenging environments for BeiDou DFMC receivers and provides valuable insights for the advancement of high-precision BeiDou applications.

1. Introduction

The Global Navigation Satellite System (GNSS) has emerged as a foundational technology for modern positioning, navigation, and timing services [1]. With the global deployment of the BeiDou Navigation Satellite System (BDS) and the ongoing refinement of its signal structure, the open service signals (B1C and B2a) [2,3] deliver improved positioning accuracy and reliability for civilian applications. These advancements also provide a richer information source for dual-frequency multi-constellation (DFMC) receivers [4]. Dual-frequency signals offer significant advantages over traditional single-frequency signals, such as GPS L1 C/A, by effectively mitigating ionospheric delays and enhancing robustness in weak signal and high-dynamic environments [5]. Despite these benefits, conventional receivers typically process signals from each frequency independently during the acquisition phase, failing to harness their cooperative potential [6]. This gap is the goal of this study. This limitation constrains acquisition sensitivity and efficiency, particularly in demanding scenarios like civil aviation, where high precision and resistance to interference are paramount.

The modulation characteristics of civilian GNSS signals are summarized in

Table 1. Comparison of signal structures.

Signal Structure	${\mathit{f}}_{\mathbf{RF}}$ (MHz)	Modulation	Power Sharing	Code Length (Chips)
				Primary	Secondary
B1C	1575.42	Pilot: QMBOC (6,1,4/33)	Pilot: 29/44 (BOC (1,1))	10,230	1800
		Data: BOC (1,1)	Data: 1/11 (BOC (6,1))	10,230	1
B2a	1176.45	Pilot: QPSK (10)	Pilot: 1/2	10,230	100
		Data: QPSK (10)	Data: 1/2	10,230	5
L1C/A	1575.42	Data: BPSK	Data: 1	1023	N/A
E1 OS	1575.42	Pilot: CBOC (6,1,1/11,−)	Pilot: 1/2	4092	N/A
		Data: CBOC (6,1,1/11,+)	Data: 1/2	4092	25

[1,2,3]. In the coming years, civil aviation is expected to adopt a new generation of DFMC receivers capable of providing signal observations across two frequency bands [7]. This capability establishes a foundation for designing flexible baseband signal processing strategies [6]. Dual-frequency observations enable the formation of ionosphere-free combinations through linear combinations, markedly enhancing positioning accuracy [8]. Numerous studies have explored cooperative techniques involving pilot and data channels on the same carrier frequency, or even across different frequency bands transmitted by the same satellite, for acquisition and tracking purposes [4,9]. Among prior methods, multi-channel joint acquisition improves performance by combining the energy of both pilot and data components [10]. However, most research to date applies the same integration time to signals from pilot and data channels, even at different frequency bands, which is ultimately constrained by the presence of navigation bits in the data channel [11]. In contrast, the pilot channel, free from navigation data modulation, can employ longer integration times, enabling more robust signal acquisition in challenging environments [12].

To maximize the mutual benefits of dual-frequency signals, this paper proposes a dual-frequency cooperative acquisition strategy. This approach aims to enhance receiver performance in complex environments by incorporating inter-frequency Doppler assistance and extending coherent integration time. A joint processing approach is employed for the B2a signal, integrating the data and pilot channels. Specifically, a non-coherent combining strategy, as proposed by Borio et al. (2009) [13], is utilized to fuse the information from these channels. By leveraging the known frequency ratio between the B2a and B1C signals, the Doppler shift estimated from the B2a signal is used to predict the corresponding Doppler shift of the B1C signal, thereby reducing the search space [9]. Subsequently, a 10 ms coherent integration is applied to the B1C signal to finalize the acquisition process and improve the detection of weak signals. Through cooperative processing across the two frequencies, it optimizes Doppler shift estimation, thereby increasing acquisition success rates and positioning accuracy. This method is not only tailored to the BeiDou system but is also adaptable to other multi-frequency GNSS receiver designs, offering potential applications in civil aviation for achieving higher-precision approach and landing navigation. Venturino et al. (2025) [14] proposed an Adaptive Robust Navigation Filter (ARNF) that couples array angle-of-arrival statistics with an adaptive filtering mechanism to achieve real-time high-precision positioning in complex spoofing environments. This method offers key theoretical support and guidance for embedding anti-jamming designs after the dual-frequency cooperative acquisition in this study.

The paper is structured into four primary sections: First, we review the fundamental properties of GNSS signals and introduce a simplified dual-channel signal correlator output model. Next, we elaborate on the dual-frequency cooperative acquisition architecture, which is based on inter-frequency Doppler assistance. Subsequently, simulation experiments are conducted to evaluate the performance improvements of the proposed strategy, confirming its robustness in weak signal conditions. Finally, conclusions and future work are provided.

2. Materials and Methods

2.1. Modulation Characteristics of GNSS Signals

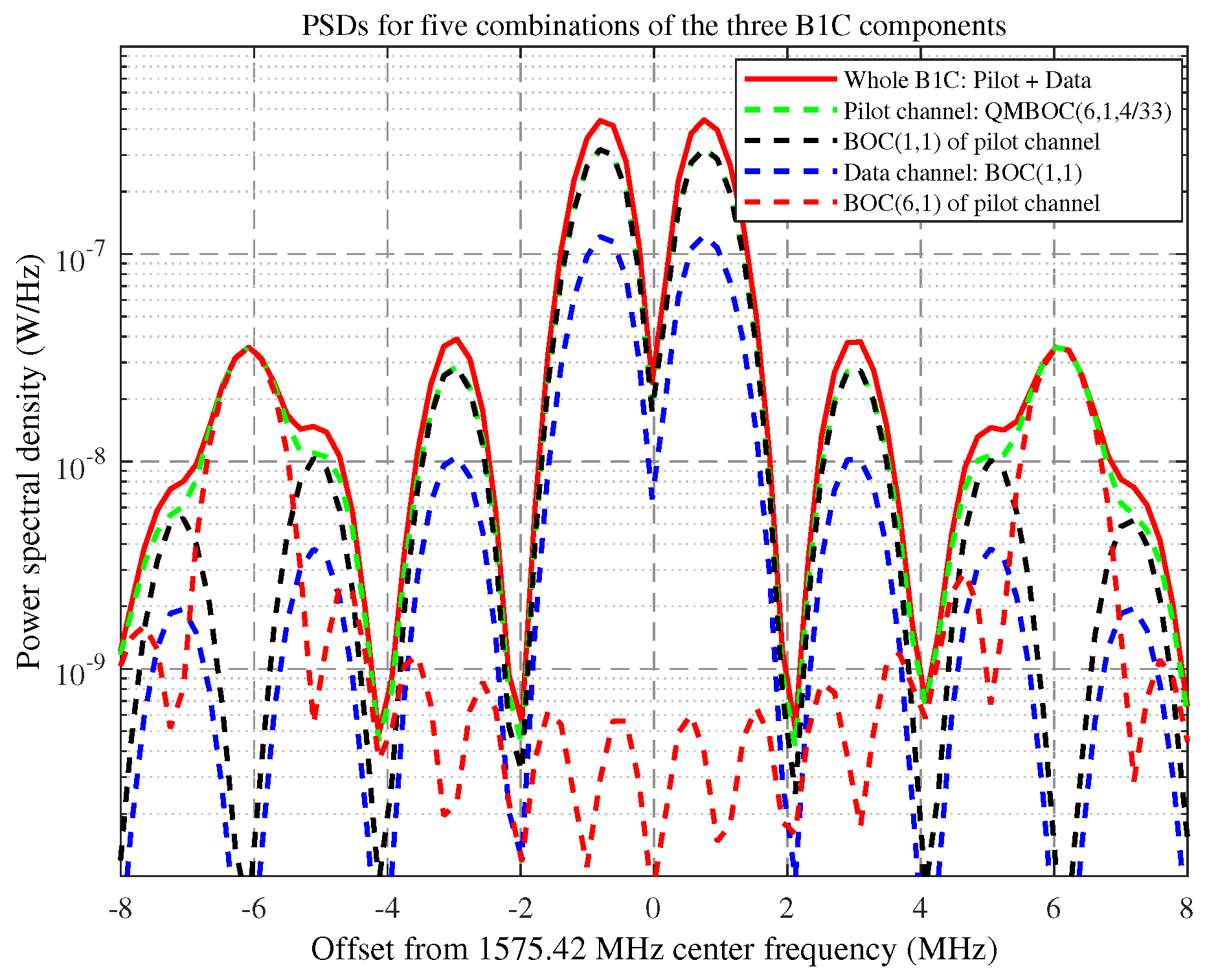
As presented in Table 1, the B1C signal’s data component employs Binary Offset Carrier (BOC) modulation with parameters BOC(1,1), while the pilot component utilizes Quadrature Multiplexed BOC (QMBOC) modulation, specifically QMBOC (6,1,4/33). The power spectral densities (PSDs) for the three B1C components and their combinations are illustrated in Figure 1. The received B1C signal, after baseband processing, can be expressed as follows [15]:

$$r_{\mathrm{B}1\mathrm{C}}=s_{\mathrm{d},n}^{\mathrm{B}1\mathrm{C}}+s_{\mathrm{p}61,n}^{\mathrm{B}1\mathrm{C}}+j·s_{\mathrm{p}11,n}^{\mathrm{B}1\mathrm{C}}+\eta$$

(1)

where $s_{\mathrm{d},n}^{\mathrm{B}1\mathrm{C}}$ represents the data component, $s_{\mathrm{p}61,n}^{\mathrm{B}1\mathrm{C}}$ and $s_{\mathrm{p}11,n}^{\mathrm{B}1\mathrm{C}}$ denote the pilot components corresponding to BOC(6,1) and BOC(1,1), respectively, and $\eta$ is the additive white Gaussian noise.

In contrast, the B2a signal’s data and pilot components both utilize Binary Phase Shift Keying (BPSK) modulation with a parameter of BPSK(10). The baseband model for the B2a signal is given by [15]:

$$r_{\mathrm{B}2\mathrm{a}}=s_{\mathrm{d},n}^{\mathrm{B}2\mathrm{a}}+j·s_{\mathrm{p},n}^{\mathrm{B}2\mathrm{a}}+\xi$$

(2)

where $s_{\mathrm{d},n}^{\mathrm{B}2\mathrm{a}}$ is the data component, $s_{\mathrm{p},n}^{\mathrm{B}2\mathrm{a}}$ is the pilot component, and $\xi$ is the additive white Gaussian noise.

Notably, the noise terms ($\eta$) in the B1C and B2a signals are statistically independent and exhibit distinct variances. Compared to the B1C signal, the B2a signal benefits from higher transmit power, a lower carrier frequency, and a higher primary code frequency. These attributes confer several potential advantages to the B2a signal, including the following:

• a stronger carrier-to-noise density ratio ($C/N_0$);
• slower carrier Doppler dynamics.

In addition, according to the Interface Control Document (ICD) [2,3], ephemeris data can be decoded from either the B1C or B2a data channels. However, the transmit power of the B1C data component is significantly lower than that of other components in both the B1C and B2a signals. Consequently, for BeiDou third-generation DFMC receivers, it is proposed that the B2a data channel be utilized to receive ephemeris data, while the B1C data channel may be disregarded. This approach simplifies the complexity of the dual-frequency receiver design. Further discussion of the B1C data channel will be omitted in subsequent chapters.

2.2. Correlator Output Model for GNSS Signals

To evaluate the acquisition performance of GNSS signals, this section introduces a dual-channel correlator output model. Drawing on the research by Macabiau et al. [16], the correlator outputs for the pilot and data components can be mathematically represented as shown in the following equation:

$$\begin{array}{c}{I}_{L5E5a}^D\left(k\right)=\sqrt{{\displaystyle \frac{P_{L5}}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D,c_D}^{L5E5a}\left({\epsilon }_{\tau }\right)+h_{20}\left(k\right){\tilde{R}}_{c_P,c_D}^{L5E5a}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)cos\left({\epsilon }_{\phi }\right)+n_{I,L5}^D\left(k\right)\\ Q_{\mathrm{L}5\mathrm{E}5a}^D\left(k\right)=\sqrt{{\displaystyle \frac{P_{L5}}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D,c_D}^{L5E5a}\left({\epsilon }_{\tau }\right)+h_{20}\left(k\right){\tilde{R}}_{c_P,c_D}^{L5E5a}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)sin\left({\epsilon }_{\phi }\right)+n_{Q,L5}^D\left(k\right)\\ I_{L5\mathrm{E}5a}^P\left(k\right)=\sqrt{{\displaystyle \frac{P_{L5}}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D,c_P}^{L5E5a}\left({\epsilon }_{\tau }\right)+h_{20}\left(k\right){\tilde{R}}_{c_P,c_P}^{L5E5a}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)\cos \left({\epsilon }_{\phi }\right)+n_{I,L5}^P\left(k\right)\\ Q_{L5\mathrm{E}5a}^P\left(k\right)=\sqrt{{\displaystyle \frac{P_{L5}}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D,c_P}^{L5E5a}\left({\epsilon }_{\tau }\right)+h_{20}\left(k\right){\tilde{R}}_{c_P,c_P}^{L5E5a}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)sin\left({\epsilon }_{\phi }\right)+n_{Q,L5}^P\left(k\right)\end{array}$$

(3)

Given that the data and pilot codes are spread using distinct pseudorandom noise (PRN) sequences, the cross-correlation between these codes is negligible in practical applications. As a result, this model can be simplified to facilitate joint acquisition analysis.

The correlator output for the data component is expressed as

$$\begin{array}{c}{I}_{L1L5}^D\left(k\right)=\sqrt{{\displaystyle \frac{P}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D{c}_D}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)\cos \left({\epsilon }_{\phi }\right)+n_I^D\left(k\right)\\ Q_{L1L5}^D\left(k\right)=\sqrt{{\displaystyle \frac{P}{4}}}\left(d\left(k\right)h_{10}\left(k\right){\tilde{R}}_{c_D{c}_D}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)sin\left({\epsilon }_{\phi }\right)+n_Q^D\left(k\right)\end{array}$$

(4)

Similarly, the correlator output for the pilot component is given by

$$\begin{array}{c}{I}_{L1L5}^P\left(k\right)=\sqrt{{\displaystyle \frac{P}{4}}}\left(h_{20}\left(k\right){\tilde{R}}_{c_P{c}_P}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)\cos \left({\epsilon }_{\phi }\right)+n_I^P\left(k\right)\\ Q_{L1L5}^P\left(k\right)=\sqrt{{\displaystyle \frac{P}{4}}}\left(h_{20}\left(k\right){\tilde{R}}_{c_P{c}_P}\left({\epsilon }_{\tau }\right)\right)sinc\left(\pi {\epsilon }_f{T}_i\right)sin\left({\epsilon }_{\phi }\right)+n_Q^P\left(k\right)\end{array}$$

(5)

In practical receivers, this assumption is generally valid due to code design and typical front-end filtering, though slight residual correlation may exist under non-ideal conditions. The variables in these equations are defined as follows:

P: total signal power at the antenna port; $d\left(k\right)$: navigation bit; $h_{10}$, $h_{20}$: secondary code bits; ${\epsilon }_{\tau }$, ${\epsilon }_f$ and ${\epsilon }_{\phi }$: code delay, frequency and phase errors, respectively; ${\tilde{R}}_{XY}$: cross-correlation function between the received filtered PRN signal X and the locally generated signal Y; $n_I^D$, $n_Q^D$, $n_I^p$, $n_Q^p$: independent additive white Gaussian noise (AWGN) terms with power ${\sigma }_n^2$, where ${\sigma }_n^2={\displaystyle \frac{\beta N_0}{4T_i}}$.

2.3. Impact of RFFE Filters on GNSS Signals

The bandwidth of the radio frequency front-end (RFFE) filter plays a critical role in determining the retention of signal energy in GNSS receivers. This effect is governed by the filter’s transfer function, $H_{RF,BB}$, and the power spectral density (PSD) of the locally generated signal, $S_{cm}$, as expressed in the following equation [11]:

$$\beta ={\int }_{-\infty }^{+\infty }{\left|H_{RF,BB}\left(f\right)\right|}^2{S}_{c_m}\left(f\right)df$$

(6)

The impact of the RFFE filter bandwidth on signal correlation is evident in the behavior of GNSS signals. As shown in Figure 2a, the cross-correlation function of the GPS L1 C/A signal attenuates as the filter bandwidth decreases. Similarly, Figure 2b illustrates the correlation characteristics of the Galileo E1 signal under a 12 MHz bandwidth, which represents the minimum allowable bandwidth for Galileo E1 receivers according to the ED-259 specification. These figures collectively highlight how RFFE bandwidth influences the correlation functions of both GPS L1 C/A and Galileo E1 signals.

The results in Figure 2 are based on theoretical, noise-free GNSS signals. In practice, increasing the bandwidth will introduce additional noise. Further analysis, presented in Figure 2c,d, reveals that a reduction in RFFE bandwidth results in increased power loss. Given these observations, the design of GNSS receivers must carefully balance filter bandwidth with signal power loss to optimize both signal acquisition and tracking performance.

2.4. Architecture of Dual-Frequency Cooperative Acquisition Strategy

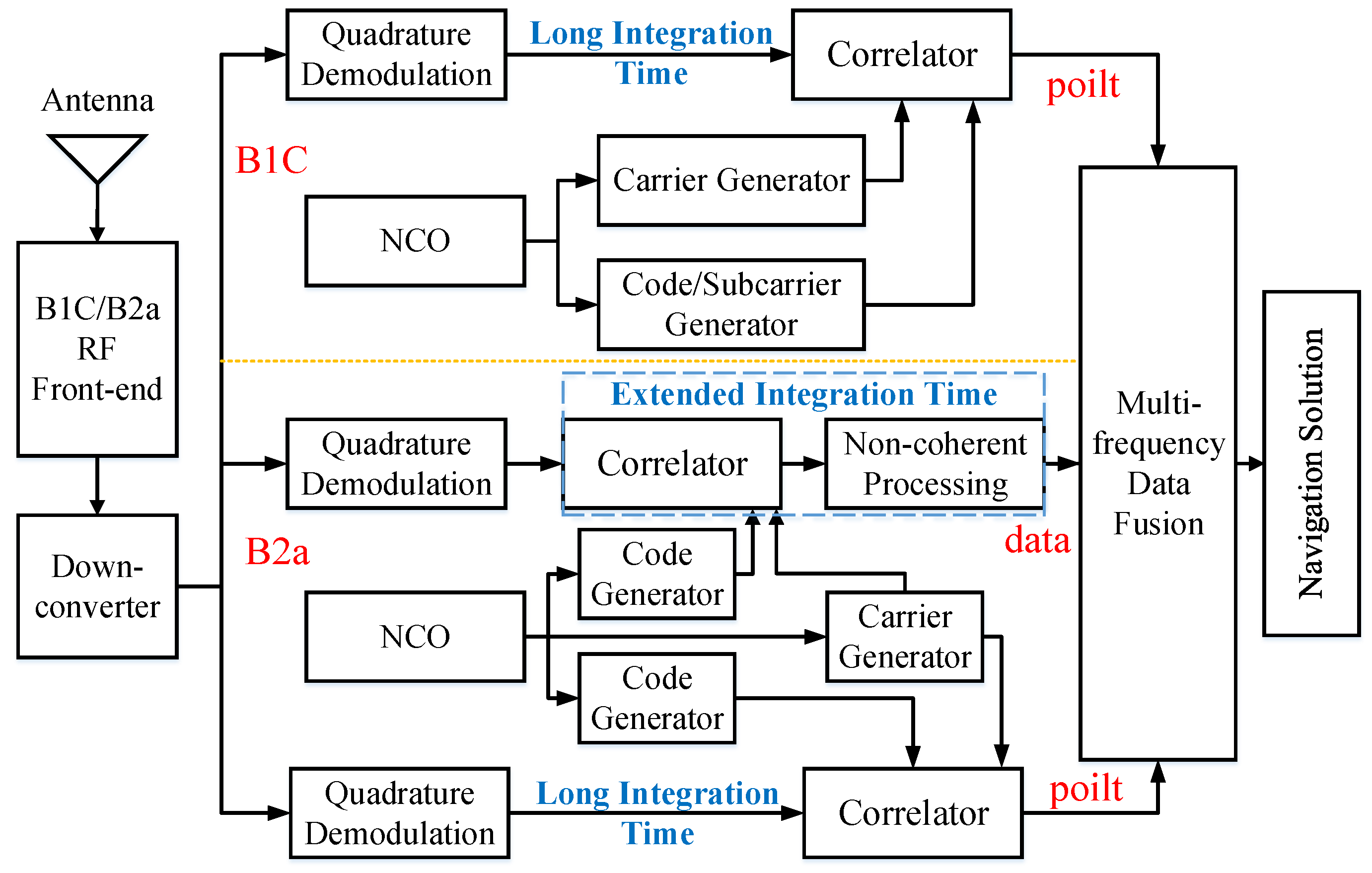
Traditional GNSS acquisition methods typically apply identical integration times to both data and pilot components of the received signals. However, the presence of navigation bit transitions in the data channel imposes constraints on extending coherent integration time, which consequently reduces acquisition sensitivity. To address this limitation and harness cooperative gains between dual-frequency signals, this study proposes a dual-frequency cooperative acquisition strategy. The architecture of this strategy is depicted in Figure 3. Dual-frequency signals from the L1 and L5 bands are received through an antenna, digitized and down-converted by the radio frequency (RF) frontend, and subsequently processed by the acquisition module.

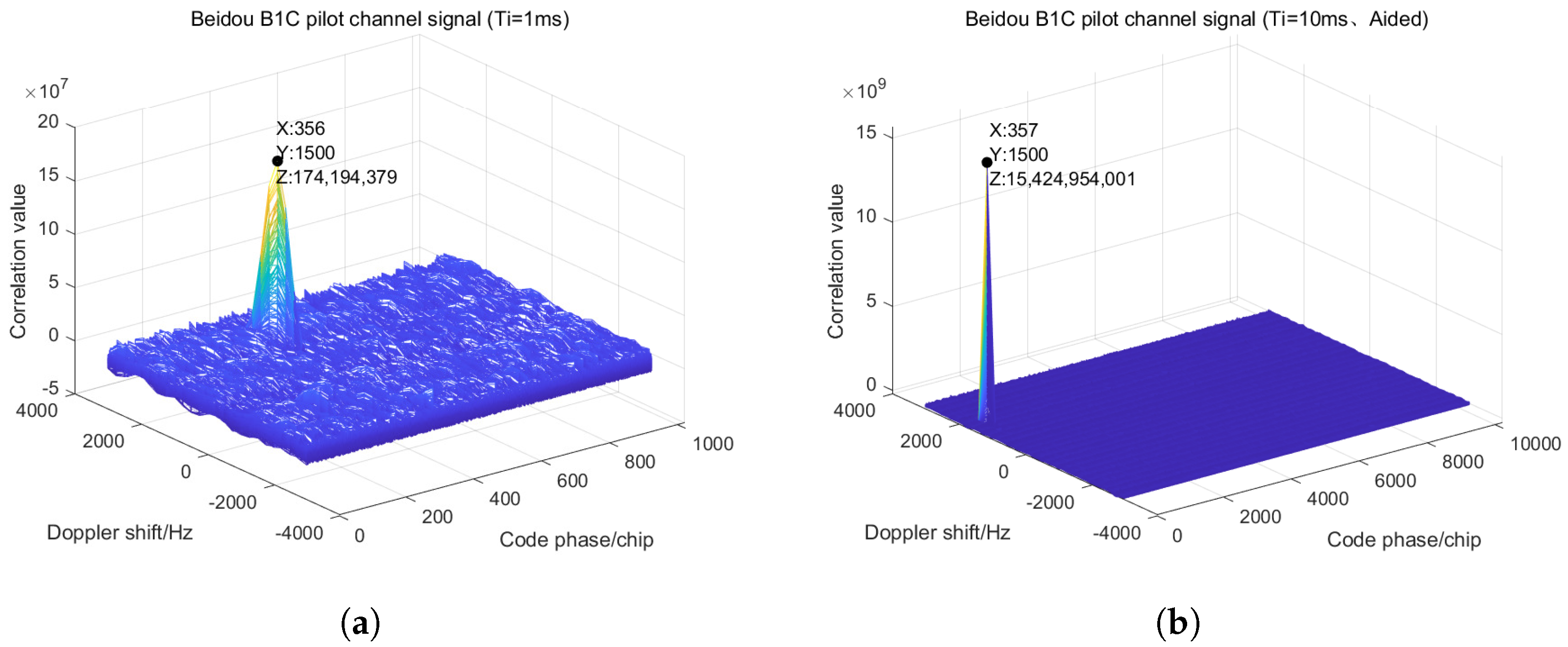
The signal acquisition process is realized through the cooperative handling of B1C and B2a signals. For the acquisition of the first satellite, the B2a signal is prioritized due to its lower observation noise and wider bandwidth. A short coherent integration time of 2 ms is employed to swiftly estimate the code phase and Doppler shift [9], ensuring an efficient initial acquisition. Leveraging the Doppler estimate derived from the B2a signal and the known frequency ratio between the dual-frequency signals, the Doppler shift of the B1C signal can be predicted. This prediction substantially narrows the search range during B1C signal acquisition. When processing the B1C signal, the predicted Doppler range enables an extended coherent integration time of 10 ms, which enhances the signal-to-noise ratio (SNR) and improves the detection of weak signals.

For subsequent satellites (e.g., the 2nd to 4th satellites), the pilot component of the B2a signal adopts long coherent integration. However, the data component of the B2a signal, constrained by navigation bit transitions, utilizes a 5 ms coherent integration time, supplemented by non-coherent accumulation to further extend the total integration duration and boost the SNR [17]. This approach significantly enhances the receiver’s sensitivity to weak signals, ensuring that a sufficient number of satellites—typically at least four—are acquired within a limited timeframe to enable positioning computation.

In contrast to the joint tracking architecture for L1/L5 frequencies proposed by Wu et al. (2019) [4,8,9], this study emphasizes cooperative processing of B1C and B2a signals specifically during the acquisition phase. By exploiting the inherent linear relationship between signals of different frequencies from the same satellite, this strategy effectively reduces uncertainty in Doppler estimates for the complementary frequency band. For additional insights into Doppler assistance architectures for L1/L5 bands, readers may refer to Bolla and Borre (2019) and Wu et al. (2019) [4,8].

2.5. Inter-Frequency Doppler Assistance Technique

The inter-frequency Doppler assistance technique capitalizes on the intrinsic linear relationship between Doppler shifts of L1 and L5 signals transmitted by the same satellite. The center frequency of the L1 band is 1575.42 MHz, while that of the L5 band is 1176.45 MHz, yielding a frequency ratio of: ${\displaystyle \frac{f_{L1}}{f_{L5}}}={\displaystyle \frac{1575.42}{1176.45}}\approx 1.34$. Similarly, the code frequency ratio is determined by the respective code rates: the B1C signal has a code rate of 1.023 MHz, and the B2a signal has a code rate of 10.23 MHz, resulting in a ratio of: ${\displaystyle \frac{f_{code,L1}}{f_{code,L5}}}={\displaystyle \frac{1.023}{10.23}}=0.1$. Thus, if the L5 signal has been acquired and its carrier Doppler shift $f_{d,L5}$ and code Doppler shift $f_{cd,L5}$ have been estimated, the corresponding Doppler shifts for the L1 signal ($f_{d,L1}$ and $f_{cd,L1}$) can be predicted as follows:

$$\left[\begin{array}{c}{f}_{cd,L1}\\ f_{d,L1}\end{array}\right]=\left[\begin{array}{cc}0.1& 0\\ 0& 1.34\end{array}\right]\left[\begin{array}{c}{f}_{cd,L5}\\ f_{d,L5}\end{array}\right]$$

(7)

Per the DO-292 standard (RTCA, 2004) [18], in the absence of clock synchronization, the Doppler estimation error for the L5 signal is $\Delta f_{d,L5}=\pm 120\mathrm{Hz}$. Consequently, the predicted carrier Doppler shift error for the L1 signal is calculated as

$$\Delta f_{d,L1}=1.34\times \Delta f_{d,L5}=1.34\times 120\approx 160.8\mathrm{Hz}$$

(8)

Compared to the conventional search range of ±1200 Hz used in traditional acquisition methods, this technique markedly reduces the number of search bins. During L1 signal acquisition, the Doppler search range is confined to the vicinity of the predicted value, thereby decreasing computational complexity and enhancing acquisition efficiency.

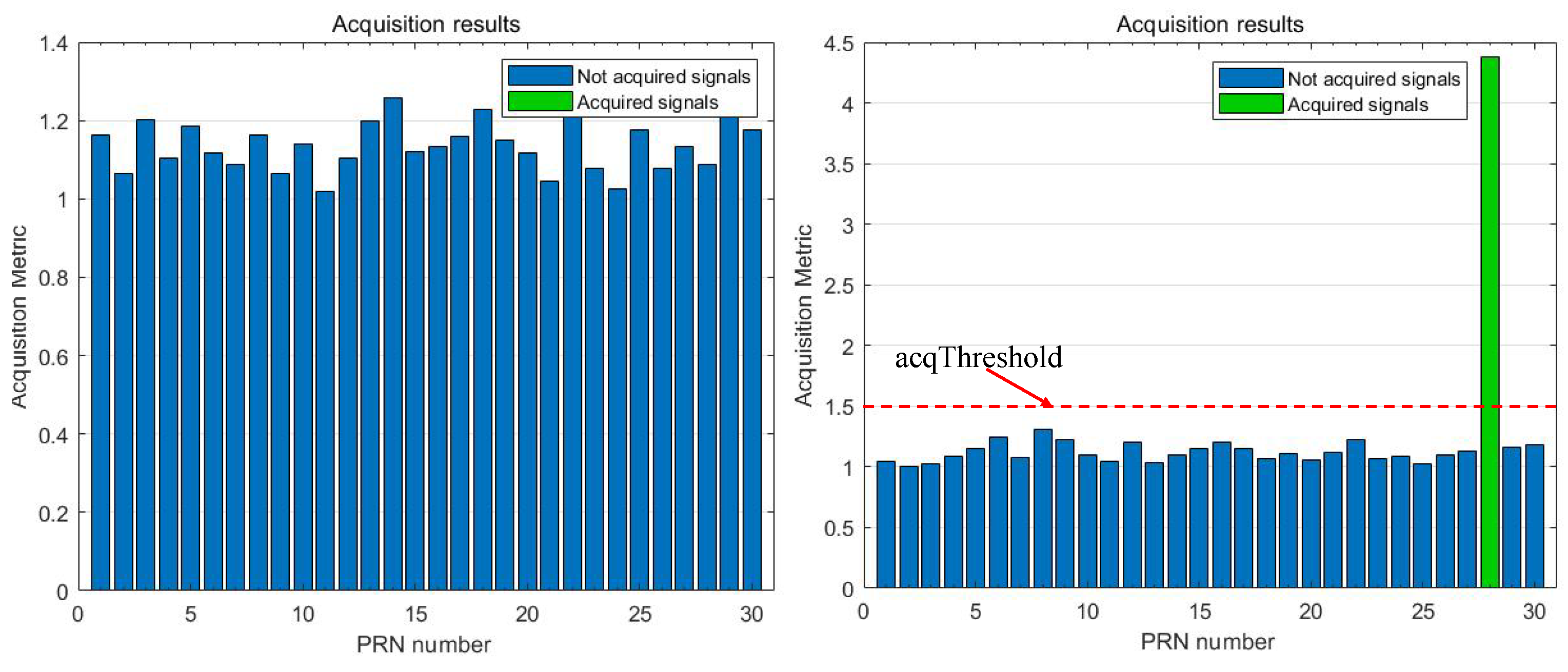
2.6. Inputs for Acquisition Threshold Calculation

Doppler uncertainty refers to the potential variation range of the actual Doppler shift of a signal, primarily induced by user dynamics (relative motion of the receiver), ephemeris errors (deviations in satellite orbit predictions), and receiver clock drift. According to RTCA DO-292 (Appendix D) [18], the velocity uncertainty for the on-ground scenario is dominated by oscillator frequency stability, resulting in a worst-case velocity uncertainty of 300 m/s. For the en-route scenario, continuous saving of navigation data by the receiver reduces the velocity uncertainty to 51 m/s, mainly due to aircraft heading uncertainty. These velocity uncertainties can be converted into frequency uncertainties, as detailed in

Table 2. Doppler uncertainty for different GNSS signals.

Frequency Band	Acquisition Type	En-Route Operations	Ground Operations
L1/E1 (Hz)	1st SV acquisition	$F=\pm 268$	$F=\pm 1500$
	2nd–4th SV acq	$F=\pm 150$	$F=\pm 150$
L5/E5a (Hz)	1st SV acquisition	$F=\pm 200$	$F=\pm 1200$
	2nd–4th SV acq	$F=\pm 120$	$F=\pm 120$

.

The total number of cells in the acquisition matrix, denoted as $N_{tot}$, is determined by the code delay uncertainty D, the frequency uncertainty F, the code delay bin width $\delta d$, and the frequency bin width $\delta f$. Mathematically, the number of cells in the acquisition matrix is expressed as

$$N_{tot}=⌈{\displaystyle \frac{D}{\delta d}}⌉\times ⌈{\displaystyle \frac{F}{\delta f}}⌉$$

(9)

where $⌈·⌉$ represents the ceiling function, rounding up to the nearest integer. The power losses resulting from code delay and frequency misalignments are given by

$$\Delta C_d={\left({\displaystyle \frac{{\tilde{R}}_X^Y\left(\frac{\delta d}{2}\right)}{{\tilde{R}}_X^Y\left(0\right)}}\right)}^2\Delta C_f=sin{c}^2\left(\pi {\displaystyle \frac{\delta f}{2}}{T}_i\right)$$

(10)

Traditional acquisition methods encounter significant challenges when addressing navigation bit transitions. For example, in the case of the GPS L1 C/A signal, the coherent integration time $T_i$ is typically set to 1 ms. According to Bastide et al. [19], the frequency bin width $\delta f$ is commonly configured as ${\displaystyle \frac{1}{2T_i}}$. This implies that extending the coherent integration time reduces $\delta f$, consequently increasing the number of Doppler frequency sets that must be searched. As noted earlier, the inter-frequency Doppler assistance technique for dual-frequency signals mitigates this limitation.

For the BeiDou B1C signal, Figure 1 and Figure 2 illustrates that the slope of its correlation function is approximately three times steeper than that of the GPS correlation function. As a result, Julien et al. [20] recommend reducing the code delay bin width by a factor of three, i.e., $\delta d={\displaystyle \frac{T_{chip}}{6}}$, where $T_{chip}$ denotes the chip period. The resulting number of cells in the acquisition matrix is summarized in

Table 3. Number of cells in the acquisition matrix.

Signal	Acquisition Type	Code Uncertainty	$\mathit{\delta }\mathit{d}$	Freq. Uncertainty	$\mathit{\delta }\mathit{f}$	Total Cells
		(Chips)	(Chip)	(Hz)	(Hz)	${\mathit{N}}_{\mathrm{tot}}$
B1C	1st SV acquisition	10,230	1/6	3000	500	368,280
	Doppler assistance acquisition	10,230	1/6	322 *	50	395,287
B2a	1st SV acquisition	10,230	1/2	2400	100	491,040
	2nd–4th SV acquisition	10,230	1/2	240	100	61,380
L1C/A	1st SV acquisition	1023	1/2	3000	500	12,276
	2nd–4th SV acquisition	1023	1/2	300	500	2046

* See Equation (8) for details. 322 Hz is the rounded total Doppler range from ±160.8 Hz.

.

2.7. Derivation of Theoretical Acquisition Thresholds

To quantitatively assess the performance of various acquisition strategies, this section derives a mathematical model for the acquisition threshold using the Neyman–Pearson detection criterion. The detection probability Pd and its relationship with the carrier-to-noise ratio ($(C/N_0)$) play a pivotal role in determining acquisition effectiveness. The objective here is to establish detection models for both single-component and dual-component acquisition scenarios, laying a theoretical groundwork for subsequent performance evaluations.

2.7.1. Detection Model

The signal acquisition problem can be modeled as a binary hypothesis test:

H₀ (Null Hypothesis): 

The target signal is absent. However, cross-correlation interference from other GNSS signals may be present.

H₁ (Alternative Hypothesis): 

The target signal is present, with the Doppler frequency and code delay of the detection cell aligning with those of the received signal. For single-component acquisition [21], the normalized detector T₁ follows a non-central chi-squared distribution with 2M_T1 degrees of freedom. The non-centrality parameter is expressed as

$${\lambda }_0^{T_1}={\displaystyle \frac{P_j}{{\sigma }_n^2}}\sum _{k=1}^{M_{T_1}}{\tilde{R}}_{C_D,J,C_D}^X{\left(0\right)}^2=2T_i{\displaystyle \frac{C_j}{N_0}}{M}_{T_1}{\left(K_j^{T_1}\right)}^2$$

(11)

$$K_j^{T_1}={\displaystyle \frac{{\tilde{R}}_{C_D,J,C_D}^X\left({\epsilon }_{\tau ,max}\right)}{{\tilde{R}}_{C_D,J,C_D}^X\left(0\right)}}$$

(12)

$${\lambda }_1^{T_1}=2M_{T_1}{\displaystyle \frac{C_{L1}}{N_0}}{\left({\displaystyle \frac{{\tilde{R}}_{C_D,C_D}^{L1}\left({\epsilon }_{\tau }\right)}{{\tilde{R}}_{C_D,C_D}^{L1}\left(0\right)}}\right)}^2{\mathrm{sinc}}^2\left({\pi \epsilon }_f{T}_i\right)$$

(13)

For dual-component acquisition, the normalized detector $T_2$ follows a non-central chi-squared distribution with $4M_{T1}$ degrees of freedom, and its non-centrality parameter is given by

$${\lambda }_0^{T_2}=2T_i{\displaystyle \frac{C_j}{N_0}}{M}_{T_2}{\left(K_j^{T_2}\right)}^2$$

(14)

$$K_j^{T_2}={\displaystyle \frac{\left({\tilde{R}}_{C_D,J,C_D}^X{\left({\epsilon }_{\tau ,max}\right)}^2+{\tilde{R}}_{C_P,J,C_D}^X{\left({\epsilon }_{\tau ,max}\right)}^2+{\tilde{R}}_{C_D,J,C_P}^X{\left({\epsilon }_{\tau ,max}\right)}^2+{\tilde{R}}_{C_P,J,C_P}^X{\left({\epsilon }_{\tau ,max}\right)}^2\right)}{{\tilde{R}}_{C_D,J,C_D}^X{\left(0\right)}^2+{\tilde{R}}_{C_P,J,C_P}^X{\left(0\right)}^2}}$$

(15)

$${\lambda }_1^{T_2}=2M_{T_2}{T}_i{\displaystyle \frac{C_X}{N_0}}\left({\tilde{R}}_{C_D,C_D}^X{\left({\epsilon }_{\tau }\right)}^2+{\tilde{R}}_{C_P,C_D}^X{\left({\epsilon }_{\tau }\right)}^2\right){\mathrm{sinc}}^2\left(\pi {\epsilon }_f{T}_i\right)$$

(16)

Here, $K_j^{T_l}(l\in \{1,2\})$ denotes the cross-correlation between the interfering signal’s PRN code and the local PRN code, and M represents the number of non-coherent integrations. The values of cross-correlation interference are consistent with those specified in RTCA standards [18,21] and the findings of Sun et al. [22], as detailed in

Table 4. Cross-correlation interference.

Signal	GPS L1 C/A	Galileo E1	BDS B1C	GPS L5 / Galileo E5a
Value	−24 dB	−29.5 dB	−28 dB	−34 dB

.

2.7.2. Calculation of Threshold and Detection Probability

Under the hypotheses $H_0$ and $H_1$, the detection probability $P_d$ is a function of the GNSS signal’s $C_X/N_0$, where X represents the target signal. The computation of $P_d$ proceeds in two steps:

Step 1: The detection threshold $T_h^l$ is derived from the distribution of the detector $T_1$ and the false alarm rate $P_{fa}$:

$$T_h={\sigma }_n^2{F}_{{\chi }^2}^{-1}\left(2l{M}_{T_l},{\lambda }_0^{T_l}\right)(1-P_{fa})$$

(17)

Step 2: Under $H_1$, the detection probability is calculated as

$$P_d\left({\displaystyle \frac{C}{N_0}},{\epsilon }_{\tau },{\epsilon }_f\right)=\mathbb{P}(T_l\ge T_h\mid H_1)=1-F_{{\chi }^2}\left(2l{M}_{T_l},{\lambda }_1^{T_l},{\displaystyle \frac{T_h}{{\sigma }_n^2}}\right)$$

(18)

Since ${\epsilon }_{\tau }$, ${\epsilon }_f$ can be treated as a uniformly distributed random variable, the average detection probability is obtained through integration:

$$P_D\left({\displaystyle \frac{C}{N_0}}\right)=\mathbb{E}\left(P_d\left({\displaystyle \frac{C}{N_0}},{\epsilon }_{\tau },{\epsilon }_f\right)\right),{\epsilon }_{\tau }\sim \mathcal{U}\left(\left[-{\displaystyle \frac{\delta d}{2}};{\displaystyle \frac{\delta d}{2}}\right]\right),{\epsilon }_f\sim \mathcal{U}\left(\left[-{\displaystyle \frac{\delta f}{2}};{\displaystyle \frac{\delta f}{2}}\right]\right)$$

(19)

where $F_{{\chi }^2}^{-1}$ is the cumulative distribution function of the chi-squared distribution. The acquisition sensitivity is defined as the minimum $C/N_0$ at which $P_d\ge 0.95$.

3. Results

The performance of signal acquisition is commonly assessed using key metrics such as detection probability, acquisition threshold, and false alarm probability. In this chapter, we concentrate on the analysis of detection probability and acquisition threshold to investigate the performance benefits offered by the dual-frequency cooperative acquisition strategy. To ensure practical relevance, the performance evaluation is conducted under a false alarm rate of $P_{fa}$ = $1\times {10}^{-3}$, a value widely adopted in system design as a reasonable compromise between sensitivity and reliability [21].

3.1. Analysis of Traditional Fixed Short-Time Integration Acquisition

Traditional acquisition methods often rely on fixed short-time integration. For instance, GPS L1 C/A signals typically employ a 1 ms coherent integration period. The performance of this approach is illustrated in Figure 4, which depicts the relationship between the detection probability ($P_d$) and the threshold $C/N_0$ for GPS L1 C/A signals under varying numbers of correlators ($N_{corr}$ ranging from 10 to 100). At a detection probability of $P_d$ = 0.95, the $C/N_0$ threshold is approximately 29.8 dB-Hz [21]. This result aligns with the performance requirements outlined in the RTCA-DO235C standard, confirming the accuracy of the simulation model. Subsequent simulations will extend this analysis to BeiDou dual-frequency signals to substantiate the superiority of the dual-frequency cooperative acquisition strategy.

3.2. Acquisition of B1C Single Pilot Component

This section evaluates the acquisition performance of the BeiDou B1C pilot component under varying coherent integration times. The analysis employs 100 parallel correlators ($N_{corr}$ = 100) to search for Doppler shifts and code phases. The performance is assessed through the relationship between the detection probability ($P_d$) and the $C/N_0$ threshold, with further optimizations achieved using inter-frequency Doppler assistance to enhance acquisition sensitivity and computational efficiency.

Figure 5 illustrates the variation in Pd with respect to the $C/N_0$ threshold for different integration times. In traditional B1C pilot channel receivers, a 1 ms coherent integration time is standard, yielding a $C/N_0$ threshold of approximately 34.0 dB-Hz at $P_d$ = 0.95 [23]. Leveraging the frequency ratio between B1C (1575.42 MHz) and B2a (1176.45 MHz) signals—approximately 1.34:1—this study applies inter-frequency Doppler assistance to extend the coherent integration time to 10 ms. This technique narrows the Doppler search range from ±1500 Hz to ±160 Hz around the predicted value, while maintaining a finer Doppler step size. Consequently, at $P_d$ = 0.95, the $C/N_0$ threshold decreases to 28.3 dB-Hz, improving acquisition sensitivity by approximately 5.7 dB. This enhancement significantly improves the receiver’s capability to detect weak signals, such as those from low-elevation satellites.

Figure 6 compares the acquisition results for coherent integration times of 1 and 10 ms, highlighting the benefits of inter-frequency Doppler assistance. With a 1 ms integration time, the acquisition peak is relatively low, indicating limited detection capability for weak signals. In contrast, a 10 ms integration time produces a substantially higher acquisition peak, reflecting improved signal resolution. This difference arises from the increased signal energy accumulated over the extended integration period and the optimized Doppler search range enabled by inter-frequency assistance. By exploiting the linear frequency relationship between B1C and B2a signals, the dual-frequency receiver enhances acquisition sensitivity and robustness under challenging conditions. Meanwhile, the computational burden for acquiring the complementary frequency band remains at a comparable level to the conventional single-frequency approach, thus avoiding significant additional hardware resource requirements.

3.3. Dual-Channel Acquisition of B2a Pilot and Data Components

Studies by Li, Shivaramaiah, and other researchers have shown that the Generalized Likelihood Ratio Test (GLRT) statistic for the non-coherent combination of dual channels significantly outperforms that of processing the data channel alone, thereby confirming the efficacy of joint acquisition strategies [10]. Figure 7 depicts the detection probability ($P_d$) as a function of the $C/N_0$ for the B2a signal under a dual-channel acquisition approach. Given that the B2a data component is subject to navigation bit transitions, the coherent integration time is limited to a maximum of 5 ms [3]. To overcome this constraint, the proposed strategy employs non-coherent integration to extend the total integration duration effectively.

As illustrated in Figure 7a, when employing a 1 ms coherent integration time, the acquisition threshold decreases progressively from 32.5 to 29.6 dB-Hz as the number of correlators increases from 100 to 1000. This reduction suggests that a higher number of correlators facilitates more parallel searches and increases the number of non-coherent integrations, thereby enhancing overall acquisition performance. Notably, at $N_{corr}$ = 1000, the threshold drops to 29.6 dB-Hz. Modern airborne receivers are capable of supporting the computational load associated with 1000 complex correlators [23], underscoring the practical viability of this approach in real-world applications.

In the design of dual-frequency receivers, a trade-off between computational complexity and performance requirements was achieved by avoiding the most stringent constraints on the number of correlators, resulting in the selection of $N_{corr}$ = 600. As illustrated in Figure 7b, an increase in the coherent integration time ($T_i$) from 1 to 5 ms leads to a significant enhancement in acquisition sensitivity. Specifically, at a detection probability of $P_d$ = 0.95, the required carrier-to-noise ratio ($C/N_0$) decreases from 30.6 dB-Hz at $T_i$ = 1 ms to 29.1 dB-Hz at $T_i$ = 5 ms, yielding a sensitivity improvement of 1.5 dB. This improvement is attributed to the extension of the total integration duration, accomplished by lengthening the coherent integration time and incorporating non-coherent integration. This approach enables the receiver to accumulate greater signal energy, thereby enhancing the signal-to-noise ratio and optimizing acquisition performance.

To further substantiate the efficacy of the proposed strategy, acquisition simulation tests were performed utilizing intermediate frequency (IF) signals collected from real-world scenarios. The IF signal data utilized in this investigation were obtained from an open-access dataset published by Li et al. [10]. Details on the experimental setup can be found in the original publication. Figure 8 presents the spectrum of the digital IF samples, revealing a distinct signal peak at 15 MHz, which confirms the presence of the BDS B2a signal. Simulation results indicate that, with a 1 ms coherent integration time, the acquisition metric fails to detect any signal. In contrast, extending the coherent integration time to 5 ms enables the acquisition metric for PRN28 (represented by a green bar) to surpass the acquisition threshold (denoted by a red dashed line), as illustrated in Figure 9. This demonstrates a significant improvement in weak signal acquisition performance achieved by lengthening the integration period.

Further evidence is provided in Figure 10, which displays the correlation results across Doppler bins for a 5 ms coherent integration. A prominent peak is observed at sample 3760, with an amplitude of approximately 16,000, well above the detection threshold. This result conclusively demonstrates successful signal acquisition under the proposed strategy.

4. Discussion

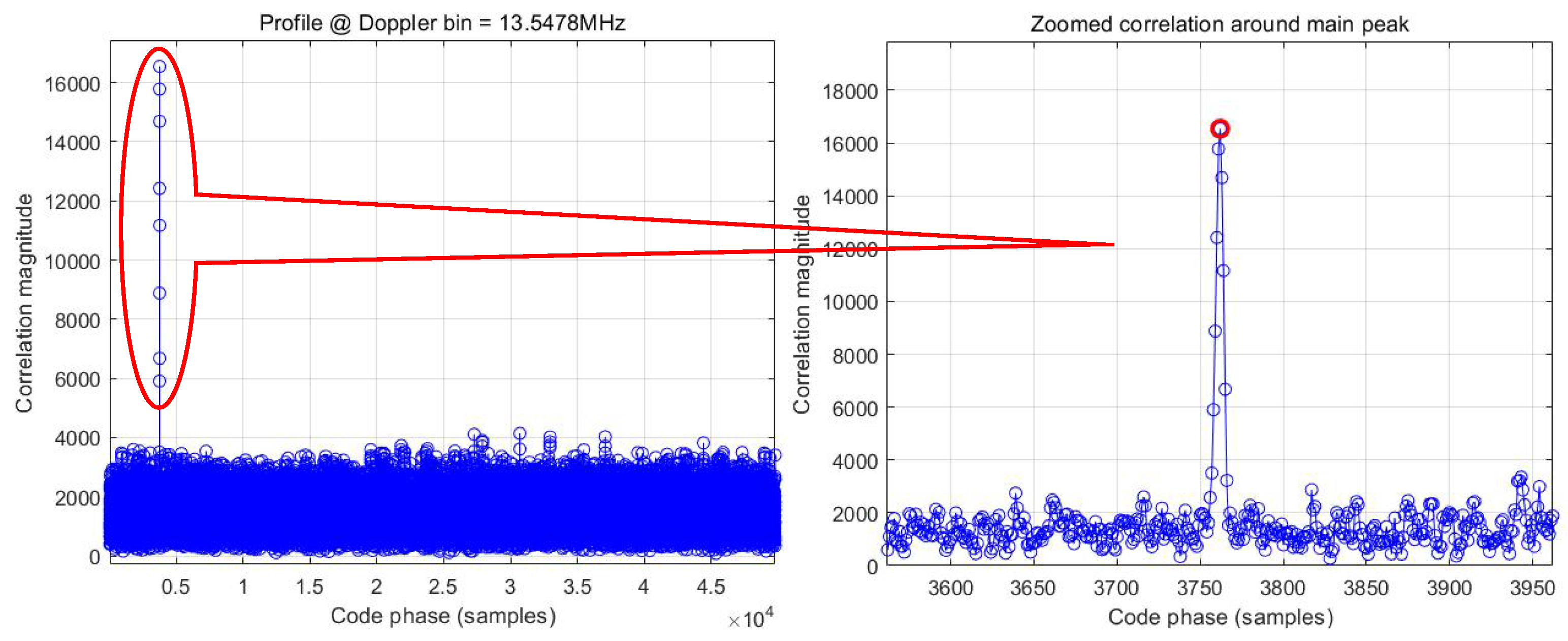
This study presents a novel dual-frequency cooperative acquisition strategy tailored for BeiDou DFMC receivers, designed to enhance signal acquisition performance in challenging weak signal environments. By leveraging inter-frequency Doppler assistance and extended coherent integration times, this approach markedly improves sensitivity compared to conventional methods. Traditional acquisition techniques often face limitations due to navigation bit transitions in the data channel, which restrict integration duration. In contrast, our strategy optimizes the processing of the B1C and B2a pilot components, effectively circumventing these constraints.

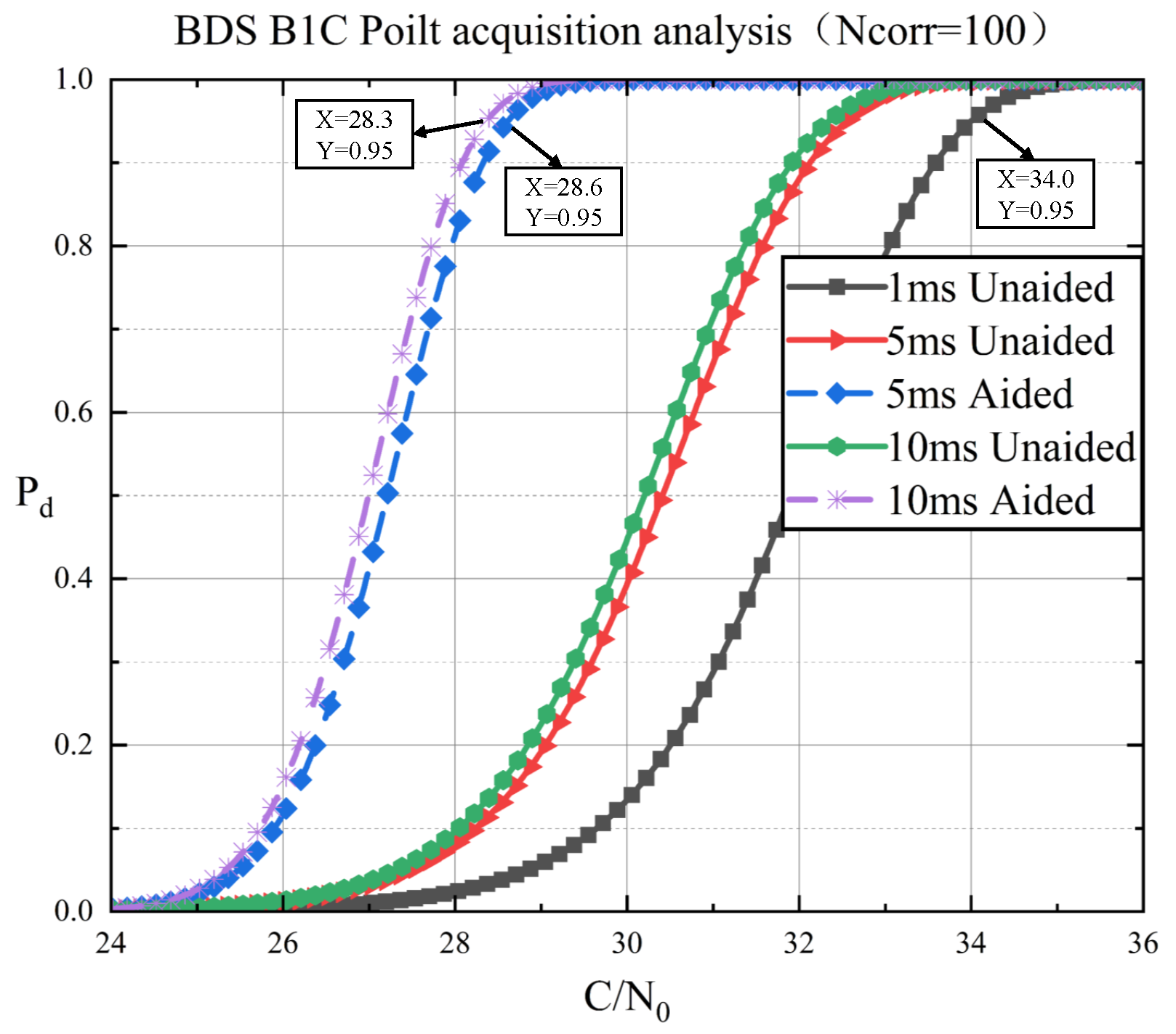
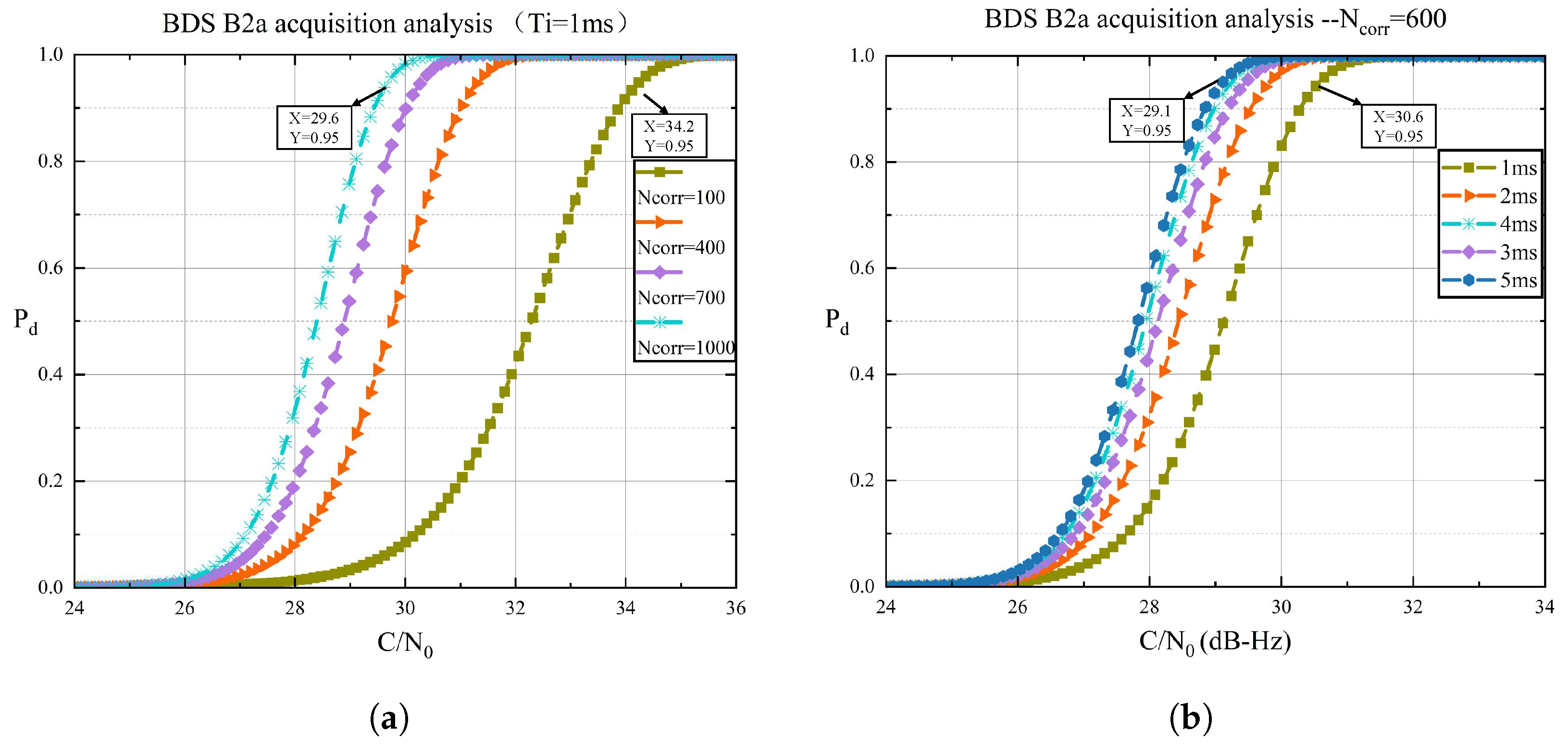
Simulation results highlight the efficacy of the proposed method. For the B1C pilot component, acquisition sensitivity improved by 5.7 dB, reducing the acquisition threshold from 34.0 to 28.3 dB-Hz. Similarly, for the B2a signal, the dual-channel cooperative approach lowered the threshold to 29.1 dB-Hz using 600 correlators—a configuration compatible with practical hardware limitations. These improvements stem from exploiting the linear frequency relationship between the B1C and B2a signals, which reduces Doppler search uncertainty. This enables longer integration periods without a proportional increase in computational overhead, making the strategy particularly effective for detecting weak signals, such as those from low-elevation satellites.

In this study, weak signal conditions are defined as scenarios in which conventional methods fail to acquire a satellite, while the proposed strategy succeeds. This practical definition avoids reliance on a fixed $C/N_0$ threshold [24]. The theoretical framework underpinning this method aligns with the RTCA-DO235C standard, reinforcing its reliability and applicability to high-precision BeiDou applications. These advancements position the strategy as a promising solution for next-generation GNSS receivers operating in diverse environments.

Looking ahead, several avenues warrant further exploration. Hardware implementation and real-world testing in scenarios such as urban canyons or high-dynamic conditions are essential to validate the strategy’s practical performance. Moreover, integrating adaptive integration times or advanced filtering techniques could bolster resilience against interference and multipath effects, further enhancing robustness. Future work will include comparisons with adaptive acquisition techniques to further assess performance. This research establishes a solid foundation for the design of BeiDou DFMC receivers and holds potential for broader application across other multi-frequency GNSS systems.

5. Conclusions

This study proposes a dual-frequency cooperative acquisition strategy for BeiDou DFMC receivers. By extending the integration time of the pilot component and leveraging inter-frequency Doppler assistance, the strategy significantly improves acquisition sensitivity in weak signal environments. Simulation results demonstrate that, for the B1C pilot component, a 10 ms coherent integration combined with inter-frequency Doppler assistance enhances the acquisition sensitivity from 34.0 to 28.3 dB-Hz, yielding a gain of 5.7 dB. For the B2a signal, the dual-channel cooperative acquisition strategy reduces the acquisition threshold to 29.1 dB-Hz with 600 correlators. The acquisition threshold is derived based on the Neyman–Pearson detection criterion, and the simulation outcomes are consistent with the RTCA-DO235C standard, confirming the model’s validity. This research provides theoretical support and simulation-based evidence for the acquisition design of BeiDou DFMC receivers, establishing a foundation for high-precision positioning applications. Nevertheless, several important aspects remain for future work. Comprehensive hardware implementation and field testing under diverse and challenging conditions will be pursued to fully validate the proposed method in practical environments. In addition, further comparative studies with other advanced acquisition techniques will be conducted to provide a more thorough performance assessment and promote broader applicability in next-generation GNSS receivers.