Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology
Abstract
1. Introduction
2. Computational Methodology
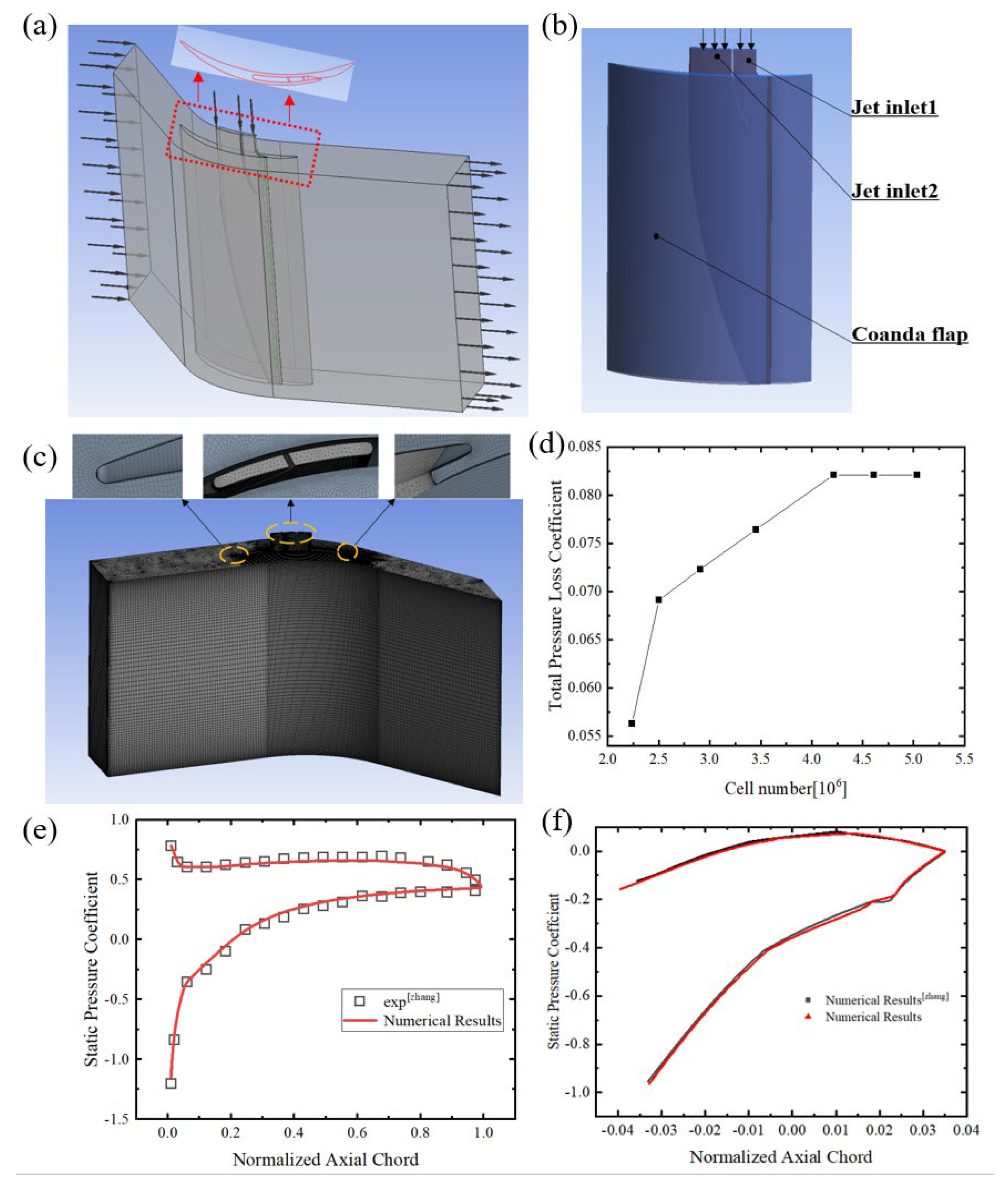
2.1. Geometry Model
2.2. Numerical Model
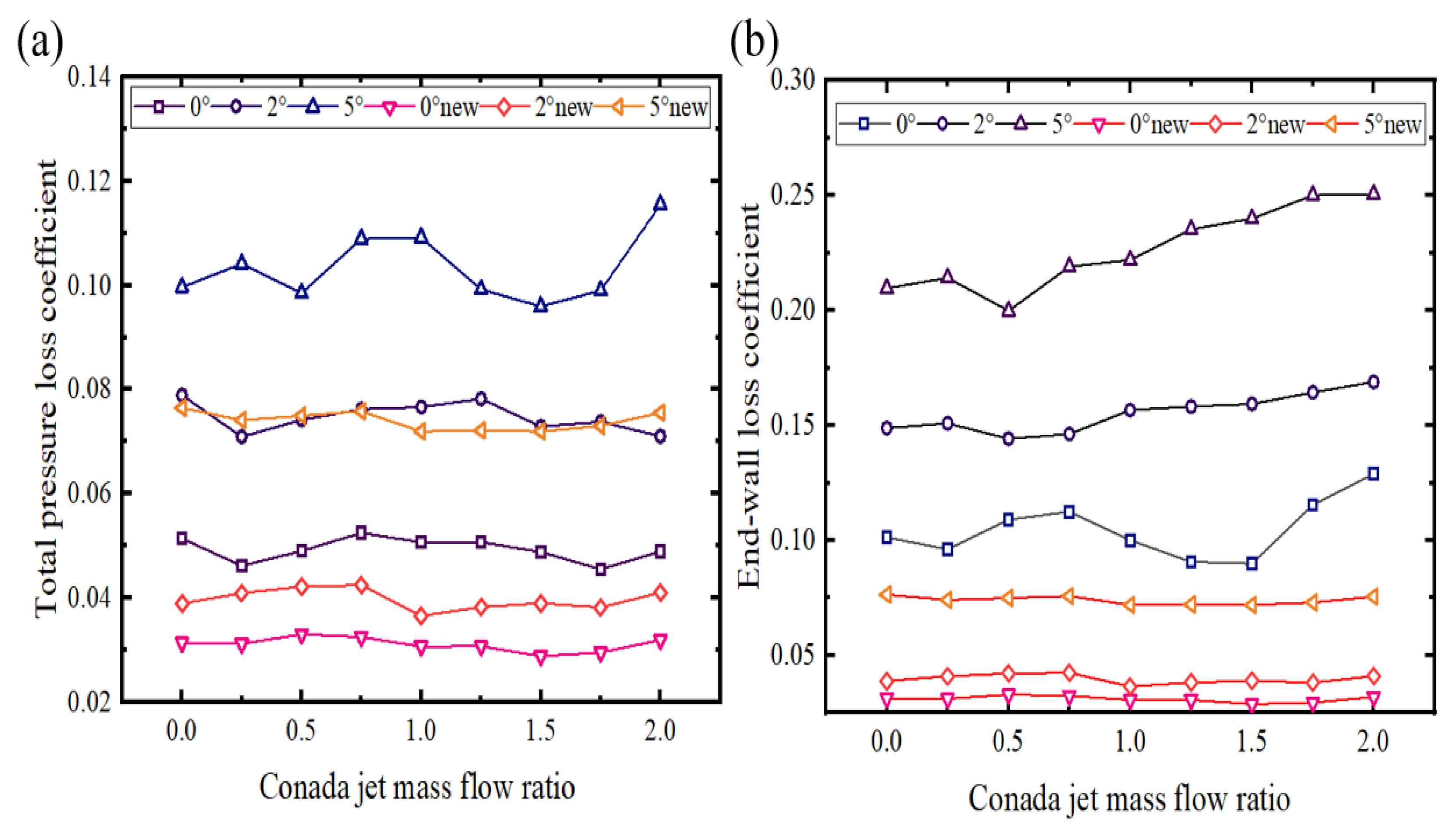
2.3. Model Verification
3. Design Optimization
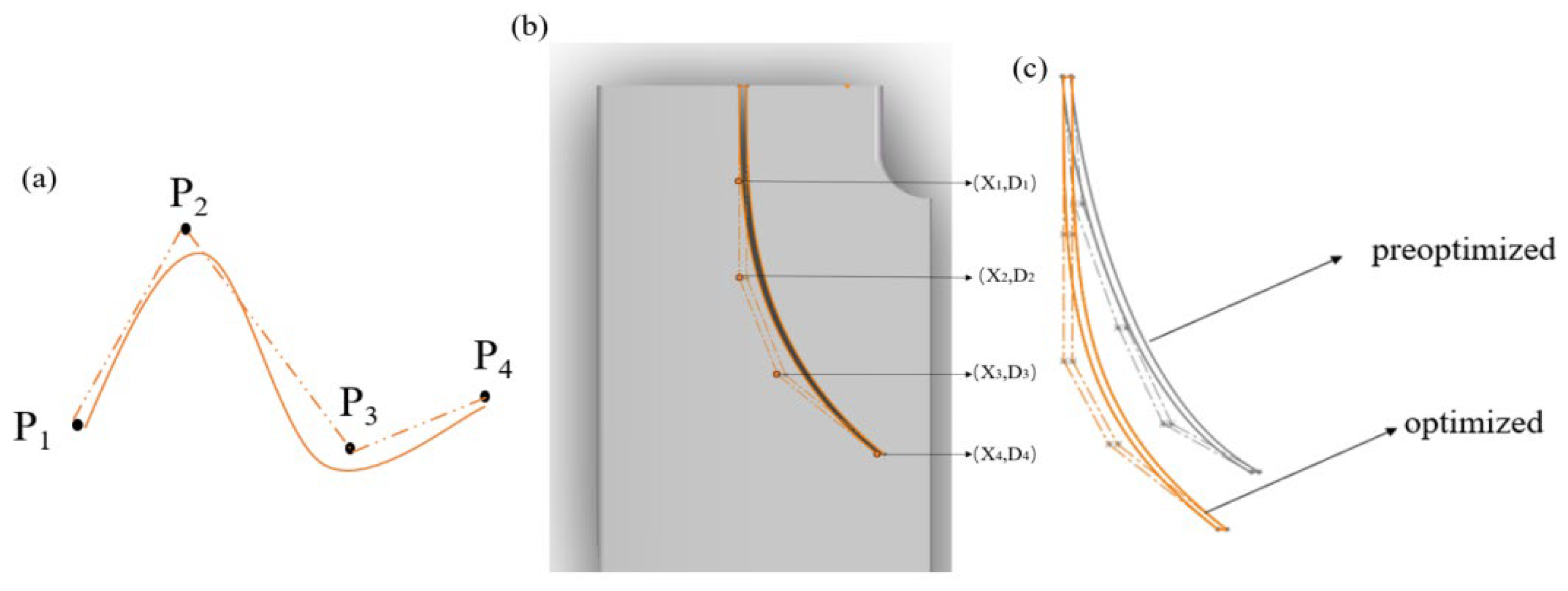
3.1. Optimization Factors
3.2. Experimental Design
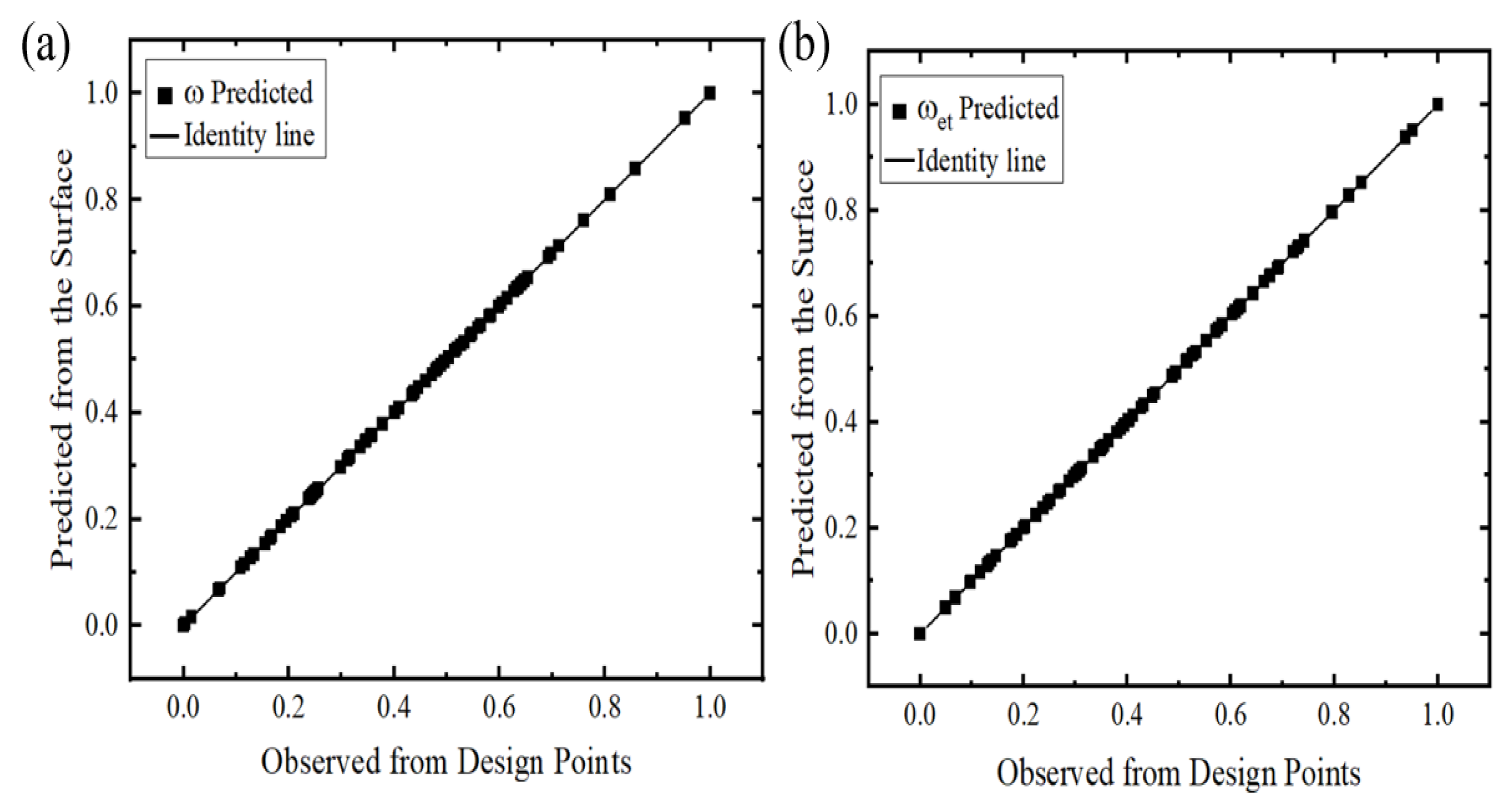
3.3. Response Surface Methodology
3.4. Multi-Objective Optimization
4. Results and Discussion
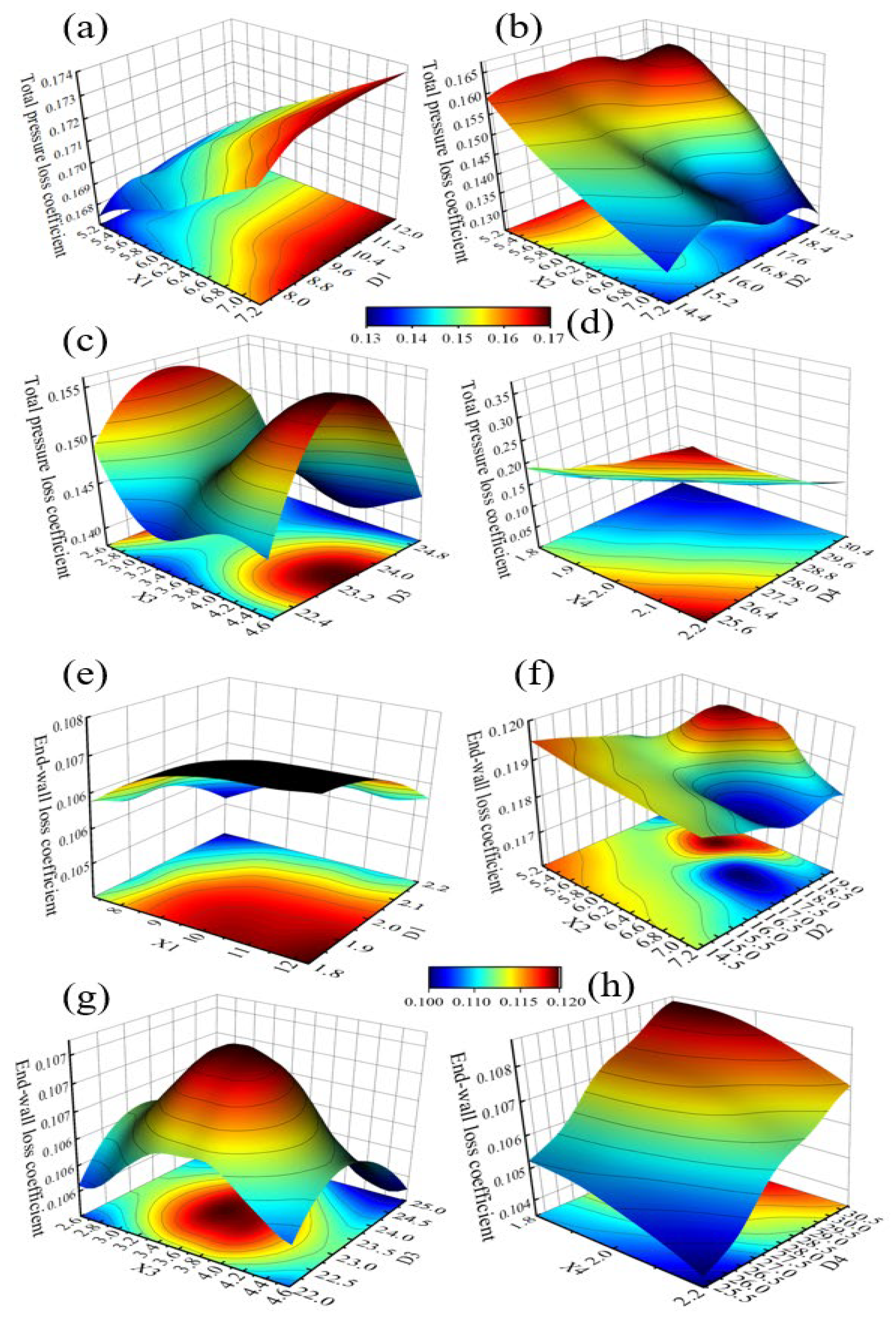
4.1. Response Surface Models
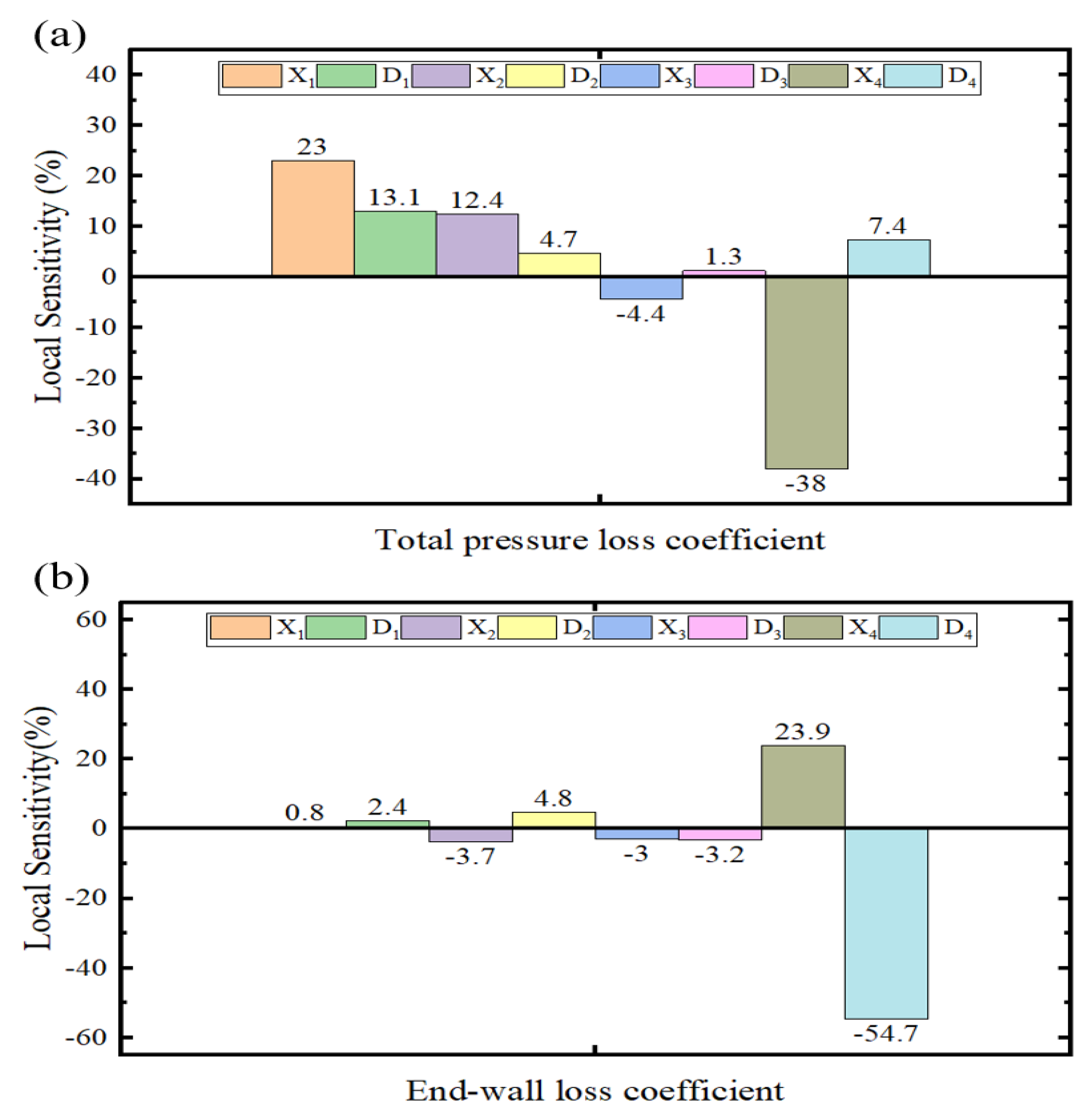
4.2. Sensitivity Analysis
4.3. Optimization Results
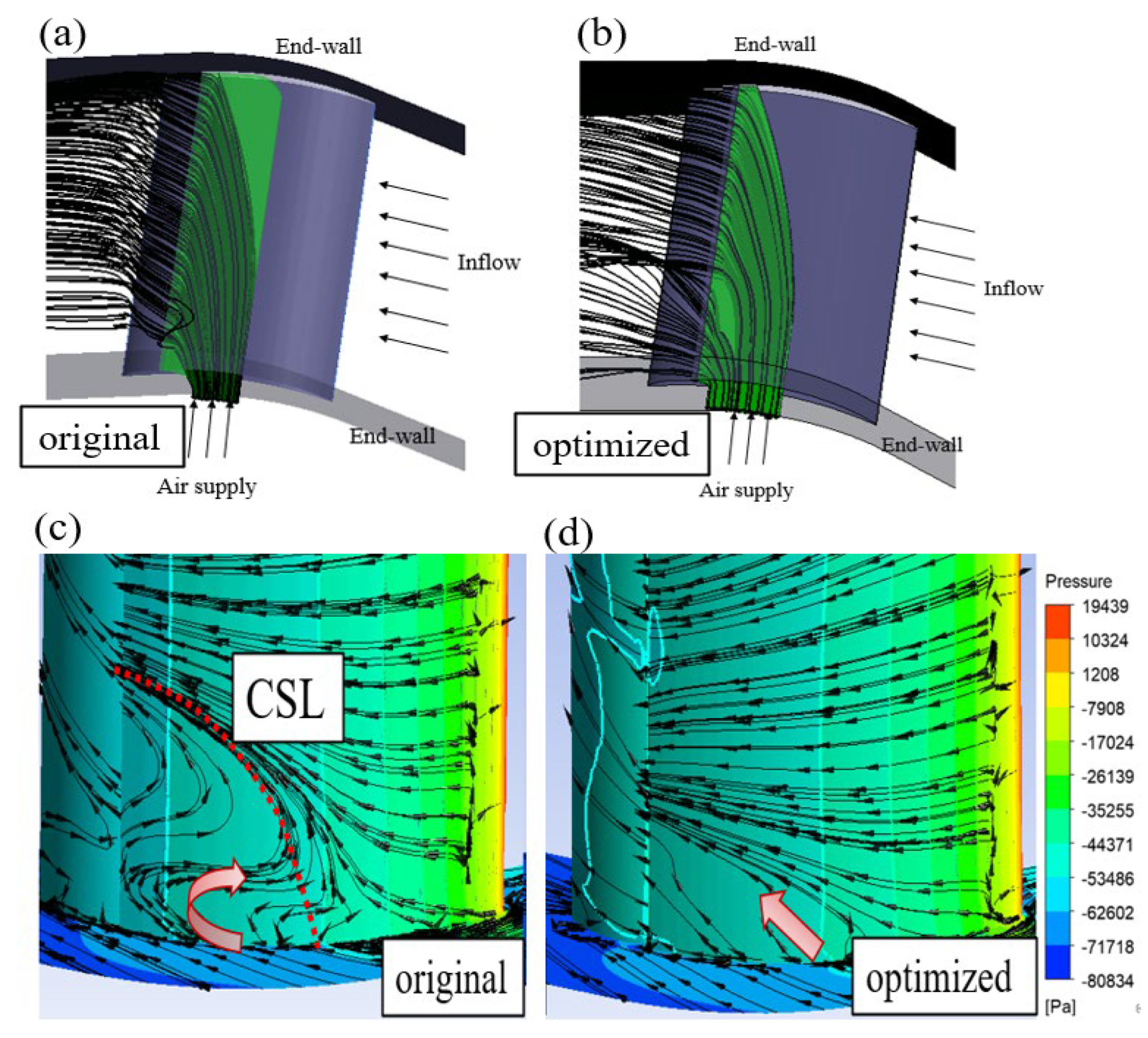
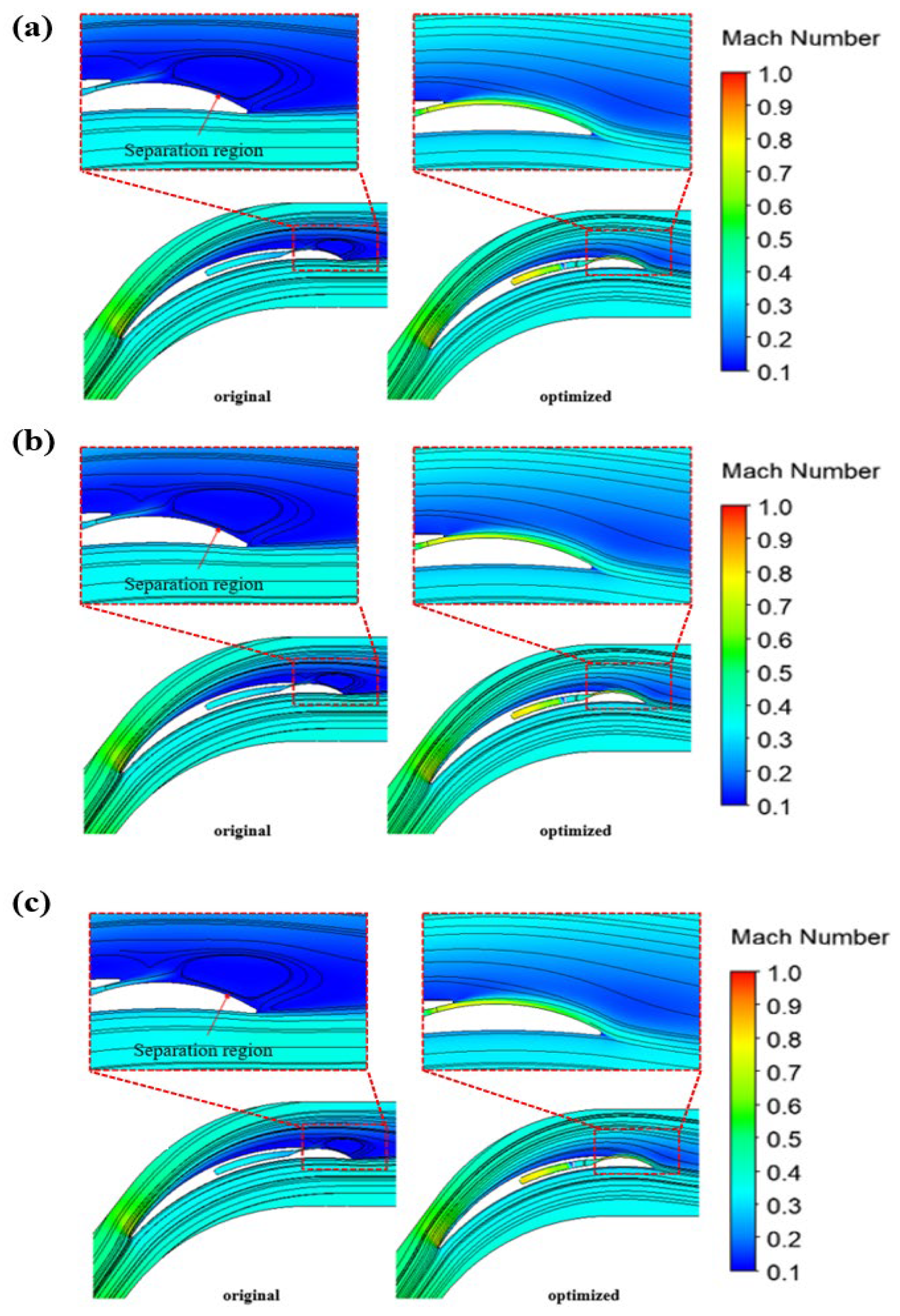
4.4. Analysis of the Flow Field Before and After Optimization
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Day, I. Stall, Surge, and 75 Years of Research. J. Turbomach. 2015, 138, 11001. [Google Scholar] [CrossRef]
- Lieblein, S. Loss and Stall Analysis of Compressor Cascades. J. Basic Eng. 1959, 81, 387–400. [Google Scholar] [CrossRef]
- Jothiprasad, G.; Murray, R.C.; Essenhigh, K.; Bennett, G.A.; Saddoughi, S.; Wadia, A.; Breeze-Stringfellow, A. Control of tip-clearance flow in a low speed axial compressor rotor with plasma actuation. J. Turbomach. 2012, 134, 021019. [Google Scholar] [CrossRef]
- Lieblein, S.; Schwenk, F.C.; Broderick, R.L. Diffusion factor for estimating losses and limiting blade loadings in axial-flow-compressor blade elements. Tech. Rep. Arch. Image Libr. 1953, NACA RM E53DOI, 10004207426. [Google Scholar]
- Lee, N.K.W.; Greitzer, E.M. Effects of endwall suction and blowing on compressor stability enhancement. J. Turbomach. 1990, 112, 133–144. [Google Scholar] [CrossRef]
- Sonoda, T.; Olhofer, M.; Hasenjaeger, M.; Schreiber, H.A. Airfoil for Axial-Flow Compressor Capable of Lowering Loss in Low Reynolds Number Region. U.S. Patent No. 8,152,459, 10 April 2012. [Google Scholar]
- Culley, D.E.; Bright, M.M.; Prahst, P.S.; Strazisar, A.J. Active Flow Separation Control of a Stator Vane Using Surface Injection in a Multistage Compressor Experiment. J. Turbomach. 2003, 36894, 1039–1050. [Google Scholar]
- Culley, D.E.; Bright, M.M.; Prahst, P.S.; Strazisar, A.J. Active Flow Separation Control of a Stator Vane Using Embedded Injection in a Multistage Compressor Experiment. Am. Soc. Mech. Eng. 2004, 126, 24–34. [Google Scholar] [CrossRef]
- Wang, B.; Wu, Y.; Spence, S. Loss reduction in a high-speed compressor cascade using an L-shaped endwall groove to generate a streamwise vortex. Aerosp. Sci. Technol. 2022, 123, 107486. [Google Scholar] [CrossRef]
- Sun, J.; Ottavy, X.; Liu, Y.; Lu, L. Corner separation control by optimizing blade end slots in a linear compressor cascade. Aerosp. Sci. Technol. 2021, 114, 106737. [Google Scholar] [CrossRef]
- Abbott, F.T., Jr.; Library, I. Test of NACA 66,2-116, a = 0.6 airfoil section fitted with pressure balanced and slotted flaps for the wing of the XP-63 airplane. Tech. Rep. Arch. 1942, 41, 47–55. [Google Scholar]
- Landsberg, T.J.; Krasnoff, E. An Experimental Study of Rectilinear Jet-Flap Cascades. J. Fluids Eng. 1972, 94, 97–104. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. Aiaa J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Dal Monte, A.; Castelli, M.R.; Benini, E. A retrospective of high-lift device technology. Int. J. Aerosp. Mech. Eng. 2012, 6, 2561–2566. [Google Scholar]
- Feng, Y.; Song, Y.; Chen, F. Numerical simulation of circulation control turbine cascade with Coanda jet and counter-flow blowing at high Mach numbers. Aeronaut. J. 2017, 121, 1239–1260. [Google Scholar] [CrossRef]
- Horn, J.; Nafploitis, N.; Goldberg, D.E. A niched Pareto genetic algorithm for multi-objectiveoptimization. In Proceedings of the First IEEE Conference onEvolutionary Computation, Orlando, FL, USA, 27–29 June 1994; IEEE Service Center: Piscataway, NJ, USA, 1994. [Google Scholar]
- Samad, A.; Kim, K.-Y. Shape Optimization of an Axial Compressor Blade by Multi-objective Genetic Algorithm. Proc. Inst. Mech. Engineers. Part A J. Power Energy 2008, 222, 599–611. [Google Scholar] [CrossRef]
- Ma, C.; Su, X.; Yuan, X. An Efficient Unsteady Adjoint Optimization System for Multistage Turbomachinery. J. Turbomach. 2017, 139, 11003. [Google Scholar] [CrossRef]
- Benini, E. Three-Dimensional Multi-Objective Design Optimization of a Transonic Compressor Rotor. J. Propuls. Power 2004, 20, 559–565. [Google Scholar] [CrossRef]
- Fonseca, C.M.; Fleming, P.J. Genetic Algorithms for Multiobjective Optimization: Formulation, Discussion and Generalization. In Proceedings of the Fifth International Conference on Genetic Algorithms, San Mateo, CA, USA, 17–21 July 1993. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Nondominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II. In Proceedings of the 6th International Conference Parallel Problem Solving from Nature-PPSN VI, Paris, France, 18–20 September 2000. [Google Scholar]
- Jameson, A. Aerodynamic Shape Optimization Using the Adjoint Method; Von Karman Institute: Brussels, Belgium, 2003. [Google Scholar]
- Luo, J.; Zhou, C.; Liu, F. Multipoint Design Optimization of a Transonic Compressor Blade by Using an Adjoint Method. J. Turbomach. 2014, 136, 051005. [Google Scholar] [CrossRef]
- Bellman, M.; Straccia, J.; Morgan, B.; Maschmeyer, K.; Agarwal, R. Improving Genetic Algorithm Efficiency with an 19 Artificial Neural Network for Optimization of Low Reynolds Number Airfoils. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Srinivas, N.; Deb, K. Multiobjective Function Optimization Using Nondominated Sorting Genetic Algorithms. Evol. Comput. 1995, 2, 221–248. [Google Scholar] [CrossRef]
- Zhang, J.; Du, J.; Zhang, M.; Chen, Z.; Zhang, H.; Nie, C. Aerodynamic Performance Improvement of a Highly Loaded Compressor Airfoil with Coanda Jet Flap. J. Therm. Sci. 2022, 31, 151–162. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Chord length | 62.1 mm |
| Pitch width | 29 mm |
| Solidity | 2.14 |
| Stagger angle | 20.5° |
| Camber angle | 65.0° |
| Aspect ratio | 1.61 |
| Inlet metal angle | 53° |
| Outlet metal angle | 12° |
| Parameter | Range (mm) |
|---|---|
| (X1, D1) | (5.2~7.2, 7.3~12.3) |
| (X2, D2) | (5.2~7.2, 14.3~19.3) |
| (X3, D3) | (2.6~4.6, 22~25) |
| (X4, D4) | (1.5~3, 26~30) |
| #1 | #2 | #3 | |
|---|---|---|---|
| (X1, D1) | (7.1864, 10.6730) | (7.1882, 9.0353) | (7.1854, 9.0939) |
| (X2, D2) | (7.1864, 19.2922) | (7.1875, 19.2439) | (7.1885, 19.2175) |
| (X3, D3) | (4.5477, 24.9869) | (3.8512, 24.9944) | (4.5672, 24.9944) |
| (X4, D4) | (1.8000, 30.7916) | (1.8003, 30.7941) | (1.8003, 30.7939) |
| ω | 0.0622 | 0.0621 | 0.0648 |
| ωet | 0.0648 | 0.0620 | 0.0647 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yue, K.; Zhang, Y. Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology. Aerospace 2025, 12, 571. https://doi.org/10.3390/aerospace12070571
Zhang H, Yue K, Zhang Y. Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology. Aerospace. 2025; 12(7):571. https://doi.org/10.3390/aerospace12070571
Chicago/Turabian StyleZhang, Hui, Kai Yue, and Yiming Zhang. 2025. "Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology" Aerospace 12, no. 7: 571. https://doi.org/10.3390/aerospace12070571
APA StyleZhang, H., Yue, K., & Zhang, Y. (2025). Geometric Optimization of Coanda Jet Chamber Fins via Response Surface Methodology. Aerospace, 12(7), 571. https://doi.org/10.3390/aerospace12070571






