A Novel Method for Aging Life Evaluation of O-Rings Based on the Sealing Performance Degradation Model and the Artificial Neural Network Model
Abstract
1. Introduction
2. Method and Models
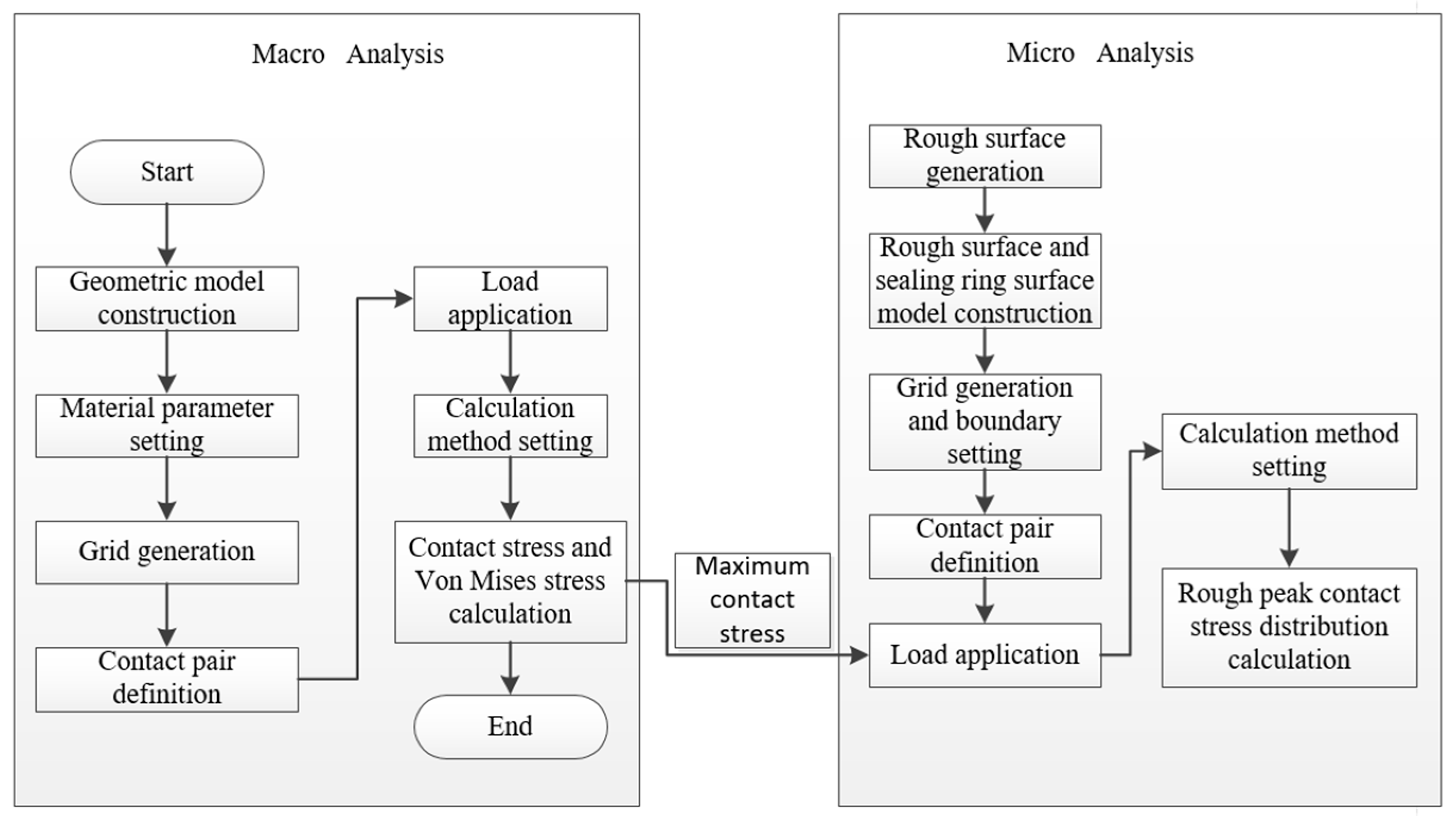
2.1. Macro–Micro Comprehensive Numerical Analysis of Typical Sealing Structures
2.1.1. Constitutive Model of Material
2.1.2. Random Rough Surface Generation
2.1.3. Macro–Micro Numerical Analysis Process
2.2. Degradation Model of the Sealing Ring
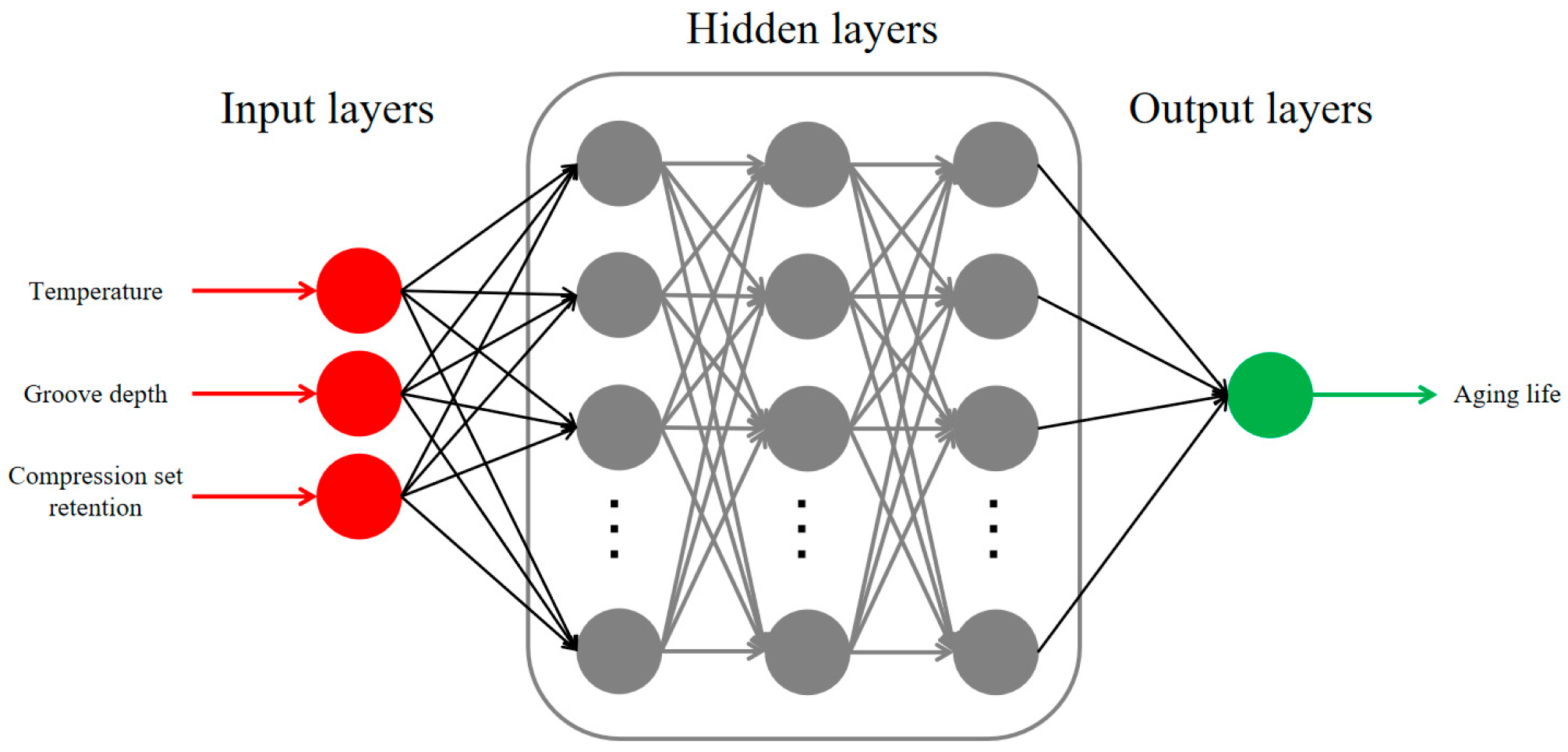
2.3. ANN-Based Aging Life Prediction Model
2.3.1. Construction of the ANN Model
2.3.2. Establishment of the Database
2.3.3. Parameter Optimization and Aging Life Prediction
3. Accelerated Thermal Aging Test
4. Results
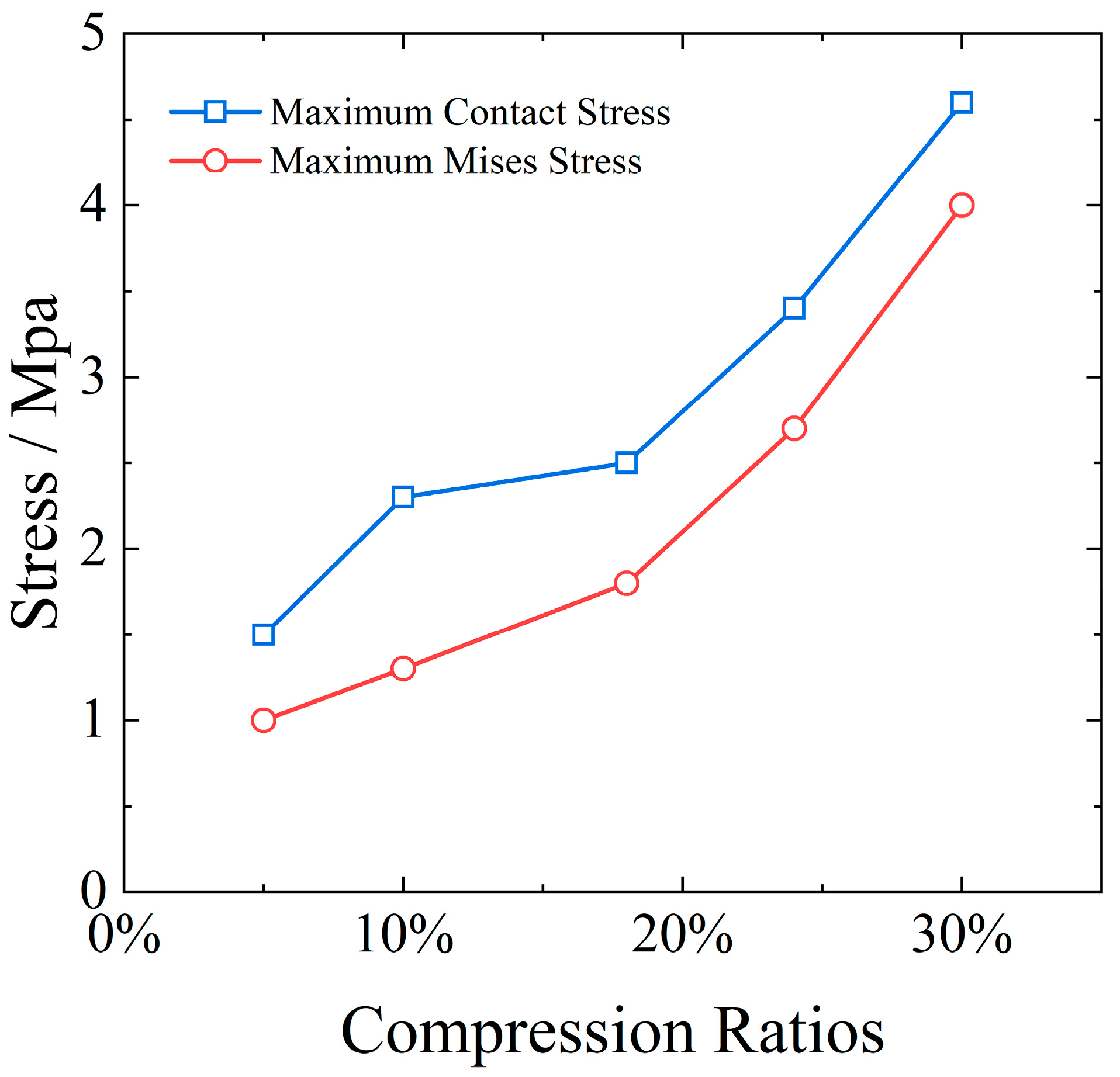
4.1. Effect of Different Compression Ratios
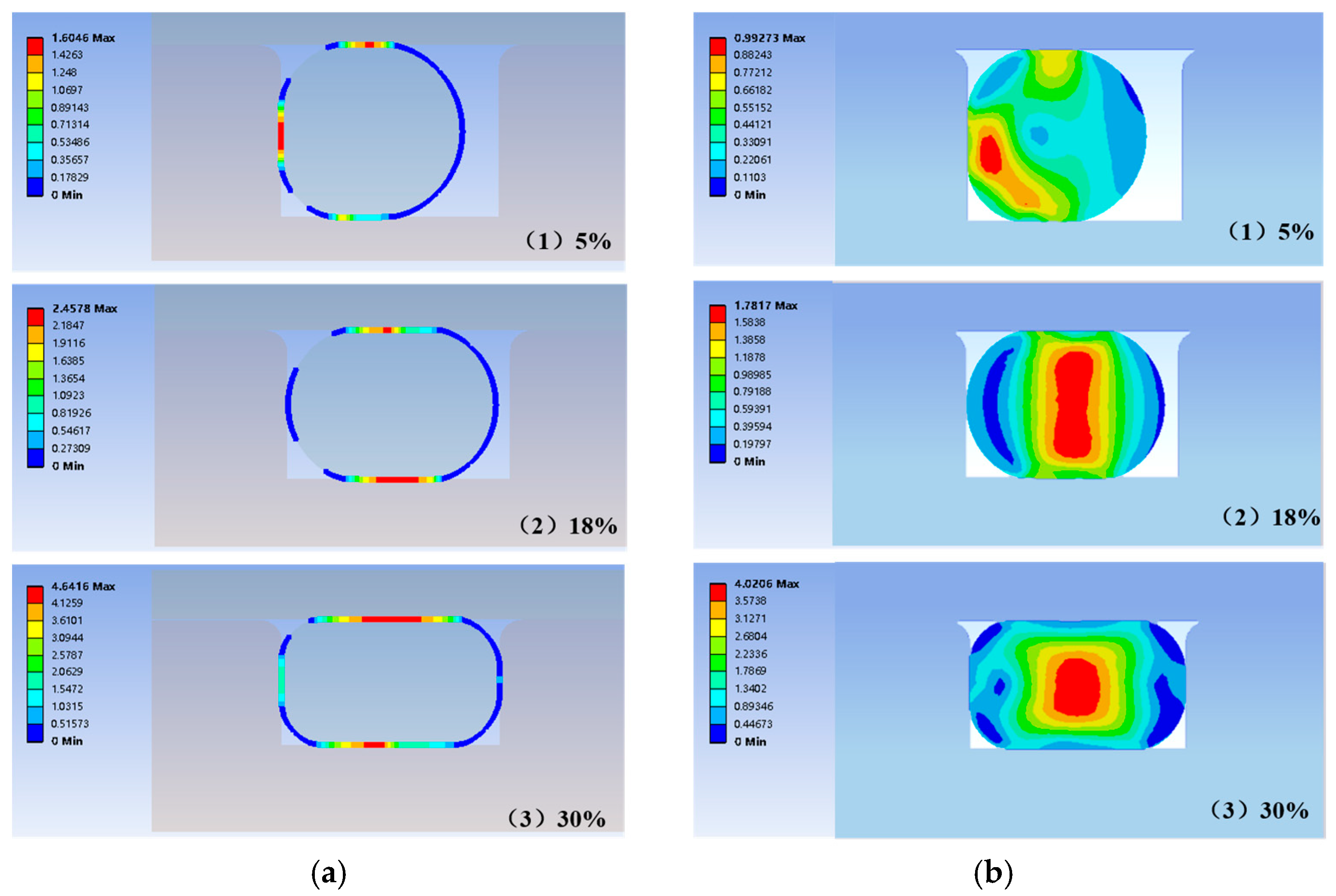
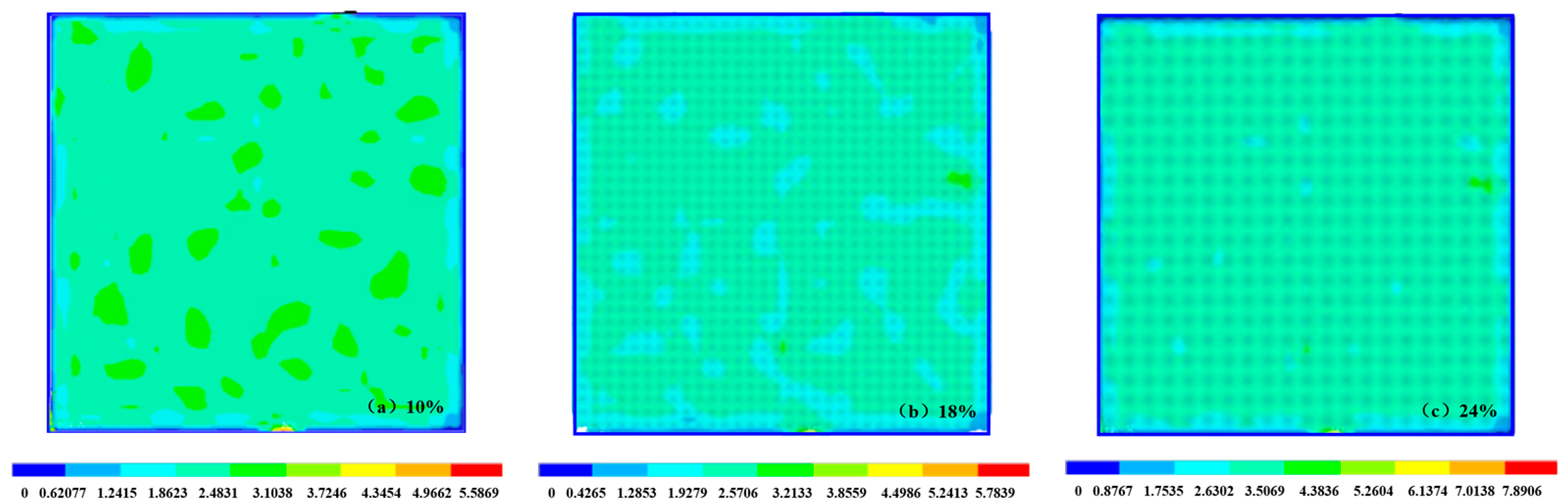
4.1.1. Results of Macro-Comprehensive Numerical Analysis
4.1.2. Results of Micro-Comprehensive Numerical Analysis
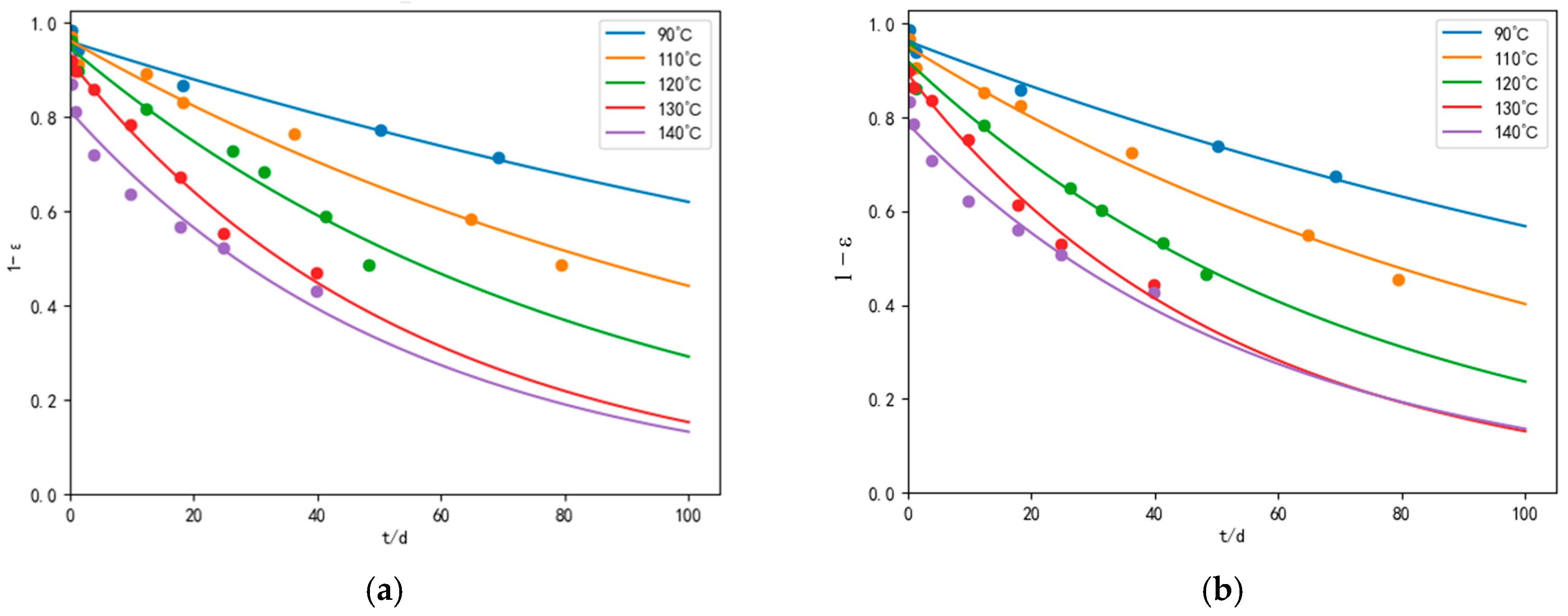
4.2. The Degradation Model of the Seal’s Performance
4.2.1. Parameter Regression of the Degradation Model
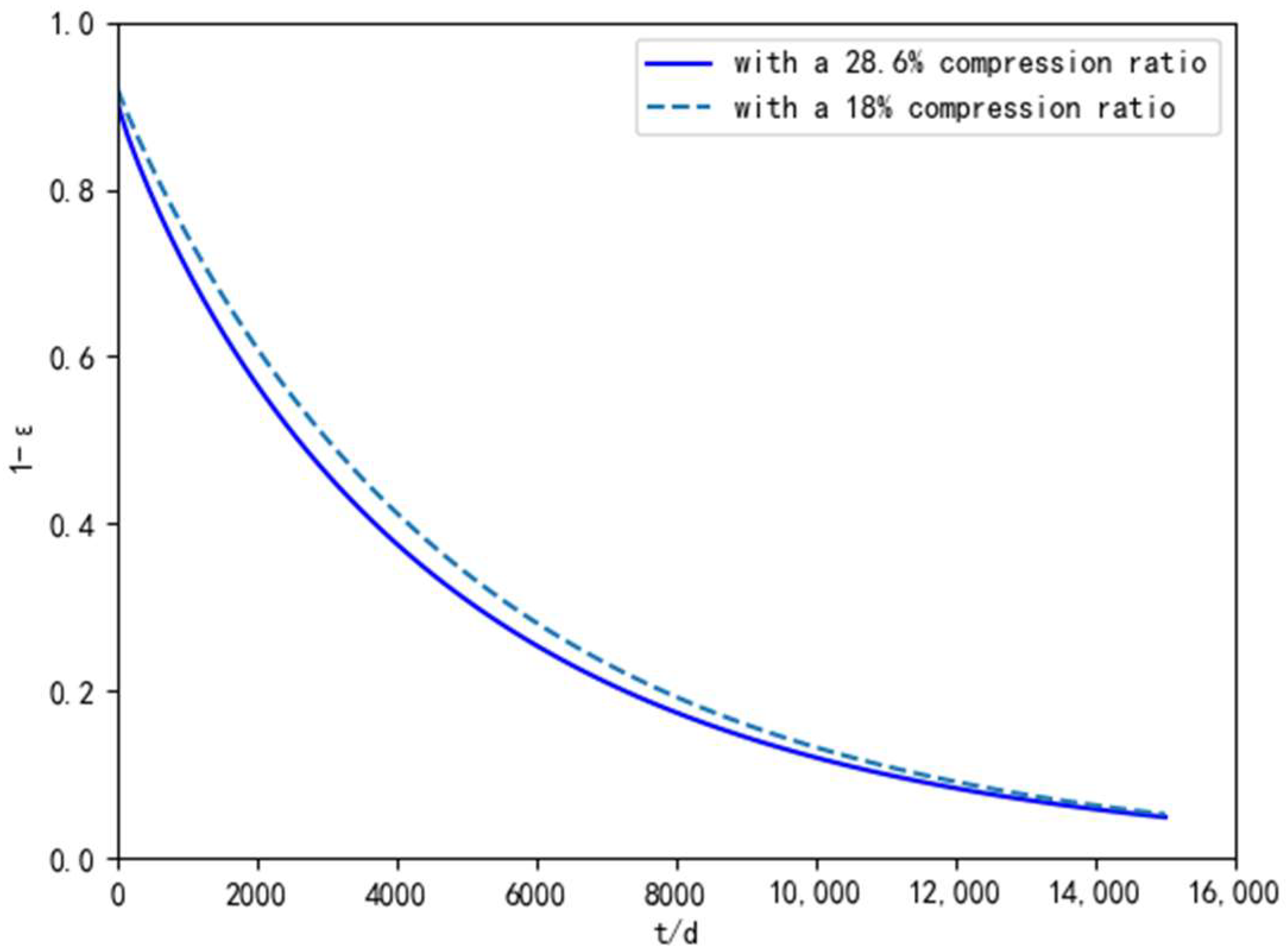
4.2.2. Aging Life Prediction Model
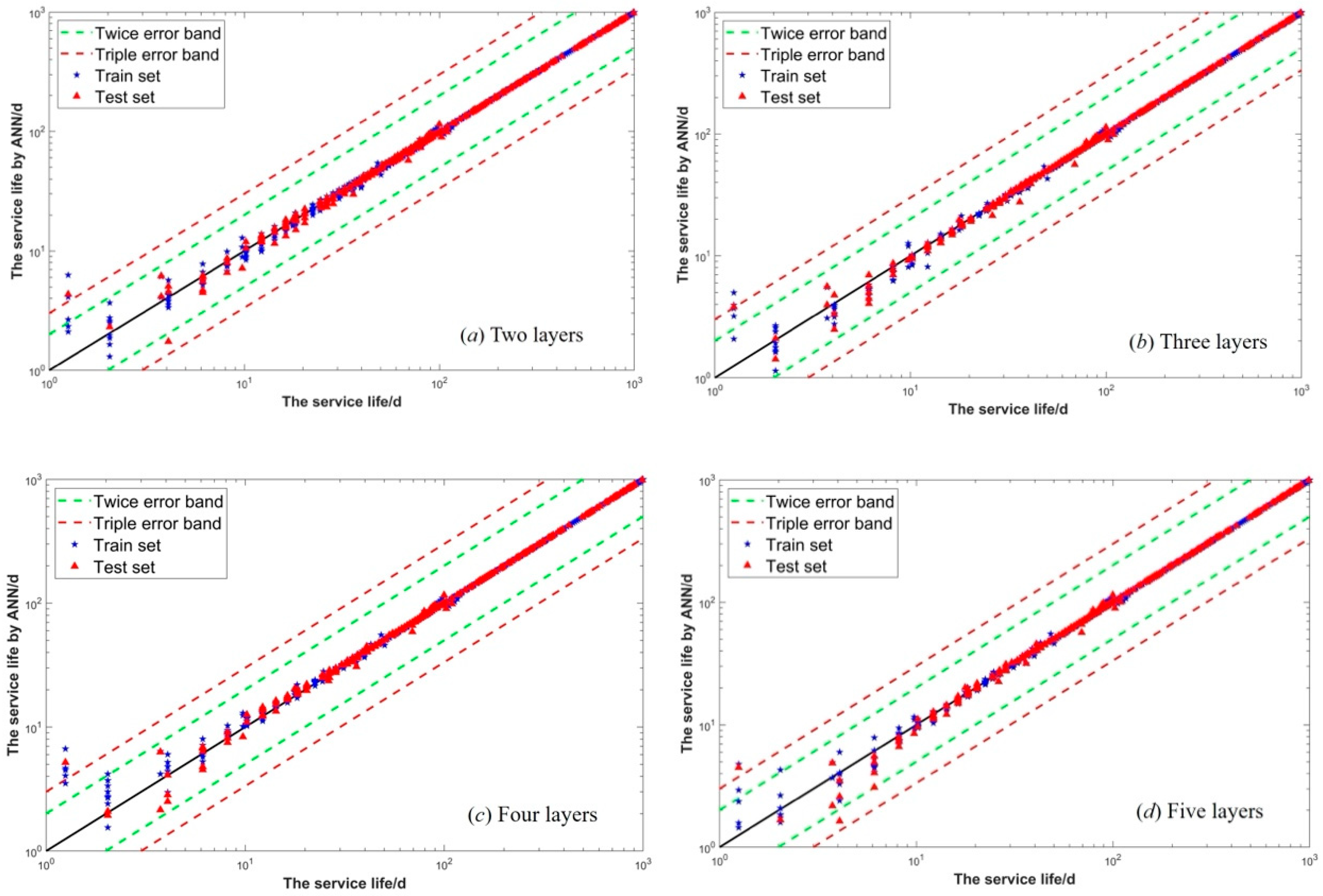
4.3. ANN-Based Aging Life Prediction Result
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahankar, P.S.; Dhoble, A.S. Review of hydraulic seal failures due to effect of medium to high temperature. Eng. Fail. Anal. 2021, 127, 105552. [Google Scholar] [CrossRef]
- Nikas, G.K. Eighty years of research on hydraulic reciprocating seals: Review of tribological studies and related topics since the 1930s. Proc. Inst. Mech. Eng. Part J. J. Eng. Tribol. 2010, 224, 1–23. [Google Scholar] [CrossRef]
- Han, C.; Zhang, J.; Liang, Z. Thermal failure of rubber bushing of a positive displacement motor: A study based on thermo-mechanical coupling. Appl. Therm. Eng. 2014, 67, 489–493. [Google Scholar] [CrossRef]
- Han, C.; Zhang, H.; Zhang, J. Structural design and sealing performance analysis of biomimetic sealing ring. Appl. Bionics Biomech. 2015, 2015, 358417. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S.; Teodoriu, C.; Ahmed, R. Performance evaluation and parametric study of elastomer seal in conventional hanger assembly. J. Pet. Sci. Eng. 2019, 175, 246–254. [Google Scholar] [CrossRef]
- Patel, H.; Salehi, S.; Ahmed, R.; Teodoriu, C. Review of elastomer seal assemblies in oil & gas wells: Performance evaluation, failure mechanisms, and gaps in industry standards. J. Pet. Sci. Eng. 2019, 179, 1046–1062. [Google Scholar]
- Jovanović, S.; Samaržija-Jovanović, S.; Marković, G.; Jovanović, V.; Adamović, T.; Marinović-Cincović, M. Mechanical properties and thermal aging behaviour of polyisoprene/polybutadiene/styrene-butadiene rubber ternary blend reinforced with carbon black. Compos. Part B Eng. 2016, 98, 126–133. [Google Scholar] [CrossRef]
- Kömmling, A.; Jaunich, M.; Wolff, D. Effects of heterogeneous aging in compressed HNBR and EPDM O-ring seals. Polym. Degrad. Stab. 2016, 126, 39–46. [Google Scholar] [CrossRef]
- Zeng, W.; Xue, Y.; Sun, Y.; Zhao, J.; Xie, H.; Ren, T. Sealing reliability assessment of deep-water oil and nature gas pipeline connector considering thermo-mechanical coupling. Proc. Inst. Mech. Eng. Part M. J. Eng. Marit. Environ. 2022, 236, 196–208. [Google Scholar] [CrossRef]
- Li, C.; Ding, Y.; Yang, Z.; Yuan, Z.; Ye, L. Compressive stress-thermo oxidative ageing behaviour and mechanism of EPDM rubber gaskets for sealing resilience assessment. Polym. Test. 2020, 84, 106366. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, J. Investigation of Static and Dynamic Seal Performances of a Rubber O-Ring. J. Tribol. 2018, 140, 042202. [Google Scholar] [CrossRef]
- Tong, G.; Zhu, X.; Liu, Y.; Lv, F.; Lu, X. Research on the Sealing Mechanism of Split-Liner High-Pressure Hydrogen Storage Cylinders. Processes 2024, 12, 554. [Google Scholar] [CrossRef]
- Wang, S.; Liu, P.; Li, D.; Dong, Z.; Li, G. Simulation and experimental study on sealing characteristics of hydro-pneumatic spring GS seal rings. Appl. Sci. 2023, 13, 11703. [Google Scholar] [CrossRef]
- Li, J.W.; Chen, G.Q.; Yang, L.; Wang, Y. Failure analysis and structural optimization of high-pressure reciprocating Y-Shaped sealing ring. J. Fail. Anal. Prev. 2024, 24, 1957–1975. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X. A novel structure of rubber ring for hydraulic buffer seal based on numerical simulation. Appl. Sci. 2021, 11, 2036. [Google Scholar] [CrossRef]
- Luo, Y.; Dong, Y.; Li, Y.; Hu, T.; Guo, Y.; Qian, C.; Zheng, H. Reliability analysis of critical systems in a fuel booster pump using advanced simulation techniques. Materials 2022, 15, 1989. [Google Scholar] [CrossRef]
- Zhu, M.; Ma, D.; Zhou, Y.; Huang, H.; Shao, Z.; Wu, F.; Li, B. The change of sealing property in the aging process of NBR sealing equipment based on finite element analysis. Coatings 2024, 14, 1178. [Google Scholar] [CrossRef]
- Yang, H.; Yao, X.F.; Ke, Y.C.; Ma, Y.J.; Liu, Y.H. Constitutive behaviors and mechanical characterizations of fabric reinforced rubber composites. Compos. Struct. 2016, 152, 117–123. [Google Scholar] [CrossRef]
- Jaunich, M.; Kömmling, A.; Horn, J.; Völzke, H.; Wolff, D. Long-term performance of elastomer seals: From aging tests to lifetime estimations.Pressure Vessels and Piping Conference. Am. Soc. Mech. Eng. 2018, 51708, V007T07A038. [Google Scholar]
- Zeng, C.; Liu, Y.; Lin, L.; Luo, H.; Lin, W.; Xiao, T.; Wang, P. Experimental research on aging and operating life of O-ring used in GIS. In Proceedings of the 4th International Conference on Electric Power Equipment-Switching Technology, Xi’an, China, 22–25 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 857–862. [Google Scholar]
- Kömmling, A.; Jaunich, M.; Pourmand, P.; Wolff, D.; Hedenqvist, M. Analysis of O-ring seal failure under static conditions and determination of end-of-lifetime criterion. Polymers 2019, 11, 1251. [Google Scholar] [CrossRef]
- Wu, D.; Wang, S.; Wang, X. A novel stress distribution analytical model of O-ring seals under different properties of materials. J. Mech. Sci. Technol. 2017, 31, 289–296. [Google Scholar] [CrossRef]
- Guo, L.; Zeng, Y.; Huang, J.; Wang, Z.; Li, J.; Han, X.; Xia, C.; Qian, L. Fatigue optimization of rotary control head rubber core based on steady sealing. Eng. Fail. Anal. 2022, 132, 105935. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, X.; Chen, X.; Liu, H. Research on key factors of sealing performance of combined sealing ring. Appl. Sci. 2022, 12, 714. [Google Scholar] [CrossRef]
- Das, S.K.; Biswal, R.K.; Sivakugan, N.; Das, B. Classification of slopes and prediction of factor of safety using differential evolution neural networks. Environ. Earth Sci. 2011, 64, 201–210. [Google Scholar] [CrossRef]
- Joshi, R.; Kumar, K.; Adhikari, V.P.S. Modelling suspended sediment concentration using Artificial Neural Networks for Gangotri glacier. Hydrol. Process. 2016, 30, 1354–1366. [Google Scholar] [CrossRef]
- Kumar, S.; Basudhar, P.K. A neural network model for slope stability computations. Geotech. Lett. 2018, 8, 149–154. [Google Scholar] [CrossRef]
- Erofeev, A.; Orlov, D.; Ryzhov, A.; Koroteev, D. Prediction of porosity and permeability alteration based on machine learning algorithms. Transp. Porous Media 2019, 128, 677–700. [Google Scholar] [CrossRef]
- Zhan, Z.; He, X.; Tang, D.; Dang, L.; Li, A.; Xia, Q.; Berto, F.; Li, H. Recent developments and future trends in fatigue life assessment of additively manufactured metals with particular emphasis on machine learning modeling. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 4425–4464. [Google Scholar] [CrossRef]
- Zhu, J.-A.; Jia, Y.; Lei, J.; Liu, Z. Deep learning approach to mechanical property prediction of single-network hydrogel. Mathematics 2021, 9, 2804. [Google Scholar] [CrossRef]
- Zhan, Z.; Ao, N.; Hu, Y.; Liu, C. Defect-induced fatigue scattering and assessment of additively manufactured 300M-AerMet100 steel: An investigation based on experiments and machine learning. Eng. Fract. Mech. 2022, 264, 108352. [Google Scholar] [CrossRef]
- Zhan, Z.; Li, H. A novel approach based on the elastoplastic fatigue damage and machine learning models for life prediction of aerospace alloy parts fabricated by additive manufacturing. Int. J. Fatigue 2021, 145, 106089. [Google Scholar] [CrossRef]
- Zhou, W.; Xie, Z. Sealing rubber ring design based on machine learning algorithm combined progressive optimization method. Tribol. Int. 2025, 201, 110173. [Google Scholar] [CrossRef]
- Jiao, K.; Yun, F.; Hao, X.; Wang, G.; Yao, S.; Jia, P.; Wang, X.; Wang, L. A fast GA-ANN model and application in multi-objective optimization of the sealing ring for the subsea pipeline connector with regard of the penetration load. J. Mech. Sci. Technol. 2024, 38, 309–322. [Google Scholar] [CrossRef]
- Pokharel, A. Application of Supervised Machine Learning Algorithms for Developing Service Life Prediction Model of Sewer Pipes. Ph.D. Thesis, The University of Texas at Arlington, Arlington, TX, USA, 2021. [Google Scholar]
- Bao, H.; Wu, S.; Wu, Z.; Kang, G.; Peng, X.; Withers, P.J. A machine-learning fatigue life prediction approach of additively manufactured metals. Eng. Fract. Mech. 2021, 242, 107508. [Google Scholar] [CrossRef]
- Manesh, K.K.; Ramamoorthy, B.; Singaperumal, M. Numerical generation of anisotropic 3D non-Gaussian engineering surfaces with specified 3D surface roughness parameters. Wear 2010, 268, 1371–1379. [Google Scholar] [CrossRef]
- Mukhopadhyay, A. Friction and wear characteristics of indegenous EPDM rubber under dry sliding condition. Asian Rev. Mech. Eng. 2014, 3, 19–25. [Google Scholar] [CrossRef]
- Zhao, L.H.; Wei, X.B.; Li, X.G. The analysis on the tribological properties of CR/EPDM blends with chrome-plated steel under dry sliding. Adv. Mater. Res. 2013, 774, 99–102. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Xu, L.; He, T. Service lifetime estimation of EPDM rubber based on accelerated aging tests. J. Mater. Eng. Perform. 2017, 26, 1735–1740. [Google Scholar] [CrossRef]
- GB/T 20028-2005; Rubber, Vulcanized or Thermos-Plastic-Estimation of Life-Time and Maximum Temperature of Use from an Arrhenius plot. China Standard Press: Beijing, China, 2005.
- Zhou, C.; Zheng, J.; Gu, C.; Zhao, Y.; Liu, P. Sealing performance analysis of rubber O-ring in high-pressure gaseous hydrogen based on finite element method. Int. J. Hydrogen Energy 2017, 42, 11996–12004. [Google Scholar] [CrossRef]
- Song, W.; Cui, W. Finite element analysis of large-sized O-rings used in deep-ocean pressure chambers. Adv. Mech. Eng. 2021, 13, 16878140211040672. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, J.; Zhang, K. Lifetime prediction of EPDM sealing materials with thermal aging under constant compression. J. Phys. Conf. Ser. 2024, 2842, 012008. [Google Scholar] [CrossRef]
- Zhou, Y.; Qiu, L.; Xu, Z.; Huang, S.; Nie, J.; Yin, H.; Zhao, Z. Thermal oxidative aging and service life prediction of commercial ethylene–propylene–diene monomer spacer damping composites for high–voltage transmission lines. Polymers 2024, 16, 1186. [Google Scholar] [CrossRef] [PubMed]









| Sample Material | Compression Ratio | Sealing Dimension | Aging Temperature |
|---|---|---|---|
| EDMP | 28.6% | Φ100 × 8.4 mm | 90 °C, 110 °C, 120 °C, 130 °C, 140 °C |
| EDMP | 18% | Φ100 × 8.4 mm | 90 °C, 110 °C, 120 °C, 130 °C, 140 °C |
| Number | Compression Value | Sealing Dimension | Environment Condition | |||
|---|---|---|---|---|---|---|
| Groove Width (mm) | Groove Depth (mm) | Compression Ratios | Diameter (mm) | Temperature (°C) | Pressure (MPa) | |
| 1 | 10 | 8.0 | 5% | 8.4 | 25 | 0.6 |
| 2 | 7.6 | 10% | ||||
| 3 | 6.9 | 18% | ||||
| 4 | 6.4 | 24% | ||||
| 5 | 5.9 | 30% | ||||
| Compression Ratios | Temperature | B | K | Correlation Coefficient |
|---|---|---|---|---|
| 28.6% | 90 | 0.9595 | 0.0044 | 0.9773 |
| 110 | 0.9613 | 0.0078 | 0.9764 | |
| 120 | 0.9461 | 0.0118 | 0.9652 | |
| 130 | 0.9175 | 0.0179 | 0.9898 | |
| 140 | 0.8120 | 0.0181 | 0.9398 | |
| 18% | 90 | 0.9623 | 0.0053 | 0.9834 |
| 110 | 0.9507 | 0.0086 | 0.9851 | |
| 120 | 0.9195 | 0.0136 | 0.9819 | |
| 130 | 0.8917 | 0.0192 | 0.9873 | |
| 140 | 0.7860 | 0.0175 | 0.9508 |
| Sealing Structure | lnA | Correlation Coefficient | |
|---|---|---|---|
| with a 28.6% compression ratio | −4616.6931 | 7.2783 | 0.9700 |
| with an 18% compression ratio | −4050.0793 | 5.9191 | 0.9367 |
| The Number of Hidden Layers | Number of Neurons in Each Hidden Layer | RMSE | R2 |
|---|---|---|---|
| 2 | 60, 60 | 2.2734 | 0.9998 |
| 3 | 60, 60, 60 | 2.2359 | 0.9998 |
| 4 | 60, 60, 60, 60 | 1.9185 | 0.9999 |
| 5 | 60, 60, 60, 60, 60 | 2.0159 | 0.9999 |
| Activation Function | Number of Hidden Layers | Number of Neurons in Each Hidden Layer | RMSE | R2 | MAPE |
|---|---|---|---|---|---|
| ReLU | 4 | 24, 91, 85, 71 | 1.8264 | 0.9999 | 8.05% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Huang, Y.; Zhang, J.; Wang, Z.; Hu, W.; Song, C. A Novel Method for Aging Life Evaluation of O-Rings Based on the Sealing Performance Degradation Model and the Artificial Neural Network Model. Aerospace 2025, 12, 570. https://doi.org/10.3390/aerospace12070570
Wang X, Huang Y, Zhang J, Wang Z, Hu W, Song C. A Novel Method for Aging Life Evaluation of O-Rings Based on the Sealing Performance Degradation Model and the Artificial Neural Network Model. Aerospace. 2025; 12(7):570. https://doi.org/10.3390/aerospace12070570
Chicago/Turabian StyleWang, Xiaojia, Yu Huang, Jianning Zhang, Zihui Wang, Weiping Hu, and Chao Song. 2025. "A Novel Method for Aging Life Evaluation of O-Rings Based on the Sealing Performance Degradation Model and the Artificial Neural Network Model" Aerospace 12, no. 7: 570. https://doi.org/10.3390/aerospace12070570
APA StyleWang, X., Huang, Y., Zhang, J., Wang, Z., Hu, W., & Song, C. (2025). A Novel Method for Aging Life Evaluation of O-Rings Based on the Sealing Performance Degradation Model and the Artificial Neural Network Model. Aerospace, 12(7), 570. https://doi.org/10.3390/aerospace12070570






