Abstract
This study introduces enhanced artificial intelligence (AI)-assisted terrain-aided navigation (TAN) for a sophisticated jet trainer, building upon our prior researchby incorporating real-flight test validation. The proposed TAN integrates a high-performance terrain server, a digital elevation model, and an efficient line-of-sight algorithm to facilitate terrain-aided navigation. The system utilizes an advanced search algorithm in conjunction with two filter designs, including adaptive filters that dynamically optimize navigation precision and operational efficiency. A significant development is the AI model’s capacity to independently alternate between the resource-intensive search algorithm and a set of filters, thereby maintaining navigational accuracy while facilitating in-flight execution without supplementary hardware requirements. Comprehensive Monte Carlo calculations, validated by flight test instrumentation (FTI) data, indicate that the proposed TAN consistently facilitates low-altitude navigation across diverse operational settings. The incorporation of actual flight data not only substantiates the system’s efficacy but also offers novel perspectives on practical implementation obstacles and improvements. These findings signify an advancement in autonomous terrain-aided navigation, connecting simulation with actual flight performance.
1. Introduction
This study presents AI-enhanced TAN designed for Hürjet (prototype 1), an advanced jet trainer aircraft seen in Figure 1, with the aim of improving navigation accuracy and operational efficiency. The system utilizes an advanced terrain server (version alpha) combined with a high-resolution digital elevation map (DEM) called digital terrain elevation data (DTED) to produce accurate height-on-terrain (HoT) and height-above-terrain (HaT) data, which are crucial for precise low-altitude aircraft navigation. Overall design of our TAN solution can be found in [1].

Figure 1.
Hürjet flying over the Bosphorus Strait.
The TAN is fundamentally based on a sophisticated technique that includes intricate filter setups. We specifically implement and evaluate banks of adaptive filters, which dynamically react to varying terrain roughness and other environmental factors. This adaptive filtering method enhances the system’s tracking accuracy and considerably improves its resilience under diverse flying situations. Additionally, the TAN incorporates an AI-driven supervisory module that can automatically switch among various software designs, providing a warrant that the system selects the most efficient mode’s output at all times. A simplified diagram of the algorithm is given in Figure 2 with latitude δL, longitude δλ, and altitude δh errors in the geodetic coordinate system. Also, hradalt is the radalt clearance measurement and is the state vector that contains positions. A sophisticated search algorithm, designed for the acquisition phase, effectively analyzes topographical data to determine safe flight paths while reducing processing demands.
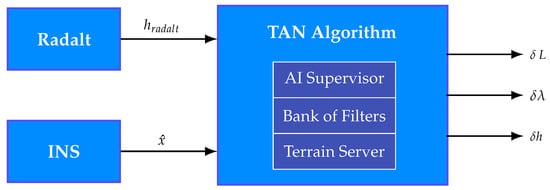
Figure 2.
Basic schematic of the TAN algorithm.
To assess the efficacy and resilience of the proposed system, we use empirical analysis bolstered by FTI data and comprehensive simulation outcomes. This dual approach highlights the practical application of our AI-enhanced TAN and illustrates its capability to satisfy the stringent certification standards necessary for sophisticated avionic systems. Our study establishes a foundation for a next-generation terrain-aided navigation system that is both safe and reliable by connecting simulation with real-world validation.
While the proposed system builds upon recent advances in adaptive filtering and AI-assisted supervisory control, it is important to acknowledge the foundational contributions in the field. Notably, the terrain contour matching (TERCOM) algorithm [1] and the Sandia inertial terrain-aided navigation (SITAN) system [2,3] have laid the groundwork for batch and recursive TAN architectures, respectively. Our study builds upon these classical methodologies, extending them through hybrid filter banks and artificial intelligence to support robust navigation in GPS-denied environments.
The real-world accuracy of the proposed TAN algorithm allows it to achieve 89% better performance in comparison to just standalone traditional filter solutions. Our extended Kalman filter has better performance than the inertial navigation system-only solution by 38%.
Our contributions in this study are summarized as follows: A hybrid TAN framework is developed and reduced navigational drift is demonstrated in environments lacking GPS signals. Our main contribution is the validation of an artificial intelligence-based supervisory system that dynamically selects appropriate navigation algorithms according to terrain characteristics and filter attributes, against real world flight test instrumentation data.
2. Previous Work
TAN is one of the methods that produces a navigation solution independently of GPS. There are many TAN algorithms in the literature, and the most famous ones are the terrain contour matching (TERCOM) [2] and Sandia inertial terrain-aided navigation (SITAN) [3,4] algorithms. TAN algorithms can be examined under three headings: batch, recursive, and hybrid algorithms. Although the first studies on TAN focused on batch or recursive algorithms, current studies generally consist of hybrid algorithms that combine different algorithms, as in this article. Moreover, gravity-aided and magnetic navigation studies are among the alternative methods that can work without GPS.
2.1. Batch TAN Algorithms
In batch TAN algorithms, the data is processed as a single group. In the TERCOM [2], a height error comparison is made using different comparison methods. In [5], it is stated that the mean absolute difference (MAD) is the most efficient and most correct combination among comparison methods for real-time applications. Ref. [6] added a maximum a posteriori (MAP) estimator to TERCOM and SITAN, and noted that improvements were achieved.
Probability-based TAN (PTAN) [7] that examines probability distribution differences is another research. The solution with the minimum probability distribution difference gives the best match. However, Ref. [5] stated that the computational load of this algorithm is very high.
Ref. [8] observed an increase in system performance using a probabilistic data association filter (PDAF) compared to TERCOM. However, there are questions marks about running this system in real time [5].
Ref. [9] proposed a computer vision-based TAN application using a charge-coupled camera. However, this method has the disadvantage of giving poor results in cases such as adverse weather conditions [5].
2.2. Recursive TAN Algorithms
In recursive TAN algorithms, the data is processed recursively when new measurement data is received. For the SITAN algorithm, different filters are compared such as the nonlinear Kalman filter (KF), extended Kalman filter (EKF), parallel Kalman filter, and particle filter (PF). Among these filter structures, the PF has the highest computational cost. Additionally, it has been observed that a divergence problem may occur in some trials. In this method, terrain linearization is one of the most important factors [4]. In [10], system models were improved with colored noises for SITAN. Also, by adding error models to SITAN, better and more realistic results are achieved [11]. In a study, terrain altitude linearization was performed [12]. It is stated that SITAN is used for AFTI/F16 [13] and a US Army UH-1 Helicopter [14]. Multi-model adaptive estimation (MMAE) and KF are used for this application [14].
In [15], the inertial terrain-aided navigation (BITAN)-II method is presented where position and speed errors are examined. Also, for navigation solutions, a bank of KFs is used. BITAN [16], which can work in both acquisition and track modes, is actually an improved version of SITAN.
In [17], the point mass filter reached the Cramer–Rao lower limit after convergence, and good results were achieved with this Bayesian method on both flat and variable terrains. However, there are computational problems due to dense meshes [5]. Ref. [18] proposed a Rao–Backwellisation technique that uses recursive Monte Carlo (MC) runs and a particle filter for position estimation.
Viterbi algorithm terrain-aided navigation (VATAN) [19] uses the Viterbi algorithm and contains dynamic programming for position estimation.
Landmark detection is performed [20] by using a probabilistic data association filter (PDAF). Moreover, a batch implementation is performed for the PDAF [8].
There are also classical TAN algorithms that perform INS correction using DTED [21,22]. In one study, it was mentioned that it provides a high level of localization accuracy [23]. In addition, there are some image-based TAN applications [24,25].
2.3. Hybrid TAN Algorithms
Hybrid TAN algorithms are composed of batch and recursive algorithms. Since they include recursive algorithms, it is also possible to consider these recursive algorithms. Hybrid TAN algorithms use KF and comparison techniques together, thus taking advantage of both batch and recursive methods. With this method, it is possible to achieve better navigation solutions [26].
In [27], on improved TERCOM, it is mentioned that velocity corrections are made as well as position correction using a Kalman filter. By incorporating this method, an improvement in accuracy and stability in the navigation solution has been achieved. It has also been stated that this method is a solution to the divergence problem encountered in TERCOM.
TERPROM® (Plymouth, UK) [28], which is used in military systems, produces navigation solutions using INS and radar measurements and digital terrain data. TERPROM®, which can also operate at low altitudes, has functions such as advanced terrain avoidance cueing (ATAC), a predictive ground collision system (PGCAS), and a terrain awareness display (TAD).
Recent studies have been proposed to enhance classical TAN systems, including hybrid filters such as batch + APF structures [29], visual TAN using structure-from-motion [30], or deep learning-based object recognition with aerial maps [31]. In particular, marginalized particle filtering (MPF) has become a popular approach to address the nonlinear nature of TAN, with several studies introducing moment-matched kernels [32], boundary flow mechanisms [33], and computationally efficient filter variants [34] to ensure robustness and efficiency. Moreover, adaptively modeling radar altimeter errors [35] and employing LSTM-based measurement models [36] have proven effective in maintaining filter consistency, especially over flat terrain.
High-altitude applications, such as aircraft-based TAN, have also benefited from slant-range measurement strategies using steerable lasers [37], which allow selective targeting of terrain gradients to maximize navigation information. These methods outperform traditional nadir TAN, both in CRLB analysis and simulation, and have been validated with real flight data. Broader perspectives, such as all-source PNT architectures [38,39], highlight the necessity of combining multiple navigation modalities—TAN, SOOP, vision, and sensor fusion—to ensure resilient performance under jamming or spoofing conditions.
TAN is not only used for airborne applications; there are some underwater TAN applications [40,41]. By using sonar and inertial measurement unit (IMU), the autonomous navigation of underwater vehicles is investigated. In [42], it is stated that a DTED map is not used; terrain height is detected thanks to sonar sensors.
2.4. Gravity-Aided and Magnetic Navigation Algorithms
Apart from TAN, efforts have been made to investigate GPS-independent solutions using gravity-aided and magnetism-based methods [43,44,45]. Gravity navigation approaches, often implemented in underwater or simulation environments, require precise, often bulky gradiometers and rely on high-resolution gravity maps, making their application on aircraft challenging in terms of both cost and platform dynamics [40,46,47,48]. Moreover, many studies in this domain still focus on improving basic matching or filtering algorithms, indicating that gravity-aided navigation remains in a relatively early stage compared to TAN systems [49]. Similar to this, magnetic navigation techniques rely on anomaly maps and are highly susceptible to magnetic disturbances caused by platforms; this is especially problematic on aircraft because of the complex and dynamic electromagnetic environments present [44,50,51]. While some successful demonstrations have been reported, including real flight tests on fighter aircraft like the F-16 [44], the calibration complexity and variability between platforms make operational deployment difficult.
Biological and marine studies further show how magnetic navigation can be effective in controlled or natural environments, but they also highlight limitations in sensor placement and environmental stability for airborne use [38,52]. However, with off-the-shelf sensors and globally accessible, current terrain databases, TAN systems that use radar altimeters and digital terrain elevation maps provide a more practical option for airplanes. Table 1 provides a comparison of algorithm types.

Table 1.
Comparison of algorithm types.
3. TAN Methodology
3.1. Modeling INS Errors Using Linearized State Equations
In an inertial navigation system (INS), the mechanization equations determine the system’s position, velocity, and orientation (attitude) within a specified reference frame. These equations exhibit significant nonlinearity, and sensor flaws, such as bias and noise, eventually degrade navigation accuracy. A typical method to model and mitigate these errors is to linearize the INS error dynamics around a nominal (presumed) trajectory. The resulting set of linear time-varying equations enables the implementation of filtering techniques, including the Kalman filter, for state estimation and error corrections [53].
Given that it is significantly easier for individuals on the Earth’s surface to conceptualize a navigation solution within the local-level frame, and considering that the computational errors in the horizontal frame are bounded (Schuler effect), it is deemed more suitable to resolve the error dynamics equations in the local-level frame for practical applications.
To formulate the error-state equations, applying a small perturbation to the state variables of the INS in its nominal trajectory, while excluding higher-order terms and negligible terms such as the terms that are multiplied by the square of the Earth’s radius, a system of linear differential equations governing the INS error dynamics can be derived. Furthermore, integrating the sensor error characteristics into this INS error dynamics with specific assumptions, such as first-order Gauss–Markov and random walk, provides the augmented state space equation. Now, using this knowledge, we will derive a linear system model of the errors of INS. Comprehensive knowledge about linearization, INS mechanization, and error dynamics derivations are available in [53], Section 2, Section 5 and Section 6.
The INS mechanization equations can be explained as a set of nonlinear differential equations constructed using IMU measurements taken by a 6-degree-of-freedom system with respect to a specified reference coordinate frame. The general form of the nonlinear ODE is given below:
where is the INS state and is the IMU input.
Let the state vector can be composed as
where is the major part and is the minor and stochastic part. can be considered the best guess of the true state (given our motion model and IMU inputs). The model we use for estimation is always subject to some modeling errors and random noises; is attributed to the small, stochastic components of the solution.
By taking this into account, linearizing the INS mechanization equations around a nominal solution, we establish that
By letting
we obtain the desired linearized form.
In the local-level frame, the mechanization equations yield a 15-dimensional error-state vector. The position error vector, denoted by , represents errors in geodetic latitude , longitude , and altitude . The velocity error vector, , accounts for errors in the north , east , and down velocity components. The attitude error vector, , captures the small-angle errors in roll , pitch , and azimuth . The gyroscope error vector, , corresponds to gyroscope biases, and the accelerometer error vector, , represents accelerometer biases resolved in an x-y-z triad. Concatenating these sub-vectors results in the 15-dimensional error-state vector After linearizing the INS trajectory along a nominal path, the linear relationship between error states and the change of error states can be expressed as follows.
where , , and , , are the autocorrelation time constants of the gyroscope and accelerometer, respectively, resolved in the x-y-z triad. , and are the standard deviations associated with the gyroscope, , and are the standard deviations associated with the accelerometer, represents the rotation matrix elements which converts the body frame to local-level frame, , and are the accelerometer readings resolved in the local NED frame, and is the unit variance Gaussian white noise.
We can express this set of linear differential equations in a compact way for filtering tasks like state estimation.
is called the dynamic matrix, which propagates the INS errors over time, and is the noise distribution matrix.
3.2. TAN Fundamentals
Terrain-aided navigation (TAN) entails determining the platform’s position by comparing the measured terrain profile with the onboard elevation data. These topographical profiles are generated utilizing data from the platform’s barometric altimeter and radar altimeter (RADALT). As depicted in Figure 3, the barometric altimeter provides altitude information relative to mean sea level , whilst the RADALT measures the platform’s elevation above the ground . The terrain elevation at the measurement location is determined by subtracting the RADALT value from the barometer altitude.
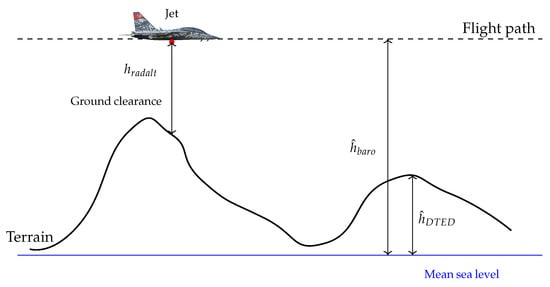
Figure 3.
Visualization of measurements.
Batch and recursive solutions have become popular in academia and industry for providing navigation solutions with predictive algorithms using terrain data. The most popular of these algorithms are TERCOM and SITAN, explained in references [2,4], respectively. The SITAN method employs EKF and local terrain linearization algorithms to analyze the terrain profile, with position updates performed as measurements become available. While favorable outcomes may be achieved in certain terrain types and mission profiles, local linearization may not comprehensively address the issue due to the discontinuous and highly nonlinear nature of terrain data in certain areas.
3.3. Terrain Server
Terrain server is a database query system that interprets DTED and provides digital elevation models (DEMs). The DTED model that is interpreted is a DTED-2 model that has 30 m spacing between grid lines. It also has 1 s latitude and longitude spacing. The database for the terrain server is stored in the onboard computer of the aircraft. It can provide responses with user datagram protocol (UDP) and distributed interactive simulation (DIS). It has several different functions that handle the LoS, HaT, and HoT.
For HaT and HoT queries, the server uses the provided data to respond with the terrain elevation of a location. It can provide this service for a single location or for a matrix centered around a location, which is mostly used for our case. LoS is used to predicted the collisions between the aircraft path and the terrain. A straight line is calculated between the aircraft’s location and the stated location, and checked against the elevation of the terrain along the path. To provide these services in a real-time environment, a cache system is used to decrease the time required to load the data into the memory. It stores the DTED in the database in the local memory and retrieves information based on these data.
3.4. Filter Formulations
The formulations of the filters used during implantation are based on the formulations described in this section and are included in the text for completeness.
3.4.1. Kalman Filter Formulation
The Kalman filter is a recursive solution to the linear quadratic estimation problem. It estimates the state of a discrete time-controlled process governed by the linear stochastic difference equation
where is the state vector at time step k, is the state transition matrix, is the control input matrix, is the control vector, and denotes the process noise, assumed to be zero mean Gaussian with covariance .
The measurement vector is defined by
where represents the observation matrix and is the measurement noise, also assumed to be zero mean Gaussian with covariance .
The Kalman filter comprises two phases: prediction and update.
In the prediction step, the state and error covariance matrix is forecast using
During the update step, the Kalman gain is computed by
after which the state estimate is updated with the new measurement according to
and finally, the error covariance is updated as
3.4.2. Unscented Kalman Filter (UKF) Formulation
The unscented Kalman filter addresses nonlinear state and measurement models by employing the unscented transform. Let the state vector be , with a prior estimate and covariance . A set of sigma points is generated as below, where is a scaling parameter.
In the prediction step, each sigma point is propagated through the nonlinear state transition function :
The predicted state and covariance are computed as
where and are the weights for the mean and covariance, and is the process noise covariance.
In the update step, each predicted sigma point is transformed through the measurement function :
The predicted measurement and its covariance are obtained by
with representing the measurement noise covariance. The cross-covariance between the state and the measurement is computed as
The Kalman gain is then given by
Finally, the state estimate and error covariance are updated as
3.4.3. Particle Filter (PF) Formulation
The particle filter approximates the posterior density
by a set of N weighted particles
where is a state candidate and is the corresponding weight.
Assuming a proposal distribution , the weights are updated as
A common choice is
which simplifies the weight update to
The weights are normalized by
The effective sample size is defined as
Resampling is performed when , where is a predefined threshold, by drawing N particles with replacement according to the weights, and resetting the weights to
4. Proposed Algorithms
4.1. Bank of Kalman Filters
In our TAN system, in order to prevent problems caused by high initial errors, different terrain structures affect our altimeter readings and linearization errors, a parallel Kalman filter structure was used, and an appropriate navigation solution was provided by making hard decisions between these filters using artificial intelligence. Here, when the three filter structures that have been explained calculate their separate solutions, the supervisor decides which filter will give better results by looking at certain metrics from the covariance matrices of these solutions, such as trace, determinant, eigenvalue, and the roughness of the terrain profile. The supervisor makes this decision by separating the latitude and longitude solutions of the filters. In other words, in each iteration, supervisor can choose the longitudinal error of one filter while choosing the latitudinal error of the other filter. In this way, by decoupling, errors that may differentially affect the latitude and longitude solutions can be eliminated. Details of EKF, stochastic linearization, and parallel filter structures can be examined in [4,5]. Details of UKF and PF are given in [5,54,55].
The terrain data used was converted into a continuous dataset using the spatial interpolation method.
4.2. Our TAN Algorithm
We choose an open-loop architecture due to the algorithm’s solution being significantly influenced by the terrain profile, which can produce inaccurate results in steep or non-unique terrains. Moreover, improperly correcting errors in a reliable INS solution, which is already equipped with high-precision, military-grade sensors, creates a risk in flight-critical scenarios. The TAN algorithm (see Figure 4) corrects the errors of INS in an open-loop configuration. It makes positional and velocity updates by subtracting the estimated error states from the INS predictions in the iteration TAN runs. In this configuration, unlike a closed loop, the navigation solution at the output has no direct relationship with the next iteration. The bank of filters produces error-state estimation outputs in the iteration where the radar measurement is received. The AI supervisor also decides which filter structure output to use. As parallel filter structures, EKF with numeric Jacobian, classic unscented Kalman filter, and particle filter were preferred.
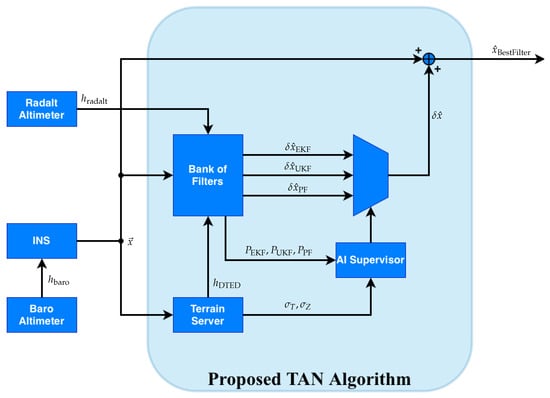
Figure 4.
Schematic of the TAN algorithm.
The primary objective of creating this structure is to minimize the risk of finding incorrect solutions in situations where error states are assumed to follow a Gaussian distribution, thereby allowing the numerical Jacobian retrieval process and the unscented transform to perform well in varying contexts, while simultaneously approximating the distribution of particles affected by noise across various terrain profiles. The measurement of the filter can be expressed as
In Equation (33), is the estimated terrain height, and is the estimated height of the terrain obtained from the aircraft’s latitude and longitude using the onboard terrain server database. Our proposed measurement function inserts the adjusted latitude and longitude values into the terrain server to estimate the height of terrain at the true position hypothesized. The input can be formulated as follows:
In Equation (34), is the measurement innovation vector between the INS predictions and the estimates of the filter. and are the latitude and longitude measurement error estimations of the error-state Kalman filter.
4.3. AI Supervisor
One way to have more precise navigation is to have better sensors or better algorithms; however, if sensors and algorithms are fixed beforehand, one can cleverly choose which algorithm serves better in which terrain conditions. This is how our AI supervisor was conceived.
As can be observed in Figure 4, our AI supervisor takes two series of inputs: the covariance matrices of the bank of filters and the roughness values of the terrain. The supervisor is a classifier model which selects the predicted best rms value-returning filter.
The outputs of the model are two label structures consisting of three classes separately on the latitude and longitude axes. Thus, a total of nine different filter configurations are obtained, and the model selects the most suitable one from these nine.
To select our model architecture, we used the hyperparameter optimization tool Optuna. Layer count, dropout layer batch size, and hidden state size are all given as a parameter to our optimization pipeline. Our final model has 3 linear layers to process the input. Each layer has a hidden layer with a fully connected (FC) layers size of 1024 and a RELU nonlinear activation function. The architecture of the supervisor model is given in Figure 5.
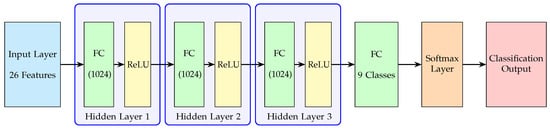
Figure 5.
Supervisor neural network architecture.
Thirteen different terrains were selected, including rough, moderate, and flat terrains. Ten Monte Carlo flights of 1000 s were performed on these terrains. Filter error metrics, covariance data, and roughness data where the flight took place were recorded. The model was then trained on this dataset collected from simulations in the environment mentioned in the Section 5.1. A total of 85% of the data was used as training data and 15% was used as test data. Training was carried out for 30 epochs using a cross-entropy loss function applied to both outputs. The model achieved a validation accuracy of 0.88, computed over the joint label space consisting of all nine class combinations. Figure 6 illustrates the learning dynamics of the proposed architecture.
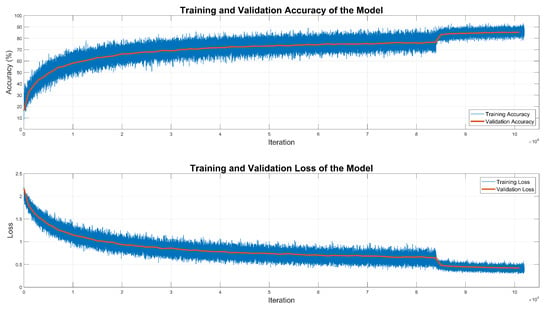
Figure 6.
Learning dynamics of the training.
5. Simulations and Results
5.1. Simulations
In this section, a simulation environment designed to provide AI training by generating the results of the aforementioned methods and filters will be explained. First of all, three different terrain models were selected for simulations: rough, moderate, and flat terrains. Then, flight trajectories were determined. While determining these trajectories, path height standard deviation and path height slope standard deviation parameters are examined. Even though both parameters are a metric of roughness, is a more significant metric in such filtering methods since algorithms such as KF use linearization methods [5]. corresponds to the standard deviation of the terrain heights on the trajectory. N is the sample, is the terrain height measurement, and is the mean height of that terrain.
By using and , the path height standard deviation can be calculated as shown below.
In order to calculate the path height slope standard deviation , slopes should be found first, and is the mean of the slopes.
By using and , the path height slope standard deviation can be calculated as shown below.
Sample and values of chosen terrains are given in Table 2.

Table 2.
Roughness values of terrains.
After the flight trajectories were selected, 1000 s flights were made on the determined paths. A trajectory sample is given in Figure 7. A path was defined for the aircraft such that there was a random acceleration on the horizontal axis. Then, the IMU was modeled to make measurements. The characteristics of the accelerometer, gyroscope, and barometric altimeter used in the simulations are given in Table 3.
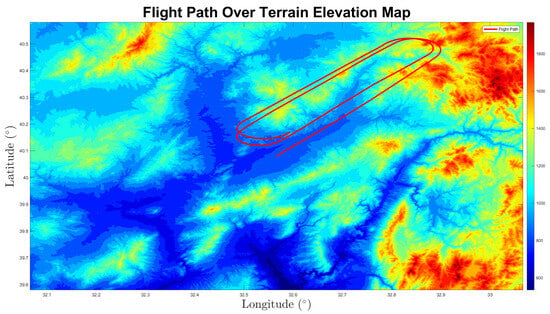
Figure 7.
Flight trajectory.

Table 3.
Simulation sensor characteristics.
5.2. Validation with Real World FTI Data
Real flight test data (FTI) from Hürjet advanced jet trainer platform projects within Turkish Aerospace was used. The TAN algorithm was run at a frequency of 20 Hz. The data were recorded with a sampling frequency of 128 Hz. There are three different navigation solutions: the free inertial solution (FI), GPS solution, and hybrid solution. The hybrid solution is a filtered version of the FI and GPS solutions and produces more accurate and reliable results compared to both solutions. Therefore, the hybrid solution was accepted as the “ground truth” while evaluating the performance of the TAN algorithm. The FI navigation solution shows drift over time due to various errors as explained in Section 3.1 and constitutes the input data that are being improved. Similarly, radalt measurements were also taken from the aircraft. When the aircraft makes high angles of roll or yaw, radalt cannot measure the HaT correctly and produces invalid data. For this reason, when the radalt measurement could not be produced, only the prediction step was applied and no correction was made.
5.3. Results
In order to compare the results of the trials, two parameters are examined: absolute error and circular error probable (CEP). Absolute error and CEP [56] are computed as shown below.
Here, and are the position errors between the ground truth and the TAN output. The standard deviations of the position errors between the ground truth, and the TAN output is denoted as and . Also, and are the means of the position errors between the ground truth and the TAN output. CEP is calculated by using coefficient .
The FTI data absolute error results are given in Figure 8 and Figure 9 for two different flights. Parallel filter solutions give better navigation solutions than INS-only solutions as proposed.
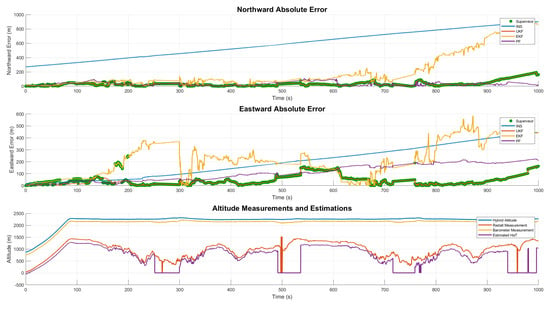
Figure 8.
Absolute error results.
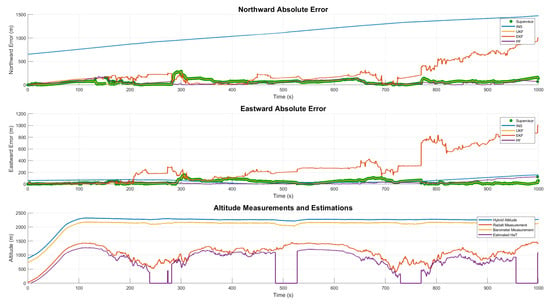
Figure 9.
Absolute error results.
In Figure 8 and Figure 9 The reason for the dips in the estimated line in the ranges of 250–300, 480–540, 720–760 and 930–1000 s is that the aircraft is performing an agile maneuver at these moments. This can be called radalt shadowing due to roll and pitch manuevers. Moreover, there is a variable called ‘radalt attitude angle’ that is dependent on the roll and pitch angles of the aircraft. When this variable is below a certain value, measurements from radalt can be accepted as correct. In the specified times listed above, the attitude angle is above the threshold, and the correction to the bank of filters can not be accepted. In order to visualize this type of manuever, the estimated HaT value is set to zero. This situation can also be validated from the dip to 0 in the Radalt measurements in the intervals mentioned above.
From CEP results given in Table 4, our AI-assisted TAN solution can be seen performing better than others, excluding . These results are highly correlated with the roughness properties of the terrain and initializations of the filters. Further analysis for real world FTI data is left as future work.

Table 4.
CEP results of simulations.
6. Conclusions
Designed for the Hürjet advanced jet trainer, this paper presents a new artificial intelligence-enhanced terrain-aided navigation (TAN) system. The TAN system improves navigation precision and computation efficiency by including adaptive filtering techniques, an advanced terrain server, and an artificial intelligence supervisory module that dynamically alternates between multiple filtering schemes (EKF, UKF, PF). Compared to conventional navigation methods (INS-only solutions), the proposed hybrid TAN method significantly increases low-altitude navigation efficacy. Emphasizing improved navigational accuracy even in GPS-denied environments, Monte Carlo simulations and empirical flight test instrumentation (FTI) data support the efficacy and viability of the AI-driven methodology. With an accuracy of around 82% in appropriate filter selection, the AI supervisor efficiently finds acceptable filters based on terrain roughness and ambient factors, hence significantly lowering absolute error values. This study provides important new insights into the issues and operational aspects related to avionics certification by using real flight data from the Hürjet platform to link theoretical modeling with pragmatic application. We understand the importance of upcoming projects and stress the change from simulation to real-time onboard applications as well as a complete certification process for the TAN integration with aircraft control systems. Appropriate for inclusion into advanced avionics systems, this work represents a notable advancement in autonomous, trustworthy, and accurate terrain-aided navigation procedures.
Author Contributions
Conceptualization, Ü.C.B. and G.I.; methodology, Ü.C.B.; software, B.T and I.E.U.; validation, I.E.U.; investigation, B.T. and I.E.U.; resources, N.A.G.; data curation, I.E.U.; writing—original draft preparation, Ü.C.B.; writing—review and editing, Ü.C.B., B.T., I.E.U. and G.I.; visualization, I.E.U.; supervision, G.I.; project administration, Ü.C.B.; funding acquisition, Ü.C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Real world flight trajectories are not available for distribution due to company restrictions.
Acknowledgments
The project was realized as part of Hürjet advanced jet trainer platform’s artificial intelligence concept projects within Turkish Aerospace. The domain experts were employees of the company. The simulation environment and flight dynamics model of the jet were provided by the company.
Conflicts of Interest
The authors declare no conflicts of interest. All the authors except Gokhan Inalhan were employed by the Turkish Aerospace company.
References
- Bekar, U.C.; Tanyeri, B.; Canoglu, A.S.; Uslu, I.E.; Gungor, N.A.; Inalhan, G. AI-assisted Digital Terrain System for an Advanced Jet Trainer. In Proceedings of the 2024 AIAA DATC/IEEE 43rd Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 29 September–3 October 2024; pp. 1–10. [Google Scholar] [CrossRef]
- Golden, J.P. Terrain contour matching (TERCOM): A cruise missile guidance aid. In Proceedings of the Image Processing for Missile Guidance, SPIE, San Diego, CA, USA, 29 July–1 August 1980; Volume 238, pp. 10–18. [Google Scholar]
- Hostetler, L.; Beckmann, R. Sandia Inertial Terrain-Aided Navigation System. 1977. Available online: https://scholar.google.com.tr/scholar?cluster=3935347283561463586&hl=tr&as_sdt=0,5 (accessed on 29 May 2025).
- Hostetler, L.; Andreas, R. Nonlinear Kalman filtering techniques for terrain-aided navigation. IEEE Trans. Autom. Control 1983, 28, 315–323. [Google Scholar] [CrossRef]
- Ekütekin, V. Navigation and Control Studies on Cruise Missiles. Ph.D. Thesis, Middle East Technical University, Ankara, Turkiye, 2007. [Google Scholar]
- Johnson, N.; Tang, W.; Howell, G. Terrain aided navigation using maximum a posteriori estimation. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20 March 1990; pp. 464–469. [Google Scholar]
- Erhui, W.; Guohua, G.; Lincheng, S.; Wensen, C. A probability-based terrain-aided navigation approach and its relative terrain navigability analysis. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT’96), Shanghai, China, 2–6 December 1996; pp. 781–785. [Google Scholar]
- Qingtang, F.; Lincheng, S.; Wenseng, C. Terrain aided navigation using PDAF. In Proceedings of the IEEE International Conference on Robotics, Intelligent Systems and Signal Processing, Changsha, China, 8–13 October 2003; Volume 2, pp. 1063–1068. [Google Scholar]
- Zhou, H.; Zhang, C.y. Terrain aided navigation based on computer vision. In Proceedings of the 4th World Congress on Intelligent Control and Automation (Cat. No. 02EX527), Shanghai, China, 10–14 June 2002; Volume 3, pp. 2164–2166. [Google Scholar]
- Chen, Z.; Yu, P. Model study for terrain aided navigation systems. In Proceedings of the IEEE International Symposium on Industrial Electronics, Xi’an, China, 25–29 May 1992; pp. 848–849. [Google Scholar]
- Wang, W.; Chen, Z. Error model identification on digital map of TAN system based on EKF. In Proceedings of the 1994 IEEE International Conference on Industrial Technology-ICIT’94, Guangzhou, Chin, 5–9 December 1994; pp. 818–822. [Google Scholar]
- Yu, P.J.; Chen, Z.; Hung, J.C. Performance evaluation of six terrain stochastic linearization techniques for TAN. In Proceedings of the IEEE 1991 National Aerospace and Electronics Conference NAECON 1991, Dayton, OH, USA, 20–24 May 1991; pp. 382–388. [Google Scholar]
- Baird, C.A.; Snyder, F.B.; Beierle, M. Terrain-aided altitude computations on the AFTI/F-16. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20 March 1990; pp. 474–481. [Google Scholar]
- Hollowell, J. Heli/SITAN: A terrain referenced navigation algorithm for helicopters. In Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1990. [Google Scholar]
- Pei, Y.; Chen, Z.; Hung, J. BITAN-II: An improved terrain aided navigation algorithm. In Proceedings of the 1996 IEEE IECON. 22nd International Conference on Industrial Electronics, Control, and Instrumentation, Taipei, Taiwan, 9 August 1996; Volume 3, pp. 1675–1680. [Google Scholar]
- Chen, Z. BUAA Inertial Terrain Aided Navigation. Icas92 1992. Available online: https://scholar.google.com.tr/scholar?q=BUAA+Inertial+Terrain+Aided+Navigation&hl=tr&as_sdt=0%2C5&as_ylo=1992&as_yhi=1992 (accessed on 29 May 2025).
- Bergman, N.; Ljung, L. Point-mass filter and Cramer-Rao bound for terrain-aided navigation. In Proceedings of the 36th IEEE Conference on Decision and Control, San Diego, CA, USA, 12 December 1997; Volume 1, pp. 565–570. [Google Scholar]
- Nordlund, P.J.; Gustafsson, F. Recursive estimation of three-dimensional aircraft position using terrain-aided positioning. In Proceedings of the 2002 IEEE International Conference on Acoustics, Speech, and Signal Processing, Orlando, FL, USA, 13–17 May 2002; Volume 2, p. II-1121. [Google Scholar]
- Enns, R.; Morrell, D. Terrain-aided navigation using the Viterbi algorithm. J. Guid. Control. Dyn. 1995, 18, 1444–1449. [Google Scholar] [CrossRef]
- Dezert, J. Improvement of strapdown inertial navigation using PDAF. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 835–856. [Google Scholar] [CrossRef]
- Madhavan, R.; Durrant-Whyte, H.; Dissanayake, G. Natural landmark-based autonomous navigation using curvature scale space. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 4, pp. 3936–3941. [Google Scholar]
- Bruder, S.B.; Wedeward, K. Terrain aided INS robot navigation: A deferred decision making approach. In Proceedings of the 42nd Midwest Symposium on Circuits and Systems (Cat. No. 99CH36356), Las Cruces, NM, USA, 8–11 August 1999; Volume 1, pp. 135–139. [Google Scholar]
- Morisue, F.; Ikeda, K. Evaluation of map-matching techniques. In Proceedings of the Conference Record of papers presented at the First Vehicle Navigation and Information Systems Conference (VNIS’89), Toronto, ON, Canada, 11–13 September 1989; pp. 23–28. [Google Scholar]
- Xu, H.; Tian, Y.; Su, J.; Tian, J.; Liu, J. Terrain matching based on imaging laser radar. In Proceedings of the 6th International Conference on Signal Processing, Beijing, China, 26–30 August 2002; Volume 2, pp. 1043–1046. [Google Scholar]
- Bevington, J.E.; Marttila, C.A. Precision aided inertial navigation using sar and digital map data. In Proceedings of the IEEE Symposium on Position Location and Navigation. A Decade of Excellence in the Navigation Sciences, Las Vegas, NV, USA, 20 March 1990; pp. 490–496. [Google Scholar]
- Metzger, J.; Wendel, J.; Trommer, G.F.; Tumbragel, F.; Taddiken, B. Hybrid terrain referenced navigation system using a bank of Kalman filters and a comparison technique. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004; pp. 1–12. [Google Scholar]
- Yoo, Y.; Lee, W.; Lee, S.; Park, C.; Kwon, J. Improvement of TERCOM aided inertial navigation system by velocity correction. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 1082–1087. [Google Scholar]
- Wilkinson, N.; Brookes, T.; Price, A.; Godfrey, M. Latest developments of the TERPROM® digital terrain system 2009. In Proceedings of the Joint Navigation Conference, Orlando, FL, USA, 2–4 June 2009. [Google Scholar]
- Lee, J.; Sung, C.K.; Oh, J.; Han, K.; Lee, S.; Yu, M.J. A Pragmatic Approach to the Design of Advanced Precision Terrain-Aided Navigation for UAVs and Its Verification. Remote Sens. 2020, 12, 1396. [Google Scholar] [CrossRef]
- Navon, D.; Rivlin, E.; Rotstein, H. A Robust Approach to Vision-Based Terrain-Aided Localization. Navig. J. Inst. Navig. 2025, 72, 683. [Google Scholar] [CrossRef]
- Bijjahalli, S.; Sabatini, R.; Gardi, A. Advances in intelligent and autonomous navigation systems for small UAS. Prog. Aerosp. Sci. 2020, 115, 100617. [Google Scholar] [CrossRef]
- Lee, J.; Sung, C.; Nam, S. CRLB analysis for a robust TRN based on a combination of RNN and PF. Int. J. Aeronaut. Space Sci. 2020, 21, 265–276. [Google Scholar] [CrossRef]
- González-García, J.; Gómez-Espinosa, A.; Cuan-Urquizo, E.; García-Valdovinos, L.G.; Salgado-Jiménez, T.; Escobedo Cabello, J.A. Autonomous underwater vehicles: Localization, navigation, and communication for collaborative missions. Appl. Sci. 2020, 10, 1256. [Google Scholar] [CrossRef]
- Kim, Y.; Back, S.; Song, D.; Lee, B.Y. Aerial Map-Based Navigation by Ground Object Pattern Matching. Drones 2024, 8, 375. [Google Scholar] [CrossRef]
- Kim, S.; Park, J.; Bang, H. Enhanced Terrain-Referenced Navigation Through Adaptive Radar Altimeter Error Estimation with Monte Carlo Sampling. Int. J. Aeronaut. Space Sci. 2025, 1–21. [Google Scholar] [CrossRef]
- Choe, Y.; Song, J.W.; Park, C.G. Lightweight marginalized particle filtering with enhanced consistency for terrain referenced navigation. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 2493–2504. [Google Scholar] [CrossRef]
- Canciani, A.J. Magnetic navigation on an F-16 aircraft using online calibration. IEEE Trans. Aerosp. Electron. Syst. 2021, 58, 420–434. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Z.; Huang, L.; Deng, Z.; Fu, M. A filtered-marine map-based matching method for gravity-aided navigation of underwater vehicles. IEEE/ASME Trans. Mechatronics 2022, 27, 4507–4517. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, H.; Yuan, K.; Zhu, L. Improved SITAN algorithm in the application of aided inertial navigation. In Proceedings of the 2012 International Conference on Measurement, Information and Control, Harbin, China, 18–20 May 2012; Volume 2, pp. 922–926. [Google Scholar]
- Wang, R.; Wang, J.; Li, Y.; Ma, T.; Zhang, X. Research Advances and Prospects of Underwater Terrain-Aided Navigation. Remote Sens. 2024, 16, 2560. [Google Scholar] [CrossRef]
- Keller, B.A.; Putman, N.F.; Grubbs, R.D.; Portnoy, D.S.; Murphy, T.P. Map-like use of Earth’s magnetic field in sharks. Current Biology 2021, 31, 2881–2886. [Google Scholar] [CrossRef]
- Newman, P.; Durrant-Whyte, H. Using sonar in terrain-aided underwater navigation. In Proceedings of the 1998 IEEE International Conference on Robotics and Automation (Cat. No. 98CH36146), Leuven, Belgium, 20 May 1998; Volume 1, pp. 440–445. [Google Scholar]
- Sung, C.K.; Lee, S.J. Moment matched Gaussian kernel and region representative likelihood for performance improvement of PMF-based TRN. Int. J. Control. Autom. Syst. 2020, 18, 1691–1704. [Google Scholar] [CrossRef]
- Luque, I.D. Planes de Contingencia GNSS a Largo Plazo. 2020. Available online: https://isdefeinnova.es/wp-content/uploads/2023/05/Planes-de-contingencia-GNSS-a-largo-plazo.pdf (accessed on 29 May 2025).
- Rodriquez, S.; Brashar, C.; Haydon, T.C.E.; Luong, A.; Pihlaja, C. PNT Resilience RFI Response. In Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Choe, Y.; Park, C.G. Point-mass filtering with boundary flow and its application to terrain referenced navigation. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3600–3613. [Google Scholar] [CrossRef]
- Li, R.K. All Source Positioning, Navigation and Timing; Artech House: Norwood, MA, USA, 2020. [Google Scholar]
- Carroll, J.D.; Canciani, A.J. Terrain-referenced navigation using a steerable-laser measurement sensor. Navigation 2021, 68, 115–134. [Google Scholar] [CrossRef]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. An improved TERCOM-based algorithm for gravity-aided navigation. IEEE Sens. J. 2016, 16, 2537–2544. [Google Scholar] [CrossRef]
- Wang, B.; Yu, L.; Deng, Z.; Fu, M. A particle filter-based matching algorithm with gravity sample vector for underwater gravity aided navigation. IEEE/ASME Trans. Mechatronics 2016, 21, 1399–1408. [Google Scholar] [CrossRef]
- Wu, L.; Ma, J.; Tian, J. A self-adaptive unscented Kalman filtering for underwater gravity aided navigation. In Proceedings of the IEEE/Ion Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 142–145. [Google Scholar]
- Bao, B.; Hua, Y.; Wang, R.; Li, D. Quantum-Based Magnetic Field Sensors for Biosensing. Adv. Quantum Technol. 2023, 6, 2200146. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yiğit, H. Arazi Verisine Dayalı Konumlandırma ve Seyrüsefer Sistemi Tasarlanması. Master’s Thesis, Havacılık ve Uzay Teknolojileri Enstitüsü, Hava Harp Okulu Komutanlığı, Istanbul, 2012. [Google Scholar]
- Turan, B. Comparison of nonlinear filtering methods for terrain referenced aircraft navigation. In Proceedings of the 2020 IEEE/Ion Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020; pp. 144–149. [Google Scholar]
- Wang, Y.Y.; Jia, X.R.; Yang, G.L.; Wang, Y.M. Comprehensive CEP evaluation method for calculating positioning precision of navigation systems. Appl. Mech. Mater. 2013, 341, 955–960. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).