Development of a Simulation Model for Blade Tip Timing with Uncertainties
Abstract
1. Introduction
2. The Principle of BTT
3. Blade Vibration Model and BTT Sampling Model
3.1. Blade Vibration Model
3.2. BTT Sampling Model
3.3. Solving the Vibration Response
3.4. Probe Trigger and Probe Mounting Angle Error Simulation
3.5. Trigger Error Simulation
3.6. Blade Mounting Angle Error Simulation
3.7. Multi-Harmonic Vibration Model
4. Comparison of Simulation and Experimental Results
4.1. Single-Mode Vibration Simulation
4.1.1. Simulation of Synchronous Vibration Based on Sinusoidal Excitation Force
4.1.2. Simulation of Synchronous Vibration Based on Multi-Source Square Wave Excitation Force
4.1.3. Effect of Trigger Position Error
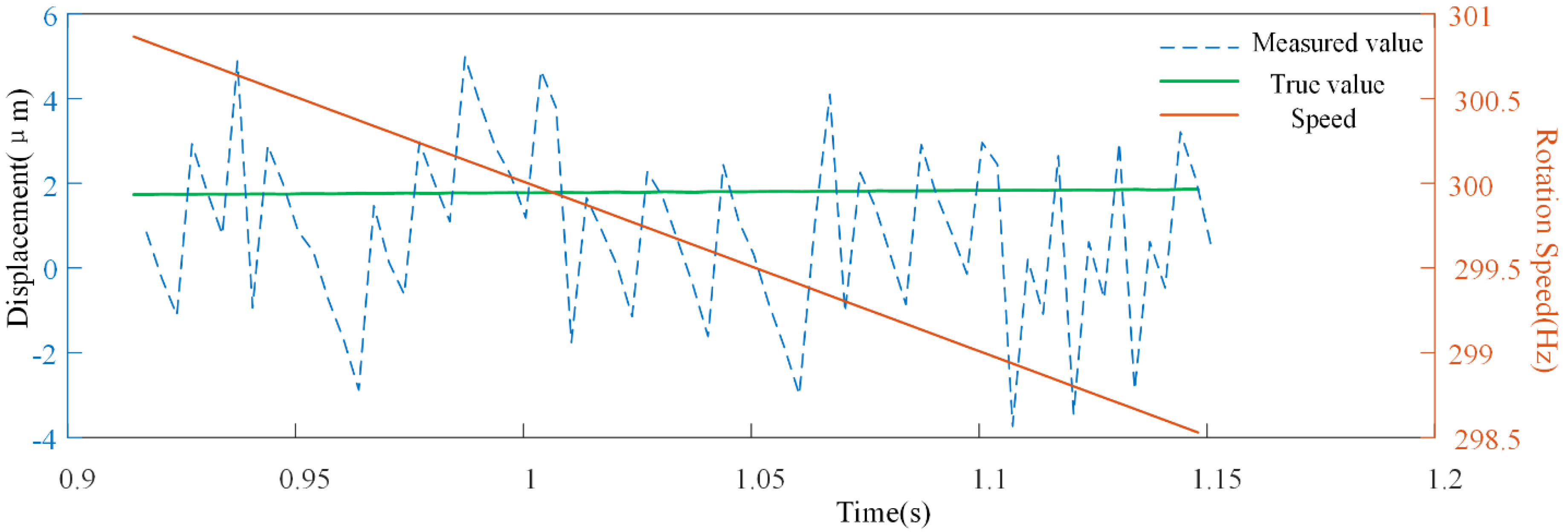
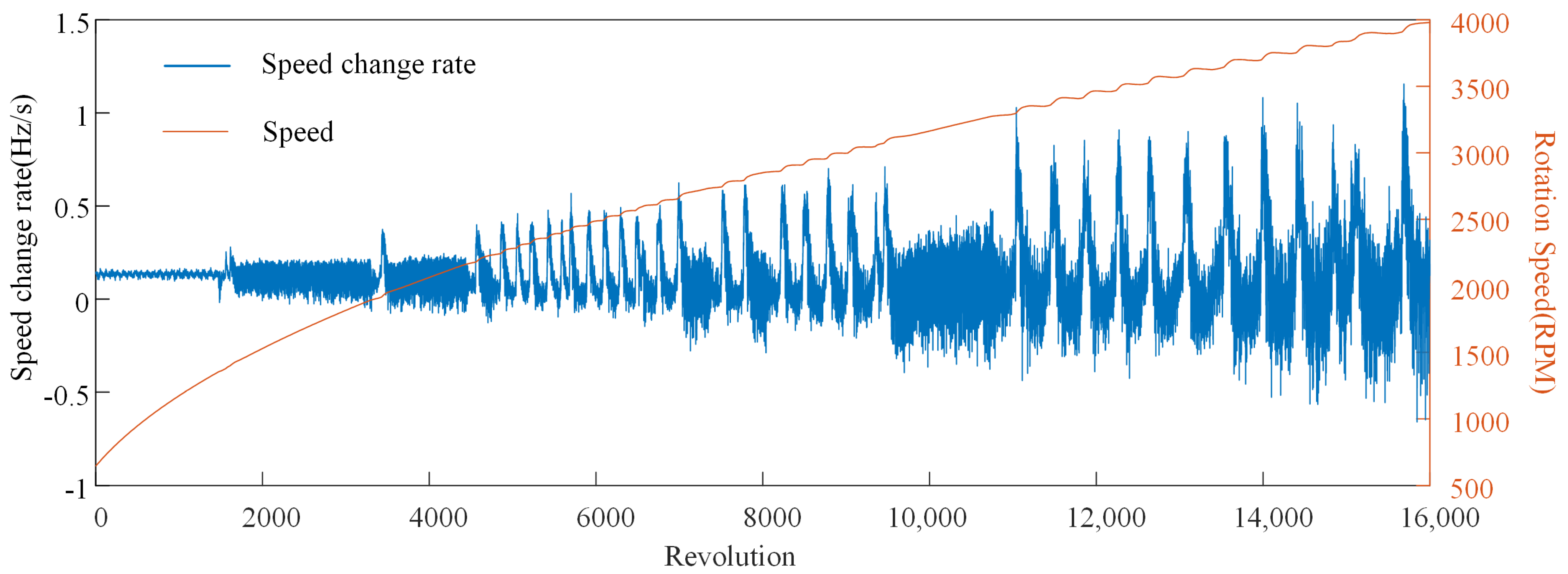
4.1.4. Speed Fluctuation
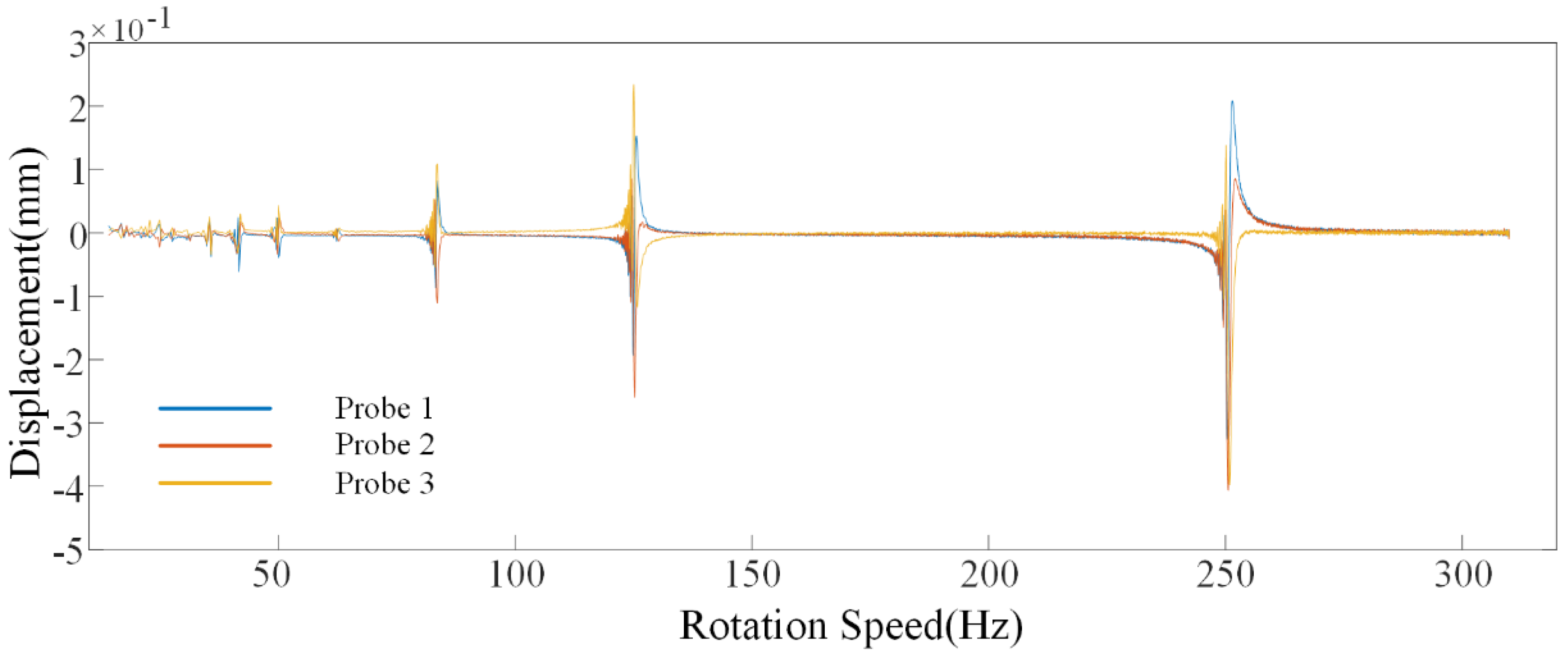
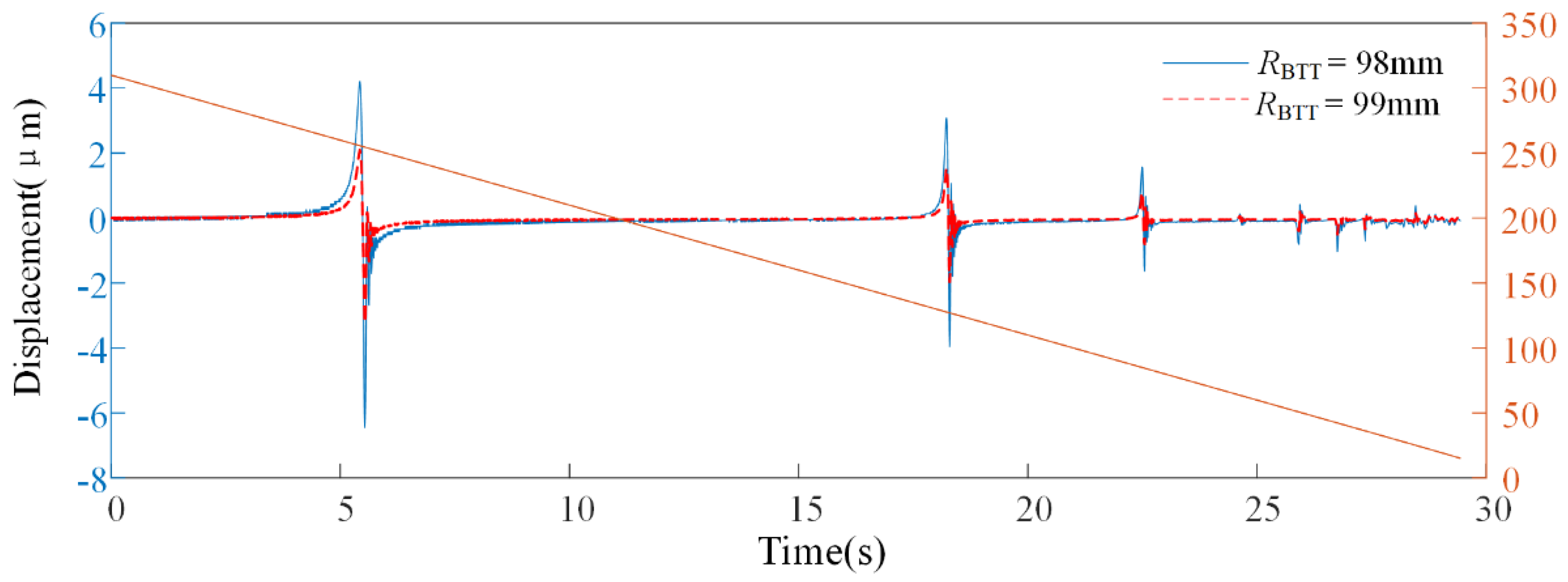
4.1.5. Effect of Changes in Blade Radius
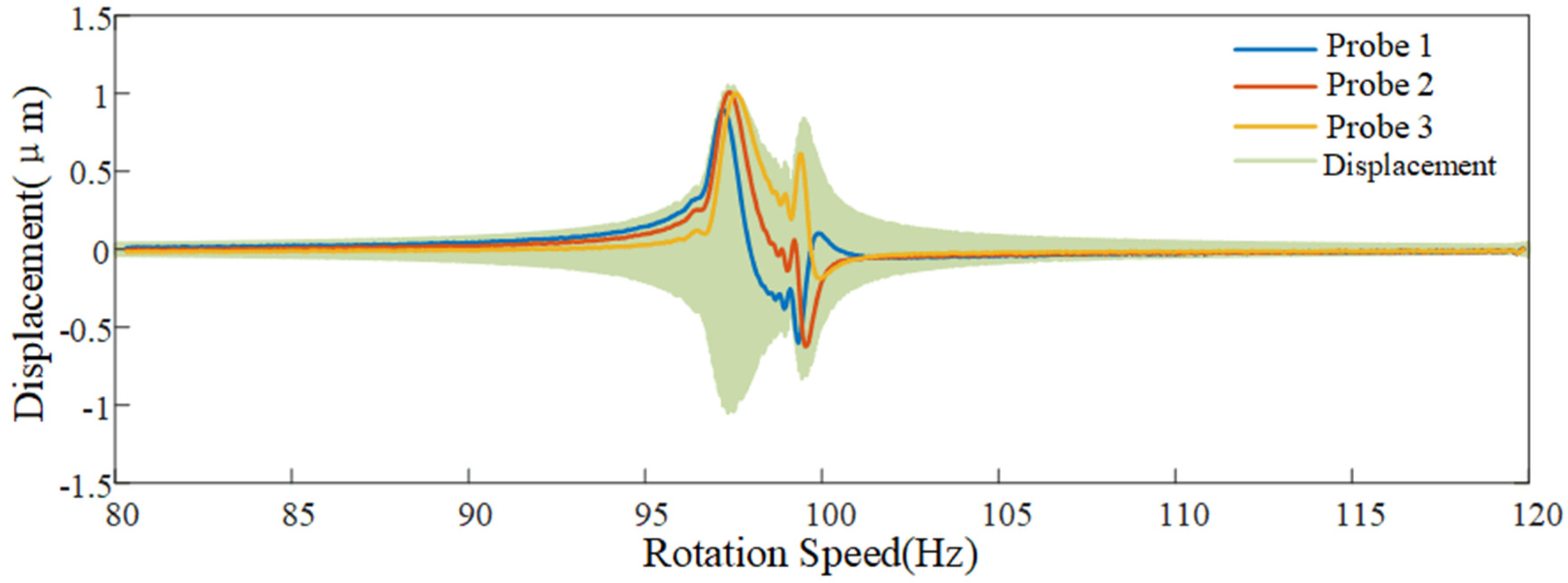
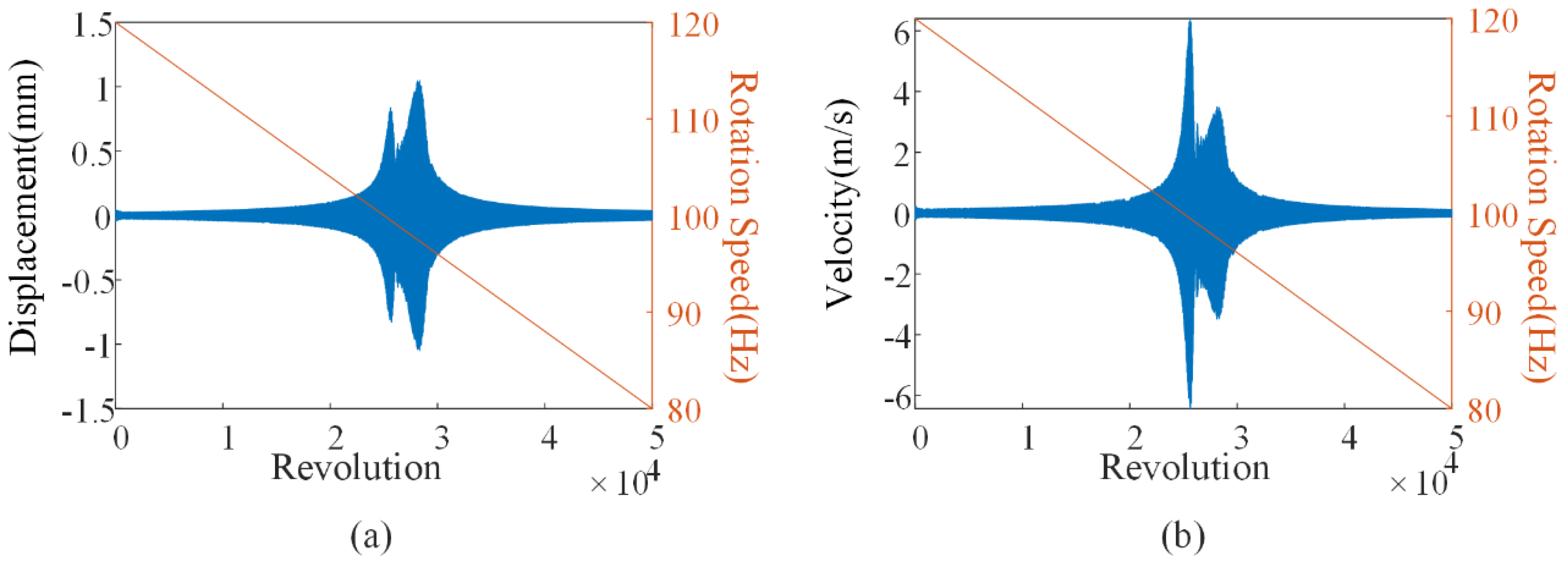
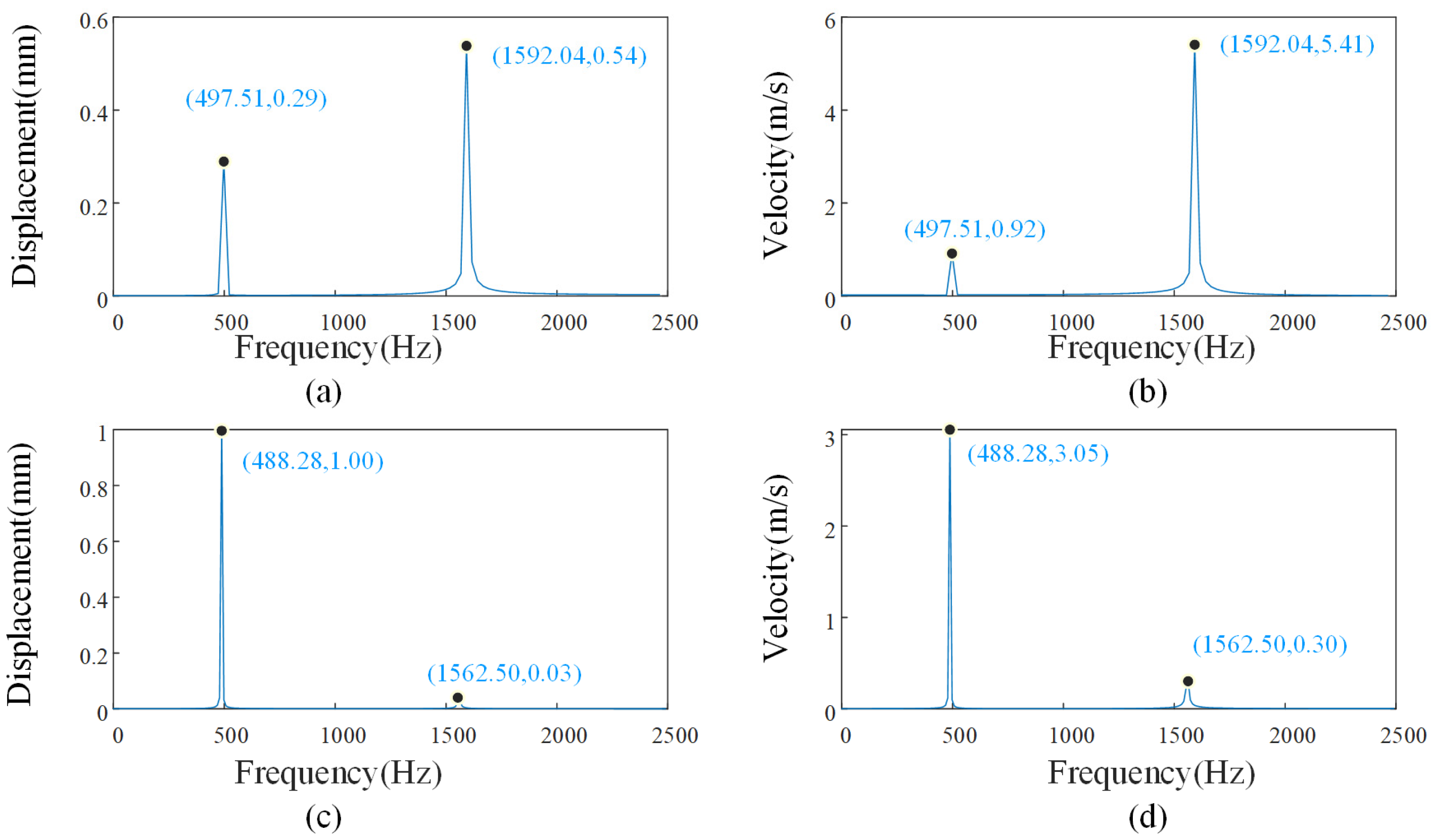
4.2. Multi-Harmonic Vibration Simulation
4.3. Comparison with Test Results
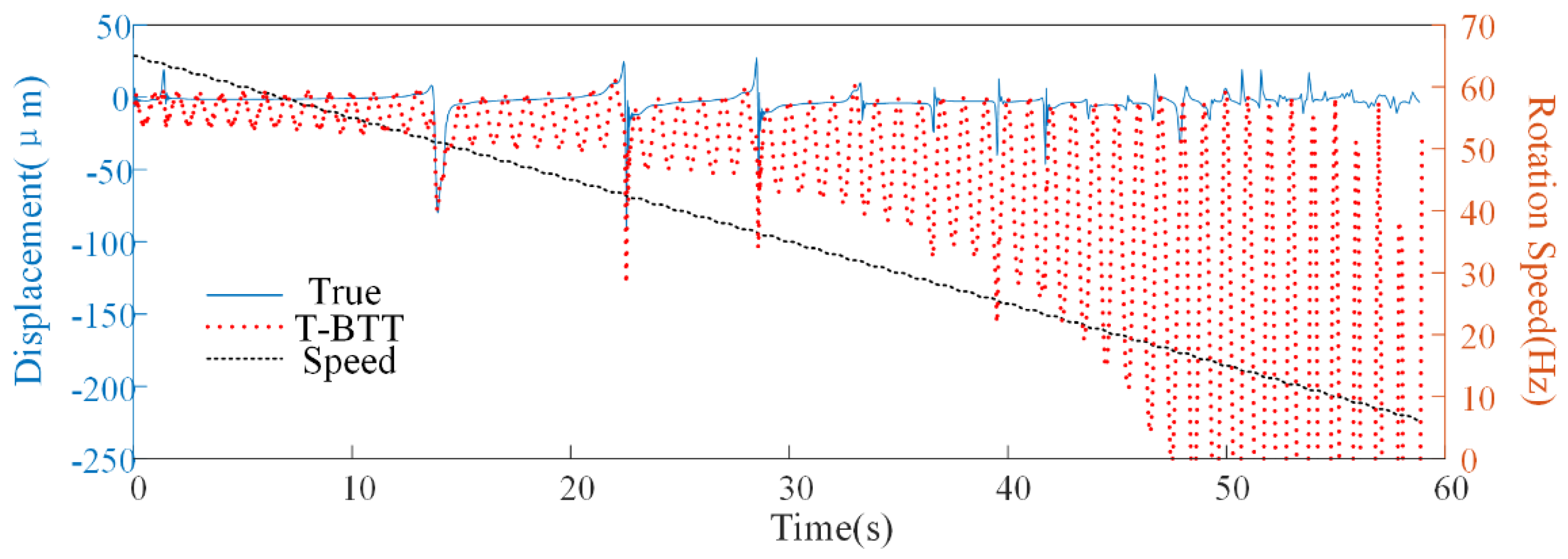
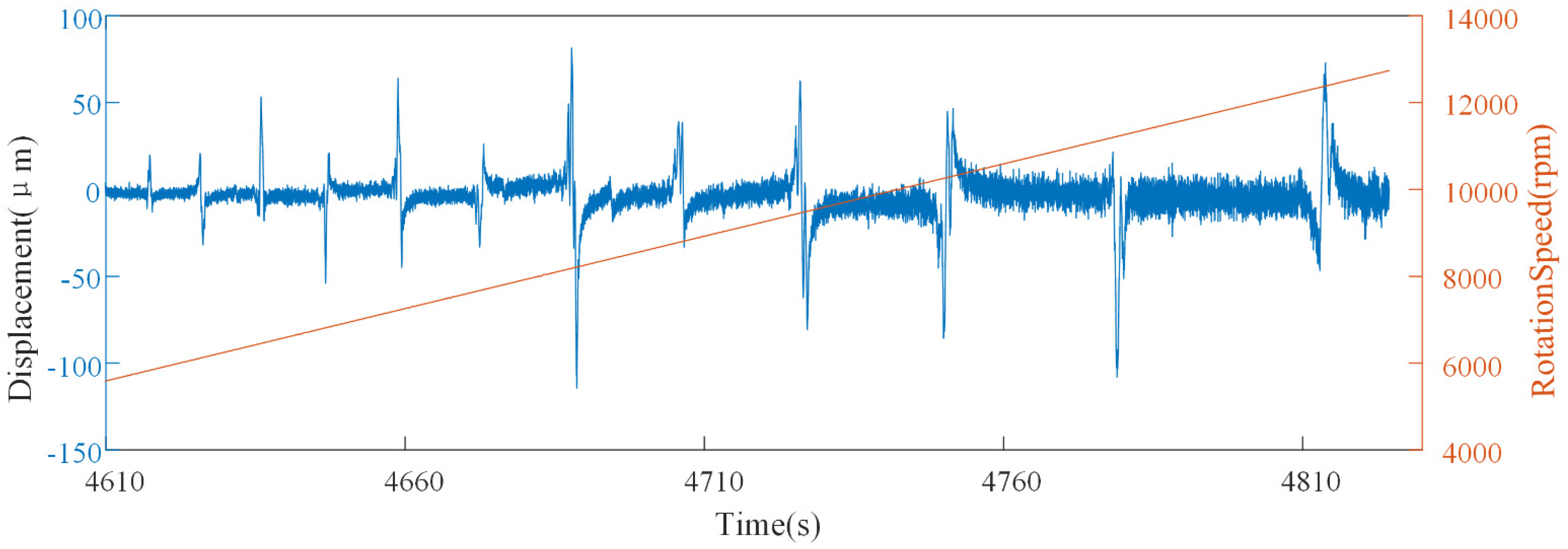
4.3.1. The Acceleration Process Verification
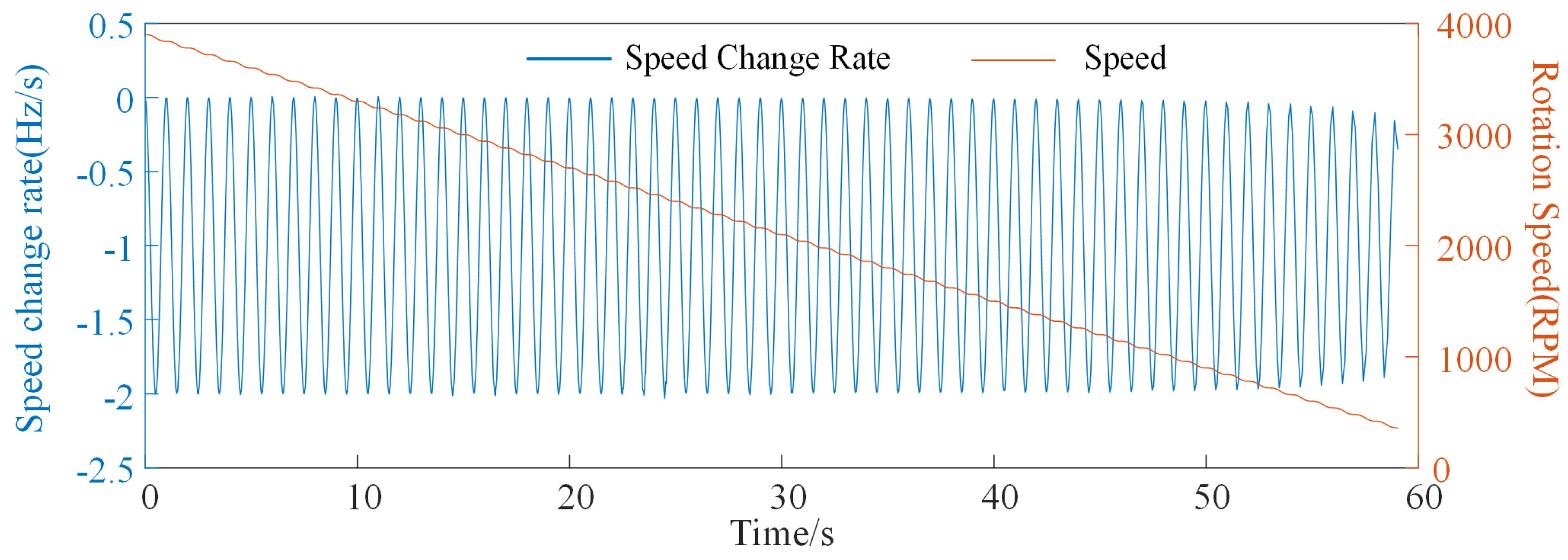
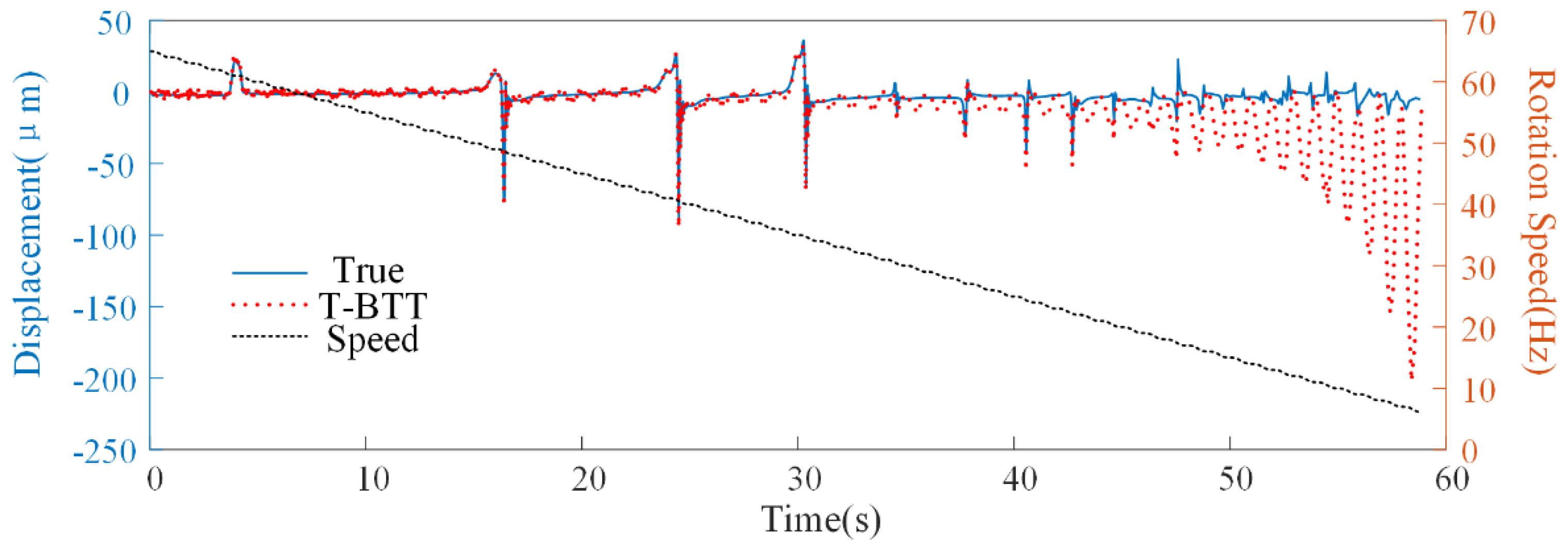
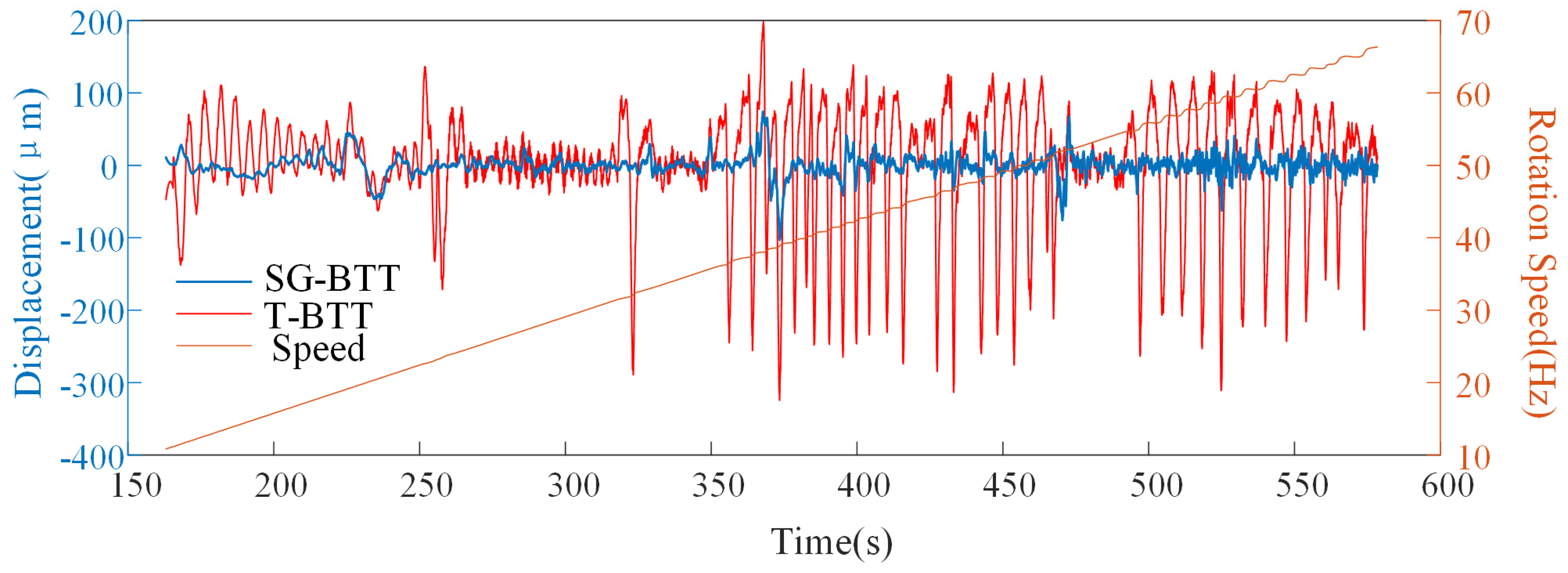
4.3.2. Verification of Speed Fluctuation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BTT | Blade Tip-Timing |
| ToA | Time of Arrival |
| OPR | Once Per Revolution |
| MDoF | Multi-Degree-of-Freedom |
| SDoF | Single-Degree-of-Freedom |
| BTC | Blade Tip Clearance |
References
- Carrington, I.B.; Wright, J.R.; Cooper, J.E.; Dimitriadis, G. A Comparison of Blade Tip Timing Data Analysis Methods. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2001, 215, 301–312. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Carrington, I.B.; Wright, J.R.; Cooper, J.E. Blade-Tip Timing Measurement of Synchronous Vibrations of Rotating Bladed Assemblies. Mech. Syst. Signal Process. 2002, 16, 599–622. [Google Scholar] [CrossRef]
- Bornassi, S.; Battiato, G.; Firrone, C.M.; Berruti, T.M. Tip-Timing Measurements of Transient Vibrations in Mistuned Bladed Disks. Int. J. Mech. Sci. 2022, 226, 107393. [Google Scholar] [CrossRef]
- Fan, Z.; Li, H.; Huang, J.; Liu, S. Blade Vibration Difference-Based Circumferential Fourier Fitting Algorithm for Synchronous Vibration Parameter Identification of Rotation Blades. Sensors 2024, 24, 8083. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Xiong, Y.; Chen, P.; Wei, C.; Liang, D.; Fan, W.; Peng, Z. Simultaneous Measurement of Blade Tip Clearance and Blade Tip Timing with Microwave Sensor. IEEE Trans. Instrum. Meas. 2024, 73, 8002412. [Google Scholar] [CrossRef]
- Heller, D.; Sever, I.A.; Schwingshackl, C.W. A Method for Multi-Harmonic Vibration Analysis of Turbomachinery Blades Using Blade Tip-Timing and Clearance Sensor Waveforms and Optimization Techniques. Mech. Syst. Signal Process. 2020, 142, 106741. [Google Scholar] [CrossRef]
- Huang, W.; Bian, Z.; Pan, M.; Xiao, B.; Li, A.; Hu, H.; Yang, Y.; Guan, F. A Novel Sparse Reconstruction Method for Under-Sampled Blade Tip Timing Signals: Integrating Vibration Displacement and Velocity. Mech. Syst. Signal Process. 2025, 229, 112543. [Google Scholar] [CrossRef]
- Nikpour, M.; Moradi, S.; Soodmand, I. A New Bladed Assembly Simulator and an Improved Two-Parameter Plot Method for Blade Tip-Timing Numerical Simulations. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2021, 235, 2135–2144. [Google Scholar] [CrossRef]
- Mohamed, M.E.; Bonello, P.; Russhard, P. An Experimentally Validated Modal Model Simulator for the Assessment of Different Blade Tip Timing Algorithms. Mech. Syst. Signal Process. 2020, 136, 106484. [Google Scholar] [CrossRef]
- Tocci, T.; Capponi, L.; Rossi, G.; Marsili, R.; Marrazzo, M. State-Space Model for Arrival Time Simulations and Methodology for Offline Blade Tip-Timing Software Characterization. Sensors 2023, 23, 2600. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Yang, Z.; Tian, S.; Teng, G.; Chen, X. Active Aliasing Technique and Risk versus Error Mechanism in Blade Tip Timing. Mech. Syst. Signal Process. 2023, 191, 110150. [Google Scholar] [CrossRef]
- Xu, J.; Qiao, B.; Wang, Y.; Liu, M.; Fu, S.; Fan, Y.; Chen, X. A Recursive Calculation Method of Vibration Displacements Using Blade Tip Timing in Angular Domain. Mech. Syst. Signal Process. 2024, 219, 111612. [Google Scholar] [CrossRef]
- Zhu, Y.; Qiao, B.; Wang, Y.; Yang, Z.; Liu, M.; Chen, X. Improved Non-Contact Vibration Measurement via Acceleration-Based Blade Tip Timing. Aerosp. Sci. Technol. 2024, 152, 109373. [Google Scholar] [CrossRef]
- Zhu, Y.; Wang, Y.; Qiao, B.; Liu, M.; Chen, X. Blade Tip Timing for Multi-Mode Identification Based on the Blade Vibration Velocity. Mech. Syst. Signal Process. 2024, 209, 111092. [Google Scholar] [CrossRef]
- Guo, S.; Xu, B. Effect of temperature and rotational speed on radial clearance of turbine blade tip. J. Propuls. Technol. 2000, 21, 51–53. [Google Scholar] [CrossRef]
- Carrington, I.B. Development of Blade Tip Timing Data Analysis Techniques. Ph.D. Thesis, University of Manchester, Manchester, UK, 2002. [Google Scholar]
- Wang, S.; Bi, C.-X.; Zi, B.; Zheng, C.-J. Vibration Characteristics of Rotating Mistuned Bladed Disks Considering the Coriolis Force, Spin Softening, and Stress Stiffening Effects. Shock. Vib. 2019, 2019, 9714529. [Google Scholar] [CrossRef]
- Ren, S.; Xiang, X.; Zhao, Q.; Wang, W.; Zhao, W.; Hao, L. Research on Active Control Method of Rotor Blade Synchronous Vibration Based on Additional Secondary Excitation Forces. J. Low Freq. Noise Vib. Act. Control. 2021, 40, 2077–2093. [Google Scholar] [CrossRef]
- Niu, G.; Duan, F.; Liu, Z.; Zhi, F.; Fu, X.; Jiang, J.; Guo, G.; Xiong, B. Identification of the Excitation Source’s Circumferential Position for Rotating Blades Based on Vibration Phase. J. Sound Vib. 2022, 520, 116628. [Google Scholar] [CrossRef]
- Bian, Z.; Yang, Y.; Guan, F.; Hu, H.; Shen, G.; Pan, M. Single-Sensor Rotating Blade Monitoring Method under Non-Stationary Conditions Based on Velocity and Displacement. ISA Trans. 2024, 152, 385–407. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Chen, K.; Zhang, X.; Li, W. A Novel Method to Improve the Precision of BTT under Rapid Speed Fluctuation Conditions. Mech. Syst. Signal Process. 2022, 177, 109203. [Google Scholar] [CrossRef]
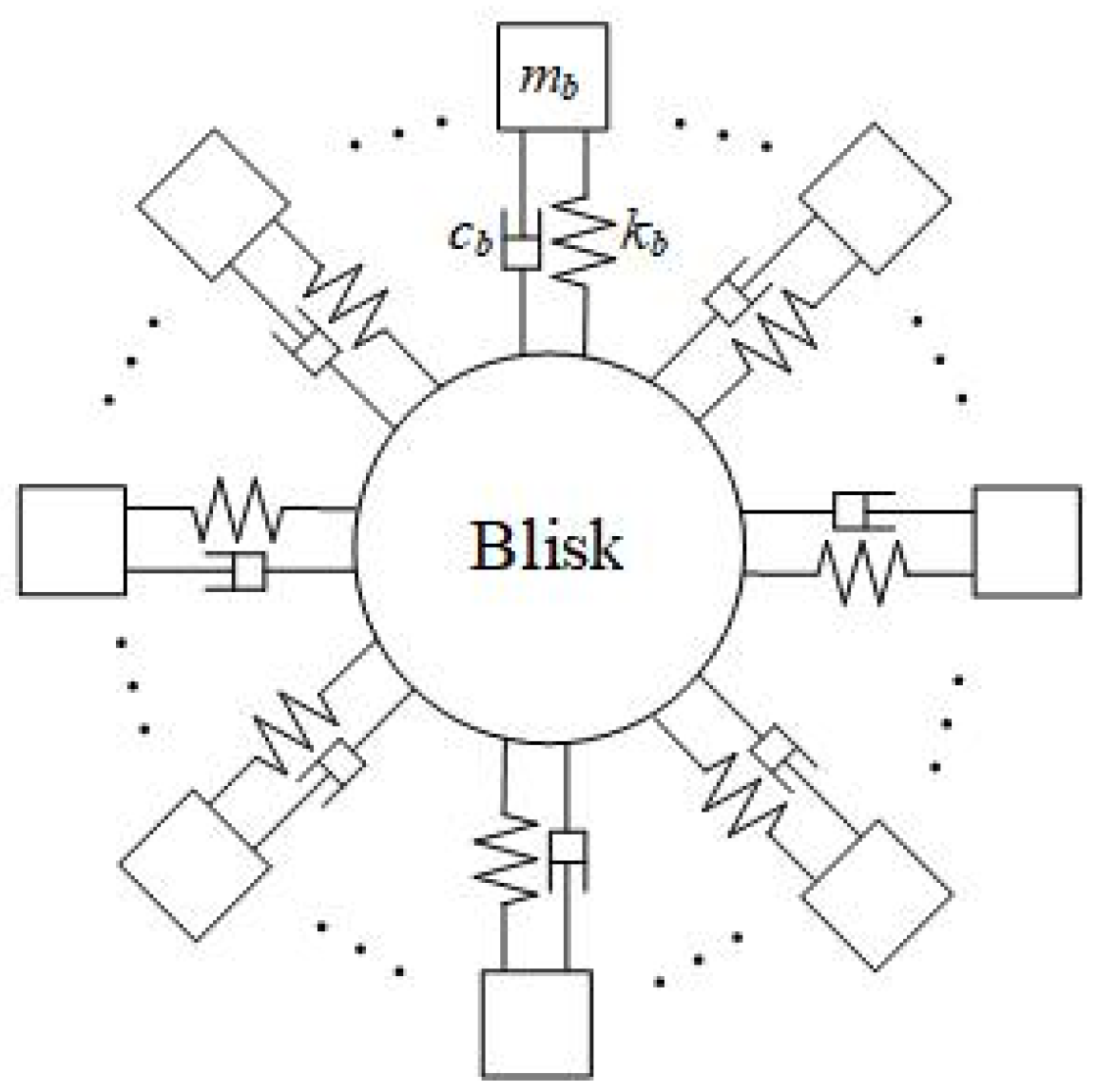
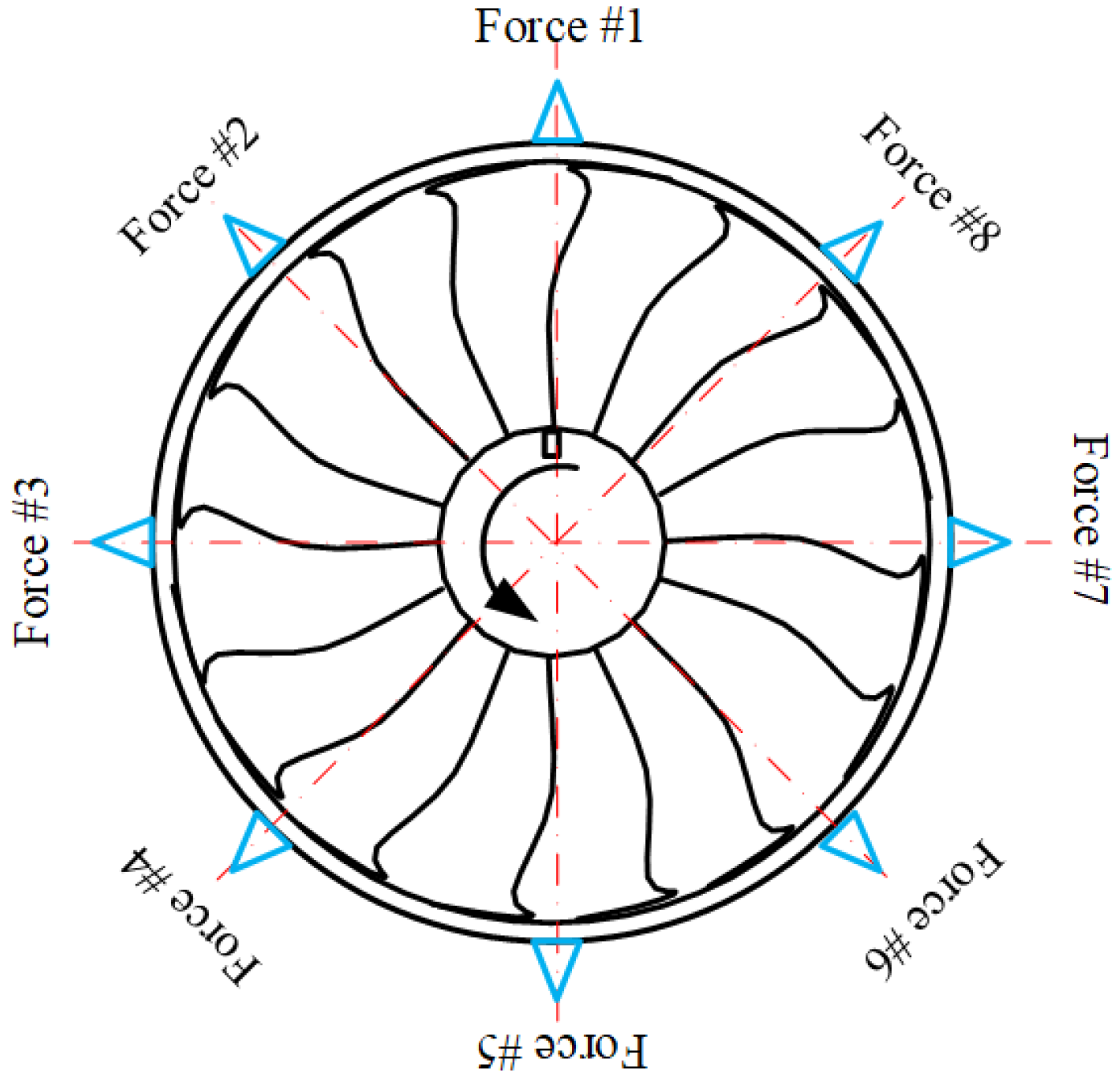

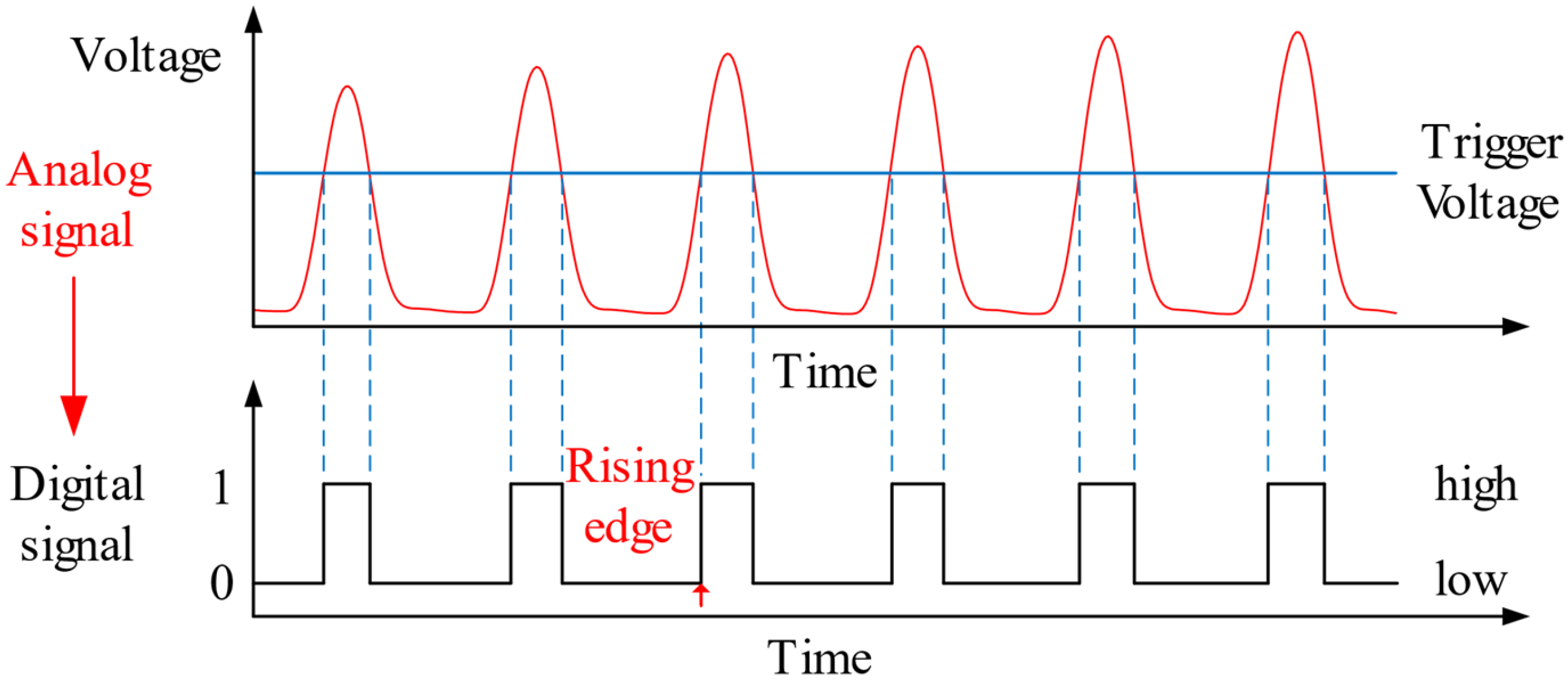
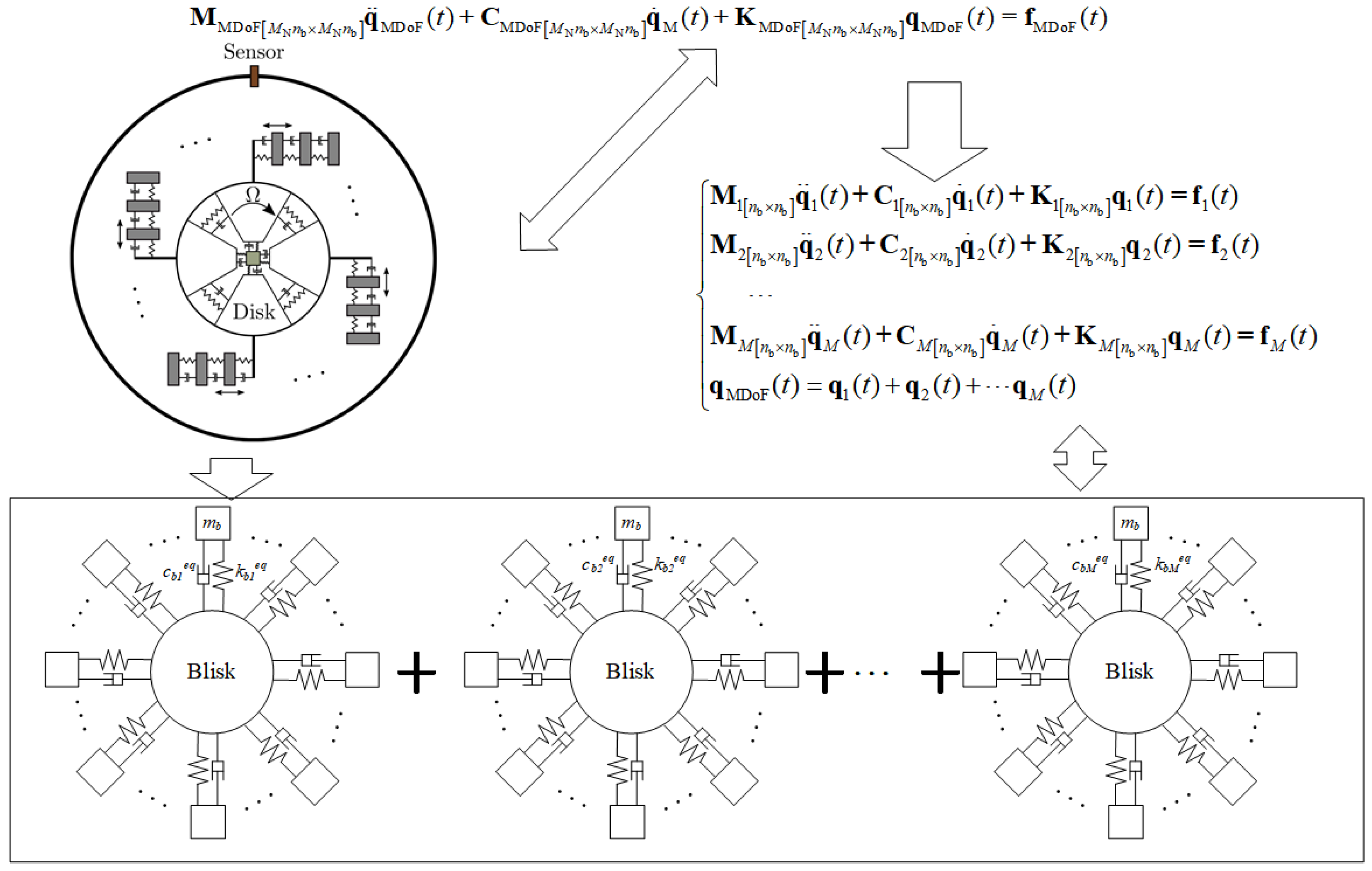
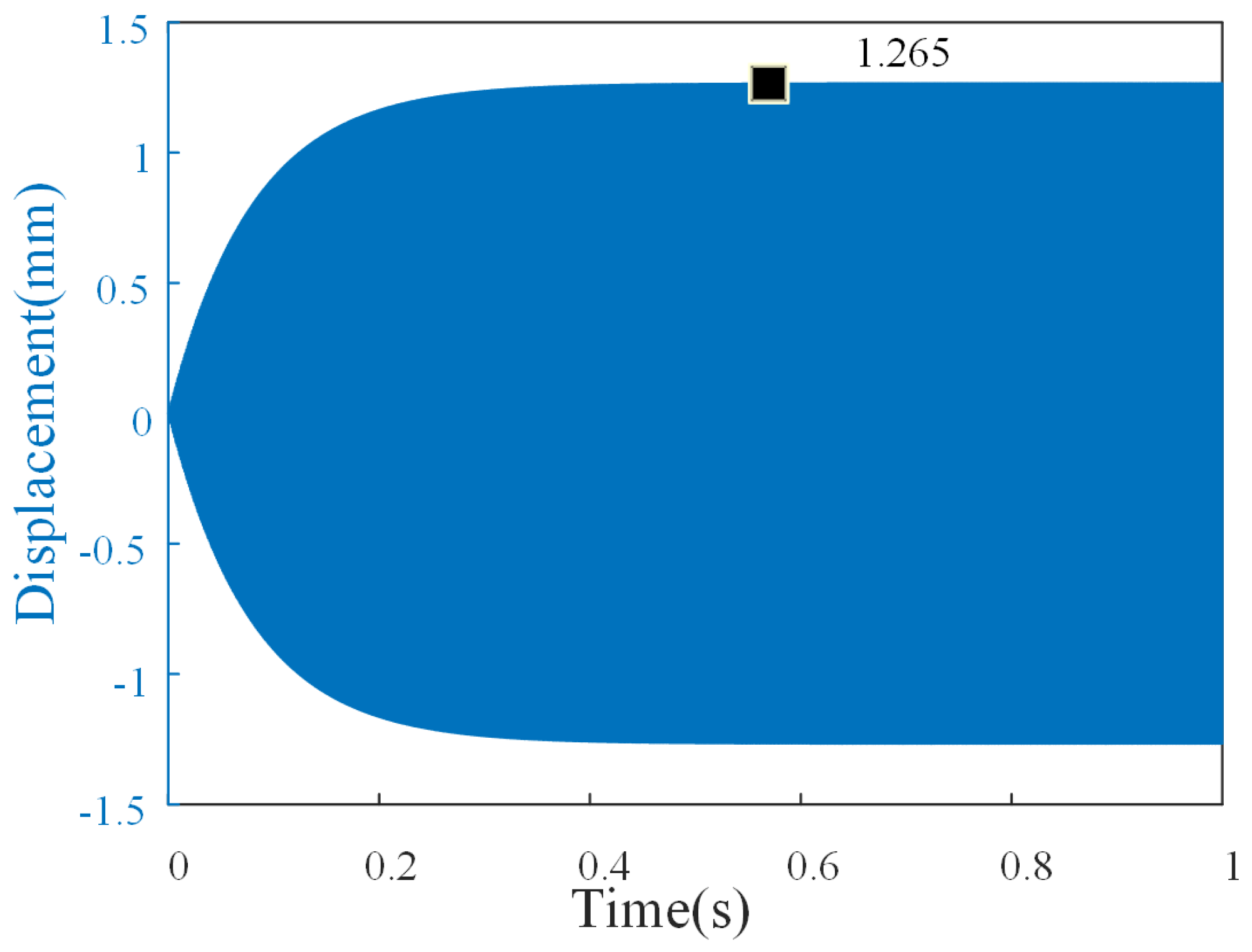


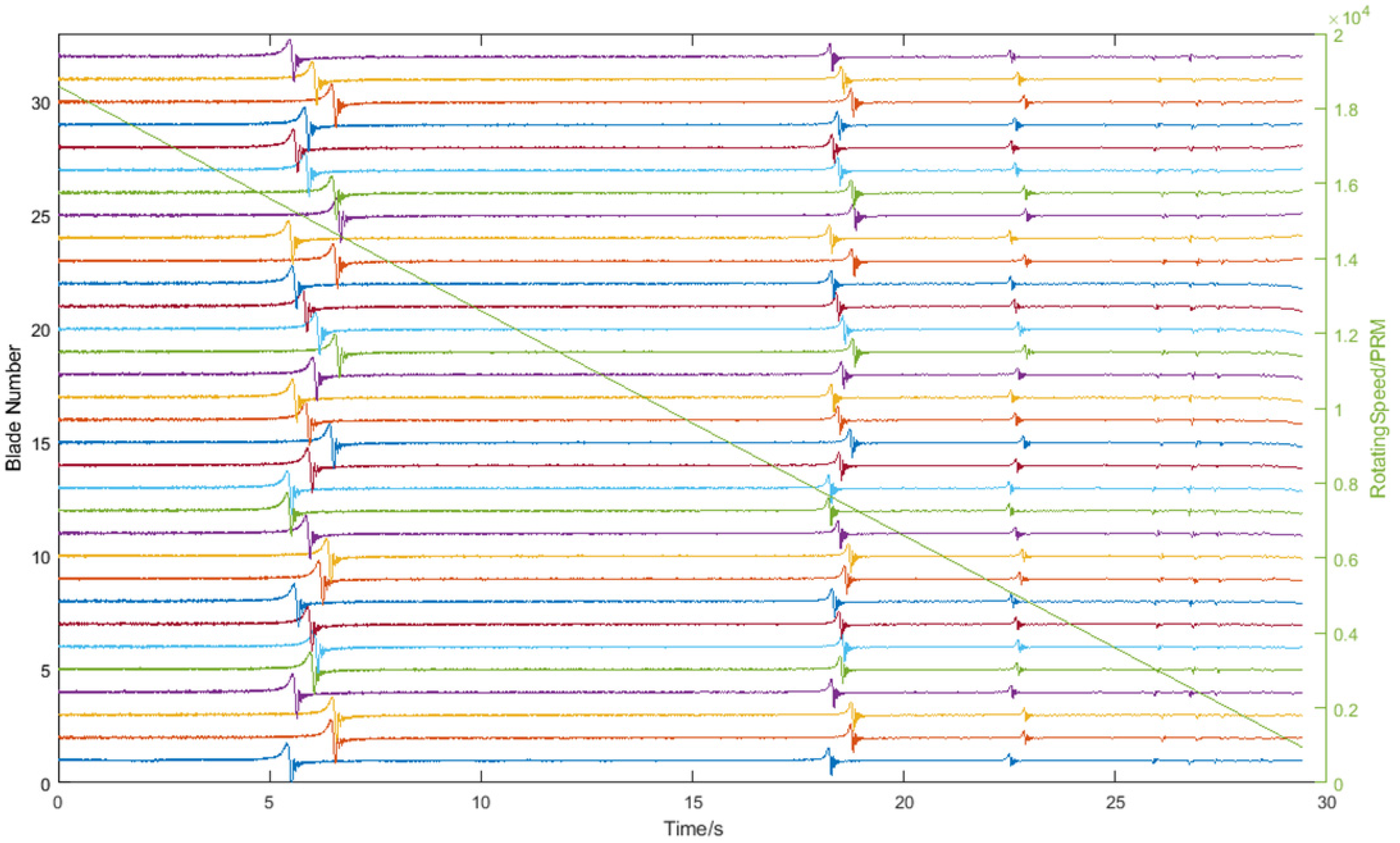
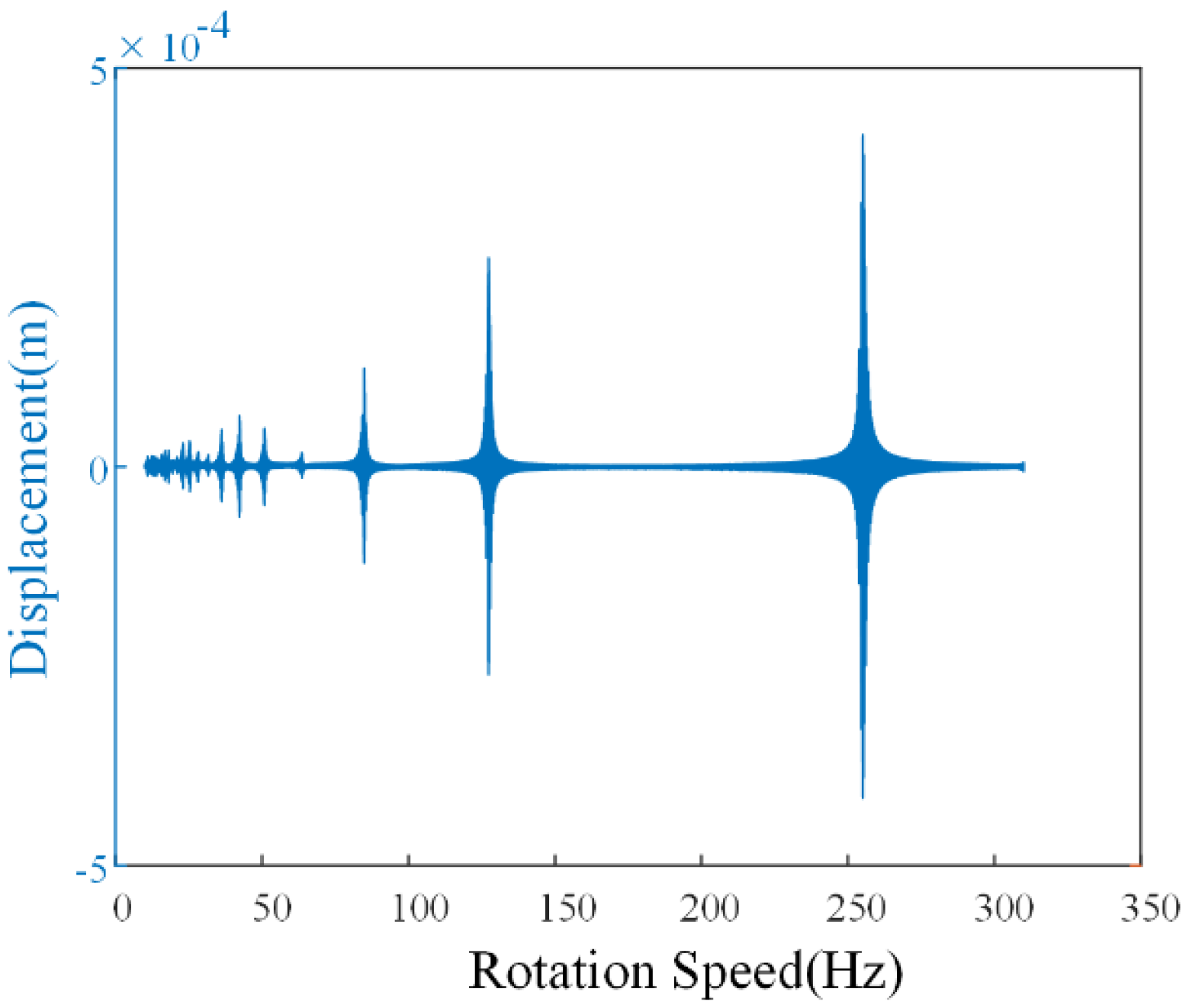
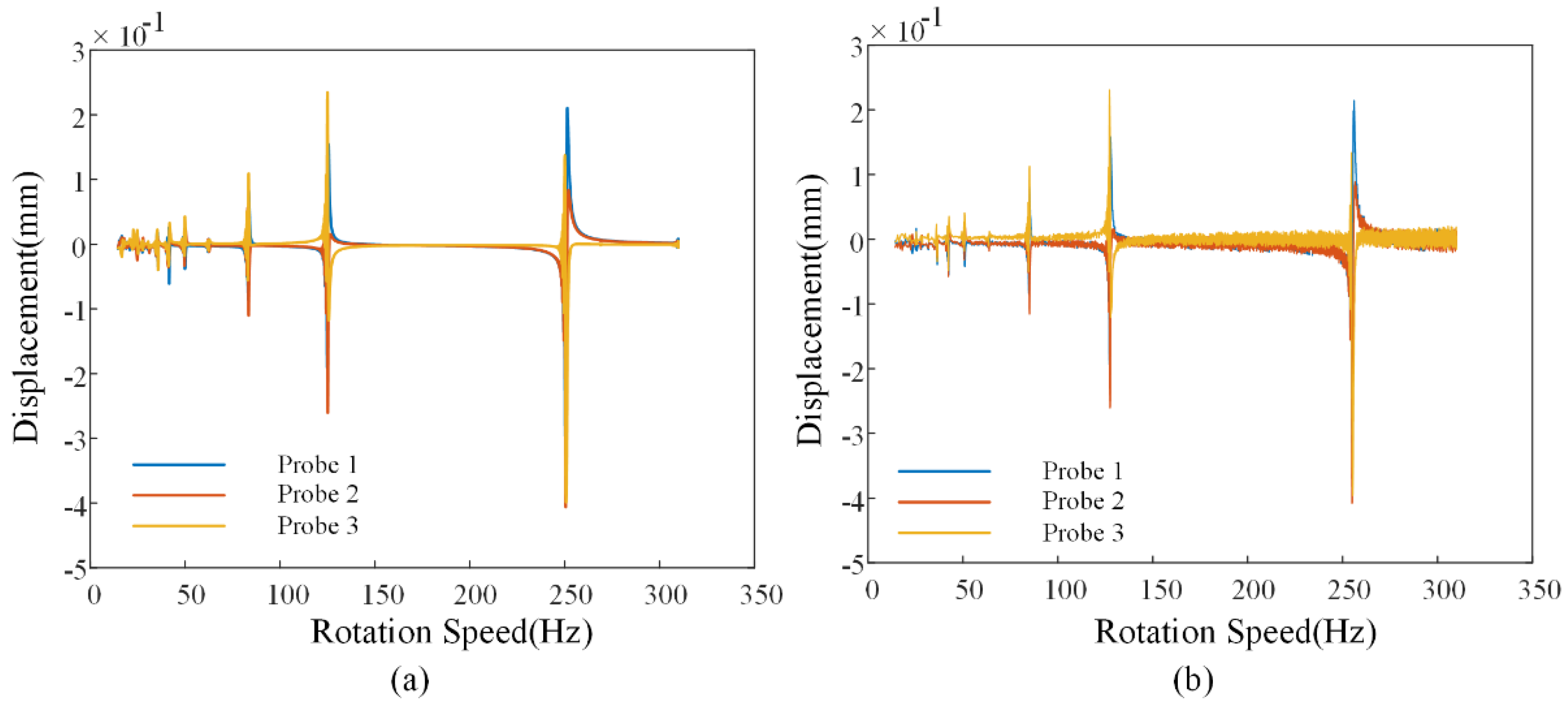








| Mass of Blades m (Unit: kg) | (Unit: Hz) | Blade Number nb | Radius of Blade Disk R (Unit: m) | (Unit: kg) | Sampling Frequency (Unit: MHz) | |
|---|---|---|---|---|---|---|
| 0.05 | 2000 | 0.001 | 32 | 0.05 | 0.05 × m | 5 |
| (Unite: N) | Start Frequency (Unite: Hz) | End Frequency (Unite: Hz) | Simulation Time (Unite: s) | |
|---|---|---|---|---|
| 20 | 20 | 95 | 105 | 10 |
| (Unit: N) | Start Frequency (Unite: Hz) | End Frequency (Unite: Hz) | Simulation Time (Unite: s) | |
|---|---|---|---|---|
| 20 | 20 | 310 | 10 | 30 |
| (Unit: N) | Start Frequency (Unite: Hz) | End Frequency (Unite: Hz) | Simulation Time (Unite: s) | |
|---|---|---|---|---|
| 20 | 20 | 310 | 10 | 30 |
| Mass of Blades m (Unit: kg) | Blade Number nb | Radius of Blade Disk R (Unit: m) | (Unit: kg) | Sampling Frequency (Unit: MHz) | Mode 1 | Mode 2 | ||
|---|---|---|---|---|---|---|---|---|
| (Unit: Hz) | (Unit: Hz) | |||||||
| 0.05 | 32 | 0.05 | 0.03 × m | 5 | 486 | 0.005 | 1587 | 0.0015 |
| (Unite: N) | (Unite: N) | Start Frequency (Unite: Hz) | End Frequency (Unite: Hz) | Simulation Time (Unite: s) | ||
|---|---|---|---|---|---|---|
| 10 | 5 | 20 | 16 | 120 | 80 | 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Xu, G.; Zhang, X.; Qu, W. Development of a Simulation Model for Blade Tip Timing with Uncertainties. Aerospace 2025, 12, 480. https://doi.org/10.3390/aerospace12060480
Chen K, Xu G, Zhang X, Qu W. Development of a Simulation Model for Blade Tip Timing with Uncertainties. Aerospace. 2025; 12(6):480. https://doi.org/10.3390/aerospace12060480
Chicago/Turabian StyleChen, Kang, Guoning Xu, Xulong Zhang, and Wei Qu. 2025. "Development of a Simulation Model for Blade Tip Timing with Uncertainties" Aerospace 12, no. 6: 480. https://doi.org/10.3390/aerospace12060480
APA StyleChen, K., Xu, G., Zhang, X., & Qu, W. (2025). Development of a Simulation Model for Blade Tip Timing with Uncertainties. Aerospace, 12(6), 480. https://doi.org/10.3390/aerospace12060480






