1. Introduction
The wind tunnel test is crucial for studying the aerodynamic characteristics of aerospace vehicles. However, the real gas effect, scale effect, wall interference, and flow similarity in ground tests can lead to significant discrepancies between the aerodynamic ground test data and the actual flight data. Analyzing the deviations between aerodynamic data from ground tests, including wind tunnel and computational fluid dynamics (CFD) data and the actual flight data, is known as a correlation study. The objective of the correlation study is to create a more precise aerodynamic database model for vehicle development to better predict aerodynamic characteristics during actual flight.
The correction or extrapolation of wind tunnel test data was one of the popular research branches of aerodynamic ground-to-flight correlation analysis [
1,
2,
3]. Recently, considerable research efforts have been devoted to problems with strongly nonlinear properties in ground effects and transonic and hypersonic flow regimes, such as using neural networks to estimate aerodynamic characteristics under the ground effect [
4], hypersonic vehicle stage separation [
5,
6], boundary layer transition [
7,
8] and CFD-based ground test data corrections for transonic business jet aircraft [
9,
10]. The main goal of ground-to-flight correlation analysis is to establish a ground aerodynamic database that can better approximate the real flight. To date, the processing methods for the ground-to-flight aerodynamic deviations can be categorized as follows:
These correction methods cannot model the overall biases between ground and real flight and are mostly used in wind tunnel test data correction. In contrast, the black box deviation modeling methods lack generalization and interpretability and require large-scale data size in modeling. The physical law mining-based method appears to address the shortcomings of both correction and black box modeling methods, and it has therefore emerged as a promising direction for studying aerodynamic ground-to-flight deviations.
The symbolic regression method can be utilized in physical law mining, which has gained significant attention since the 1990s [
22,
23] and has been widely applied in various fields, such as chemical systems [
24], fluid dynamics [
25], dynamical systems [
26,
27,
28,
29] and natural science modeling [
30]. The early application of the genetic-based evolutionary symbolic regression algorithm was limited to the difficulty of realizing the tree-structured formula expression in universal programming languages (UPLs). Consequently, several improvements have been made to the structure of the formula. For instance, attempts have been made to use binary coding to replace the tree structure [
31] and a parse matrix-based encoding and decoding method to map from a two-dimensional matrix to function expression [
20]. França [
32] proposed a greedy search tree heuristic algorithm to exclude a region of rugged search space and complicated expressions. Cozad and Sahinidis [
33] put forward a deterministic optimization algorithm, namely a mixed-integer nonlinear programming (MINLP) approach, to avoid the stochastic nature of genetic algorithms in symbolic regression and verified the method’s performance in eliminating formula redundancies and symmetries. Additionally, Petersen et al. [
34] introduced reinforcement learning in symbolic regression to realize the best search direction autoregression. In the comparison between symbolic regression and neural networks, it was found that symbolic regression methods based on evolutionary algorithms could obtain a mathematical–physical model with stronger interpretability [
35]. However, the issues of fitting accuracy and efficiency for high-dimensional space have remained a focus of research in symbolic regression.
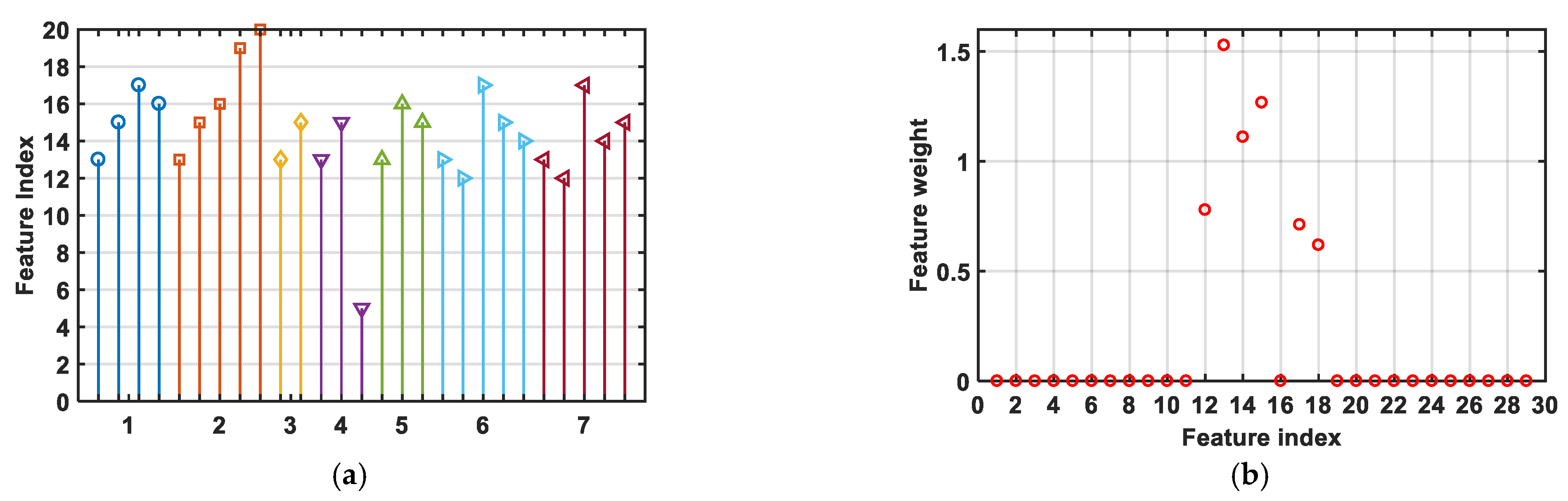
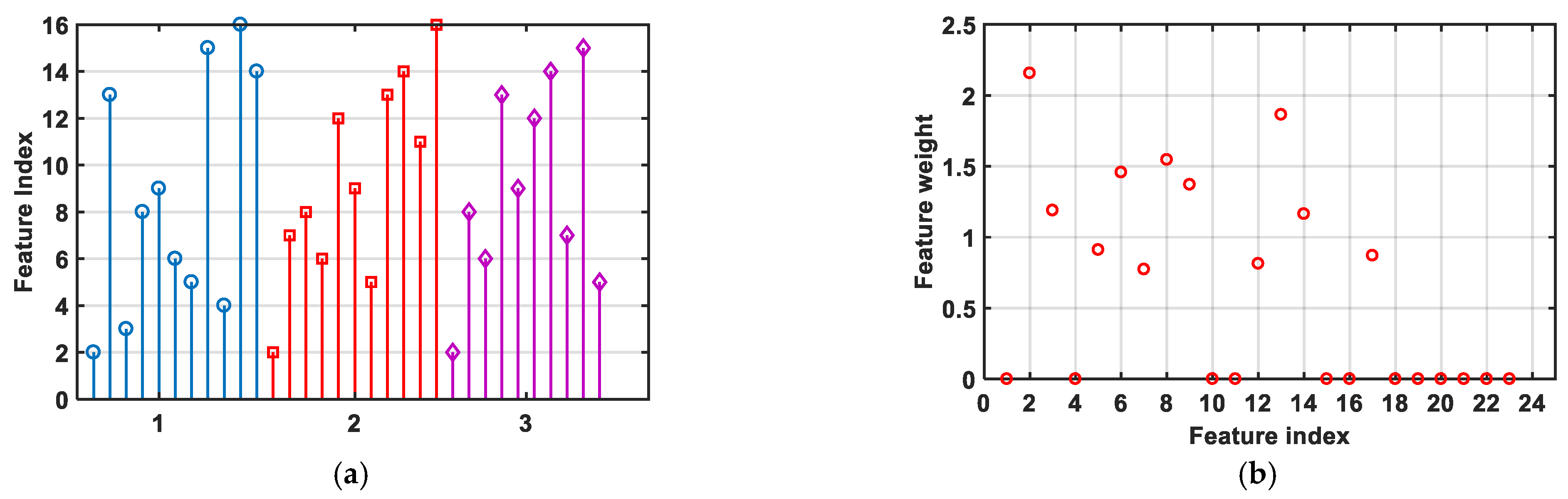
Current studies on the ground-to-flight correlation of aircraft aerodynamic characteristics mainly focus on wind tunnel test data corrections and theoretical analysis, while data-driven modeling mostly adopts black box models. This paper proposes conducting research on physical mechanism exploration and mathematical modeling of ground-to-flight deviations in aircraft aerodynamic characteristics of aerospace vehicles, aiming to establish an interpretable mathematical model with explicit physical significance. Such research remains relatively scarce in current academic investigations. The symbolic regression method is applicable for modeling the correlation between the aerodynamic ground test data and flight test data, but the challenge of efficiently extracting concise and physically interpretable mathematical expressions from high-dimensional flight state spaces remains to be addressed. To address this issue, a dimensional reduction technique is applied in this paper to enhance the efficiency of symbolic regression. The study faces another challenge in ground-to-flight correlation research: the unavailability of obtaining extensive flight test data due to the costs. Therefore, based on assumptions of flow similarity and the intrinsic physical connections between flight tests and ground tests for the same vehicle, this study combines correlation feature extraction with symbolic regression to address the challenges of physical law modeling from the aerodynamic ground-to-flight deviations in high-dimensional state space and with finite flight test data. The universality and effectiveness of this methodology is validated by two distinct types of aerospace vehicles. The findings demonstrate that the method can rapidly and efficiently identify physical laws governing the ground-to-flight deviation across the entire state space of different aerospace vehicles.
The paper is organized as follows: first,
Section 2 introduces the symbolic regression tool and feature extraction method. Next, the two methods are validated using simulation data and applied on real flight deviations in the
Section 3. Finally, the paper concludes with the
Section 4.
4. Discussion
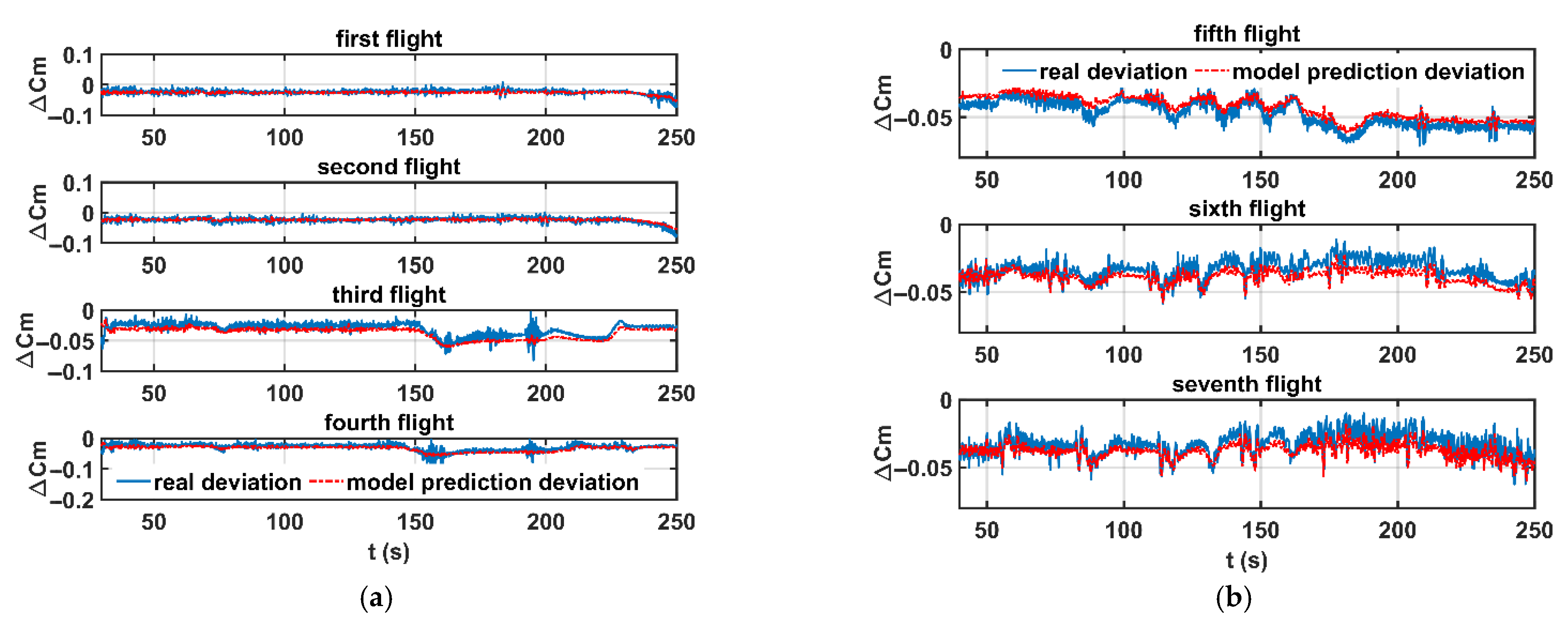
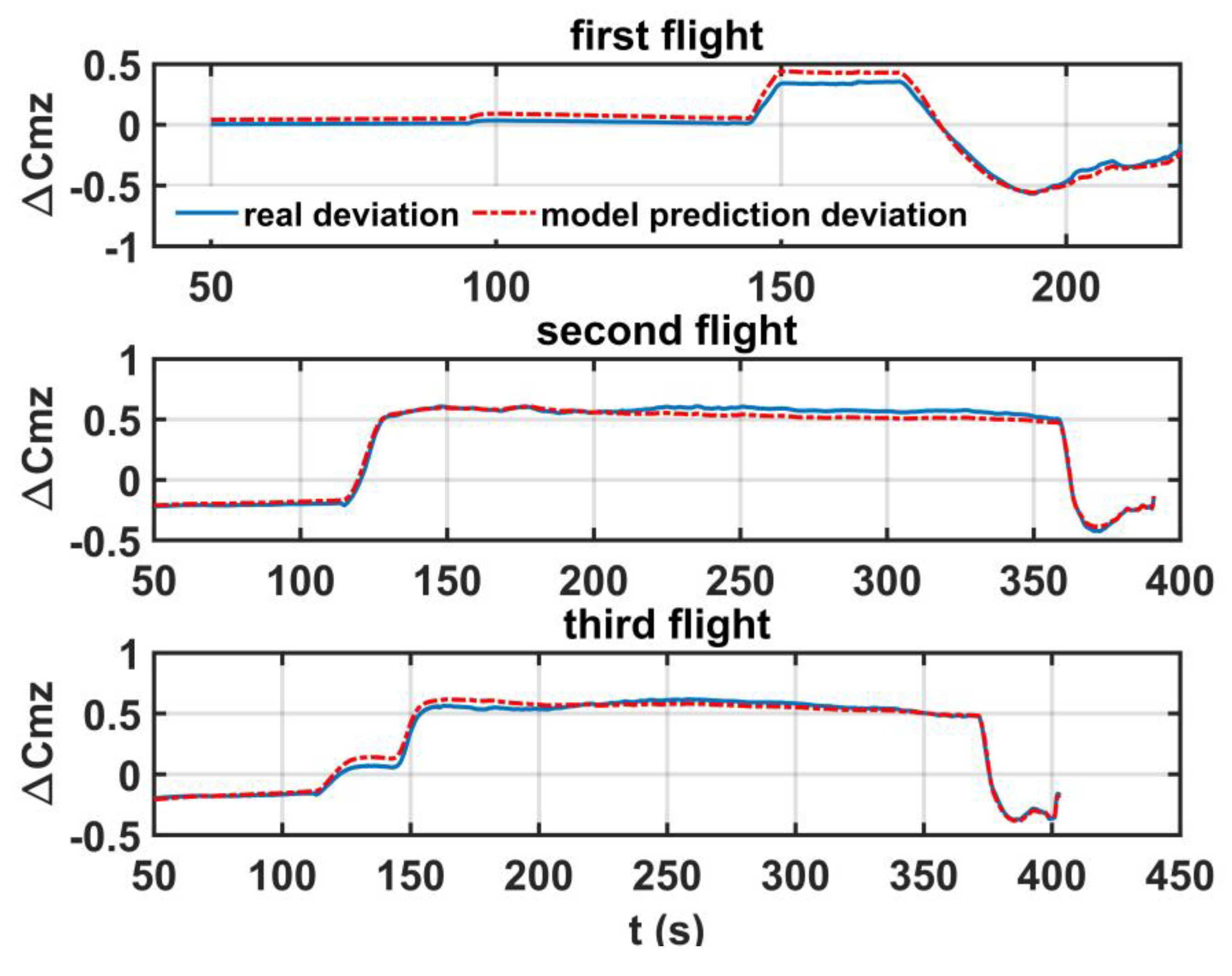
The paper discusses data analysis and modeling for studying the aerodynamic characteristics correlation between ground and flight of aerospace vehicles. The paper explores the feasibility and effectiveness of symbolic regression and the NCA method in modeling the physical correlation for ground-to-flight deviations of aerodynamic coefficients in high dimensional flight state space. Simulation examples validate the symbolic regression toolbox GPSR and NCA method. Then, the tool and the method are applied to model the aerodynamic ground-to-flight deviation of pitching moment coefficients existing in the actual flight test data of a UAV and an XRLV. The paper compares the prediction accuracy of the spatial dimensionality reduction-based symbolic regression for actual flight tests with three typical data-driven models and demonstrates its successful application in finite flight test data modeling. The mathematical model delivers a multi-fold enhancement in fitting accuracy over data-driven methods for all fight cases. For UAV flight test data, the RMSE of the mathematical model demonstrates a maximum improvement of 37% in accuracy compared to three data-driven methods. For XRLV flight test data, the prediction accuracy of the mathematical model shows an enhancement exceeding 80% relative to Gaussian kernel SVM and Gaussian process data-driven models.
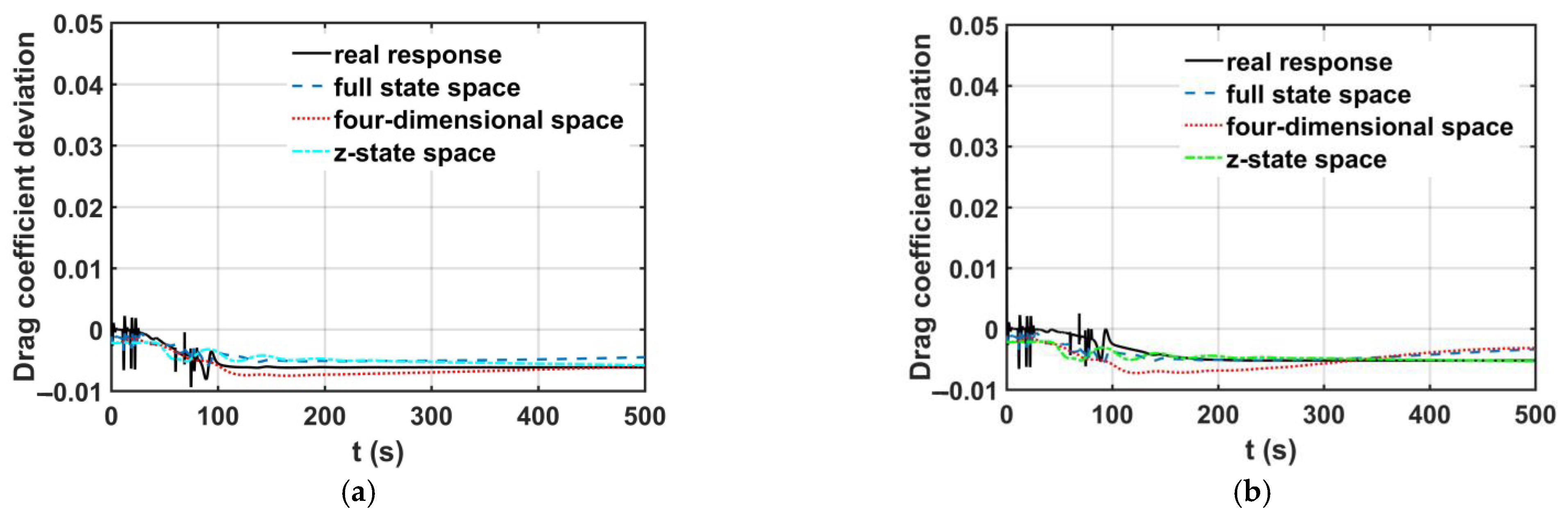
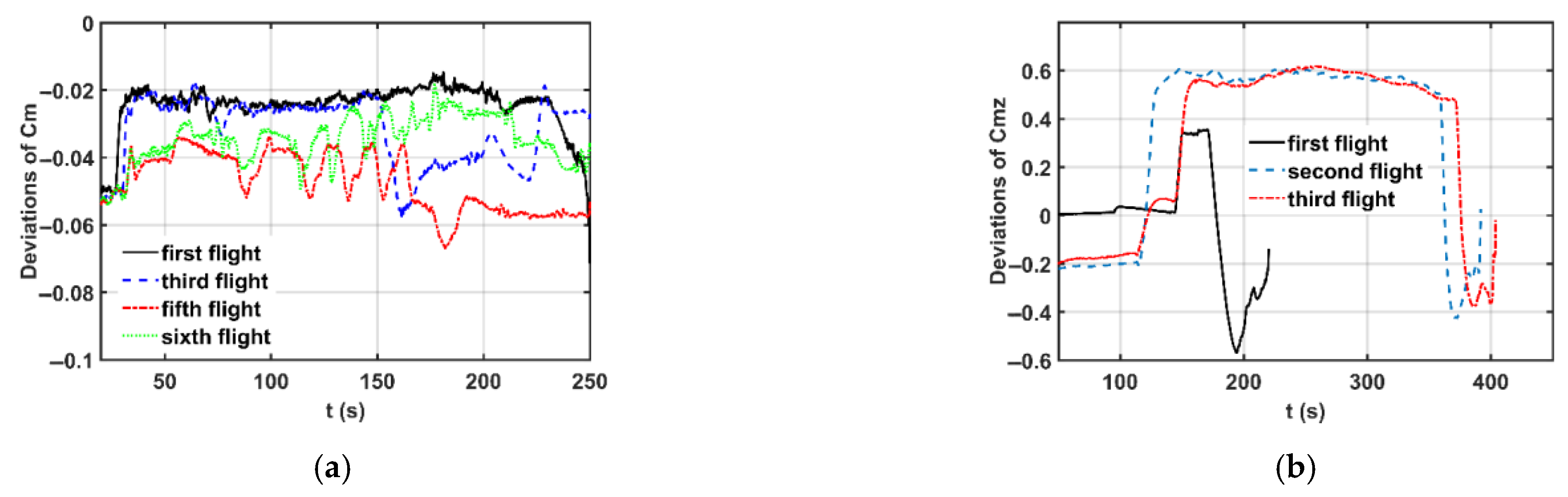
The study establishes that flow similarity plays a significant role in the vehicle’s aerodynamic characteristics correlation between ground and flight. Due to wall interference and blockage effects in ground wind tunnel tests, the aerodynamic characteristics of aerospace vehicles in the testing environment differ significantly from those under real atmospheric conditions, and simple wall interference corrections cannot fully eliminate the ground-to-flight discrepancies. Because of the internal physical connection between the multiple flight test data with the ground test data of the same type of vehicle, the modeling methodology can dig out a similar physical law in aerodynamic ground-to-flight deviations despite different flight conditions. For the pitching moment coefficient deviations between flight and ground, the methodology proposed in this paper ultimately establishes two similar mathematical models solely related to the angle of attack for two distinct vehicle configurations. Physically, the angle of attack is one of the most significant state variables affecting the aerodynamic characteristics of aerospace vehicles in pitch motion, and it also serves as a critical factor in ground wind tunnel experiments for investigating aerodynamic characteristics. The mathematical models developed through the symbolic regression methodology in this study effectively reveal the physical principles governing the influence of angle of attack on pitching moment coefficient deviations under different testing conditions.
This paper aims to combine the data feature extraction method with symbolic regression to mine aerospace vehicles’ aerodynamic ground-to-flight deviation laws. These methods show an application prospect for similar data modeling problems with limited data samples and strong physical correlations. However, when the assumptions of flow similarity and intrinsic physical connections are not satisfied, this methodology may fail. Additionally, the limitations of symbolic regression-based approaches, including computational inefficiency and reduced interpretability of results caused by inherent randomness, also exist in this methodology. The methods have only been applied to model typical flight scenarios for two types of vehicles. Subsequently, the application of the methods is anticipated to be expanded to encompass a wider variety of aerospace vehicle types and a broader spectrum of highly nonlinear flight scenarios, including large-angle-of-attack maneuvers, tailspin rotations, in-flight system failures, and hypersonic flight conditions. Modeling and analysis of data physical laws can be further developed to address these problems and extreme cases.