Numerical Investigation of Fuel Cooling in Sudden Expansion Structures of Scramjet Engines
Abstract
1. Introduction
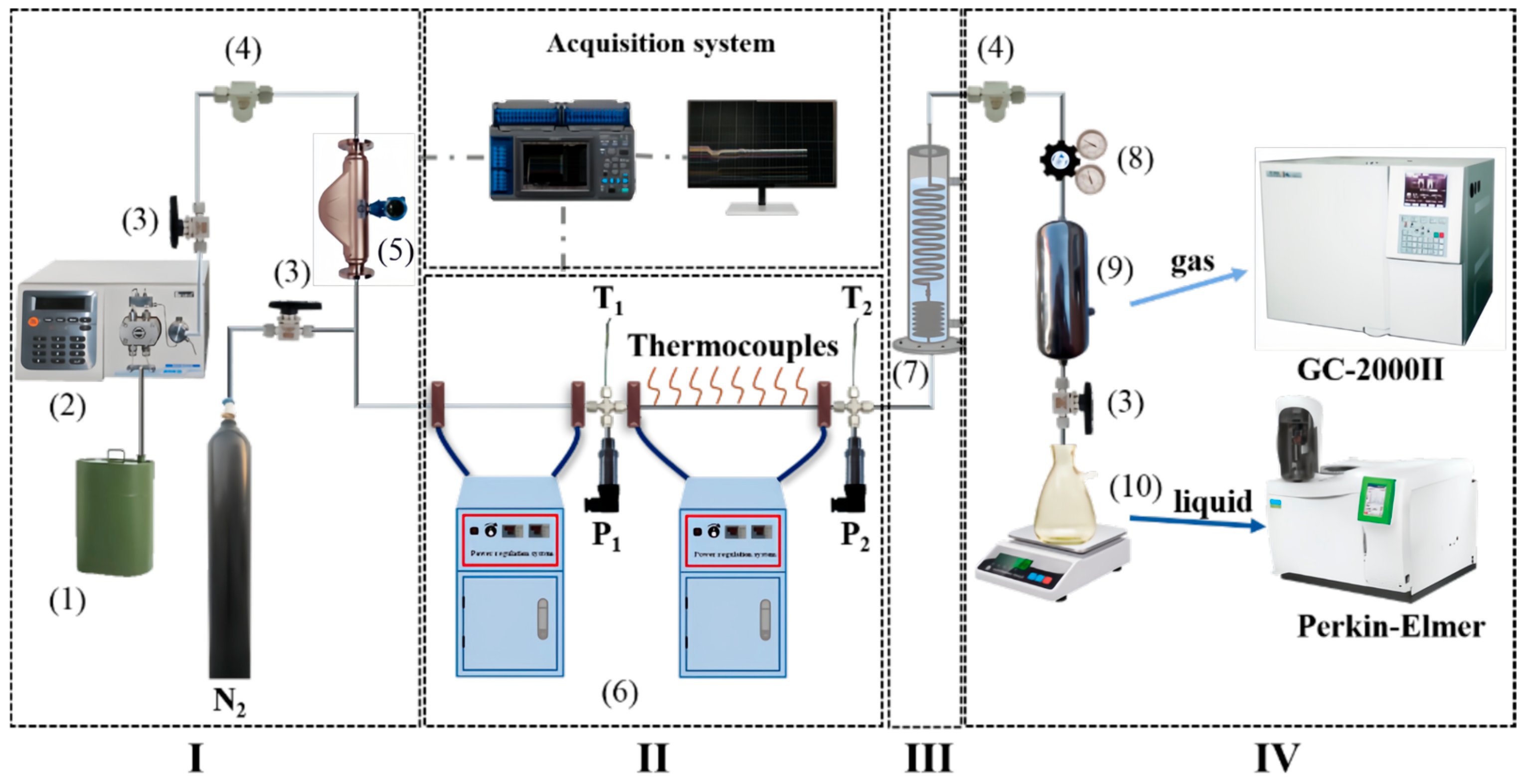
2. Model Description
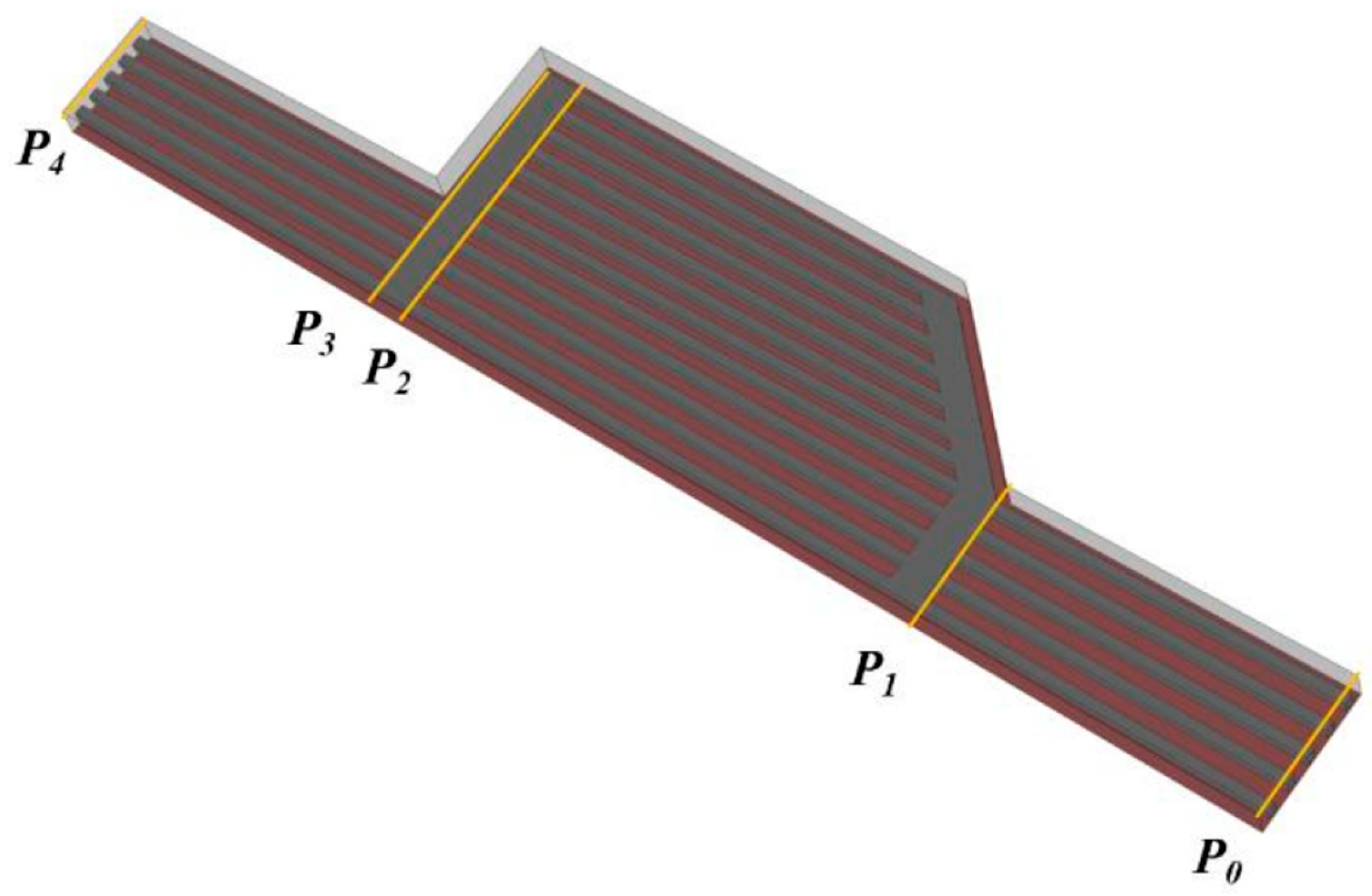
2.1. Geometry Model and Thermal Environment
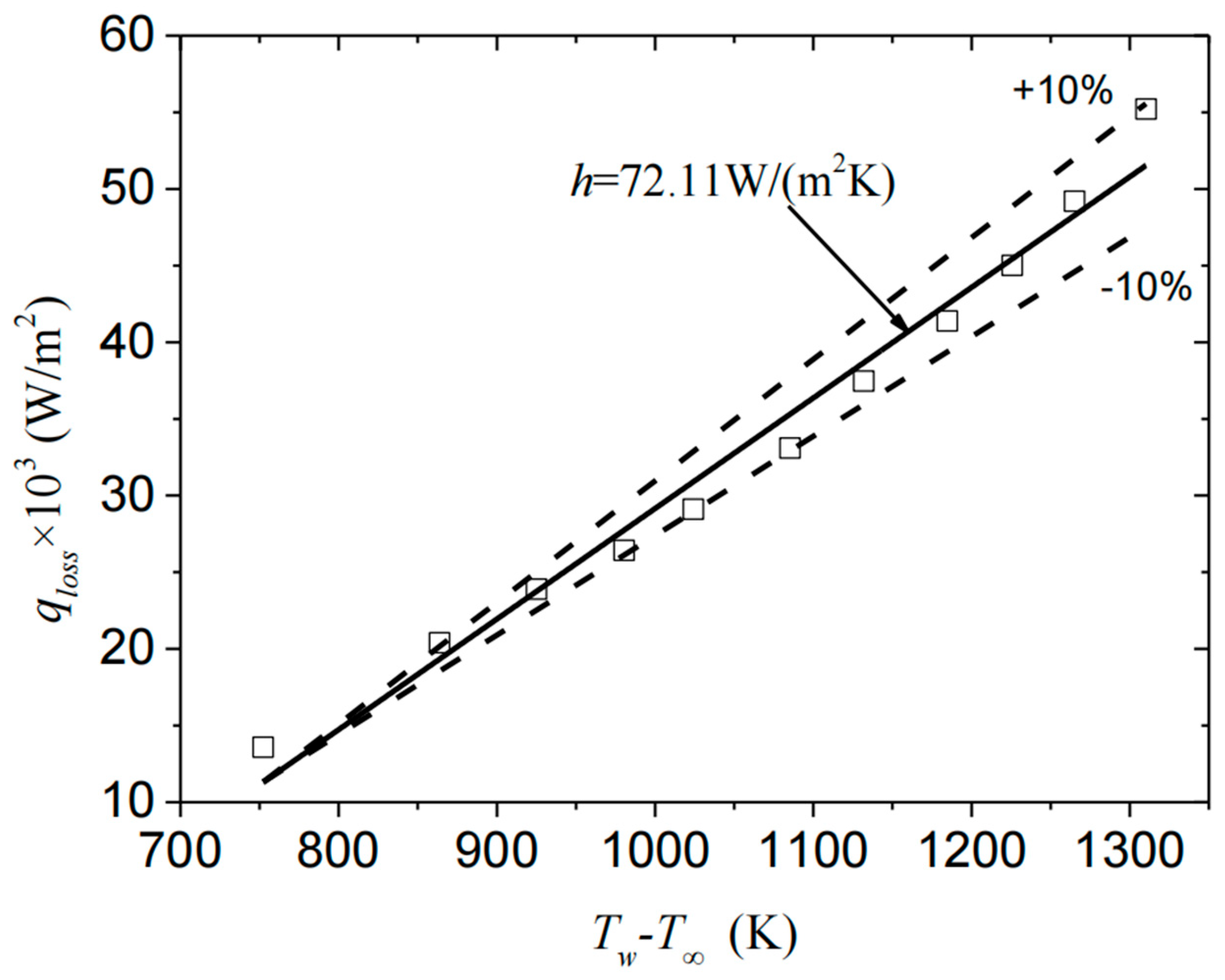
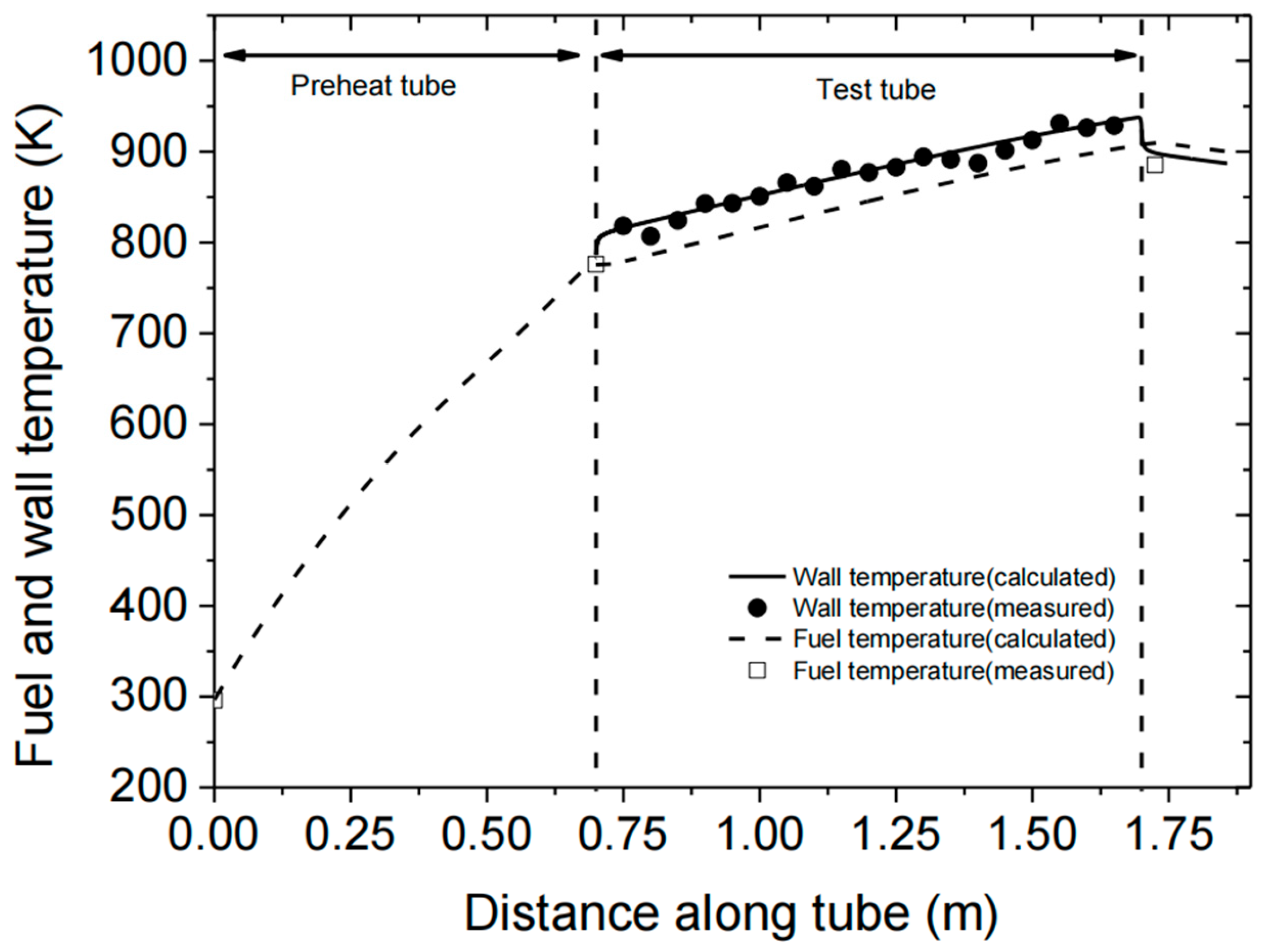
2.2. Validation of the Numerical Model
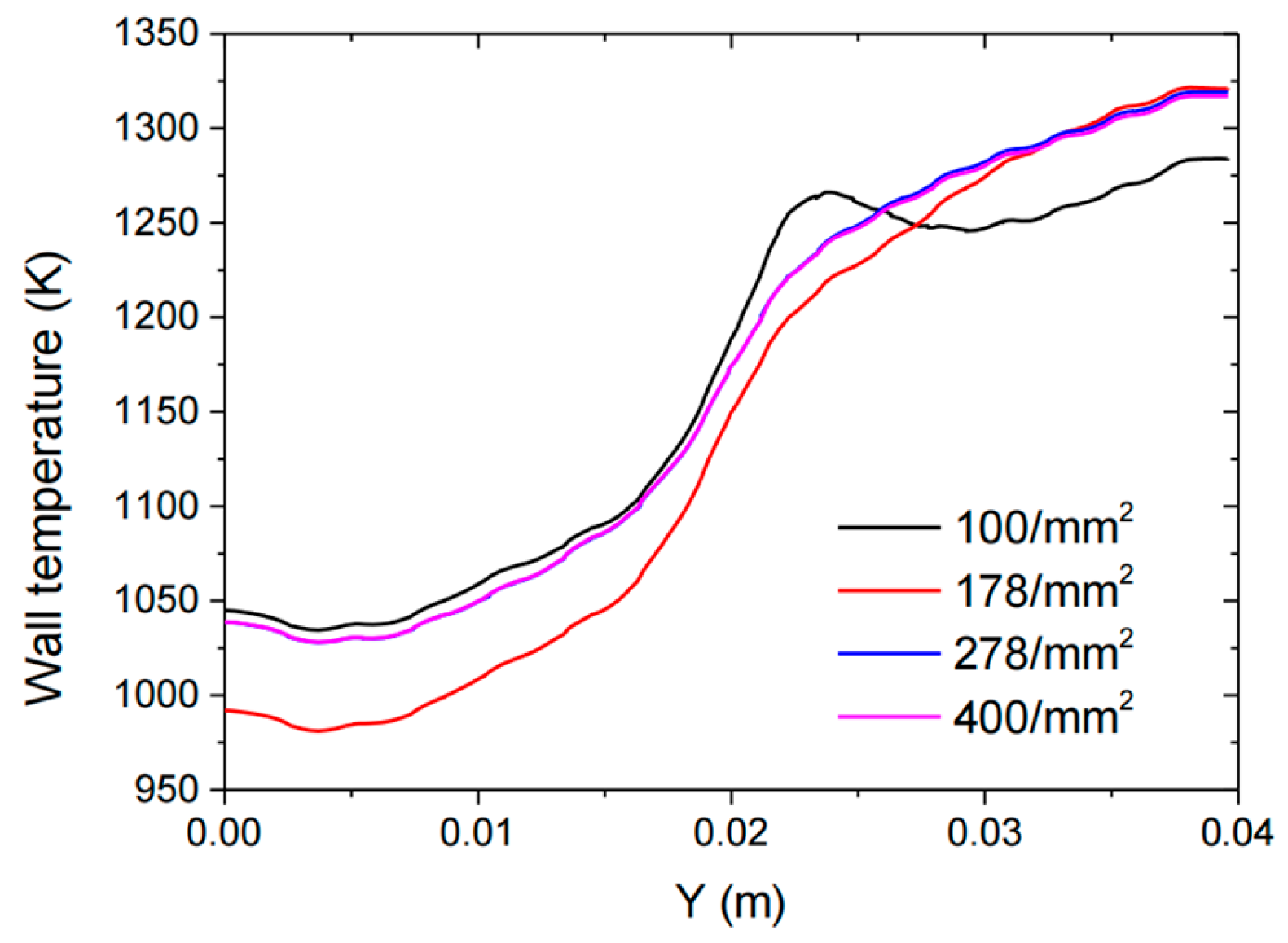
2.3. Grid Convergence
3. Results and Discussion
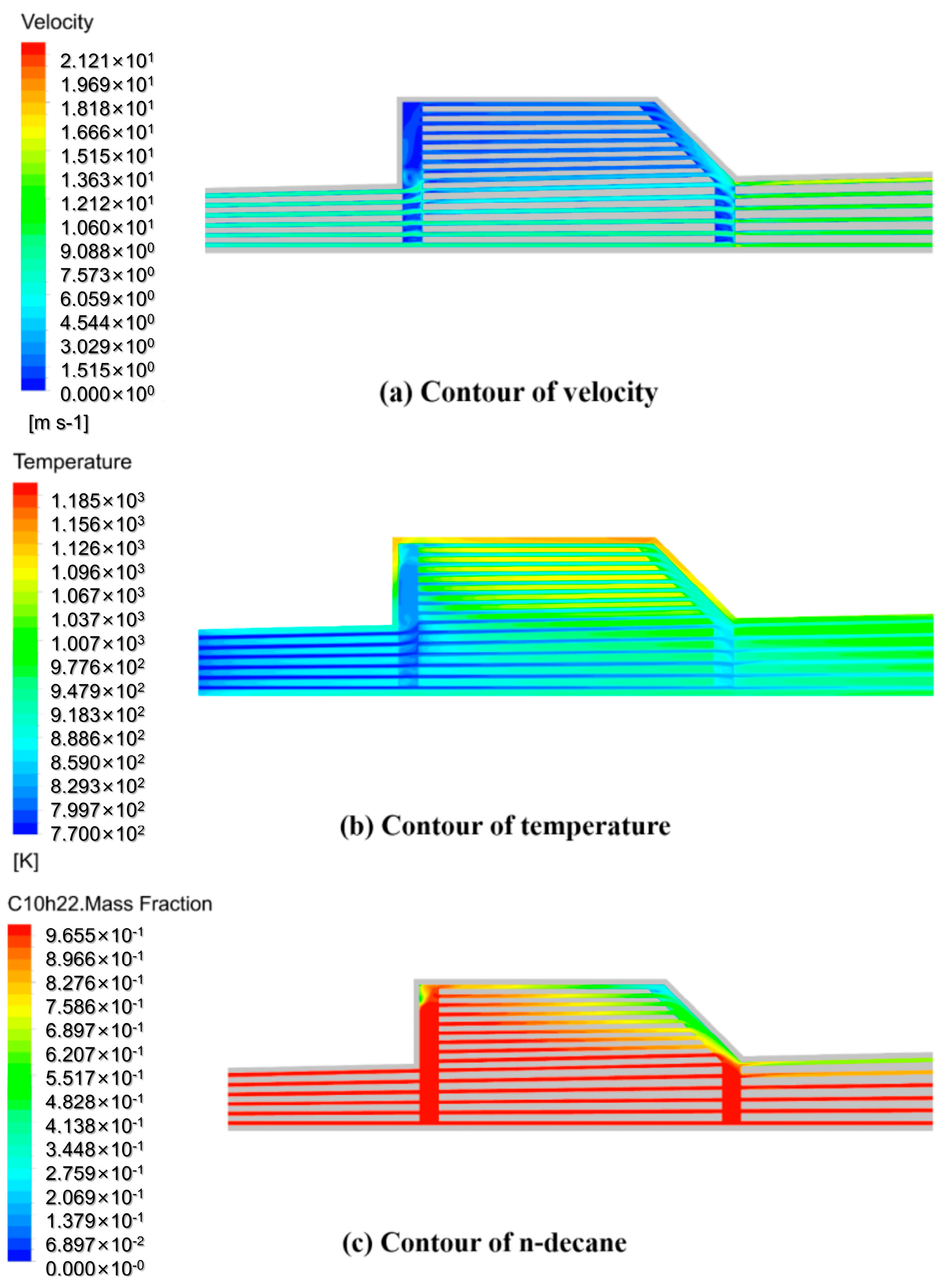
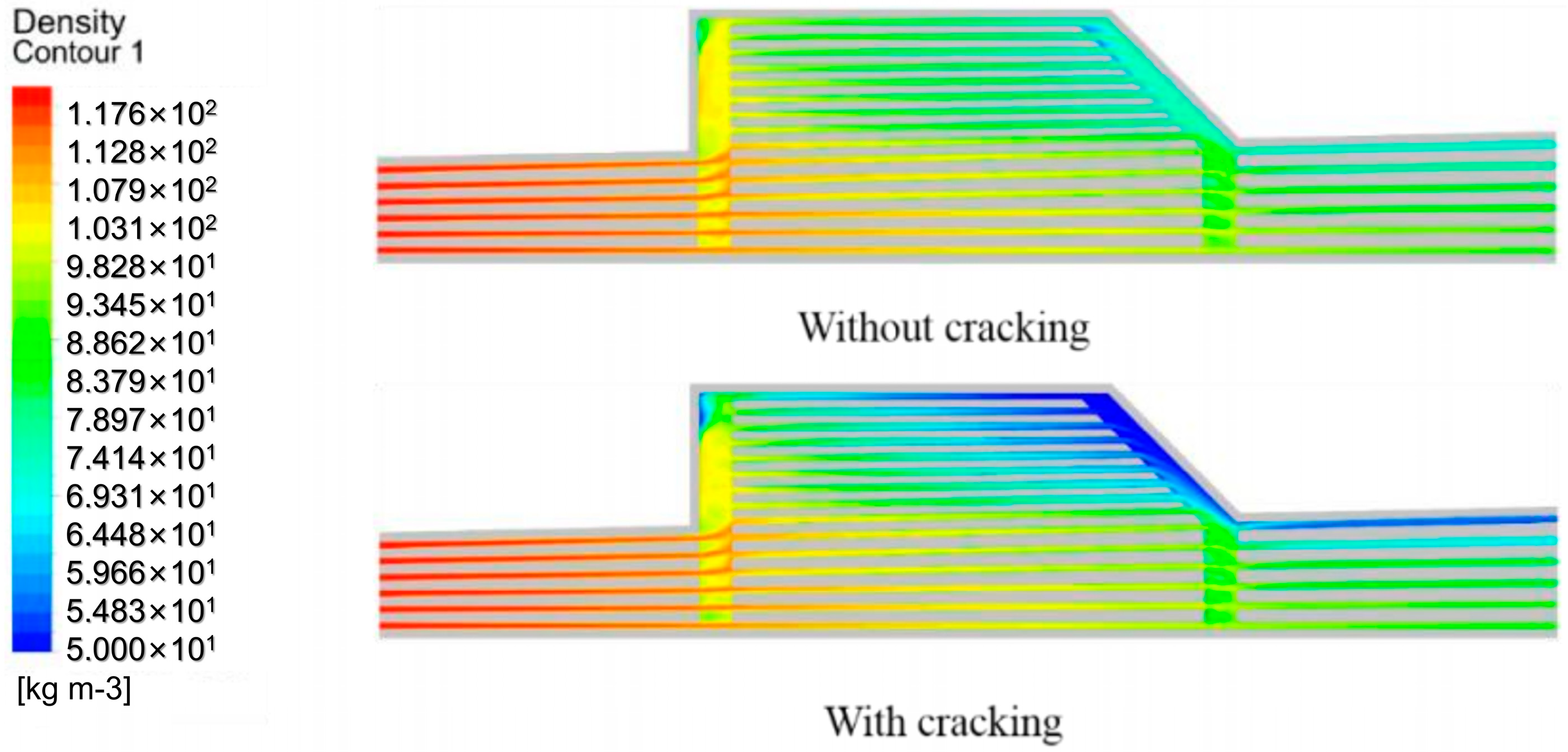
3.1. Main Characteristics of Flow Distribution in Suddenly Expanded Structure
3.2. Effect of Channel Parameters on Flow Distribution
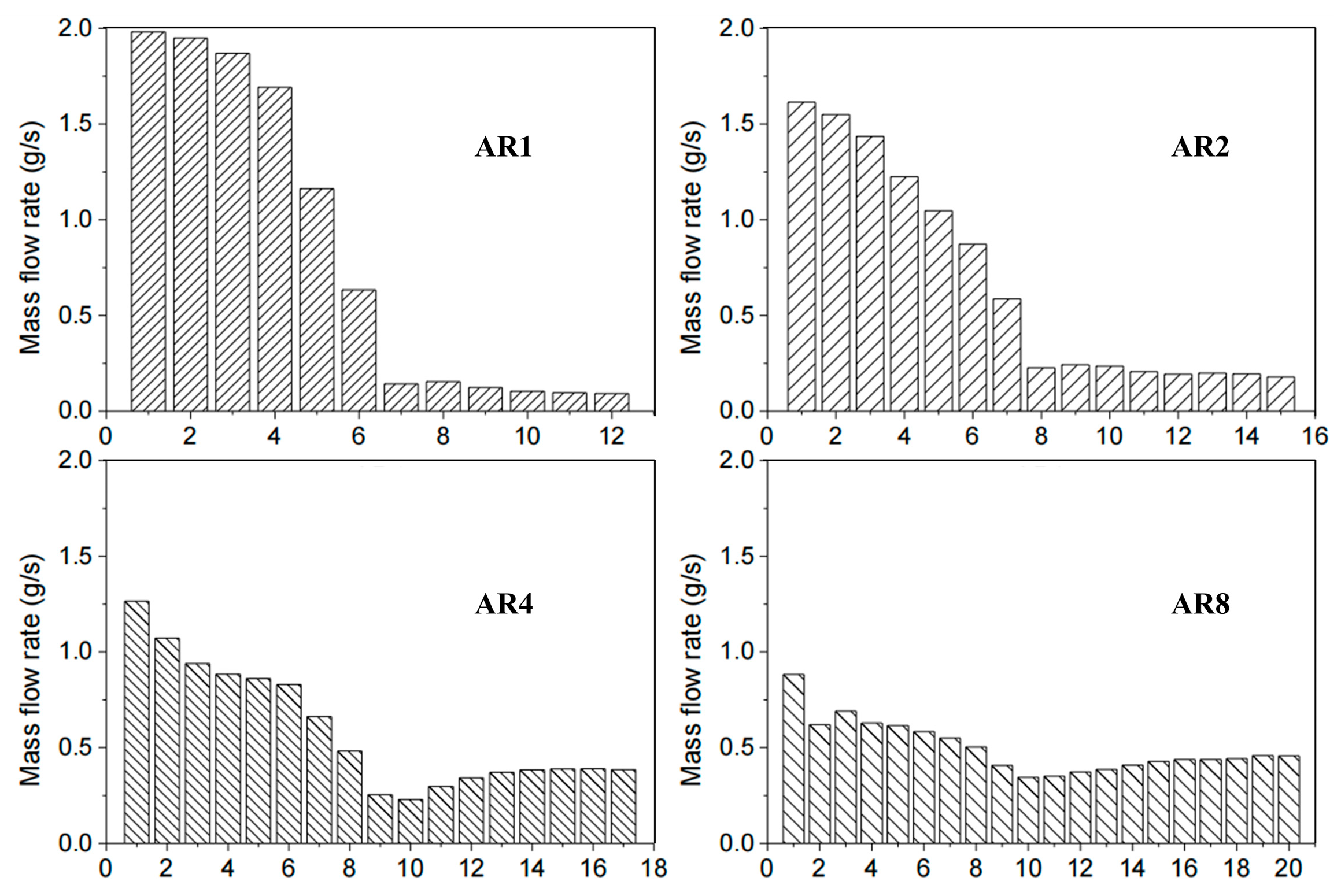
| ϕm (Without Cracking) | ϕm (With Cracking) | |
|---|---|---|
| AR1 | 0.843 | 0.954 |
| AR2 | 0.783 | 0.817 |
| AR4 | 0.409 | 0.428 |
| AR8 | 0.181 | 0.181 |
3.3. Effect of Channel Parameters on Thermal Cracking
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | channel cross-sectional area, m2 |
| AR | aspect ratio |
| C | channel perimeter, m |
| cp | specific heat, J/(kg·K) |
| Dh | hydraulic diameter, m |
| Ea | activation energy, J/mol |
| h | enthalpy, J/mol |
| hG | heat transfer coefficient, W/(m2·K) |
| H | plate height, m |
| la | channel width, m |
| lb | channel height, m |
| k | pre-exponential factor, s−1 |
| m | mass flow rate, g/s |
| Ma | Mach number |
| nc | channel number |
| q | heat flux W/m2 |
| Q | heat absorption, W |
| Re | Reynolds number |
| St | Stanton number |
| Sw | heated wall thickness |
| tw | rib thickness, m |
| u | velocity of fuel, m/s |
| V | velocity of air, m/s |
| volume of fuel, (m3) | |
| W | distribution chamber width, m |
| Y | mass fraction |
| ρ | density, kg/m3 |
| λ | thermal conductivity, W/(m·K) |
| μ | dynamic viscosity, Pa·s |
| ω | acentric factor |
| ΔP | pressure drop, Pa |
| Subscripts | |
| aw | Adiabatic |
| comb | combustion chamber |
| c | critical |
| eff | effective |
| i | species |
| channel number index | |
| ideal | ideal gas |
| s | solid |
| single | |
| w | wall |
References
- Curran, E. Scramjet Engines: The First Forty Years. J. Propuls. Power 2001, 17, 1138–1148. [Google Scholar] [CrossRef]
- Valdevit, L.; Vermaak, N.; Hsu, K.; Zok, F.; Evans, A. Design of Actively Cooled Panels for Scramjets. In Proceedings of the 14th AIAA/AHI Space Planes and Hypersonic Systems and Technologies Conference, AIAA Meeting Paper 2006-8069, Canberra, Australia, 6–9 November 2006. [Google Scholar]
- Jiang, J.; Zhang, R.-L.; Le, J.-L. Calculational tool of thermal structure design for regeneratively cooled scramjet. Shiyan Liuti Lixue/J. Exp. Fluid Mech. 2006, 20, 1–7. [Google Scholar]
- Zhang, D.; Yang, S.; Zhang, S.; Qin, J.; Bao, W. Thermodynamic analysis on optimum performance of scramjet engine at high Mach numbers. Energy 2015, 90, 1046–1054. [Google Scholar] [CrossRef]
- Yang, Q.; Bao, W.; Chetehouna, K.; Zhang, S.; Gascoin, N. Thermal behavior of an isolator with mode transition inducing back-pressure of a dual-mode scramjet. Chin. J. Aeronaut. 2017, 30, 595–601. [Google Scholar] [CrossRef]
- Yang, Q.; Chetehouna, K.; Gascoin, N.; Bao, W. Experimental study on Combustion modes and thrust performance of a staged-combustor of the scramjet with dual-strut. Acta Astronaut. 2016, 122, 28–34. [Google Scholar] [CrossRef]
- Feng, Y.; Liu, S.; Qin, J.; Cao, Y.; Jiang, Y.; Zhang, S. Numerical study on the influence of turbulence on the pyrolysis of hydrocarbon fuel in mini-channel. Int. J. Heat Mass Transf. 2018, 119, 768–776. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Meng, H. Numerical study of conjugate heat transfer of cryogenic methane in rectangular engine cooling channels at supercritical pressures. Appl. Therm. Eng. 2013, 54, 237–246. [Google Scholar] [CrossRef]
- Taddeo, L.; Gascoin, N.; Fedioun, I.; Chetehouna, K.; Lamoot, L.; Fau, G. Dimensioning of automated regenerative cooling: Setting of high-end experiment. Aerosp. Sci. Technol. 2015, 43, 350–359. [Google Scholar] [CrossRef]
- Fry, R. A Century of Ramjet Propulsion Technology Evolution. J. Propuls. Power 2004, 20, 27–58. [Google Scholar] [CrossRef]
- Feng, Y.; Cao, Y.; Qin, J.; Hemeda, A.; Ma, Y. The influence of coking on heat transfer in turbulent reacting flow of supercritical hydrocarbon fuels. Int. J. Heat Mass Transf. 2019, 144, 118623. [Google Scholar] [CrossRef]
- Zhang, C.; Qin, J.; Yang, Q.; Zhang, S.; Bao, W. Design and heat transfer characteristics analysis of combined active and passive thermal protection system for hydrogen fueled scramjet. Int. J. Hydrogen Energy 2015, 40, 675–682. [Google Scholar] [CrossRef]
- Tong, J.; Sparrow, E.; Abraham, J. Geometric strategies for attainment of identical outflows through all of the exit ports of a distribution manifold in a manifold system. Appl. Therm. Eng. 2009, 29, 3552–3560. [Google Scholar] [CrossRef]
- Tonomura, O.; Tanaka, S.; Noda, M.; Kano, M.; Hasebe, S.; Hashimoto, I. CFD Based Optimal Design of Manifold in Plate-Fin Microdevices. Chem. Eng. J 2004, 101, 397–402. [Google Scholar] [CrossRef]
- Wang, C.-C.; Yang, K.S.; Tsai, J.-S.; Chen, I. Characteristics of flow distribution in compact parallel flow heat exchangers, part II: Modified inlet header. Appl. Therm. Eng. 2011, 31, 3235–3242. [Google Scholar] [CrossRef]
- Kumaran, R.; Kumaraguruparan, G.; Sornakumar, T. Experimental and numerical studies of header design and inlet/outlet configurations on flow mal-distribution in parallel micro-channels. Appl. Therm. Eng. 2013, 58, 205–216. [Google Scholar] [CrossRef]
- Luo, L.; Fan, Z.; Gall, H.; Zhou, X.; Yuan, W. Experimental study of constructal distributor for flow equidistribution in mini crossflow heat exchanger (MCHE). Chem. Eng. Process. Process Intensif. 2008, 47, 229–236. [Google Scholar] [CrossRef]
- Yue, J.; BOICHOT, R.; Luo, L.; Gonthier, Y.; Chen, G.; Yuan, Q. Flow Distribution and Mass Transfer in a Parallel Microchannel Contactor Integrated with Constructal Distributors. AIChE J. 2009, 56, 298–317. [Google Scholar] [CrossRef]
- Wen, J.; Li, Y.; Wang, S.; Zhou, A. Experimental investigation of header configuration improvement in plate–fin heat exchanger. Appl. Therm. Eng. 2007, 27, 1761–1770. [Google Scholar] [CrossRef]
- Luo, L.; Wei, M.; Fan, Y. Design and optimization of baffled fluid distributor for realizing target flow distribution in a tubular solar receiver. Energy 2017, 136, 126–134. [Google Scholar]
- Wei, M.; Boutin, G.; Fan, Y.; Luo, L. Numerical and experimental investigation on the realization of target flow distribution among parallel mini-channels. Chem. Eng. Res. Des. 2016, 113, 74–84. [Google Scholar] [CrossRef]
- Wang, J. Pressure drop and flow distribution in parallel-channel configurations of fuel cells: U-type arrangement. Int. J. Hydrogen Energy 2008, 33, 6339–6350. [Google Scholar] [CrossRef]
- Bi, W.; Li, J.; Lin, Z. Flow uniformity optimization for large size planar solid oxide fuel cells with U-type parallel channel designs. J. Power Sources 2010, 195, 3207–3214. [Google Scholar] [CrossRef]
- Afshari, E.; Ziaei-Rad, M.; Shariati, Z. A study on using metal foam as coolant fluid distributor in the polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2015, 41, 1902–1912. [Google Scholar] [CrossRef]
- Hossain, M.S.; Shabani, B.; Cheung, S. Enhanced gas flow uniformity across parallel channel cathode flow field of Proton Exchange Membrane fuel cells. Int. J. Hydrogen Energy 2016, 42, 5272–5283. [Google Scholar] [CrossRef]
- Xu, K.; Meng, H. Numerical study of fluid flows and heat transfer of aviation kerosene with consideration of fuel pyrolysis and surface coking at supercritical pressures. Int. J. Heat Mass Transf. 2016, 95, 806–814. [Google Scholar] [CrossRef]
- Qin, J.; Jiang, Y.; Feng, Y.; Li, X.; Haowei, L.; Xu, Y.; Bao, W.; Zhang, S.; Han, J. Flow rate distribution of cracked hydrocarbon fuel in parallel pipes. Fuel 2015, 161, 105–112. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, S.; Feng, Y.; Cao, J.; Qin, J.; Bao, W. A control method for flow rate distribution of cracked hydrocarbon fuel in parallel channels. Appl. Therm. Eng. 2016, 105, 153–536. [Google Scholar] [CrossRef]
- Chen, Y.; Lei, Z.; Zhang, T.; Zhu, Q.; Bao, Z.; Zhang, Q.; Li, X.-Y. Flow Distribution of Hydrocarbon Fuel in Parallel Mini-Channels Heat Exchanger. AIChE J. 2018, 64, 2781–2791. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, B.; Lei, Z.; Zhang, Q.; Zhu, Q.; Bao, Z.; Li, X.-Y. A control method for flow distribution in fuel-cooled plate based on choked flow effect. Appl. Therm. Eng. 2018, 142, 127–137. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Bao, Z.; Zhang, Q.; Li, X.-Y. Numerical investigation of flow distribution and heat transfer of hydrocarbon fuel in regenerative cooling panel. Appl. Therm. Eng. 2015, 98, 628–635. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Y.; Qin, J.; Zhang, S.; Chetehouna, K.; Gascoin, N.; Bao, W. The flow rate distribution of hydrocarbon fuel in parallel channels with different cross section shapes. Appl. Therm. Eng. 2018, 137, 173–183. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, J.; Chetehouna, K.; Gascoin, N.; Bao, W. Parametric study on the hydrocarbon fuel flow rate distribution and cooling effect in non-uniformly heated parallel cooling channels. Int. J. Heat Mass Transf. 2018, 126, 267–276. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, J.; Chetehouna, K.; Gascoin, N.; Bao, W. Effect of geometry parameters on the hydrocarbon fuel flow rate distribution in pyrolysis zone of SCRamjet cooling channels. Int. J. Heat Mass Transf. 2019, 141, 1114–1130. [Google Scholar] [CrossRef]
- Jiang, Y.; Qin, J.; Xu, Y.; Yu, W.; Zhang, S.; Chetehouna, K.; Gascoin, N.; Bao, W. The influences of variable sectional area design on improving the hydrocarbon fuel flow distribution in parallel channels under supercritical pressure. Fuel 2018, 233, 442–453. [Google Scholar] [CrossRef]
- Niu, J.; Piao, Y. Numerical Simulation of Liquid Kerosene Combustion in a Dual-Mode Scramjet Combustor Using Flamelet/Progress Variable Approach. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar]
- Yan, Z.; Lin, Y.; Wei, L.; Jianchen, W.; Yongsheng, Z. Numerical Simulation of a Dual-Mode Scramjet Combustor Using Flamelet Scheme. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- Swithenbank, J. Hypersonic Air-Breathing Propulsion; AIAA Education Series; AIAA: Washington, DC, USA, 1994. [Google Scholar]
- Eckert, E.R.G. Engineering Relations for Heat Transfer and Friction in High-Velocity Laminar and Turbulent Boundary-Layer Flow Over Surfaces with Constant Pressure and Temperature. Trans. Am. Soc. Mech. Eng. 1956, 78, 1273–1283. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Liang, C.; Zhang, Q.; Li, X. Heat transfer analysis of n-decane with variable heat flux distributions in a mini-channel. Appl. Therm. Eng. 2018, 144, 695–701. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Xie, G.; Sunden, B. Effect of thermal pyrolysis on heat transfer and upward flow characteristics in a rectangular channel using endothermic hydrocarbon fuel. Chem. Eng. Sci. 2021, 244, 116806. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, R.; Wang, J.; Li, X. Numerical Investigations on the Molecular Reaction Model for Thermal Cracking of n-Decane at Supercritical Pressures. ACS Omega 2022, 7, 22351–22362. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- TChung, H.; Lee, L.L.; Starting, K.E. Applications of Kinetic Gas Theories and Multiparameter Correlation for Prediction of Dilute Gas Viscosity and Thermal Conductivity. Ind. Eng. Chem. Fundam. 1984, 23, 8–13. [Google Scholar] [CrossRef]
- Menter, F. Influence of Freestream Values on k-omega Turbulence Model Predictions. AIAA J. 1992, 30, 1657–1659. [Google Scholar] [CrossRef]
- Sparrow, E.; Tong, J.; Abraham, J. Fluid Flow in a System with Separate Laminar and Turbulent Zones. Numer. Heat Transf. Part A Appl. 2008, 53, 341–353. [Google Scholar] [CrossRef]
- Ruan, B.; Meng, H. Supercritical Heat Transfer of Cryogenic-Propellant Methane in Rectangular Engine Cooling Channels. J. Thermophys. Heat Transf. 2012, 26, 313–321. [Google Scholar] [CrossRef]
- Qin, J.; Zhang, S.; Bao, W.; Zhou, W.; Yu, D. Thermal management method of fuel in advanced aeroengines. Energy 2013, 49, 459–468. [Google Scholar] [CrossRef]
- Zhang, S.; Qin, J.; Bao, W.; Feng, Y.; Xie, K. Thermal management of fuel in advanced aeroengine in view of chemical recuperation. Energy 2014, 77, 201–211. [Google Scholar] [CrossRef]
- Feng, Y.; Qin, J.; Zhang, S.; Bao, W.; Cao, Y.; Huang, H. Modeling and analysis of heat and mass transfers of supercritical hydrocarbon fuel with pyrolysis in mini-channel. Int. J. Heat Mass Transf. 2015, 91, 520–531. [Google Scholar] [CrossRef]



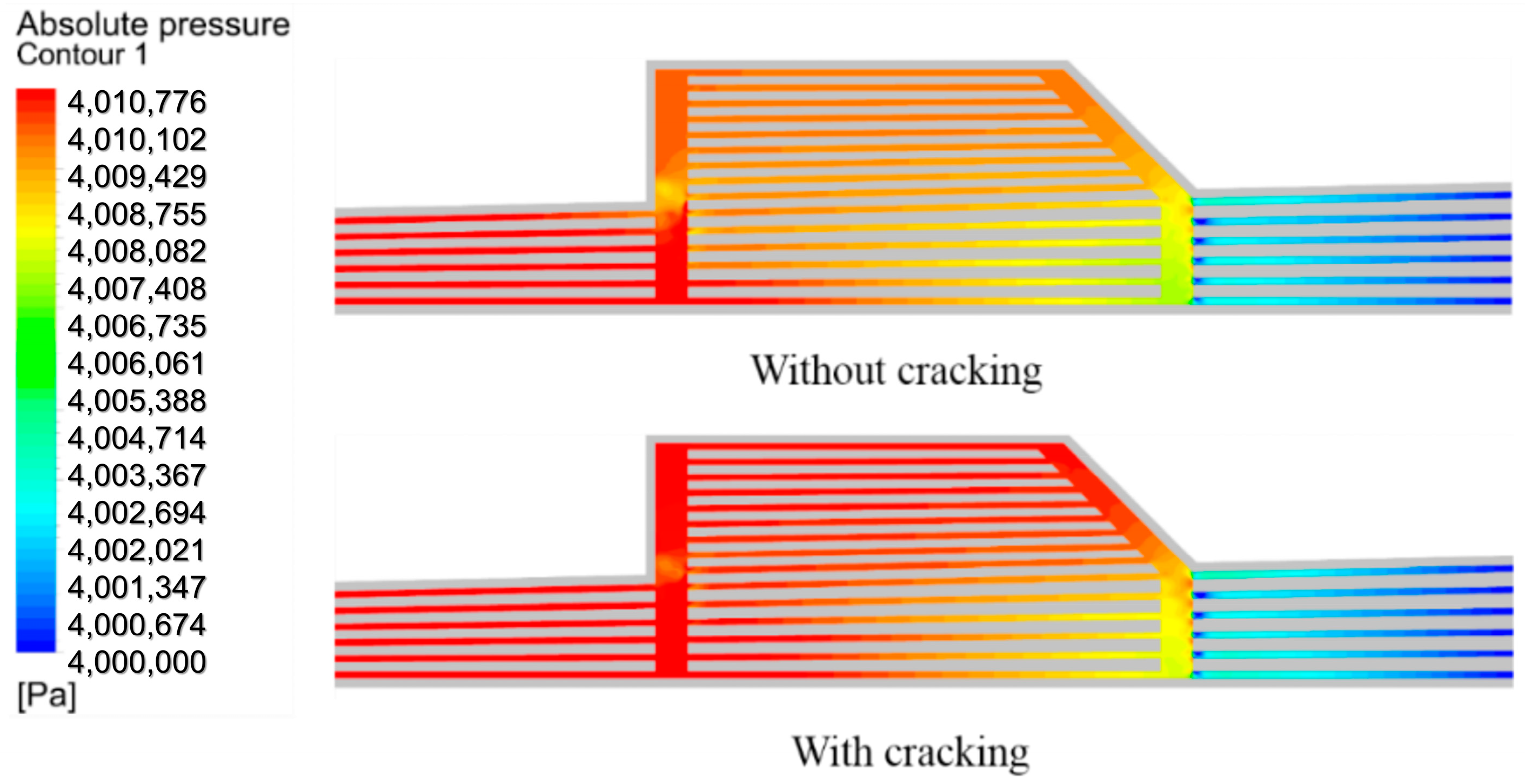
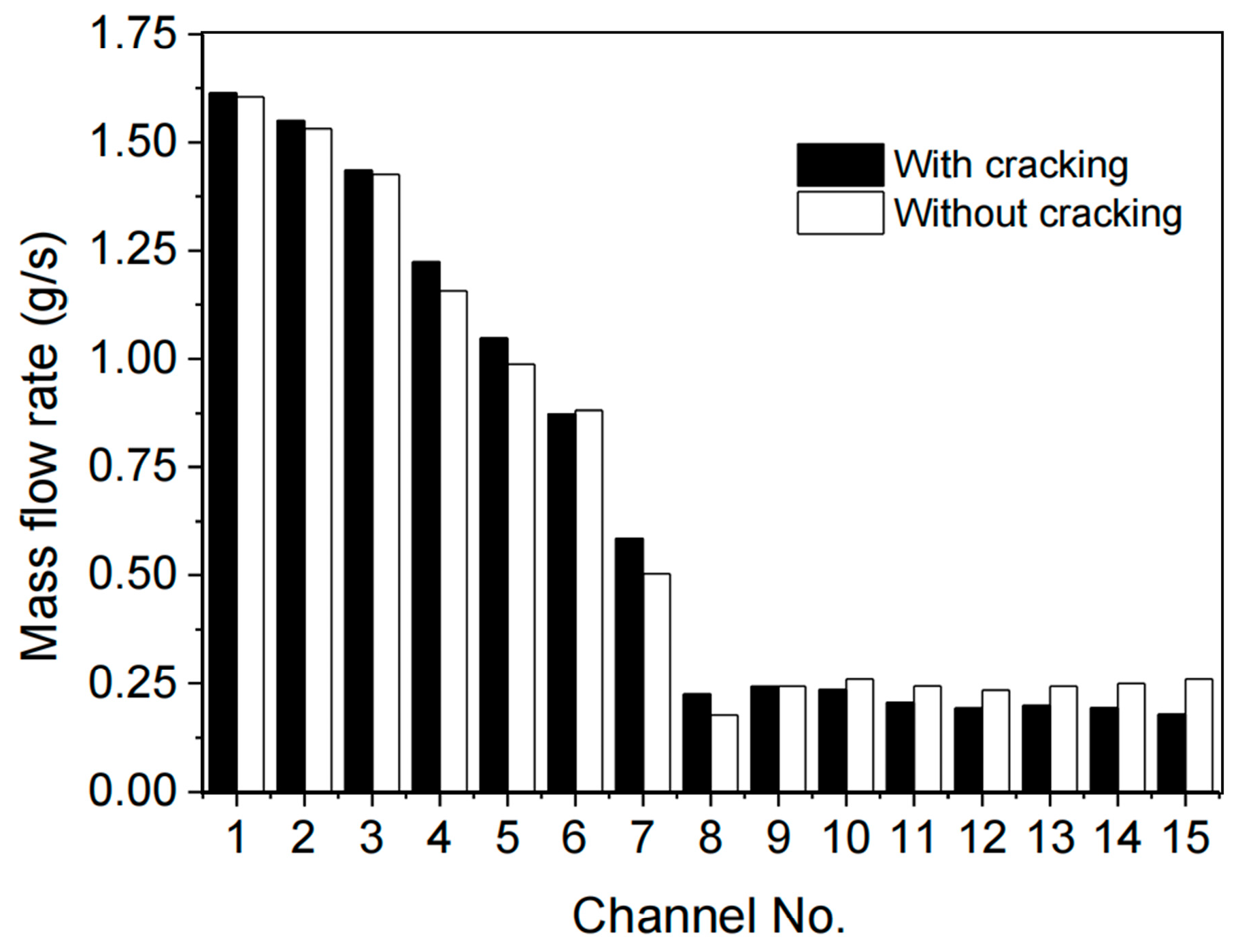
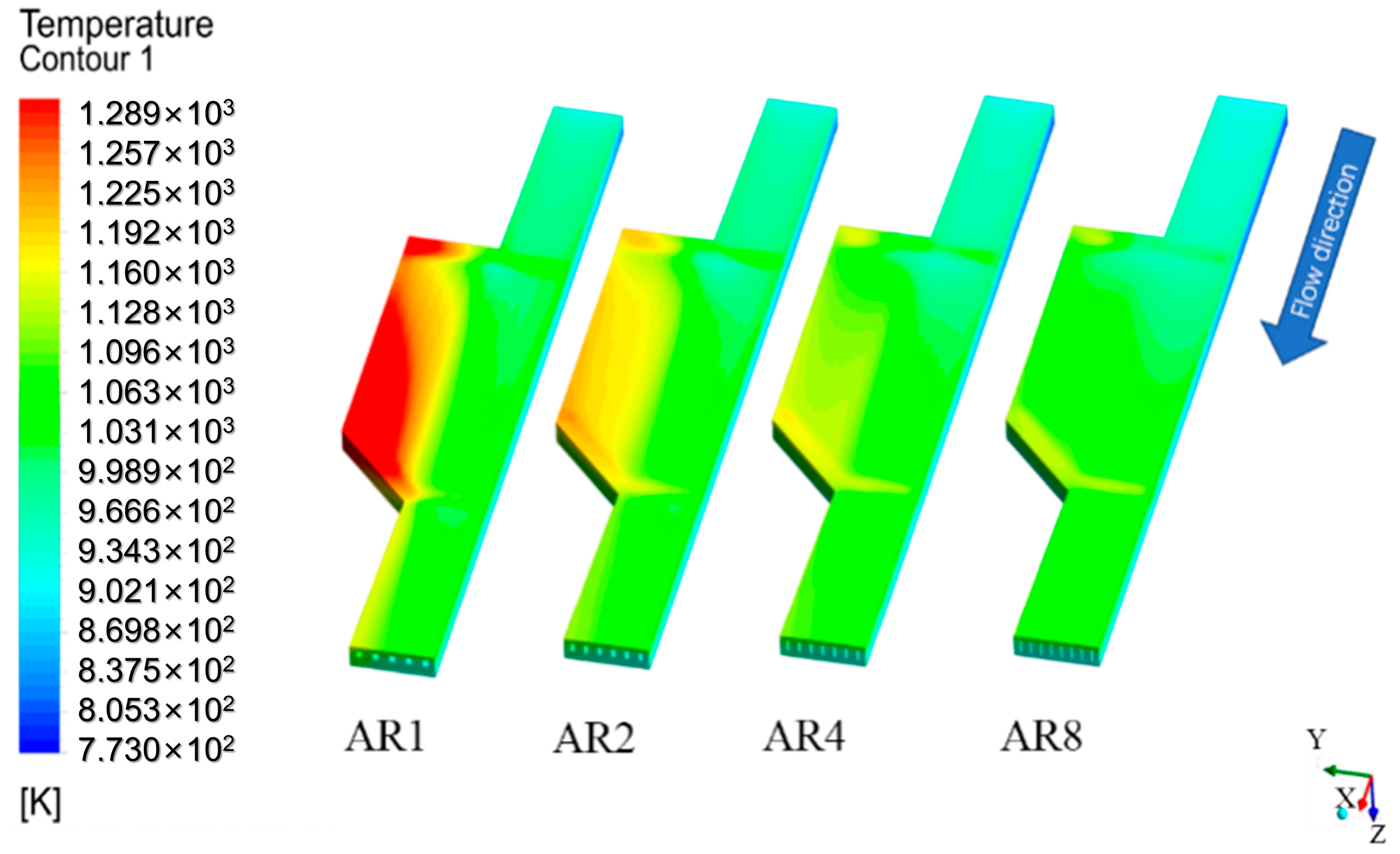

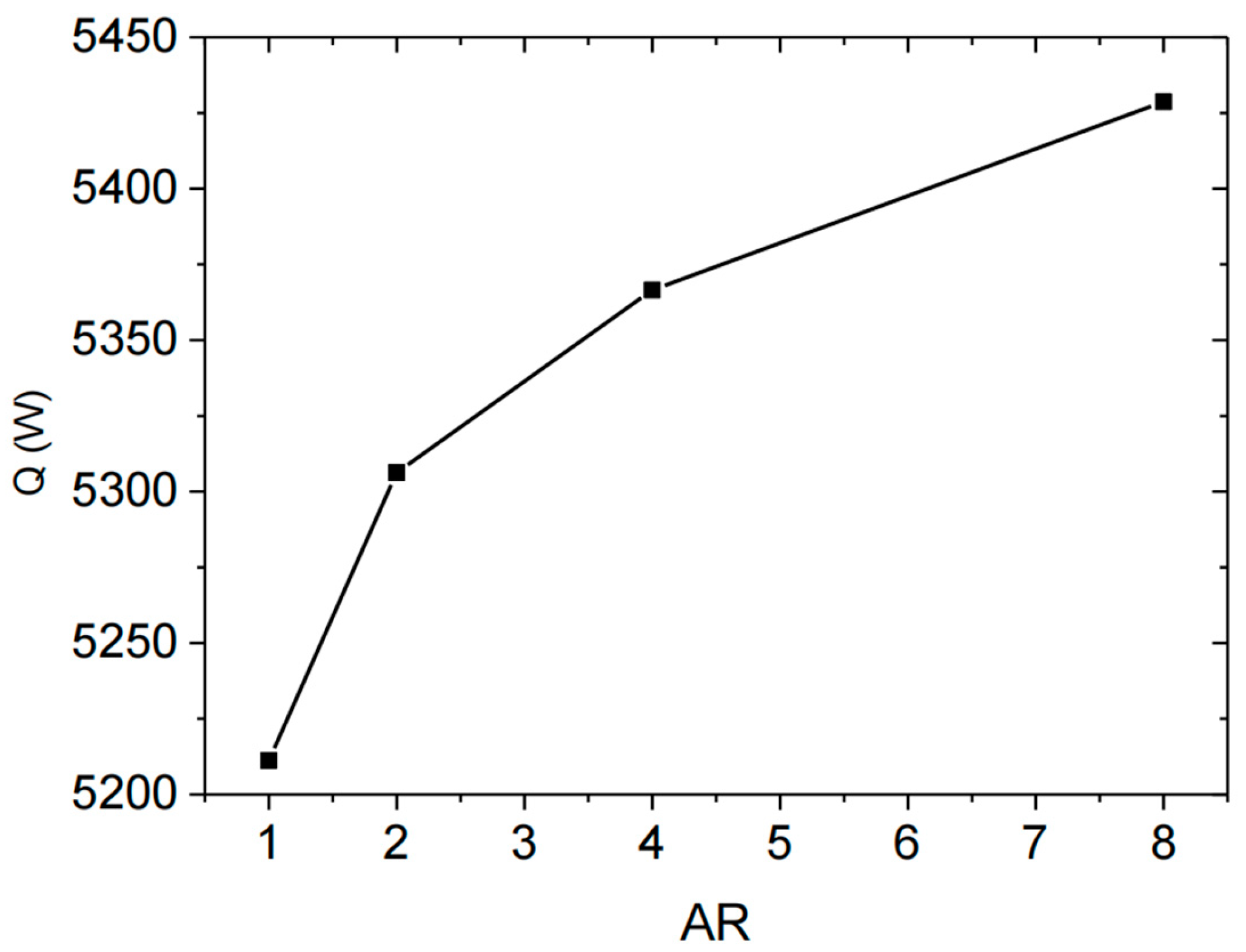
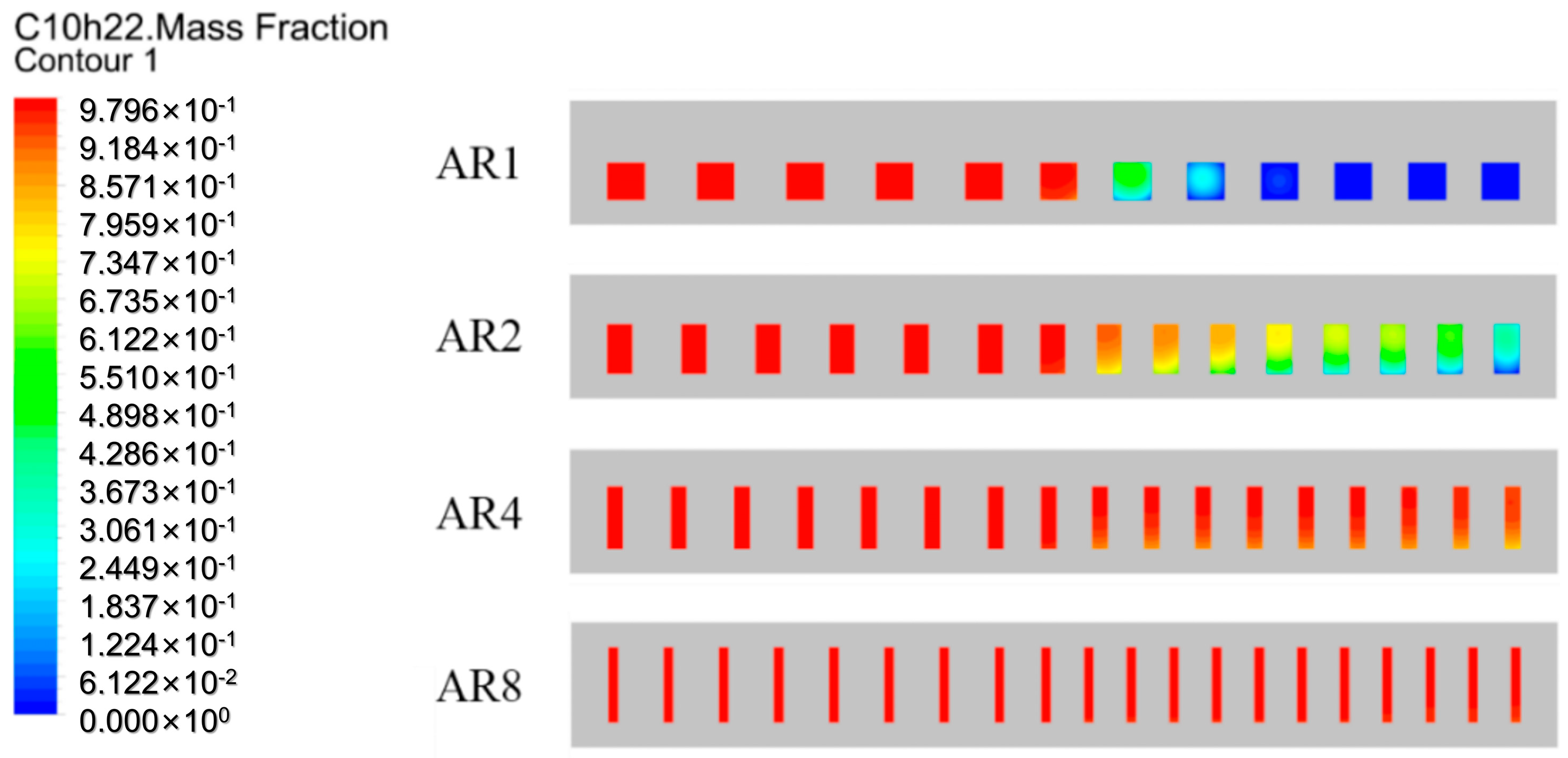
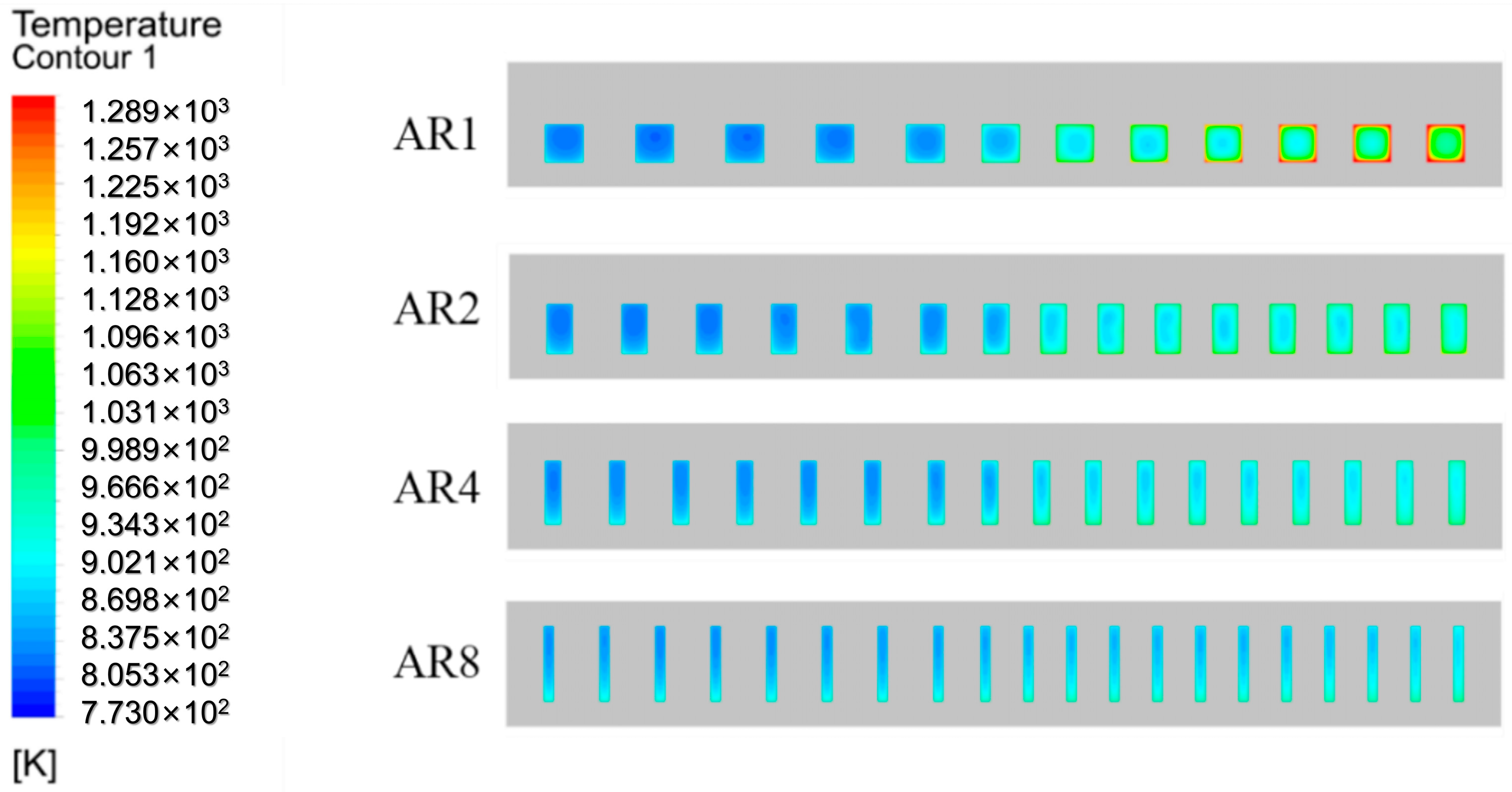
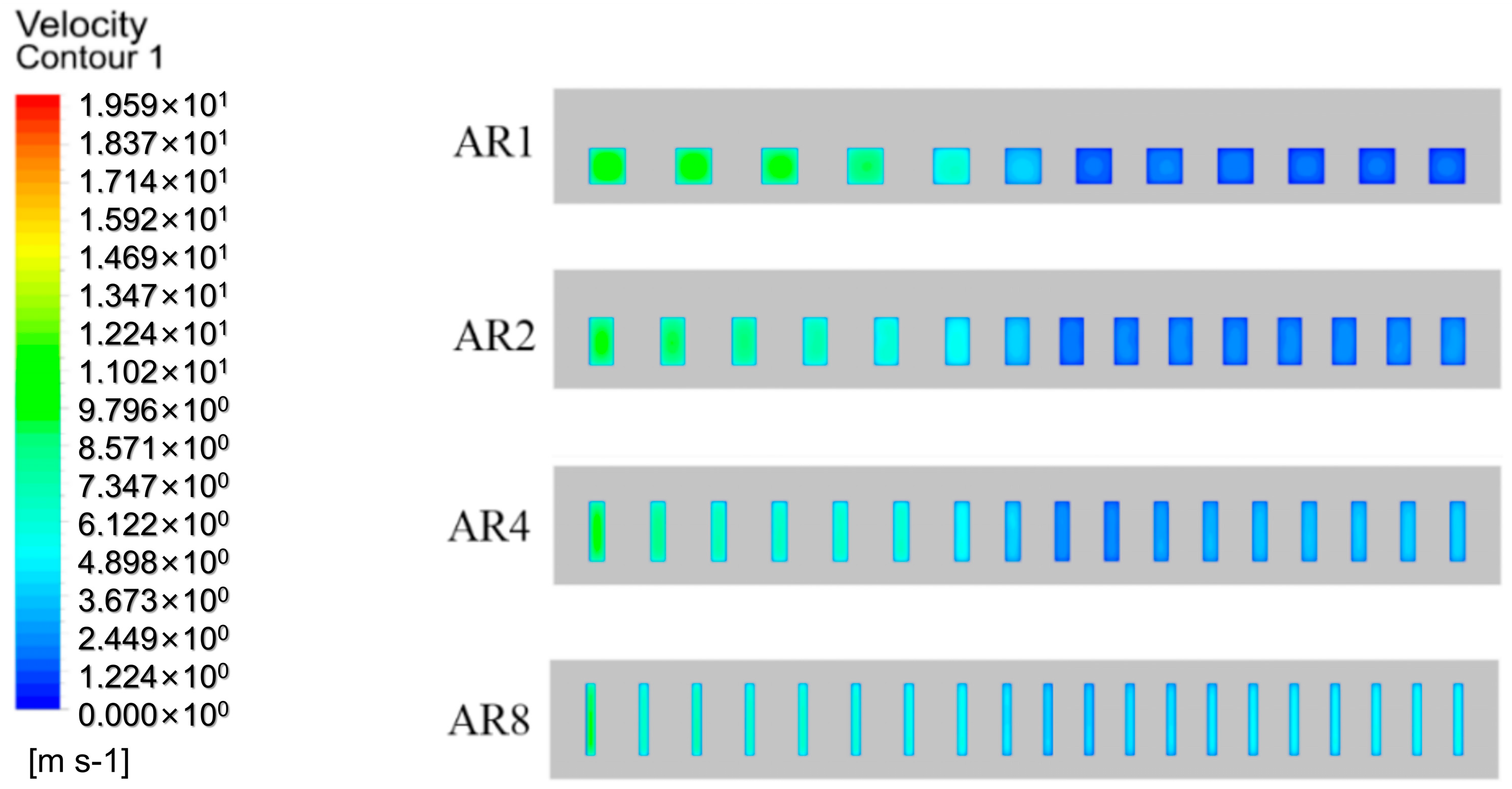
| AR | la (mm) | lb (mm) | nc | Dh (mm) | A (mm2) | C (mm) | ms (g/s) | mf (g/s) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.5 | 1.5 | 5-12-5 | 1.5 | 2.25 | 6 | 2.0 | 10.0 |
| 2 | 1 | 2 | 6-15-6 | 1.333 | 2 | 6 | 1.667 | |
| 4 | 0.625 | 2.5 | 7-17-7 | 1 | 1.563 | 6.25 | 1.429 | |
| 8 | 0.375 | 3 | 8-20-8 | 0.667 | 1.125 | 6.75 | 1.25 |
| No. | Reaction Equation | k, 1/s or m3/mol·s | Ea, kcal/mol |
|---|---|---|---|
| 1 | 0.415H2 + 0.2CH4 + 0.39C2H4 + 0.3C2H6 + 0.37C3H6 + 0.10C3H8 + 0.16C4H8 + 0.04C4H10 + 0.04C4H6 + C6H12 + 0.005C10H14 | 6.21 × 1015 | 59,350.29 |
| 2 | H2 + C2H4 | 4.65 × 1013 | 50,250.83 |
| 3 | CH4 + C3H8 | 3.75 × 1018 | 65,203.15 |
| 4 | C4H6 | 1.02 × 1018 | 41,260.84 |
| 5 | C3H6 + CH4 | 7.08 × 1019 | 60,430.21 |
| 6 | C2H4 + CH4 | 4.69 × 1010 | 50,600.71 |
| 7 | C3H6 + H2 | 5.89 × 1010 | 51,290.47 |
| 8 | C2H6 + C3H6 | 2.54 × 1019 | 59,060.50 |
| 9 | 0.12C10H14 + 0.24C6H12 + 0.36CH4 | 1.42 × 1013 | 54,490.63 |
| 10 | 3C2H4 | 7.39 × 1017 | 59,390.26 |
| 11 | C2H2 + CH4 | 7.28 × 1013 | 55,800.46 |
| 12 | C4H8 + CH4 | 1.00 × 1022 | 56,200.17 |
| 13 | C3H6 + CH4 | 7.00 × 1012 | 59,640.79 |
| 14 | 2C2H4 + H2 | 7.00 × 1014 | 70,680.03 |
| 15 | C2H4 + C2H6 | 4.10 × 1014 | 61,631.14 |
| 16 | C4H8 + H2 | 1.64 × 1012 | 62,060.48 |
| 17 | H2 + C4H6 | 1.00 × 1010 | 50,000.26 |
| 18 | 0.1C10H14 + 0.5C6H12 + 0.3H2 | 1.11 × 1011 | 53,560.59 |
| 19 | C6H6 + 2H2 | 1.08 × 1020 | 36,600.43 |
| 20 | C7H8 + 2H2 | 9.74 × 1019 | 36,900.81 |
| 21 | C8H10 + 2H2 | 1.36 × 1021 | 52,200.32 |
| 22 | 0.094H2 + 0.3CH4 + 0.1C2H2 + 0.4C2H4 + 0.2C2H6 + 0.3C3H6 + 0.1C3H8 + 0.2C4H8 + 0.04C4H10 + 0.04C4H6 + 0.198C10H14 | 1.80 × 1013 | 44,080.21 |
| 23 | C2H4 + C4H8 | 2.35 × 1012 | 55,071.11 |
| 24 | CH4 + C2H4 + C3H6 | 4.00 × 1018 | 55,071.23 |
| 25 | 2C3H6 | 1.00 × 1012 | 57,066.42 |
| 26 | C2H2 + 2CH4 | 7.00 × 1016 | 59,640.25 |
| Case Number | Run 1 | Run 2 | Run 3 | Run 4 |
|---|---|---|---|---|
| Mf (g/s) | 2.00 | 1.51 | 0.97 | 0.48 |
| Tin (K) | 776 | 781 | 776 | 780 |
| Tout, exp (K) | 885 | 896 | 902 | 925 |
| Tout, cal (K) | 910 | 916 | 931 | 947 |
| Relative error | 2.75% | 2.18% | 3.11% | 2.23% |
| Yn-decane, exp | 85.18% | 77.88% | 63.09% | 27.64% |
| Yn-decane, cal | 94.64% | 90.93% | 76.61% | 40.97% |
| Relative error | 9.99% | 14.41% | 17.65% | 32.54% |
| Average Pressure (×103 Pa) | ||||
|---|---|---|---|---|
| AR1 | AR2 | AR4 | AR8 | |
| P0 | 4000 | 4000 | 4000 | 4000 |
| P1 | 4003.54 | 4003.72 | 4005.98 | 4013.70 |
| P2 | 4010.30 | 4010.90 | 4015.97 | 4029.57 |
| P3 | 4011.19 | 4011.79 | 4017.13 | 4031.05 |
| P4 | 4014.17 | 4014.98 | 4021.77 | 4041.58 |
| ΔP2,1 | 6.67 | 7.18 | 9.99 | 15.87 |
| ΔP3,2 | 0.89 | 0.89 | 1.16 | 1.48 |
| ΔPratio | 0.133 | 0.124 | 0.116 | 0.093 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Hu, M.; Quan, Z.; Chen, Y. Numerical Investigation of Fuel Cooling in Sudden Expansion Structures of Scramjet Engines. Aerospace 2025, 12, 456. https://doi.org/10.3390/aerospace12060456
Wang Q, Hu M, Quan Z, Chen Y. Numerical Investigation of Fuel Cooling in Sudden Expansion Structures of Scramjet Engines. Aerospace. 2025; 12(6):456. https://doi.org/10.3390/aerospace12060456
Chicago/Turabian StyleWang, Qingjun, Minglei Hu, Zongjie Quan, and Yu Chen. 2025. "Numerical Investigation of Fuel Cooling in Sudden Expansion Structures of Scramjet Engines" Aerospace 12, no. 6: 456. https://doi.org/10.3390/aerospace12060456
APA StyleWang, Q., Hu, M., Quan, Z., & Chen, Y. (2025). Numerical Investigation of Fuel Cooling in Sudden Expansion Structures of Scramjet Engines. Aerospace, 12(6), 456. https://doi.org/10.3390/aerospace12060456





