GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks
Abstract
1. Introduction
- Proposing an Eclipse-Aware Routing (EAR) algorithm that considers both satellite battery levels and eclipse conditions for energy-efficient path selection in LEO satellite networks.
- Implementing a BFS-based K-Shortest Path (KSP) algorithm optimized for GPU-based parallel processing to enable real-time routing.
- Demonstrating the feasibility of the proposed method through integration with a SpaceWire-based onboard system and dynamic routing table updates.
2. Problem Description
2.1. Routing Problem in the LEO Network
2.2. Energy Efficiency Problem in the LEO Network
| Algorithm 1. Eclipse Aware Routing—Pseudo-code representing the Eclipse Aware Routing method. | |
| Input | eclipseMatrix[time][nodes] KShortestPaths[] sampleTime NoE, TxE, RxE nTimeStep |
| Output | minPath |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. | Initialize Constants: NoE, TxE, RxE Initialize Data Structures: expectedConsumedEnergy[][] <= 0; For pathIndex = 0 ~ topPath testingPath <= shortestPaths[pathIndex]; For satIndex = 0 ~ num_sats_in_path testingSat <= testingPath[satIndex]; If eclipseMatrix[timeIndex, testing Sat] == 1 Determine eclipseStartIndex and eclipseEndIndex; eclipseTime = (eclipseEndIndex − eclipseStartIndex) * sampleTime; expectedTxNum = round(eclipseTime * randi(10, 1, 1) * 0.01); Compute Energy Consumption: NominalE = eclipseTime * NoE; CommunicationE = (expectedNum + 1) * (TxE + RxE) ExpectedConsumedEnergy[pathIndex, satIndex] = NominalE + CommunicationE; End if End for End for Compute Maximum Energy Consumtion per Path: For pathIndex = 0 ~ topPath maxEnergy[pathIndex] = max(ExpectedConsumedEnergy[pathInex]); End for Select Optimal Path: minPath <= pathIndex with min(maxEnergy); Return minPath; |
2.3. Overall Structure of the Algorithm and the Need for Parallelization
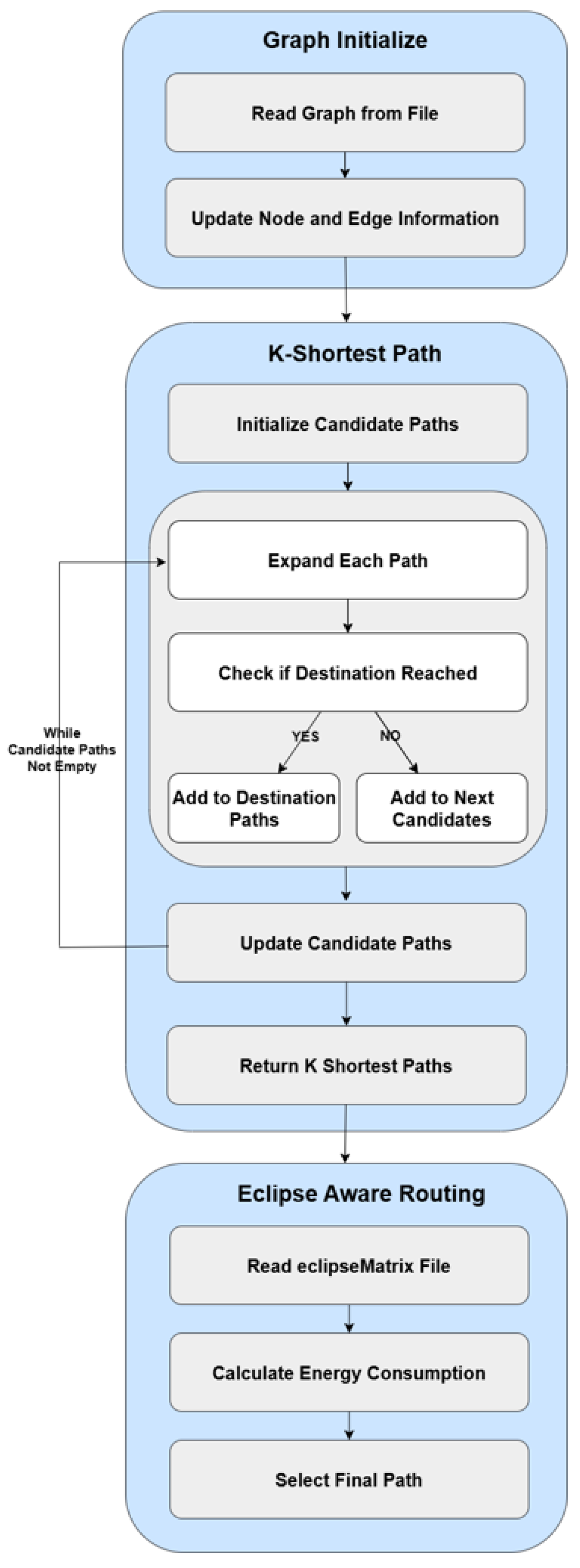
3. Proposed Method
3.1. BFS-Based K-Shortest Path Algorithm
| Algorithm 2. BFS-based K-Shortest Path Algorithm in CPU—Pseudo-code representing the BFS-based K-Shortest Path algorithm in CPU. | |
| Input | graph_adj[] src, dst, k num_nodes |
| Output | k_paths[] |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. | Initialize candidate_paths with {src} Initialize destination paths as empty list While candidate_paths is not empty AND size(destination_paths) < k Initialize next_candidate_paths as empty list For each path in candidate_paths last_node = last node in path For each neighbor in graph_adj[last_node] If neighbor is NOT in path (prevent cycles) new_path = path + neighbor new_path_cost = path.cost + edge_cost(last_node, neighbor) If neighbor == dst Add new_path to destination_paths Else Add new_path to next_candidate_paths End End End candidate_paths = next_candidate_paths End Sort destination_paths by cost Return K paths from destination_paths |
3.2. Graph Representation
3.3. Configuration of the CUDA Kernel
| Algorithm 3. BFS-based K-Shortest Path Algorithm in GPU—Pseudo-code representing the BFS-based K-Shortest Path algorithm in GPU. | |
| Input | graph_offsets[], graph_edges[] src, dst, k num_nodes |
| Output | k_paths[] |
| 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. 32. 33. 34. 35. 36. 37. 38. 39. | Copy graph data to GPU memory Initialize device candidate_paths with {src} Initialize device destination_paths as empty list Initialize device new_candidates as empty list While candidate_paths is not empty AND size(destination_paths) < k Set new_candidate_count = 0 Launch CUDA kernel: For each path in candidate_paths (Parallelized by threadIdx.x) last_node = last node in path start_idx = graph_offsets[last_node] end_idx = graph_offsets[last_node + 1] For i = start_idx to end_idx neighbor = graph_edges[i] If neighbor is NOT in path (prevent cycles) new_path = path + neighbor new_path_cost = path.cost + edge_cost(last_node, neighbor) If neighbor == dst AtomicAdd(destination_paths_count) Store new_path in destination_paths Else AtomicAdd(new_candidate_count) Store new_path in new_candidates End End End End End Swap candidate_paths with new_candidates End Copy destination_paths to CPU memory Sort destination_paths by cost Return K paths from destination_paths |
4. Experimental Results
4.1. Experimental Setups
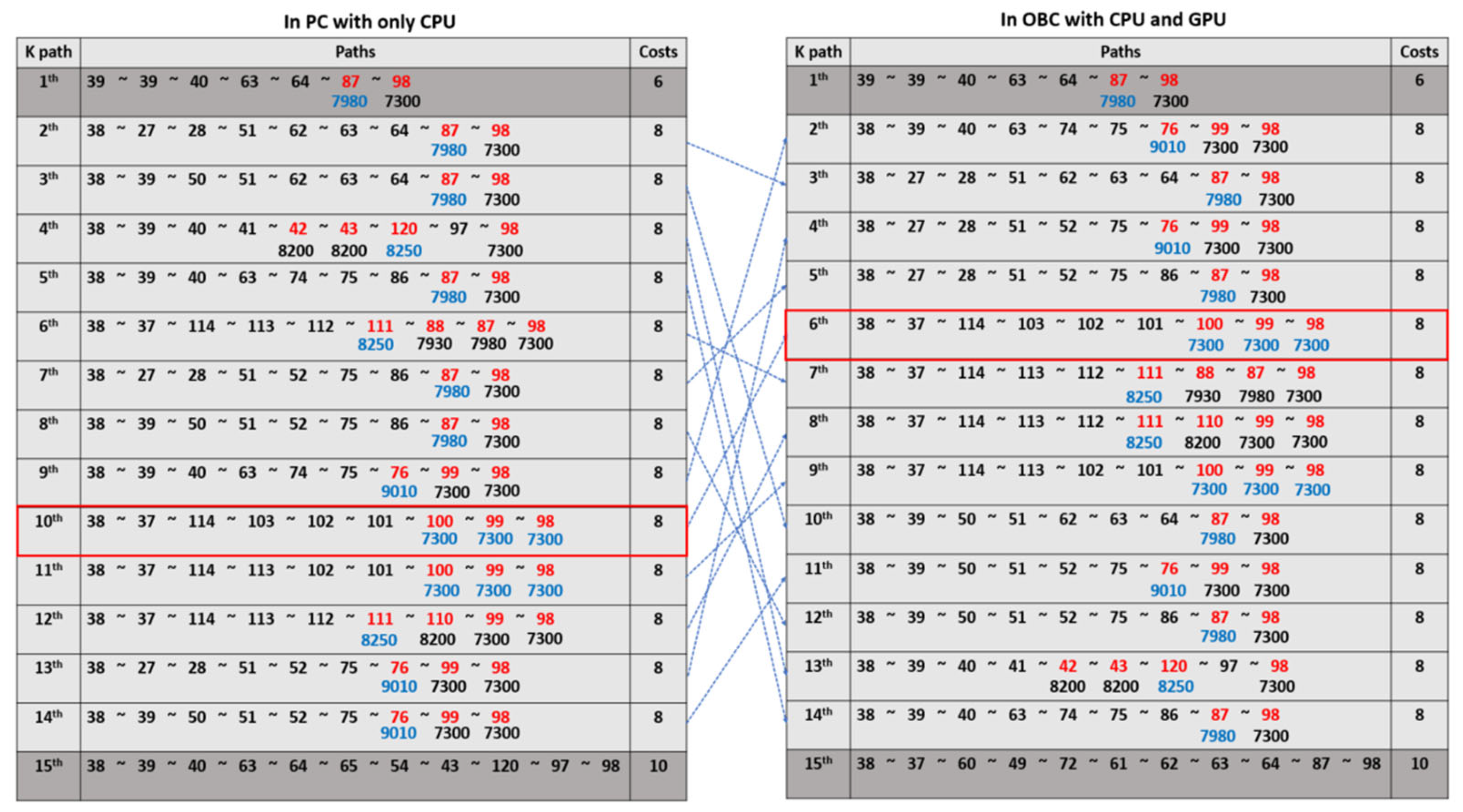
4.2. Eclipse-Aware Routing Results
4.3. SpaceWire-Based Experiment Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hassan, N.U.L.; Huang, C.; Yuen, C.; Ahmad, A.; Zhang, Y. Dense Small Satellite Networks for Modern Terrestrial Communication Systems: Benefits, Infrastructure, and Technologies. IEEE Wirel. Commun. 2020, 27, 96–103. [Google Scholar] [CrossRef]
- Cheng, H.; Xu, Z.; Guo, X.; Yang, J.; Xu, K.; Liu, S.; Jin, Z.; Jin, X. Research on Routing Equalization Algorithm of Inter-Satellite Partition for Low-Orbit Micro-Satellites. Future Internet 2022, 14, 207. [Google Scholar] [CrossRef]
- Darwish, T.; Kurt, G.K.; Yanikomeroglu, H.; Bellemare, M.; Lamontagne, G. LEO Satellites in 5G and Beyond Networks: A Review from a Standardization Perspective. IEEE Access 2022, 10, 35040–35060. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhang, T.; Shi, D.; Liu, F. A LEO Satellite Network Capacity Model for Topology and Routing Algorithm Analysis. In Proceedings of the 14th International Wireless Communications & Mobile Computing Conference (IWCMC), Limassol, Cyprus, 25–29 June 2018; pp. 1431–1436. [Google Scholar] [CrossRef]
- Ferreira, A.; Galtier, J.; Penna, P. Topological Design, Routing, and Handover in Satellite Networks. In Handbook of Wireless Networks and Mobile Computing; Wiley: Hoboken, NJ, USA, 2002; pp. 473–493. [Google Scholar] [CrossRef]
- Gounder, V.V.; Prakash, R.; Abu-Amara, H. Routing in LEO-Based Satellite Networks. In Proceedings of the 1999 IEEE Emerging Technologies Symposium, Wireless Communications and Systems (IEEE Cat. No.99EX297), Richardson, TX, USA, 18–21 October 1999; pp. 22.1–22.6. [Google Scholar] [CrossRef]
- Yang, Y.; Guo, X.; Xu, Z.; Zhu, Y.; Yi, X. Design and Implementation of LEO Micro-Satellite Network Routing Protocol Based on Virtual Topology. In Proceedings of the 2021 IEEE 5th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Xi’an, China, 15–17 October 2021; pp. 1490–1496. [Google Scholar] [CrossRef]
- Tan, H.; Zhu, L. A Novel Routing Algorithm Based on Virtual Topology Snapshot in LEO Satellite Networks. In Proceedings of the 2014 IEEE 17th International Conference on Computational Science and Engineering, Chengdu, China, 19–21 December 2014; pp. 357–361. [Google Scholar] [CrossRef]
- Mota Macambira, R.N.; Carvalho, C.B.; Rezende, J.F. Energy-Efficient Routing in LEO Satellite Networks for Extending Satellites Lifetime. Comput. Commun. 2022, 195, 463–475. [Google Scholar] [CrossRef]
- Hussein, M.; Jakllari, G.; Paillassa, B. On Routing for Extending Satellite Service Life in LEO Satellite Networks. In Proceedings of the 2014 IEEE Global Communications Conference, Austin, TX, USA, 8–12 December 2014; pp. 2832–2837. [Google Scholar] [CrossRef]
- Shergill, M.; Thompson, Z.; Song, G.; Zhu, T. Energy Efficient LoRaWAN in LEO Satellites. arXiv 2024, arXiv:2412.20660. [Google Scholar] [CrossRef]
- Huang, G.; Lu, W.; Jidong, X.; Zhang, G. Improved Route Selection Strategy Based on K Shortest Path. In Proceedings of the 2019 International Symposium on Networks, Computers and Communications (ISNCC), Istanbul, Turkey, 18–20 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, S.; Chen, Q.; Wang, H.; Wang, M.; Liu, N. Computing-Aware Routing for LEO Satellite Networks: A Transmission and Computation Integration Approach. IEEE Trans. Veh. Technol. 2023, 72, 16607–16623. [Google Scholar] [CrossRef]
- Yu, C.; Kim, D.; Lee, H.; Han, M. GPU-Accelerated CNN Inference for Onboard DQN-Based Routing in Dynamic LEO Satellite Networks. Aerospace 2024, 11, 1028. [Google Scholar] [CrossRef]
- ECSS-E-ST-50-12C; SpaceWire Standard. ECSS-Space Engineering. SpaceWire-Links Nodes Routers and Networks. Publications Division ESTEC: Noordwijk, The Netherlands, 2008; pp. 11–12.
- STAR-Dundee. SpaceWire Brick Mk4 Datasheet. Available online: https://www.star-dundee.com/wp-content/star_uploads/product_resources/datasheets/SpaceWire-Brick-Mk4.pdf (accessed on 7 May 2025).
- Pizzi, S.; Rinaldi, F.; Iera, A.; Molinaro, A.; Araniti, G. Tackling Satellite Mobility in LEO-Based Non-Terrestrial Networks: Principles and Enhancements of Feeder Link Switch. IEEE Veh. Technol. Mag. 2024, 19, 83–91. [Google Scholar] [CrossRef]
- Xiao, Z.; Yang, J.; Mao, T.; Xu, C.; Zhang, R.; Han, Z.; Xia, X.G. LEO Satellite Access Network (LEO-SAN) Toward 6G: Challenges and Approaches. IEEE Wirel. Commun. 2024, 31, 89–96. [Google Scholar] [CrossRef]
- Yen, J.Y. Finding the k Shortest Loopless Paths in a Network. Manag. Sci. 1971, 17, 712–716. [Google Scholar] [CrossRef]
- Eppstein, D. Finding the k Shortest Paths. SIAM J. Comput. 1998, 28, 652–673. [Google Scholar] [CrossRef]
- Katoh, N.; Ibaraki, T.; Mine, H. An Efficient Algorithm for K Shortest Simple Paths. ACM Trans. Algorithms 2007, 3, 41. [Google Scholar] [CrossRef]
- Liu, H.; Jin, C.; Yang, B.; Zhou, A. Finding Top-k Shortest Paths with Diversity. IEEE Trans. Knowl. Data Eng. 2017, 30, 488–502. [Google Scholar] [CrossRef]
- Tsuchida, H.; Kawamoto, Y.; Kato, N.; Kaneko, K.; Tani, S.; Hangai, M.; Aruga, H. Improvement of Battery Lifetime Based on Communication Resource Control in Low-Earth-Orbit Satellite Constellations. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1388–1398. [Google Scholar] [CrossRef]
- Bell, N.; Garland, M. Efficient Sparse Matrix-Vector Multiplication on CUDA; Nvidia Technical Report NVR-2008-004; Nvidia Corporation: Santa Clara, CA, USA, 2008; Volume 2, p. 5. [Google Scholar]
- Jang, B.; Schaa, D.; Mistry, P.; Kaeli, D. Exploiting Memory Access Patterns to Improve Memory Performance in Data-Parallel Architectures. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 105–118. [Google Scholar] [CrossRef]
- Harish, P.; Narayanan, P.J. Accelerating Large Graph Algorithms on the GPU Using CUDA. In International Conference on High-Performance Computing; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]





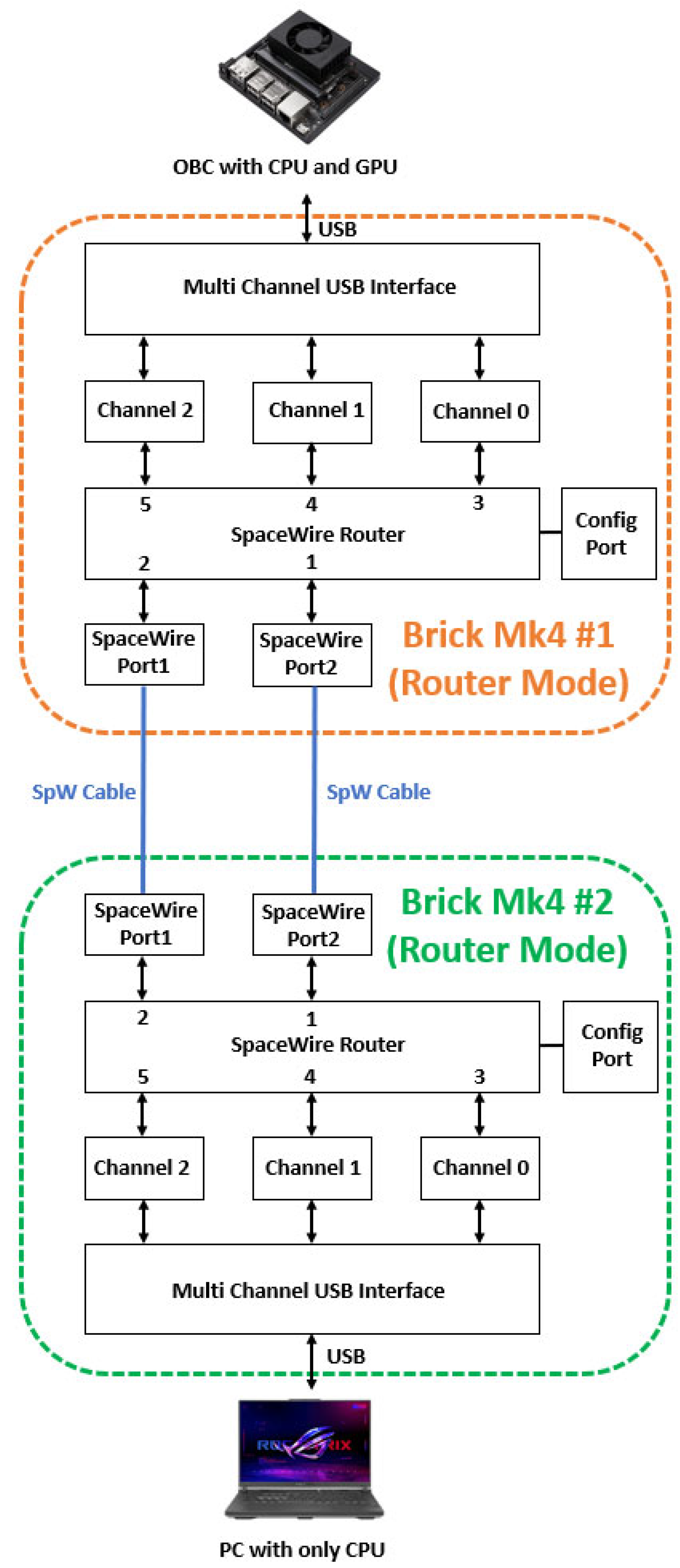




| MODE | 20 W 6CORE |
| CUDA Version | 10.2v |
| AI Performance | 21TOPS |
| GPU | 384-core NVIDIA Volta GPU (48 Tensor Cores) |
| CPU | 6CORE NVIDIA Carmel ARM v8.2 64-bit |
| Memory | 16 GB 128-bit LPDDR4x (59.7 GB/s) |
| Power consumption | 10 W–20 W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Lee, H.; Han, M. GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks. Aerospace 2025, 12, 422. https://doi.org/10.3390/aerospace12050422
Kim H, Lee H, Han M. GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks. Aerospace. 2025; 12(5):422. https://doi.org/10.3390/aerospace12050422
Chicago/Turabian StyleKim, Hyeonwoo, Heoncheol Lee, and Myonghun Han. 2025. "GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks" Aerospace 12, no. 5: 422. https://doi.org/10.3390/aerospace12050422
APA StyleKim, H., Lee, H., & Han, M. (2025). GPU-Accelerated Eclipse-Aware Routing for SpaceWire-Based OBC in Low-Earth-Orbit Satellite Networks. Aerospace, 12(5), 422. https://doi.org/10.3390/aerospace12050422







