Abstract
In this study, two-dimensional airfoil shapes obtained in aerodynamic optimizations are converted to three-dimensional wing models and then their aerodynamic and sonic boom performance are evaluated. The airfoil shapes analyzed are the diamond, Busemann, new supersonic biplane (NSB), and triplane airfoil configurations. The NSB is a modified version of the Busemann biplane airfoil proposed in previous studies. The triplane airfoil configuration is obtained in this study by maximizing the lift-to-drag ratio using an aerodynamic topology optimization method. Based on the obtained two-dimensional airfoil shapes, three-dimensional multiple (biplane/triplane) wing configurations are designed. The aerodynamic and sonic boom performance of these configurations is evaluated in detail through three-dimensional flow analyses as well as acoustic propagation analyses. The aerodynamic superiority of the multiple wing configurations is confirmed in this study.
1. Introduction
The primary advantage of supersonic transports (SSTs) is that they can drastically reduce travel time from departure to destination by cruising at supersonic speeds. For this reason, various research efforts have been conducted since the 1950s to realize the SST. In 1976, the Concorde was put into commercial operation. This SST could cruise at a Mach number of 2.0, shortening the travel time between London and New York from approximately seven hours for conventional transonic aircraft to approximately three and a half hours. However, problems arose due to shock waves generated in the supersonic cruising. These shock waves increase supersonic wave drag on the aircraft. This wave drag deteriorates the fuel efficiency of the SST aircraft, leading to higher airfares. In addition, shock waves cause a loud noise on the ground, known as a sonic boom. Because of the sonic boom, supersonic flight over land was prohibited for the Concorde, and then the Concorde was not commercially successful because it could not fully utilize its capability of supersonic cruising. Due to these issues, Concorde was retired in 2003, and as of 2025, no SST aircrafts have been operated commercially since then.
As globalization progresses, it is expected that the demand for long-distance travel for business and leisure will continue to increase. Therefore, the excellent transport speed of the SST aircraft can be a major advantage, and many research and development are being conducted with the aim of reviving its commercial operation [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. In order to realize the commercial operation of the SST, it is necessary to improve its profitability and reduce the noise of the sonic boom. To improve the profitability, it is necessary to improve its fuel efficiency by increasing the lift-to-drag ratio during the supersonic cruising [1,2,4,6,7,9]. To reduce the strength of the sonic boom, it is necessary to tailorize the pressure waveform propagating to the ground while maintaining the lift force required for the cruising. The physical mechanisms of the sonic boom are as follows: shock waves generated from an SST propagate towards the ground, and due to their nonlinearity, they finally integrate into strong pressure variations at the front and rear ends of the waveform on the ground, resulting in two loud noises. Taking into account these circumstances, research on the sonic boom reduction technology has been actively conducted in recent years [1,3,5,6,8,9,10]. The main research being conducted is to control the generation pattern of shock and expansion waves near the aircraft by devising the aircraft shape to delay the integration of shock waves propagating towards the ground.
As an innovative configuration for the low-drag and low-boom SST, a twin-body/biplane wing SST model has been proposed [16,18]. The configuration of this SST model has been proposed by combining supersonic twin-body theory [15] and supersonic biplane wing theory [11,12,13,14], and has been designed to reduce the supersonic wave drag. The supersonic twin-body theory is an approach to reduce volume-dependent wave drag of the fuselage, while the supersonic biplane wing theory is an approach to reduce both volume and lift dependent wave drag of the wing. According to [16], the total drag of the twin-body/biplane wing SST model was 38% lower than that of a conventional SST model consisting of a single-body/diamond wedge wing under the same conditions of volume and fuselage length. A 38% reduction in maximum pressure rise has also been confirmed in the twin-body/biplane wing SST model as a metric of the sonic boom strength.
As a means of designing innovative airfoil configurations under supersonic flow conditions, topology optimization approaches have attracted attention [20,21,22,23,24,25]. One such approach is the global topology optimization method called FANTOM (black-box function aerodynamic topology optimization algorithm using machine learning technologies), which utilizes machine learning technologies [23]. The usefulness of the FANTOM has been demonstrated through solving the optimization problem of minimizing inviscid drag in a two-dimensional (2D) supersonic flow. The resulting optimal airfoil topology was similar to that of the Busemann biplane airfoil. The Busemann biplane airfoil is known as a theoretical optimal airfoil configuration minimizing the supersonic wave drag in linear theory.
In another previous study [26], a new supersonic biplane (NSB) airfoil configuration has been proposed. The conventional Buemann biplane airfoil has a symmetrical topology consisting of two triangular airfoils, which can achieve successful interaction of shock waves between them. Under off-design conditions, however, a choking phenomenon occurs due to its small ratio of throat area to inlet area, which results in a drastic increase in wave drag. The NSB was theoretically designed to improve its off-design performance while retaining the excellent characteristics of the conventional Buemann biplane airfoil. In the design of the NSB, the upper airfoil of the conventional Busemann biplane airfoil is removed and a flat plate is placed in the central region. This topology maintains a similar interaction effect of shock waves as the conventional Busemann biplane airfoil under design conditions, while increasing the ratio of throat area to inlet area, which results in the mitigation of the choking phenomenon under off-design conditions. Due to its smaller wetted area than that of the conventional Busemann biplane airfoil, its skin friction drag is also smaller. Therefore, the NSB is a promising candidate for supersonic wing design, and it may be able to achieve higher performance than conventional wing designs. However, since its three-dimensional (3D) effects and sonic boom performance have not yet been clarified, its additional investigation is required.
As described above, the modified Busemann biplane airfoil configuration, NSB, has been proposed and various new airfoil topologies can also be proposed utilizing topology optimization methods. In this study, aiming to achieve low-drag/low-boom SST aircraft, promising supersonic airfoil topologies are designed using aerodynamic optimization approaches. Obtained promising 2D airfoil configurations are converted into 3D wing and wing–body models, and then 3D computational fluid dynamics (CFD) simulations as well as acoustic propagation analyses are performed to discuss those aerodynamic performance and sonic boom characteristics.
The remainder of this paper is organized as follows. In Section 2, numerical methods utilized in this research are concisely introduced. In Section 3 and Section 4, two supersonic airfoil topologies are designed using aerodynamic optimization methods. In Section 5, 3D wing and wing–body designs of the obtained airfoils are introduced. Section 6 presents the results of the 3D CFD and sonic boom analyses. Finally, Section 7 and Section 8, respectively, present the comprehensive discussion and conclusions of this study.
2. Numerical Methods
2.1. The Topology Optimization Approach
In this study, we apply the black-box function aerodynamic topology optimization algorithm FANTOM [22,23,25], which utilizes surrogate models and machine learning technologies. The FANTOM is a global optimization method, which has been developed to efficiently solve high-dimensional discontinuous optimization problems involving infeasible regions. This method is an optimization method integrating EGODISC [27], a global optimization method using a classification method, and EGOCCS [28], a global optimization method using a clustering method and classification method. In this approach, various topologies are generated by a kind of level-set methods utilizing a NURBS surface. Design variables are used to set the locations of control points for the NURBS surface. When the NURBS surface is constructed, an airfoil topology is extracted by cutting the NURBS surface to satisfy a user-specified sectional area. The details of the algorithm of FANTOM are given in [23].
For this aerodynamic topology optimization, 2D inviscid compressible flow simulations are used for aerodynamic performance evaluations. 2D compressible Euler equations are solved using a gridless method [19,22,29]. Approximately 20,000 computational points are distributed around supersonic airfoils in this aerodynamic evaluation. In [22], a convergence study for the computational point resolution was performed, and the present resolution of computational points is selected considering both the accuracy and the computational cost. The numerical flux at the intermediate position of two computational points is calculated using Roe’s approximate Riemann solver, which has second-order spatial accuracy. Temporal discretization is performed using a four-stage Runge–Kutta scheme.
2.2. Three-Dimensional CFD Method
3D supersonic inviscid flows around SST aircrafts are analyzed using an unstructured grid CFD solver of TAS (Tohoku University Aerodynamic Simulation)-code [30]. Governing equations are 3D compressible Euler equations, which are discretized using a cell-vertex finite volume method. The inviscid flux is evaluated by an approximate Riemann solver of Harten–Lax–van Leer–Einfelds–Wada (HLLEW). The second-order spatial accuracy is achieved using the Unstructured Monotone Upwind Schemes for Conservation Laws (U-MUSCL). To stabilize the CFD simulations, a limiter function of Venkatakrishnan is applied. The LU-SGS implicit method is used for the time integration. 3D unstructured grids are generated using MEGG3D (version 6.9), which uses the advancing front method to generate surface/volume grids [31,32].
Since the viscous effects are neglected in this study, the successful interaction effect between shock/expansion waves may be weakened due to the existence of boundary layers, which can reduce the aerodynamic performance in viscous simulations. According to [13], however, Cp distributions of a biplane airfoil obtained from inviscid simulations were qualitatively similar to those obtained from viscous simulations, which implies that the present inviscid simulations are reasonable for evaluating the aerodynamic performance in this study.
2.3. Estimation of Skin Friction Drag
In this study, we use an algebraic model to estimate the skin friction drag of designed airfoils/SST aircrafts. Assuming that the boundary layer on the SST is turbulent, the skin friction drag coefficient can be estimated as follows:
where Cf is the average turbulent skin friction coefficient on the object. Swet and Sref are the wetted area and reference area of the object, respectively. Cf is calculated using the Prandtl–Schlichting flat-plate skin friction formula [33,34] as follows:
where Re and M∞ are the Reynolds number and uniform flow Mach number, respectively. The Reynolds number is calculated from the cruising condition of the Concorde (fuselage length l = 62 [m]) under the design Mach number of 1.7. The sound speed and dynamic viscosity at the altitude of 18,000 [m] are 295.069 [m/s] and 1.1686 × 10−4 [m2/s], respectively. The Reynolds number for the fuselage can be calculated as follows:
In references [11,13], the accuracy of the algebraic skin friction drag model was compared with viscous CFD results, and the effectiveness of this algebraic model was demonstrated.
2.4. Evaluation of Sonic Boom Strength
The propagation of the sonic boom to the ground is analyzed using the nonlinear acoustic propagation analysis software Xnoise (version 1.6) [35,36] developed by Japan Aerospace eXploration Agency (JAXA). The Xnoise calculates the propagation of pressure waveforms toward the ground by solving the extended Burgers equation using an operator splitting method. The extended Burgers equation takes into account nonlinear effects, geometric spreading effects, effects of inhomogeneity of atmosphere, thermoviscous attenuation as well as molecular vibration relaxation. In this approach, the pressure distribution below the aircraft extracted from CFD analysis is used as the initial (input) pressure waveform for the propagation analysis (in this study, the pressure waveform extracted at the position two fuselage lengths below is used as the input). The pressure waveform on the ground is obtained by analyzing the propagation using the extended Burgers equation. Finally, the maximum pressure rise Pmax and the A-weighted sound exposure level (ASEL) are evaluated from the ground pressure waveform as metrics of the sonic boom strength. Pmax is simply given from the maximum value of the pressure waveform on the ground, which corresponds to a physical metric of the sonic boom strength. ASEL is, on the other hand, an annoyance-based metric calculated from the pressure waveform on the ground taking into account the relative loudness perceived by the human ear. In this sonic-boom analysis, standard atmosphere temperature/humidity profiles are assumed. The fuselage length and the cruise altitude of SSTs are, respectively, set to 62 [m] and 18,000 [m], that are the conditions of the Concorde.
2.5. Validity of Numerical Methods
The validity of the 2D inviscid simulation and the estimation method of the skin friction drag was investigated by comparing with a viscous CFD simulation result of a diamond airfoil (10% thickness), that were given in [13]. Aerodynamic performance was evaluated at an M∞ of 1.7, an angle of attack (AoA) of 2 degrees, and Re of 32 million, and results are summarized in Table 1. In the present approach, the inviscid CFD approach introduced in Section 2.1 is utilized to evaluate the pressure lift coefficient (Clp) and pressure drag coefficient (Cdp). The skin friction drag (Cdf) is estimated by using the algebraic model of Section 2.3, and then its effect is included to evaluate the lift-to-drag ratio L/D(=Cl/Cd = Clp/(Cdp + Cdf)). The effect of the skin friction on the lift coefficient can be neglected (Cl = Clp). We can confirm that the present inviscid simulation approach and the estimation method of the skin friction drag can predict aerodynamic performance reasonably well.

Table 1.
Aerodynamic performance of a diamond airfoil comparing with a viscous CFD result.
The validity of the 3D inviscid simulation and the analysis method of the sonic boom was investigated by comparing with experimental data obtained in the drop test of axisymmetric bodies performed in the low sonic boom design concept demonstration project (D-SEND#1) of JAXA [3,37,38]. In this project, two models are investigated, that are referred to as an N-wave model (NWM) and a low-boom model (LBM). The NWM is an axisymmetric body which generates a typical N-type pressure waveform, while the LBM is an axisymmetric body that has been designed using low sonic boom design technology to reduce sonic boom strength. In this experiment, sonic booms generated at Mach numbers of 1.58–1.59 were investigated for the two models. The sonic boom waveforms were measured at a position approximately 3500 [m] away from the bodies. In this analysis, CFD analyses are firstly performed as shown in Figure 1. Then, input pressure distributions are extracted from the CFD results. Acoustic propagation analyses are performed from the input pressure distributions to obtain the waveforms at the position approximately 3500 [m] away from the bodies. A comparison of the experimental and numerical results is shown in Figure 2. Some differences in the waveforms are observed in the range of 0.03–0.05 [s], which is considered to be due to the influence of atmospheric turbulence. The experimental and numerical results are found to qualitatively agree for both the NWM and LBM models. These results demonstrate the validity of the numerical methods used in this study.
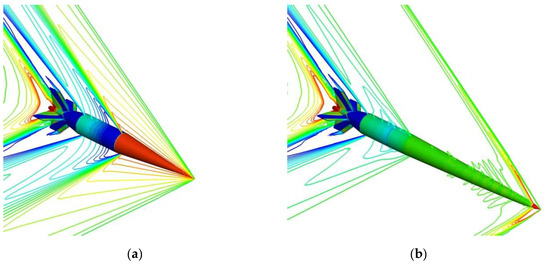
Figure 1.
Pressure distributions around two models used in the D-SEND#1 project. (a) The N-wave model; (b) the low-boom model.
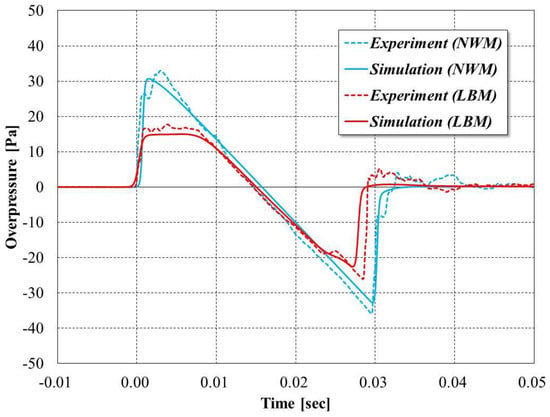
Figure 2.
Comparison of experimental and numerical waveforms at a position approximately 3500 m away from models.
3. Shape Optimization of NSB Airfoil
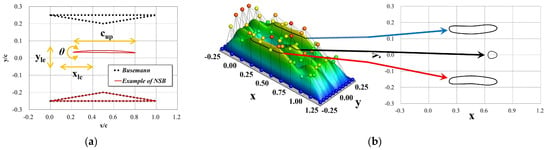
Since the original NSB airfoil has been designed using a flat plate for its upper airfoil element [26], it is difficult to construct realistic 3D wing models. In this section, therefore, the NSB airfoil configuration is designed under the condition where the upper airfoil element has a thickness. When the lower airfoil element is fixed to the triangular shape of the Busemann biplane airfoil, the upper airfoil element is designed as to have a 2% thickness with respect to its chord length. While its lower surface is flattened, its upper surface is set as the radius distribution of the Sears–Haack body. The NSB airfoil configuration is designed by using an aerodynamic shape optimization method [39] with four design variables, that are x and y locations of leading edge (xle, yle), chord length (cup) and setting angle () of the upper airfoil element. The schematic sketch of the definition of design variables is shown in Figure 3a. The objective function is to maximize L/D at an M∞ of 1.7 and an AoA of 2 degrees. In this optimization, the inviscid CFD approach of Section 2.1 is utilized to evaluate Clp and Cdp. Cdf is estimated by using the algebraic model of Section 2.3, and then its effect is included to evaluate L/D(=Clp/(Cdp + Cdf)).
The shape of the obtained optimal airfoil is shown in Figure 4, which is referred to as NSB1 airfoil hereafter. The aerodynamic performance and flow visualization of the NSB1 airfoil are compared with those of the diamond airfoil (10% thickness) and the Busemann biplane airfoil (5% thickness for each element) in Table 2 and Figure 5. Since other representative airfoils have the same total sectional area of 0.05 (as a non-dimensional value), the NSB2 airfoil has been defined for comparison purposes, which also has the same total sectional area of 0.05. This has been achieved by enlarging the shape of the NSB1 airfoil while maintaining its geometric similarity. It can be confirmed that successful interaction of shock waves is achieved around the NSB1/NSB2 airfoil configurations, which is consistent with the flow field of the original NSB airfoil [26]. In Figure 6, L/D values are compared within the range of 0 AoA 3 degrees, which shows better aerodynamic performance of the NSB1/NSB2 airfoils than the diamond and Busemann biplane airfoil configurations.
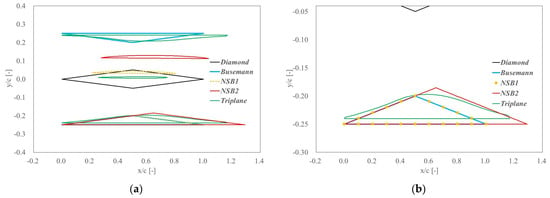
Figure 4.
Comparison of representative airfoil configurations. (a) General view; (b) Enlarged view at the lower region.

Table 2.
Comparison of aerodynamic performance values of representative airfoil configurations at an AoA of 2 degrees. Best values are displayed in boldface type.
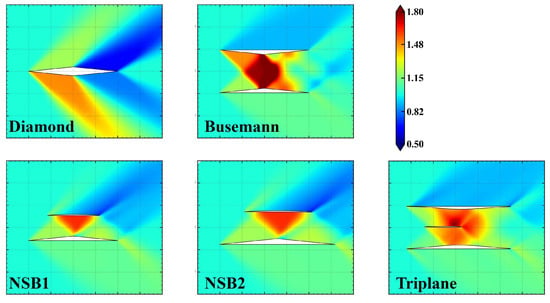
Figure 5.
Comparison of pressure distributions around representative airfoil configurations at an AoA of 2 degrees.
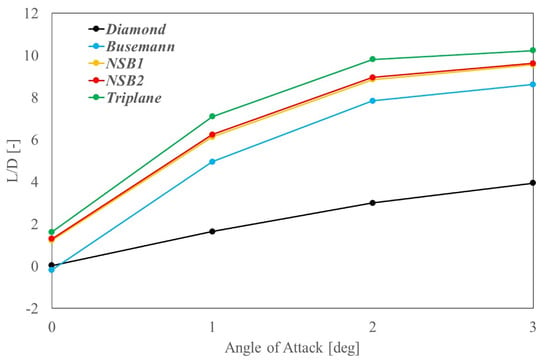
Figure 6.
Comparison of L/D values obtained by 2D CFD evaluations.
4. Topology Optimization of Supersonic Airfoil Configuration
An aerodynamic topology optimization is also performed using the FANTOM approach which was introduced in Section 2.1. The objective function is to maximize the lift-to-drag ratio at an M∞ of 1.7 and an AoA of 2 degrees. A total of 70 design variables is used to define the arrangement of control points for a NURBS surface. The cross-sectional shape of the NURBS surface ensuring its total sectional area of 0.05 is used to define various 2D shapes/topologies. The schematic sketch of the definition of design variables is shown in Figure 3b.
The obtained optimal airfoil topology is shown in Figure 4. The obtained optimal topology consists of three objects, which is referred to as triplane airfoil configuration hereafter. The aerodynamic performance and flow visualization of the triplane airfoil are also indicated in Figure 5 and Figure 6 and Table 2. By introducing a small object in the central region, a pressure reduction on the upper surface of the lower airfoil and a pressure increase on the lower surface of the upper airfoil are confirmed, which increases the lift force. Although the introduction of the third object increases the skin friction drag due to a larger wetted area, an increase in L/D can be confirmed in the obtained triplane airfoil configuration. The features of the representative airfoil configurations that are used in the following sections are summarized in Table 3.

Table 3.
Summary of representative airfoil configurations.
5. Three-Dimensional Wing/Wing–Body Model Design
3D wing models are designed for the obtained optimal airfoil configurations referring the conditions given in [16]. For the wing design in this study, a tapered wing planform without a swept back angle is adopted. This is because the aerodynamic performance of unswept tapered wings has been shown to be better in previous studies [12]. The aspect ratio and taper ratio are set to 7 and 0.25, respectively. The chord length of the main wing at the root is set to one-sixth of the fuselage length (10.3 [m]) for the models of diamond, Busemann and NSB1 airfoil models. Since the effectiveness of wing tip plates on Busemann biplane wings has been demonstrated in [11], a vertical plate is added to the wing tips of the models to enhance the two-dimensionality of the flow around them, except for the diamond wing model. Regarding the design of the wing tip plate, its inner surface is flattened while its outer surface is convex to have a thickness. To realize the appropriate interaction of shock waves, a dihedral angle is given on the lower wing at the wing tip side, which makes that the non-dimensional cross-sectional airfoil shape is equivalent at all spanwise positions. The 3D wing models of the five representative airfoils are constructed in the same manner, that are schematically shown in Figure 7.
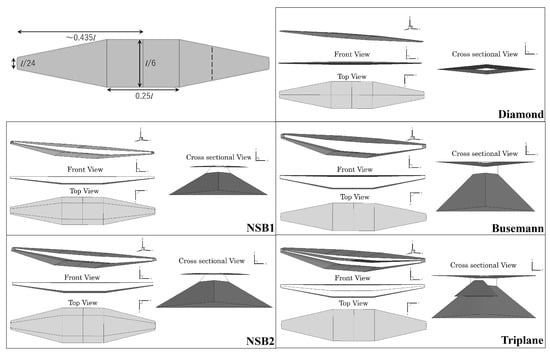
Figure 7.
3D wing designs using representative airfoil configurations.
In the design of 3D wing–body models, the Sears–Haack body is used for the fuselage. The fuselage volume is set to accommodate 200 passengers according to [18]. However, the Sears–Haack body designed for 200 passengers cannot be properly combined with the Busemann biplane wing used in this study. This is because that the maximum diameter of the Sears–Haack body is insufficient for a proper wing-fuselage combination with the Busemann biplane wing, which has the largest distance between upper/lower elements. Therefore, in order to maintain the volume while still allowing a proper combination, the cross-sectional shape of the Sears–Haack body is deformed from a true circular shape to an elliptical shape (the ratio of the major axis to the minor axis of the ellipse is designed to be 4:3). With respect to the attachment position of the wings, the centers of the wings are set 65% from the head of the fuselage according to [18]. With respect to the vertical direction, the diamond, Busemann, and triplane wings are attached as that their centers coincide with the center of the fuselage. The NSB1 and NSB2 wings are attached as that the vertical positions of the lower surfaces of the lower wings coincide with that of the Busemann biplane wing. The 3D wing–body models of the five representative airfoils are schematically shown in Figure 8.
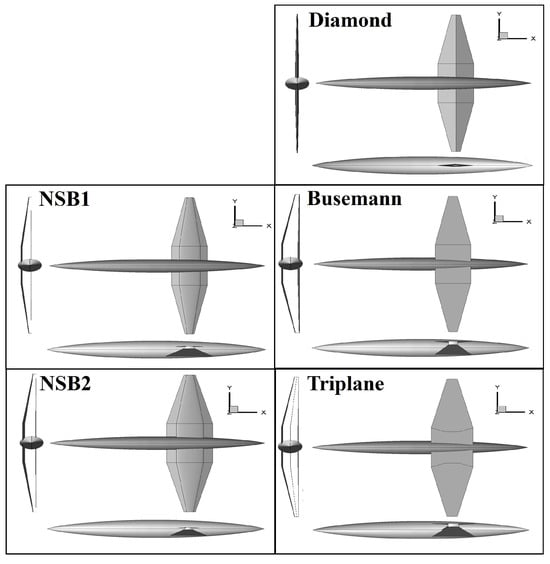
Figure 8.
3D wing–body designs using representative airfoil configurations.
Computational grids are generated using the MEGG3D, and the prism elements are generated in the direction of shock wave propagation to accurately evaluate the pressure distribution at the outer (lower) region [16]. The number of grid points is set to approximately one million for wing models and two million for wing–body models. The computational grid around a wing–body model is visualized in Figure 9.
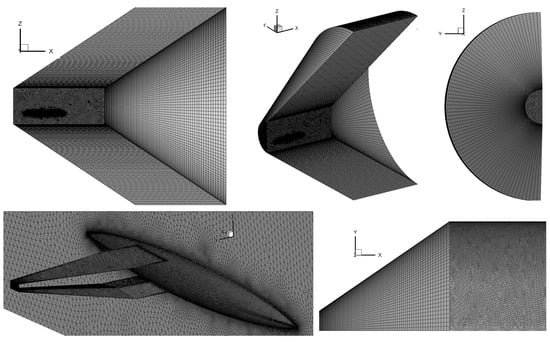
Figure 9.
Computational grid around a 3D wing–body model.
To validate the present grid resolution, a finer computational grid of the wing–body model for the Busemann biplane, which has approximately five million grid points, has also been generated as shown in Figure 10. Obtained CFD results at an M∞ of 1.7 and an AoA of 2 degrees are compared in Table 4. Since the difference in the L/D value was less than 1%, the present grid resolution can be considered acceptable for this study.

Figure 10.
Visualization of utilized computational grids around the wing–body model of the Busemann biplane.

Table 4.
Effect of computational grid resolution on aerodynamic performance values.
Additionally, to validate the sonic boom analysis method, the effect of the position to extract the pressure waveform () is investigated. Obtained pressure waveforms on the ground at = 1.5, 2.0 and 2.5 are compared in Figure 11, indicating qualitative agreement between them. Therefore, the extraction of the pressure waveform at = 2.0 can be considered sufficient for this study.
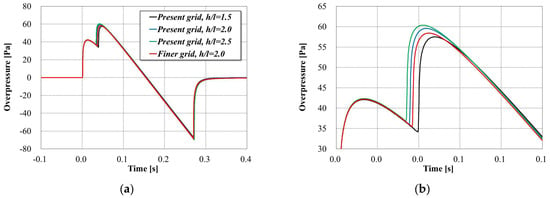
Figure 11.
Comparison of pressure waveforms on the ground for the wing–body model of the Busemann biplane. (a) general view; (b) enlarged view.
6. Results of Three-Dimensional Computations
6.1. 3D Simulations of Wing Models
In this section, results of 3D wing models at an M∞ of 1.7 are discussed. Pressure distributions at 0, 50 and 90% semi-span sections are shown in Figure 12. It can be confirmed that obtained pressure distributions are qualitatively similar to those of the 2D cases (Figure 5). The aerodynamic performance of the five designs is compared in Table 5 and Figure 13. In the 3D wing analysis, the NSB2 showed the highest L/D among the five wing models. The triplane, which showed the highest L/D in the 2D analysis, performed worse than the NSB1 and NSB2 models. This is due to the increase in CDP compared to the 2D analysis, which is considered to be due to the influence of the three-dimensionality of the flow. Although the triplane wing still has the highest inviscid lift–drag ratio (defined as CLP/CDP) in the 3D wing analysis, its CDP value is not the smallest, and it has the largest CDf value, which yields that the L/D value considering viscosity is lower than that of the NSB wings. It can be observed from Figure 12 that the pressure distributions of the triplane wing change relatively in the spanwise direction (the high pressure areas on the upper side of the middle object are weakened on the outer wing side). This is thought to be because the influence of the three dimensionality of the flow becomes more significant in the complex triplane models, which has a strong influence on the interference of shock waves.
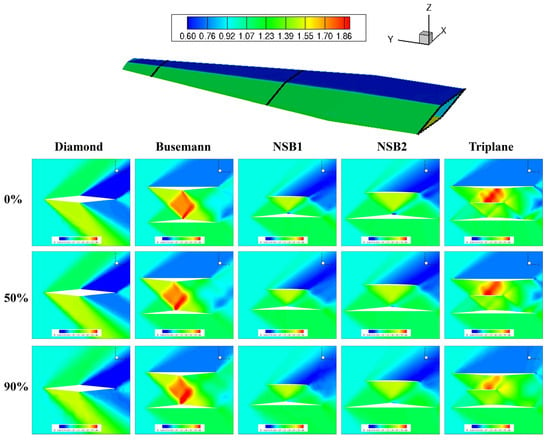
Figure 12.
Pressure distributions at 0, 50 and 90% semi-span sections of 3D wing models.

Table 5.
Comparison of aerodynamic performance values of wing models at an AoA of 2 degrees. Best values are displayed in boldface type.
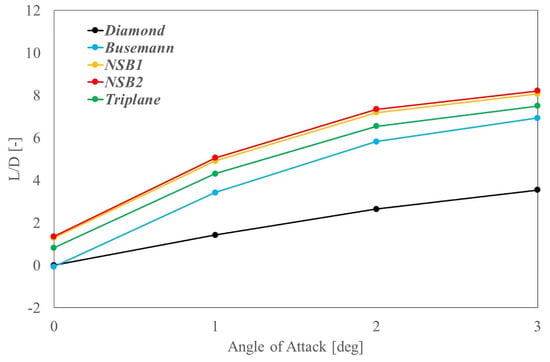
Figure 13.
Comparison of L/D values obtained by 3D CFD evaluations of wing models.
6.2. 3D Simulations of Wing–Body Models
In this section, results of 3D wing–body models at an M∞ of 1.7, as visualized in Figure 14, are discussed. With respect to the wing–body model of the Busemann biplane, a choking phenomenon occurred at the condition of an AoA of 3 degrees. This is due to the change in the flow field caused by the introduction of the fuselage. In the results presented hereafter, therefore, comparisons and discussions are performed without the case of the Busemann biplane model at an AoA of 3 degrees.
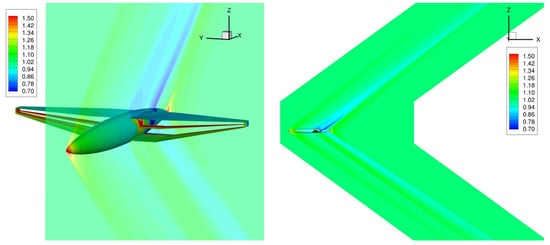
Figure 14.
Visualization of pressure distributions around a triplane wing–body model.
The aerodynamic performance of the five wing–body models is compared in Table 6 and Figure 15. The introduction of the fuselage increases the drag components compared to the wing models, which results in lower values of L/D. In the 3D wing–body analysis, NSB2 exhibited the highest L/D among the five models, which is consistent with the result of the 3D wing analysis results. This implies that the enhancement of lift force provided by biplane/triplane wing configurations is effective even in wing–body models. The interaction effect of shock waves also occurs effectively in the wing–body models, which demonstrates the effectiveness of the NSB and triplane wing configurations for the wing–body models.

Table 6.
Comparison of aerodynamic performance values of wing–body models at an AoA of 2 degrees. Best values are displayed in boldface type.
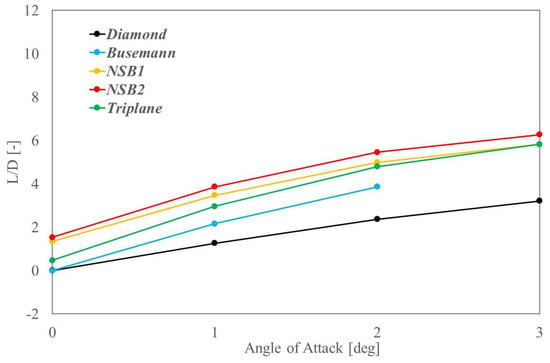
Figure 15.
Comparison of L/D values obtained by 3D CFD evaluations of wing–body models.
The sonic boom performance is also evaluated for the wing–body models. In Figure 16, pressure distributions around the five models are visualized. Pressure waveforms extracted from the CFD results are used as the input information for the sonic boom analysis. In Figure 17a, the near-field pressure waveforms extracted from the location of two fuselage lengths below are compared. In Figure 17a, the first peak appears near x = 30 [m], which is due to the shock wave generated from the head of the fuselage. This can be confirmed from the visualization of the pressure distributions of Figure 16. The second peaks observed in the range 50 < x < 80 [m] are due to shock waves generated from the main wings, that can also be confirmed from the visualization of Figure 16. It can be confirmed from Figure 16 that the shock waves generated from the main wings wrap around the fuselage, which makes high-pressure regions corresponding to the second peak. Therefore, the shock waves generated from the main wings have a significant impact on the near-field pressure waveform of the wing–body models. Specifically, the diamond wing model exhibited the largest second peak, whereas the waveforms were comparable for the biplane/triplane wing models.
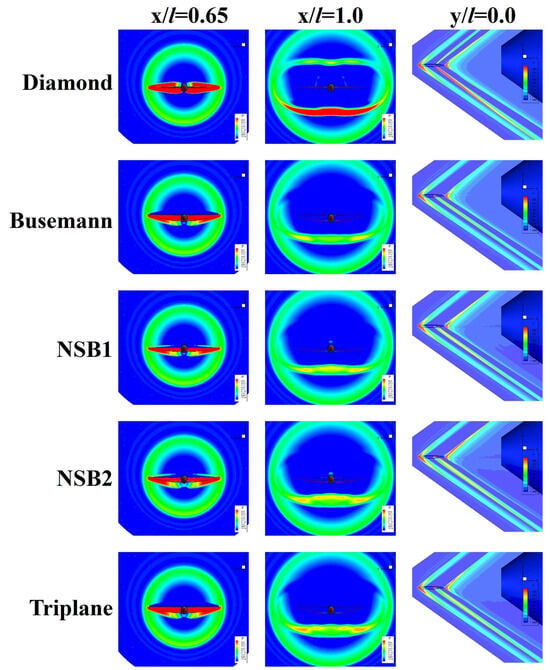
Figure 16.
Pressure distributions around five wing–body models at an AoA of 2 degrees.
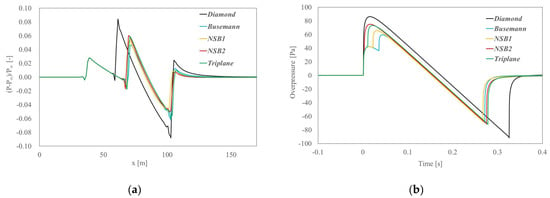
Figure 17.
Sonic boom analysis for 3D wing–body models at an AoA of 2 degrees. (a) Near-field pressure waveforms extracted from two fuselage lengths below; (b) pressure waveforms on the ground.
In Figure 17b, pressure waveforms on the ground are compared. As the metrics of the sonic boom strength, Pmax and ASEL are evaluated from the ground pressure waveforms, that are also indicated in Table 6. The diamond/NSB2 models exhibit typical N-wave distributions, whereas the other models have two peaks in their distributions. When comparing the five models, the Busemann model showed the best results in terms of Pmax, while the biplane/triplane wing models were comparable in terms of ASEL. In Figure 18, ASEL values are compared within the range of 0 AoA 3 degrees, which demonstrates the superior sonic boom performance of biplane/triplane wing configurations compared to the diamond wing configuration.
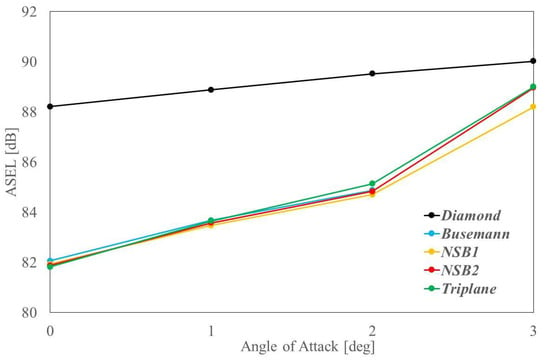
Figure 18.
Comparison of ASEL values obtained by 3D CFD evaluations of wing–body models.
7. Comprehensive Discussion
In this study, we investigated the impact of airfoil configurations on the aerodynamic and sonic boom performance of supersonic transport aircraft. The characteristics of the diamond, Busemann, NSB1, NSB2 and triplane configurations were evaluated through 2D and 3D CFD analyses. For more comprehensive discussion, the correlations between the obtained performance metrics are summarized in Figure 19. Correlations between L/D values obtained by 2D, 3D wing and 3D wing–body models are shown in Figure 19a–c. Figure 19d shows the correlation between L/D and ASEL of the wing–body models. In these graphs, the performance values of each model within the range of 0 AoA 3 degrees are indicated.
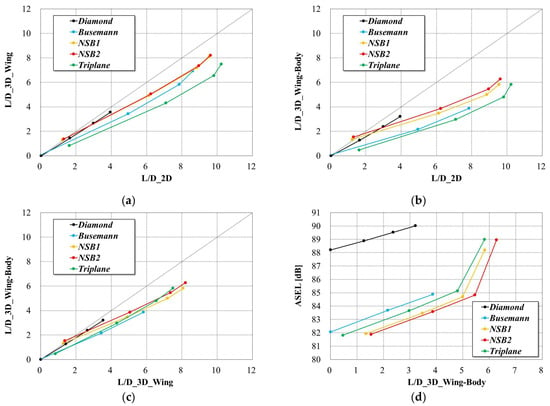
Figure 19.
Correlation between obtained performance metrics. (a) L/D of 2D airfoil and 3D wing models; (b) L/D of 2D airfoil and 3D wing–body models; (c) L/D of 3D wing and 3D wing–body models; (d) L/D and ASEL of 3D wing–body models.
As shown in Figure 19, for all configurations and all performance evaluation methods, L/D values increased with a higher AoA, and L/D values were the highest at an AoA of 3 degrees. When comparing the 2D and 3D L/D values, the triplane configuration exhibited the highest L/D in 2D, whereas the NSB2 was superior in 3D cases. This is considered to be due to the influence of the three dimensionality of the flow caused by the complexity of the triplane configuration. On the other hand, the reduction rate in L/D due to the introduction of a fuselage body was comparable between all configurations. Regarding the sonic boom performance, the boom strength increases with increasing AoA, indicating a tradeoff relationship between L/D and ASEL.
Overall, when comparing the investigated configurations, it can be confirmed that the multiple wing configurations are effective/promising under supersonic flow conditions. Among the multiple wing configurations, the NSB2 configuration has the highest L/D in the 3D analyses, and is considered to be relatively insensitive to the effects of the three dimensionality of the flow. Since the NSB2 configuration had a comparable boom strength to the other multiple wing configurations, it is considered the most promising model in this study and its low-boom design optimization can be considered as a future prospect.
8. Conclusions
In this study, multiple wing configurations were examined to improve the aerodynamic and sonic boom performance of the next-generation supersonic transport aircraft. Promising airfoil configurations were explored using optimization techniques, and 2D optimal airfoil configurations of the NSB1, NSB2 and triplane were obtained. 3D wing and wing–body models were created for the representative 2D airfoil configurations of diamond, Busemann, NSB1, NSB2 and triplane, and their aerodynamic and sonic boom performance was investigated.
In 2D CFD analyses, the interference effect of shock waves was notable in the multiple airfoil configurations. In particular, the introduction of a middle object to the central region of the triplane airfoil configuration achieved increased lift and reduced drag through complex shock wave interference, resulting in the highest L/D in the 2D CFD analyses.
In 3D wing model analyses, the triplane wing configuration was significantly affected by the three-dimensionality of the flow due to the complexity of its shape and of the flow field, and then L/D was decreased. On the other hand, the NSB2 wing exhibited the highest L/D in the 3D wing model analyses. In the wing–body model analyses, although the L/D was decreased with the introduction of the fuselage, the trend of the aerodynamic performance was similar to that of the wing model analyses, and the effect of improving aerodynamic performance due to the multiple wing configurations was also confirmed in the wing–body model analyses. Regarding sonic boom performance, the significant impact of shock waves generated from the main wing was confirmed, and a reduction in sonic boom strength was confirmed in the multiple wing configurations.
Overall, it was confirmed that the multiple wing configurations were effective/promising for the wing of SSTs. Among the multiple wing configurations, NSB2 had the highest L/D in the 3D analyses, and was considered to be relatively insensitive to the effects of the three dimensionality of the flow. As for future prospects, it is necessary to investigate the wing planform shape and consider ways for further suppression/successful interaction of shock waves generated from the main wing. It is also important to suppress the performance degradation when converting 2D optimal airfoil shapes into 3D wing models. Additionally, as the introduction of the fuselage caused a significant decrease in aerodynamic performance, it is also necessary to introduce a more sophisticated fuselage body to realize further improvement in aerodynamic performance. Another area for future work is multi-objective/robust design optimizations to realize low-boom/low-drag NSB configurations with improved off-design performance.
Author Contributions
Conceptualization, W.Y. and S.I.; methodology, W.Y.; software, W.Y.; validation, W.Y.; formal analysis, S.I.; investigation, S.I. and W.Y.; resources, W.Y.; data curation, S.I. and W.Y.; writing—original draft preparation, W.Y. and S.I.; writing—review and editing, W.Y.; visualization, S.I.; supervision, W.Y.; project administration, W.Y.; funding acquisition, W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by JSPS KAKENHI, grant numbers 22K03874 and 22H00184.
Data Availability Statement
Data are contained within this article.
Acknowledgments
The authors are grateful for Japan Aerospace Exploration Agency about the support to utilize the software of MEGG3D (version 6.9) and Xnoise (version 1.6).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ueno, A.; Watanabe, Y.; Din, I.S.E.; Grenon, R.; Carrier, G. Low Boom/Low Drag Small Size Supersonic Aircraft Design. In Proceedings of the VII European Congress on Computational Methods in Applied Sciences and Engineering, Crete, Greece, 5–10 June 2016. [Google Scholar]
- Quagliarella, D.; Iuliano, E. UQ Sensitivity Analysis and Robust Design Optimization of a Supersonic Natural Laminar Flow Wing-Body. Notes Numer. Fluid Mech. Multidiscip. Des. 2018, 140, 601–628. [Google Scholar] [CrossRef]
- Honda, M.; Yoshida, K. D-SEND Project for Low Sonic Boom Design Technology. In Proceedings of the 28th ICAS Congress, Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Bons, N.; Martins, J.; Mader, C.A.; McMullen, M.S.; Suen, M. High-fidelity Aerostructural Optimization Studies of the Aerion AS2 Supersonic Business Jet. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 15–19 June 2020. [Google Scholar] [CrossRef]
- Liebhardt, B.; Lütjens, K.; Ueno, A.; Ishikawa, H. JAXA’s S4 Supersonic Low-Boom Airliner—A Collaborative Study on Aircraft Design, Sonic Boom Simulation, and Market Prospects. In Proceedings of the AIAA Aviation 2020 Forum, Virtual, 15–19 June 2020. [Google Scholar] [CrossRef]
- Jim, T.M.S.; Faza, G.A.; Palar, P.S.; Shimoyama, K. A Multiobjective Surrogate-assisted Optimisation and Exploration of Low-Boom Supersonic Transport Planforms. Aerosp. Sci. Technol. 2022, 128, 107747. [Google Scholar] [CrossRef]
- Liu, C.; Meng, X.; Liu, J.; Zhou, J.; Bai, P. Experimental Investigation for Subsonic, Transonic, and Supersonic Performances of Double-Swept Waverider. AIAA J. 2023, 61, 4247–4258. [Google Scholar] [CrossRef]
- Chen, Q.; Han, Z.H.; Ding, Y.L.; Jianling, Q.; Song, K.; Song, W. Low-Boom Design of a T-tail Supersonic Transport Configuration. In Proceedings of the APISAT 2023, Lingshui, China, 16–18 October 2023. [Google Scholar]
- Buyanbaatar, N.; Yamazaki, W. Efficient Multi-objective Aerodynamic Shape Optimization of 3D Supersonic Transport Using Proper Orthogonal Decomposition. Trans. Jpn. Soc. Aeronaut. Space Sci. 2023, 66, 147–155. [Google Scholar] [CrossRef]
- Bonavolontà, G.; Lawson, C.; Riaz, A. Review of Sonic Boom Prediction and Reduction Methods for Next Generation of Supersonic Aircraft. Aerospace 2023, 10, 917. [Google Scholar] [CrossRef]
- Kusunose, K. Aerodynamic Design of Supersonic Biplane: Cutting Edge and Related Topic; Tohoku University Press: Sendai, Japan, 2007. [Google Scholar]
- Yonezawa, M.; Obayashi, S. Reducing Drag Penalty in the Three-Dimensional Supersonic Biplane. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2009, 223, 891–899. [Google Scholar] [CrossRef]
- Kusunose, K.; Matsushima, K.; Maruyama, D. Supersonic biplane—A review. Prog. Aerosp. Sci. 2011, 47, 53–87. [Google Scholar] [CrossRef]
- Hu, R.; Jameson, A.; Wang, Q. Adjoint-Based Aerodynamic Optimization of Supersonic Biplane Airfoils. J. Aircr. 2012, 49, 802–814. [Google Scholar] [CrossRef]
- Yamazaki, W.; Kusunose, K. Aerodynamic Study of Twin-Body Fuselage Configuration for Supersonic Transport. Trans. Jpn. Soc. Aeronaut. Space Sci. 2013, 56, 229–236. [Google Scholar] [CrossRef]
- Yamazaki, W.; Kusunose, K. Aerodynamic/Sonic Boom Performance Evaluation of Innovative Supersonic Transport Configurations. J. Aircr. 2016, 53, 942–950. [Google Scholar] [CrossRef]
- Patidar, V.K.; Yadav, R.; Joshi, S. Numerical Investigation of the Effect of Stagger on the Aerodynamic Characteristics of a Busemann Biplane. Aerosp. Sci. Technol. 2016, 55, 252–263. [Google Scholar] [CrossRef]
- Ban, N.; Yamazaki, W.; Kusunose, K. Low-Boom/Low-Drag Design Optimization of Innovative Supersonic Transport Configuration. J. Aircr. 2018, 55, 1071–1081. [Google Scholar] [CrossRef]
- Hanazaki, K.; Yamazaki, W. Robust Design Optimization of Supersonic Biplane Airfoil Using Efficient Uncertainty Analysis Method for Discontinuous Problem. Aerospace 2024, 11, 64. [Google Scholar] [CrossRef]
- Payot, A.D.; Rendall, T.C.S.; Allen, C.B. Restricted Snakes Volume of Solid (RSVS): A Parameterisation Method for Topology Optimisation of External Aerodynamics. Comput. Fluids 2019, 102, 60–84. [Google Scholar] [CrossRef]
- Wood, M.J.; Rendall, T.C.S.; Allen, C.B.; Taylor, N.J.; Fincham, J.; Leppard, N. Gradient-Based Aerodynamic Optimisation for Two- and Three-Dimensional Supersonic Flows Using a Volume-of-Solid Parameterisation. In Proceedings of the AIAA Scitech 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Ban, N. Efficient Aerodynamic Topology Optimization on Supersonic Flow Field via Machine Learning Technologies. Ph.D. Thesis, Nagaoka University of Technology, Niigata, Japan, 2019. [Google Scholar]
- Ban, N.; Yamazaki, W. Black-box Function Aerodynamic Topology Optimization Algorithm via Machine Learning Technologies. AIAA J. 2021, 59, 5174–5185. [Google Scholar] [CrossRef]
- Liao, P.; Song, W.; Du, P.; Feng, F.; Zhang, Y. Aerodynamic Intelligent Topology Design (AITD)-A Future Technology for Exploring the New Concept Configuration of Aircraft. Aerospace 2023, 10, 46. [Google Scholar] [CrossRef]
- Hirose, K.; Suzuki, K.; Yamazaki, W. Aerodynamic Topology Optimization of Supersonic Airfoils using Feature Extraction via Dimensionality Reduction Methods. In Proceedings of the APISAT 2024, Adelade, Australia, 28–30 October 2024. [Google Scholar]
- Zhai, J.; Zhang, C.A.; Wang, F.M.; Zhang, W.W. Design of New Supersonic Biplane. Acta Astronaut. 2020, 175, 216–233. [Google Scholar] [CrossRef]
- Ban, N.; Yamazaki, W. Development of Efficient Global Optimization Method for Discontinuous Optimization Problems with Infeasible Region via Classification Method. J. Adv. Mech. Des. Syst. Manuf. 2019, 13, JAMDSM0017. [Google Scholar] [CrossRef]
- Ban, N.; Yamazaki, W. Efficient Global Optimization Method via Clustering/Classification Methods and Exploration Strategy. Optim. Eng. 2021, 22, 521–553. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, H.; Zhou, C. A Study of Point Moving Adaptivity in Gridless Method. Comput. Meth. Appl. Mech. Eng. 2008, 197, 1926–1937. [Google Scholar] [CrossRef]
- Yamazaki, W.; Matsushima, K.; Nakahashi, K. Drag Prediction, Decomposition and Visualization in Unstructured Mesh CFD Solver of TAS-Code. Int. J. Numer. Methods Fluids 2008, 57, 417–436. [Google Scholar] [CrossRef]
- Ito, Y.; Nakahashi, K. Direct Surface Triangulation Using Stereolithography Data. AIAA J. 2002, 40, 490–496. [Google Scholar] [CrossRef]
- Ito, Y.; Nakahashi, K. Surface Triangulation for Polygonal Models Based on CAD Data. Int. J. Numer. Methods Fluids 2002, 39, 75–96. [Google Scholar] [CrossRef]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 4th ed.; AIAA: Reston, VA, USA, 2006; pp. 327–330. [Google Scholar]
- Krasnov, N.F. Aerodynamics of Bodies of Revolution; Elsevier: New York, NY, USA, 1970; pp. 379–385. [Google Scholar]
- Yamamoto, M.; Hashimoto, A.; Takahashi, T.; Kamamura, T.; Sakai, T. Long-range Sonic Boom Prediction Considering Atmospheric Effects. In Proceedings of the InterNoise 2011, Osaka, Japan, 4–7 September 2011. [Google Scholar]
- Yamamoto, M.; Hashimoto, A.; Takahashi, T.; Kamakura, T.; Sakai, T. Numerical Simulations for Sonic Boom Propagation through an Inhomogeneous Atmosphere with Winds. In Proceedings of the 19th International Symposium on Nonlinear Acoustics, Tokyo, Japan, 21–24 May 2012. [Google Scholar]
- Naka, Y. Sonic Boom Data from D-SEND#1. JAXA Research and Development Memorandum, JAXA RM-11-010E; JAXA: Tokyo, Japan, 2012. [Google Scholar]
- JAXA D-SEND Database Website. Available online: http://d-send.jaxa.jp/d_send_1.html (accessed on 31 March 2025).
- Yamazaki, W.; Mavriplis, D.J. Derivative-enhanced Variable Fidelity Surrogate Modeling for Aerodynamic Functions. AIAA J. 2013, 51, 126–137. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).