End-to-End GNC Solution for Reusable Launch Vehicles
Abstract
1. Introduction
1.1. Background and State of the Art
1.2. Notation
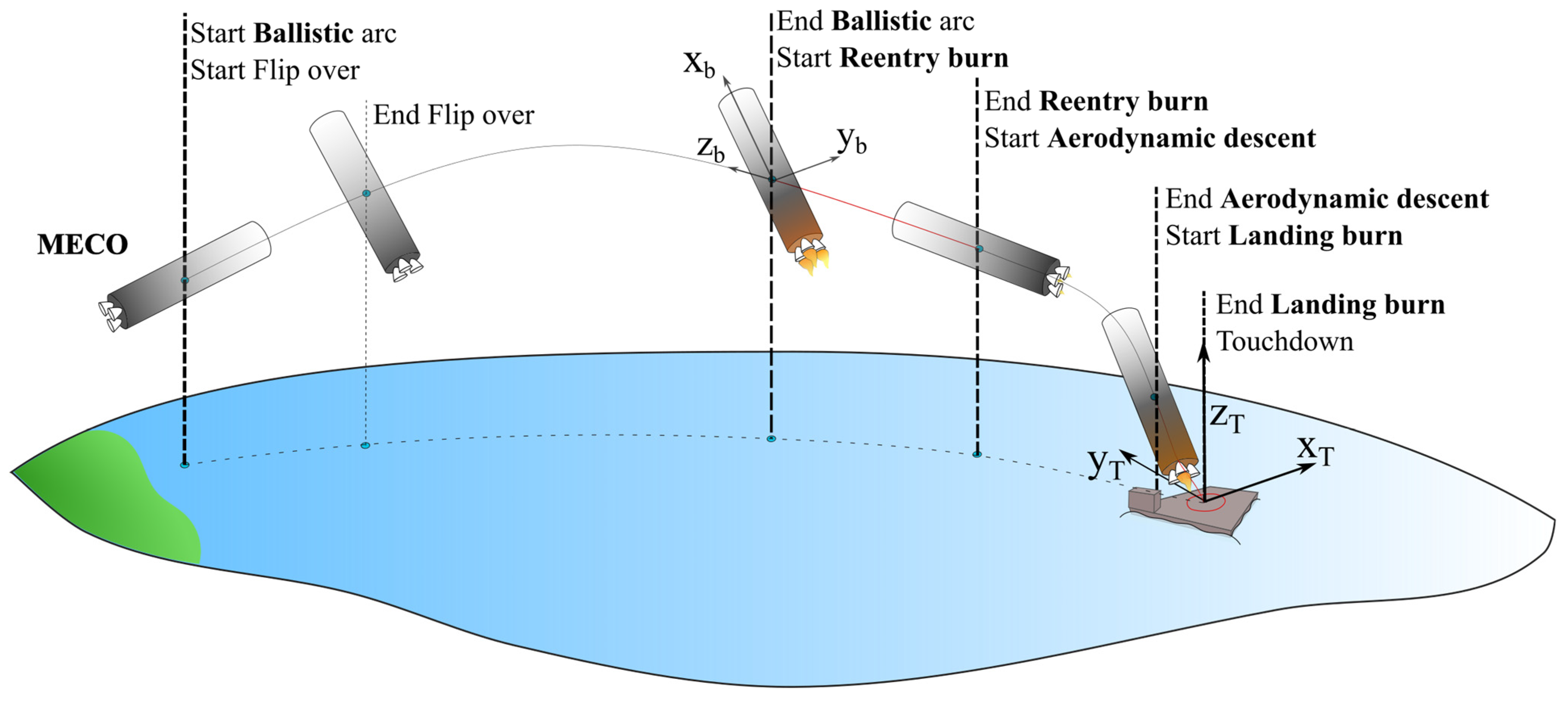
2. Reference Mission and Configuration Overview
3. Guidance, Navigation, and Control Architecture
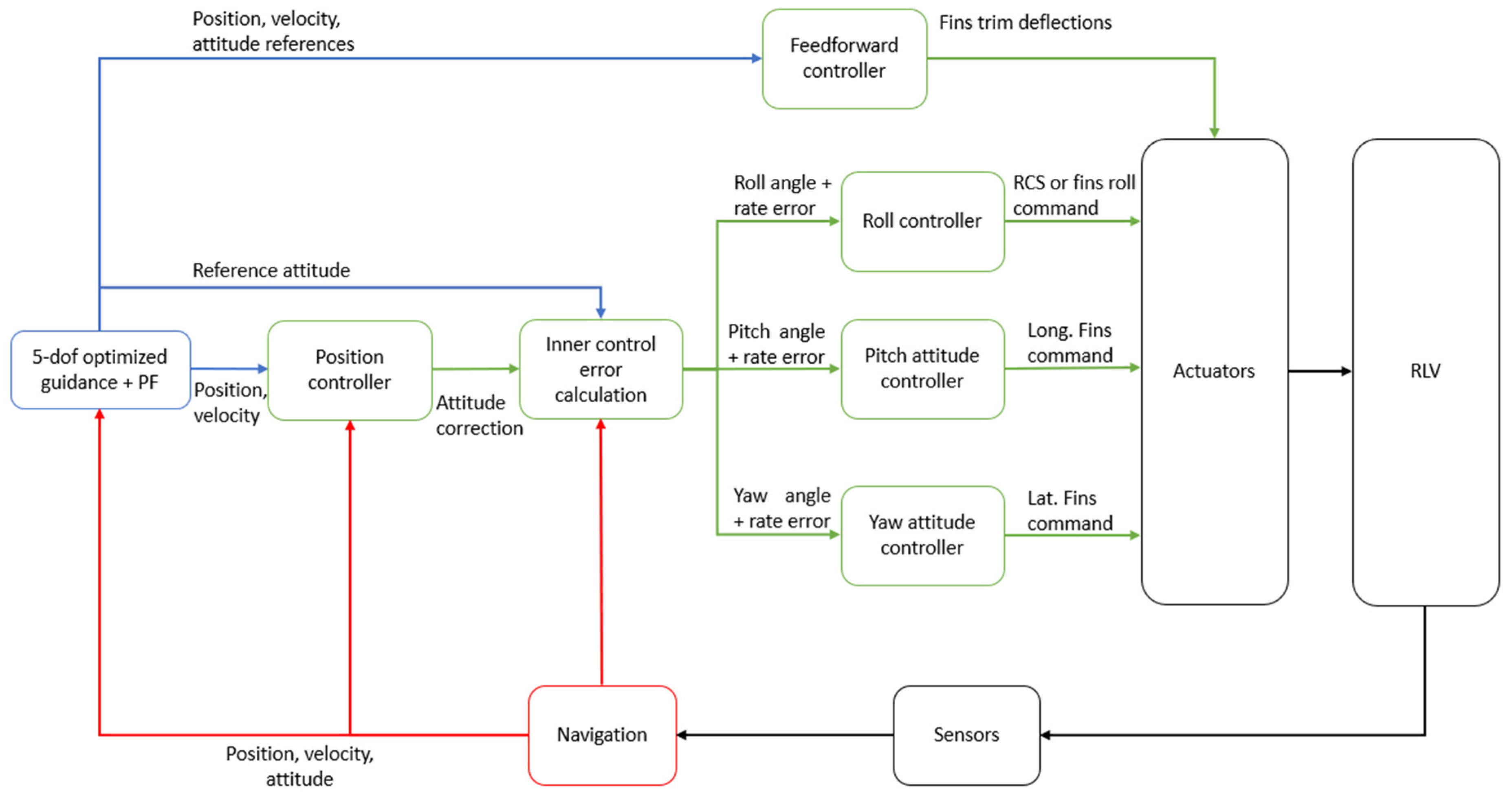
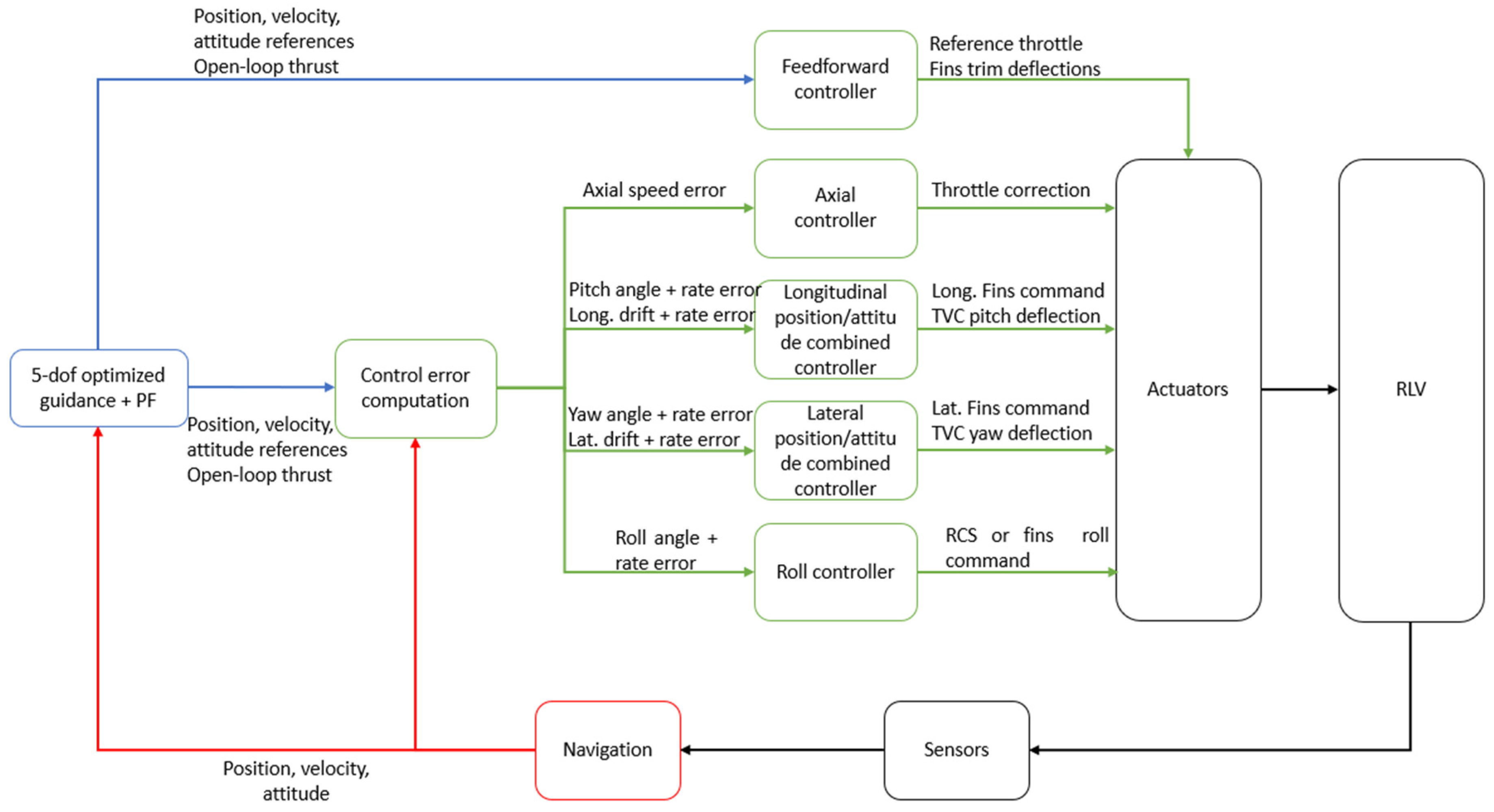
3.1. GNC Functional Architecture
- Flight Management (FM): The FM oversees both the internal status and data from all the other functions and defines the functional modes of each of them depending on the phase and the conditions of flight. The FM interacts with the Mission Vehicle Management (MVM), which manages the interaction of the GNC with other vehicles subsystems.
- Guidance: The objective of the guidance algorithm is to define the reference trajectory and the control actions required to track it. This shall be designed so as to allow for the vehicle to arrive at the designated target site, satisfying the mission and flight path constraints.
- Navigation: The navigation function estimates the current state of the system. The navigation solution is served primarily by the inertial measurement unit (IMU or INS (inertial navigation system)), which is hybridized with a (D)GNSS receiver. Navigation could also make use of other sensors (e.g., FADS (Flush Airdata Sensing), altimeter), if available, depending on the mission phase, even if they are not strictly required.
- Control: The control function task is to ensure a correct tracking of the reference states generated by the guidance using the GNC’s available actuators.
3.2. GNC Modes
- High-altitude ballistic flight: During this phase, neither thrust nor aerodynamic forces are available to perform trajectory control. The control function actuates the RCS to perform a flip-over and aligns the vehicle to the reference attitude for the re-entry burn. During this phase, the aerodynamic control surfaces (ACSs) are deployed. The navigation function continues estimating the position, velocity, and attitude, making use of inertial measurements fused with (D)GNSS updates.
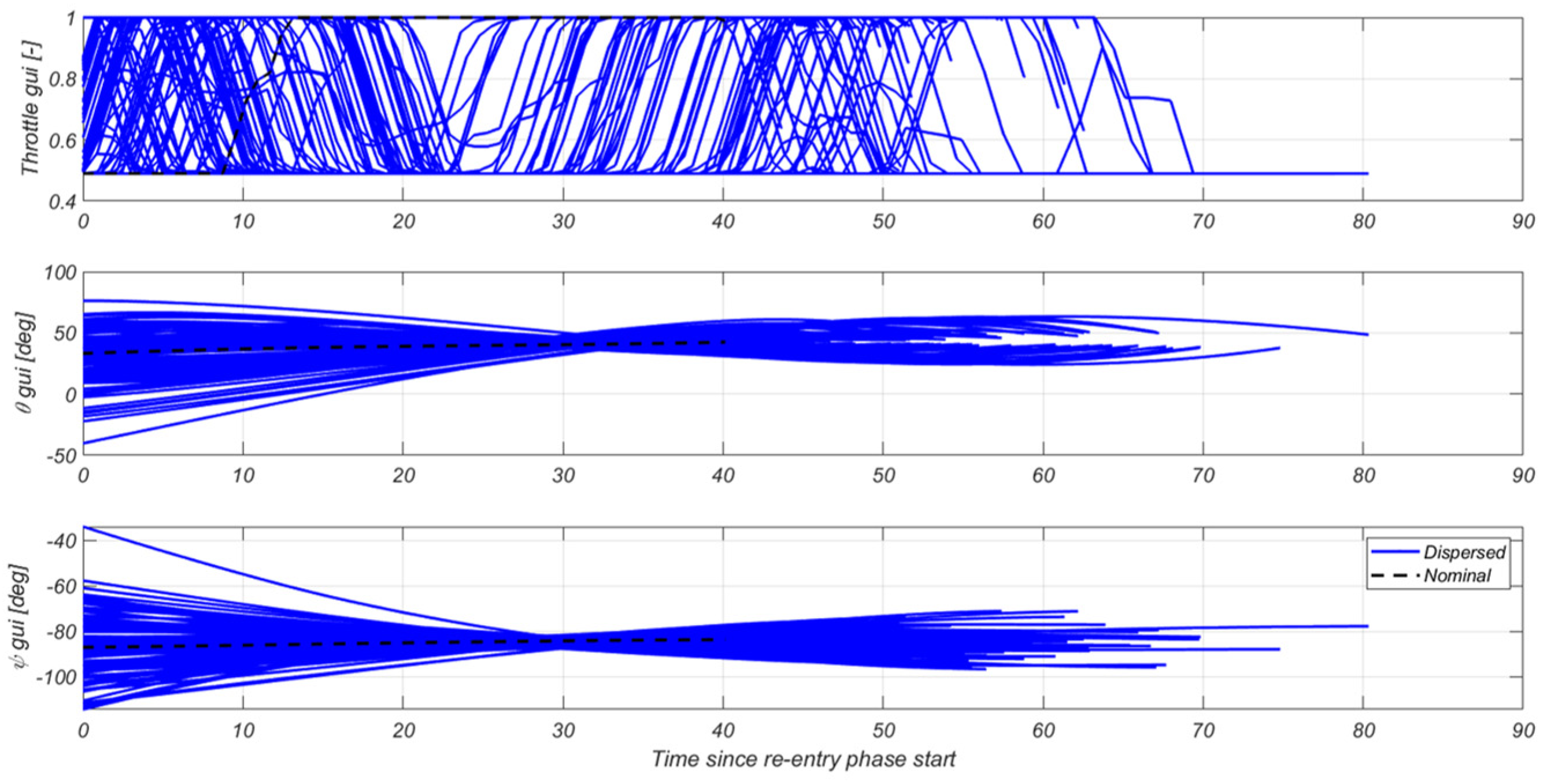
- Re-entry burn: During the re-entry burn, the vehicle carries out a retro-propulsion braking maneuver to reduce the velocity of the booster and limit the aerodynamic load. When this mode is triggered, the guidance function generates a trajectory (position, velocity, attitude, and throttle profile) accounting for the vehicle’s initial conditions and operational constraints, and the control function takes care of orienting and steering the vehicle using the TVC, RCS, and throttle modulation (the effectiveness of the ACS is too low during this phase). The navigation function continues estimating the position, velocity, and attitude, making use of inertial measurements fused with (D)GNSS updates.
- Aerodynamic phase: During the aerodynamic phase, the guidance function outputs a reference trajectory to target the correct location at the start of the landing burn by modulating the attitude. The control function uses fins and RCS to correct the vehicle drift with respect to the guidance reference. The navigation function continues estimating the position, velocity, and attitude, making use of inertial measurements fused with (D)GNSS updates and with (F)ADS measurements, if available.
- Landing burn: During the landing phase, the guidance function commands the nominal throttle profile and thrust orientation required to perform a safe approach to the recovery barge and achieve pinpoint landing. The control function uses the TVC, ACS, RCS, and throttle modulation to perform the required maneuvers and track the desired path. The navigation function could use an altimeter and (F)ADS, if available, to further improve the accuracy of the estimation approaching the landing site.
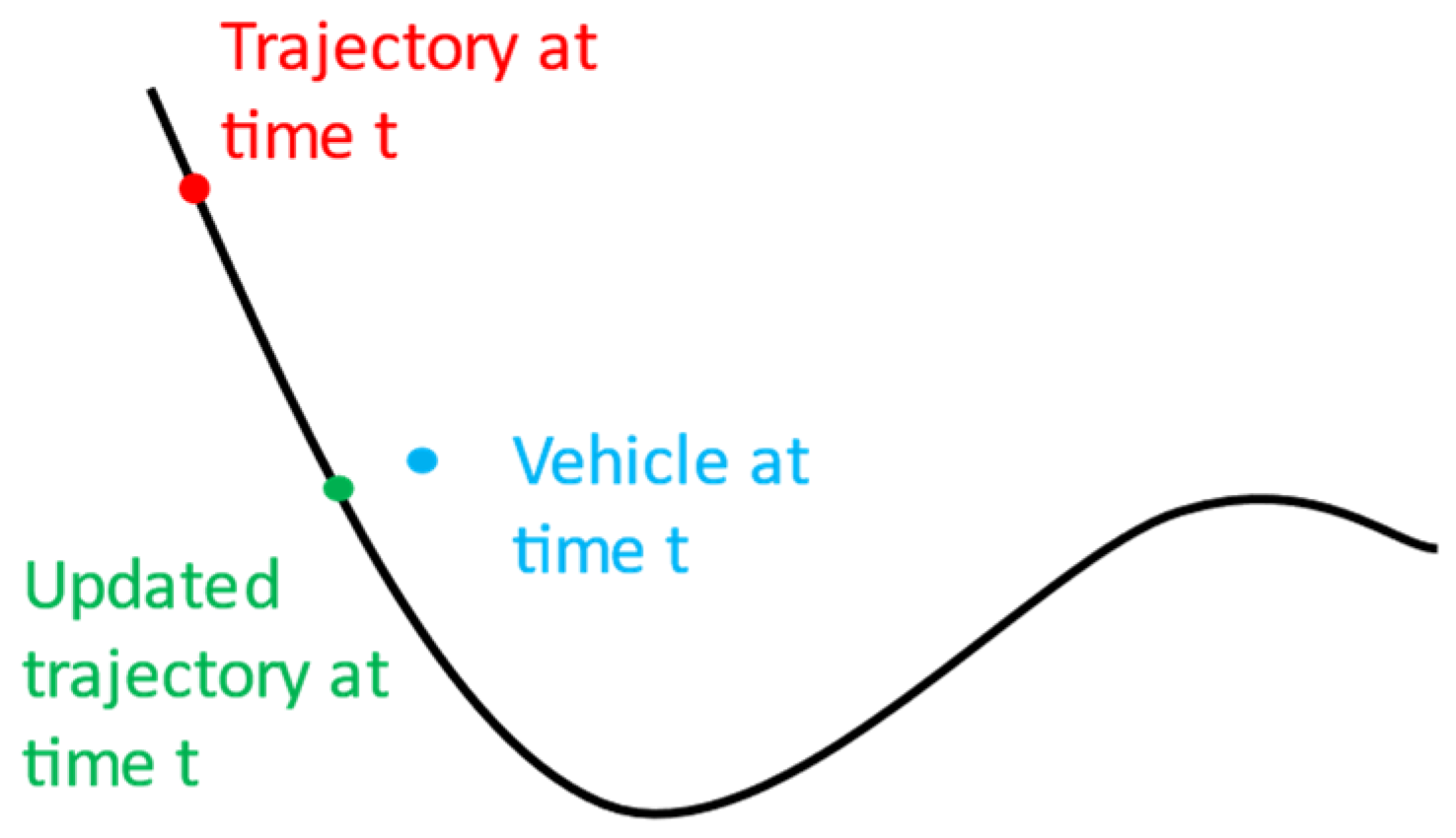
3.3. Sequential Convex Programming (SCP) Onboard Guidance
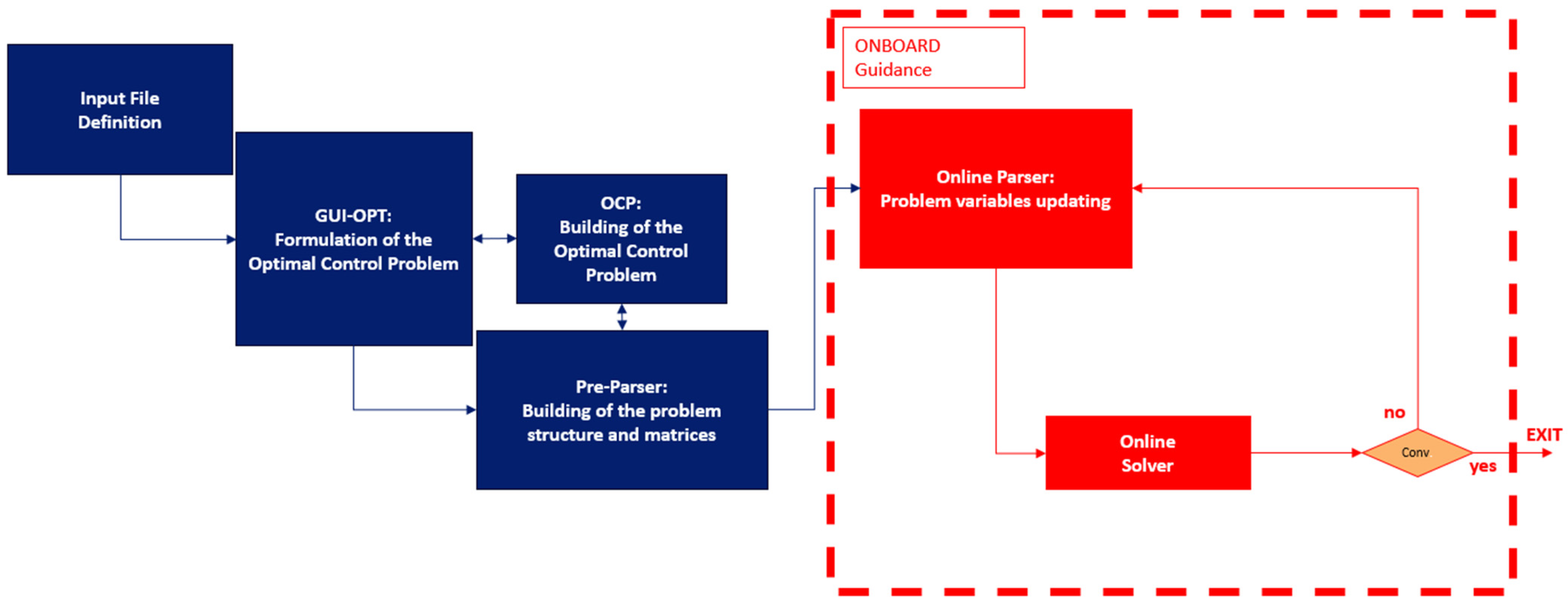
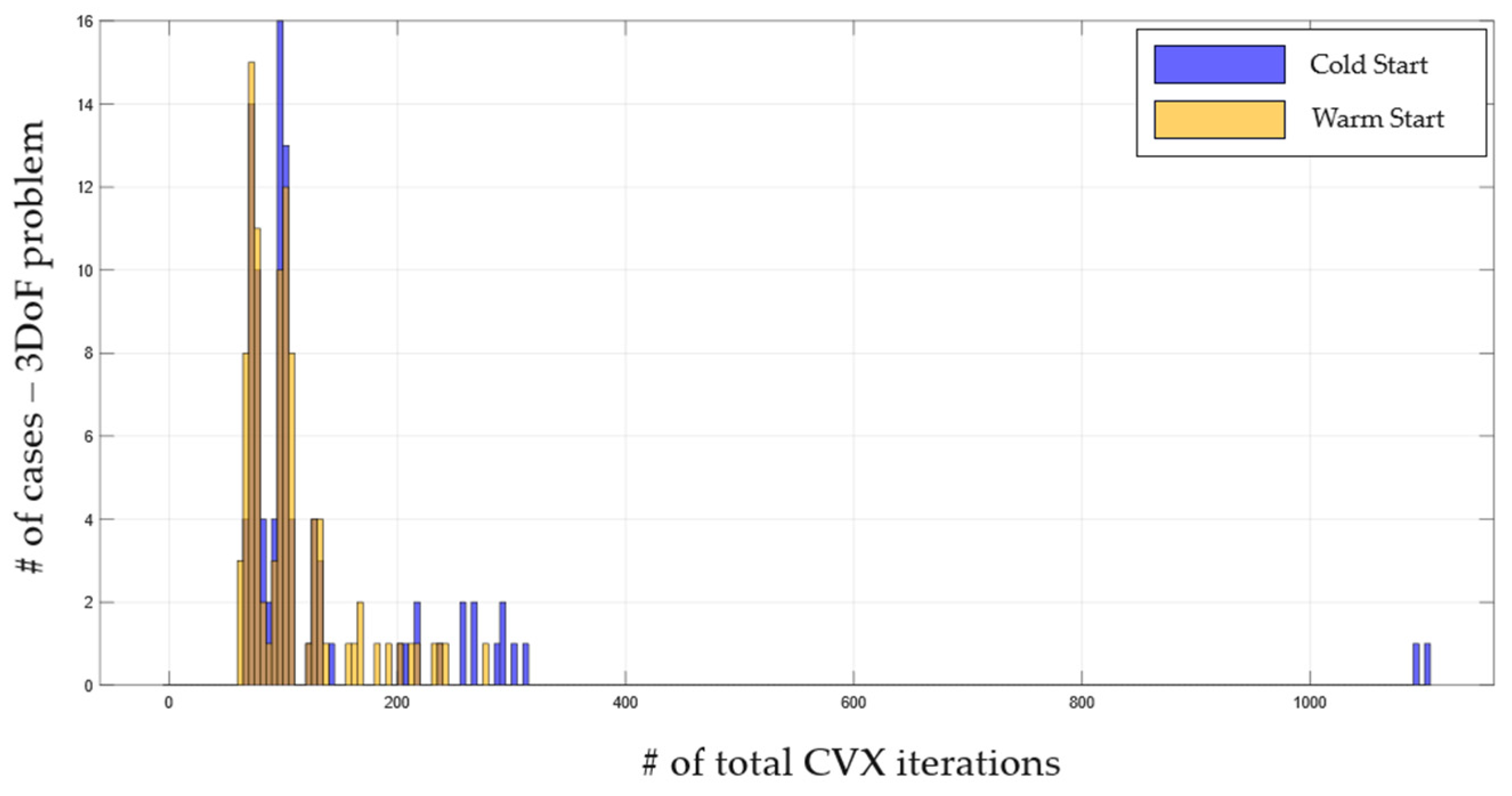
3.4. Real-Time Implementation and PIL Integration
3.4.1. Offline Pre-Parsing
3.4.2. Online Parsing and Solving
3.5. Control Methods Overview
3.5.1. Control Problem Formulation
- Setpoint tracking: Of paramount importance to ensure good accuracy in terms of either position or attitude reference profile tracking.
- Disturbance attenuation: The control system must be capable of rejecting external perturbations.
- Control effort moderation: The control system actuators present a physical limitation. This limitation must be accounted for during the tuning process.
- Stability margins: It is of paramount importance that the closed loop is stable in presence of unmodelled effects and parametric uncertainties. Robustness can be quantified via classical gain and phase margins or disk margins.
| High Level Objective | Synthesis Objective |
|---|---|
| Setpoint tracking | |
| Disturbance attenuation | |
| Control effort moderation | |
| Stability margins at input | |
| Stability margins at output | |
| Setpoint tracking |
3.5.2. Control-Oriented Modelling
4. Guidance and Control Design
4.1. Flip-Over and Ballistic Phase
4.1.1. Scheduling LUT
4.1.2. Slew Maneuver Design
4.1.3. Flip-Over Control Design
4.2. Re-Entry Burn Phase
4.2.1. Powered Re-Entry Guidance Design
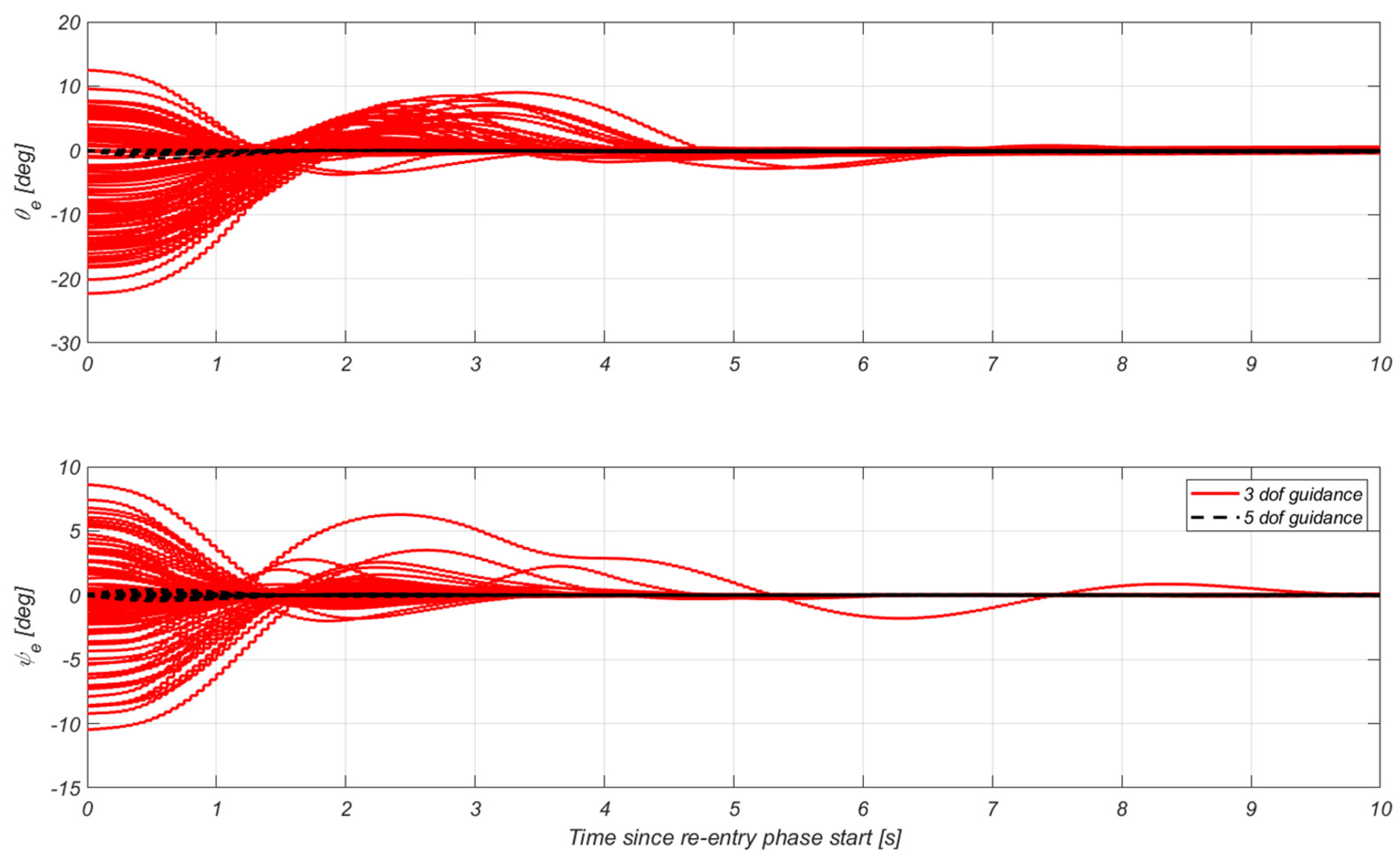
4.2.2. 3DoF vs. 5DoF Guidance Problem Formulation
4.2.3. Re-Entry Powered Control Design
4.2.4. Path-Following Logic
4.2.5. Re-Entry G&C Specific Results
4.3. Aerodynamic Phase
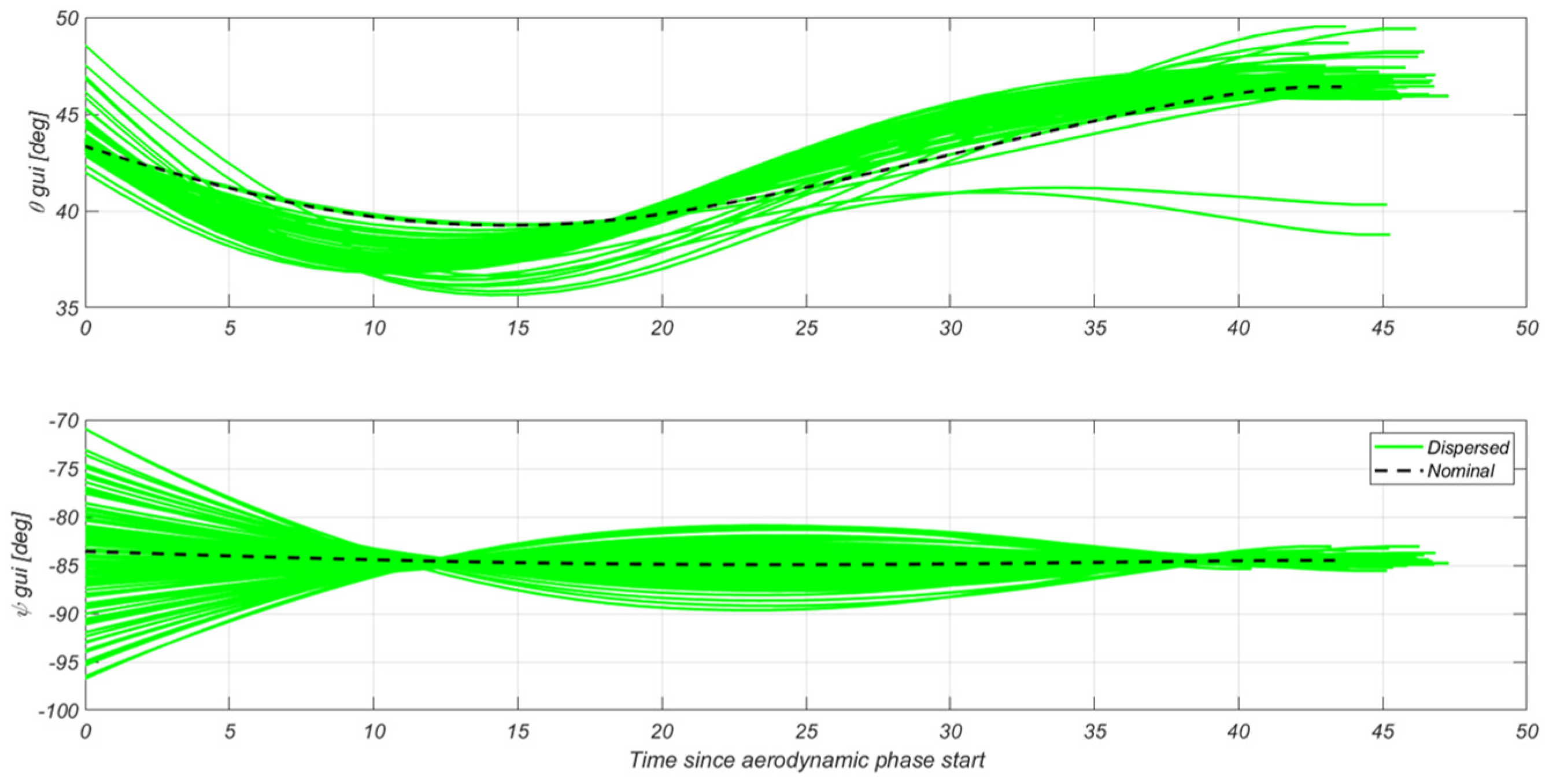
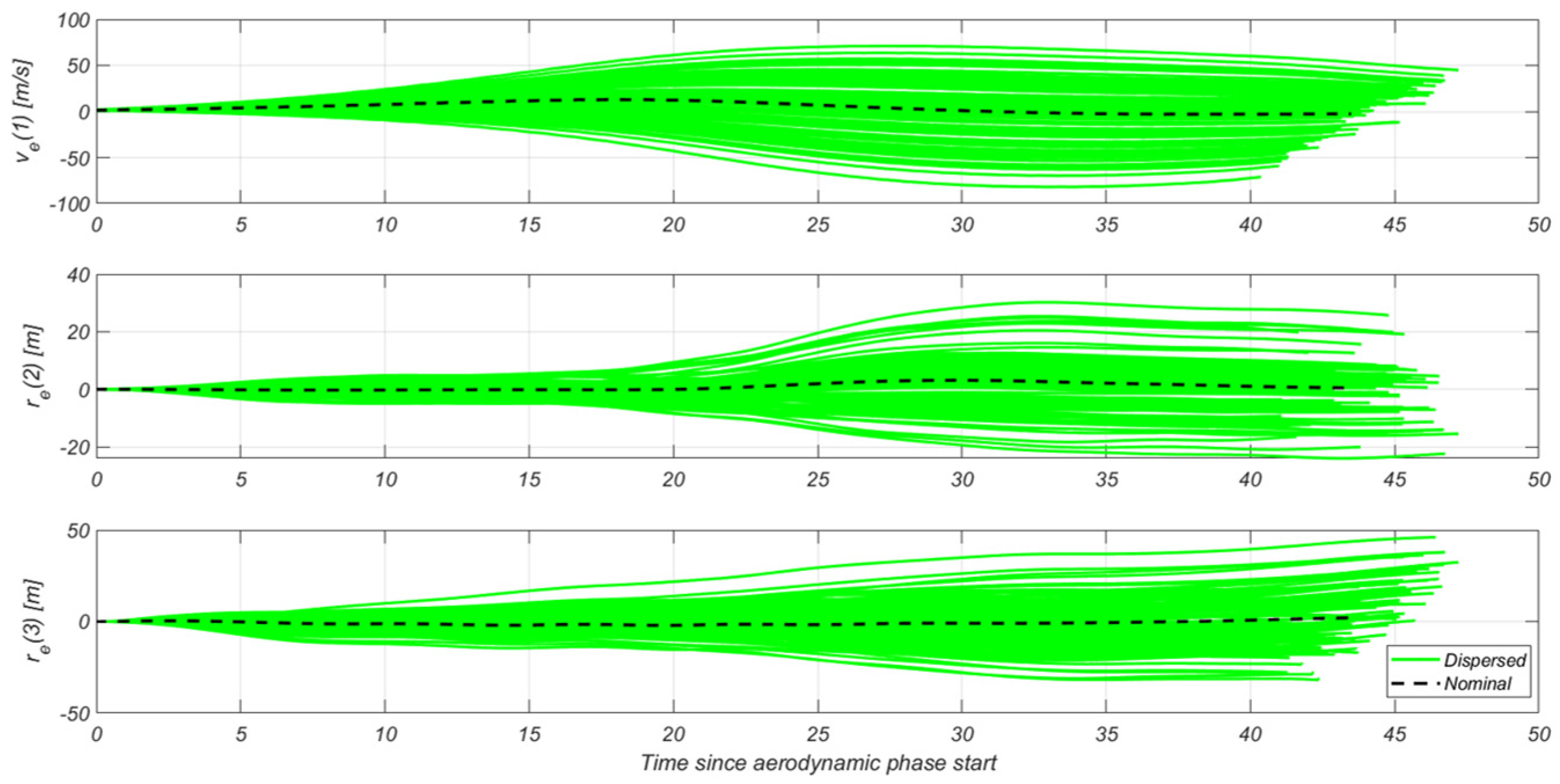
4.3.1. Aerodynamic Descent Guidance Design
4.3.2. Roll Command for Zero-Sideslip
- The vehicle is symmetrical, so its aerodynamic properties are optimal. To make this assumption, we neglect the impact of the fins on the AEDB symmetry characteristics and winds (which we assume negligible compared to the airspeed for guidance purposes for this phase of flight).
- The roll angle is such that the sideslip angle is zero. The value of this angle can be found via the definition of the sideslip angle as
4.3.3. Aerodynamic Descent Control Design
4.3.4. Aerodynamic G&C-Specific Results
4.4. Landing Burn Phase
4.4.1. Powered Landing Guidance Design
- The aerodynamics coefficients are approximated with splines in order to have smoother profiles. In this phase, the side force is also taken into account, and due to the symmetry of the vehicle, is modelled as the .
- Since a wind profile is considered, the velocity of the vehicle with respect to the ground and the one respect to the air do not coincide, so
- The wind speed profile is assumed to be a function of the altitude only. The guidance knows the mean wind value at the mission epoch (Figure 16). During the simulations, uncertainties on the wind are considered.
- The formulation of the dynamics equation by considering the relative velocity introduces additional terms in the computation of the Jacobians during the convexification step, since
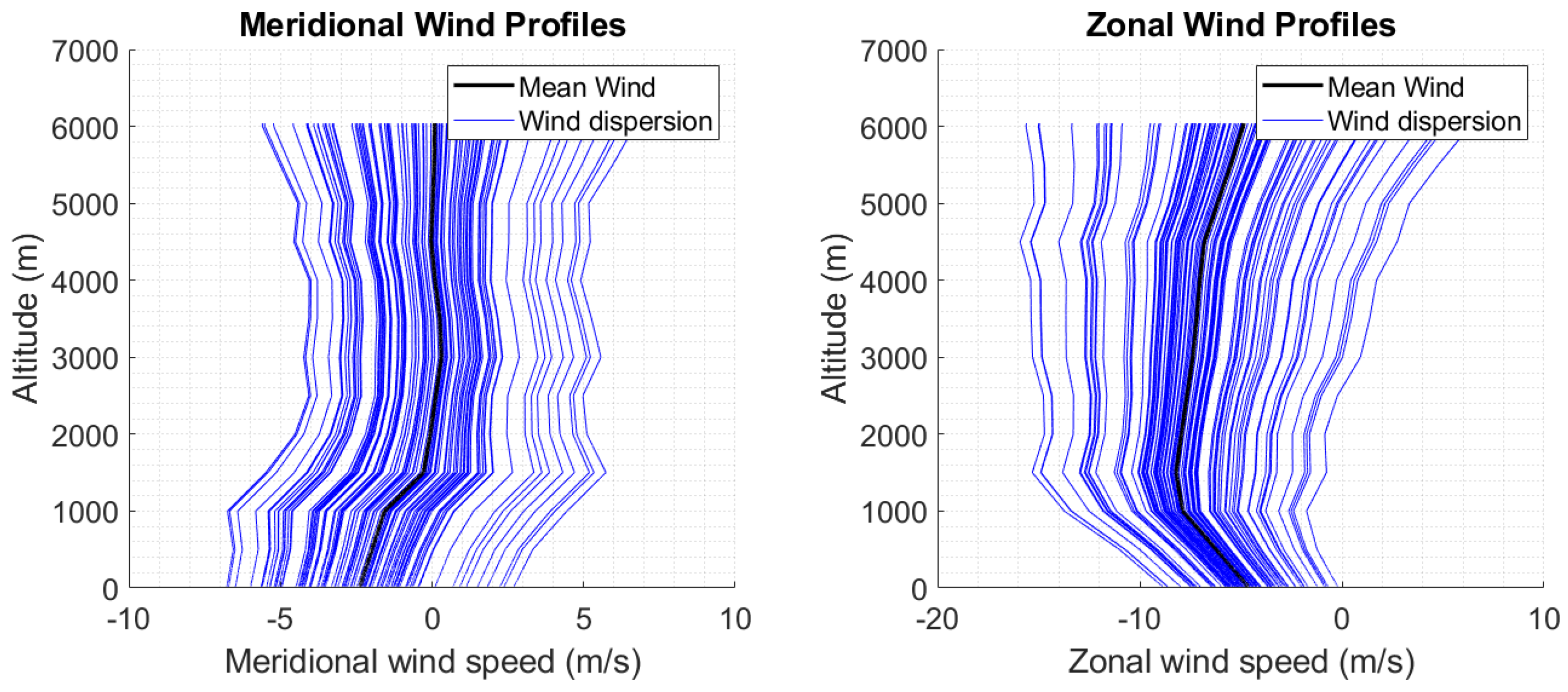
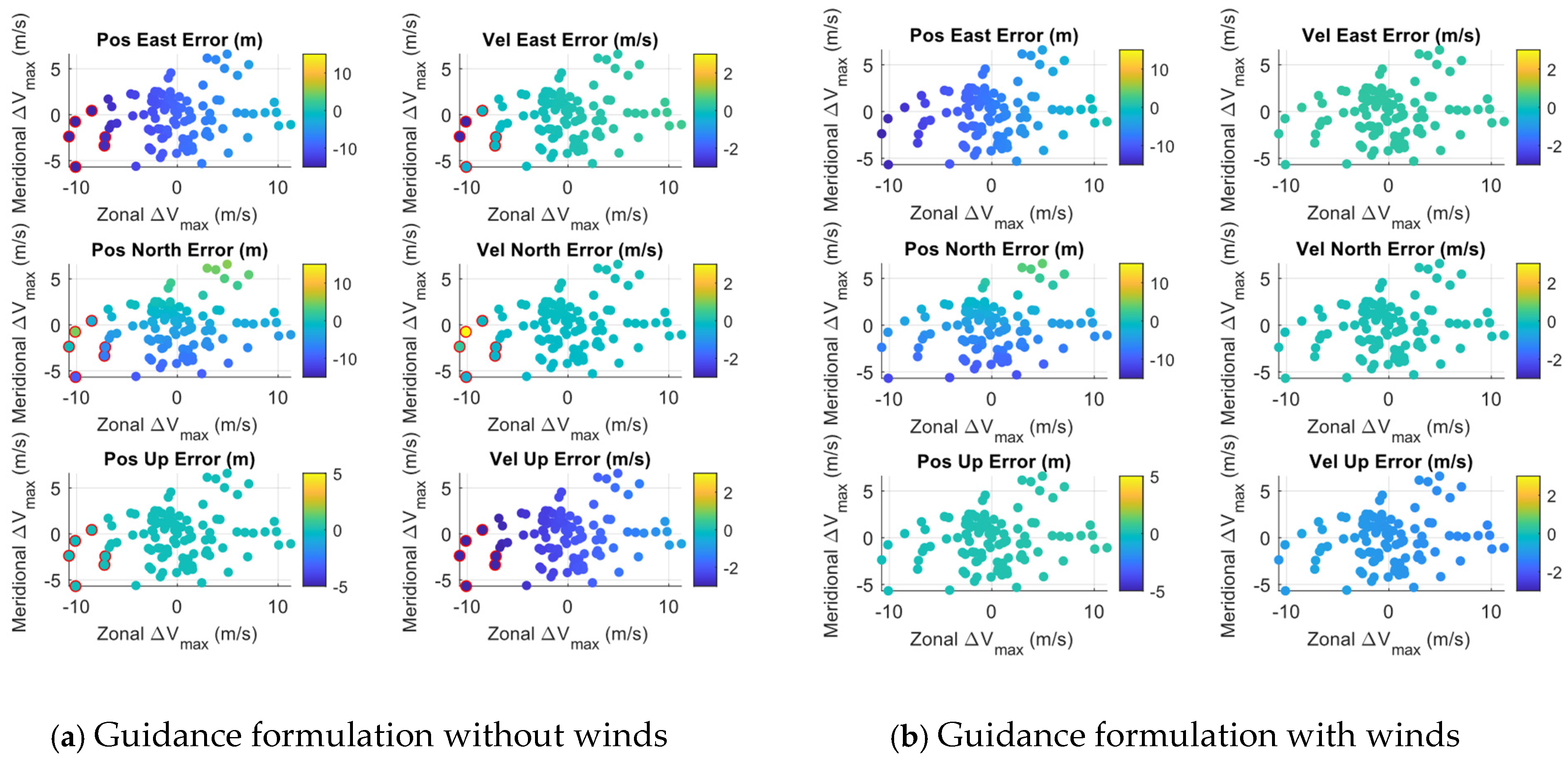
4.4.2. Benefits of the Wind Knowledge in the Landing Guidance
| Landing Requirements | Value |
|---|---|
| East position | |
| North position | |
| East velocity | |
| North velocity | |
| Vertical velocity | |
| Pitch |
4.4.3. Landing Powered Control Design
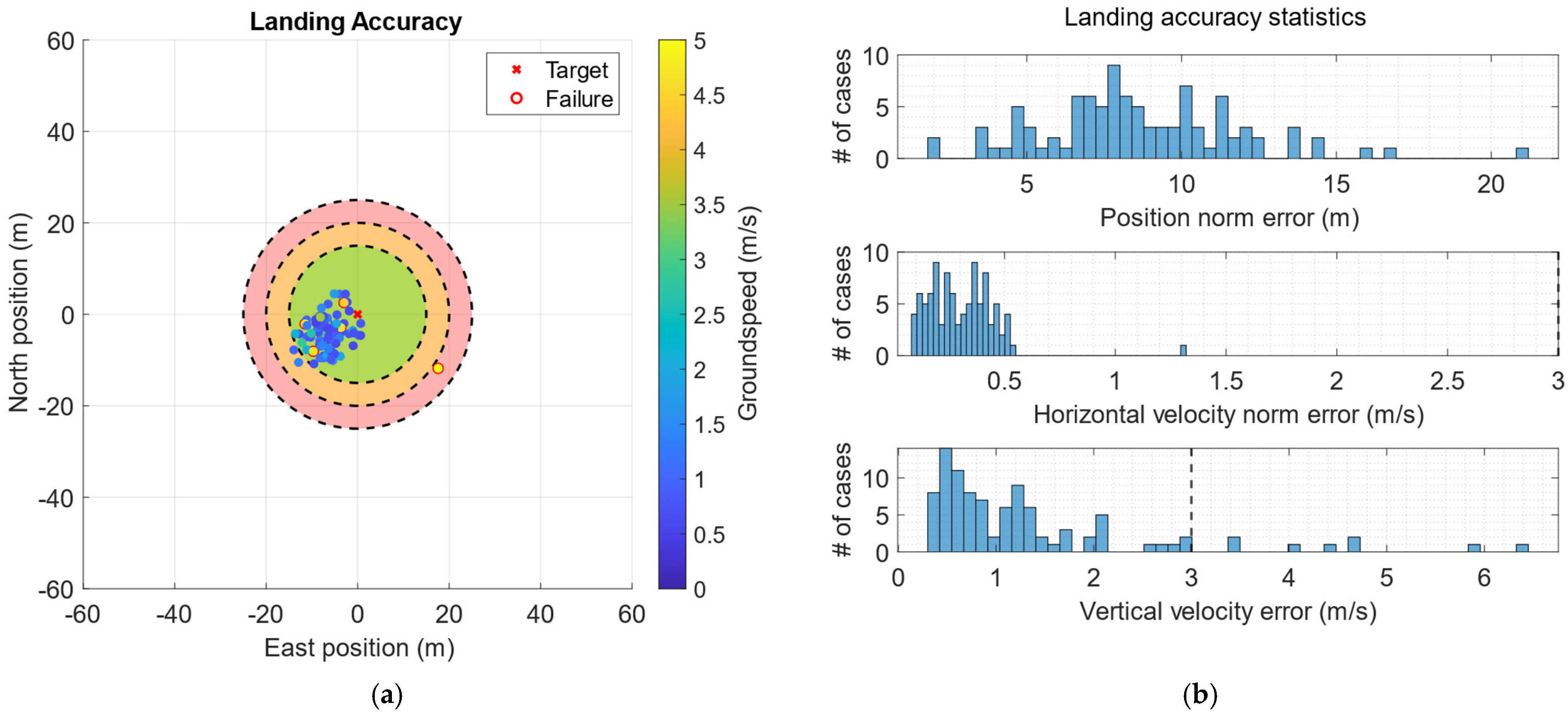
4.4.4. Landing G&C Specific Results
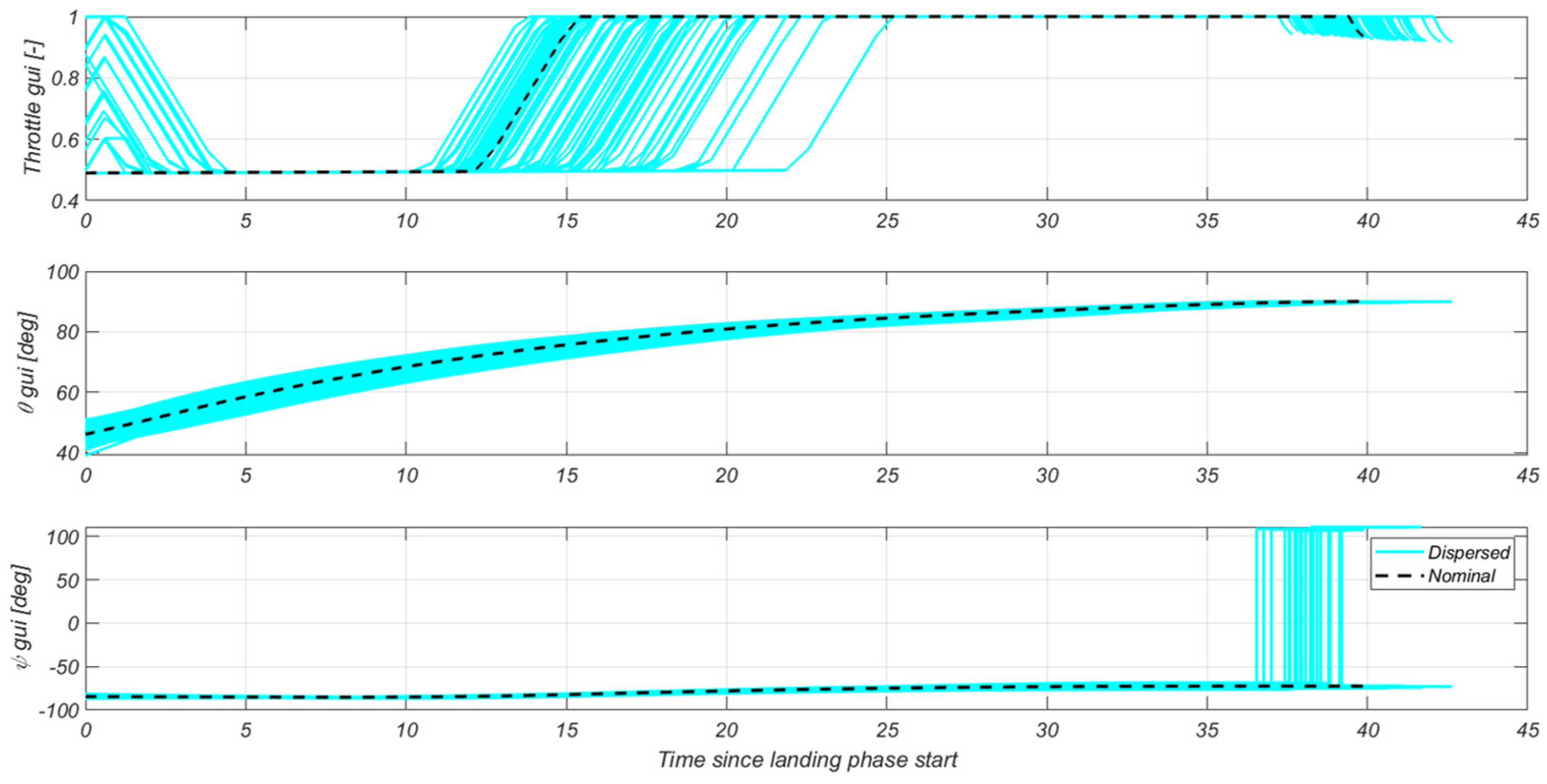
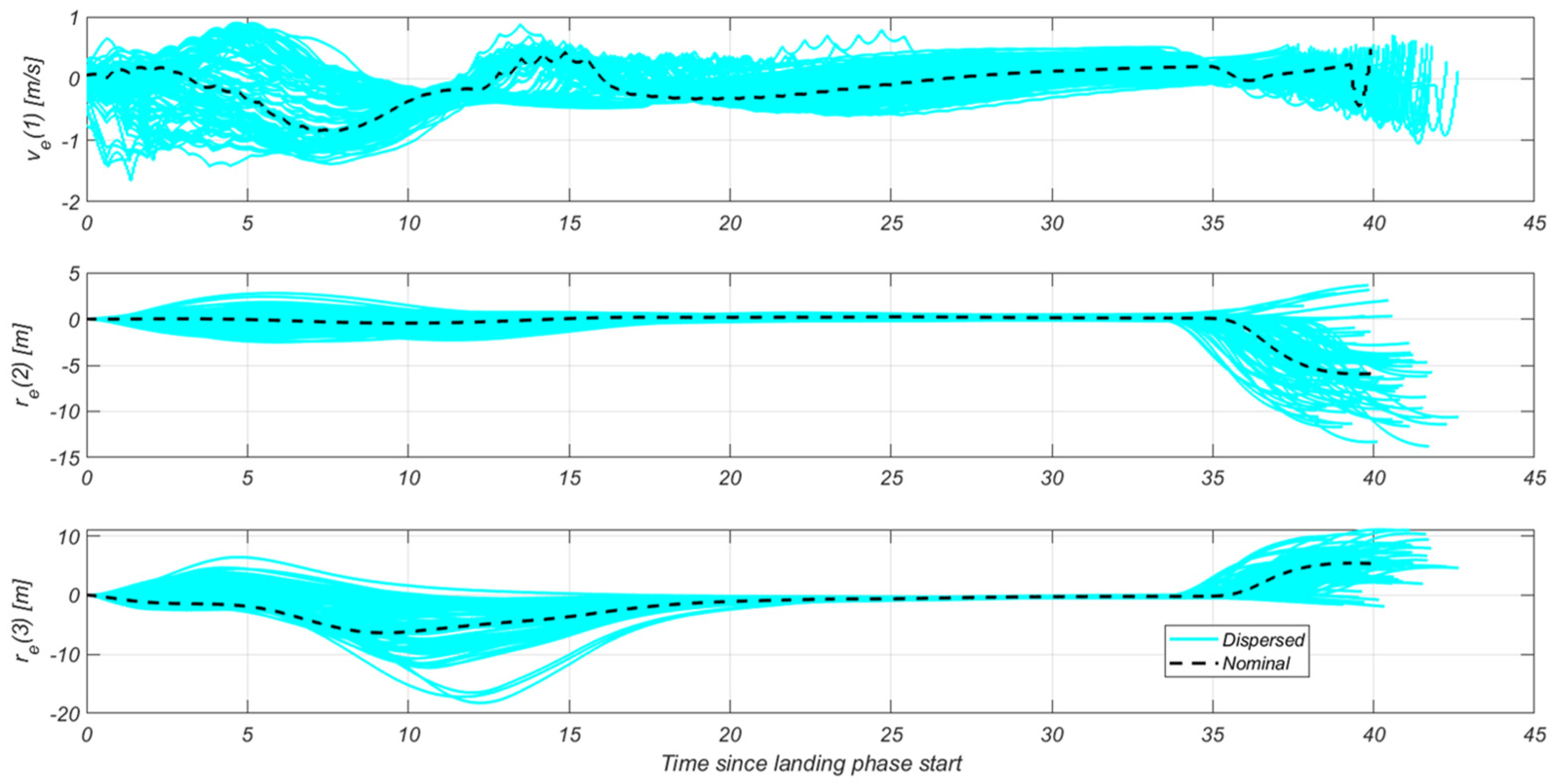
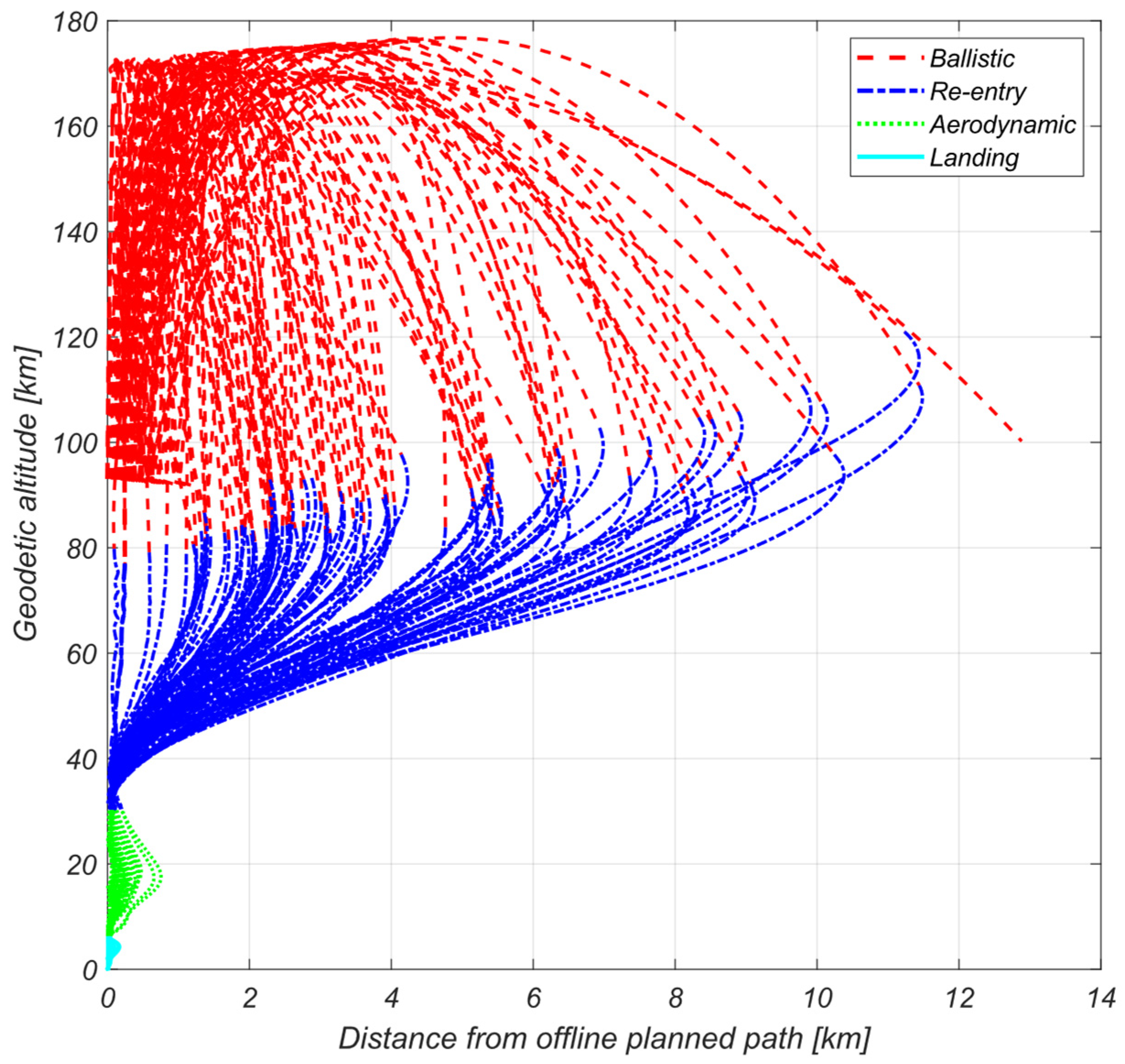
5. Robustness Analysis Results
5.1. Scenario Description
5.2. Results
6. Conclusions and Future Developments
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Mirand, A.P.; Bahu, J.M.; Gogdet, O. Ariane Next, a vision for the next generation of Ariane Launcher. Acta Astronaut. 2020, 170, 735–749. [Google Scholar] [CrossRef]
- Marwege, A.; Gülhan, A.; Klevansky, J.; Hantz, C.; Karl, S.; Laureti, M.; De Zaiacomo, G.; Vos, J.; Jevons, M.; Thies, C.; et al. RETALT: Review of technologies and overview of design changes. CEAS Space J. 2022, 14, 433–445. [Google Scholar] [CrossRef] [PubMed]
- SALTO-reuSable strAtegic Space Launcher Technologies & Operations, Salto Consortium Associated Partners. Available online: https://salto-project.eu/ (accessed on 6 April 2025).
- De Zaiacomo, G.; Arnao, G.B.; Bund, R.; Bonetti, D. Mission engineering for the RETALT VTVL launcher. CEAS Space J. 2022, 14, 533–549. [Google Scholar] [CrossRef]
- Guadagnini, J.; Lavagna, M.; Rosa, P. Model predictive control for reusable space launcher guidance improvement. Acta Astronaut. 2022, 193, 767–778. [Google Scholar] [CrossRef]
- Szmuk, M.; Reynolds, T.P.; Acikmese, B. Successive Convexification for Real-Time Six-Degree-of-Freedom Powered Descent Guidance with State-Triggered Constraints. J. Guid. Control Dyn. 2020, 43, 1399–1413. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.; Szmuk, M.; Lew, T.; Bonalli, R.; Pavone, M.; Açıkmeşe, B. Convex Optimization for Trajectory Generation. IEEE Control Syst. Mag. 2022, 42, 20–113. [Google Scholar] [CrossRef]
- Mao, Y.; Szmuk, M.; Acikmese, B. Successive convexification of non-convex optimal control problems and its convergence properties. In Proceedings of the IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016. [Google Scholar] [CrossRef]
- Wang, J.; Cui, N.; Wei, C. Optimal Rocket Landing Guidance Using Convex Optimization and Model Predictive Control. J. Guid. Control Dyn. 2019, 42, 1078–1092. [Google Scholar] [CrossRef]
- Simplicio, P. Guidance and Control Elements for Improved Access to Space from Planetary Landers to Reusable Launchers. Ph.D. Thesis, University of Bristol, Department of Aerospace Engineering, Bristol, UK, November 2019. [Google Scholar]
- Szmuk, M.; Acikmese, B. Successive Convexification for 6-DoF Mars Rocket Powered Landing with Free-Final-Time. In Proceedings of the 2018 AIAA Guidance, Navigation and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.; Szmuk, M.; Mesbahi, M.; Acikmese, B.; Carson, J.M. Discretization Performance and Accuracy Analysis for the Rocket Powered Descent Guidance Problem. In Proceedings of the AIAA SCITECH 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Sagliano, M.; Heidecker, A.; Hernández, J.M.; Farí, S.; Schlottere, M.; Woicke, S.; Seelbinder, D.; Dumont, E. Onboard Guidance for Reusable Rockets: Aerodynamic Descent and Powered Landing. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, Orlando, FL, USA, 11–21 January 2021. [Google Scholar] [CrossRef]
- Bucchioni, G.; Innocenti, M. Rendezvous in Cis-Lunar Space near Rectilinear Halo Orbit: Dynamics and Control Issues Aerospace. Aerospace 2021, 8, 68. [Google Scholar] [CrossRef]
- Mooij, E. Linear Quadratic Regulator Design for an Unpowered, Winged Re-Entry Vehicle; Delft University Press: Delft, The Netherlands, 1997. [Google Scholar]
- Lu, P. Regulation About Time-Varying Trajectories: Precision Entry Guidance Illustrated in Guidance. In Proceedings of the Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999. [Google Scholar] [CrossRef]
- Pascucci, C.A.; Bennani, S.; Bemporad, A. Model predictive control for powered descent guidance and control. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 12–15 June 2015. [Google Scholar] [CrossRef]
- Jung, Y.; Bang, H. Mars precision landing guidance based on model predictive control approach. Proc. Inst. Mech. Eng. 2015, 230, 2048–2062. [Google Scholar] [CrossRef]
- Sagliano, M.; Tsukamoto, T.; Ishimoto, S.; Farì, S.; Dumont, E.; Seelbinder, D.; Schlotterer, M.; Heidecker, A.; Macés-Hernández, J.A.; Woicke, S. Robust Control for reusable rockets via structured H-infinity Synthesis. In Proceedings of the ESA GNC 2021, Virtual, 22–25 June 2021. [Google Scholar]
- Sagliano, M.; Macés, A.J.H.; Farí, S.; Heidecker, A.; Schlotterer, M.; Woicke, S.; Seelbinder, D.; Krummen, S.; Dumont, E. Unified-Loop Structured H-Infinity Control for Aerodynamic Steering of Reusable Rockets. J. Guid. Control Dyn. 2023, 46, 815–837. [Google Scholar] [CrossRef]
- Ghignoni, P.; Botelho, A.; Recupero, C.; Fernandez, V.; Fabrizi, A.; De Zaiacomo, G. RETALT: Recovery GNC for the Retro-Propulsive Vertical Landing of an Orbital Launch Vehicle. In Proceedings of the 2nd International Conference on High-Speed Vehicle 1227 Science Technology, Bruges, Belgium, 11–16 September 2022. [Google Scholar] [CrossRef]
- Vandersteen, J.; Bennani, S.; Roux, C. Robust Rocket Navigation with Sensor Uncertainties: Vega Launcher Application. J. Spacecr. Rocket. 2018, 55, 153–166. [Google Scholar] [CrossRef]
- Spada, F.; Ghignoni, P.; Botelho, A.; De Zaiacomo, G.; Rosa, P. Successive Convexification-based Fuel-Optimal High-Altitude Guidance of the RETALT Reusable Launcher. In Proceedings of the ESA 12th International Conference on Guidance Navigation and Control and 9th International Conference on Astrodynamics Tools and Techniques, Sopot, Poland, 12–16 June 2023. [Google Scholar] [CrossRef]
- Reynolds, T.; Malyuta, D.; Mesbahi, M.; Acikmese, B.; Carson, J.M. A Real-Time Algorithm for Non-Convex Powered Descent Guidance In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A software framework for nonlinear optimization and optimal control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP solver for embedded systems. In Proceedings of the European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013. [Google Scholar] [CrossRef]
- Apkarian, P.; Noll, D. Nonsmooth H-infinity Synthesis. IEEE Trans. Autom. Control 2006, 51, 71–86. [Google Scholar] [CrossRef]
- Apkarian, P.; Gahinet, P.; Buhr, C. Multi-model, multi-objective tuning of fixed-structure controllers. In Proceedings of the European Control Conference (ECC), Strasbourg, France, 24–27 June 2014. [Google Scholar] [CrossRef]
- Simplicio, P.; Bennani, S.; Marcos, A.; Roux, C.; Lefort, X. Structured Singular-Value Analysis of the Vega Launcher in Atmospheric Flight. J. Guid. Control Dynamcis 2016, 39, 1342–1355. [Google Scholar] [CrossRef]
- De Zaiacomo, G.; Medici, G.; Princi, A.; Ghignoni, P.; Botelho, A.; Arlandis, M.M.; Recupero, C.; Fabrizi, A.; Fernandez, V.; Guidotti, G. RETALT: Development of Key Flight Dynamics and GNC Technologies for Reusable Launchers. In Proceedings of the 73rd International Astronautical Congress (IAC), Paris, France, 18–22 September 2022. [Google Scholar] [CrossRef]
- De Oliveira, A.M.A. Guidance and Control System Design for Reusable Launch Vehicle Descent and Precise Landing. Ph.D. Thesis, Politecnico di Milano, Milano, Italy, 2024. [Google Scholar]
- Watcher, A.; Biegler, L.T. On the Implementation of an Interior-Point Filter Line-Search Algorithm for Large-Scale Nonlinear Programming. Math. Program. 2006, 106, 25–57. [Google Scholar] [CrossRef]
- Spada, F.; Sagliano, M.; Topputo, F. Direct-Indirect Hybrid Strategy for Optimal Powered Descent and Landing. J. Spacecr. Rocket. 2023, 60, 1787–1804. [Google Scholar] [CrossRef]
- Malyuta, D.; Acikmese, B. Fast Homotopy for Spacecraft Rendezvous Trajectory Optimization with Discrete Logic. J. Guid. Control Dyn. 2023, 46, 1262–1279. [Google Scholar] [CrossRef]
- Landis Markley, F.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Korzun, A.M.; Cruz, J.R.; Braun, R.D. A Survey of Supersonic Retropropulsion Technology for Mars Entry, Descent, and Landing. In Proceedings of the IEEE Aerospace, Big Sky, MT, USA, 1–8 March 2008. [Google Scholar] [CrossRef]
- Brendel, E.; Hérissé, B.; Bourgeois, E. Optimal guidance for toss back concepts of Reusable Launch Vehicles. In Proceedings of the 8th European Conference for Aeronautics and Aerospace Sciences (EUCASS), Madrid, Spain, 1–4 July 2019. [Google Scholar]
- Navarro-Tapia, D. Robust and Adaptive TVC Control Design Approaches for the VEGA Launcher. Ph.D. Thesis, University of Bristol, Bristol, UK, 2019. [Google Scholar]
- Cunha, R.; Duarte, A.; Gomes, P.; Silvestre, C. A Path-Following Preview Controller for Autonomous Air Vehicles. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar]
- Mathematics, E.O. The European Mathematical Society. Available online: http://encyclopediaofmath.org/index.php?title=Cardano_formula&oldid=29227 (accessed on 9 January 2025).
- Horizontal Wind Model 14 Website U.S. Naval Research Laboratory. Available online: https://map.nrl.navy.mil/map/pub/nrl/HWM/HWM14/ (accessed on 31 January 2024).
- Charbonnier, D.; Vos, J.B.; Marwege, A.; Hantz, C. Computational fluid dynamics investigations of aerodynamic control surfaces of a vertical landing configuration. CEAS Space J. 2022, 14, 1–16. [Google Scholar] [CrossRef]
- Marwege, A.; Hantz, C.; Kirchheck, D.; Klevanski, J.; Gulhan, A.; Charbonnier, D.; Von, J.B. Wind tunnel experiments of interstage segments used for aerodynamic control of retro-propulsion assisted landing vehicles. CEAS Space J. 2022, 14, 447–471. [Google Scholar] [CrossRef]
- NRLMSIS-00 Atmospheric Model Community Coordinated Modeling Center Website. Available online: https://ccmc.gsfc.nasa.gov/models/NRLMSIS~00/ (accessed on 31 January 2024).
- Blackmore, L. Autonomous precision landing of space rockets. Bridge 2016, 4, 15–20. [Google Scholar]
- Kamath, A.G.; Elango, P.; Yu, Y.; Mceowen, S.; Chari, G.M.; Carson, J.M., III; Acikmese, B. Real-Time Sequential Conic Optimization for Multi-Phase Rocket Landing Guidance. IFAC-PapersOnLine 2023, 56, 3118–3125. [Google Scholar] [CrossRef]









| Initial Conditions | Nominal Value | Std. Dev. |
|---|---|---|
| Geodetic altitude | 93,057 m | 540 |
| Longitude | −51.97° | - |
| Geodetic latitude | 5.21° | - |
| Airspeed | 2217 m/s | 18 |
| Flight path angle | 31.77° | 0.29° |
| Heading angle | 94.64° | 0.22° |
| Angle of attack | 0° | - |
| Sideslip angle | 0° | - |
| Bank angle | 0° | - |
| Waypoint | Reference Position [m] | Reference Velocity [m/s] | Reference Pitch [°] |
|---|---|---|---|
| Re-entry burn start | [−88,960; 6730; 76,350] | [1901; −177; −1254] | 33.4° |
| Aerodynamic descent start | [−25,701; 2404; 30,110] | [790; −74; −757] | 43.2° |
| Landing burn start | [−2386; 223; 6038] | [199; −18; −251] | 51.5° |
| Touchdown | [0; 0; 0] | [0; 0; 0] | 90° |
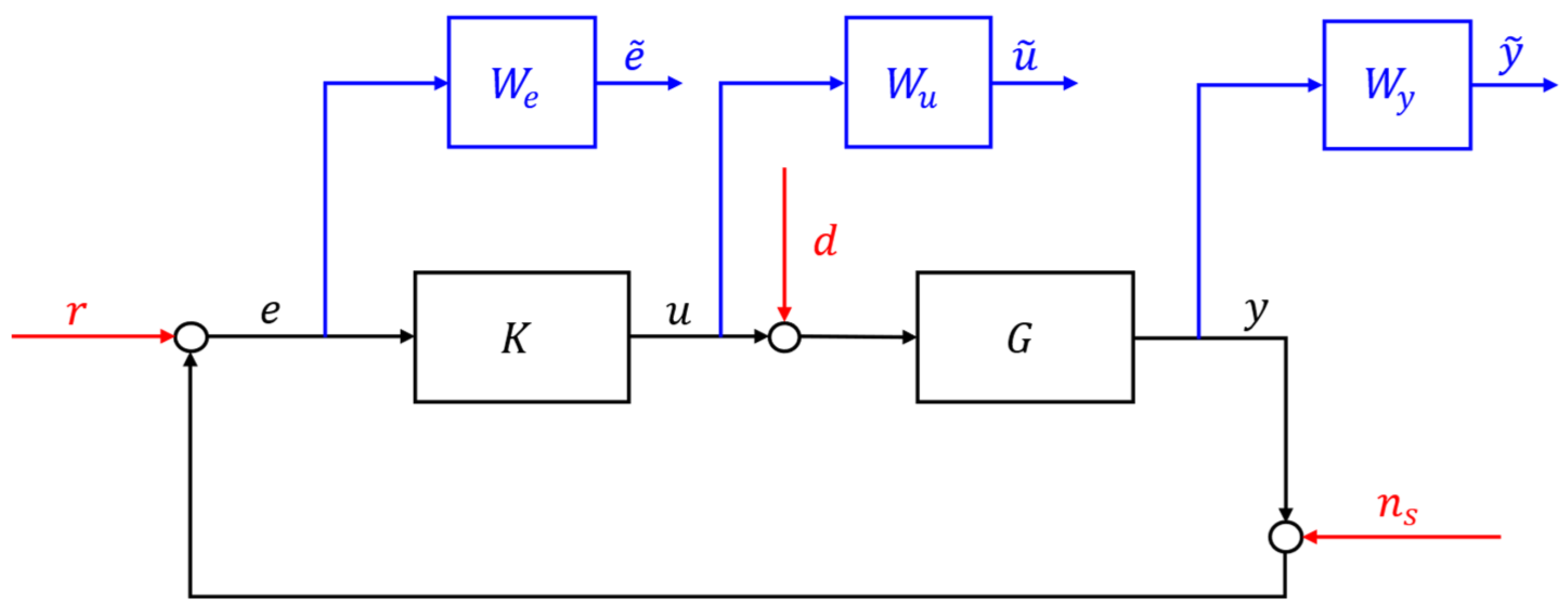
| Elements | Description |
|---|---|
| Reference signal to be tracked when closing the loop | |
| Control error | |
| Filtered control error | |
| Controller output (plant input) | |
| Filtered control output | |
| Plant disturbance | |
| Measurement (or estimate) available for control | |
| Filtered measurement | |
| Measurement noise | |
| Controller | |
| Plant (linearized) | |
| Weight on control error | |
| Weight on control signal | |
| Weight on measurement | |
| Controller |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guadagnini, J.; Ghignoni, P.; Spada, F.; De Zaiacomo, G.; Botelho, A. End-to-End GNC Solution for Reusable Launch Vehicles. Aerospace 2025, 12, 339. https://doi.org/10.3390/aerospace12040339
Guadagnini J, Ghignoni P, Spada F, De Zaiacomo G, Botelho A. End-to-End GNC Solution for Reusable Launch Vehicles. Aerospace. 2025; 12(4):339. https://doi.org/10.3390/aerospace12040339
Chicago/Turabian StyleGuadagnini, Jacopo, Pietro Ghignoni, Fabio Spada, Gabriele De Zaiacomo, and Afonso Botelho. 2025. "End-to-End GNC Solution for Reusable Launch Vehicles" Aerospace 12, no. 4: 339. https://doi.org/10.3390/aerospace12040339
APA StyleGuadagnini, J., Ghignoni, P., Spada, F., De Zaiacomo, G., & Botelho, A. (2025). End-to-End GNC Solution for Reusable Launch Vehicles. Aerospace, 12(4), 339. https://doi.org/10.3390/aerospace12040339







