Aerodynamic Analysis of a Hexacopter with an Inner Tilted-Rotor Configuration During Hovering
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometry Models
2.1.1. Propeller Geometry
2.1.2. The Structure of the Inner Tilted Hexacopter
2.2. Experimental Setup
2.3. Numerical Simulations
2.3.1. CFD Methodology
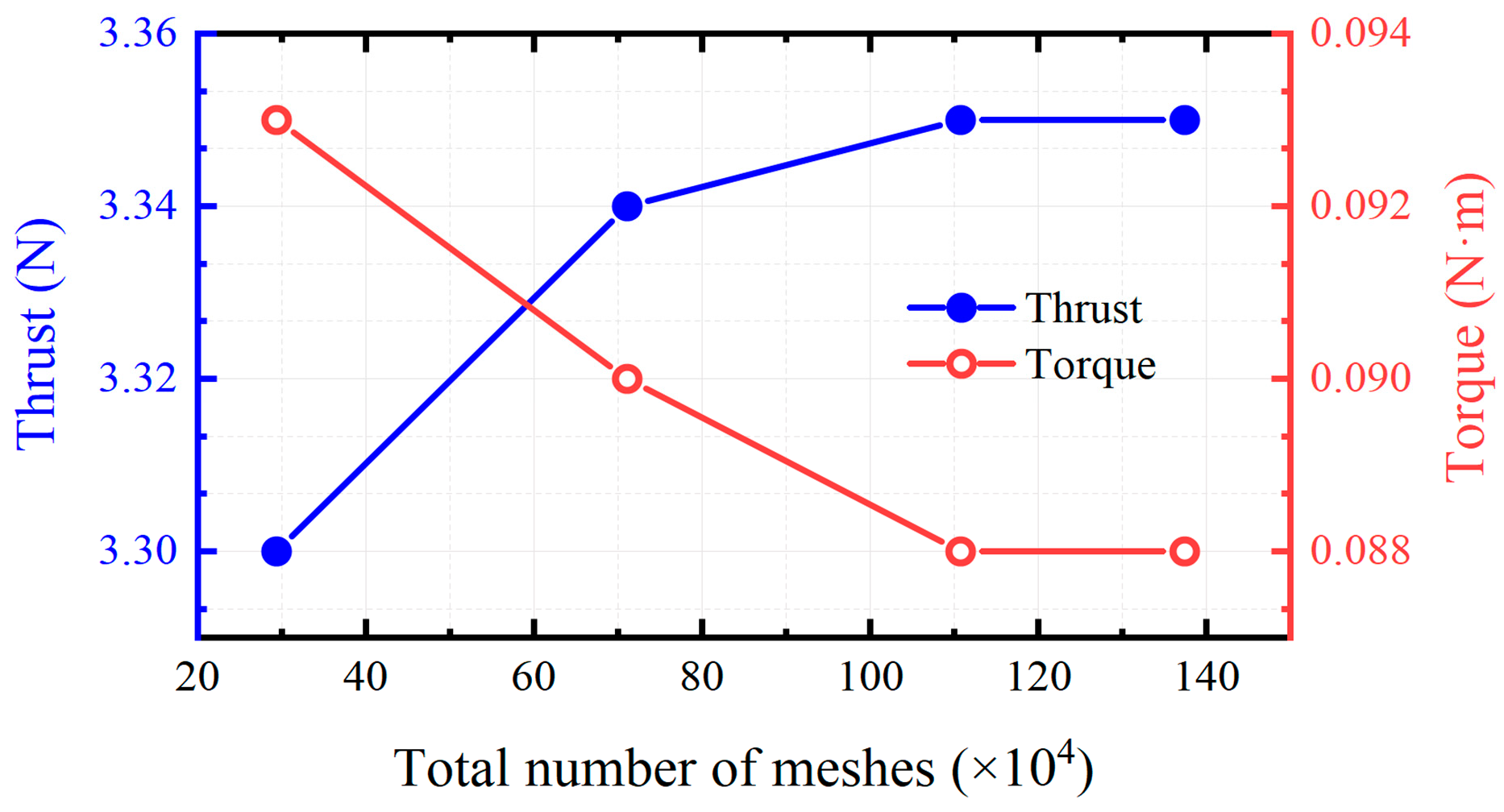
2.3.2. Mesh Sensitivity Study
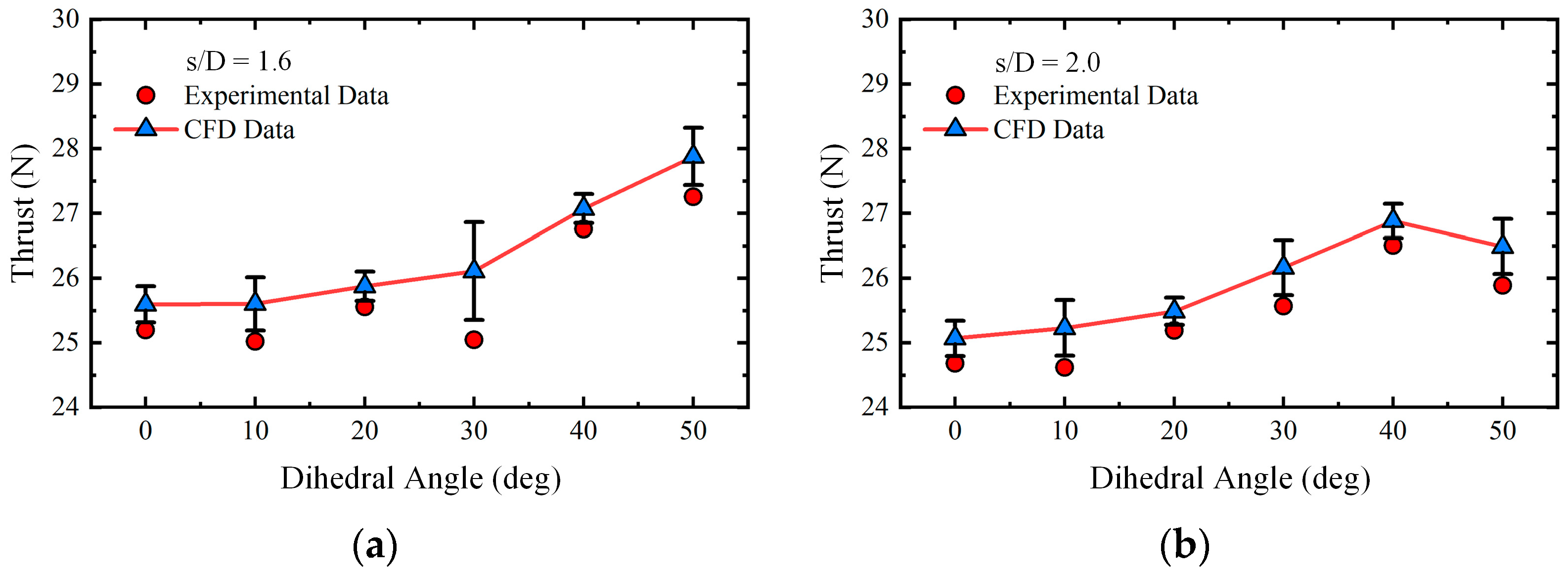
2.4. Data Validation
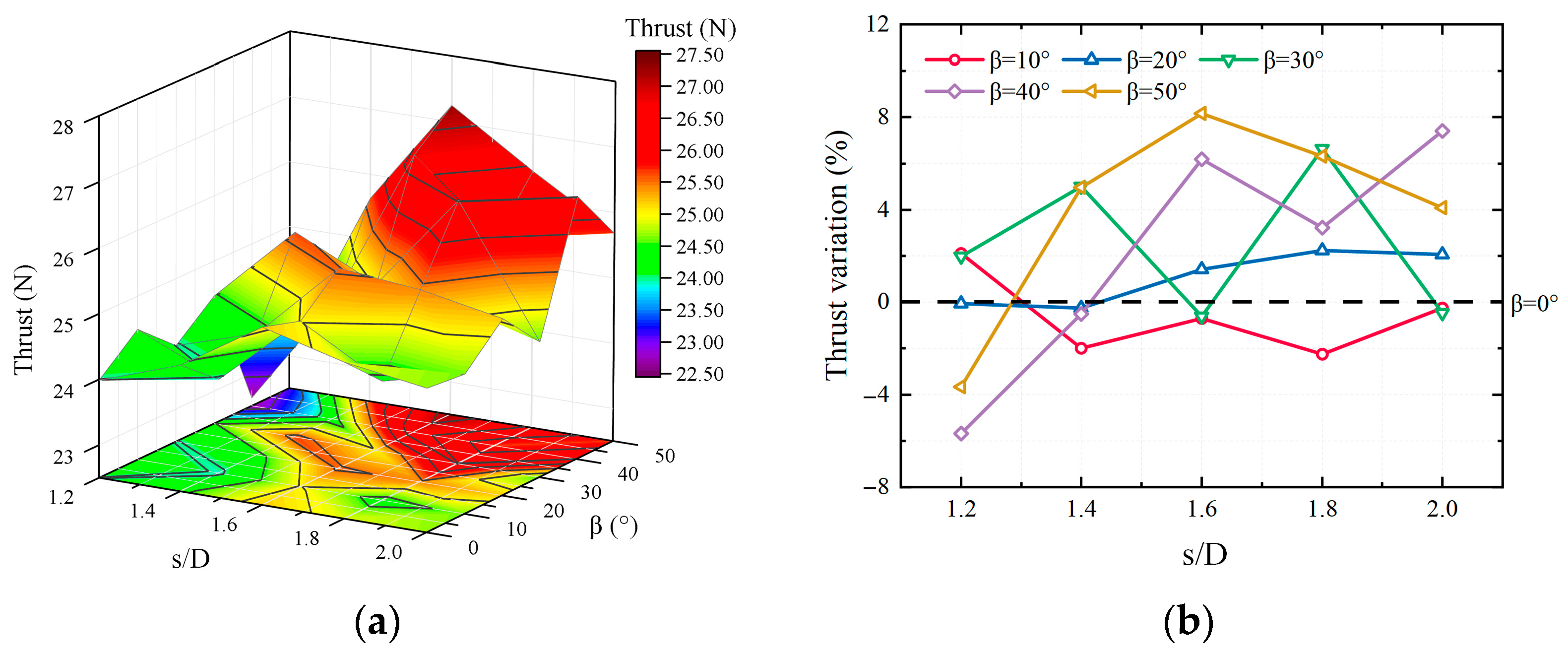
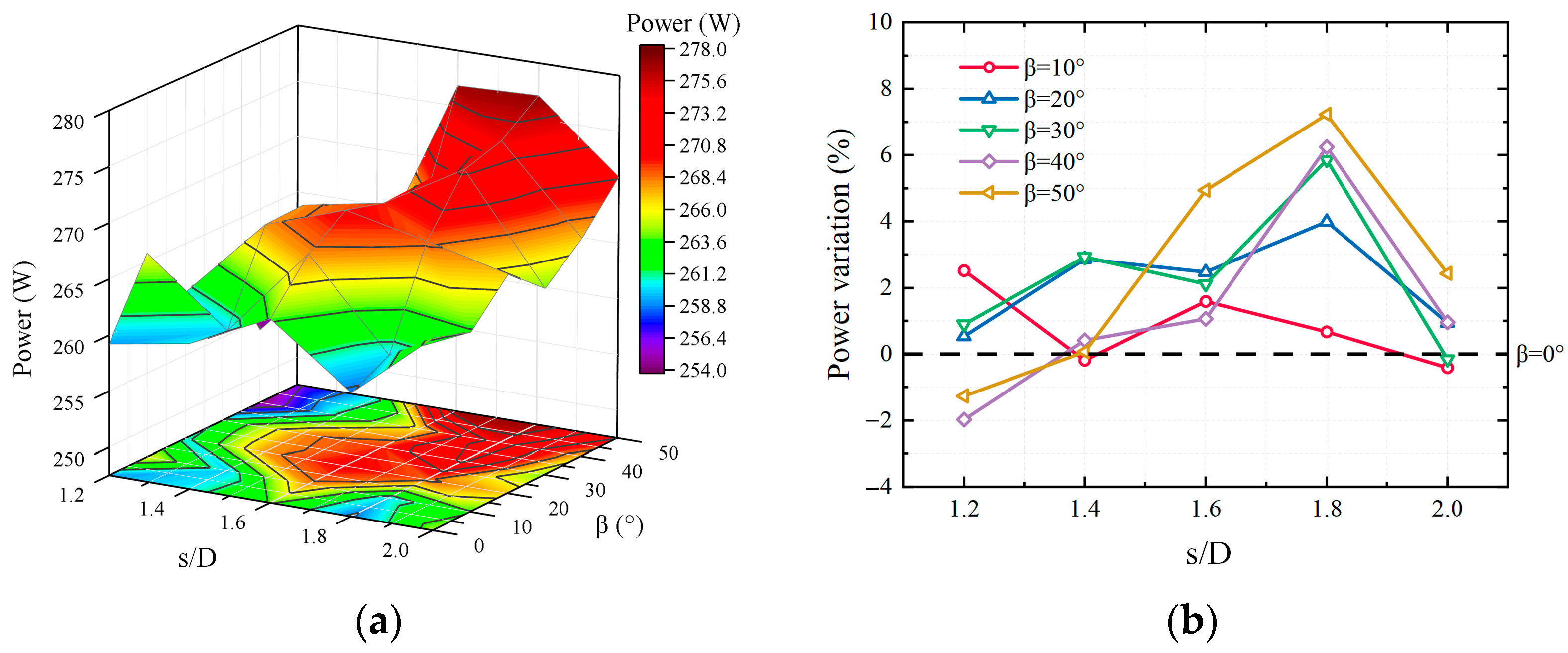
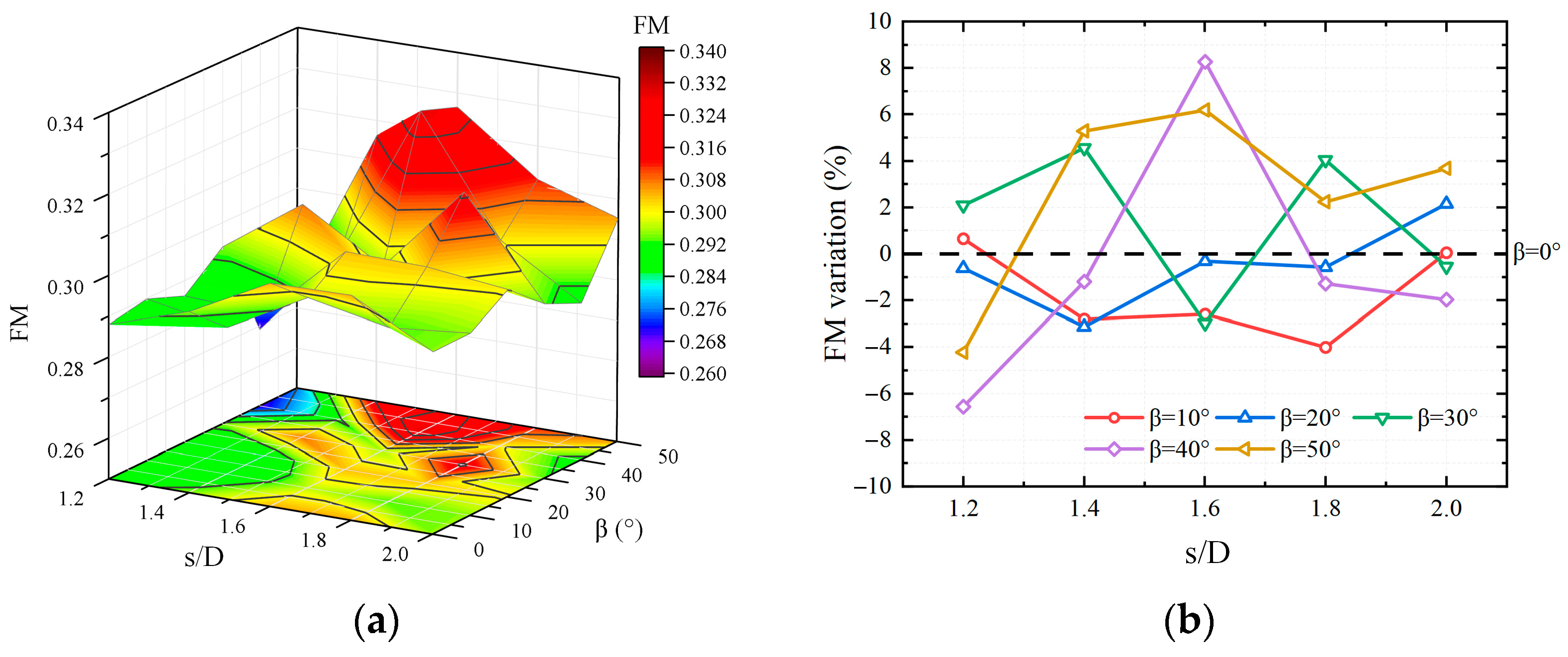
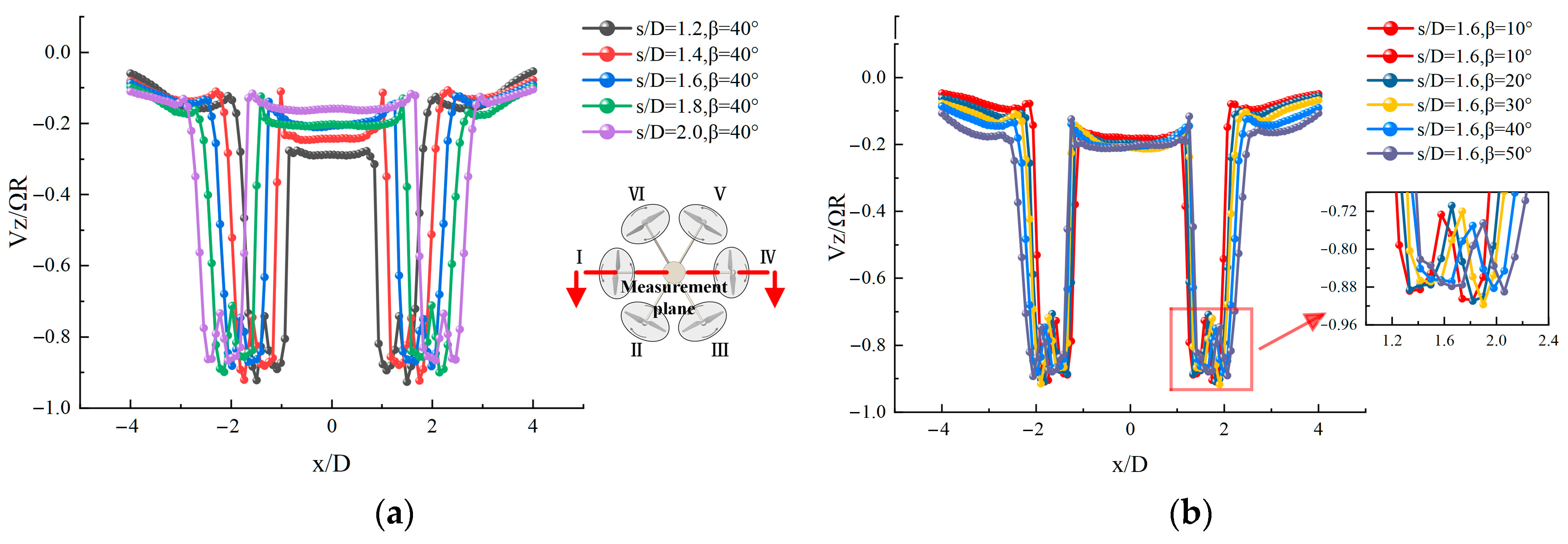
3. Results and Discussion
3.1. Experimental Results
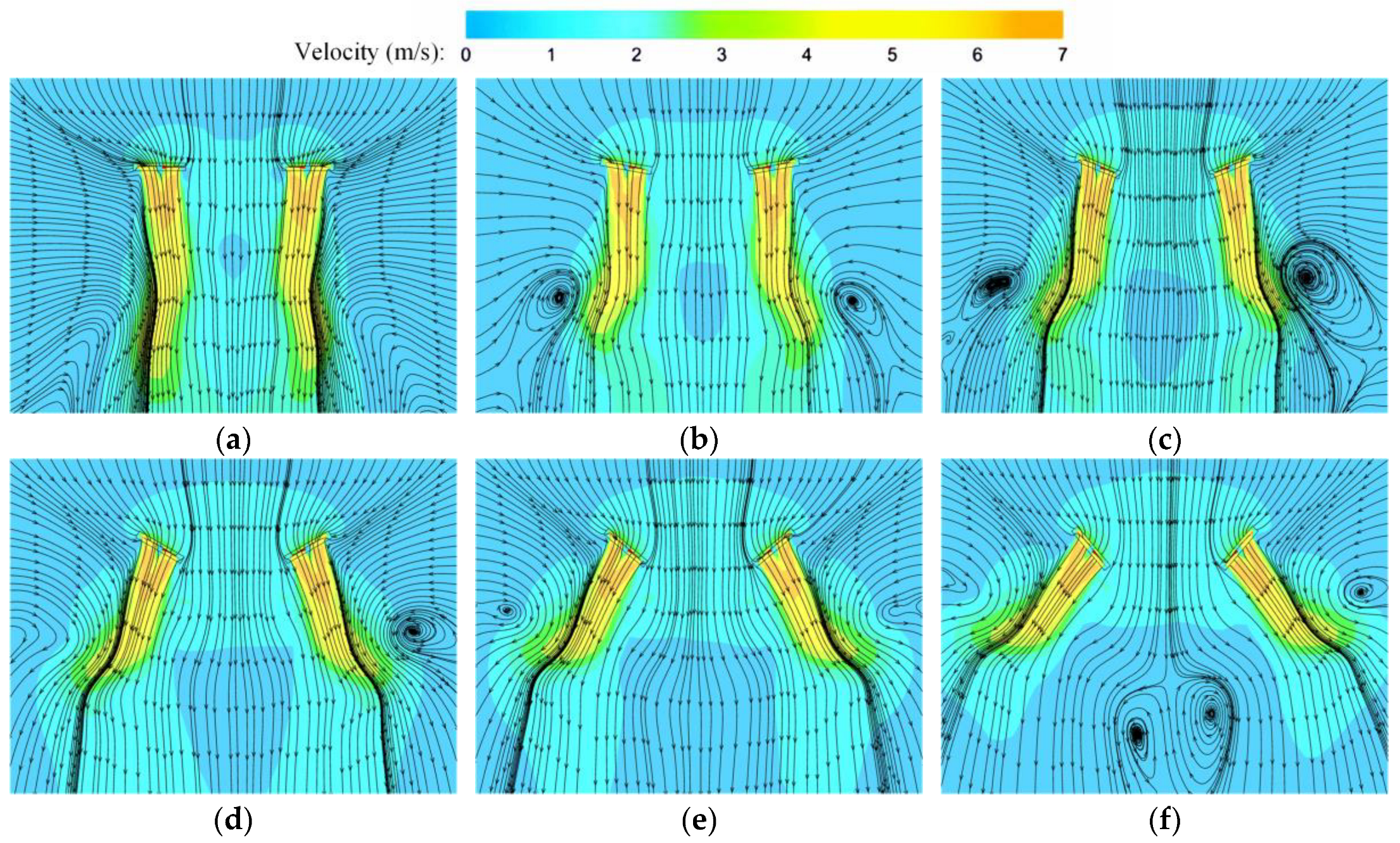
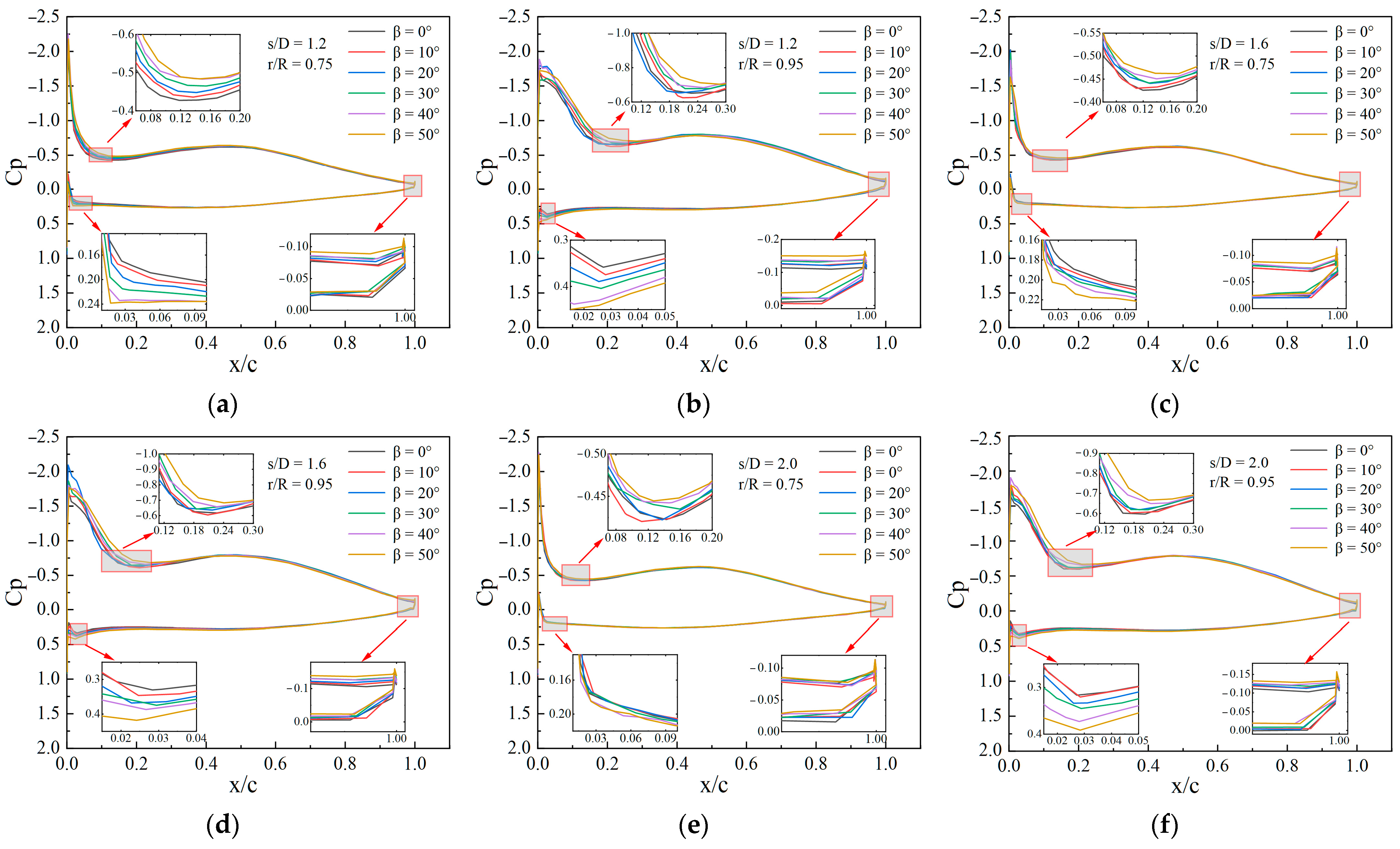
3.2. Numerical Simulation Results
4. Conclusions
- (1)
- The optimal combination of rotor spacing and the dihedral angle will improve the aerodynamic performance of the inner tilted-rotor hexacopter with appropriate rotor interference to enhance thrust generation.
- (2)
- The inflows of the inner tilted-rotor hexacopter interfere with each other, which increases the complexity of the flow field. It reaches a steady state when the rotor spacing ratio (s/D) is less than 1.6, and aerodynamic interference is balanced with thrust increments and power decrements.
- (3)
- Smaller spacings lead to increased mutual interference between rotors, and the presence of vortices produces an unsteady wake behavior that reduces the overall aerodynamic efficiency, whereas larger spacings reduce this interference effect and improve aerodynamic efficiency.
- (4)
- For the inner tilted rotor, the thrust can be decomposed, which promotes a positive effect on the manipulation of the hexacopter. The experimental results show that it has a better performance compared to the conventional hexacopter, with s/D = 1.6 and β = 40°.
- (5)
- An optimal dihedral angle at a smaller spacing will improve the hover efficiency. However, too large of a dihedral angle will lead to increasing drag, which is not of benefit for thrust generation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Floreano, D.; Wood, R.J. Science, Technology and the Future of Small Autonomous Drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Yang, X.; Luo, Z.; Guan, T. Application of Unmanned Aerial Vehicle (UAV) Thermal Infrared Remote Sensing to Identify Coal Fires in the Huojitu Coal Mine in Shenmu City, China. Sci. Rep. 2020, 10, 13895. [Google Scholar] [CrossRef]
- Zhu, M.; Yu, X.; Tan, H.; Yuan, J. Integrated High-Precision Monitoring Method for Surface Subsidence in Mining Areas Using D-InSAR, SBAS, and UAV Technologies. Sci. Rep. 2024, 14, 12445. [Google Scholar] [CrossRef]
- De Boer, G.; Calmer, R.; Jozef, G.; Cassano, J.J.; Hamilton, J.; Lawrence, D.; Borenstein, S.; Doddi, A.; Cox, C.; Schmale, J.; et al. Observing the Central Arctic Atmosphere and Surface with University of Colorado Uncrewed Aircraft Systems. Sci. Data 2022, 9, 439. [Google Scholar] [CrossRef]
- Achermann, F.; Stastny, T.; Danciu, B.; Kolobov, A.; Chung, J.J.; Siegwart, R.; Lawrance, N. WindSeer: Real-Time Volumetric Wind Prediction over Complex Terrain Aboard a Small Uncrewed Aerial Vehicle. Nat. Commun. 2024, 15, 3507. [Google Scholar] [CrossRef]
- Bodie, K.; Brunner, M.; Pantic, M.; Walser, S.; Pfandler, P.; Angst, U.; Siegwart, R.; Nieto, J. Active Interaction Force Control for Contact-Based Inspection with a Fully Actuated Aerial Vehicle. IEEE Trans. Robot. 2021, 37, 709–722. [Google Scholar] [CrossRef]
- Praveen, A.; Ma, X.; Manoj, H.; Venkatesh, V.L.; Rastgaar, M.; Voyles, R.M. Inspection-on-the-Fly Using Hybrid Physical Interaction Control for Aerial Manipulators. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020; IEEE: Las Vegas, NV, USA, 2020; pp. 1583–1588. [Google Scholar]
- Tognon, M.; Chavez, H.A.T.; Gasparin, E.; Sable, Q.; Bicego, D.; Mallet, A.; Lany, M.; Santi, G.; Revaz, B.; Cortes, J.; et al. A Truly-Redundant Aerial Manipulator System With Application to Push-and-Slide Inspection in Industrial Plants. IEEE Robot. Autom. Lett. 2019, 4, 1846–1851. [Google Scholar] [CrossRef]
- Rashad, R.; Goerres, J.; Aarts, R.; Engelen, J.B.C.; Stramigioli, S. Fully Actuated Multirotor UAVs: A Literature Review. IEEE Robot. Autom. Mag. 2020, 27, 97–107. [Google Scholar] [CrossRef]
- Voyles, R.; Jiang, G. Hexrotor UAV Platform Enabling Dextrous Interaction with Structures—Preliminary Work. In Proceedings of the 2012 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), College Station, TX, USA, 5–8 November 2012; IEEE: College Station, TX, USA, 2012; pp. 1–7. [Google Scholar]
- Jiang, G.; Voyles, R. Hexrotor UAV Platform Enabling Dextrous Interaction with Structures-Flight Test. In Proceedings of the 2013 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Linköping, Sweden, 21–26 October 2013; IEEE: Linkoping, Sweden, 2013; pp. 1–6. [Google Scholar]
- Jiang, G.; Voyles, R. A Nonparallel Hexrotor UAV with Faster Response to Disturbances for Precision Position Keeping. In Proceedings of the 2014 IEEE International Symposium on Safety, Security, and Rescue Robotics (2014), Hokkaido, Japan, 27–30 October 2014; IEEE: Hokkaido, Japan, 2014; pp. 1–5. [Google Scholar]
- Rajappa, S.; Ryll, M.; Bulthoff, H.H.; Franchi, A. Modeling, Control and Design Optimization for a Fully-Actuated Hexarotor Aerial Vehicle with Tilted Propellers. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; IEEE: Seattle, WA, USA, 2015; pp. 4006–4013. [Google Scholar]
- Giljarhus, K.E.T.; Porcarelli, A.; Apeland, J. Investigation of Rotor Efficiency with Varying Rotor Pitch Angle for a Coaxial Drone. Drones 2022, 6, 91. [Google Scholar] [CrossRef]
- Jiang, G.; Voyles, R.; Sebesta, K.; Greiner, H. Estimation and Optimization of Fully-Actuated Multirotor Platform with Nonparallel Actuation Mechanism. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Vancouver, BC, Canada, 2017; pp. 6843–6848. [Google Scholar]
- Jiang, G.; Voyles, R.M.; Choi, J.J. Precision Fully-Actuated UAV for Visual and Physical Inspection of Structures for Nuclear Decommissioning and Search and Rescue. In Proceedings of the 2018 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Philadelphia, PA, USA, 6–8 August 2018; IEEE: Philadelphia, PA, USA, 2018; pp. 1–7. [Google Scholar]
- Michieletto, G.; Ryll, M.; Franchi, A. Fundamental Actuation Properties of Multirotors: Force–Moment Decoupling and Fail–Safe Robustness. IEEE Trans. Robot. 2018, 34, 702–715. [Google Scholar] [CrossRef]
- Deng, J.; Fan, F.; Liu, P.; Huang, S.; Lin, Y. Aerodynamic Characteristics of Rigid Coaxial Rotor by Wind Tunnel Test and Numerical Calculation. Chin. J. Aeronaut. 2019, 32, 568–576. [Google Scholar] [CrossRef]
- Lei, Y.; Zhao, X. The Aerodynamic Performance of a Novel Overlapping Octocopter in Hover. Aerospace 2024, 11, 737. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, C.; Wang, W.; An, C. An Experimental and Numerical Evaluation of the Aerodynamic Performance of a UAV Propeller Considering Pitch Motion. Drones 2023, 7, 447. [Google Scholar] [CrossRef]
- Rostami, M. Propeller Effects and Elasticity in Aerodynamic Analysis of Small Propeller-Driven Aircraft and UAVs. Aerospace 2024, 11, 664. [Google Scholar] [CrossRef]
- Vargas Loureiro, E.; Oliveira, N.L.; Hallak, P.H.; De Souza Bastos, F.; Rocha, L.M.; Grande Pancini Delmonte, R.; De Castro Lemonge, A.C. Evaluation of Low Fidelity and CFD Methods for the Aerodynamic Performance of a Small Propeller. Aerosp. Sci. Technol. 2021, 108, 106402. [Google Scholar] [CrossRef]
- Aziz, A.; Shi, Y. Impact of Rotor-to-Rotor Interactions on the Tonal Noise Characteristics of Different Octocopter Configurations. Aerospace 2024, 11, 1022. [Google Scholar] [CrossRef]
- Ventura Diaz, P.; Yoon, S. High-Fidelity Computational Aerodynamics of Multi-Rotor Unmanned Aerial Vehicles. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Kissimmee, FL, USA, 2018. [Google Scholar]
- Garofano-Soldado, A.; Sanchez-Cuevas, P.J.; Heredia, G.; Ollero, A. Numerical-Experimental Evaluation and Modelling of Aerodynamic Ground Effect for Small-Scale Tilted Propellers at Low Reynolds Numbers. Aerosp. Sci. Technol. 2022, 126, 107625. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries: La Cañada, CA, USA, 2000; ISBN 978-0-9636051-5-3. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Kutty, H.; Rajendran, P. 3D CFD Simulation and Experimental Validation of Small APC Slow Flyer Propeller Blade. Aerospace 2017, 4, 10. [Google Scholar] [CrossRef]
- Paz, C.; Suárez, E.; Gil, C.; Vence, J. Assessment of the Methodology for the CFD Simulation of the Flight of a Quadcopter UAV. J. Wind Eng. Ind. Aerodyn. 2021, 218, 104776. [Google Scholar] [CrossRef]
- Li, C.; Xue, C.; Bai, Y. Experimental Investigation on Aerodynamics of Nonplanar Rotor Pairs in a Multi-Rotor UAV. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; IEEE: Xi’an, China, 2019; pp. 911–915. [Google Scholar]
- Dougherty, S.; Oo, N.L.; Zhao, D. Effects of Propeller Separation and Onset Flow Condition on the Performance of Quadcopter Propellers. Aerosp. Sci. Technol. 2024, 145, 108837. [Google Scholar] [CrossRef]
- Sagaga, J.; Lee, S. High-Fidelity Computational Study of Aerodynamic Noise of Side-by-Side Rotor in Full Configuration. J. Sound Vib. 2024, 592, 118607. [Google Scholar] [CrossRef]
- Yoon, S.; Lee, H.C.; Pulliam, T.H. Computational Analysis of Multi-Rotor Flows. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics: San Diego, CA, USA, 2016. [Google Scholar]
- Chiew, J.J.; Aftosmis, M.J. Efficient Simulation of Multi-Rotor Vehicles with Low Reynolds Number Propellers. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Atlanta, GA, USA, 2018. [Google Scholar]
- Fengbo, Y.; Xinyu, X.; Ling, Z.; Zhu, S. Numerical Simulation and Experimental Verification on Downwash Air Flow of Six-Rotor Agricultural Unmanned Aerial Vehicle in Hover. Int. J. Agric. Biol. Eng. 2017, 10, 41–53. [Google Scholar] [CrossRef]
- Shen, A.; Zhou, S.; Peng, S. Atmospheric Environment Detection Method Based on Multi-Rotor Uav Platform. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, XLII-3/W5, 67–71. [Google Scholar]
- Grande, E.; Shubham, S.; Avallone, F.; Ragni, D.; Casalino, D. Computational Aeroacoustic Study of Co-Rotating Rotors in Hover. Aerosp. Sci. Technol. 2024, 153, 109381. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, J.; Wang, L.; Wu, J.; He, L. Rotor Airfoil Aerodynamic Design Method and Wind Tunnel Test Verification. Chin. J. Aeronaut. 2020, 33, 2123–2132. [Google Scholar] [CrossRef]
- Jing, S.M.; Zhao, G.Q.; Zhao, Q.J. Numerical Research on Secondary Peak of Aerodynamic Forces of Airfoil Under Dynamic Stall. J. Nanjing Univ. Aeronaut. Astronaut. 2022, 54, 191–202. (In Chinese) [Google Scholar] [CrossRef]
- Okulov, V.L.; Sørensen, J.N. Stability of Helical Tip Vortices in a Rotor Far Wake. J. Fluid Mech. 2007, 576, 1–25. [Google Scholar] [CrossRef]
- Inagaki, K.; Hamba, F. Modeling the Energy Flux Enhanced in Rotating Inhomogeneous Turbulence. In Progress in Turbulence VIII, Proceedings of the iTi Conference in Turbulence 2018, Bertinoro, Italy, September 2018; Örlü, R., Talamelli, A., Peinke, J., Oberlack, M., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 139–144. [Google Scholar]
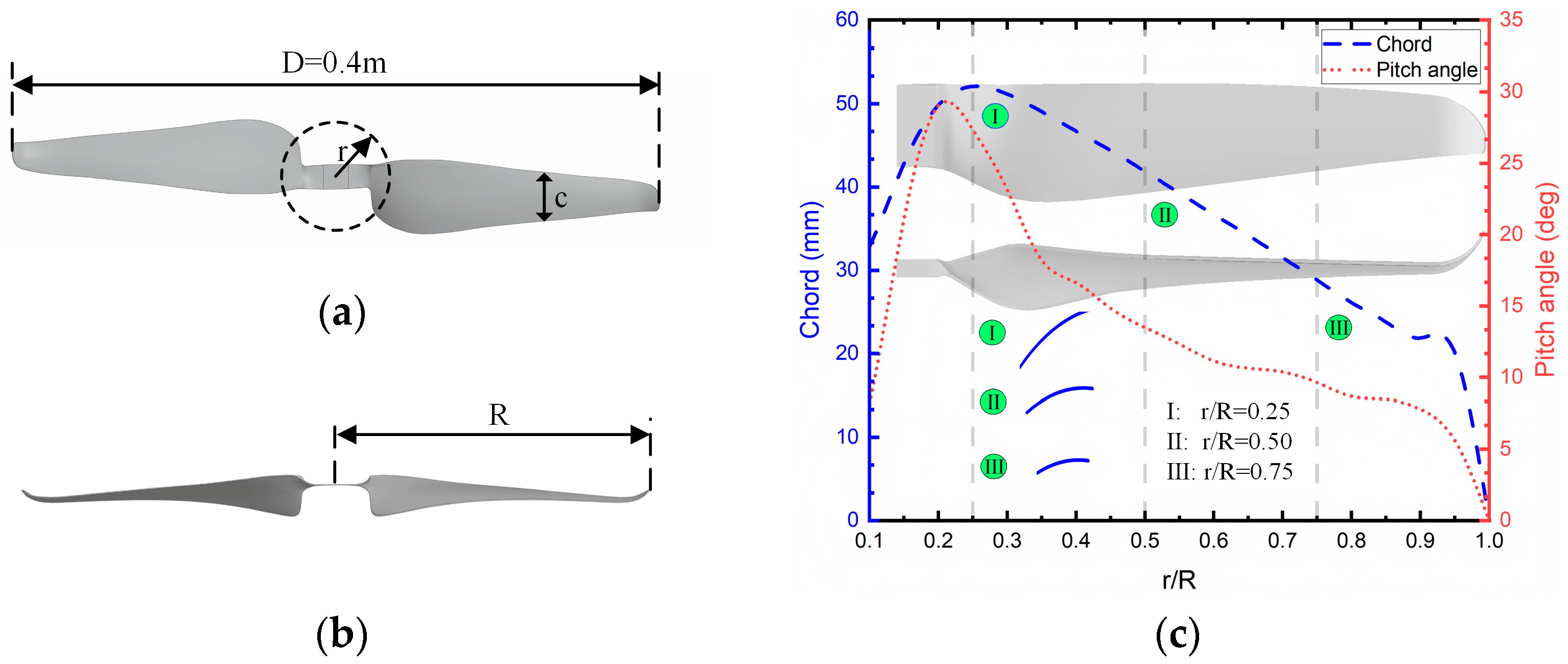

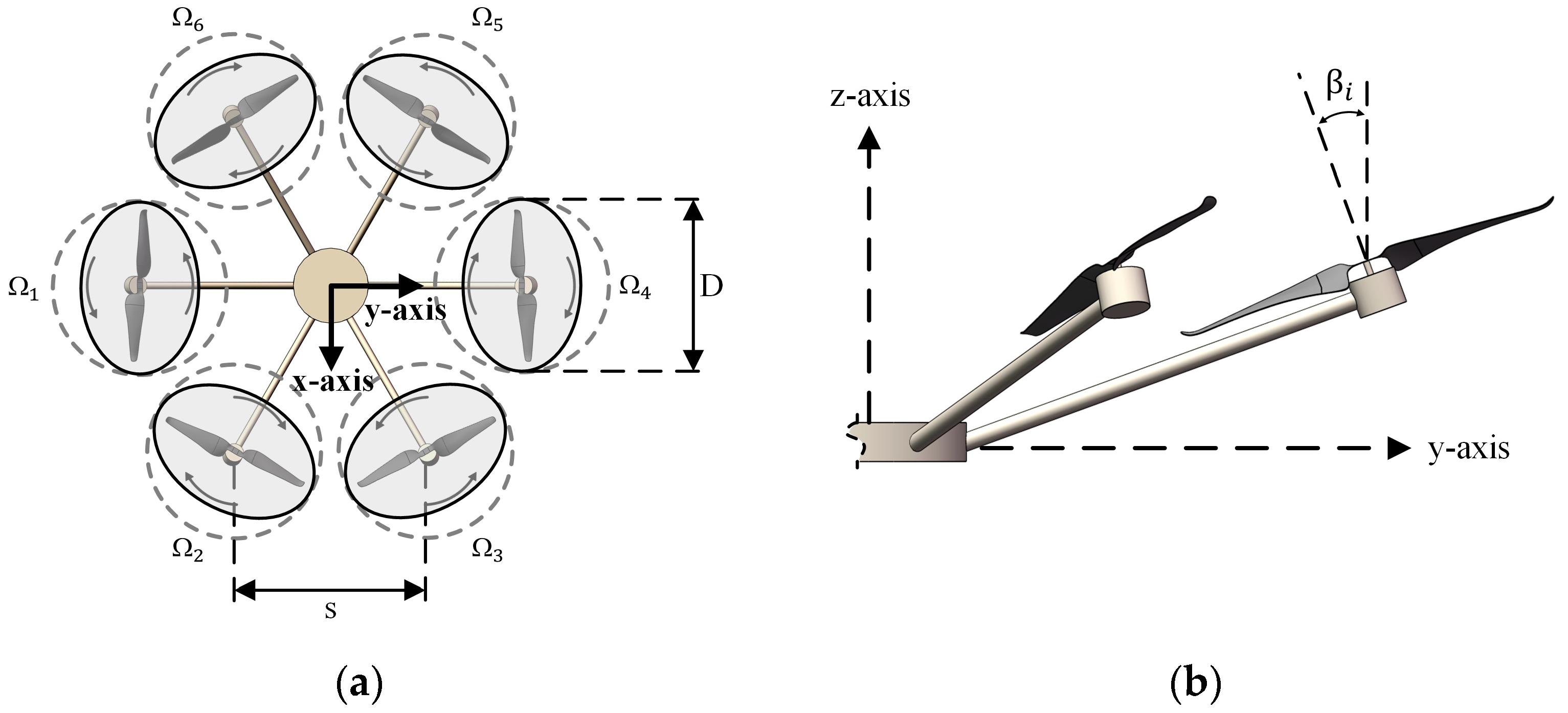
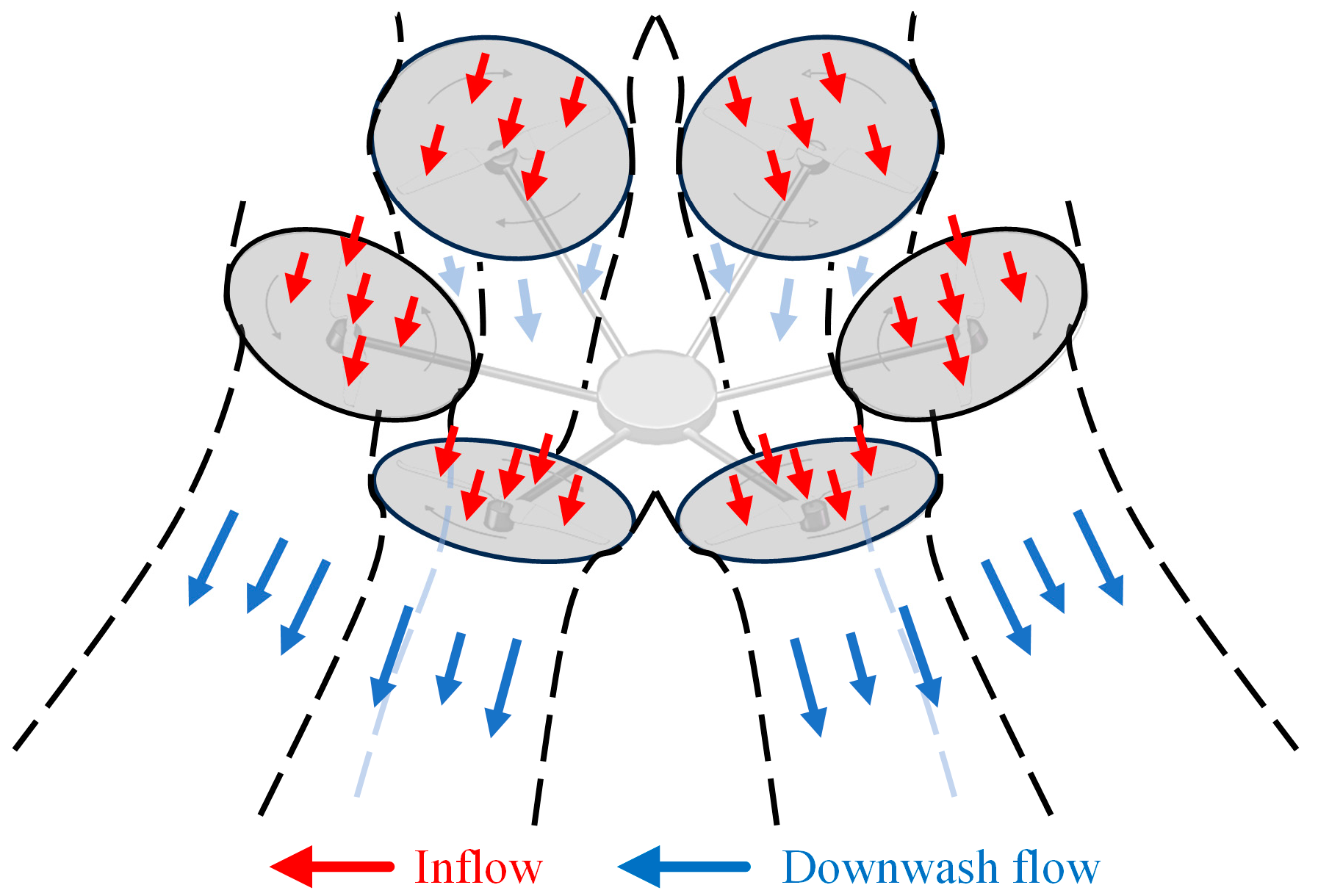
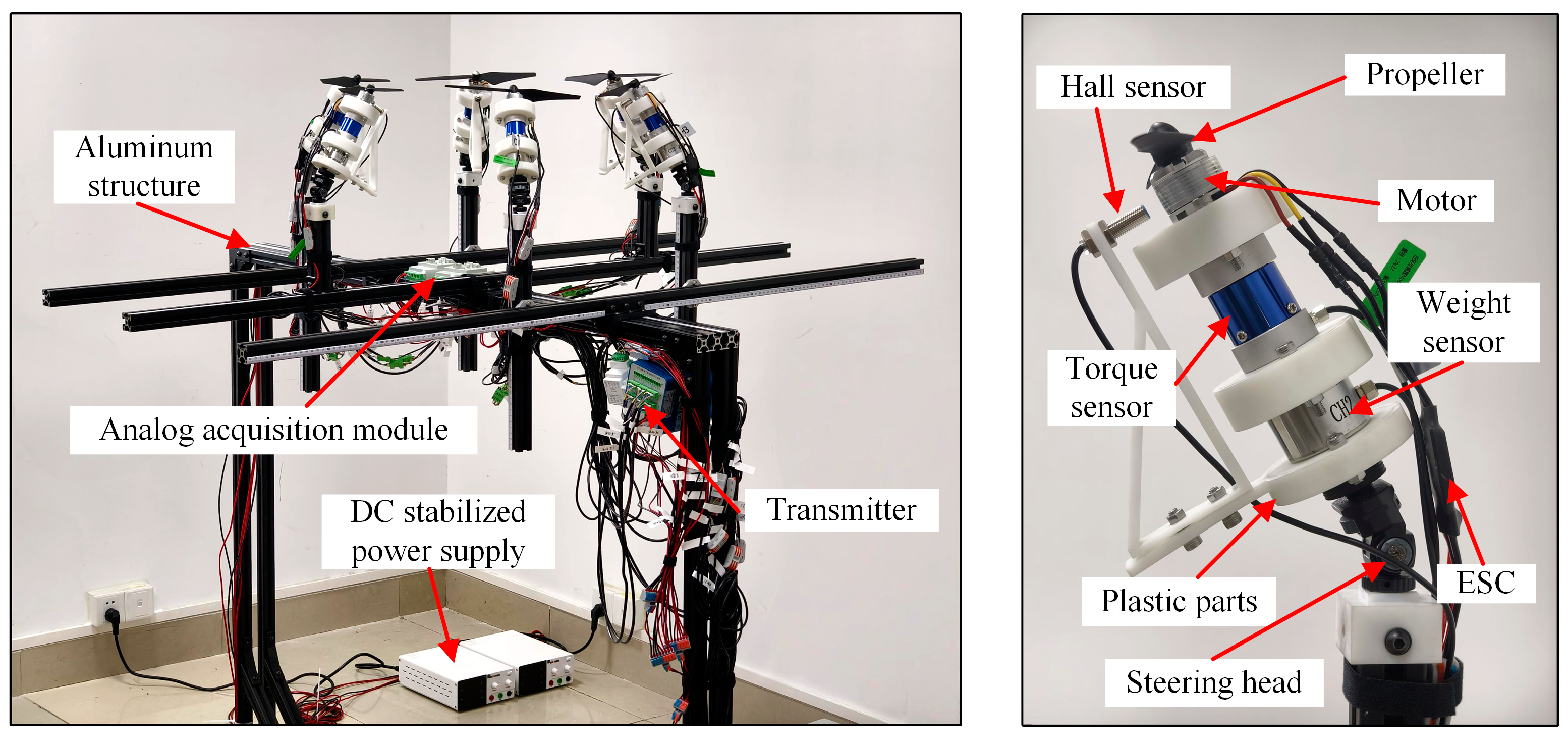
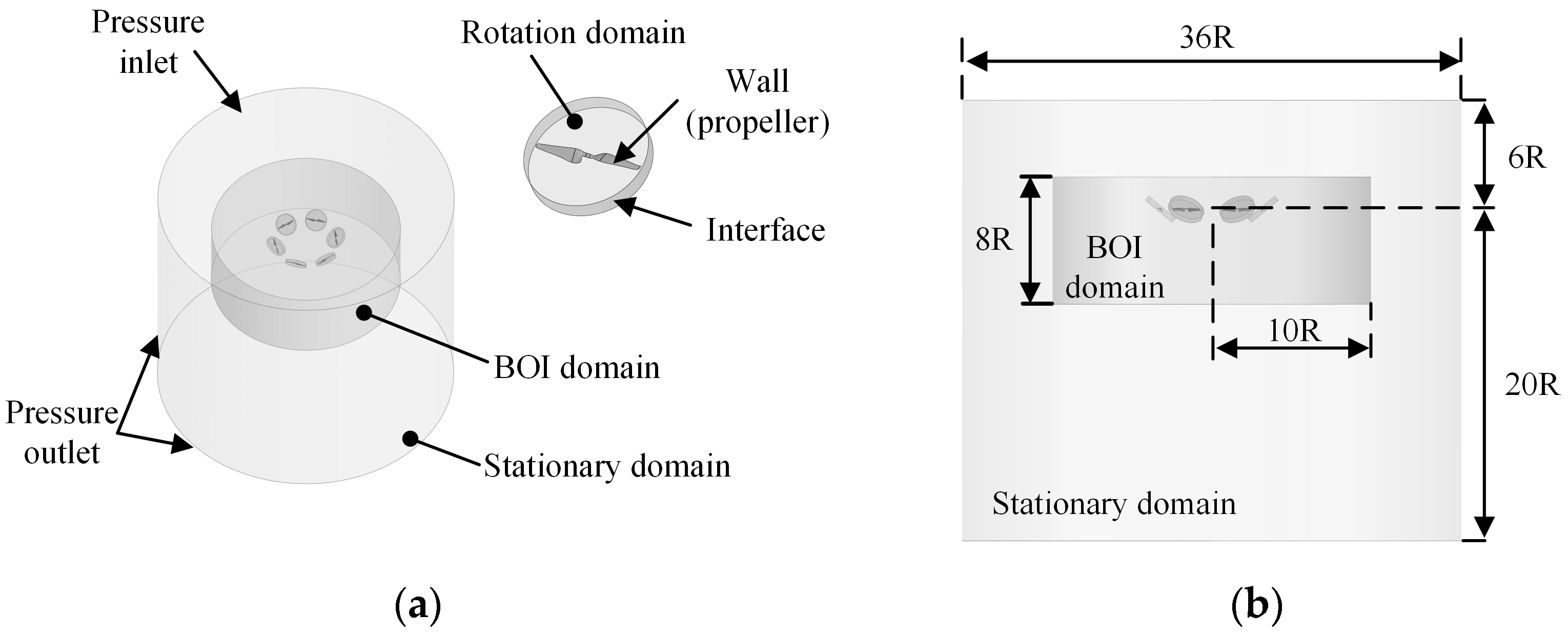
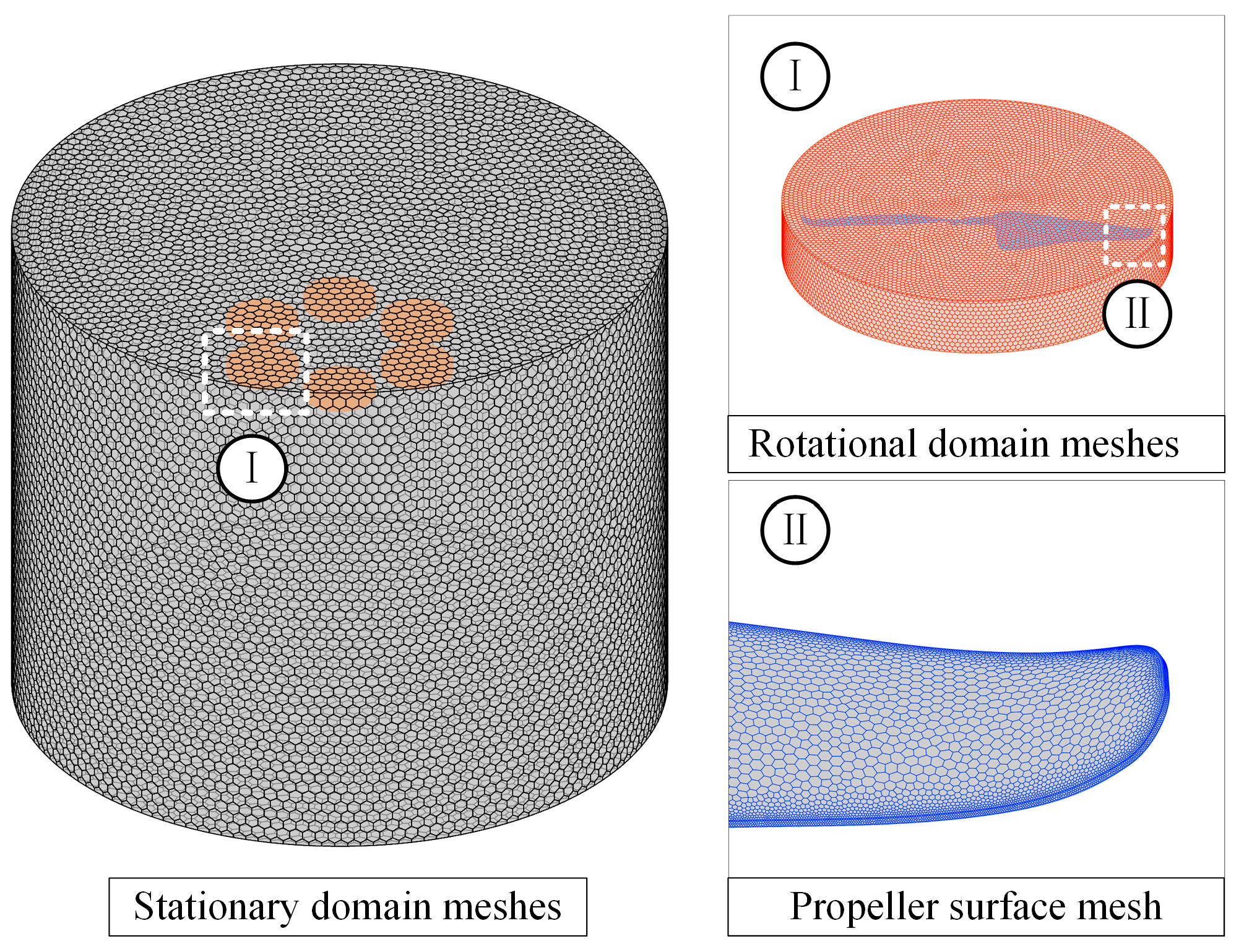

| Parameters | Unit | Value |
|---|---|---|
| Diameter | m | 0.4 |
| Blade Pitch | m | 0.157 |
| Chord (0.75R) | m | 0.026 |
| Chord (average) | m | 0.035 |
| Weight | kg | 0.015 |
| Uniform Thickness | % | 2.5 |
| Uniform Curvature | % | 4.5 |
| Solidity | % | 0.128 |
| Facility | Model | Scope | Accurate Value |
|---|---|---|---|
| Weight Sensor | DYZ-101 | 0–10 N | 0.05% |
| Hall Sensor | NJK-8001C | 10–9999 RPM | 0.1% |
| Torque Sensor | DYJN-104 | 0–0.5 N·m | 0.05% |
| Electronic Speed Control | YK-PWM1041 | 1–99 KHz | 1% |
| Parameters | Unit | Value |
|---|---|---|
| Propeller speed () | rpm | 2200 |
| Dihedral angle () | deg | 0, 10, 20, 30, 40, 50 |
| Rotor spacing ratio (s/D) | - | 1.2, 1.4, 1.6, 1.8, 2.0 |
| Mesh Model | Surface Mesh (mm) | Total Elements (×104) | Thrust (N) | Torque (N·m) | Averaged y-Plus |
|---|---|---|---|---|---|
| Mesh 1 | 6 | 29.36 | 3.30 | 0.093 | 32.82 |
| Mesh 2 | 4 | 71.06 | 3.34 | 0.090 | 32.66 |
| Mesh 3 | 2 | 110.70 | 3.35 | 0.088 | 32.34 |
| Mesh 4 | 1 | 137.37 | 3.35 | 0.088 | 31.39 |
| Mesh Model | Rotational Domain Meshes (×104) | Stationary Domain Meshes (×104) | Total Number of Meshes (×104) | Thrust (N) |
|---|---|---|---|---|
| Coarse mesh | 476.70 | 606.21 | 1082.91 | 23.97 |
| Medium mesh | 606.25 | 852.36 | 1458.61 | 24.04 |
| Fine mesh | 760.53 | 1009.82 | 1770.35 | 24.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Y.; Luan, C. Aerodynamic Analysis of a Hexacopter with an Inner Tilted-Rotor Configuration During Hovering. Aerospace 2025, 12, 317. https://doi.org/10.3390/aerospace12040317
Lei Y, Luan C. Aerodynamic Analysis of a Hexacopter with an Inner Tilted-Rotor Configuration During Hovering. Aerospace. 2025; 12(4):317. https://doi.org/10.3390/aerospace12040317
Chicago/Turabian StyleLei, Yao, and Chunfeng Luan. 2025. "Aerodynamic Analysis of a Hexacopter with an Inner Tilted-Rotor Configuration During Hovering" Aerospace 12, no. 4: 317. https://doi.org/10.3390/aerospace12040317
APA StyleLei, Y., & Luan, C. (2025). Aerodynamic Analysis of a Hexacopter with an Inner Tilted-Rotor Configuration During Hovering. Aerospace, 12(4), 317. https://doi.org/10.3390/aerospace12040317








