Integrated Aircraft Engine Energy Management Based on Game Theory
Abstract
1. Introduction
2. System Modeling
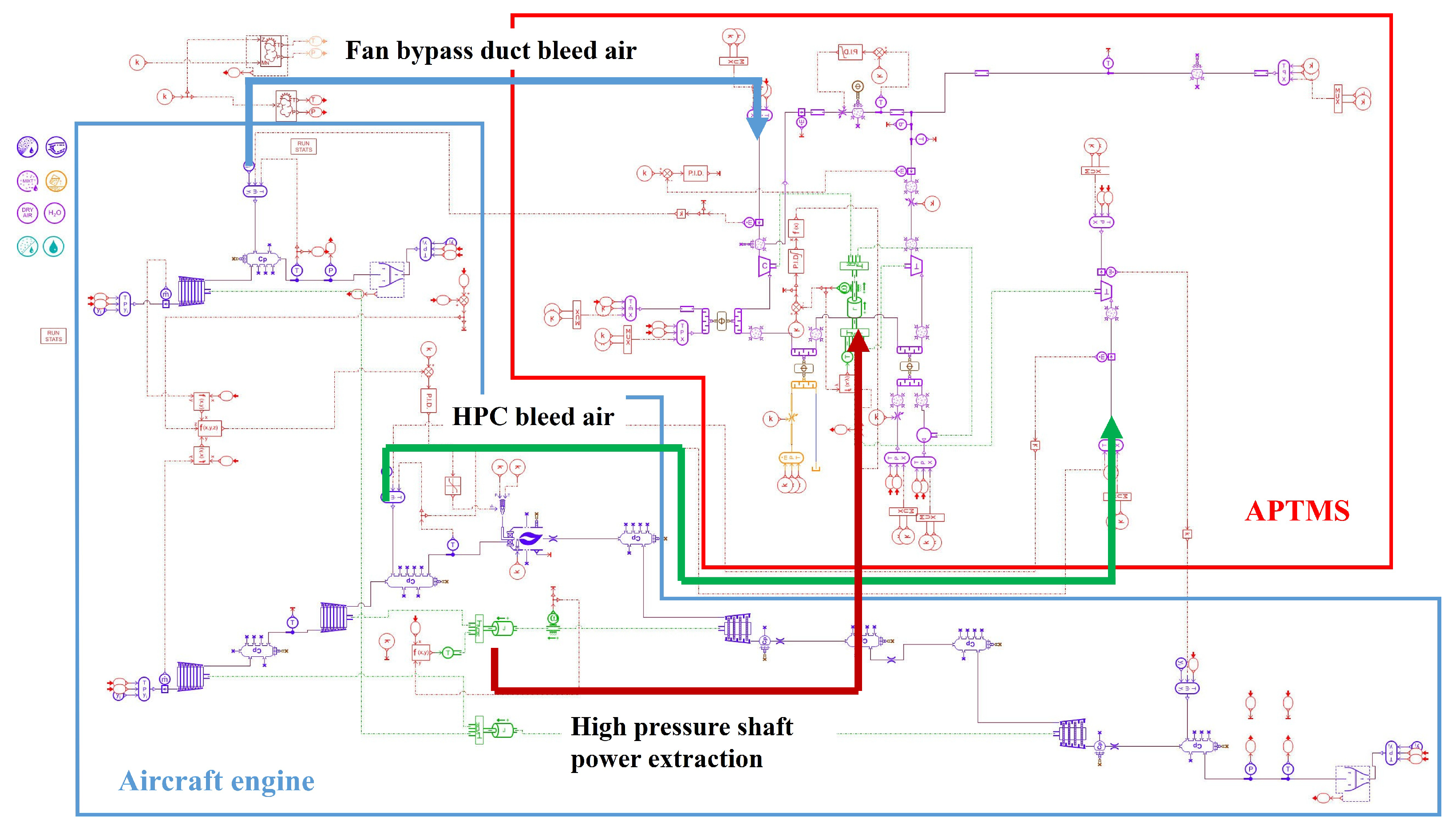
2.1. Aircraft Engine Modeling
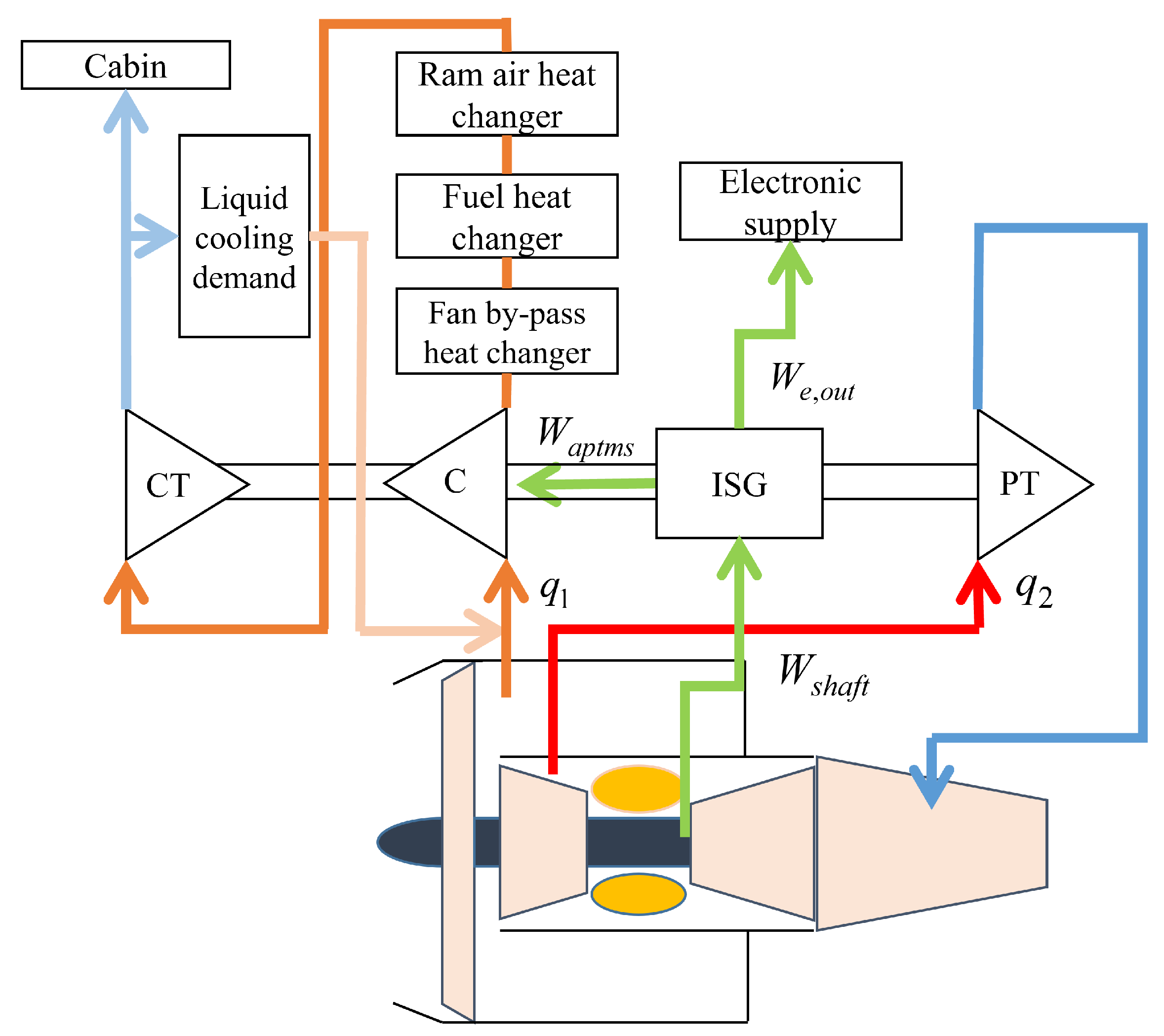
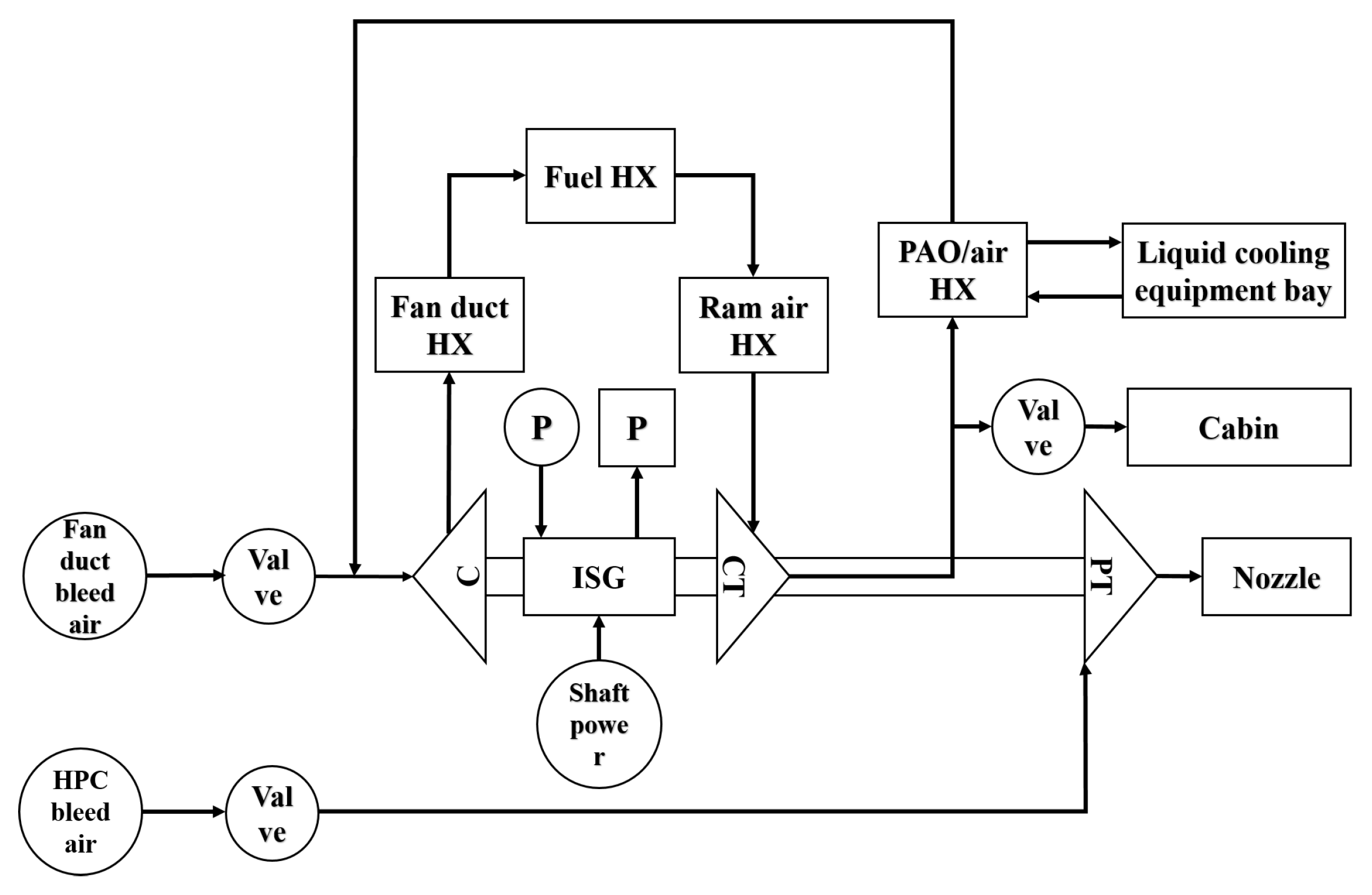
2.2. APTMS System Modeling
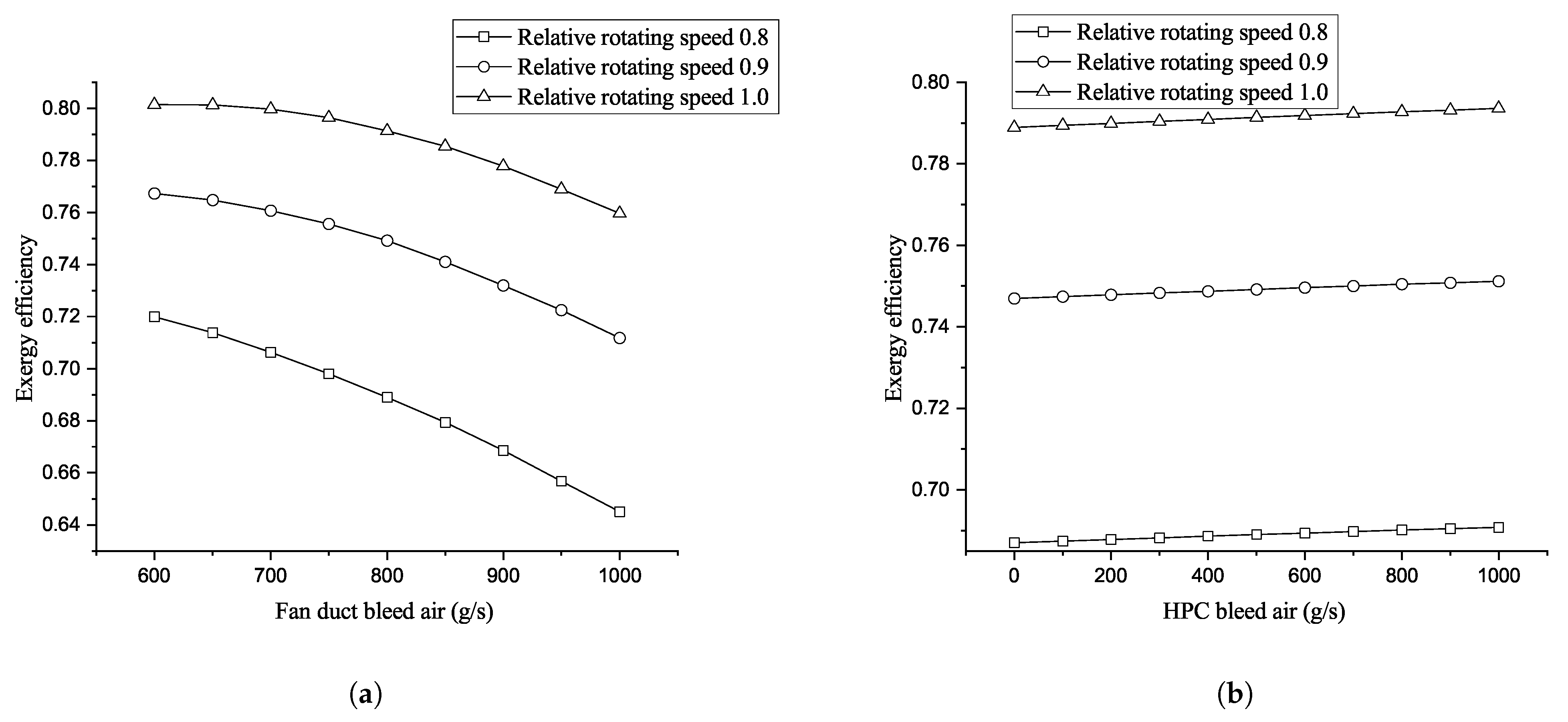
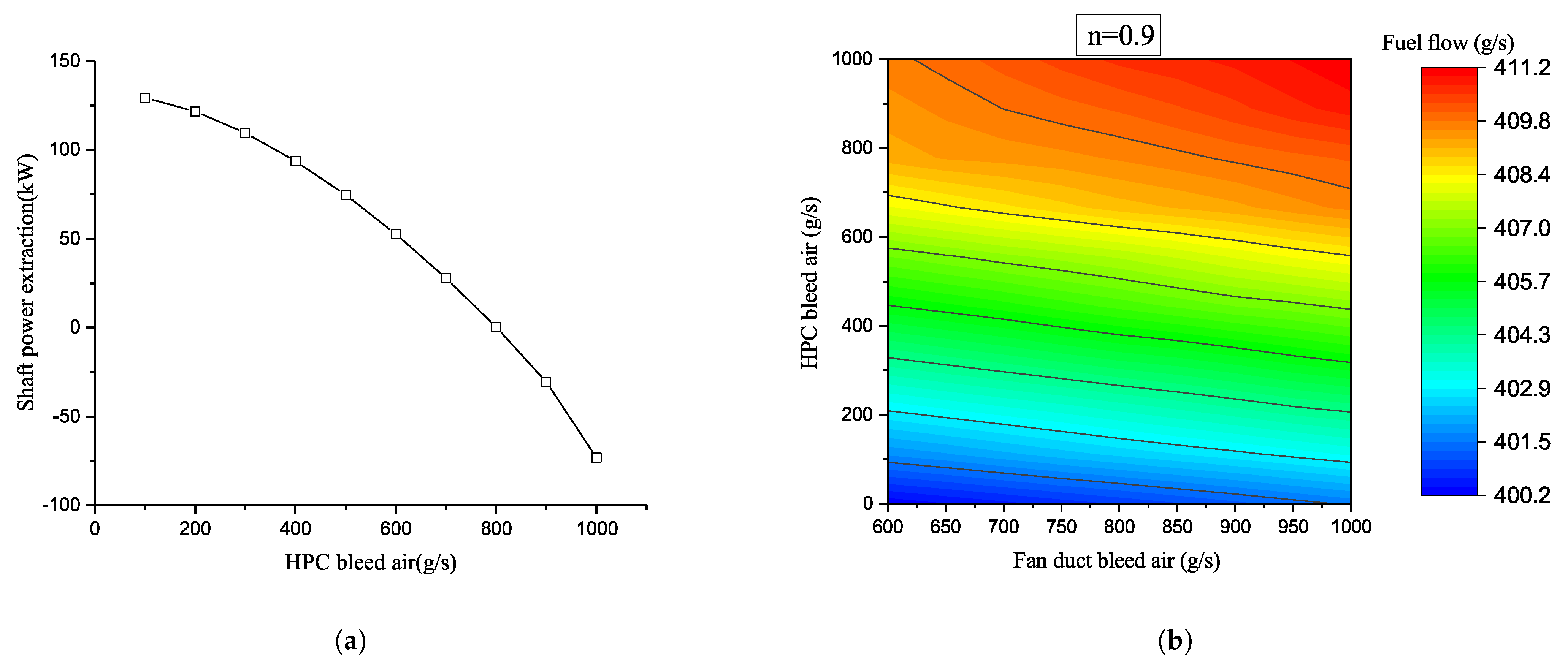
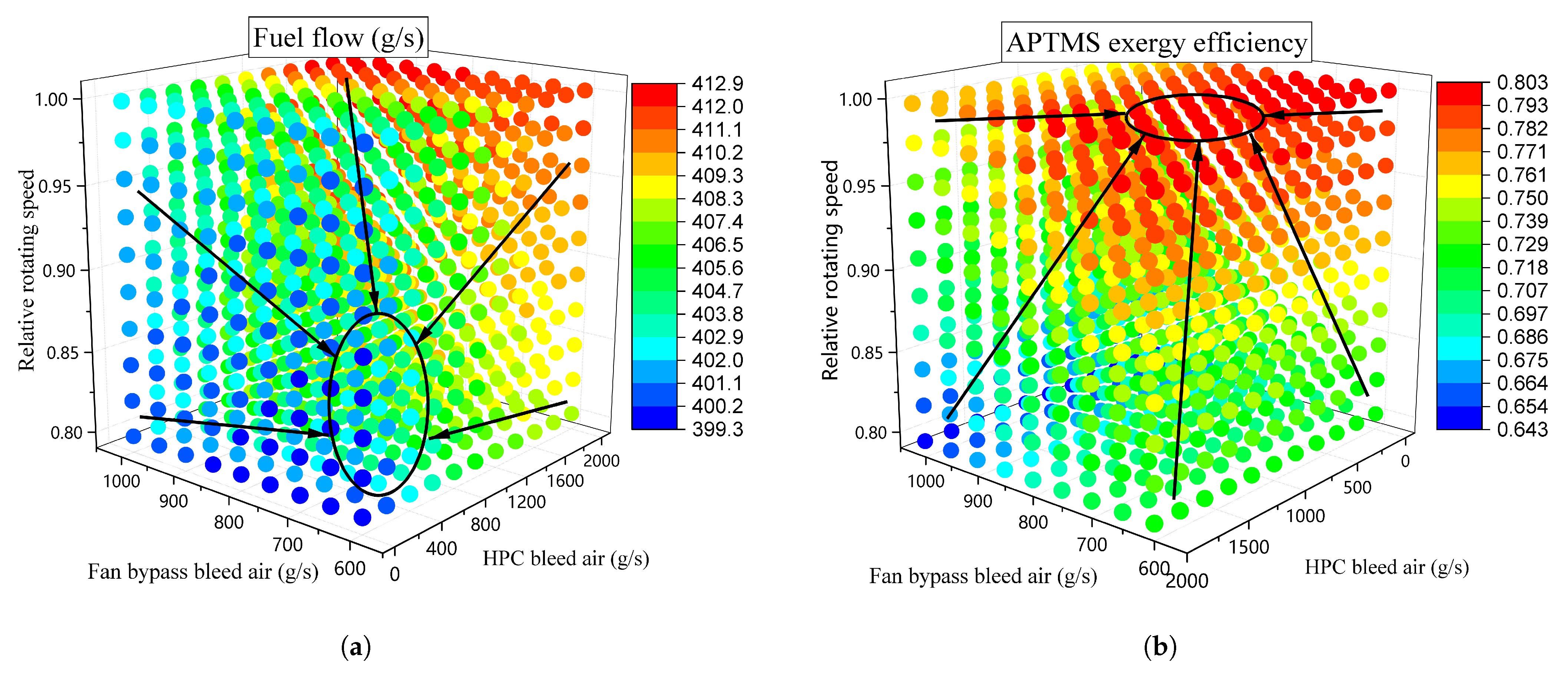
3. Coupling Influence Between the Aircraft Engine and APTMS
4. Stackelberg Game and Adaptive Chaotic Particle Swarm Algorithm
4.1. Stackelberg Game
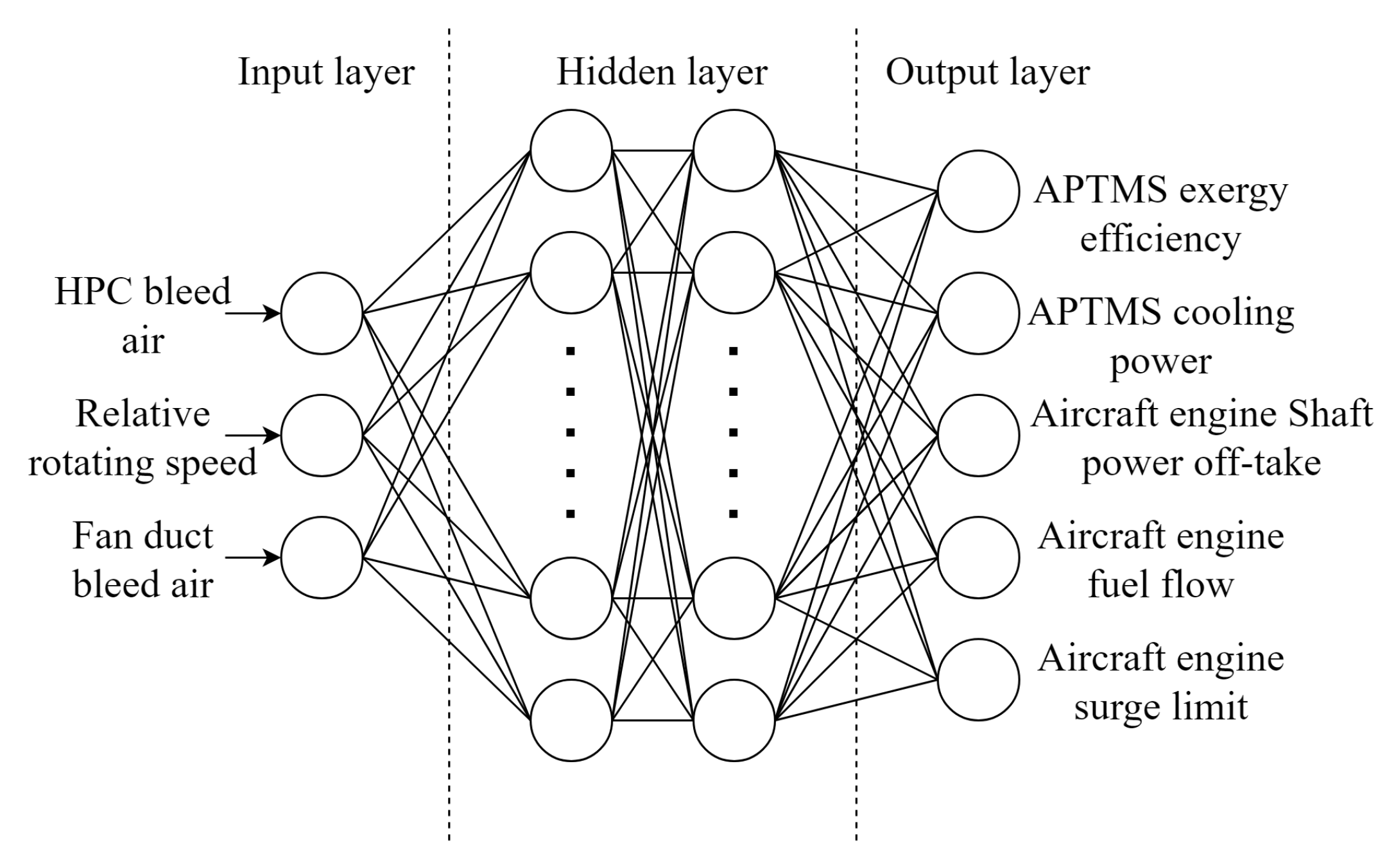
4.2. ANN-Based APTMS-Engine Performance Surrogate Model
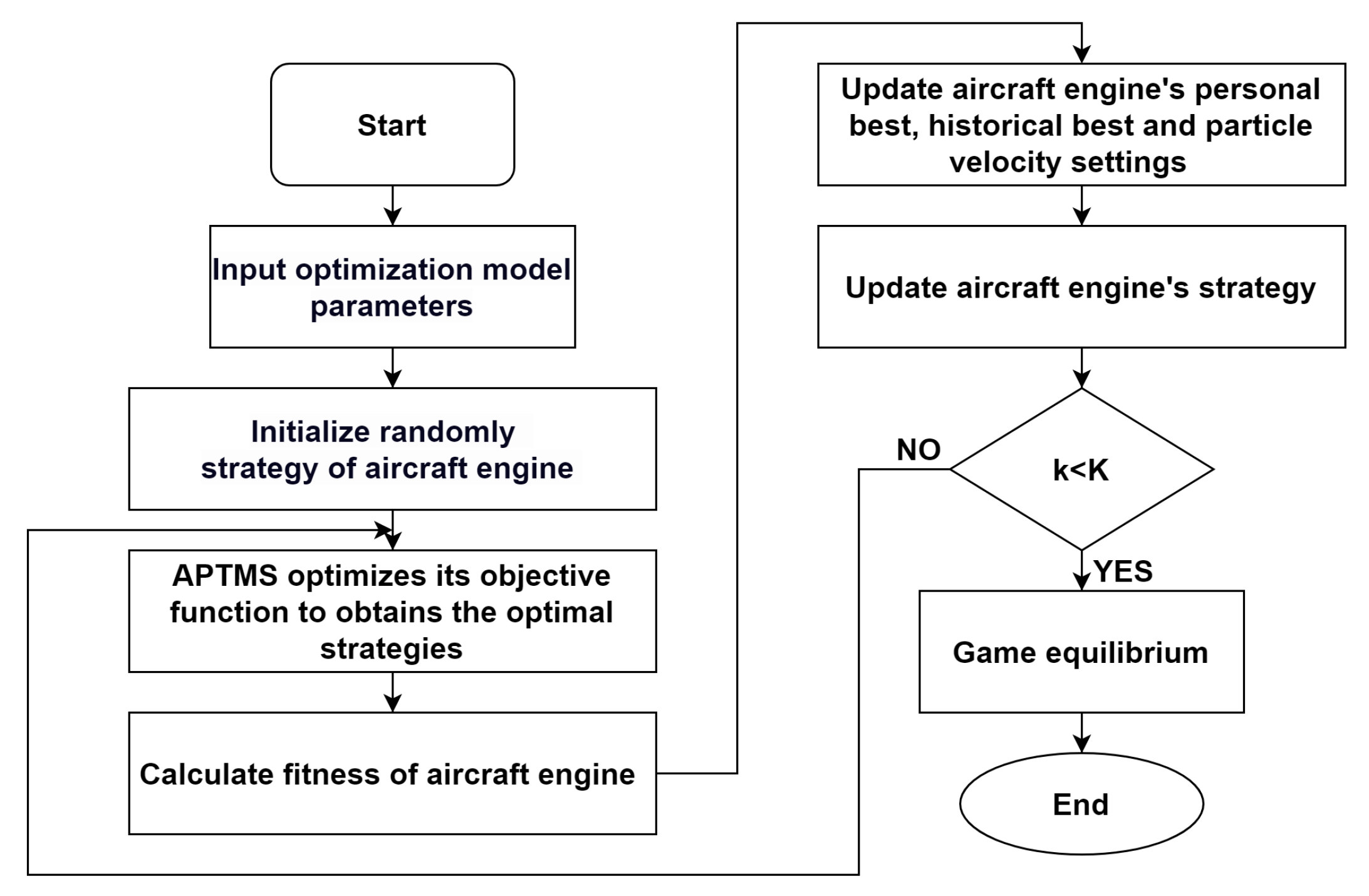
4.3. Adaptive Chaotic Particle Swarm Algorithm
- (1)
- Set the environmental parameters for the system model: flight altitude, flight Mach number, and energy demand. Set the iteration parameters for the ACPSO: particle count and maximum iteration number.
- (2)
- Randomly generate as strategies for the aircraft engine and pass the parameters to the APTMS system.
- (3)
- The APTMS system employs the ACPSO algorithm to determine strategies that maximize exergy efficiency, resulting in optimal rotational speed n and fan bleed air that meets cooling power demand.
- (4)
- APTMS’s strategies are passed to the aircraft engine and calculate the fitness and the fuel flow.
- (5)
- Update the aircraft engine’s particle swarm personal best set and group best set. Update the particle swarm velocities.
- (6)
- According to the new velocities, and calculate the aircraft engine’s new strategies.
- (7)
- Check if the number of iterations k has reached the maximum limit or if the fuel economy of the aircraft engine and the exergy efficiency of the APTMS system have achieved equilibrium. If either condition is met, output the results. If not, continue iterating.
- (8)
- Re-update the strategies and repeat steps (3) to (7).
5. Simulation
5.1. Cruise Simulation
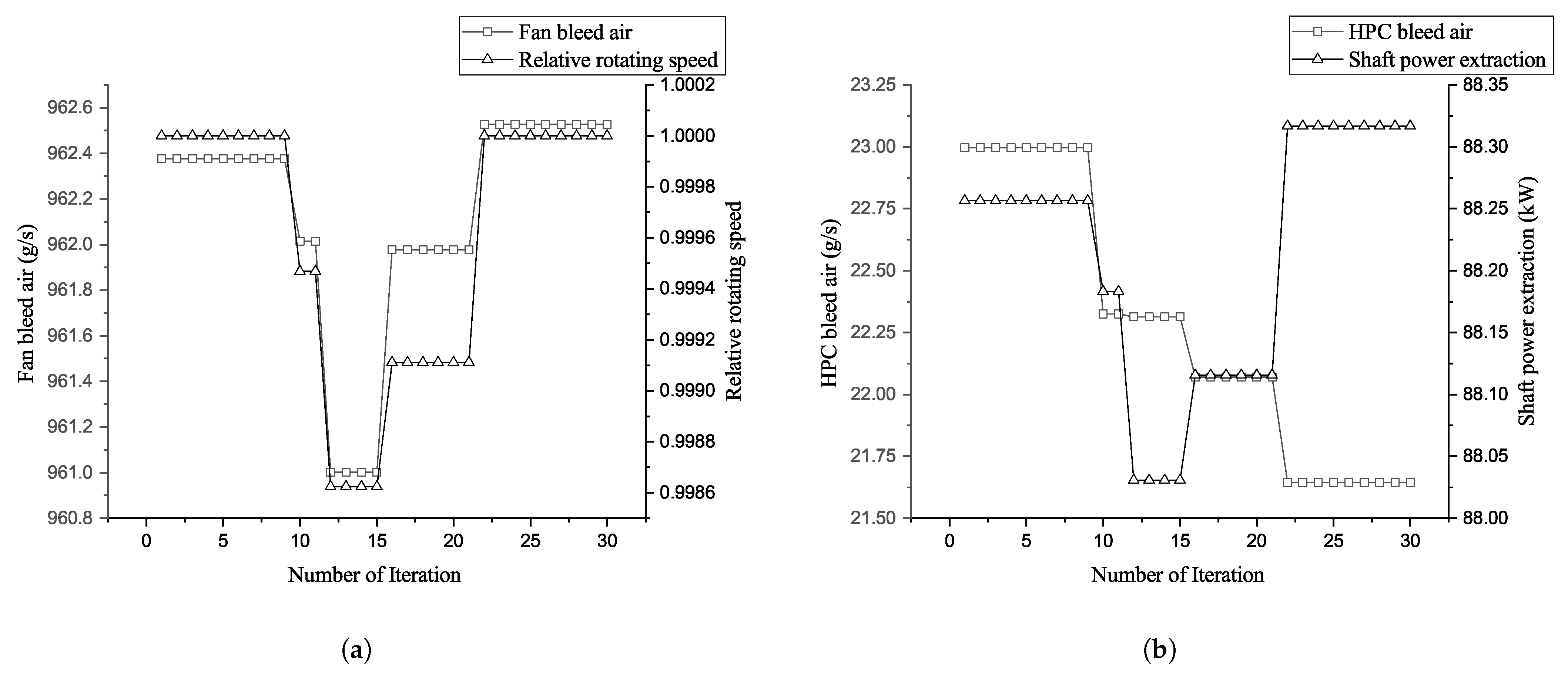
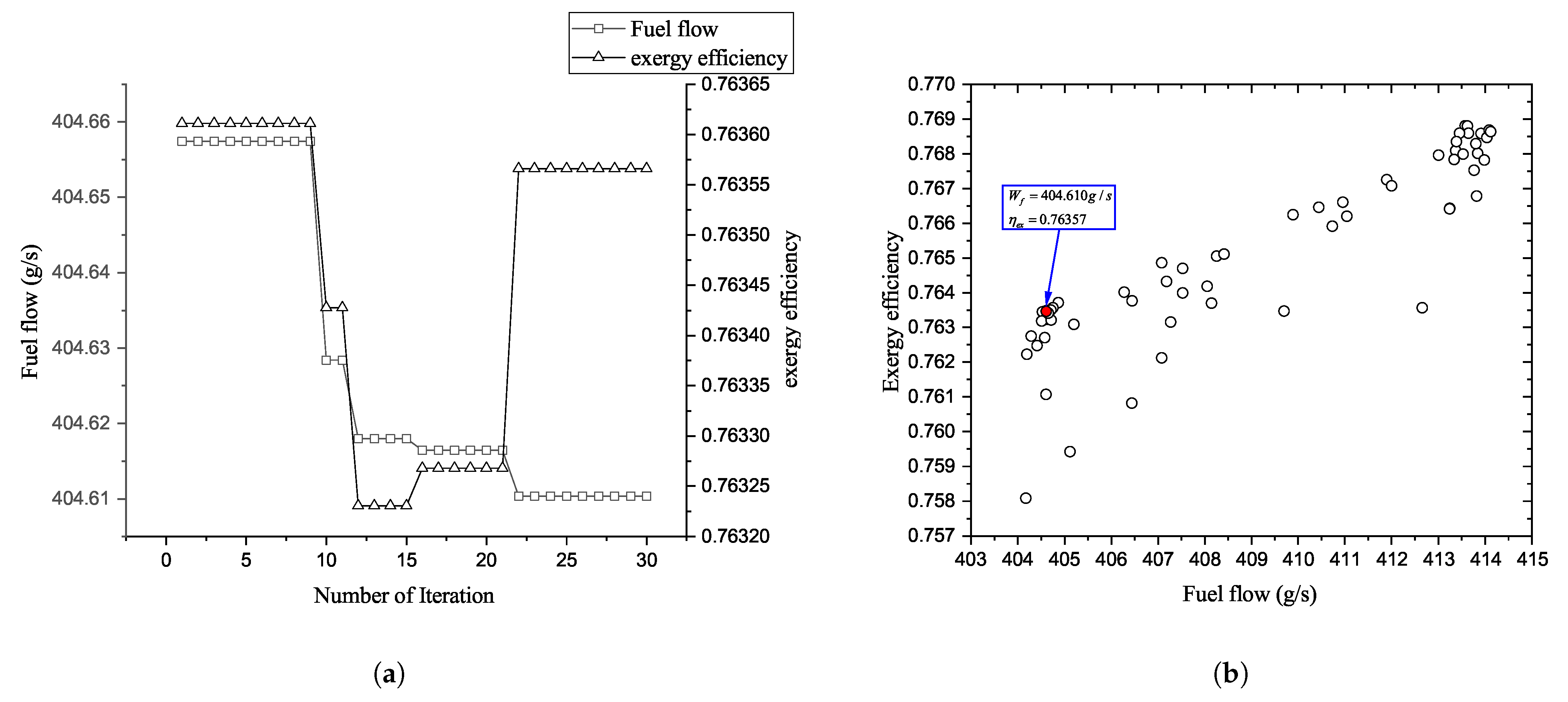
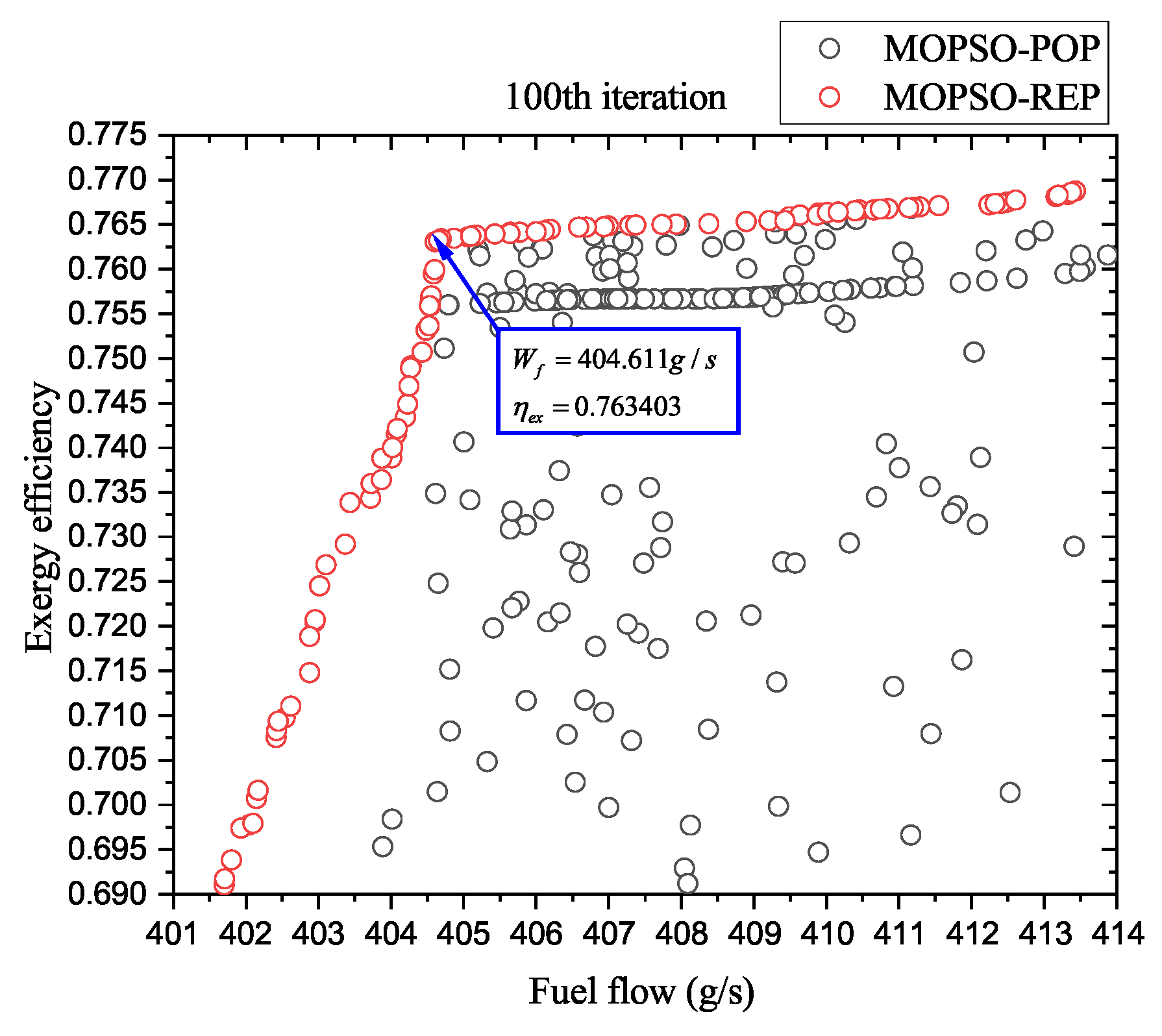
5.2. Comparison Between MOPSO, Cournot–ACPSO, and Stackelberg–ACPSO
5.3. Flight Mission Simulation
6. Conclusions
- (1)
- There is a significant performance conflict between the aircraft engine and the APTMS system, as their optimization objectives are fundamentally opposed within the operational envelope. An improvement in exergy efficiency inevitably leads to a decline in fuel economy.
- (2)
- This article proposes an energy management strategy based on the Stackelberg game to mitigate the performance conflicts between the APTMS system and the aircraft engine. Furthermore, it introduces an enhanced Particle Swarm Optimization (PSO) method that incorporates adaptive chaos search, inertia coefficient, and adjustable learning factors to determine the Stackelberg equilibrium effectively.
- (3)
- Through simulation and calculation, the optimization effects of Stackelberg–ACPSO were found to be superior to those of Cournot–ACPSO and MOPSO.
- (4)
- Optimal strategy selection relies on thrust-dependent characteristics and cooling power demand through parametric mission profile simulations under Stackelberg game energy management.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| APMTS | Adaptive Power and Thermal Management System |
| PSO | Particle Swarm Optimization |
| ACPSO | Adaptive Chaotic Particle Swarm Optimization |
| T/EMM | Power and Thermal Management Components |
| CT | Cooling turbine |
| PT | Power turbine |
| HPC | High-pressure compressor |
| LPC | Low-pressure compressor |
| HPT | High-pressure turbine |
| LPT | Low-pressure turbine |
| ISG | Integrated starter-gene |
| SFC | Specific fuel consumption |
| HX | Heat exchanger |
| CPU | Combine power unit |
| MOPSO | Multi-objective Particle Swarm Optimization |
References
- Guo, S.; Wang, Y.; Pan, J.; Li, A. Integrated Technology of Aircraft Electromechanical Fluid System, 1st ed.; Shanghai Scientific & Technical Publishers: Shanghai, China, 2020. (In Chinese) [Google Scholar]
- Scholz, D.; Seresinhe, R.; Staack, I.; Lawson, C. Fuel Consumption Due to Shaft Power Off-Takes from the Engine; Shaker Verlag: Düren, Germany, 2013. [Google Scholar] [CrossRef]
- Slingerland, R.; Zandstra, S. Bleed Air versus Electric Power Off-takes from a Turbofan Gas Turbine over the Flight Cycle. In Proceedings of the 7th AIAA ATIO Conf, 2nd CEIAT Int’l Conf on Innov and Integr in Aero Sciences, 17th LTA Systems Tech Conf; Followed by 2nd TEOS Forum, Belfast, Northern Ireland, 18–20 September 2007. [Google Scholar] [CrossRef]
- Van Heerden, A.; Judt, D.; Jafari, S.; Lawson, C.; Nikolaidis, T.; Bosak, D. Aircraft Thermal Management: Practices, Technology, System Architectures, Future Challenges, and Opportunities. Prog. Aerosp. Sci. 2022, 128, 100767. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, X.; Huang, C. Adaptive Power and Thermal Management System for New Generation Aircraft. Aeronaut. Sci. Technol. 2012, 5, 38–41. (In Chinese) [Google Scholar]
- Roberts, R.A.; Decker, D.D. Control Architecture Study Focused on Energy Savings of an Aircraft Thermal Management System. J. Dyn. Syst. Meas. Control 2014, 136, 041003. [Google Scholar] [CrossRef]
- Stoia, M.F.; Ek, G.W.; Bowcutt, K.G.; Needels, J.T. Integrated Power and Thermal Management System for High Speed Aircraft. In Proceedings of the AIAA Propulsion and Energy 2021 Forum, Virtual Event, 9–11 August 2021. [Google Scholar] [CrossRef]
- Hu, X. Modeling and Performance Analysis of Power Thermal Management System Based on MATLAB Simulation Platform. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2018. (In Chinese). [Google Scholar]
- Zhuang, L.; Xu, G.; Dong, B.; Liu, Q.; Huang, C.; Wen, J. Study on performance and mechanisms of a novel integrated model with Power & Thermal Management system and turbofan engine. Appl. Therm. Eng. 2023, 219, 119481. [Google Scholar] [CrossRef]
- Rong, A.; Pang, L.; Jiang, X.; Qi, B.; Shi, Y. Analysis and Comparison of Potential Power and Thermal Management Systems for High-Speed Aircraft with an Optimization Method. Energy Built Environ. 2021, 2, 13–20. [Google Scholar] [CrossRef]
- Lei, Y. Research on Scheme of Integrated Thermal and Energy Management System of Aircraft. Master’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2016. (In Chinese). [Google Scholar]
- Lei, T.; Min, Z.; Gao, Q.; Song, L.; Zhang, X.; Zhang, X. The Architecture Optimization and Energy Management Technology of Aircraft Power Systems: A Review and Future Trends. Energies 2022, 15, 4109. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, F.; Chen, Y.; Zhang, J.; Cheng, F.; Zhang, J. A Two-Stage Energy Management for Integrated Thermal/Energy Optimization of Aircraft Airborne System Based on Stackelberg Game. Energy 2023, 269, 126506. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. A Two-Stage Energy Management for Heat-Electricity Integrated Energy System Considering Dynamic Pricing of Stackelberg Game and Operation Strategy Optimization. Energy 2022, 244, 122576. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Qian, T.; Wu, X. Energy Management in Microgrids Based on Generalized Stackelberg Game Theory. Electr. Power Autom. Equip. 2022, 42, 171–177. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, B.; Peng, H.; Zang, T.; Zhang, Y.; Zhao, W.; Cao, Q. Peer-to-Peer Trade Strategy for Multi-microgrid System Based on Stackelberg Game. Proc. CSU-EPSA 2023, 35, 103–111. (In Chinese) [Google Scholar] [CrossRef]
- Chen, L.; Fan, Y.; Li, G.; Li, F.; Zhao, D. Energy Optimization Management Strategy of Photovoltaic Hydrogen Production System Based on Stackelberg Game. Mod. Electr. Power 2024, 41, 507–516. (In Chinese) [Google Scholar] [CrossRef]
- Chen, W.; Luo, W.; Liang, K.; Bai, C. Research on New Energy Investment Strategy Based on Non-cooperative and Cooperative Bimatrix Games. J. Syst. Sci. Math. Sci. 2024, 44, 3557–3572. (In Chinese) [Google Scholar] [CrossRef]
- Lin, J.; Li, G. Power Allocation Based on Stackelberg Game in Wireless Location Network. In Proceedings of the 14th Annual Conference on Satellite Communications; College of Communications Engineering, Army Engineering University of PLA: Nanjing, China, 2018; pp. 397–404. (In Chinese). [Google Scholar]
- Zhang, X.; Wang, Y.; Zhang, H.; Zhao, J.; Jia, R. Research on High-Speed Automatic Lane Change Decision-Making and Planning Considering Driving Style. Automob. Technol. 2024, 1, 17–28. (In Chinese) [Google Scholar] [CrossRef]
- Xu, H.; Chen, p.; Li, X.; Wang, P.; Ma, L. Charging Management Strategy of Electric Vehicle Based on Stackelberg Game. Comput. Appl. Softw. 2024, 41, 382–388. (In Chinese) [Google Scholar] [CrossRef]
- Soleymani, M.; Mostafavi, V.; Hebert, M.; Kelouwani, S.; Boulon, L. Hydrogen Propulsion Systems for Aircraft, a Review on Recent Advances and Ongoing Challenges. Int. J. Hydrogen Energy 2024, 91, 137–171. [Google Scholar] [CrossRef]
- Tiwari, S.; Pekris, M.J.; Doherty, J.J. A Review of Liquid Hydrogen Aircraft and Propulsion Technologies. Int. J. Hydrogen Energy 2024, 57, 1174–1196. [Google Scholar] [CrossRef]
- Zhang, J.; Roumeliotis, I.; Zolotas, A. Model-Based Fully Coupled Propulsion-Aerodynamics Optimization for Hybrid Electric Aircraft Energy Management Strategy. Energy 2022, 245, 123239. [Google Scholar] [CrossRef]
- He, L.; Chen, F.; Tian, P.; Gou, H. An Improved Energy Management Strategy for Hybrid Electric Powered Aircraft Based on Deep Reinforcement Learning. Aerosp. Sci. Technol. 2024, 149, 109137. [Google Scholar] [CrossRef]
- Yang, C.; Lu, Z.; Wang, W.; Li, Y.; Chen, Y.; Xu, B. Energy Management of Hybrid Electric Propulsion System: Recent Progress and a Flying Car Perspective under Three-Dimensional Transportation Networks. Green Energy Intell. Transp. 2023, 2, 100061. [Google Scholar] [CrossRef]
- Hayes, D.; Lone, M.; Whidborne, J.F.; Camberos, J.; Coetzee, E. Adopting Exergy Analysis for Use in Aerospace. Prog. Aerosp. Sci. 2017, 93, 73–94. [Google Scholar] [CrossRef]
- Ge, Y.; Song, B.; Pei, Y. Analysis Method of More-electric Aircraft Energy Efficiency Based on Exergy. Acta Aeronaut. Astronaut. Sin. 2014, 35, 1276–1283. (In Chinese) [Google Scholar] [CrossRef]
- Da Costa Baptista, F.M. A 0-D Off-Design Performance Prediction Model of the CFM56-5B Turbofan Engine. Ph.D. Thesis, Techico Lisboa, Lisboa, Portugal, 2017. [Google Scholar]
- Quevedo-Reina, R.; Álamo, G.M.; Aznárez, J.J. ANN-based Surrogate Model for the Structural Evaluation of Jacket Support Structures for Offshore Wind Turbines. Ocean Eng. 2025, 317, 119984. [Google Scholar] [CrossRef]
- Candon, M.; Esposito, M.; Fayek, H.; Levinski, O.; Koschel, S.; Joseph, N.; Carrese, R.; Marzocca, P. Advanced Multi-Input System Identification for next Generation Aircraft Loads Monitoring Using Linear Regression, Neural Networks and Deep Learning. Mech. Syst. Signal Process. 2022, 171, 108809. [Google Scholar] [CrossRef]
- Cao, J.; Yang, D.; Dehghanian, P. Co-Optimization of Multiple Virtual Power Plants Considering Electricity-Heat-Carbon Trading: A Stackelberg Game Strategy. Int. J. Electr. Power Energy Syst. 2023, 153, 109294. [Google Scholar] [CrossRef]
- Raju, V.A.G.; Nayak, J.; Dash, P.B.; Mishra, M. Short-Term Solar Irradiance Forecasting Model Based on Hyper-Parameter Tuned LSTM via Chaotic Particle Swarm Optimization Algorithm. Case Stud. Therm. Eng. 2025, 69, 105999. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, J.; Guo, R.; Gao, Z.; Niu, Y. An Adaptive Chaotic Particle Swarm Optimization Based Scheduling Strategy for Combined Cooling, Heating and Power System. Mod. Electr. Power 2020, 37, 551–558. (In Chinese) [Google Scholar] [CrossRef]
- Dong, C.; Cheng, H.; Wang, S.; He, C.; Wang, B.; Shao, X.C. Comprehensive Energy System Optimization Based on CIPSO Algorithm. J. Zhejiang Univ. Technol. 2024, 52, 196–202+229. [Google Scholar]
- Lampl, T.S.; Muschkorgel, S.; Hornung, M. Parameterized Flight Mission for Secondary Power Requirement Estimations of Commercial Transport Aircraft. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Z. Power Management Problem for Civil Aircraft under More Electric Environment. Int. J. Aerosp. Eng. 2020, 2020, 8474375. [Google Scholar] [CrossRef]





| Equilibrium | Equation |
|---|---|
| High-pressure rotor shaft power balance | |
| Low-pressure rotor shaft power balance | |
| Combustor outlet flow balance | |
| HPT outflow balance | |
| Fan outflow balance | |
| Nozzle inflow and outflow balance | |
| Fan duct airflow balance | |
| HPC airflow balance |
| Parameters | Value |
|---|---|
| Turbine entry temperature | 1696 K |
| Combustion chamber efficiency | 0.99 |
| Pressure ratio of HPC | 10.668 |
| Pressure ratio of outer fan | 1.69 |
| Pressure ratio of inner fan | 3.197 |
| High-pressure shaft speed | 14,736 r/min |
| Low-pressure shaft speed | 5057 r/min |
| Power turbine entry temperature | 473.15 K |
| Cool side airflow of fan bypass duct HX | 2 kg/s |
| Cool side airflow of fuel HX | 2 kg/s |
| Fuel temperature | 298.15 K |
| Standard atmosphere pressure | 101,325 Pa |
| Standard shaft speed | 22,500 r/min |
| Performance | Fuel Flow (g/s) | Exergy Efficiency |
|---|---|---|
| Stackelberg–ACPSO | 404.610 | 0.76357 |
| Cournot–ACPSO | 405.04 | 0.76316 |
| Condition | Altitude/m | Ma |
|---|---|---|
| 1 | 9250 | 0.76 |
| 2 | 9250 | 0.78 |
| 3 | 9250 | 0.8 |
| 4 | 9500 | 0.76 |
| 5 | 9500 | 0.78 |
| …………… | ||
| 12 | 10,000 | 0.80 |
| Condition | Time (s) | Ma | Altitude (m) | Net Thrust (kN) | Electrical Power Demand (kW) | Cooling Power Demand (kW) |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 110 | 46.9515 | 22.25 |
| 2 | 120.4 | 0.24173 | 0 | 90 | 38.36303 | 21.5 |
| 3 | 287.4 | 0.41336 | 1524.19645 | 65 | 39.33459 | 23 |
| 4 | 443.2 | 0.50232 | 3048 | 60 | 47.59906 | 23.75 |
| 5 | 481.2 | 0.541 | 3279.53766 | 26 | 44.04975 | 23.75 |
| 6 | 630 | 0.60323 | 4840.75 | 48.3 | 38.39962 | 24.5 |
| 7 | 779.4 | 0.66421 | 6402.02515 | 42 | 38.19671 | 27.5 |
| 8 | 1021 | 0.74748 | 8274.13592 | 34.1 | 37.28203 | 27.7 |
| 9 | 1262.8 | 0.78107 | 9754.34236 | 20.5 | 36.6321 | 31.25 |
| 10 | 3450 | 0.78107 | 9754.34236 | 20.5 | 36.6321 | 31.25 |
| 11 | 3471.6 | 0.78035 | 9754.34236 | 17 | 36.83725 | 31.25 |
| 12 | 3780.7 | 0.72301 | 7728.64632 | 17 | 36.37847 | 27.7 |
| 13 | 4089.8 | 0.63155 | 5574.80629 | 17 | 36.57198 | 27.5 |
| 14 | 4666 | 0.44218 | 2665.65876 | 17 | 42.88959 | 23.750 |
| 15 | 5243.8 | 0.23248 | 457.02513 | 17 | 34.72716 | 23 |
| 16 | 5444 | 0.23248 | 0 | 17 | 40.4565 | 22.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Luo, C.; Li, X.; Li, R.; Fan, Z. Integrated Aircraft Engine Energy Management Based on Game Theory. Aerospace 2025, 12, 328. https://doi.org/10.3390/aerospace12040328
Zhang H, Luo C, Li X, Li R, Fan Z. Integrated Aircraft Engine Energy Management Based on Game Theory. Aerospace. 2025; 12(4):328. https://doi.org/10.3390/aerospace12040328
Chicago/Turabian StyleZhang, Hong, Chenyang Luo, Xiangping Li, Runcun Li, and Zhilong Fan. 2025. "Integrated Aircraft Engine Energy Management Based on Game Theory" Aerospace 12, no. 4: 328. https://doi.org/10.3390/aerospace12040328
APA StyleZhang, H., Luo, C., Li, X., Li, R., & Fan, Z. (2025). Integrated Aircraft Engine Energy Management Based on Game Theory. Aerospace, 12(4), 328. https://doi.org/10.3390/aerospace12040328








