Abstract
This research investigates the optimization of airfoil design for fixed-wing drones, aiming to enhance aerodynamic efficiency and reduce drag. The research employs Kulfan CST and Bézier surface parameterization methods combined with global sensitivity analysis (GSA) and machine learning techniques to improve airfoil performance under various operational conditions. Particle swarm optimization (PSO) is utilized to optimize the airfoil design, minimizing drag in cruise and ascent conditions while ensuring lift at takeoff. Computational fluid dynamics (CFD) simulations, primarily using XFOIL, validate the aerodynamic performance of the optimized airfoils. This study also explores the generative design approach using a neural network trained on 10 million airfoil simulations to predict airfoil geometry based on desired performance criteria. The results show important improvements in drag reduction, especially during low-speed cruise and ascent phases, contributing to extended flight endurance and efficiency. These results can be used for small unmanned aerial vehicles (UAVs) in real-world applications to develop better-performance UAVs under mission-specific constraints.
1. Introduction
Airfoil design plays a crucial role in the broader field of aircraft design. Airfoils are integral to the wings, horizontal and vertical stabilizers (or other possible empennage configurations), rotor blades in helicopters or drones, blades in wind turbines, aerodynamic components of racing cars such as those in Formula One, and even hydrofoil boats. Historically, airfoil designs were developed primarily through wind tunnel experiments. However, these methods were expensive, time-consuming, and required large, sophisticated facilities. In recent decades, computational aerodynamics has increasingly taken over, with numerical optimization being used to automatically find optimal shapes or generate potential designs for refinement through wind tunnel testing.
Airfoil shape optimization began in the 1970s with the pioneering work of Hicks et al. [1], who used the method of feasible directions to optimize a transonic airfoil. Although the results were satisfactory, the process encountered several difficulties and unexpected outcomes. The same researchers later attempted to incorporate multiple design conditions into the optimization process to achieve low drag at high Mach numbers while minimizing adverse effects at lower Mach numbers. They also improved shape functions to expand the range of achievable airfoils [2]. These early works were characterized by a limited number of design parameters and were constrained by the computational resources available at the time.
More recent studies have been more comprehensive and have achieved better results. For example, optimization was used in the design of the MIT Daedalus, a human-powered aircraft that successfully flew from Crete to mainland Greece [3]. Later, the same designer, Drela [4] performed a detailed study of both the advantages and limitations of the optimization process. He concluded that while optimization can indeed produce airfoils with good performance, especially when multiple operating points or non-aerodynamic design drivers are considered, the optimizer may perform poorly outside the targeted operating condition. It may also exploit minute flow phenomena, leading to noisy outputs. These issues can be mitigated by selecting a set of operating conditions for multi-point optimization and by performing checks or smoothing on the resulting geometry. Other researchers [5,6], have also explored multi-point optimization, improving performance across a range of operating conditions with varying Mach numbers and flight conditions.
The choice of optimizer in airfoil design varies widely in the literature. Some authors prefer gradient-based optimization, supported by finite differences or more advanced methods for gradient calculation [7,8]. Gradient methods offer high convergence rates and fast calculations but can suffer from issues related to automatic differentiation. On the other hand, many researchers opt for metaheuristic approaches, such as genetic algorithms [9] or particle swarm algorithms [10,11], which do not require the gradients of the objective function and make no assumptions about its differentiability. Mirjalili et al. [12] provide a good review of the state of the art of both algorithms on the airfoil design application.
The global sensitivity analysis is also a tool that has been gaining traction recently, and its effectiveness is proven in systems that can be defined by a reduced set of parameters. Although this method is typically employed in other fields, there are several applications within the aerodynamics domain. One of them is the analysis of wings, or blades in the case of wind turbines, as demonstrated by Echeverría et al. [13], in which the twist, chord, and airfoil representation parameters based on B-splines are selected as parameters. Another application could be the parametric analysis of a high-lift system, as shown in the work of Siddique et al. [14], where the sensitivity of aerodynamic coefficients to changes in the geometrical position of the flap and slat are assessed. Global sensitivity analysis typically requires a large number of samples, particularly when multiple parameters are involved, which limits its use in fields where obtaining high volumes of data is challenging. However, new methods involving emulators, which replace complex models with simpler ones, are emerging as a solution. Various types of emulators exist, such as smoothing splines with high-dimensional model representation and Gaussian processes. Storlie et al. [15] reviewed and compared different emulators.
Recently, machine learning has been increasingly employed to speed up the optimization process. While the initial cost of training a model is significant, the reduction in optimization time often justifies the investment. The literature typically implements this by creating a surrogate model that approximates the more computationally expensive CFD or XFOIL simulations. Several approaches exist for this task. Neural networks, in particular, show promise due to their ability to handle large datasets [16,17,18]. Training data is usually derived from RANS CFD simulations, which typically include fewer than 50,000 samples [18,19], or from XFOIL or other fast airfoil solvers, which may involve up to millions of samples [20]. The challenge of training models with limited samples across diverse conditions and geometries means that neural network training in RANS is often focused on specific applications. Machine learning has also been applied to assist in airfoil parametrization, by learning from shape variations within existing databases [21]. This method enables a compact representation but at the cost of limiting the geometries of airfoils that can be modeled.
Another approach to incorporating this technology involves the generative design of airfoils directly in an inverse-design manner. Most authors acknowledge the potential of traditional design methods based on particle swarm optimization (PSO), Differential Evolution (DE), or other techniques enhanced by generative design [21,22,23,24]. Sekar et al. [25] demonstrated the use of Convolutional Neural Networks (CNNs) for inverse airfoil design, successfully mapping desired pressure distributions to airfoil shapes. However, their approach, which represented airfoils as images, faced challenges such as high dimensionality and potential smoothness issues. Yilmaz and German [17] pioneered the application of Conditional Generative Adversarial Networks (CGANs) to airfoil inverse design. This architecture has since been adopted by other researchers, yielding promising results [26]. A significant advancement in the field was the introduction of Bézier-GAN [22]. By integrating Bézier curves into the GAN framework, Bézier-GAN ensured the generation of smooth airfoil shapes. While these methods show promising results, they are not without limitations. Training GANs can be computationally intensive, and ensuring diversity in the generated designs remains a challenge. Additionally, training typically requires large datasets of possible airfoil shapes. Most studies rely on the UIUC database, often using a subset of 1500 or fewer airfoils to train neural networks. This limitation restricts the accuracy of the models and the diversity of the generated airfoils. Expanding the dataset by creating new airfoils that share characteristics with those in the database could improve model performance and accuracy. Furthermore, selecting a simpler architecture is advantageous for minimizing training time and ensuring stability.
Therefore, there are several optimization and analysis methods available for airfoil design. It is valuable to explore the potential of these methods, particularly the application of global sensitivity analysis (GSA) for this purpose. In addition, the impact of parameterization on the optimization process is highly relevant not only to the accuracy of the representation but also to the optimization results and warrants further investigation. Lastly, while the use of generative designs for airfoil optimization in drones is gaining traction, current approaches often rely on a limited number of airfoils from open-access databases. This constraint restricts the accuracy of the models and the diversity of the generated airfoils. Expanding the dataset while employing a simple architecture could yield promising results without incurring significant training costs. In light of these observations, the objectives of the present study are (i) to develop an airfoil optimization algorithm based on pattern search and compare its performance with expertly designed airfoils; (ii) to provide a comparison between two popular airfoil parametrization methods, Kulfan and Bézier; (iii) to use global sensitivity analysis to obtain a quantitative assessment of the influence of several airfoil parameters; and (iv) to implement generative design using machine learning to generate valid airfoils for a specific application. The remainder of this paper is organized as follows: In Section 2, the airfoil parametrization methods, global sensitivity analysis, and generative design techniques are presented, along with the case study that is addressed. Section 3 presents the results, which are divided into pattern swarm optimization and validation, global sensitivity analysis, and generative design. The main conclusions and suggestions for future work are provided in Section 4.
2. Numerical Model
2.1. Airfoil Parametrization
There are various methods for representing airfoil geometry, ranging from general techniques to those specifically designed for airfoils. These methods can be broadly categorized into two types: constructive methods, which define an airfoil shape using parameter values, and deformative methods, which modify an existing airfoil to create a new shape [27].
The contemporary literature offers a range of robust and efficient methods for airfoil representation, each varying in accuracy and application. Notable techniques include Hicks and Henne’s analytical method with bump functions [28], the free-form deformation (FFD) method [29], the PARSEC method using 6th-degree polynomials [30], B-splines, the Bézier curves method [31], and Kulfan’s CST method [32]. Some of these methods are less suited for optimization and may require more variables to achieve the same level of accuracy.
Masters et al. [27] conducted a comprehensive analysis of seven airfoil shape parameterization methods, evaluating a total of 2174 airfoils. The study concluded that to approximate 95% of the airfoils in the UIUC library [33] within Kulfan’s tolerance, Singular Value Decomposition (SVD) was the most efficient parameterization, followed by Kulfan’s CST method and Bézier curves. Achieving this level of accuracy required between 15 and 20 variables. Additional comparison studies offer further insights. Manohara [34] found that the CST and Hicks–Henne methods outperformed others, both in terms of the number of parameters needed to achieve a given tolerance and the computational cost of the parameterization. Similarly, Sripawadkul et al. [35], using four different evaluation metrics, identified CST as the top performer, with Bézier ranking third. Both CST and Bézier excelled in two key aspects: completeness, i.e., the ability to describe any airfoil up to a certain tolerance—and flawlessness, i.e., avoiding ill-behaved shapes. The CST and Bézier methods are therefore attractive due to their simplicity and strong performance. They have been widely adopted in recent studies, such as [36,37] for CST, and [21,38,39] for Bézier.
2.1.1. CST Method
The CST method is a type of constructive parameterization that allows for the representation of various shapes, including airfoils as well as square-like and circle-like objects. It was proposed by Kulfan in 2008 [32] and is defined as
where S is the CST shape function, and define the trailing edge thickness and C is the class function. The parameters and control the shape of the parameterization; a value of 1 produces a sharp edge, while a value of 0.5 results in a rounded one. Therefore, for an airfoil class, and are typically used to achieve the characteristic rounded leading edge and sharp trailing edge. The class function is represented as follows:
The CST shape function is defined as a linear combination of Bernstein polynomials, expressed as:
with B as
where represents the Bernstein coefficients, and n denotes the degree of the polynomial. The class of Bernstein polynomials is -continuous and is defined on the interval . Additionally, an extra coefficient for the leading edge can be introduced to improve the accuracy of the parameterization. The shape function then becomes
In the present work, this enhanced shape function with the extra leading edge coefficient will be used. As a result, a total of 18 coefficients are considered: 8 for the lower surface, 8 for the upper surface, one for the leading edge, and another to account for the trailing edge thickness.
2.1.2. Bézier Surface
Bézier curves are a type of parametric curve used in various fields, including computer graphics, and were introduced by Pierre Bézier. Given control points , the Bézier curve of degree n is defined as [27]:
where the basis functions are the Bernstein polynomials, expressed as
The De Casteljau algorithm is a numerically stable method used to evaluate the point on a Bézier curve corresponding to a parameter . It provides a simple and robust computational implementation [31].
The implementation of Bézier curves in this work is based on selecting 8 control points for the lower surface and another 8 for the upper surface. To better approximate the geometry, several constraints are imposed on the control points. For both the upper and lower surfaces, the first control point is positioned at the leading edge, which corresponds to the point (0,0). The second point defines the tangent and curvature of the leading edge and is placed on the vertical line passing through the leading edge. The final point is located at the trailing edge.
A comparison of both methods is presented in Figure 1. As shown, both methods are capable of accurately approximating the SD7003 airfoil, with only minor differences observed at the leading and trailing edges. While these differences may slightly affect the airfoil’s performance and optimization, the associated additional variables would complicate the optimization process without significantly improving accuracy, as shown in [27].
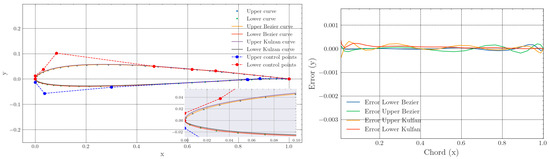
Figure 1.
Comparison of the CST and Berzier curves to approximate the geometry of the SD7003 airfoil [40]. The discrete points that correspond to the desired geometry are also shown.
2.2. Global Sensitivity Analysis
Sensitivity analysis examines the impact that each parameter has on a model, specifically how the model’s variability is influenced by uncertainty in the inputs [41]. Sensitivity analysis is applied across various industries and sectors, from atmospheric chemistry to radioactive waste management [42]. In airfoil design, global sensitivity analysis is particularly valuable for quantitatively evaluating the effects of fundamental design choices on airfoil performance, enabling better design decisions. In this way, the most critical design parameters for optimization can be identified, ranked by their importance, and their interactions evaluated. Similarly, irrelevant parameters can be excluded from consideration. The most basic and relevant parameters used to characterize an airfoil are camber and thickness. In fact, NACA airfoils are named after these two parameters. Therefore, the effects of maximum camber, maximum thickness, and their non-dimensional positions are considered in this study, along with one additional parameter, the trailing edge gap, which is also important in assessing manufacturing feasibility.
From a black box perspective, the GSA can be viewed as an attempt to identify the sensitivity of the function , where are the design parameters, and are the performance parameters. Therefore, the sensitivity of with respect to is [43]:
where and denote the expected value and variance, respectively. and refer to the first-order and second-order interactions of and . The total effect measures the remaining uncertainty when the true values of all inputs except are known:
To calculate the sensitivity indices, the high-dimensional model representation (HDMR) method [43,44] is employed, significantly reducing the number of samples required. The general approach involves decomposing the system into a linear combination of input terms and interactions of increasing order while neglecting higher-order contributions. The decomposition of is given as
In the HDMR framework, spline functions are used to approximate the HDMR component functions. As a result, the first, second, and third-order component functions are expressed as
with , , and as constants to be determined and m as the number of knots. These component functions are then determined by backfitting, allowing the sensitivity indices to be calculated. Three indices are defined, representing the total, structural (uncorrelated), and correlative contributions for an input or subset of inputs . The indices are computed as
where is the average value of y. The total indices are obtained by summing all the sensitivity indices that include .
2.3. Generative Design
The goal of the generative design workflow is to create a set of designs optimized for specific performance criteria. A neural network (NN) is trained on a dataset of airfoil simulations to output an airfoil geometry based on the desired performance. Although training the model can be computationally expensive, the inference process is extremely fast, enabling the generation of thousands of potential airfoils in less than a second. To mitigate the computational cost, a simple architecture is selected and trained on a large dataset of airfoils. This approach ensures diversity in the generated airfoils and addresses the common issue of data scarcity when relying solely on the airfoils available in the UIUC database. To build this dataset, each data point represents a realization of a parameterized airfoil, where the parameters define the airfoil geometry, and corresponds to its performance. The parameters include 8 upper Kulfan parameters , 8 lower Kulfan parameters , the trailing edge Kulfan parameter , the leading edge Kulfan parameter , and the angle of attack . The performance metrics are , , and , which characterize the airfoil’s performance under specific operating conditions.
Airfoil simulations were performed using XFOIL, with a total of 10 million simulations conducted across variations of the 1600 airfoils from the UIUC database [33], removing the ones destined for propellers and wind turbines. These airfoils were converted into Kulfan representations using the AeroSandbox library [20]. The airfoil generation process begins by randomly selecting three parent airfoils from the UIUC database. Random weights are applied to combine the Kulfan parameters (which define the airfoil shape) of the parent airfoils through a weighted average. The resulting airfoil is then scaled and further modified by introducing random deviations based on the covariance matrix of the original airfoils, thereby adding variability. This method generates new, unique airfoil shapes that blend characteristics of the parent airfoils with randomized perturbations. To guarantee that the newly generated airfoils are geometrically feasible, a series of checks are performed. The maximum and minimum thickness and camber are calculated, followed by the verification of the sharpness of both the leading and trailing edges. If the airfoil does not meet the constraints, the airfoil is not added to the dataset.
After the dataset is generated, the airfoils are simulated using XFOIL under the conditions specified in Table 1. XFOIL achieves good accuracy compared with the experimental data for airfoils in the original UIUC database, as demonstrated, for example, in [40]. The simulation parameters are set as follows: a time limit of 5 s per simulation, a maximum of 200 iterations, an ncrit value of 9, and an angle of attack ranging from −10° to 15° with 20 points sampled within this range. Airfoils that fail to converge within the specified time limit or iteration count are removed from the dataset.

Table 1.
Operative points for the optimization analysis.
The neural network consists of five hidden layers, each containing 256 neurons, and uses Rectified Linear Unit (ReLU) activation functions. For the i-th layer:
where are the weights and the bias vectors. The network is compiled using the Adam optimizer and mean squared error (MSE) as the loss function.
with being the true value and the predicted value. The NN was trained over 1000 epochs with a batch size of 256, using 80% of the data for training and the remaining 20% for validation. The number of layers, neurons, and batch size were determined through extensive experimentation and optimization. For instance, using a much smaller case consisting of 4 layers of 64 neurons results in approximately double the errors but with a much smaller training cost. The dependence of the results on the number of samples is also present. A minimum amount of 500,000 samples should be used to obtain a set of airfoils with errors lower than 50%, and the procedure is explained in Section 3.3.
2.4. Particle Swarm
In this work, the particle swarm optimization (PSO) algorithm is used to optimize the airfoil design. Initially proposed by Kennedy et al. [45] to simulate social behavior, the algorithm has seen extensive use in recent years. PSO works by maintaining a population of candidate solutions, or particles, that move around the search space based on the best-known positions of both the entire swarm and the individual particles. As better positions are discovered, the swarm adjusts its movement accordingly. This process continues until termination conditions are met.
PSO is particularly advantageous for airfoil optimization [12], as it does not require gradient information. This is useful given the limitations of XFOIL, the simulation tool used to calculate the aerodynamic coefficients. Firstly, XFOIL exhibits hysteresis, meaning slightly different solutions can be obtained for the same geometry and flight conditions, leading to non-unique results. This occurs because XFOIL uses the last converged solution to perform its Newton iterations. Secondly, XFOIL is non-differentiable, preventing the direct calculation of gradients. Finally, XFOIL’s solutions lack continuity, resulting in inaccurate automatic differentiation.
The PSO algorithm is implemented using the pyswarm 1.3.0 Python library [46]. The setup includes a population of 30 particles, 1000 iterations, and a termination condition based on an objective function tolerance of 0.001.
2.5. Case Study
The case study involves the design of a fixed-wing drone intended for firefighting activities. Its purpose is to provide real-time observation and control of fire spread, allowing valuable information to be gathered without human intervention. The drone needs to be small, with the capability of flying for extended periods, making efficiency and optimized aerodynamic performance critical.
The following design parameters were considered: the aircraft’s mean aerodynamic chord is 0.2 m, with an operational weight of 5 kg and a wing surface area of 0.3 m2, resulting in a wing loading of 16.66 kg/m2. The drone will operate at sea level. There are four primary operational points: cruise at full speed, cruise at a lower speed, ascent, and takeoff. These points will be incorporated into the optimization process, as outlined in Table 1. For the first three points, drag will be minimized, while for the fourth, lift will be maximized. Each operational point will have an associated weight WW, depending on its relative importance. The objective function is therefore
Several constraints are introduced in the optimization process to address potential manufacturing challenges and ensure adequate performance. The optimization will tend to favor designs with low drag and high efficiency, which could lead to a significant reduction in thickness. To prevent this, the thickness is constrained between 8% and 20%, and the local thickness at is required to be greater than 0.01 to avoid producing a trailing edge too thin for manufacturing. The moment coefficient is also limited to . Additionally, the Bézier and Kulfan coefficients are constrained to improve optimization performance, with absolute value limits of 0.2 and 0.05, respectively.
Another common issue in airfoil optimization is the so-called “wiggliness” w, which results from artifacts in the airfoil representation [47]. A common method for measuring this effect is provided by [48]
which is approximated and limited to a value four times as big as in the original airfoil [47]. The aerodynamic coefficients of the airfoils are calculated using XFOIL, a FORTRAN program for the analysis of subsonic isolated airfoils [49]. Developed by Mark Drela, XFOIL has been extensively used in numerous studies and projects. Its accuracy in predicting aerodynamic coefficients is highly regarded and has been shown to outperform RANS simulations [50] while having a computational cost several orders of magnitude lower.
The choice of the initial airfoil for the optimization process is also critical, as it will influence the quality of the final design. An airfoil well suited for the described application is the SD7003 [40], which is optimized for low Reynolds number applications. With low drag, high efficiency at standard cruise angles of attack, and a moment coefficient greater than −0.08, this airfoil is ideal for small drones requiring extended range and endurance.
3. Results
3.1. Optimization
To verify the process outlined in Section 2.5, a case from the literature is first tested. This case, documented in Drela’s study [4], involves the optimization of the MIT Daedalus, a human-powered aircraft designed by Mark Drela. The airfoil DAE-11, used in the Daedalus, was originally developed using traditional inverse-design methods and direct geometry manipulation techniques. This makes it an ideal benchmark for validating the optimization process. The constraints applied in this case are significant from an optimization perspective and are detailed in Drela [4]. The optimization constraints are as follows: the selected regime is characterized by a Reynolds number and a Mach number . Six operating points are considered in the optimization.
Subject to ; ; ; at and at , where t denotes the non-dimensional thickness. The results of this optimization are shown in Figure 2, where the similarity to the DAE-11 airfoil is evident; only a small discrepancy is observed at the leading edge. This demonstrates that the optimization process is capable of producing an airfoil that closely resembles DAE-11 in a reduced amount of time. The initial guess for the optimization was the SD7003 airfoil, which has a distinctly different shape and purpose, highlighting the optimizer’s robustness, as it was able to converge on an optimal design regardless of the starting point. In terms of performance, both airfoils exhibit similar behaviors, as shown in the polars in Figure 3. The main performance parameters for each of the six operating points are plotted, showing variations due to changes in Reynolds number. The optimized airfoil achieves a lower moment coefficient, particularly at angles of attack below 6 degrees. As expected, the curve remains unchanged. Additionally, the drag polar shows differences: the optimized airfoil performs better at lower values, especially below . At higher values, the performance of both airfoils is very similar, with a slight advantage for the expertly designed DAE-11. When the objective function for both airfoils is calculated, the DAE-11 achieves , while the optimized airfoil achieves . Based on the objective function alone, the optimized airfoil performs slightly better. In this way, the optimization algorithm was able to produce an airfoil that rivals the DAE-11 in performance, achieving even better results in terms of the objective function, and did so in a short amount of time with significantly less effort compared with traditional design methods.
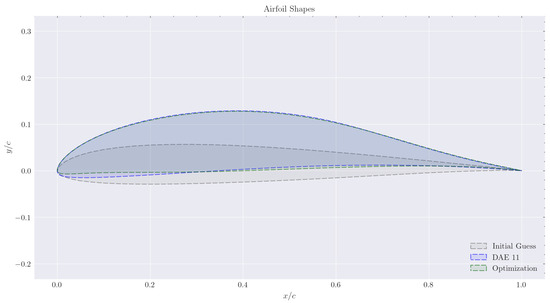
Figure 2.
Comparison of the geometries of the optimized airfoil and the DAE-11.
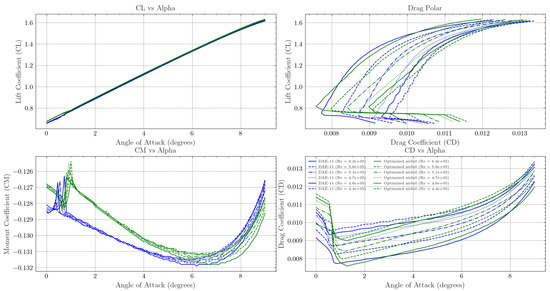
Figure 3.
Polars of the optimized designs compared with the DAE-11 airfoil.
Now, the optimization process is used to enhance the performance of the SD7003 airfoil across the operational points described in Table 1. The optimization process for one of the designs is illustrated in Figure 4, where the process terminated after 273 iterations. The result is an improvement of 17.183% over the original design. Initially, performance improved rapidly, but it eventually plateaued, indicating diminishing returns. If needed, another optimization algorithm could be employed from the final design to perform a local search for further enhancements.
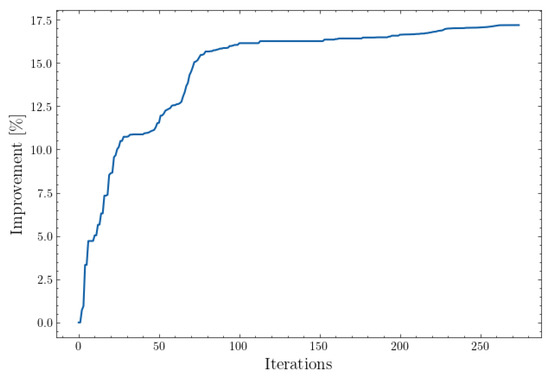
Figure 4.
Optimization timeline: the improvement with respect to the original airfoil is shown.
Both Bézier and Kulfan CST parameterizations were used in the optimization process, resulting in distinctly different airfoil geometries, as shown in Figure 5. Significant differences, especially in camber and thickness, were observed between the Bézier and Kulfan airfoils, with the latter exhibiting a larger thickness. The polars of the optimized airfoils are presented in Figure 6, and the performance improvements are shown in Table 2. The moment is calculated with respect to the quarter-chord point. When compared with the original SD7003 airfoil, the redesigned airfoils demonstrated a slight reduction in drag during cruise conditions, leading to increased efficiency, extended autonomy, and range. Although the reduction at full-speed conditions was lower, the CST optimization achieved up to a 2.3% reduction in drag at lower speeds, while the Bézier optimization achieved a similar improvement. The original airfoil was already a well-optimized low-Reynolds-number airfoil, which limited the scope for further drag reduction. However, at lower cruise speeds, the drag reduction was significant: up to 25.3% for the CST optimization and 19.6% for the Bézier optimization, greatly enhancing the drone’s efficiency. During ascent, the Bézier curves representation achieved a 55.5% reduction in drag, while the Kulfan CST achieved a 55.6% reduction. Both airfoils also demonstrated a 5.2% increase in lift compared with the original airfoil. The moment coefficients of the optimized airfoils remained within acceptable limits, with the Bézier and Kulfan airfoils having and , respectively, at a lift coefficient of for operational condition 1. Both designs stayed well within the stipulated moment coefficient limit of , suggesting no significant impact on stability. The original airfoil had a moment coefficient of , slightly better than the optimized airfoils despite its lower camber and maximum lift.
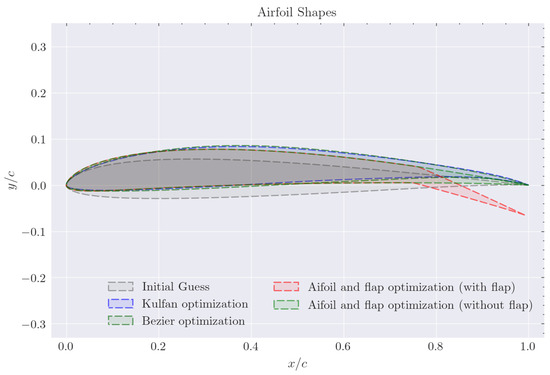
Figure 5.
Geometry comparison of the optimized and original designs.
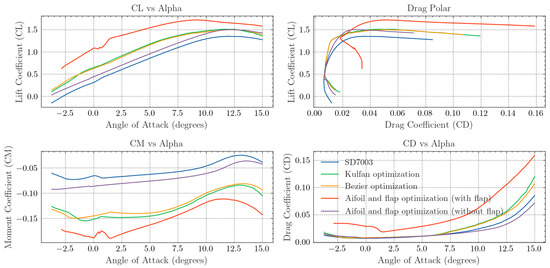
Figure 6.
Polars of the optimized designs compared with the base SD7003 airfoil.

Table 2.
Performance improvement of the optimized airfoils for each operation condition.
Both the Bézier and CST airfoil representations achieved improved designs compared with the original SD7003 airfoil. The CST airfoil focuses more on reducing drag at cruise conditions, while the Bézier airfoil achieved substantial drag reduction during ascent. Both methods had similar effects on maximum lift. The small differences can be attributed to the distinct airfoil representations and the inherent randomness of particle swarm optimization. By adjusting the weighting factors , it would be possible to further refine the designs, prioritizing performance at higher velocities or ascent conditions. Both solutions are valid and usable.
An additional optimization analysis was conducted to consider the presence of a flap, a device essential for increasing lift during takeoff, especially when runway length is limited or when low flight speeds are required for specific tasks like terrain measurements. The optimization was extended to include an additional operational point at deg, targeting a lift coefficient of . The optimization is conducted in the same way as before but with the additional operation condition.
The results are shown in Figure 6 and the corresponding geometry in Figure 5. The flap-optimized airfoil is very similar to the Bézier airfoil, with the most noticeable difference at the leading edge. In terms of performance without the flap, the drag remains nearly identical across the first three operational points compared with the previous Kulfan and Bézier optimizations, with only a slight increase. However, the maximum lift coefficient increased to , a slight improvement over the previous designs. The moment coefficient at settled around , slightly lower in absolute value compared with the other designs. With the flap deployed, the drag more than doubled, but the lift coefficient increased by 16.7%, reaching at the desired angle of attack of 9°. The optimized flap angle was set to 15°. The small drop in the airfoil lift with the flap at around 1°, can be attributed to inaccuracies in XFOIL. Therefore, this tool demonstrated its effectiveness in optimizing airfoils across multiple operational points and considering the inclusion of a flap for specific flight conditions.
3.2. Global Sensitivity Analysis
The global sensitivity analysis using High Dimensional Model Representation (HDMR) was conducted on the SD7003 airfoil, modifying the camber, maximum camber location, thickness, maximum thickness location, and trailing edge thickness. The objective was to evaluate the effects of these parameters on the objective function presented in Equation (18), as well as to analyze the interactions between inputs and their influence on output variance. A total of 10,000 samples were used, varying all five parameters through Latin hypercube sampling [51] within the bounds shown in Table 3. The decision to use 10,000 samples was based on achieving good accuracy and a low confidence interval. The results are shown in Figure 7, where bars represent the contributions of specific parameters or groups of parameters. These values are also summarized in Table 4. Each index is depicted with different colors, accompanied by a black line indicating the confidence interval. Four sensitivity indices were calculated for each of the five design parameters: the uncorrelated contribution term , the correlated contribution term , the total contribution term S (the sum of and ), and the total contribution of a particular parameter . Additionally, the same sensitivity indices were computed for each possible second-order interaction between pairs of design parameters, resulting in a total of 10 interactions.

Table 3.
Range of variation of the parameters used for the global sensitivity analysis.
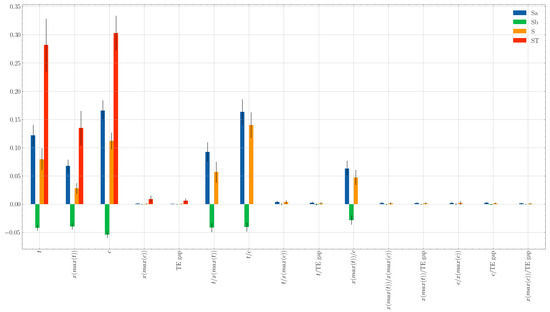
Figure 7.
Global sensitivity analysis for the selected parameters. The first- and second-order interactions are included.

Table 4.
Global sensitivity analysis results.
Focusing on the first-order indices, represented by the first five groups in Figure 7, it is clear that the first three inputs—thickness, camber, and maximum thickness location—dominate the objective function. Thickness and camber have high S indices (orange bars), indicating their strong influence on performance, specifically the airfoil’s drag and lift in the selected operational conditions. In both of them, the blue bar, i.e., the uncorrelated contribution, is significantly larger than the correlated term. This implies that both parameters are independently driving the performance. The position of maximum thickness also contributes significantly, though to a lesser extent than the first two parameters. Notably, the correlated and uncorrelated contributions for this parameter are more balanced, indicating that both direct and interaction effects are important. In contrast, the position of maximum camber and trailing edge thickness have minimal S indices, suggesting that their influence on airfoil performance is negligible.
Also, the total index (red bars) for the first three parameters—thickness, camber, and maximum thickness location—exceeds their respective S indices (orange bars), indicating that higher-order effects or interactions between parameters play a significant role. This is further supported by the second-order interaction results, shown in columns 6 to 15 of Figure 7, where several notable interactions are observed. Firstly, there is a strong second-order interaction between thickness t and maximum thickness location , which is expected. The performance of an airfoil is not only dependent on thickness but also on where the maximum thickness occurs along the chord. For example, a thin airfoil might reduce drag and improve performance, but if the maximum thickness is located too close to the leading edge, the aerodynamic design could be compromised. Therefore, the impact of thickness on performance depends on the position of maximum thickness. In this case, the correlated and uncorrelated effects are of similar magnitude, confirming the importance of both direct and interaction effects. A strong second-order interaction also exists between thickness and camber, with this interaction having an even larger impact than the first-order effects of these parameters. This is because both parameters significantly influence airfoil performance. For instance, an airfoil with low thickness and high camber may perform similarly to one with greater thickness but lower camber. Alternatively, an airfoil with very low camber may not generate sufficient lift regardless of its thickness. These simplified examples illustrate the complex second-order interactions between thickness and camber that influence performance. Additionally, the maximum thickness location is correlated with camber, leading to similar conclusions. The position of maximum thickness affects the airfoil geometry, thereby influencing how camber affects performance. Once again, the correlated and uncorrelated contributions are closely matched.
The remaining second-order interactions are relatively insignificant, indicating that the corresponding parameters can be considered largely independent one from another. Surprisingly, there is no significant second-order interaction between maximum camber and camber c, suggesting that these values act independently despite both contributing to the camber line’s shape. In this study, only first- and second-order indices were considered, while higher-order indices were neglected. However, higher-order effects are generally small, which can be confirmed by summing the first and second-order indices for each parameter and comparing this sum to the total index (red bars). In this case, the values are close, reinforcing that the higher-order contributions are negligible.
The airfoil design presented in the previous section is compared with the original SD7003 airfoil. According to the global sensitivity analysis (GSA), the most influential geometric properties for airfoil performance are thickness, camber, and, to a lesser extent, the position of maximum thickness. These findings are corroborated by the optimization process, as these parameters underwent significant changes in the optimized airfoil. The original SD7003 airfoil features a thickness of 8.51% located at 24.72% of the chord and a camber of 1.48%. In contrast, the optimized airfoil has a thickness of 9.12% at 31.37% of the chord and a camber of 4.19%. The notable modification of these three parameters, particularly the camber, reinforces their critical role in airfoil design, as highlighted by the GSA results in Figure 7. Conversely, the GSA identified minimal influence from the trailing edge (TE) gap, which is consistent with the optimization results; both the original and optimized airfoils feature a TE gap of 0.
3.3. Generative Design
In this section, generative designs are created based on a set of input parameters, i.e., , and . As mentioned above, an architecture of 5 layers of 256 neurons is used. It is possible to use smaller and fewer layers at the expense of accuracy. A 4-layer architecture with 64 neurons doubles the errors, while 5 layers with 128 neurons gives about 10% more errors. Conversely, using 512 neurons results in a negligible increase in accuracy. A total of 10,000 designs were generated using the NN. This batch of designs, once the model is created, can be obtained in less than a second, which makes it considerably faster than the Xfoil optimization or even a simulation, in which the latter could last 5–10 s on average. In this way, this generative process is several orders of magnitude faster than a traditional design process, with higher exploration capabilities. Figure 8 provides an overview of the distributions of individual Kulfan parameters for designs generated for different target values. The blue designs correspond to high-velocity cruise conditions, with target values, , and . The red designs represent ascent conditions, with target values , and . A variety of design parameter combinations can be realized for each set of target labels. As seen in the histograms, certain parameters exhibit narrower distributions, characterized by a higher concentration of vertical bars, such as . In contrast, other parameters show broader distributions, such as , suggesting greater variability in the designs. When comparing the two operating conditions, the ascent condition (red bars) shows more dispersed Kulfan parameters, indicating greater variability in the generated designs. Additionally, some Kulfan parameters have more influence on the airfoil designs than others. For example, the upper Kulfan parameters, particularly to , display similar distributions for both conditions, suggesting that these parameters are less influenced by performance label selections during airfoil design or optimization.
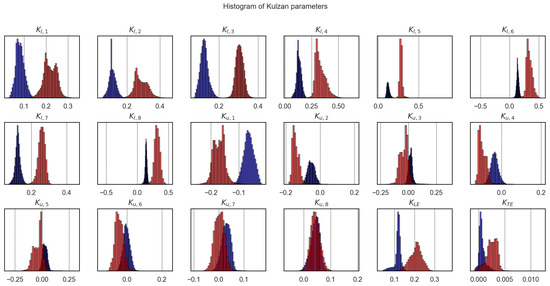
Figure 8.
Generative design of the airfoil according to two sets of conditions represented in blue and red.
Accuracy is a key concern in generative design tools, as there is no inherent guarantee that the generated designs will meet the performance labels. To assess this, the error between the generated designs and accurate simulations using Xfoil was calculated. Figure 9 illustrates the error distribution for both operating conditions, showing the deviation from the target performance labels. The majority of the designs have low errors, with mean percentage errors for lift, drag, and moment coefficients falling below 10%, and a significant number of designs achieving errors below 5%. However, some designs exhibit higher errors, exceeding 20%, indicating that further review may be necessary to ensure that these designs meet the required performance criteria. When comparing the two operating conditions, the ascent condition (red bars) shows lower average errors. This is likely due to the challenge of meeting the low drag requirement of for high-velocity cruise conditions. Despite these challenges, this generative tool proves highly effective in rapidly producing thousands of potential airfoils that approximate a given performance criterion. These generated designs serve as a valuable starting point for further detailed analysis, refinement, and optimization. Compared with other methods in the literature that require the pressure coefficient distribution as input [17,25], this procedure can directly obtain the desired geometry for a desired set of performance coefficients as input. In addition, the resulting geometry is obtained directly without an optimization process, as in [18]. The errors obtained are generally small, with all designs constrained to less than 25% errors in the first case. This is lower than the more than 100% errors in the model of [26].
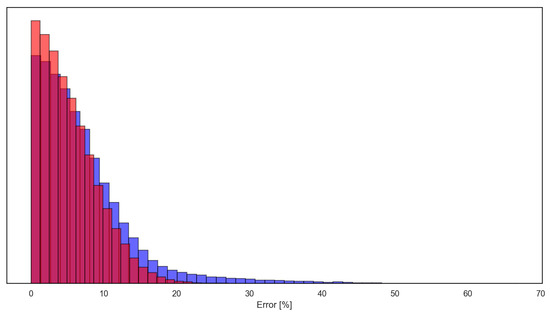
Figure 9.
Error on the predicted and real aerodynamic performance on the two sets of conditions.
To evaluate the performance of airfoils generated through the generative design process, a comparison is made between the particle swarm optimization method based on Kulfan parametrization (Section 3.1) and the generative design method discussed in this section, using the first operative point from Table 1. Both methods were applied, yielding airfoils with the performance metrics shown in Figure 10. In this comparison, only drag at cruise conditions is considered, without accounting for maximum lift.
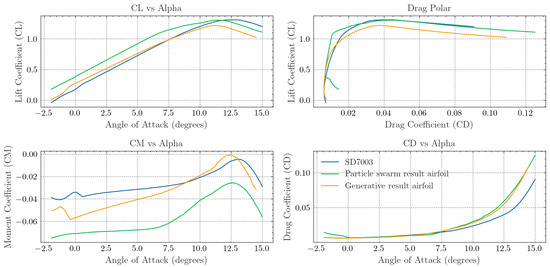
Figure 10.
Polars of the airfoils obtained by the particle-swarm optimization based on Kulfan parametrization and the generative design.
As shown in Figure 10, both approaches successfully improved upon the baseline SD7003 airfoil for the operating point defined in Table 1. For this condition, both airfoils achieve a drag coefficient of . The generative design method results in a lower moment coefficient, while the particle-swarm approach achieves a slightly higher lift. Nevertheless, given the focus on cruise conditions, both methods achieve similar aerodynamic performance. Notably, the generative design approach demonstrates significant efficiency, generating the optimized airfoil in under one second, a stark contrast to the longer computation time required by the traditional particle-swarm optimization. This highlights the potential of generative design as a rapid and effective tool for airfoil optimization.
4. Conclusions
The research presented in this manuscript focuses on the aerodynamic optimization of airfoils specifically for fixed-wing drones designed for firefighting operations. The primary goal was to achieve improved aerodynamic performance, particularly in terms of drag reduction, without compromising the lift characteristics crucial for takeoff and ascent. The optimization of airfoils, such as the SD7003, is performed using advanced methodologies including the Kulfan CST and Bézier curve parameterization, combined with a particle swarm optimization (PSO) algorithm. This study also incorporates a global sensitivity analysis (GSA) to better understand the effects of key design parameters, providing a holistic approach to airfoil optimization.
One of the key conclusions of our research is the demonstration of the effectiveness of combining multiple optimization techniques. The Kulfan CST and Bézier surface methods, both commonly used in airfoil design, were employed to optimize different aspects of the airfoil’s geometry. The results indicate that both parameterization methods can achieve substantial drag reduction, particularly in the cruise and ascent phases. However, each method exhibited different strengths: the Kulfan CST airfoil showed a significant drag reduction during cruise conditions, achieving up to 23.5% improvement at lower speeds; on the other hand, the Bézier airfoil excelled during ascent, with a drag reduction of 52.2%, making it more suitable for scenarios requiring sustained climbing performance. These differences highlight the importance of selecting the right parameterization method based on the specific operational requirements of the UAV.
The application of particle swarm optimization (PSO) in airfoil design was another critical aspect of this study. PSO is a metaheuristic optimization technique well suited for problems where gradient information is either unavailable or unreliable, as is the case with XFOIL-based simulations. This research demonstrated that PSO could efficiently navigate the complex design space, producing optimized airfoil geometries that outperformed the baseline designs. This approach was particularly valuable in addressing the non-linearity and discontinuities present in the aerodynamic performance data. The PSO algorithm also provided a robust method for balancing trade-offs between lift and drag, which are often in conflict in aerodynamic optimization.
Global sensitivity analysis (GSA) played an important role in quantifying the impact of various design parameters on airfoil performance. By analyzing the sensitivity of parameters such as thickness, camber, and the location of maximum thickness and maximum camber, this research identified which design choices most influenced the overall aerodynamic characteristics. The results show that thickness and camber were the dominant parameters, contributing significantly to both lift and drag performance. The interactions between these parameters were also notable, particularly the second-order interactions between thickness and camber. This interaction highlights the complex nature of airfoil optimization, where changes in one parameter can have cascading effects on overall performance. The insights gained from GSA enable more informed design decisions, allowing for targeted modifications that provide the greatest performance benefits.
The generative design approach, using a neural network trained on a large dataset of airfoil simulations, offers a novel pathway for future airfoil optimization. By leveraging machine learning techniques, this study was able to generate thousands of potential airfoil designs that approximate the desired aerodynamic performance. While the neural network predictions showed reasonable accuracy, with most designs achieving errors below 10%, some discrepancies were noted, particularly for high-velocity cruise conditions where drag reduction was more challenging. Despite these limitations, the generative design method proved to be a valuable tool for rapidly exploring a wide range of design possibilities, providing a solid foundation for further refinement through more detailed optimization processes.
The inclusion of a flap in the airfoil optimization process added an additional layer of complexity and realism to the study. Flaps are essential for improving lift during takeoff, especially in situations where runway length is limited or low-speed flight is required. The results of the flap-optimized airfoil show that while drag increased with the deployment of the flap, the lift coefficient improved by 16.7%, achieving the target lift value at an angle of attack of 9°. This balance between lift enhancement and drag penalties is a critical consideration in the design of UAVs for firefighting operations, where precise control over flight dynamics is essential for mission success.
Overall, this study contributes to the growing body of knowledge on airfoil optimization for small UAVs, particularly those used in specialized applications like firefighting. The integration of multiple advanced techniques, including Kulfan CST and Bézier parameterizations, PSO, GSA, and generative design, provides a comprehensive framework for optimizing airfoil performance across a range of operational conditions. The findings highlight the importance of selecting appropriate optimization strategies based on the specific mission profile of the UAV, ensuring that performance is maximized where it matters most.
Future research could focus on further refining the neural network-based generative design approach, possibly incorporating other more complex architectures and performing sensitivity analysis of the data and architecture. In addition, the inclusion of more complex flight conditions, such as turbulent flow or varying atmospheric conditions, could improve the robustness of the optimization framework and make it more applicable to real-world UAV operations. Other parameterization methods could be considered, such as the Bezier PARSEC method [52], which provides a more intuitive representation of the airfoil characteristics.
Author Contributions
Conceptualization, P.R. and F.A.-A.; funding acquisition, P.O.-C.; methodology, P.R. and P.O.-C.; project administration, P.O.-C. and F.A.-A.; resources, P.O.-C., G.D.R.G. and F.A.-A.; software, P.R. and G.D.R.G.; validation, F.A.-A.; visualization, G.D.R.G.; writing—original draft, P.R.; writing—review and editing, P.O.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Hicks, R.; Murman, E.; Vanderplaats, G. An Assessment of Airfoil Design by Numerical Optimization; NASA: Mountain View, CA, USA, 1974. [Google Scholar]
- Hicks, R.M.; Vanderplaats, G.N. Application of Numerical Optimization to the Design of Supercritical Airfoils without Drag-Creep. In Proceedings of the SAE Technical Paper Series, 400 Commonwealth Drive, Warrendale, PA, USA, 3–4 January 1977. [Google Scholar]
- Drela, M. Low-Reynolds-number airfoil design for the M.I.T. Daedalus prototype—A case study. J. Aircr. 1988, 25, 724–732. [Google Scholar] [CrossRef]
- Drela, M. Pros & Cons of Airfoil Optimization. In Frontiers of Computational Fluid Dynamics 1998; World Scientific: Singapore, 1998; pp. 363–381. [Google Scholar]
- Li, W.; Huyse, L.; Padula, S. Robust airfoil optimization to achieve drag reduction over a range of Mach numbers. Struct. Multidiscip. Optim. 2002, 24, 38–50. [Google Scholar] [CrossRef]
- Zingg, D.; Elias, S. On Aerodynamic Optimization Under a Range of Operating Conditions. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar]
- Mirzaei, M.; Nasrin Hosseini, S.; Roshanian, J. Single and multi-point optimization of an airfoil using gradient method. Aircr. Eng. Aerosp. Technol. 2007, 79, 611–620. [Google Scholar] [CrossRef]
- Ulker, F.D.; Doostan, A.; Drela, M. Stochastic Gradient Optimization of Transonic Airfoils. In Proceedings of the AIAA Scitech 2021 Forum, Reston, VA, USA, 11–21 January 2021. [Google Scholar]
- Vicini, A.; Quagliarella, D. Inverse and direct airfoil design using a multiobjective genetic algorithm. AIAA J. 1997, 35, 1499–1505. [Google Scholar] [CrossRef]
- Wang, Y.-Y.; Zhang, B.-Q.; Chen, Y.-C. Robust airfoil optimization based on improved particle swarm optimization method. Appl. Math. Mech. 2011, 32, 1245–1254. [Google Scholar] [CrossRef]
- Wickramasinghe, U.K.; Carrese, R.; Li, X. Designing airfoils using a reference point based evolutionary many-objective particle swarm optimization algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation, Barcelona, Spain, 18–23 July 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Mirjalili, S.; Dong, J.S.; Lewis, A. Nature-Inspired Optimizers: Theories, Literature Reviews and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Echeverría, F.; Mallor, F.; San Miguel, U. Global sensitivity analysis of the blade geometry variables on the wind turbine performance. Wind Energy 2017, 20, 1601–1616. [Google Scholar] [CrossRef]
- Mohamed Abubacker Siddique, P.M.; Prince Raj, L. Sensitivity analysis of geometric parameters on the aerodynamic performance of a multi-element airfoil. Aerosp. Sci. Technol. 2023, 132, 108074. [Google Scholar] [CrossRef]
- Storlie, C.B.; Swiler, L.P.; Helton, J.C.; Sallaberry, C.J. Implementation and evaluation of nonparametric regression procedures for sensitivity analysis of computationally demanding models. Reliab. Eng. Syst. Saf. 2009, 94, 1735–1763. [Google Scholar] [CrossRef]
- Ribeiro, A.; Awruch, A.; Gomes, H. An airfoil optimization technique for wind turbines. Appl. Math. Model. 2012, 36, 4898–4907. [Google Scholar] [CrossRef]
- Yilmaz, E.; German, B. A Convolutional Neural Network Approach to Training Predictors for Airfoil Performance. In Proceedings of the 18th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Du, X.; He, P.; Martins, J.R. Rapid airfoil design optimization via neural networks-based parameterization and surrogate modeling. Aerosp. Sci. Technol. 2021, 113, 106701. [Google Scholar] [CrossRef]
- Bouhlel, M.A.; He, S.; Martins, J.R.R.A. Scalable gradient–enhanced artificial neural networks for airfoil shape design in the subsonic and transonic regimes. Struct. Multidiscip. Optim. 2020, 61, 1363–1376. [Google Scholar] [CrossRef]
- Sharpe, P.D. Accelerating Practical Engineering Design Optimization with Computational Graph Transformations. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2024. [Google Scholar]
- Chen, W.; Chiu, K.; Fuge, M.D. Airfoil Design Parameterization and Optimization Using Bézier Generative Adversarial Networks. AIAA J. 2020, 58, 4723–4735. [Google Scholar] [CrossRef]
- Chen, W.; Chiu, K.; Fuge, M. Aerodynamic Design Optimization and Shape Exploration using Generative Adversarial Networks. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Wang, J.; Li, R.; He, C.; Chen, H.; Cheng, R.; Zhai, C.; Zhang, M. An inverse design method for supercritical airfoil based on conditional generative models. Chin. J. Aeronaut. 2022, 35, 62–74. [Google Scholar] [CrossRef]
- Sun, K.; Wang, W.; Cheng, R.; Liang, Y.; Xie, H.; Wang, J.; Zhang, M. Evolutionary generative design of supercritical airfoils: An automated approach driven by small data. Complex Intell. Syst. 2023, 10, 1167–1183. [Google Scholar] [CrossRef]
- Sekar, V.; Zhang, M.; Shu, C.; Khoo, B.C. Inverse Design of Airfoil Using a Deep Convolutional Neural Network. AIAA J. 2019, 57, 993–1003. [Google Scholar] [CrossRef]
- Achour, G.; Sung, W.J.; Pinon-Fischer, O.J.; Mavris, D.N. Development of a Conditional Generative Adversarial Network for Airfoil Shape Optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Masters, D.A.; Taylor, N.J.; Rendall, T.; Allen, C.B.; Poole, D.J. A geometric comparison of aerofoil shape parameterisation methods. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Hicks, R.; Henne, P. Wing design by numerical optimization. In Proceedings of the Aircraft Systems and Technology Meeting, Seattle, WA, USA, 22–24 August 1977. [Google Scholar]
- Rendall, T.C.S.; Allen, C.B. Unified fluid–structure interpolation and mesh motion using radial basis functions. Int. J. Numer. Methods Eng. 2007, 74, 1519–1559. [Google Scholar] [CrossRef]
- Sobieczky, H. Parametric Airfoils and Wings. In Notes on Numerical Fluid Mechanics (NNFM); Vieweg+Teubner Verlag: Wiesbaden, Germany, 1999; pp. 71–87. [Google Scholar]
- Prautzsch, H.; Paluszny, M.; Böhm, W. Métodos de Bézier y B-Splines; KIT Scientific Publishing: Singapore, 2005. [Google Scholar]
- Kulfan, B.; Bussoletti, J. “Fundamental” Parameteric Geometry Representations for Aircraft Component Shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006. [Google Scholar]
- Selig, M. UIUC Airfoil Data Site; University of Illinois Urbana-Champaign: Champaign, IL, USA, 2024. [Google Scholar]
- Selvan, K.M. On The Effect Of Shape Parameterization On Aerofoil Shape Optimization. Int. J. Res. Eng. Technol. 2015, 4, 123–133. [Google Scholar] [CrossRef]
- Sripawadkul, V.; Padulo, M.; Guenov, M. A Comparison of Airfoil Shape Parameterization Techniques for Early Design Optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010. [Google Scholar]
- Song, X.; Wang, L.; Luo, X. Airfoil optimization using a machine learning-based optimization algorithm. J. Phys. Conf. Ser. 2022, 2217, 012009. [Google Scholar] [CrossRef]
- Akram, M.T.; Kim, M.H. Aerodynamic Shape Optimization of NREL S809 Airfoil for Wind Turbine Blades Using Reynolds-Averaged Navier Stokes Model—Part II. Appl. Sci. 2021, 11, 2211. [Google Scholar] [CrossRef]
- Fatchulloh, M.A.; Arini, N.R. Airfoil profile modifications based on Bezier Curve and Optimization using PSO. In Proceedings of the 2024 International Electronics Symposium (IES), Denpasar, Indonesia, 6–8 August 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 100–106. [Google Scholar]
- Ümütlü, H.C.A.; Kiral, Z. Airfoil Shape Optimization Using Bézier Curve And Genetic Algorithm. Aviation 2022, 26, 32–40. [Google Scholar] [CrossRef]
- Selig, M.S. Summary of Low Speed Airfoil Data; Soartech: Ann Arbor, MI, USA, 1995. [Google Scholar]
- Le Gratiet, L.; Marelli, S.; Sudret, B. Metamodel-Based Sensitivity Analysis: Polynomial Chaos Expansions and Gaussian Processes. In Handbook of Uncertainty Quantification; Springer International Publishing: Cham, Switzerland, 2017; pp. 1289–1325. [Google Scholar]
- Saltelli, A. Global sensitivity analysis: An introduction. In Proceedings of the 4th International Conference on Sensitivity Analysis of Model Output (SAMO 2004), Santa Fe, NM, USA, 8–11 March 2004. [Google Scholar]
- Rabitz, H.; Aliş, Ö.F. General foundations of high-dimensional model representations. J. Math. Chem. 1999, 25, 197–233. [Google Scholar] [CrossRef]
- Rabitz, H. Global Sensitivity Analysis for Systems with Independent and/or Correlated Inputs. Procedia-Soc. Behav. Sci. 2010, 2, 7587–7589. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Miranda, L.J.V. PySwarms, a research-toolkit for Particle Swarm Optimization in Python. J. Open Source Softw. 2018, 3, 433. [Google Scholar] [CrossRef]
- Sharpe, P.D. AeroSandbox: A Differentiable Framework for Aircraft Design Optimization. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2021. [Google Scholar]
- Wahba, G. Spline Models for Observational Data; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1990. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar] [CrossRef]
- Coder, J.G.; Maughmer, M.D. Comparisons of Theoretical Methods for Predicting Airfoil Aerodynamic Characteristics. J. Aircr. 2014, 51, 183–191. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239. [Google Scholar] [CrossRef]
- Derksen, R.; Rogalsky, T. Bezier-PARSEC: An optimized aerofoil parameterization for design. Adv. Eng. Softw. 2010, 41, 923–930. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).