Aerodynamic Characteristics of the Opposing Jet Combined with Magnetohydrodynamic Control in Hypersonic Nonequilibrium Flows
Abstract
1. Introduction
2. Numerical Approach
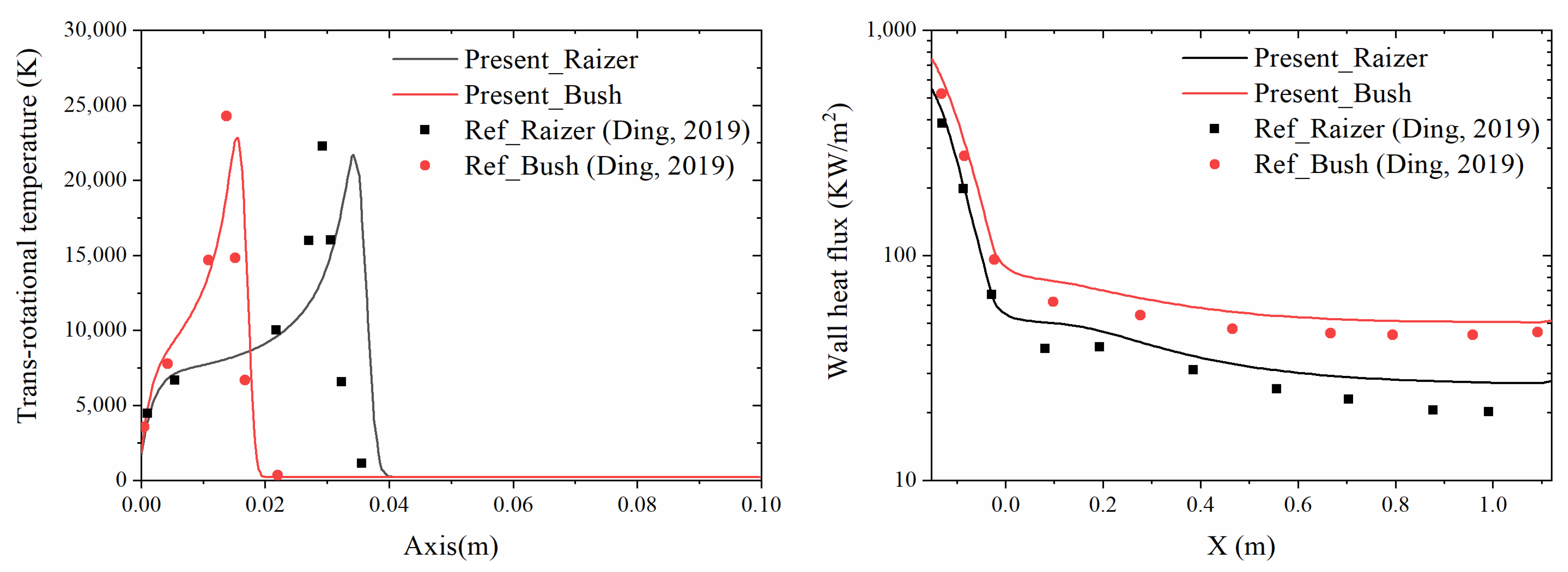
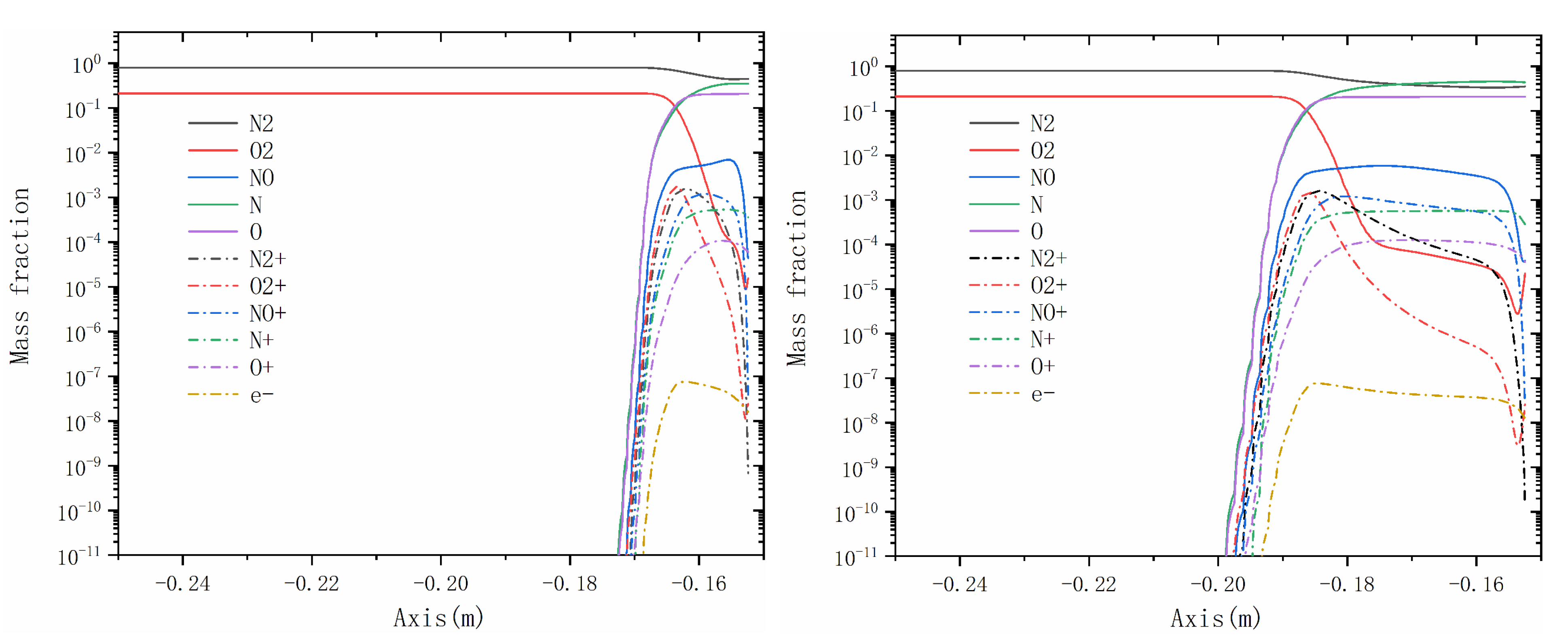
3. Computational Model Validation
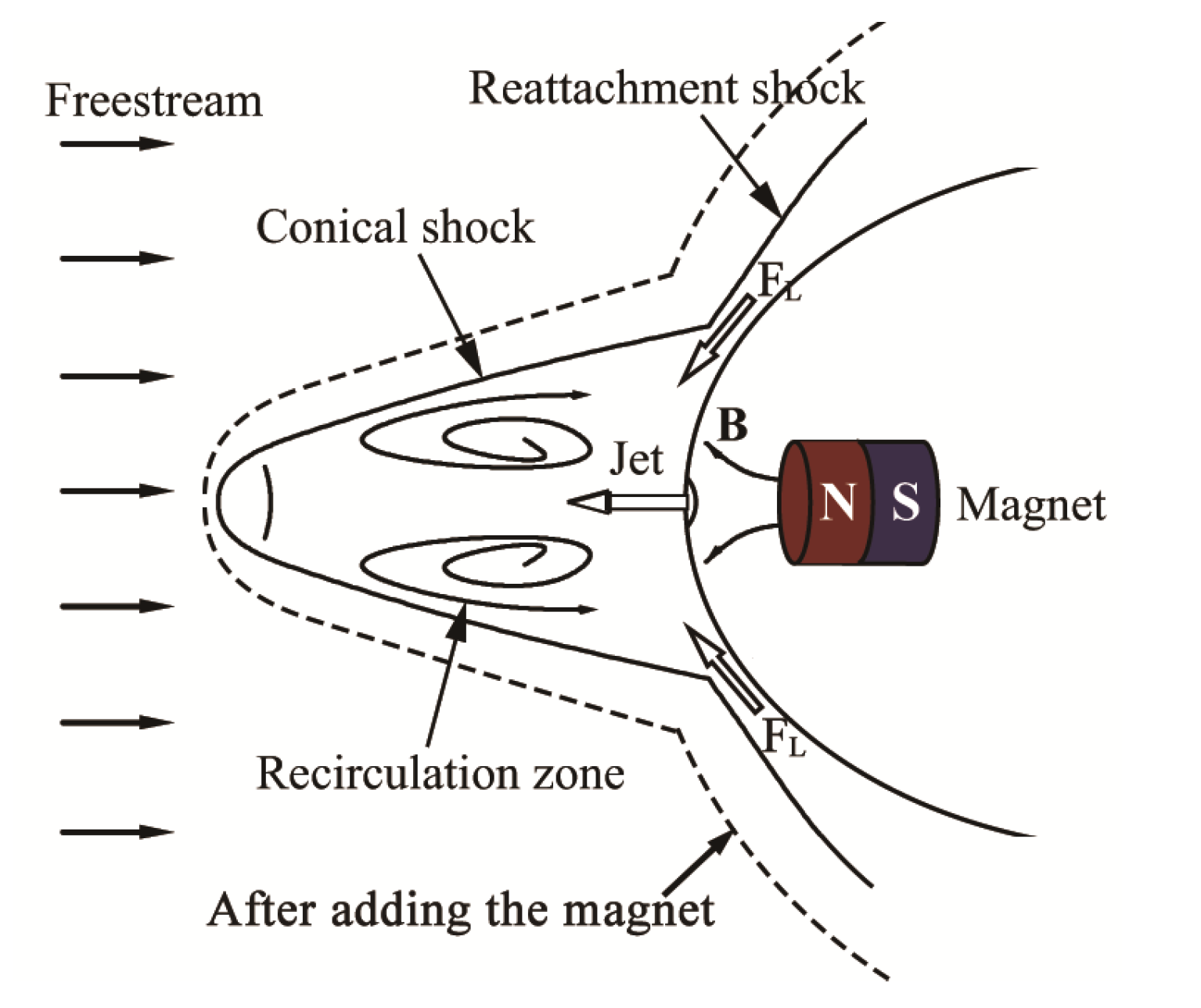
4. Physical Description
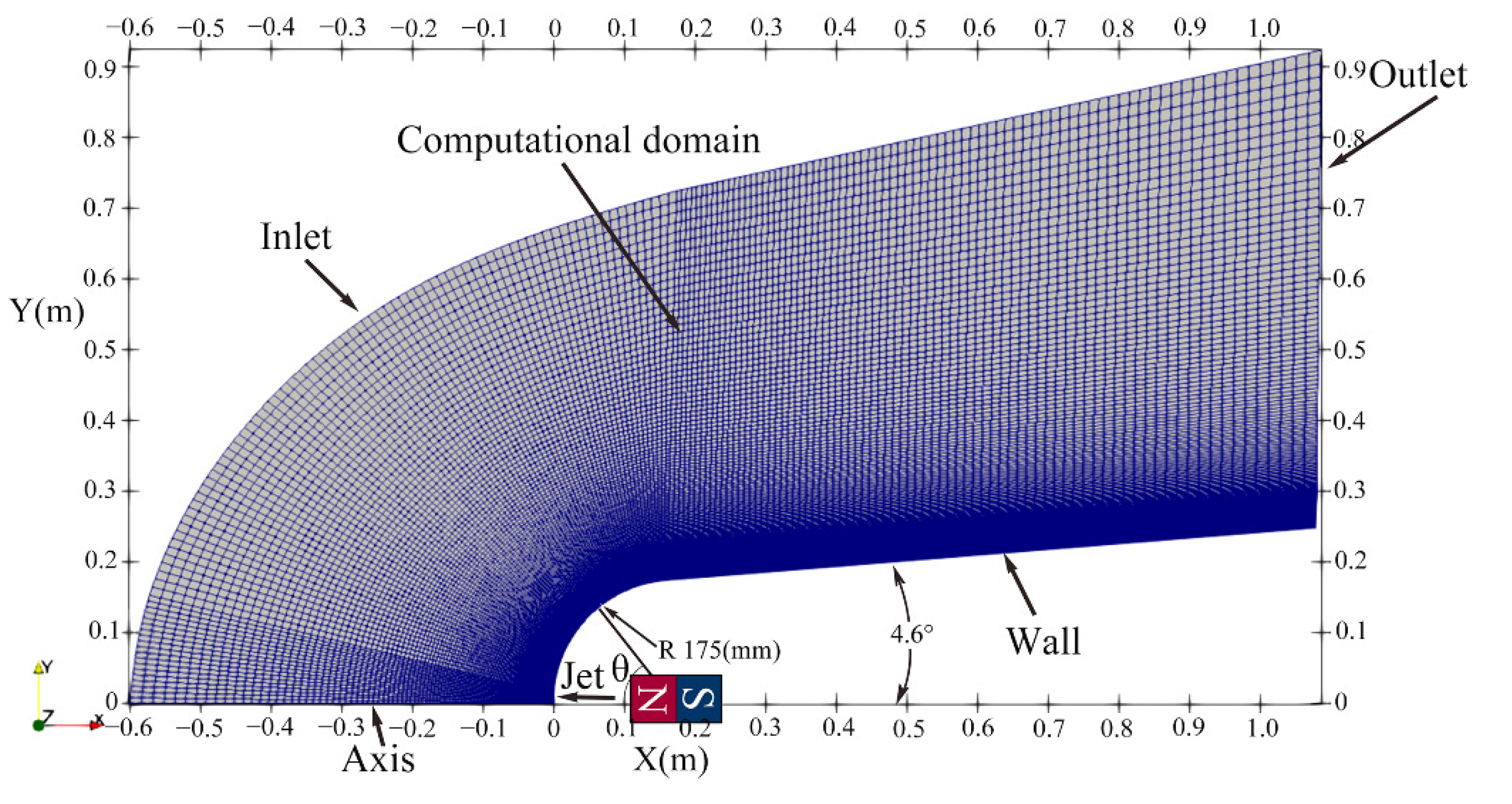
4.1. Geometric Model and Grid
4.2. Cases Design and Boundary Conditions
5. Results and Discussions
5.1. Flowfield Analysis with MHD Control Technology
5.2. Jet Characteristics and Aerodynamic Performances with the Opposing Jet Combined with MHD Control Technology
5.2.1. Jet Characteristics
5.2.2. Aerodynamic Heat
5.2.3. Aerodynamic Drag
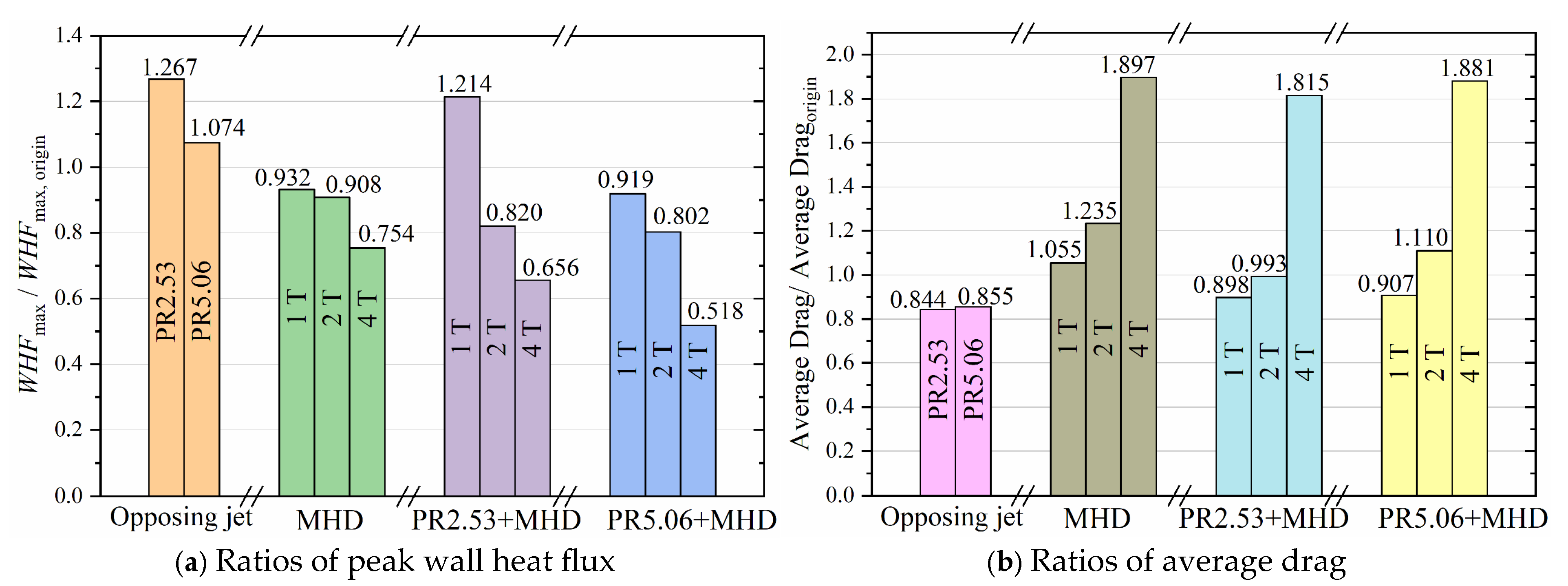
5.3. Comprehensive Evaluation of the Aerodynamic Performances
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MHD | magnetohydrodynamic |
| LPM | long penetration mode |
| SPM | short penetration mode |
| SSDPR | shock standoff distancepressure ratio |
| Nomenclature | |
| J | electric current density vector |
| B | magnetic field vector |
| E | electric field vector |
| σ | electrical conductivity |
| reference electrical conductivity | |
| γ | ratio constant |
| ρs | density of species s |
| ui, uj | velocity vectors |
| p | pressure |
| E | total energy per unit volume |
| Eve | vibro-electronic energy per unit volume |
| eve,s | vibro-electronic energy per unit mass of species s |
| Js,j | mass diffusion flux |
| δij | Kronecker delta |
| τij | shear stress tensor |
| qj | total heat conduction vector |
| qve,j | vibro-electronic heat conduction vector |
| hs | enthalpy per unit mass of species s |
| chemical source term | |
| T0 | reference temperature |
| Ttr | trans-rotational temperature |
| n | constant |
| B0 | magnetic field strength of the reference point |
| r0 | distance between the reference point and the dipole magnet center |
| r | position vector |
| ǀrǀ | magnitude of the r |
| m | angle vector between the dipole magnet and the flow field axis |
References
- Qi, Y.; Ma, X.; Jiang, P.; Zhu, Y. Review on heat-to-power conversion technologies for hypersonic vehicles. Chin. J. Aeronaut. 2024, 37, 148–179. [Google Scholar] [CrossRef]
- van Heerden, A.S.J.; Judt, D.M.; Jafari, S.; Lawson, C.P.; Nikolaidis, T.; Bosak, D. Aircraft thermal management: Practices, technology, system architectures, future challenges, and opportunities. Prog. Aerosp. Sci. 2022, 128, 100767. [Google Scholar]
- Zhang, S.; Li, X.; Zuo, J.; Qin, J.; Cheng, K.; Feng, Y.; Bao, W. Research progress on active thermal protection for hypersonic vehicles. Prog. Aerosp. Sci. 2020, 119, 100646. [Google Scholar]
- Liu, S.; Yan, C.; Kang, D.; Jiang, Z.; Sun, M. Opposing jets for heat flux reduction and uncertainty analysis on a V-shaped blunt leading edge. Aerosp. Sci. Technol. 2023, 138, 108353. [Google Scholar] [CrossRef]
- Hayashi, K.; Aso, S.; Tani, Y. Experimental Study on Thermal Protection System by Opposing Jet in Supersonic Flow. J. Spacecr. Rocket. 2006, 43, 233–235. [Google Scholar]
- Daso, E.O.; Pritchett, V.E.; Wang, T.S.; Ota, D.K.; Blankson, I.M.; Auslender, A.H. Dynamics of Shock Dispersion and Interactions in Supersonic Freestreams with Counterflowing Jets. AIAA J. 2009, 47, 1313–1326. [Google Scholar]
- Huang, W.; Zhang, R.R.; Yan, L.; Ou, M.; Moradi, R. Numerical experiment on the flow field properties of a blunted body with a counterflowing jet in supersonic flows. Acta Astronaut. 2018, 147, 231–240. [Google Scholar]
- Bibi, A.; Maqsood, A.; Sherbaz, S.; Dala, L. Drag reduction of supersonic blunt bodies using opposing jet and nozzle geometric variations. Aerosp. Sci. Technol. 2017, 69, 244–256. [Google Scholar] [CrossRef]
- Sriram, R.; Jagadeesh, G. Film cooling at hypersonic Mach numbers using forward facing array of micro-jets. Int. J. Heat Mass Transf. 2009, 52, 3654–3664. [Google Scholar]
- Ji, C.; Liu, B.; Huang, W.; Li, S.; Meng, Z.; Yan, L.; Choubey, G. Design exploration on the drag reduction and thermal protection over a blunted waverider with multiple opposing jets. Aerosp. Sci. Technol. 2022, 124, 107519. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Zhang, Z.; Han, F.; Zhao, S. Heat and drag reduction of single and combined opposing jets in hypersonic nonequilibrium flows. Aerosp. Sci. Technol. 2022, 121, 107194. [Google Scholar]
- Eghlima, Z.; Mansour, K.; Fardipour, K. Heat transfer reduction using combination of spike and counterflow jet on blunt body at high Mach number flow. Acta Astronaut. 2018, 143, 92–104. [Google Scholar]
- Huang, J.; Yao, W.; Shan, X. Coupled fluid-thermal investigation on non-ablative thermal protection system with spiked body and opposing jet combined configuration. Chin. J. Aeronaut. 2019, 32, 1390–1402. [Google Scholar]
- Vali, S.E.; Abbasi, S. Hypersonic drag and heat reduction mechanism of a new hybrid method of spike, multi-row discs and opposing jets aerodynamic configuration. Int. J. Heat Mass Transf. 2022, 194, 123034. [Google Scholar]
- Wang, Z.; Zhang, X. Research on a novel combined shock control mechanism for thermal protection and drag reduction in hypersonic compressible flow field. Int. J. Heat Mass Transf. 2023, 201, 123592. [Google Scholar]
- Huang, W.; Yan, L.; Liu, J.; Jin, L.; Tan, J. Drag and heat reduction mechanism in the combinational opposing jet and acoustic cavity concept for hypersonic vehicles. Aerosp. Sci. Technol. 2015, 42, 407–414. [Google Scholar]
- Zhang, R.; Dong, M.; Huang, W.; Li, S.; Du, Z.; Liao, J. Drag and heat flux reduction mechanism induced by the combinational forward-facing cavity and pulsed counterflowing jet configuration in supersonic flows. Acta Astronaut. 2019, 160, 62–75. [Google Scholar]
- Sudarshan, B.; Rao, S.M.V.; Jagadeesh, G.; Saravanan, S. Effect of the axial cavity with an opposing high-pressure jet combination in a Mach 6 flow condition. Acta Astronaut. 2021, 178, 335–348. [Google Scholar]
- Fujita, M. Axisymmetric oscillations of an opposing jet from a hemispherical nose. In Proceedings of the 32nd Aerospace Science Meeting & Exhibit, Reno, NV, USA, 10–13 January 1994. [Google Scholar]
- Deng, F.; Xie, F.; Huang, W.; Dong, H.; Zhang, D. Numerical exploration on jet oscillation mechanism of counterflowing jet ahead of a hypersonic lifting-body vehicle. Sci. China Technol. Sci. 2018, 61, 1056–1071. [Google Scholar] [CrossRef]
- Kim, Y.; Roh, T.-S.; Lee, H.J. Mechanism and prediction of flow oscillation based on counter-flow jet for drag reduction in hypersonic flow. Aerosp. Sci. Technol. 2022, 126, 107603. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Zhang, Z.; Su, T. Numerical Investigation on the Jet Characteristics and the Heat and Drag Reductions of Opposing Jet in Hypersonic Nonequilibrium Flows. Aerospace 2022, 9, 554. [Google Scholar] [CrossRef]
- Zhao, K.; Ming, M.; Li, F.; Lu, Y.; Zhou, T.; Wang, K.; Meng, N. Experimental study on plasma jet deflection and energy extraction with MHD control. Chin. J. Aeronaut. 2020, 33, 1602–1610. [Google Scholar]
- Schramm, J.M.; Hannemann, K. Study of MHD Effects in the High-Enthalpy Shock Tunnel Göttingen (HEG) Using a 30 T-Pulsed Magnet System. In Proceedings of the 31st International Symposium on Shock Waves, Nagoya, Japan, 9–14 July 2017. [Google Scholar]
- Ziemer, R.W.; Bush, W.B. Magnetic Field Effects on Bow Shock Stand-Off Distance. Phys. Rev. Lett. 1958, 1, 58–59. [Google Scholar]
- Smith, D.R.; Gildfind, D.E.; Jacobs, P.A.; Cullen, T.G.; Mcintyre, T.J. Magnetohydrodynamic Drag Measurements in an Expansion Tunnel with Argon Test Gas. AIAA J. 2020, 58, 4495–4504. [Google Scholar]
- Smith, D.R.; Gildfind, D.E.; James, C.M.; Mcintyre, T.J.; Wheatley, V. Magnetohydrodynamic drag force measurements in an expansion tube. In Proceedings of the 2018 Flow Control Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Gong, G.; Li, Y.W.; Wang, Y.T.; Kuang, P. Investigation on wedge shock wave control by surface MHD actuation. AIP Adv. 2020, 10, 005212. [Google Scholar]
- Jiang, H.; Liu, J.; Che, X.; Du, Y.; Huang, W.; Ding, F.; Zhang, T. Magnetic field control of high-enthalpy shock wave/boundary-layer interactions using a fully implicit thermochemical non-equilibrium solver. Aerosp. Sci. Technol. 2023, 141, 108507. [Google Scholar]
- Luo, S.; Wu, L.; Chang, Y.; Li, X. Thermochemical non-equilibrium and electromagnetic effects of double-cone in hypervelocity flow. Aerosp. Sci. Technol. 2023, 132, 108041. [Google Scholar]
- Wang, D.; Wang, J.; Li, L. Electromagnetic field/hypersonic flow field coupled algorithm and its application in the magnetic controlled inlet design. Aerosp. Sci. Technol. 2022, 126, 107598. [Google Scholar]
- Park, C. Assessment of two-temperature kinetic model for dissociating and weakly-ionizing nitrogen. J. Thermophys. Heat Transf. 1987, 2, 8–16. [Google Scholar]
- Muir, H.A.; Nikiforakis, N. Numerical modeling of imposed magnetohydrodynamic effects in hypersonic flows. Phys. Fluids 2022, 34, 107114. [Google Scholar]
- Zhang, W.; Zhang, Z.; Wang, X.; Su, T. A review of the mathematical modeling of equilibrium and nonequilibrium hypersonic flows. Adv. Aerodyn. 2022, 4, 38. [Google Scholar]
- Bisek, N.J.; Boyd, I.D.; Poggie, J. Numerical Study of Electromagnetic Aerodynamic Control of Hypersonic Vehicles. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Otsu, H.; Konigorski, D.; Abe, T. Influence of Hall Effect on Electrodynamic Heat Shield System for Reentry Vehicles. AIAA J. 2010, 48, 2177–2186. [Google Scholar]
- Nagata, Y.; Otsu, H.; Yamada, K.; Abe, T. Influence of Hall Effect on Electrodynamic Flow Control for Weakly Ionized Flow. In Proceedings of the 43rd AIAA Plasmadynamics and Lasers Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar]
- Fujino, T.; Matsumoto, Y.; Kasahara, J.; Ishikawa, M. Numerical Studies of Magnetohydrodynamic Flow Control Considering Real Wall Electrical Conductivity. J. Spacecr. Rocket. 2007, 44, 625–632. [Google Scholar]
- Casseau, V. An Open-Source CFD Solver for Planetary Entry. Ph.D. Thesis, University of Strathclyde, Glasgow, Scotland, 2017. [Google Scholar]
- Ding, M.S.; Jiang, T.; Liu, Q.Z.; Dong, W.Z.; Gao, T.S.; Fuyang, A.Y. Impact of simulation of electrical conductivity on hypersonic MHD control. Acta Aeronaut. Astronaut. Sin. 2019, 40, 123009. (In Chinese) [Google Scholar]
- Muylaert, J.; Walpot, L.; Haeuser, J.; Sagnier, P.; Devezeaux, D.; Papirnyk, O.; Lourme, D. Standard model testing in the European High Enthalpy Facility F4 andextrapolation to flight. In Proceedings of the AIAA 17th Aerospace Ground Testing Conference, Nashville, TN, USA, 6–8 July 1992. [Google Scholar]
- Smith, D.R.; Gildfnd, D.E.; McIntyre, T.J.; Mee, D.J.; James, C.M.; Andrianatos, A. Magnetohydrodynamic drag force measurements in expansion tunnels using an accelerometer-based force balance. Exp. Fluids 2019, 60, 183. [Google Scholar]
- Kim, Y.; Roh, T.-S.; Huh, H.; Lee, H.J. Study on the combined effect of various injection conditions on the drag reduction by a counter-flow jet in supersonic flow. Aerosp. Sci. Technol. 2020, 98, 105580. [Google Scholar]
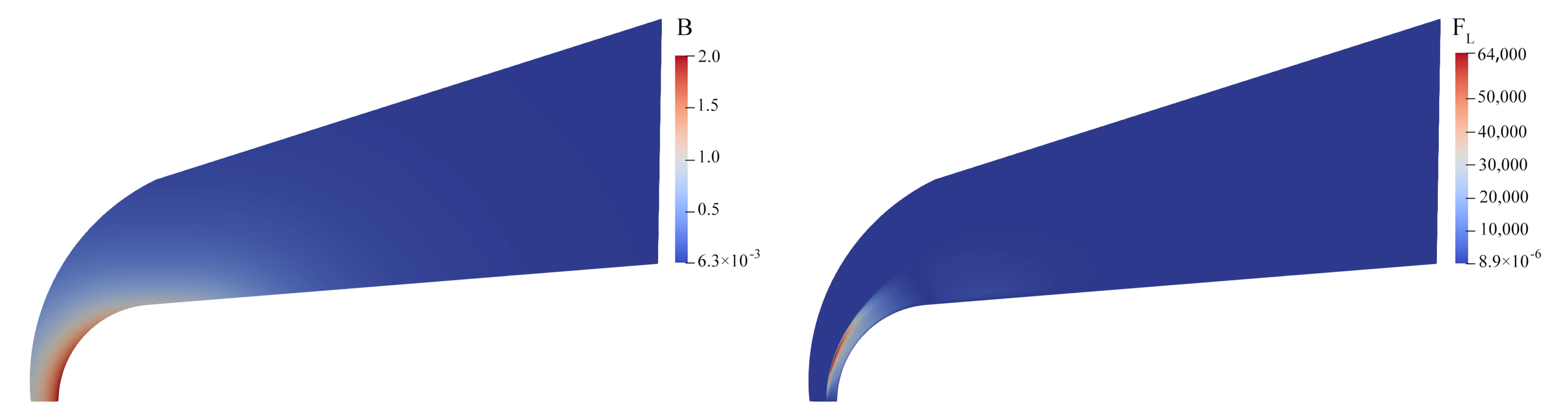
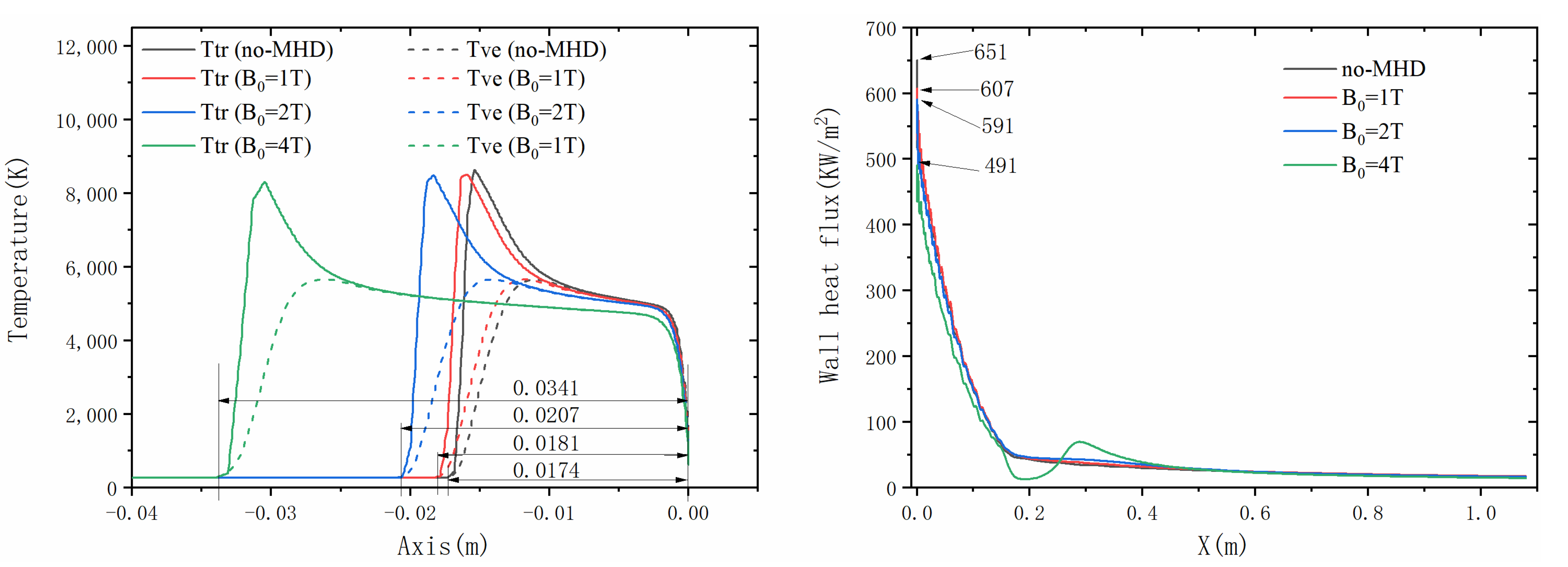
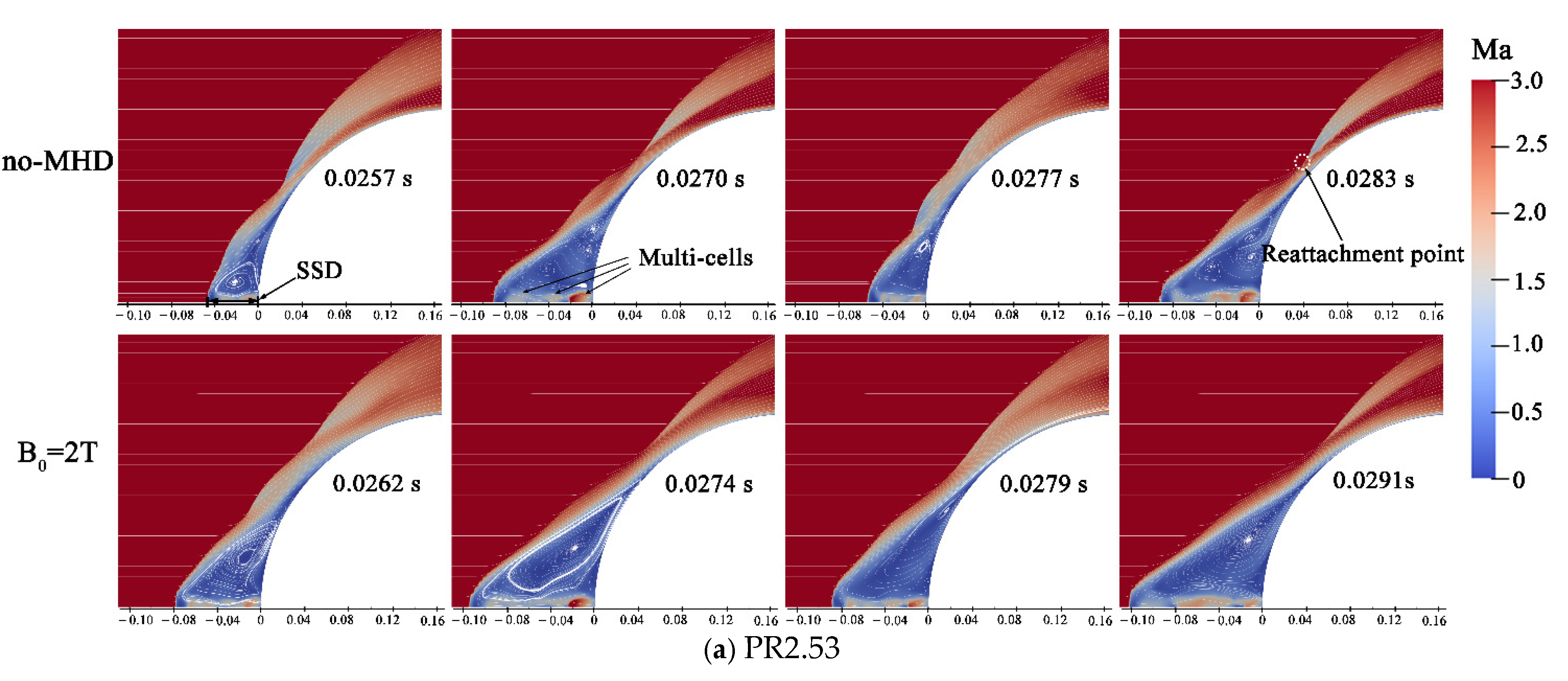
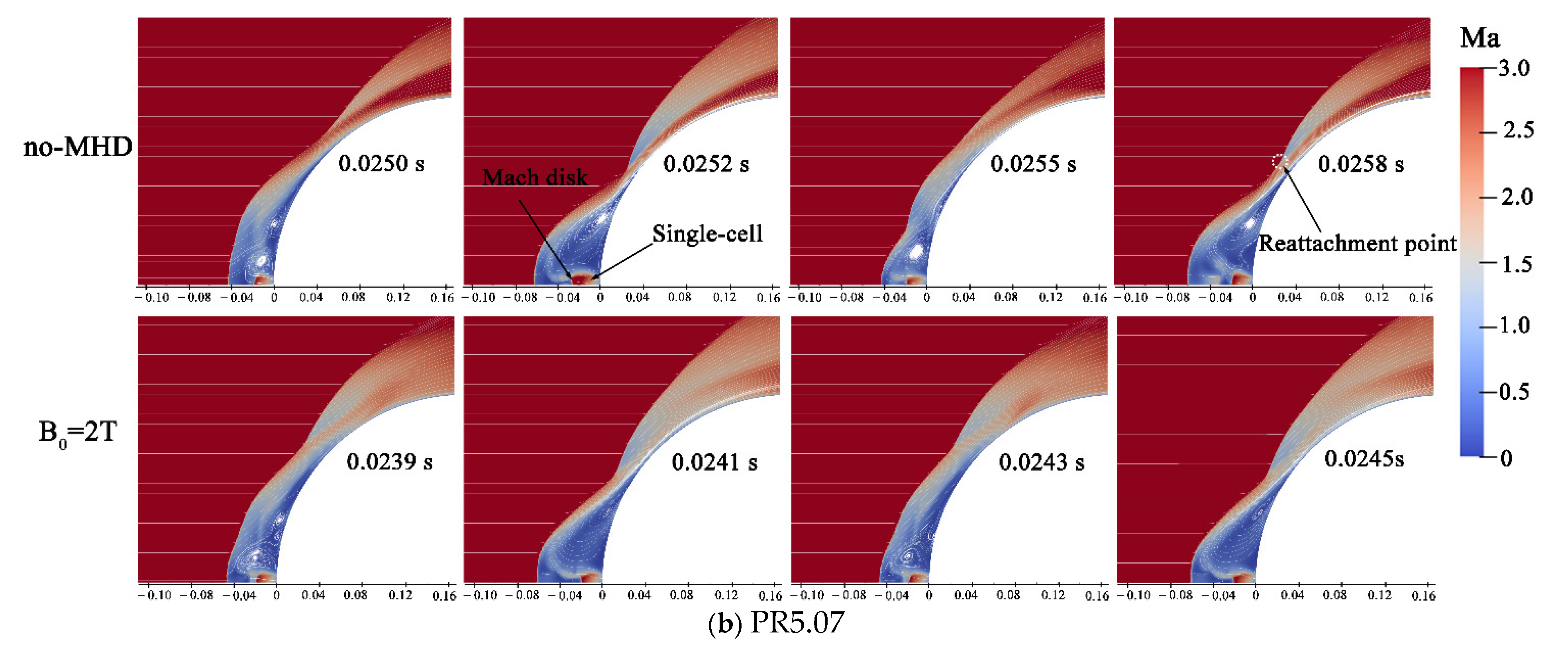
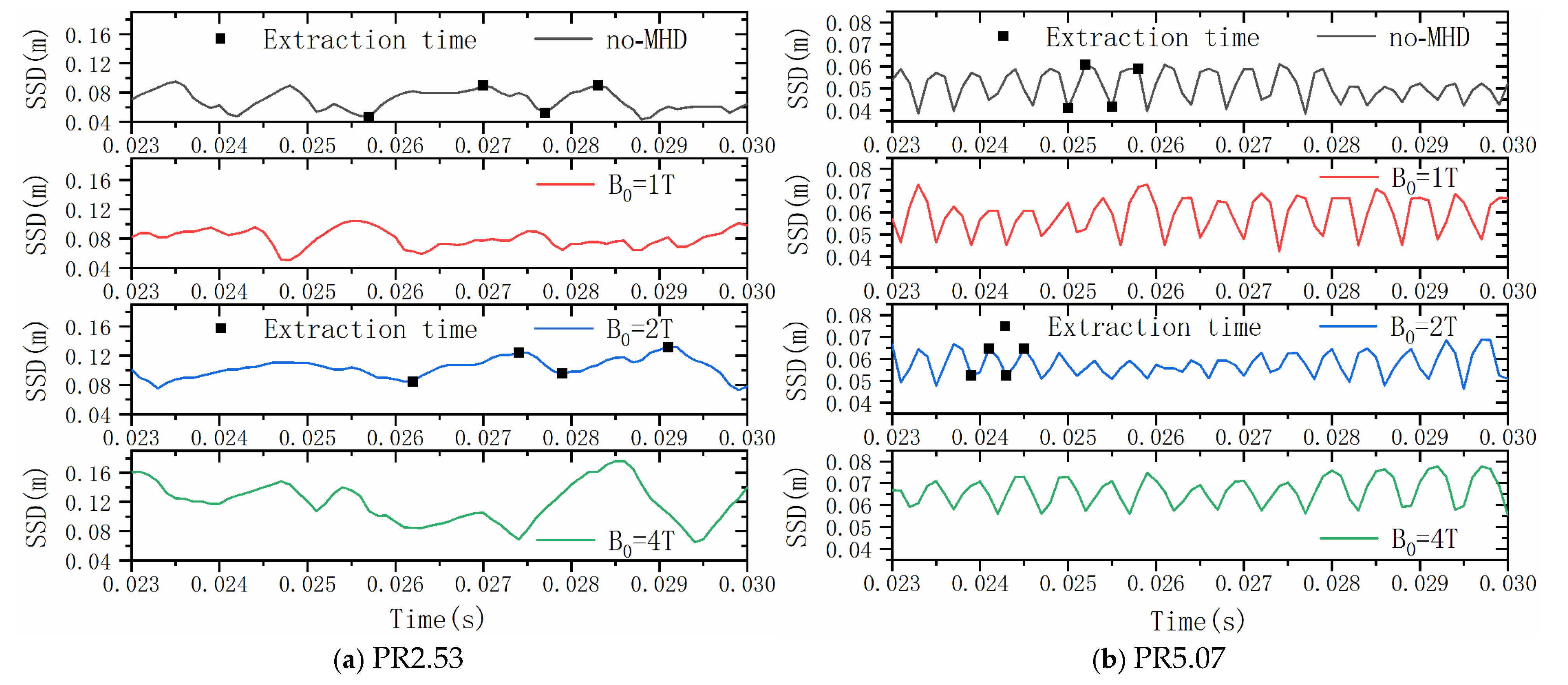


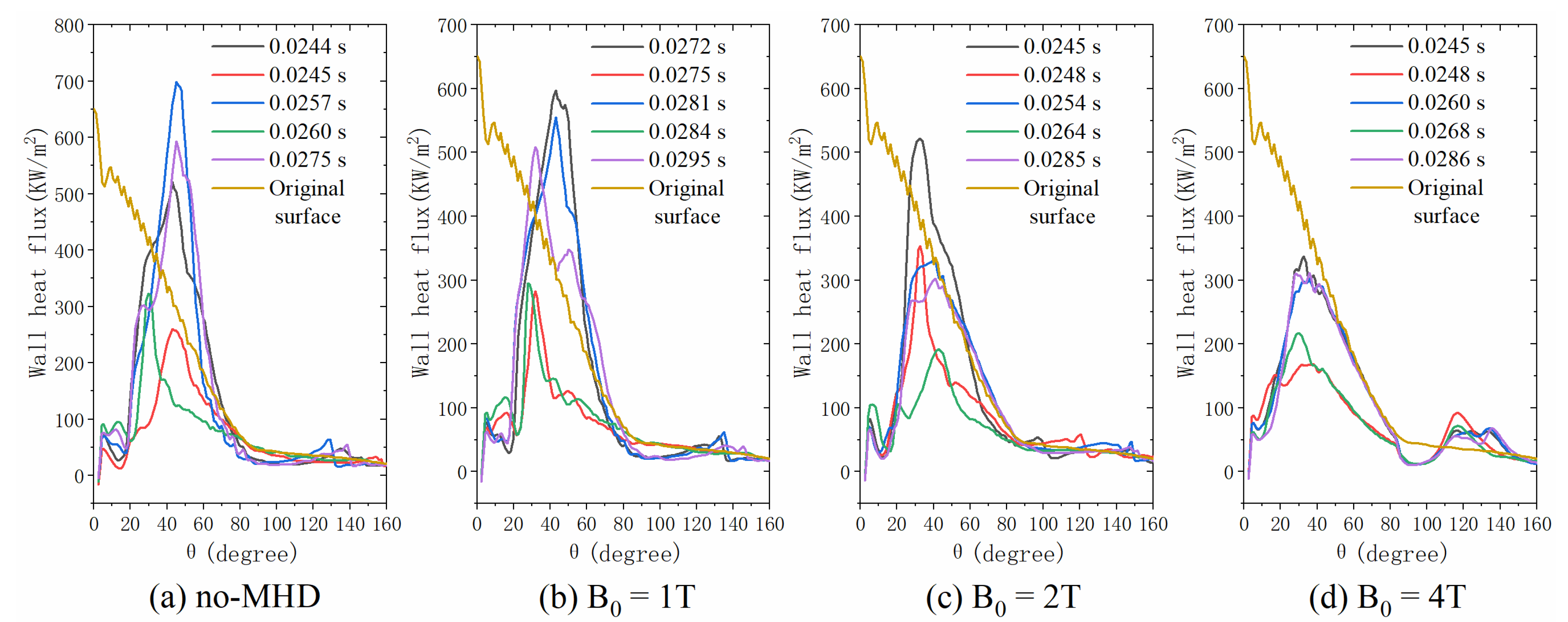
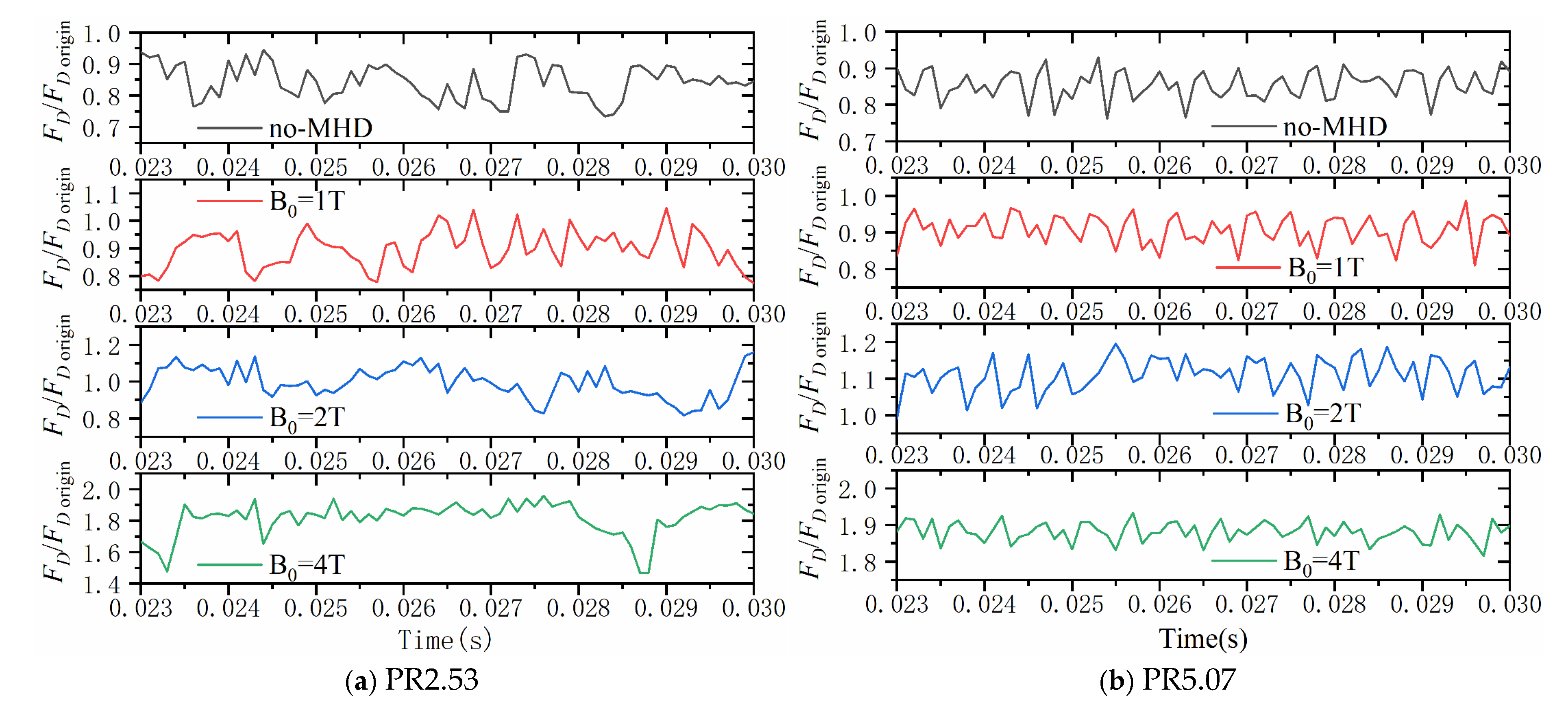
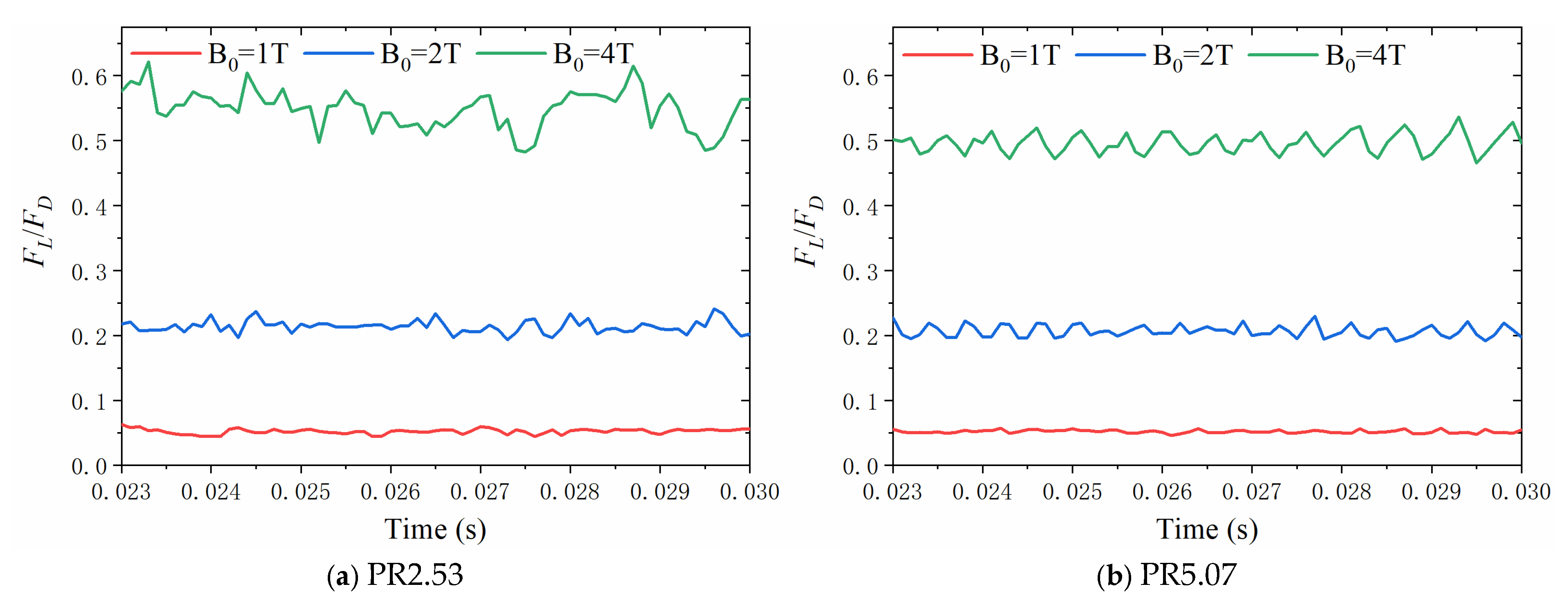
| Inlet | Wall | Jet | Magnetic Field | ||
|---|---|---|---|---|---|
| Mach Number | 13 | 0 | 1 | 1 | no-MHD; B0 = 1 T; B0 = 2 T; B0 = 4 T |
| Static Pressure (Pa) | 52.8 | ∂p/∂n = 0 | 13,922 | 27,844 | |
| Static Temperature (K) | 265 | 343 | 343 | 343 | |
| Pressure Ratio | --- | --- | 2.53 | 5.07 | |
| Species | 78% N2 + 22% O2 | ∂Y/∂n = 0 | N2 | N2 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhang, Z.; Gao, W. Aerodynamic Characteristics of the Opposing Jet Combined with Magnetohydrodynamic Control in Hypersonic Nonequilibrium Flows. Aerospace 2025, 12, 308. https://doi.org/10.3390/aerospace12040308
Zhang W, Zhang Z, Gao W. Aerodynamic Characteristics of the Opposing Jet Combined with Magnetohydrodynamic Control in Hypersonic Nonequilibrium Flows. Aerospace. 2025; 12(4):308. https://doi.org/10.3390/aerospace12040308
Chicago/Turabian StyleZhang, Wenqing, Zhijun Zhang, and Weifeng Gao. 2025. "Aerodynamic Characteristics of the Opposing Jet Combined with Magnetohydrodynamic Control in Hypersonic Nonequilibrium Flows" Aerospace 12, no. 4: 308. https://doi.org/10.3390/aerospace12040308
APA StyleZhang, W., Zhang, Z., & Gao, W. (2025). Aerodynamic Characteristics of the Opposing Jet Combined with Magnetohydrodynamic Control in Hypersonic Nonequilibrium Flows. Aerospace, 12(4), 308. https://doi.org/10.3390/aerospace12040308






