Adaptive UAV Control with Sensor and Actuator Faults Recovery
Abstract
1. Introduction
- An adaptive fault-tolerant control strategy is proposed, which integrates radial basis function neural networks with a nonlinear dynamic inversion controller. The approach is specifically tailored for fixed-wing UAVs and ensures accurate attitude and velocity control even under simultaneous nonlinear actuator and sensor faults.
- A nonlinear perturbation observer is developed for sensor fault detection and estimation to mitigate sensor faults. The observer is integrated into the fault-tolerant control strategy and is characterised by a simple design, high effectiveness and guaranteed convergence.
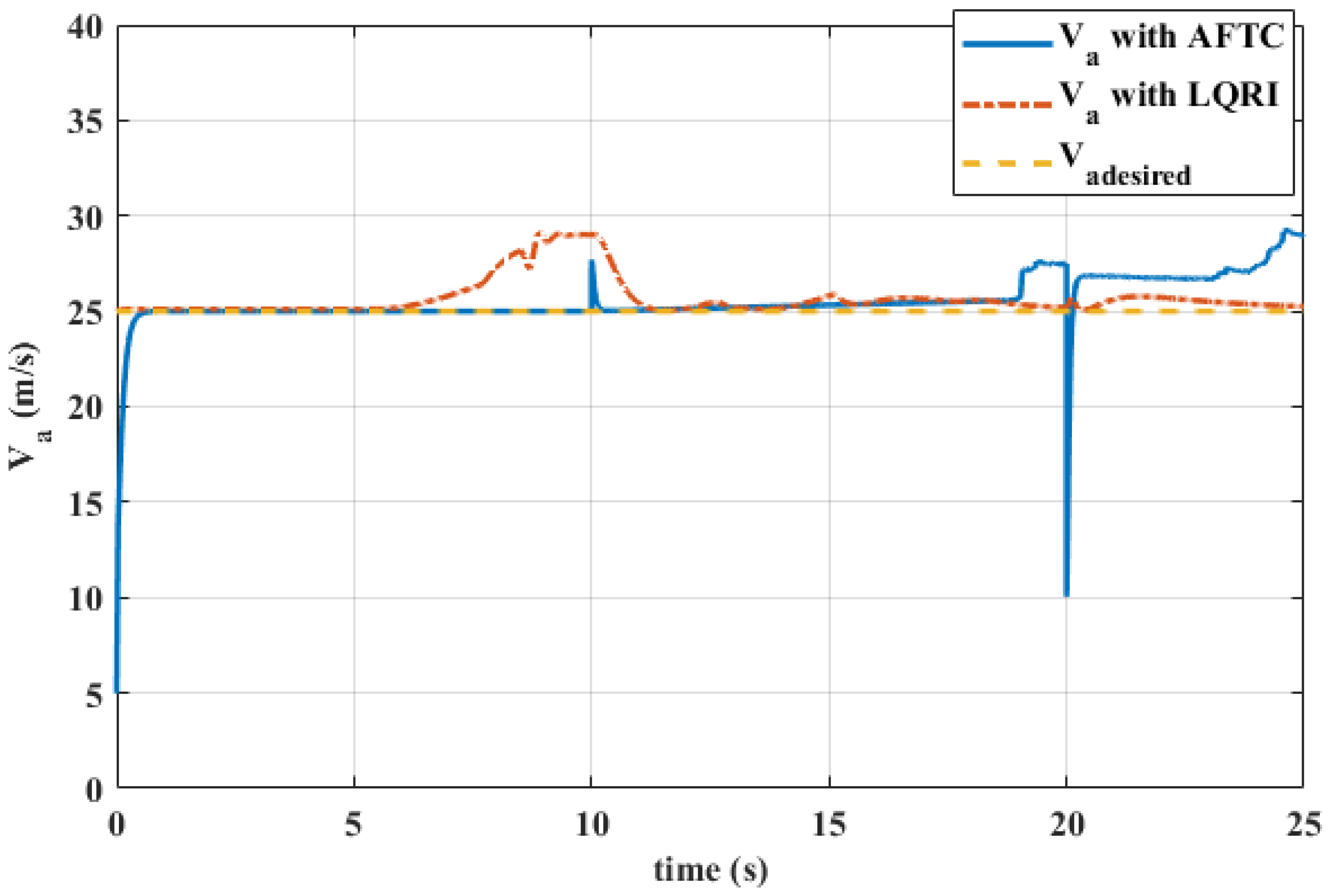
- The proposed control strategy simultaneously addresses actuator and sensor faults, unlike most existing works that treat them separately [25,30]. This holistic approach significantly improves fault tolerance capabilities and ensures robust performance in challenging scenarios. Simulation results show that the artificial intelligence (AI)-enhanced observer-based fault-tolerant controller maintains a safe UAV flight in a condition where the same controller without a sensor fault detection and estimation fails.
2. Problem Formulation
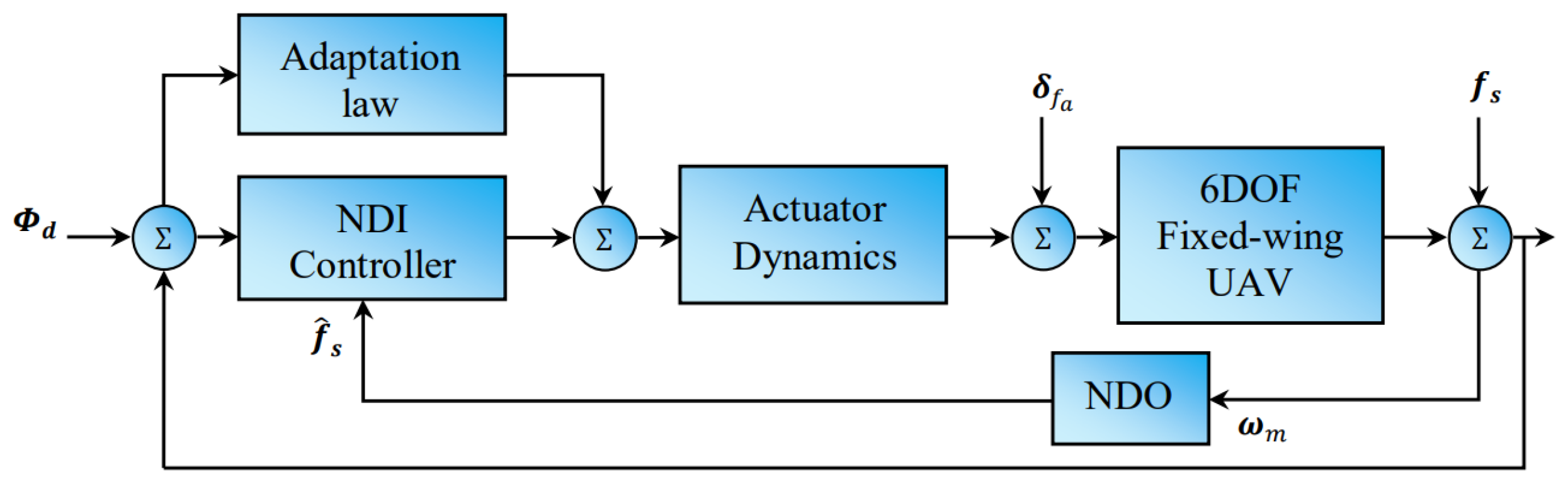
3. Adaptive FTC Design
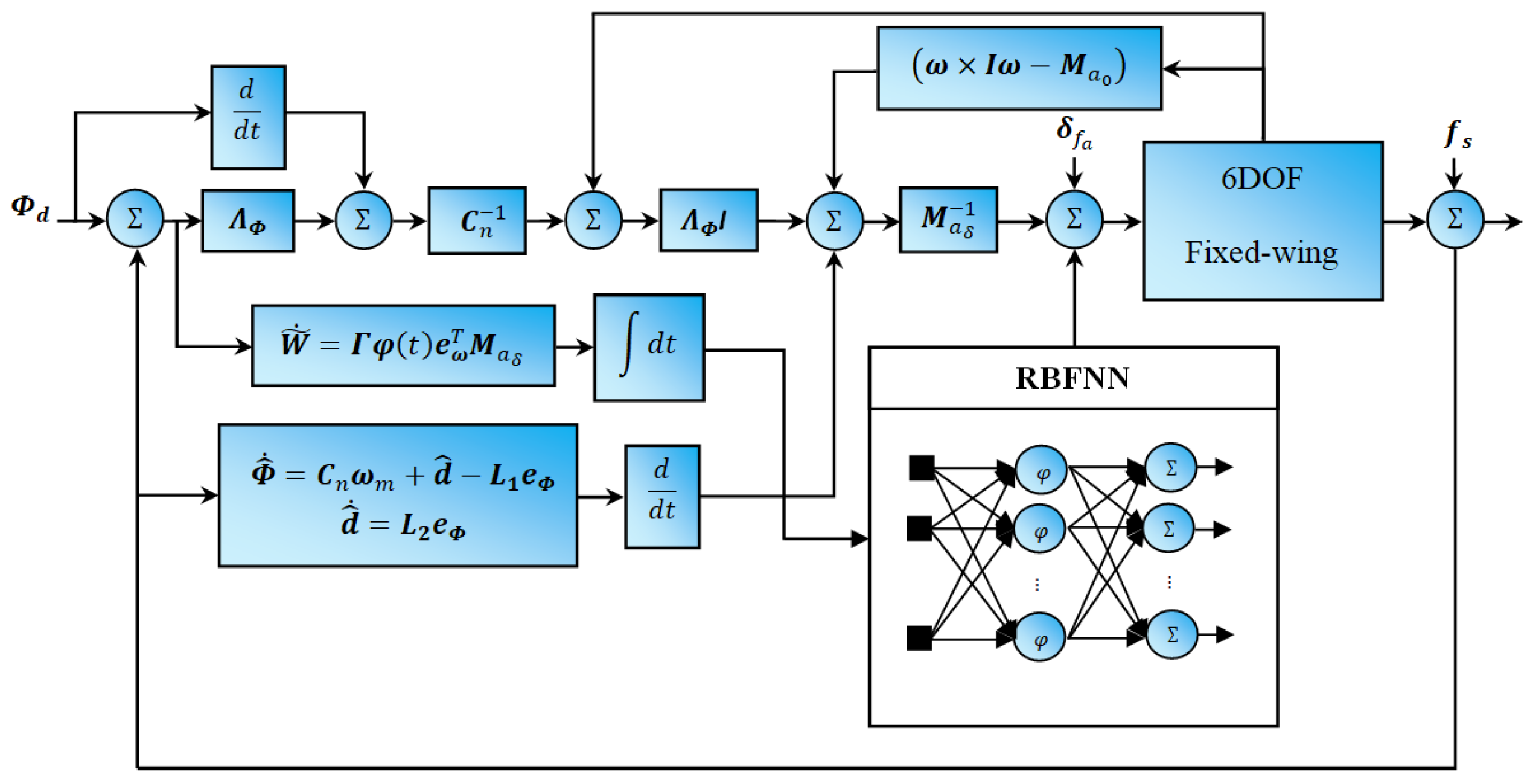
3.1. Nonlinear Disturbance Observer Design
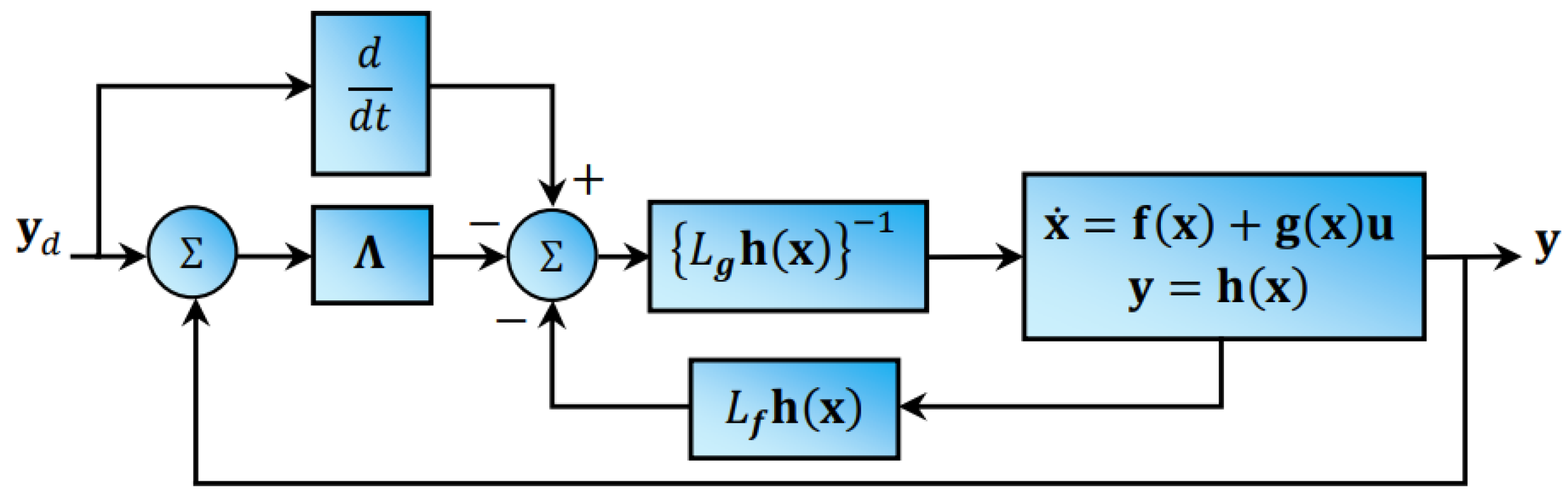
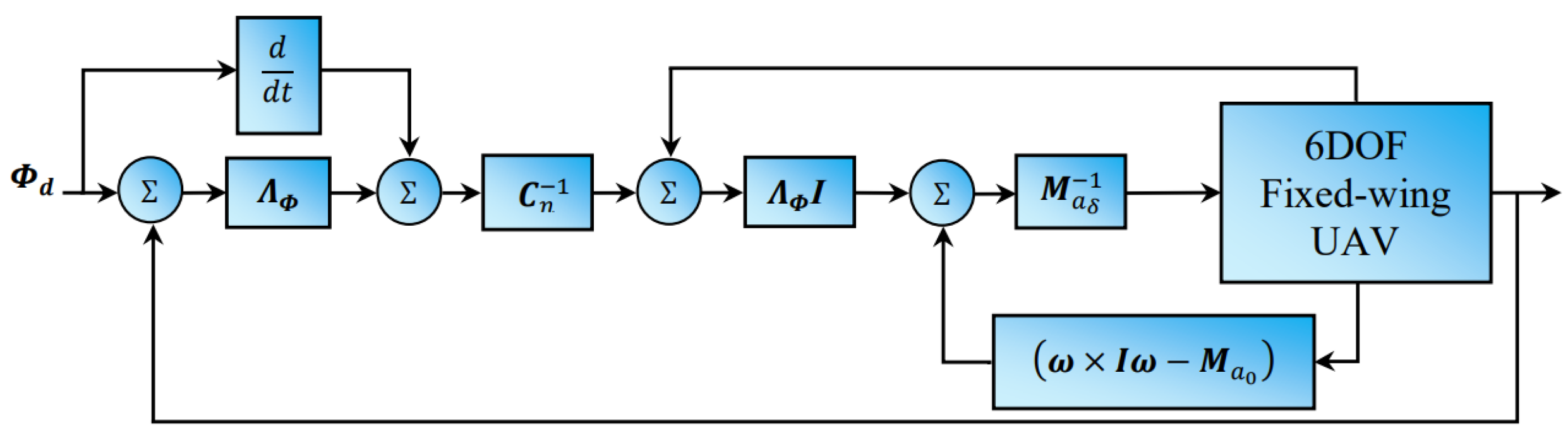
3.2. Nonlinear Dynamic Inversion Control Design
3.3. RBF Neural Network
3.4. Adaptive FTC Control Design
3.5. Airspeed Control Design
4. Linear Quadratic Regulator with Integral Action Design
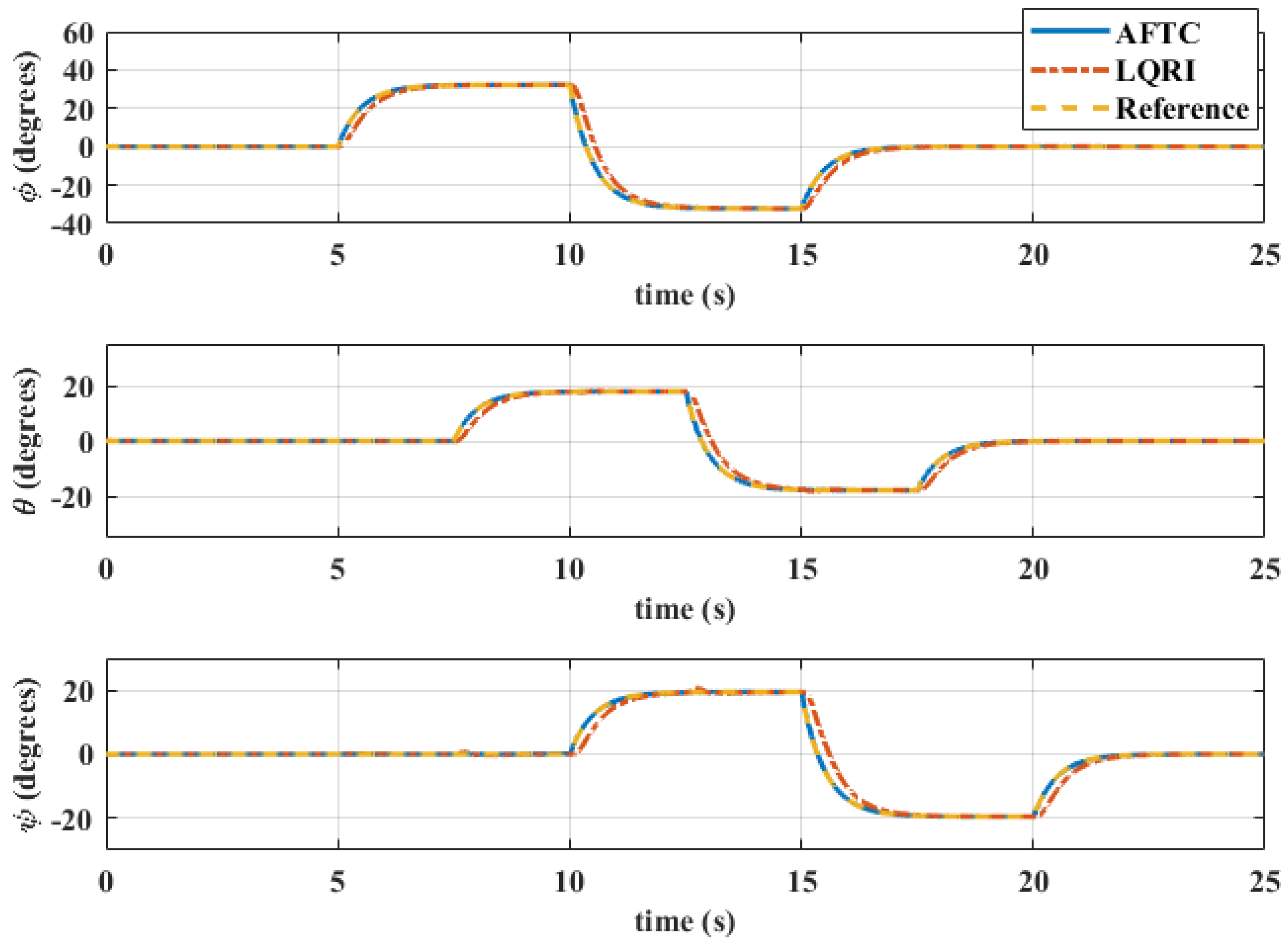
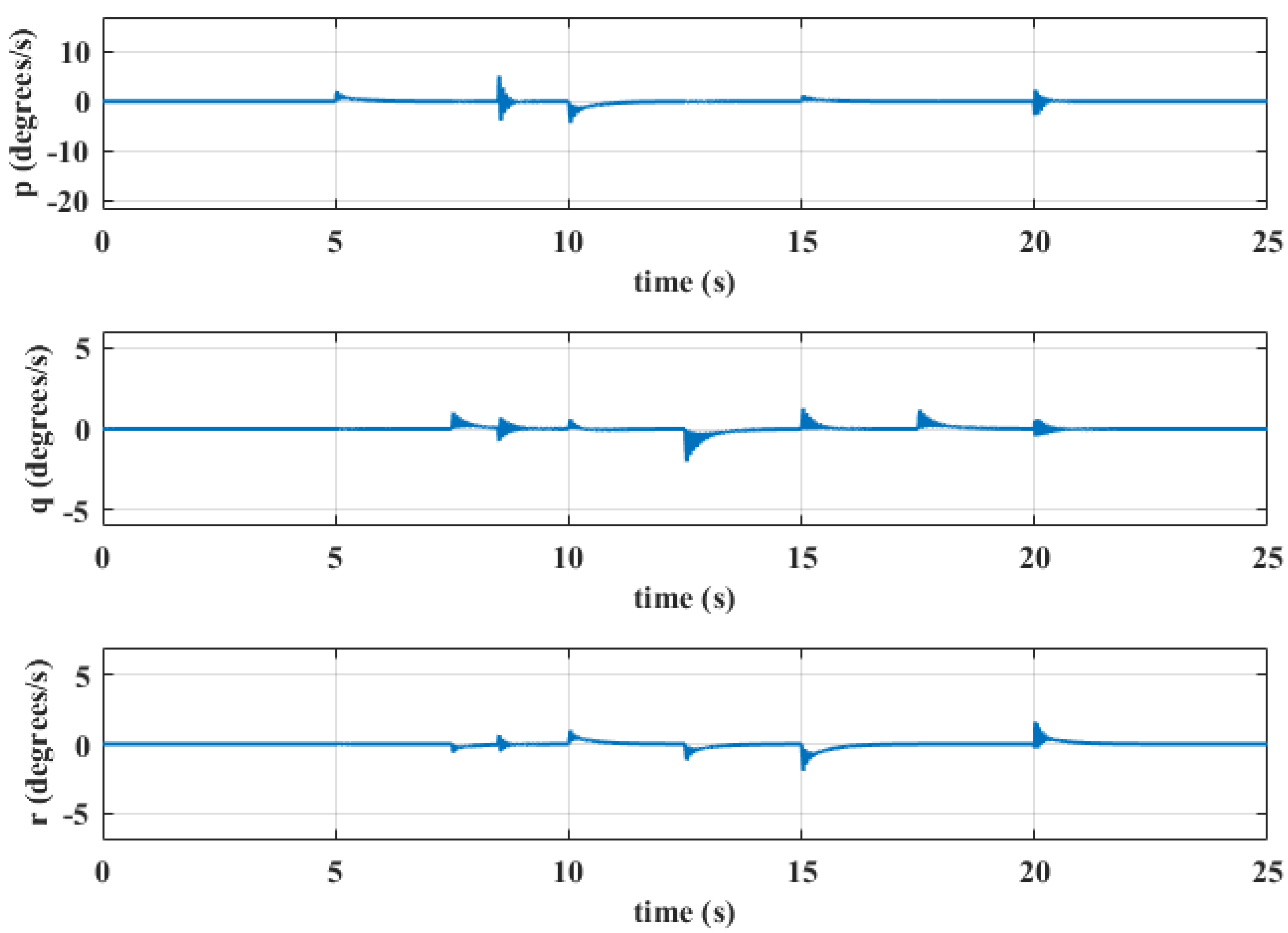
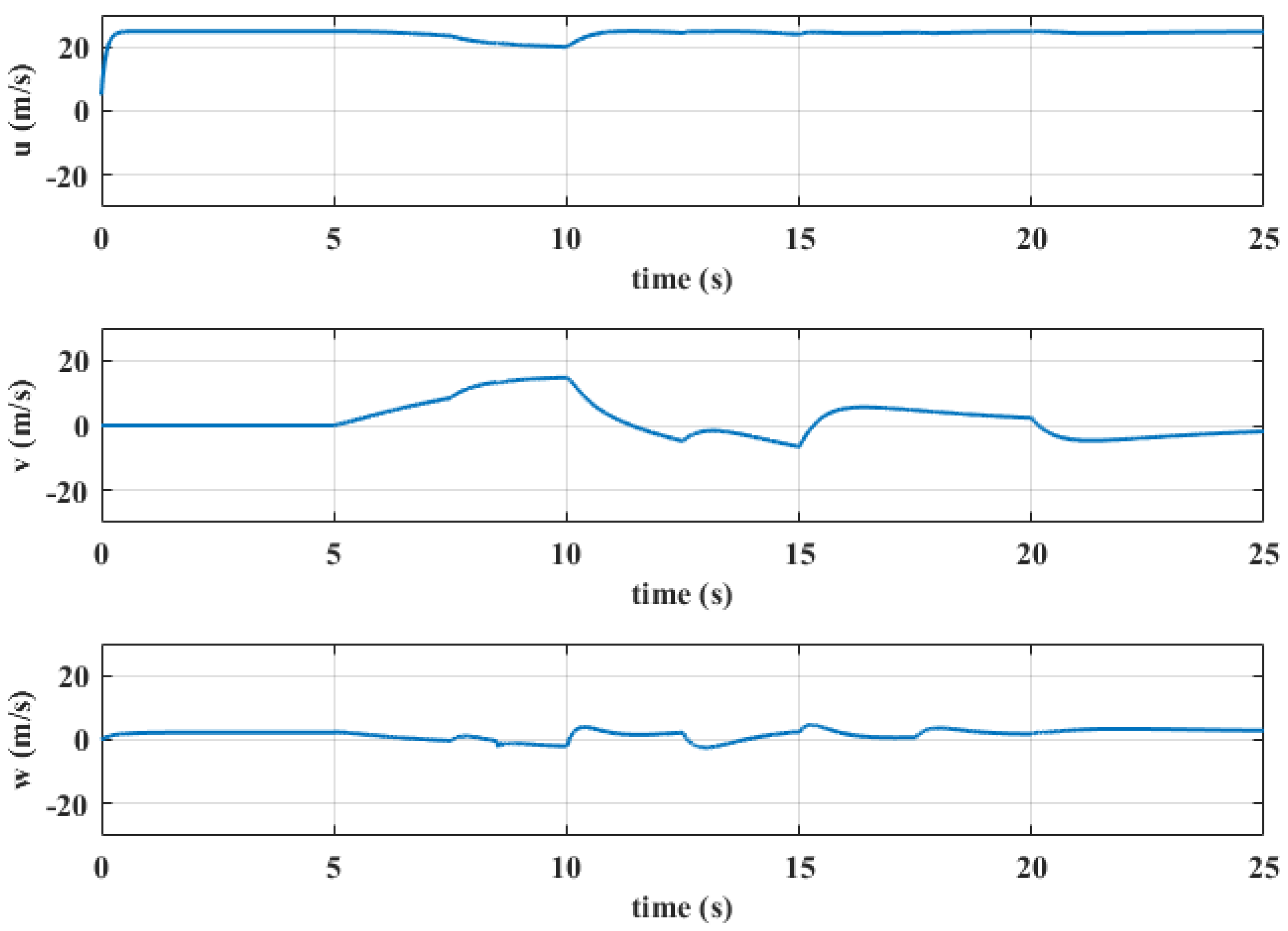
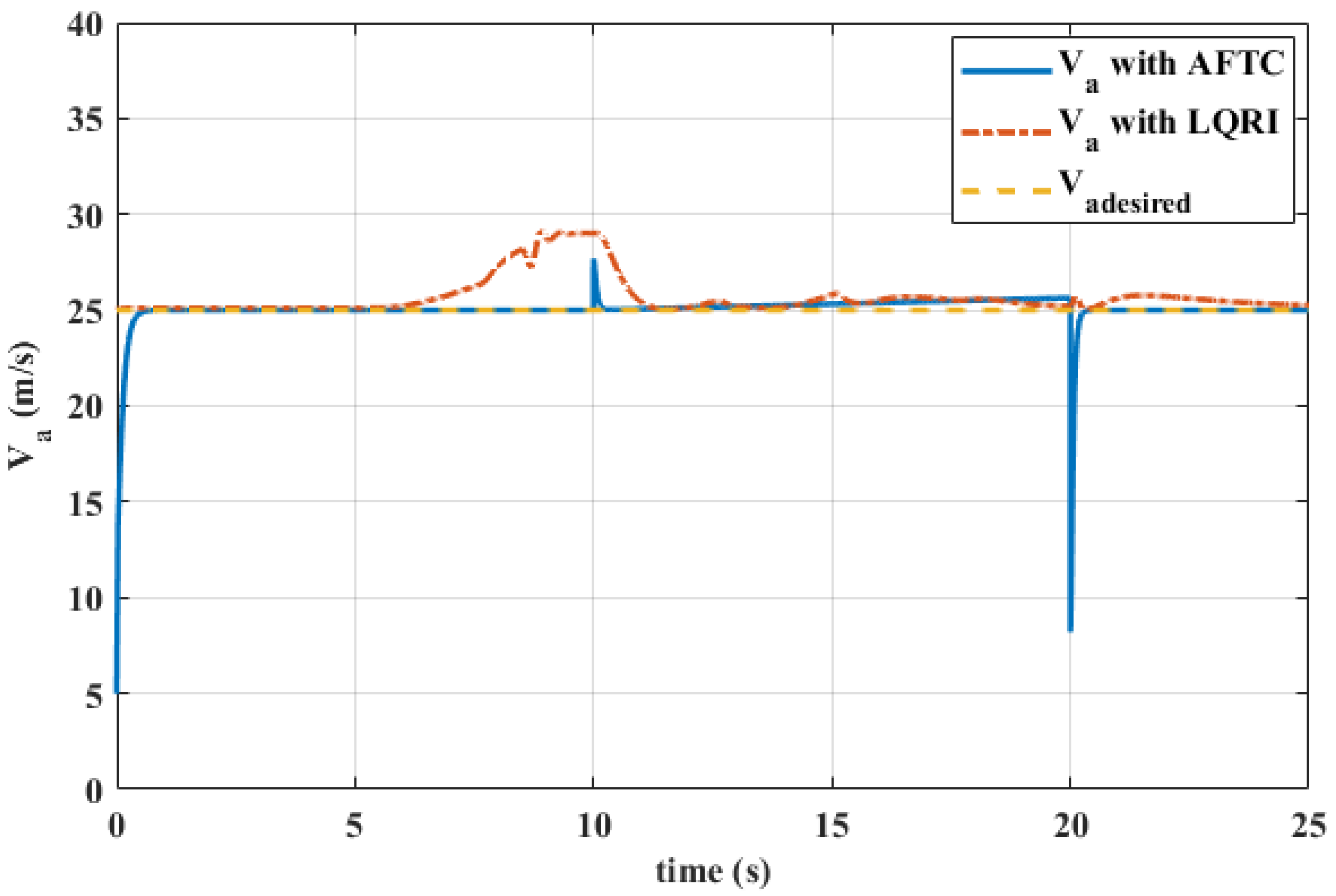
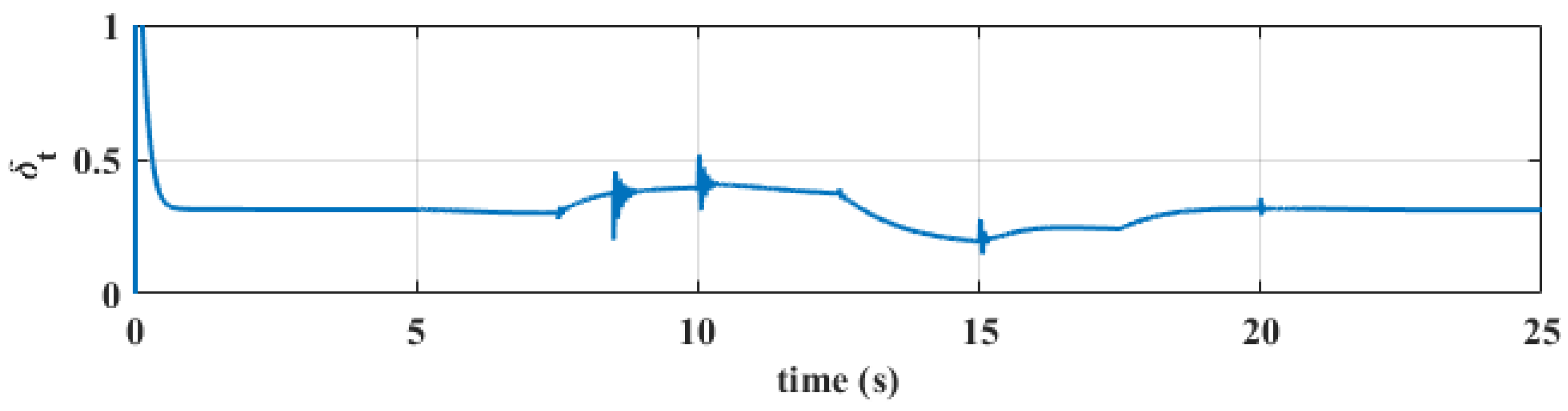
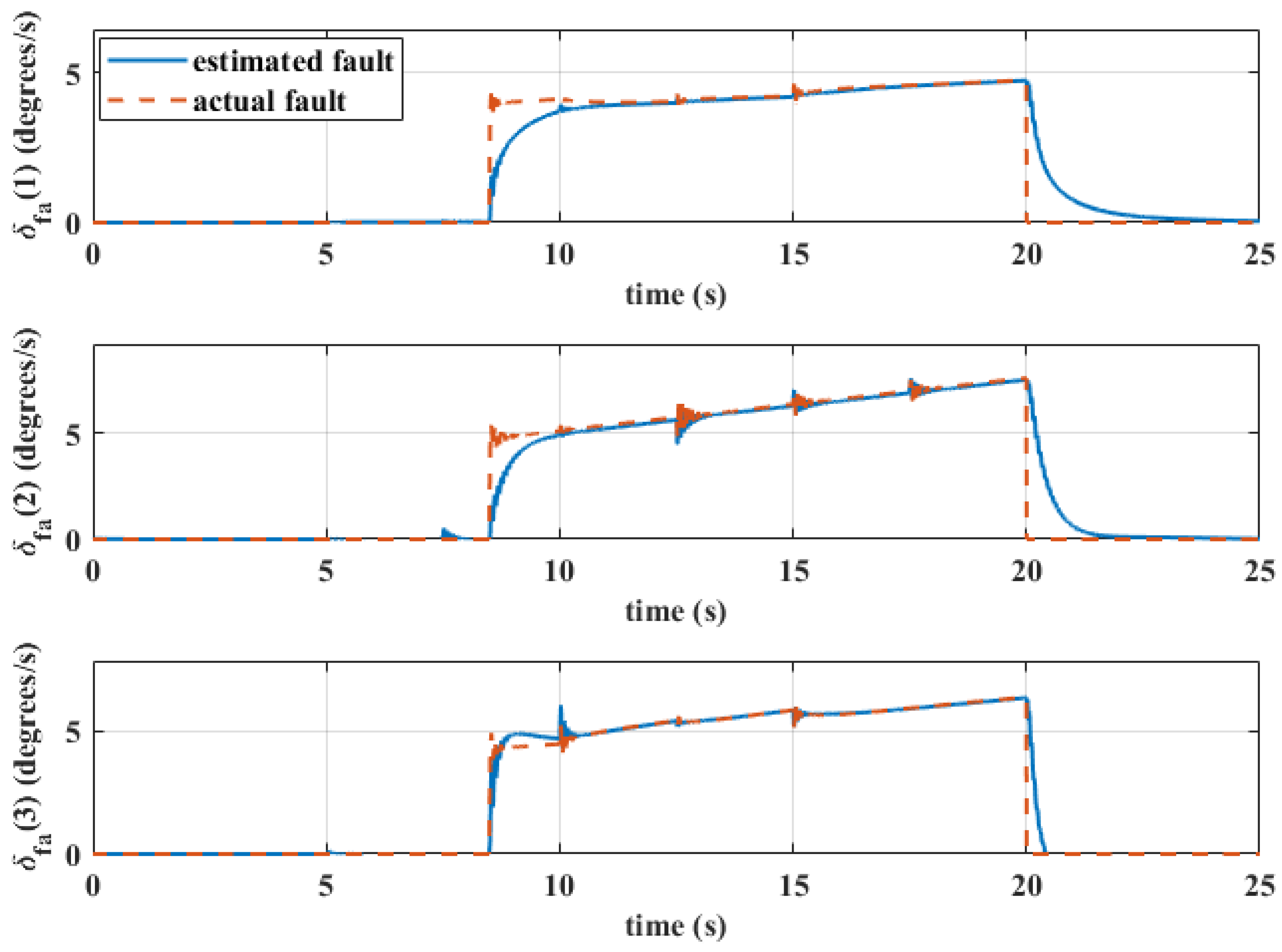
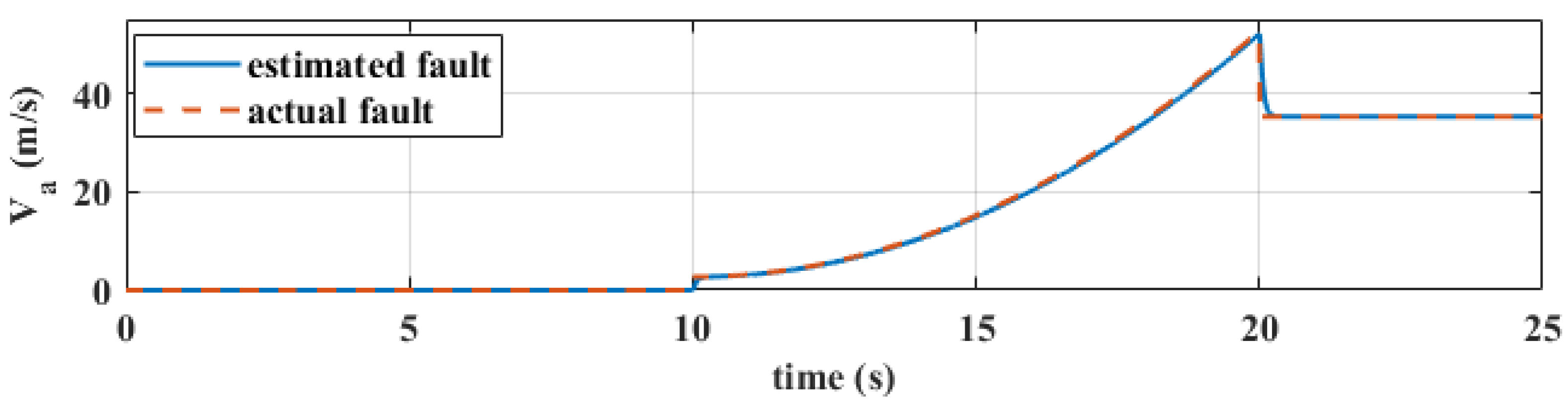
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicles |
| DOF | Degree Of Freedom |
| FTC | Fault-Tolerant Control |
| RBF | Radial Basis Function |
| NDI | Nonlinear Dynamic Inversion |
| NDO | Nonlinear Disturbance Observer |
| LQR | Linear Quadratic Regulator |
| LQRI | Linear Quadratic Regulator with Integral Action |
| ARE | Algebraic Riccati Equation |
Appendix A. Trimming Conditions and Linearised Model
References
- Kim, J.; Kim, S.; Ju, C.; Son, H.I. Unmanned aerial vehicles in agriculture: A review of perspective of platform, control, and applications. IEEE Access 2019, 7, 105100–105115. [Google Scholar] [CrossRef]
- Lyu, M.; Zhao, Y.; Huang, C.; Huang, H. Unmanned aerial vehicles for search and rescue: A survey. Remote Sens. 2023, 15, 3266. [Google Scholar] [CrossRef]
- Greenwood, W.W.; Lynch, J.P.; Zekkos, D. Applications of UAVs in civil infrastructure. J. Infrastruct. Syst. 2019, 25, 04019002. [Google Scholar] [CrossRef]
- Vasiloni, A.; Guyvenchy, F.; Pașcalău, R.; Șmuleac, A. Use of UAV technology for environmental conservation. Res. J. Agric. Sci. 2023, 55, 4. [Google Scholar]
- Telli, K.; Kraa, O.; Himeur, Y.; Ouamane, A.; Boumehraz, M.; Atalla, S.; Mansoor, W. A comprehensive review of recent research trends on unmanned aerial vehicles (UAVs). Systems 2023, 11, 400. [Google Scholar] [CrossRef]
- Fourlas, G.K.; Karras, G.C. A survey on fault diagnosis and fault-tolerant control methods for unmanned aerial vehicles. Machines 2021, 9, 197. [Google Scholar] [CrossRef]
- Henna, H.; Toubakh, H.; Kafi, M.R.; Sayed-Mouchaweh, M. Towards fault-tolerant strategy in satellite attitude control systems: A review. Annu. Conf. PHM Soc. 2020, 12, 14. [Google Scholar] [CrossRef]
- Zogopoulos-Papaliakos, G.; Karras, G.C.; Kyriakopoulos, K.J. A fault-tolerant control scheme for fixed-wing with flight envelope awareness. J. Intell. Robot. Syst. 2021, 102, 46. [Google Scholar] [CrossRef]
- Hann, R.; UNTNU. 2nd international UAV Icing Workshop: Book of abstracts. UAV Icing Workshop, Trondheim, Norway. 3 December 2024. Available online: https://zenodo.org/records/14274740 (accessed on 1 March 2025).
- Souanef, T. Adaptive Guidance and Control of Small Unmanned Aerial Vehicles. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2019. [Google Scholar]
- Souanef, T. L1 Adaptive Output Feedback Control of Small Unmanned Aerial Vehicles. Unmanned Syst. 2023, 11, 249–260. [Google Scholar] [CrossRef]
- Emami, S.; Banazadeh, A. Fault-tolerant predictive trajectory tracking of an air vehicle based on acceleration control. IET Control Theory Appl. 2020, 14, 750–762. [Google Scholar] [CrossRef]
- Hu, X.; Zong, G.; Deng, X.; Wang, W. Model predictive control-based non-linear fault-tolerant control for air-breathing hypersonic vehicles. IET Control Theory Appl. 2014, 8, 1147–1153. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, G.; Dong, Q. Fixed-time disturbance observer-based nearly optimal control for reusable launch vehicle with input constraints. ISA Trans. 2022, 122, 182–197. [Google Scholar] [CrossRef]
- Almutairi, S.H.; Aouf, N. Fault-tolerant flight control design against actuator impairments using optimal control and fault compensation. In Proceedings of the 11th IEEE International Conference on Control & Automation (ICCA), Taichung, Taiwan, 18–20 June 2014. [Google Scholar]
- Zhang, Y.; Tang, S.; Guo, J. Adaptive-gain fast super-twisting sliding mode fault-tolerant control for a reusable launch vehicle in reentry phase. ISA Trans. 2017, 71, 380–390. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zhang, Y.; Zhang, B.; Peng, Y. Fixed-time observer-based fault-tolerant attitude control for reusable launch vehicle with actuator faults. Aerosp. Sci. Technol. 2020, 107, 106314. [Google Scholar] [CrossRef]
- Mahboub, M.A.; Rouabah, B.; Kafi, M.R.; Toubakh, H. Health management using fault detection and fault-tolerant control of multicellular converter applied in more electric aircraft system. Diagnostyka 2022, 23, 2. [Google Scholar] [CrossRef]
- Ma, X.; Liu, S.; Cheng, H. Civil aircraft fault-tolerant attitude tracking based on extended state observers and nonlinear dynamic inversion. J. Syst. Eng. Electron. 2022, 33, 180–187. [Google Scholar] [CrossRef]
- Meng, Y.; Jiang, B.; Qi, R. Adaptive fault-tolerant attitude tracking control of hypersonic vehicle subject to unexpected centroid-shift and state constraints. Aerosp. Sci. Technol. 2019, 95, 105515. [Google Scholar] [CrossRef]
- Saied, M.; Belkacem, A.; Khenfouch, M. BFA fuzzy logic-based control allocation for fault-tolerant control of multirotor UAVs. Aeronaut. J. 2019, 123, 1356–1373. [Google Scholar] [CrossRef]
- Long, H.; Wang, Z.; Guo, L.; Li, J. Fixed-time adaptive fuzzy fault-tolerant control of flapping wing MAVs with wing damage. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 6594–6607. [Google Scholar] [CrossRef]
- Zhang, C.; Luo, H.; Li, J.; Wang, Z. Neural-networks and event-based fault-tolerant control for spacecraft attitude stabilization. Aerosp. Sci. Technol. 2021, 114, 106746. [Google Scholar] [CrossRef]
- Lombaerts, T.; Ankersen, F.; Mulder, T.; Voskuijl, M. Dynamic inversion based full envelope flight control for an eVTOL vehicle using a unified framework. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Dong, Z.; Liu, K.; Wang, S. Sliding mode disturbance observer-based adaptive dynamic inversion fault-tolerant control for fixed-wing UAV. Drones 2022, 6, 295. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, J.; Ma, H.; Dai, G.; Tong, S. Research on fault-tolerant control of combined airframe damage of electric aircraft. Aerospace 2023, 10, 611. [Google Scholar] [CrossRef]
- Jiang, F.; Liu, X.; Chen, T.; Li, K. Research on an Ice Tolerance Control Method for Large Aircraft Based on Adaptive Dynamic Inversion. Actuators 2024, 227. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, X.; Tian, Y. Robust adaptive fault-tolerant control using RBF-based neural network for a rigid-flexible robotic system with unknown control direction. Int. J. Robust Nonlinear Control 2022, 32, 1272–1302. [Google Scholar] [CrossRef]
- Hou, Z.; Lan, X. Adaptive sliding mode and RBF neural network-based fault-tolerant attitude control for spacecraft with unknown uncertainties and disturbances. Adv. Space Res. 2024, 74, 1680–1692. [Google Scholar] [CrossRef]
- Ding, S.; Zhai, Q.; Liu, J.; Ma, J.; Qiu, Y. Disturbance observer design for nonlinear systems represented by input–output models. IEEE Trans. Ind. Electron. 2019, 67, 1222–1232. [Google Scholar] [CrossRef]
- He, Q.; Zhao, J.; Hu, X.; Wang, G.; Yan, J. Reconfigurable nonlinear dynamic inversion for attitude control of a structurally damaged aircraft. IEEE Access 2020, 8, 199931–199943. [Google Scholar] [CrossRef]
- Xue, Y.X.; Yan, L.; Sun, X.; Ma, D. Adaptive fault-tolerant control for carrier-based UAV with actuator failures. Aerosp. Sci. Technol. 2020, 107, 106227. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, H.; Guo, H. 1 adaptive output-feedback fault-tolerant control for uncertain nonlinear systems subject to unmodeled actuator dynamics and faults. Trans. Inst. Meas. Control 2022, 44, 2177–2192. [Google Scholar] [CrossRef]
- Iglesis, E.; Horri, N.; Brusey, J.; Dahia, K.; Piet-Lahanier, H. Simultaneous actuator and sensor faults estimation for aircraft using a jump-Markov regularized particle filter. In Proceedings of the 2021 IEEE International Conference on Prognostics and Health Management (ICPHM), Detroit (Romulus), MI, USA, 7–9 June 2021. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Cecilia, A. Advances in Nonlinear Observer Design for State and Parameter Estimation in Energy Systems; Springer Nature: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Snell, S.A. Nonlinear Dynamic-Inversion Flight Control of Supermaneuverable Aircraft; University of Minnesota: Minneapolis, MN, USA, 1991. [Google Scholar]
- Safwat, E.; Farag, M.; El-Bardini, M.; Bayoumi, A. Robustness analysis of modified incremental nonlinear dynamic inversion for small UAVs. Autom. Control. Comput. Sci. 2020, 54, 128–138. [Google Scholar] [CrossRef]
- Lavretsky, E.; Wise, K.A. Robust and Adaptive Control with Aerospace Applications; Springer: London, UK, 2013. [Google Scholar]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Souanef, T. Multiple model l 1 adaptive fault-tolerant control of small unmanned aerial vehicles. J. Aerosp. Eng. 2024, 37, 04023103. [Google Scholar] [CrossRef]




| Coefficient | Value | Coefficient | Value |
|---|---|---|---|
| 0.28 | 0 | ||
| 0.03 | −0.98 | ||
| −0.02338 | −0.12 | ||
| 3.45 | 0.25 | ||
| 0.30 | 0 | ||
| −0.38 | −0.26 | ||
| 0 | 0.022 | ||
| 0 | 0 | ||
| −3.6 | 0.14 | ||
| −0.36 | −0.35 | ||
| 0 | 0 | ||
| −0.5 | 0.08 | ||
| −0.032 | 0.06 | ||
| 0 | −0.17 | ||
| 0 | 0.105 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | b | ||
| S |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bekhiti, A.; Souanef, T.; Toubakh, H.; Horri, N.; Kafi, M.R.; Bouzid, Z. Adaptive UAV Control with Sensor and Actuator Faults Recovery. Aerospace 2025, 12, 261. https://doi.org/10.3390/aerospace12030261
Bekhiti A, Souanef T, Toubakh H, Horri N, Kafi MR, Bouzid Z. Adaptive UAV Control with Sensor and Actuator Faults Recovery. Aerospace. 2025; 12(3):261. https://doi.org/10.3390/aerospace12030261
Chicago/Turabian StyleBekhiti, Abdellah, Toufik Souanef, Houari Toubakh, Nadjim Horri, Mohamed Redouane Kafi, and Zakaria Bouzid. 2025. "Adaptive UAV Control with Sensor and Actuator Faults Recovery" Aerospace 12, no. 3: 261. https://doi.org/10.3390/aerospace12030261
APA StyleBekhiti, A., Souanef, T., Toubakh, H., Horri, N., Kafi, M. R., & Bouzid, Z. (2025). Adaptive UAV Control with Sensor and Actuator Faults Recovery. Aerospace, 12(3), 261. https://doi.org/10.3390/aerospace12030261









