Adaptive Incremental Nonlinear Dynamic Inversion Control with Guaranteed Stability for Aerial Manipulators
Abstract
1. Introduction
2. INDI for UAMs
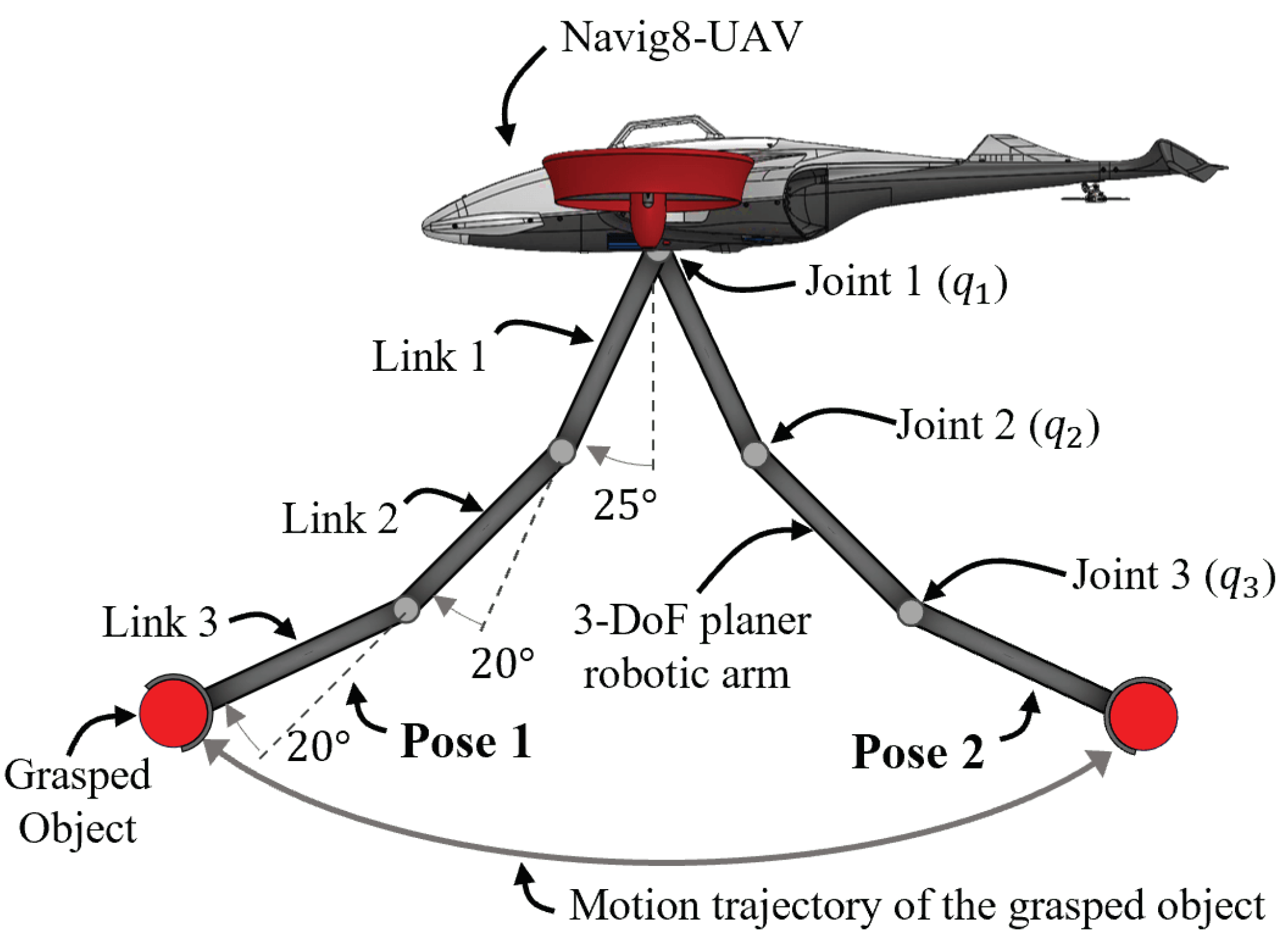
2.1. Navig8-UAM System
2.2. INDI for UAMs
2.3. Stability Criterion for INDI
3. Adaptive INDI with Guaranteed Stability
3.1. Stability Analysis of the Proposed INDI for the Navig8-UAM
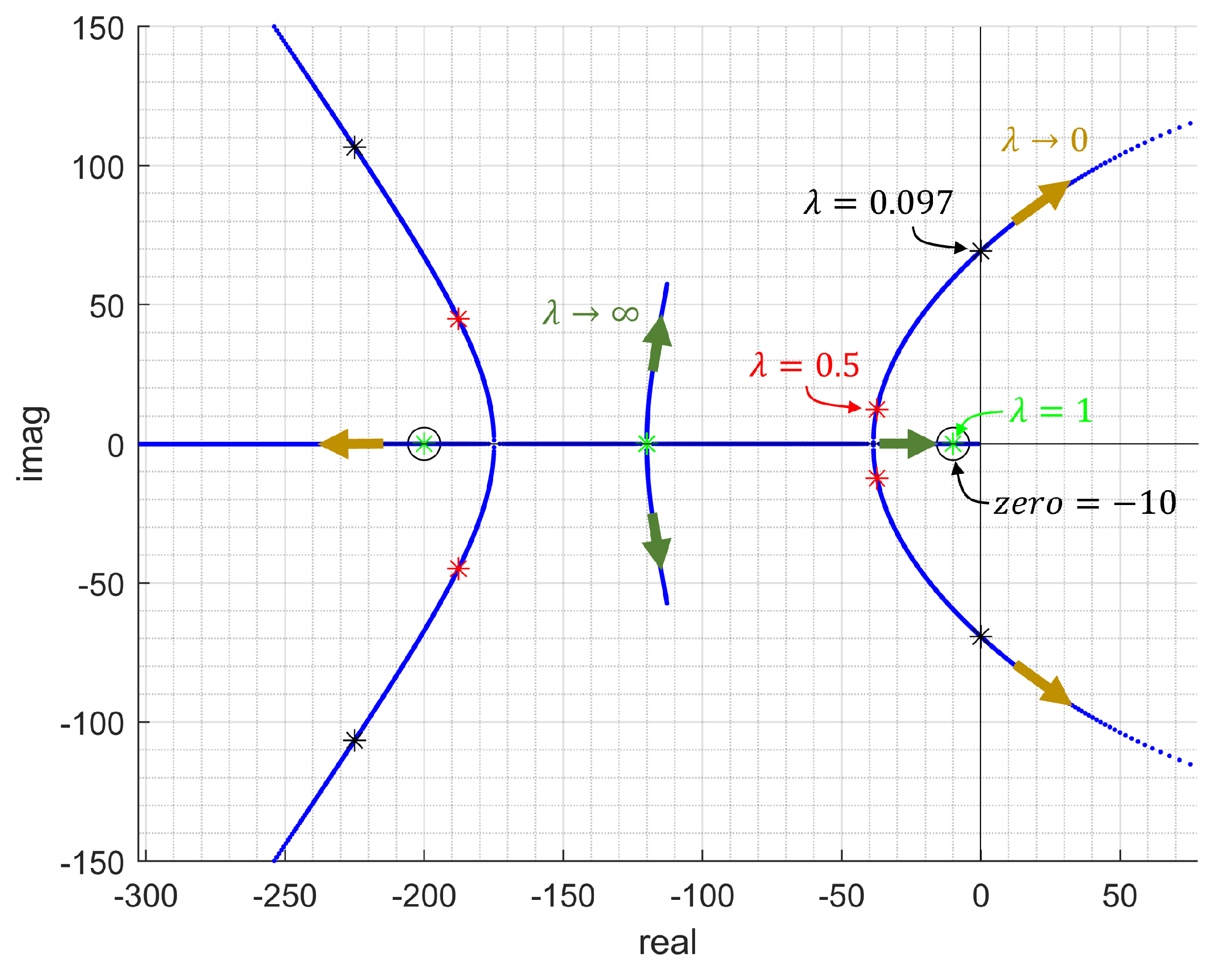
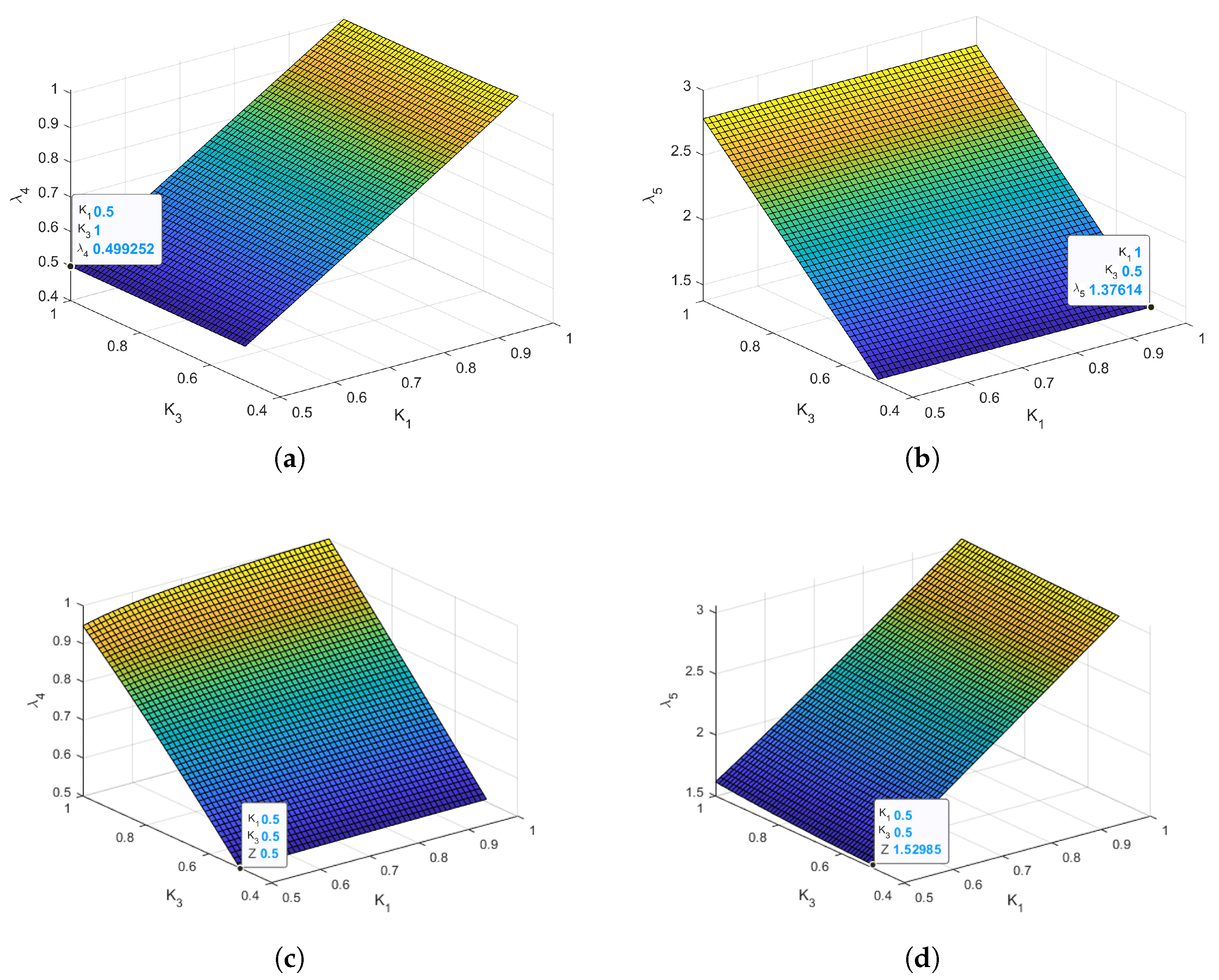
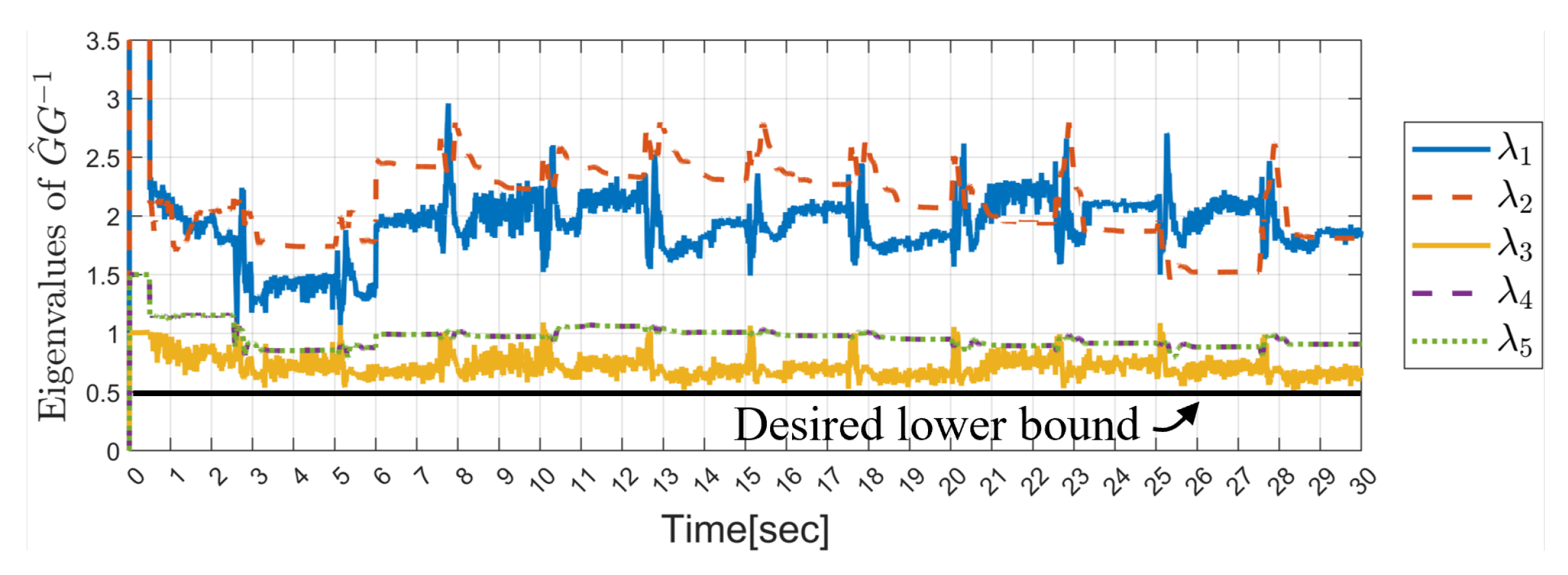
3.2. Bounds on K to Ensure Stability with Control Performance Considerations
3.3. Constrained Kalman Filter
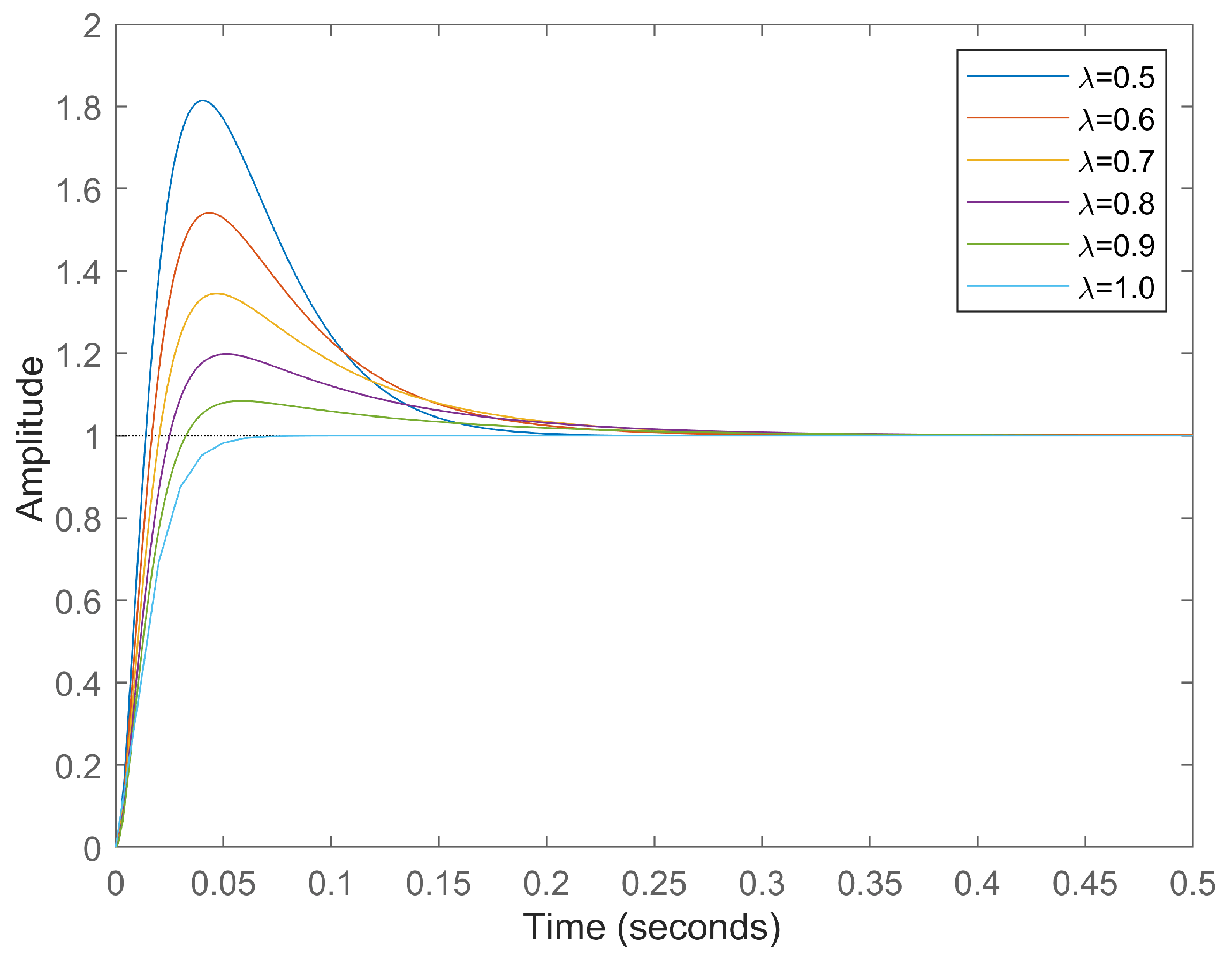
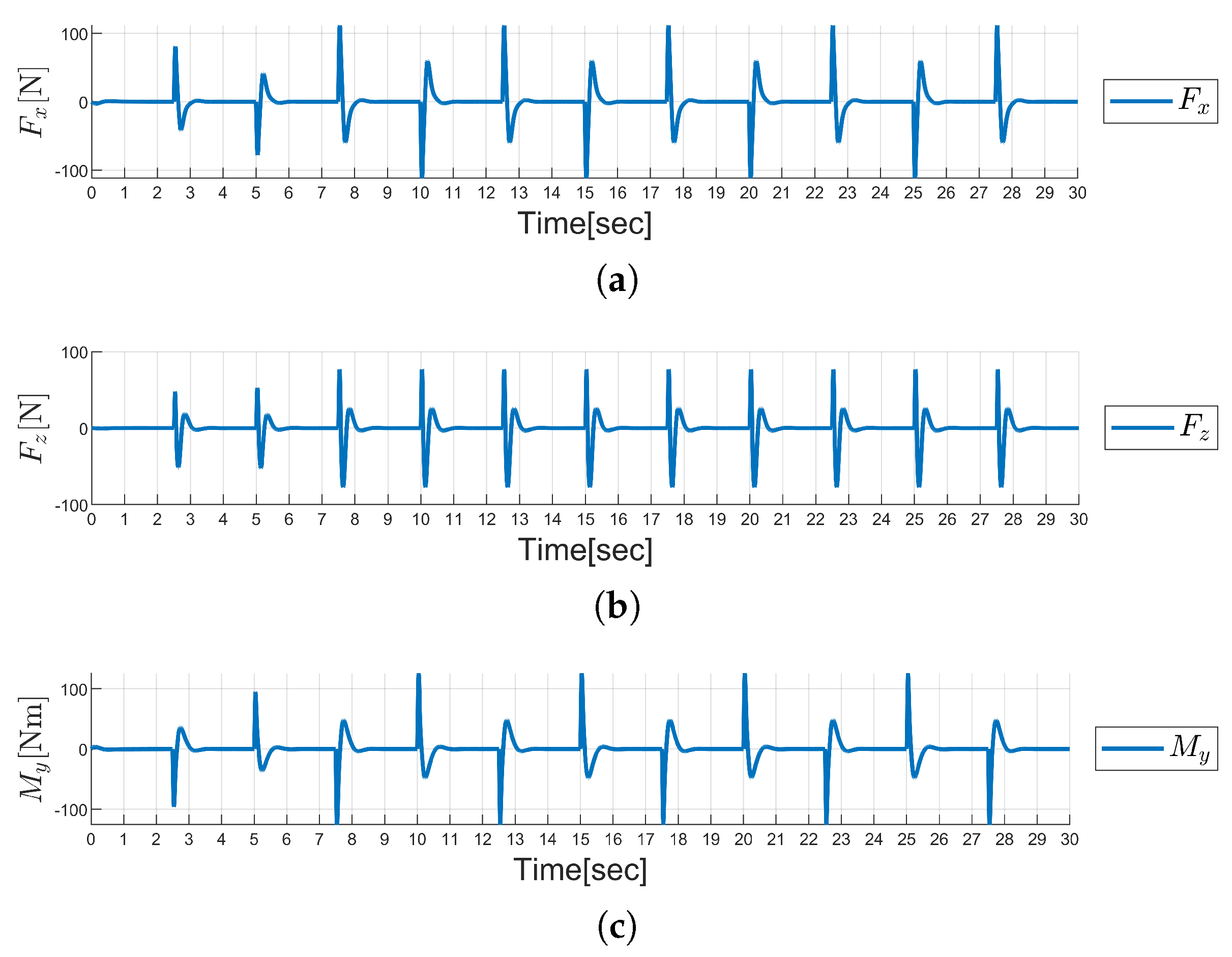
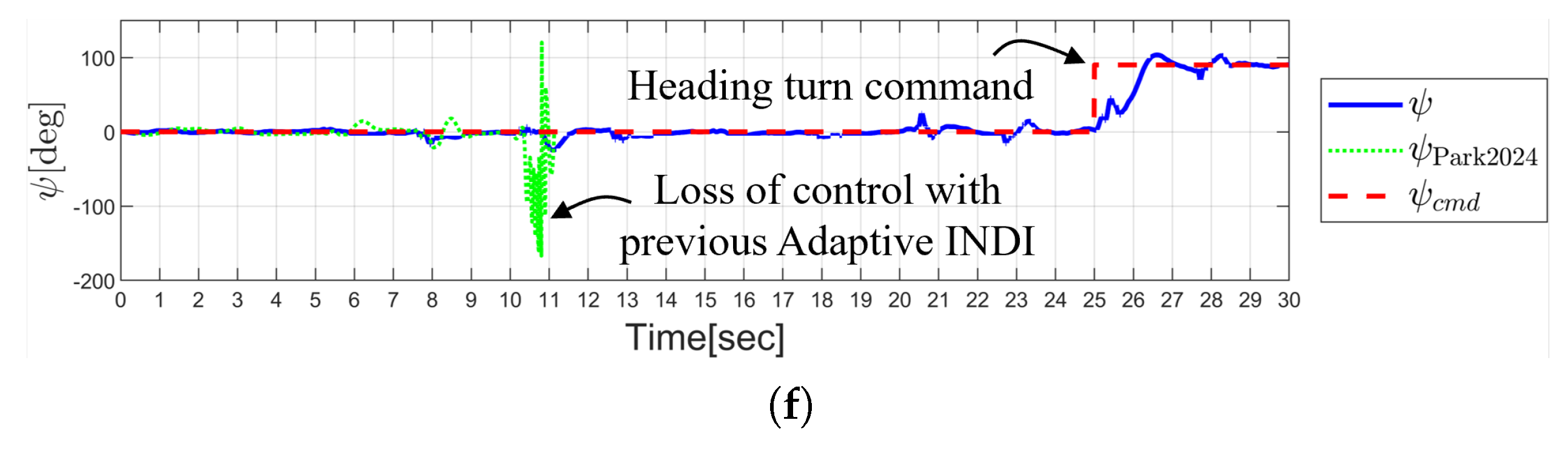
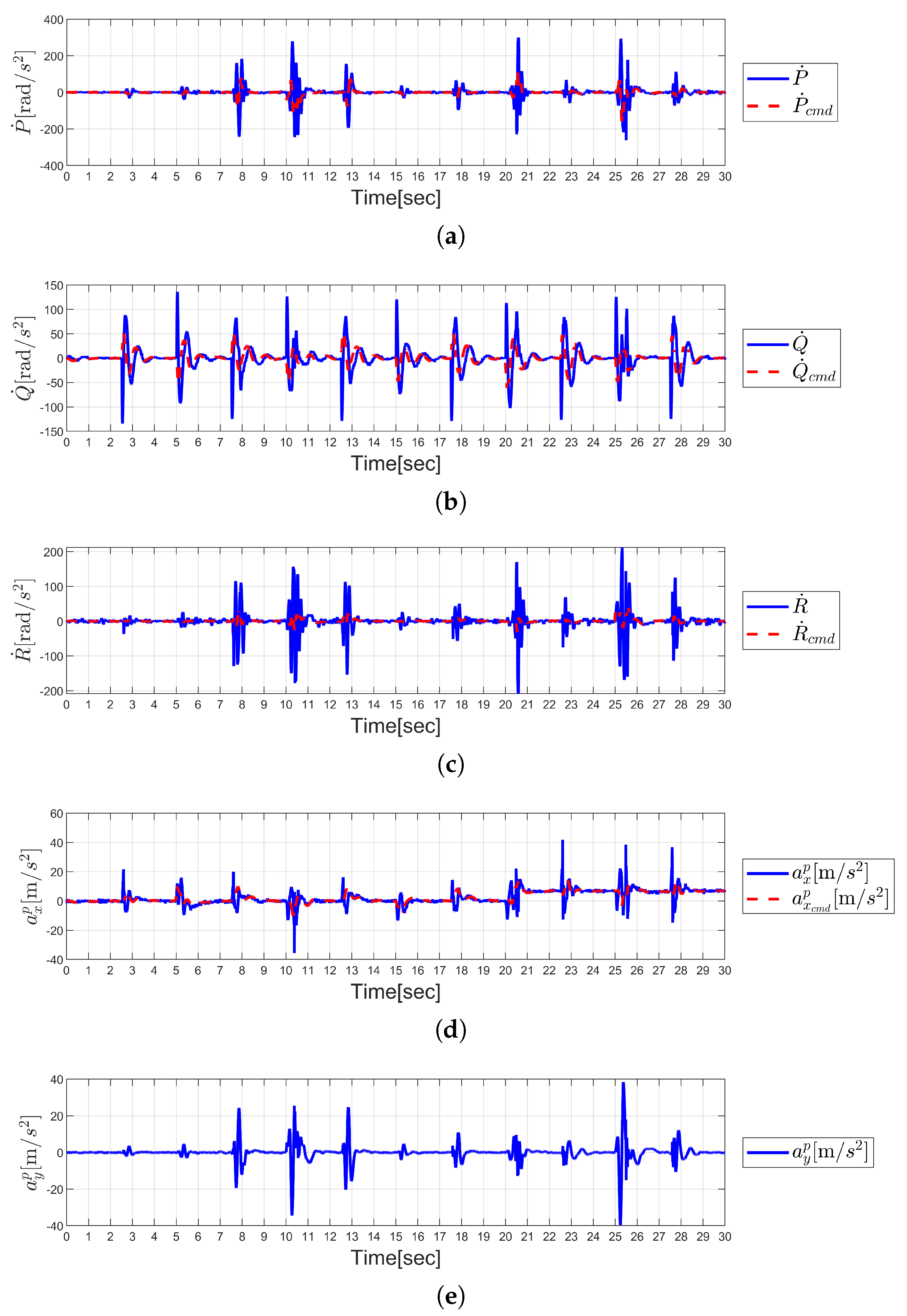
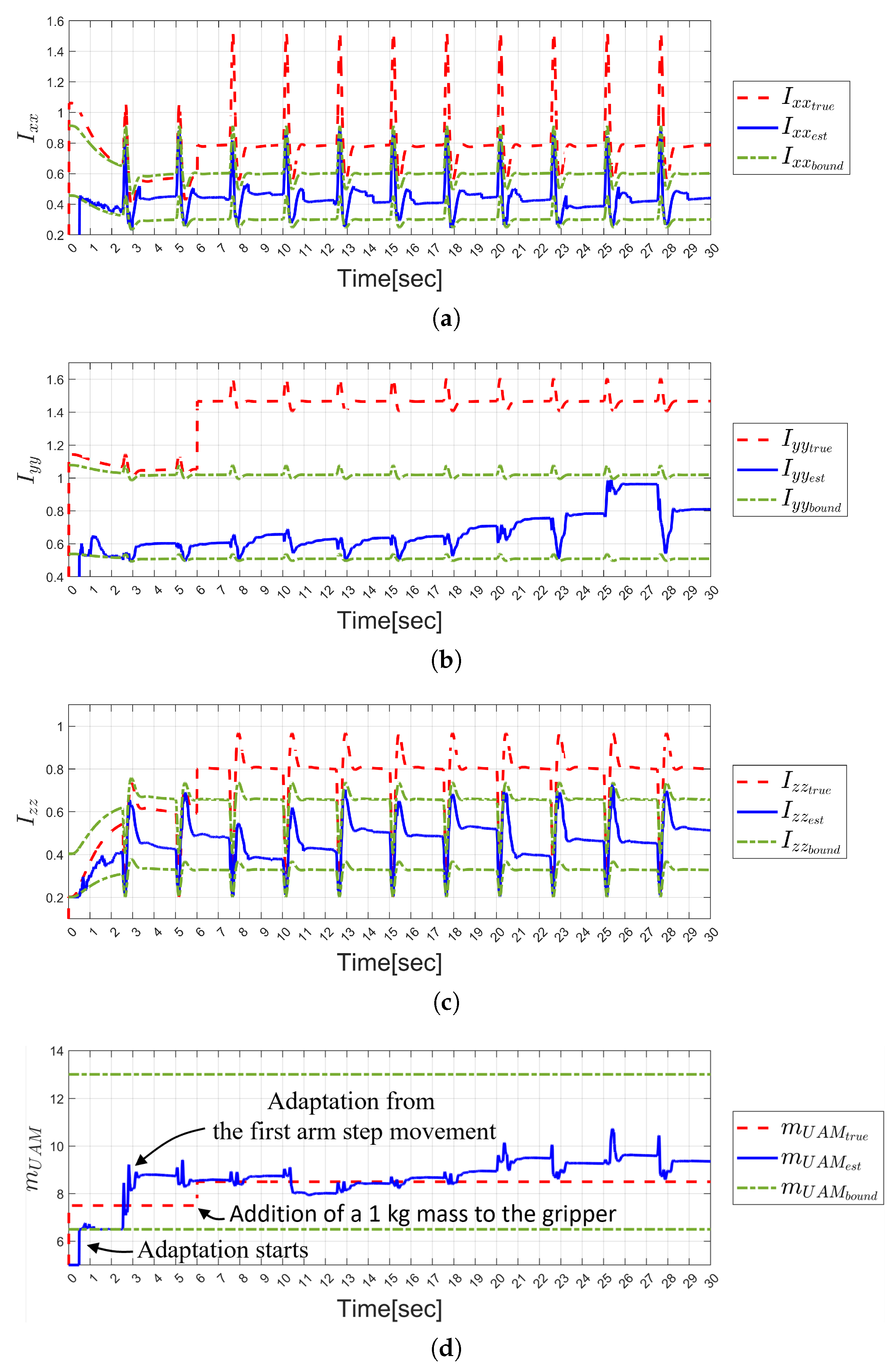
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Konert, A.; Balcerzak, T. Military autonomous drones (UAVs)-from fantasy to reality. Legal and Ethical implications. Transp. Res. Procedia 2021, 59, 292–299. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A Survey on Civil Applications and Key Research Challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Craig, J.J.; Hsu, P.; Sastry, S.S. Adaptive control of mechanical manipulators. Int. J. Robot. Res. 1987, 6, 16–28. [Google Scholar]
- Wang, C.; Nahon, M.; Trentini, M. Controller development and validation for a small quadrotor with compensation for model variation. In Proceedings of the 2014 International Conference on Unmanned Aircraft Systems (ICUAS), Orlando, FL, USA, 27–30 May 2014; pp. 902–909. [Google Scholar] [CrossRef]
- Wang, C.; Song, B.; Huang, P.; Tang, C. Trajectory tracking control for quadrotor robot subject to payload variation and wind gust disturbance. J. Intell. Robot. Syst. 2016, 83, 315–333. [Google Scholar] [CrossRef]
- Baraban, G.; Sheckells, M.; Kim, S.; Kobilarov, M. Adaptive parameter estimation for aerial manipulation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 614–619. [Google Scholar] [CrossRef]
- Lee, H.; Kim, H.J. Estimation, control, and planning for autonomous aerial transportation. IEEE Trans. Ind. Electron. 2016, 64, 3369–3379. [Google Scholar] [CrossRef]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Estimation of Time-Varying Inertia of Aerial Manipulators Performing Manipulation of Unknown Objects. In Proceedings of the 10th International Conference of Control Systems, and Robotics (CDSR’23), Ottawa, ON, Canada, 1–3 June 2023; p. 209. [Google Scholar] [CrossRef]
- Enns, D.; Bugajski, D.; Hendrick, R.; Stein, G. Dynamic inversion: An evolving methodology for flight control design. Int. J. Control 1994, 59, 71–91. [Google Scholar] [CrossRef]
- Lombaerts, T.; Chu, P.; Mulder, J.A.; Joosten, D. Flight Control Reconfiguration based on a Modular Approach. IFAC Proc. Vol. 2009, 42, 259–264. [Google Scholar] [CrossRef]
- Simplício, P.; Pavel, M.; VanKampen, E.; Chu, Q. An acceleration measurements-based approach for helicopter nonlinear flight control using incremental nonlinear dynamic inversion. Control Eng. Pract. 2013, 21, 1065–1077. [Google Scholar] [CrossRef]
- Sun, S.; Romero, A.; Foehn, P.; Kaufmann, E.; Scaramuzza, D. A comparative study of nonlinear mpc and differential-flatness-based control for quadrotor agile flight. IEEE Trans. Robot. 2022, 38, 3357–3373. [Google Scholar] [CrossRef]
- Tal, E.; Karaman, S. Accurate tracking of aggressive quadrotor trajectories using incremental nonlinear dynamic inversion and differential flatness. IEEE Trans. Control Syst. Technol. 2020, 29, 1203–1218. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Z.; Zhao, J.; Wang, Z.; Ding, Y.; Wang, Y. INDI-based aggressive quadrotor flight control with position and attitude constraints. Robot. Auton. Syst. 2023, 159, 104292. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, J.; Yang, J. INDI-based transitional flight control and stability analysis of a tail-sitter UAV. In Proceedings of the 2020 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Toronto, ON, Canada, 11–14 October 2020; pp. 1420–1426. [Google Scholar] [CrossRef]
- Smeur, E.J.; de Croon, G.C.; Chu, Q. Cascaded incremental nonlinear dynamic inversion for MAV disturbance rejection. Control Eng. Pract. 2018, 73, 79–90. [Google Scholar] [CrossRef]
- Kim, H.J.; Lombaerts, T.; Looye, G. Design and Evaluation of Nonlinear Inversion Based Automated Landing Control for an Airliner in a High Crosswind Scenario. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 0079. [Google Scholar]
- Smeur, E.J.; Chu, Q.; DeCroon, G.C. Adaptive incremental nonlinear dynamic inversion for attitude control of micro air vehicles. J. Guid. Control Dyn. 2016, 39, 450–461. [Google Scholar] [CrossRef]
- Cao, S.; Shen, L.; Zhang, R.; Yu, H.; Wang, X. Adaptive Incremental Nonlinear Dynamic Inversion Control Based on Neural Network for UAV Maneuver. In Proceedings of the 2019 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Hong Kong, China, 8–12 July 2019; pp. 642–647. [Google Scholar] [CrossRef]
- Ahmadi, K.; Asadi, D.; Nabavi-Chashmi, S.-Y.; Tutsoy, O. Modified adaptive discrete-time incremental nonlinear dynamic inversion control for quad-rotors in the presence of motor faults. Mech. Syst. Signal Process. 2023, 188, 109989. [Google Scholar] [CrossRef]
- Atmaca, D.; Van Kampen, E.-J. Fault Tolerant Control for the Flying-V Using Adaptive Incremental Nonlinear Dynamic Inversion. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 0081. [Google Scholar]
- van’t Veld, R.; Van Kampen, E.-J.; Chu, Q.P. Stability and robustness analysis and improvements for incremental nonlinear dynamic inversion control. In Proceedings of the 2018 AIAA Guidance, Navigation,and Control Conference, Kissimmee, FL, USA, 8–12 January 2018; p. 1127. [Google Scholar] [CrossRef]
- Wang, X.; Kampen, E.-J.v.; Chu, Q.; Lu, P. Incremental sliding-mode fault-tolerant flight control. J. Guid. Control Dyn. 2019, 42, 244–259. [Google Scholar] [CrossRef]
- Wang, X.; VanKampen, E.-J.; Chu, Q.; Lu, P. Stability analysis for incremental nonlinear dynamic inversion control. J. Guid. Control Dyn. 2019, 42, 1116–1129. [Google Scholar] [CrossRef]
- Chang, J.; DeBreuker, R.; Wang, X. Discrete-time design and stability analysis for nonlinear incremental fault-tolerant flight control. In Proceedings of the AIAA SciTech 2022 Forum, San Diego, CA, USA and Virtual, 3–7 January 2022; p. 2034. [Google Scholar]
- Chang, J.; DeBreuker, R.; Wang, X. Adaptive nonlinear incremental flight control for systems with unknown control effectiveness. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 228–240. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Pool, D.M.; Stroosma, O.; Chu, Q. Time-delay margin and robustness of incremental nonlinear dynamic inversion control. J. Guid. Control. Dyn. 2022, 45, 394–404. [Google Scholar] [CrossRef]
- Taherinezhad, M.; Ramirez-Serrano, A. An Enhanced Incremental Nonlinear Dynamic Inversion Control Strategy for Advanced Unmanned Aircraft Systems. Aerospace 2023, 10, 843. [Google Scholar] [CrossRef]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Adaptive Incremental Nonlinear Dynamic Inversion Control for Aerial Manipulators. Aerospace 2024, 11, 671. [Google Scholar] [CrossRef]
- Park, C.; Ramirez-Serrano, A.; Bisheban, M. Advanced Adaptive INDI for UAMs. In Proceedings of the 2025 AIAA Scitech, AIAA, Orlando, FL, USA, 6–10 January 2025; pp. 4916–4921. [Google Scholar] [CrossRef]
- Jansen, F.; Ramirez-Serrano, A. Agile unmanned vehicle navigation in highly confined environments. In Proceedings of the 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AK, USA, 9–12 October 2011; pp. 2381–2386. [Google Scholar] [CrossRef]
- Amiri, N.; Ramirez-Serrano, A.; Davies, R.J. Integral backstepping control of an unconventional dual-fan unmanned aerial vehicle. J. Intell. Robot. Syst. 2013, 69, 147–159. [Google Scholar] [CrossRef]
- Majnoon, M.; Samsami, K.; Mehrandezh, M.; Ramirez-Serrano, A. Mobile-Target Tracking via Highly-Maneuverable VTOL UAVs with EO Vision. In Proceedings of the 2016 13th Conference on Computer and Robot Vision (CRV), Victoria, BC, Canada, 1–3 June 2016; pp. 260–265. [Google Scholar] [CrossRef]
- Yavari, M.; Gupta, K.; Mehrandezh, M.; Ramirez-Serrano, A. Optimal real-time trajectory control of a pitch-hover UAV with a two link manipulator. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 930–938. [Google Scholar] [CrossRef]
- Sieberling, S.; Chu, Q.P.; Mulder, J.A. Robust Flight Control Using Incremental Nonlinear Dynamic Inversion and Angular Acceleration Prediction. J. Guid. Control Dyn. 2010, 33, 1732–1742. [Google Scholar] [CrossRef]
- Prussing, J.E. The principal minor test for semidefinite matrices. J. Guid. Control. Dyn. 1986, 9, 121–122. [Google Scholar] [CrossRef]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Keesman, K.J.; Keesman, K.J. Time-varying Dynamic Systems Identification. In System Identification: An Introduction; Springer: London, UK, 2011; pp. 195–221. [Google Scholar] [CrossRef]
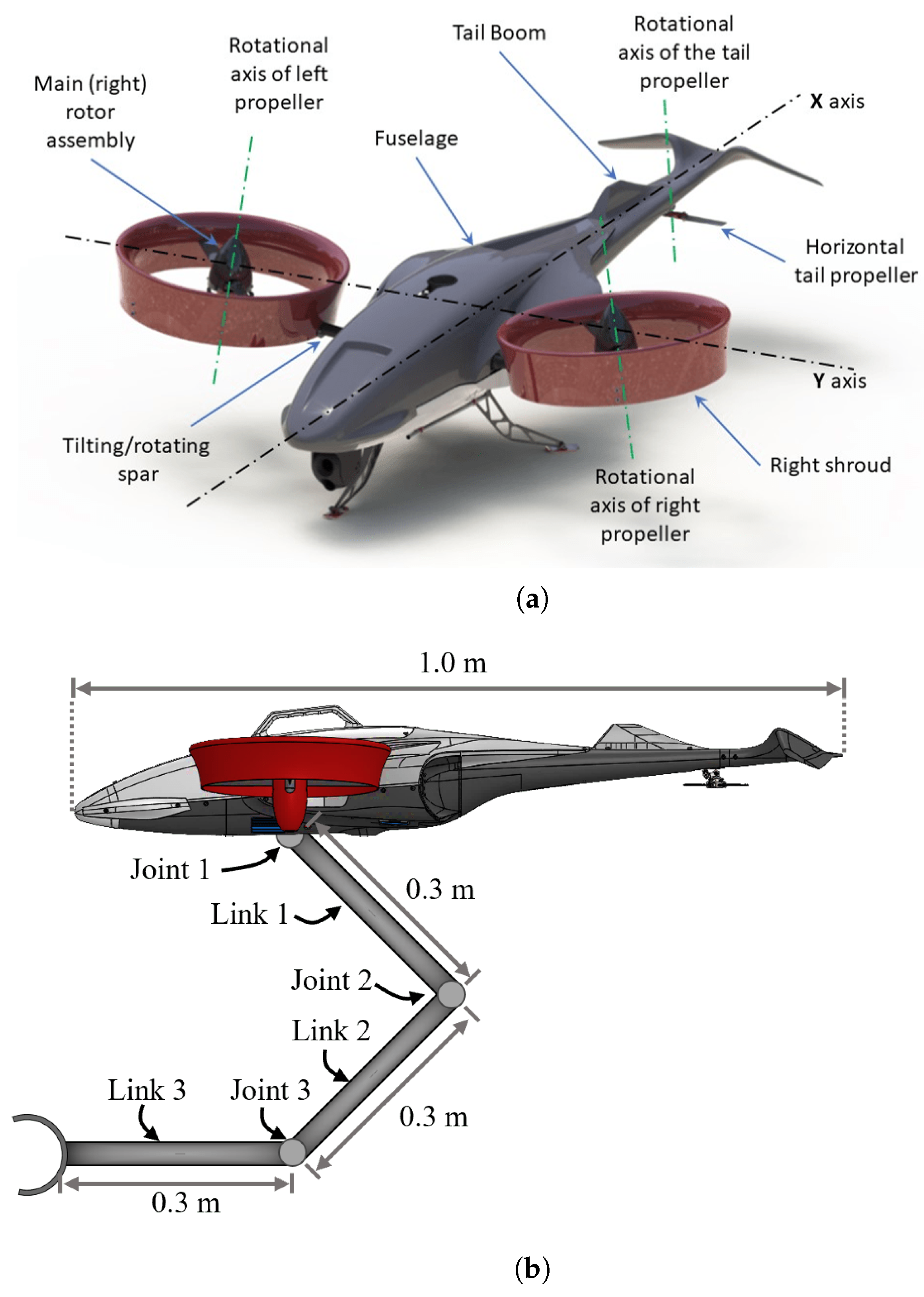
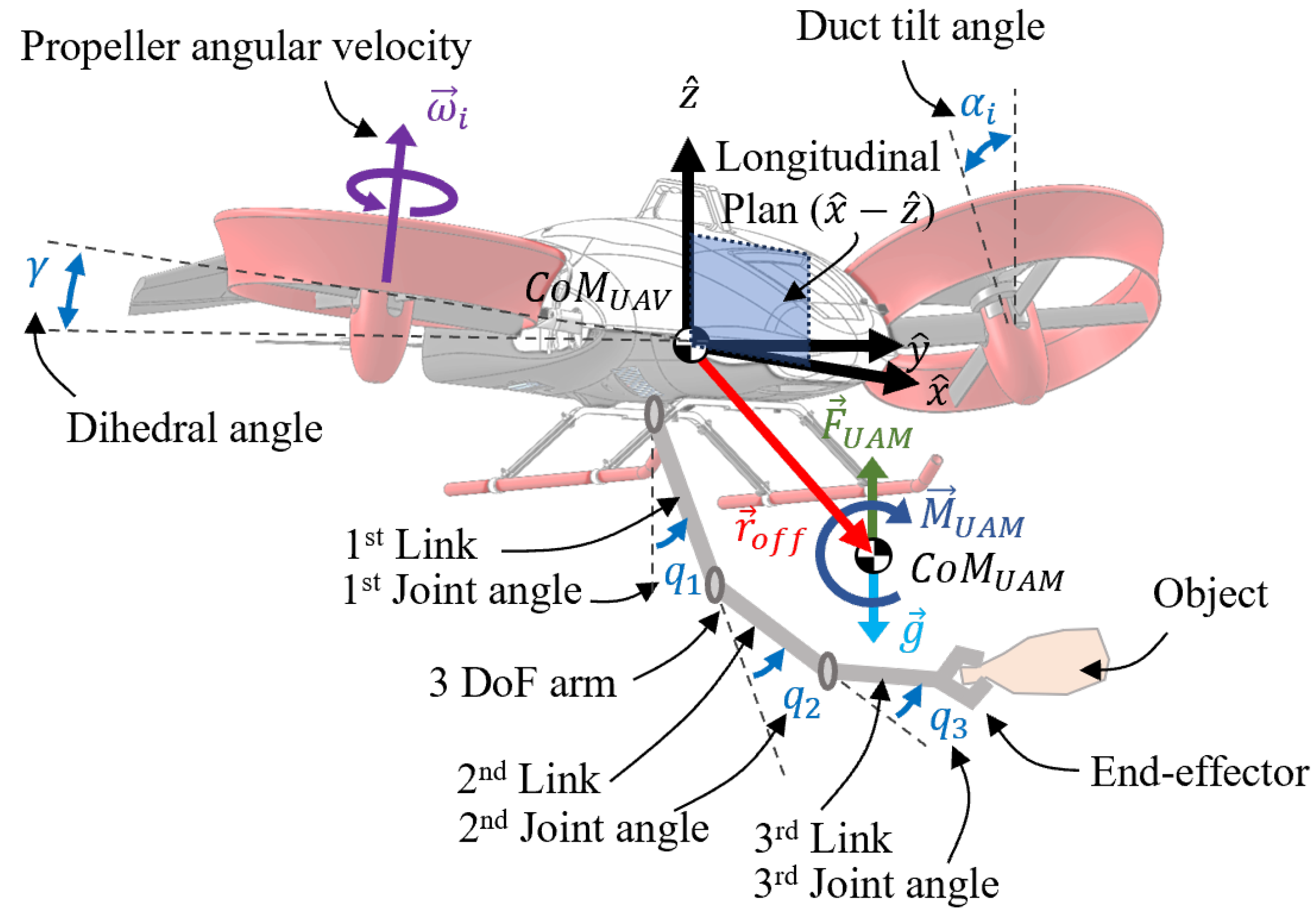







| Size [m] | Mass [kg] | [] | [] | [] | [] | [] | [] | |
|---|---|---|---|---|---|---|---|---|
| Navig8-UAV | Length: 1.0 Width: 0.8 Height: 0.2 | 5.0 | 0.0667 | 0.1492 | 0.2019 | 0.0147 | 0 | 0 |
| Each arm linkage | Length: 0.3 | 0.5 | 0.0037 | 0.0037 | 0 | 0 | 0 | 0 |
| Object (Sphere) | Radius: 0.05 | 1→2 | 0.001 | 0.001 | 0.001 | 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, C.; Ramirez-Serrano, A.; Bisheban, M. Adaptive Incremental Nonlinear Dynamic Inversion Control with Guaranteed Stability for Aerial Manipulators. Aerospace 2025, 12, 312. https://doi.org/10.3390/aerospace12040312
Park C, Ramirez-Serrano A, Bisheban M. Adaptive Incremental Nonlinear Dynamic Inversion Control with Guaranteed Stability for Aerial Manipulators. Aerospace. 2025; 12(4):312. https://doi.org/10.3390/aerospace12040312
Chicago/Turabian StylePark, Chanhong, Alex Ramirez-Serrano, and Mahdis Bisheban. 2025. "Adaptive Incremental Nonlinear Dynamic Inversion Control with Guaranteed Stability for Aerial Manipulators" Aerospace 12, no. 4: 312. https://doi.org/10.3390/aerospace12040312
APA StylePark, C., Ramirez-Serrano, A., & Bisheban, M. (2025). Adaptive Incremental Nonlinear Dynamic Inversion Control with Guaranteed Stability for Aerial Manipulators. Aerospace, 12(4), 312. https://doi.org/10.3390/aerospace12040312







