Formation Flight of Fixed-Wing UAVs: Dynamic Modeling, Guidance Design, and Testing in Realistic Scenarios
Abstract
1. Introduction
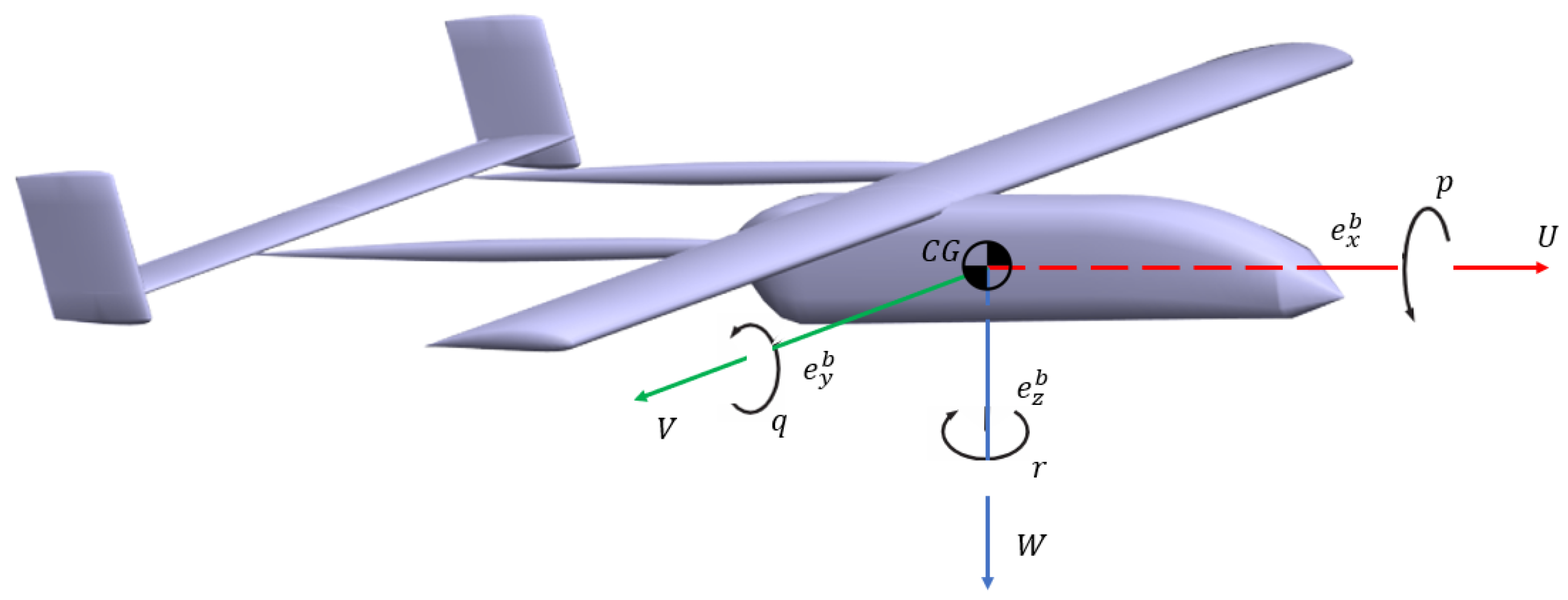
2. Flight Dynamics Model
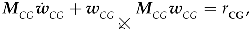
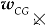 represents the generalized velocity vector with the southwest cross product operator applied. This operator rearranges the sub-vectors and in a six-by-six matrix, filling it with their skew-symmetric forms, i.e., and , as the three-by-three antisymmetric matrices composed of their respective sub-vector components. More explicitly,
represents the generalized velocity vector with the southwest cross product operator applied. This operator rearranges the sub-vectors and in a six-by-six matrix, filling it with their skew-symmetric forms, i.e., and , as the three-by-three antisymmetric matrices composed of their respective sub-vector components. More explicitly,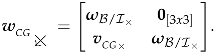

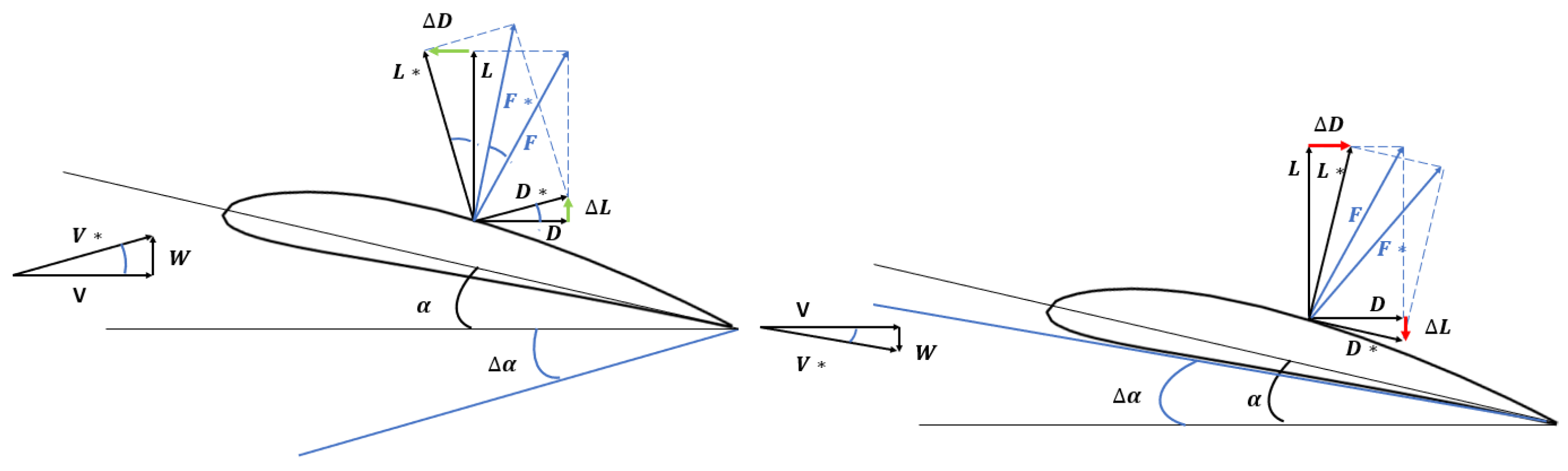
3. Aerodynamic Modeling
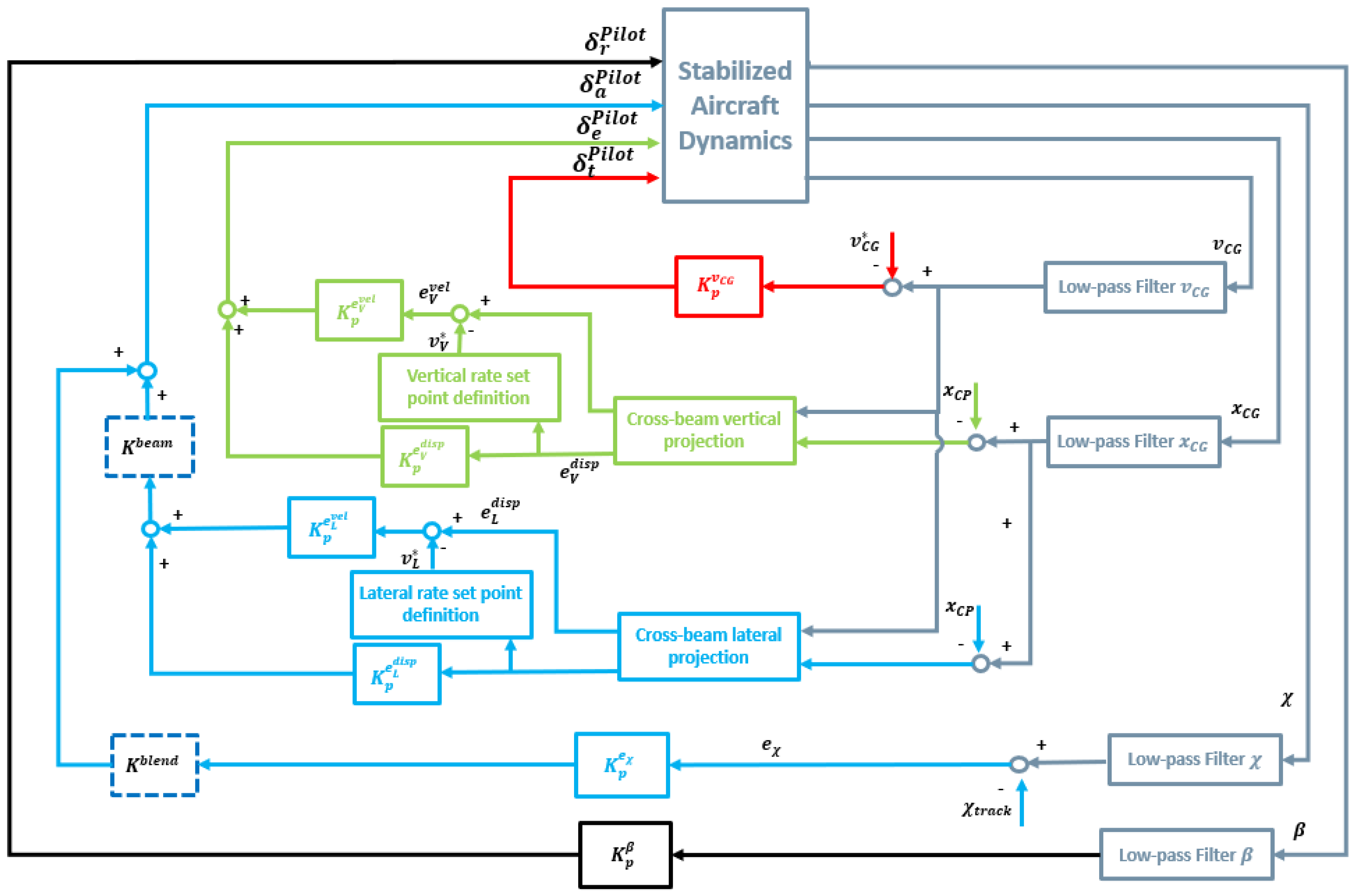
4. Formation Guidance and Coordination in Different Mission Phases
4.1. Guidance Mode (GM)
- Beam tracking navigation. Employed during the cruise phase or linear ground reconnaissance. Described in Section 4.1.1 and Section 4.1.2.
- Circular trajectory tracking. Availed of during loitering or orbital reconnaissance around a fixed target. Described in Section 4.1.3.
- Rendezvous guidance. Implementing a specific control to reduce the space and time required for in-flight formation assembly. Described in Section 4.1.4.
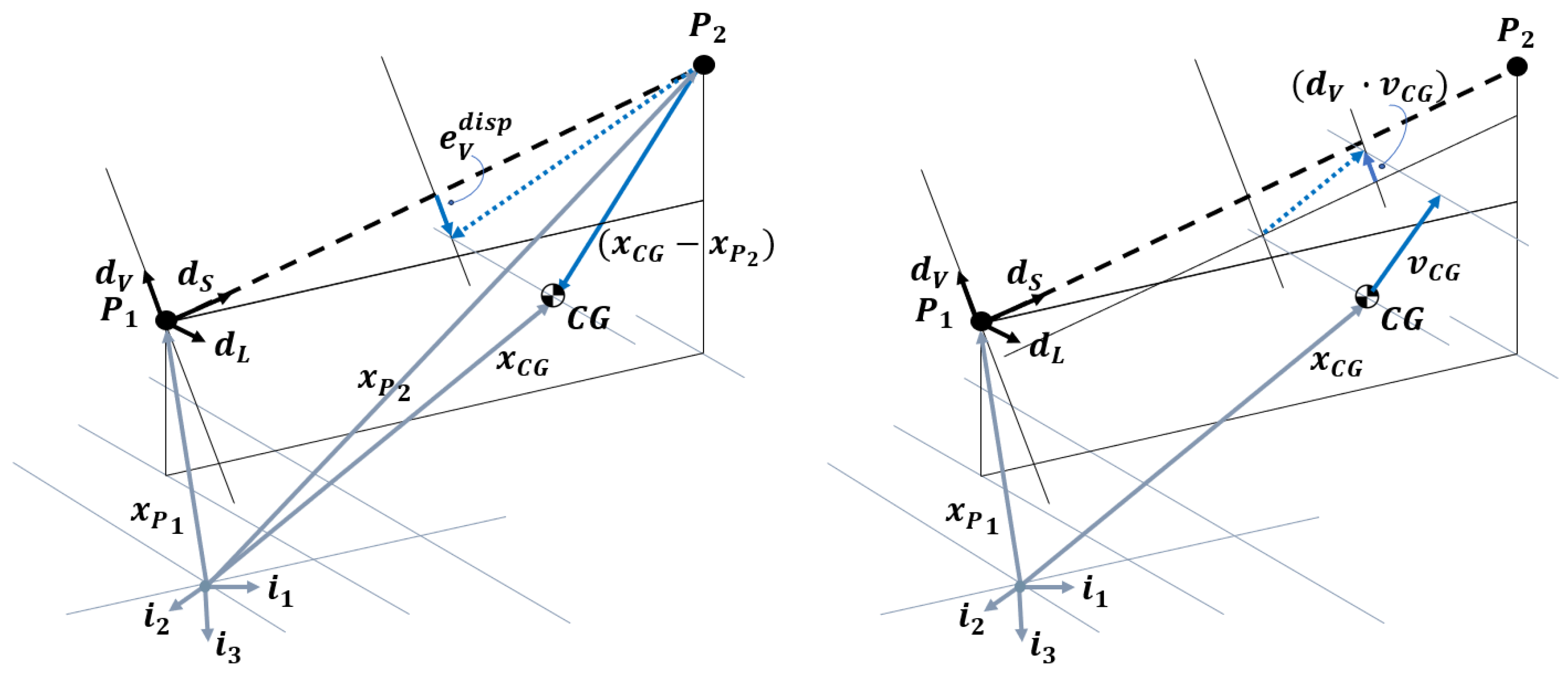
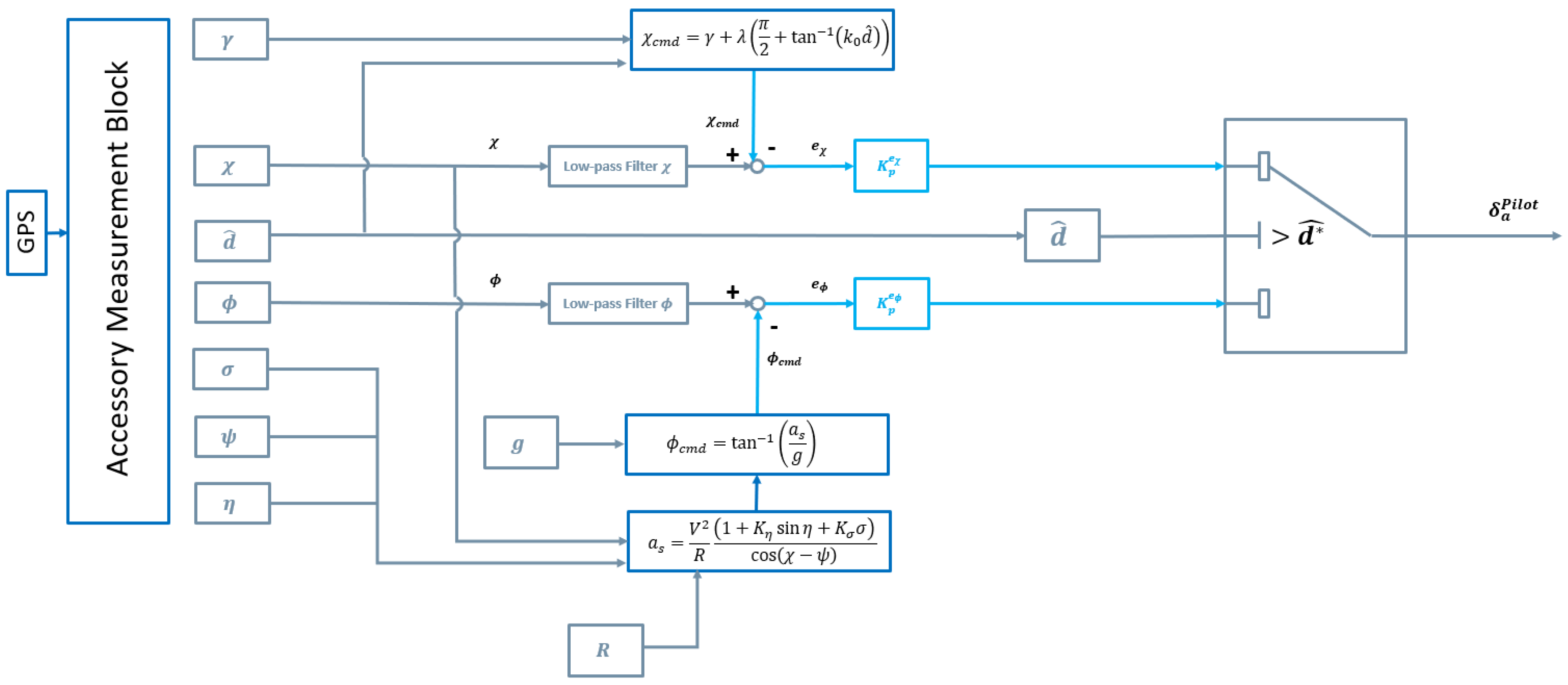
4.1.1. Beam Tracking
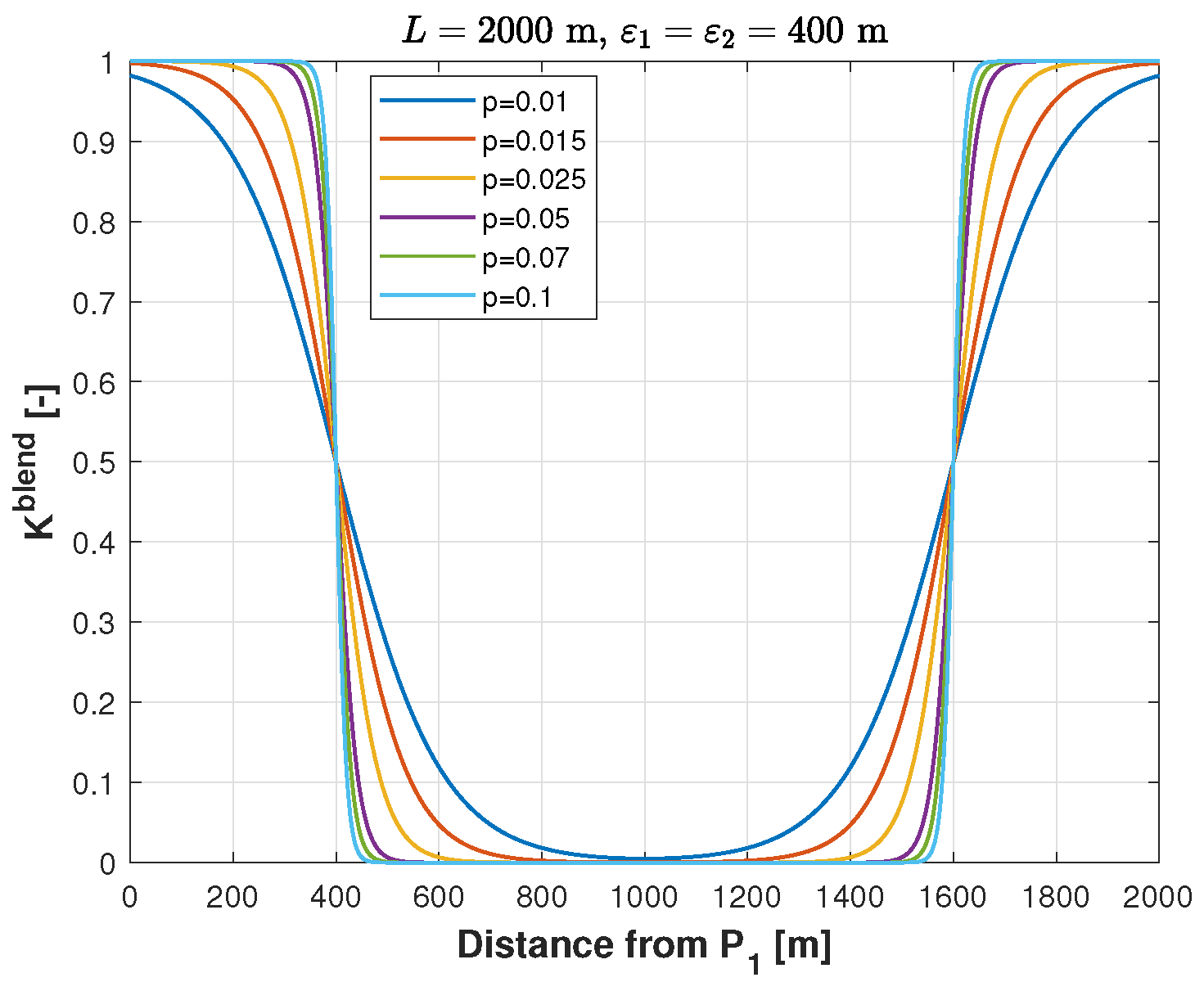
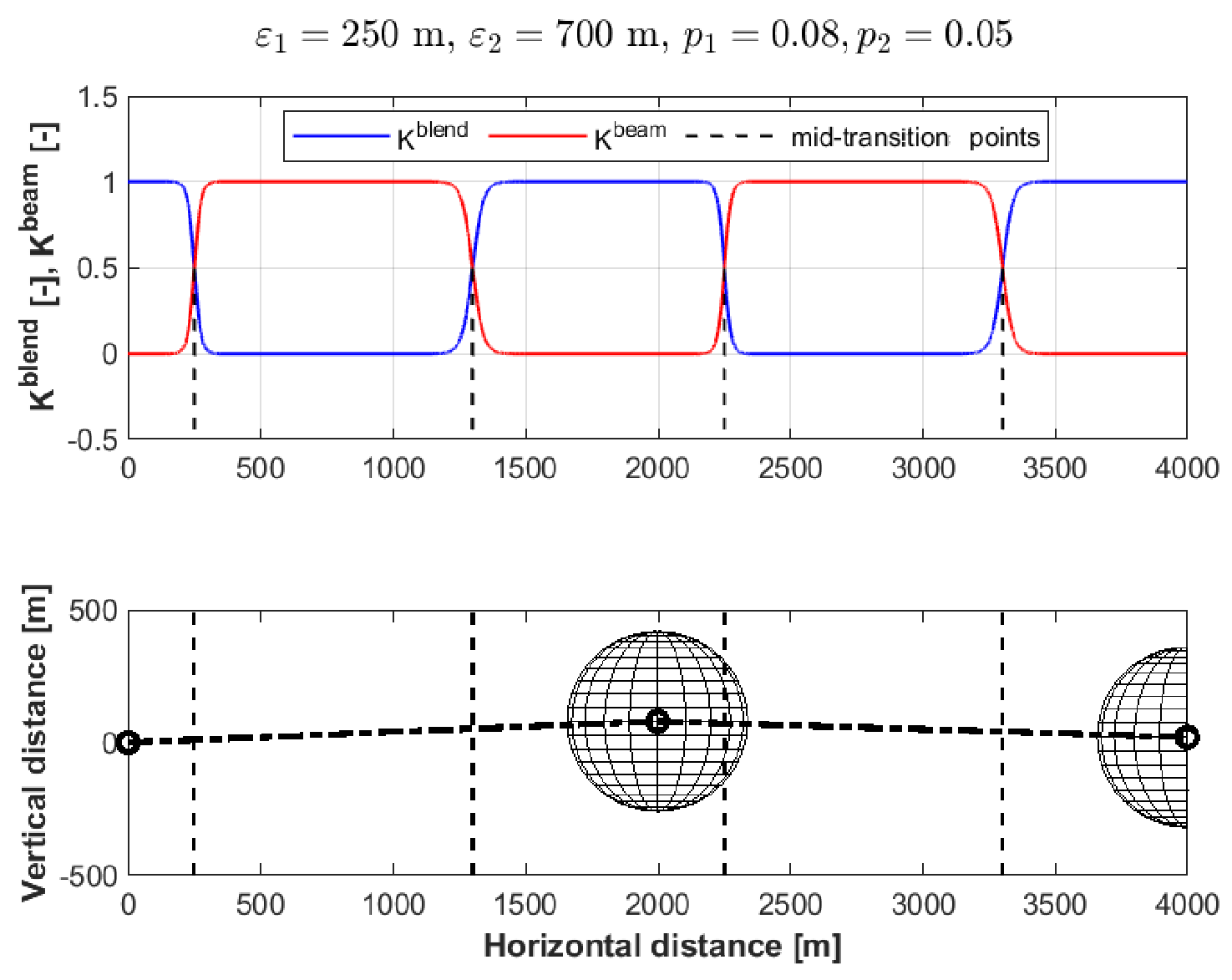
4.1.2. Trajectory Blending
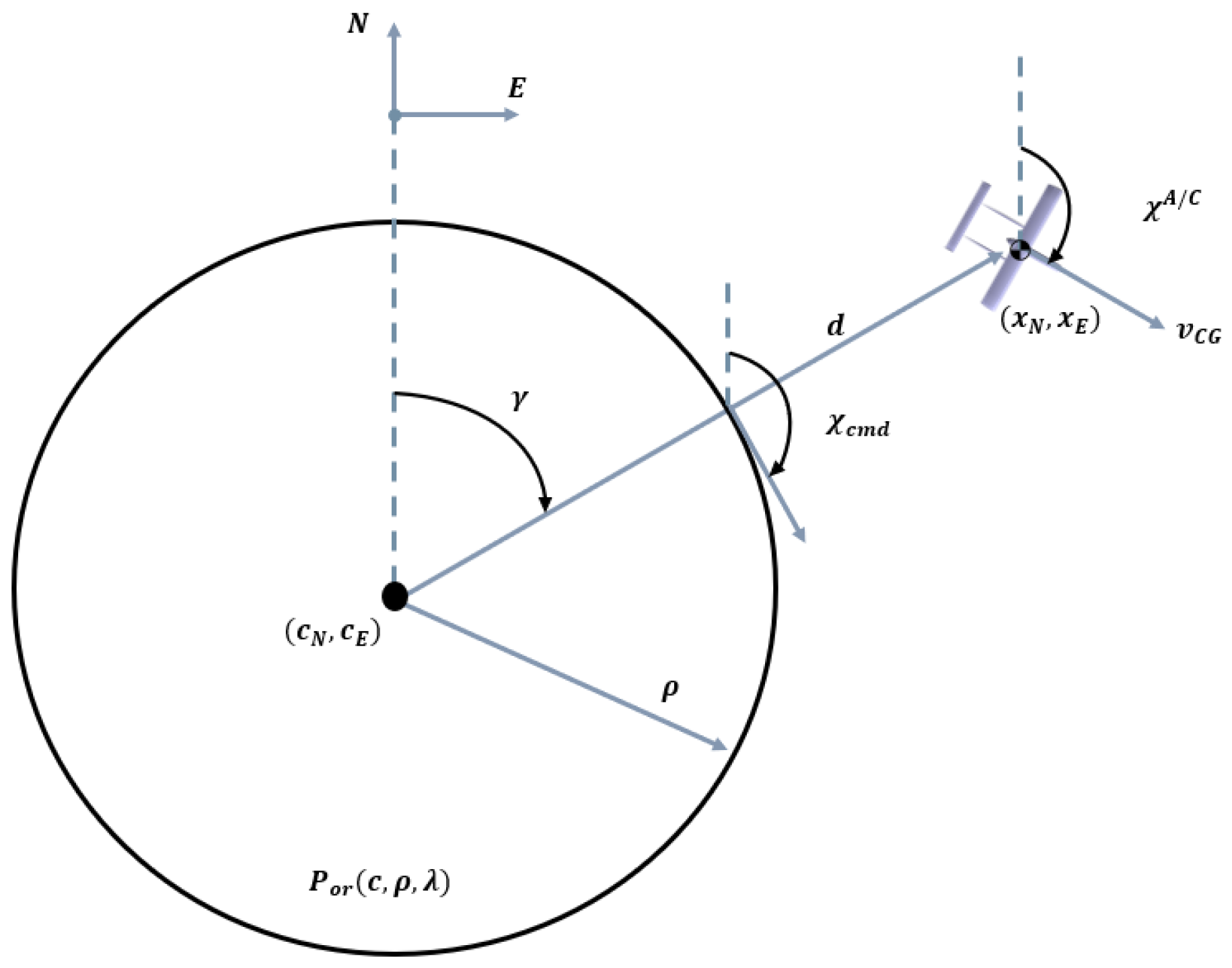
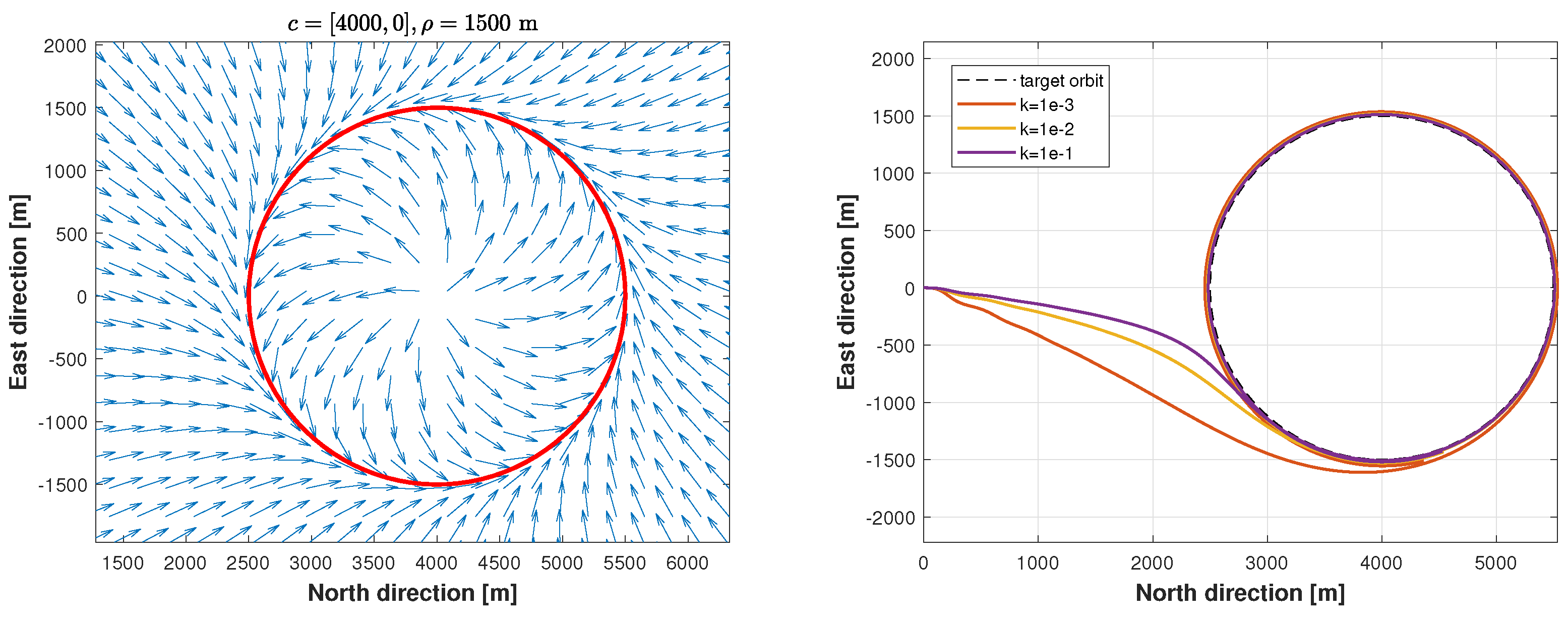
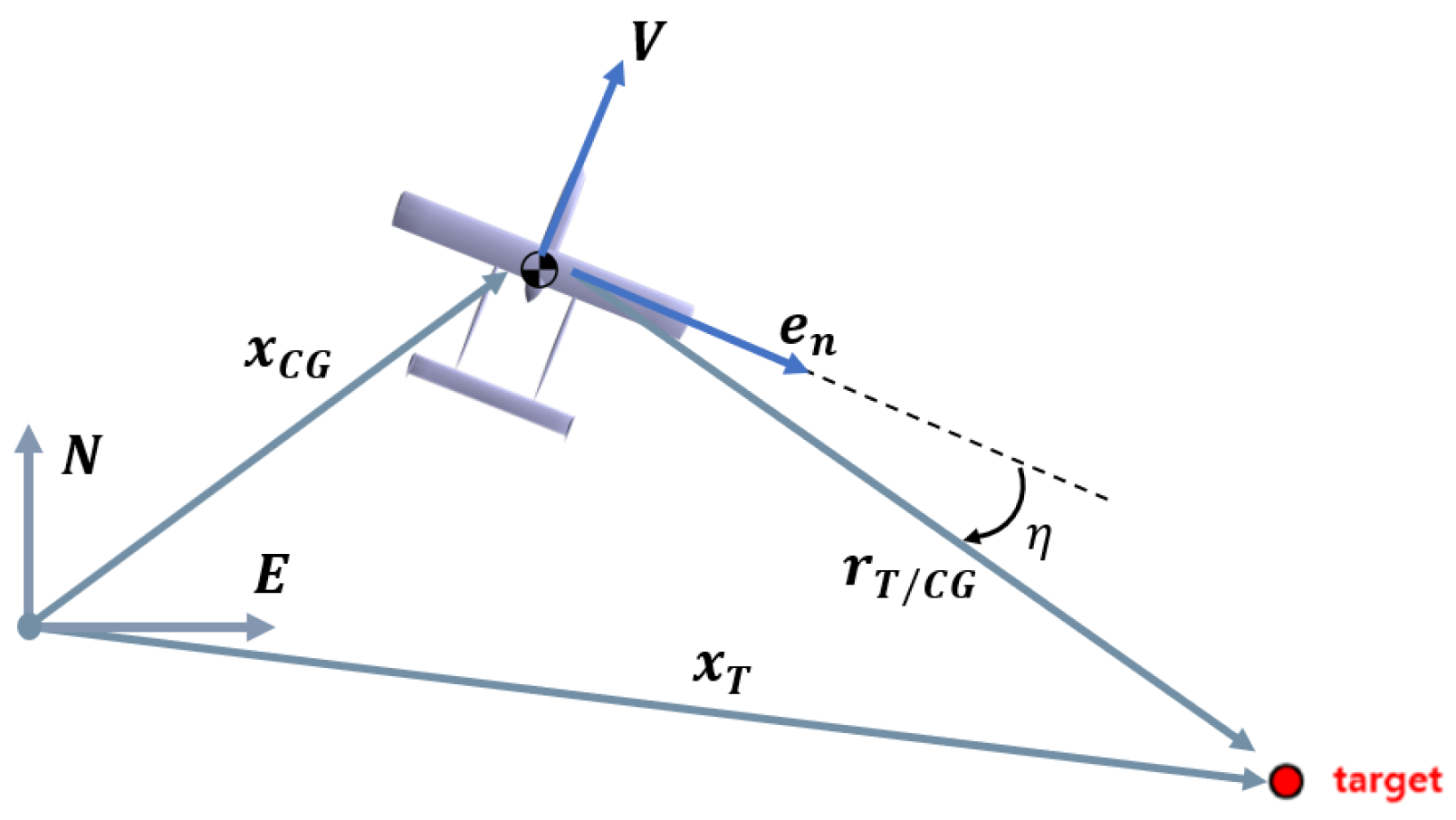
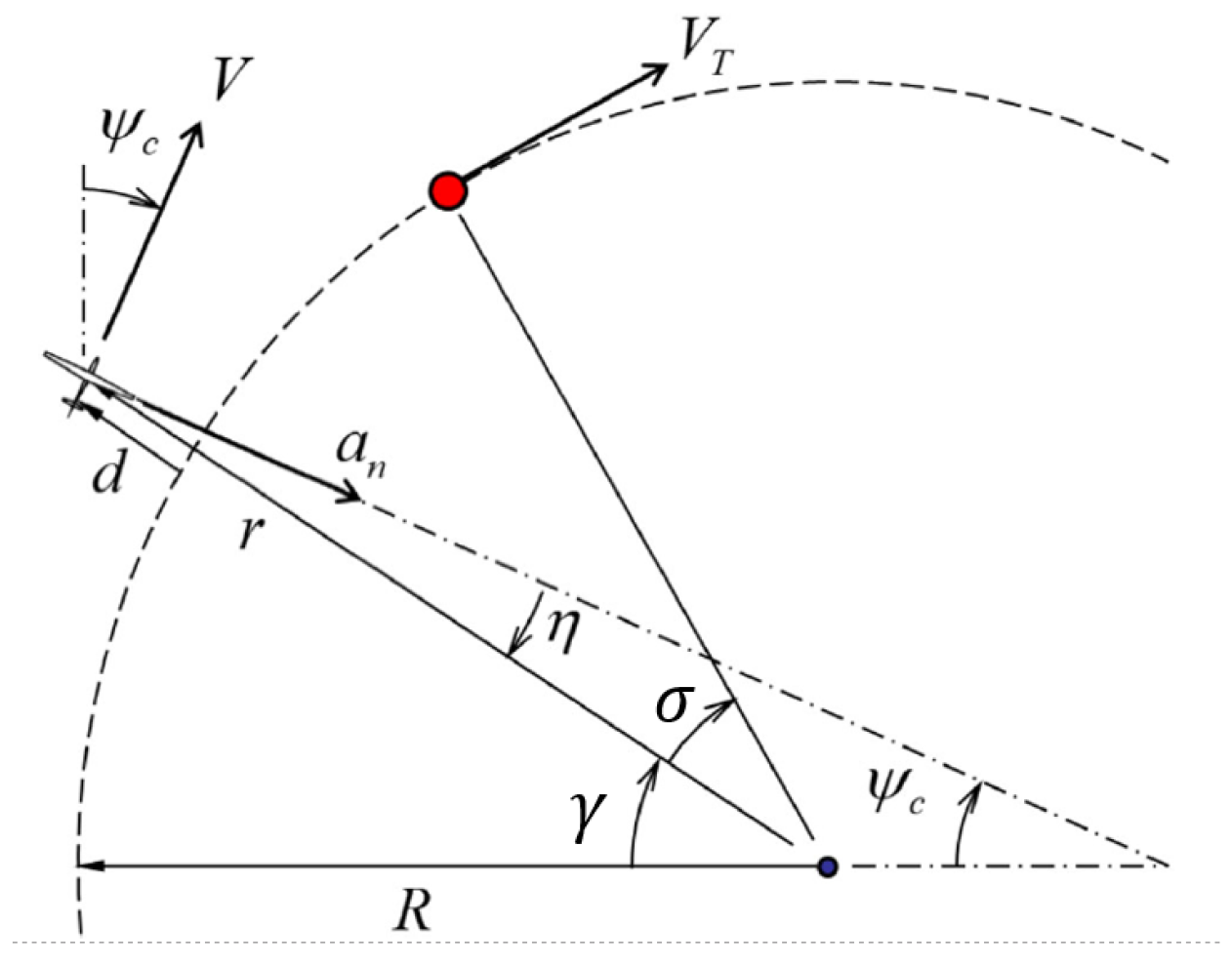
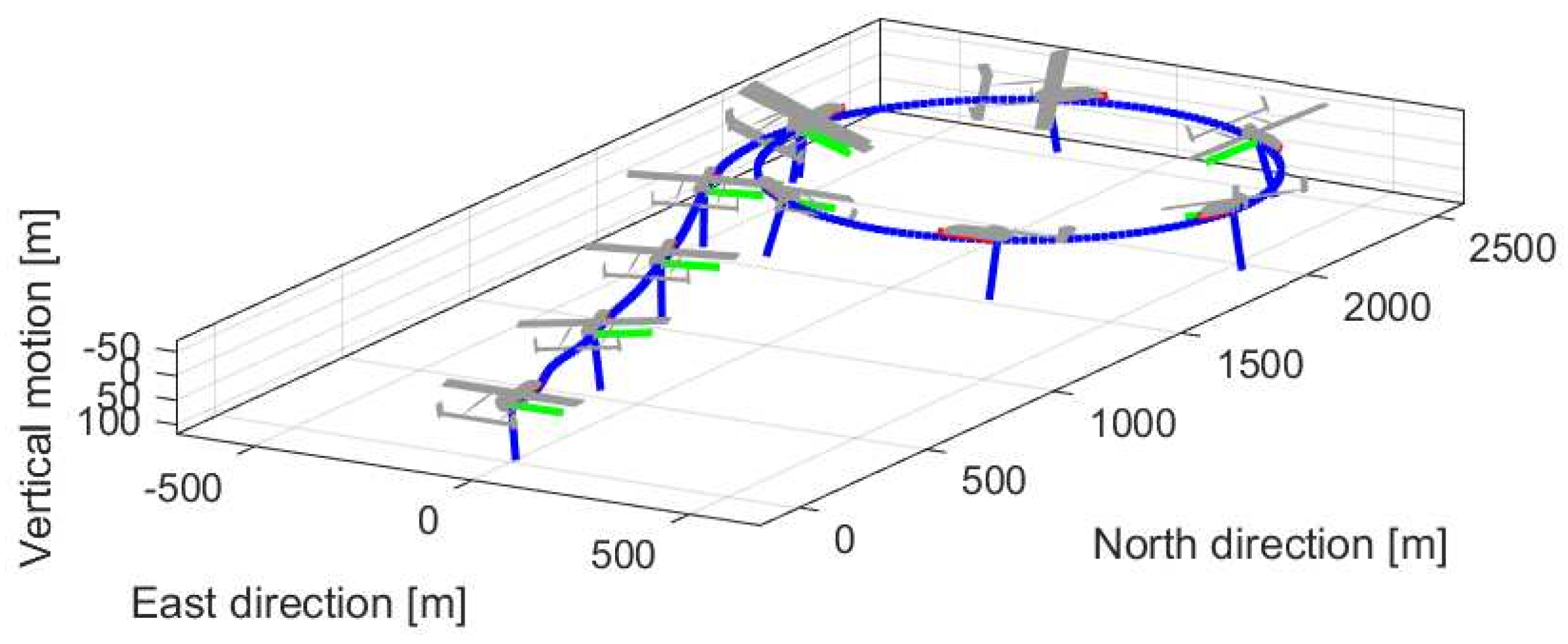
4.1.3. Circular Trajectory Tracking
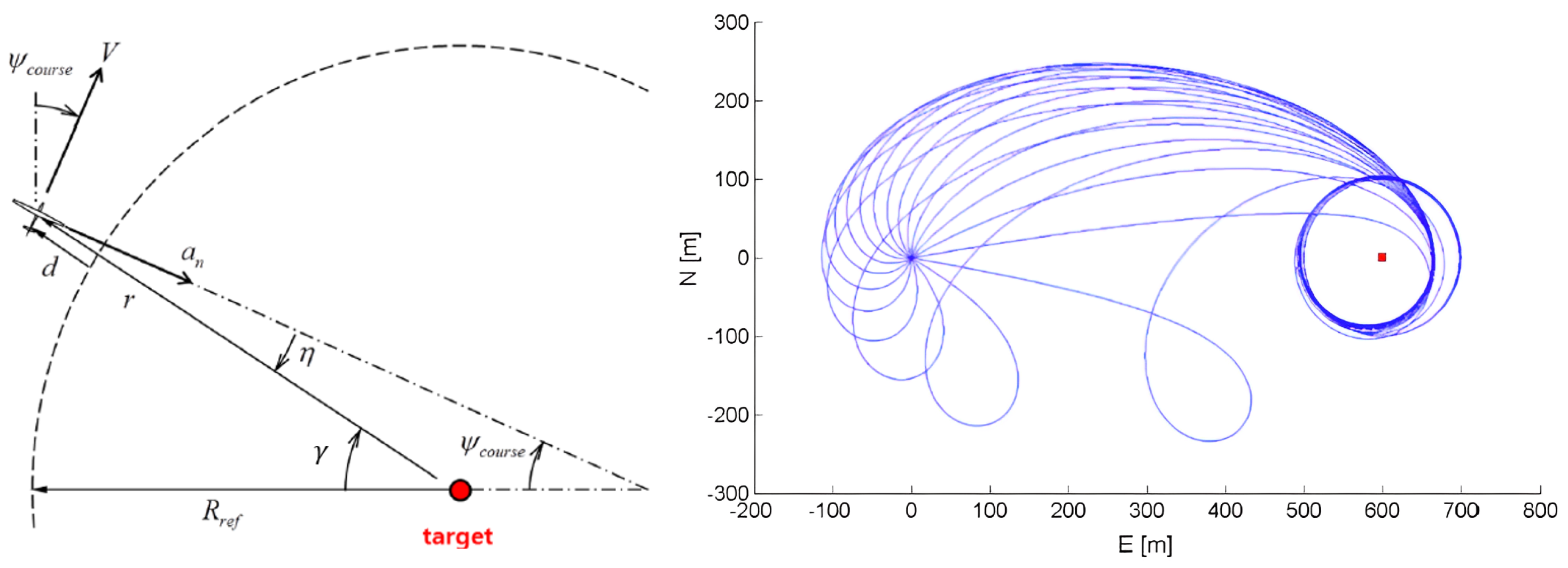
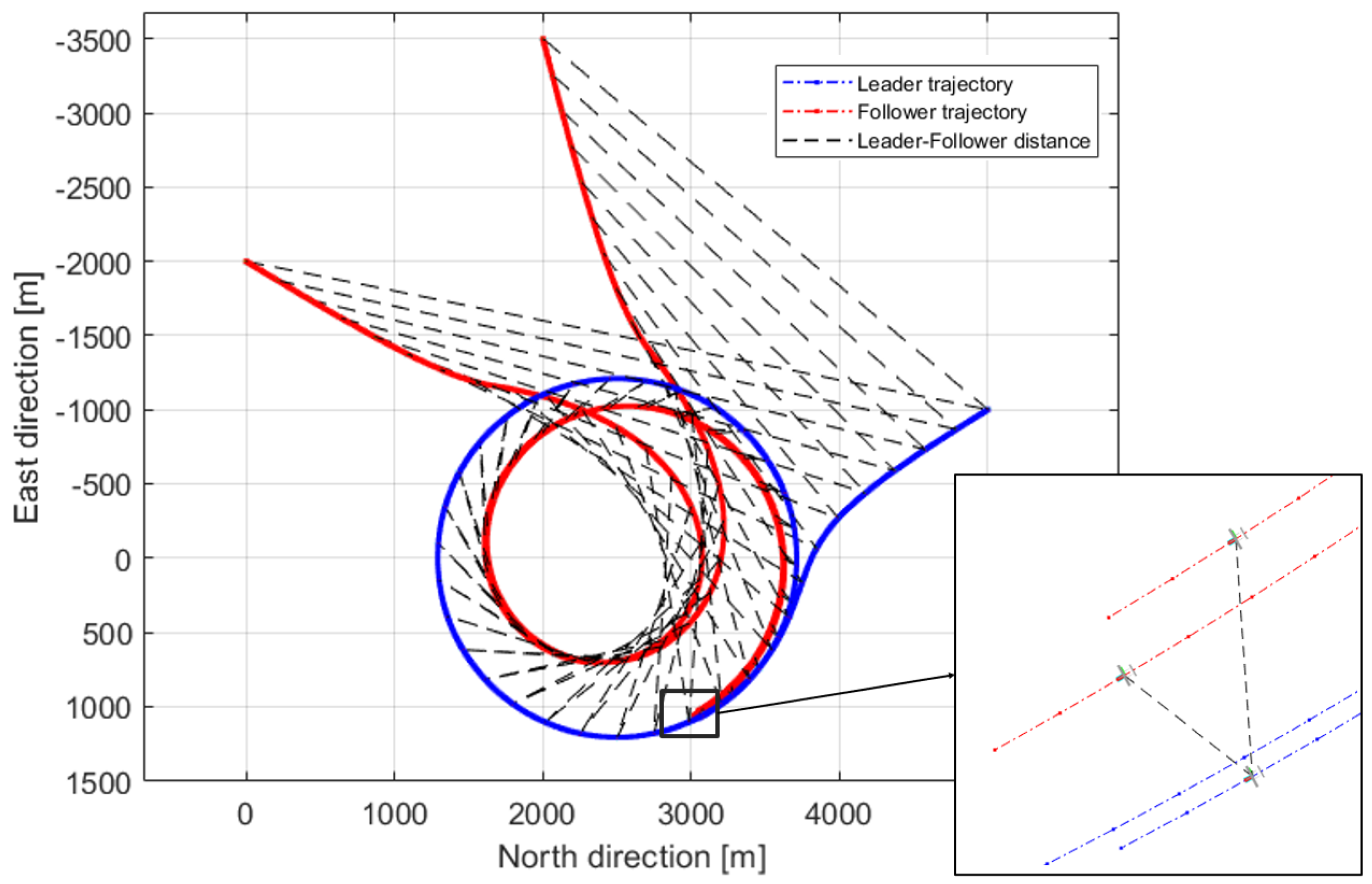
4.1.4. Rendezvous Guidance
- Linear rendezvous. In the linear rendezvous technique, multiple aircraft converge on a common point along a straight line. This approach is characterized by its simplicity and is suitable for scenarios where vehicles need to assemble quickly. Among the basic advantages of this technique are its simplicity in planning and execution, as well as the ability to cater for an arbitrary number of components in the formation. Furthermore, this trajectory minimizes the travel distance. On the cons side, a straight trajectory is predictable and hence easy to intercept, and wind may hinder the rendezvous maneuver.
- Circular rendezvous. This technique involves aircraft converging on a central point along the circumference of a circle. The major advantages of this maneuver rest in the ease of constant communication with multiple neighbors and the chance to complete the assembly phase of the swarm within a relatively compact space, thus reducing the chance of encroaching into hostile territory or collisions due to orographic constraints. Conversely, on the cons side is the potentially longer time for completing the rendezvous maneuver compared to a straight-trajectory maneuver.
4.2. Formation Control Mode (FCM)
- Enhanced resilience and fault tolerance. Each aircraft can continue operating autonomously, even if other aircraft in the formation become unavailable. This ensures a higher level of resilience and fault tolerance.
- Reduced computational complexity. Each aircraft processes only local information and interacts with neighboring aircraft, reducing the computational complexity compared to a centralized approach.
- Increased scalability. Aircraft can be added to or removed from the formation without the need to reconfigure the entire control system.
- A position error, as previously described;
- A path error, measured with respect to the course angle and climb angle of the leader;
- An attitude error, measured with respect to the roll angle and pitch angle of the leader.
4.3. Flying over Target: Guidance Mode (GM) vs. Formation Control Mode (FCM)
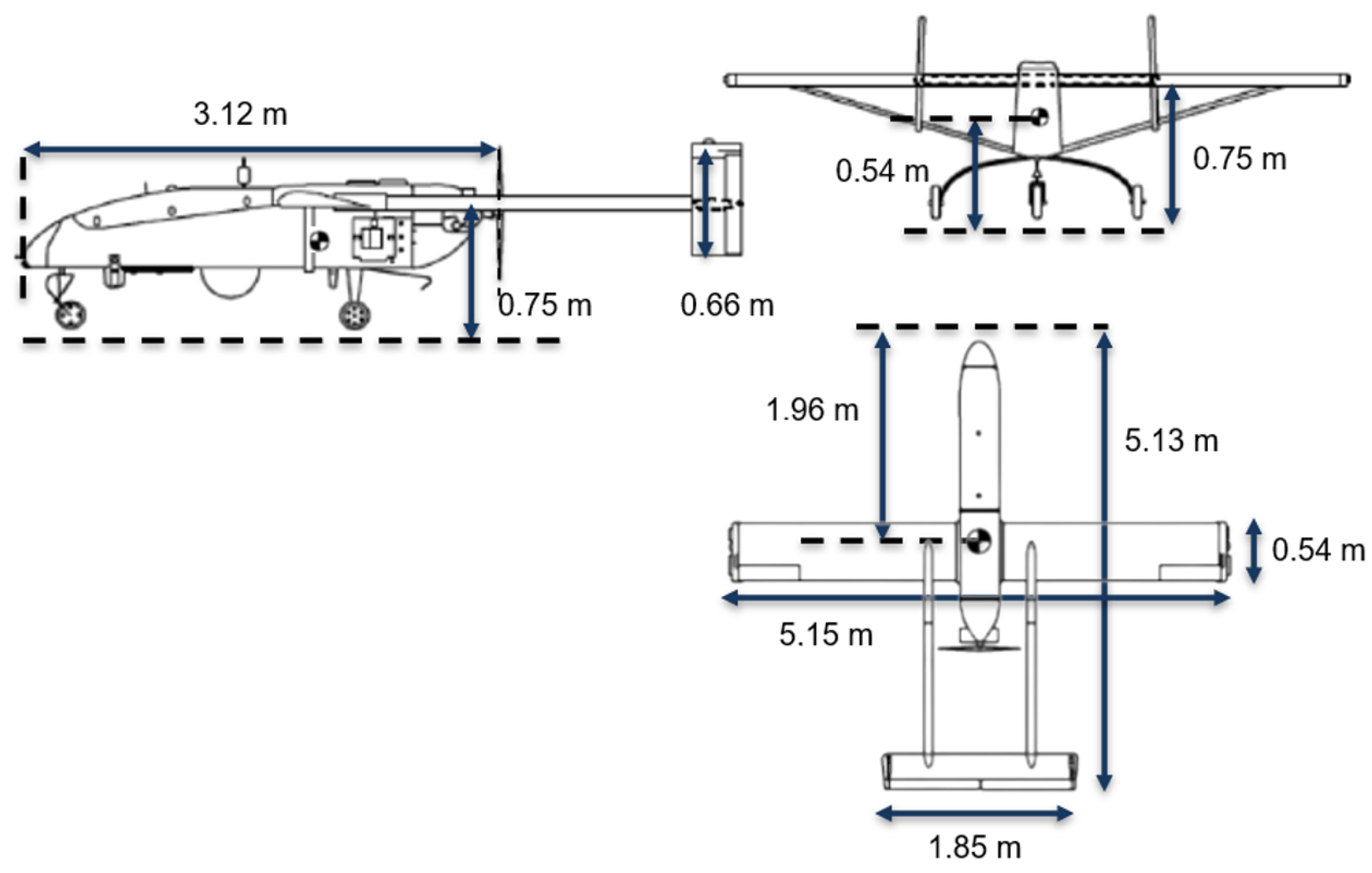
5. Application Results
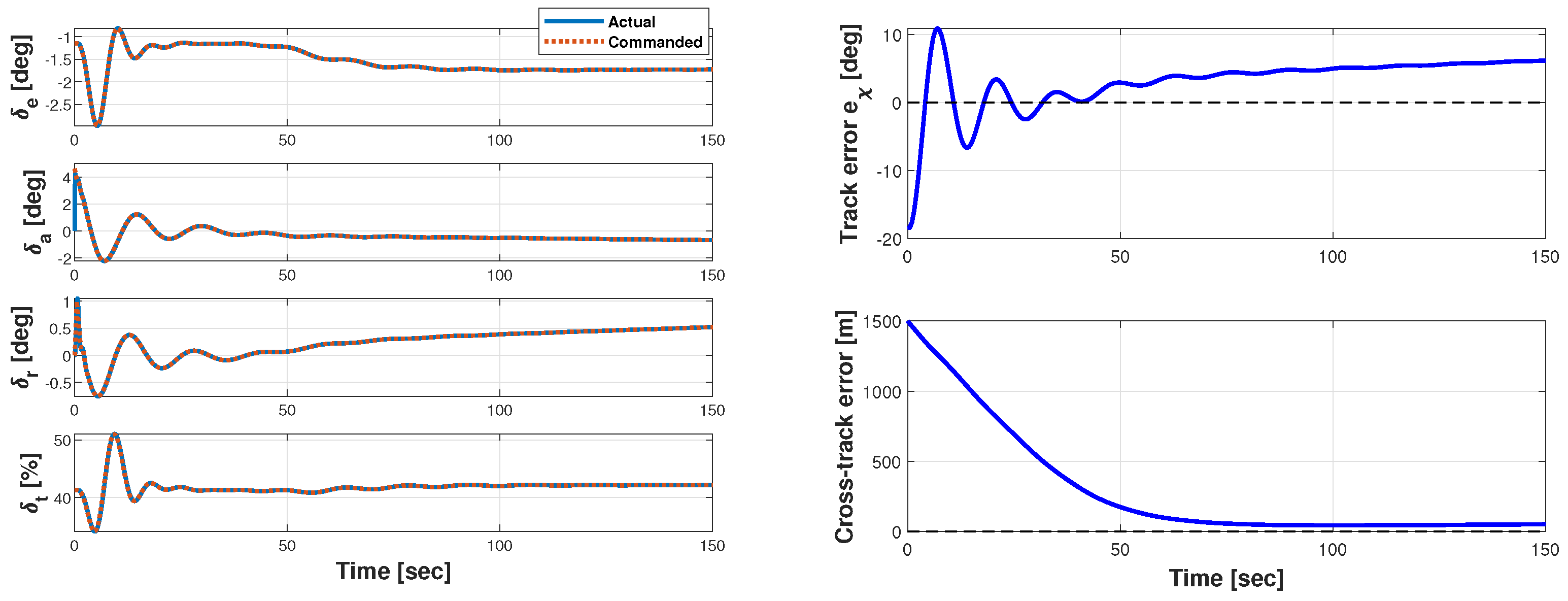
5.1. Single-Aircraft Guidance Testing
5.1.1. Beam Tracking Testing
5.1.2. Circular-Trajectory-Tracking Testing
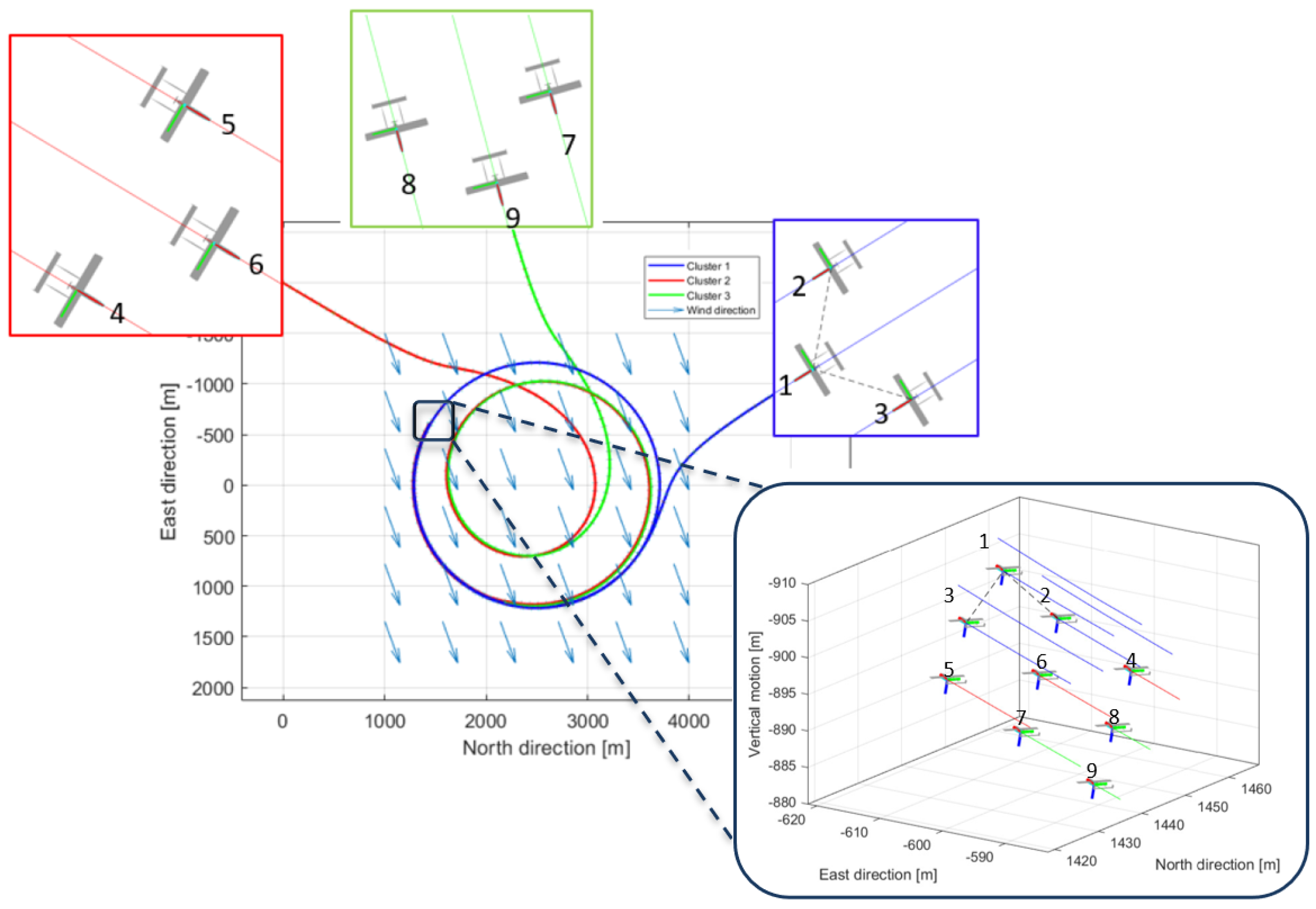
5.2. Rendezvous Testing
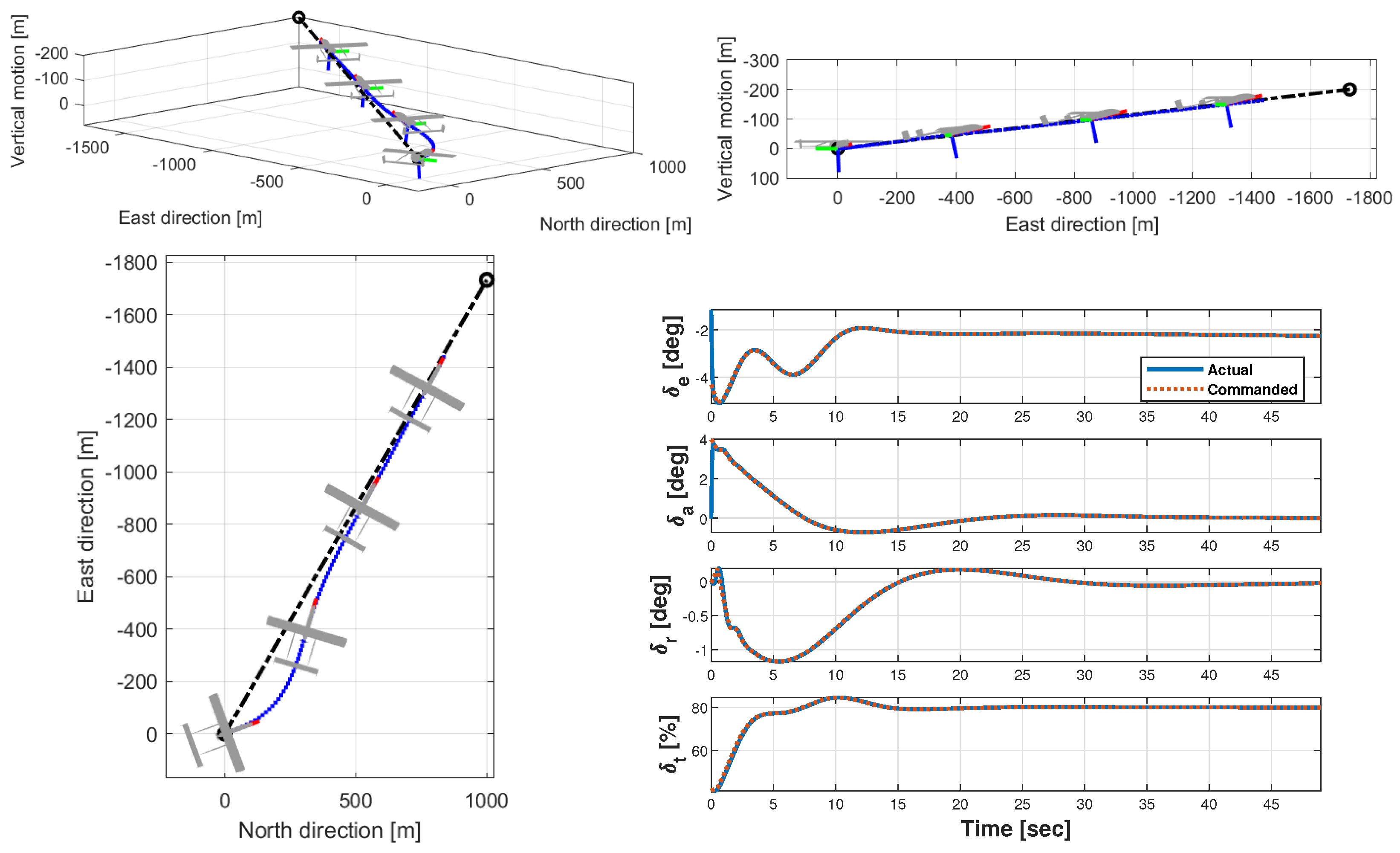
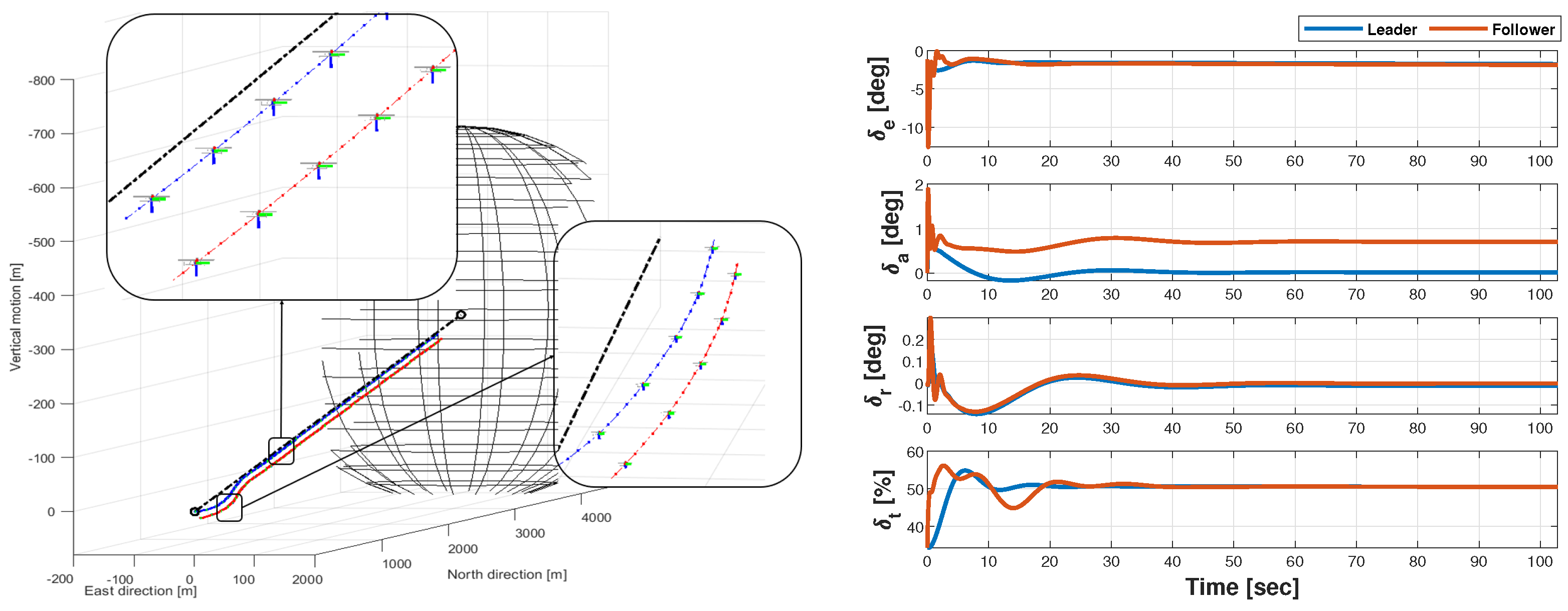
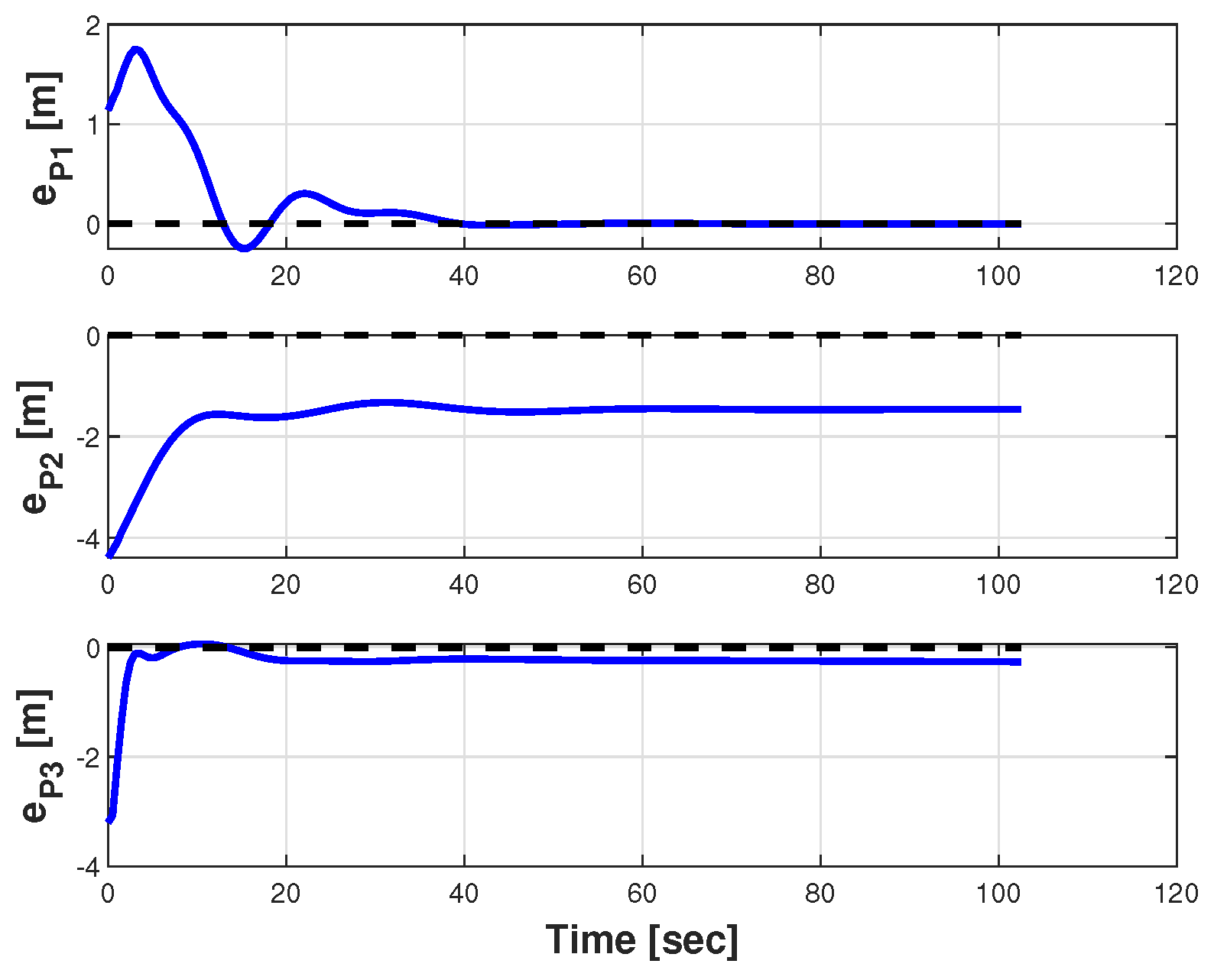
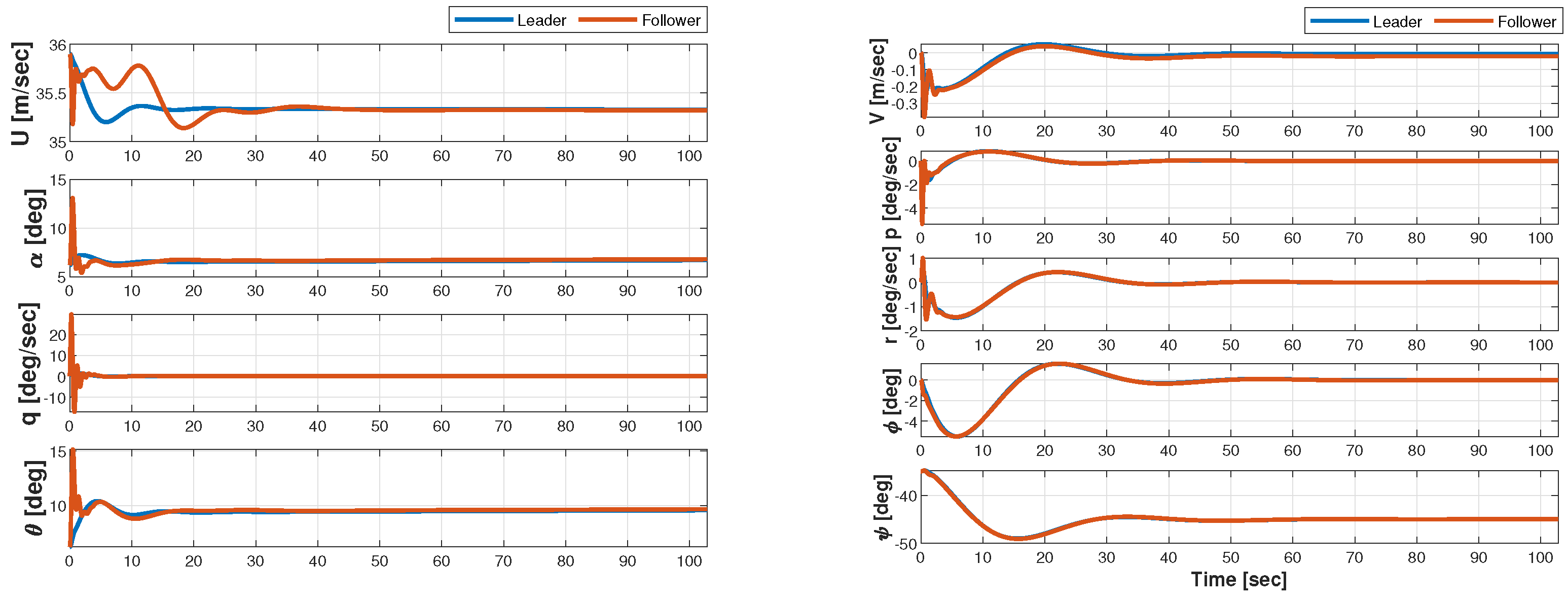
5.3. Formation Flight Testing Along a Rectilinear Leg
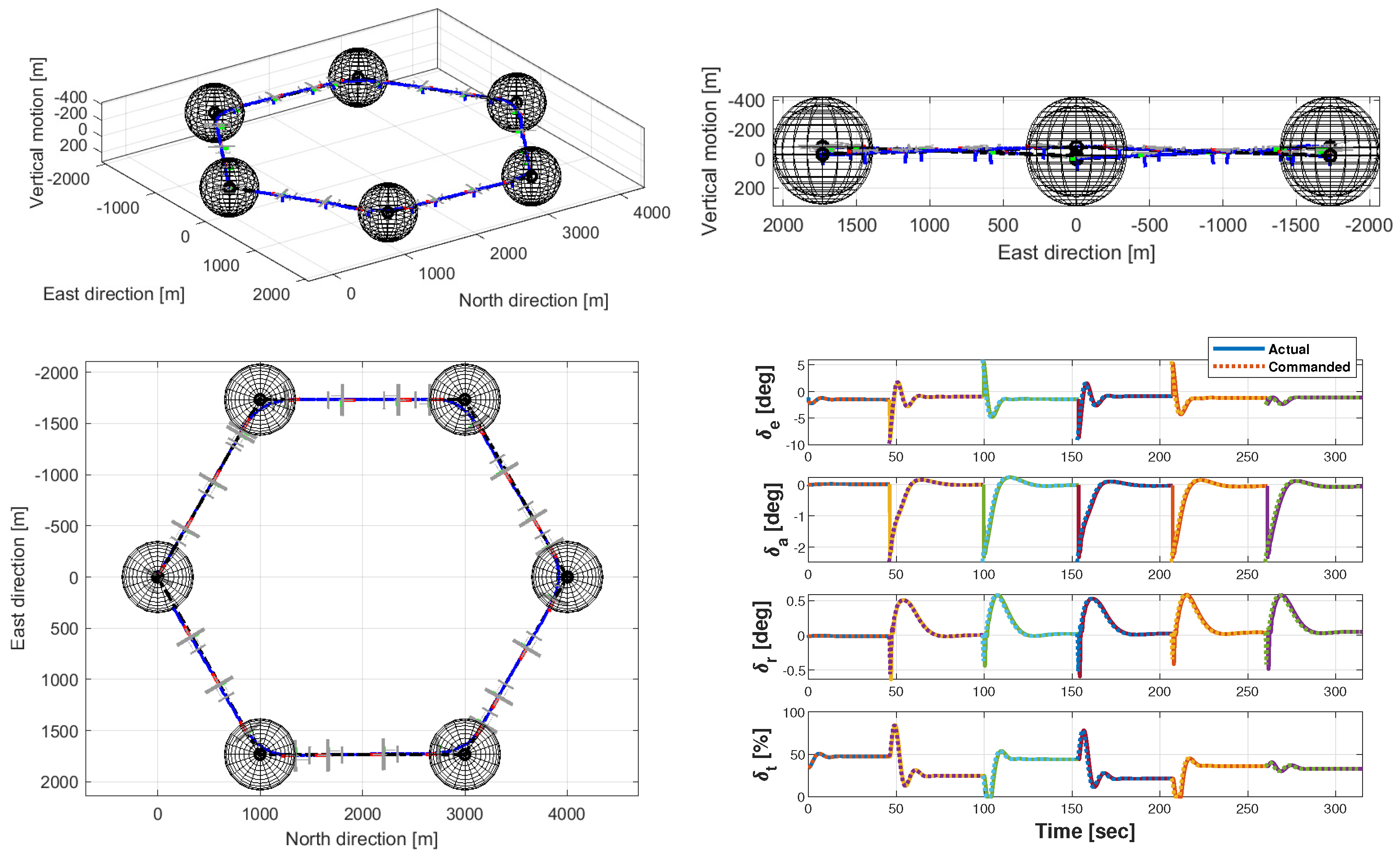
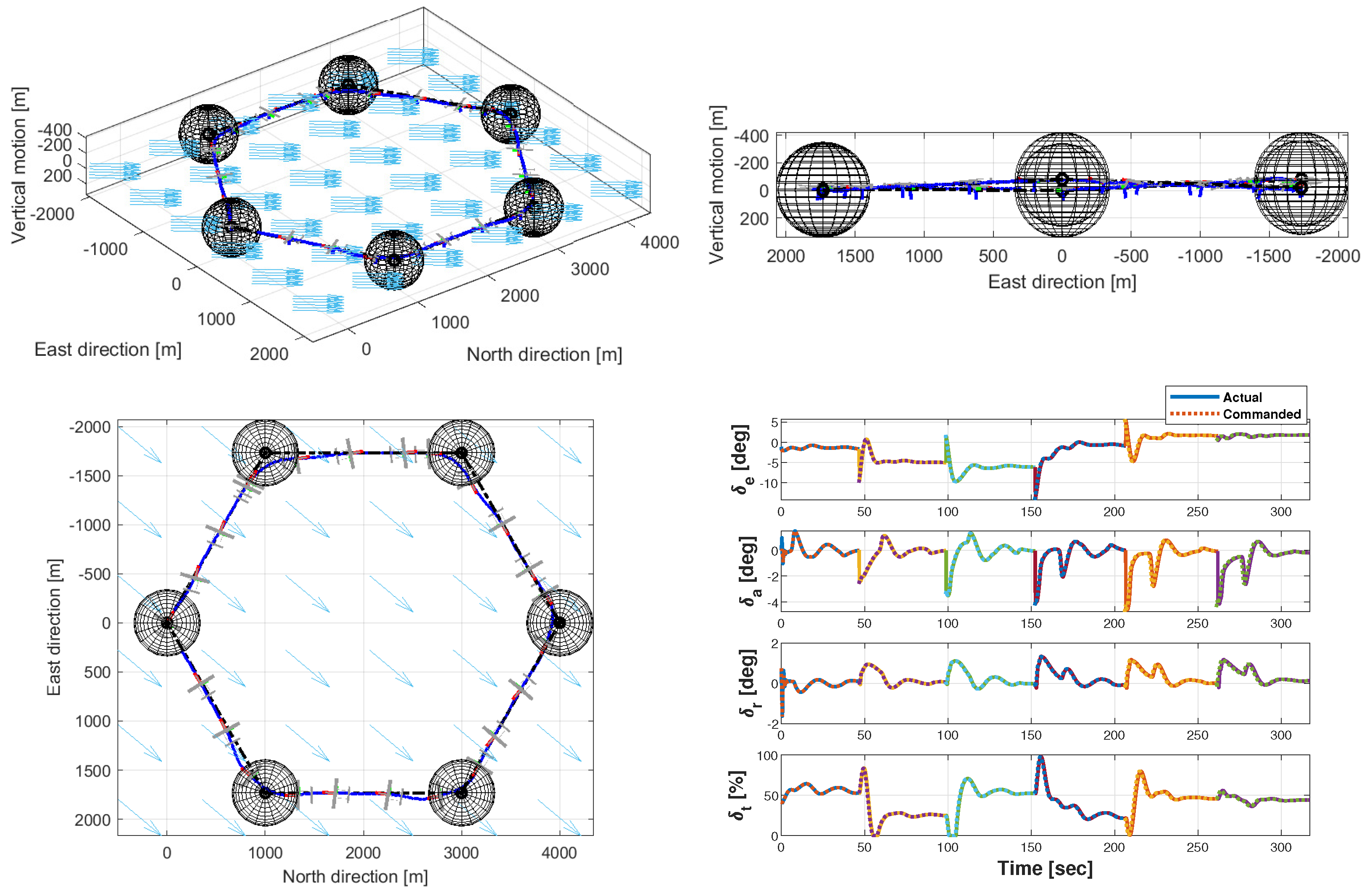
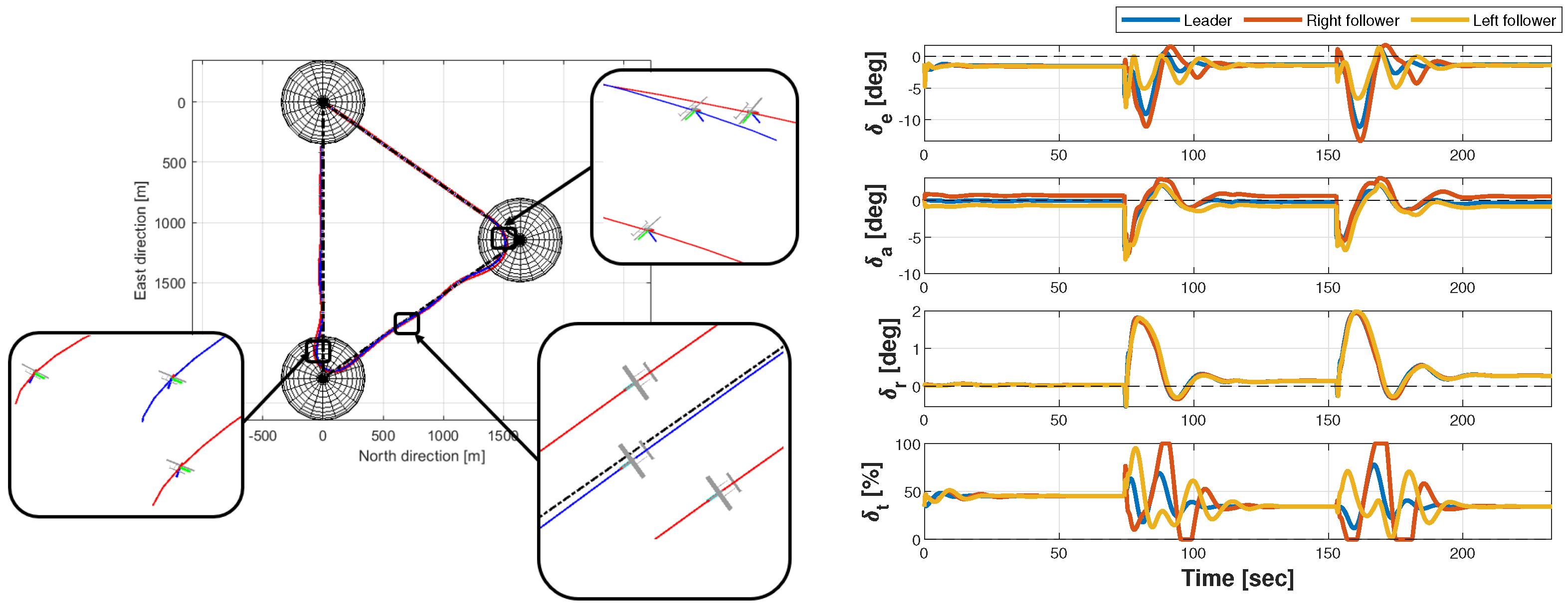
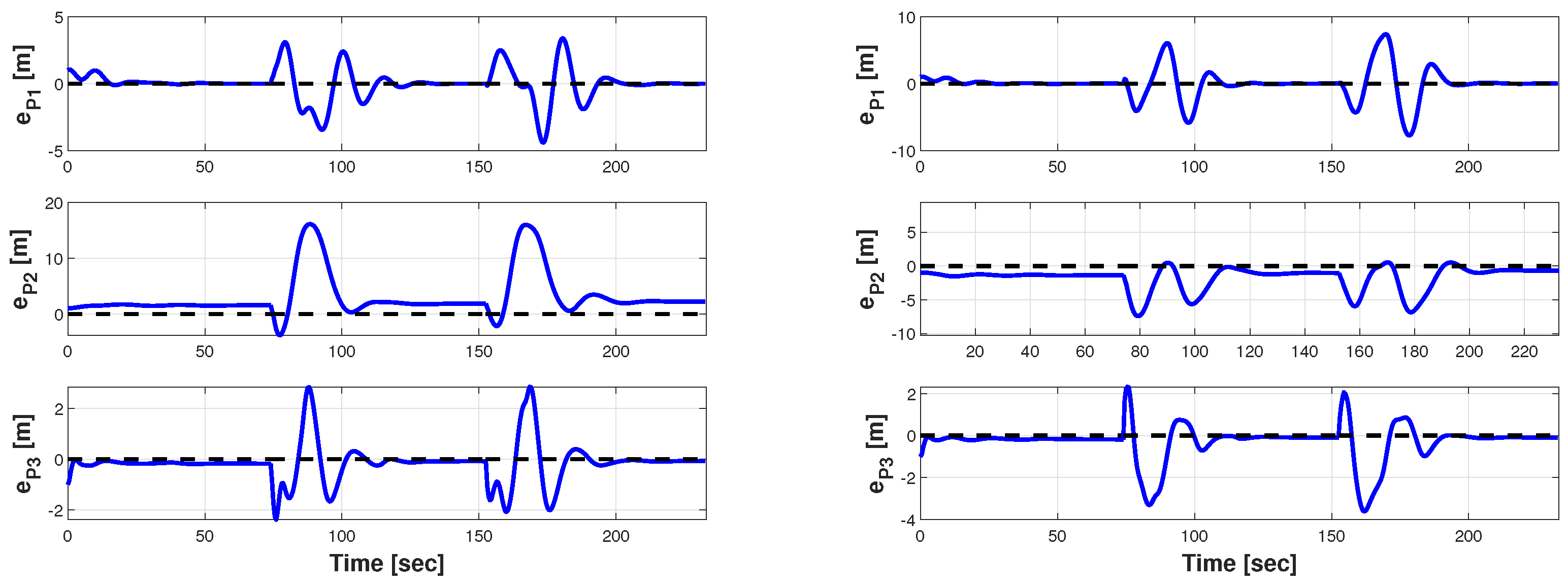
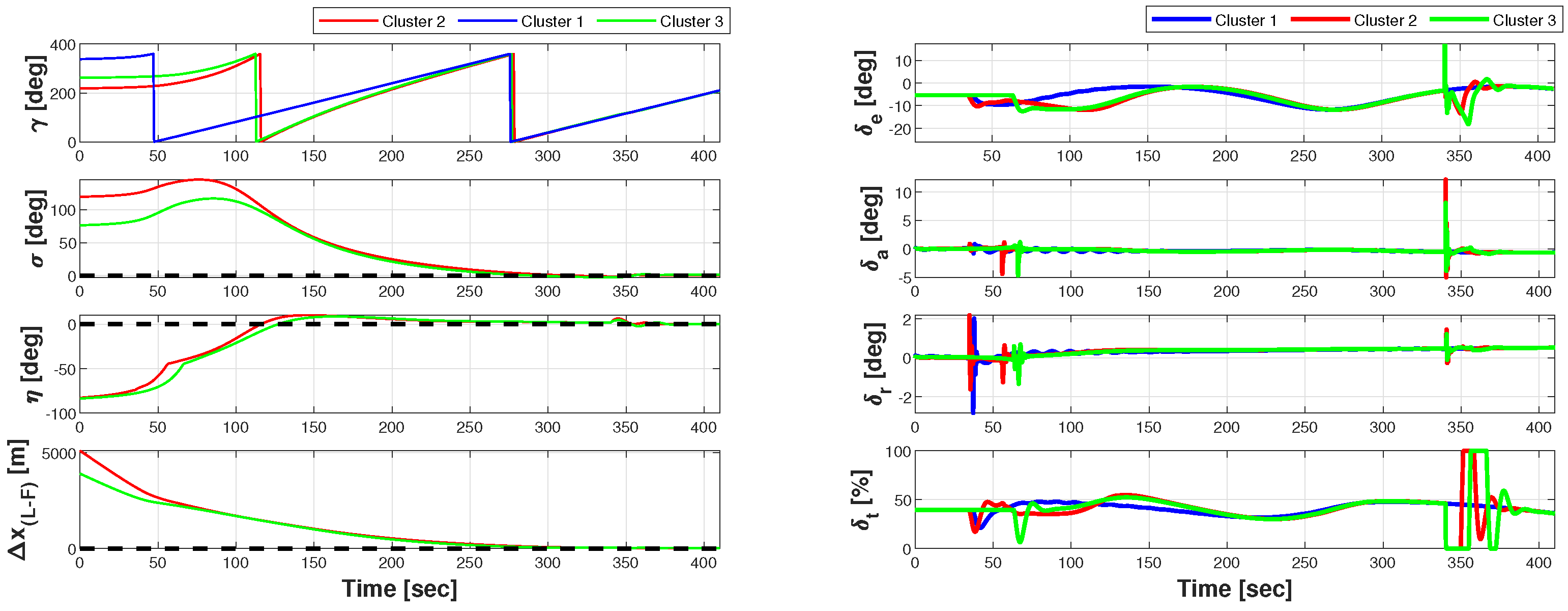
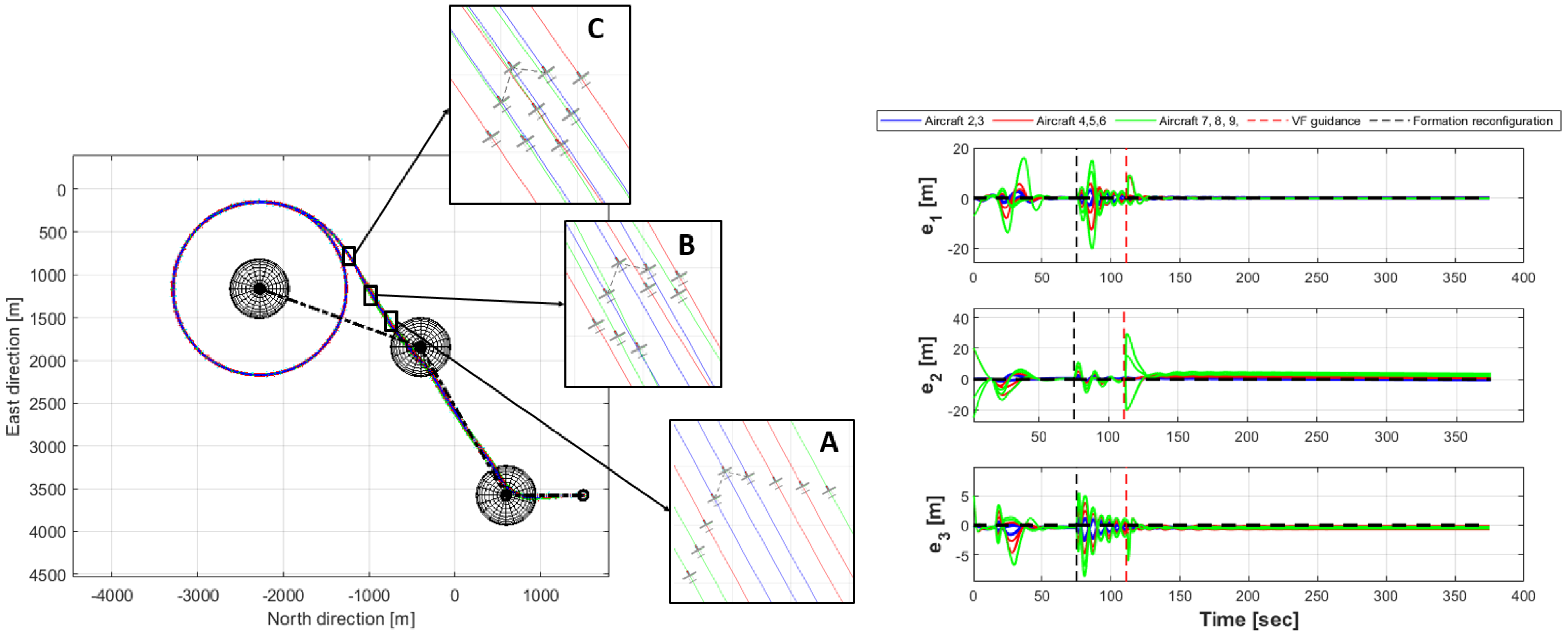
5.4. Realistic Mission Simulation
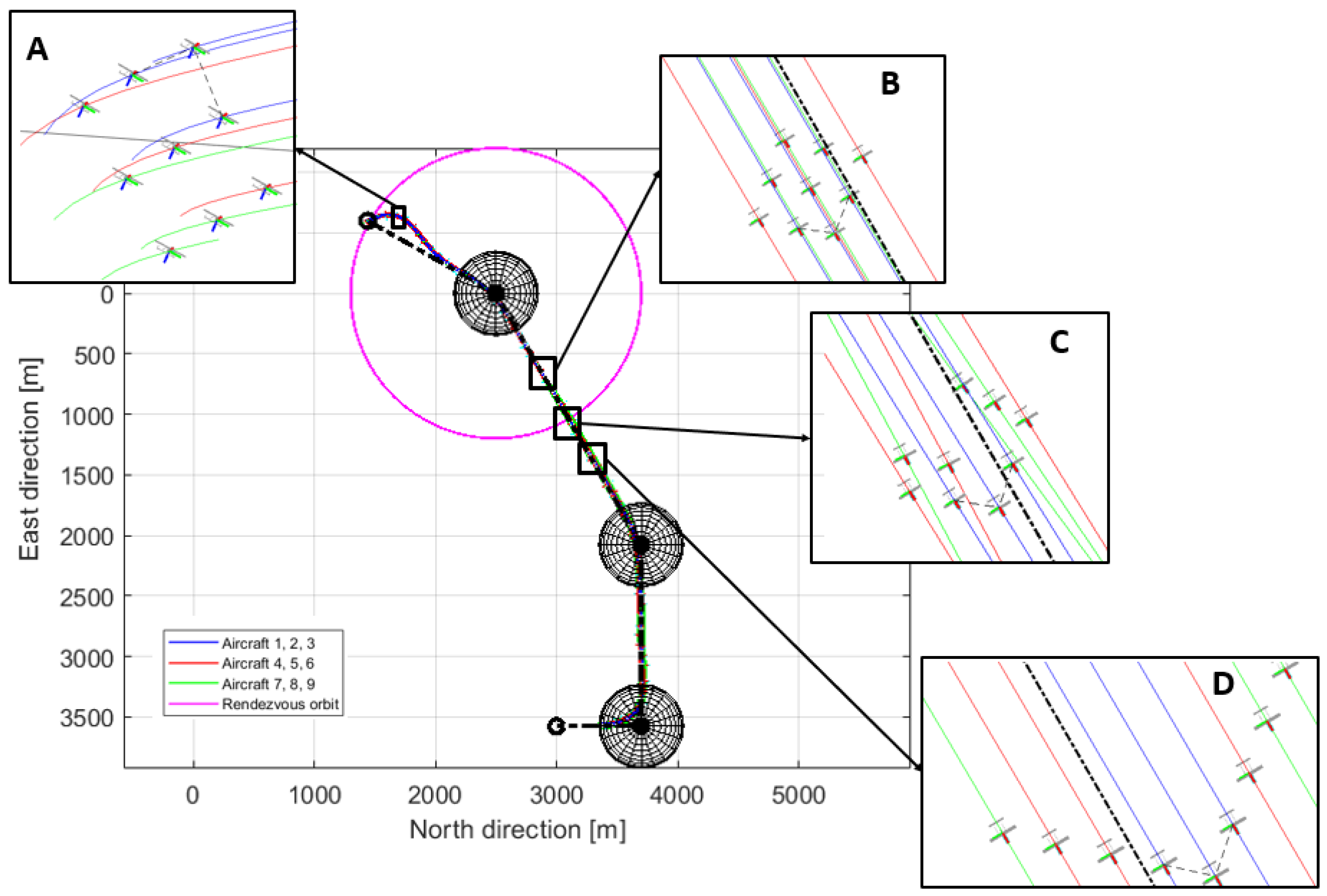
5.4.1. Phase 1: Rendezvous
5.4.2. Phase 2: Waypoint Navigation
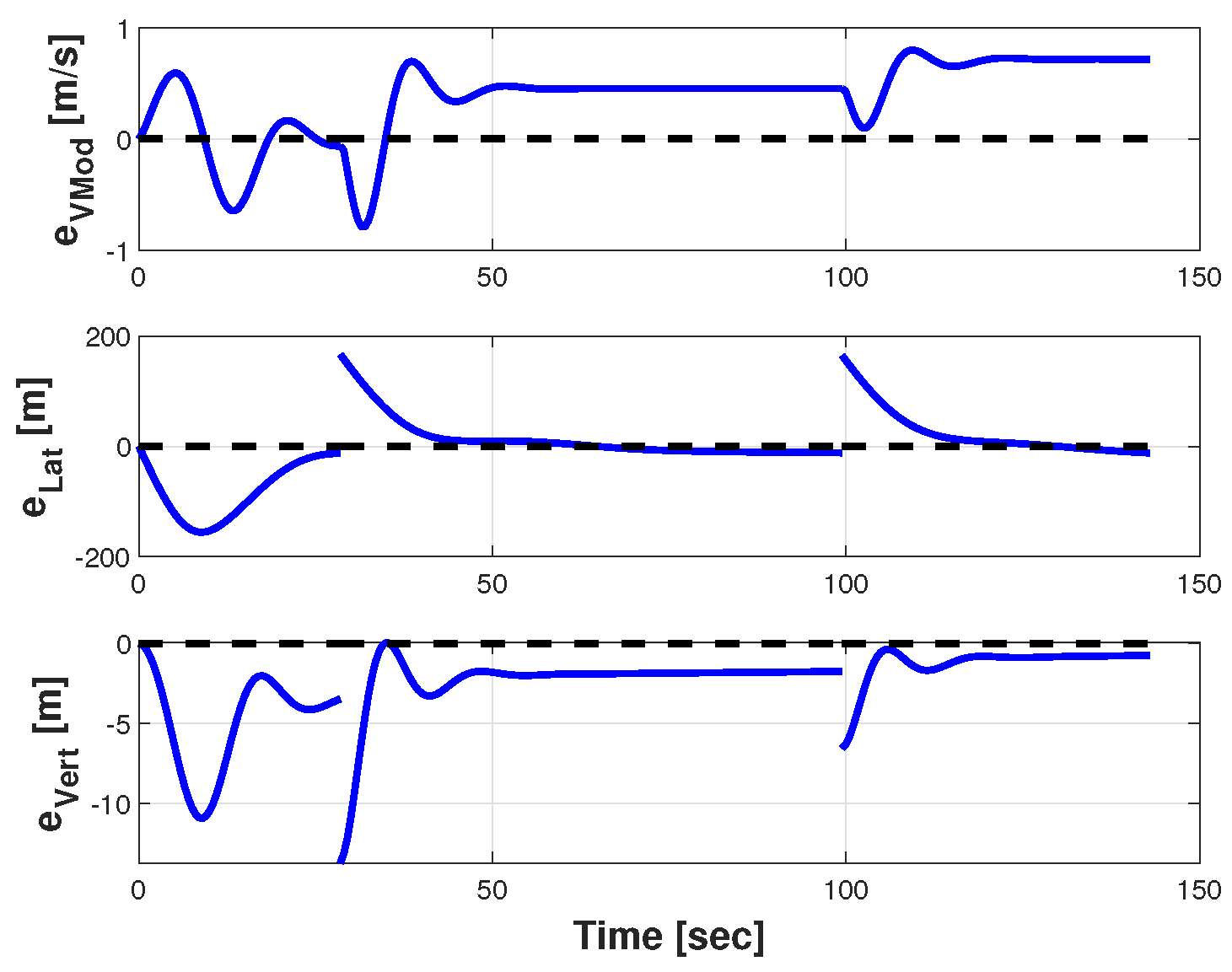
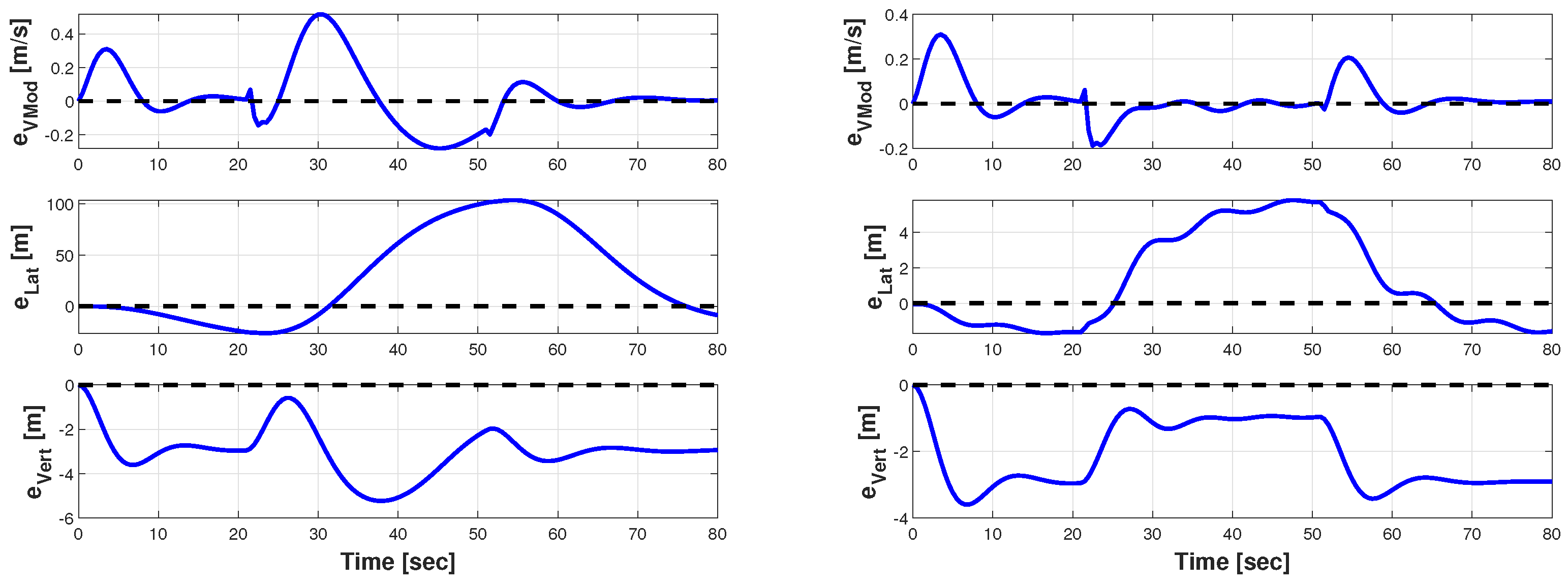
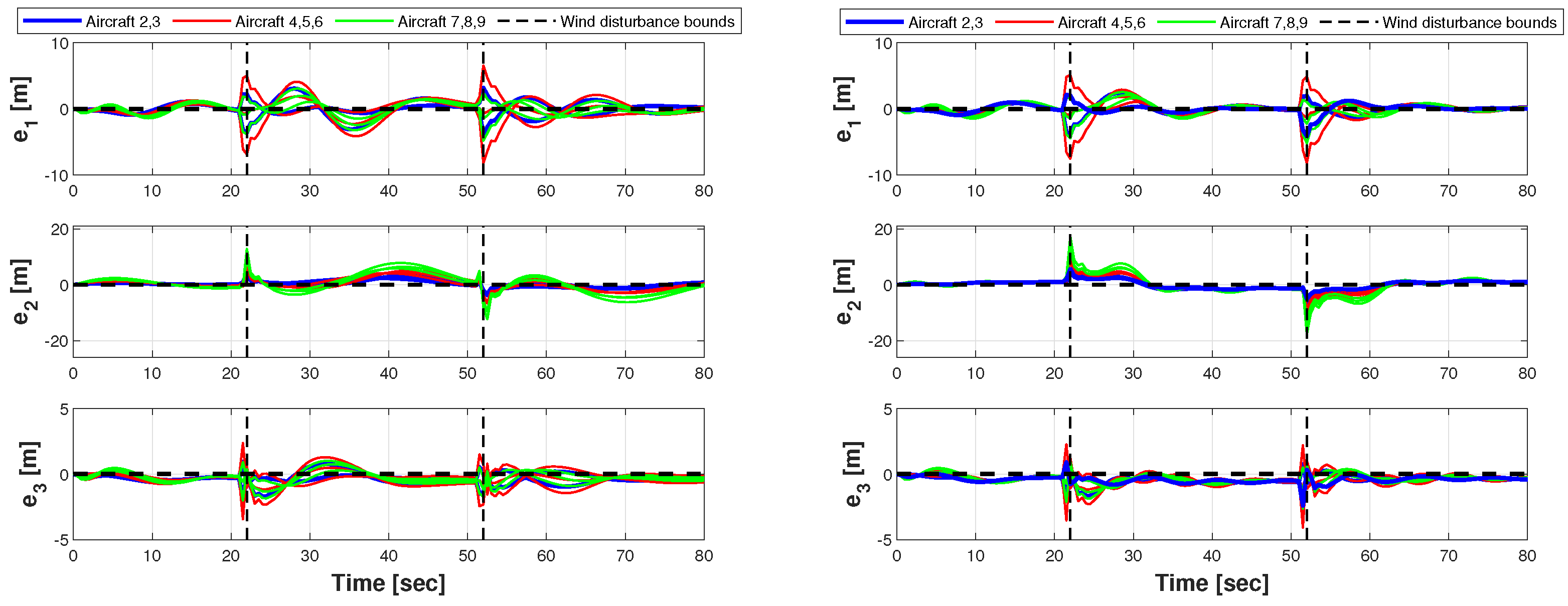
5.4.3. Phase 3.a: Target 1 Overflight with Crosswind
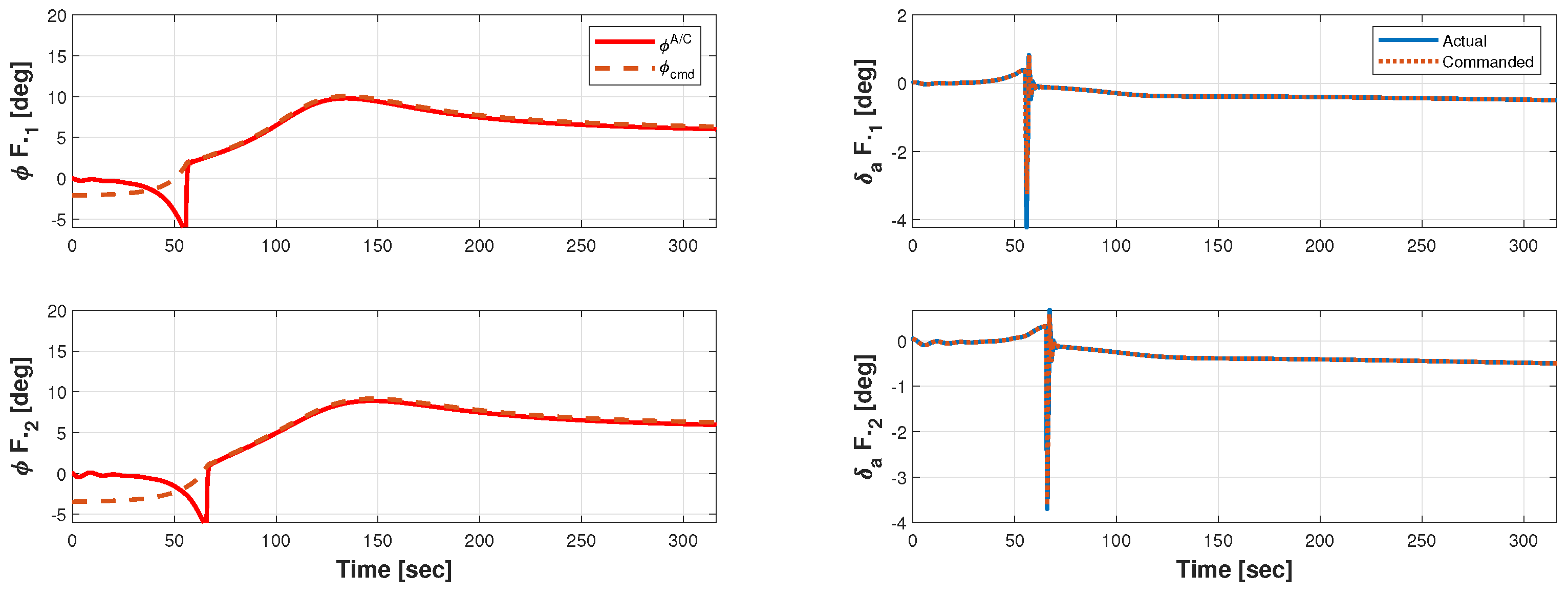
5.4.4. Phase 3.b: Target 1 Overflight with Leader’s Guidance Mode (GM) Failure
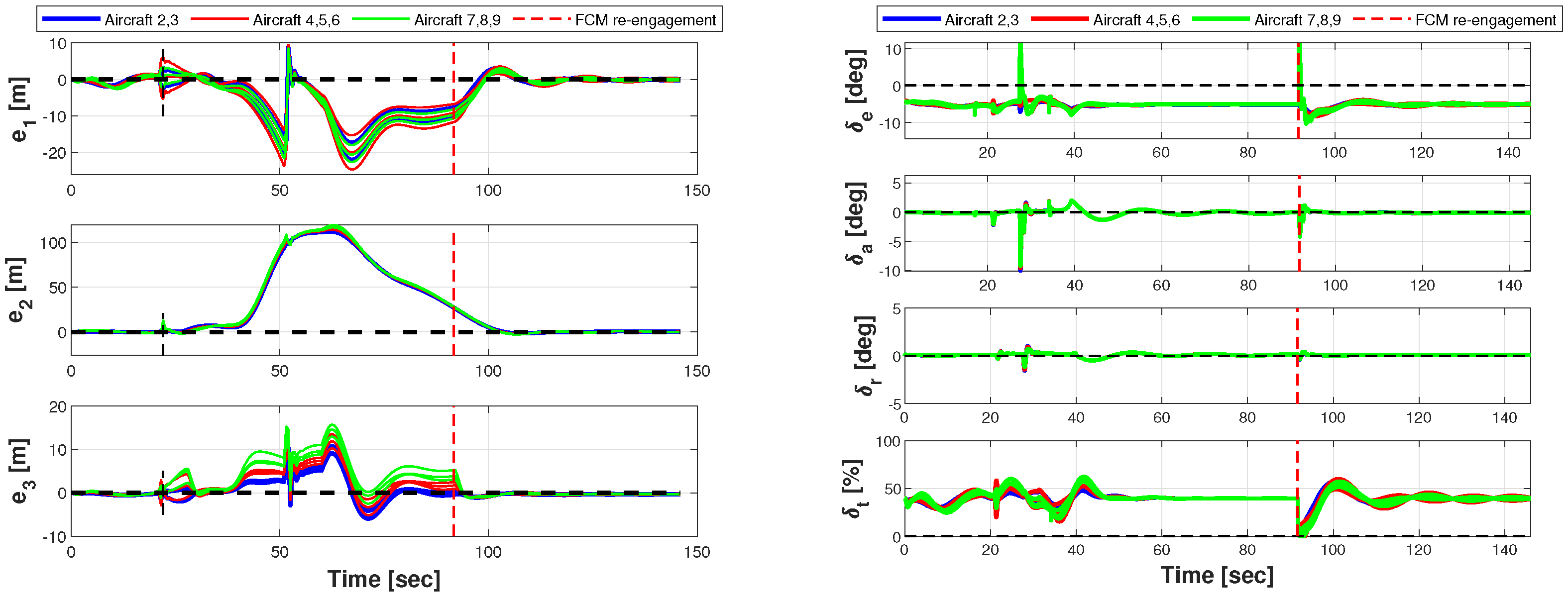
5.4.5. Phase 4: Target 2 Overflight
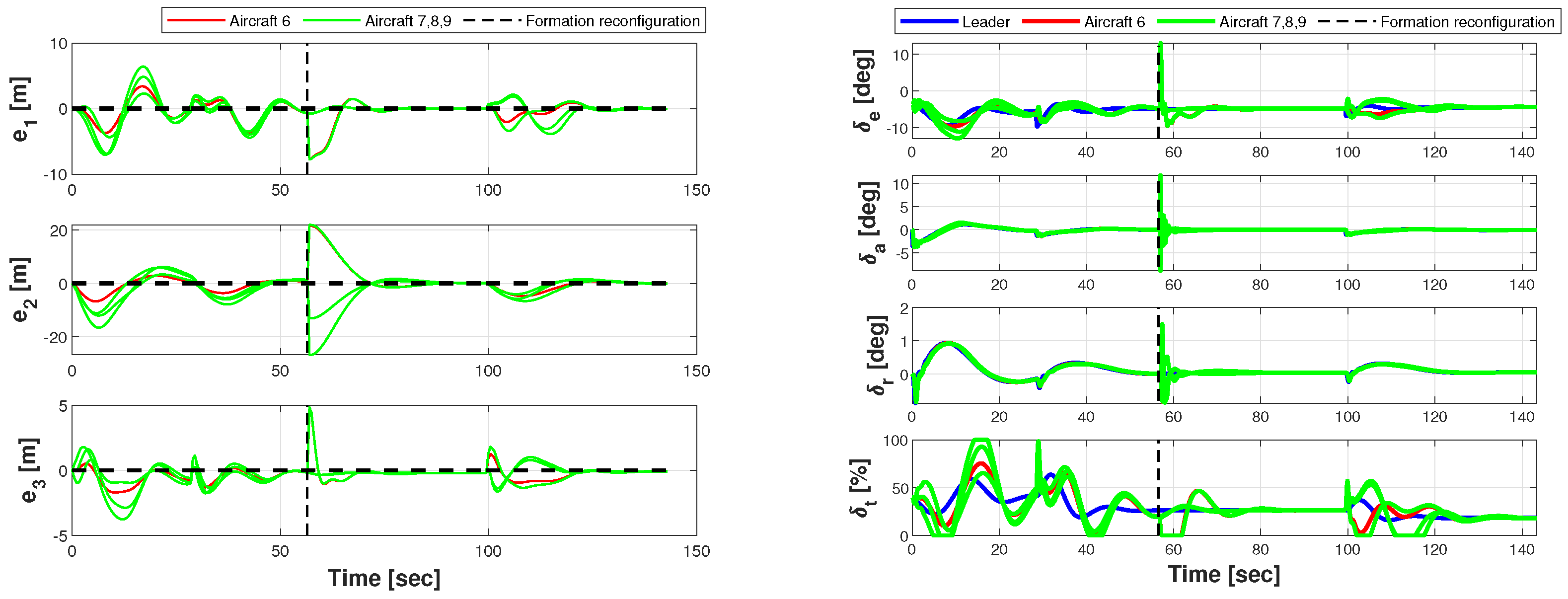
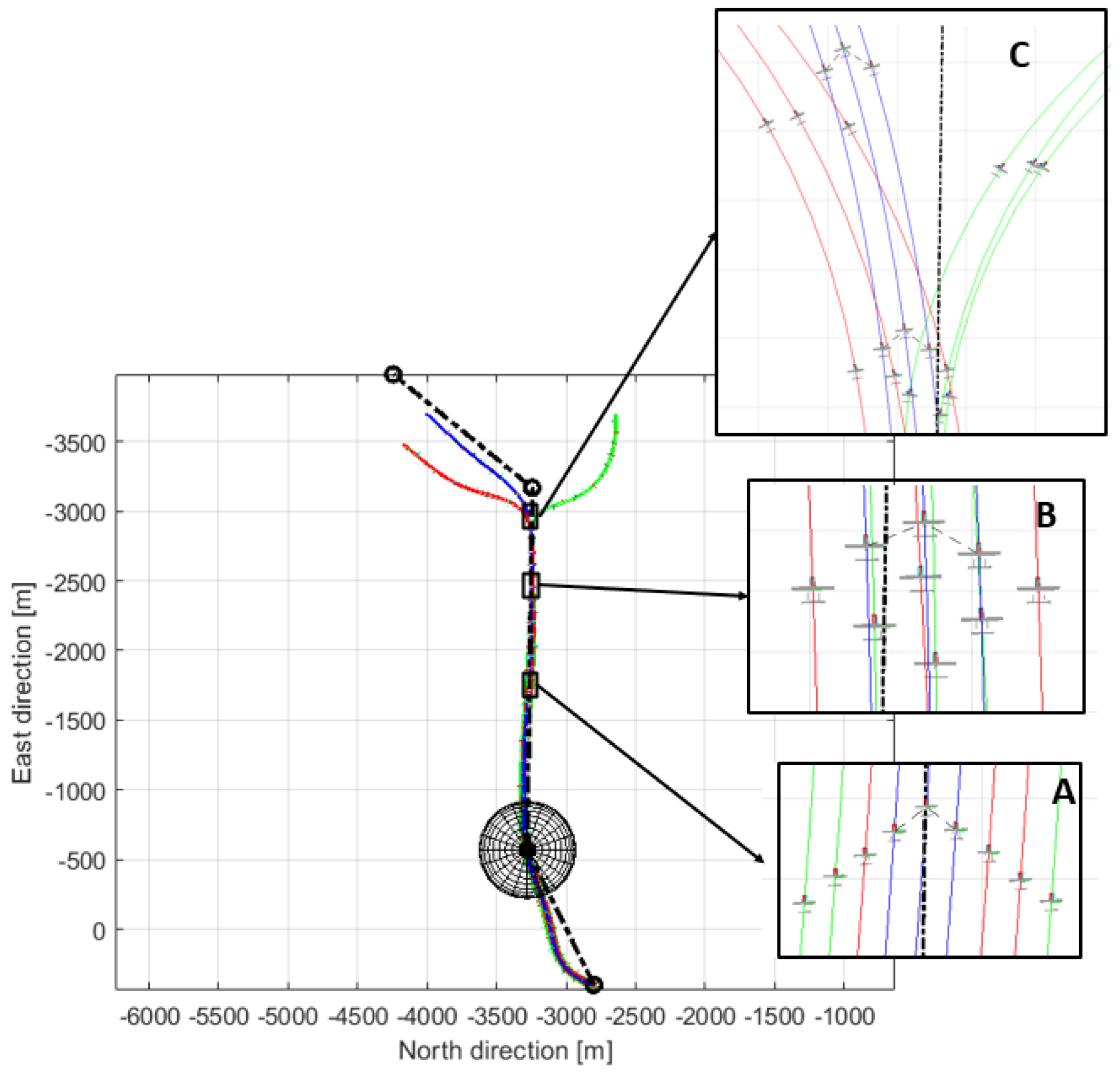
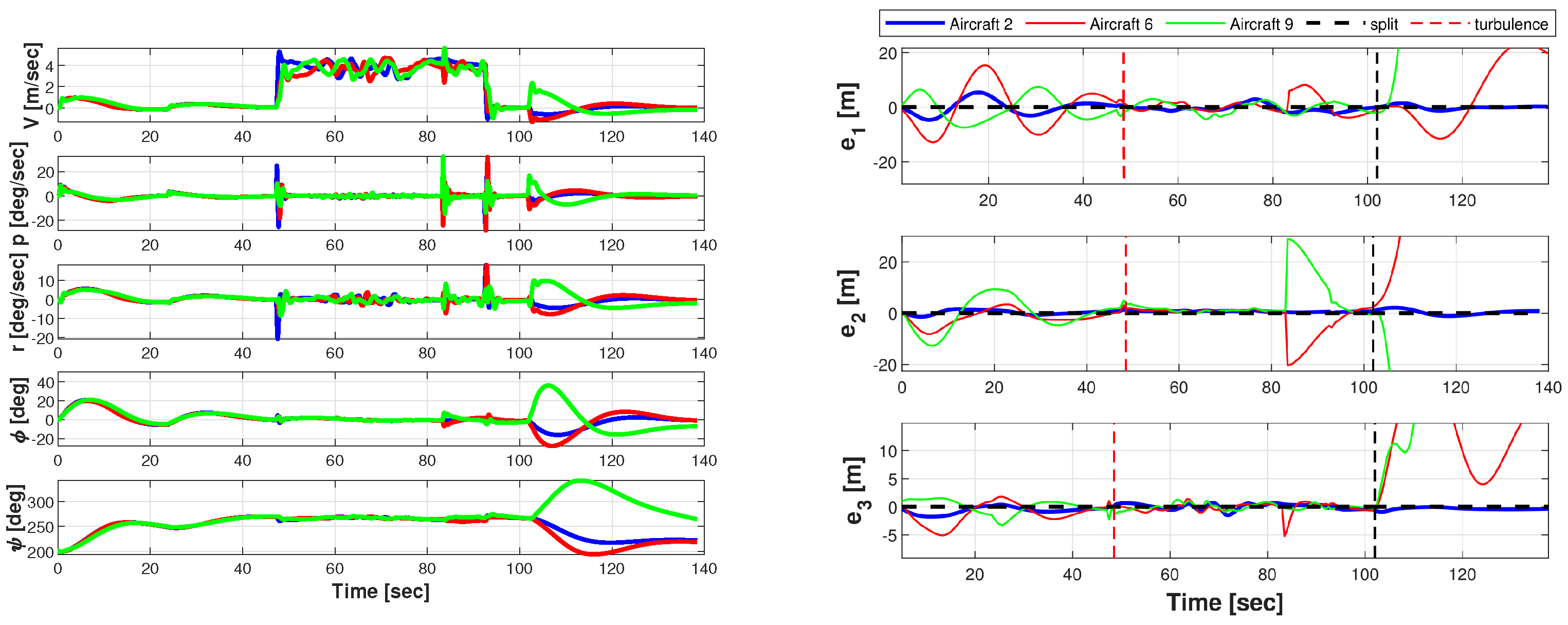
5.4.6. Phase 5: Disengagement and Formation Splitting
6. Conclusions
Future Perspectives
- Firstly, the possibility of significantly increasing the number of aircraft units within the swarm while establishing a proper hierarchy to ensure stability and robustness.
- Secondly, an analysis of potential swarm reconfiguration strategies in case of signal loss. For future research, an exploration of coordination logic based on local distance measurements using lasers, as opposed to relying solely on GPS data, could be pursued. This approach not only mitigates the risk of signal interception but also holds promise for enhanced operational security in military contexts.
- The potential implementation of additional control techniques for collision avoidance, both among swarm units and with environmental obstacles, as well as guidance strategies aiming at the mitigation of risk and discomfort induced by the overflight of unmanned machines and by noise, respectively, could represent a significant contribution to this research domain. These techniques and strategies aim to refine automation and enhance the system reliability in increasingly complex scenarios.
- Lastly, the optimal tuning of the control systems could be pursued to enhance their performance across a wide range of deployment scenarios. This could involve conducting extensive simulations to identify the optimal control settings and refine the control algorithms with the aim of maximizing the effectiveness, efficiency, and adaptability of the control systems in different mission scenarios.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Wang, X.; Shen, L.; Zhao, S.; Cong, Y.; Li, J.; Yin, D.; Jia, S.; Xiang, X. Mission Oriented Miniature Fixed-wing UAV Swarms: A Multi-layered and Distributed Architecture. IEEE Trans. Syst. Man Cybern. Syst. 2019, 52, 1588–1602. [Google Scholar] [CrossRef]
- Pham, H.X.; La, H.M.; Feil-Seifer, D.; Deans, M.C. A Distributed Control Framework of Multiple Unmanned Aerial Vehicles for Dynamic Wildfire Tracking. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 1537–1548. [Google Scholar] [CrossRef]
- Kubyshkin, E.P.; Kazakov, L.N.; Sterin, D.I. Mathematical modeling of flight reconfiguration of a unmanned aerial vehicles group. In Proceedings of the 2018 Systems of Signal Synchronization, Generating and Processing in Telecommunications (SYNCHROINFO), Minsk, Belarus, 4–5 July 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Qu, Y.; Zhang, Y.; Zhang, Y. A global path planning algorithm for fixed-wing UAVs. J. Intell. Robot. Syst. 2018, 91, 691–707. [Google Scholar] [CrossRef]
- Huang, C. A Novel Three-Dimensional Path Planning Method for Fixed-Wing UAV Using Improved Particle Swarm Optimization Algorithm. Int. J. Aerosp. Eng. 2021, 2021, 7667173. [Google Scholar] [CrossRef]
- Wang, X.; Shen, L.; Liu, Z.; Zhao, S.; Cong, Y.; Li, Z.; Jia, S.; Chen, H.; Yu, Y.; Chang, Y. Coordinated flight control of miniature fixed-wing UAV swarms: Methods and experiments. Sci. China Inf. Sci. 2019, 62, 212204. [Google Scholar] [CrossRef]
- Zhou, Y.; Rao, B.; Wang, W. UAV swarm intelligence: Recent advances and future trends. IEEE Access 2020, 8, 183856–183878. [Google Scholar] [CrossRef]
- Tang, J.; Duan, H.; Lao, S. Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review. Artif. Intell. Rev. 2023, 56, 4295–4327. [Google Scholar] [CrossRef]
- Abdelkader, M.; Samet, G.; Jaleel, H.; Shamma, J.S. Aerial swarms: Recent applications and challenges. Curr. Robot. Rep. 2021, 2, 309–320. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Layout analysis and optimization of airships with thrust-based stability augmentation. Aerospace 2022, 9, 393. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A.; Galbersanini, D. Retrofitting of an ultralight aircraft for unmanned flight and parachute cargo drops. J. Aerosp. Eng. 2023, 36, 04023029. [Google Scholar] [CrossRef]
- Salucci, F.; Riboldi, C.E.D.; Trainelli, L.; Rolando, A.; Mariani, L. A noise estimation procedure for electric and hybrid-electric aircraft. In Proceedings of the AIAA SciTech 2021 Forum, Online, 1–15 & 19–21 January 2021; p. 0258. [Google Scholar] [CrossRef]
- Rolando, A.; Rossi, F.; Riboldi, C.E.D.; Trainelli, L.; Grassetti, R.; Leonello, D.; Redaelli, M. The pilot acoustic indicator: A novel cockpit instrument for the greener helicopter pilot. In Proceedings of the 41st European Rotorcraft Forum, Munich, Germany, 1–4 September 2015. [Google Scholar]
- Trainelli, L.; Gennaretti, M.; Bernardini, G.; Rolando, A.; Riboldi, C.E.D.; Redaelli, M.; Riviello, L.; Scandroglio, A. Innovative helicopter in-flight noise monitoring systems enabled by rotor-state measurements. Noise Mapp. 2016, 3, 190–215. [Google Scholar] [CrossRef]
- Farì, S. Guidance and Control for a Fixed-Wing UAV. Master’s Thesis, Politecnico di Milano, Milano, Italy, 2016. [Google Scholar]
- Beard, R.W.; McLain, T.W. Small Unmanned Aircraft: Theory and Practice, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Israr, A.; Alkhammash, E.H.; Hadjouni, M. Guidance, Navigation, and Control for Fixed-Wing UAV. Math. Probl. Eng. 2021, 2021, 4355253. [Google Scholar] [CrossRef]
- Dat, N.T.; Son, T.N.; Tra, D.A. Development of a flight dynamics model for fixed wing aircraft. In Proceedings of the 10th International Conference on Computer Modeling and Simulation (ICCMS 2018), Sydney, Australia, 8–10 January 2018; pp. 202–205. [Google Scholar] [CrossRef]
- Mobarez, E.N.; Sarhan, A.; Ashry, M.M. Modeling of fixed wing UAV and design of multivariable flight controller using PID tuned by local optimal control. In Proceedings of the 18th International Conference on Aerospace Sciences & Aviation Technology, Cairo, Egypt, 9–11 April 2019. [Google Scholar] [CrossRef]
- Parunak, V.; Purcell, M.; O’Connell, R. Digital Pheromones for Autonomous Coordination of Swarming UAV’s. In Proceedings of the AIAA 1st Technical Conference and Workshop on Unmanned Aerospace Vehicles, Porstmouth, VA, USA, 20–23 May 2002. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Trainelli, L.; Capocchiano, C.; Cacciola, S. A model-based design framework for rotorcraft trim control laws. In Proceedings of the 43rd European Rotorcraft Forum (ERF 2017), Milan, Italy, 12–15 September 2017. [Google Scholar]
- Jin, Y.; Song, T.; Dai, C.; Wang, K.; Song, G. Autonomous UAV Chasing with Monocular Vision: A Learning-Based Approach. Aerospace 2024, 11, 928. [Google Scholar] [CrossRef]
- Chen, H.; Wang, X.; Shen, L.; Cong, Y. Formation flight of fixed-wing UAV swarms: A group-based hierarchical approach. Chin. J. Aeronaut. 2021, 34, 504–515. [Google Scholar] [CrossRef]
- Suo, W.; Wang, M.; Zhang, D.; Qu, Z.; Yu, L. Formation Control Technology of Fixed-Wing UAV Swarm Based on Distributed Ad Hoc Network. Appl. Sci. 2022, 12, 535. [Google Scholar] [CrossRef]
- Wang, P.K.C. Navigation Strategies for Multiple Autonomous Mobile Robots Moving in Formation. J. Robot. Syst. 1991, 8, 177–195. [Google Scholar] [CrossRef]
- Marina, H.G.D.; Kapitanyuk, Y.A.; Bronz, M.; Hattenberger, G.; Cao, M. Guidance algorithm for smooth trajectory tracking of a fixed wing UAV flying in wind flows. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2017), Singapore, 29 May–3 June 2017. [Google Scholar] [CrossRef]
- Siwek, M. Consensus-Based Formation Control with Time Synchronization for a Decentralized Group of Mobile Robots. Sensors 2024, 24, 3717. [Google Scholar] [CrossRef]
- Pamadi, B.N. Performance, Stability, Dynamics, and Control of Airplanes, 2nd ed.; AIAA Education Series; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2004. [Google Scholar]
- Riboldi, C.E.D. Flight Dynamics: Modeling, Characterization and Performance; Esculapio: Bologna, Italy, 2024. [Google Scholar]
- Vechtel, D.; Fischenberg, D.; Schwithal, J. Flight dynamics simulation of formation flight for energy saving using LES-generated wake flow fields. CEAS Aeronaut. J. 2018, 9, 735–746. [Google Scholar] [CrossRef]
- Bangash, Z.A.; Sanchez, R.P.; Ahmed, A.; Khan, M.J. Aerodynamics of formation flight. J. Aircr. 2006, 43, 907–912. [Google Scholar] [CrossRef]
- Larson, G.; Schkolnik, G. Autonomous Formation Flight. Presentation from the transcripts of MIT Course 16.886 on Air Transportation Systems Architecting. 2004. Available online: https://ocw.mit.edu/courses/16-886-air-transportation-systems-architecting-spring-2004/1265be456f2d57218356ad48572ad150_02_greg_larson1.pdf (accessed on 9 March 2025).
- Singh, D.; Antoniadis, A.F.; Tsoutsanis, P.; Shin, H.S.; Tsourdos, A.; Mathekga, S.; Jenkins, K.W. A Multi-Fidelity Approach for Aerodynamic Performance Computations of Formation Flight. Aerospace 2018, 5, 66. [Google Scholar] [CrossRef]
- Giulietti, F.; Innocenti, M.; Napolitano, M.; Pollini, L. Dynamic and control issues of formation flight. Aerosp. Sci. Technol. 2005, 9, 65–71. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Rolando, A. Thrust-Based Stabilization and Guidance for Airships without Thrust-Vectoring. Aerospace 2023, 10, 344. [Google Scholar] [CrossRef]
- Riboldi, C.E.D.; Tomasoni, M. Dynamic Simulation, Flight Control and Guidance Synthesis for Fixed Wing UAV Swarms. In Proceedings of the Joint 10th European Conference for Aerospace Sciences (EUCASS) and 9th Conference of the Council of European Aerospace Societies (CEAS), Lausanne, Switzerland, 10–13 July 2023. [Google Scholar]
- Blakelock, J.H. Automatic control of Aircraft and Missiles, 2nd ed.; John Wiley and Sons, Inc.: New York, NY, USA, 1991. [Google Scholar]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems, 3rd ed.; Wiley-Blackwell: Hoboken, NJ, USA, 2015. [Google Scholar]
- Griffiths, S.R. Vector Field Approach for Curved Path Following for Miniature Aerial Vehicles. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Park, S. Rendezvous Guidance on Circular Path for Fixed-Wing UAV. Int. J. Aeronaut. Space Sci. 2021, 22, 129–139. [Google Scholar] [CrossRef]
- Park, S. Circling over a target with relative side bearing. J. Guid. Control. Dyn. 2016, 39, 1450–1456. [Google Scholar] [CrossRef]
- Bray, R.M. A Wind Tunnel Study of the Pioneer Remotely Piloted Vehicle. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 1991. [Google Scholar]
- Melin, T. Tornado 1.0 User’s Guide. Reference Manual; KTH—Institutionen för flygteknik Teknikringen: Stockholm, Sweden, 2000. [Google Scholar]











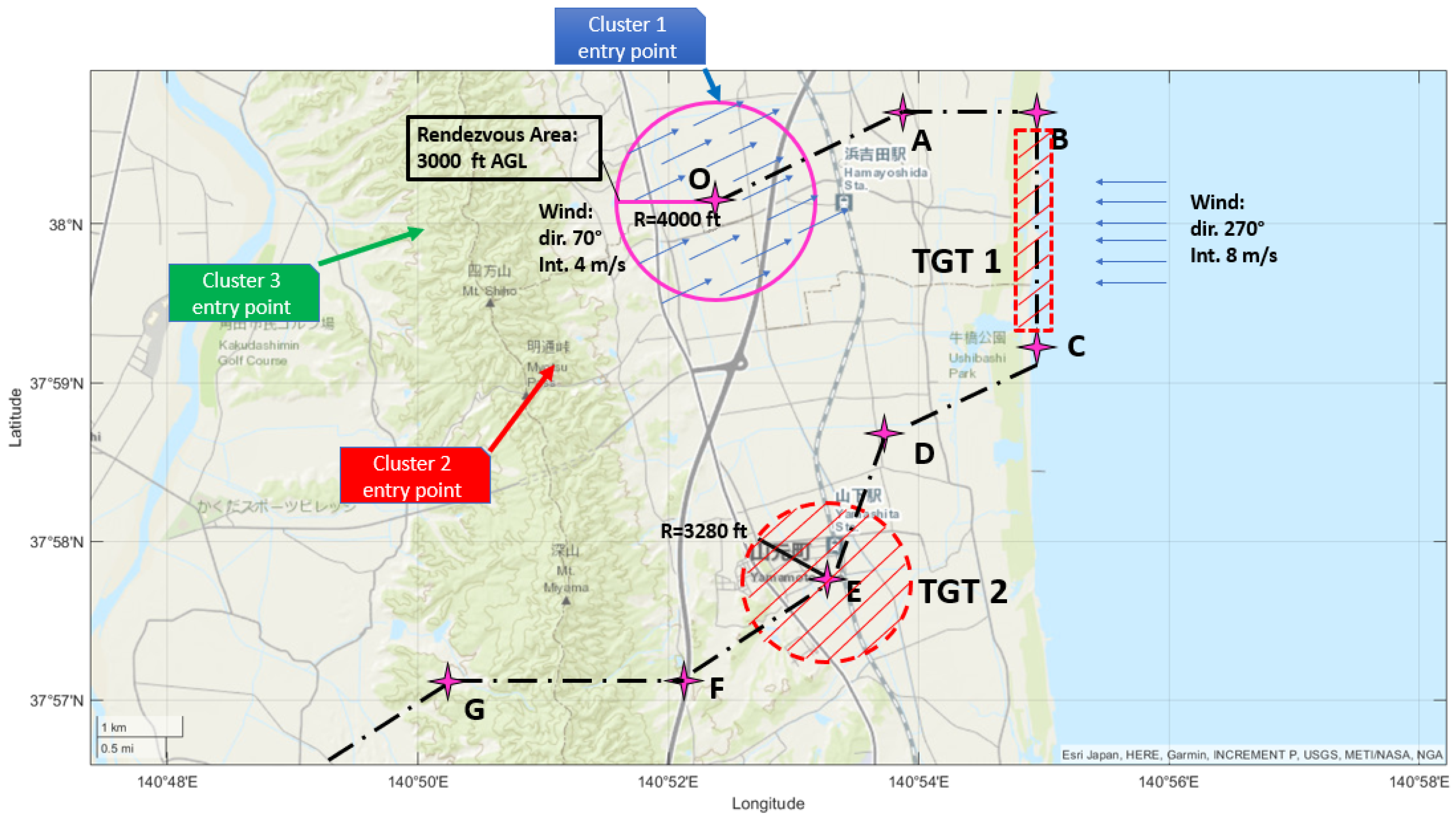


| Rendezvous | ||||
|---|---|---|---|---|
| Orbit center | Orbit radius | Altitude | Velocity | Additional notes |
| 38°01′ N, 140°53′ E | 1200 m | 900 m | 120 km/h | Wind: deg, int. 4 m/s |
| Waypoint navigation | ||||
| Leg | Length | Velocity | Additional notes | |
| O-A, deg | 2400 m | m | 130 km/h | Formation geom. switch—V. |
| A-B, deg | 1500 m | m | 130 km/h | - |
| B-C, deg | 3100 m | m | 130 km/h | Wind: , int. 8 m/s |
| C-D, deg | 2000 m | m | 130 km/h | Formation geom. switch—D. |
| D-E, deg | 2000 m | m | 130 km/h | - |
| Loiter | ||||
| Orbit center | Orbit radius | Altitude | Velocity | Additional notes |
| 37°57′ N, 140°53′ E | 1000 m | 400 m | 120 km/h | - |
| Waypoint navigation | ||||
| Leg | Length | Velocity | Additional notes | |
| E-F, deg | 2000 m | m | 130 km/h | Formation geom. switch—V. |
| F-G, deg | 2600 m | m | 130 km/h | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riboldi, C.E.D.; Tomasoni, M. Formation Flight of Fixed-Wing UAVs: Dynamic Modeling, Guidance Design, and Testing in Realistic Scenarios. Aerospace 2025, 12, 260. https://doi.org/10.3390/aerospace12030260
Riboldi CED, Tomasoni M. Formation Flight of Fixed-Wing UAVs: Dynamic Modeling, Guidance Design, and Testing in Realistic Scenarios. Aerospace. 2025; 12(3):260. https://doi.org/10.3390/aerospace12030260
Chicago/Turabian StyleRiboldi, Carlo E.D., and Marco Tomasoni. 2025. "Formation Flight of Fixed-Wing UAVs: Dynamic Modeling, Guidance Design, and Testing in Realistic Scenarios" Aerospace 12, no. 3: 260. https://doi.org/10.3390/aerospace12030260
APA StyleRiboldi, C. E. D., & Tomasoni, M. (2025). Formation Flight of Fixed-Wing UAVs: Dynamic Modeling, Guidance Design, and Testing in Realistic Scenarios. Aerospace, 12(3), 260. https://doi.org/10.3390/aerospace12030260







