Electromechanical Resonant Ice Protection Systems Using Extensional Modes: Optimization of Composite Structures
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Background
2.1.1. Extensional and Flexural Modes Decoupling
2.1.2. Substrate Material Selection
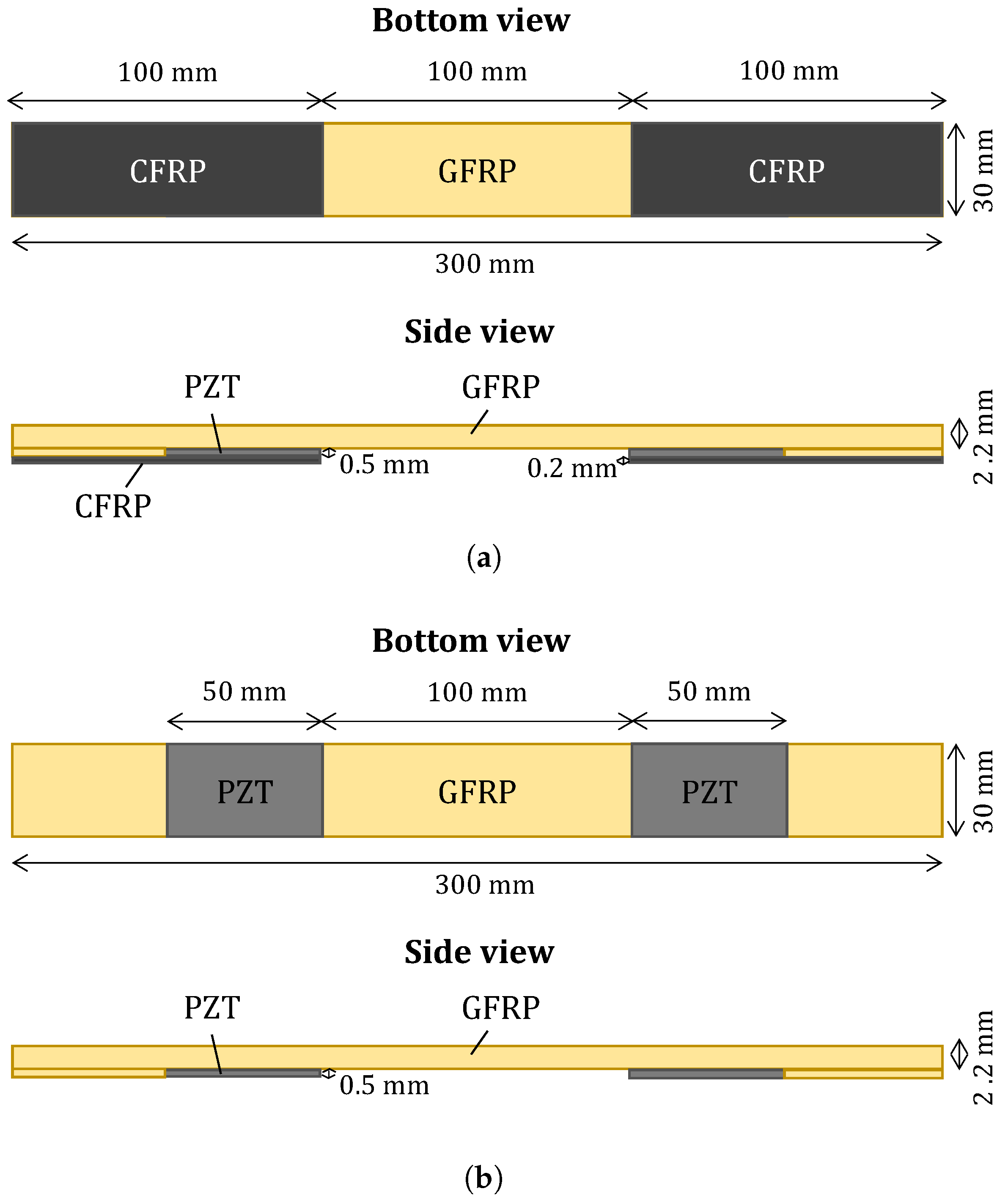
2.2. Beam—Preliminary Study and Fabrication
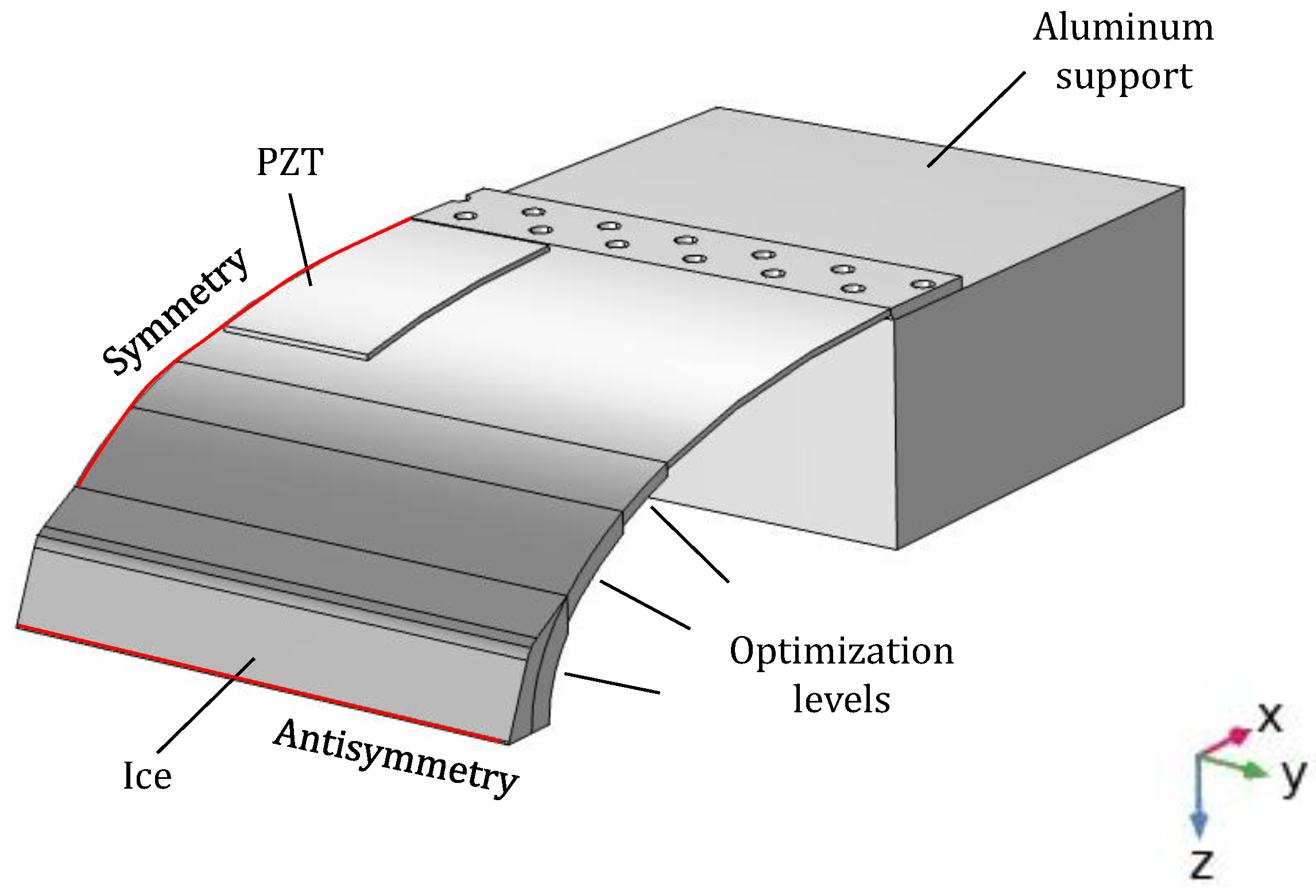
2.3. Curved Composite Structure Study
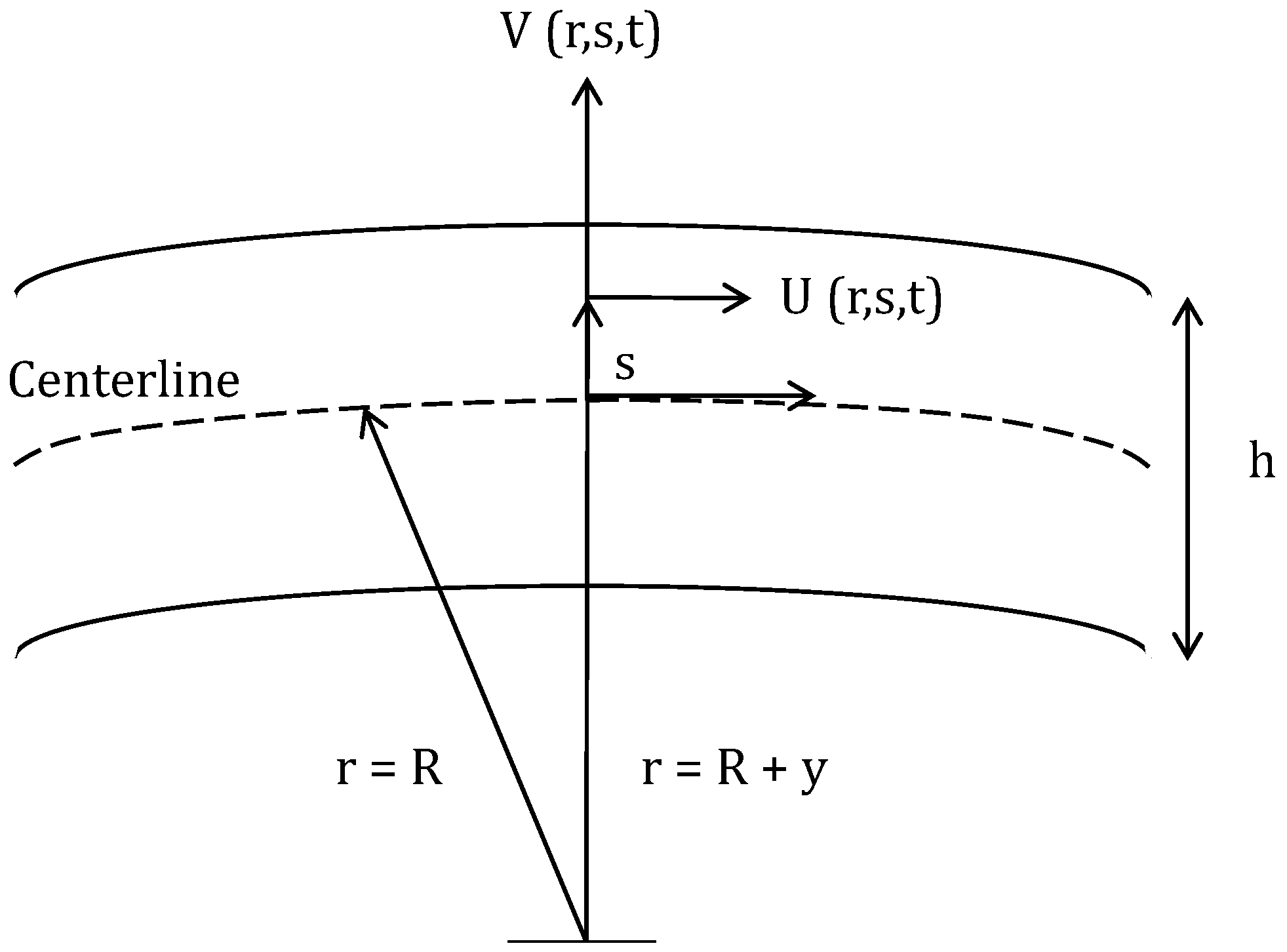
2.3.1. Coupled Wave Equations
2.3.2. Coupling Analysis with Rayleigh Method
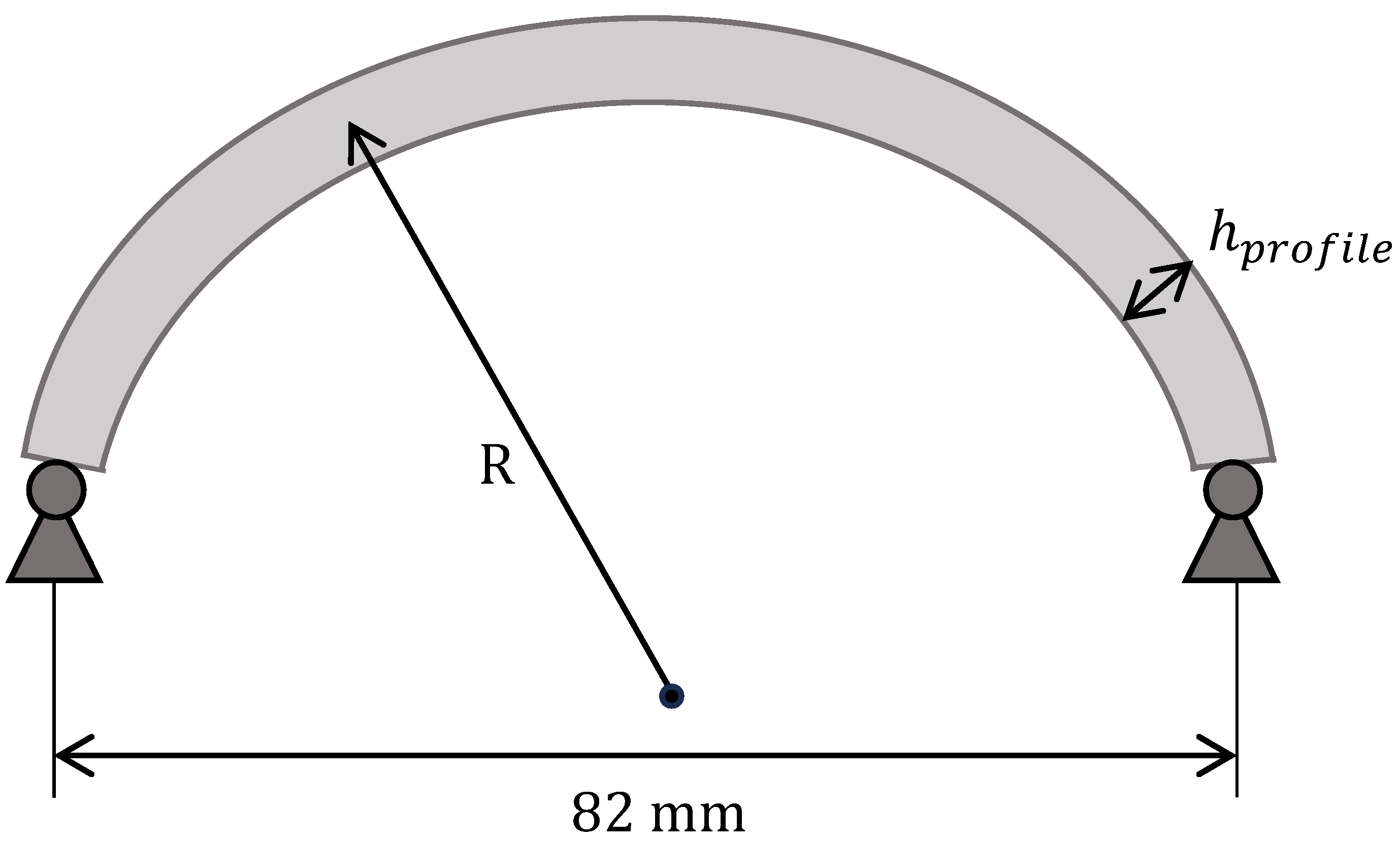
2.3.3. Case Study
3. Results and Discussion
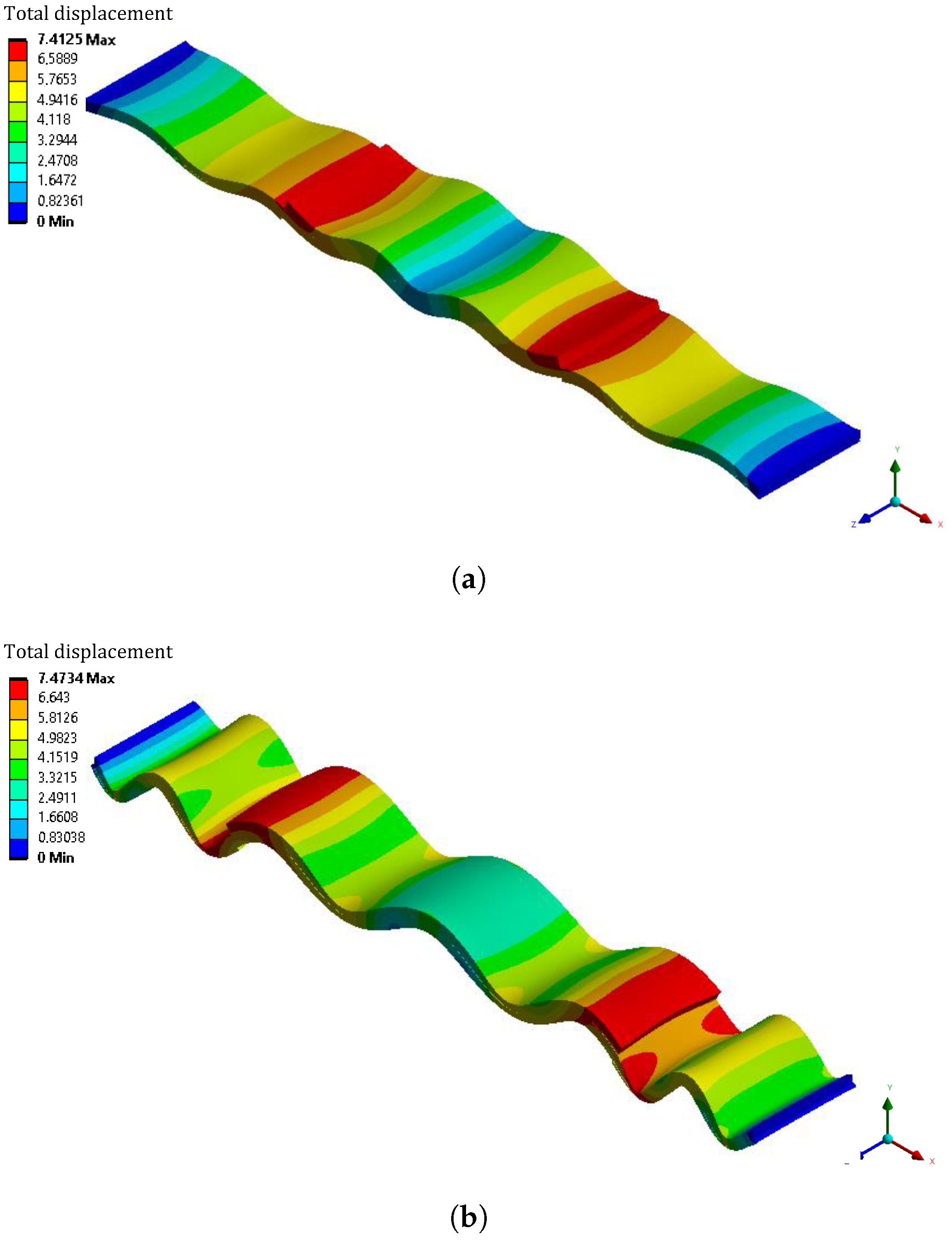
3.1. Beam—Numerical Study and Experimental Validation
3.1.1. Numerical Study
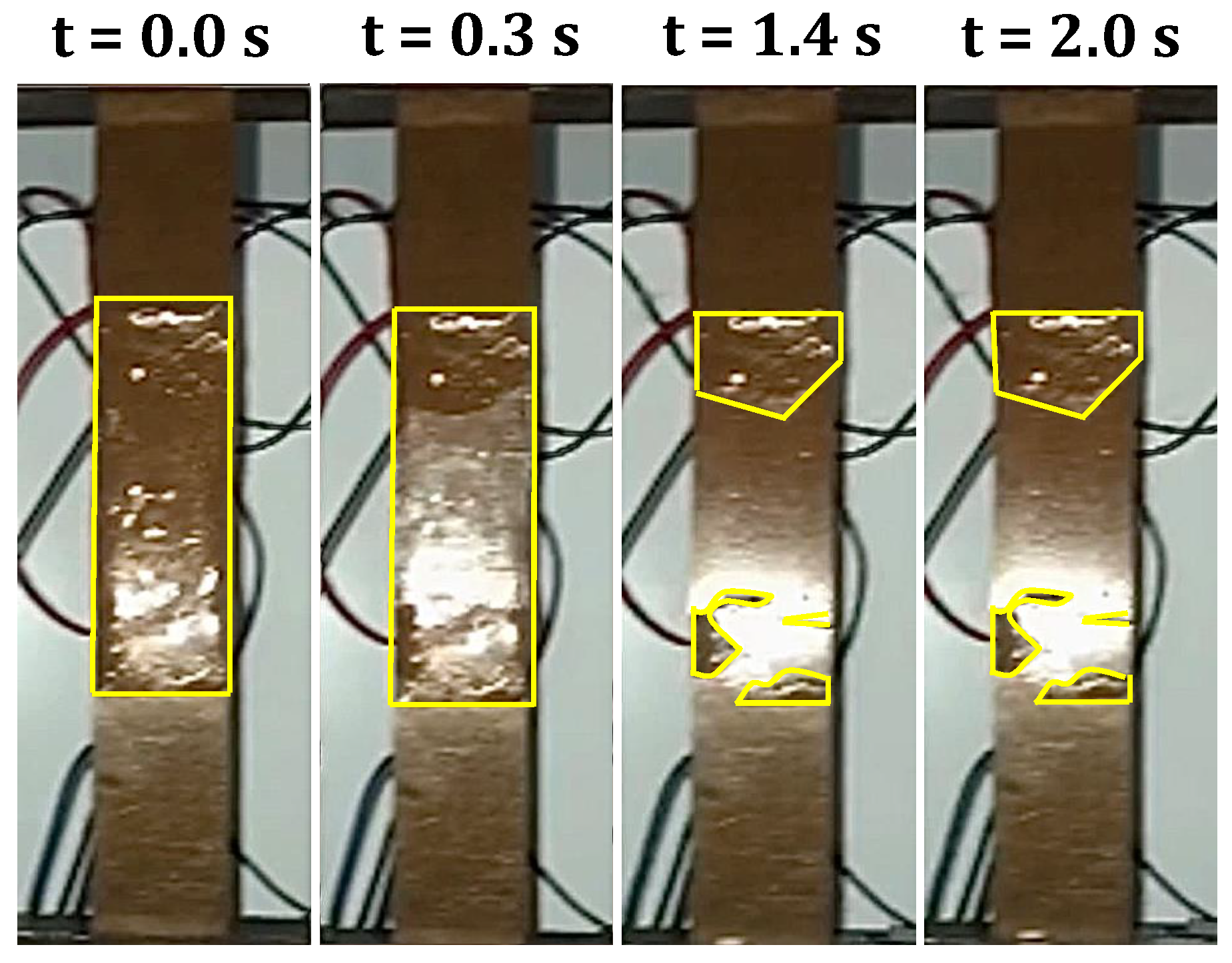
3.1.2. Experimental Validation
3.1.3. Discussion
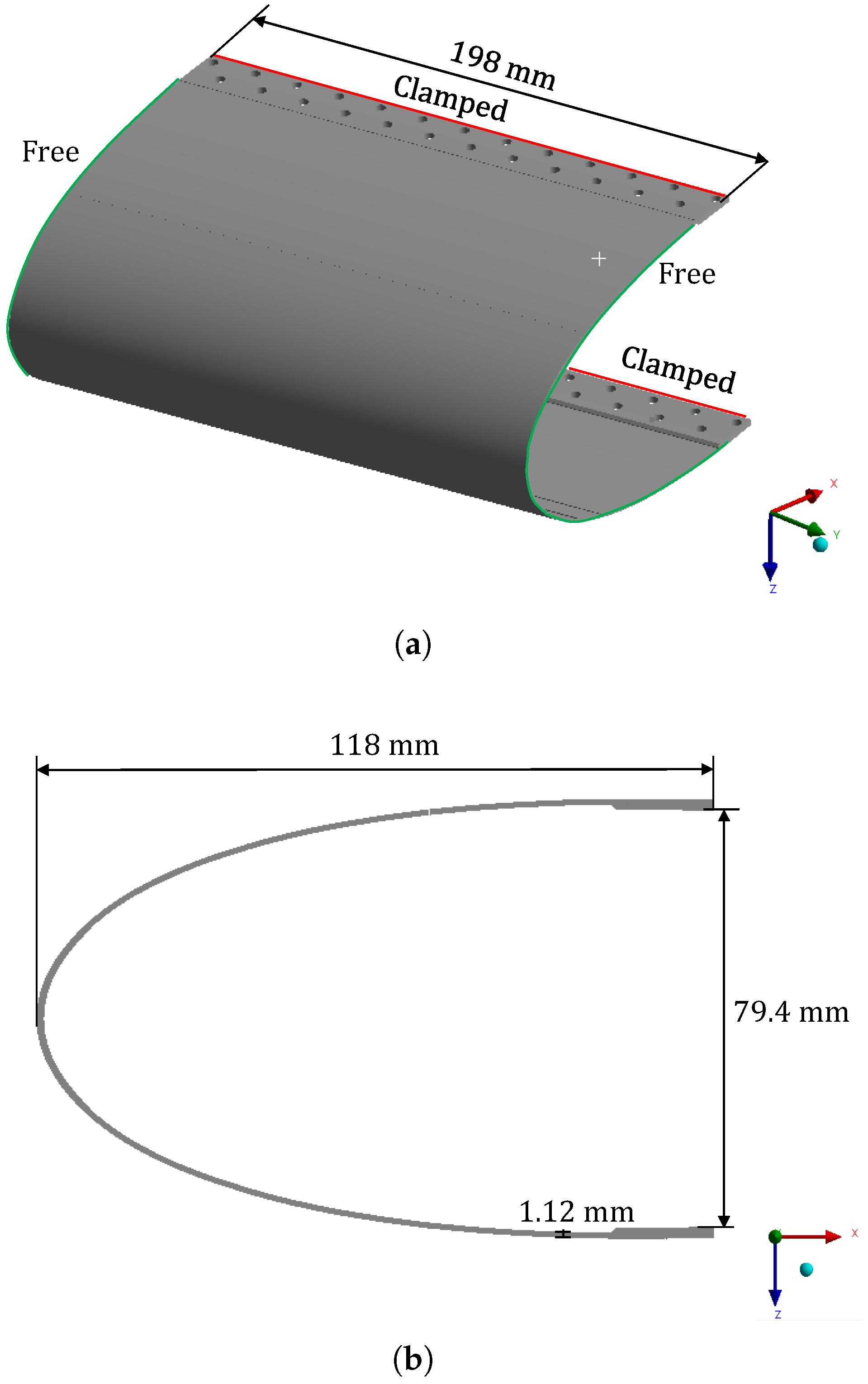
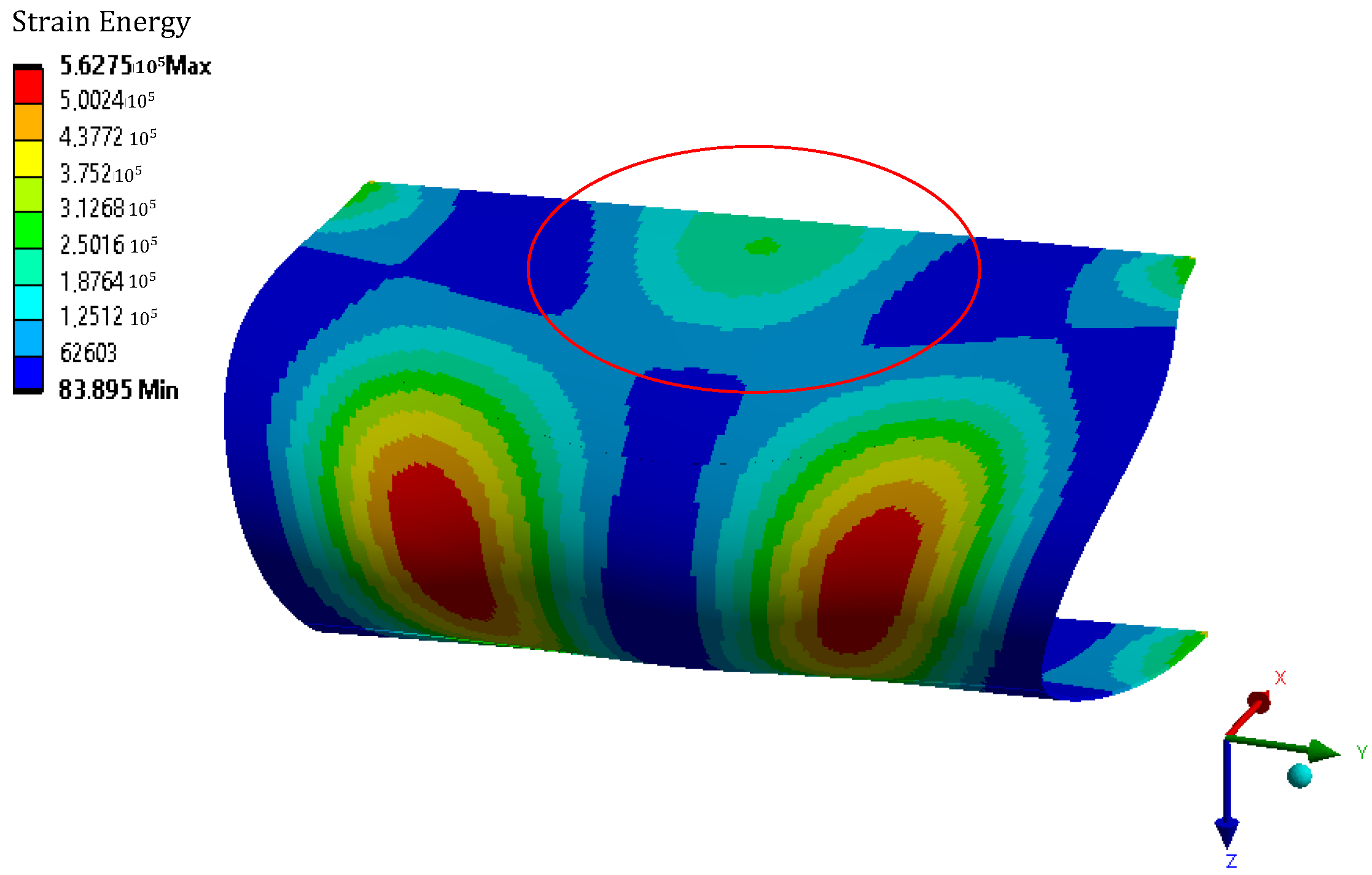
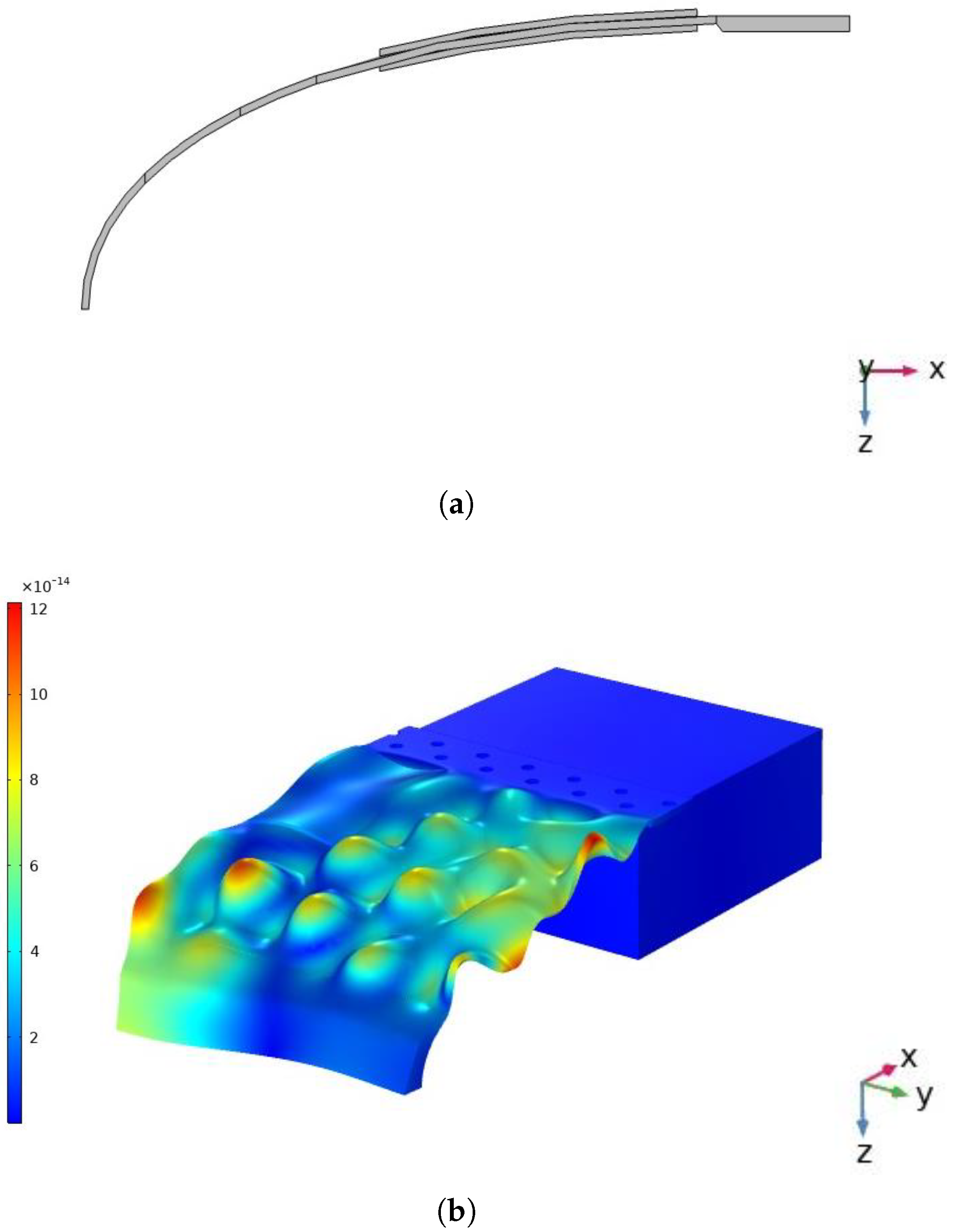
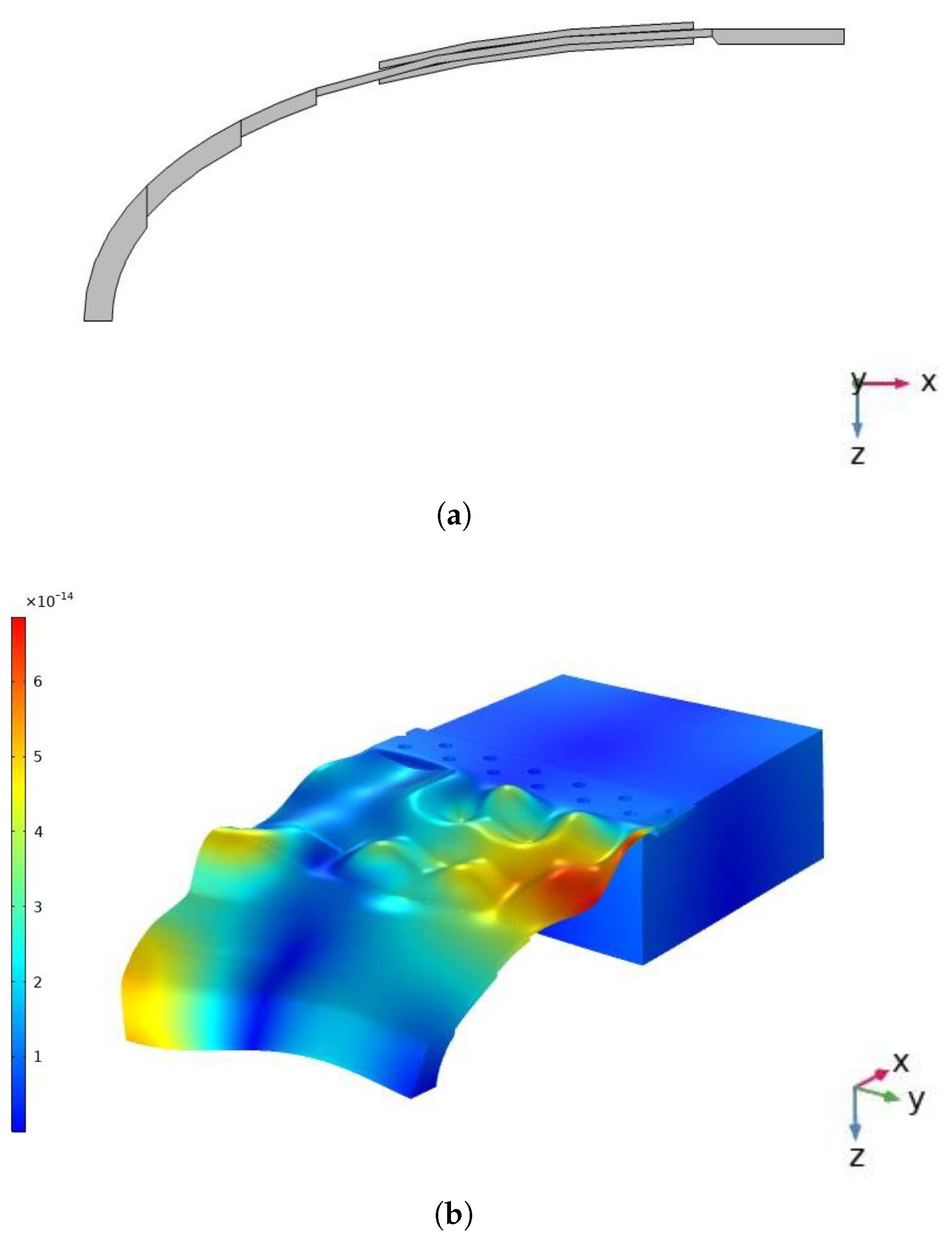
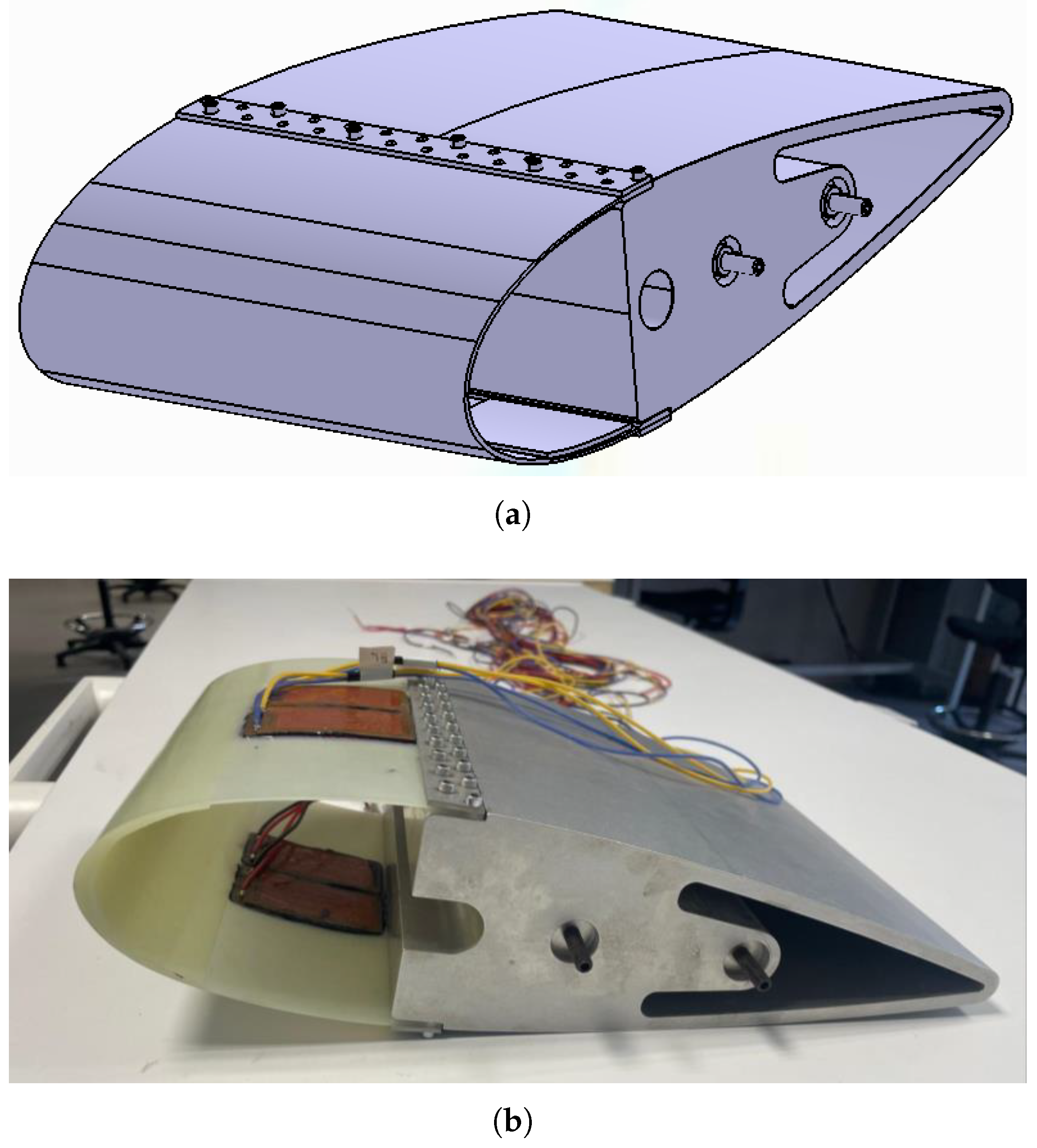
3.2. Leading Edge—Numerical Study and Experimental Validation
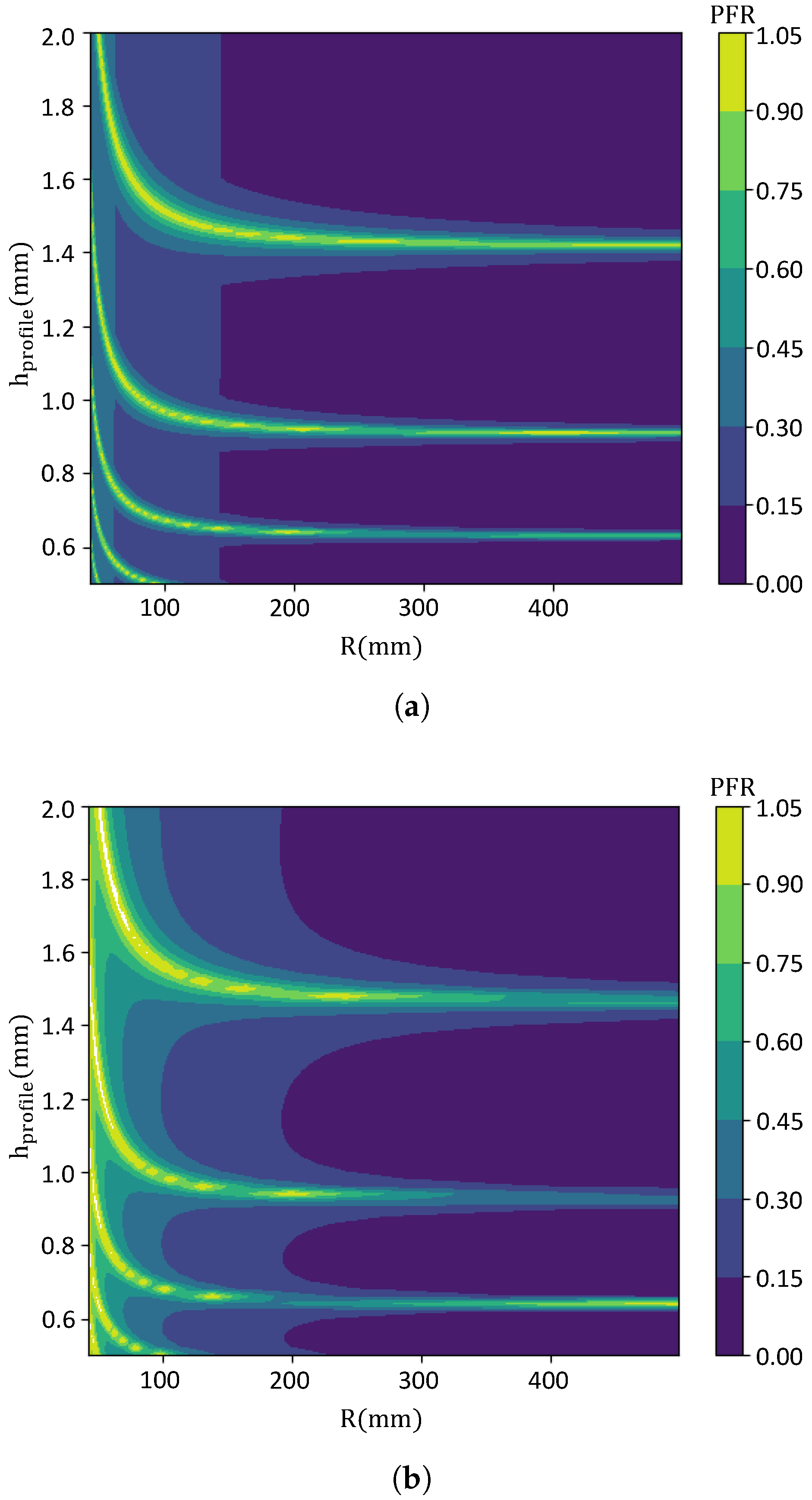
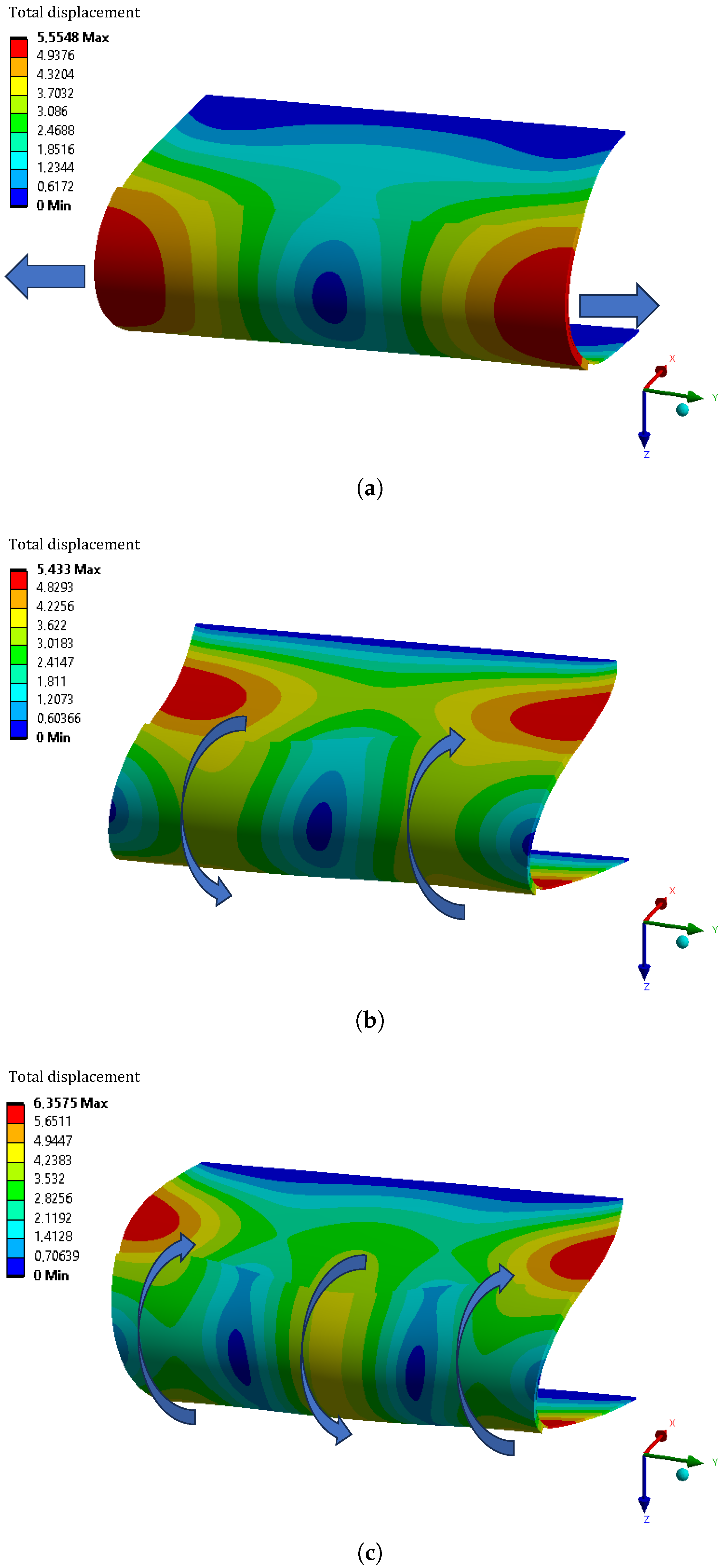
3.2.1. Numerical Study
3.2.2. Experimental Validation
3.2.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IWT | Icing Wind Tunnel |
| LWC | Liquid Water Content |
| MVD | Median Volumetric Diameter |
| PFR | Parasitic Flexural Ratio |
| CFRP | Carbon-Fiber-Reinforced Polymer |
| GFRP | Glass-Fiber-Reinforced Polymer |
| FEM | Finite Element Method |
| PZT | Lead Zirconate Titanate |
References
- Gent, R.W.; Dart, N.P.; Cansdale, J.T. Aircraft icing. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2000, 358, 2873–2911. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Lynch, F.T.; Khodadoust, A. Effects of ice accretions on aircraft aerodynamics. Prog. Aerosp. Sci. 2001, 37, 669–767. [Google Scholar] [CrossRef]
- Bragg, M.B.; Broeren, A.P.; Blumenthal, L.A. Iced-airfoil aerodynamics. Prog. Aerosp. Sci. 2005, 41, 323–362. [Google Scholar] [CrossRef]
- Vercillo, V.; Karpen, N.; Laroche, A.; Guillén, J.A.M.; Tonnicchia, S.; de Andrade Jorge, R.; Bonaccurso, E. Analysis and modelling of icing of air intake protection grids of aircraft engines. Cold Reg. Sci. Technol. 2019, 160, 265–272. [Google Scholar] [CrossRef]
- Thomas, S.K.; Cassoni, R.P.; MacArthur, C.D. Aircraft anti-icing and de-icing techniques and modeling. J. Aircr. 1996, 33, 841–854. [Google Scholar] [CrossRef]
- Sinnett, M. 787 no-bleed systems: Saving fuel and enhancing operational efficiencies. Aero Q. 2007, 18, 6–11. [Google Scholar]
- Meier, O.; Scholz, D. A Handbook Method for the Estimation of Power Requirements for Electrical De-Icing Systems; DLRK: Hamburg, Germany, 2010; Volume 31. [Google Scholar]
- Gallia, M.; Guardone, A.; Congedo, P.M. Novel Framework for the Robust Optimization of the Heat Flux Distribution for an Electro-Thermal Ice Protection System and Airfoil Performance Analysis; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 2023. [Google Scholar]
- Hann, R.; Enache, A.; Nielsen, M.C.; Stovner, B.N.; van Beeck, J.; Johansen, T.A.; Borup, K.T. Experimental heat loads for electrothermal anti-icing and de-icing on UAVs. Aerospace 2021, 8, 83. [Google Scholar] [CrossRef]
- Martin, C.A.; Putt, J.C. Advanced pneumatic impulse ice protection system (PIIP) for aircraft. J. Aircr. 1992, 29, 714–716. [Google Scholar] [CrossRef]
- Palanque, V.; Planès, T.; Pommier-Budinger, V.; Budinger, M.; Delbecq, S. Piezoelectric resonant ice protection systems Part 2/2: Evaluation of benefits at aircraft level. Chin. J. Aeronaut. 2024, 37, 92–103. [Google Scholar] [CrossRef]
- Ramanathan, S.; Varadan, V.V.; Varadan, V.K. Deicing of helicopter blades using piezoelectric actuators. In Proceedings of the Smart Structures and Materials 2000: Smart Electronics and MEMS, Newport Beach, CA, USA, 6–8 March 2000; International Society for Optics and Photonics: Newport Beach, CA, 2000; Volume 3990, pp. 281–292. [Google Scholar]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Instantaneous de-icing of freezer ice via ultrasonic actuation. AIAA J. 2011, 49, 1158–1167. [Google Scholar] [CrossRef]
- Palacios, J.; Smith, E.; Rose, J.; Royer, R. Ultrasonic de-icing of wind-tunnel impact icing. J. Aircr. 2011, 48, 1020–1027. [Google Scholar] [CrossRef]
- Bai, T.; Zhu, C.; Miao, B.; Li, K.; Zhu, C. Vibration de-icing method with piezoelectric actuators. J. Vibroeng. 2015, 17, 61–73. [Google Scholar]
- Villeneuve, E.; Harvey, D.; Zimcik, D.; Aubert, R.; Perron, J. Piezoelectric deicing system for rotorcraft. J. Am. Helicopter Soc. 2015, 60, 1–12. [Google Scholar] [CrossRef]
- Villeneuve, E.; Volat, C.; Ghinet, S. Numerical and experimental investigation of the design of a piezoelectric de-icing system for small rotorcraft part 3/3: Numerical model and experimental validation of vibration-based de-icing of a flat plate structure. Aerospace 2020, 7, 54. [Google Scholar] [CrossRef]
- Palanque, V.; Pothin, J.; Pommier-Budinger, V.; Budinger, M. Piezoelectric resonant ice protection systems–Part 1/2: Prediction of power requirement for de-icing a NACA 0024 leading edge. Chin. J. Aeronaut. 2024, 37, 92–103. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Lei, Y. An effect assessment and prediction method of ultrasonic de-icing for composite wind turbine blades. Renew. Energy 2018, 118, 1015–1023. [Google Scholar] [CrossRef]
- Zhu, Y.; Palacios, J.; Rose, J.; Smith, E. De-icing of multi-layer composite plates using ultrasonic guided waves. In Proceedings of the 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 16th AIAA/ASME/AHS Adaptive Structures Conference, 10th AIAA Non-Deterministic Approaches Conference, 9th AIAA Gossamer Spacecraft Forum, 4th AIAA Multidisciplinary Design Optimization Specialists Conference, Schaumburg, IL, USA, 7–10 April 2008; p. 1862. [Google Scholar]
- Budinger, M.; Pommier-Budinger, V.; Bennani, L.; Rouset, P.; Bonaccurso, E.; Dezitter, F. Electromechanical resonant ice protection systems: Analysis of fracture propagation mechanisms. AIAA J. 2018, 56, 4412–4422. [Google Scholar] [CrossRef]
- Budinger, M.; Pommier-Budinger, V.; Reysset, A.; Palanque, V. Electromechanical resonant ice protection systems: Energetic and power considerations. AIAA J. 2021, 59, 2590–2602. [Google Scholar] [CrossRef]
- Gastaldo, G.; Budinger, M.; Rafik, Y.; Pommier-Budinger, V.; Palanque, V.; Yaich, A. Full instantaneous de-icing using extensional modes: The role of architectured and multilayered materials in modes decoupling. Ultrasonics 2024, 138, 107264. [Google Scholar] [CrossRef]
- Palanque, V.; Villeneuve, É.; Budinger, M.; Pommier-Budinger, V.; Momen, G. Experimental measurement and expression of atmospheric ice Young’s modulus according to its density. Cold Reg. Sci. Technol. 2023, 212, 103890. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology optimization I—homogenization theory for media with periodic structure. Comput. Struct. 1998, 69, 707–717. [Google Scholar] [CrossRef]
- Hassani, B.; Hinton, E. A review of homogenization and topology opimization II—analytical and numerical solution of homogenization equations. Comput. Struct. 1998, 69, 719–738. [Google Scholar] [CrossRef]
- Andreassen, E.; Andreasen, C.S. How to determine composite material properties using numerical homogenization. Comput. Mater. Sci. 2014, 83, 488–495. [Google Scholar] [CrossRef]
- Gay, D. Composite Materials: Design and Applications; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Weaver, W., Jr.; Timoshenko, S.P.; Young, D.H. Vibration Problems in Engineering; John Wiley & Sons: Hoboken, NJ, USA, 1991. [Google Scholar]
- Palanque, V. Design of Low Consumption Electro-Mechanical De-Icing Systems. Ph.D. Thesis, Université de Toulouse, Toulouse, France, ISAE-Supaero, Toulouse, France, 2022. [Google Scholar]



| Ef (GPa) | (kg/m3) | Vf (%) | Em (GPa) | (kg/m3) | |
|---|---|---|---|---|---|
| GFRP | 74 | 2580 | 58 | 4.67 | 1301 |
| CFRP | 231 | 1770 | 55.29 | 4.67 | 1301 |
| Eeq (GPa) | (kg/m3) | (m/s) | |
|---|---|---|---|
| GFRP | 17.1 | 1826 | 3060 |
| CFRP | 67 | 1570 | 6532 |
| hice | 2 mm | 2.5 mm | 3 mm | 3.5 mm | 4 mm | 4.5 mm |
|---|---|---|---|---|---|---|
| PFR—Unoptimized | 0.35 | 0.64 | 0.32 | 0.27 | 0.18 | 0.24 |
| PFR—Optimized | 0.15 | 0.27 | 0.11 | 0.08 | 0.07 | 0.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gastaldo, G.; Rafik, Y.; Budinger, M.; Pommier-Budinger, V. Electromechanical Resonant Ice Protection Systems Using Extensional Modes: Optimization of Composite Structures. Aerospace 2025, 12, 255. https://doi.org/10.3390/aerospace12030255
Gastaldo G, Rafik Y, Budinger M, Pommier-Budinger V. Electromechanical Resonant Ice Protection Systems Using Extensional Modes: Optimization of Composite Structures. Aerospace. 2025; 12(3):255. https://doi.org/10.3390/aerospace12030255
Chicago/Turabian StyleGastaldo, Giulia, Younes Rafik, Marc Budinger, and Valérie Pommier-Budinger. 2025. "Electromechanical Resonant Ice Protection Systems Using Extensional Modes: Optimization of Composite Structures" Aerospace 12, no. 3: 255. https://doi.org/10.3390/aerospace12030255
APA StyleGastaldo, G., Rafik, Y., Budinger, M., & Pommier-Budinger, V. (2025). Electromechanical Resonant Ice Protection Systems Using Extensional Modes: Optimization of Composite Structures. Aerospace, 12(3), 255. https://doi.org/10.3390/aerospace12030255






