Experimental Validation of Clamping-Type Mesh Fastening Method Using Thin Plates and Push-Button Rivets for Deployable Mesh Antennas
Abstract
1. Introduction
2. Design Description of the Clamping-Type Mesh Fastening Method
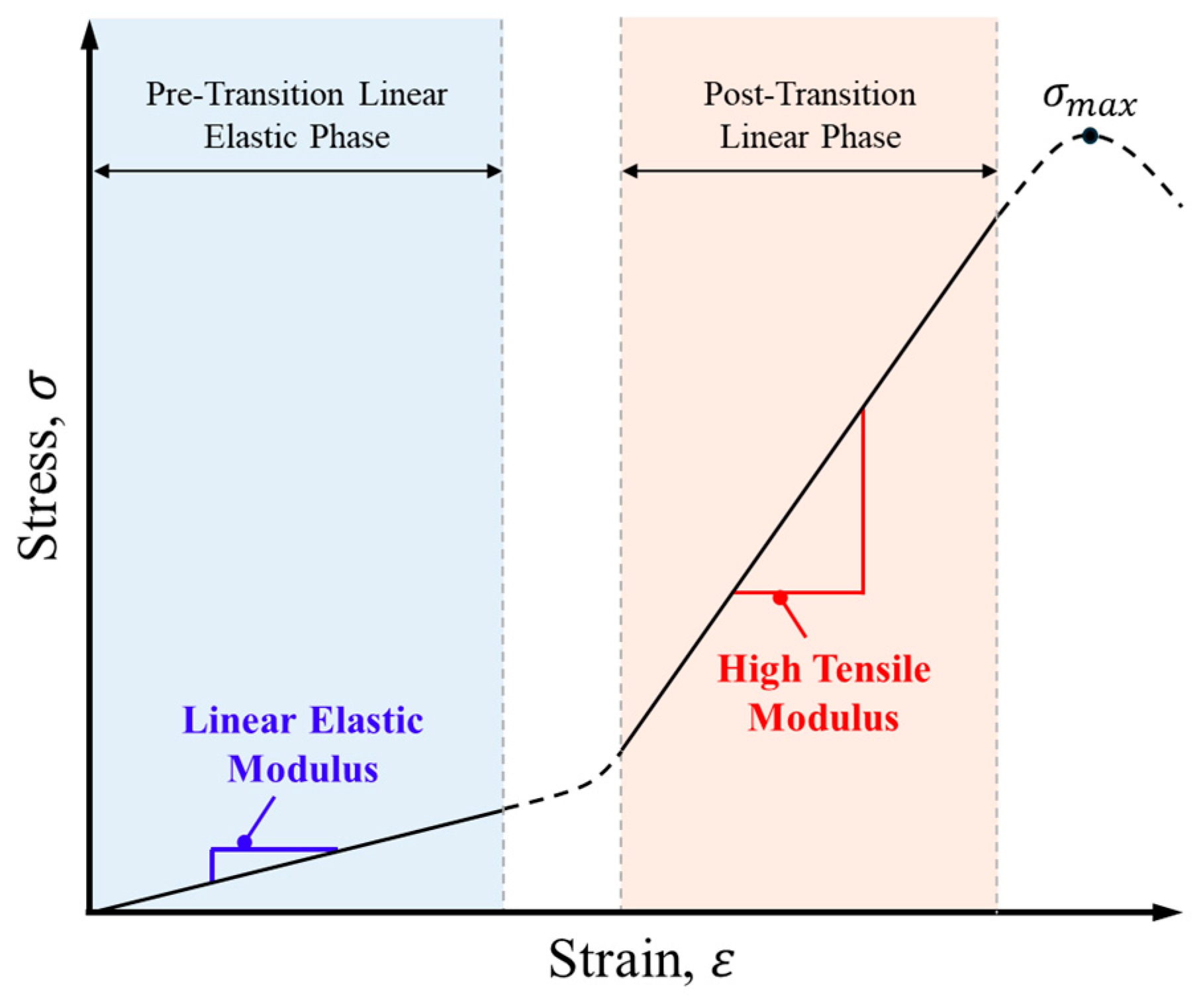
2.1. Overview of Mesh Fabrics for Space Applications
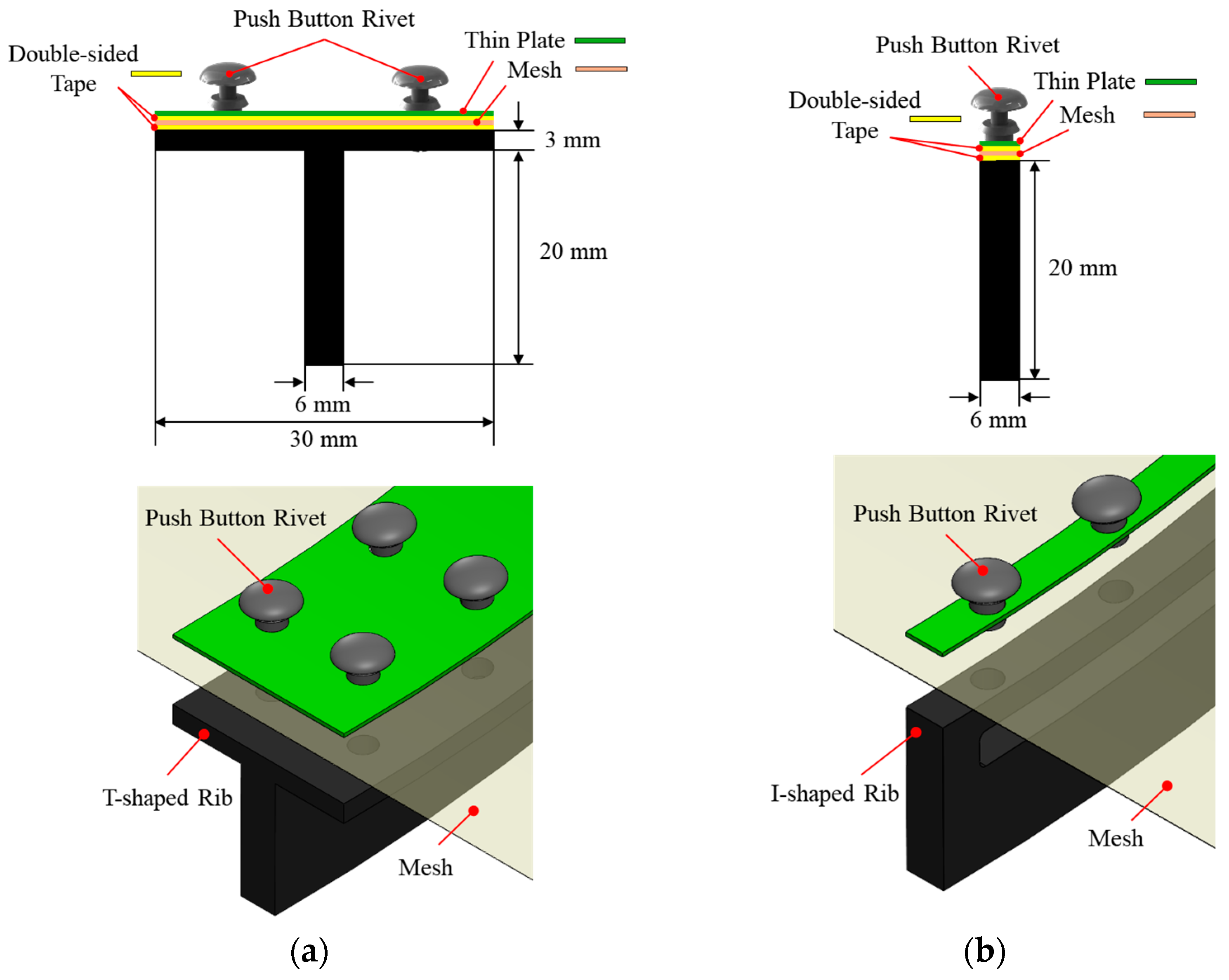
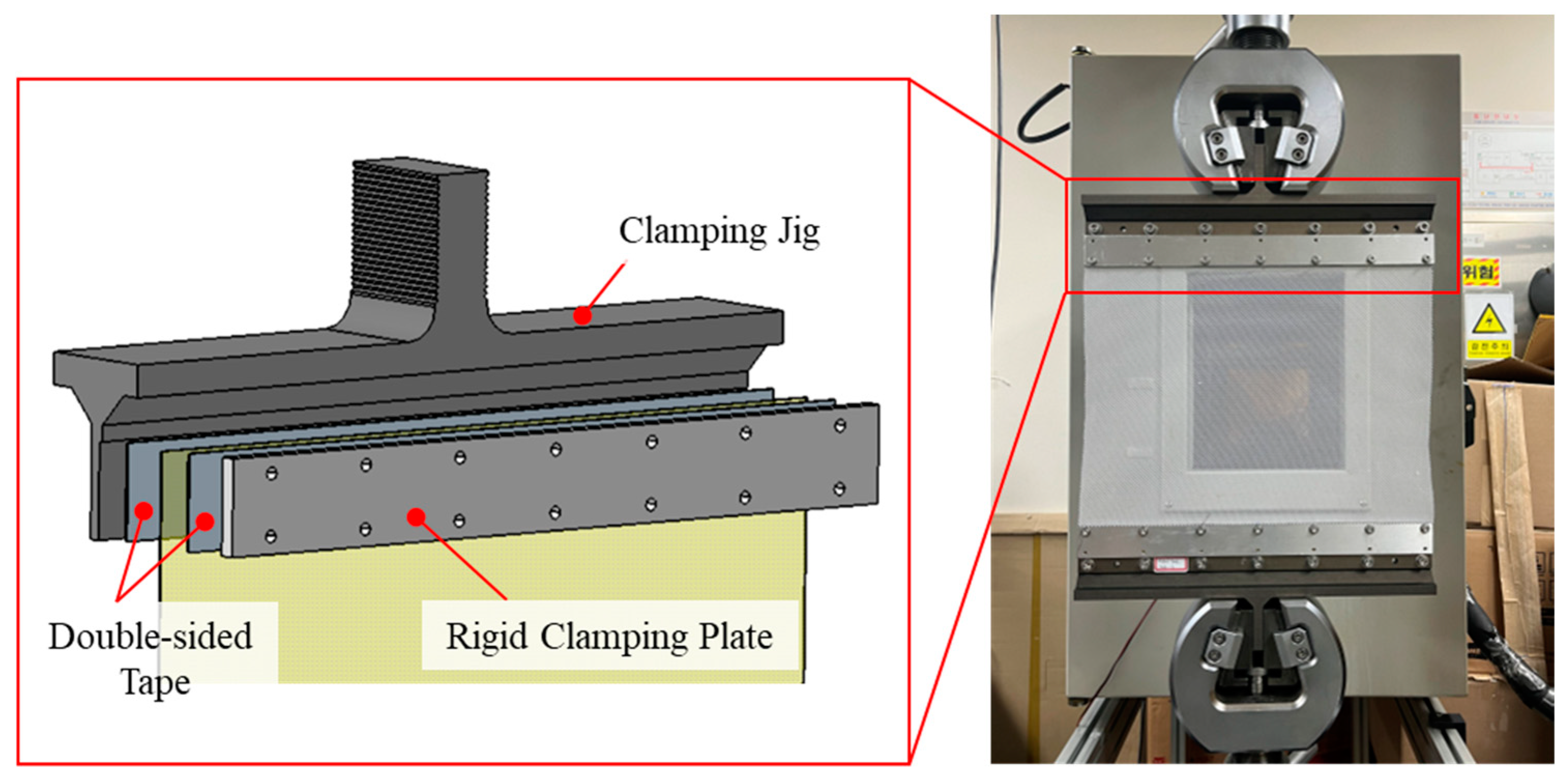
2.2. Design of the Clamping-Type Mesh Fastening Method
3. Experimental Validation of the Clamping-Type Fastening Method
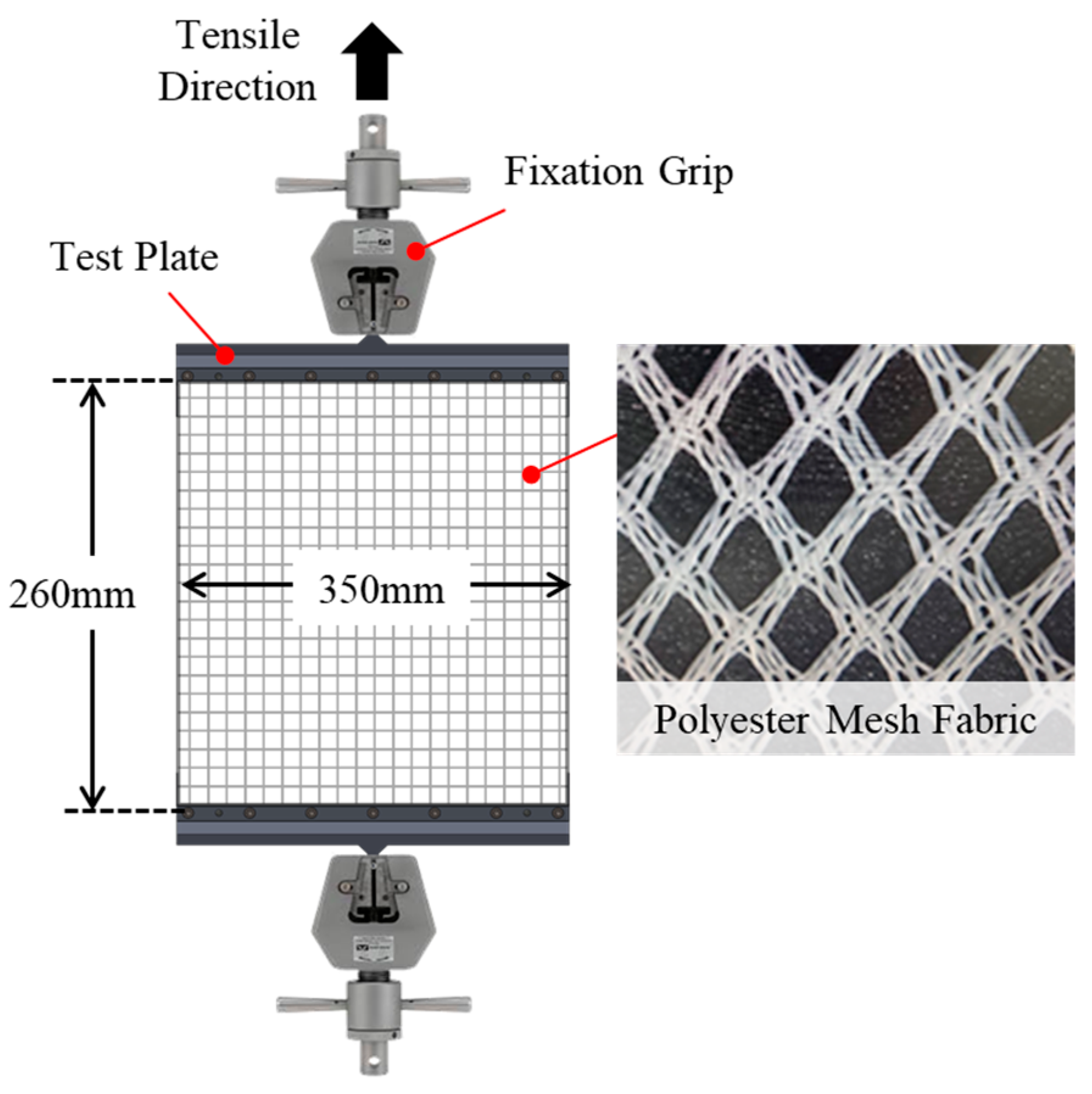
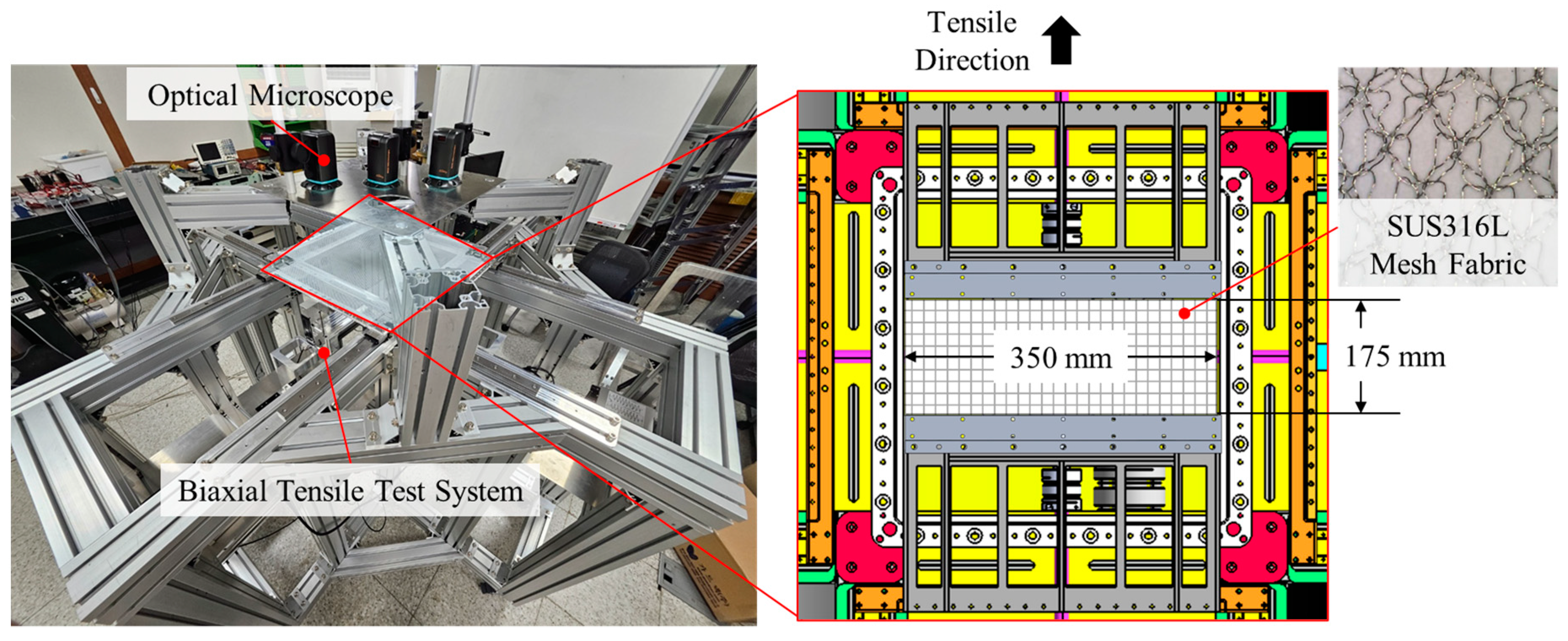
3.1. Tensile Strength Test Overview
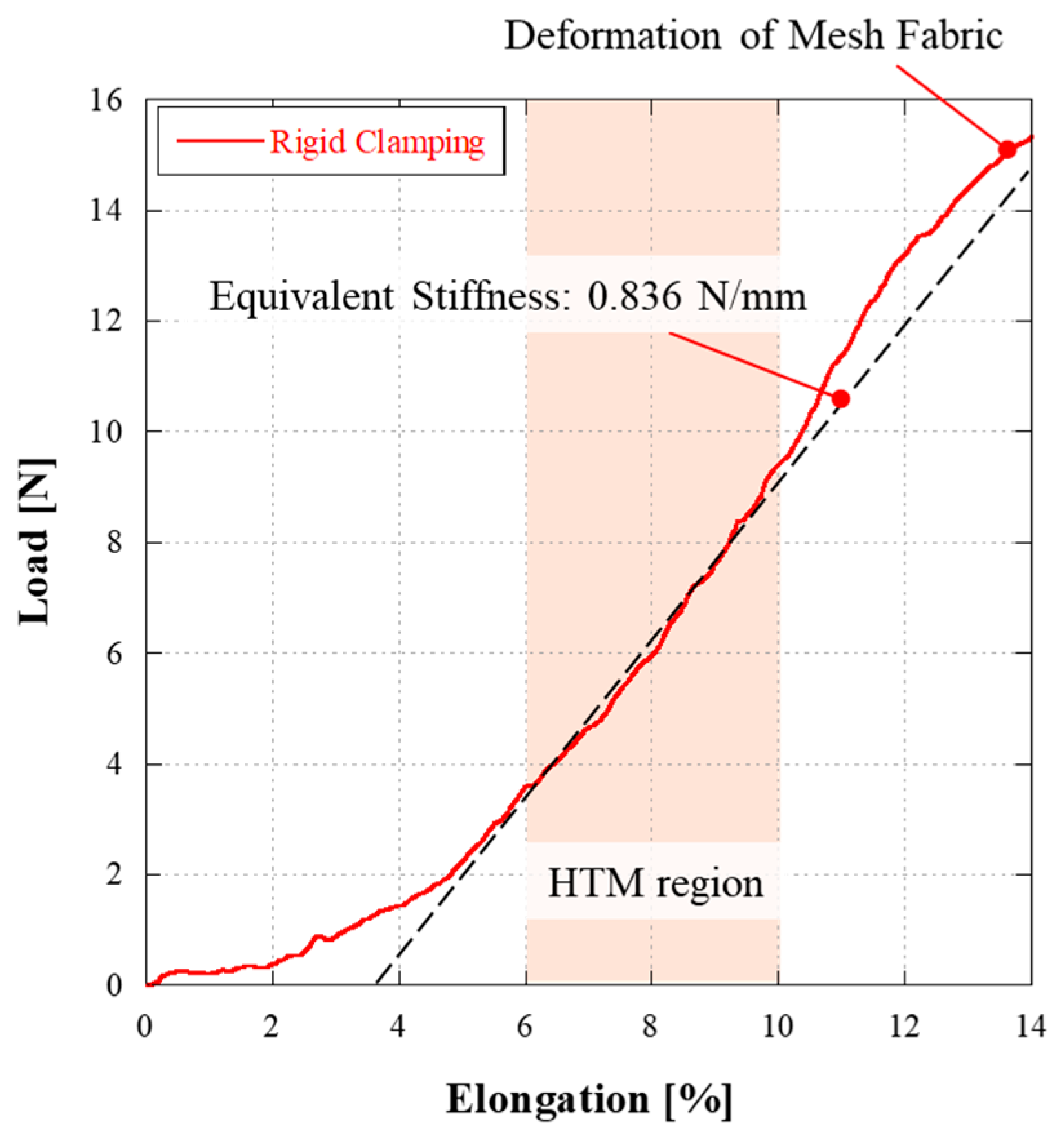
3.2. Tensile Strength Test Results
3.3. Repeated Tensile Test Overview
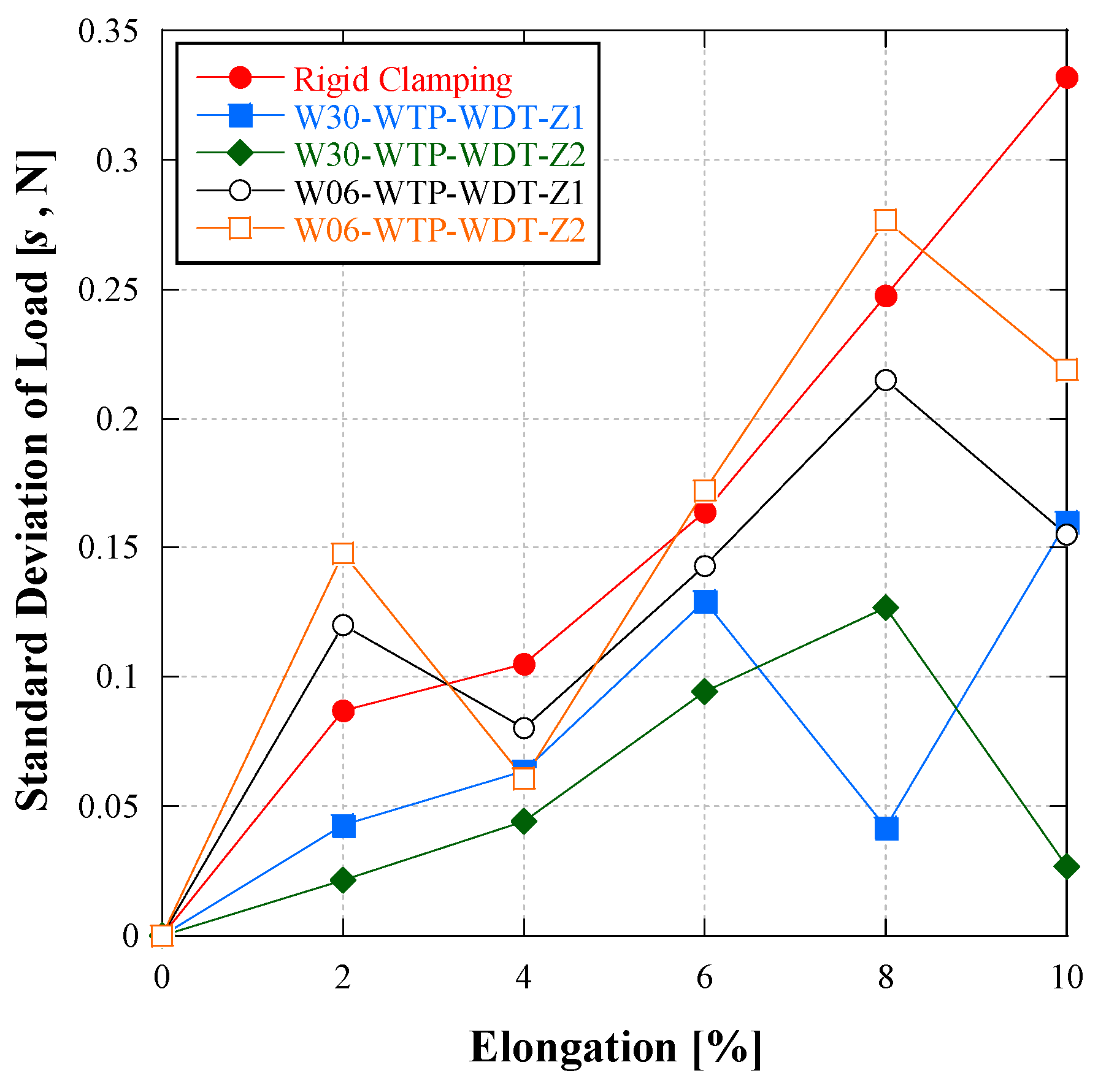
3.4. Repeated Tensile Test Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- The Newspace Paradigm: SpaceX Is Just the Beginning. Available online: http://trinitamonti.org/2020/07/15/the-newspace-paradigm-spacex-is-just-the-beginning/ (accessed on 30 December 2024).
- Zancan, V.; Paravano, A.; Locatelli, G.; Trucco, P. Evolving governance in the space sector: From legacy space to new space models. Acta Astronaut. 2024, 225, 515–523. [Google Scholar] [CrossRef]
- Lappas, V.; Kostopoulos, V. A survey on small satellite technologies and space missions for geodetic applications. In Satellite Missions and Technologies for Geosciences; IntechOpen: London, UK, 2020; Volume 8, pp. 123–144. [Google Scholar]
- Ince, F. Nano and micro satellites as the pillar of the “new space” paradigm. J. Aeronaut. Space Technol. 2020, 13, 235–250. [Google Scholar]
- Logue, T.J.; Pelton, J. Overview of commercial small satellite systems in the “new space” age. In Handbook of Small Satellites; Springer Nature: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Rahmat-Samii, Y.; Manohar, V.; Kovitz, J.M.; Hodges, R.E.; Freebury, G.; Peral, E. Development of highly constrained 1m Ka-band mesh deployable offset reflector antenna for next generation CubeSat radars. IEEE Trans. Antennas Propag. 2019, 67, 6254–6266. [Google Scholar] [CrossRef]
- Rao, S.; Shafai, L.; Sharma, S. Handbook of Reflector Antennas and Feed Systems Volume III: Applications of Reflectors; Artech: London, UK, 2013. [Google Scholar]
- Focardi, P.; Brown, P.R.; Rahmat-Samii, Y. Deployable mesh reflector antennas for space applications: RF characterizations. In Space Antenna Handbook; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lopatin, A.V.; Morozov, E.V.; Kazantsev, A.; Berdnikova, N.A. Deployment analysis of a composite thin-walled toroidal rim with elastic hinges: Application to an umbrella-type reflector of spacecraft antenna. Compos. Struct. 2023, 306, 116566. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Yang, D. Form-finding design of cable-mesh deployable reflector antennas considering wire mesh properties. AIAA J. 2019, 57, 5027–5041. [Google Scholar] [CrossRef]
- Goddard Space Flight Center. Final Report for ATS F&G. Available online: https://ntrs.nasa.gov/api/citations/19710001365/downloads/19710001365.pdf (accessed on 30 December 2024).
- Lockheed Missiles & Space Company, Inc. Method of Attaching Antenna Mesh. Available online: https://patentimages.storage.googleapis.com/3c/c0/68/2e64b91bba0518/US5456779.pdf (accessed on 30 December 2024).
- Thomson, M.W. Mechanical vs. Inflatable Deployable Structures for Large Apertures or Still No Simple Answers. In Proceedings of the Large Space Apertures Workshop California Institute of Technology, Pasadena, CA, USA, 10–11 November 2008. [Google Scholar]
- Bettermann, I.; Löcken, H.; Greb, C.; Gries, T.; Oses, A.; Pauw, J.; Maghaldadze, N.; Datashvili, L. Review and evaluation of warp-knitted patterns for metal-based large deployable reflector surfaces. CEAS Space J. 2023, 15, 477–493. [Google Scholar] [CrossRef]
- Scialino, G.L.; Salvini, P.; Migliorelli, M.; Pennestri, E.; Valentini, P.P.; van’t Klooster, K.; Santiago-Prowald, J.; Rodrigues, G.; Gloy, Y. Structural characterization and modeling of metallic mesh material for large deployable reflectors. In Proceedings of the 2nd International Conference: Advanced Lightweight Structures and Reflector Antennas, Tbilisi, Georgia, 1–3 October 2014; pp. 182–192. [Google Scholar]
- Mueller, K.M.A.; Mulderrig, S.; Najafian, S.; Hurvitz, S.B.; Sodhani, D.; Mela, P.; Stapleton, S.E. Mesh manipulation for local structural property tailoring of medical warp-knitted textiles. J. Mech. Behav. Biomed. Mater. 2022, 128, 105117. [Google Scholar] [CrossRef] [PubMed]
- Hasan, A.; Ragaert, K.; Swieszkowski, W.; Selimović, Š.; Paul, A.; Camci-Unal, G.; Mofrad, M.R.K.; Khademhosseini, A. Biomechanical properties of native and tissue engineered heart valve constructs. J. Biomech. 2014, 47, 1949–1963. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Feng, X.; Rogers, J.A.; Huang, Y.; Zhang, Y. Design and application of ‘J-shaped’ stress-strain behavior in stretchable electronics: A review. Lab Chip. 2017, 17, 1689–1704. [Google Scholar] [CrossRef] [PubMed]
- 3MTM Adhesive Transfer Tape 966. Available online: https://multimedia.3m.com/mws/media/2365951O/3m-adhesive-transfer-tape-966.pdf?&fn=3M-Adhesive-Transfer-Tape-966_R1.pdf (accessed on 30 December 2024).
- Choi, J.S.; Park, T.Y.; Chae, B.G.; Oh, H.U. Development of lightweight 6 m deployable mesh reflector antenna mechanisms based on superelastic shape memory alloy. Aerospace 2024, 11, 738–759. [Google Scholar] [CrossRef]
- Shi, H.; Yuan, S.; Yang, B. New methodology of surface mesh geometry design for deployable mesh reflectors. J. Spacecr. Rocket. 2018, 55, 266–281. [Google Scholar] [CrossRef]



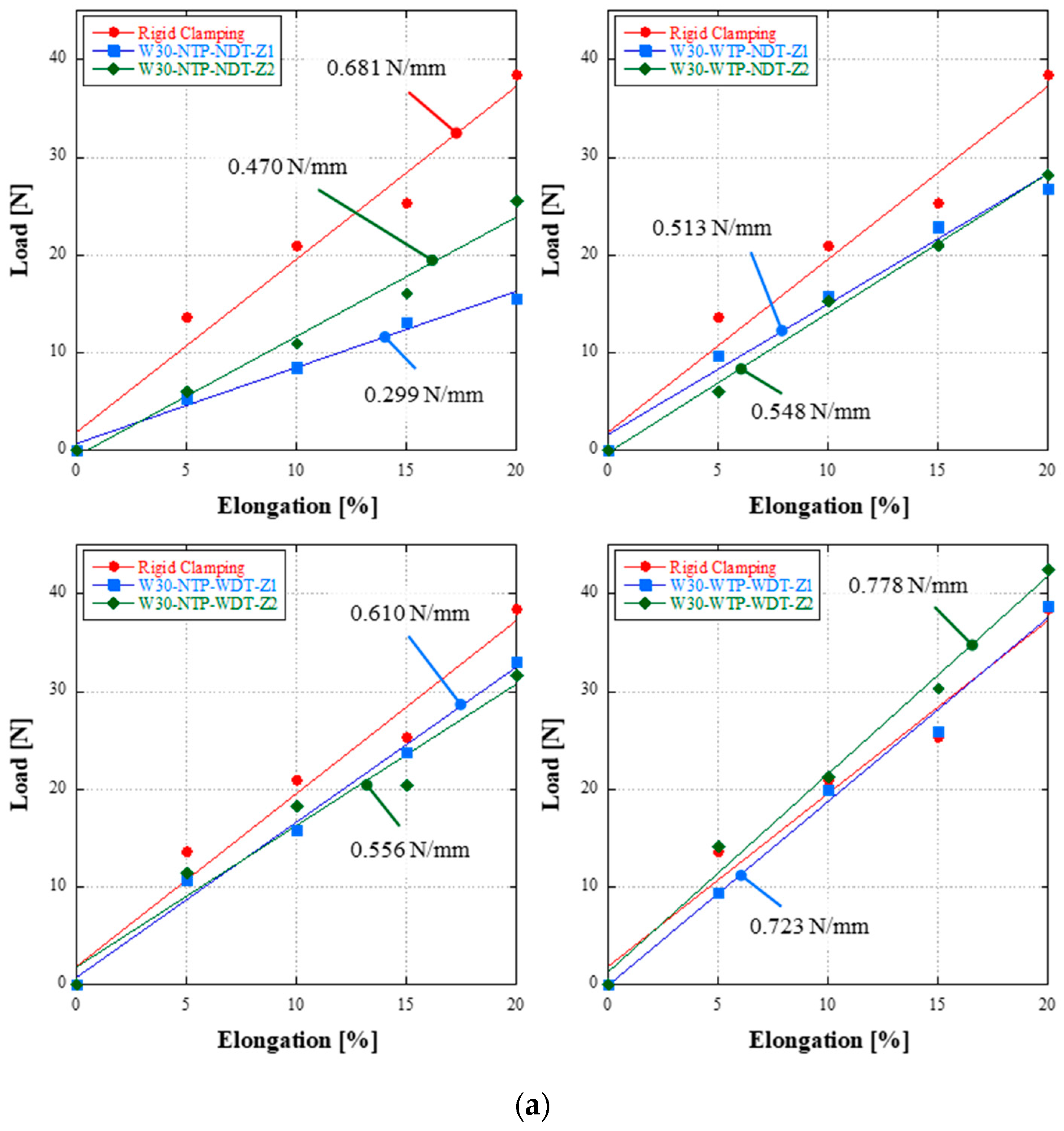
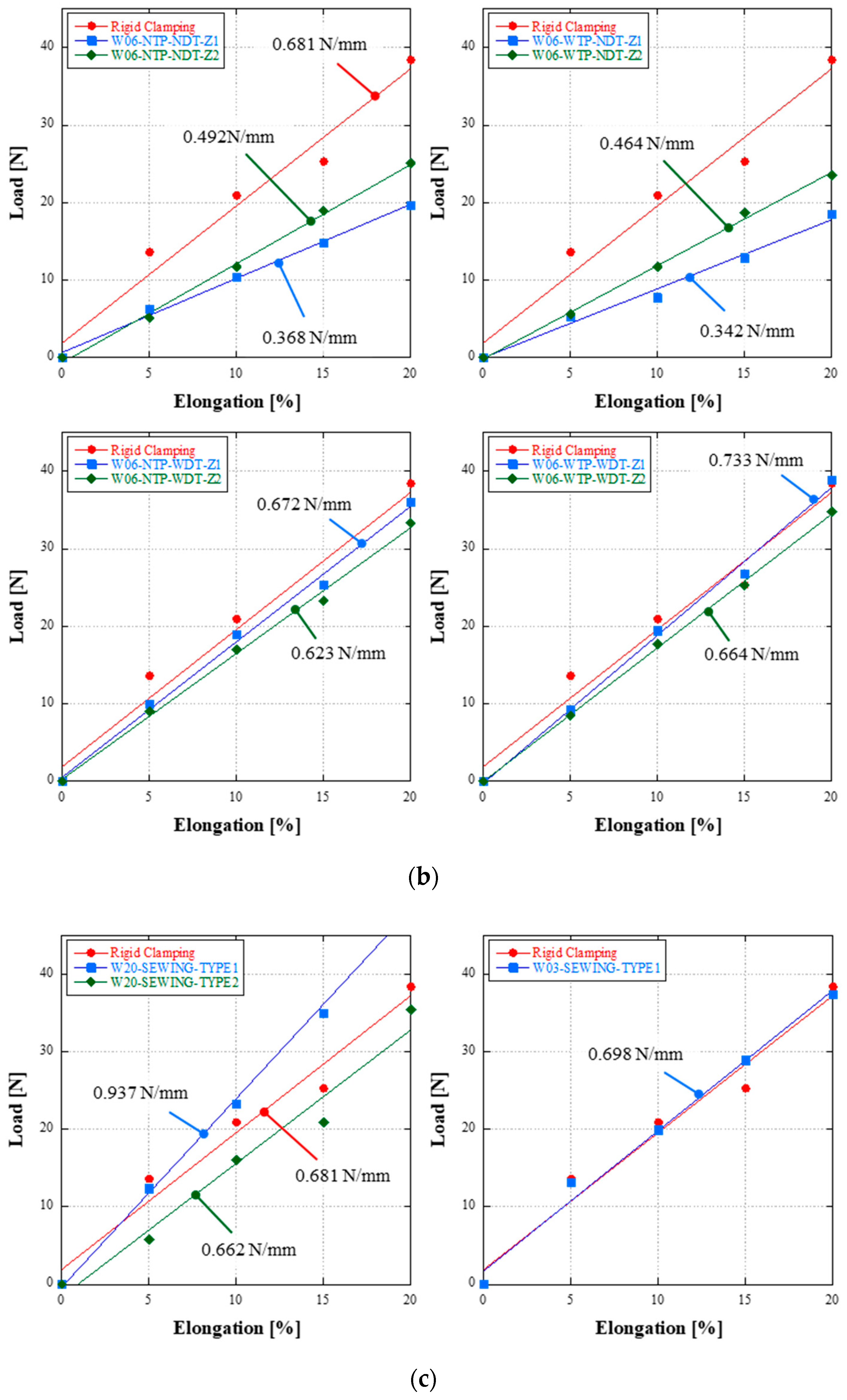



| Case | Test ID |
|---|---|
| 1 | W30-NTP-NDT-Z1 |
| 2 | W30-NTP-NDT-Z2 |
| 3 | W30-WTP-NDT-Z1 |
| 4 | W30-WTP-NDT-Z2 |
| 5 | W30-NTP-WDT-Z1 |
| 6 | W30-NTP-WDT-Z2 |
| 7 | W30-WTP-WDT-Z1 |
| 8 | W30-WTP-WDT-Z2 |
| 9 | W06-NTP-NDT-Z1 |
| 10 | W06-NTP-NDT-Z2 |
| 11 | W06-WTP-NDT-Z1 |
| 12 | W06-WTP-NDT-Z2 |
| 13 | W06-NTP-WDT-Z1 |
| 14 | W06-NTP-WDT-Z2 |
| 15 | W06-WTP-WDT-Z1 |
| 16 | W06-WTP-WDT-Z2 |
| 17 | W20-SEWING-TYPE1 |
| 18 | W20-SEWING-TYPE2 |
| 19 | W03-SEWING-TYPE1 |
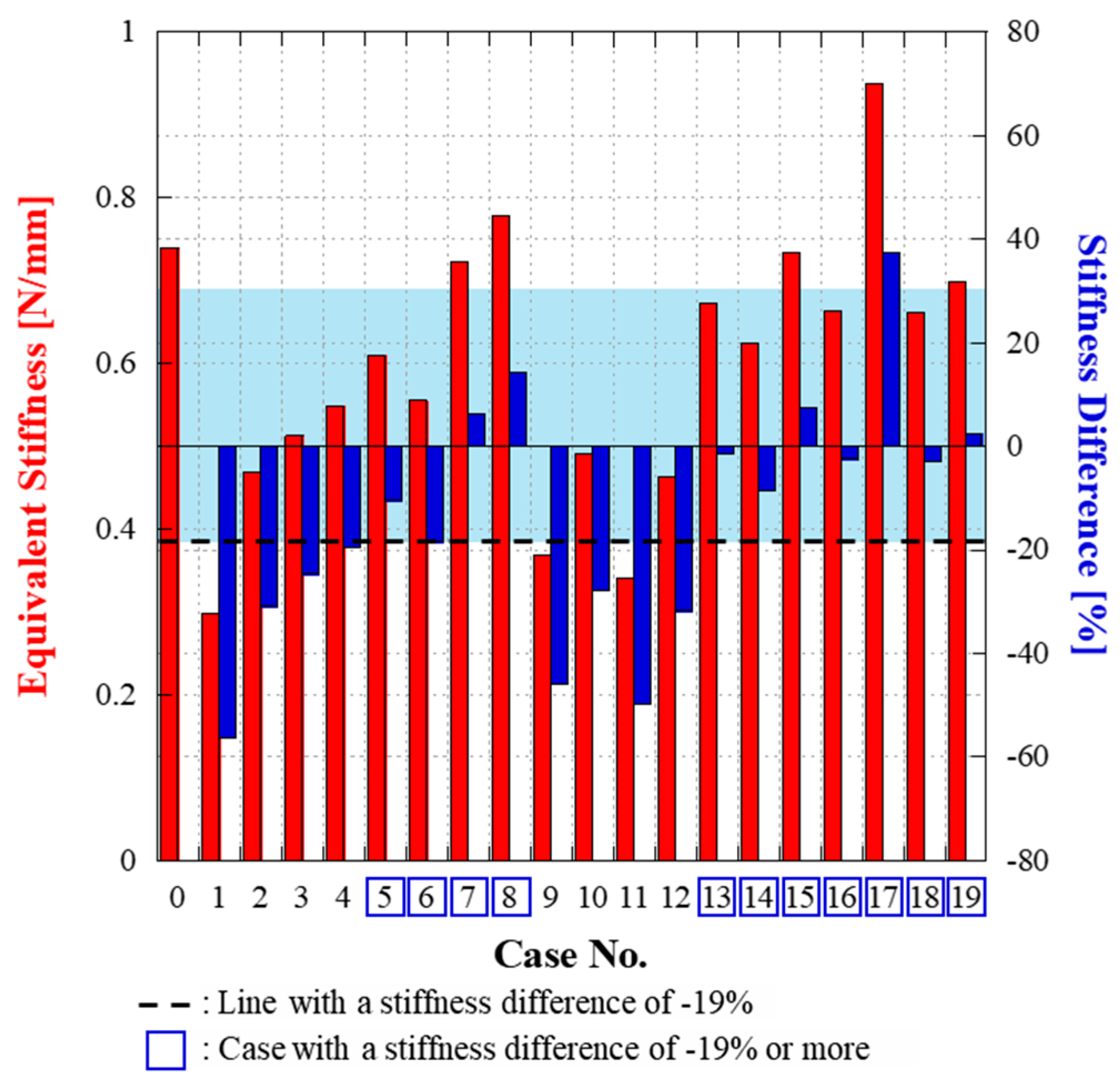
| Case | Test ID | Equivalent Stiffness [N/mm] | Rib Shape | Riveting Distance [mm] | Remark |
|---|---|---|---|---|---|
| Ref. | Rigid Clamping | 0.681 | - | - | - |
| 1 | W30-NTP-NDT-Z1 | 0.470 | T-shaped | 330 | w/o Thin Plate w/o Double-sided Tape |
| 2 | W30-NTP-NDT-Z2 | 0.299 | 165 | w/o Thin Plate w/o Double-sided Tape | |
| 3 | W30-WTP-NDT-Z1 | 0.513 | 330 | w/Thin Plate w/o Double-sided Tape | |
| 4 | W30-WTP-NDT-Z2 | 0.548 | 165 | w/Thin Plate w/o Double-sided Tape | |
| 5 | W30-NTP-WDT-Z1 | 0.610 | 330 | w/o Thin Plate w/Double-sided Tape | |
| 6 | W30-NTP-WDT-Z2 | 0.556 | 165 | w/o Thin Plate w/Double-sided Tape | |
| 7 | W30-WTP-WDT-Z1 | 0.723 | 330 | w/Thin Plate w/Double-sided Tape | |
| 8 | W30-WTP-WDT-Z2 | 0.778 | 165 | w/Thin Plate w/Double-sided Tape | |
| 9 | W06-NTP-NDT-Z1 | 0.368 | I-shaped | 330 | w/o Thin Plate w/o Double-sided Tape |
| 10 | W06-NTP-NDT-Z2 | 0.492 | 165 | w/o Thin Plate w/o Double-sided Tape | |
| 11 | W06-WTP-NDT-Z1 | 0.342 | 330 | w/Thin Plate w/o Double-sided Tape | |
| 12 | W06-WTP-NDT-Z2 | 0.464 | 165 | w/Thin Plate w/o Double-sided Tape | |
| 13 | W06-NTP-WDT-Z1 | 0.672 | 330 | w/o Thin Plate w/Double-sided Tape | |
| 14 | W06-NTP-WDT-Z2 | 0.623 | 165 | w/o Thin Plate w/Double-sided Tape | |
| 15 | W06-WTP-WDT-Z1 | 0.733 | 330 | w/Thin Plate w/Double-sided Tape | |
| 16 | W06-WTP-WDT-Z2 | 0.664 | 165 | w/Thin Plate w/Double-sided Tape | |
| 17 | W20-SEWING-TYPE1 | 0.937 | T-shaped | - | Sewing Method |
| 18 | W20-SEWING-TYPE2 | 0.662 | - | Sewing Method | |
| 19 | W03-SEWING-TYPE1 | 0.698 | I-shaped | - | Sewing Method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.-S.; Chae, B.-G.; Oh, H.-U. Experimental Validation of Clamping-Type Mesh Fastening Method Using Thin Plates and Push-Button Rivets for Deployable Mesh Antennas. Aerospace 2025, 12, 248. https://doi.org/10.3390/aerospace12030248
Choi J-S, Chae B-G, Oh H-U. Experimental Validation of Clamping-Type Mesh Fastening Method Using Thin Plates and Push-Button Rivets for Deployable Mesh Antennas. Aerospace. 2025; 12(3):248. https://doi.org/10.3390/aerospace12030248
Chicago/Turabian StyleChoi, Jae-Seop, Bong-Geon Chae, and Hyun-Ung Oh. 2025. "Experimental Validation of Clamping-Type Mesh Fastening Method Using Thin Plates and Push-Button Rivets for Deployable Mesh Antennas" Aerospace 12, no. 3: 248. https://doi.org/10.3390/aerospace12030248
APA StyleChoi, J.-S., Chae, B.-G., & Oh, H.-U. (2025). Experimental Validation of Clamping-Type Mesh Fastening Method Using Thin Plates and Push-Button Rivets for Deployable Mesh Antennas. Aerospace, 12(3), 248. https://doi.org/10.3390/aerospace12030248







