Preliminary Design of Regional Aircraft—Integration of a Fuel Cell-Electric Energy Network in SUAVE
Abstract
1. Introduction
1.1. Research Focus and Aircraft Configuration
- Reference configuration: A reverse-engineered ATR 72-500-like aircraft serves as the basis for the other configurations.
- Baseline configuration: An ATR 72-500-like aircraft with a state-of-the-art turboprop with an entry-in-service date equal to the lead configuration, which serves as a benchmark for comparison.
- Lead configuration: A design utilizing DEP powered by an FC electric powertrain.
1.2. State of the Art and Motivation
- Thermal management of electric and hydrogen-based systems
- Multi-functional structural design to reduce weight and enhance efficiency
- Aerodynamic interactions between the airframe and propulsion systems
- Advanced acoustic modeling for noise reduction
2. Materials and Methods
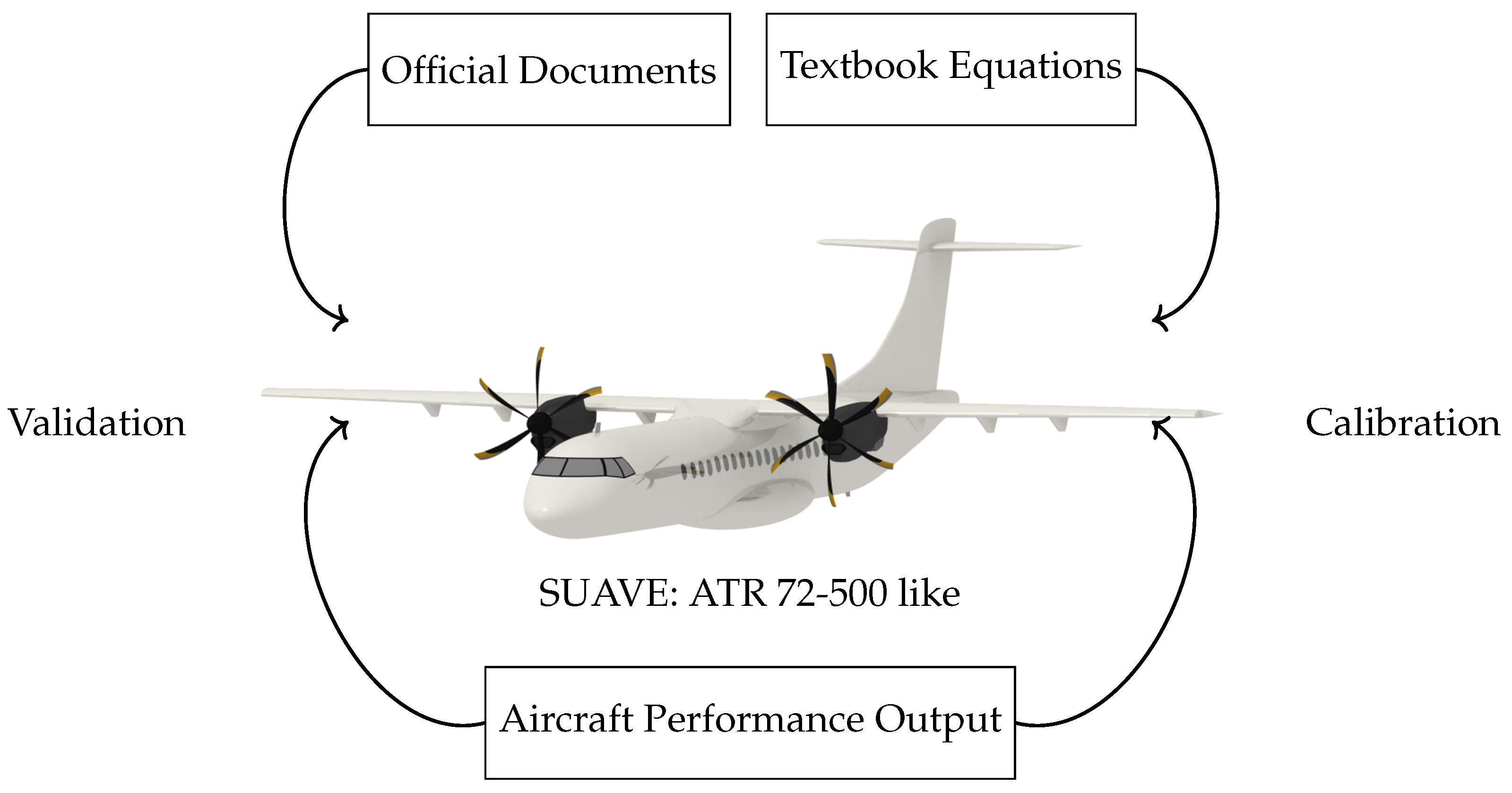
2.1. Design and Calibration in SUAVE
2.2. Method Calibration
2.3. Impact of the New Propulsion Architecture
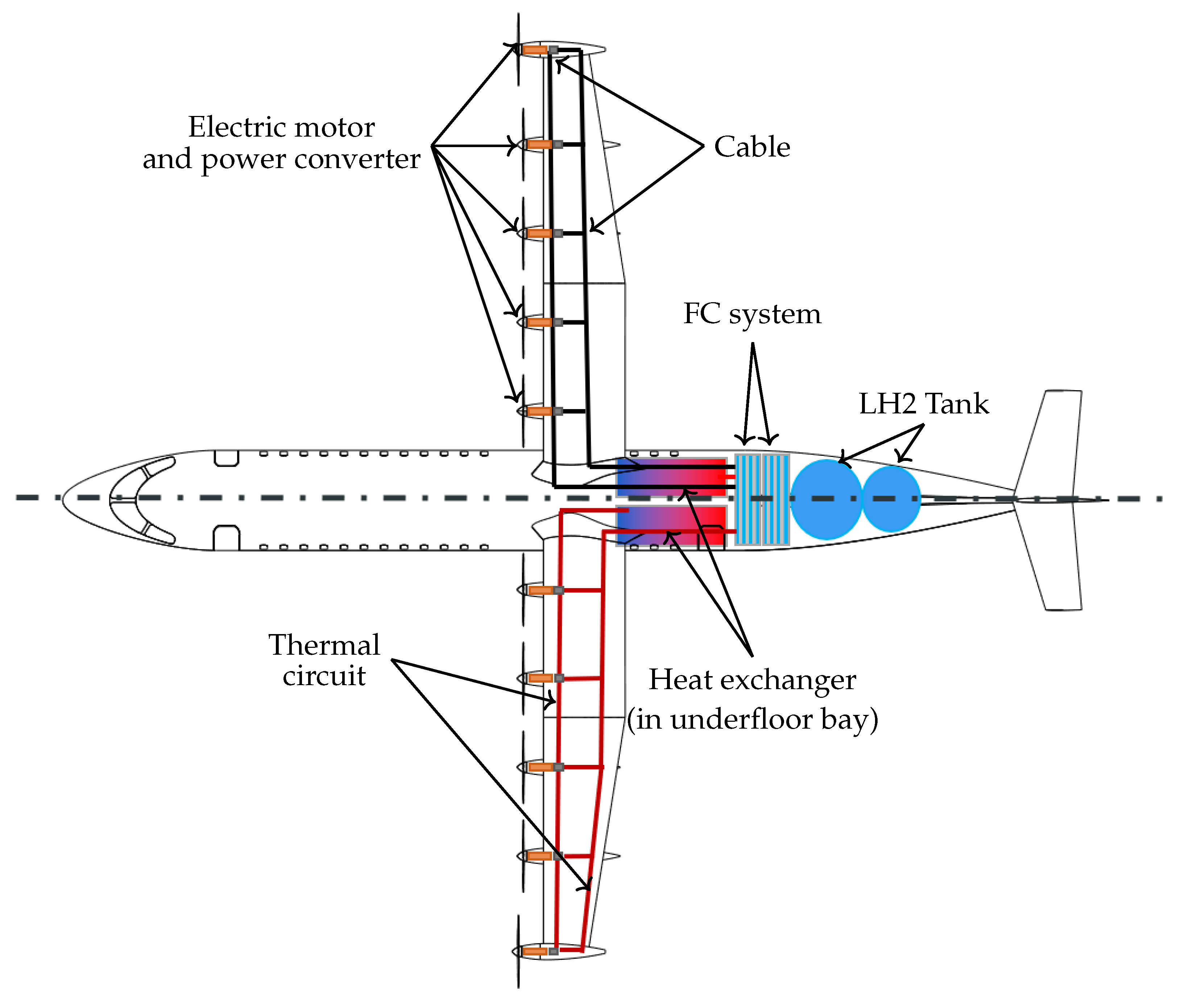
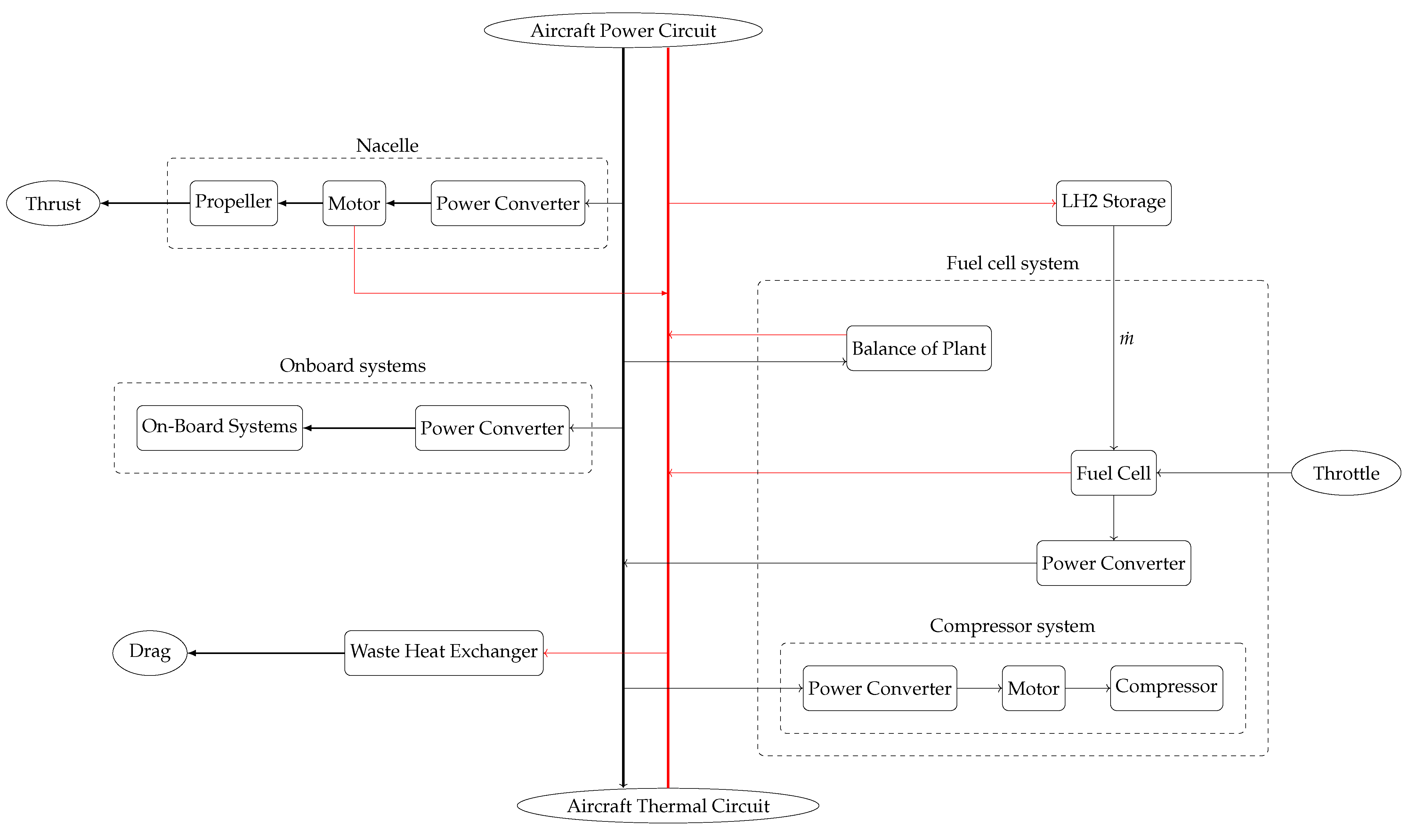
2.4. Aircraft Energy System Model
2.4.1. Integration Aspects of Energy Network
2.4.2. Energy Network Model
2.5. Assessment and Figure of Merit
2.5.1. Energy Specific Air Range
2.5.2. Improvements for the Off-Design Assessment
3. Results
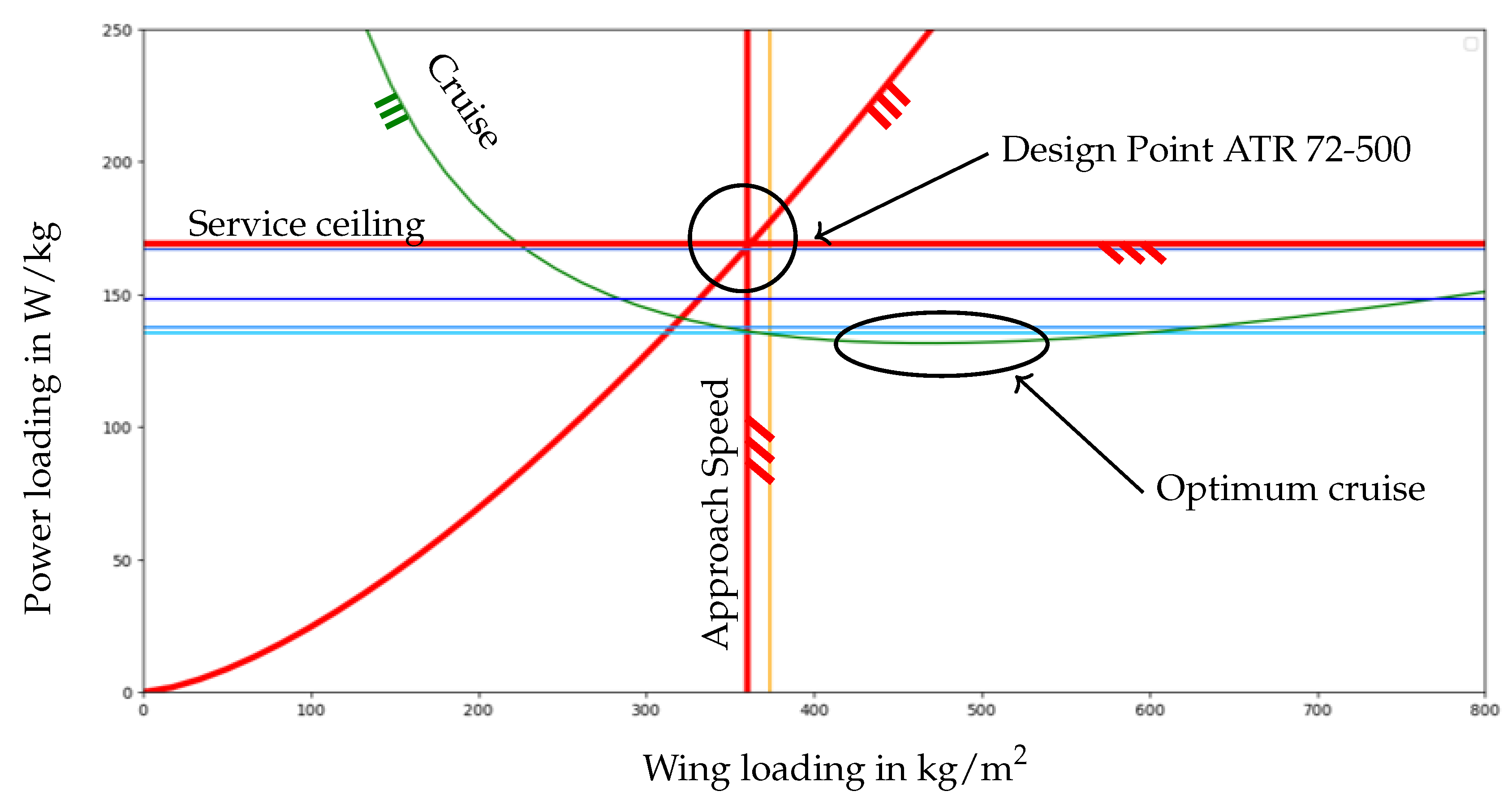
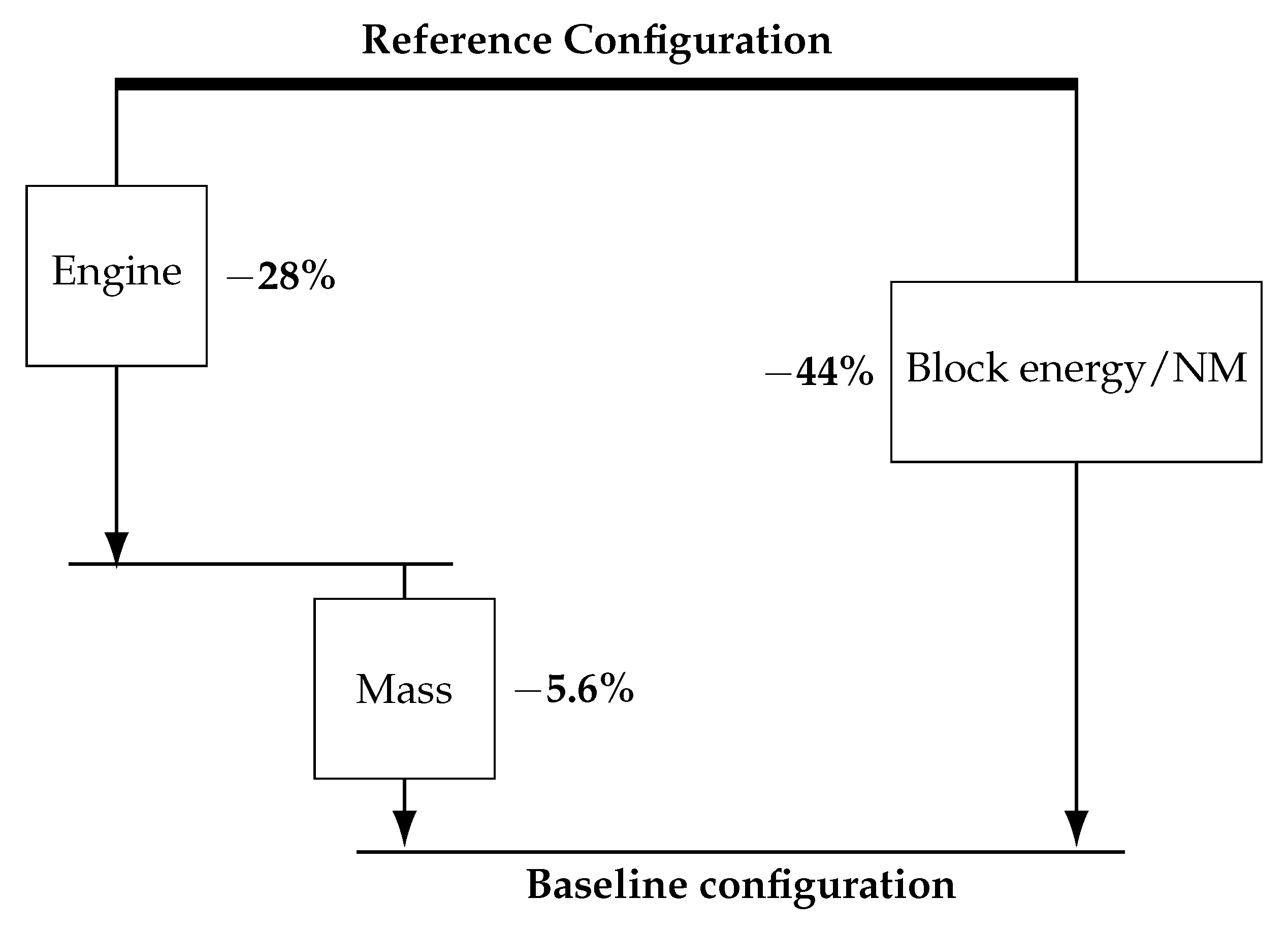
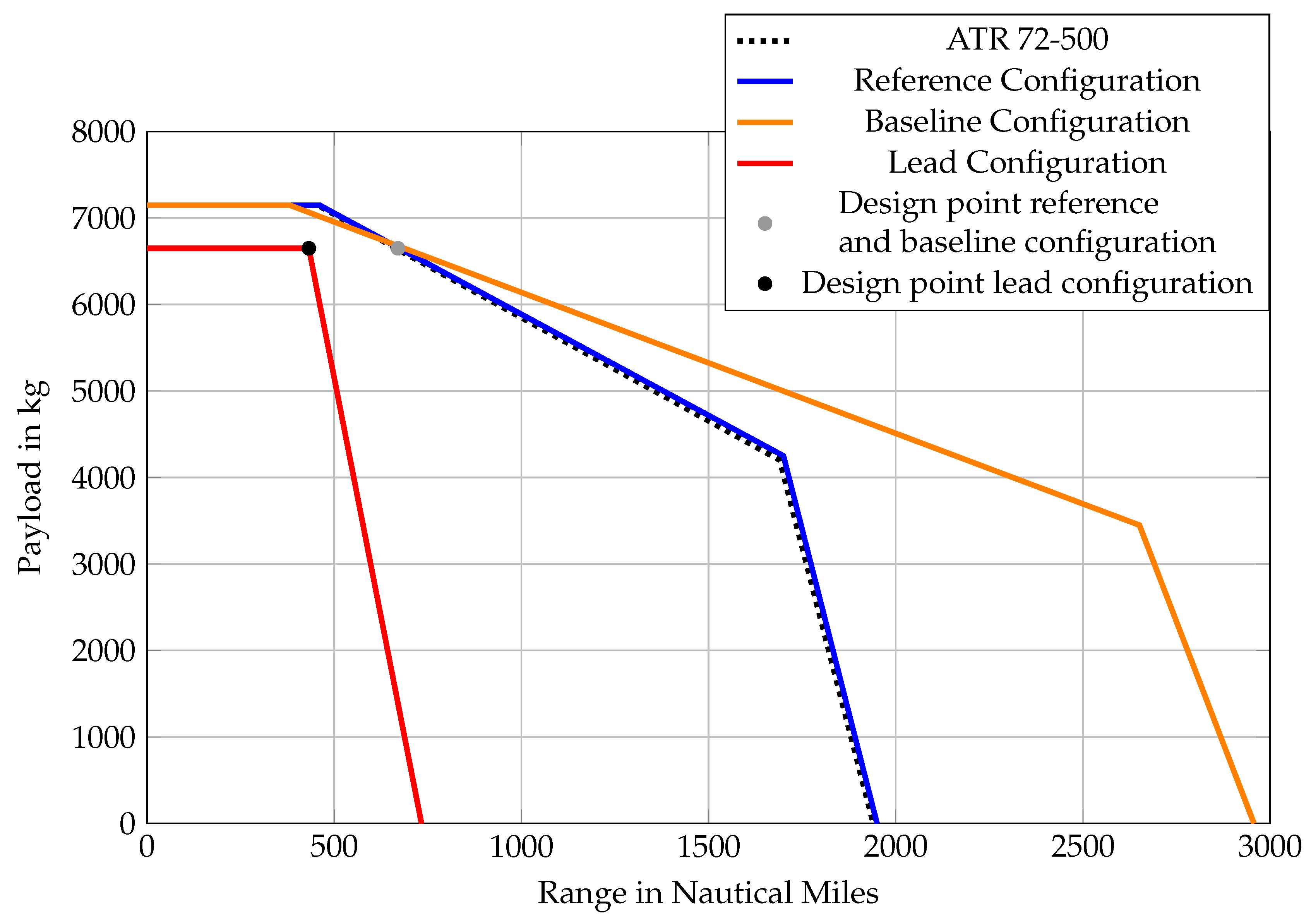
3.1. Reference Configuration
3.2. Baseline Configuration
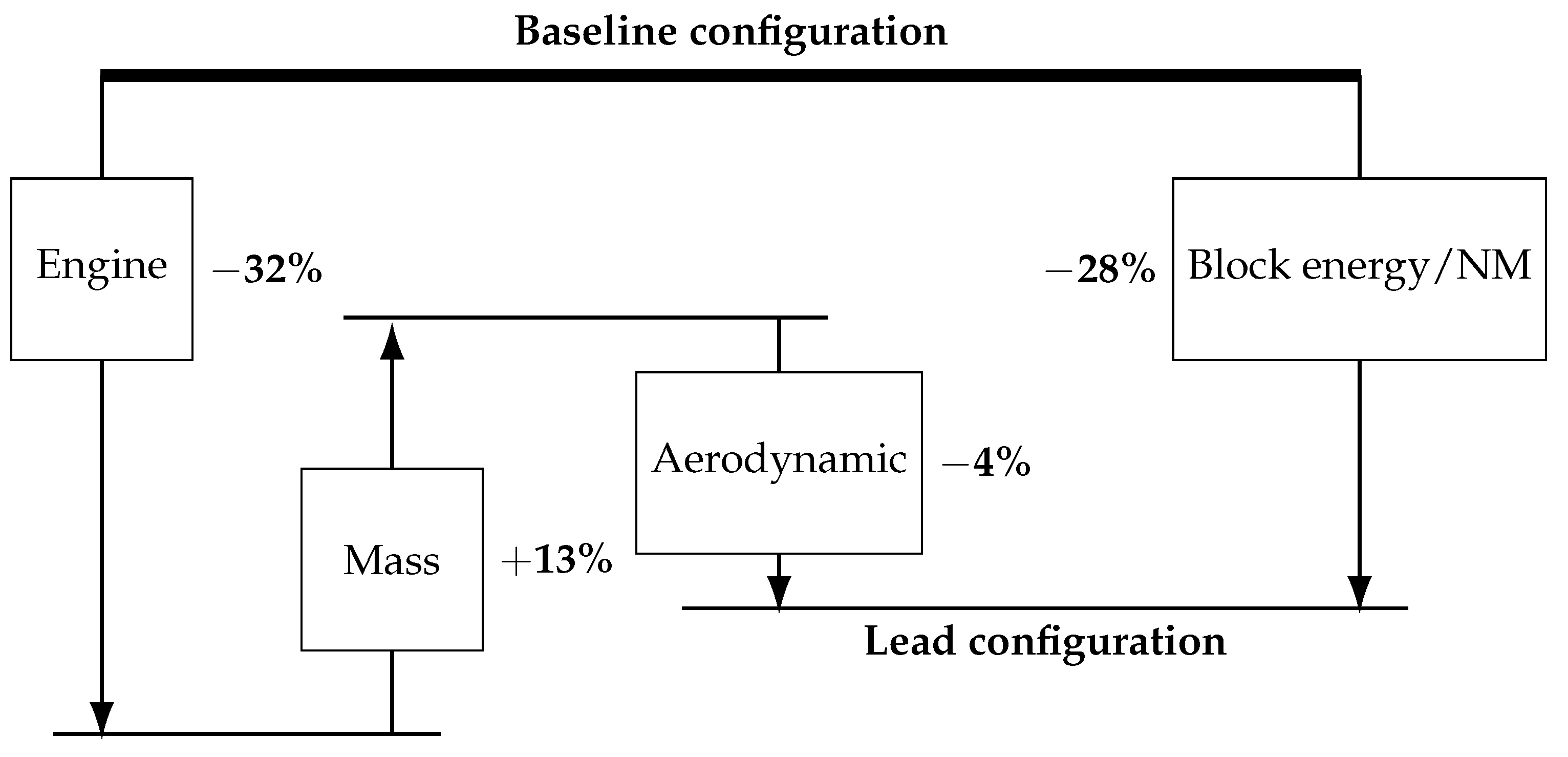
3.3. Lead Configuration
4. Discussion
4.1. Comparison
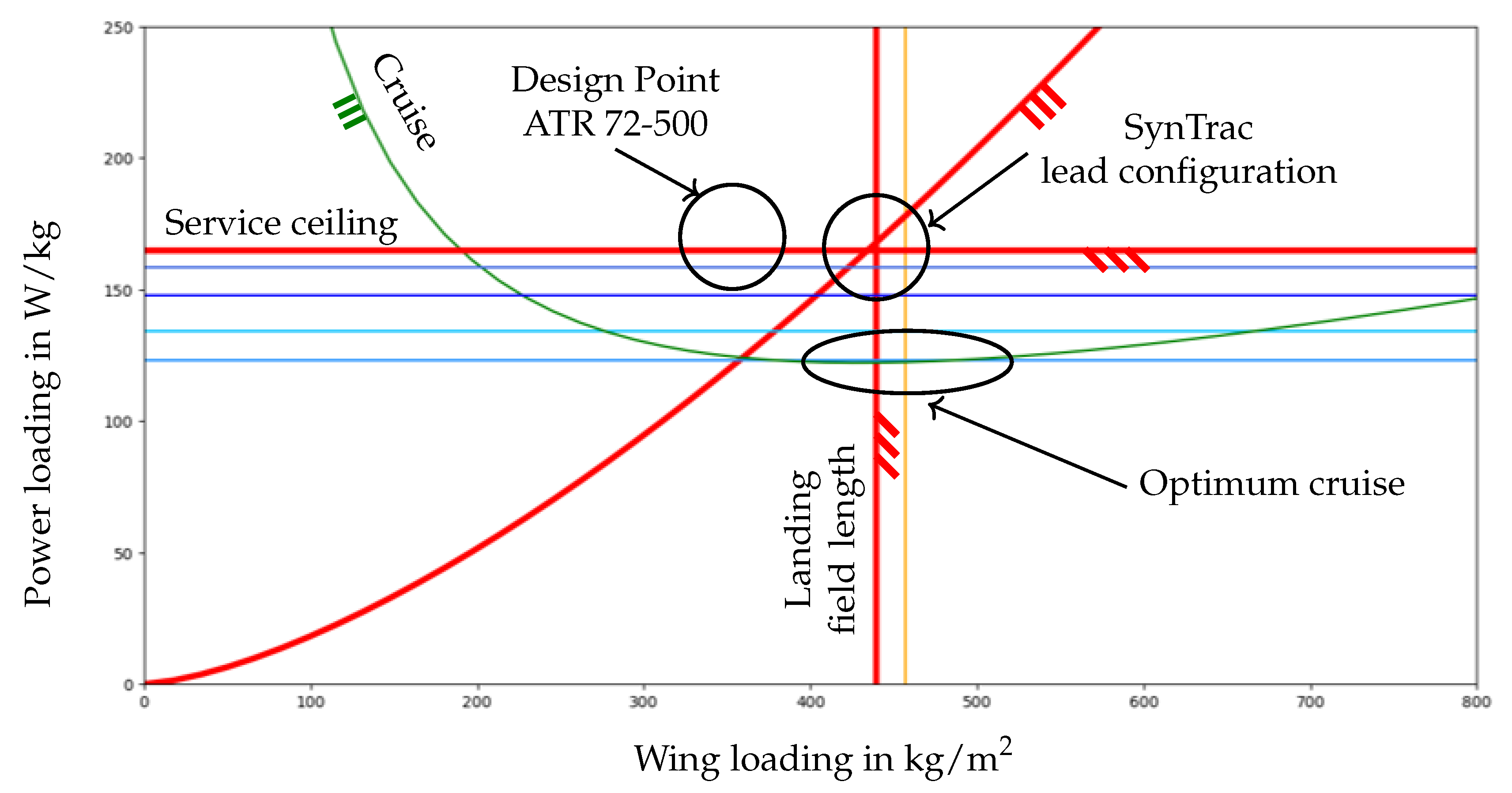
4.2. Off-Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ATR | French: Avions de Transport Régional, |
| Italian: Aerei da Trasporto Regionale, | |
| lit.: ‘Regional Transport Airplanes’ | |
| APC | Aircraft Power Circuit |
| ATC | Aircraft Thermal Circuit |
| BOP | Balance of Plant |
| Maximum Lift Coefficient | |
| CG | Center of Gravity |
| DEP | Distributed Electric Propulsion |
| EASA | European Union Aviation Safety Agency |
| EIS | Entry Into Service |
| ESAR | Energy Specific Air Range |
| ESPAR | Energy Specific Payload Air Range |
| FC | Fuel Cell |
| FC-PC | Fuel Cell-Power Converter |
| HTP | Horizontal Tail Plane |
| ISA | International Standard Atmosphere |
| LH2 | Liquid Hydrogen |
| MAC | Mean Aerodynamic Chord |
| MTOM | Maximum Take-Off Mass |
| NM | Nautical Mile |
| OAD | Overall Aircraft Design |
| OEM | Operating Empty Mass |
| PM | Propulsion Motor |
| POT | Power Off-Take |
| PSFC | Power Specific Fuel Consumption |
| SAR | Specific Air Range |
| SUAVE | Stanford University Aerospace Vehicle Environment |
| SynTrac | Synergies of Highly Integrated Transport Aircraft |
| TMS | Thermal Management System |
| TRL | Technology Readiness Level |
| VTP | Vertical Tail Plane |
| WHex | Waste Heat Exchanger |
Appendix A. Model Derivation and Parameters
Appendix A.1. Fuel Cell Equations

Appendix A.2. Energy-Related Parameters
| Symbol | Name/Meaning | Value | Ref. |
|---|---|---|---|
| Efficiency of propulsion motor (in %) | 95 | [36] | |
| Efficiency of propulsion motor power converters (in %) | 99 | [36] | |
| Efficiency of Aircraft Power Circuit (in %) | 99.5 | [36] | |
| Efficiency of fuel cell power converters (in %) | 97 | [36] | |
| Specific electric energy from fuel cell feed (kWh/kg) | 20 | [37] | |
| Factor for variable specific energy from fuel cell feed | −0.5 | [37] | |
| Specific total energy from fuel cell feed (kWh/kg) | 33.3 | [37] | |
| Fuel cell air demand factor (kgAir/kgH2) | 60 | [38] | |
| Factor for BOP power demand (kW/kW) | 0.01 | [37] | |
| Efficiency of air compressor (in %) | 87 | [39] | |
| Efficiency of air compressor motor (in %) | 95 | [36] | |
| Efficiency of air compressor motor power converters (in %) | 99 | [36] | |
| Constant power off-take (kW) | 150 | [40] | |
| Efficiency of consumer power converters (in %) | 97 | [36] | |
| Specific vaporization enthalpy of H2 (kWh/kg) | 0.125 | [41] | |
| Isobaric heat capacity of air (kWh/kgK) | [42] | ||
| Isentropic exponent of air | 1.4 | [42] | |
| Sizing factor for buffer battery (h) | 0.15 | [43] | |
| F | Faraday constant kAs/kmol | 96,485 | [31] |
| Molar mass kg/kmol | 2 | [31] |
Appendix A.3. Mass-Related Formulation and Parameters
| Symbol | Name/Meaning | Value | Ref. |
|---|---|---|---|
| Gravimetric power density Fuel Cell (kW/kg) | 3.5 | [37] | |
| Gravimetric power density Fuel Cell converters (kW/kg) | 25 | [36] | |
| Gravimetric power density Fuel Cell balance of plant (kW/kg) | 10 | [37] | |
| Gravimetric power density air compressor (kW/kg) | 12 | [44] | |
| Gravimetric power density air compressor motor (kW/kg) | 10 | [36] | |
| Gravimetric power density air compressor motor power converter (kW/kg) | 100 | [36] | |
| Specific Energy battery (kWh/kg) | 0.3 | [43] | |
| Gravimetric power density battery converters (kW/kg) | 25 | [36] | |
| Gravimetric power density heat exchanger (kW/kg) | 2 | [37] | |
| Gravimetric power density aircraft thermal circuit (kW/kg) | 5.5 | [37] | |
| Gravimetric power density consumer power converters (kW/kg) | 25 | [36] | |
| Gravimetric power density aircraft power circuit (kW/kg) | 500 | [36] | |
| Gravimetric power density propulsion motor power converters (kW/kg) | 100 | [36] | |
| Gravimetric power density propulsion motor (kW/kg) | 10 | [36] | |
| LH2 gravimetric storage density (kg/kg) | 1 | [45] |
Appendix A.4. Volume-Related Formulation and Parameters
| Symbol | Name/Meaning | Value | Ref. |
|---|---|---|---|
| Volumetric power density Fuel Cell (kW/m3) | 5000 | [46] | |
| Volumetric power density Fuel Cell power converters (kW/m3) | 3500 | [47] | |
| Volumetric power density Fuel Cell balance of plant (kW/m3) | 2000 | [37] | |
| Volumetric power density air compressor (kW/m3) | 5000 | [44] | |
| Volumetric power density air compressor motor (kW/m3) | 4500 | [48] | |
| Volumetric power density air compressor motor power converter (kW/m3) | 2500 | [49] | |
| Energy density battery (kWh/m3) | 200 | [50] | |
| Volumetric power density battery power converters (kW/m3) | 3500 | [47] | |
| Volumetric heat Volumetric power density heat exchanger (kW/m3) | 400 | [51] | |
| Volumetric heat Volumetric power density aircraft thermal circuit (kW/m3) | - | - | |
| Volumetric power density consumer power converters (kW/m3) | 3500 | [47] | |
| Volumetric power density aircraft power circuit (kW/m3) | - | - | |
| Volumetric power density propulsion motor power converters (kW/m3) | 2500 | [49] | |
| Volumetric power density propulsion motor (kW/m3) | 4500 | [48] | |
| LH2 volumetric storage density (kg/m3) | 50 | [45] |
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. Climate Change 2021: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- United Nations. Paris Agreement; United Nations: New York, NY, USA, 2015. [Google Scholar]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015. [Google Scholar]
- United Nations. Sustainable Development Goals; United Nations: New York, NY, USA, 2015. [Google Scholar]
- European Commission. The European Green Deal; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- European Commission and Directorate-General for Research and Innovation. Fly the Green Deal—Europe’s Vision for Sustainable Aviation; Publications Office of the European Union: Luxembourg, 2022. [Google Scholar] [CrossRef]
- TRR-SynTrac. TRR-SynTrac Project; TU Braunschweig, Institut für Akustik und Dynamik: Braunschweig, Germany; Universität Stuttgart, Institut für Luftfahrtantriebe: Stuttgart, Germany, 2025. [Google Scholar]
- Eissele, J.; Lafer, S.; Mejía Burbano, C.; Schließus, J.; Wiedmann, T.; Mangold, J.; Strohmayer, A. Hydrogen-Powered Aviation—Design of a Hybrid-Electric Regional Aircraft for Entry into Service in 2040. Aerospace 2023, 10, 277. [Google Scholar] [CrossRef]
- Ansell, P.J. Hydrogen-electric aircraft technologies and integration: Enabling an environmentally sustainable aviation future. IEEE Electrif. Mag. 2022, 10, 6–16. [Google Scholar] [CrossRef]
- Wu, S.; Li, Y. Fuel cell applications on more electrical aircraft. In Proceedings of the 2014 17th International Conference on Electrical Machines and Systems (ICEMS), Hangzhou, China, 22–25 October 2014; pp. 198–201. [Google Scholar] [CrossRef]
- Kim, H.; Perry, A.; Ansell, P. A Review of Distributed Electric Propulsion Concepts for Air Vehicle Technology. In Proceedings of the AIAA AIAA/IEEE Electric Aircraft Technologies Symposium, Cincinnati, OH, USA, 9–11 July 2018. [Google Scholar] [CrossRef]
- Vechtel, D.; Buch, J.P. Aspects of yaw control design of an aircraft with distributed electric propulsion. Ceas Aeronaut. J. 2022, 13, 847–860. [Google Scholar] [CrossRef] [PubMed]
- Asli, M.; König, P.; Sharma, D.; Pontika, E.; Huete, J.; Konda, K.R.; Mathiazhagan, A.; Xie, T.; Höschler, K.; Laskaridis, P. Thermal management challenges in hybrid-electric propulsion aircraft. Prog. Aerosp. Sci. 2024, 144, 100967. [Google Scholar] [CrossRef]
- Macdonald, T.; Clarke, M.; Botero, E.; Vegh, J.; Alonso, J. SUAVE: An Open-Source Environment Enabling Multi-fidelity Optimization. In Proceedings of the AIAA SciTech Forum, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Stanford University Department of Aeronautics and Astronautics. SUAVE: Aerospace Vehicle Environment; Stanford University Department of Aeronautics and Astronautics: Stanford, CA, USA, 2024. [Google Scholar]
- FutPrInt50 Consortium. FutPrInt50—Greening Tomorrow’s Aviation. An EU-Funded Collaborative Research Project Focused on Technologies and Configurations for Hybrid-Electric Aircraft up to 50 Seats. Online Resource. Available online: https://futprint50.eu/about/project-overview (accessed on 1 December 2024).
- Mangold, J.; Eisenhut, D.; Brenner, F.; Moebs, N.; Strohmayer, A. Preliminary Hybrid-Electric Aircraft Design with Advancements on the Open-Source Tool SUAVE. J. Phys. Conf. Ser. 2023, 2526, 012022. [Google Scholar] [CrossRef]
- Raymer, D.P. Aircraft Design: A Conceptual Approach; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2012. [Google Scholar]
- ATR. ATR 72-500 Performance Data; ATR: Blagnac, France, 1997. [Google Scholar]
- ATR. ATR 72-600 Flight Crew Operating Manual; ATR: Blagnac, France, 2011. [Google Scholar]
- ATR. ATR 72 Flight Crew Operating Manual; ATR: Blagnac, France, 1996. [Google Scholar]
- Jackson, P. Jane’s All the World’s Aircraft 2006–2007; Jane’s Information Group: Croydon, UK, 2007. [Google Scholar]
- European Union Aviation Safety Agency. Type Certificate Data Sheet for ATR 42 and ATR 72, EASA.A.084, Issue 12; European Union Aviation Safety Agency: Cologne, Germany, 2023. [Google Scholar]
- European Union Aviation Safety Agency. AMC and GM to Annex VII (Part-NCO) to Commission Regulation (EU) No 965/2012—Issue 2, Amendment 12; European Union Aviation Safety Agency: Cologne, Germany, 2022. [Google Scholar]
- Brenner, F.; Mangold, J.; Eisenhut, D.; Moebs, N.; Strohmayer, A. Deriving a year 2040 reference aircraft from a modern turboprop, implemented and calibrated in SUAVE. J. Phys. Conf. Ser. 2023, 2526, 012009. [Google Scholar] [CrossRef]
- Keller, D. Aerodynamic Investigation of the High-Lift Performance of a Propeller-Driven Regional Transport Aircraft with Distributed Propulsion. J. Phys. Conf. Ser. 2023, 2526, 012007. [Google Scholar] [CrossRef]
- Dietz, M. Einführung in den Flugzeugentwurf. In Aerodynamik des Fliegens: Von den Grundlagen bis zur Flugzeugauslegung; Springer: Berlin/Heidelberg, Germany, 2024; pp. 637–670. [Google Scholar] [CrossRef]
- European Union Aviation Safety Agency. Certification Specifications for Large Aeroplanes (CS-25); European Union Aviation Safety Agency: Cologne, Germany, 2007. [Google Scholar]
- Loftin, L. Subsonic aircraft: Evolution and the matching of size to performance. In National Aeronauticsand Space Administration, Reference Publication 1060; NASA Langley Research Center: Hampton, VA, USA, 1980. [Google Scholar]
- Brewer, G.D. Hydrogen Aircraft Technology; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A. Fuel Cell Systems Explained, 2nd ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
- Chapman, J.; Schulo, S.; Nitzsche, M. Development of a Thermal Management System for Electrified Aircraft; Technical Report, NASA TM 2020-220473; NASA: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Schmitz, O.; Hornung, M. Unified Applicable Propulsion System Performance Metrics. J. Eng. Gas Turbines Power 2013, 135, 111201. [Google Scholar] [CrossRef]
- Seitz, A.; Schmitz, O.; Isikveren, A.T.; Hornung, M. Electrically Powered Propulsion: Comparison and Contrast to Gas Turbines. In Proceedings of the Deutscher Luft- und Raumfahrtkongress 2012, Berlin, Germany, 10–12 September 2012. [Google Scholar]
- Kazula, S.; Staggat, M.; De Graaf, S. Functional and Safety Challenges of Hydrogen Fuel Cell Systems for Application in Electrified Regional Aircraft. J. Phys. Conf. Ser. 2023, 2526, 012063. [Google Scholar] [CrossRef]
- Ebersberger, J.; Fauth, L.; Keuter, R.; Cao, Y.; Freund, Y.; Hanke-Rauschenbach, R.; Ponick, B.; Friebe, J. Power Distribution and Propulsion System for an All-Electric Short-Range Commuter Aircraft—A Case Study. IEEE Access 2022, 10, 114514–114539. [Google Scholar] [CrossRef]
- Palladino, V.; Jordan, A.; Bartoli, N.; Schmollgruber, P.; Pommier-Budinger, V.; Benard, E. Preliminary studies of a regional aircraft with hydrogen-based hybrid propulsion. In Proceedings of the AIAA AVIATION 2021 FORUM. American Institute of Aeronautics and Astronautics, Virtual Event, 2–6 August 2021; pp. 1–29. [Google Scholar] [CrossRef]
- Schröder, M.; Becker, F.; Kallo, J.; Gentner, C. Optimal operating conditions of PEM fuel cells in commercial aircraft. Int. J. Hydrogen Energy 2021, 46, 33218–33240. [Google Scholar] [CrossRef]
- Fu, J.; Wang, H.; Bao, H.; Sun, X.; Liu, J. Multi-parameter optimization for the performance of the fuel cell air compressor. Therm. Sci. Eng. Prog. 2023, 44, 102057. [Google Scholar] [CrossRef]
- Buticchi, G.; Wheeler, P.; Boroyevich, D. The More-Electric Aircraft and Beyond. Proc. IEEE 2022, 111, 356–370. [Google Scholar] [CrossRef]
- VDI. VDI-Wärmeatlas; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Langeheinecke, K.; Jany, P.; Thieleke, G.; Langeheinecke, K.; Kaufmann, A. Thermodynamik für Ingenieure; Springer Fachmedien Wiesbaden: Wiesbaden, Germany, 2013. [Google Scholar] [CrossRef]
- Stückl, S.; Lobentanzer, H. Voltair—The all-electric propulsion concept platform—A vision for atmospheric friendly flight. In Proceedings of the 4th International Conference on Aerospace, Augsburg, Germany, 13–14 November 2012; pp. 2737–2747. [Google Scholar]
- Teichel, S.; Dörbaum, M.; Misir, O.; Merkert, A.; Mertens, A.; Seume, J.; Ponick, B. Design considerations for the components of electrically powered active high-lift systems in civil aircraft. Ceas Aeronaut. J. 2014, 6, 49–67. [Google Scholar] [CrossRef]
- Kadyk, T.; Winnefeld, C.; Hanke-Rauschenbach, R.; Krewer, U. Analysis and design of fuel cell systems for aviation. Energies 2018, 11, 375. [Google Scholar] [CrossRef]
- Tongsh, C.; Wu, S.; Jiao, K.; Huo, W.; Du, Q.; Park, J.; Xuan, J.; Wang, H.; Brandon, N.; Guiver, M. Fuel cell stack redesign and component integration radically increase power density. Joule 2023, 8, 175–192. [Google Scholar] [CrossRef]
- Beiranvand, H.; Rokrok, E.; Liserre, M. Volume optimization in Si IGBT-based dual-active-bridge converters. In Proceedings of the PEDSTC, Shiraz, Iran, 12–14 February 2019; pp. 577–582. [Google Scholar] [CrossRef]
- Wolnik, T.; Jarek, T.; Golec, J.; Topolewski, R.; Jastrzębski, D. High power density motor for light electric aircraft—Design study and lab tests. In Proceedings of the 2023 WEMDCD, Newcastle upon Tyne, UK, 13–14 April 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Itoh, J.-i.; Araki, T. Volume evaluation of a PWM inverter with wide band-gap devices for motor drive system. In Proceedings of the 2013 ECCE-Asia, Melbourne, VIC, Australia, 3–6 June 2013; pp. 372–378. [Google Scholar] [CrossRef]
- Zhang, X.; Gong, Y.; Xu, C.; Qu, P.; Wang, G. Thickness dependence of high volumetric energy density lithium ion battery based on Sn–Zn eutectic alloy foil anode. Ionics 2022, 28, 2685–2692. [Google Scholar] [CrossRef]
- PowerCell. PowerCell S3 Datasheet. 2018. Available online: https://www.powercell.se/wordpress/wp-content/uploads/2018/12/S3-Produktblad-190430.pdf (accessed on 1 December 2024).
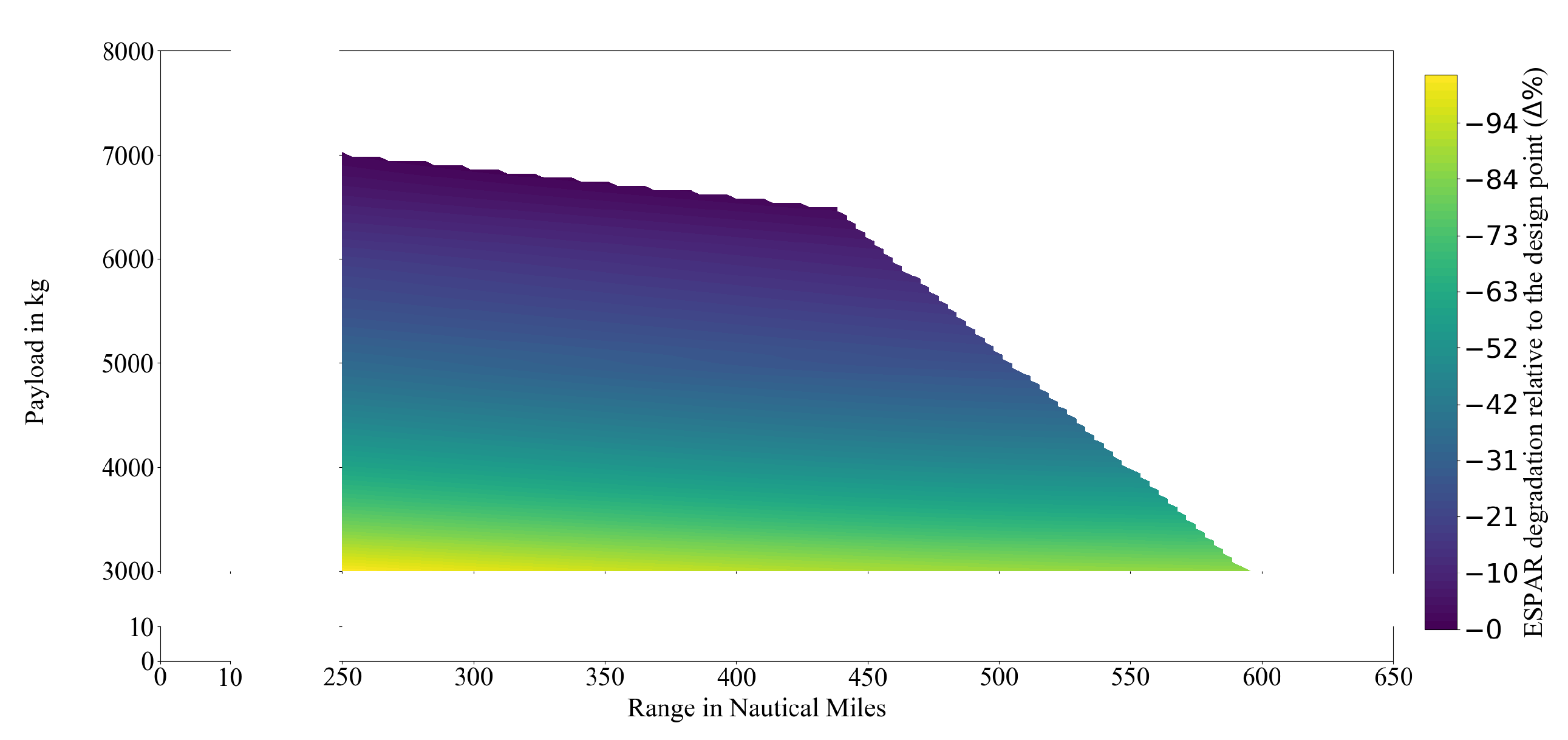
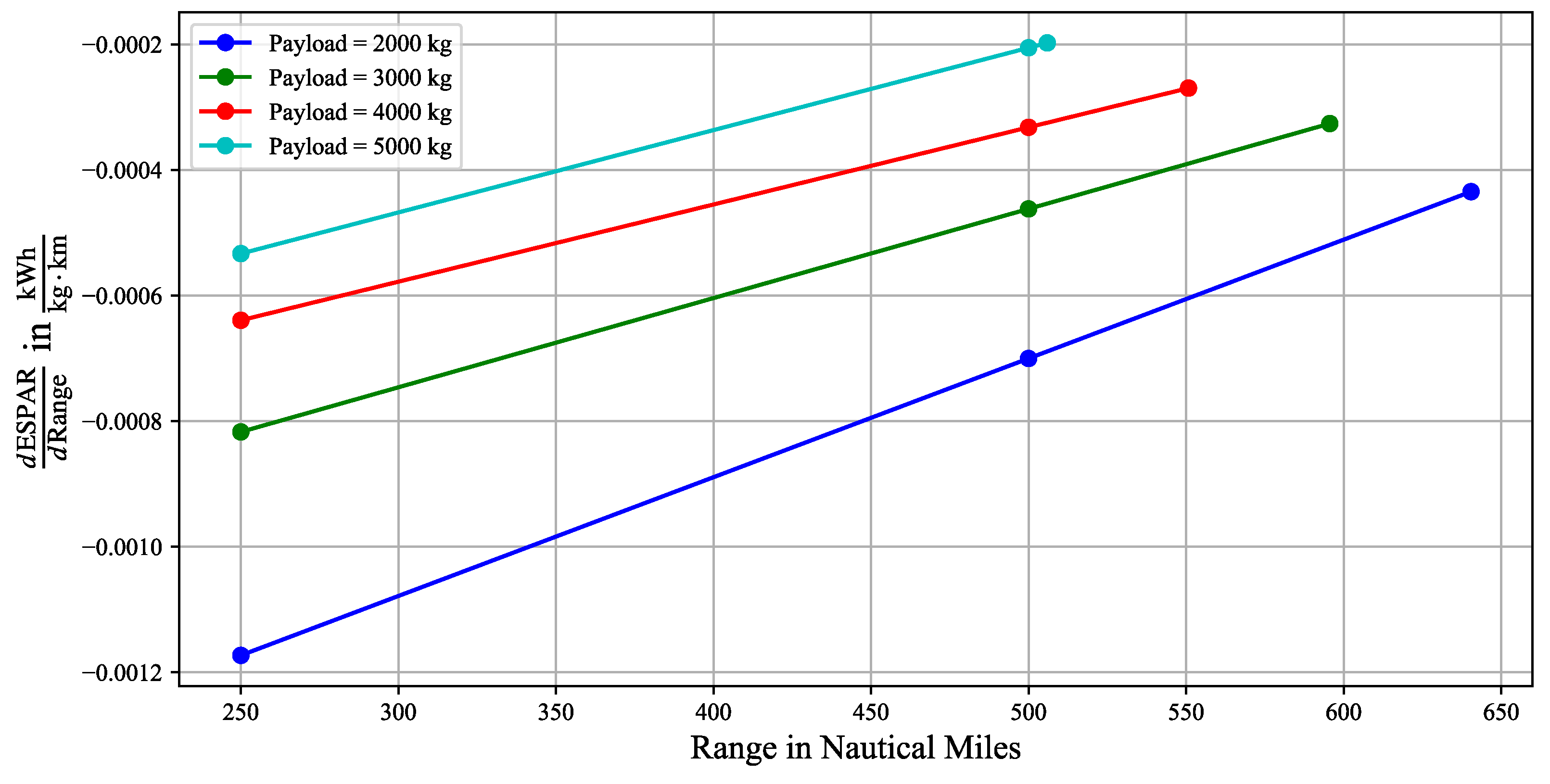
| Parameter | ATR 72-500 | Reference |
|---|---|---|
| Top of Climb | ||
| Altitude | 22,000 ft | [19] |
| Climb rate | 500 ft/min | [19] |
| Service Ceiling | ||
| Altitude | 25,000 ft | [19] |
| Climb rate | 300 ft/min | [19] |
| Design Mission | ||
| Passengers (à 95 kg) | 70 | |
| Payload | 6650 kg | [19] |
| Range | 670 NM | [19] |
| Cruise Mach number (speed) | 0.44 (265 kts) | [19] |
| Take-off and Landing | ||
| Take-off field length | 1300 m (ISA +0) | [21] |
| Landing field length | 1000 m (ISA +0) | [21] |
| Approach speed | 115 kts | [21] |
| Certification basis | CS-25 | [23] |
| Max payload | 7200 kg | [20] |
| OEI net ceiling (95% MTOM, ISA +10) | 7700 ft | [19] |
| Entry-Into-Service | 1997 | [23] |
| Maximum take-off mass | 22,500 kg | [19] |
| Operating empty mass | 12,850 kg | [19] |
| Maximum fuel mass | 5000 kg | [19] |
| Maximum operational Mach number | 0.55 Ma | [19] |
| Design Mach number | 0.44 Ma | [19] |
| Reference wing area | 61.00 | [19] 1 |
| Wing loading | 352.4 | [19] 1 |
| Engine (SLS, SA) | 2051 kW (each) | [19] |
| Power loading | 0.18 kW/kg | [19] 1 |
| Volume coefficient horizontal stabilizer | 1.07 | [21] 1 |
| Volume coefficient vertical stabilizer | 0.124 | [21] 1 |
| Final reserve fuel/energy | 45 min at holding speed | [24] |
| Alternate | 87 NM | [19] |
| Component | Mass Calibration Factor |
|---|---|
| Operational items | 1.15 |
| Landing gear | 0.94 |
| Main wing | 1.38 |
| Fuselage | 0.81 |
| Horizontal stabilizer | 1.12 |
| Vertical stabilizer | 1.03 |
| Propulsion system | 0.99 |
| Flight Segment | Drag Counts per Flight Segment |
|---|---|
| Take-off | 150 |
| Second segment | 6 |
| Climb | 6 |
| Cruise | 1 |
| Descent | 6 |
| Landing | 190 |
| Component | Reference | Baseline | Lead | |||
|---|---|---|---|---|---|---|
|
Mass in kg |
X-Axis CG in m |
Mass in kg |
X-Axis CG in m |
Mass in kg |
X-Axis CG in m | |
| Main wing | 1973 | 12.37 | 2119 | 12.40 | 1883 | 15.08 |
| Fuselage | 2078 | 12.29 | 2136 | 12.29 | 2259 | 13.25 |
| VTP | 222 | 23.94 | 238 | 24.00 | 209 | 25.82 |
| HTP | 132 | 25.23 | 147 | 25.26 | 123 | 27.80 |
| Nose landing gear | 115 | 4.09 | 119 | 4.09 | 125 | 4.80 |
| Main landing gear | 557 | 12.81 | 585 | 12.84 | 627 | 15.81 |
| Crew | 313 | 8.19 | 313 | 8.19 | 313 | 8.83 |
| Propulsion System | 1644 | 10.20 | 1736 | 10.20 | 5674 | 18.9 |
| Systems | 4422 | 11.67 | 4436 | 11.67 | 4382 | 12.77 |
| Operational items | 1022 | 10.92 | 1022 | 10.92 | 1022 | 11.77 |
| Design Fuel | 1800 | 12.23 | 2601 | 12.26 | 373 | 20.35 |
| Design Payload | 6650 | 12.29 | 6650 | 12.29 | 6650 | 13.25 |
| OEM | 12,478 | 11.88 | 12,851 | 11.93 | 16,617 | 15.38 |
| MTOM | 20,928 | 12.04 | 22,102 | 12.08 | 23,640 | 14.86 |
| Key Fact | Reference | Baseline | Lead |
|---|---|---|---|
| MTOM CG in percent MAC | 15 | 15 | 15 |
| MTOM CG in m | 12.08 | 12.04 | 14.86 |
| OEM in kg | 12,851 | 12,478 | 16,617 |
| Main Wing in m2 | 62 | 59 | 54 |
| Span in m | 27.4 | 26.6 | 27.05 |
| VTP in m2 | 16.2 | 15.0 | 14.9 |
| HTP in m2 | 12.0 | 11.0 | 10.8 |
| Design fuel energy in kWh (670 NM) 1 | 29,886 | 20,682 | n/a |
| Design fuel energy in kWh (432 NM) 1 | 22,727 | 15,764 | 12,309 |
| Total installed shaft power in kW | 4120 | 3902 | 4408 |
| Fuselage length in m | 27 | 27 | 29.44 |
| L/D Cruise | 16.8 | 16.8 | 17.3 |
| max CL | 2.6 | 2.6 | 3.3 |
| Main Wing Origin | 11.45 m | 11.45 m | 14.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlittenhardt, J.; Freund, Y.; Mangold, J.; Hanke-Rauschenbach, R.; Strohmayer, A. Preliminary Design of Regional Aircraft—Integration of a Fuel Cell-Electric Energy Network in SUAVE. Aerospace 2025, 12, 249. https://doi.org/10.3390/aerospace12030249
Schlittenhardt J, Freund Y, Mangold J, Hanke-Rauschenbach R, Strohmayer A. Preliminary Design of Regional Aircraft—Integration of a Fuel Cell-Electric Energy Network in SUAVE. Aerospace. 2025; 12(3):249. https://doi.org/10.3390/aerospace12030249
Chicago/Turabian StyleSchlittenhardt, Jakob, Yannik Freund, Jonas Mangold, Richard Hanke-Rauschenbach, and Andreas Strohmayer. 2025. "Preliminary Design of Regional Aircraft—Integration of a Fuel Cell-Electric Energy Network in SUAVE" Aerospace 12, no. 3: 249. https://doi.org/10.3390/aerospace12030249
APA StyleSchlittenhardt, J., Freund, Y., Mangold, J., Hanke-Rauschenbach, R., & Strohmayer, A. (2025). Preliminary Design of Regional Aircraft—Integration of a Fuel Cell-Electric Energy Network in SUAVE. Aerospace, 12(3), 249. https://doi.org/10.3390/aerospace12030249







