Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III
Abstract
1. Introduction
- Theoretical contribution: The UAM corridor network design problem is mathematically formulated as a multi-objective optimization framework, balancing travel time efficiency, ground risk, and implementation costs, while considering constraints such as available airspace. This framework presents a novel theoretical approach to UAM corridor network design, fostering the application of multi-objective optimization in this domain.
- Method contribution: By combining node position vectors and edge connection vectors into a fixed-length encoding vector, the encoding scheme allows for the representation of UAM corridor networks with variable corridor counts, thereby significantly enhancing the diversity and flexibility of network designs. With the proposed encoding scheme, this study presents a UAM corridor network design approach based on the unified non-dominated sorting genetic algorithm III (U-NSGA-III).
- Application contribution: This study demonstrates the application of the proposed UAM corridor network design method in a real-world case study in Chengdu. Beyond improving efficiency, our method achieves substantial reductions in risk and cost. The results demonstrate that, compared to the traditional method, our approach reduces ground risk by 37.8%, reduces implementation costs by 69.9%, and increases time savings by 4.7%. This result validates the effectiveness of the proposed method and showcases its substantial potential in real-world applications.
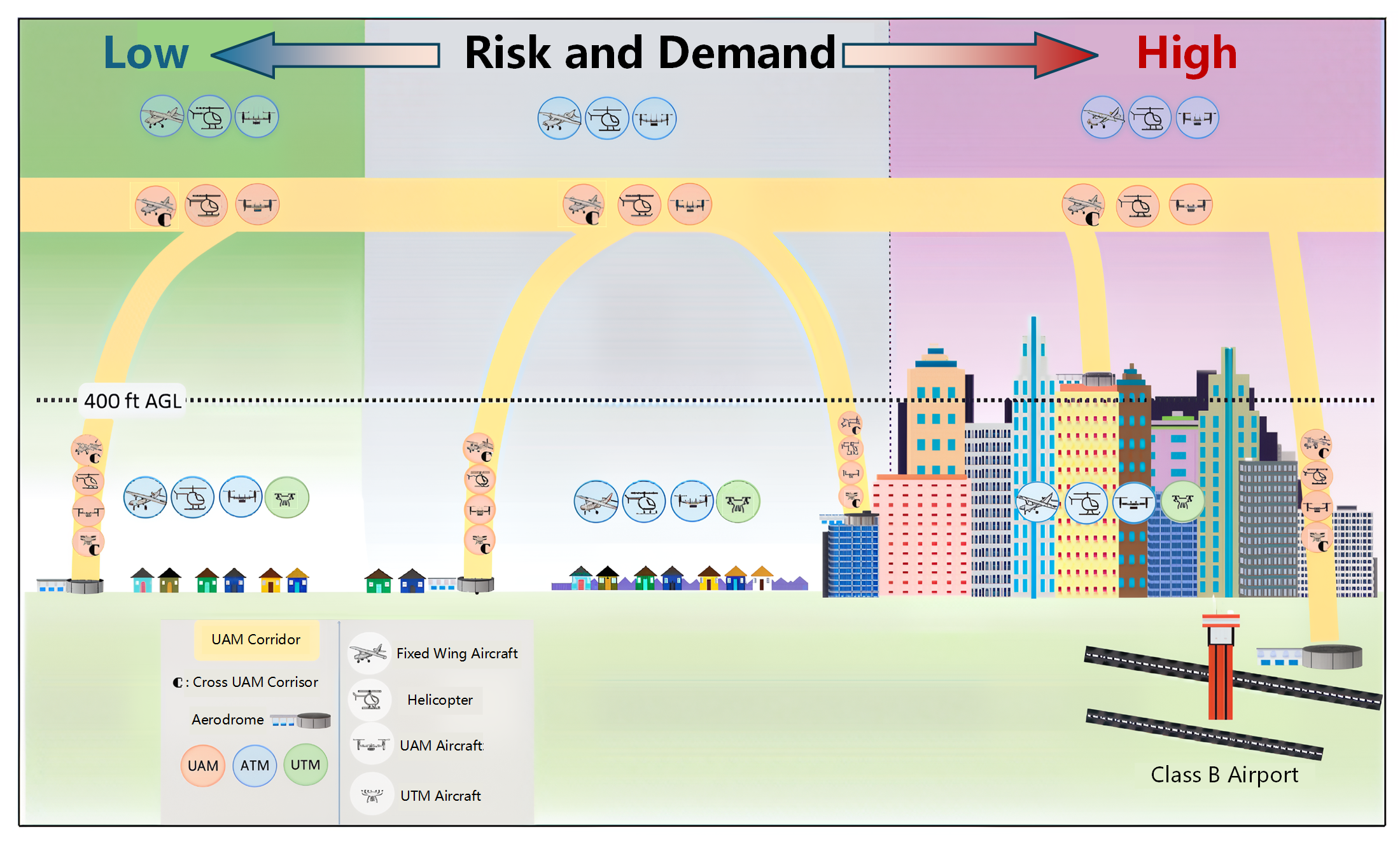
2. Problem Formulation
2.1. Multi-Objective Optimization Problem of Corridor Network Design
2.2. Optimal Objective Setting
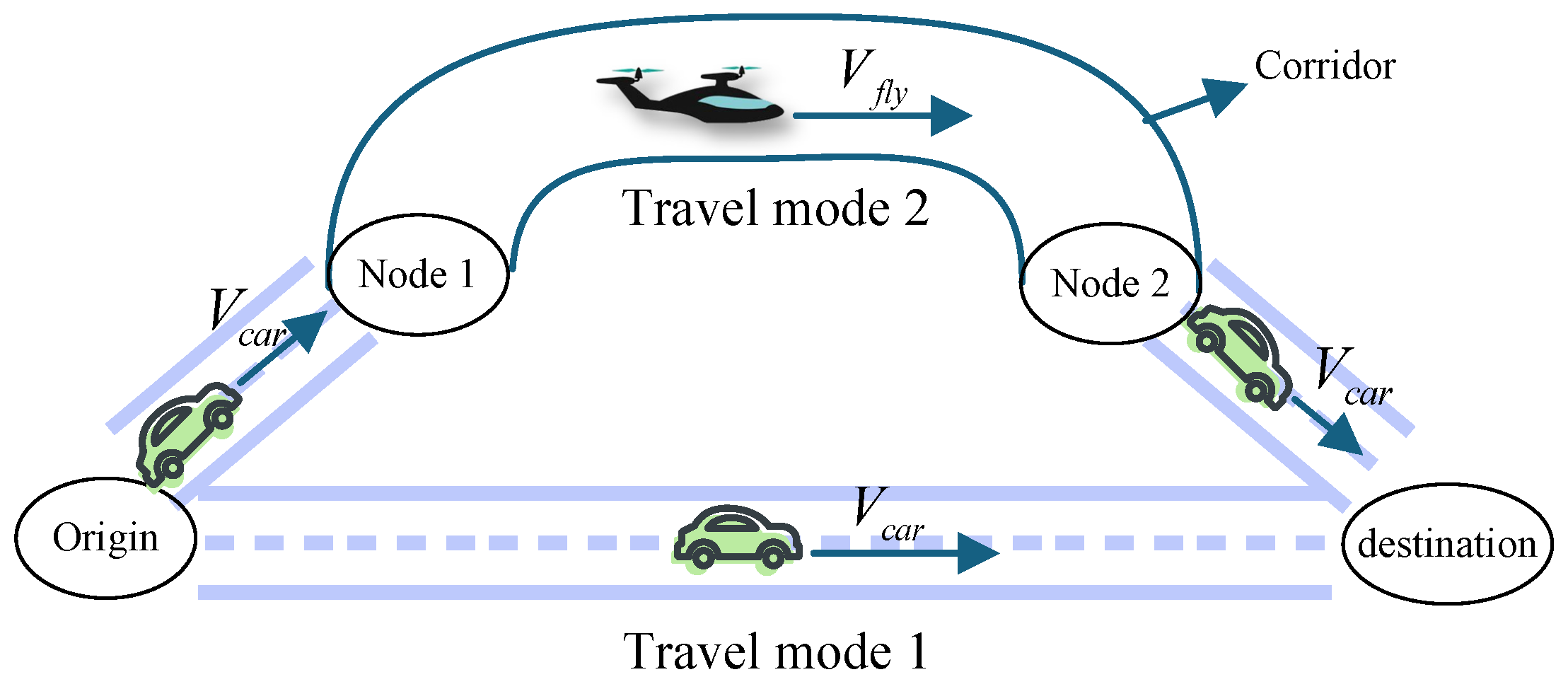
2.2.1. Travel Time-Saving Rate
2.2.2. Ground Risk
2.2.3. Implementation Cost
2.3. Constraint Setting
- No-fly zone constraint (): Each corridor in the network must avoid passing through no-fly zones, as shown in Equation (11).where represents the grid matrix of the no-fly zone, and denotes the intersection of grid cells occupied by the corridor network X and those belonging to the no-fly zones.
- Connectivity constraint (): All nodes within the corridor network must form a connected structure. The connectivity of the corridor network is expressed as follows:where denotes a path from node u to node v. denotes an edge with nodes and as the starting and ending points.
- Minimum length constraint (): The length of each corridor in the network must be no less than , as shown in Equation (12).where denotes determining whether it is true. If true, then plus 1.
3. Methods
3.1. Overview of Multi-Objective Optimization Methods
3.2. Non-Dominated Sorting Genetic Algorithm
3.3. Encoding Scheme
3.4. Algorithm Flow and Parameter Setting
| Algorithm 1 U-NSGA-III algorithm. |
|
Initialization: 1: Generate reference points with 2: Randomly initialize with Main loop: 3: 4: whiledo 5: generate offspring population with . 6: Combine and . 7: For X in : Filter out X that do not meet . 8: Perform non-dominated sorting on by . 9: Calculate the population fitness of by . 10: Select the next-generation population with . 11: Update the reference points with . 12: . 13: end while Output: 14: Return the final set of non-dominated solutions . |
4. Case Analysis
4.1. Data Collection and Processing
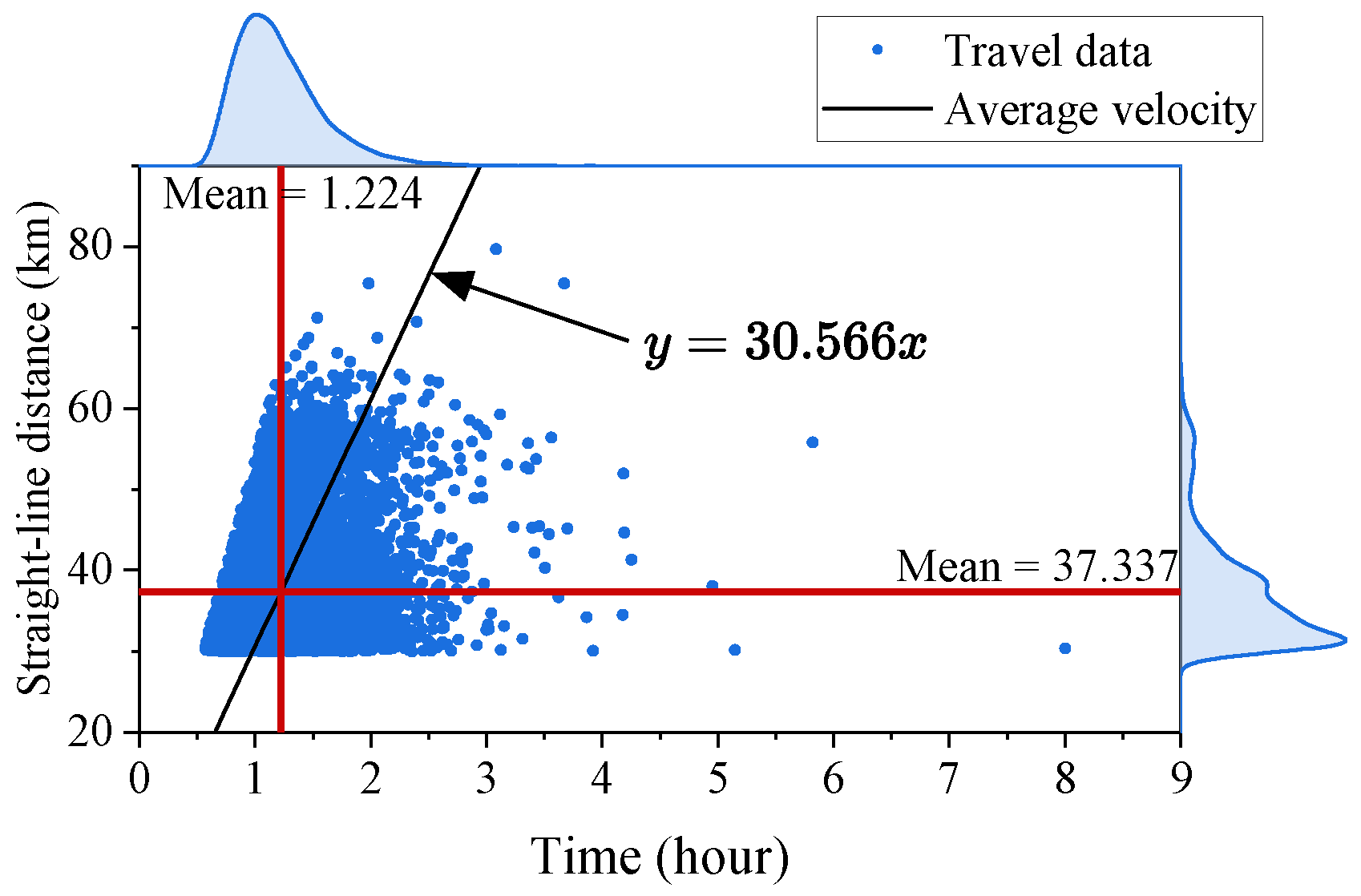
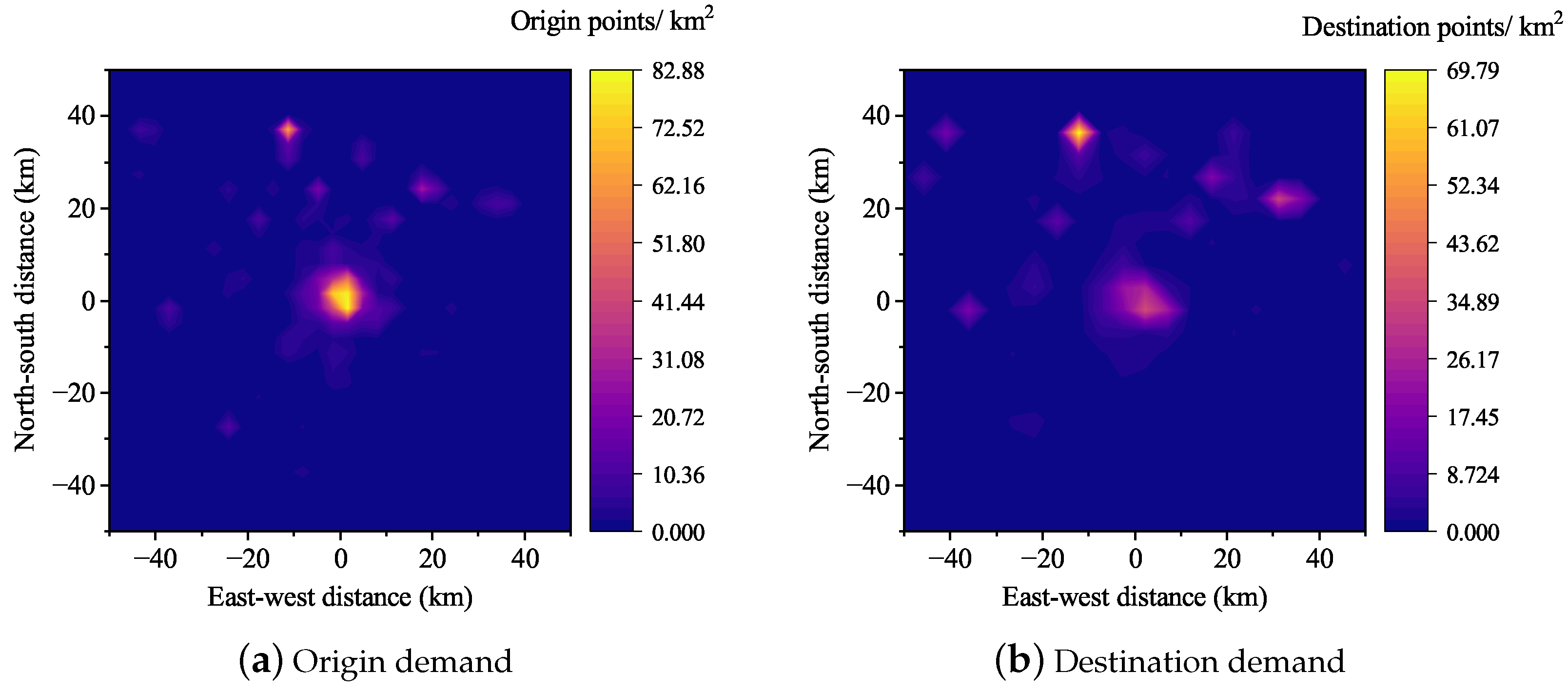
4.1.1. Travel Demand Data
- Travel distance filtering: Identify trips with a straight-line distance greater than 30 km.
- Travel scope filtering: Select trips where both the origin and destination lie within Chengdu’s main urban area, defined as a square region extending 50 km in all four directions (north, south, east, and west) from the city center (Tianfu Square).
- Outlier Removal: Clean and filter out abnormal data.
4.1.2. Population Distribution Data
- Travel scope filtering: This involves filtering mobile signaling data to include only locations within Chengdu’s main urban area, represented as a square area extending 50 km in all four directions (north, south, east, and west) from the city center (Tianfu Square).
- Outlier removal: This involves cleaning and filtering out abnormal data.
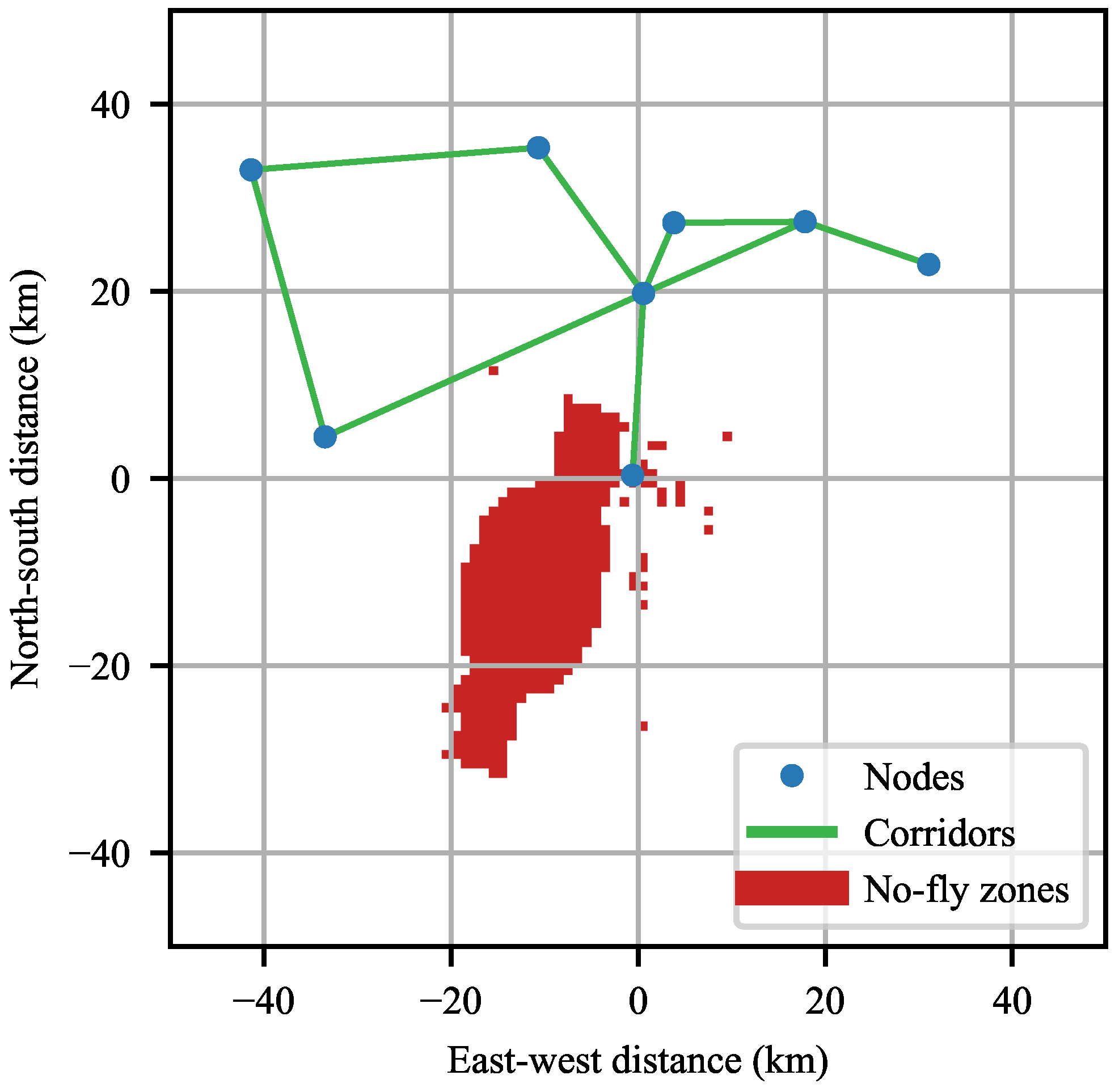
4.1.3. No-Fly Zone Data
4.2. Result of U-NSGA-III
4.2.1. Experiment on Selecting Crossover and Mutation Probabilities
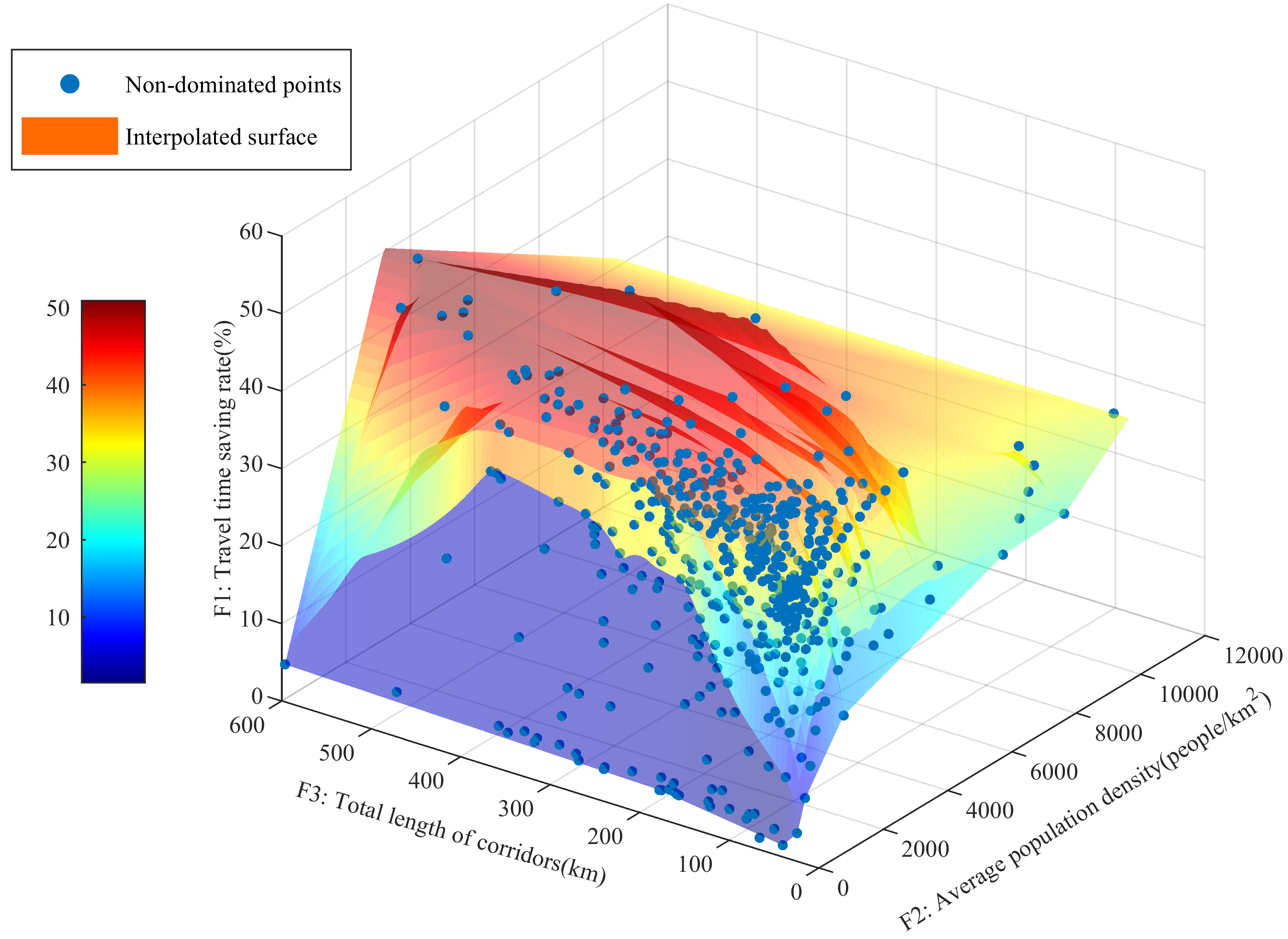
4.2.2. Pareto Front and Corridor Design Result
4.3. Comparison of K-Means Clustering Method
5. Discussion
- Non-linear corridor design: The current model assumes linear connections between nodes. Future studies could explore non-linear pathways to enhance coverage, particularly in areas with numerous no-fly zones or geographical constraints.
- Dynamic factors: Incorporating dynamic elements such as weather conditions, time-varying demands, and real-time traffic data could improve the robustness and adaptability of the corridor network.
- Additional objectives: Expanding the optimization framework to include objectives like noise pollution, environmental impact, and social equity would provide a more comprehensive assessment of UAM network performance.
- Implementation feasibility: Further research is necessary to evaluate the practical feasibility of deploying the optimized network, including aspects of regulatory compliance, public acceptance, and economic viability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- China Academy of Urban Planning and Design. Commuter Monitoring Report of Major Chinese Cities in 2024; Technical report; China Academy of Urban Planning and Design: Beijing, China, 2024. [Google Scholar]
- Niklaß, M.; Dzikus, N.; Swaid, M.; Berling, J.; Lührs, B.; Lau, A.; Terekhov, I.; Gollnick, V. A Collaborative Approach for an Integrated Modeling of Urban Air Transportation Systems. Aerospace 2020, 7, 50. [Google Scholar] [CrossRef]
- Altun, A.T.; Hasanzade, M.; Saldiran, E.; Guner, G.; Uzun, M.; Fremond, R.; Tang, Y.; Bhundoo, P.; Su, Y.; Xu, Y.; et al. AMU-LED Cranfield Flight Trials for Demonstrating the Advanced Air Mobility Concept. Aerospace 2023, 10, 775. [Google Scholar] [CrossRef]
- Gordo, V.; Becerra, I.; Fransoy, A.; Ventas, E.; Menendez-Ponte, P.; Xu, Y.; Tojal, M.; Perez-Castan, J.; Perez Sanz, L. A Layered Structure Approach to Assure Urban Air Mobility Safety and Efficiency. Aerospace 2023, 10, 609. [Google Scholar] [CrossRef]
- Qu, W.; Xu, C.; Tan, X.; Tang, A.; He, H.; Liao, X. Preliminary Concept of Urban Air Mobility Traffic Rules. Drones 2023, 7, 54. [Google Scholar] [CrossRef]
- Holden, J.; Goel, N. Fast-Forwarding to a Future of on-Demand Urban Air Transportation; Technical report; Uber Elevate: San Francisco, CA, USA, 2016. [Google Scholar]
- NASA. UAM Vision Concept of Operations (ConOps) UAM Maturity Level (UML) 4; Technical report; NASA: Washington, DC, USA, 2021. [Google Scholar]
- FAA. NextGen Concept of Operations for Urban Air Mobility (UAM) v1.0; Technical report; FAA: Washington, DC, USA, 2020. [Google Scholar]
- FAA. Urban Air Mobility (UAM) Concept of Operations 2.0; Technical Report; FAA: Washington, DC, USA, 2023. [Google Scholar]
- SESAR. U-Space Concept of Operations (Conops), 4th ed.; Technical Report; SESAR: Brussels, Belgium, 2023. [Google Scholar]
- Verma, S.; Dulchinos, V.; Wood, R.D.; Farrahi, A.; Mogford, R.; Shyr, M.; Ghatas, R. Design and Analysis of Corridors for UAM Operations. In Proceedings of the 2022 IEEE/AIAA 41st Digital Avionics Systems Conference (DASC), Portsmouth, VA, USA, 18–22 September 2022; pp. 1–10. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, T. Strategic Integration of Vertiport Planning in Multimodal Transportation for Urban Air Mobility: A Case Study in Beijing, China. J. Clean. Prod. 2024, 467, 142988. [Google Scholar] [CrossRef]
- Jin, Z.; Ng, K.K.; Zhang, C. Robust Optimisation for Vertiport Location Problem Considering Travel Mode Choice Behaviour in Urban Air Mobility Systems. J. Air Transp. Res. Soc. 2024, 2, 100006. [Google Scholar] [CrossRef]
- Kitthamkesorn, S.; Chen, A. Maximum Capture Problem for Urban Air Mobility Network Design. Transp. Res. Part E Logist. Transp. Rev. 2024, 187, 103569. [Google Scholar] [CrossRef]
- Wei, Q.; Gao, Z.; Clarke, J.P.; Topcu, U. Risk-Aware Urban Air Mobility Network Design with Overflow Redundancy. Transp. Res. Part B Methodol. 2024, 185, 102967. [Google Scholar] [CrossRef]
- Barsotti, M.; Gao, Z.; Clarke, J.P. An Eco-Social Approach to Sustainable UAM Network Design. In Proceedings of the AIAA AVIATION Forum and ASCEND 2024, Las Vegas, NV, USA, 29 July–2 August 2024. [Google Scholar] [CrossRef]
- Bauranov, A.; Rakas, J. Designing Airspace for Urban Air Mobility: A Review of Concepts and Approaches. Prog. Aerosp. Sci. 2021, 125, 100726. [Google Scholar] [CrossRef]
- Jiao, Q.; Liu, Y.; Zheng, Z.; Sun, L.; Bai, Y.; Zhang, Z.; Sun, L.; Ren, G.; Zhou, G.; Chen, X.; et al. Ground Risk Assessment for Unmanned Aircraft Systems Based on Dynamic Model. Drones 2022, 6, 324. [Google Scholar] [CrossRef]
- Wisely, D.; Wang, N.; Tafazolli, R. Capacity and Costs for 5G Networks in Dense Urban Areas. IET Commun. 2018, 12, 2502–2510. [Google Scholar] [CrossRef]
- EHang. The Future of Transportation: White Paper on Urban Air Mobility Systems; EHang: Guangzhou, China, 2020. [Google Scholar]
- Deb, K.; Sindhya, K.; Hakanen, J. Multi-objective optimization. In Decision Sciences; CRC Press: Boca Raton, FL, USA, 2016; pp. 161–200. [Google Scholar]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Kasimbeyli, R.; Ozturk, Z.K.; Kasimbeyli, N.; Yalcin, G.D.; Erdem, B.I. Comparison of some scalarization methods in multiobjective optimization: Comparison of scalarization methods. Bull. Malays. Math. Sci. Soc. 2019, 42, 1875–1905. [Google Scholar] [CrossRef]
- Sharma, S.; Kumar, V. A Comprehensive Review on Multi-objective Optimization Techniques: Past, Present and Future. Arch. Comput. Methods Eng. 2022, 29, 5605–5633. [Google Scholar] [CrossRef]
- Deb, K. Multiobjective Optimization: Interactive and Evolutionary Approaches; Lecture Notes in Computer Science Series; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Seada, H.; Deb, K. A Unified Evolutionary Optimization Procedure for Single, Multiple, and Many Objectives. IEEE Trans. Evol. Comput. 2016, 20, 358–369. [Google Scholar] [CrossRef]
- Tian, Y.; Xiang, X.; Zhang, X.; Cheng, R.; Jin, Y. Sampling Reference Points on the Pareto Fronts of Benchmark Multi-Objective Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Deb, K.; Sindhya, K.; Okabe, T. Self-Adaptive Simulated Binary Crossover for Real-Parameter Optimization. In Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 1187–1194. [Google Scholar] [CrossRef]
- Carles-Bou, J.L.; Galán, S.F. Self-Adaptive Polynomial Mutation in NSGA-II. Soft Comput. 2023, 27, 17711–17727. [Google Scholar] [CrossRef]
- Didi Chuxing. Didi Gaia Data Open Plan. 2017. Available online: https://outreach.didichuxing.com/research/opendata (accessed on 20 December 2024).
- Wei, B.; Su, G.; Liu, F. Dynamic Assessment of Spatiotemporal Population Distribution Based on Mobile Phone Data: A Case Study in Xining City, China. Int. J. Disaster Risk Sci. 2023, 14, 649–665. [Google Scholar] [CrossRef]
- ICAO. Annex14-Aerodromes Volume I; ICAO: Montréal, QC, USA, 2018. [Google Scholar]
- China Civil Aviation Website. The Civil Aviation Administration Has Announced the Protection Zones for Obstacle Limitation Surfaces at Civil Airports. 2017. Available online: https://www.ccaonline.cn/news/hot/332813.html (accessed on 20 December 2024).
- SKYDB. Chengdu—Buildings—Skyscrapers—High-Rise-Buildings. Available online: https://www.skydb.net/city/598504688/chengdu/ (accessed on 20 December 2024).
- Fonseca, C.; Paquete, L.; Lopez-Ibanez, M. An Improved Dimension-Sweep Algorithm for the Hypervolume Indicator. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; pp. 1157–1163. [Google Scholar] [CrossRef]
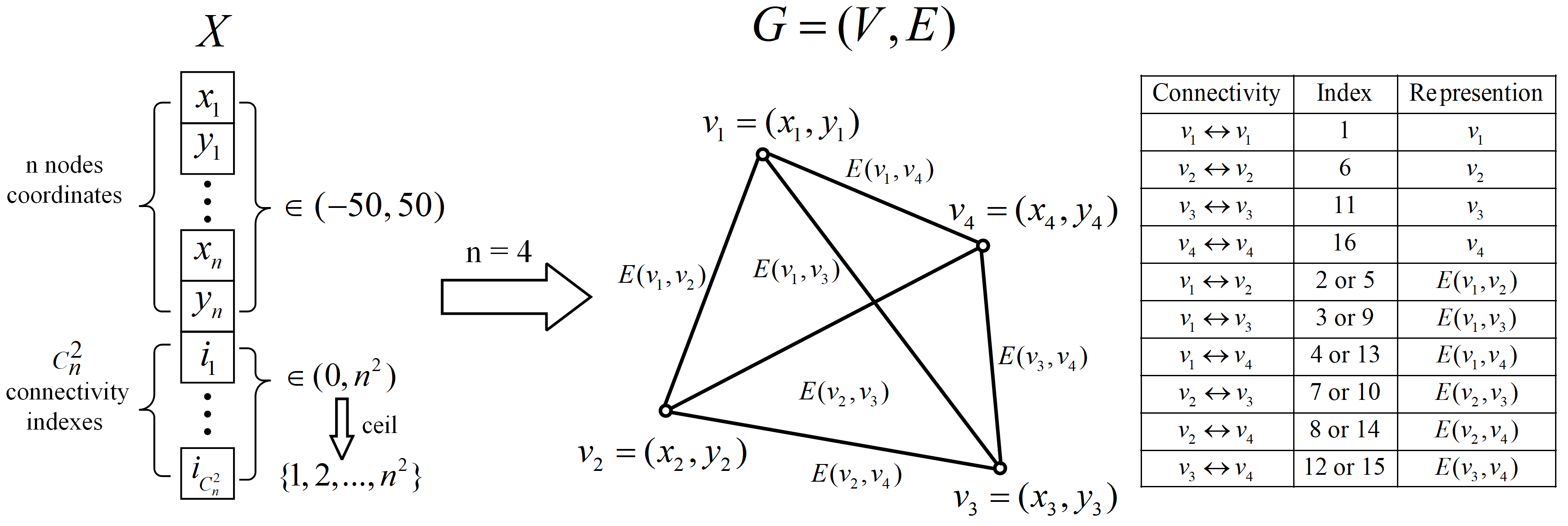





| Name | Symbol | Value |
|---|---|---|
| Velocity of fling in corridors | 240 km/h | |
| Minimum length of a corridor | 8 km | |
| The number of nodes | [4–8] | |
| Population size | ||
| Population generation number | 1000 | |
| Reference direction division number | 20 | |
| Crossover probability | [0.2–0.8] | |
| Mutation probability | [0.2–0.8] |
| Name | Height | Latitude | Longitude |
|---|---|---|---|
| Chengdu Greenland Tower | 468 | 30.61055 | 104.1408 |
| Tiantou International Business Center | 284 | 30.42122 | 104.0730 |
| International Commerce Center | 280 | 30.63604 | 104.1115 |
| Chengdu IFS Tower | 247 | 30.65705 | 104.0780 |
| Global Times Center | 243 | 30.55739 | 104.0628 |
| Western IFC Conrad Hotel | 241 | 30.65101 | 104.0808 |
| Tianxi Twin Towers | 222 | 30.63745 | 104.0933 |
| Tianfu IFC | 220 | 30.58707 | 104.0643 |
| Waldorf Astoria Chengdu | 220 | 30.58685 | 104.0665 |
| Oriental Hope Intertek Plaza | 219 | 30.55477 | 104.0656 |
| Minyoun Financial Plaza | 206 | 30.64957 | 104.0886 |
| OPPO Headquarters | 206 | 30.58233 | 104.0673 |
| Chengdu Fantasia Meinian Plaza | 204 | 30.53615 | 104.0660 |
| Sichuan Airlines Plaza | 204 | 30.66147 | 104.0678 |
| Huarun Tower | 201 | 30.65247 | 104.1135 |
| Pinnacle One | 200 | 30.65258 | 104.0816 |
| Chengdu World Financial Center | 200 | 30.55341 | 104.0608 |
| Twin Rivers International Office Tower | 200 | 30.56217 | 104.0550 |
| Palm Springs International Center | 200 | 30.55763 | 104.0672 |
| 0.2 | 0.4 | 0.6 | 0.8 | ||
|---|---|---|---|---|---|
| 0.2 | 0.886 | 0.914 | 0.926 | 0.921 | |
| 0.4 | 0.868 | 0.879 | 0.895 | 0.884 | |
| 0.6 | 0.845 | 0.868 | 0.883 | 0.875 | |
| 0.8 | 0.825 | 0.842 | 0.837 | 0.855 | |
| Number of Clusters (K) | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|
| Travel time-saving rate () | 30.9% | 33.7% | 35.7% | 38.5% | 42.4% |
| e population density () | 2488.4 | 2968.1 | 3609.5 | 3059.3 | 2164.9 |
| Total corridor length () | 112.3 | 225.4 | 412.7 | 445.2 | 636.2 |
| Demand coverage rate | 77.9% | 82.6% | 87.8% | 89.7% | 90.6% |
| Travel time-saving rate of covered demands | 37.3% | 39.0% | 39.2% | 41.7% | 45.5% |
| Evaluation Metrics | U-NSGA-III | K-Means |
|---|---|---|
| Travel time-saving rate () | 47.1% | 42.4% |
| Average population density () | 1346.1 | 2164.9 |
| Total corridor length () | 191.6 | 636.2 |
| Demand coverage rate | 88.1 | 90.6% |
| Travel time-saving rate of covered demands | 51.9 | 45.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zheng, Y.; Li, C.; Jiang, B.; Li, Y. Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III. Aerospace 2025, 12, 229. https://doi.org/10.3390/aerospace12030229
Zhang Z, Zheng Y, Li C, Jiang B, Li Y. Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III. Aerospace. 2025; 12(3):229. https://doi.org/10.3390/aerospace12030229
Chicago/Turabian StyleZhang, Zhiyuan, Yuan Zheng, Chenglong Li, Bo Jiang, and Yichao Li. 2025. "Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III" Aerospace 12, no. 3: 229. https://doi.org/10.3390/aerospace12030229
APA StyleZhang, Z., Zheng, Y., Li, C., Jiang, B., & Li, Y. (2025). Designing an Urban Air Mobility Corridor Network: A Multi-Objective Optimization Approach Using U-NSGA-III. Aerospace, 12(3), 229. https://doi.org/10.3390/aerospace12030229






