The Assembly, Integration and Test of the DORA Telescope, a Deployable Optics System in Space for Remote Sensing Applications
Abstract
1. Introduction
2. Mission Requirements
3. Instrument Requirements and Optical Design
4. Mechanical Design
4.1. Telescope Structure
- -
- a baseplate hosting the primary mirror and MIMA interface plate; four opening pockets of 45 × 20 mm allow for the actuators passage.
- -
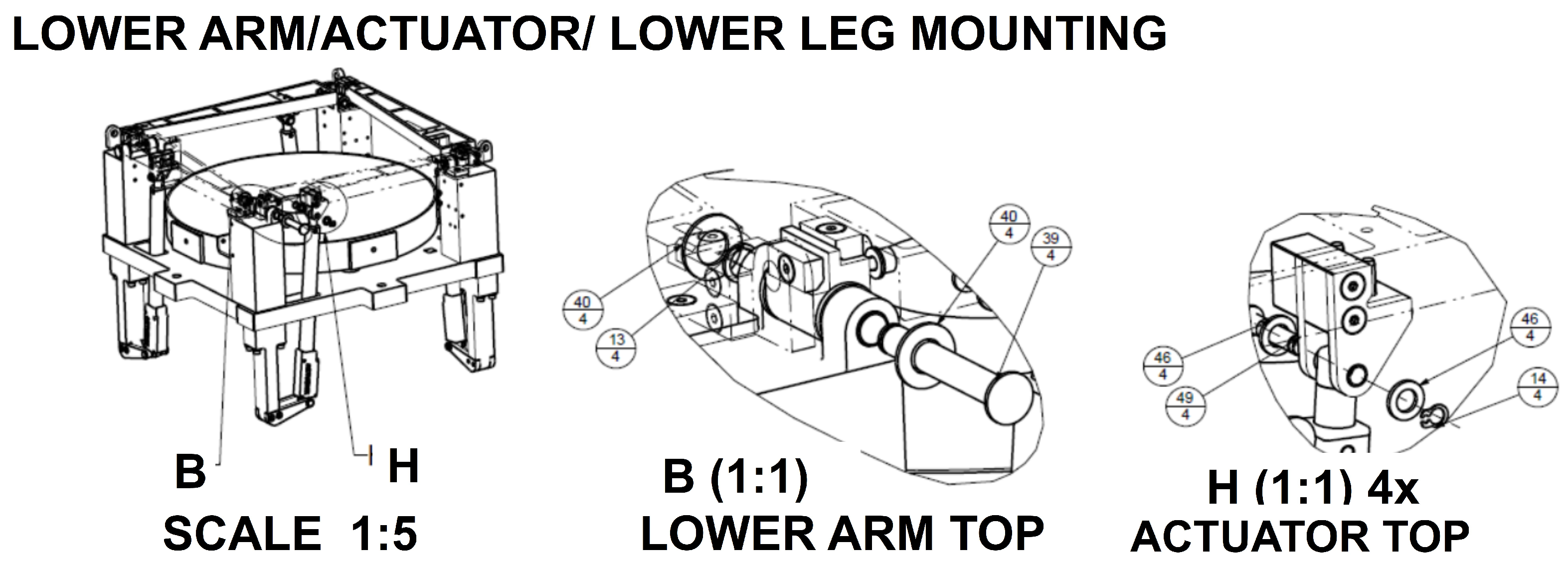
- four supporting blocks respectively for the actuators and the articulated lower arms, containing the revolute joints to carry out the deployment motion.
- -
- four upper articulating arms with hinges connected to the top ring with the secondary mirror subunit.
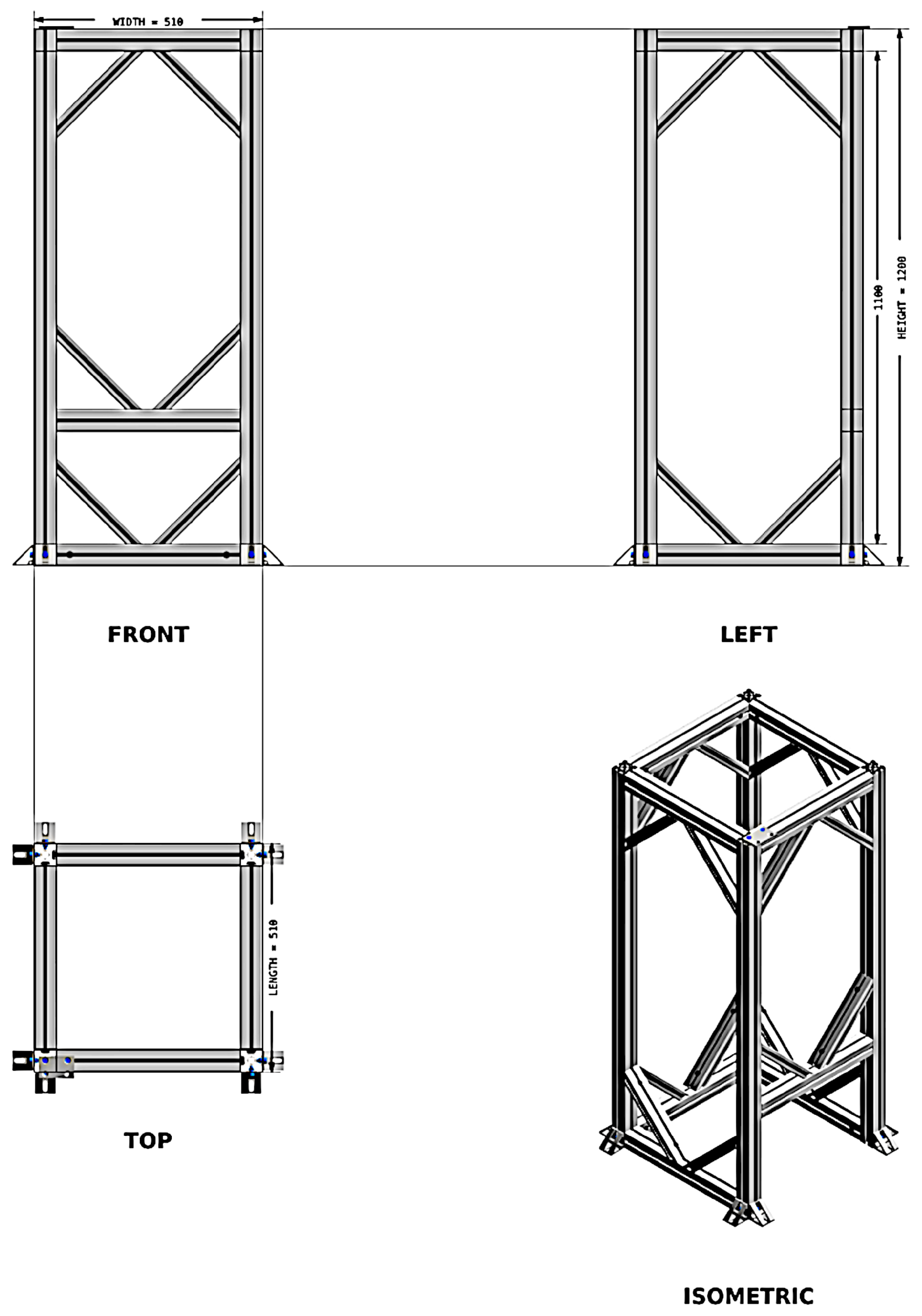
4.2. Supporting Frame Structure
4.3. The Primary and Secondary Mirrors
5. Assembling Procedure
Mechanical Assembling
6. Test Procedure
6.1. Measurements Methodology
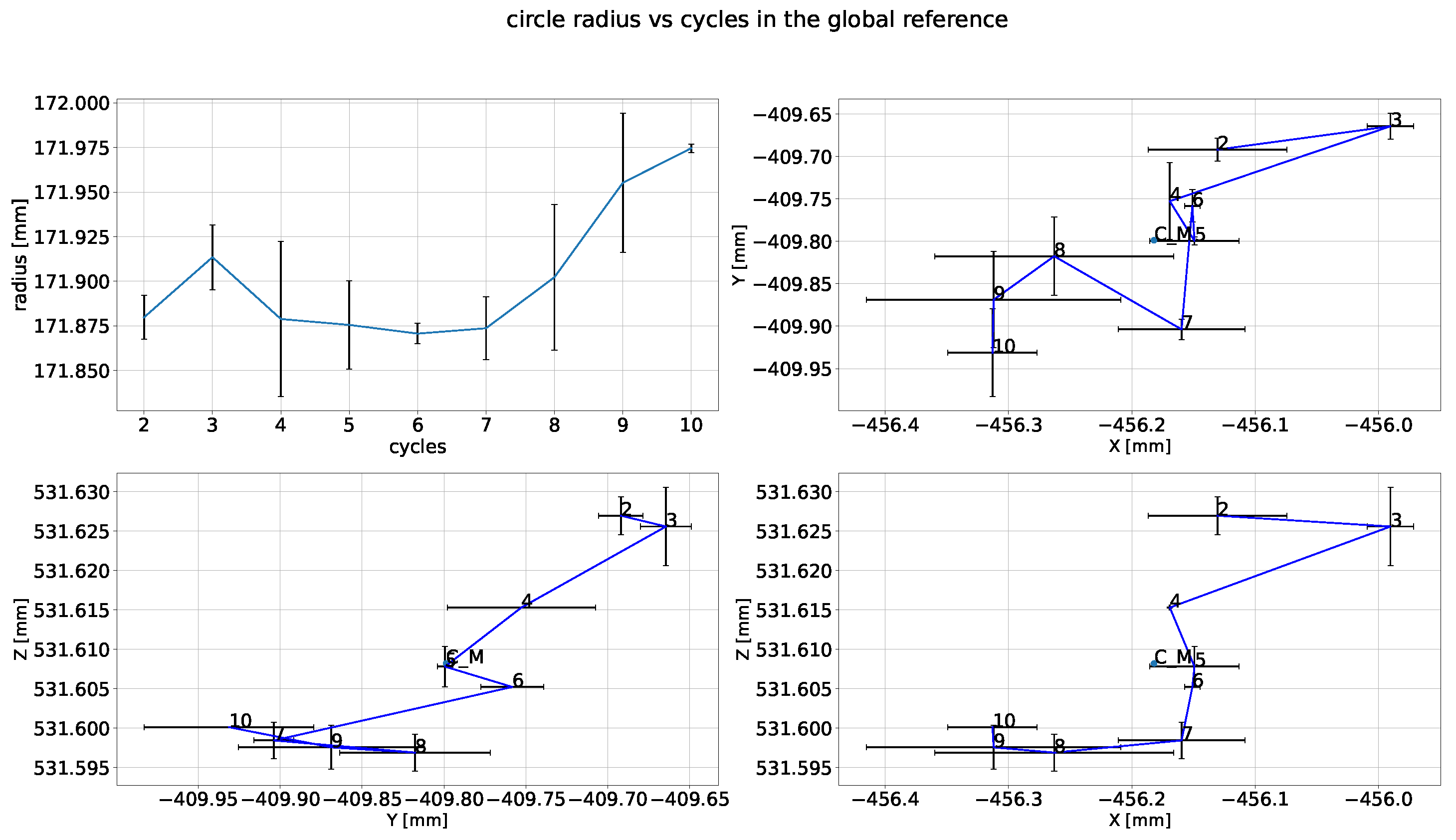
6.2. Outcomes from Data Analysis
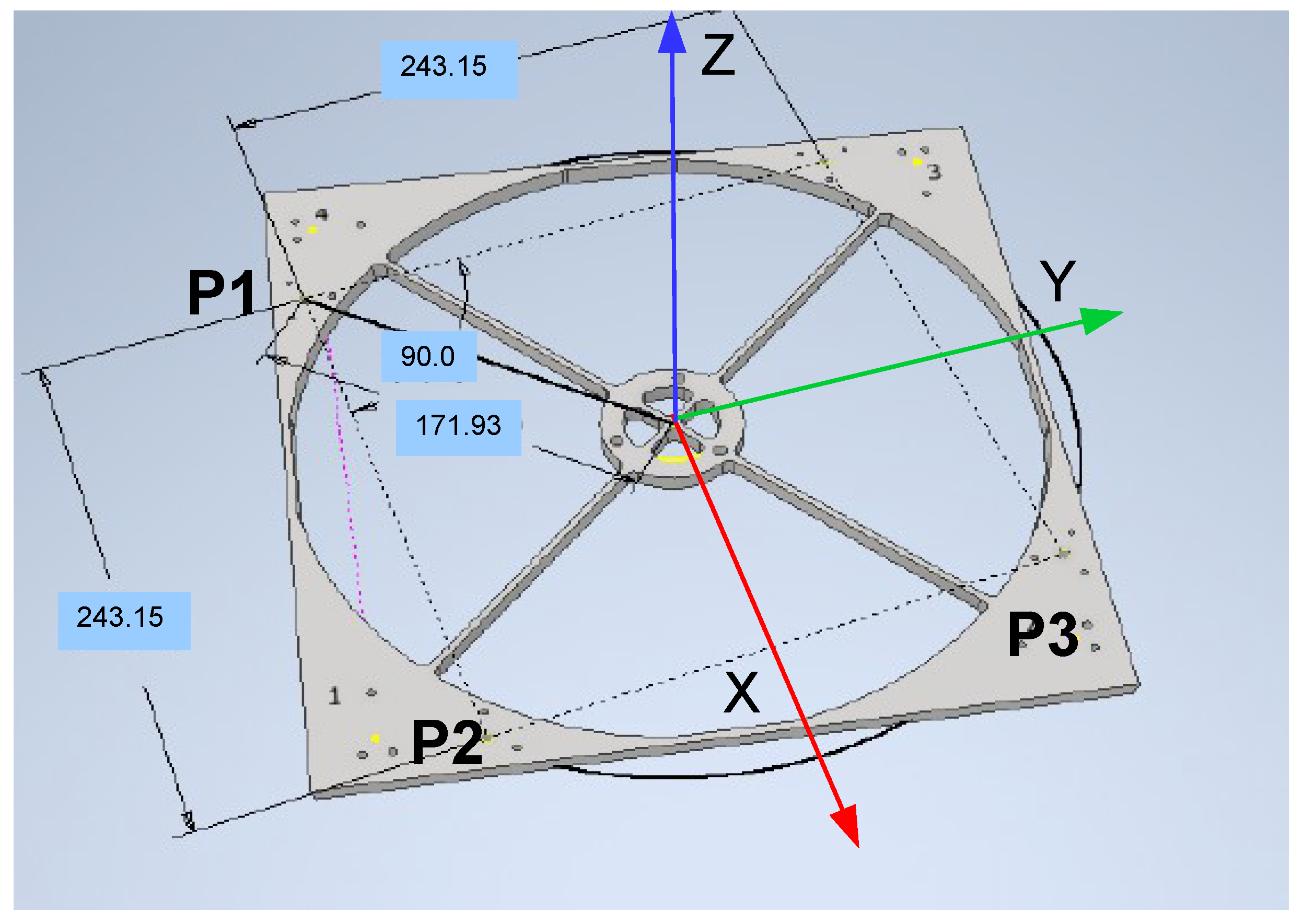
6.2.1. Analyzing the Pin Positions
6.2.2. Displacements and Euler Angles Calculation
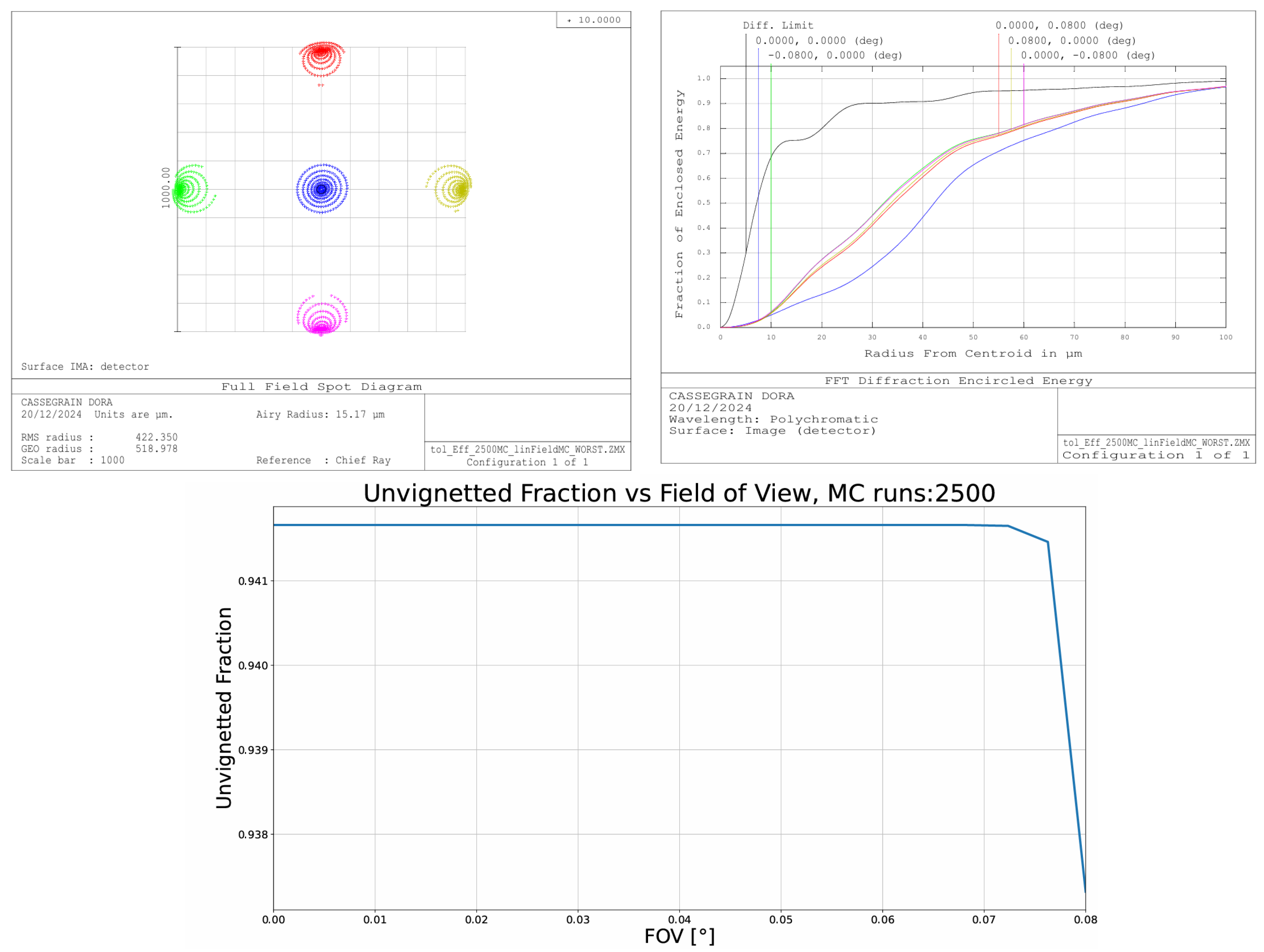
6.3. Updating the Tolerance Analysis
7. Conclusions
- Reducing backlash in each of the supporting blocks for the lower arms or replacing them with four whole blocks (which now, instead, consist of 3 components).
- Introducing a smart hexapod structure behind M2: it can be either a miniaturized platform like the one provided by Physik Instrumente (PI) with six degrees of freedom capability or the one offered by Smaract company, the Smarpod model, which is equivalent to a hexapod but with 3 multi-linear stages at 120°. This item, which has been investigated for its limited envelope, has a baseplate diameter of ∅ 70 mm interfacing with the fixed top ring assembly and a ∅ 45 mm flange diameter interfacing with M2. It would represent the best tradeoff solution, as it is a fully controlled 5 dof platform with a minimum number of interface parts to manufacture, rather compact, which can be quickly plugged in and calibrated, and incorporates optical and inductive sensors. In particular, the Smarpod 70.42 type, weighing about 200 g, would be suitable [17].
- An alternative solution with respect to the Hexapod involves two different types of piezoactuators currently adopted in various astronomical instruments: two multistacked PI-601.3SL for correction along the X and Y directions and three APA-120S from Cedrat Technologies for providing Z motion and tilts around X and Y. The shell shaped APA type of piezoactuators, providing three degrees of freedom compensation (Z, , ), has been deployed to steer M5 for ELT [18]. They all incorporate sensors for closed-loop control and have to come precalibrated for the specific application and need, including strain gages, an amplifier, and controller boards.
- For both solutions, an additional mechanical interface is needed, consequently increasing the distance between the top ring plate and the primary mirror cell.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Muslimov, E.R.; Sakhabutdinov, A.Z.; Morozov, O.G.; Pavlycheva, N.K.; Akhmetov, D.M.; Kharitonov, D.Y. Digital Holographic Positioning Sensor for a Small Deployable Space Telescope. Appl. Sci. 2022, 12, 4427. [Google Scholar] [CrossRef]
- Xue, Y.; Li, Y.; Guang, J.; Zhang, X.; Guo, J. Small satellite remote sensing and applications—History, current and future. Int. J. Remote. Sens. 2008, 29, 4339–4372. [Google Scholar] [CrossRef]
- Bellucci, G.; Saggin, B.; Fonti, S.; Biondi, D.; Cerulli, P.; Luca, M.; Altieri, F.; Mattana, A.; Alberti, A.; Marzo, G.; et al. MIMA, a miniaturized Fourier infrared spectrometer for Mars ground exploration: Part I. Concept and expected performance. In Sensors, Systems, and Next-Generation Satellites XI, Florence, Italy, 17–20 September 2007; SPIE: Bellingham, WA, USA, 2007. [Google Scholar] [CrossRef]
- Saggin, B.; Alberti, E.; Comolli, L.; Tarabini, M.; Bellucci, G.; Fonti, S. MIMA, a miniaturized infrared spectrometer for Mars ground exploration: Part III. Thermomechanical design. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XI, Florence, Italy, 17–20 September 2007; Habib, S., Meynart, R., Neeck, S.P., Shimoda, H., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2007; Volume 6744, p. 67441S. [Google Scholar] [CrossRef]
- Fonti, S.; Marzo, G.A.; Politi, R.; Bellucci, G.; Saggin, B. MIMA, a miniaturized Fourier spectrometer for Mars ground exploration: Part II. Optical design. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XI, Florence, Italy, 17–20 September 2007; Habib, S., Meynart, R., Neeck, S.P., Shimoda, H., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2007; Volume 6744, p. 67441R. [Google Scholar] [CrossRef]
- Martellato, E.; Piccirillo, A.M.; Ferraioli, G.; Rotundi, A.; Della Corte, V.; Palumbo, P.; Alcaras, E.; Appolloni, L.; Aulicino, G.; Bertini, I.; et al. A New Orbiting Deployable System for Small Satellite Observations for Ecology and Earth Observation. Remote Sens. 2022, 14, 2066. [Google Scholar] [CrossRef]
- Capaccioni, F.; Bellucci, G.; Rinaldi, G.; Saggin, B.; Valnegri, P.; Filacchione, G.; Della Corte, V.; Magrin, D.; Angarano, M.; Filippetto, D.; et al. DORA: Deployable Optics for Remote sensing Applications. In Proceedings of the European Planetary Science Congress, Online, 21 September–9 October 2020; Volume 14. EPSC2020-1003. [Google Scholar] [CrossRef]
- Villalba, V.; Kuiper, H.; Gill, E. Review on thermal and mechanical challenges in the development of deployable space optics. J. Astron. Telesc. Instruments Syst. 2020, 6, 010902. [Google Scholar] [CrossRef]
- Valnegri, P.; Saggin, B.; Scaccabarozzi, D.; Corti, M.; Capaccioni, F.; Bellucci, G.; Rinaldi, G. Comparison of candidate mechanism concepts for a deployable space telescope. In Proceedings of the 2021 IEEE 8th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 23–25 June 2021; pp. 92–96. [Google Scholar] [CrossRef]
- Rinaldi, G.; Capaccioni, F.; Bellucci, G.; Filacchione, G.; Di Varano, I.; Magrin, D.; Saggin, B.; Valnegri, P.; Della Corte, V.; Piccirillo, A.M.; et al. Deployable Telescope for Remote Sensing Applications. Opt. Express, 2025; in preparation. [Google Scholar]
- Ansys Zemax. OpticStudio User Manual. Ansys Inc. 2023. Available online: https://www.ansys.com/products/optics/ansys-zemax-opticstudio (accessed on 31 October 2024).
- Francis, W.; Lake, M.; Peterson, L.; Hinkle, J. Development of an Elastic Memory Composite Self-Locking Linear Actuator for Deployable Optics. In Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference, Palm Springs, CA, USA, 19–22 April 2004. [Google Scholar] [CrossRef]
- Valnegri, P.; Saggin, B.; Scaccabarozzi, D.; Arrigoni, S.; Capaccioni, F.; Bellucci, G.; Rinaldi, G. DORA telescope project: Preliminary characterization of the deployment mechanism. In Proceedings of the 2022 IEEE 9th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Pisa, Italy, 27–29 June 2022; pp. 550–555. [Google Scholar] [CrossRef]
- Di Varano, I.; Capaccioni, F.; Filacchione, G.; Rinaldi, G.; Bellucci, G.; Morbidini, A.; Saggin, B. Investigation of optical error budget for the DORA telescope. In Proceedings of the 2023 IEEE 10th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Milan, Italy, 19–21 June 2023; pp. 84–88. [Google Scholar] [CrossRef]
- Andersen, T.; Enmark, A. Integrated Modeling of Telescopes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 377. [Google Scholar] [CrossRef]
- Di Varano, I.; Yuan, S.; Woche, M.; Strassmeier, K.G.; Weber, M. ELT-HIRES the high-resolution spectrograph for the ELT: Simulation results of polarimetric aberrations for the polarimetric module. In Proceedings of the Modeling Aspects in Optical Metrology VII, Munich, Germany, 24–27 June 2019; Society of Photo-Optical Instrumentation Engineers (SPIE) Conference, Series. Bodermann, B., Frenner, K., Silver, R.M., Eds.; SPIE: Bellingham, WA, USA, 2019; Volume 11057, p. 1105715. [Google Scholar] [CrossRef]
- Technical Datasheet: Smarpod-70-42.pdf. SmarAct GmbH. 2024. Available online: https://www.smaract.com/en/smarpod/product/smarpod-70-42 (accessed on 15 June 2024).
- Company Weblink. 2024. Available online: https://cedrat-technologies.com/wp-content/uploads/downloads/piezo_actuators_for_astronomical_instrumentation.pdf (accessed on 31 October 2024).
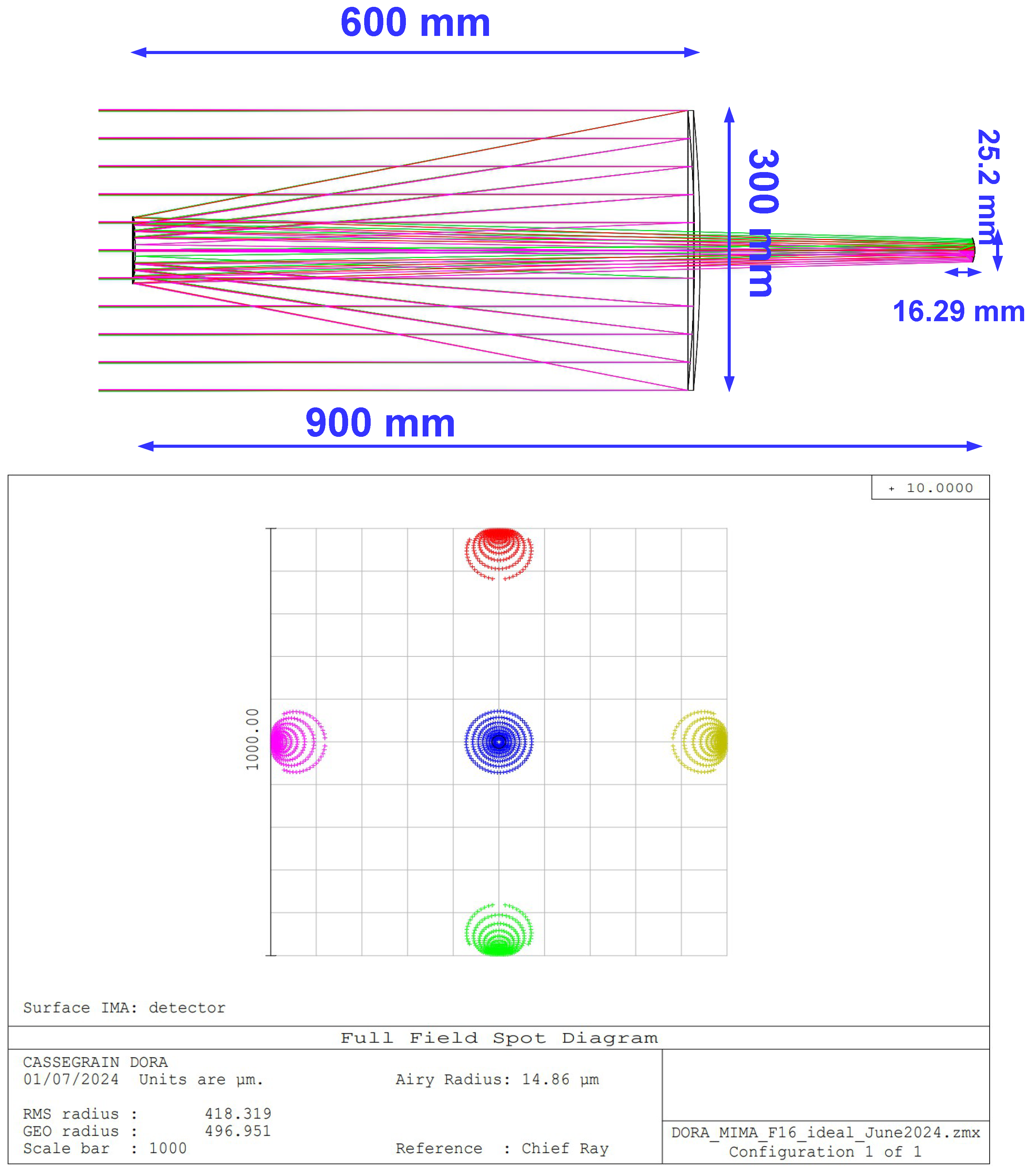
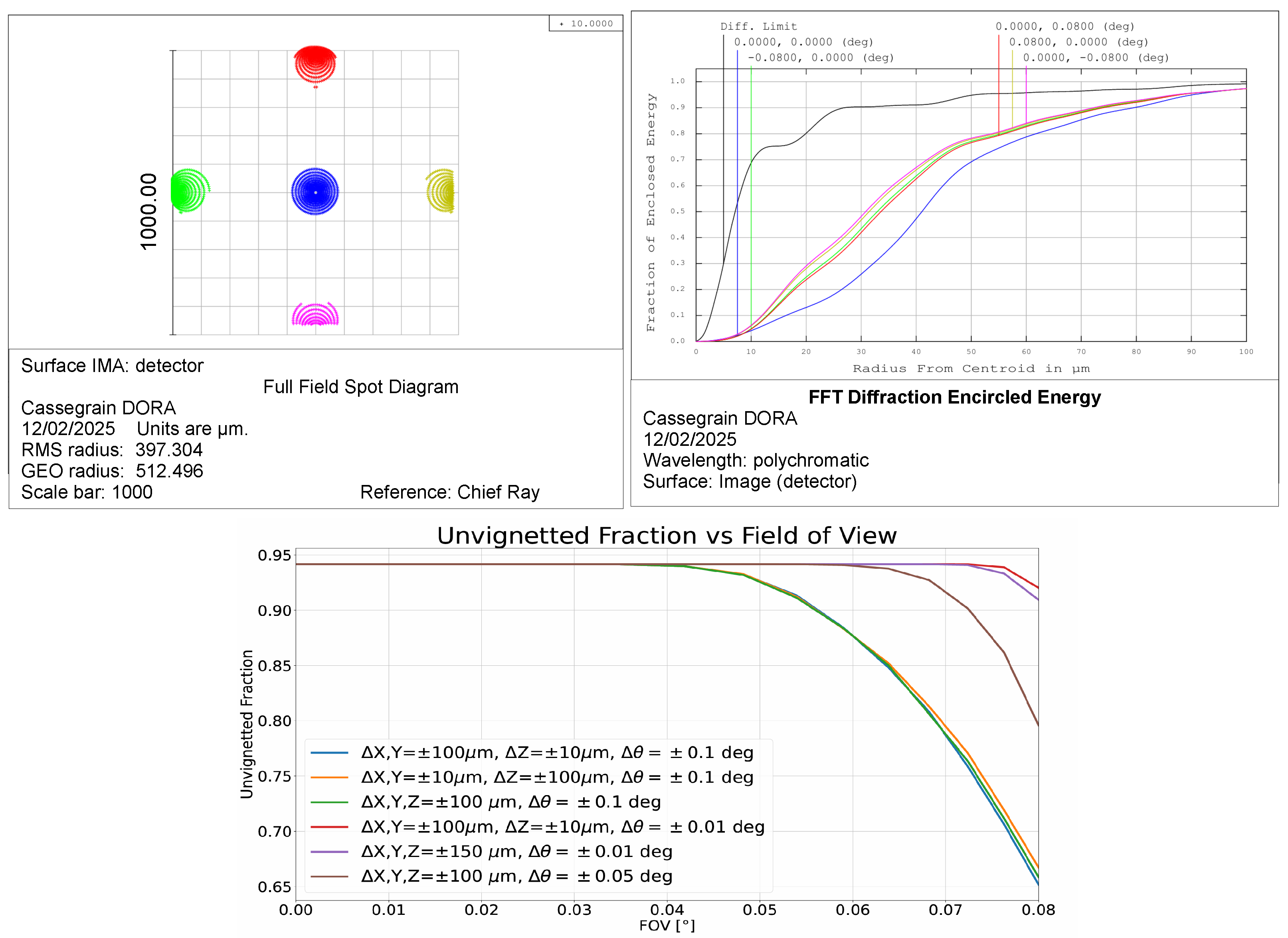








| MIMA | |
|---|---|
| Spectral range | 5–25 m |
| Spectral resolution | 5 cm−1 for atmospheric sounding |
| 10 cm−1 for geologic mapping | |
| Entrance pupil diameter | 26.4 mm |
| Focal length | 17.5 mm |
| Etendue (AΩ) | 0.01654 sr cm2 |
| FOV | 3.2° ( 56 mrad) |
| Detector size | 1 mm2 |
| Detector | PbSe |
| Telescope | |
| f/# | 16.21 |
| Optical efficiency | 0.6 |
| Maximum entrance pupil | 300 mm |
| Central bore diameter | 60 mm |
| Exit pupil diameter | 79.142 mm |
| Effective focal length | 4863.287 mm |
| Back focal length | 1124.61 mm |
| Maximum radial field | 0.08° |
| Spatial resolution | <6 km @700 km |
| FOV | 0.16° |
| Overall dimensions | 320 × 320 × 800 mm |
| Equivalent f/# telescope + MIMA | 1.25 |
| Euler Displacements | st. dev. P1 | st. dev. P2 | st. dev. P3 | Average of the Absolute Values | Euler Standard Deviation | P-V | |
|---|---|---|---|---|---|---|---|
| [mm] | −2.7970 × | 0.010 | 0.005 | 0.025 | 5.15311480 × | 5.85475931 × | 1.74670486 × |
| −7.8780 × | 0.048 | 0.055 | 0.035 | ||||
| 2.1274 × | 0.010 | 0.025 | 0.050 | ||||
| −1.3788 × | 0.085 | 0.040 | 0.035 | ||||
| −3.2729 × | 0.085 | 0.021 | 0.105 | ||||
| −7.8625 × | 0.0082 | 0.025 | 0.0249 | ||||
| 6.7116 × | 0.029 | 0.041 | 0.0679 | ||||
| 4.7604 × | 0.005 | 0.045 | 0.100 | ||||
| 9.5890 × | 0.05 | 0.020 | 0.100 | ||||
| [mm] | −9.9461 × | 0.020 | 0.065 | 0.015 | 6.49705303 × | 7.36597189 × | 2.27605805 × |
| −7.7048 × | 0.026 | 0.030 | 0.024 | ||||
| −3.9517 × | 0.005 | 0.100 | 0.025 | ||||
| 5.8891 × | 0.025 | 0.065 | 0.080 | ||||
| −7.6346 × | 0.015 | 0.020 | 0.010 | ||||
| 7.3216 × | 0.016 | 0.073 | 0.033 | ||||
| 3.3226 × | 0.049 | 0.157 | 0.026 | ||||
| 5.1883 × | 0.065 | 0.115 | 0.045 | ||||
| 1.2814 × | 0.050 | 0.010 | 0.030 | ||||
| [mm] | −1.870 × | 0.005 | 0.005 | 0.0 | 9.5138551 × | 1.10244034 × | 3.00122214 × |
| −1.7073 × | 0.0 | 0.0188 | 0.004 | ||||
| −7.0235 × | 0.005 | 0.020 | 0.005 | ||||
| 4.6162 × | 0.0 | 0.005 | 0.0 | ||||
| 2.9650 × | 0.005 | 0 | 0.0 | ||||
| 9.6382 × | 0.0 | 0.004 | 0.004 | ||||
| 1.1304 × | 0.008 | 0.004 | 0.094 | ||||
| 1.0474 × | 0.0 | 0.005 | 0.005 | ||||
| 7.9764 × | 0.005 | 0 | 0.005 | ||||
| [arcsec] | −2.31319279 | 6.0926 | 8.66167075 | 3.00122214 × | |||
| 1.90047357 × | |||||||
| −1.51306623 × | |||||||
| −2.35251697 | |||||||
| 6.11046078 | |||||||
| −5.24722085 | |||||||
| 0.43148227 | |||||||
| −2.40424968 | |||||||
| 1.83889158 | |||||||
| [arcsec] | 7.71040722 | 9.49810788 | 1.31833530 × | 4.35996864 × | |||
| 3.43675620 × | |||||||
| −7.74680198 | |||||||
| 6.38635058 × | |||||||
| −3.65250933 | |||||||
| −9.23212436 | |||||||
| −6.44188792 | |||||||
| −7.83445282 | |||||||
| −7.85859018 | |||||||
| [arcsec] | 14.17840657 | 5.07874334 × | 6.44609936 × | 2.14035969 × | |||
| −7.07562743 × | |||||||
| 7.85410568 | |||||||
| 5.81705298 × | |||||||
| 6.15844734 × | |||||||
| 8.03693703 × | |||||||
| 6.30875773 | |||||||
| −2.41983835 × | |||||||
| −1.33666599 × |
| Minimum | Maximum | |||||||
|---|---|---|---|---|---|---|---|---|
| Type | Value | Criterion | Change | Value | Criterion | Change | ||
| TTHI | 2 | 3 | −0.01102400 | 0.03829310 | 0.00059871 | 0.01102400 | 0.03709693 | −0.00059745 |
| TEDX | 4 | 4 | −0.05850000 | 0.03769497 | 0.05850000 | 0.03769497 | ||
| TEDX | 3 | 3 | −0.05850000 | 0.03768540 | 0.05850000 | 0.03768540 | ||
| TEDY | 4 | 4 | −0.07360000 | 0.03769393 | 0.07360000 | 0.03769651 | ||
| TEDY | 3 | 3 | −0.07360000 | 0.03733470 | −0.00035969 | 0.07360000 | 0.03802683 | 0.00033244 |
| TETX | 3 | 3 | −0.00240600 | 0.03759846 | 0.00240600 | 0.03778812 | ||
| TETZ | 3 | 3 | −0.01790000 | 0.03769439 | 0.01790000 | 0.03769439 | ||
| TETY | 3 | 3 | −0.00366100 | 0.03769184 | 0.00366100 | 0.03769184 | ||
| TIRR | 2 | −0.25000000 | 0.04471511 | 0.00702072 | 0.25000000 | 0.03088357 | −0.00681082 | |
| Worst offenders: | ||||||||
| Type | Value | Criterion | Change | |||||
| TIRR | 2 | −0.25000000 | 0.04471511 | 0.00702072 | ||||
| TTHI | 2 | 3 | −0.01102400 | 0.03829310 | 0.00059871 | |||
| TEDY | 3 | 3 | 0.07360000 | 0.03802683 | 0.00033244 | |||
| TETX | 3 | 3 | 0.00240600 | 0.03778812 | ||||
| TEDY | 4 | 4 | 0.07360000 | 0.03769651 | ||||
| TEDX | 4 | 4 | 0.05850000 | 0.03769497 | ||||
| TEDX | 4 | 4 | −0.05850000 | 0.03769497 | ||||
| TETZ | 3 | 3 | −0.01790000 | 0.03769439 | ||||
| TETZ | 3 | 3 | 0.01790000 | 0.03769439 | ||||
| TEDY | 4 | 4 | −0.07360000 | 0.03769393 | ||||
| Estimated Performance Changes based upon Root-Sum-Square method: | ||||||||
| Nominal RMS Spot Radius: | 0.03769439 | |||||||
| Estimated change: | 0.00695166 | |||||||
| Estimated RMS Spot Radius: | 0.04464605 | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Varano, I.; Capaccioni, F.; Rinaldi, G.; Filacchione, G.; Biondi, D.; Bellucci, G.; Morbidini, A.; Saggin, B. The Assembly, Integration and Test of the DORA Telescope, a Deployable Optics System in Space for Remote Sensing Applications. Aerospace 2025, 12, 224. https://doi.org/10.3390/aerospace12030224
Di Varano I, Capaccioni F, Rinaldi G, Filacchione G, Biondi D, Bellucci G, Morbidini A, Saggin B. The Assembly, Integration and Test of the DORA Telescope, a Deployable Optics System in Space for Remote Sensing Applications. Aerospace. 2025; 12(3):224. https://doi.org/10.3390/aerospace12030224
Chicago/Turabian StyleDi Varano, Igor, Fabrizio Capaccioni, Giovanna Rinaldi, Gianrico Filacchione, David Biondi, Giancarlo Bellucci, Alfredo Morbidini, and Bortolino Saggin. 2025. "The Assembly, Integration and Test of the DORA Telescope, a Deployable Optics System in Space for Remote Sensing Applications" Aerospace 12, no. 3: 224. https://doi.org/10.3390/aerospace12030224
APA StyleDi Varano, I., Capaccioni, F., Rinaldi, G., Filacchione, G., Biondi, D., Bellucci, G., Morbidini, A., & Saggin, B. (2025). The Assembly, Integration and Test of the DORA Telescope, a Deployable Optics System in Space for Remote Sensing Applications. Aerospace, 12(3), 224. https://doi.org/10.3390/aerospace12030224








