Aerodynamic Characteristics and Dynamic Stability of Coning Motion of Spinning Finned Projectile in Supersonic Conditions
Abstract
1. Introduction
2. Theoretical Basis
2.1. Governing Equations
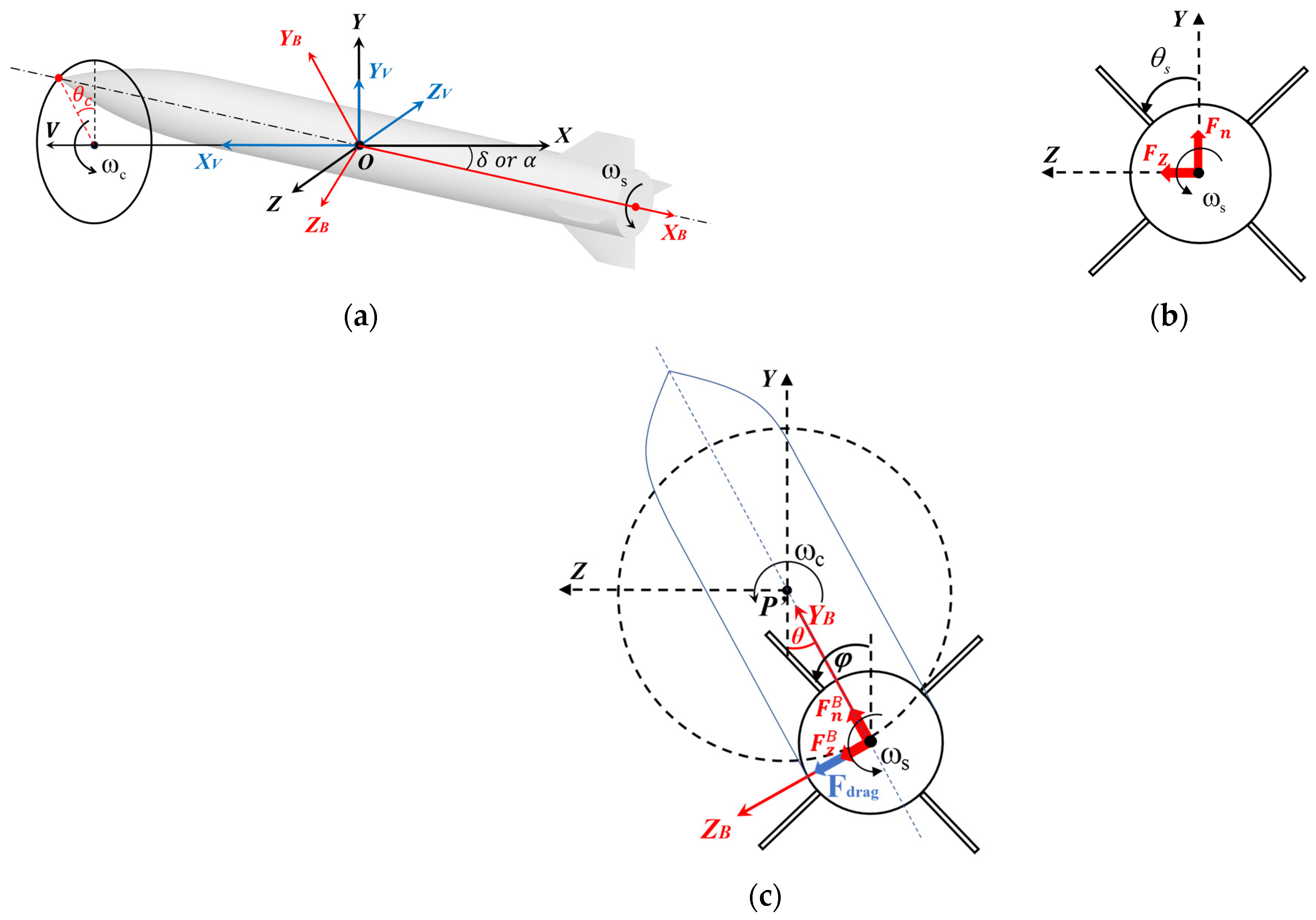
2.2. Coupled Spinning–Coning Motion Mode
2.3. Angular Motion Theory
3. Numerical Approach and Validation
3.1. Numerical Algorithm
3.2. Computational Model, Grid, and Conditions
3.3. Validation of Numerical Approach
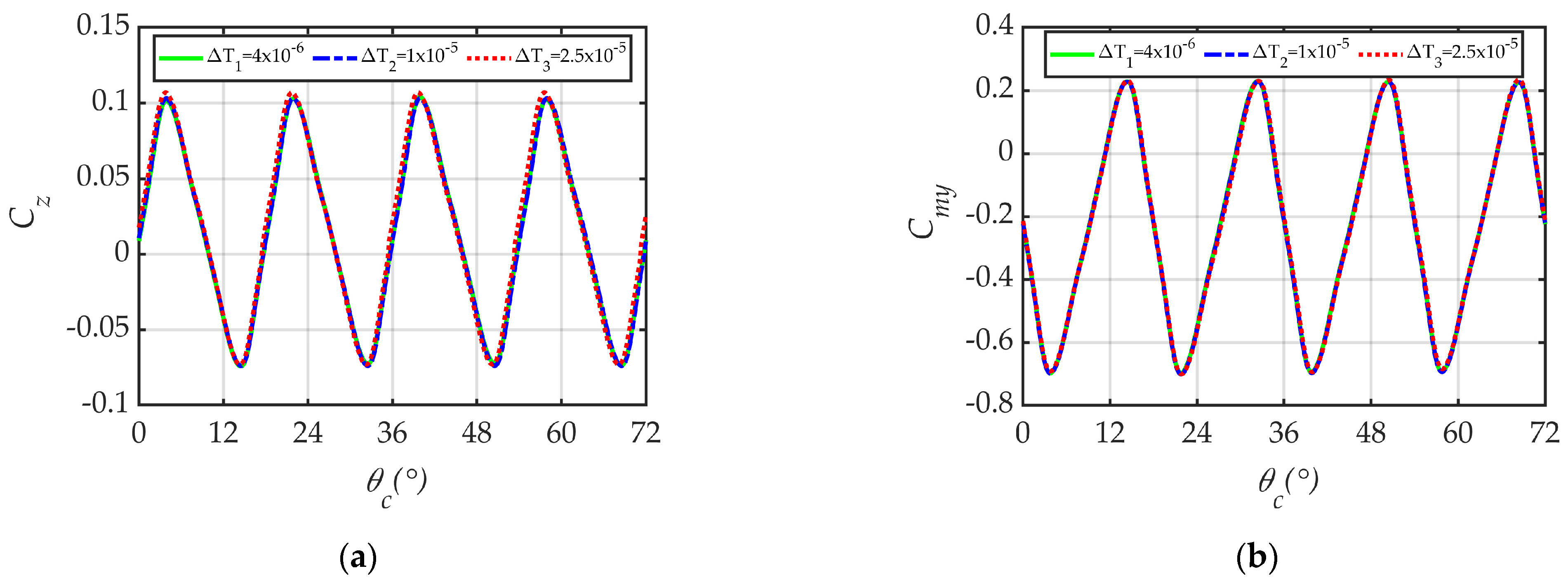
3.3.1. Grid Independence and Time-Step Independence
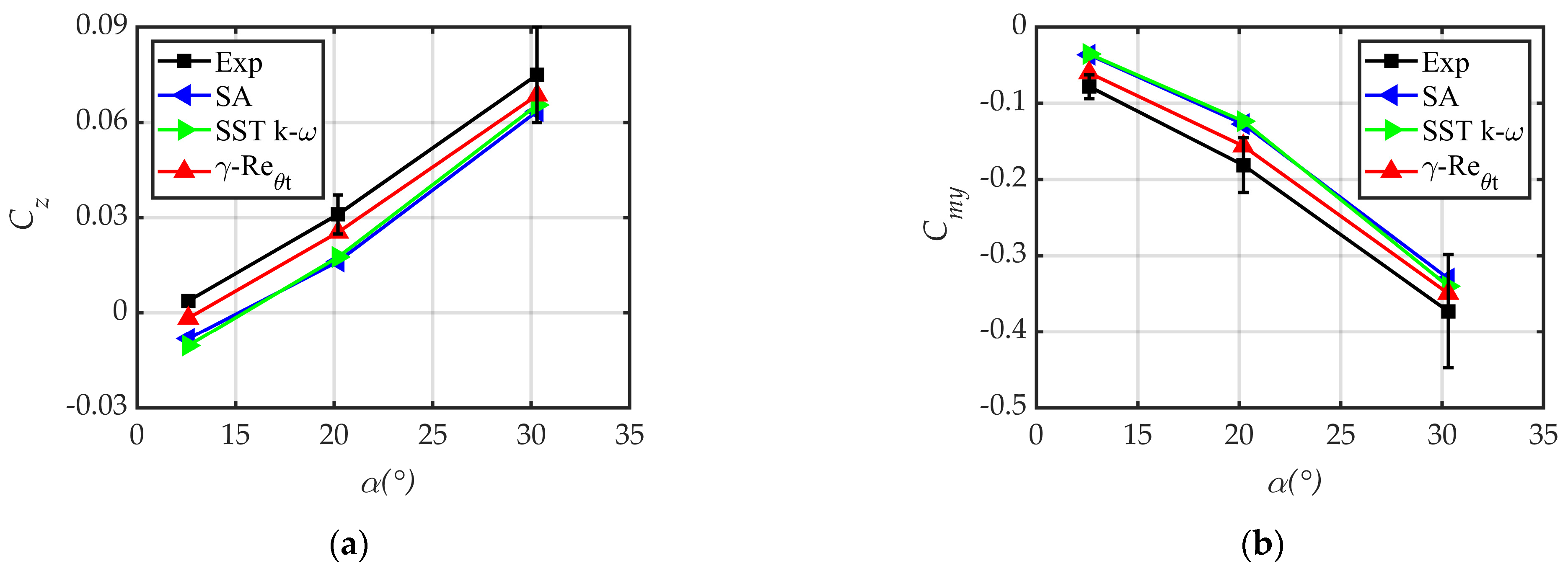
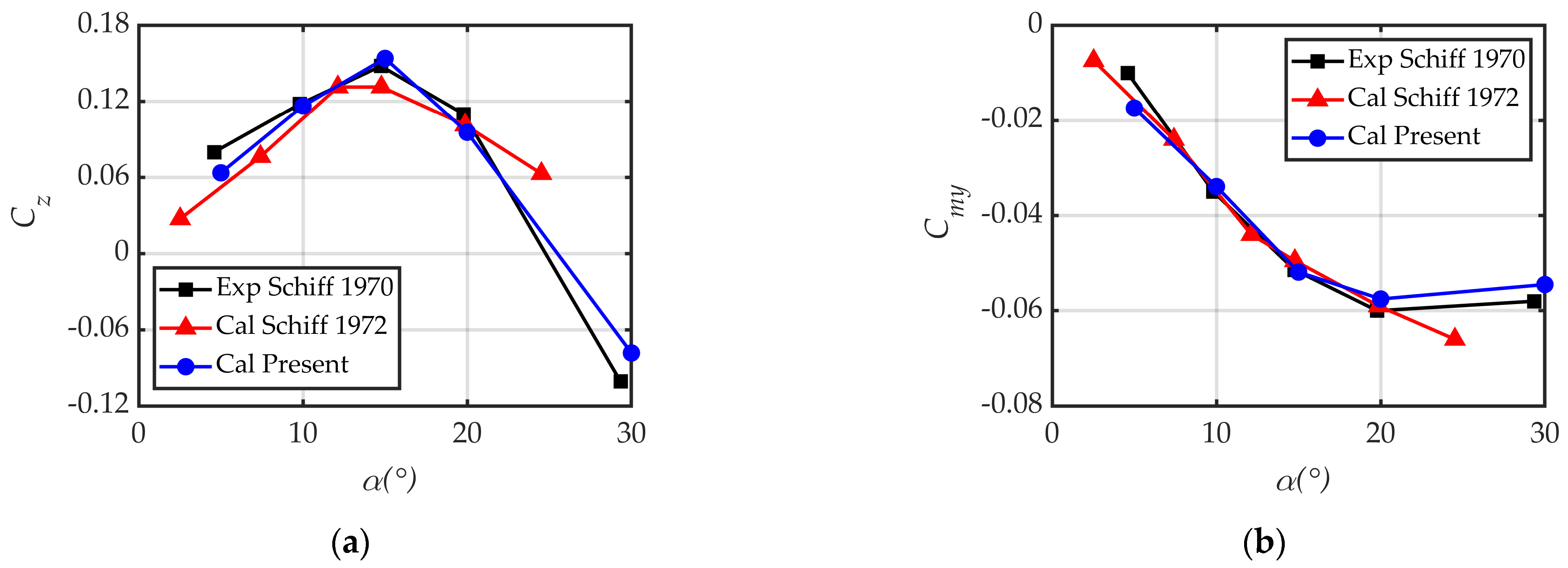
3.3.2. Validation of Unsteady Numerical Method
Spin-Induced Lateral Force and Yawing Moment
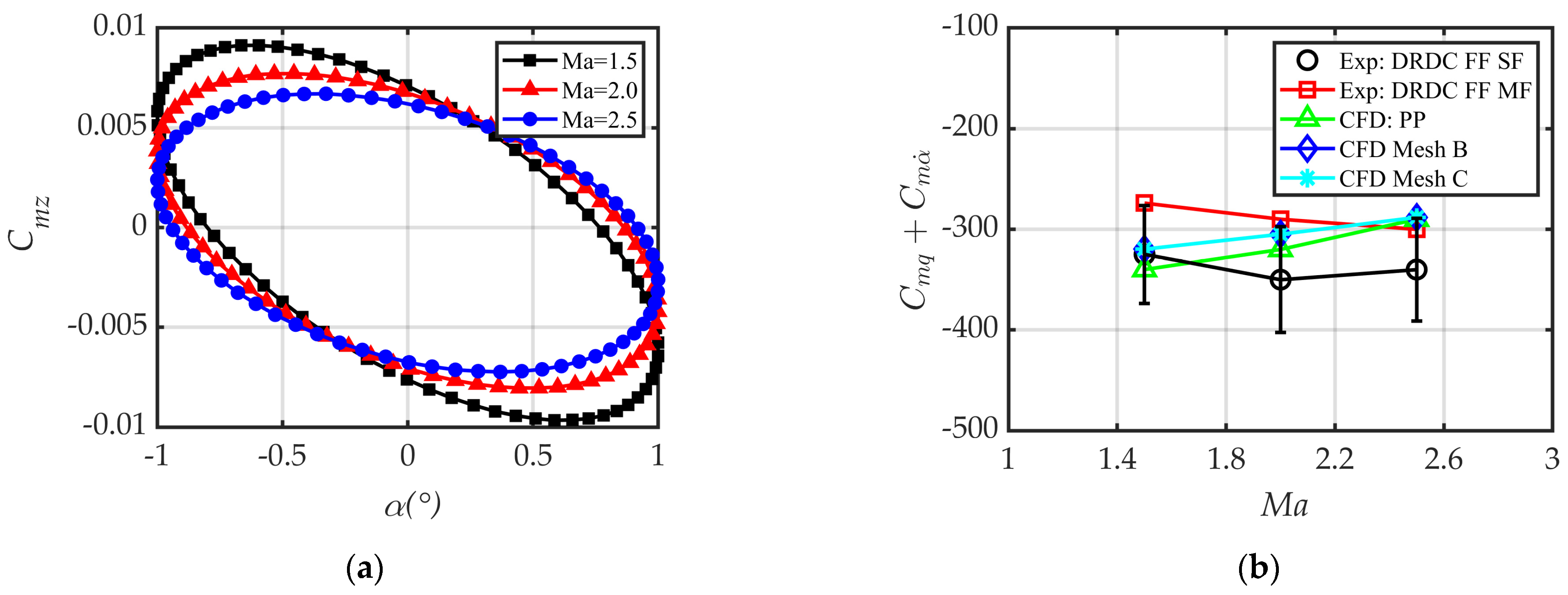
Pitch Damping Characteristics
Lunar Coning Induced Lateral Force and Yawing Moment
4. Results and Discussion
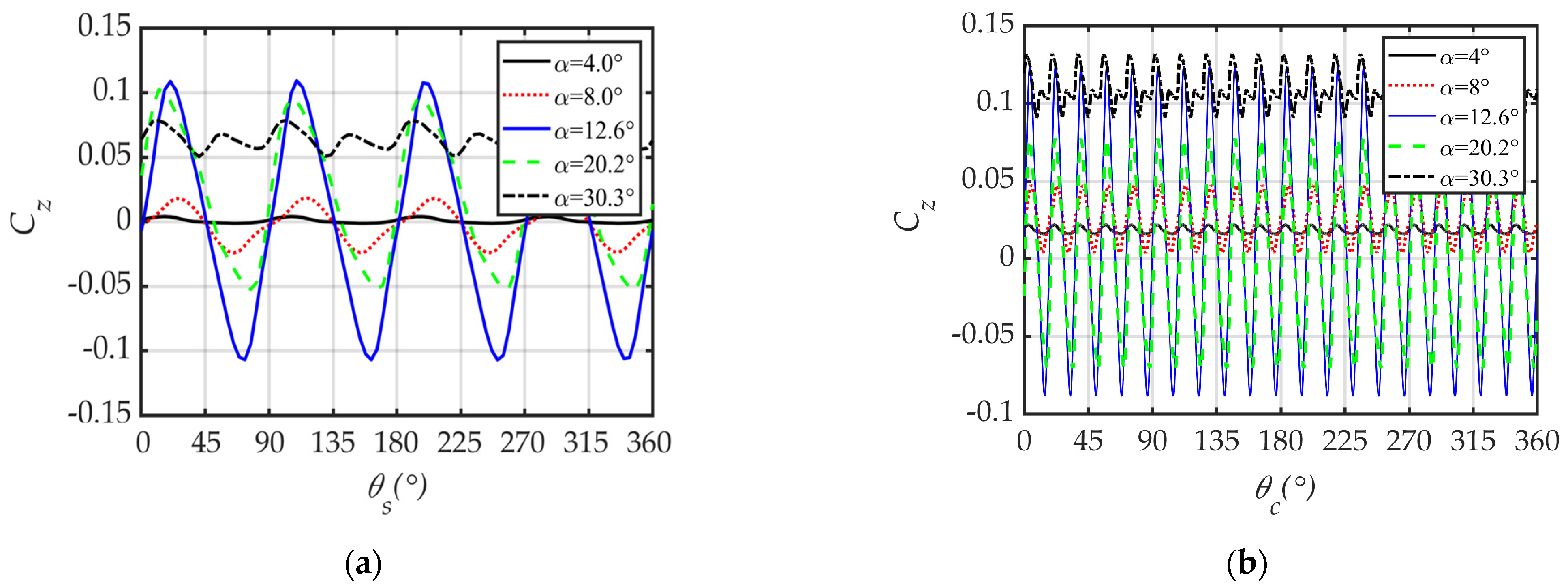
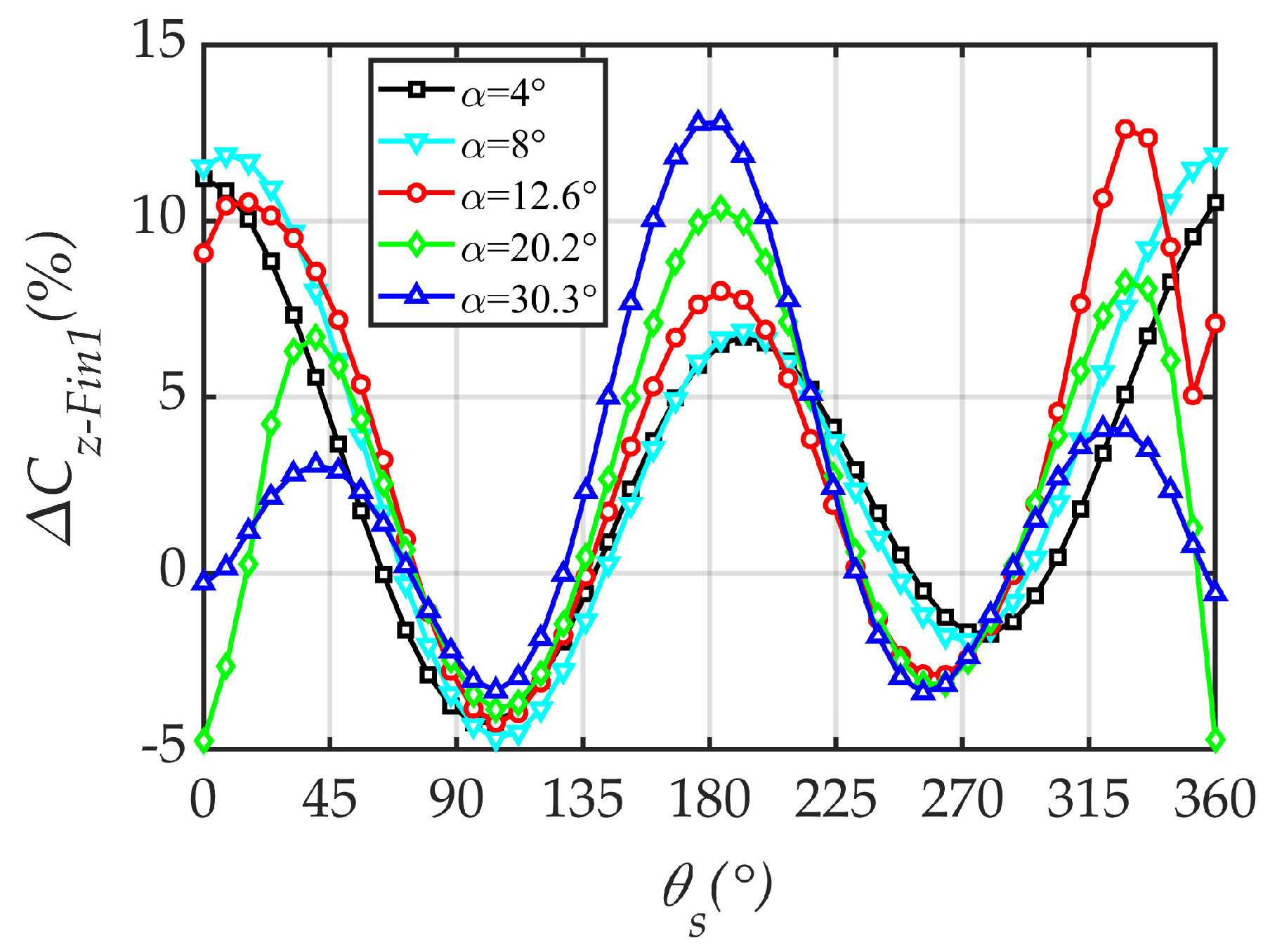
4.1. Effect of AoA
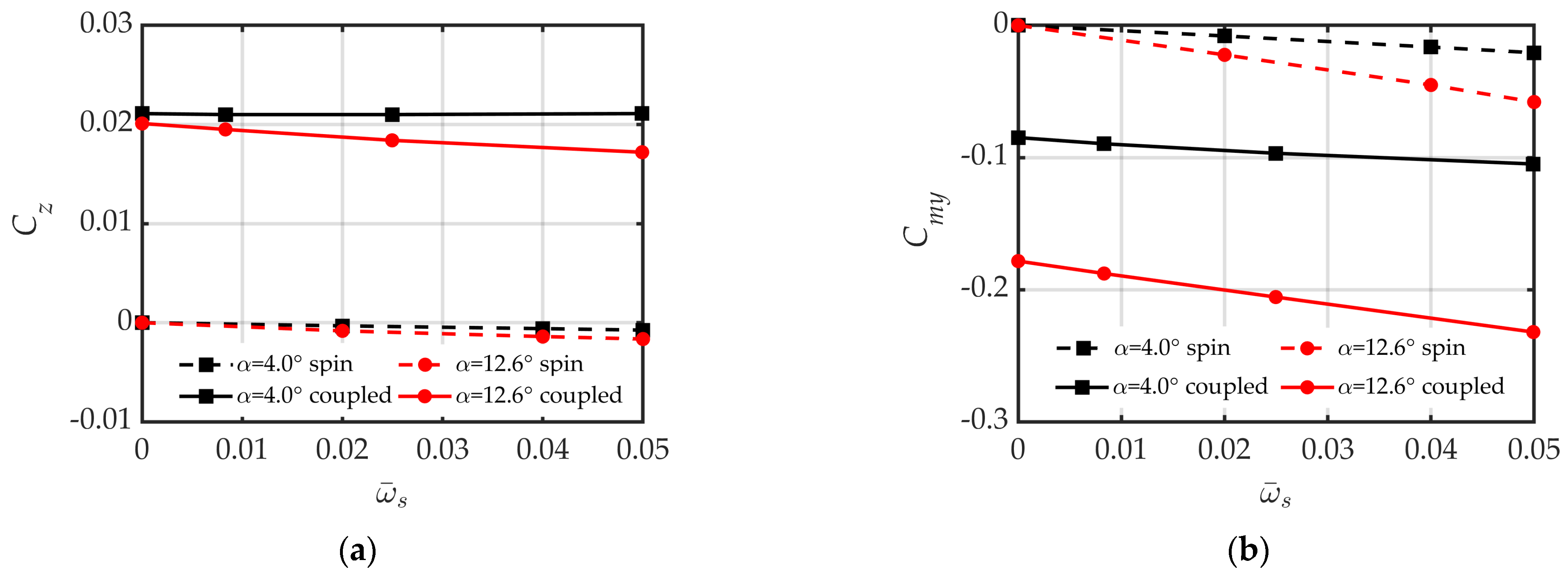
4.2. Effect of Non-Dimensional Spin Rate
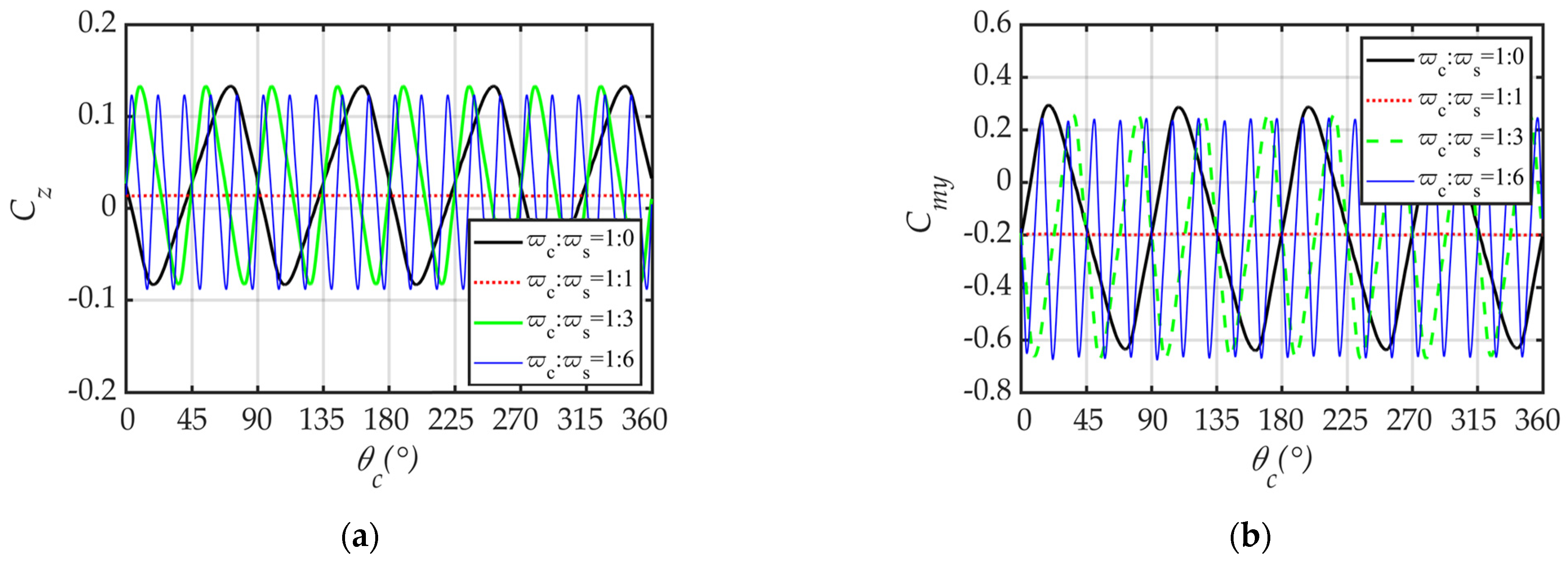
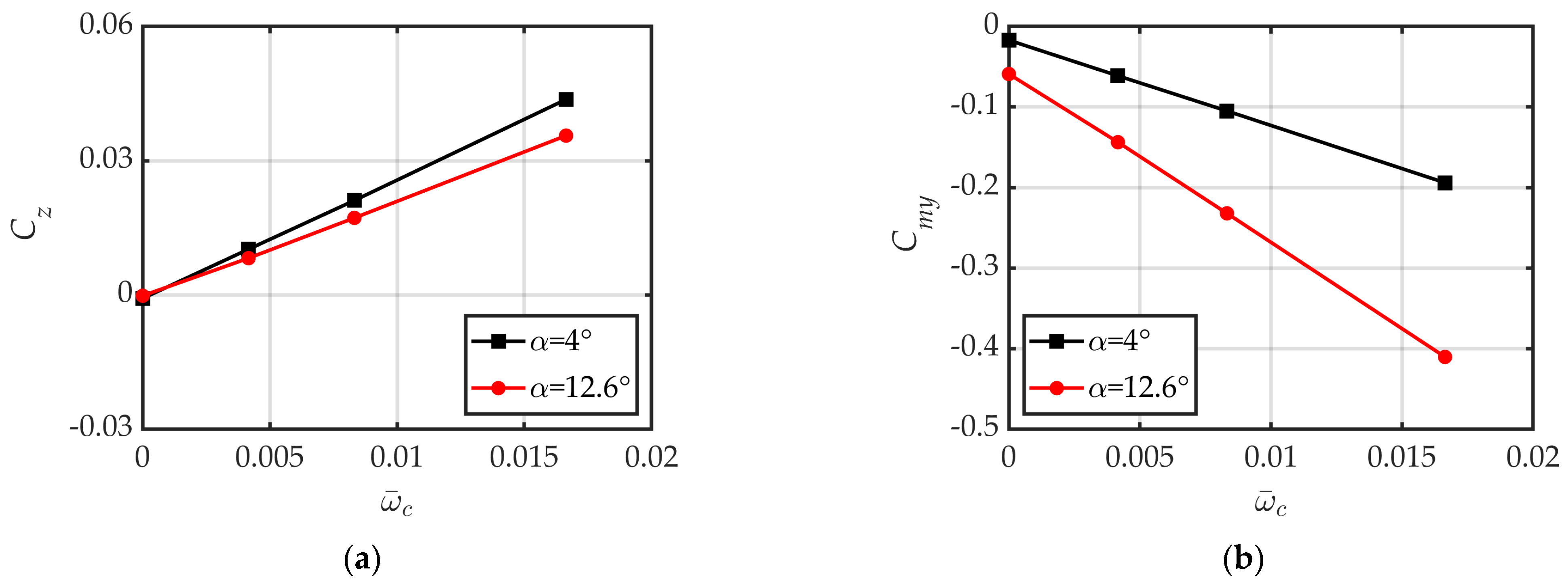
4.3. Effect of Non-Dimensional Cone Rate
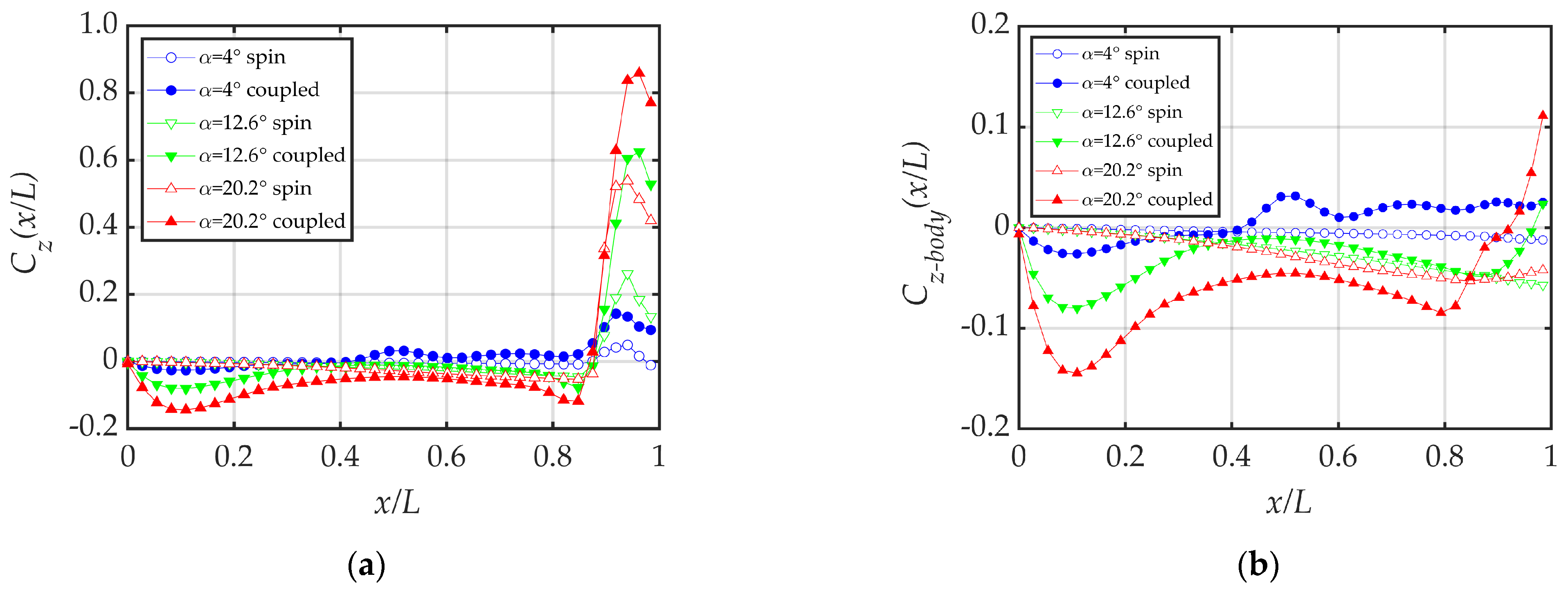
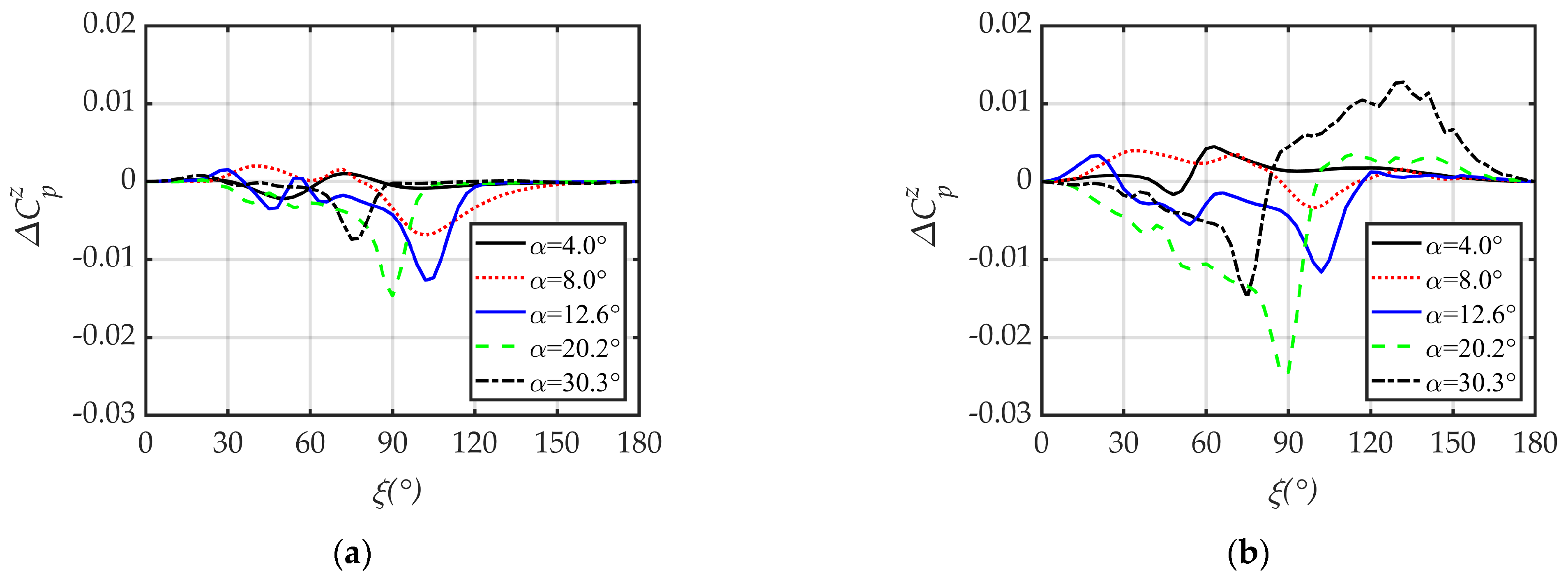
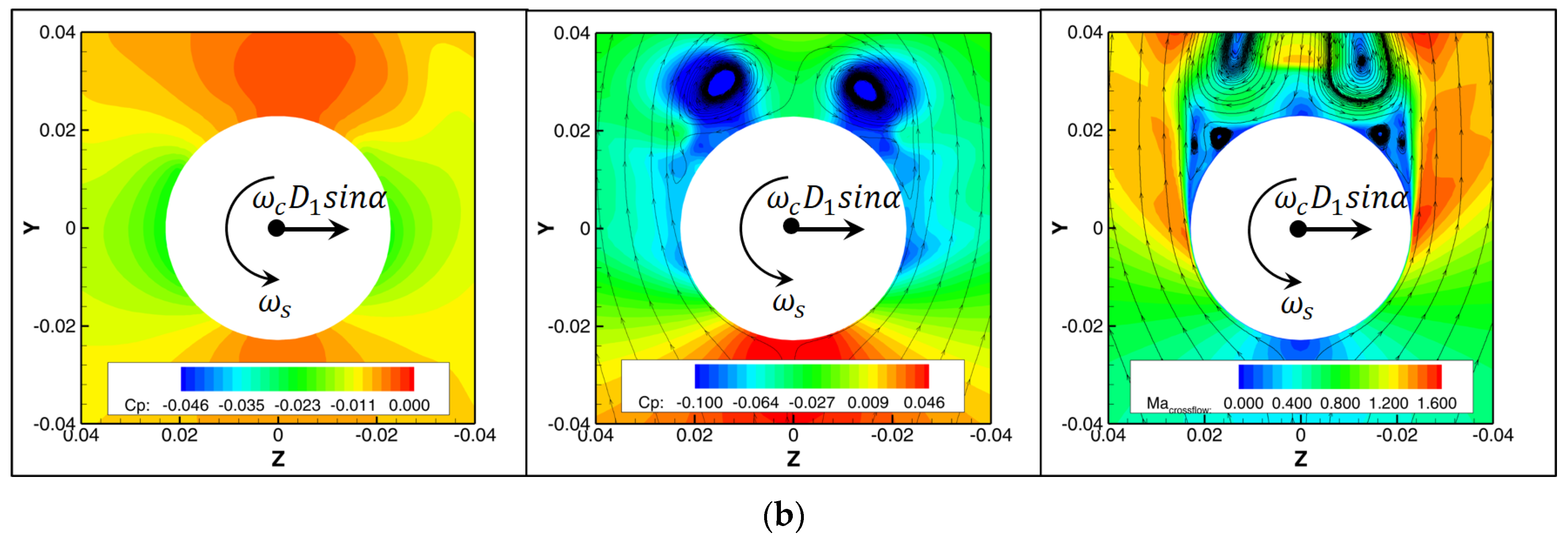
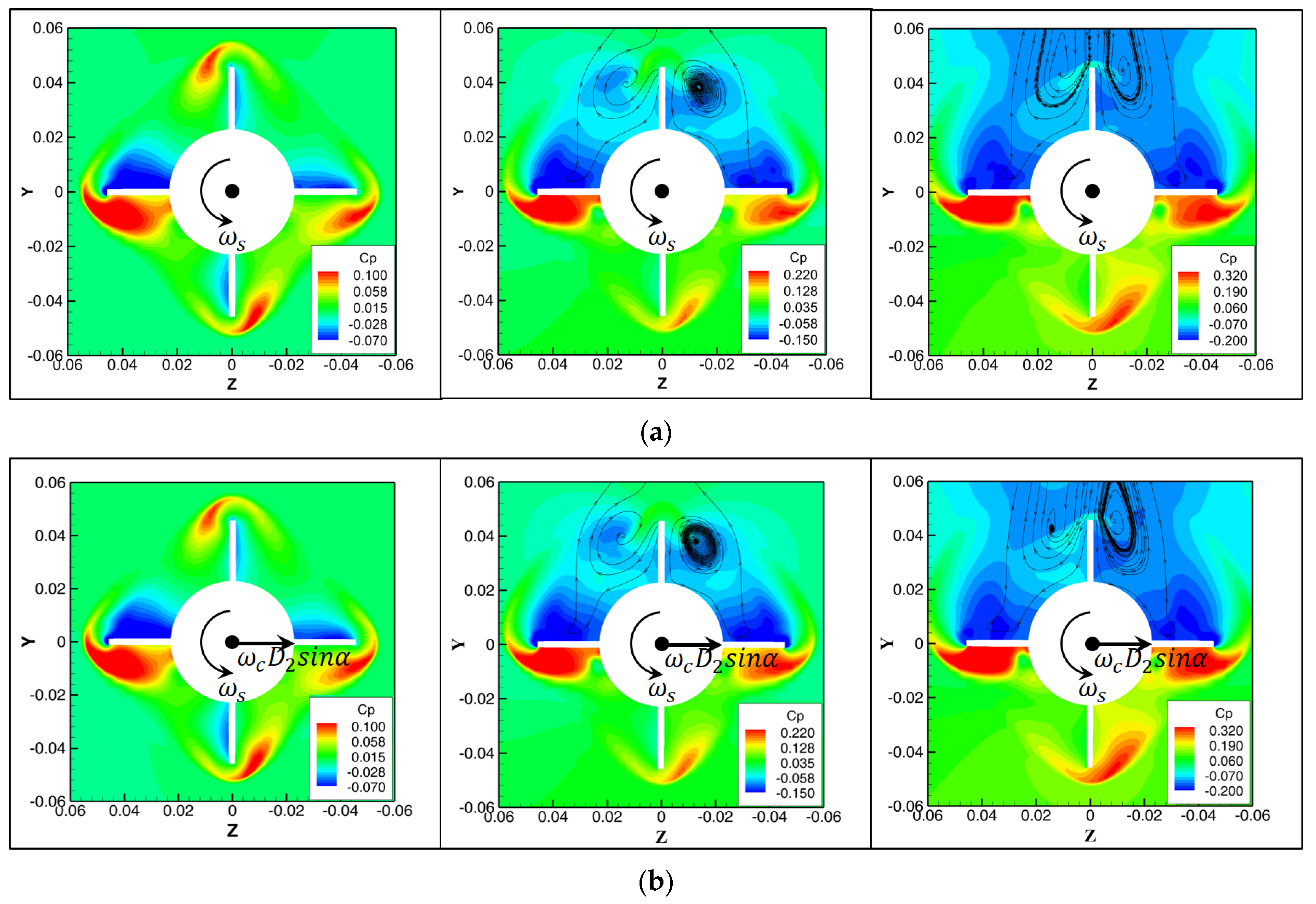
4.4. Mechanism of Coning Motion on Lateral Force
4.5. Flight Response Analysis
4.5.1. Modified Expression of Yawing Moment
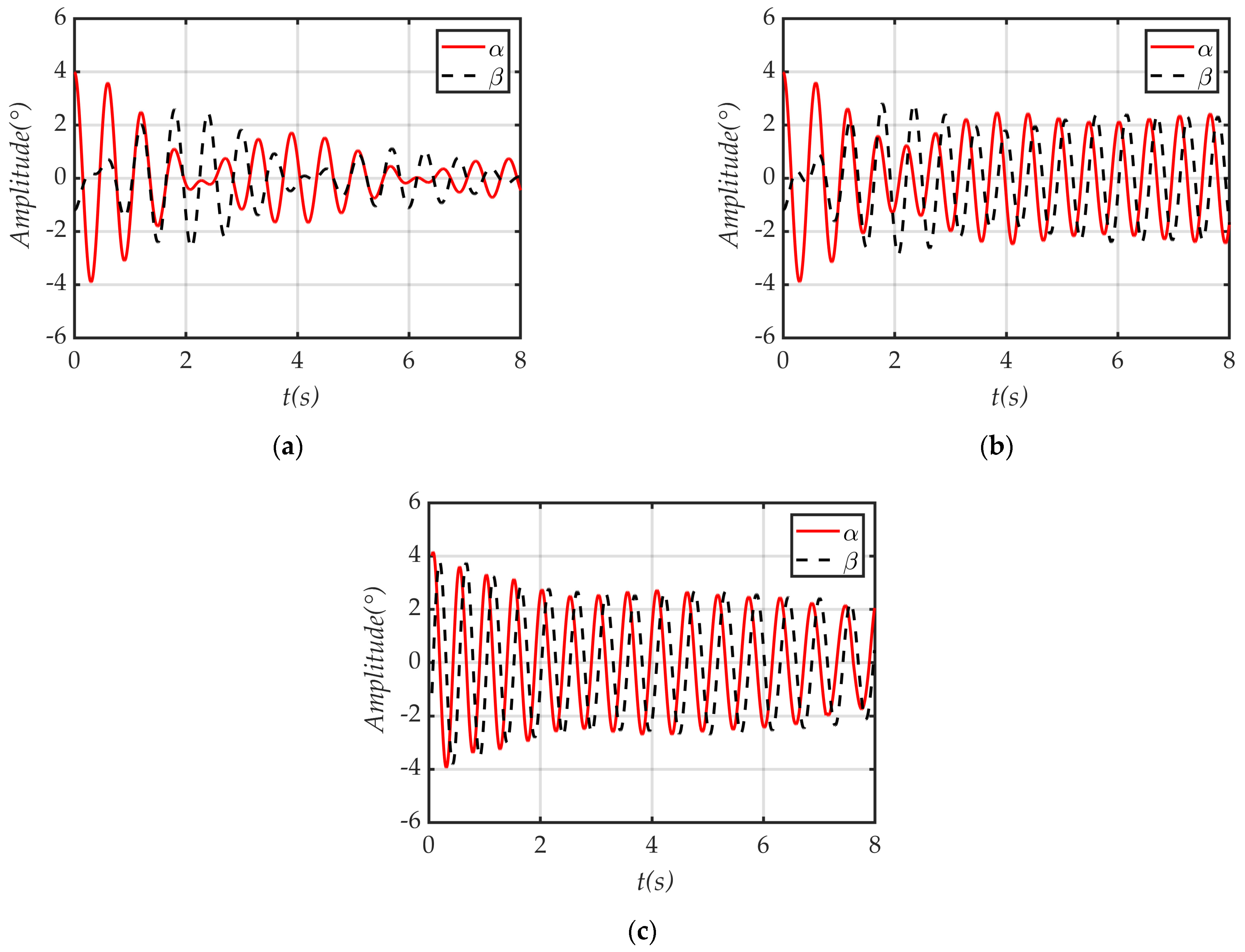
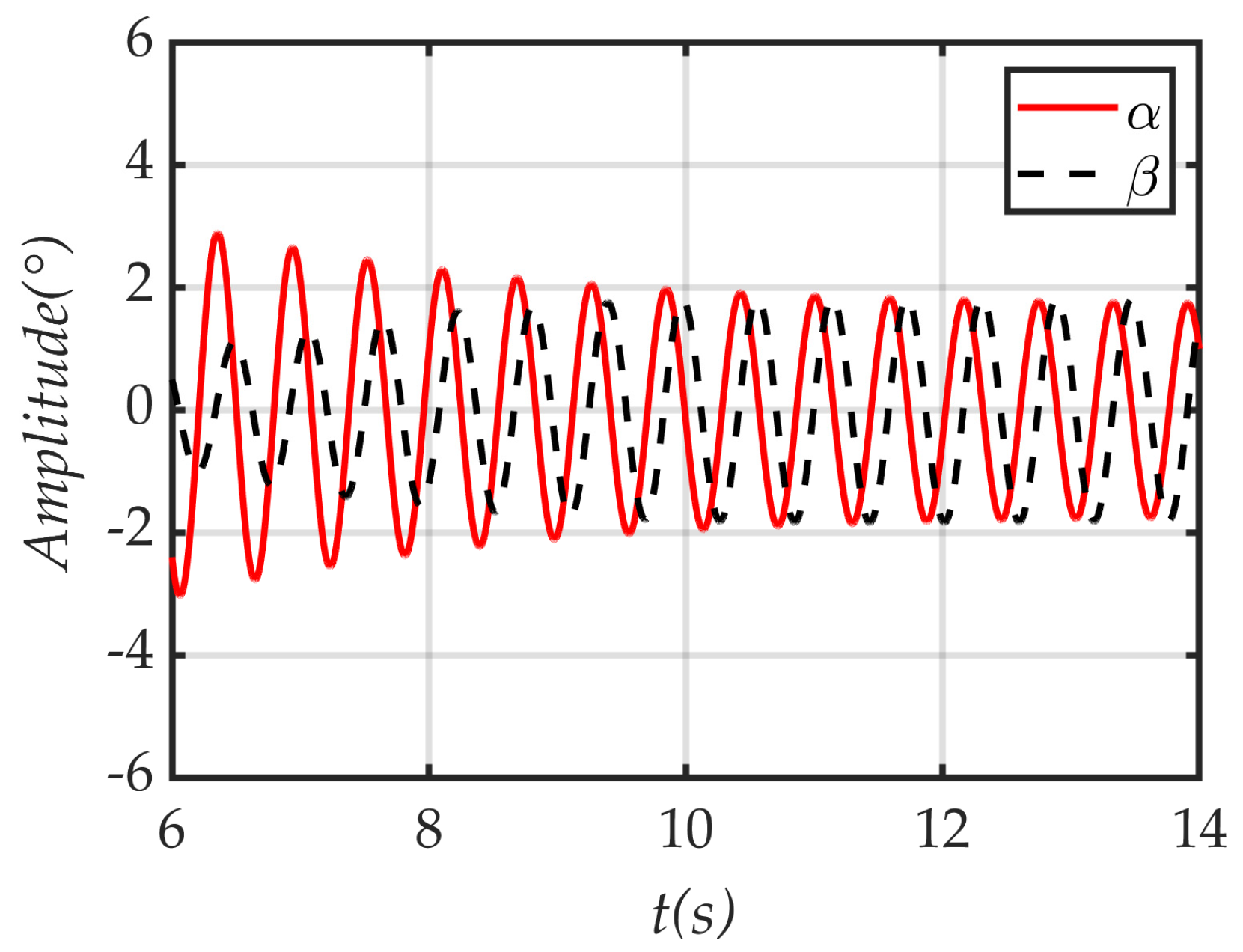
4.5.2. Angular Motion Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| URANS | Unsteady Reynolds-Averaged Navier–Stokes Equations |
| AoA | Angle of Attack |
| AoS | Angle of Sideslip |
| CFD | Computational Fluid Dynamics |
| RBD | Rigid Body Dynamics |
Nomenclature
| A | Pitching amplitude | Components of volumetric heat per unit mass in three directions | |
| CD | Drag coefficient, drag force/qSref | Reynolds number based on projectile diameter, | |
| Lift coefficient derivative, | Sref | Reference aera, m2 | |
| Cn | Normal force coefficient, normal force/qSref | T | Static temperature, K |
| Cz | Lateral (Magnus) force coefficient, lateral force/qSref | Velocity components in three directions | |
| Moment coefficient at zero angle of attack | Characteristics velocity, , | ||
| Moment coefficient induced by angle of attack | Velocity vector of fluid | ||
| Pitch damping coefficient | v | Projectile velocity, m/s | |
| Cmy | Yawing (Magnus) moment coefficient, yawing moment/qLrefSref | Freestream velocity, m/s | |
| Yawing (Magnus) moment coefficient derivative, | x | Coordinate in longitudinal direction, m | |
| Yawing (Magnus) moment coefficient derivative, | y+ | Non-dimensional distance from wall to viscous sublayer, | |
| Cmz | Pitching moment coefficient, pitching moment/qLrefSref | Mean angle of attack during planar pitching motion, deg | |
| Pitching moment coefficient derivative, f | Flight angle of attack, deg | ||
| Cp | Pressure coefficient, | Additional sideslip angle induced by cone rate, | |
| Distance between fixed point O and characteristic profile | Cone angle, equal to , deg | ||
| D | Projectile diameter, 0.04572 m | Rolling angle for coning motion, deg | |
| e | Total energy per unit mass, J/kg | Rolling angle in quasi-body coordinate system, deg | |
| h | Height of the first layer grid, m | Circumferential angle for projectile body, equal to , deg | |
| Moment of inertia, | Complex angle of attack, | ||
| Reduced pitch frequency, | Kinematic viscosity, , m2/s | ||
| l | Length of 10° half-angle cone, 0.58 m | Air density, kg/m3 | |
| L | Total length of missile, 0.4572 m | Stress terms between fluid units | |
| m | Projectile mass, kg | Wall shear stress | |
| Lref | Reference length, equal to projectile diameter, m | Pitching frequency, rad/s | |
| Ma | Mach number | Pitch rate, | |
| Outside boundary normal direction | Non-dimensional cone rate, | ||
| N | Number of integration time steps per oscillation | Non-dimensional spin rate, | |
| P | Static pressure, Pa | ||
| Freestream static pressure, Pa | Time step, s | ||
| q | Dynamic pressure, |
References
- Sturek, W.B.; Dwyer, H.A.; Kayser, L.D.; Nietubicz, C.J.; Reklis, R.P.; Opalka, K.O. Computations of Magnus effects for a yawed, spinning body of revolution. AIAA J. 1978, 16, 687–692. [Google Scholar] [CrossRef]
- Curry, W.H.; Uselton, J.C. Some comments on the aerodynamic characteristics of the Tomahawk sounding rocket. In Proceedings of the Sounding Rocket Vehicle Technology Specialist Conference, Williamsburg, VA, USA, 27 February–1 March 1967. [Google Scholar] [CrossRef][Green Version]
- Uselton, J.C.; Carman, J.B. A study of the Magnus effects on a sounding rocket at supersonic speeds. J. Spacecr Rocket. 1971, 8, 28–34. [Google Scholar] [CrossRef]
- Platou, A.S. Magnus characteristics of finned and nonfinned projectiles. AIAA J. 1965, 3, 83–90. [Google Scholar] [CrossRef]
- Klatt, D.; Hruschka, R.; Leopold, F. Investigation of the Magnus effect of a generic projectile at Mach 3 Up to 16 degrees angle of attack. J. Appl. Mech. 2014, 80, 031603. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, X.S.; Yin, J.T.; Yao, R. Effect of transition on the aerodynamic characteristics of a spinning cone. P. I. Mech. Eng. G—J. Aer. 2018, 232, 2048–2058. [Google Scholar] [CrossRef]
- Cayzac, R.; Carette, E.; Denis, P.; Guillen, P. Magnus effect: Physical origins and numerical prediction. J. Appl. Mech. 2011, 78, 051005. [Google Scholar] [CrossRef]
- Yin, J.T.; Lei, J.M.; Wu, X.S. Body-fin interference on the Magnus effect of spinning projectile in supersonic flows. Eng. Appl. Comp. Fluid. 2017, 11, 496–512. [Google Scholar] [CrossRef]
- Blades, E.L.; Marcum, D.L. Numerical simulation of a spinning missile with dithering canards using unstructured grids. J. Spacecr Rocket. 2004, 41, 248–256. [Google Scholar] [CrossRef]
- Yin, J.T.; Wu, X.S.; Lei, J.M.; Liu, X.D. Canards interference on the Magnus effect of a fin-stabilized spinning missile. Adv. Mech. Eng. 2018, 10, 1687814018790865. [Google Scholar] [CrossRef]
- Yin, J.T.; Lei, J.M.; Jiang, S.J.; Yin, X.Z. The aerodynamic characteristics and its estimation method of finned missile experiencing spin-deformation coupling motion. Aerosp. Sci. Technol. 2021, 115, 106806. [Google Scholar] [CrossRef]
- Ding, Y.Y.; Wang, J.; Jiang, B.Y.; Xiao, Q.H.; Yang, X.P.; Wu, L.Y.; Xie, B.C. Numerical investigation of the effect of blade distortion laws on the corner flow separation of the axial-flow fan. Aerosp. Sci. Technol. 2023, 138, 108296. [Google Scholar] [CrossRef]
- Liu, Q.; Lei, J.M.; Yu, Y.; Yin, J.T. Effect of bending deformation on the lateral force of spinning projectiles with large aspect ratio. Aerospace 2023, 10, 810. [Google Scholar] [CrossRef]
- Yong, Z.; Lei, J.M.; Yin, J.T. The generation mechanism of the side force and yawing moment of a rotating missile with wrap-around fins. Aerospace 2024, 11, 765. [Google Scholar] [CrossRef]
- Silton, S.I. Numerical experiments on finned bodies. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar] [CrossRef]
- Lu, T.Y.; Wu, X.S.; Lei, J.M.; Yin, J.T. Numerical study on the aerodynamic coupling effects of spinning and coning motions for a finned vehicle. Aerosp. Sci. Technol. 2018, 77, 399–408. [Google Scholar] [CrossRef]
- Pang, C.B.; Kang, S.; Zhao, C.; Jiang, S.J.; Dang, M.L. Research on aerodynamic characteristics of spinning projectile in coning motion. J. Proj. Rockets Missiles Guid. 2019, 39, 50–56. [Google Scholar] [CrossRef]
- Murphy, C.H. Free Flight Motion of Symmetric Missiles; Ballistic Research Laboratory: Aberdeen Proving Ground, MD, USA, 1963. [Google Scholar]
- Nicolaides, J.D. Two Non-Linear Problems in the Flight Dynamics of Modern Ballistic Missiles; Bureau of Ordnance, Department of the Navy: Arlington, VA, USA, 1958.
- Han, Z.P. External Ballistics; Beijing Institute of Technology Press: Beijing, China, 2008; pp. 145–149. [Google Scholar]
- Morote, J.; Liaño, G. Stability analysis and flight trials of a clipped wrap around fin configuration. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar] [CrossRef]
- Murphy, C.H.; Mermagen, W.H. Spin-yaw lock-in of a rotationally symmetric missile. J. Guid Control Dynam. 2009, 32, 377–382. [Google Scholar] [CrossRef]
- Morote, J.; Garcia-Ybarra, P.L.; Castillo, J.L. Large amplitude oscillations of cruciform tailed missiles Part 1: Catastrophic yaw fundamental analysis. Aerosp. Sci. Technol. 2013, 25, 145–151. [Google Scholar] [CrossRef]
- Morote, J.; Garcia-Ybarra, P.L.; Castillo, J.L. Large amplitude oscillations of cruciform tailed missiles Part 2: Catastrophic yaw avoidance. Aerosp. Sci. Technol. 2013, 26, 1–9. [Google Scholar] [CrossRef]
- Costello, M.; Sahu, J. Using computational fluid dynamic/rigid body dynamic results to generate aerodynamic models for projectile flight simulation. P. I. Mech. Eng. G—J. Aer. 2008, 222, 1067–1078. [Google Scholar] [CrossRef]
- Sahu, J. Time-accurate numerical prediction of free-flight aerodynamics of a finned projectile. J. Spacecr Rocket. 2008, 45, 946–954. [Google Scholar] [CrossRef]
- DeRango, S.; Zingg, D.W. Improvements to a dual-time-stepping method for computing unsteady flows. AIAA J. 1997, 35, 1548–1550. [Google Scholar] [CrossRef]
- Jenke, L.M. Experimental Roll-Damping, Magnus, and Static-Stability Characteristics of Two Slender Missile Configurations at High Angles of Attack (0 to 90 Deg) and Mach Numbers 0.2 Through 2.5 (AEDC-TR-76-58); National Technical Information Service: Springfield, VA, USA, 1976.
- Bhagwandin, V.A. Numerical prediction of roll damping and Magnus dynamic derivatives for finned projectiles at angle of attack. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012. [Google Scholar] [CrossRef]
- DeSpitito, J.; Silton, S.; Weinacht, P. Navier-Stokes predictions of dynamic stability derivatives: Evaluation of steady-state method. J. Spacecr Rocket. 2009, 46, 1142–1154. [Google Scholar] [CrossRef]
- Bhagwandin, V.A.; Sahu, J. Numerical prediction of pitch damping stability derivatives for finned projectiles. J. Spacecr Rocket. 2014, 51, 1603–1618. [Google Scholar] [CrossRef]
- Schiff, L.B.; Tobak, M. Results from a New Wind-Tunnel Apparatus for Studying Coning and Spinning Motions of Bodies of Revolution. AIAA J. 1970, 8, 1953–1957. [Google Scholar] [CrossRef]
- Schiff, L.B. Nonlinear Aerodynamics of Bodies in Coning Motion. AIAA J. 1972, 10, 1517–1522. [Google Scholar] [CrossRef]






| Mesh A | Mesh B | Mesh C | |
|---|---|---|---|
| Axial (body) | 200 | 340 | 470 |
| Spanwise | 36 | 56 | 76 |
| Circumferential | 120 | 196 | 276 |
| Total (mil.) | 5.12 | 11.27 | 25.81 |
| Effect of or | , , , , | |
| Effect of | , | |
| Effect of | , |
| Mesh Type | Time Step | |||
|---|---|---|---|---|
| Grid independence | Mesh A Mesh B Mesh C | |||
| Time-step independence | Mesh B |
| Cn | Cz | Cmz | Cmy | |
|---|---|---|---|---|
| Mesh A | 3.7005 | 0.0017 | 2.1591 | −0.3361 |
| Mesh B | 3.6845 | 0.0018 | 2.1685 | −0.3263 |
| Mesh C | 3.6313 | 0.00185 | 2.1819 | −0.3143 |
| (Mesh A-Mesh B)/Mesh A | 0.43% | −5.88% | −0.44% | 2.92% |
| (Mesh A-Mesh C)/Mesh A | 1.87% | −8.82% | −1.06% | 6.49% |
| (Mesh B-Mesh C)/Mesh B | 1.44% | −2.78% | −0.62% | 3.68% |
| Structural Parameter | Values | Aerodynamic Parameter | Spinning Motion | Spinning–Coning Coupled Motion |
|---|---|---|---|---|
| L (m) | 0.4572 | 0.415 | 0.394 | |
| m (kg) | 2.48 | 5.821 | 5.878 | |
| (kg∙m2) | 0.001 | −0.326 | −0.339 | |
| (kg∙m2) | 0.354 | −0.527 | −0.527 | |
| (kg∙m3) | 3700 | - | −14.902 | |
| 0.5 | −1.301 | −1.301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, J.; Jiang, S.; Hu, Y.; Zhang, J.; Miao, H.; Lei, J. Aerodynamic Characteristics and Dynamic Stability of Coning Motion of Spinning Finned Projectile in Supersonic Conditions. Aerospace 2025, 12, 225. https://doi.org/10.3390/aerospace12030225
Yin J, Jiang S, Hu Y, Zhang J, Miao H, Lei J. Aerodynamic Characteristics and Dynamic Stability of Coning Motion of Spinning Finned Projectile in Supersonic Conditions. Aerospace. 2025; 12(3):225. https://doi.org/10.3390/aerospace12030225
Chicago/Turabian StyleYin, Jintao, Shengju Jiang, Yaowei Hu, Jiawei Zhang, Haochun Miao, and Juanmian Lei. 2025. "Aerodynamic Characteristics and Dynamic Stability of Coning Motion of Spinning Finned Projectile in Supersonic Conditions" Aerospace 12, no. 3: 225. https://doi.org/10.3390/aerospace12030225
APA StyleYin, J., Jiang, S., Hu, Y., Zhang, J., Miao, H., & Lei, J. (2025). Aerodynamic Characteristics and Dynamic Stability of Coning Motion of Spinning Finned Projectile in Supersonic Conditions. Aerospace, 12(3), 225. https://doi.org/10.3390/aerospace12030225






