Abstract
Adhesively bonded joints are essential in the aeronautical industry, offering benefits such as weight reduction and enhanced sustainability. However, certifying these joints is challenging due to unreliable methods for assessing their strength and the development of predictive models for fatigue-driven disbonding remains an ongoing effort. This manuscript presents the implementation and validation of a cohesive zone model for studying high-cycle fatigue disbonding under Mode I and Mixed-Mode loading. The model was integrated into the commercial finite element analysis software Abaqus using user-defined material subroutine (UMAT). Two modelling approaches were investigated: one replacing the adhesive with a cohesive layer, and the other incorporating a cohesive layer at the adhesive’s mid-plane while modelling its entire thickness, using both 2D and 3D techniques. Validation was conducted against experimental data from the literature that examined the influence of adhesive thickness on fatigue behaviour in DCB and CLS tests. The findings of this study confirm that the model accurately predicts fatigue disbonding across all cases examined. Additionally, the analysis reveals that modelling adhesive thickness plays a critical role in the simulation’s outcomes. Variations in adhesive thickness can significantly alter the crack growth behaviour, highlighting the importance of carefully considering this parameter in future assessments and applications.
1. Introduction
Over the past two decades, the aerospace industry has been actively seeking environmentally friendly innovations to significantly reduce emissions and achieve carbon neutrality. A major driving force behind the development of “green aviation” comes from global initiatives, such as the Clean Aviation programme funded by the European Union. This programme is focused on making aviation a sustainable and climate-neutral sector. Established in 2021, it is a public–private partnership that involves the European Commission and the aeronautics industry, which includes small and medium-sized enterprises, research centres, and academic institutions. Clean Aviation builds upon the success of its predecessor, Clean Sky 2. The main goal of the programme is to develop and integrate innovative aeronautic technologies that significantly reduce aircraft emissions and noise. This effort contributes to the EU’s climate goals. Specifically, Clean Aviation aims to decrease fuel consumption and related emissions by 30–50% by the year 2050, as well as lower noise levels in future aircraft. Reducing aircraft emissions primarily involves optimising structural designs by utilising lightweight, high-strength, and stiff materials.
Aeronautic structures have traditionally been manufactured using metallic materials due to their strength, toughness, and fatigue resistance. However, they face limitations in achieving minimal weight despite numerous advancements over the years. In this regard, composite materials, particularly carbon fibre-reinforced plastics (CFRPs), have gained considerable importance. These advanced materials offer superior strength-to-weight ratios compared to conventional metallic alloys such as aluminium and titanium. Consequently, they enhance fuel efficiency, reduce operational costs, and extend the fatigue life of aircraft components. Modern airliners, including the Airbus A350 XWB and the Boeing 787 Dreamliner, illustrate this trend, with more than 50% of their airframes built with composite materials.
The increasing use of composite materials has spurred innovation in joining techniques. While traditional methods, such as riveting, are reliable and widely utilised in metals, they present significant challenges when performed on composites. Drilling holes for rivets can compromise the integrity of composite fibres, inducing defects like delamination, burrs, tearing, surface cavities, glass transition failure, and borehole damages [1]. These defects may lead to stress concentrations that may result in premature failure. Alternative joining methods tailored for composite materials have been proposed to address these issues. Adhesive bonding is the most commonly used method due to its advantages, such as eliminating the necessity for drilled holes and causing no damage to the structure. Furthermore, adhesives distribute loads evenly across the bonded surfaces, minimising stress concentrations caused by localised loading. This facilitates the creation of lighter, more efficient designs. Nevertheless, adhesive bonding also poses certain challenges. Currently, there is a lack of reliable inspection methods to establish a minimum load capability of bonded joints through non-destructive inspection (NDI) technologies [2]. Existing methods, i.e., ultrasound and radiography, are not fully capable of detecting manufacturing defects such as voids, porosity, disbonds, bubbles, intrusions, or contamination, which can adversely affect the bond strength and may go unnoticed. Additionally, this lack of control over the adhesive’s bond quality leads to unpredictable behaviour under fatigue loading which is still under investigation [3]. This limitation adds complexity to the certification process for aviation authorities, including the European Union Aviation Safety Agency (EASA) and the Federal Aviation Administration (FAA). Therefore, at the moment, most of the adhesive use is limited to secondary structures.
Addressing these challenges is crucial for the widespread adoption of adhesive bonding in aerospace primary structures and repairs. Researchers are exploring advanced inspection techniques, i.e., ultrasonic testing and infrared thermography, to enhance the detection of bond defects [4,5,6]. Concurrently, efforts are focused on developing robust fatigue life prediction models that leverage computational simulations and experimental validation. Since conducting experimental assessments of fatigue crack initiation and propagation is often impractical, researchers increasingly rely on analytical and numerical models to predict adhesive behaviour.
Numerical models designed to investigate fatigue crack growth in adhesively bonded joints need to accurately represent the complex interactions between stresses, material properties, and adhesive behaviour. The literature offers a variety of models that can be classified into four primary categories: stress/strain-based models, fracture mechanics-based models, extended finite element method (XFEM) models, and cohesive zone models (CZMs).
The stress/strain methods are among the earliest approaches and are based on the correlation between delamination growth and the stress or strain values within the material. These methods are primarily suited for static delamination. In the case of fatigue applications, they are typically employed to determine the fatigue life of a component rather than to predict crack growth and, therefore, cannot be used for understanding the disbonding behaviour [7,8,9].
The fracture mechanics-based methods study crack growth by utilising properties such as the stress intensity factor (SIF) and the strain energy release rate (SERR). The SERR is usually more suitable for non-homogeneous materials, such as composites, and can be easily obtained experimentally. These methods derive from the application of the fracture mechanics techniques to investigate metals under fatigue loading conditions [10,11,12].
XFEM is an advanced finite element model (FEM) technique designed to accurately represent discontinuities, such as cracks, at arbitrary locations within a material. Contrary to traditional FEM that is limited to boundaries and predefined crack paths, XFEM allows for the propagation of cracks without the need for remeshing [13,14]. This is achieved by incorporating enrichment functions into specific nodes of the FEM, allowing the crack to propagate freely through the elements instead of strictly along its edges. Additionally, it is possible to combine XFEM with cohesive laws [15] or a cohesive zone model [16] to simulate crack opening. This approach captures the cohesive behaviour of the material or adhesive, providing a detailed representation of the material’s response at the crack tip. In general, XFEM is a particularly effective method for simulating complex crack paths and interactions within heterogeneous materials.
The cohesive zone models (CZMs) is the most widely used technique and combines fracture mechanics-based models and continuum damage mechanics [17]. CZMs employ finite element modelling techniques to represent the interface between two fictitious surfaces called the cohesive zone. Unlike traditional methods, where the stiffness in the region is constant, in this method the stiffness is reduced following a constitutive law. A damage parameter is usually introduced to progressively reduce the stiffness of the zone, thereby simulating the advancement of damage. The concept was originally introduced by Barenblatt [18], and its application was later expanded to perfectly plastic materials by Dugdale [19], whilst it was first implemented within the FEM framework by Hillerborg et al. [20] to investigate crack growth in concrete. In this case, a bi-linear traction–separation law (BTSL) was employed for the first time to describe the constitutive law of the material within the cohesive zone. Subsequent researchers expanded upon the model by introducing various traction–separation functions, such as exponential, polynomial, constant, tri-linear, and bi-linear, each differing in their description of the elastic and softening behaviours [21,22,23]; however, the fundamental concept remained unchanged.
CZMs have been used to assess the fatigue life of adhesive-bonded joints, with the cohesive properties of the adhesive degrading during the analysis due to fatigue loads. Robinson et al. [24] and Tumino and Cappello [25] developed fatigue damage models based on maximum fatigue load conditions. However, these models require additional parameters and a calibration process to ensure accuracy and reliability in practical applications. Other authors have modelled the fatigue loading on a cycle-by-cycle basis [26,27,28,29], resulting in a computationally expensive solution. Furthermore, this approach does not apply to High Cycle Fatigue (HCF), for which cyclic extrapolation techniques are more suitable [30,31]. In this kind of model, damage parameters that consider both static and fatigue degradation are employed. Its main disadvantage is the high dependence on experimental fatigue data.
Whilst CZMs have been demonstrated to accurately simulate fatigue crack growth in adhesively bonded joints, they possess an important limitation: crack propagation occurs along a predefined path, typically representing cohesive failure. This constraint restricts the model’s ability to capture complex behaviours of crack propagation that can occur in real-world applications, particularly due to defects and stress concentrations within the material. Nevertheless, CZMs still provide valuable and reliable data for studying the adhesive behaviour under complex loadings, including fatigue.
The effect of the adhesive layer thickness on fatigue crack growth has been investigated in several studies [32,33]. In general, an increase in thickness results in reduced fatigue crack growth rates and enhanced fracture toughness. This phenomenon occurs because the adherents constrain the size of the plastic zone within the adhesive layer, limiting the adhesive’s capacity to dissipate energy through mechanisms other than fracture. As the thickness increases, the level of constraint diminishes, allowing for greater plasticity, which subsequently decreases the fatigue crack growth rate. Whilst some authors have found clear evidence of an existing optimal thickness [34,35,36], this behaviour may be material-dependent [37]. Furthermore, variations in adhesive thickness affect the driving force for crack growth due to the varying stress distribution [38,39]. It remains unclear whether this concept applies to cohesive cracks within the adhesive layer; however, it does help to explain the observed increase in fracture toughness values at greater thicknesses. Nevertheless, the impact of specific thicknesses varies depending on both the adhesive material and the geometry of the joint.
This manuscript presents the implementation of a numerical model to simulate fatigue crack growth in adhesively bonded joints under Mode I and Mixed-Mode (Mode I + Mode II) loading conditions. The first case is based on the experimental work of Pascoe et al. [40] and Zavatta [41] whilst the Mixed-Mode loading is based on the experimental work of Zavatta [41] and van Teeseling [42]. The model was implemented into a user-defined subroutine (UMAT) in the commercial FEM software Abaqus.
2. Cohesive Zone Models (CZMs)
Efforts to develop CZMs for simulating HCF have been mainly focused on composite delamination but are also applicable for adhesive disbonding. Most proposed formulations over the years are extensions of earlier models designed for quasi-static loading, such as that by Camanho et al. [43]. The first fatigue cohesive zone model was introduced by Robinson et al. [24], who implemented an exponential damage function based on parameters fitted from experimental data. Subsequently, Turon et al. [30,44] presented the first fatigue model that linked Paris’ law to the damage growth rate, also allowing for the simulation of Mixed-Mode loading and different fatigue displacement/load ratios. Their work proposed a damage model based on CZMs validated with experimental data from carbon-fibre-reinforced epoxy laminates under Mode I, Mode II, and Mixed-Mode fatigue loading, demonstrating that the model could effectively capture crack propagation under fatigue loading.
Many researchers have referenced the work of Turon et al. [30] to enhance specific aspects, as Pirondi and Moroni [45] who calculated the Strain Energy Release Rate (SERR) for the Paris’ Law with the J-integral and assumed that the cohesive area linked to the damage growth rate was constant throughout the simulation. Similarly, Harper and Hallett [46] proposed an improved estimation of the cohesive length considering unwanted fatigue damage, whilst Kawashita and Hallett [47] introduced a crack tip tracking algorithm to determine the effective cohesive length to improve the damage growth rate accuracy, and other authors have mainly focused on the crack front shape [48,49].
Recently, Dávila and Joosten [50] proposed the CF20 model, which continues to utilise the approach of Turon et al. [30] to calculate the stiffness reduction, but it no longer relies on the Paris’ Law for determining the fatigue damage growth rate. Instead, it uses the material’s S-N curve (stress–life curve) for this purpose and has been validated by other researchers [51,52].
The numerical model used in this manuscript for quasi-static and HCF loading is based on the work of the aforementioned Turon et al. [30,44]. The numerical implementation is discussed in detail in the following subsections.
2.1. Numerical Implementation of Cohesive Zone Models for Quasi-Static Loading
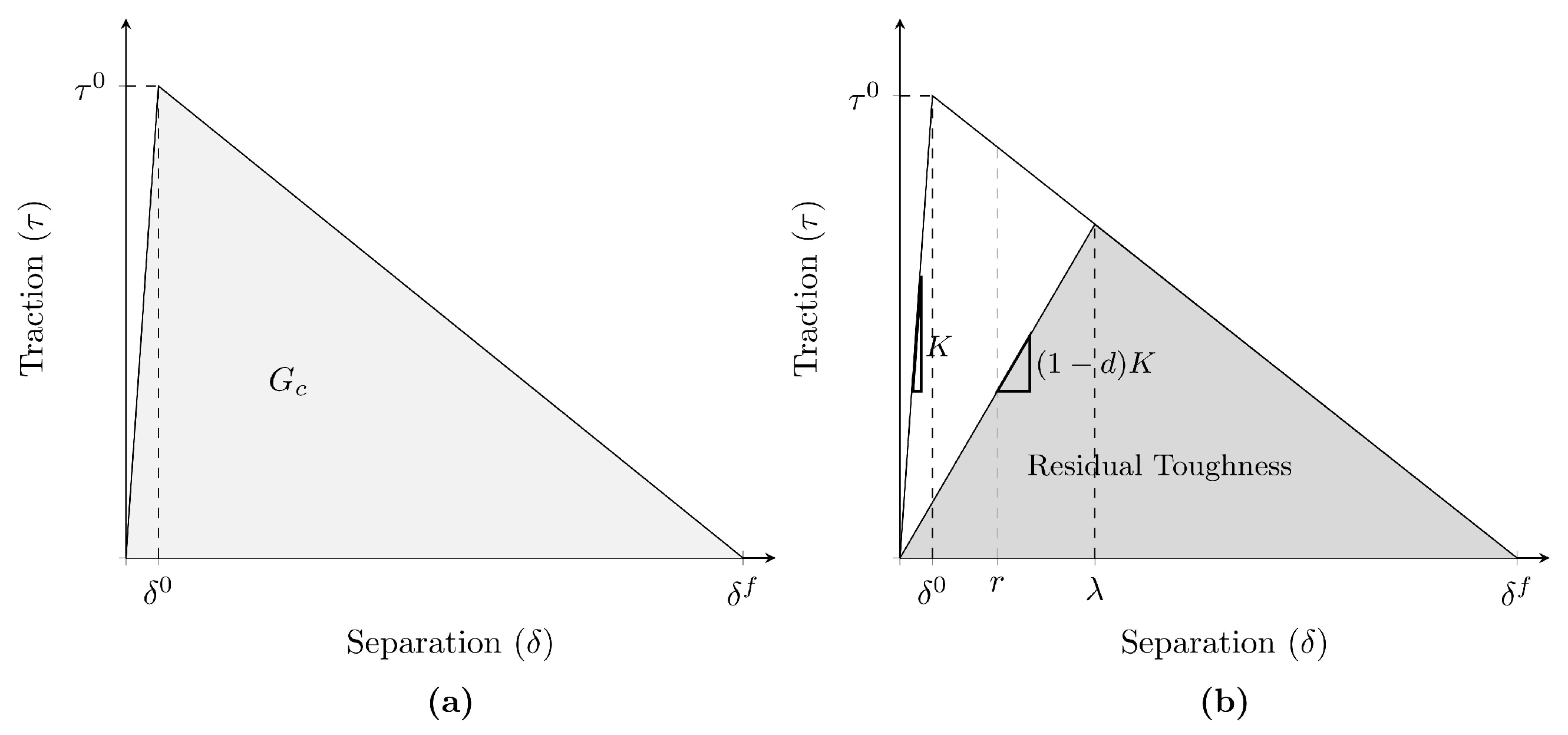
The evolution of damage within the cohesive zone is governed by traction–separation laws, which establish the relationship between the maximum traction and critical energy release rate, with the tractions and relative displacements in the cohesive zone. For adhesives, the bi-linear traction separation law (BTSL) is commonly used (See Figure 1a) [53], and is consistent with the framework presented by Turon et al. [30,44].
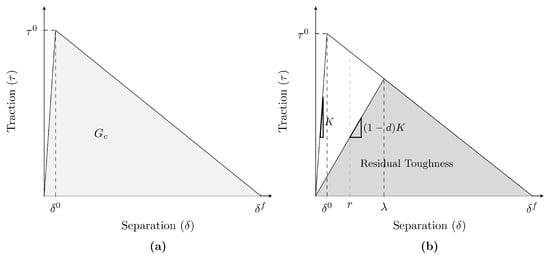
Figure 1.
Visual representation of the bi-linear traction–separation law, non-damaged (a); damaged, illustrating stiffness reduction (b); where is the onset displacement, is the propagation displacement, is the displacement jump, r is the damage threshold, is the maximum traction, K is the stiffness of the cohesive zone, d is the damage, and the fracture energy.
Figure 1a illustrates two distinct regions of the BTSL: a linear–elastic region and a damaged region, which is also referred to as softening region in the literature. In the linear–elastic region, no damage is accumulated until the maximum traction () is reached at the onset displacement (), which is computed as follows:
where K is the stiffness of the cohesive zone. This stiffness can be estimated with Equation (2), and it depends on the Young’s Modulus of the material (E), the thickness of the cohesive zone (t), and a correction factor (), which is greater than 1, calibrated to capture crack initiation.
Beyond the onset displacement, the damaged region begins. In this region, as the relative displacement increases, the damage increases, leading to a reduction in the maximum traction that the zone can sustain. This results in a progressive decrease in stiffness (K). When the propagation displacement () is reached, the zone can no longer sustain any loads, resulting in the growing of the crack. The energy required to propagate the crack is known as the fracture toughness () and it corresponds to the area under the BTSL curve. The propagation displacement can be determined as follows:
During the implementation of the numerical model, where computations are performed increment-by-increment (i), it is essential to consider the damage state from the previous increment (). Given that damage within the cohesive zone is irreversible, it cannot decrease even if the subsequent load is reduced. Therefore, it is crucial to compute the threshold at which damage can increase. This threshold (r), which differs from the onset displacement in already damaged zones, is defined as follows:
To compute the damage due to quasi-static loads () at increment i, Equation (5) is used. This equation, derived from the BTSL, evaluates damage based on the current displacement jump () and the damage threshold (r), considering both the onset and propagation displacements.
This formulation effectively models the transition from linear–elastic behaviour to softening as damage initiates and evolves, reflecting changes in material properties under quasi-static loading. Damage is interpreted as a reduction in stiffness, leading to a decrease in fracture toughness (residual toughness) in the analysed region, as illustrated in Figure 1b.
In summary, by utilising the bi-linear traction–separation law and the associated damage equation, the transition from linear–elastic behaviour to softening can be effectively modelled. This approach accurately captures the material’s response under static loads and its damage evolution.
2.2. Numerical Implementation of Cohesive Zone Models for Fatigue Loading
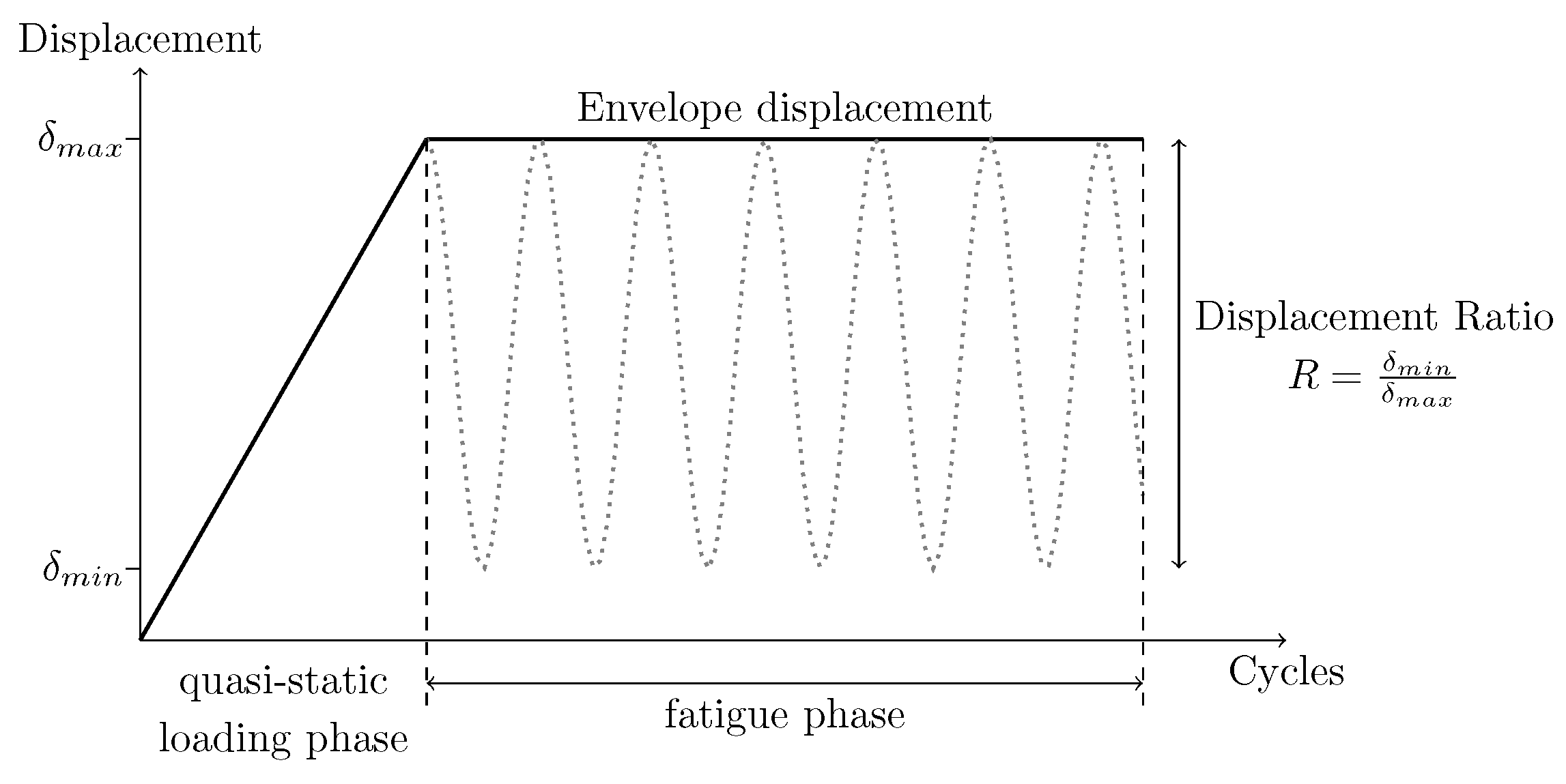
CZMs are a powerful framework for simulating crack initiation and propagation under fatigue loading. In the work by Turon et al. [30,44], only constant amplitude loading is considered during fatigue cycling. This simplification allows for modelling focusing solely on the envelope of forces or displacements, as illustrated in Figure 2. In this approach, only the maximum load and its variation are considered.
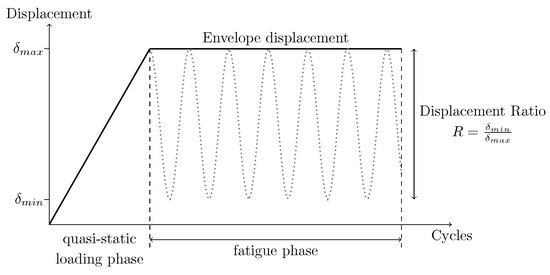
Figure 2.
Fatigue loading diagram, displacement number of cycles, illustrating the displacement’s envelope and ratio (variation) during the fatigue loading phase.
The total damage at any given increment is defined as the sum of damage contributions from both quasi-static and cyclic loads, reflecting the different damage mechanisms involved. This decoupling of quasi-static and fatigue loading is represented in the following equation:
The fatigue damage () is calculated with Equation (7), where damage accumulates with respect to the value computed in the previous increment (). To further simplify the modelling process, the envelope approach is employed, allowing for the implementation of a cycle jump strategy (further discussed in Section Cycle Jump Strategy). With this strategy, a specified number of cycles () are simulated per increment (i).
where represents the damage growth rate. Damage growth rate links the experimental data and the computational modelling with the following relationship:
where is the crack growth rate determined from experimental fatigue testing using Paris’ Law (See Equation (9)). Conversely, represents the relation between damage and damaged length (), which is computed with Equation (15).
where C and m are material constants; G is the strain energy release rate (SERR). The crack growth rate is valid between the no-crack growth SERR threshold () and the fracture toughness ().
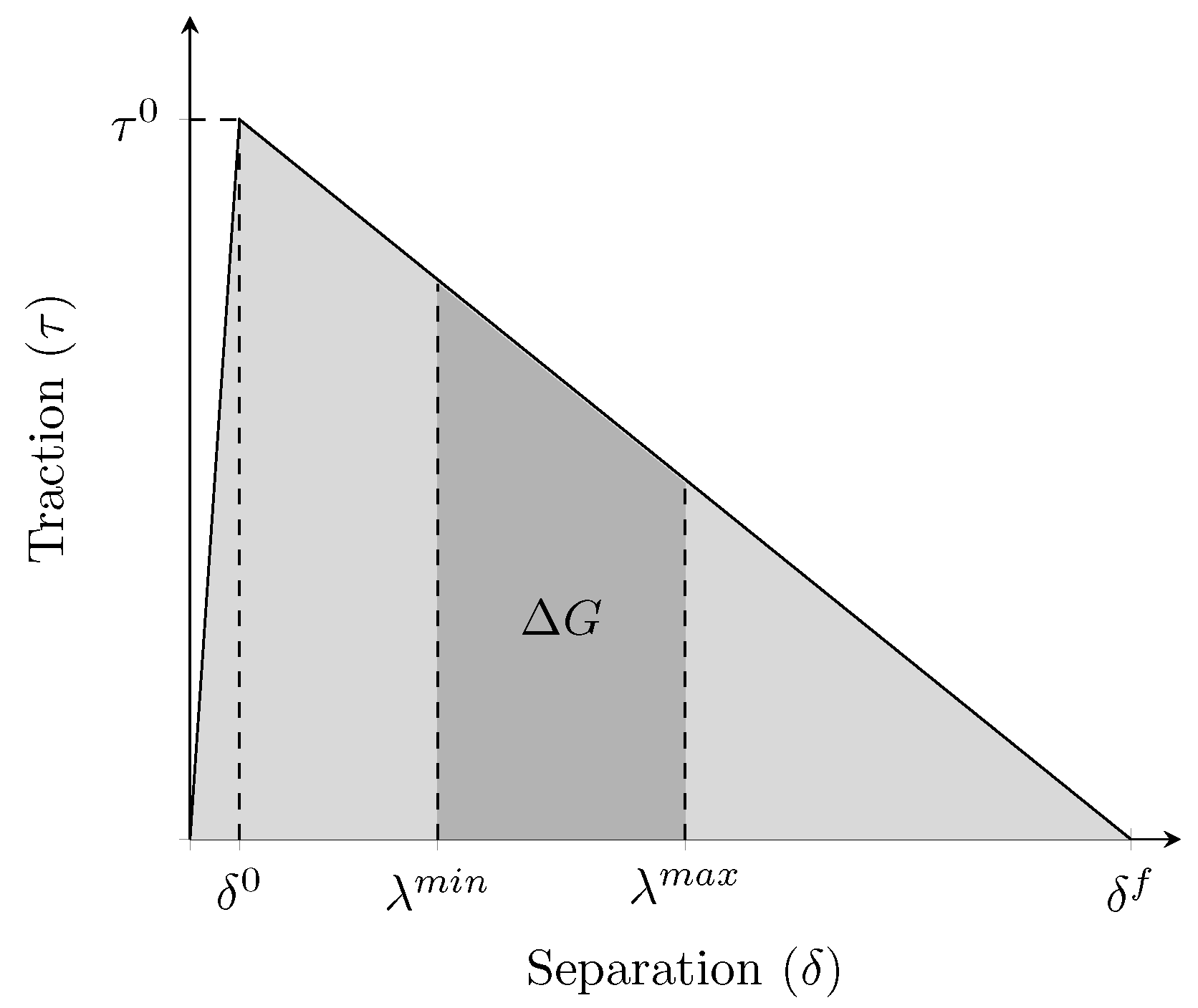
The cyclic variation of the SERR () is computed between the maximum and minimum displacement during the fatigue cycling. Considering the BTSL, it corresponds to the area under the curve between these displacements and is illustrated in Figure 3.
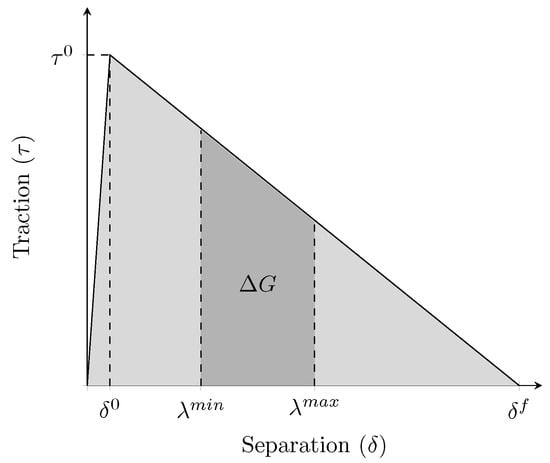
Figure 3.
Visual representation of the cyclic variation of the strain energy release rate () of the bi-linear traction separation law, where is the minimum and the maximum displacement jump during the cyclic loading.
Mathematically, the strain energy release rate is defined as follows:
Its cyclic variation can be defined as in Equation (11), exploiting the displacement or loading ratio R.
where the maximum strain energy release rate can be computed as follows [30,54,55]:
To capture small variations in the computation of during fatigue cycling, Kawashita and Hallett [47] suggested employing the midpoint rule, considering the current and previous displacement jump and residual strength (). The latter is computed considering the damaged state of the region as described in Equation (14).
Finally, the relation between the damage and damaged length represents a material property dependent on the BTSL and the length of the cohesive zone ().
The cohesive zone length, as defined by Harper and Hallett [55], refers to a zone where elements experience irreversible deformation (already damaged elements) ahead of the crack tip. Its estimation has been widely discussed in the literature [20,55,56,57,58] and the importance of having a fine mesh in the cohesive zone, to accurately capture crack growth, has been highlighted by Turon et al. [58]. The general definition is described in Equation (16), where M is a parameter that is adjusted to the loading condition and geometry.
Cycle Jump Strategy
One of the main advantages of implementing HCF simulation with CZMs is exploiting the displacement or loading envelope to determine the degradation due to fatigue for a certain number of cycles, avoiding a cycle-by-cycle analysis, which is computationally expensive. This strategy is called Cycle Jump, implemented by Turon et al. [30], based on the work from Van Paepegem and Degrieck [59], and it determines the number of cycles for which the accuracy for the damage calculation is respected considering the damage growth , as follows:
It is important to note that this is valid as long as the displacement or load ratio is constant.
2.3. Adapting Numerical Model for Different Loading Modes
Each specific loading condition necessitates an adjustment of some parameters described in the previous section. The convention used to specify the direction of relative displacements in the cohesive zone is for the normal direction and for the in-plane directions. Conversely, tractions, SERR, and the elastic moduli are determined by the loading mode; thus, indicates Mode I loading, and correspond to the shear loading modes. The stiffness (K) is directly specified by the normal () or shear () directions.
2.3.1. Mode I Loading
Mode I loading considers only tractions and displacements in the normal direction and all the equations discussed previously shall be adjusted accordingly. An adaptation shall be performed for the displacement jump, which is calculated as follows:
where the MacAuley brackets indicate that only tensile loading is considered.
2.3.2. Mixed-Mode Loading
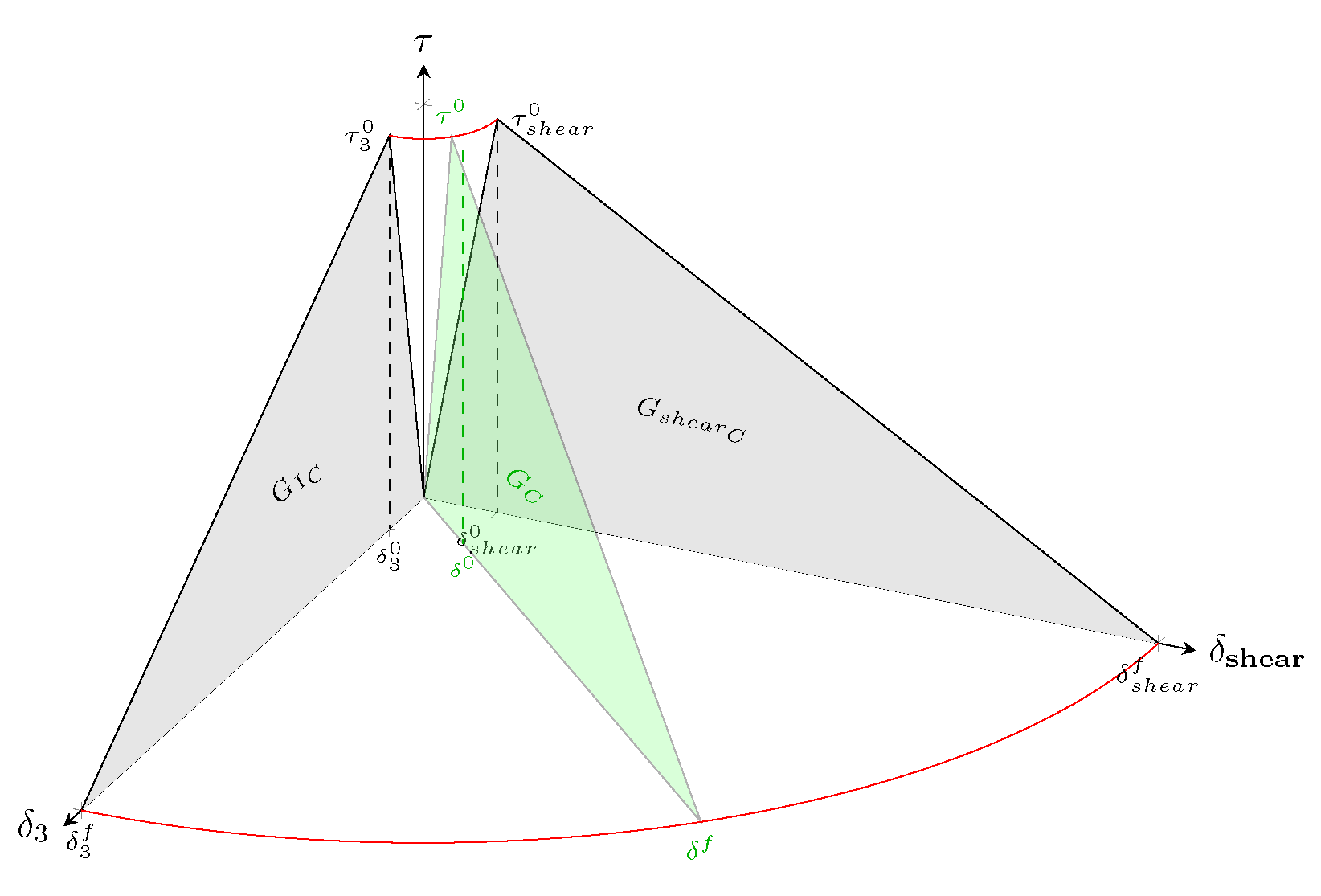
Mixed-mode loading considers tractions and displacements in all directions, incorporating both normal and shear. In this manuscript, the Mode II and Mode III loading-related parameters are treated equally (e.g., ). Figure 4 illustrates the bi-linear traction separation law for Mixed-Mode loading, with the equivalent curve highlighted in green.
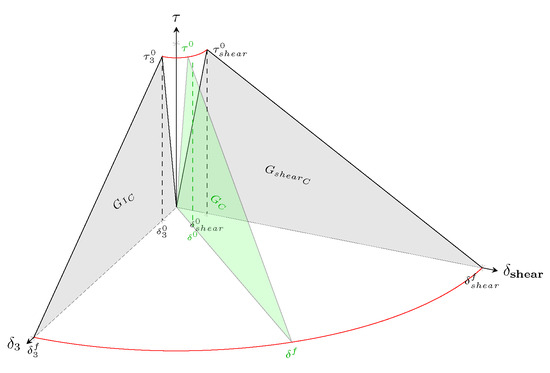
Figure 4.
Visual representation of the bi-linear traction separation law highlighting in green the equivalent displacement mode for Mixed-Mode loading considering Mode I and Shear.
The equivalent displacement jump is calculated using the following equation:
where .
The relative displacement in each direction facilitates the determination of the Mixed-Mode ratio (), which quantifies the contribution of strain energy release rate due to Mode II loading (See Equation (20)).
where is the total strain energy release rate. If , only Mode II loading is present; if , there is only Mode I, and any intermediate values indicate Mixed-Mode loading. As suggested by Turon et al. [61], the computation may be also performed with the relative displacements (), as seen in Equation (21).
By determining the Mixed-Mode ratio, the Mixed-Mode stiffness [61] and elastic modulus [62] can be computed with the following expressions:
where and with .
The Benzeggagh and Kenane criterion (B-K criterion) [63] describes how the different loading modes interact, as seen in the following equation:
The criterion may be employed to determine the maximum Mixed-Mode traction through Equation (25). Additionally, the onset and propagation displacements, and , can be calculated with Equations (26) and (27), respectively.
For the numerical implementation of the fatigue model under Mixed-Mode loading, Paris’ Law to describe the crack growth in Equation (9) must be modified to account for these effects. Various authors have proposed modifications with limitations in mode interaction [64,65,66,67,68]. This manuscript adopts the model proposed by Bürger [69], which is tailored for adhesive bonding and validated through an experimental campaign demonstrating accurate predictions even with variable mode ratios. The model relies on the computation of the principal stresses, assuming that it is a suitable parameter to describe disbonding. In terms of SERR, the maximum is calculated as follows:
The cyclic variation of the SERR is then computed as follows:
This leads to the modified Paris’ Law expression:
where . The C and m parameters for Paris’ Law are derived from Mode I () and Mode II () testing.
The M parameter to estimate the cohesive length may vary since research has mostly focused on either Mode I or Mode II loading [62]. For the case studied in this manuscript, the M parameter will be calibrated accordingly.
3. Methods
The implementation of the CZM described in Section 2 was implemented on adhesively bonded joints under Mode I and Mixed-Mode loading. The adhesive where fatigue crack growth was simulated and studied was an epoxy film adhesive from Solvay, FM94K, a high-performance adhesive used in the aerospace industry. Its mechanical and interfacial cohesive properties are summarised in Table 1.

Table 1.
Mechanical/cohesive properties of adhesive FM94K.
3.1. FEA Modelling
Each specimen analysed under Mode I and Mixed-Mode loading was simulated using four distinct approaches in order to validate the implemented model. When using CZM to simulate adhesive bonding, cohesive elements are typically used in place of the adhesive.
This manuscript specifically investigates the modelling of the cohesive zone in the mid-plane of the adhesive. In this approach, the adhesive is modelled with its actual thickness and a thin cohesive zone is introduced at the mid-plane. This approach was considered both in 2D and 3D models and it provides an insight on the effect of modelling the adhesive thickness on fatigue disbonding.
The analyses were all performed with Abaqus 2024 Standard/Implicit. Table 2 summarises the characteristics of the four modelled cases, including the mesh size and element type for each region. It is important to note that mesh size in the cohesive zone was refined in order to improve the accuracy of crack growth analysis.

Table 2.
Summary of the modelling characteristics of the adhesive, adherents, and cohesive zone.
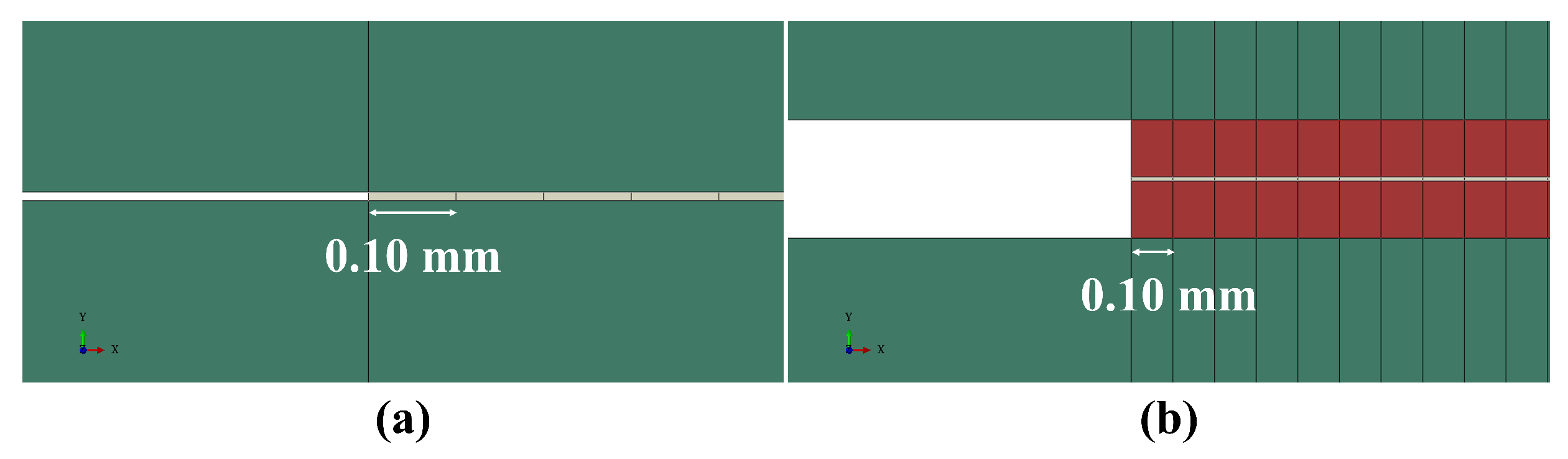
For the models where the adhesive is completely replaced (as illustrated in Figure 5a), the properties of the adhesive’s material are implemented in the cohesive elements. In comparison, Figure 5b illustrates a focus of the models where the adhesive is modelled considering its entire thickness, with a thin layer of cohesive elements on its mid-plane simulating the crack growth path. In this situation, refining the mesh on the adherent was necessary to improve the stress distribution output.
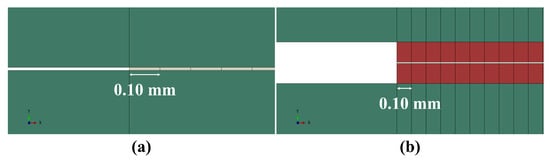
Figure 5.
Modelling approaches to the cohesive zone: Cohesive zone replacing the adhesive (a); Cohesive zone located along the mid-plane of the adhesive (b); in green the adherent, in red the adhesive, and in grey the cohesive zone.
3.2. User-Defined Material Subroutine (UMAT) Implementation
User-defined material subroutines (UMAT) in Abaqus define the mechanical constitutive behaviour of materials at each integration point, including the cohesive behaviour of a material. This type of subroutine requests two outputs from the model: the stress tensor () and the Jacobian matrix of the constitutive model (also known as the tangent stiffness matrix, ). The subroutine returns time-step and strain-related variables.
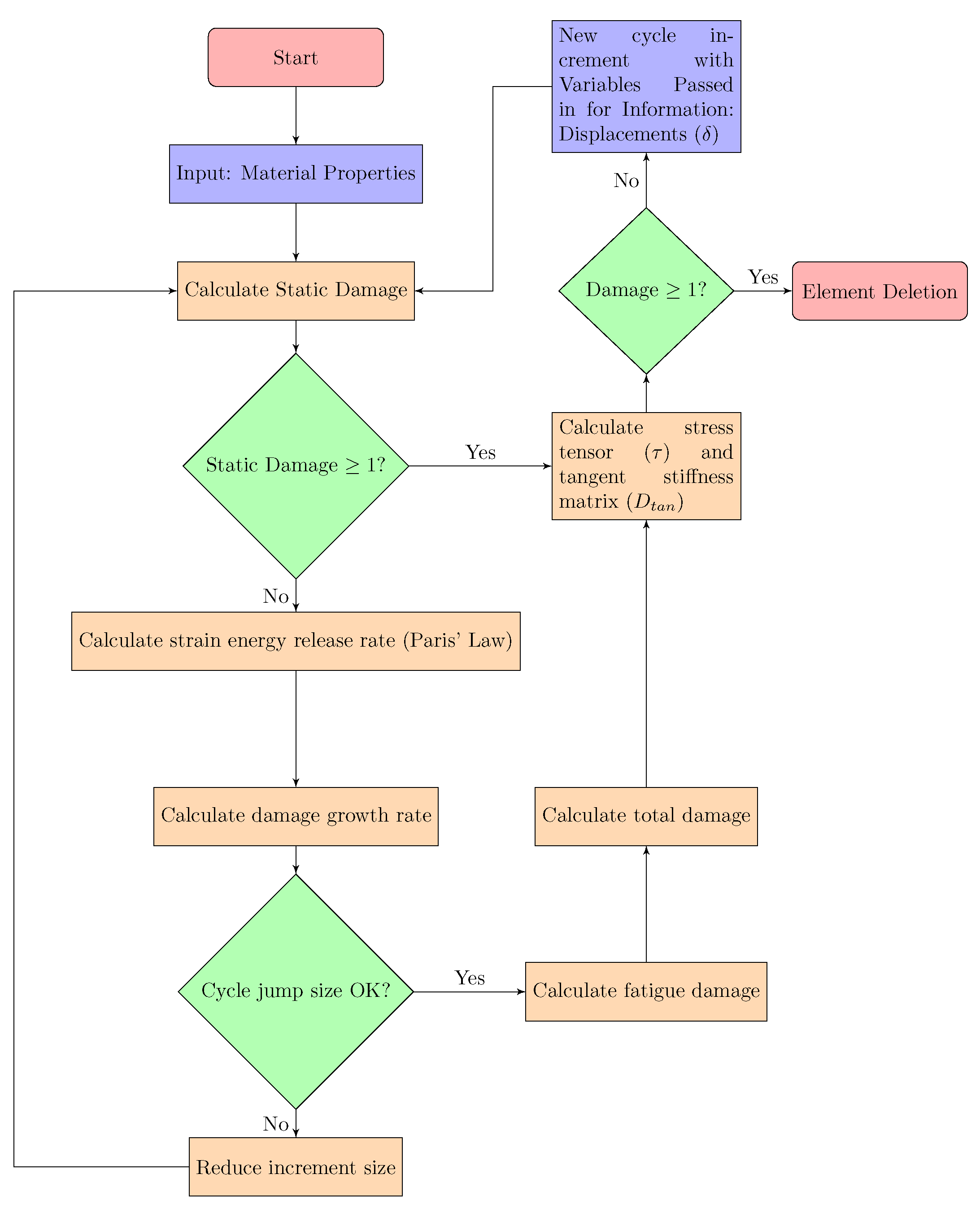
The numerical model for simulating HCF, detailed in Section 2, was implemented using a UMAT. The chart illustrated in Figure 6 shows the implemented model workflow considering the calculation of the stress tensor and tangent stiffness. The specific loading cases will be discussed in detail in the following subsection.
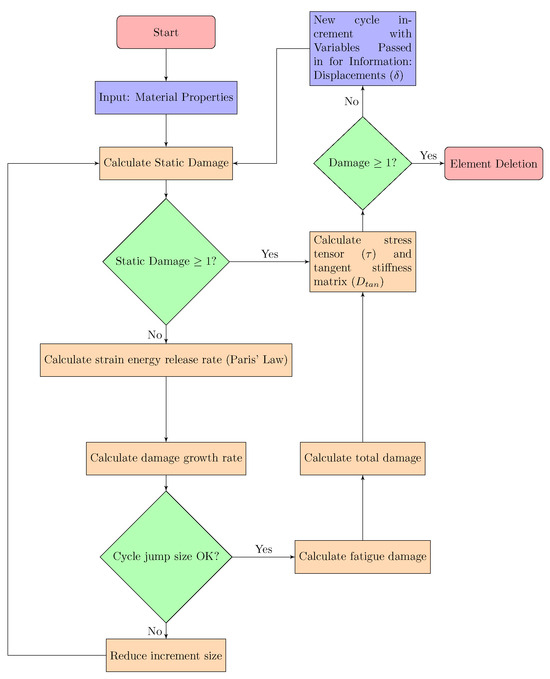
Figure 6.
UMAT implementation workflow for the simulation of high cycle fatigue with cohesive zone models.
3.3. Test Cases
3.3.1. Mode I—Double Cantilever Beam (DCB)
The implementation of the CZM for Mode I loading was validated with the experimental data from Pascoe et al. [40] and Zavatta [41]. These authors conducted tests on double-cantilever beams (DCBs) with adherents manufactured with aluminium 2024-T3 and the FM94K adhesive. The DCB specimens measured 270 mm in length, 6 mm in thickness per adherent, and 25 mm in width, with an initial crack length () of 50 mm. Different adhesive thicknesses were used to evaluate their effects on the fatigue disbonding. The loading properties, adhesive thickness, and the parameters for Paris’ Law for each simulated specimen are described in Table 3. The data provided pertain to tests conducted under displacement-controlled conditions for a total of 375,000 cycles. It is important to note that the Paris’ Law parameters (C, m) are for the normalised cyclic variation of the SERR, represented as .

Table 3.
Summary of the modified Paris’ Law parameters, fatigue load conditions, and adhesive thickness of different simulated specimens.
The stress tensor for Mode I only is calculated as follows:
where the stiffness matrix () in matrix notation, considering the condition of tensile loading ( and compression loading (), is defined as follows:
While the tangent stiffness matrix for Mode I loading is defined as follows:
In matrix notation:
3.3.2. Mixed-Mode—Cracked Lap Shear (CLS)
The implementation of the CZM for Mixed-Mode loading was validated with the experimental data from Zavatta [41] and van Teeseling [42]. These authors conducted tests on Crack Lap Shear (CLS) specimens. This specimen was first proposed by Lai et al. [71] in 1996 to assess the Mixed-Mode bond fracture strength and then adhesive joint disbonding. In the work by Zavatta [41] and van Teeseling [42], the adherents were manufactured with GLARE 2A-4/3-0.4, a fibre metal laminate (FML) composed of aluminium sheets and glass fibre prepreg, and the FM94K adhesive. In the CLS specimens, each adherent measured 212.50 mm in length, 2.50 mm in thickness, 43.56 mm in width, whilst the adhesive had a thickness of 0.1 mm and an initial crack length () of 30 mm. A singular experimental test was selected for comparison with the numerical results. The loading characteristics and the parameters related to Paris’ Law for each modelling technique, which were simulated for 160,000 cycles under load-controlled conditions, are presented in Table 4.

Table 4.
Summary of the modified Paris’ Law parameters for Bürger’s model where the strain energy release rate is in [J/] and crack growth rate is in [m/cycle]; and fatigue loads with .
4. Results
The results are organised into two sections based on the type of loading: Mode I for the DCB and Mixed Mode for the CLS. In both cases, the numerical analysis outcomes are compared against the experimental results.
4.1. Mode I—Double-Cantilever Beam (DCB)
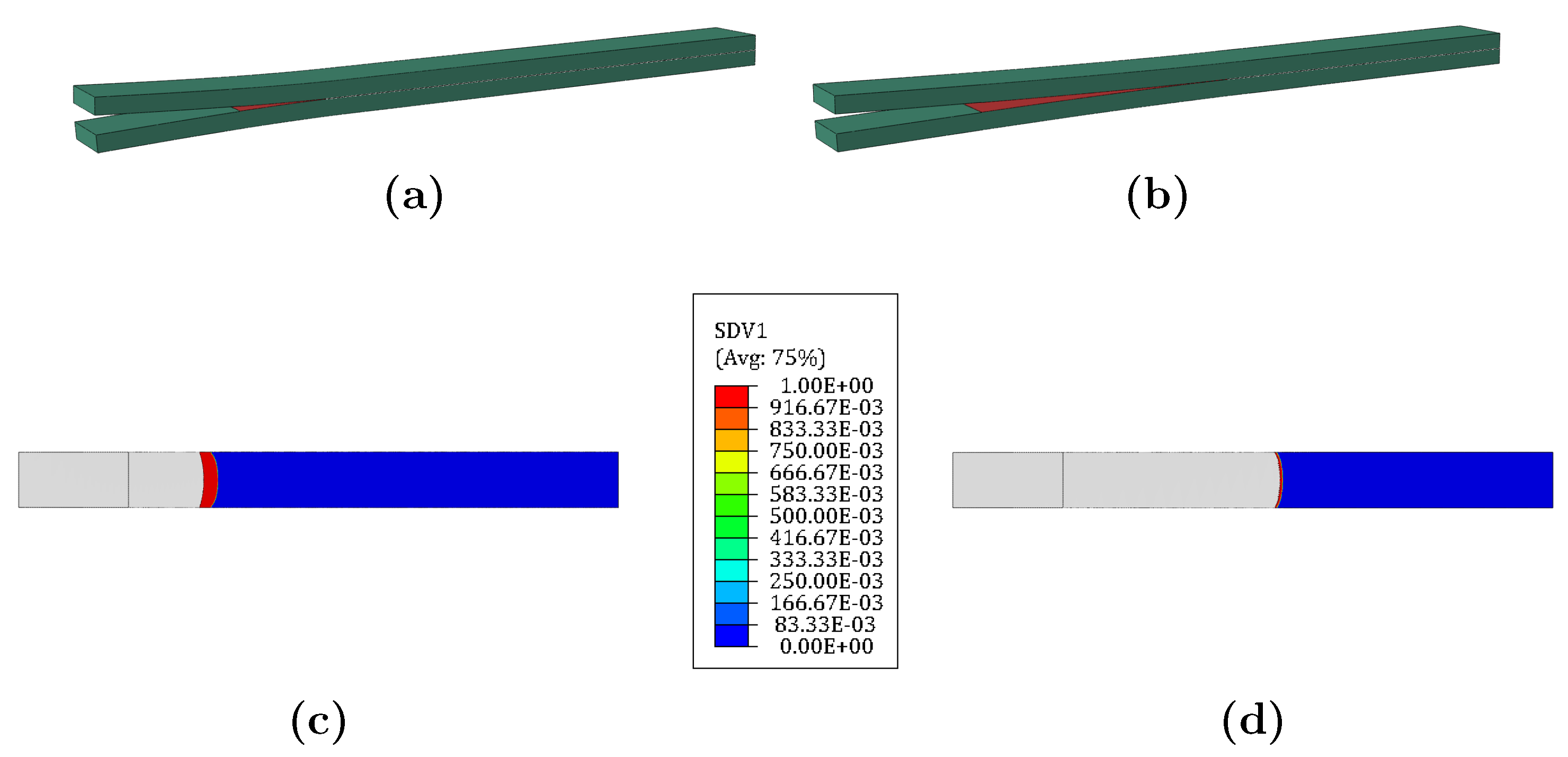
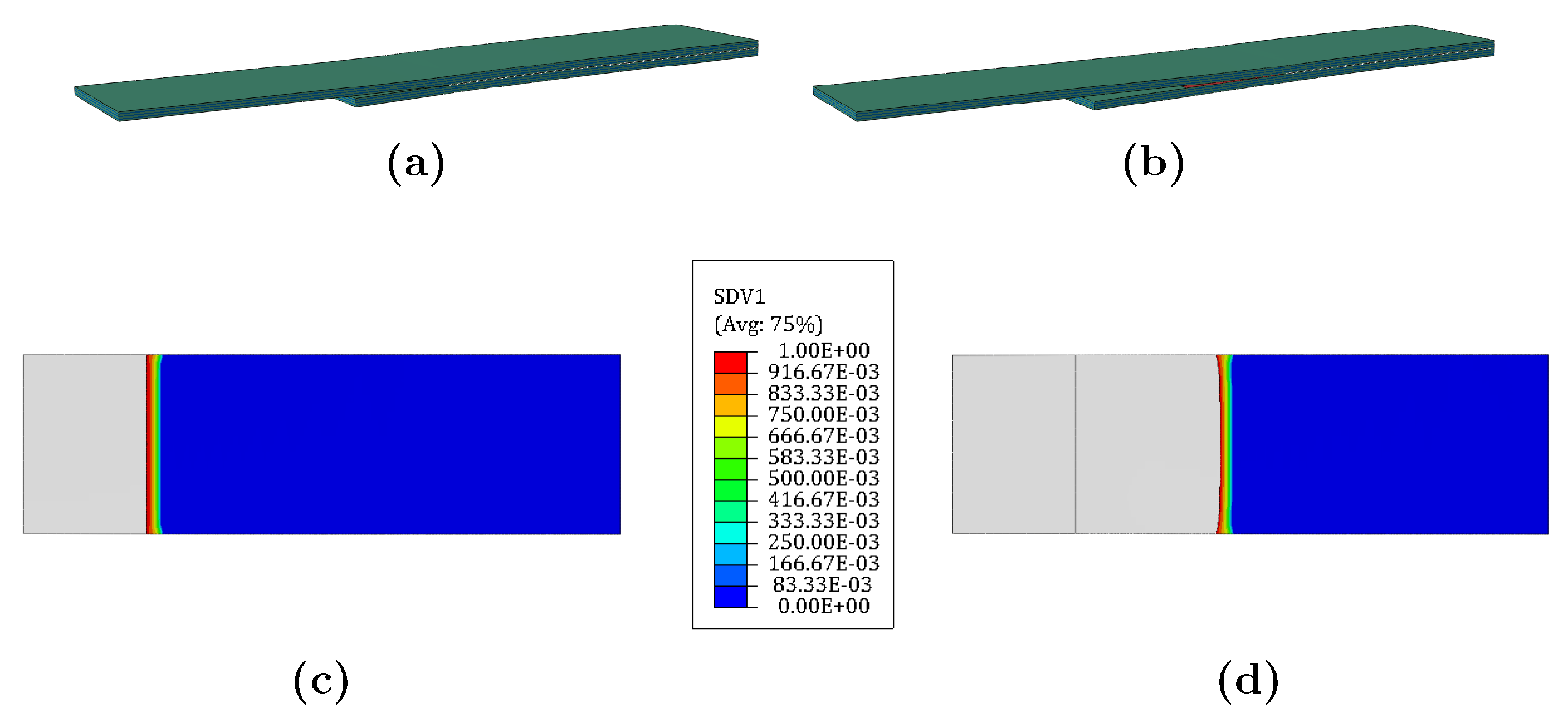
The implementation of the numerical model for Mode I loading captured fatigue disbonding growth for all the simulated cases. The evolution of the disbonding during fatigue cycling is illustrated in Figure 7, where (a) refers to the state of the specimen and (c) to the damage state variable (SDV1) of the cohesive elements that simulate the adhesive behaviour and the crack front shape at the beginning of the fatigue step; (b) illustrates the state of the specimen and (d) the final damage state of the cohesive elements and its crack shape after reaching 375,000 fatigue cycles. A non-damaged region is represented by SDV1 = 0 (shown in blue in the Figure) whilst a fully damaged region is represented by SDV1 = 1.00 (in red); when all the integration points in the element reach this value, it is deleted in the subsequent increment. All values between 0 and 1 represent the softening region (also known as process zone) in the adhesive. (c,d) show a different size of the non-damaged region due to the evolution of the crack growth rate as the fatigue cycles increase. In displacement-controlled testing of Mode I under fatigue, the crack growth rate decreases due to the lower SERR [72].
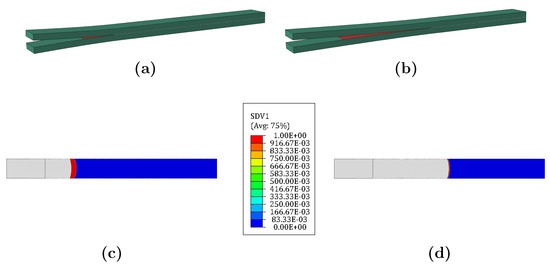
Figure 7.
Visual representation of the DCB during disbonding during fatigue cycling at N = 0 (a); at N = 375,000 (b); damage distribution in cohesive zone at N = 0 (c); and at N = 375,000 (d).
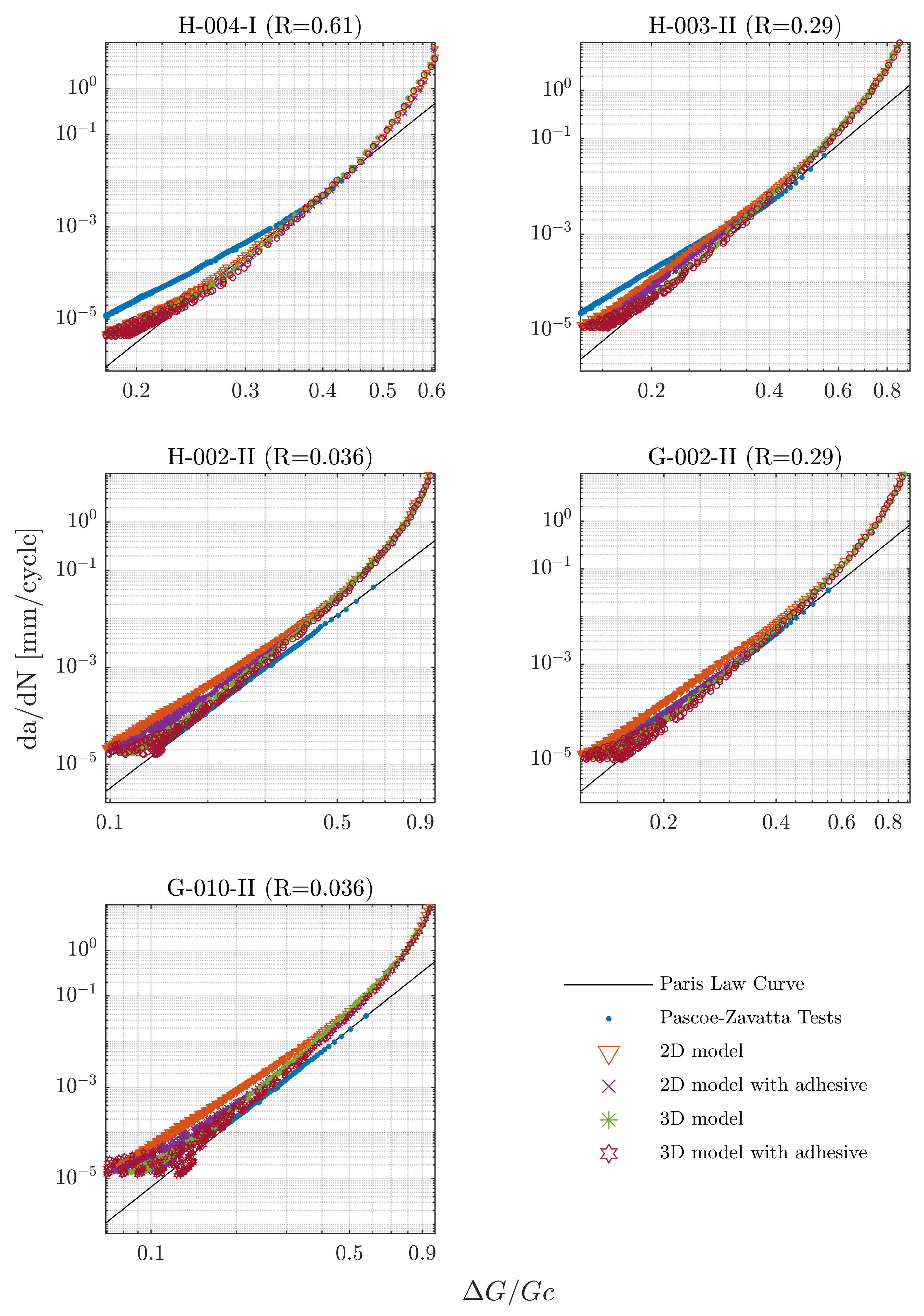
The results of all four models are summarised in Figure 8 compared with the experimental results from Pascoe et al. [40]. The Paris’ Law parameters used for the numerical model (and summarised in Table 3) were obtained from the fitting of the experimental test data (in blue) with the fitting function (in black), obtaining a high correlation between both ().
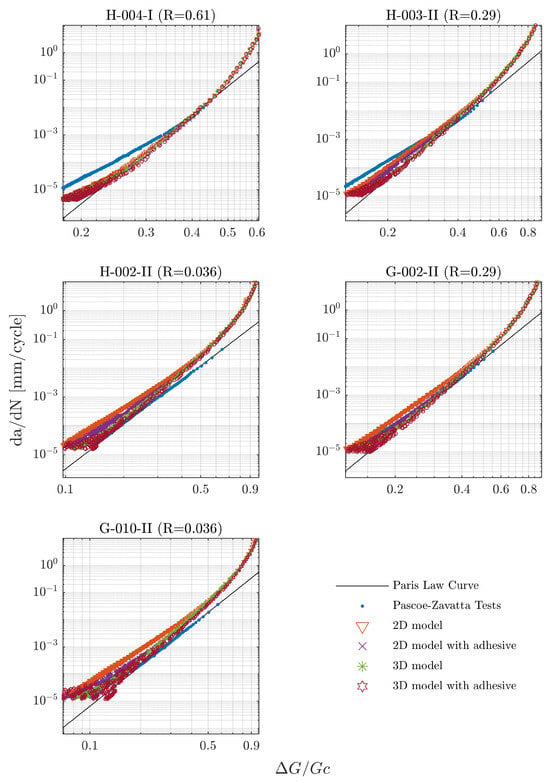
Figure 8.
Crack growth rate as a function of normalised cyclic variation of the strain energy release rate. Results are divided by specimen name and by the different testing configurations.
All the simulated specimens correctly captured fatigue disbonding initiation, highlighted in values of normalised cyclic SERR () greater than 0.5 (Figure 8). This region is also known in the literature as the "stable-tearing crack growth" region. Stable propagation is noticed in lower normalised cyclic SERR values, which align with the trend of the Paris’ Law curve. Due to the absence of experimental data for the initiation stages, there is a discrepancy observed in this region regarding the presented experimental results.
The effect of modelling the adhesive thickness is particularly evident at low crack propagation rates (∼ mm/cycle), where both the 2D and 3D models exhibit oscillatory behaviour. These oscillations can be attributed to the slow redistribution of stresses and strains within the cohesive elements at the crack front. These stresses and strains differ from those in models where the adhesive thickness was not modelled. In the first case, in fact, the cohesive elements are in direct contact with the adhesive instead of the aluminium adherents.
Furthermore, the additional thickness introduced by the adhesive influences the load distribution within the cohesive zone. At low crack growth rates, particularly near the specimen’s no-growth region (SERR threshold), this variation enhances the model’s sensitivity to small displacements. The oscillatory effect related to the load distribution is more pronounced in thicker specimens (e.g., H-002-II compared to G-010-II). These effects may be mitigated by using a finer mesh, as this allows for faster redistribution of stresses and strains particularly at low crack propagation rates.
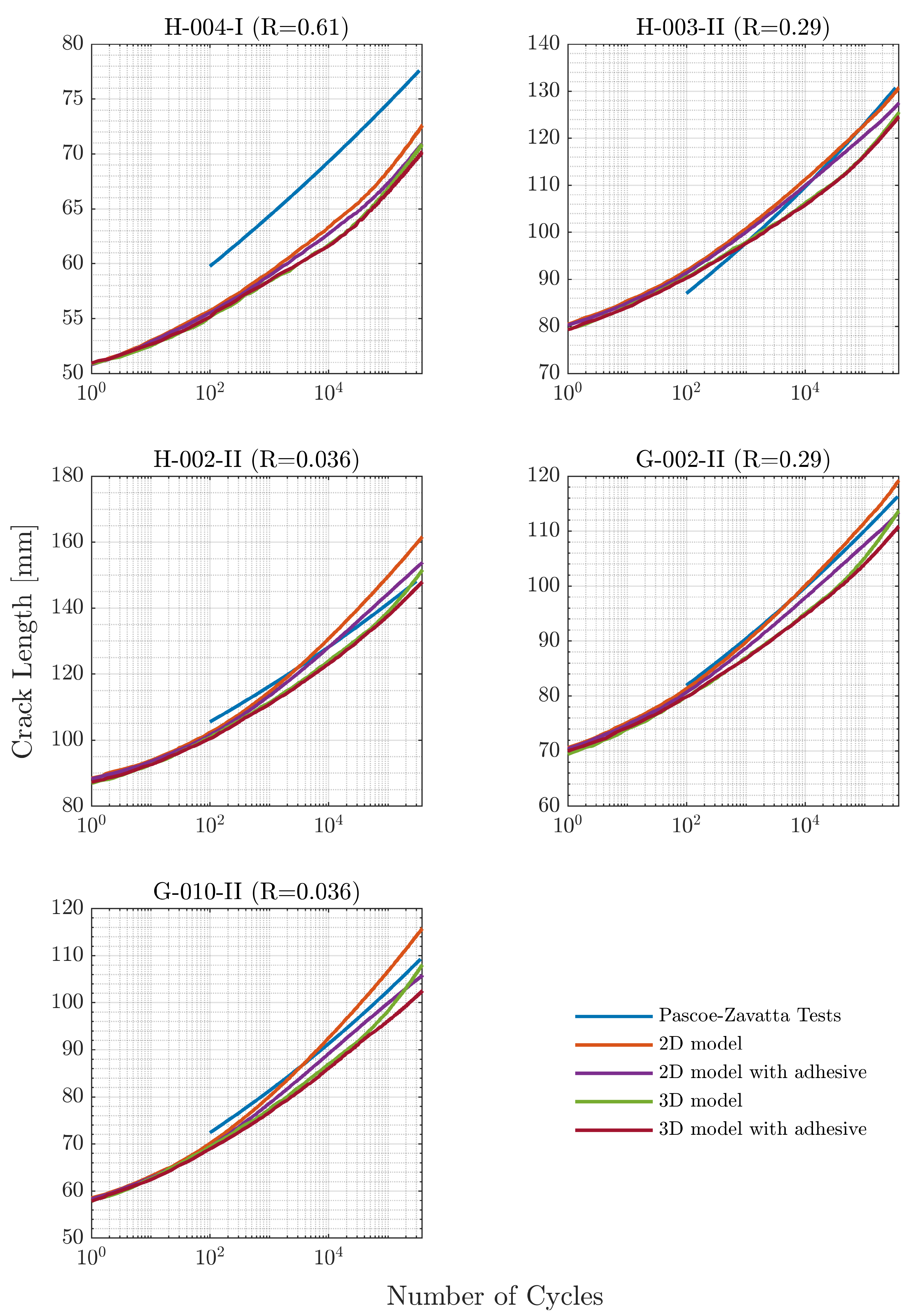
The results comparing crack length to the number of fatigue cycles for all modelling techniques across all specimens are presented in Figure 9. The relative error of the final crack length between the experimental results and the different modelling techniques after 375,000 fatigue cycles is summarised in Table 5. In general, all the modelling techniques and specimens showed a good agreement with the experimental results, with a maximum average deviation of . The differences observed may be attributed to the parameters of Paris’ Law, particularly at low crack growth rates, where the experimental results deviate the most from the fitted curve. For specimen H-004-I, there is a significant difference, almost a deviation in crack length, because this specimen was pre-cracked differently during the experimental test by Pascoe et al. [40] to eliminate the effects of a resin-rich area at the crack front; however, this difference is not documented. Therefore, the maximum deviation between the experimental final crack length and that coming from the simulated cases does not exceed , excluding from the analysis specimen H-004-I.
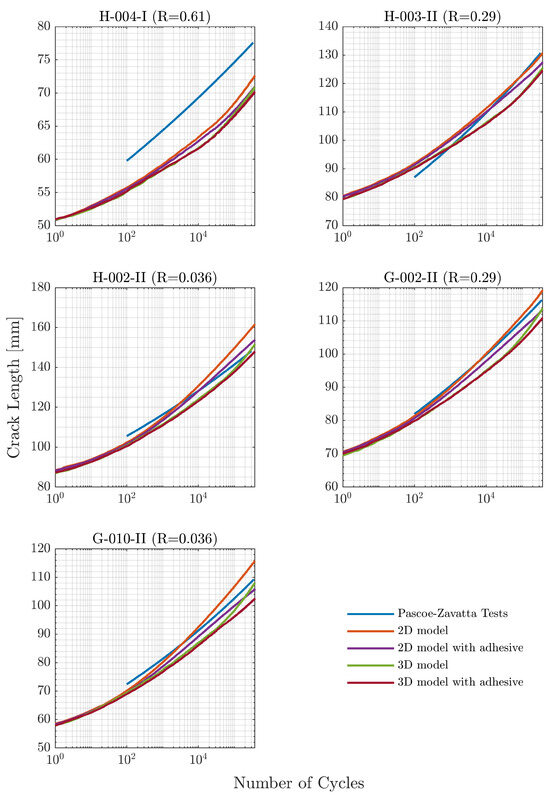
Figure 9.
Crack length as a function of the number of fatigue cycles. Results divided by specimen name and by the different testing configurations.

Table 5.
Relative error of the final crack length between experimental results and different modelling techniques divided by specimen name.
The results summarised in Table 5 may appear counter-intuitive, as the highest average error is associated to the most detailed modelling technique, the 3D model where the adhesive thickness was included. As previously discussed, this was due to the significant deviation on specimen H-004-I. When excluding H-004-I from the average error analysis, the 2D model is the least accurate but still presents a small average relative error. Conversely, the most accurate models were the 3D model and 2D model where the adhesive thickness was included, both exhibiting a relative average error of around .
4.2. Mixed-Mode—Cracked Lap Shear (CLS)
The numerical model for Mixed-Mode loading effectively captured fatigue disbonding growth for all the modelling techniques. The evolution of the disbonding during fatigue cycling is illustrated in Figure 10, where (a) illustrates the state of the specimen and (c) the damage state (SDV1) of the cohesive elements at the beginning of the fatigue step; (b) illustrates the state of the specimen and (d) the final damage state of the cohesive elements and the crack shape after reaching 160,000 fatigue cycles. In contrast to what was observed in the Mode I loading case, the damaged area shows only minor changes after 160,000 cycles, since this type of test is force-controlled (meaning the applied load remains constant throughout the experiment). Since the strain energy release rate (SERR) is proportional to the square of the applied force (), the crack growth rate does not vary significantly.
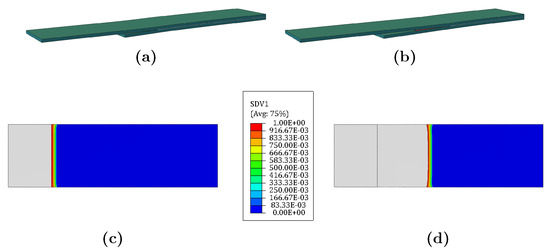
Figure 10.
Visual representation of the CLS during disbonding during fatigue cycling at N = 0 (a); at N = 160,000 (b); damage distribution in cohesive zone at N = 0 (c); and at N = 160,000 (d).
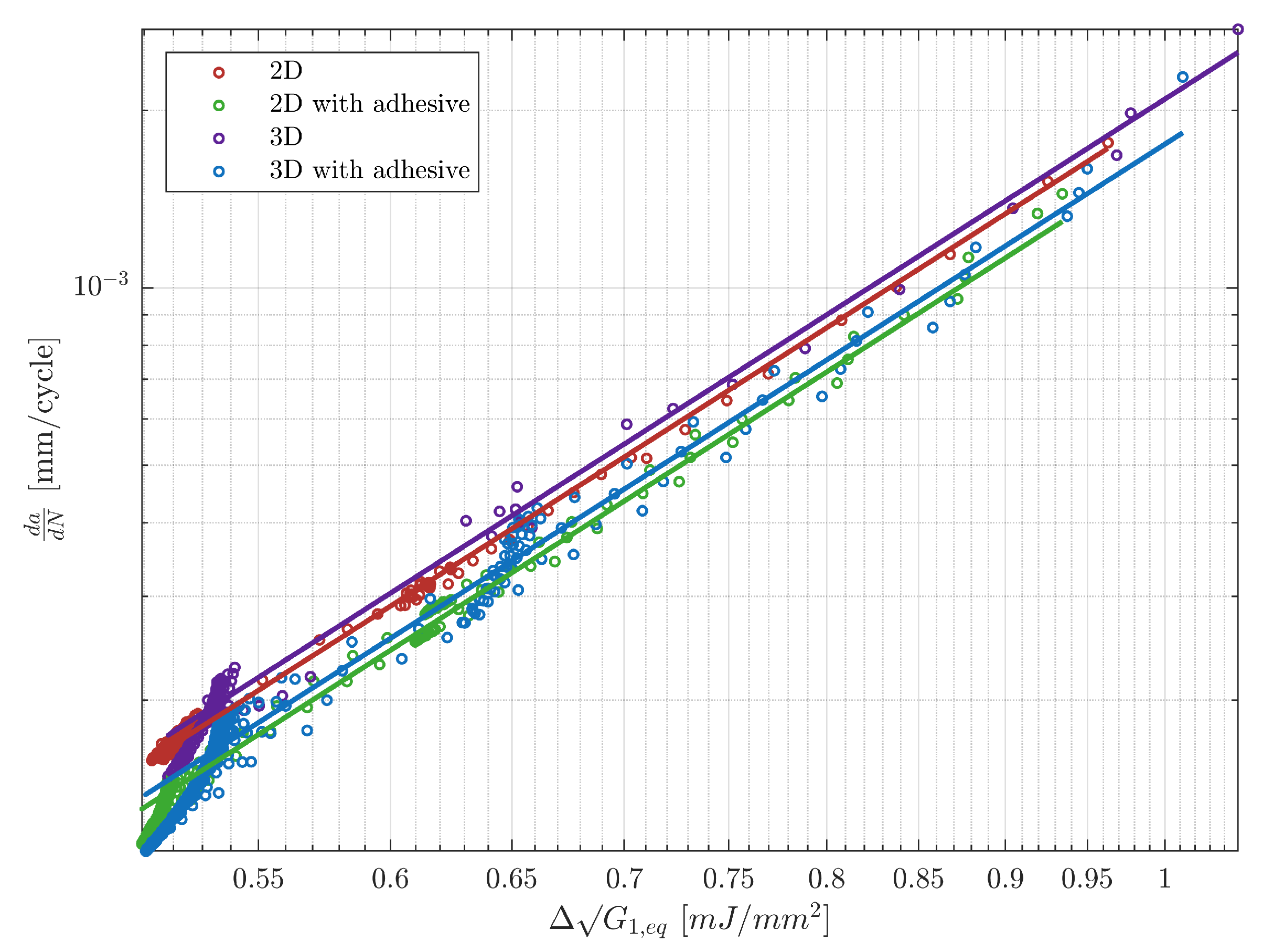
As illustrated in Figure 11, the crack growth rate throughout the entire simulation consistently falls within the same order of magnitude (), which supports the discussion presented earlier. The modified Paris’ Law by Bürger (See Equation (30)) has demostrated to accurately capture fatigue disbonding under Mixed-Mode loading implemented to a CZM and the plot demonstrates that modelling the adhesive thickness affects the fatigue disbonding captured by the model. The solid lines on the plot represent the equivalent Paris’ Law curve and its parameters with the respective equivalent Mixed-Mode ratio are summarised in Table 6 showing a high correlation between the data and fit (). The difference between the models with and without the adhesive thickness is due to the distribution of the Mixed-Mode ratio distribution on the cohesive layer, which is the main factor affecting the computation of the crack growth rate at the same equivalent SERR.
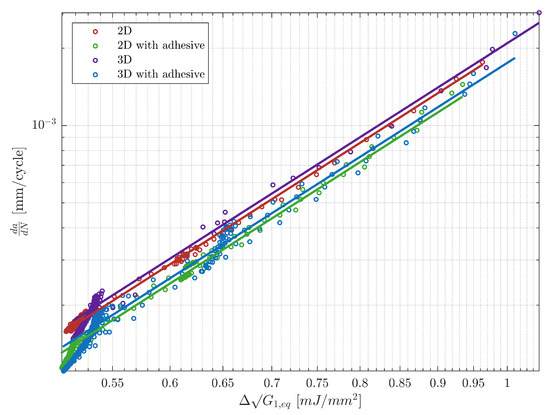
Figure 11.
Crack growth rate as a function of normalised cyclic variation of the strain energy release rate. Results are divided by specimen name and by the different modelling configurations. Solid lines represent the interpolation for each model.

Table 6.
Equivalent Paris’ Law parameters from different model configurations from Figure 11 with .
Additionally, discrepancies between the 2D and 3D are evident in the data dispersion. The interaction in the out-of-plane direction, which is simulated in the 3D case, also influences the Mixed-Mode ratio distribution in the adhesive layer. As discussed in the Mode I loading scenario, the redistribution of stresses and strains within the elements at the cohesive front has an impact on this dispersion which can be minimised with a finer mesh. No experimental data were available to directly compare the crack growth rate against the equivalent cyclic behaviour. Therefore, only the different modelling techniques were compared.
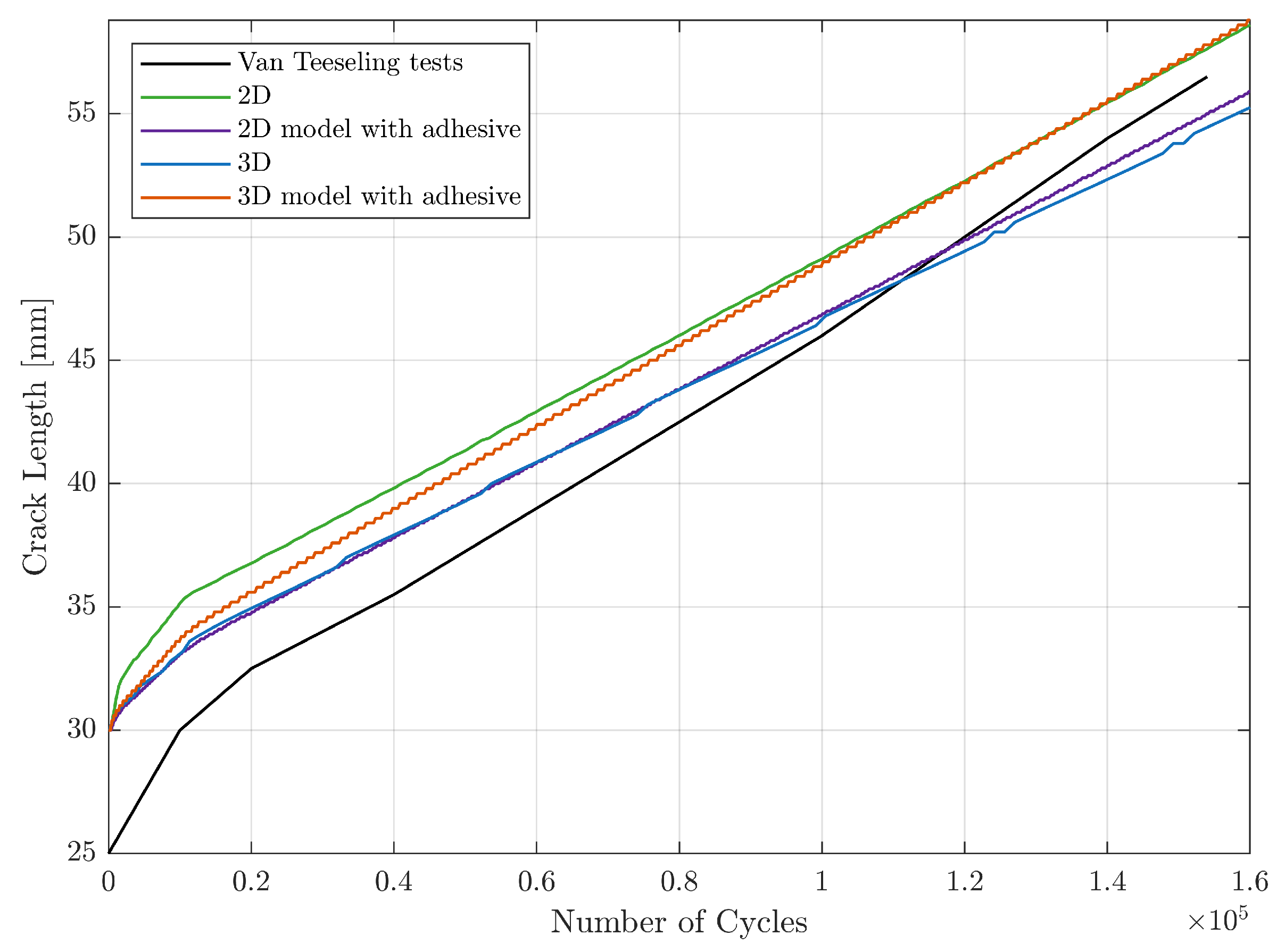
Figure 12 shows the relationship between crack length and the number of fatigue cycles. The relative error of the final crack length between the experimental results and the different modelling techniques after 150,000 cycles is summarised in Table 7. In general, all four modelling techniques showed a good agreement with the experimental results, with a maximum deviation of . The experimental data indicate an initial crack length of 25 mm. The specimen tested by van Teeseling [42] had a 10 mm saw-tooth crack front design to facilitate crack initiation. For the sake of simplicity, all modelled cases were represented with a straight crack front measuring 30 mm.
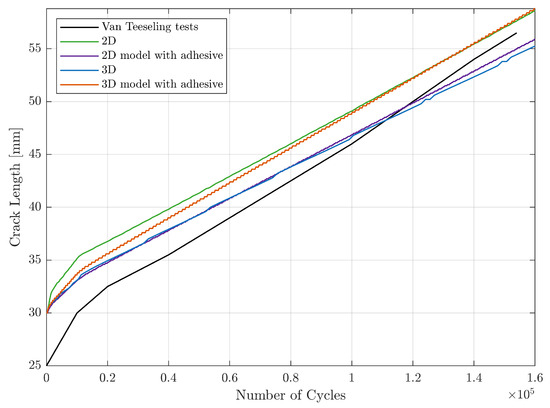
Figure 12.
Crack length as a function of the number of fatigue cycles. Results divided by the different modelling configurations.

Table 7.
Relative error of the final crack length between experimental results and different modelling techniques.
Variation in the slope of the four modelled cases can be attributed to both out-of-plane effects and changes in Mixed-Mode ratio due to the added thickness, as well as the estimation of the cohesive length. Specifically, the M parameter from Equation (16) can be dynamically adjusted and calibrated based on the Mixed-Mode ratio from the cohesive layer. In scenarios where a constant M was selected, the modelling technique that most accurately represents crack growth behaviour was the 2D model, with a deviation, followed by the 3D model, which incorporates the adhesive with a deviation. This approach has been proven to effectively capture the effects of both the out-of-plane direction and the added thickness during fatigue disbonding.
5. Conclusions
This study demonstrated the successful implementation of user-defined subroutines in Abaqus to simulate high cycle fatigue disbonding in adhesively bonded joints under Mode I and Mixed-Mode conditions. Both loading scenarios were validated against experimental data in the literature.
The manuscript explored four different modelling techniques, including both 2D and 3D approaches, with and without consideration of the adhesive thickness. Special emphasis was placed on the models that included the adhesive thickness, as this is the least explored technique in the literature. This approach provides a more realistic representation of load distribution during disbonding.
The results from Mode I simulations indicated that the additional thickness of the adhesive affects how the load is distributed within the cohesive zone. At low crack growth rates, the influence of this load distribution on the crack growth rate is more pronounced in specimens with greater thickness.
Bürger’s model, which is a modified version of Paris’ Law, effectively captured fatigue disbonding. Additionally, this model demonstrated that, under Mixed-Mode loading, the inclusion or exclusion of the adhesive thickness influenced the Mixed-Mode distribution, leading to variations in fatigue crack growth rates.
Although both 2D and 3D models have demonstrated good accuracy, the importance of 3D models lies in the possible insights they provide regarding the out-of-plane direction, particularly in relation to the shape of the crack front and its implications. Conversely, 2D models offer a more time-efficient simulation method, enabling quick iterations during the developing phase whilst still maintaining adequate accuracy compared to experimental data.
The main disadvantages of the cohesive zone model described in this manuscript for fatigue disbonding relates to the high reliance on experimental data. For each test case, the simulation requires the Paris’ Law curve parameters, limiting the possibilities of the user to test different loading conditions. For instance, without experimental data, it is not possible to simulate the effect of different bond thicknesses. Furthermore, crack propagation is constrained to occur at a predefined plane, simulating cohesive failure; however, this does not always reflect the reality, as cracks could deviate or the failure could be an adhesion failure.
The authors recommend extending this study at an element level to further investigate the model’s capabilities, in particular its accuracy with more complex geometries to help certify the use of adhesive bondings on primary aerospace structures.
Author Contributions
J.B.: Conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing—original draft preparation, writing—review and editing; M.P.F.: Methodology, visualization, writing—review and editing; E.T.: Methodology, supervision, project administration, funding acquisition, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
European Union—NextGenerationEU through the Italian Ministry of University and Research under PNRR—Mission 4 Component 1, Investment 4.1 “Extension of the number of PhD programmes and innovative PhD programmes for Public Administration and cultural heritage” and Investment 3.4 “Advanced university education and skills–Support to PhD programmes for digital and environmental transition”. MOST—Sustainable Mobility National Research Center and received funding from the European Union—NextGenerationEU (PIANO NAZIONALE DI RIPRESA E RESILIENZA (PNRR)—MISSIONE 4 COMPONENTE 2, INVESTIMENTO 1.4—D.D. 1033 17/06/2022, CN00000023) CUP: J33C22001120001. This manuscript reflects only the authors’ views and opinions, neither the European Union nor the European Commission can be considered responsible for them.
Data Availability Statement
The data presented in this article are not readily available because they are part of an ongoing study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| B-K criterion | Benzeggagh and Kenane criterion |
| BTSL | Bi-linear Traction–Separation Law |
| CFRP | Carbon Fibre-Reinforced Plastics |
| CLS | Cracked Lap Shear |
| CZM | Cohesive Zone Model |
| Cyclic variation of the strain energy release rate | |
| d | Damage |
| R | Displacement/Load Ratio |
| DCB | Double-Cantilever Beam |
| Displacement jump | |
| EASA | European Union Aviation Safety Agency |
| FAA | Federal Aviation Administration |
| FEA | Finite Element Analysis |
| FEM | Finite Element Method |
| FML | Fibre Metal Laminate |
| Fracture toughness | |
| HCF | High Cycle Fatigue |
| Length of the cohesive zone | |
| Maximum traction | |
| Mixed-Mode ratio | |
| NDI | Non-Destructive Inspection |
| Onset displacement | |
| Propagation displacement | |
| K | Stiffness |
| SERR and G | Strain Energy Release Rate |
| SIF | Stress Intensity Factor |
| XFEM | Extended Finite Element Method |
References
- Xu, J.; Yin, Y.; Paulo Davim, J.; Li, L.; Ji, M.; Geier, N.; Chen, M. A critical review addressing drilling-induced damage of CFRP composites. Compos. Struct. 2022, 294, 115594. [Google Scholar] [CrossRef]
- Crane, R.L.; Hart-Smith, J.; Newman, J. 8—Nondestructive inspection of adhesive bonded joints. In Adhesive Bonding, 2nd ed.; Adams, R.D., Ed.; Woodhead Publishing Series in Welding and Other Joining Technologies; Woodhead Publishing: Duxford, UK, 2021; pp. 215–256. [Google Scholar] [CrossRef]
- Malekinejad, H.; Carbas, R.J.C.; Akhavan-Safar, A.; Marques, E.A.S.; Castro Sousa, F.; da Silva, L.F.M. Enhancing Fatigue Life and Strength of Adhesively Bonded Composite Joints: A Comprehensive Review. Materials 2023, 16, 6468. [Google Scholar] [CrossRef] [PubMed]
- Jasiūnienė, E.; Yilmaz, B.; Smagulova, D.; Bhat, G.A.; Cicėnas, V.; Žukauskas, E.; Mažeika, L. Non-Destructive Evaluation of the Quality of Adhesive Joints Using Ultrasound, X-ray, and Feature-Based Data Fusion. Appl. Sci. 2022, 12, 12930. [Google Scholar] [CrossRef]
- Yılmaz, B.; Jasiūnienė, E. Advanced ultrasonic NDT for weak bond detection in composite-adhesive bonded structures. Int. J. Adhes. Adhes. 2020, 102, 102675. [Google Scholar] [CrossRef]
- Schroeder, J.A.; Ahmed, T.; Chaudhry, B.; Shepard, S. Non-destructive testing of structural composites and adhesively bonded composite joints: Pulsed thermography. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1511–1517. [Google Scholar] [CrossRef]
- Liniecki, A.; Hsu, T.; Li, W. Fatigue Strength of Adhesive Bonded Aluminum Joints. J. Test. Eval. 1995, 23, 453–468. [Google Scholar] [CrossRef]
- Imanaka, M.; Iwata, T. Fatigue Failure Criterion of Adhesively-Bonded Joints Under Combined Stress Conditions. J. Adhes. 1996, 59, 111–126. [Google Scholar] [CrossRef]
- Ishii, K.; Imanaka, M.; Nakayama, H.; Kodama, H. Evaluation of the fatigue strength of adhesively bonded CFRP/metal single and single-step double-lap joints. Compos. Sci. Technol. 1999, 59, 1675–1683. [Google Scholar] [CrossRef]
- Paris, P.; Gomez, M.; Anderson, W. A rational analytic theory of fatigue. Trend Inf. Eng. 1961, 13, 9–14. [Google Scholar]
- Paris, P.; Erdogan, F. A Critical Analysis of Crack Propagation Laws. J. Basic Eng. 1963, 85, 528–533. [Google Scholar] [CrossRef]
- Paris, P.C. The fracture mechanics approach to fatigue. In Fatigue: An Interdisciplinary Approach: Proceedings of the 10th Sagamore Army Materials Research Conference, Sagamore Conference Center, Raquette Lake, NY, USA, 13–16 August 1963; Syracuse University Press: Syracuse, NY, USA, 1964. [Google Scholar]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Duarte, C.A.; Oden, J.T. H-p clouds—An h-p meshless method. Numer. Methods Partial Differ. Equ. 1996, 12, 673–705. [Google Scholar] [CrossRef]
- Moës, N.; Belytschko, T. Extended finite element method for cohesive crack growth. Eng. Fract. Mech. 2002, 69, 813–833. [Google Scholar] [CrossRef]
- Ling, D.; Yang, Q.; Cox, B. An augmented finite element method for modeling arbitrary discontinuities in composite materials. Int. J. Fract. 2009, 156, 53–73. [Google Scholar] [CrossRef]
- Khoramishad, H.; Crocombe, A.D.; Katnam, K.B.; Ashcroft, I.A. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. In Advances in Applied Mechanics; Dryden, H.L., von Kármán, T., Kuerti, G., van den Dungen, F.H., Howarth, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1962; Volume 7, pp. 55–129. [Google Scholar] [CrossRef]
- Dugdale, D.S. Yielding of steel sheets containing slits. J. Mech. Phys. Solids 1960, 8, 100–104. [Google Scholar] [CrossRef]
- Hillerborg, A.; Modéer, M.; Petersson, P.E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Concr. Res. 1976, 6, 773–781. [Google Scholar] [CrossRef]
- Needleman, A. A Continuum Model for Void Nucleation by Inclusion Debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Needleman, A. An analysis of decohesion along an imperfect interface. Int. J. Fract. 1990, 42, 21–40. [Google Scholar] [CrossRef]
- Chandra, N.; Li, H.; Shet, C.; Ghonem, H. Some issues in the application of cohesive zone models for metal–ceramic interfaces. Int. J. Solids Struct. 2002, 39, 2827–2855. [Google Scholar] [CrossRef]
- Robinson, P.; Galvanetto, U.; Tumino, D.; Bellucci, G.; Violeau, D. Numerical simulation of fatigue-driven delamination using interface elements. Int. J. Numer. Methods Eng. 2005, 63, 1824–1848. [Google Scholar] [CrossRef]
- Tumino, D.; Cappello, F. Simulation of Fatigue Delamination Growth in Composites with Different Mode Mixtures. J. Compos. Mater. 2007, 41, 2415–2441. [Google Scholar] [CrossRef]
- Maiti, S.; Geubelle, P.H. A cohesive model for fatigue failure of polymers. Eng. Fract. Mech. 2005, 72, 691–708. [Google Scholar] [CrossRef]
- Nguyen, O.; Repetto, E.; Ortiz, M.; Radovitzky, R. A cohesive model of fatigue crack growth. Int. J. Fract. 2001, 110, 351–369. [Google Scholar] [CrossRef]
- Roe, K.L.; Siegmund, T. An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng. Fract. Mech. 2003, 70, 209–232. [Google Scholar] [CrossRef]
- Siegmund, T. A numerical study of transient fatigue crack growth by use of an irreversible cohesive zone model. Int. J. Fatigue 2004, 26, 929–939. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.P.; Dávila, C.G. Simulation of delamination in composites under high-cycle fatigue. Compos. Part A Appl. Sci. Manuf. 2007, 38, 2270–2282. [Google Scholar] [CrossRef]
- Ural, A.; Krishnan, V.R.; Papoulia, K.D. A cohesive zone model for fatigue crack growth allowing for crack retardation. Int. J. Solids Struct. 2009, 46, 2453–2462. [Google Scholar] [CrossRef]
- Azari, S.; Papini, M.; Spelt, J.K. Effect of adhesive thickness on fatigue and fracture of toughened epoxy joints—Part I: Experiments. Eng. Fract. Mech. 2011, 78, 153–162. [Google Scholar] [CrossRef]
- Azari, S.; Papini, M.; Spelt, J.K. Effect of adhesive thickness on fatigue and fracture of toughened epoxy joints—Part II: Analysis and finite element modeling. Eng. Fract. Mech. 2011, 78, 138–152. [Google Scholar] [CrossRef]
- Kin Loch, A.J.; Shaw, S.J. The Fracture Resistance of a Toughened Epoxy Adhesive. J. Adhes. 1981, 12, 59–77. [Google Scholar] [CrossRef]
- Wang, S.S.; Mandell, J.F.; McGarry, F.J. An analysis of the crack tip stress field in DCB adhesive fracture specimens. Int. J. Fract. 1978, 14, 39–58. [Google Scholar] [CrossRef]
- Chai, H. On the correlation between the mode I failure of adhesive joints and laminated composites. Eng. Fract. Mech. 1986, 24, 413–431. [Google Scholar] [CrossRef]
- Azari, S.; Ameli, A.; Papini, M.; Spelt, J. Analysis and design of adhesively bonded joints for fatigue and fracture loading: A fracture-mechanics approach. J. Adhes. Sci. Technol. 2013, 27, 1681–1711. [Google Scholar] [CrossRef]
- Chiu, W.K.; Jones, R. A numerical study of adhesively bonded lap joints. Int. J. Adhes. Adhes. 1992, 12, 219–225. [Google Scholar] [CrossRef]
- Gleich, D.M.; Van Tooren, M.J.L.; Beukers, A. Analysis and evaluation of bondline thickness effects on failure load in adhesively bonded structures. J. Adhes. Sci. Technol. 2001, 15, 1091–1101. [Google Scholar] [CrossRef]
- Pascoe, J.A.; Zavatta, N.; Troiani, E.; Alderliesten, R.C. The effect of bond-line thickness on fatigue crack growth rate in adhesively bonded joints. Eng. Fract. Mech. 2020, 229, 106959. [Google Scholar] [CrossRef]
- Zavatta, N. Crack Growth in Adhesively Bonded Joints Under Quasi-Static and Fatigue Loading. Ph.D. Thesis, Alma Mater Studiorum-Università di Bologna, Bologna, Italy, 2020. [Google Scholar] [CrossRef]
- van Teeseling, I. Towards the Certification of Bonded Primary Fiber Metal Laminate Structures by Bolted Disbond Arrest Features. Master’s Thesis, TU Delft, Delft, The Netherlands, 2019. [Google Scholar]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical Simulation of Mixed-Mode Progressive Delamination in Composite Materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.P.; Davila, C.G. Simulation of Delamination Propagation in Composites Under High-Cycle Fatigue by Means of Cohesive-Zone Models; Technical Report L-19304; NASA Langley Research Center: Hampton, VA, USA, 2006.
- Pirondi, A.; Moroni, F. A Progressive Damage Model for the Prediction of Fatigue Crack Growth in Bonded Joints. J. Adhes. 2010, 86, 501–521. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. A fatigue degradation law for cohesive interface elements—Development and application to composite materials. Int. J. Fatigue 2010, 32, 1774–1787. [Google Scholar] [CrossRef]
- Kawashita, L.F.; Hallett, S.R. A crack tip tracking algorithm for cohesive interface element analysis of fatigue delamination propagation in composite materials. Int. J. Solids Struct. 2012, 49, 2898–2913. [Google Scholar] [CrossRef]
- Bak, B.L.V.; Turon, A.; Lindgaard, E.; Lund, E. A simulation method for high-cycle fatigue-driven delamination using a cohesive zone model. Int. J. Numer. Methods Eng. 2016, 106, 163–191. [Google Scholar] [CrossRef]
- Carreras, L.; Bak, B.L.V.; Turon, A.; Renart, J.; Lindgaard, E. Point-wise evaluation of the growth driving direction for arbitrarily shaped delamination fronts using cohesive elements. Eur. J. Mech.-A/Solids 2018, 72, 464–482. [Google Scholar] [CrossRef]
- Dávila, C.G.; Joosten, M.W. A cohesive fatigue model for composite delamination based on a new material characterization procedure for the Paris law. Eng. Fract. Mech. 2023, 284, 109232. [Google Scholar] [CrossRef]
- Raimondo, A.; Dávila, C.G.; Bisagni, C. Cohesive analysis of a 3D benchmark for delamination growth under quasi-static and fatigue loading conditions. Fatigue Fract. Eng. Mater. Struct. 2022, 45, 1942–1952. [Google Scholar] [CrossRef]
- Leciñana, I.; Carreras, L.; Renart, J.; Zurbitu, J.; Tijs, B.H.A.H.; Turon, A. A simulation strategy for fatigue modeling of delamination in composite structures under multiple loading conditions considering loading history and R-curve effects. Compos. Part A Appl. Sci. Manuf. 2024, 186, 108402. [Google Scholar] [CrossRef]
- Abdel Wahab, M.M. 11—Simulating mode I fatigue crack propagation in adhesively-bonded composite joints. In Fatigue and Fracture of Adhesively-Bonded Composite Joints; Vassilopoulos, A.P., Ed.; Woodhead Publishing: Duxford, UK, 2015; pp. 323–344. [Google Scholar] [CrossRef]
- Pirondi, A.; Moroni, F. Improvement of a Cohesive Zone Model for Fatigue Delamination Rate Simulation. Materials 2019, 12, 181. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. Cohesive zone length in numerical simulations of composite delamination. Eng. Fract. Mech. 2008, 75, 4774–4792. [Google Scholar] [CrossRef]
- Yang, Q.; Cox, B. Cohesive models for damage evolution in laminated composites. Int. J. Fract. 2005, 133, 107–137. [Google Scholar] [CrossRef]
- Yang, Q.D.; Cox, B.N.; Nalla, R.K.; Ritchie, R.O. Fracture length scales in human cortical bone: The necessity of nonlinear fracture models. Biomaterials 2006, 27, 2095–2113. [Google Scholar] [CrossRef] [PubMed]
- Turon, A.; Dávila, C.G.; Camanho, P.P.; Costa, J. An engineering solution for mesh size effects in the simulation of delamination using cohesive zone models. Eng. Fract. Mech. 2007, 74, 1665–1682. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Degrieck, J. Fatigue degradation modelling of plain woven glass/epoxy composites. Compos. Part A Appl. Sci. Manuf. 2001, 32, 1433–1441. [Google Scholar] [CrossRef]
- Falk, M.L.; Needleman, A.; Rice, J.R. A Critical Evaluation of Cohesive Zone Models of Dynamic Fracture. J. Phys. IV France 2001, 11, Pr5-43–Pr5-50. [Google Scholar] [CrossRef]
- Turon, A.; González, E.V.; Sarrado, C.; Guillamet, G.; Maimí, P. Accurate simulation of delamination under mixed-mode loading using a cohesive model with a mode-dependent penalty stiffness. Compos. Struct. 2018, 184, 506–511. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.P.; Maimí, P. Analytical and Numerical Investigation of the Length of the Cohesive Zone in Delaminated Composite Materials. In Proceedings of the Mechanical Response of Composites; Camanho, P.P., Dávila, C.G., Pinho, S.T., Remmers, J.J.C., Eds.; Computational Methods in Applied Sciences; Springer: Dordrecht, The Netherlands, 2008; pp. 77–97. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Ramkumar, R.L.; Whitcomb, J.D. Characterization of Mode I and Mixed-Mode Delamination Growth in T300/5208 Graphite/Epoxy; NASA Langley Research Center: Hampton, VA, USA, 1985.
- Gustafson, C.G.; Hojo, M. Delamination Fatigue Crack Growth in Unidirectional Graphite/Epoxy Laminates. J. Reinf. Plast. Compos. 1987, 6, 36–52. [Google Scholar] [CrossRef]
- Russell, A.; Street, K. Predicting Interlaminar Fatigue Crack Growth Rates in Compressively Loaded Laminates. In Composite Materials: Fatigue and Fracture, Second Volume; Lagace, P., Ed.; ASTM International: West Conshohocken, PA, USA, 1989; Volume STP1012-EB, pp. 162–178. [Google Scholar] [CrossRef]
- Kenane, M.; Benzeggagh, M.L. Mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites under fatigue loading. Compos. Sci. Technol. 1997, 57, 597–605. [Google Scholar] [CrossRef]
- Allegri, G.; Wisnom, M.R.; Hallett, S.R. A new semi-empirical law for variable stress-ratio and mixed-mode fatigue delamination growth. Compos. Part A Appl. Sci. Manuf. 2013, 48, 192–200. [Google Scholar] [CrossRef]
- Bürger, D.B. Mixed-Mode Fatigue Disbond on Metallic Bonded Joints. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 2015. [Google Scholar]
- Naik, S.H.; Javagal, S. Analytical Study of the Effects of Delamination in Glare Fiber-Metal Laminate using Modified Virtual Crack Closure Technique (MVCCT). Procedia Struct. Integr. 2019, 14, 900–906. [Google Scholar] [CrossRef]
- Lai, Y.H.; Dwayne Rakestraw, M.; Dillard, D.A. The cracked lap shear specimen revisited—A closed form solution. Int. J. Solids Struct. 1996, 33, 1725–1743. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Sato, C. Effect of Bond-Line Thickness on Fatigue Crack Growth of Structural Acrylic Adhesive Joints. Materials 2021, 14, 1723. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).