Radiometric Interferometry for Deep Space Navigation Using Geostationary Satellites

Abstract

Deep space navigation, defined as spacecraft position tracking beyond the lunar orbit, presents significant challenges due to the extremely weak Global Navigation Satellite System (GNSS) signals and severe signal attenuation over interplanetary distances. Traditional terrestrial systems, such as NASA’s Deep Space Network (DSN) and ESA’s ESTRACK, rely on Very Long Baseline Interferometry (VLBI) for angular positioning. However, these systems are limited by relatively short baselines, atmospheric distortions requiring extensive calibration, and reduced line-of-sight (LOS) availability due to Earth’s rotation. Because VLBI angle measurements require at least two simultaneously visible stations, the measurement duty cycle is inherently constrained. This research proposes a complementary deep space navigation approach using space-based interferometry, in which radio signals from the spacecraft are received and cross-correlated onboard Geostationary Earth Orbit (GEO) satellites. By replacing terrestrial VLBI stations with dual GEO platforms, the method significantly extends the effective baseline, removes atmospheric phase errors, and provides near-continuous visibility to deep space targets. Unlike Earth-based systems, GEO-based interferometry maintains persistent mutual visibility between stations, enabling higher measurement availability and more flexible mission support. A complete system model is presented, including the principles of dual-frequency phase-based angular tracking and a structured error budget analysis. Theoretical error analysis indicates that the GEO-based system achieves a total angular error better than 4 nanoradians—within the same order of magnitude as terrestrial VLBI. In particular, the space-based architecture nearly doubles the geometric availability for interferometric tracking while eliminating the need for atmospheric calibration. These results support the feasibility of the GEO-based VLBI concept and motivate continued research, including detailed simulations, hardware implementation, and field validation.

1. Introduction

Deep space navigation presents significant challenges, particularly for small spacecraft with limited transmission power and onboard resources [1,2]. Traditional Global Navigation Satellite Systems (GNSSs), widely used for orbit determination (OD) of Earth-orbiting satellites in LEO, MEO, and GEO regimes, and even in specific lunar missions, can still be detected beyond GEO with high-sensitivity receivers. However, their severely attenuated signal power and weak geometric coverage make them unsuitable for deep space navigation [3]. The primary limitation is the substantial free-space path loss, which scales with distance as $1/R^2$; for example, an electromagnetic signal propagating over 1 million km suffers roughly 190 dB of power loss. In addition, unfavorable triangulation geometry results in narrow vertex angles and high Geometric Dilution of Precision (GDOP), further reducing the achievable accuracy of GNSS-based solutions at interplanetary distances.

As a result, alternative navigation methods are required. Optical navigation [4] and radiometric interferometry, which utilize phase measurements of electromagnetic waves [5,6], are commonly used techniques for deep space orbit determination [7]. The most established radiometric approach is NASA’s Deep Space Network (DSN) [8] and its European counterpart, ESA’s ESTRACK [9], both of which rely on Very Long Baseline Interferometry (VLBI) performed by ground-based stations. The DSN, in particular, consists of globally distributed antenna arrays with dish diameters up to 70 m, designed to support deep space communications and navigation [10]. While these terrestrial systems have demonstrated exceptional accuracy, they are fundamentally constrained by their ground-based nature.

The primary limitations of DSN and ESTRACK in deep space navigation include the following:

• Short baselines in deep space scenarios: Although VLBI accuracy improves with increasing baseline length, the maximum baseline achievable by ground-based stations is limited to Earth’s diameter (∼12,700 km). The baseline of terrestrial systems is typically ∼8000 km. This constraint limits the angular resolution for deep space targets.
• Atmospheric distortions: Ionospheric and tropospheric effects introduce phase errors that require extensive calibration, increasing the complexity of measurement processing and potentially degrading final accuracy.
• Limited simultaneous station visibility: VLBI requires that at least two stations have concurrent line-of-sight to the target spacecraft. Due to Earth’s curvature and rotation, this condition is satisfied only about 50% of the time during a diurnal cycle. As a result, observation windows are inherently limited and fragmented, which reduces the overall availability of angular measurement opportunities for navigation.
• High demand and limited access: DSN and ESTRACK assets are heavily utilized for mission-critical operations across multiple agencies. As a result, obtaining sufficient observation time on these networks is increasingly difficult, posing a significant barrier to navigation support for additional missions.

To overcome these constraints, this research proposes an alternative deep space navigation approach based on space-based radio interferometry. Specifically, this method replaces terrestrial VLBI stations with phase sensors onboard Geostationary Earth Orbit (GEO) satellites. This configuration offers several key advantages:

• Extended baselines: The separation between GEO satellites can exceed 80,000 km—an order of magnitude greater than the terrestrial systems limited by Earth’s diameter—creating substantial potential for improving angular measurement precision.
• Elimination of atmospheric distortions: Since GEO-based interferometry operates in space, it avoids ionospheric and tropospheric distortions, eliminating the need for complex atmospheric calibration.
• Higher system availability: Unlike ground stations, GEO satellites maintain near-continuous line-of-sight (LOS) to deep space targets, mitigating Earth-based LOS constraints and ensuring more frequent angular measurements.
• Independent space-based navigation infrastructure: By reducing reliance on Earth-based VLBI networks, this method enables a more autonomous and scalable deep space navigation system.

A small number of space VLBI efforts demonstrate that off-Earth baselines are feasible, but none match the GEO-to-GEO navigation-focused geometry considered here. Early demonstrations used a space-to-ground baseline with NASA’s TDRSS to test VLBI techniques [11]; likewise, the Japanese HALCA/VSOP mission flew in a highly elliptical orbit and correlated with ground stations for radio astronomy imaging [12], and Spektr R/RadioAstron (and the planned Spektr M/Millimetron targeted astronomy with space-to-ground baselines [13]. Recently, the SunRISE mission has enabled the formation of a low-frequency interferometric array near GEO to study solar radio bursts and CMEs at about 0.1 to 25 MHz, roughly three orders of magnitude below the X/Ka-band spacecraft tones considered here, and it is not aimed at navigation [14]. In all these cases, the primary objective is radio astronomy rather than navigation; at least one element of the baseline is ground-based (SunRISE is an exception, but operates at very low frequencies), and the operating frequencies and signal structures differ substantially from the narrowband spacecraft downlinks considered here. To the best of the authors’ knowledge, a fully space-based, dual GEO VLBI configuration that cross-correlates spacecraft signals specifically for deep space navigation has not been implemented or reported.

The remainder of this paper is structured as follows: the next section outlines the fundamental principles of terrestrial VLBI and its limitations for deep space navigation. Section 3 introduces the proposed space-based VLBI system, detailing its measurement methodology, system architecture, and key design considerations. Section 4 discusses the individual and aggregated error contributions and the resulting expected performance. Section 5 presents preliminary simulation results, demonstrating the feasibility of GEO-based phase sensors, with analysis of system availability improvements and phase noise characteristics. Finally, Section 6 summarizes the findings and discusses future research directions.

2. Fundamentals of VLBI for Deep Space Navigation

Very Long Baseline Interferometry (VLBI) is a well-established technique originally developed in the latter half of the 20th century for applications in radio astronomy and geodesy [15], which was later extended to satellite orbit determination. Traditional and more recent applications of VLBI in satellite tracking are well documented; for instance, see [16].

In the context of deep space navigation, VLBI is employed to determine the angular position of a distant spacecraft relative to a known terrestrial baseline [17]. This section outlines the fundamental principles and derivations used in terrestrial VLBI systems to extract such angular information. Since the proposed space-based method builds upon the same core principles, this section provides a technical foundation for comparison with the RINGS concept introduced later in Section 3. The contrast serves to highlight the advantages and novel capabilities of the GEO-based interferometric approach.

2.1. Angle Measurement by VLBI

VLBI relies on two widely separated high-gain receiving antennas that capture and record the spacecraft’s signal within a specific frequency band. These signals are subsequently processed using a software correlator to extract the Differential One-Way Ranging (DOR) data between the antennas, enabling precise determination of the spacecraft’s direction. The principles of VLBI-based direction finding have been thoroughly discussed in [5,17].

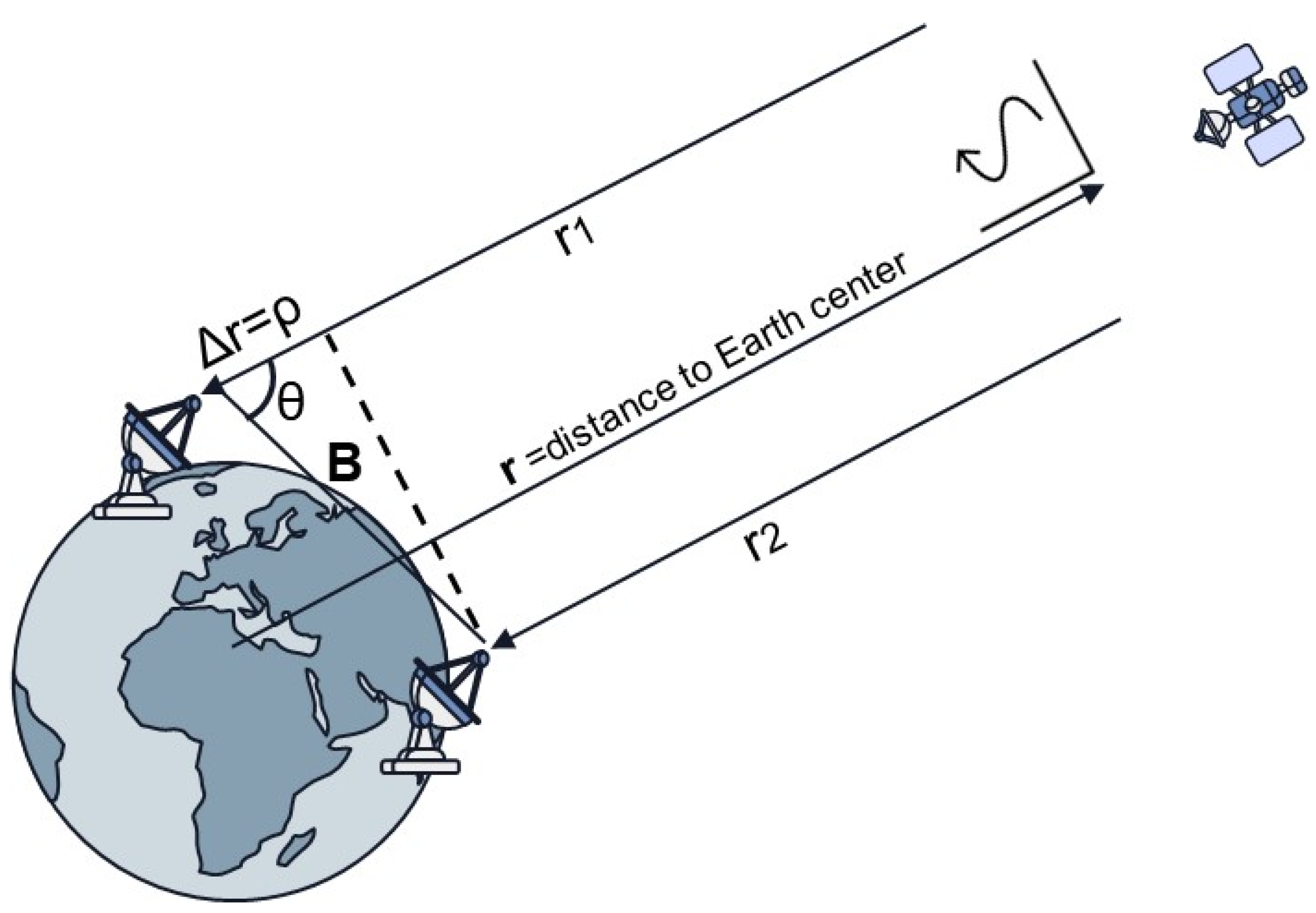
As illustrated in Figure 1, DOR measurements are taken simultaneously by two Earth-based stations at precisely known locations. The spacecraft’s direction of arrival (DOA) relative to the baseline is denoted by $\theta$ and is given by

$$\Delta r=c\Delta t=Bcos\theta$$

(1)

$$cos\theta ={\displaystyle \frac{c\Delta t}{B}}$$

(2)

$$\theta =arccos{\displaystyle \frac{c\Delta t}{B}}$$

(3)

where B is the baseline vector connecting the two receivers, $\Delta r$ is the measured range difference in the direction of the spacecraft, $\Delta t$ is the measured time difference, and c is the speed of light.

Measurement Sensitivity

The sensitivity of the estimated $\theta$ to time difference errors is derived by differentiating Equation (2) with respect to $\Delta t$ [17]:

$${\displaystyle \frac{d\theta }{d\Delta t}}=-{\displaystyle \frac{c}{Bsin\theta }}.$$

(4)

For small angles, $sin\theta$ can be approximated using the first-order terms of its Taylor expansion, $sin\theta \approx \theta -{\theta }^3/6$, leading to

$${\displaystyle \frac{d\theta }{d\Delta t}}=-{\displaystyle \frac{c}{B}}{\displaystyle \frac{1}{\theta \left(1-\frac{{\theta }^2}{6}\right)}}.$$

(5)

This expression shows that the sensitivity of $\theta$ to errors in $\Delta t$ is inversely proportional to the baseline length B and the angle $\theta$. Since $\theta$ is bounded within $[0,\pi ]$ and the singularity at $\theta =0$ is generally avoided in practice, the dominant factor in reducing sensitivity to errors is an increase in B.

2.2. Electromagnetic Phase Measurement in VLBI

The fundamental observable in a VLBI system is the phase of the electromagnetic wave received at each ground-station antenna. Under the far-field approximation, the incoming wavefront can be represented as a planar electromagnetic wave, expressed as

$$E_i(t,r)=E_0{e}^{j(\overrightarrow{k}·\overrightarrow{r}-\omega t)},$$

(6)

where the following applies:

• $E_0$ is the amplitude of the electric field.
• $\overrightarrow{k}$ is the wave vector, with a magnitude of $2\pi /\lambda$.
• $\overrightarrow{r}$ is the propagation distance.
• $\omega =2\pi f_c$ is the angular frequency of the wave.
• t is the time coordinate.

The phase term, which carries the interferometric measurement information, is given by

$${\varphi }_i=\overrightarrow{k}·\overrightarrow{r_i}-\omega t+{\varphi }_0.$$

(7)

By computing the phase difference between two receivers (Station 1 and Station 2), one obtains

$$\Delta \varphi ={\displaystyle \frac{2\pi }{\lambda }}{r}_1-{\displaystyle \frac{2\pi }{\lambda }}{r}_2=\Delta r{\displaystyle \frac{2\pi }{\lambda }}.$$

(8)

Substituting the geometrical relation between the differential distance and the baseline projection gives

$$\Delta \varphi ={\displaystyle \frac{2\pi }{\lambda }}Bcos\theta ,$$

(9)

and solving for the source angle yields

$$cos\theta ={\displaystyle \frac{\Delta \varphi \lambda }{2\pi B}}={\displaystyle \frac{c}{B}}{\displaystyle \frac{\Delta \varphi }{2\pi f}}.$$

(10)

It should be emphasized that Equation (6) relies on the far-field approximation, which simplifies the incident wavefront to a plane wave. This assumption is convenient and widely adopted in interferometric analyses; however, it is not strictly valid for the extremely long baselines encountered in deep space VLBI. The Fraunhofer distance generally defines the transition from near field to far field:

$$R_{FF}={\displaystyle \frac{2B^2}{\lambda }},$$

(11)

where B is the interferometric baseline, and $\lambda$ is the wavelength.

For baselines of the order of tens of thousands of kilometers, $R_{FF}$ becomes astronomically large. As an illustrative example, consider a GEO–GEO baseline of $B=8\times {10}^7$ m with a Ka-band carrier at $\lambda =0.01$ m. Substituting into Equation (11) yields

$$R_{FF}\approx {\displaystyle \frac{2{(8\times {10}^7)}^2}{0.01}}\approx 1.3\times {10}^{18}\mathrm{m},$$

(12)

which is more than six orders of magnitude larger than 1 AU (∼1.5 ×${10}^{11}$ m). Thus, even spacecraft located anywhere within the inner solar system do not satisfy the formal far-field condition relative to such baselines.

In practice, the planar wave assumption is retained for analytical tractability and system modeling. Nevertheless, a rigorous formulation of the VLBI measurement process must account for near-field effects, where the curvature of the spherical wavefront and associated corrections become significant. Such corrections directly impact the accuracy of angle-of-arrival estimation. In operational systems, these limitations are typically mitigated through proper calibration procedures, most notably by referencing extragalactic quasars. Quasar phase measurements serve as highly stable calibration references, enabling the correction of systematic errors and compensation for deviations from the idealized far-field assumption [18]. This approach is particularly relevant to the proposed RINGS system, which uses GEO-based baselines at Ka-band frequencies for deep space navigation (see Section 3).

2.3. Ambiguity Resolution in VLBI Phase Measurements

One of the major challenges in phase-based interferometry is phase ambiguity, which arises because phase measurements are inherently modulo $2\pi$. The measured phase difference $\Delta \varphi$ alone does not provide the integer number of full wavelengths between receivers.

To resolve this ambiguity, multiple site locations, multiple frequencies, or a combination of both can be used [5,6]. The dual-frequency approach provides an effective solution by computing the group delay:

$$\Delta \Delta \varphi =Bcos\theta \left({\displaystyle \frac{2\pi }{{\lambda }_1}}-{\displaystyle \frac{2\pi }{{\lambda }_2}}\right)=2\pi {\displaystyle \frac{B}{c}}cos\theta (f_1-f_2).$$

(13)

Rearranging, we have

$$cos\theta ={\displaystyle \frac{c}{B}}{\displaystyle \frac{\Delta \Delta \varphi }{2\pi \Delta f_c}}.$$

(14)

For a dual-frequency system, the final ambiguity-free angular measurement is

$$\theta =arccos\left({\displaystyle \frac{c}{B}}{\displaystyle \frac{\Delta \Delta \varphi }{2\pi \Delta f_c}}\right).$$

(15)

This technique dramatically reduces ambiguity effects, shifting the uncertainty from the scale of the carrier wavelength $\lambda$ to the much larger synthetic wavelength $c/\Delta f_c$; this enables robust and precise deep space angle measurements.

2.4. Doppler Effect Analysis in Terrestrial VLBI

In VLBI systems, the Doppler effect introduces a frequency shift in the received signal due to the relative motion between the spacecraft and each receiving station. For Earth-based systems, this relative motion is primarily governed by Earth’s rotation, which imparts differing velocities to spatially separated antennas.

The received frequency $f_d$, including special relativity effects, is given by

$$f_d=f_0{\displaystyle \frac{\sqrt{1-v^2/c^2}}{1-v_r\left(t\right)/c}}$$

(16)

where $f_d$ and $f_0$ are the received and transmitted frequencies, respectively; v is the station’s total velocity in an inertial frame; $v_r\left(t\right)$ is the radial component of the velocity vector, defined as the projection of the station’s velocity along the line-of-sight to the spacecraft; and c is the speed of light.

Since $v^2/c^2\ll 1$ for both spacecraft and stations (typically of the order of ${10}^{-10}$), relativistic corrections can be neglected, yielding the classic Doppler shift:

$$f_d=f_0\left(1+{\displaystyle \frac{v_r\left(t\right)}{c}}\right)$$

(17)

The corresponding frequency offset, defined by $f_d-f_0$, is

$$\Delta f_d=f_0{\displaystyle \frac{v_r\left(t\right)}{c}}={\displaystyle \frac{v_r\left(t\right)}{{\lambda }_0}}$$

(18)

Since VLBI measures signal phase, the Doppler effect modifies the effective wavelength at each station:

$${\lambda }_d={\displaystyle \frac{c}{f_d}}={\displaystyle \frac{c}{f_i\left(1+\frac{v_{r_j}}{c}\right)}},$$

(19)

where $f_i$ denotes the signal carrier frequency, and $j=1,2$ indexes the receiving stations. The received phase at station j is given by

$${\varphi }_{f_{i,j}}={\displaystyle \frac{2\pi f_i}{c}}\left(1+{\displaystyle \frac{v_{r_j}}{c}}\right)r_j,$$

(20)

with $r_j$ being the distance from station j to the spacecraft and $v_{r_j}$ its radial velocity component.

The phase difference between the two stations at frequency $f_1$ is

$$\Delta {\varphi }_{f_1}={\displaystyle \frac{2\pi f_1}{c}}\left[\left(1+{\displaystyle \frac{v_{r_1}}{c}}\right)r_1-\left(1+{\displaystyle \frac{v_{r_2}}{c}}\right)r_2\right],$$

(21)

and similarly, for $f_2$,

$$\Delta {\varphi }_{f_2}={\displaystyle \frac{2\pi f_2}{c}}\left[\left(1+{\displaystyle \frac{v_{r_1}}{c}}\right)r_1-\left(1+{\displaystyle \frac{v_{r_2}}{c}}\right)r_2\right].$$

(22)

Subtracting these gives the dual-frequency phase difference:

$$\Delta \Delta \varphi =\Delta {\varphi }_{f_1}-\Delta {\varphi }_{f_2}={\displaystyle \frac{2\pi }{c}}\Delta f_c\left[\left(1+{\displaystyle \frac{v_{r_1}}{c}}\right)r_1-\left(1+{\displaystyle \frac{v_{r_2}}{c}}\right)r_2\right],$$

(23)

where $\Delta f_c=f_1-f_2$ is the frequency separation.

We define the baseline projection as $r_1-r_2=Bcos\theta$, where B is the baseline length and $\theta$ is the angle between the baseline vector and the line-of-sight to the source, as illustrated in Figure 1. When involving the products $r_1{v}_{r_1}$ and $r_2{v}_{r_2}$, we can assume that $r_1\approx r_2\approx r$, maintaining $r_1+r_2=2r$; therefore, the expression simplifies to

$$\begin{array}{cc}\hfill \Delta \Delta \varphi & ={\displaystyle \frac{2\pi \Delta f_c}{c}}\left[Bcos\theta +{\displaystyle \frac{r}{c}}\left(v_{r_1}-v_{r_2}\right)\right]\hfill \end{array}$$

(24)

We now define the vectorial radial velocity difference as

$$\Delta V_r\triangleq V_{r_1}·\widehat{s}-V_{r_2}·\widehat{s}=v_{r_1}-v_{r_2},$$

(25)

where $\widehat{s}$ is the unit vector pointing from the observer toward the spacecraft, and $V_{r_j}$ are the velocity vectors of the stations. Then,

$$\Delta \Delta \varphi ={\displaystyle \frac{2\pi \Delta f_c}{c}}\left[Bcos\theta +{\displaystyle \frac{r}{c}}\Delta V_r\right]$$

(26)

This general expression shows that the differential phase $\Delta \Delta \varphi$ includes two additive components:

• An undistorted geometric term, identical to the basic Equation (13) and proportional to $Bcos\theta$, which captures the baseline projection along the source direction.
• A Doppler-induced correction term proportional to $r\Delta V_r/c$, which reflects the differential motion of the receiving stations along the line-of-sight.

While Doppler contributions may not be the dominant term in interferometric phase measurements, they are non-negligible and must be explicitly modeled to ensure accurate data interpretation. In terrestrial VLBI systems, the differential Doppler effect is typically smaller, primarily due to the modest tangential velocities introduced by Earth’s rotation. Nevertheless, for high-precision angular estimation, even these small Doppler components must be corrected to avoid systematic bias.

In space-based VLBI configurations—such as those involving GEO satellites or other high-velocity platforms—the differential radial velocity, denoted $\Delta V_r$, between observing stations can become a significant contributor to the measured phase. The proper modeling of this effect is essential to achieve measurement accuracy.

This general Doppler formulation will be later applied to the specific case of a symmetric GEO-based VLBI geometry.

3. Proposed System: Radiometric Interferometry Navigation Using GEO Satellites (“RINGS”)

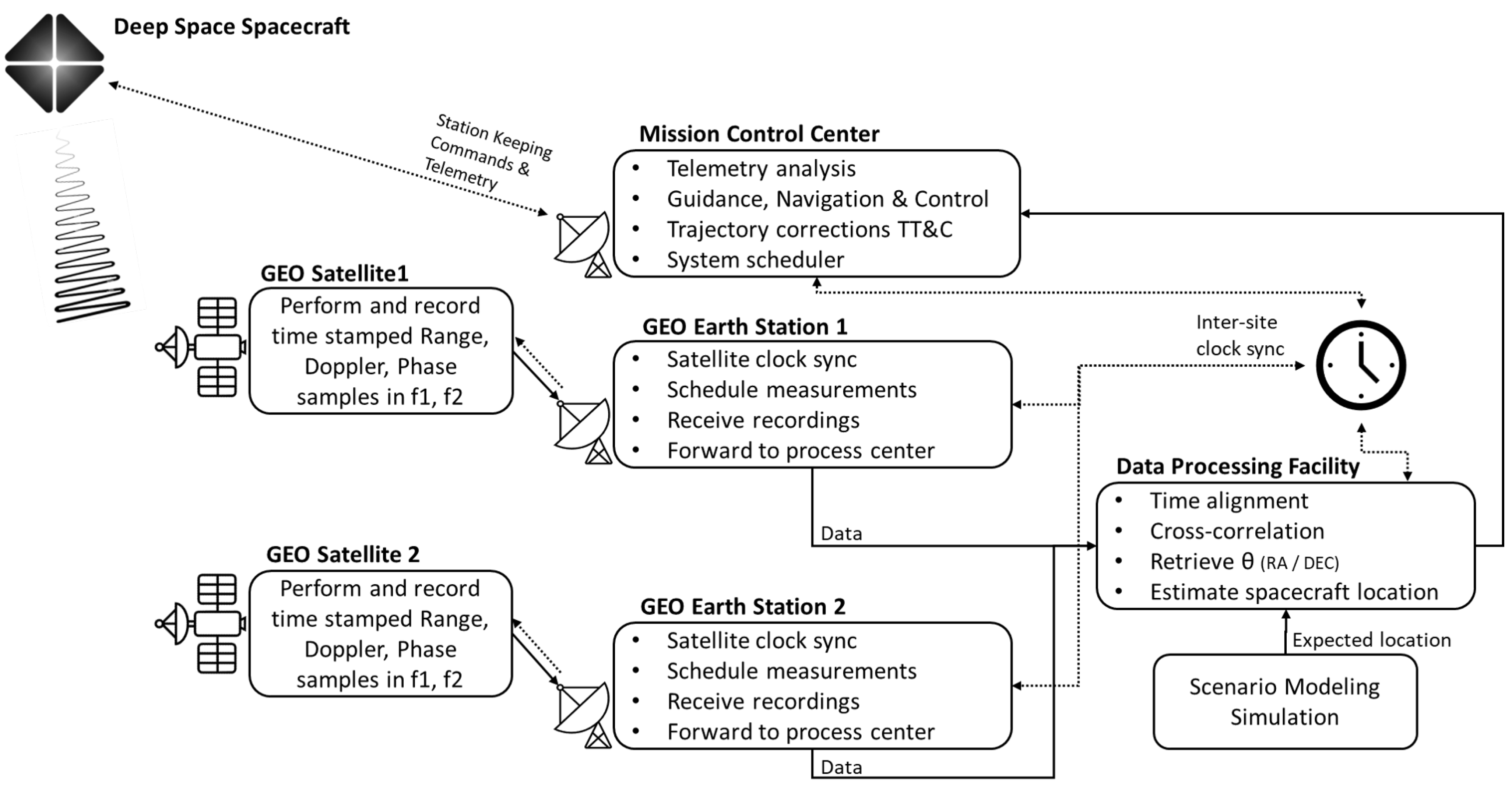
This section outlines the proposed method, including the system architecture, principles of operation, and data-processing approach used to obtain angular measurements of a spacecraft’s position in space. We introduce a new VLBI configuration that replaces terrestrial baselines with a dual-geostationary (GEO) satellite setup. The two satellites, positioned at widely separated longitudes, form a space-based interferometric baseline significantly longer than any feasible ground-based system, as illustrated in Figure 2. A high-level functional overview of the system’s components and data flow is shown in Figure 3.

During a typical measurement session (lasting approximately 2 to 5 min), the target spacecraft’s radio signal is simultaneously received by both GEO satellites. Each satellite time-stamps the signal with high precision and stores it onboard. These recorded observations are subsequently downloaded through GEO-compatible ground stations and forwarded to a central processing facility. There, the signals are time-aligned and cross-correlated to extract phase differences, which are used for precise angular localization. The resulting navigation solution is delivered to the Mission Control Center to support real-time Guidance and Control (G&C) operations, such as orbit correction commands.

3.1. Advantages of the RINGS Architecture

The RINGS concept offers several key advantages over terrestrial VLBI systems:

• Extended baselines: GEO satellite separations can exceed 80,000 km, approximately 10 times the maximum baselines achievable on Earth. This increased baseline length allows for significantly improved angular resolution in interferometric measurements.
• Elimination of atmospheric distortions: Because the system operates entirely in space, it is unaffected by ionospheric and tropospheric phase delays. This eliminates the need for complex atmospheric correction models, which are essential in ground-based VLBI systems.
• Higher system availability: GEO satellites maintain nearly continuous line-of-sight to deep space targets, unlike terrestrial antennas that are limited by Earth’s rotation and horizon. This allows for more frequent angular measurements. Furthermore, ground-based VLBI systems require periodic calibration using quasars, which forces them to alternate between tracking the spacecraft and the calibration source. As a result, only about half of the time is effectively used for actual navigation measurements, making the GEO-based approach significantly more efficient.
• Improved performance in low SEP configurations: For missions directed toward the Sun from Earth’s perspective, such as solar probes or inner solar system missions, the use of GEO satellites increases the effective Sun–Earth–Probe (SEP) angle. The higher SEP angle improves angular discrimination between the spacecraft and the Sun, thereby reducing the thermal solar background and enhancing the SNR in these challenging observation scenarios.
• Independent space-based navigation infrastructure: By minimizing reliance on ground-based VLBI networks, the proposed system enables a more autonomous, scalable architecture for deep space navigation.

3.2. Challenges and Limitations

Despite its advantages, the RINGS approach introduces several technical and research-related challenges:

• Orbital position uncertainty: Inaccuracies in the known position of GEO satellites relative to Earth-fixed reference points introduce angular measurement errors.
• Reduced antenna gain: GEO satellite antennas typically have smaller apertures than terrestrial VLBI dishes, resulting in lower signal-to-noise ratio (SNR) at the receiver.
• Limited time-based synchronization: Precise cross-correlation requires high-accuracy clock alignment between satellites, which is difficult to achieve without robust inter-satellite timing solutions.
• Phase ambiguity scaling: Phase ambiguity increases with baseline length, making cycle resolution and phase unwrapping more challenging in space-based configurations.
• Lack of space-based VLBI datasets: Unlike terrestrial VLBI systems, which benefit from decades of accumulated phase measurement data, there is currently no accessible database of phase observations collected from space-based platforms. This presents a significant research limitation, as it restricts the ability to analyze real-world stochastic characteristics, verify phase stability, and refine processing algorithms. Future deployment of experimental space-based assets could help address this gap and enable empirical validation of the proposed method.
• Data acquisition and transfer constraints: Digitizing and transferring wideband 32 GHz signals from GEO requires high-rate sampling and significant data throughput. Even moderate bandwidths can generate multi-gigabit data rates, comparable to those in RadioAstron. As in terrestrial VLBI (e.g., DSN and ESTRACK), RINGS phase data are not transmitted in real time but are recorded onboard and later downlinked to the GEO ground segment for correlation. Given the slow dynamics of deep space targets, several hours are available for processing, which relaxes telemetry demands but still calls for efficient onboard compression and high-capacity optical or Ka-band links.

In the following sections, we address these constraints and systematically assess the feasibility of space-based VLBI for deep space navigation. The next section focuses on the primary contributors to interferometric error in the proposed system, including signal-to-noise ratio, Doppler-induced phase biases, time synchronization errors, orbital position uncertainty, and the total system-level error budget.

4. Performance Analysis Discussion

This section applies the structured error estimation methodology developed and used by NASA and ESA [19,20] for terrestrial VLBI and Delta-DOR systems to the proposed GEO-based VLBI concept. Following the methodology introduced and elaborated by various authors [5,6,17,19,21], we adopt the same framework to evaluate the dominant error sources contributing to the total phase and angular uncertainty in the RINGS system.

This approach ensures consistency with established ground-based VLBI error budgets, facilitating direct comparison between terrestrial and space-based configurations. The analysis identifies the critical factors limiting system performance and highlights areas where the space-based VLBI architecture offers inherent advantages. Key contributors to error include signal-to-noise ratio limitations, Doppler-induced phase shifts, clock synchronization uncertainty, and orbit determination errors for GEO satellites. Each component is examined to derive a comprehensive error budget that supports system-level performance predictions.

4.1. Evaluation of Signal-to-Noise Ratio (SNR)

A primary contributor to the error budget in the satellite-based VLBI configuration is the relatively low received signal power from deep space spacecraft. This, combined with systematic noise sources, results in a modest signal-to-noise ratio (SNR), which directly impacts the accuracy of phase extraction in the interferometric process.

The total system noise arises primarily from two independent sources:

1.

Thermal noise: This is determined using the receiver’s ambient noise temperature and the cosmic background radiation incident on the antenna aperture.

2.

Phase noise: This originates from imperfections in the onboard oscillators and stochastic propagation effects such as scintillation and plasma-induced variations.

In this section, we quantify the contribution of each noise source and compute the resulting effective system noise. We then derive the received signal power based on standard link budget formulations. Finally, the SNR is obtained by comparing the received signal power to the combined noise power, establishing a baseline for subsequent phase error and angular uncertainty analysis.

4.1.1. Thermal Noise Power

The total system noise temperature is given by the sum of the receiver’s ambient noise and the cosmic background noise received by the antenna aperture. Unlike terrestrial VLBI systems, there is no atmospheric absorption that attenuates the incoming signal, nor is there atmospheric emission that increases the system temperature, as is commonly accounted for in ground-based models [18]. Contributions from planetary bodies and the Sun’s blackbody radiation are neglected due to their relatively small angular coverage compared to the antenna’s field of view. Therefore,

$$T_{op}=T_{amb}+T_{sky}$$

(27)

where $T_{amb}\approx 290\mathrm{K}$ is the receiver’s ambient noise temperature, and $T_{sky}=2.7\mathrm{K}$ represents the cosmic microwave background observed by the antenna aperture. Thus,

$$T_{op}\approx 290+2.7=292.7\mathrm{K}$$

(28)

The thermal noise power at the receiver input is given by the Johnson–Nyquist equation [22]:

$$N_{\mathrm{T}}=k_B{T}_{op}BW$$

(29)

where $k_B=1.38\times {10}^{-23}\mathrm{J}/\mathrm{K}$ is Boltzmann’s constant, and $BW$ is the receiver bandwidth—a variable system parameter, temporarily set to $1\mathrm{kHz}$. Substituting the values yields

$$N_{\mathrm{T}}=(1.38\times {10}^{-23})\times \left(292.7\right)\times \left({10}^3\right)\approx 4.04\times {10}^{-18}\mathrm{W}(-174\mathrm{dBW})$$

(30)

4.1.2. Phase Noise Contribution

Phase noise arises from two primary sources:

• Internal phase noise: Generated by oscillator instabilities in both the transmitter and receiver. Since the same transmitted signal is received at both GEO satellites, any static or slowly varying transmitter phase noise is effectively canceled in the differential measurement. However, rapid fluctuations or time-dependent variations may still introduce residual errors.
• External phase noise: Introduced by the propagation medium, primarily due to interplanetary plasma fluctuations, scintillations, and other stochastic effects along the wavefront. These effects are not common to both receivers and, thus, contribute directly to phase measurement uncertainty.

For the purpose of a preliminary noise budget, we adopted a conservative upper bound for the total phase noise variance. This serves as a rough order-of-magnitude estimate and will later be refined based on the actual signal-to-noise ratio (SNR) and expected dispersion conditions. In practice, phase noise variance should be derived from oscillator stability specifications and propagation models or inferred from historical data.

Therefore, we assume that accumulated phase uncertainty follows a zero-mean Gaussian distribution with variance [18]:

$${\sigma }_{\varphi }^2\approx {10}^{-2}{\mathrm{rad}}^2.$$

(31)

4.1.3. Effective Noise Power Including Phase Noise

When both thermal noise and phase noise are significant, the total effective noise power is given by the sum of the thermal and phase noise powers in quadrature, as the two components are statistically independent and uncorrelated:

$$N_{\mathrm{RF}}=\sqrt{N_{\mathrm{T}}^2+N_{\mathrm{PH}}^2}.$$

(32)

where $N_{\mathrm{T}}$ denotes the thermal noise power and $N_{\mathrm{PH}}$ represents the equivalent phase noise contribution, expressed in power units as

$$N_{\mathrm{PH}}=2S{\sigma }_{\varphi }^2,$$

(33)

where S is the received signal power, and ${\sigma }_{\varphi }^2$ is the phase variance (in ${\mathrm{radians}}^2$). This relation follows from the high-SNR approximation ${\sigma }_{\varphi }^2\approx 1/\left(2\mathrm{SNR}\right)$, which allows phase fluctuations to be represented as an equivalent power degradation term.

Therefore, the effective SNR for a single interferometric phase sample is given by

$${\mathrm{SNR}}_{\mathrm{eff}}={\displaystyle \frac{S}{\sqrt{N_{\mathrm{T}}^2+N_{\mathrm{PH}}^2}}}.$$

(34)

For low phase noise variance (${\sigma }_{\varphi }^2\ll 1$), the impact of phase noise on the overall SNR is typically minor. However, if phase noise increases beyond a certain threshold, it may significantly degrade the system’s ability to extract accurate phase measurements.

Since the phase noise contribution is usually small compared to the thermal noise power in deep space scenarios, the expression can be approximated as

$${\mathrm{SNR}}_{\mathrm{eff}}\approx {\displaystyle \frac{S}{N_{\mathrm{T}}}}.$$

(35)

4.1.4. SNR and Link Budget Calculation

The received signal power S is computed using the Friis transmission equation [23]:

$$S={\displaystyle \frac{P_t{G}_t{G}_r{\lambda }^2}{{\left(4\pi R\right)}^2}}$$

(36)

where the following applies:

• $P_t=20$ W is the spacecraft transmission power.
• $G_t$ is the transmit antenna gain, given by

  $$G_t={\displaystyle \frac{4\pi A}{{\lambda }^2}},A=\pi {\left({\displaystyle \frac{D}{2}}\right)}^2.$$

  (37)
  For a spacecraft parabolic antenna of approximately 0.8 to 1 m in diameter, this results in

  $$G_t\approx 47\mathrm{dBi}.$$

  (38)
• $G_r$ is the receive antenna gain, assuming a 5-m parabolic dish onboard each GEO satellite:

  $$G_r\approx 60-64\mathrm{dBi}.$$

  (39)
• $R=1.0\times {10}^{11}$ m (0.7 AU).
• $\lambda ={\displaystyle \frac{c}{f}}=9.4\times {10}^{-3}$ m (Ka-band, 32 GHz).

Substituting into Equation (36), we have

$$S={\displaystyle \frac{\left(20\right)\left({10}^{4.7}\right)\left({10}^{6.2}\right){(9.4\times {10}^{-3})}^2}{{\left(4\pi (1.0\times {10}^{11})\right)}^2}}$$

(40)

$$S\approx 1.13\times {10}^{-20}\mathrm{W}\mathrm{or}-169.5\mathrm{dBW}.$$

(41)

Using the simplified logarithmic form of Equation (35), the single-sample signal-to-noise ratio (SNR) in dB units is calculated as

$${\mathrm{SNR}}_{\mathrm{eff}}=S_{\mathrm{dB}}-N_{\mathrm{T},\mathrm{dB}}.$$

(42)

For the case of a 0.7 AU deep space link, the received signal power and thermal noise power are given by

$$S_{\mathrm{dB}}=-169.5\mathrm{dBW},N_{\mathrm{T},\mathrm{dB}}=-174\mathrm{dBW}.$$

(43)

Substituting these values into Equation (42), the effective single-sample SNR is

$${\mathrm{SNR}}_{\mathrm{eff}}=(-169.5)-(-174)=4.5\mathrm{dB}.$$

(44)

The key link budget parameters used for this calculation are summarized in

Table 1. Link budget parameters for a 0.7 AU deep space mission.

Parameter	Symbol	Value	Unit
Distance	R	$1.0\times {10}^{11}$	m
Transmit antenna diameter	$D_t$	0.8–1	m
Transmit antenna gain	$G_t$	47	dBi
Receive antenna diameter	$D_r$	5	m
Receive antenna gain	$G_r$	60–64	dBi
System noise temperature	$T_{op}$	292.7	K
Receiver bandwidth	$BW$	$1.0\times {10}^3$	Hz
Thermal noise power	$N_{\mathrm{T}}$	−174	dBW
Received signal power	S	−169.5	dBW
Phase noise variance	${\sigma }^2$	$1.0\times {10}^{-2}$	${\mathrm{rad}}^2$
Effective SNR	${\mathrm{SNR}}_{\mathrm{eff}}$	4.5	dB

.

4.1.5. Aggregated SNR Effect on Phase Difference Estimation

While the single-sample SNR defines the instantaneous measurement quality, the aggregate accuracy improves with coherent integration over multiple samples. The 4.5 dB SNR value used in this study refers to the single-sample power ratio (instantaneous SNR). When phase measurements are accumulated over a total integration time $T_{\mathrm{int}}$, the number of independent samples $N=T_{\mathrm{int}}/T_s$ increases, and the effective SNR improves proportionally to N, or equivalently, the standard deviation of the phase estimate decreases as $1/\sqrt{N}$. In other words, the SNR is not independent of $T_s$: the initially quoted 4.5 dB applies per sample, while the integrated effective SNR over the full interval $T_{\mathrm{int}}$ is higher due to coherent averaging.

For N-independent and Gaussian-distributed phase samples, a lower bound for the variance of an unbiased phase estimator is given by the Cramér–Rao Lower Bound (CRLB). For long-baseline, dual-station interferometry under Gaussian noise dominance, the CRLB for phase difference estimation is expressed as [24]:

$$\mathrm{Var}(\Delta \varphi )\ge CRLB={\displaystyle \frac{1}{N·\mathrm{SNR}}},$$

(45)

where $\mathrm{Var}(\Delta \varphi )$ is the phase difference error variance, N is the number of coherently integrated samples, and SNR is the single-sample signal-to-noise ratio (in linear scale).

The corresponding standard deviation (1$\sigma$ error) in radians is

$${\sigma }_{\Delta \varphi }=\sqrt{{\displaystyle \frac{1}{N·\mathrm{SNR}}}}.$$

(46)

Numerical Estimation for RINGS

Assuming a sampling interval of 1 ms ($T_s=1\mathrm{ms}$), as well as an integration time of $T_{\mathrm{int}}=120$ to 300 s (2–5 min), the number of samples is

$$N={\displaystyle \frac{T_{\mathrm{int}}}{T_s}}={\displaystyle \frac{120}{0.001}}\mathrm{to}{\displaystyle \frac{300}{0.001}}\Rightarrow N=120,000\mathrm{to}300,000.$$

(47)

Given the single-sample SNR of 4.5 dB, corresponding to

$${\mathrm{SNR}}_{\mathrm{linear}}={10}^{4.5/10}\approx 2.82,$$

(48)

The CRLB-based phase standard deviation becomes

• For $N=120,000$ (2 min):

  $${\sigma }_{\Delta \varphi }=\sqrt{{\displaystyle \frac{1}{120,000\times 2.82}}}\approx 0.0054\mathrm{rad}(\sim 0.{31}^{\circ })$$

  (49)
• For $N=300,000$ (5 min):

  $${\sigma }_{\Delta \varphi }=\sqrt{{\displaystyle \frac{1}{300,000\times 2.82}}}\approx 0.0034\mathrm{rad}(\sim 0.{20}^{\circ })$$

  (50)

These results quantify the minimum achievable phase error due to SNR-limited thermal noise under Gaussian assumptions. Even with a modest single-sample SNR of 4.5 dB, the accumulation of ${10}^5$–$3\times {10}^5$ samples through coherent integration reduces the phase error to below $0.3^{\circ }$, demonstrating the critical role of long integration times in enhancing measurement precision. This represents only the noise-limited contribution; additional error sources are addressed in the following sections.

4.2. Doppler Effect in GEO-Based VLBI

Geostationary Earth Orbit (GEO) satellites move at approximately $V_{\mathrm{GEO}}=3075\mathrm{m}/\mathrm{s}$ in an Earth-Centered Inertial (ECI) frame, introducing significant Doppler shifts compared to terrestrial VLBI stations. In space-based Very Long Baseline Interferometry (VLBI), this Doppler effect must be carefully modeled, as it contributes a systematic bias to the measured phase.

The general expression for the dual-frequency differential phase, derived previously for a generic two-station configuration (see Equation (26)), is recalled here for reference:

$$\Delta \Delta \varphi ={\displaystyle \frac{2\pi \Delta f_c}{c}}\left[Bcos\theta +{\displaystyle \frac{r}{c}}\Delta V_r\right]$$

where B is the baseline length, $\theta$ is the angle between the baseline and the line-of-sight to the target, r is a nominal range to the spacecraft, and $\Delta V_r=v_{r_1}-v_{r_2}$ is the differential radial velocity between the two stations.

In a symmetric GEO-based configuration, the two satellites are separated by ${180}^{\circ }$ in longitude. Their radial velocities relative to the target are

$$v_{r_1}=V_{\mathrm{GEO}}sin\theta ,v_{r_2}=-V_{\mathrm{GEO}}sin\theta$$

(51)

such that

$$\Delta V_r=v_{r_1}-v_{r_2}=2V_{\mathrm{GEO}}sin\theta$$

(52)

In this configuration, the differential range satisfies

$$r_1\left(t\right)-r_2\left(t\right)=Bcos\theta ,$$

(53)

but this applies only to the range difference, not to the individual ranges.

Substituting the expressions for $\Delta V_r$ and the geometry into the general phase equation yields

$$\Delta \Delta \varphi ={\displaystyle \frac{2\pi \Delta f_c}{c}}\left[Bcos\theta +{\displaystyle \frac{r}{c}}·2V_{\mathrm{GEO}}sin\theta \right]=\Delta \Delta {\varphi }_{\mathrm{static}}+\Delta {\varphi }_{\mathrm{error}}$$

(54)

where the second term represents the Doppler-induced phase error accumulated over time.

To analyze this time-dependent component, we begin from the instantaneous Doppler frequency:

$$\Delta f_{\mathrm{Doppler}}={\displaystyle \frac{\Delta f_c}{c}}·\Delta V_r={\displaystyle \frac{2\Delta f_c{V}_{\mathrm{GEO}}sin\theta }{c}}$$

(55)

The corresponding instantaneous phase rate is

$${\displaystyle \frac{d{\varphi }_{\mathrm{error}}}{dt}}=2\pi \Delta f_{\mathrm{Doppler}}={\displaystyle \frac{4\pi \Delta f_c{V}_{\mathrm{GEO}}sin\theta }{c}}$$

(56)

Integrating over the interferometric integration time T gives the accumulated phase error:

$$\Delta {\varphi }_{\mathrm{error}}={\int }_0^T{\displaystyle \frac{d{\varphi }_{\mathrm{error}}}{dt}}dt={\displaystyle \frac{4\pi \Delta f_c{V}_{\mathrm{GEO}}sin\theta }{c}}·T$$

(57)

This expression defines the Doppler-induced phase drift over time for a dual-GEO VLBI system. It is linearly proportional to the radial velocity difference and integration duration, and thus, geometry-dependent.

We evaluate $\Delta {\varphi }_{\mathrm{error}}$ for three representative angles using the following parameters:

$$\Delta f_c={10}^5\mathrm{Hz},V_{\mathrm{GEO}}=3075\mathrm{m}/\mathrm{s},T=300\mathrm{s},c=3\times {10}^8\mathrm{m}/\mathrm{s}.$$

As seen, the Doppler-induced phase error increases monotonically with angle $\theta$, reaching its maximum near ${85}^{\circ }$, where the relative radial velocity is largest. At this angle, the accumulated phase exceeds 500 radians (more than 80 cycles). At $\theta ={45}^{\circ }$, the Doppler contribution remains substantial, corresponding to approximately 364 radians (58 cycles). Even at small look angles (e.g., $\theta =5^{\circ }$), the effect is non-negligible for VLBI systems, resulting in about 45 radians (7 cycles) of phase error.

This analysis shows that Doppler contributions in GEO-based VLBI are strongly geometry-dependent and must be precisely modeled. Even in symmetric configurations, the velocity-induced phase drift may dominate the error budget. Consequently, resolving the inherent $2\pi$ phase ambiguity through phase tracking, unwrapping, or a priori modeling is essential to preserve measurement integrity.

Table 2. Doppler-induced phase error at various target angles.

$\mathit{\theta }$ (deg)	$\mathit{\Delta }{\mathit{V}}_{\mathit{r}}$ [m/s]	$\mathit{\Delta }{\mathit{\varphi }}_{\mathbf{error}}$ [rad]	Cycles
5	536.0	44.90	7.15
45	4348.7	364.32	57.98
85	6126.6	513.26	81.69

demonstrates some numerical examples for resulted phase errors in several aspect angles to the target.

Once corrected, the residual phase error can be interpreted as a small angular offset. The corresponding angular deviation is approximately

$$\Delta \theta \approx {\displaystyle \frac{\lambda }{2\pi Bcos\theta }}·\Delta {\varphi }_{\mathrm{error}}$$

(58)

where $\lambda$ is the signal wavelength, B is the interferometric baseline, and $\theta$ is the nominal angle about which variations occur. This relation will be used in later sections to translate phase noise or post-correction residuals into angular uncertainty bounds.

4.3. Time Synchronization and Clock Instability in GEO-Based VLBI

Precise time synchronization between the two GEO satellites is a fundamental requirement in the RINGS system, as interferometric phase measurements are highly sensitive to clock offsets. Unlike terrestrial VLBI, which utilizes ultra-stable ground-based hydrogen masers with timing stability below ${10}^{-14}$ over 1000 s, spaceborne platforms must rely on smaller, more practical clocks compatible with space constraints. This introduces unique challenges due to size, weight, and power-consumption limitations, as well as the inability to maintain continuous line-of-sight between the satellites for direct synchronization.

4.3.1. Clock Stability and Timing Error Sources

The total timing uncertainty in the RINGS system arises from both intrinsic clock instability and limitations in inter-satellite or ground-based synchronization.

(1)

Onboard Clock Instability

Onboard atomic clocks determine the short-term coherence of the interferometric measurements. Three classes of frequency standards are relevant:

• Rubidium (Rb): Commonly used in communication satellites, with a typical Allan deviation of $\sim {10}^{-12}$ over 1000 s. This corresponds to a drift of $\sim 3.6$ ns over one hour, or about 725 radians of phase error at 32 GHz.
• Cesium (Cs): Provides an order-of-magnitude improvement in stability, with an Allan deviation of $\sim {10}^{-13}$. Over one hour, this yields $\sim 0.36$ ns timing drift ($\sim 72$ radians, or $\sim 11$ phase cycles). With post-processing and GNSS-assisted calibration, the residual uncertainty can be reduced to $\sim 30$ ps, corresponding to $\sim 6$ radians of phase error.
• Maser-class clocks: Active or passive hydrogen masers achieve stabilities of ${10}^{-15}$-${10}^{-16}$ over 1000 s, as demonstrated in missions such as RadioAstron and the planning for Millimetron. These devices could further reduce residual phase noise below one radian over similar timescales.

The current RINGS performance estimates are based on a Cesium-class clock, which provides sufficient stability for the expected integration intervals. Future studies will extend the analysis to include maser-grade references to quantify potential gains in coherence.

(2)

Time Transfer and Synchronization Limitations

Without continuous synchronization, any residual clock offset accumulates as phase error. Conventional methods, such as GNSS-based calibration, mitigate long-term drift but leave short-term relative errors between updates. We adopted a conservative post-calibrated timing uncertainty of $\sim 100$ ps for initial error budgeting, corresponding to

$$\Delta {\varphi }_{\mathrm{clk}}=2\pi f_0\Delta t_{\mathrm{clk}}=2\pi \times 32\times {10}^9\times {10}^{-10}\approx 20\mathrm{rad},$$

(59)

equivalent to roughly three phase cycles. This level of error can be corrected or unwrapped during the post-correlation phase processing.

4.3.2. Synchronization Strategies

Multiple approaches are considered for maintaining synchronization between the two GEO stations:

(1)

Autonomous Direct Synchronization (Line-of-Sight Required)

This method involves real-time bidirectional communication between the GEO satellites:

• One-way time transfer: A master satellite transmits a timing reference to synchronize the secondary node.
• Two-way time transfer: Bidirectional exchange of timing signals allows real-time drift estimation and compensation.

In the RINGS geometry with ∼${180}^{\circ }$ separation, Earth obstructs direct line-of-sight, making this approach infeasible without an intermediate relay satellite.

(2)

Hybrid Internal–External Synchronization

A practical alternative combines stable onboard clocks with periodic external corrections:

• GNSS-based calibration: Each GEO independently receives GNSS signals for periodic clock updates, maintaining long-term stability but not real-time coherence.
• Post-processing correlation: Residual offsets are estimated and removed during ground-based correlation, correcting slow drifts without degrading phase integrity.

4.3.3. Inter-Satellite Synchronization Links

Advanced synchronization links can further enhance coherence:

• Relay via a third GEO satellite: A third node at an intermediate longitude can enable continuous two-way time transfer.
• Optical or RF cross-links: Two-way inter-satellite links can achieve tens-of-picoseconds precision by canceling path delays, offering real-time phase alignment.

Combining high-stability onboard clocks (currently cesium; potentially maser-class) with periodic GNSS calibration, post-correlation correction, and inter-satellite synchronization provides a robust framework with which to minimize timing-induced phase errors in the RINGS system.

4.4. Satellite Orbit Determination (OD) Accuracy

A key differentiator between terrestrial and satellite-based VLBI lies in the accuracy of station positions. Ground VLBI antennas are surveyed with centimeter-level precision. In contrast, the positions of GEO satellites are typically known to 10–100 m, unless dedicated tracking systems, such as GPS, Satellite Laser Ranging (SLR), or inter-satellite links, are employed.

In conventional GEO operations, a 10–100 m position error is common and would impose a significant limitation on VLBI performance. The uncertainty in the baseline vector B directly translates into angular measurement error via the linearized relation:

$$\delta \theta \approx {\displaystyle \frac{\delta B}{B}}·\theta ,$$

(60)

For example, assuming a 10-m orbit determination error over an $80,000$ km GEO-GEO baseline, we have

$${\displaystyle \frac{10}{80,000,000}}=1.25\times {10}^{-7}\Rightarrow \delta \theta \approx 125\mathrm{prad}\mathrm{for}\theta =1\mathrm{mrad}.$$

(61)

This level of error is unacceptably large for precision deep space VLBI applications.

However, since the RINGS system is specifically designed for VLBI navigation and GEO satellite locations are needed a posteriori (at the time of measurement correlation rather than in real time), we assume a dedicated orbit determination process is employed. This includes precise GNSS-based tracking, laser ranging when applicable, and fusion with inter-satellite link data. As a result, we conservatively assume that a post-processed orbital knowledge of 0.5 m (50 cm) is achievable.

For a 0.5-m OD error, the resulting angular error is

$${\displaystyle \frac{0.5}{80,000,000}}=6.25\times {10}^{-9}\Rightarrow \delta \theta \approx 6.25\mathrm{nrad}\mathrm{for}\theta =1\mathrm{mrad}.$$

(62)

This level of station location uncertainty, while still larger than that for ground VLBI, is consistent with the overall system error budget and can be mitigated through post-correlation analysis. It represents the value adopted for the final performance estimation in

Table 3. Comparison of terrestrial VLBI and satellite-based VLBI error budgets.

Error Source	Terrestrial VLBI (ns)	Satellite VLBI (ns)
Quasar-SNR (QSNR)	0.033	-
Spacecraft SNR	0.019	0.030
Clock Instability	0.004	0.300
Dispersive Phase	0.030	0.030
Station Location Uncertainty	0.010	1.000
Earth Orientation	0.013	0.013
Troposphere Systematic (Zenith)	0.012	-
Troposphere Fluctuations	0.019	-
Ionospheric Effects	0.019	-
Solar Plasma Effects	0.006	0.006
Quasar Coordinates	0.020	-
Root Sum Square (RSS)	0.063	1.044
Angular Error (nanoradians)	2.35	3.92

.

4.5. Elimination of Atmospheric Path Errors

An important advantage of the proposed RINGS architecture is the complete elimination of tropospheric and ionospheric phase delay errors. In terrestrial VLBI, these effects constitute significant components of the total error budget:

• Tropospheric wet delay: Up to 20–30 ps RMS.
• Ionospheric group delay: Up to 15–20 ps, especially at X-band.
• Solar plasma effects: Variable and geometry-dependent.

Since the GEO satellites operate entirely above the Earth’s atmosphere, these contributions vanish. This removes the need for auxiliary calibration systems such as microwave radiometers, water vapor profilers, or dual-frequency plasma compensation links.

Thus, while the RINGS system introduces new error sources (e.g., clock and OD uncertainty), it also removes several dominant ones from the classical ground-based budget. This tradeoff is a key feature of the proposed space-based VLBI paradigm.

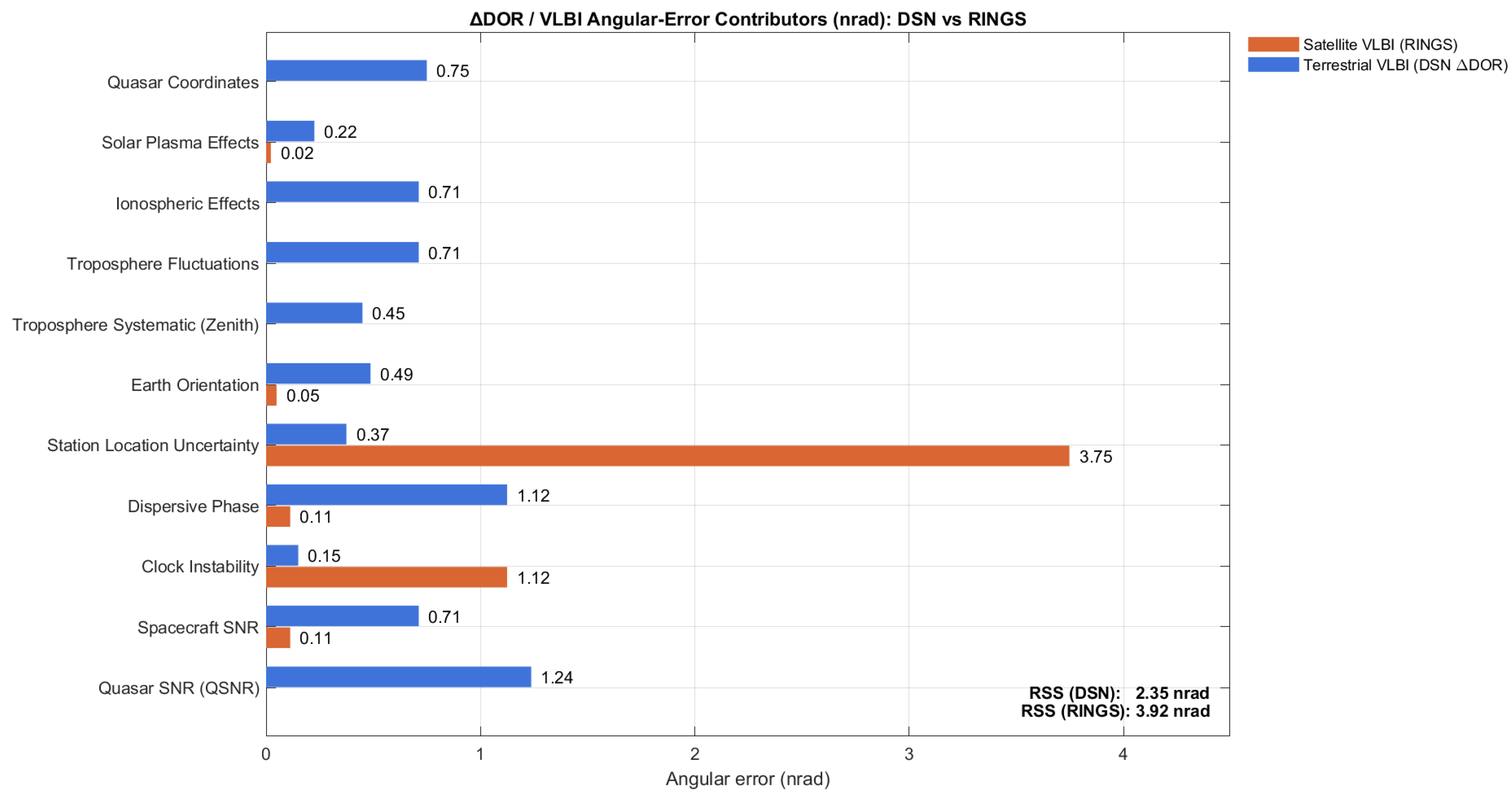
4.6. Error Budget Summary and Analysis

Table 3 summarizes the error contributions for both traditional terrestrial VLBI and the proposed GEO-based VLBI configuration (RINGS). We adopted the same error budget methodology used for ground-based VLBI and Delta-DOR systems, as extensively detailed in [5,6,17,19,21,25]. This ensures a direct and consistent comparison between terrestrial and space-based architectures.

For the terrestrial case, the Root Sum Square (RSS) timing error is approximately 0.063 ns, corresponding to an angular uncertainty of 2.39 nanoradians. In contrast, the GEO-based RINGS system yields an RSS of 1.044 ns, resulting in an angular uncertainty of approximately 3.92 nanoradians.

The dominant contributors to the satellite-based VLBI error budget are as follows:

• Spacecraft SNR contribution: Derived from the Cramér–Rao Lower Bound (CRLB) for phase estimation under Gaussian noise conditions. For a 2 to 5-min integration time and a sampling interval of 1 millisecond, the accumulated phase error is between 0.0054 and 0.0034 radians. Converting this to timing uncertainty at Ka-band ($f_0=32$ GHz) yields

  $$\Delta t_{\mathrm{SNR}}={\displaystyle \frac{\Delta \varphi }{2\pi f_0}}$$
  Using the worst case (shorter integration time), this results in

  $$\Delta t_{\mathrm{SNR}}\approx {\displaystyle \frac{0.0054}{2\pi \times 32\times {10}^9}}\approx 27\mathrm{ps}$$
  For conservatism, we round to $\Delta t_{\mathrm{SNR}}\approx 30\mathrm{ps}$.
• Clock instability: The use of space-qualified rubidium clocks onboard the GEO satellites introduces residual timing errors after GNSS-based correction and post-correlation calibration. The residual clock error is estimated at approximately 300 ps, corresponding to a phase error of about 20 radians at 32 GHz.
• Station location uncertainty: Unlike terrestrial VLBI antennas, the positions of which are known to centimeter accuracy, satellite-based systems suffer from orbit determination limitations. While standard GEO orbit knowledge is typically in the 10–100 m range, the RINGS system assumes dedicated post-processed orbit determination, achieving 0.5-m accuracy. For an 80,000 km baseline, this leads to

  $${\displaystyle \frac{0.5}{80,000,000}}=6.25\times {10}^{-9}$$
  Translating this into timing error over light speed yields

  $$\delta t_{\mathrm{OD}}\approx 1\mathrm{ns}$$
  This is currently the dominant contributor to the overall error budget.

Several error sources present in terrestrial VLBI, such as tropospheric fluctuations, ionospheric delays, and quasar coordinate uncertainties [25], are effectively eliminated or negligible in the RINGS system, since the receivers operate in space and directly observe the spacecraft signal.

While the absolute Root Sum Square (RSS) error is higher in the GEO-based scenario, the system still meets the angular accuracy requirements for deep space navigation. Moreover, the inherent advantages of space-based VLBI, including continuous target visibility, immunity to atmospheric effects, and extended baselines, help compensate for much of the increased error budget.

Future improvements may include the deployment of higher-precision onboard clocks (e.g., space-qualified cesium or H-maser standards), inter-satellite synchronization links, and further enhancements in GEO orbit determination accuracy.

Figure 4 illustrates the error-budget comparison shown in Table 3.

According to this analysis, the GEO-based VLBI system (RINGS) exhibits a higher overall Root Sum Square (RSS) error compared to traditional terrestrial VLBI, primarily due to clock instability and station location uncertainty. The calculated satellite-based RSS timing error is 1.044 ns, corresponding to an angular uncertainty of 3.92 nanoradians compared to the terrestrial VLBI error of 0.063 ns and 2.39 nrad, respectively.

However, the space-based system still maintains error levels within the same order of magnitude as terrestrial VLBI. If spacecraft-based VLBI is combined with periodic quasar calibration, further improvements in angular resolution could be achieved, particularly in correcting baseline and clock biases.

Although the GEO-based VLBI configuration exhibits a slightly higher error floor, its additional advantages—including continuous observation windows, significantly reduced effects of atmospheric noise, and the potential for higher Sun–Earth–Probe (SEP) angles—strongly justify continued development and field experimentation. The proposed method offers a promising alternative to Earth-based VLBI, especially in scenarios where terrestrial station geometry limits availability or accuracy.

5. Simulation and Modeling

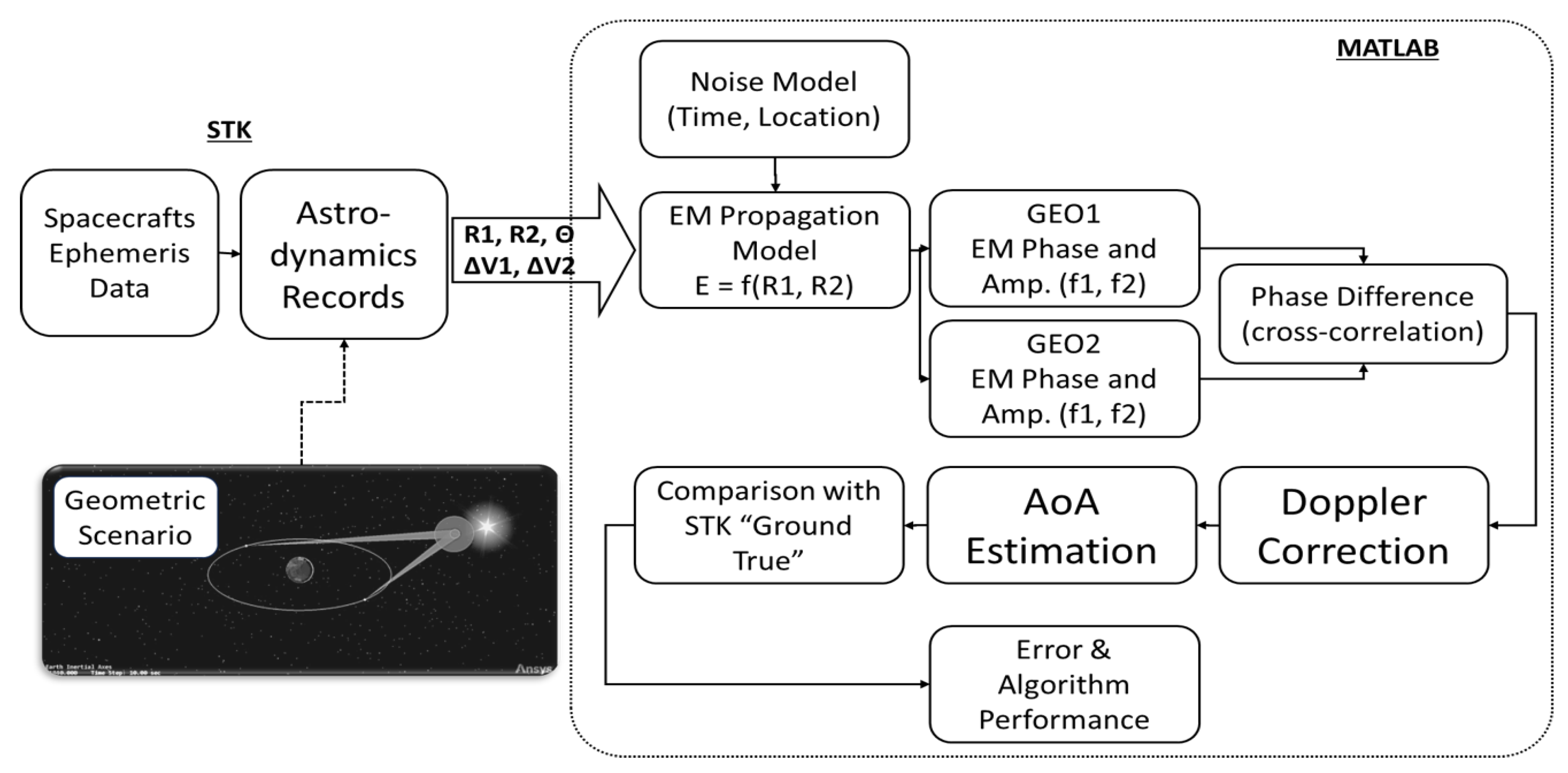
To validate the proposed RINGS concept, a dedicated simulation framework was developed combining the Ansys/AGI System Tool Kit (STK version 12.5) and MATLAB (version R2024a). The goal was to assess system performance under realistic orbital conditions and quantify both angular measurement accuracy and system availability.

5.1. Simulation Structure

The simulation consists of two integrated components:

• STK orbital scenario: A representative deep space mission geometry was modeled using the Sun–Earth Lagrangian point L1 (SEL1) as an example target. Two GEO satellites were placed in dual longitude slots, creating a long interferometric baseline. STK provides the orbital dynamics, including relative positions, velocities, and baseline–spacecraft angles ($\theta$). While SEL1 is used as a reference case, the geometric considerations and availability analysis are generally applicable to any deep space target located in the ecliptic plane.
• MATLAB interferometric model: Custom MATLAB code emulates the full radiometric interferometry process. The model includes electromagnetic wave propagation from the spacecraft, phase sampling at the GEO receivers, dual-frequency processing, and cross-correlation to extract the differential phase. The simulation structure is illustrated in Figure 5.

The simulation accounts for Doppler correction, phase ambiguity handling, and basic noise sources, such as clock biases and J2 perturbations. At this stage, perfect time synchronization was assumed.

5.2. Preliminary Angular Estimation Results

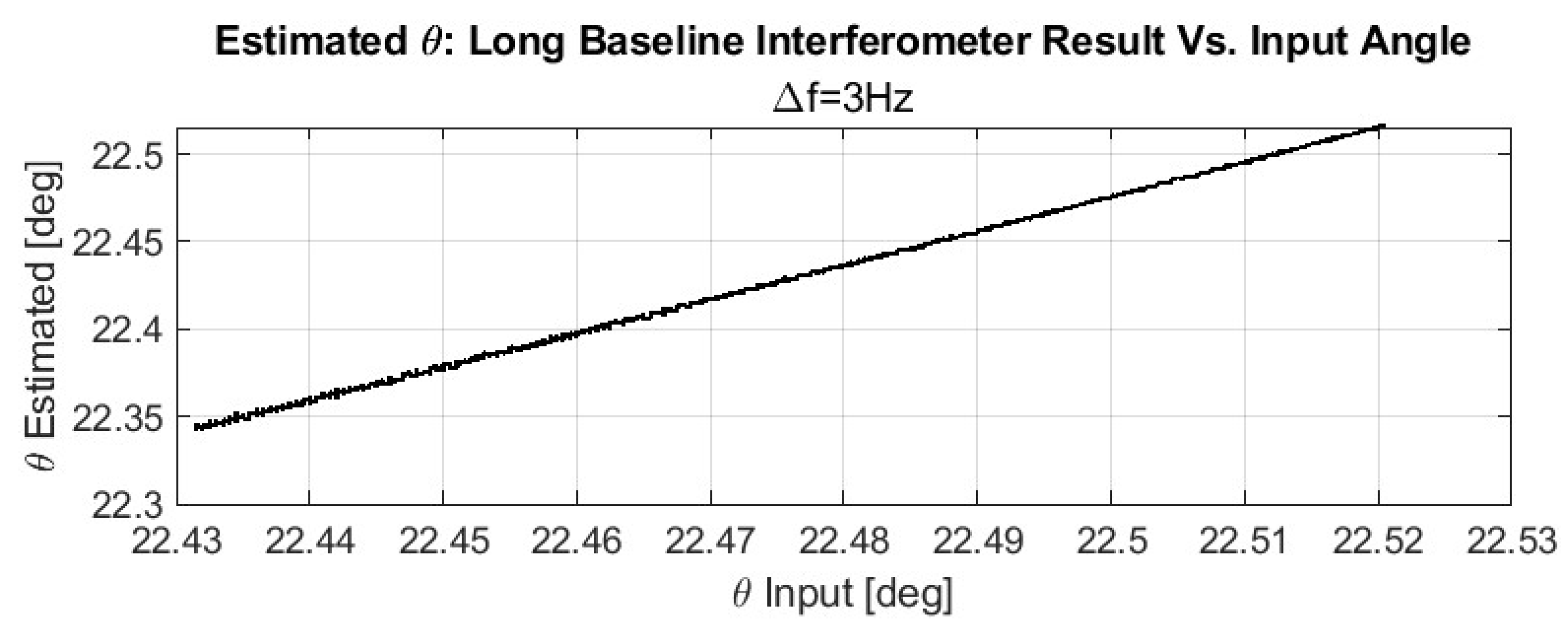
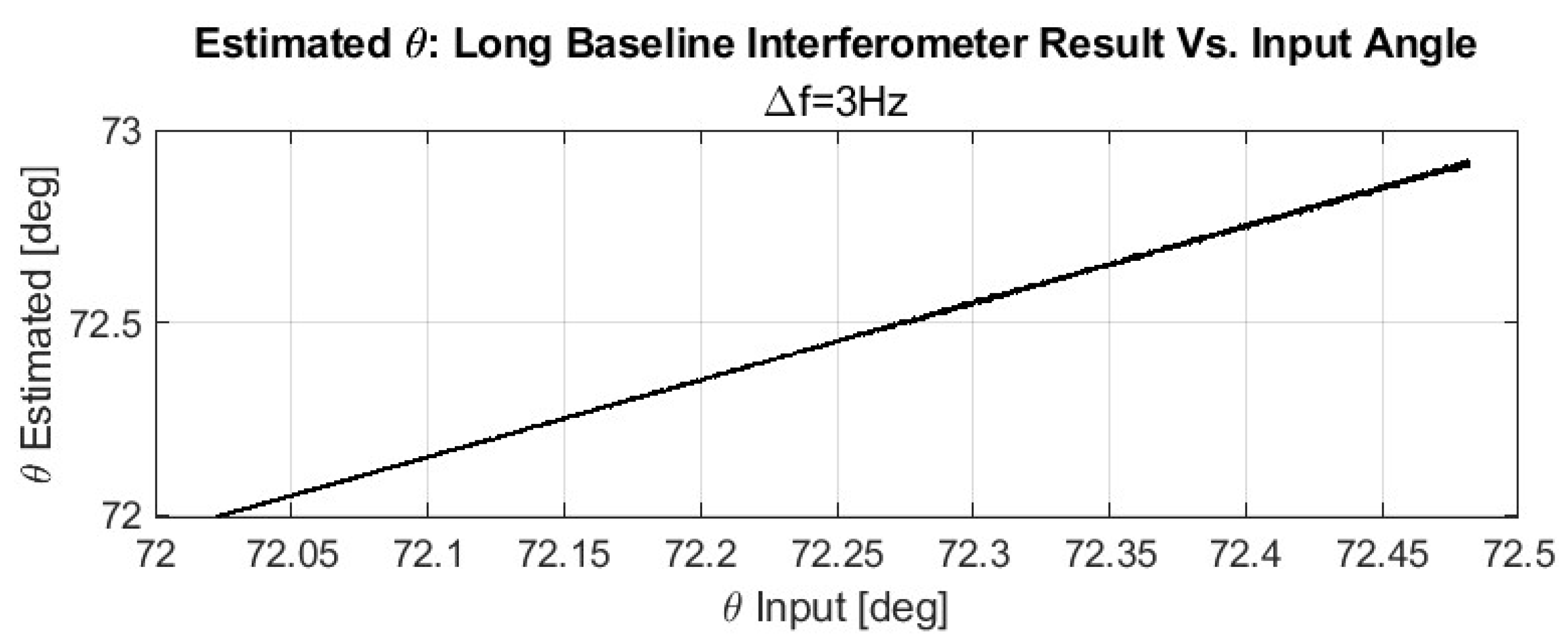
We evaluated the interferometric angle-of-arrival (AoA) estimator for two representative baseline–spacecraft geometries: (i) $\theta \approx {22}^{\circ }$ (short projected baseline; elevation-sensitive) and (ii) $\theta \approx {72}^{\circ }$ (long projected baseline; azimuth-sensitive). Each session used $T_{\mathrm{int}}=120$ s with two sampling cadences, $T_s\in \{10\mathrm{ms},1\mathrm{ms}\}$ (100 Hz and 1 kHz). For this first-stage demonstration, we chose an S-band carrier at $f_0=3$ GHz (rather than the Ka-band used in the error analysis) to operate within a more relaxed ambiguity and link-budget regime while keeping the same estimation principles; the methodology directly carries over to higher frequencies.

All results below reflect raw, epoch-wise phase differences with no sequential filtering, no ambiguity management, and no smoothing; consequently, the residuals can be viewed as a conservative upper bound before estimator refinement. In a nominal Monte Carlo run (NMC $=200$) with perfect clock alignment, accurate baseline knowledge, and resolved phase ambiguity, the mean angular error is ∼$0.{0318}^{\circ }$, with a standard deviation of ∼$0.{0330}^{\circ }$. Sensitivity checks show that injecting zero-mean baseline errors with ${\sigma }_B=0.5$ m or modest inter-satellite timing noise (bias std ${10}^{-12}$, drift std ${10}^{-13}$ over the 120 s window) changes the mean and standard deviation only at the ${10}^{-5}$ deg level, with worst-case excursions of ∼$4\times {10}^{-5}$ deg. Applying both error types together produces essentially the same statistics, indicating no adverse coupling at the tested levels for the chosen geometry and interval. A summary appears in

Table 4. Preliminary Monte Carlo results ($T_{\mathrm{int}}=120$ s, $f_0=3$ GHz, NMC $=200$).

Configuration	Mean AoA Error [deg]	Std [deg]	Worst-Case [deg]
Nominal (reference)	0.0318	0.0330	–
Baseline error (${\sigma }_B=0.5$ m)	∼$1.0\times {10}^{-5}$	∼$1.2\times {10}^{-5}$	$4.0\times {10}^{-5}$
Clock error (bias ${10}^{-12}$, drift ${10}^{-13}$)	∼$1.0\times {10}^{-5}$	∼$1.1\times {10}^{-5}$	$4.0\times {10}^{-5}$
Baseline + clock (combined)	∼$1.0\times {10}^{-5}$	∼$1.2\times {10}^{-5}$	$4.0\times {10}^{-5}$

.

Figure 6 and Figure 7 (S-band, $T_{\mathrm{int}}=120$ s) illustrate convergence in both geometries, with dispersion dominated by phase-ambiguity handling, as is expected for long baselines. These plots do not yet include averaging gains from sequential estimation (e.g., batch/recursive least squares or Kalman filtering) or dual-frequency synthetic-wavelength strategies for robust cycle resolution. Incorporating those standard elements is expected to drive the dispersion toward the CRLB scaling ${\sigma }_{\Delta \varphi }\propto 1/\sqrt{NSNR}$ discussed in Section 4. This also explains why the preliminary S-band simulation errors reported here are looser than the aggregate error budget in Section 4: the latter reflects a theoretical boundary under matured processing chain, whereas the present MATLAB results are deliberately unfiltered to demonstrate that the core GEO-based VLBI concept functions as intended. A flight-like system will implement the full processing pipeline and be evaluated accordingly in future work.

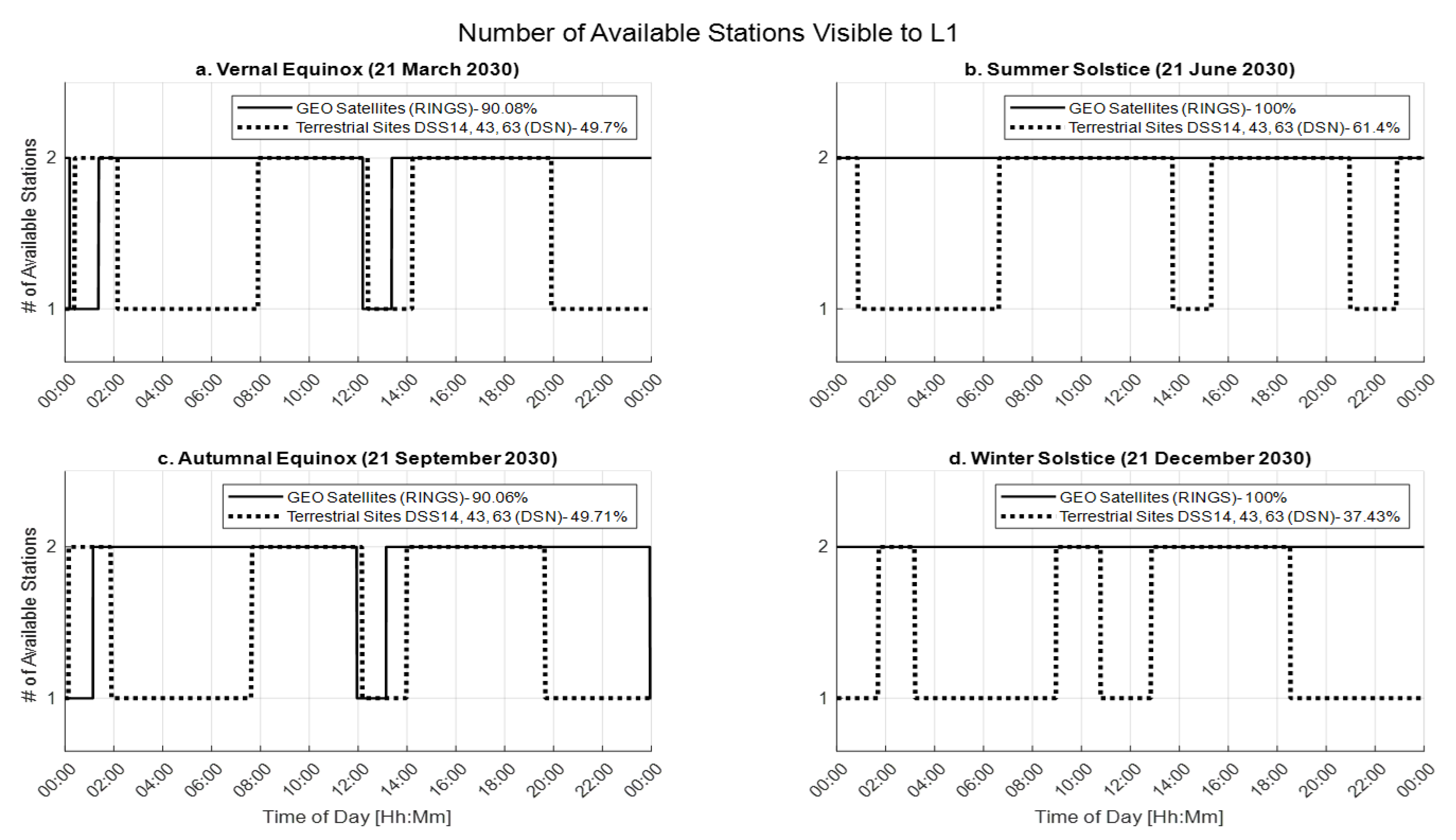
5.3. System Availability Simulation

Beyond angular estimation, the simulation was also used to evaluate system availability in comparison to terrestrial VLBI arrays. In this context, “availability” refers to the geometric condition of simultaneous line-of-sight (LOS) from both stations to the spacecraft. It does not account for hardware reliability or system uptime. Any time allocated to on-line calibration with an external radio source, if required, would reduce the total availability by subtracting from periods suitable for target observation.

Two GEO satellites were positioned at ${100}^{\circ }$ West and ${80}^{\circ }$ East, yielding an orbital separation of approximately ${180}^{\circ }$. For terrestrial comparison, the Deep Space Network (DSN) stations located in Goldstone, Canberra, and Madrid were modeled.

A full-year simulation for 2030 was conducted using STK, sampling LOS conditions every 10 min. While SEL1 served as the reference target, similar availability outcomes are expected for any deep space mission within the ecliptic plane, given the geometry of GEO satellite coverage.

Availability Results

• Terrestrial VLBI: Achieves approximately 49.66% availability due to Earth rotation and geographic constraints (see Figure 8 dashed lines). Typical daily operation involves three 4-h overlap episodes between DSN stations.
• GEO-based VLBI: Provides 98% availability, with only short interruptions during GEO eclipses near equinoxes (see Figure 8, solid lines). For certain targets such as SEL1, the system also offers a favorable Sun–Earth–Probe (SEP) angle, reducing solar proximity effects on RF measurements.

This substantial improvement in geometric availability translates into higher measurement duty cycles, fewer operational constraints, and greater support for continuous deep space navigation. It represents one of the principal operational advantages of the RINGS concept over traditional ground-based VLBI.

6. Conclusions

Radiometric interferometry is a fundamental tool for deep space navigation and spacecraft orbit determination. In this paper, we proposed and analyzed a system concept in which two geostationary satellites serve as an interferometric baseline to enable continuous angular tracking of deep space targets. This GEO-based Very Long Baseline Interferometry (VLBI) configuration, termed RINGS, introduces a new architecture that extends the capabilities of existing ground-based VLBI systems.

Using a structured error budget analysis consistent with NASA and ESA methodologies for VLBI and Delta-DOR systems, we evaluated the dominant error sources in the RINGS system. The total Root Sum Square (RSS) timing error was found to be 1.044 ns, corresponding to an angular uncertainty of 3.92 nanoradians. For comparison, the equivalent RSS error in terrestrial VLBI systems is approximately 0.063 ns (or 2.35 nanoradians). Despite this increase, the RINGS system remains within the same order of magnitude—a notable result given the unique advantages of the space-based configuration.

Several contributing factors were analyzed in detail:

• Signal-to-noise ratio (SNR): For a 2- to 5-min integration time with a 1 kHz sampling rate, the phase error due to SNR was computed to be approximately 0.0054 radians, resulting in a timing uncertainty of about 30 ps.
• Clock instability: Post-GNSS correction and post-processing calibration leave a residual clock error estimated at 300 ps, corresponding to approximately 20 radians of phase uncertainty at Ka-band.
• Orbit determination (OD) uncertainty: Assuming a dedicated post-processed OD solution with 0.5-m baseline knowledge, the resulting error contribution is 1 ns, dominating the baseline uncertainty term.

In addition to the quantitative error analysis, availability simulations demonstrated a significant operational advantage. The GEO-based system achieves approximately 98% time availability for interferometric observations of SEL1, compared to 49.66% for traditional terrestrial VLBI sites. This enhanced visibility opens new opportunities for continuous tracking and improved duty cycles, particularly for missions where Earth-based line-of-sight is periodically unavailable.

This work demonstrates that GEO-based VLBI is both theoretically feasible and practically promising for deep space navigation. While the initial error budget shows a slightly higher absolute error than ground-based VLBI, the system remains in the same performance order, with substantial potential for improvement. Future enhancements, such as higher-precision spaceborne clocks, dedicated inter-satellite synchronization links, and advanced post-processing techniques, can further reduce the error contribution.

As the number of deep space and interplanetary missions continues to grow, the development of space-based navigation infrastructure becomes increasingly relevant. The RINGS concept offers a complementary approach to existing ground-based VLBI systems, reducing reliance on terrestrial stations and enabling continuous deep space tracking with extended availability and improved baseline geometry.

Further research, extended simulation campaigns, and eventual field experimentation are warranted to refine this approach and assess its operational potential for future space navigation architectures.

An important opportunity for the scientific community is to expand access to radiometric phase measurements from spaceborne platforms. While terrestrial VLBI benefits from decades of accumulated data, space-based systems still lack flight-proven phase observations. Including phase-sensing capabilities, even as secondary payloads, in future deep space or lunar missions could help to close this gap. Such data would support the validation of processing techniques and advance the development of space-based interferometric navigation systems.